Mapping rainfall hazard based on rain gauge data: an objective cross-validation framework for model selection

We propose an objective framework for selecting rainfall hazard mapping models in a region starting from rain gauge data. Our methodology is based on the evaluation of several goodness-of-fit scores at regional scale in a cross-validation framework, allowing us to assess the goodness-of-fit of the rainfall cumulative distribution functions within the region but with a particular focus on their tail. Cross-validation is applied both to select the most appropriate statistical distribution at station locations and to validate the mapping of these distributions. To illustrate the framework, we consider daily rainfall in the Ardèche catchment in the south of France, a 2260 km² catchment with strong inhomogeneity in rainfall distribution. We compare several classical marginal distributions that are possibly mixed over seasons and weather patterns to account for the variety of climatological processes triggering precipitation, and several classical mapping methods. Among those tested, results show a preference for a mixture of Gamma distribution over seasons and weather patterns, with parameters interpolated with thin plate spline across the region.

1 Introduction

In recent years, Mediterranean storms involving various spatial and temporal scales have hit many locations in southern Europe, causing casualties and damages (Ramos et al., 2005; Ruin et al., 2008; Ceresetti et al., 2012a). Assessing the frequency of occurrence of extreme rainfall in a region is usually done by the computation of return level maps. This requires relating any (large) amount of rainfall at a given location to its return level, i.e., to the frequency at which such an amount is expected to occur on average at this location. In other words, it requires knowledge of the cumulative distribution function (CDF) of extreme rainfall at any grid point of the map. However, there are other situations when not only the largest rainfalls are of interest, but also smaller and even zero rainfall values. This is for example the case in rainfall simulation frameworks, e.g., when rainfalls are input of spatially distributed hydrological models. In such a case one needs to be able to simulate any possible rainfall field. This implies knowing both the local occurrence of any rainfall value with the right frequency, and not only the largest ones, and their spatial co-occurrence. Other domains include the evaluation of numerical weather simulations (e.g., Froidurot et al., 2018) or the investigation of the climatology of rainfall events in a region.

A difficulty in producing rainfall return level maps is that knowing the CDF at any grid point ideally requires observation of rainfall on a grid scale. However, long-enough gridded data with good-enough quality are often lacking. Radar and satellite estimations are usually available for about 10 years at best, and only for selected regions. In addition, rainfall estimation in complex topography is particularly tricky, e.g., due to the mountain ranges shielding the radar beam (Germann et al., 2006), or to the complex relationship between satellite-measured radiances and rainfall reaching the ground (Tian and Peters-Lidard, 2010). On the other hand, rain gauge networks are usually operational for 50 to 100 years in the main part of the world, at least at daily scale, but they only provide point observations. Thus, two main methods are usually adopted for estimating the CDF of rainfall at any location when observations are only available at selected locations. The first one resorts to the spatial interpolation of point data supplied by rain gauges. This allows transformation of point observations into gridded ones, and so estimation of gridded CDFs of rainfall. Among the best performing methods for spatial interpolation of daily rainfall are kriging, inverse distance weighting and spline-surface fitting (e.g., Camera et al., 2014; Creutin and Obled, 1982; Goovaerts, 2000; Ly et al., 2011; Rogelis and Werner, 2013). In complex topography, there may be some gain in applying these methods locally, e.g., considering local precipitation altitude gradients (Frei and Schär, 1998; Gottardi et al., 2012; Lloyd, 2010). However, none of the above statistical methods is able to fully account for the statistical properties of rainfall fields. A first difficulty is due to the presence of zeros, which complicates interpolation and can lead to negative interpolated rainfalls – although this could be partially overcome by using analytical transformation of the raw variable. A second difficulty is that rainfall distribution is usually heavy tailed, and interpolation methods, by smoothing values, lack quality for representing the most extreme events (Delrieu et al., 2014).

A second way of mapping rainfall hazard is, rather than interpolating the point observations, to map the parameters of CDFs fitted on rain gauge series. In addition to the choice of interpolation models comes now the choice of the marginal model of rainfall amounts on wet days (referred to as nonzero rainfalls). The most commonly used CDFs at daily scale include the exponential, Gamma, lognormal, Pareto, Weibull and Kappa models (Papalexiou et al., 2013). Noting that these distributions tend to underestimate extreme rainfall amounts (Katz et al., 2002), a recent flurry of research developed hybrid models based on mixtures of distributions for low and heavy amounts (Vrac and Naveau, 2007; Furrer and Katz, 2008; Li et al., 2012). More recently Naveau et al. (2016) proposed a family of distributions that is able to model the full spectrum of rainfall, while avoiding the use of mixtures of distributions. Several studies compared marginal models for rainfall (e.g., Mielke and Johnson, 1974; Swift and Schreuder, 1981; Cho et al., 2004; Husak et al., 2007; Papalexiou et al., 2013), but focusing usually on a couple of CDFs. Other studies compared methods for mapping rainfall hazard, and particularly extreme rainfall, assuming a given CDF (Beguería and Vicente-Serrano, 2006; Beguerïa et al., 2009; Szolgay et al., 2009; Blanchet and Lehning, 2010; Ceresetti et al., 2012b). However, there is, to the best of our knowledge, no study assessing the goodness-of-fit of the full procedure of rainfall hazard mapping, i.e., from marginal modeling to the production of hazard maps.

Our study aims at filling this gap by proposing an objective cross-validation framework that is able to validate the full procedure of rainfall hazard mapping starting from point observations. Our framework features three characteristics: (i) it selects both the marginal and mapping models, (ii) it validates the full spectrum of rainfall, from short- to long-term extrapolated amounts, and (iii) it applies on a regional scale. The framework is illustrated on the Ardèche catchment in the south of France. Despite its relatively small size, this test case is particularly challenging as it shows extraordinarily strong inhomogeneity in rainfall statistics at a very short distance. Following previous studies in the region (Evin et al., 2016; Garavaglia et al., 2010, 2011; Gottardi et al., 2012), the compared marginal distributions involve seasonal and weather pattern subsampling, considering different models for the subclass-dependent distributions. However, the proposed cross-validation framework is general, as it involves objective criteria, and could likewise be used to select among any other distribution. Section 2 presents the data. Sections 3.1 and 3.2 describe the marginal distributions and mapping models considered in this study and present the cross-validation scores of model selection. Section 3.3 details the procedure of model selection from marginal modeling to hazard mapping. Section 4 gives extensive results for the Ardèche catchment. Section 5 concludes the study.

2 Data

We illustrate our framework on the Ardèche catchment (2260 km²) located in the south of France (see Fig. 1). The region includes part of the southeastern edge of the Massif Central, where the highest peaks of the region are located (more than 1500 m a.s.l), and the Rhône Valley (down to 10 m a.s.l). The southeastern slope of the Massif Central is known to experience most of the extreme storms and resulting flash floods (Fig. 2 of Nuissier et al., 2008). These so-called “Cévenol” events are produced by quasi-stationary mesoscale convective systems that stabilize over the region during several tens of hours. The positioning and stationarity of these systems are largely influenced by the topography of the surrounding mountain massifs (Nuissier et al., 2008). We use two daily rain gauge networks maintained, respectively, by Electricité de France and Météo-France. We consider the 15 rain gauges inside the catchment, together with the 27 stations located less than 15 km outside. This gives a total of 42 stations with 20 to 64 years of data between 1 January 1948 and 31 December 2013. In both databases, daily values are recorded every day at 06:00 UTC, corresponding to rainfall accumulation between 06:00 UTC of the previous day and 06:00 UTC of the present day.

Table 1 Considered models for the marginal distributions of nonzero rainfall. Γ in the Gamma density is the complete Gamma function $\mathrm{\Gamma }\left(\mathit{\kappa }\right)=\underset{\mathrm{0}}{\overset{\mathrm{\infty }}{\int }}{r}^{\mathit{\kappa }-\mathrm{1}}{e}^{-r}\mathrm{d}r$.

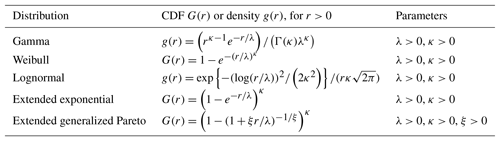
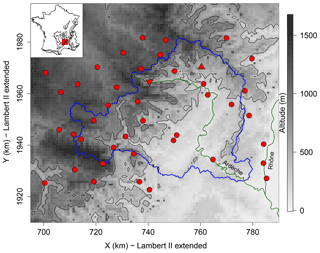
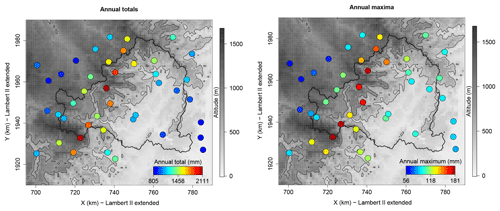
Figure 1 Region of analysis. The blue polygon is the Ardèche catchement. The red points show the locations of the stations. The upper triangle is station Antraigues and the lower triangle station Mayres (both lie at about 500 m a.s.l.). The background shows the altitude in gray scale (1 km raster cells). The top left insert shows a map of France with the studied region in red. The black lines are the 400 and 800 m a.s.l. isolines.

The Ardèche catchment is chosen for illustration purposes and because, despite its relatively small size, it shows strong inhomogeneity in rainfall distribution. To illustrate this, we show in Fig. 2 the averages of annual totals and annual maximum daily rainfalls for each station. Computing the ratios between the largest and lowest values in Fig. 2 gives ratios of 2.6 for the annual totals and 3.2 for the annual maxima. For comparison the latter ratio is barely lower than the ratio found over the whole of France, which amounts to 4. For both annual totals and annual maxima, the strongest values in the region are concentrated along the Massif Central ridge, while much smaller values are found a few kilometers apart in the Massif Central plateau or in the Piémont. Concentration of daily rainfall and particularly of extreme daily rainfall along the Massif Central ridge has already been documented in many studies; see, e.g., Fig. 10 of Blanchet et al. (2016). We assume in this study temporal stationarity of rainfall. A case of potential nonstationarity due to climate change will be discussed in Sect. 5.

Figure 2 Panel (a): averages of annual totals (mm). Panel (b): averages of annual maximum daily rainfalls (mm).

3 Method

3.1 Marginal distribution of rainfall

3.1.1 Considered marginal models

Let R be the random variable of daily rainfall amount at a given station. R is zero with probability p⁰ and, for any r>0, we have the following decomposition:

$$\begin{array}{}\text{(1)}& {\displaystyle }{\displaystyle }\mathrm{pr}(R\le r)=p^{\mathrm{0}}+\left(\mathrm{1}-p^{\mathrm{0}}\right)G\left(r\right),\end{array}$$

where G is the CDF of nonzero rainfall at the considered station. Choice of G is an issue. One of the difficulties is that we wish to model adequately both the bulk of the distribution of nonzero rainfall and its tail, i.e., the probability of extreme rainfall occurring. The most common models for nonzero rainfall include the Gamma, Weibull and lognormal models (Papalexiou et al., 2013), whose CDF G(r) or densities $g\left(r\right)=\partial G\left(r\right)/\partial r$, r>0 are given in Table 1. Although less common, another family of models for nonzero rainfall relies on univariate extreme value theory, which tells that probabilities of the form $\mathrm{pr}(R\le r|r>q)$, with q large, can be approximated by either an exponential or a generalized Pareto tail (Coles, 2001, Sect. 4). This led Naveau et al. (2016) to propose the extended exponential and extended generalized Pareto distributions, whose CDF is given in Table 1. Note that less parsimonious models are given in Naveau et al. (2016), but they are not considered in the present study. The extended exponential and extended generalized Pareto distributions of Table 1 ensure that the occurrence probability of small (but nonzero) rainfall amounts is driven by κ, while the upper tail of nonzero rainfall is equivalent to a generalized Pareto tail. The extended exponential model is also called “generalized exponential” and has been used previously for extreme rainfall in Madi and Raqab (2007) and Kazmierczak and Kotowski (2015).

In the models of Table 1, rainfall is implicitly assumed to come from a single distribution. This assumption may be questioned. Indeed, different climatological processes trigger precipitation, leading to the occurrence of rainfall of different natures and intensities (e.g., convective vs. stratiform precipitation). Furthermore, rainfall occurrence and intensities often vary with season, reflecting both variations in temperature and in storm tracks, for example. For this reason, Garavaglia et al. (2010) proposed for the same region the use of subsampling based on seasons and weather patterns (WP) (see also Brigode et al., 2014; Blanchet et al., 2015, respectively, in Canada and Norway). Each day of the record period is assigned to a WP. If S seasons and K WP are considered, then days are classified into S×K subclasses. The law of total probability gives, for all r>0,

$$\begin{array}{}\text{(2)}& {\displaystyle }{\displaystyle }\mathrm{pr}(R\le r)=\sum _{s=\mathrm{1}}^S\sum _{k=\mathrm{1}}^K\mathrm{pr}(R\le r|\mathrm{season}=s,\mathrm{WP}=k)p_{s,k},\end{array}$$

where p_s,k is the probability that a given day is in season s and in WP k (thus $\sum _s\sum _k{p}_{s,k}=\mathrm{1}$). Following Eq. (1), R in season s and WP k is zero with probability $p_{s,k}^{\mathrm{0}}$ and, for any r>0, we have the decomposition

$${\displaystyle }{\displaystyle }\mathrm{pr}(R\le r|\mathrm{season}=s,\mathrm{WP}=k)=p_{s,k}^{\mathrm{0}}+\left(\mathrm{1}-p_{s,k}^{\mathrm{0}}\right)G_{s,k}(r),$$

where G_s,k is the CDF of nonzero rainfall at the considered station for a day in season s and WP k. This gives in Eq. (2), for all r>0,

$$\begin{array}{}\text{(3)}& {\displaystyle }{\displaystyle }\mathrm{pr}(R\le r)=p^{\mathrm{0}}+\sum _{s=\mathrm{1}}^S\sum _{k=\mathrm{1}}^K{p}_{s,k}\left(\mathrm{1}-p_{s,k}^{\mathrm{0}}\right)G_{s,k}\left(r\right),\end{array}$$

where $p^{\mathrm{0}}=\sum _{s=\mathrm{1}}^S\sum _{k=\mathrm{1}}^K{p}_{s,k}{p}_{s,k}^{\mathrm{0}}$ is the probability of any day being dry. Nonzero precipitation amounts defined by Eq. (3) have CDF

$$\begin{array}{}\text{(4)}& {\displaystyle }{\displaystyle }G\left(r\right)=\mathrm{pr}(R\le r|R>\mathrm{0})=\sum _{s=\mathrm{1}}^S\sum _{k=\mathrm{1}}^K{p}_{s,k}^{\prime }{G}_{s,k}(r),\end{array}$$

where $p_{s,k}^{\prime }=p_{s,k}(\mathrm{1}-p_{s,k}^{\mathrm{0}})/(\mathrm{1}-p^{\mathrm{0}})$. Equation (4) defines a mixture of S×K distributions, e.g., a mixture of S×K Gamma distributions. Analogously, the CDF of nonzero precipitation amounts in a given season s is written as

$$\begin{array}{}\text{(5)}& {\displaystyle }{\displaystyle }{G}_s\left(r\right)=\mathrm{pr}(R\le r|R>\mathrm{0},\mathrm{season}=s)=\sum _{k=\mathrm{1}}^K{p}_{s,k}^{\prime \prime }{G}_{s,k}(r),\end{array}$$

where $p_{s,k}^{\prime \prime }=p_{s,k}(\mathrm{1}-p_{s,k}^{\mathrm{0}})/(\mathrm{1}-\sum _{k=\mathrm{1}}^K{p}_{s,k}{p}_{s,k}^{\mathrm{0}})$. A similar idea is used in Wilks (1998) for example, but considering a mixture of two (exponential) distributions in an unsupervised way, i.e., without relying on a priori subsampling. It shows the advantage of not requiring prior knowledge on the classification, but it is at the same time more difficult to estimate, in particular if the models for different seasons and WP do not differ much.

Table 2 Summary of the considered scores for evaluating marginal and mapping models.

In this article, we will consider the supervised case (Eq. 3), with S=2 seasons and K=3 WP, considering the five models of Table 1 for the distribution of precipitation amounts G_s,k (see Sect. 3.3). This implies that estimation of G_s,k can be made independently of each others, by considering only the days of the record belonging to season s and WP k. A variety of inference methods exists. For rainfall analysis, two options are popular: maximum likelihood (ML) estimation and a method of moments based on probability weighted moments (PWMs). However, as noted in Naveau et al. (2016), ML estimation may fail for rainfall because the discretization due to instrumental precision strongly affects low values, which biases ML estimation if not accounted for. One way to circumvent this issue is to resort to censored likelihood but choice of the censoring threshold is in itself an issue. Results on our data (not shown) reveal that the threshold has to be no smaller than 5 mm. PWM, on the other side, is much more robust against discretization since it is based on summary statistics, rather than on the exact values of observations (Naveau et al., 2016). For this reason, we estimate in this study the distributions of precipitation amounts G_s,k by PWM, while $p_{s,k}^{\mathrm{0}}$ at a given station is estimated empirically as ${\widehat{p}}_{s,k}^{\mathrm{0}}=d_{s,k}^{\mathrm{0}}/d$ where d is the number of observations and $d_{s,k}^{\mathrm{0}}$ is the number of zero values in season s and WP k. Combining estimations in Eq. (3) gives an estimation of the rainfall CDF at the considered station, and in Eq. (4) an estimation of the CDF of nonzero rainfall.

Estimates of return levels are then obtained as follows. The T-year return level r_T is the level expected to be exceeded on average once every T years. It satisfies the relationship $\mathrm{pr}(R\le r_T|R>\mathrm{0})=\mathrm{1}-\mathrm{1}/(T\mathit{\delta })$, where δ is the mean number of nonzero rainfall per year at the considered station. When subsampling Eq. (4) is considered, there is no explicit formulation, and estimation of r_T is obtained numerically by solving $\mathrm{pr}(R\le r_T|R>\mathrm{0})=\mathrm{1}-\mathrm{1}/(T\mathit{\delta })$ in Eq. (4).

3.1.2 Evaluation at regional scale in a cross-validation framework

The goal of this evaluation is to assess which marginal model performs better at the regional scale, i.e., for a set of n stations taken as a whole, rather than individually. We follow the split sample evaluation proposed in Garavaglia et al. (2011) and Renard et al. (2013). We divide the data for each station i into two subsamples, $C_i^{\left(\mathrm{1}\right)}$ and $C_i^{\left(\mathrm{2}\right)}$, and consider nonzero rainfall for these two subsamples. We fit a given competing model on each of the subsamples, giving two estimated distributions of G in Eq. (4): ${\widehat{G}}_i^{\left(\mathrm{1}\right)}$, estimated on $C_i^{\left(\mathrm{1}\right)}$, and ${\widehat{G}}_i^{\left(\mathrm{2}\right)}$, estimated on $C_i^{\left(\mathrm{2}\right)}$. Our goal is to test the consistency between validation data and predictions of the estimates, both for the core and tail of the distributions, and the stability of the estimates when calibration data changes, focusing particularly on the tail which is usually less stable.

As shown in Table 2, three families of scores are computed, assessing, respectively, (i) accuracy of the estimations along the full range of observations (MEAN(NRMSE)), (ii) reliability of the tail of the estimated distribution, checking in particular systematic over- or under-estimation of the observations (AREA(FF) and AREA(N_T)), and (iii) stability of the tail at extrapolation (MEAN(SPAN)). The scores relating the tail of the distribution have been proposed and used in Garavaglia et al. (2011), Renard et al. (2013) and Blanchet et al. (2015). In the split sample evaluation framework, four scores can be derived of a given score Sc: Sc⁽¹²⁾ is the regional score when $G_i^{\left(\mathrm{2}\right)}$ is validated on the nonzero rainfall subsample $C_i^{\left(\mathrm{1}\right)}$. Sc⁽²¹⁾, Sc⁽¹¹⁾ and Sc⁽²²⁾ are obtained symmetrically. Sc⁽¹¹⁾ and Sc⁽²²⁾ are calibration scores, while Sc⁽¹²⁾ and Sc⁽²¹⁾ are cross-validation scores. For the sake of conciseness, we detail below the case of Sc⁽¹²⁾ for the different scores.

The NRMSE (normalized root mean squared error) evaluates the reliability of the fits in the whole observed range of nonzero rainfall, by comparing observed and predicted return levels of daily rainfall. For a given station i∈{1, …, Q},

$$\begin{array}{}\text{(6)}& {\displaystyle }{\displaystyle }{\mathrm{NRMSE}}_i^{\left(\mathrm{12}\right)}={\left\{{\displaystyle \frac{\mathrm{1}}{n_i^{\left(\mathrm{1}\right)}}}\sum _{k=\mathrm{1}}^{n_i^{\left(\mathrm{1}\right)}}{\left(r_{i,T_k}^{\left(\mathrm{1}\right)}-{\widehat{r}}_{i,T_k}^{\left(\mathrm{2}\right)}\right)}^{\mathrm{2}}\right\}}^{\mathrm{1}/\mathrm{2}}/{\displaystyle \frac{\mathrm{1}}{n_i^{\left(\mathrm{1}\right)}}}\sum _{k=\mathrm{1}}^{n_i^{\left(\mathrm{1}\right)}}{r}_{i,T_k}^{\left(\mathrm{1}\right)},\end{array}$$

where $n_i^{\left(\mathrm{1}\right)}$ is the number of nonzero rainfall in $C_i^{\left(\mathrm{1}\right)}$ for station i, T_k ranges the observed return periods of nonzero rainfall in $C_i^{\left(\mathrm{1}\right)}$, $r_{i,T_k}^{\left(\mathrm{1}\right)}$ is the observed daily rainfall associated with the return period T_k for the subsample $C_i^{\left(\mathrm{1}\right)}$ and ${\widehat{r}}_{i,T_k}^{\left(\mathrm{2}\right)}$ is the T_k-year return period derived from the estimated ${\widehat{G}}_i^{\left(\mathrm{2}\right)}$. Without loss of generality we assume T₁, …, $T_{n_i^{\left(\mathrm{1}\right)}}$ to be sorted in descending order (so T₁ is associated with the maximum over $C_i^{\left(\mathrm{1}\right)}$). If station i has δ_i nonzero rainfall per year on average, usual practice is to consider the kth largest return period as $T_k=(n_i^{\left(\mathrm{1}\right)}+\mathrm{1})/\left({\mathit{\delta }}_{i}k\right)$, k=1, …, $n_i^{\left(\mathrm{1}\right)}$, and to estimate $r_{i,T_k}^{\left(\mathrm{1}\right)}$ as the kth largest observed rainfall over $C_i^{\left(\mathrm{1}\right)}$. Estimate ${\widehat{r}}_{i,T_k}^{\left(\mathrm{2}\right)}$ is obtained numerically from ${\widehat{G}}_i^{\left(\mathrm{2}\right)}$ as described in Sect. 3.1.1. The normalization by the mean rainfall of $C_i^{\left(\mathrm{1}\right)}$ in Eq. (6) allows comparison of NRMSE over stations with different pluviometry. The smaller NRMSE${}_i^{\left(\mathrm{12}\right)}$, the better ${\widehat{G}}_i^{\left(\mathrm{2}\right)}$ fits the rainfalls over $C_i^{\left(\mathrm{1}\right)}$. For the set of Q stations, we obtain a vector of NRMSE⁽¹²⁾ of length Q which should remain reasonably close to zero. A regional score is obtained by computing the mean of the Q values:

$$\begin{array}{}\text{(7)}& {\displaystyle }{\displaystyle }\mathrm{MEAN}\left({\mathrm{NRMSE}}^{\left(\mathrm{12}\right)}\right)={\displaystyle \frac{\mathrm{1}}{Q}}\sum _{i=\mathrm{1}}^Q{\mathrm{NRMSE}}_i^{\left(\mathrm{12}\right)}.\end{array}$$

For competing models, the closer the mean is to 0, the better the goodness-of-fit.

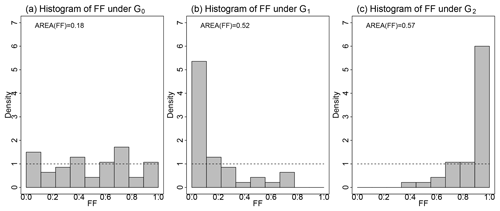
Figure 3 Illustration of the FF score when the true CDF G₀ is extended exponential with λ=20 and κ=0.3. The CDF G₁ underestimates G₀ (λ=25) while G₂ overestimates G₀ (λ=15). (a) Histogram of {G₀(m)}ⁿ where m are 42 realizations of $G_{\mathrm{0}}^n$ and n=4000. (b) Histogram of {G₁(m)}ⁿ. (c) Histogram of {G₂(m)}ⁿ. The horizontal dashed lines show the uniform density on (0, 1).

NRMSE assesses goodness-of fit of the whole distribution in the observed range. Now let us have a closer look at the tail of the distribution, and in particular at the maximum over $C_i^{\left(\mathrm{1}\right)}$; i.e., at $r_{i,T_{\mathrm{1}}}^{\left(\mathrm{1}\right)}$ in Eq. (6), that for shortness we denote $m_i^{\left(\mathrm{1}\right)}$. If G_i is the true distribution of nonzero rainfall, then the corresponding random variable $M_i^{\left(\mathrm{1}\right)}$ has distribution G_i to the power $n_i^{\left(\mathrm{1}\right)}$, whose variance is large. Thus computing error based on the single realization $m_i^{\left(\mathrm{1}\right)}$ would be very uncertain. For this reason, Renard et al. (2013) proposed to make evaluation by pulling together the maxima of the Q stations, after transformation to make them on the same scale. It is based on the idea that if X has CDF F, then F(X) follows the uniform distribution on (0, 1). Taking $X=M_i^{\left(\mathrm{1}\right)}$ and $F=(G_i{)}^{n_i^{\left(\mathrm{1}\right)}}$ implies that, if ${\widehat{G}}_i^{\left(\mathrm{2}\right)}$ is a perfect estimate of G_i, then

$$f{f}_i^{\left(\mathrm{12}\right)}=\mathit{\left\{}{\widehat{G}}_i^{\left(\mathrm{2}\right)}\right(m_i^{\left(\mathrm{1}\right)}){\mathit{\}}}^{n_i^{\left(\mathrm{1}\right)}}$$

should be a realization of the uniform distribution. For the set of Q stations, this gives a uniform sample ff⁽¹²⁾ of size Q. Hypothesis testing for assessing the validity of the uniform assumption is challenging because the $f{f}_i^{\left(\mathrm{12}\right)}$ are not independent from site to site, due to the spatial dependence between data. Thus Blanchet et al. (2015) proposed to base comparison on the divergence of the density of the ff⁽¹²⁾ to the uniform density. A reasonable estimate of the latter is obtained by computing the empirical histogram of the ff⁽¹²⁾ with 10 equal bins between 0 and 1. As illustrated in Fig. 3, if ${\widehat{G}}_i^{\left(\mathrm{2}\right)}$ are good estimates of G_i, i=1, …, Q, the histogram of ff⁽¹²⁾ should be reasonably uniform on (0, 1). If the histogram is left-skewed, then ${\widehat{G}}_i^{\left(\mathrm{2}\right)}\left(m_i^{\left(\mathrm{1}\right)}\right)$ tends to overestimate the true $G_i^{\left(\mathrm{1}\right)}\left(m_i^{\left(\mathrm{1}\right)}\right)$, or in other words the return period of the maximum over $C_i^{\left(\mathrm{1}\right)}$ tends to be underestimated (case of over-estimated risk). If the histogram is right-skewed, the return period of the maximum over $C_i^{\left(\mathrm{1}\right)}$ tends to be over-estimated (case of under-estimated risk). Although any scenario of misfitting could theoretically be possible, in practice the histograms of ff⁽¹²⁾ show mainly the three above alternatives: either a good fit (flat histogram), or a tendency towards a systematic under- or over-estimation (left- or right-skewed histograms). By focusing of maximum values, the histogram of ff⁽¹²⁾ can be seen as a way of assessing systematic bias in the far tail of the distribution. For a more quantitative assessment, we compute the area between the density of the ff⁽¹²⁾ and the uniform density as follows:

$$\begin{array}{}\text{(8)}& {\displaystyle }{\displaystyle }\mathrm{AREA}\left(F{F}^{\left(\mathrm{12}\right)}\right)={\displaystyle \frac{\mathrm{1}}{\mathrm{18}}}\sum _{c=\mathrm{1}}^{\mathrm{10}}\left|\mathrm{10}{\displaystyle \frac{\mathrm{card}\left(B_c\right)}{n}}-\mathrm{1}\right|,\end{array}$$

where card(B_c) is the number of $f{f}_i^{\left(\mathrm{12}\right)}$ in the cth bin, for c=1, …, 10. The term inside the absolute value in Eq. (8) is the difference between densities in the cth bin. The division by 18 forces the score to lie in the range (0, 1), with lower values indicating better fits (the worst case being all values lying in the same bin). Figure 3 shows that, when Q=42 stations are considered, a value of AREA(FF⁽¹²⁾) around 0.2 corresponds to no systematic bias in the very tail of the distribution at regional scale, whereas a value around 0.5 corresponds to a strong over- or under-estimation. In the latter case, only looking at the histogram can inform about whether over- or under-estimation applies.

The N_T criterion is an alternative to FF assessing reliability of the fit of the tail but focusing on prescribed (large) quantiles rather than on the overall maximum. It applies the same principle as FF, involving a transformation of X to F(X), but considering X as $K_{i,T}^{\left(\mathrm{1}\right)}$, the random variable of the number of exceedances over ${\text{C}}_i^{\left(\mathrm{1}\right)}$ of the T-year return level, i.e., $K_{i,T}^{\left(\mathrm{1}\right)}=\mathrm{card}\left(\mathit{\right\{}{R}_{i,j}\in C_i^{\left(\mathrm{1}\right)}$; $G_i\left(R_j\right)>\mathrm{1}-\mathrm{1}/\left(T{\mathit{\delta }}_i\right)\mathit{\left\}}\right)$, in which case F is the binomial distribution $B_i^{\left(\mathrm{1}\right)}$ with parameters ($n_i^{\left(\mathrm{1}\right)}$, 1∕(Tδ_i)). Thus, if ${\widehat{G}}_i^{\left(\mathrm{2}\right)}$ is a perfect estimate of G_i, then $n_{i,T}^{\left(\mathrm{12}\right)}=B_i^{\left(\mathrm{1}\right)}\left(k_{i,T}^{\left(\mathrm{12}\right)}\right)$, where

$${\displaystyle }{\displaystyle }{k}_{i,T}^{\left(\mathrm{12}\right)}=\mathrm{card}\left(\left\{r_{i,j}\in C_i^{\left(\mathrm{1}\right)};{\widehat{G}}_i^{\left(\mathrm{2}\right)}left(r_{i,j}\right)>\mathrm{1}-\mathrm{1}/\left({\mathit{\delta }}_{i}T)\right\}\right),$$

should be a realization of the discrete uniform distribution. Randomization to transform $n_{i,T}^{\left(\mathrm{12}\right)}$ to a continuous uniform variate on (0, 1) is proposed in Renard et al. (2013) and extensively described in Blanchet et al. (2015). For i ranging over the set of Q stations, we thus obtain a sample of Q uniform variates. Scores are calculated as for FF by comparing the empirical densities of $N_T^{\left(\mathrm{12}\right)}$ to the theoretical uniform density, giving the scores AREA($N_T^{\left(\mathrm{12}\right)}$). Taking T as, e.g., half to one-quarter the length of the observations allows assessment of the reliability of the close tail of the distribution. As such, it is a good complement to FF that focuses on the far tail (i.e., on the maximum).

Last but not least, the SPAN criterion evaluates the stability of the return level estimation, when using data for each of the two subsamples. More precisely, for a given return period T and station i,

$$\begin{array}{}\text{(9)}& {\displaystyle }{\displaystyle }{\mathrm{SPAN}}_{i,T}={\displaystyle \frac{|{\widehat{r}}_{i,T}^{\left(\mathrm{1}\right)}-{\widehat{r}}_{i,T}^{\left(\mathrm{2}\right)}|}{\mathrm{1}/\mathrm{2}\left\{{\widehat{r}}_{i,T}^{\left(\mathrm{1}\right)}+{\widehat{r}}_{i,T}^{\left(\mathrm{2}\right)}\right\}}},\end{array}$$

where ${\widehat{r}}_{i,T}^{\left(\mathrm{1}\right)}$; e.g., is the T-year return level for the distribution G estimated on subsample $C_i^{\left(\mathrm{1}\right)}$ of station i, i.e., such that ${\widehat{G}}_i^{\left(\mathrm{1}\right)}\mathit{\left\{}{\widehat{r}}_{i,T}^{\left(\mathrm{1}\right)}\mathit{\right\}}=\mathrm{1}-\mathrm{1}/\left(T{\mathit{\delta }}_i\right)$. SPAN_i,T is the relative absolute difference in T-year return levels estimated on the two subsamples. It ranges between 0 and 2; the closer to 0, the more stable the estimations for station i. For the set of Q stations, we obtain a vector of SPAN_T of length Q with a distribution which should remain reasonably close to zero. A rough summary of this information is obtained by computing the mean of the Q values of SPAN_i,T, i=1, …, Q:

$$\begin{array}{}\text{(10)}& {\displaystyle }{\displaystyle }\mathrm{MEAN}\left({\mathrm{SPAN}}_T\right)={\displaystyle \frac{\mathrm{1}}{Q}}\sum _{i=\mathrm{1}}^Q{\mathrm{SPAN}}_{i,T}.\end{array}$$

For competing models, the closer the mean is to 0, the more stable the model is. When T is larger than the observed range of return periods, MEAN(SPAN_T) evaluates the stability of the return levels in extrapolation. Note that it is by definition 0 in calibration, and thus it is only useful in cross-validation.

For the sake of concision, in the rest of this article the scores MEAN(NRMSE), AREA(FF), AREA(N_T) and MEAN(SPAN_T) will be referred to as the NRMSE, FF, N_T and SPAN_T scores.

3.2 Mapping of the margins

3.2.1 Considered mapping models

Let R_i be the random variable of daily rainfall at station i, i=1, …, Q. Applying Sect. 3.1 at station i gives an estimate ${\widehat{G}}_i\left(r\right)$ of the CDF $G_i\left(r\right)=\mathrm{pr}(R_i\le r|R_i>\mathrm{0})$. Our goal is to derive an estimate of the CDF of nonzero daily rainfall at any location l of the region, $\mathrm{pr}\left(R\right(l)\le r|R\left(l\right)>\mathrm{0})$, based on the Q estimated CDFs ${\widehat{G}}_i\left(r\right)$. Location l refers here to the three coordinates of ground projection coordinates and altitude, that we write l=(x, y, z). Let ${\widehat{\mathit{\theta }}}_i$ be the set of estimated parameters for station i and ${\widehat{\mathit{\theta }}}_{i,j}$ its jth element. ${\widehat{\mathit{\theta }}}_i$ is composed of the S×K probability of zero rainfall $p_{s,k}^{\mathrm{0}}$ and the $\mathrm{2}\times S\times K$ or $\mathrm{3}\times S\times K$ parameters of the distributions G_s,k, depending on the marginal distribution (see Table 1). We assume the θ_i,j ordered so that the first S×K elements are the $p_{s,k}^{\mathrm{0}}$. We aim at estimating the surface response θ_j(l) at any l of the region, knowing ${\mathit{\theta }}_j\left(l_i\right)={\widehat{\mathit{\theta }}}_{i,j}$. In this study we consider three of the most popular method: kriging interpolation, linear regression methods and thin plate spline regressions. However, the parameters θ_js are constrained, whereas these models apply the unbounded variables: the probabilities $p_{s,k}^{\mathrm{0}}$ lie in (0, 1), while the parameters of Table 1 are all positive. Therefore we apply the mapping models to transformations of θ_j, i.e., to ψ_j=transf(θ_j), where “transf” maps the range of values of θ_j to (−∞, +∞). In this study we consider ψ_j(l)=Φ{θ_j(l)} if $j\le S\times K$ (i.e., if θ_j is any $p_{s,k}^{\mathrm{0}}$), where Φ is the standard Gaussian CDF, and to ψ_j(l)=log {θ_j(l)} otherwise. Other transformations would be possible, in particular $p_{s,k}^{\mathrm{0}}$ may be transformed with the logit function, but will not be considered here for the sake of concision. Thus we aim at estimating ${\stackrel{\mathrm{̃}}{\mathit{\psi }}}_j\left(l\right)$ given values ${\mathit{\psi }}_j\left(l_i\right)={\widehat{\mathit{\psi }}}_{i,j}$ at station locations, with obvious notations. If $l\le S\times K$, estimates of θ_j(l) are then obtained as ${\stackrel{\mathrm{̃}}{\mathit{\theta }}}_j\left(l\right)={\mathrm{\Phi }}^{-\mathrm{1}}\left({\stackrel{\mathrm{̃}}{\mathit{\psi }}}_j\right(l\left)\right)$. Otherwise surface response estimates are obtained as ${\stackrel{\mathrm{̃}}{\mathit{\theta }}}_j\left(l\right)=\exp \left({\stackrel{\mathrm{̃}}{\mathit{\psi }}}_j\right(l\left)\right)$. For the sake of clarity, we omit below the index j, considering a surface ψ(l) to be estimated for all l in the region, given values $\mathit{\psi }\left(l_i\right)={\widehat{\mathit{\psi }}}_i$.

The considered mapping models are listed in Table 3. Three families of method are considered: kriging, linear regression and thin plate spline. Additionally to how they map values, there is a fundamental difference between these models: kriging is an exact interpolation, i.e., $\stackrel{\mathrm{̃}}{\mathit{\psi }}\left(l_i\right)={\widehat{\mathit{\psi }}}_i$ at any station location l_i used to estimate the model. By contrast, the linear regression models and thin plate splines provide inexact interpolations: in the great majority of the time, $\stackrel{\mathrm{̃}}{\mathit{\psi }}\left(l_i\right)\ne {\widehat{\mathit{\psi }}}_i$ (the goal being obviously to minimize the overall error).

Table 3 Mapping models considered in this study, with involved coordinates. Kriging method provides exact interpolation, unlike the linear regression and thin plate spline.

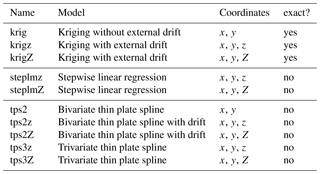
For the kriging interpolation, cases with and without external drift are tested (Sect. 3.6 of Diggle and Ribeiro, 2007). The external drift, if any, is modeled as a linear function of altitude (i.e., of the form a₀+a₁ζ), considering ζ as either the altitude of the station (z) or, following Hutchinson, 1998, as a smoothed altitude (Z) derived by smoothing a 1 km digital elevation model (DEM) with 5 km moving windows (i.e., taking Z as the average altitude of 25 DEM grid points). The results that will be presented below correspond to the case of an exponential covariance function of the form $\mathit{\rho }\left(h\right)=e^{-h/\mathit{\beta }}$, with β>0. We also considered the case of a powered exponential covariance function $\mathit{\rho }\left(h\right)=e^{-(h/\mathit{\beta }{)}^{\mathit{\nu }}}$ with $\mathrm{0}<\mathit{\nu }\le \mathrm{2}$, but this resulted in a slight loss of stability due to the additional degree of freedom, without improving the accuracy at regional scale. For the sake of concision, these results are not presented here. Combining alternatives for the drift part gives a total of three kriging interpolation models with two to three unknown parameters each, for each ψ. Estimations of the kriging models are made by maximizing the likelihood associated with the ${\widehat{\mathit{\psi }}}_i$, assuming that ψ(l) is a Gaussian process (see Sect. 5.4 of Diggle and Ribeiro, 2007). Alternatives are to estimate drifts and variograms by least squares in different steps, with the risk of biasing estimates (Sect. 5.1 to 5.3 of Diggle and Ribeiro, 2007). Both estimation methods are available in R package “geoR” (e.g., functions “likfit” and “variofit”). In the case without drift, prediction at any site l of the region is obtained as

$$\begin{array}{}\text{(11)}& {\displaystyle }{\displaystyle }\stackrel{\mathrm{̃}}{\mathit{\psi }}\left(l\right)=\sum _{i=\mathrm{1}}^Q{w}_i\left(h_i\right){\widehat{\mathit{\psi }}}_i,\end{array}$$

where the weights w_i(h_i) are derived from the kriging equations and satisfy $\sum _{i=\mathrm{1}}^Q{w}_i\left(h_i\right)=\mathrm{1}$. The weights depend on the estimated covariance function and on the distance h_i between l and station location l_i in the (x, y) space (i.e., $h_i^{\mathrm{2}}=(x-x_i{)}^{\mathrm{2}}+(y-y_i{)}^{\mathrm{2}}$). In the case with external drift, prediction at any location l of the region is then obtained as

$$\begin{array}{}\text{(12)}& {\displaystyle }{\displaystyle }\stackrel{\mathrm{̃}}{\mathit{\psi }}\left(l\right)=a_{\mathrm{1}}\mathit{\zeta }+\sum _{i=\mathrm{1}}^Q{w}_i\left(h_i\right)\left({\widehat{\mathit{\psi }}}_i-a_{\mathrm{1}}{\mathit{\zeta }}_i\right),\end{array}$$

where ζ is the altitude at location l (i.e., either z or Z). Predictions (Eqs. 11 and 12) are exact: $\stackrel{\mathrm{̃}}{\mathit{\psi }}\left(l_i\right)={\widehat{\mathit{\psi }}}_i$, and consequently $\stackrel{\mathrm{̃}}{\mathit{\theta }}\left(l_i\right)={\widehat{\mathit{\theta }}}_i$.

For the linear regression models, we start from regressions of the form $\mathit{\psi }\left(l\right)=a_{\mathrm{0}}+a_{\mathrm{1}}x+a_{\mathrm{2}}y+a_{\mathrm{3}}\mathit{\zeta }+a_{\mathrm{4}}{x}^{\mathrm{2}}+a_{\mathrm{5}}{y}^{\mathrm{2}}+a_{\mathrm{6}}xy+a_{\mathrm{7}}x\mathit{\zeta }+a_{\mathrm{8}}y\mathit{\zeta }+\mathit{ϵ}\left(l\right)$, where ϵ(l)∼N(0, σ²) and ζ is, as before, either the altitude of the station (z) or the smoothed altitude (Z). We consider the Akaike information criterion (AIC), defined as AIC = 2η−2log L, where η is the number of parameters (10 at the start) and L is the maximum likelihood value of the regression model. The lower AIC, the better the model. Then we repeatedly drop the variable that increases most the AIC – if any –, and add the variable that decreases most the AIC – if any. This stepwise method is implemented in the “step” function of R package “stats”. At algorithm stop, the model may contain 1 to 10 parameters, for each ψ. Predictions $\stackrel{\mathrm{̃}}{\mathit{\theta }}\left(l\right)$ are then obtained as the back transformation of the estimated regressions.

Last but not least, bivariate and trivariate thin plate splines are considered for ψ(l) (Boer et al., 2001; Hutchinson, 1998). These methods are implemented in function “Tps” of R package “fields”. In the bivariate case, ψ(l) is modeled as $\mathit{\psi }\left(l\right)=u(x,y)+\mathit{ϵ}(x,y)$, where u is an unknown smooth function and ϵ(x,y) are uncorrelated errors with zero means and equal variances. The function u is estimated by minimizing

$$\begin{array}{ll}{\displaystyle }\sum _{i=\mathrm{1}}^Q& {\displaystyle }{\left({\widehat{\mathit{\psi }}}_i-u\left(x_i,y_i\right)\right)}^{\mathrm{2}}+\mathit{\lambda }\underset{-\mathrm{\infty }}{\overset{+\mathrm{\infty }}{\int }}\underset{-\mathrm{\infty }}{\overset{+\mathrm{\infty }}{\int }}\left\{{\left({\displaystyle \frac{{\partial }^{\mathrm{2}}u(x,y)}{\partial x^{\mathrm{2}}}}\right)}^{\mathrm{2}}\right.\\ \text{(13)}& {\displaystyle }& {\displaystyle }\left.+\mathrm{2}{\left({\displaystyle \frac{{\partial }^{\mathrm{2}}u(x,y)}{\partial x\partial y}}\right)}^{\mathrm{2}}+{\left({\displaystyle \frac{{\partial }^{\mathrm{2}}u(x,y)}{\partial y^{\mathrm{2}}}}\right)}^{\mathrm{2}}\right\}\mathrm{d}x\mathrm{d}y,\end{array}$$

where λ is the so-called smoothing parameter, which controls the trade-off between smoothness of the estimated function and its fidelity to the observations. It can be estimated by generalized cross-validation. Then predictions are obtained as

$$\begin{array}{}\text{(14)}& {\displaystyle }{\displaystyle }\stackrel{\mathrm{̃}}{\mathit{\psi }}\left(l\right)=a_{\mathrm{0}}+a_{\mathrm{1}}x+a_{\mathrm{2}}y+\sum _{i=\mathrm{1}}^Q{b}_i{h}_i^{\mathrm{2}}\log \left(h_i\right),\end{array}$$

where h_i is the Euclidean distance in the (x, y) space between l and station location l_i. The partial trivariate case assumes that ψ(l)−a₃ζ is a bivariate thin plate spline, where a₃ is fixed and ζ is either z or Z. To make the connection with kriging, ψ(l) can thus also be seen as a bivariate thin plate spline with (fixed) drift in ζ. The coefficient a₃ is estimated in a preliminary step by regressing ${\widehat{\mathit{\psi }}}_i$ against ζ_i. Estimation of the bivariate thin plate spline for ψ(l)−a₃ζ is made as described above given the values of ${\widehat{\mathit{\psi }}}_i-a_{\mathrm{3}}{\mathit{\zeta }}_i$. Predictions are obtained as

$$\begin{array}{}\text{(15)}& {\displaystyle }{\displaystyle }\stackrel{\mathrm{̃}}{\mathit{\psi }}\left(l\right)=a_{\mathrm{0}}+a_{\mathrm{1}}x+a_{\mathrm{2}}y+a_{\mathrm{3}}\mathit{\zeta }+\sum _{i=\mathrm{1}}^Q{b}_i{h}_i^{\mathrm{2}}\log \left(h_i\right).\end{array}$$

Finally in the trivariate case, we have $\mathit{\psi }\left(l\right)=u(x,y,\mathit{\zeta })+\mathit{ϵ}(x,y,\mathit{\zeta })$. The minimization problem is similar to Eq. (13) with a penalization enlarged by several terms (Wahba and Wendelberger, 1980). Predictions are then obtained as

$$\begin{array}{}\text{(16)}& {\displaystyle }{\displaystyle }\stackrel{\mathrm{̃}}{\mathit{\psi }}\left(l\right)=a_{\mathrm{0}}+a_{\mathrm{1}}x+a_{\mathrm{2}}y+a_{\mathrm{3}}\mathit{\zeta }+\sum _{i=\mathrm{1}}^Q{b}_i{h}_i^{\prime },\end{array}$$

where $h_i^{\prime }$ is the Euclidean distance in the (x, y, ζ) space between l and station location l_i, scaling the altitude by a factor of 10 following Boer et al. (2001) and Hutchinson (1998) (i.e., $h{{}^{\prime }}_i^{\mathrm{2}}=(x-x_i{)}^{\mathrm{2}}+(y-y_i{)}^{\mathrm{2}}+\mathrm{100}(\mathit{\zeta }-{\mathit{\zeta }}_i{)}^{\mathrm{2}}$). Coefficients a_i and b_i in Eqs. (14) to (16) are estimated by solving a linear system of order Q involving the smoothing parameter λ. Note that the trivariate case (Eq. 16) differs from the bivariate case with drift (Eq. 15) in two ways. First, Eq. (16) considers distance in the (x, y, ζ) space, whereas Eq. (15) considers distance in the (x, y) space. Second, in Eq. (16), the weights associated with the stations are linear functions of the distance, unlike in Eq. (15) (see the term $h_i^{\mathrm{2}}\log \left(h_i\right)$ vs. $h_i^{\prime }$).

3.2.2 Evaluation at regional scale in a cross-validation framework

Evaluation is performed in two ways. The first one is a leave-one-out cross-validation scheme aiming to test at regional scale how the interpolated distributions are able to fit the data of the stations when these data are left out for estimating the mapping model. The second step assesses spatial stability by comparing the interpolated distributions obtained at a given station whether the data of this station are used or not in the mapping estimation. In other words, it is a comparison between leave-one-out and leave-zero-out mappings. So the two evaluations differ in that the first one compares an interpolated distribution to data, while the second step compares two interpolated distributions.

First, let us consider a given parameter estimate ${\widehat{\mathit{\theta }}}_{i,j}^{\left(\mathrm{1}\right)}$ obtained at station i based on the subsample $C_i^{\left(\mathrm{1}\right)}$ (for a given marginal model). We apply a leave-one-out cross-validation scheme: for each station i₀ alternatively, we use the set of ${\widehat{\mathit{\theta }}}_{i,j}^{\left(\mathrm{1}\right)}$, i≠i₀ to estimate the surface response ${\stackrel{\mathrm{̃}}{\mathit{\theta }}}_j^{\left(\mathrm{1}\right)}\left(l\right)$. We store the value of this estimate at station location i₀, i.e., ${\stackrel{\mathrm{̃}}{\mathit{\theta }}}_j^{\left(\mathrm{1}\right)}\left(l_{i_{\mathrm{0}}}\right)={\stackrel{\mathrm{̃}}{\mathit{\theta }}}_{i_{\mathrm{0}},j}^{\left(\mathrm{1}\right)}$. Repeating this for every parameter θ_j gives an estimation of the full set of parameters at station i₀, i.e., estimation ${\stackrel{\mathrm{̃}}{G}}_{i_{\mathrm{0}}}^{\left(\mathrm{1}\right)}$ of $G_{i_{\mathrm{0}}}$. Iterating over the stations, we obtain new estimates ${\stackrel{\mathrm{̃}}{G}}_{\mathrm{1}}^{\left(\mathrm{1}\right)}$, …, ${\stackrel{\mathrm{̃}}{G}}_Q^{\left(\mathrm{1}\right)}$ of G₁, …, G_Q. Applying similarly for the subsample $C_i^{\left(\mathrm{2}\right)}$ gives estimates ${\stackrel{\mathrm{̃}}{G}}_{\mathrm{1}}^{\left(\mathrm{2}\right)}$, …, ${\stackrel{\mathrm{̃}}{G}}_Q^{\left(\mathrm{2}\right)}$. We can assess the reliability of these estimates at the regional scale by computing the scores Sc⁽¹¹⁾, Sc⁽²²⁾, Sc⁽¹²⁾ and Sc⁽²¹⁾ of Sect. 3.1.2, where ${\widehat{G}}_i$ is replaced by ${\stackrel{\mathrm{̃}}{G}}_i$. Note that all these scores are cross-validation scores since the estimates ${\stackrel{\mathrm{̃}}{G}}_{\mathrm{1}}^{\left(\mathrm{1}\right)}$ and ${\stackrel{\mathrm{̃}}{G}}_{\mathrm{1}}^{\left(\mathrm{2}\right)}$ are computed without using any data of station i.

Second, we consider the set of all ${\widehat{\mathit{\theta }}}_{i,j}^{\left(\mathrm{1}\right)}$, i=1, …, Q to estimate the surface response ${\stackrel{\mathrm{̃}}{\mathit{\theta }}}_j^{\left(\mathrm{1}\right)}\left(l\right)$. We store the value of this function at every station location, giving new estimates ${\stackrel{\mathrm{̃}}{G}}_{\mathrm{1}}^{*\left(\mathrm{1}\right)}$, …, ${\stackrel{\mathrm{̃}}{G}}_Q^{*\left(\mathrm{1}\right)}$. Note that in the particular case of kriging, ${\stackrel{\mathrm{̃}}{G}}_i^{*\left(\mathrm{1}\right)}$ is exactly ${\widehat{G}}_i^{\left(\mathrm{1}\right)}$ since it is an exact interpolation method, so every ${\widehat{\mathit{\theta }}}_{i,j}^{\left(\mathrm{1}\right)}$ equals ${\stackrel{\mathrm{̃}}{\mathit{\theta }}}_{i,j}^{*\left(\mathrm{1}\right)}$. We can assess the stability of the interpolated distributions at a given location l_i when observations are available or not at this location by comparing ${\stackrel{\mathrm{̃}}{G}}_i^{*\left(\mathrm{1}\right)}\left(r\right)$ and ${\stackrel{\mathrm{̃}}{G}}_i^{\left(\mathrm{1}\right)}\left(r\right)$ for all r. For this we discretize r between 0 and 450 mm (which is the overall maximum rainfall) with 1 mm step and we compute the total variation distance (TVD) between ${\stackrel{\mathrm{̃}}{G}}_i^{*\left(\mathrm{1}\right)}$ and ${\stackrel{\mathrm{̃}}{G}}_i^{\left(\mathrm{1}\right)}$ and the Kullback–Leibler divergence (KLD, Weijs et al., 2010) from ${\stackrel{\mathrm{̃}}{G}}_i^{*\left(\mathrm{1}\right)}$ to ${\stackrel{\mathrm{̃}}{G}}_i^{\left(\mathrm{1}\right)}$, which are given by

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }{\mathrm{TVD}}_i^{\left(\mathrm{1}\right)}=\underset{r}{sup}\left|{\stackrel{\mathrm{̃}}{G}}_i^{*\left(\mathrm{1}\right)}\right(r)-{\stackrel{\mathrm{̃}}{G}}_i^{\left(\mathrm{1}\right)}(r\left)\right|,\\ {\displaystyle }& {\displaystyle }{\mathrm{KLD}}_i^{\left(\mathrm{1}\right)}=\underset{r}{\int }{\stackrel{\mathrm{̃}}{g}}_i^{*\left(\mathrm{1}\right)}\left(r\right)\log {\displaystyle \frac{{\stackrel{\mathrm{̃}}{g}}_i^{*\left(\mathrm{1}\right)}\left(r\right)}{{\stackrel{\mathrm{̃}}{g}}_i^{\left(\mathrm{1}\right)}\left(r\right)}}\mathrm{d}r,\end{array}$$

where, e.g., ${\stackrel{\mathrm{̃}}{g}}_i^{\left(\mathrm{1}\right)}$ is the density function associated with ${\stackrel{\mathrm{̃}}{G}}_i^{\left(\mathrm{1}\right)}$. Note that the KLD is not symmetric. Written as such, it can be interpreted as the amount of information lost when ${\stackrel{\mathrm{̃}}{G}}_i^{\left(\mathrm{1}\right)}$ is used to approximate ${\stackrel{\mathrm{̃}}{G}}_i^{*\left(\mathrm{1}\right)}$, so considering ${\stackrel{\mathrm{̃}}{G}}_i^{*\left(\mathrm{1}\right)}$ as the “true” distribution of data. TVD and KLD differ in that TVD focuses on the largest deviation between the two CDFs, whereas KLD somewhat integrates deviations along rainfalls. Obviously, one would like the interpolation to be as stable as possible when data are available or not at station i, i.e., that the lower TVD_i and KLD_i, the more stable the interpolation at station i.

Regional scores MEAN(TVD${}_i^{\left(\mathrm{1}\right)}$) and MEAN(KLD${}_i^{\left(\mathrm{1}\right)}$) are then obtained by computing the mean of the Q values. MEAN(TVD${}_i^{\left(\mathrm{2}\right)}$) and MEAN(KLD${}_i^{\left(\mathrm{2}\right)}$) are obtained similarly for the subsample C⁽²⁾. For competing models, the closer the means are to 0, the more spatially stable is the interpolation. For shortness, we will refer to MEAN(TVD) and MEAN(KLD) as the TVD and KLD scores, respectively (Table 2).

Figure 4 (a) Monthly percentage of occurrence of the three WPs. (b) Boxplot of the monthly averages of daily nonzero rainfall. Each boxplot contains 42 points (one point per station).

3.3 Procedure of model selection at regional scale

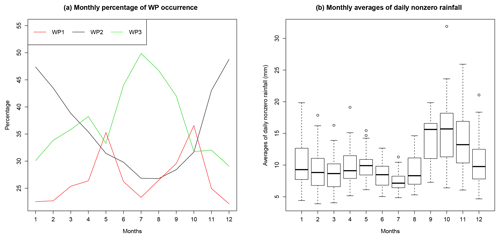
We wish to evaluate and compare the performance of both marginal and mapping models for estimating rainfall frequency across the region. We consider models both with and without season/WPs. For the cases involving the use of WPs, we use the WP classification described in Garavaglia et al. (2010), which is obtained by clustering synoptic situations (geopotential heights) for France and surrounding areas into eight classes. However, a grouping of the eight WPs into three is made in order to improve the robustness of the method while conserving the diversity of the rainy synoptic situations. The choice of the grouped WPs is made in a separate analysis based on the spatial correlation of rainfall in the different WPs. The range of spatial correlation is twice as big in WP1 as in WP2, and 3 times as big in WP1 as in WP3. The occurrence statistics of the three WPs for the period 1948–2013 are presented in Fig. 4. The yearly occurrence of the three WPs is roughly similar (27 % for WP1, 36 % for WP2, 37 % for WP3). However, the WPs show very different seasonality. In particular, WP1 is more frequent in spring and autumn, which correspond to wetter periods, particularly in autumn (see the monthly averages of nonzero rainfall in Fig. 4). WP3 is more frequent in summer, which is the driest season, while WP2 features almost a reversed seasonality compared to WP3. This shows that, although based on the spatial dependence, the WPs are linked to the seasonality of rainfall in the region.

In cases where subsampling is also undertaken by season, we impose a restriction of S being two seasons, representing the season-at-risk during which most of the annual maxima are observed, and the season-not-at-risk. Furthermore, we impose the season-at-risk to be the same for all the stations due to the little extent of the region. Based on Fig. 4, we define the season-at-risk as the three months of September, October and November, as in Garavaglia et al. (2010) and Evin et al. (2016) for example. Alternative for bigger regions would be to select the months composing the season-at-risk following the procedure described in Blanchet et al. (2015).

3.3.1 Marginal selection procedure

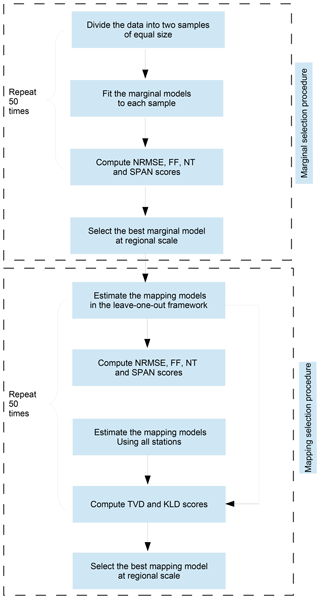
The full cross-validation procedure for selecting both the marginal and mapping models is summarized in Fig. 5. First we consider the marginal distributions of Table 1 and select the best of them at regional scale, as described in Sect. 3.1.2:

1. We divide the days of 1948-2013 into two subsamples of equal size, denoted C⁽¹⁾ and C⁽²⁾. Given the weak temporal dependence of rainfall in the region (80 % of the wet periods have length lower than 3), division is made by randomly choosing blocks of five consecutive days to compose C⁽¹⁾, the remaining blocks composing C⁽²⁾.

2. For every station i, we consider the set of observed days in C⁽¹⁾ and C⁽²⁾, giving $C_i^{\left(\mathrm{1}\right)}$ and $C_i^{\left(\mathrm{2}\right)}$.

3. We fit each distribution of Table 1 to the two subsamples, getting estimates ${\widehat{G}}_i^{\left(\mathrm{1}\right)}$ and ${\widehat{G}}_i^{\left(\mathrm{2}\right)}$ of each distribution and for every station.

4. We compute the scores of Sect. 3.1.2, getting two calibration scores – (11) and (22) – of NRMSE, FF and N_T, and two cross-validation scores – (12) and (21) – of NRMSE, FF, N_T and SPAN_T. For N_T, we consider T=5 years, which is lower than the minimum length of the calibration data and allows one to focus on the tail but still have several exceedances of the T-year return level at every station. So FF, by focusing on the maximum of roughly 10 to 30 years of data, can be seen as an evaluation score for the far tail, while N₅ can be seen as an evaluation score for the close tail. For SPAN_T, we consider T=100 and T=1000 years in order to test extrapolation far in the tail but at a scale still commonly used for engineering purposes (dam building, protections, etc., Paquet et al., 2013).

5. We repeat 50 times steps 1–4.

We obtain 100 values of each calibration score and 100 values of each cross-validation score. We apply this procedure to the four distributions of Table 1, considering the four alternatives: no season nor WP (S=1, K=1), two seasons but no WP (S=2, K=1), no season but three WPs (S=1, K=3), two seasons and three WPs (S=2, K=3). Comparing the distributions of the scores of the 16 models allows us the select the marginal distribution yielding to the best fit at regional scale. We select this marginal model for further consideration.

Figure 5 Schematic summary of the full cross-validation procedure for selecting both the marginal and mapping models.

3.3.2 Mapping selection procedure

Second we consider the mapping models of Sect. 3.2.1 for interpolating the selected marginal model, and we select the best of them in two ways, as described in Sect. 3.2.2.

1. We consider the estimates ${\widehat{G}}_i^{(\mathrm{1},t)}$, i=1, …, Q, obtained at the tth iteration of the marginal selection procedure, and corresponding to the subsamples $C_i^{(\mathrm{1},t)}$, i=1, …, Q.

2. We estimate the mapping models of Sect. 3.2.1 following the leave-one-out cross-validation framework of Sect. 3.2.2. We obtain new estimates ${\stackrel{\mathrm{̃}}{G}}_i^{(\mathrm{1},t)}$ for each station i and each mapping model. Each ${\stackrel{\mathrm{̃}}{G}}_i^{(\mathrm{1},t)}$ is a cross-validation estimation of both $G_i^{\left(\mathrm{1}\right)}$ and $G_i^{\left(\mathrm{2}\right)}$ since the computation of ${\stackrel{\mathrm{̃}}{G}}_i^{(\mathrm{1},t)}$ did not use any data of station i.

3. We compute the scores of Sect. 3.1.2 associated with ${\stackrel{\mathrm{̃}}{G}}_i^{(\mathrm{1},t)}$, i=1, …, Q. We obtain for each score two values (e.g., FF⁽¹¹⁾ and FF⁽²¹⁾ when considering ${\stackrel{\mathrm{̃}}{G}}_i^{(\mathrm{1},t)}$ and the maximum value over either C⁽¹⁾ or C⁽²⁾). All these scores are cross-validation scores.

4. We estimate the mapping models of Sect. 3.2.1, using all the stations to make interpolation. We obtain new estimates ${\stackrel{\mathrm{̃}}{G}}_i^{*(\mathrm{1},t)}$ for each station i and each mapping model.

5. We compute the spatial means of the TVD and KLD scores of Sect. 3.2.2, comparing ${\stackrel{\mathrm{̃}}{G}}_i^{*(\mathrm{1},t)}$ to ${\stackrel{\mathrm{̃}}{G}}_i^{(\mathrm{1},t)}$, for, i=1, …, Q.

6. We repeat steps 1–5 for the estimates ${\stackrel{\mathrm{̃}}{G}}_i^{(\mathrm{2},t)}$ corresponding to the subsample $C_i^{(\mathrm{2},t)}$.

7. We repeat steps 1–6 for each of the 50 subsamples.

We obtain 200 values of each cross-validation score NRMSE, FF, N_T and SPAN, and 100 values of the TVD and KLD scores. Comparing the distributions of these scores allows us the select the mapping model yielding the smallest score, for the selected marginal model. We select this mapping model for further consideration.

At this step we have selected the best marginal model and the best mapping model (among those tested) for our data.

3.3.3 Final regional model

Finally, we consider the whole sample of data and apply the selected marginal distribution and mapping model.

1. We estimate the selected marginal distribution ${\widehat{G}}_i^{*}$ based on the full data, giving parameters ${\widehat{\mathit{\theta }}}_{ij}^{*}$, i=1, …, Q.

2. We estimate the mapping model associated with each marginal parameter, using all ${\widehat{\mathit{\theta }}}_{ij}^{*}$, i=1, …, Q, to estimate the surface response ${\stackrel{\mathrm{̃}}{\mathit{\theta }}}_j^{*}\left(l\right)$.

We obtain estimates of $\mathrm{pr}\left(R\right(l)\le r|R\left(l\right)>\mathrm{0})$ for every l within the region, making full use of the observations. Estimation of pr(R(l)≤r) is obtained straightforwardly from Eq. (3). Although not considered in this study, confidence intervals could be obtained by bootstrapping within these two last steps.

Figure 6 Scores of cross-validation when G_s,k are Gamma distributions and the number of seasons and WP varies: S∈{1, 2} and K∈{1, 3}. The values of (S, K) are indicated in the x labels. Each boxplot contains 100 points.

4 Results

4.1 Selection of the marginal distribution

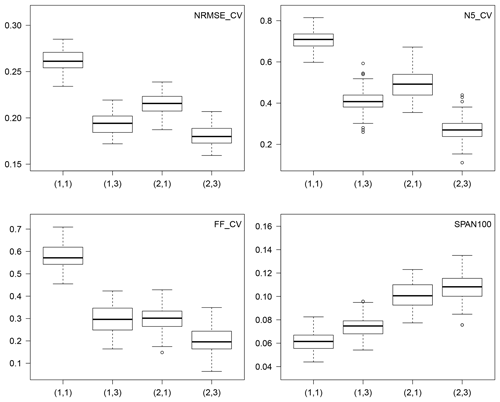
We show in Fig. 6 the influence of considering seasons and/or WPs in the marginal distributions, in the case of the Gamma distribution for illustration, but similar patterns are found with the other distributions. Figure 6 depicts the cross-validation scores of NRMSE, FF and N₅ and the reliability score SPAN₁₀₀ for the 100 split samples C⁽¹⁾ and C⁽²⁾. Calibration scores are not shown because they are very similar to the cross-validation scores (correlation 91 % between validation and calibration scores). For the stability criteria, we only show the values of SPAN₁₀₀, which corresponds to 3 to 10 times the length of calibration data, but actually values for T=1000 years lead to the same conclusions (correlation 99.9 % between SPAN₁₀₀ and SPAN₁₀₀₀).

Comparing the reliability scores NRMSE, FF and N₅ when neither season nor WP is used – case (1, 1) – with cases when either WPs – case (1, 3) – or seasons (case (2, 1)) are considered shows there is at regional scale a clear improvement in using a mixture of Gamma distributions rather than considering a single Gamma for the whole year. Reliability criteria are slightly better (i.e., lower) when WPs are considered rather than season, but this is more marked for the bulk of the distribution (represented by the NRMSE scores) than for its tail (FF and N₅). Reliability scores are even better when both seasons and WPs are considered – case (2, 3) –, particularly for the tail of the distribution.

Obviously, there is a loss of stability when considering seasons and/or WPs due to the increased number of parameters. However, the score of SPAN₁₀₀ ranges from 0.08 to 0.14, which means that the two estimates of the 100-year return levels over C⁽¹⁾ and C⁽²⁾ differ by 8 % to 14 %, which seems acceptable.

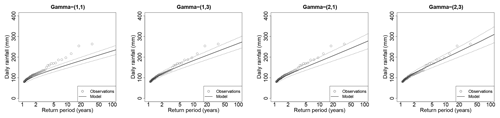
Figure 7 Case of Antraigues when G_s,k are Gamma distributions and the number of seasons and WP varies: S∈{1, 2} and K∈{1, 3}. The values of (S, K) are indicated in the title. The dotted lines show the 95 % envelope of return level estimates over the 100 subsamples. The plain line shows the median estimates. The gray points show the full sample (35 years). Each estimation is based on half of these points.

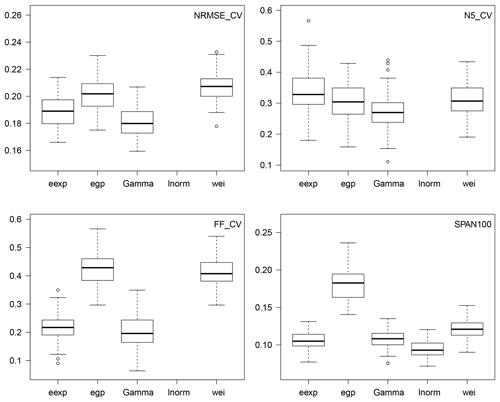
Figure 8 Scores of cross-validation when G_s,k is either the extended exponential (eexp), extended generalized Pareto (egp), Gamma (gamma), lognormal (lnorm) or Weibull (wei) distribution, with S=2 and K=3. Each boxplot contains 100 points. The boxplots of reliability scores in the lognormal case are missing because they lie far above the upper range of depicted values.

We illustrate the quality of the fit for station Antraigues, located in the very foothills of the Massif Central slope (see Fig. 1), which shows among the largest annual maxima (see Fig. 2). We focus on the tail of the distribution by looking at the return level plot (here beyond the yearly return period). Of course, some variability is found in the return level estimations depending on the subsample used for estimation. Figure 7 illustrates this by showing the 95 % envelope of return level estimations over the 100 subsamples on either C⁽¹⁾ or C⁽²⁾ together with the full sample of 35 years. Note that the envelopes do not show confidence intervals (that could be obtained by bootstrapping for example), but variability when only half the data are used from calibration. Thus, more than goodness-of-fit assessment, the plots of Fig. 7 allow us to assess the quality of the fits at close extrapolation (i.e., when extrapolating at twice the length of the data). The plots clearly show that considering seasons and WPs allows us to get heavier-tailed distributions. The median estimates with two seasons and three WPs follow most closely the empirical points, even the largest ones, showing the quality of the fits for extrapolating at twice the length of the data. However, we note that the return level plots of Fig. 7 all appear approximately linear for high values, meaning that none of the Gamma mixtures is able to produce heavy tails in the sense of extreme value theory. It is possible that return levels at extrapolation far beyond the observed return periods are underestimated. Figure 7 also shows that variability is relatively low in all cases, although it naturally increases for the marginal models involving more parameters. In particular, the coefficient of variation of the 100-year return level with two seasons and three WPs is less than 7 %, in coherence with the SPAN₁₀₀ of Fig. 6 at regional scale.

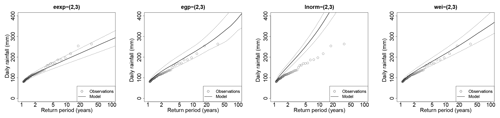
Figure 9 Case of Antraigues when G_s,k is either the extended exponential (eexp), extended generalized Pareto (egp), lognormal (lnorm) or Weibull (wei) distribution, with S=2 and K=3. The dotted lines show the 95 % envelope of return level estimates over the 100 subsamples. The plain line shows the median estimates. The gray points show the full sample (35 years). Each estimation is based on half these points. The case of the Gamma distribution is shown in panel (d) of Fig. 7.

Due to its better fit for the Gamma model (Figs. 6 and 7) as for the other distributions (not shown), we select the mixture model with S=2 seasons and K=3 WPs for further investigation. Figure 8 shows the scores of cross-validation when the parent distribution G_s,k is either the extended exponential, extended generalized Pareto, Gamma, lognormal or Weibull distribution. The reliability scores NRMSE, FF and N₅ in the lognormal case are missing because they lie far above the upper range of the depicted values (e.g., the median NRMSE is about 0.7), which clearly rules out the use of the lognormal model for this region. The reliability criteria of the four other distributions all show the same pattern: a better performance of the Gamma model, closely followed by the extended exponential case. Then comes the extended generalized Pareto, itself closely followed by the Weibull model. A closer look at the values of ff_i and n_i,5 for all stations and samples reveals that the weaker reliability of the Weibull and extended generalized Pareto models is due to their tendency to systematically overestimate the probability of occurrence of large values (i.e., to underestimate their return period), with ff_i and n_i,5 tending to be too frequently small (see case G₁ of Fig. 3). Note that the lack of reliability of the extended generalized Pareto in the upper tail is at least partially attributable to being based on fitting the entire range of rainfall values, which leads to a systematic overestimation of the shape parameter ξ in Table 1 compared to when fitting a generalized Pareto distribution on the upper tail of the data (not shown).

Stability score SPAN₁₀₀ in Fig. 8 shows that the most stable model is the lognormal case, but this is because the lognormal distribution gives unreasonably huge estimates of large return values (as illustrated in Fig. 9 for station Antraigues, for example), giving very large normalization terms in the SPAN criteria (see Eq. 9). The fact that the lognormal model has by far the worst reliability scores but the best stability score preaches for the conjoint use of these two families of scores not to misinterpret results. The stabilities of the Gamma and extended exponential distributions are very similar and fairly less good than the lognormal case. Then comes the Weibull distribution, and finally the generalized Pareto distribution, which is clearly the least stable.

Figure 9 illustrates the quality and spread of the fits depending on the distribution for station Antraigues, when estimation is made on either subsample. Compared to Fig. 7, it confirms that the Gamma and extended exponential models perform almost alike. Median estimations differ by about 5 % for the 100-year return level (303 mm for the Gamma vs. 287 mm for the extended exponential model) and by about 7 % for the 1000-year return level (414 mm vs. 386 mm), with very similar widths of the 95 % envelopes (e.g., ±40 mm for the 100-year return level). The lognormal model clearly fails to reproduce return periods larger than 1 year, giving much too heavy tails despite a reasonably good fit of the bulk. Actually the skewness – which informs somehow about the “ asymmetry of the bulk” – is reasonably well estimated, whereas the kurtosis – which informs about the heaviness of the tail – is much overestimated. This is in line with Fig. 2 of Hanson and Vogel (2008), which shows that when the skewness of daily rainfall across the US is well estimated by the lognormal distribution, then the kurtosis is much overestimated. Note that Papalexiou et al. (2013) did not find such ill-fitted tails with the lognormal distribution, but in their case fitting is made on the tail (i.e., on the largest values), whereas the lognormal model seems to fail when adjusting both the bulk and the tail of rainfall distribution. The Weibull and extended generalized Pareto models give very similar fits up to the 50-year return period, but the return level plot of the extended generalized Pareto model is more convex (i.e., it shows a heavier tail) than for the Weibull model, giving a median estimation 8 % larger for the 100-year return level (390 mm vs. 358 mm) and 35 % larger for the 1000-year return level (799 mm vs. 522 mm). The width of the 95 % envelope is also larger in both absolute and relative values, in coherence with the SPAN₁₀₀ of Fig. 8 at regional scale. Finally, both the Weibull and extended generalized Pareto models overestimate the return levels associated with 1–5 years, unlike the Gamma and extended exponential models. This tendency towards overestimation of the tail is actually a quite general feature observed for most the stations, giving too frequently low values of ff_i and n_i,T, as already stated.

The results of Figs. 8 and 9 lead us to conclude that the best performance for the region is achieved by the Gamma and extended exponential models, which actually perform very similarly for Antraigues station. Note that exactly the same conclusions hold when focusing on the season-at-risk rather than considering the whole year, i.e., when computing the cross-validation scores for the estimated seasonal distribution G_s in (5) rather than for the year-round distribution G in Eq. (4. Due to its slightly better performance at regional scale for adjusting the tail of the distribution (FF and N₅ in Fig. 8), we select the Gamma model (with two seasons and three WPs) for further consideration.

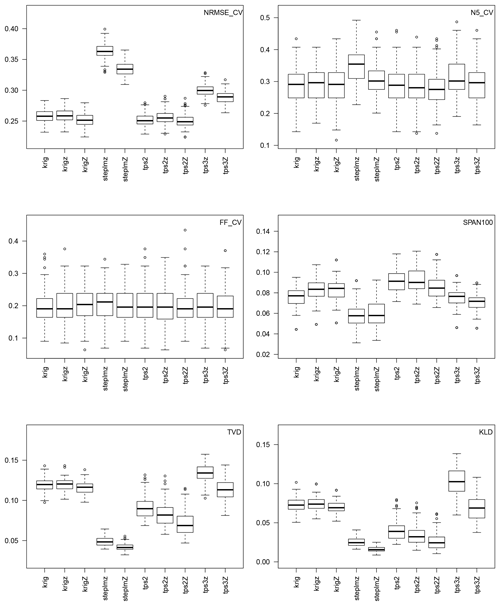
Figure 10 Scores of mapping when G_s,k are Gamma distributions with S=2 and K=3 whose parameters are interpolated with the mapping models of Table 3. The first two rows show leave-one-out cross-validation scores. Each boxplot contains 200 points. The third row compares interpolations at a given station whether the data of this station are used or not in the interpolation. Each boxplot contains 100 points.

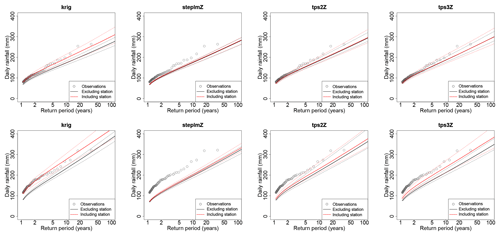
Figure 11 Cases of Antraigues (panels a–d) and Mayres (panels e–h) when G_s,k are Gamma distributions with S=2 and K=3 whose parameters are interpolated with either kriging without external drift (krig), a stepwise linear model (steplmZ), a bivariate thin plate spline with drift (tps2Z), or a trivariate thin plate spline (tps3Z). The dotted lines show the 95 % envelope of return level estimates over the 100 subsamples. The plain line shows the median estimates. In black, each interpolation is based on half the data of the other stations, excluding the considered station. In red, interpolation is based on half the data of all the stations, including the considered station. The gray points show the full sample (35 years for both stations).

4.2 Selection of the mapping model

Figure 10 shows the 10 scores of evaluation of the mapping models of Table 3. The first comment is that, compared to Fig. 8, the FF scores of leave-one-out cross-validation are for any mapping method on the same order as for the local fits, while the SPAN scores are even slightly better. This means that (i) no mapping method gives systematic over- or under-estimation of the very tail, and (ii) mapping gives more stable estimations by smoothing out the sampling effect. However, NMRSE scores are all larger, meaning that any mapping gives less accurate estimations of the full distributions than the local fits. Loss in accuracy is equivalent and relatively small for all kriging interpolations and the bivariate thin plate splines (with or without drift), while the trivariate thin plate spline and even more the linear model are less accurate. A closer look at the fits of all stations reveals that the strong loss in NRMSE for these two methods is actually due to a few stations that are systematically very badly fitted – among them the station of Mayres of Fig. 11 –, which strongly deteriorates the spatial mean of the scores. Their less good performance is due to a lack of flexibility, which prevents them from adapting to local features. However, at the same time, the lack of flexibility of these methods allows for slightly increased stability in the tail, as shown by the SPAN scores in Fig. 10.

Back to the kriging methods, the three tested alternatives give very similar fits, with slightly less stability when considering a drift in station altitude z, while considering the smoothed altitude Z is useless because a₁ in Eq. (12) is almost always zero. The best kriging method for our region study in thus the simple kriging interpolation. This method is only slightly beaten in accuracy by the bivariate thin plate spline (with or without drift), but which is slightly less stable. However, the TVD and KLD scores comparing the spatial stability of the mappings show that the bivariate thin plate splines are clearly more stable in space than all kriging methods. The linear model is even more stable but, as already said, it is much less accurate. Finally, comparing the five cases of thin plate spline shows that the three bivariate cases clearly outperform the trivariate case, both in terms of accuracy and stability. Comparing the bivariate case with drift (Eq. 15) to the the trivariate case (Eq. 16) shows the usefulness of considering nonlinear weights of the distance (through the term $h_i^{\mathrm{2}}\log \left(h_i\right)$ vs. $h_i^{\prime }$). Last but not least, whatever the method but particularly for the thin plate spline, better accuracy and stability is achieved when the smoothed altitude Z is considered rather than the station altitude z, as also found in Hutchinson (1998) for interpolating rainfall data.

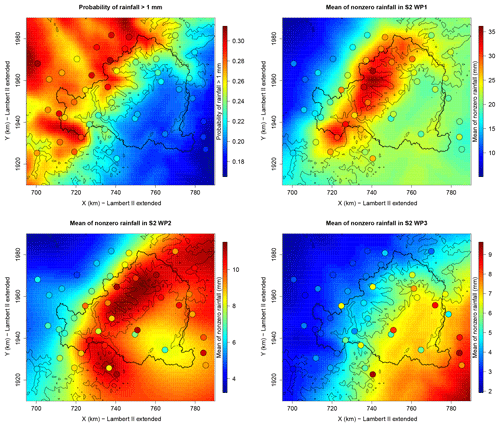
Figure 12 Map of the probability of daily rainfall exceeding 1 mm and of the mean of nonzero rainfall in the three WPs of the season-at-risk. The points are colored with respect to the empirical estimates.

We illustrate the results in Fig. 11 for the Antraigues station, adding to that the case of the worst fit of the thin plate spline, which is for the station of Mayres. Mayres lies at about 500 m a.s.l., as does Antraigues, but it is located at the end of a funnel-shaped valley surrounded by steep slopes (see Fig. 1). This creates favorable conditions to the orographic intensification of rainfall, with the consequence that Mayres receives more rainfall than expected at this altitude, as also confirmed by Fig. 2. For this reason, although the local fit of the Gamma model is reasonably good, the interpolated distributions underestimate the empirical values, even the small ones. This can be seen in Fig. 11 by comparing the black curves, which were obtained independently of the data of Mayres, to the red curves of the kriging case, which are equal to the local fits since kriging is an exact interpolation. Although return levels are underestimated with all models, kriging and the bivariate thin plate spline manage however better the fit the data of Mayres in the leave-one-out framework, in coherence with the NMRSE values of Fig. 10 at regional scale. For station Antraigues, underestimation is also found for all methods due to smoothing, but with a much smaller extent than for Mayres. For both stations, comparing the red and black curves shows that kriging and the trivariate thin plate spline are too dependent on the data used for fitting since large differences are obtained whether the station is included or not in the estimation, in coherence with the TVD and KLD values of Fig. 10 at regional scale. Finally, comparing the envelope widths in red and black in Fig. 11 confirms that interpolation increases stability of the estimates, as also revealed by the SPAN score of Fig. 11.

We conclude following the results of Figs. 10 and 11 that the best interpolation method (among those tested) is the bivariate thin plate spline with drift in smoothed altitude, which is slightly more accurate but much more spatially stable than the kriging method. The trivariate thin plate spline and the linear model should be avoided for our data due to their lack of flexibility.

4.3 Final regional model

Figure 12 illustrates the final regional models when both the Gamma parameters and the mapping models are estimated using all the available data. The map of the probability of daily rainfall exceeding 1 mm is obtained from Eq. (3) with r=1 mm. The maps of the mean nonzero rainfall in the WPs of the season-at-risk (S2) are obtained as the product ${\mathit{\lambda }}_{\mathrm{2},k}{\mathit{\kappa }}_{\mathrm{2},k}$, k=1, …, 3, with the notations of Table 1. The four maps of Fig. 12 reveal the double effect of the Massif Central ridge, which both creates a climatological border and enhances orographic precipitation. The map of rainfall probability conforms to the climatology of the region (as shown by the colored points), with a smaller probability of rainfall in the Rhône Valley and increased probability when approaching the relief due to orographic effect. Being more exposed to the western fluxes – which are the most common in the region –, the western side of the Massif Central undergoes more frequent rainfall events. Comparing the three maps of mean nonzero rainfall reveals very different ranges of values depending on the WP, with WP1 showing much larger values than the other WPs all across the region. Recall that the WPs were constructed based on the spatial correlation of rainfall, with WP1 showing a spatial correlation of rainfall twice as big as in WP2 and 3 times as big as in WP3. Remarkably, roughly the same factors are found when comparing the range of values of the means (respectively, 5–36, 3–11, and 2–10 mm). There is thus a strong link between the spatial correlation of rainfall and the mean amounts. However, the WPs do not only differ in the range of values of the mean amounts but, also, and maybe even more, in the way these amounts are usually distributed over the region. This emphasizes once again the usefulness of considering subsampling over WPs in order to distinguish a contrasted spatial pattern. The map of WP1 shows a strong intensification of rainfall along the Massif Central slope, while a clear decrease in the mean rainfall is found when passing the Massif Central ridge both towards the Massif Central plateau with means divided by 3 in 20 km and towards the Rhône Valley with means divided by 2 in 20 km. In WP2 the topography builds somehow a mask effect. The larger means are found along the Massif Central slope with a fast break when passing the Massif Central ridge. Daily means in the Massif Central plateau are half the values of the slope, while daily means in the Rhône Valley are just slightly lower than in the slope. Finally, the map of the mean nonzero rainfall in WP3 shows an inverse pattern to that of the probability of rainfall. The mean almost linearly decreases from the Rhône Valley to the Massif Central plateau, while the probability of rainfall almost linearly increases. The largest rainfall events in this WP are usually convective events of small extent occurring mainly in the Rhône Valley, the reason why the mean values are larger in this area, although the probability of rainfall is relatively low.

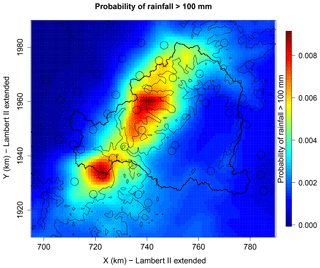
Last but not least, Fig. 13 shows the map of the probability of daily rainfall exceeding 100 mm. It reveals a clear concentration of higher probabilities of exceedance along the Massif Central ridge, with actually quite similar patterns as the averages of annual totals and annual maxima in Fig. 2, with however much more pronounced disparities. It is up to 10 times less likely to exceed 100 mm rainfall in the Rhône Valley than along the ridge, and up to 1000 times less likely in the Massif Central plateau. Actually, 100 mm is expected to be exceeded several times a year along the ridge, about every year on the slope, and on average every 100 to 1000 years in the Massif Central plateau.

Figure 13 Map of the probability of daily rainfall exceeding 100 mm. The points show the locations of the stations.

5 Conclusion and discussion

In this article we have presented an objective framework for selecting rainfall hazard mapping models in a region starting from rain gauge data. For this we have proposed an objective procedure involving split sampling cross-validation and using several evaluation scores allowing us to validate the accuracy of both the bulk and tail of the distribution and the stability of these estimates when calibration data change. We have applied this procedure to daily rainfall in the Ardèche catchment in southern France, a particularly challenging test case subject to strong inhomogeneity of rainfall at a very short distance. For illustration purposes, we chose to compare several classical marginal distributions, which are possibly mixed over seasons and weather patterns to account for the variety of climatological processes triggering precipitation, and several classical mapping methods. Our results show that for this region, the best marginal model (among those tested) is a mixture of Gamma distributions over seasons and weather patterns, and that the best mapping method (among those tested) is the bivariate thin plate spline. However, the goal of this paper was neither to be exhaustive nor to find the best hazard mapping model for the region. Obviously, other choices may be worth investigating.

A possible direction of improvement for the study region regards the choice of the marginal distribution. Although the Gamma mixture was selected according to the cross-validation scores, we noted a possible underestimation of return levels at far extrapolation since the model is unable to produce heavy tails in the sense of extreme value theory. It could be worth considering hybrid models based on combining distributions for low and heavy amounts (Vrac and Naveau, 2007; Furrer and Katz, 2008; Li et al., 2012), although robustness might be an issue. Another possibility includes considering less parsimonious versions of the extended generalized Pareto distribution (Naveau et al., 2016) to improve reliability in the upper tail. Further investigations may also be conducted regarding the choice of the spatial covariates to be used in the interpolation method. There might be more relevant covariates than the geographical coordinates used in this study, e.g., considering atmospheric and terrain characteristics (Carreau et al., 2013; Kyriakidis et al., 2001). Finding good gridded covariates (and good regression models) is a subject of research in itself, and it is particularly tricky in areas with complex topography (Prudhomme and Reed, 1999; Weisse and Bois, 2001; Drogue et al., 2002; Beguerïa et al., 2009; Rogelis and Werner, 2013). The geographical distance itself might also be improved, e.g., by better accounting for the terrain characteristics (Gottardi et al., 2012; Evin et al., 2016) or by considering statistical distance (Ahrens, 2006). Also, more robust estimates of the marginal parameters at station locations (i.e., of the $\widehat{\mathit{\theta }}s$) might be obtained by gathering observations of neighbor stations in order to increase the sample size, following the concept of regions-of-influence proposed by Burn (1990). Such idea has been quite widely used in the context of rainfall extremes (e.g., Carreau et al., 2013; Evin et al., 2016, for the studied region). However, we anticipate the gain to be much less pregnant when interest is in modeling any rainfall – as in this study –, and not only the extreme ones since parameter estimation is already based on many data (several thousands).

Despite the above reservations of prudence, some other results seem to us to be generalizable, in particular regarding the mapping step. Among these is the fact that the kriging method gives usually too patchy maps of rainfall hazard by sticking the observations, unless nugget effects are considered (which was not the case in this study). Finally, the linear model with spatial covariates usually fails to map rainfall hazard because it is highly unlikely to be ruled by simple-enough physics for the parameters to be well represented as linear functions of the covariates, in particular in such complex topography (Carreau et al., 2013).

Last for not least, we put this study in a framework of temporal stationarity and we addressed the question of the spatial nonstationarity of the margins. Yet several studies showed temporal trend in the rainfall distribution in the region, particularly since the 1980s and particularly along the Massif Central slope where daily rainfall is usually more intense (Blanchet et al., 2018; Tramblay et al., 2011, 2013; Vautard et al., 2015). Extending the proposed procedure to the case of nonstationary rainfall would be possible by considering the marginal parameters as parametric functions of time, e.g., linear models. This would increase the number of parameters but the split sample framework would still be valid. However, the scores would have to be adapted to account for changing distributions. One way of doing this would be to transform the rainfall at time t to some variate independent of t. For example, considering $R_t^{\prime }=\exp \mathit{\{}-\exp (-G_t\left(R_t\right)\left)\mathit{\right\}}$ would transform R_t with CDF G_t to a stationary Gumbel variate, to which the scores presented in this article could be applied for model evaluation and selection. A drawback however would be that the value of the scores would depend upon the chosen transformation. Also, the SPAN score might have to be thought over because return levels in changing climates are not meaningful for quantifying risk (Katz, 2013).