the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Model representation of the coupling between evapotranspiration and soil water content at different depths
Wade T. Crow
Jianzhi Dong
Grey S. Nearing
Soil water content (θ) influences the climate system by controlling the fraction of incoming solar and longwave energy that is converted into evapotranspiration (ET). Therefore, investigating the coupling strength between θ and ET is important for the study of land surface–atmosphere interactions. Physical models are commonly tasked with representing the coupling between θ and ET; however, few studies have evaluated the accuracy of model-based estimates of θ ∕ ET coupling (especially at multiple soil depths). To address this issue, we use in situ AmeriFlux observations to evaluate θ ∕ ET coupling strength estimates acquired from multiple land surface models (LSMs) and an ET retrieval algorithm – the Global Land Evaporation Amsterdam Model (GLEAM). For maximum robustness, coupling strength is represented using the sampled normalized mutual information (NMI) between θ estimates acquired at various vertical depths and surface evaporation flux expressed as a fraction of potential evapotranspiration (fPET, the ratio of ET to potential ET). Results indicate that LSMs and GLEAM are generally in agreement with AmeriFlux measurements in that surface soil water content (θs) contains slightly more NMI with fPET than vertically integrated soil water content (θv). Overall, LSMs and GLEAM adequately capture variations in NMI between fPET and θ estimates acquired at various vertical depths. However, GLEAM significantly overestimates the NMI between θ and ET, and the relative contribution of θs to total ET. This bias appears attributable to differences in GLEAM's ET estimation scheme relative to the other two LSMs considered here (i.e., the Noah model with multi-parameterization options and the Catchment Land Surface Model, CLSM). These results provide insight into improved LSM model structure and parameter optimization for land surface–atmosphere coupling analyses.
- Article
(4249 KB) - Full-text XML
-
Supplement
(354 KB) - BibTeX
- EndNote
Soil water content (θ) modulates water and energy feedbacks between the land surface and the lower atmosphere by determining the fraction of incoming solar energy that is converted into evapotranspiration (ET; Seneviratne et al., 2010, 2013). In water-limited regimes, θ exhibits a dominant control on ET, and therefore exerts significant terrestrial control on the Earth's water and energy cycles. Accurately representing θ ∕ ET coupling in land surface models (LSMs) is therefore expected to improve our ability to project the future frequency of extreme climates (Seneviratne et al., 2013).
A key question is how the constraint of θ on ET and sensible heat (H) varies as θ is vertically integrated over deeper vertical soil depths. Given the tendency for the timescales of θ dynamics to vary strongly with depth, the degree to which the ET is coupled with vertical variations in θ determines the temporal scale at which θ variations are propagated into the lower atmosphere. Therefore, in order to represent θ ∕ ET coupling, and thus land–atmosphere interactions in general, LSMs must accurately capture the relationship between vertically varying θ values and ET. Unfortunately, their ability to do so remains an open question.
Recently, land surface–atmosphere coupling strength has been investigated by sampling mutual information proxies (e.g., correlation coefficient or other coupling indices) between time series of θ and ET observations (or air temperature proxies for ET). Results suggest that, even when confined to very limited vertical support (e.g., within the top 5 cm of the soil column), surface θ estimates retain significant information for describing overall θ control on local climate (Ford and Quiring, 2014; Qiu et al., 2014; Dong and Crow, 2018, 2019). These findings are in contrast with the common perception that ET is constrained only by θ values within deeper soil layers (Hirschi et al., 2014). Hence, it is necessary to examine whether LSMs can realistically reflect observed variations of θ ∕ ET coupling strength within the vertical soil profile.
Previous studies examining the θ ∕ ET relationship have generally been based on Pearson product–moment correlation (Basara and Crawford, 2002; Ford et al., 2014), which captures only the strength of a linear relationship between two variables. However, the coupling between θ and ET is generally nonlinear. Therefore, non-parametric mutual information measures are generally more appropriate. Nearing et al. (2018) used information theory metrics (transfer entropy, in particular) to measure the strength of direct couplings between different surface variables, including soil water content, and surface energy fluxes at short timescales in several LSMs. They found that the LSMs are generally biased as compared with the strengths of couplings in observation data, and that these biases differ across different study sites. However, they did not look specifically at the effect of vertical water content profiles or of subsurface soil water content on partitioning surface energy fluxes.
Here we apply the information theory-based methodology of Qiu et al. (2016) to examine the relationship between the vertical support of θ estimates and their mutual information (MI) with respect to ET. Our approach is based on analyzing the MI content between ET and θ time series acquired from both LSMs, and ET retrieval algorithm – the Global Land Evaporation Amsterdam Model (GLEAM) – and AmeriFlux in situ observations. MI values are then normalized by entropy in the corresponding ET time series to remove the effect of inter-site variations to generate estimates of normalized mutual information (NMI) between θ and ET. Both surface (roughly 0–10 cm) soil water content (θs) and vertically integrated (0–40 cm) soil water content (θv) are considered to capture the impact of depth on NMI results. AmeriFlux-based NMI results are then compared with analogous NMI results obtained from LSM-based and GLEAM-based θ and ET time series.
The AmeriFlux network provides temporally continuous measurements of θ, surface energy fluxes and related environmental variables for sites located in a variety of North American ecosystem types, e.g., forests, grasslands, croplands, shrublands and savannas (Boden et al., 2013). To minimize sampling errors, AmeriFlux sites lacking a complete 3-year summer months (June, July and August) daily time series between the years of 2003 and 2015 (i.e., daily observations in total) of θs, θv and latent heat flux (LE) are excluded here, resulting in the 34 remaining eligible AmeriFlux sites listed in Table 1. These sites cover a variety of climate zones within the contiguous United States (CONUS). Table 1 gives background information on these 34 sites including local land-cover information. Hydro-climatic conditions in each site are characterized using the aridity index (AI), calculated using CRU (Climate Research Unit, v4.02) monthly precipitation and potential evaporation (PET) datasets.
As described above, θ ∕ ET coupling assessments made using AmeriFlux observations are compared with those using state-of-the-art LSMs including the Noah model with multi-parameterization options (NOAHMP) and Catchment Land Surface Model (CLSM). In addition, θ and ET retrievals provided by the Global Land Evaporation Amsterdam Model (GLEAM) are also considered. See below for details on all three approaches. To avoid any spurious correlations between θ and ET due to seasonality, all NMI analyses are performed on θ and ET time series anomalies acquired during the period 2003–2015. The θ and ET anomalies are calculated by removing the seasonal cycle – defined as 31 d window averages centered on each day of the year sampled across all years of the 2003–2015 historical data record – from the raw θ and ET time series data. The analysis is limited to the CONUS during summer months (June, July and August) when θ ∕ ET coupling is expected to be maximized.
Table 1Attributes of selected AmeriFlux sites.
a Was 5 cm prior to 13 April 2005. b Was 25 cm prior to 13 April 2005. c Was 5 cm prior to 1 January 2006. d Was 0–30 cm prior to 2007. e Unavailable prior to 2007. NA = not available.
2.1 Ground-based AmeriFlux measurements
The Level 2 (L2) AmeriFlux LE and H flux observations are based on high-frequency (typically > 10 Hz) eddy covariance measurements processed into half-hourly averages by individual AmeriFlux investigators. LE and θ observations at a half-hour time step and without gap-filling procedures are collected from the AmeriFlux Site and Data Exploration System (see http://ameriflux.ornl.gov/, last access: November 2018). The LE and θ observations are further aggregated into daily (00:00 to 24:00 UTC) values, and daily LE is converted into daily ET using the latent heat of vaporization. Daily ET values based on less than 30 % half-hourly coverage (i.e., < 15 half-hourly observations per day) are considered not representative at a daily timescale and are therefore excluded.
Soil water content measurements are generally available at two discrete depths that vary between the AmeriFlux sites (Table 1). Here, the top (i.e., closest to the surface) soil water content observation is always used to represent surface soil water content (θs). Since the depth of this top-layer measurement varies between 0 and 15 cm (see Table 1), we consider the surface-layer measurement θs to be roughly representative of 0–10 cm (vertically integrated) θ. For more details on AmeriFlux sites utilized here, see Raz-Yaseef et al. (2015).
Given variations in the depth of the lower AmeriFlux θ observations (see Table 1), we applied a variety of approaches for estimating vertically integrated soil water content (θv). Our first approach, hereinafter referred to as Case I, is based on the application of an exponential filter (Wagner et al., 1999; Albergel et al., 2008) to extrapolate θs to a consistent 40 cm bottom-layer depth. Therefore, only θs is used to derive θv and the bottom-layer (or second-layer) AmeriFlux θ measurement is neglected in this case. The application of the exponential filter requires a single timescale parameter T. Since θ measurements from the United States Department of Agriculture's Soil Climate Analysis Network (SCAN) are taken at fixed soil depth, we utilized this dataset to determine the most appropriate parameter T at AmeriFlux sites. Following Qiu et al. (2014), first, we estimated the optimal parameter T (Topt) for the extrapolation of θ measurements from 10 to 40 cm depth and established a global relationship between Topt and site-based NDVI (MOD13Q1 v006, 250 m, 16 d; (NDVI +0.6271)) +2.766). Then, this global relationship (goodness of fit R2: 0.85) is applied to AmeriFlux sites to extrapolate 0–10 cm θs time series into 0–40 cm θv.
Previous research has suggested that such a filtering approach does not significantly squander ET information present in actual measurements of θv (Qiu et al., 2014, 2016). Nevertheless, since the quality of θv estimates is important in our analysis, we also calculated two additional cases where 0–40 cm θv is estimated using (1) the bottom-layer soil water content measurement acquired at each AmeriFlux site (hereinafter, Case II) and (2) linear interpolation of θs, and the bottom-layer AmeriFlux soil water content measurement (hereinafter, Case III). The sensitivity of key results to these various cases is discussed below.
2.2 LSM- and GLEAM-based simulations
Simulations are acquired from the NOAHMP (Niu et al., 2011) and CLSM (Koster et al., 2000) LSMs embedded within the NASA Land Information System (LIS, Kumar et al., 2006) and the GLEAM ET retrieval algorithm (Miralles et al., 2011). Both NOAHMP and CLSM are set up to simulate 0.125∘ θ profiles at a 15 min time step using North America Land Data Assimilation System, Phase 2 (NLDAS-2) forcing data. A 10-year model spin-up period (1992 to 2002) is applied for NOAHMP and CLSM.
NOAHMP numerically solves the one-dimensional Richards equation within four soil layers of thicknesses of 0–10, 11–30, 31–60 and 61–100 cm. Major parameterization options relevant to θ simulation include options for canopy stomatal resistance parameterization and schemes controlling the effect of θ on the vegetation stress factor β. Here we employed the Ball–Berry-type stomatal resistance scheme and Noah-type soil water content factor controlling the β factor. The specific expressions are as follows:
where θwilt and θref are, respectively, soil water content at the wilting point (m3 m−3) and reference soil water content (m3 m−3), which is set as field capacity during parameterization. θi and Δzi are soil water content (m3 m−3) and soil depth (cm) at ith layer, Nroot and zroot are total number of soil layers with roots and total depth (cm) of root zone, respectively.
Following the Ball–Berry stomatal resistance scheme, the θ-controlled β factor and other multiplicative factors including temperature and foliage nitrogen simultaneously determine the maximum carboxylation rate Vmax as follows:
where Vmax25 is maximum carboxylation rate at 25 ∘C (µmol CO2 m−2 s−1), αvmax is a parameter sensitive to vegetation canopy surface temperature Tv, f(N) is a factor representing foliage nitrogen and f(Tv) is a function that mimics thermal breakdown of metabolic processes. Based on Vmax, photosynthesis rates per unit leaf area index (LAI) including carboxylase-limited (Rubisco limited, denoted by AC) type and export-limited (for C3 plants, denoted by AS) type are calculated, respectively. The minimum of AC, AS and the light-limited photosynthesis rate determines stomatal resistance rs, and consequently affects ET over vegetated areas. For the complete NOAHMP configuration, please see Table S1 in the Supplement.
CLSM simulates the 0–2 and 0–100 cm soil water content and evaporative stress as a function of simulated θ and environmental variables. ET is then estimated based on the estimated evaporative stress and land–atmosphere humidity gradients. Energy and water flux estimates are iterated with soil state estimates (e.g., θ and soil temperature) to ensure closure of surface energy and water balances. For a detailed explanation of CLSM physics, please refer to Koster et al. (2000).
GLEAM is a set of algorithms dedicated to the estimation of terrestrial ET and root-zone θ from satellite data. In this study, the latest version of this model (v3.2a) is employed. In GLEAM, the configuration of soil layers varies as a function of the land-cover type. Soil stratification is based on three soil layers for tall vegetation (0–10, 10–100 and 100–250 cm), two layers for low vegetation (0–10 and 10–100 cm) and only one layer for bare soil (0–10 cm; Martens et al., 2017).
The cover-dependent PET (mm d−1) of GLEAM is calculated using the Priestley and Taylor (1972) equation based on observed air temperature and net radiation. Following this, estimates of PET are converted into actual transpiration or bare soil evaporation (depending on the land-cover type, ET (mm d−1)), using a cover-dependent, multiplicative stress factor S (–), which is calculated as a function of microwave vegetation optical depth (VOD) and root-zone θ (Miralles et al., 2011). The related expressions are as follows:
where Ei is rainfall interception (mm), S essentially represents the fPET (see Sect. 2.3) estimated by GLEAM, θc (m3 m−3) is the critical soil water content and θω (m3 m−3) is the soil water content of the wettest layer, assuming that plants withdraw water from the layer that is most accessible. Based on Eq. (4), GLEAM S (or fPET) tends to become more sensitive to θ in areas of low VOD seasonality (i.e., low differences between VOD and VODmax). As for bare soil conditions, S is linearly related to surface soil water content (θ1):
To resolve variations in the vertical discretization of θ applied by each model, we linearly interpolated NOAHMP, CLSM and GLEAM outputs into daily 0–10 and 0–40 cm soil water content values using depth-weighted averaging.
2.3 Variable indicating soil water content and surface flux coupling
Soil water content–ET coupling can be diagnosed using a variety of different variables derived from ET, e.g., the fraction of PET (fPET, the ratio of ET and PET) or the evaporative fraction (EF, the ratio of LE and the sum of LE and sensible heat). Since ET is strongly tied to net radiation (Rn; Koster et al., 2009), both fPET and EF are advantageous in that they normalize ET by removing the impact of non-soil water content influences on ET (e.g., net radiation, wind speed and soil heat flux (G)). However, since sensible heat flux is not provided in the GLEAM dataset, we are restricted here to using fPET.
It should be noted that the applied meteorological forcing data for NOAHMP and CLSM are somewhat different from those used for GLEAM. Therefore, to minimize the impact of this difference, NOAHMP and CLSM fPET are computed from North American Regional Reanalysis (NARR) using the modified Penman scheme of Mahrt and Ek (1984), while GLEAM fPET is calculated using its own internal PET estimates. To examine the impact of the PET source on the results, AmeriFlux fPET calculations are duplicated using both GLEAM- and NARR-based PET values.
2.4 Information measures
Mutual information (MI; Cover and Thomas, 1991) is a nonparametric measure of correlation between two random variables. MI and the related Shannon-type entropy (SE; Shannon, 1948) are calculated as follows. Entropy about a random variable ζ is a measure of uncertainty according to its distribution pζ and is estimated as the expected amount of information from pζ sample:
Likewise, MI between ζ and another variable ψ can be thought of as the expected amount of information about variable ζ contained in a realization of ψ and is measured by the expected Kullback–Leibler (KL) divergence (Kullback and Leibler, 1951) between the conditional and marginal distributions over ζ:
In this context, the generic random variables ζ and ψ represent fPET and θ (soil water content), respectively. The observation space of the target random variable fPET is discretized using a fixed bin width. As bin width decreases, entropy increases but mutual information asymptotes to a constant value. On the other hand, increased bin width requires a greater sample size, which cannot always be satisfied. The trick is choosing a bin width where the NMI values stabilize with sample size. After a careful sensitivity analysis, we choose a fixed bin width of 0.25 [–] for fPET and make sure that each AmeriFlux site had enough samples to accurately estimate the NMI, and change of this constant bin width from 0.1 to 0.5 [–] will not significantly alter our conclusions. Following Nearing et al. (2016), a bin width of 0.01 m3 m−3 (1 % volumetric water content) for θ is applied. Integrations required for MI calculation in Eq. (7) are then approximated as summations over the empirical probability distribution function bins (Paninski, 2003).
By definition, the MI between two variables represents the amount of entropy (uncertainty) in either of the two variables that can be reduced by knowing the other. Therefore, the MI normalized by the entropy of the AmeriFlux-based fPET measurements represents the fraction of uncertainty in fPET that is resolvable given knowledge of the soil water content state (Nearing et al., 2013). Unlike Pearson's correlation coefficient, MI is insensitive to the impact of nonlinear variable transformations. Therefore, it is well suited to describe the strength of the (potentially non-linear) relationship between θ and fPET.
Here, we applied this approach to calculate the MI content between soil water content representing different vertical depths (as reflected by θs and θv) and fPET at each AmeriFlux site. All estimated site-specific MI are normalized by the entropy of the corresponding AmeriFlux-based fPET measurements to remove the effect of inter-site entropy variations on the magnitude of NMI differences. The resulting normalized MI calculations between both θs and θv and fPET are denoted as NMI(θs, fPET) and NMI(θv, fPET), respectively.
The underestimation of observed θ ∕ ET coupling via the impact of mutually independent θ and ET errors in AmeriFlux observations (Crow et al., 2015) is minimized by focusing on the ratio between NMI(θS, fPET) and NMI (θv, fPET). Therefore, relative comparisons between NMI(θs, fPET) and NMI(θv, fPET) are based on examining the size of their mutual ratio NMI(θS, fPET) ∕ NMI (θv, fPET). To quantify the standard error of NMI differences between various soil water content products, we applied a nonparametric, 500-member bootstrapping approach and calculated the pooled average of sampling errors across all sites assuming spatially independent sampling error.
Finally, we also examined the impact of potential nonlinearity in the θ ∕ ET relationship by comparing non-parametric NMI results with comparable inferences based on a conventional Pearson's correlation calculation. The correlation-based coupling strength between θs and fPET is denoted as R(θs, fPET) and between θv and fPET as R(θv, fPET).
3.1 Comparison of NMI(θs, fPET) and NMI(θv, fPET)
Figure 1 contains boxplots of modeled and observed NMI(θs, fPET) and NMI(θv, fPET), i.e., the relative magnitude of fPET information contained in surface soil water content and vertically integrated (0–40 cm) soil water content estimated from Case I, sampled across all the AmeriFlux locations listed in Table 1. According to the AmeriFlux ground measurements, median values of NMI(θs, fPET) and NMI(θv, fPET; across all sites) are near 0.3 [–]. This suggests that approximately 30 % of the uncertainty (i.e., entropy at this particular bin width of 0.25 [–]) in fPET can be eliminated given knowledge of either surface or vertically integrated soil water content state. This is consistent with earlier results in Qiu et al. (2016) who used similar metrics to evaluate θ ∕ EF (evaporative fraction) coupling strength. The sampled medians of NMI(θs, fPET) and NMI(θv, fPET) estimated by the NOAHMP and CLSM models are similar to these (observation-based) AmeriFlux values. With the single exception that the CLSM predicts much larger site-to-site variation in NMI(θs, fPET).
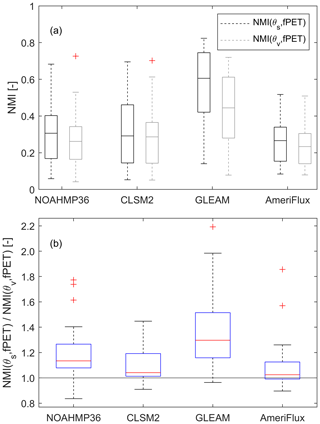
Figure 1The θ ∕ ET coupling strengths for summertime anomaly time series acquired from various LSMs, GLEAM and AmeriFlux measurements: (a) NMI(θs, fPET) and NMI(θv, fPET) individually and (b) NMI(θs, fPET) normalized by NMI(θv, fPET).
In contrast, NMI(θs, fPET) and NMI(θv, fPET) values sampled from GLEAM θ and fPET estimates show positive biases (with median θ of about 0.5 and 0.4 [–] for NMI(θs, fPET) and NMI(θv, fPET), respectively) with respect to all other estimates.
Using the 34 AmeriFlux site-collocated samples pixels for a paired t test, both LSMs and GLEAM overall exhibit significantly (at the 0.05 level) higher NMI(θs, fPET) compared to NMI(θv, fPET), implying the surface soil water content observations contain more fPET information than vertically integrated soil water content observations. However, the observed difference between NMI(θs, fPET) and NMI(θv, fPET) is less discernible in AmeriFlux measurements (Fig. 1a).
Here, AmeriFlux observations are used as a baseline for LSM and GLEAM evaluation. However, it should be stressed that random observation errors in θ and fPET will introduce a low bias into AmeriFlux-based estimates of both NMI(θs, fPET) and NMI(θv, fPET; Crow et al., 2015) and thus their difference as well. To address this concern, Fig. 1b plots the ratio of NMI(θs, fPET) and NMI(θv, fPET), which effectively normalizes (and therefore minimizes) the impact of random observation errors. As discussed above, these ratio results illustrate the general tendency for NMI(θs, fPET) to exceed NMI(θv, fPET). They also highlight the tendency for GLEAM to overvalue θs (relative to θv) when estimating fPET. A second approach for reducing the random error of θ and fPET measurement errors is the correction based on triple collocation (TC) applied in Crow et al. (2015). However, this approach is currently restricted to linear correlations and cannot be applied to estimate NMI. Future work will examine extending the information-based TC approach of Nearing et al. (2017) to the examination of NMI.
3.2 Sensitivity of AmeriFlux-based NMI(θs, fPET) ∕ NMI(θV, fPET)
As mentioned in Sect. 2.1, an important concern is the impact of interpolation errors used to estimate 0–40 cm θv from AmeriFlux θs observations acquired at non-uniform depths. To ensure that different methods for calculating AmeriFlux θv values do not affect the main conclusion of this study, we configured three cases for θv calculation, and compared their NMI(θS, fPET) ∕ NMI(θv, fPET) results in Fig. 2. Case I reflects the baseline use of the exponential filter described in Sect. 2.1. However, slight changes to AmeriFlux results are noted if alternative approaches are used. Specifically, AmeriFlux-based NMI(θv, fPET) increases and closes the gap with NMI(θs, fPET) if the bottom-layer soil water content measurements are instead directly used as θv (Case II) or if 0–40 cm θv is based on the linear interpolation of the two AmeriFlux θ observations (Case III); the impact of this modest sensitivity on key results is discussed below.
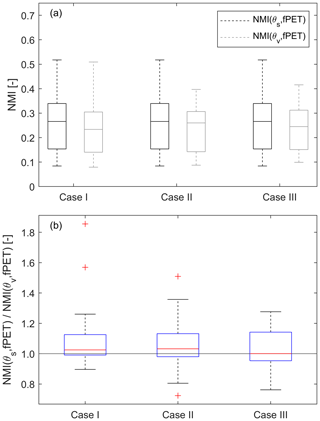
Figure 2The θ ∕ ET coupling strengths for summertime anomaly time series from AmeriFlux measurements using three different θv calculation methods: (a) NMI(θs, fPET) and NMI(θv, fPET) individually and (b) NMI(θs, fPET) divided by NMI(θv, fPET) for multiple θv cases. Case I is based on the application of an exponential filter to extrapolate 0–10 cm θs to a consistent 0–40 cm bottom-layer depth, while Cases II and III refer to the direct use of only the bottom-layer measurement and a linear interpolation of both the top and bottom layer, respectively, to calculate θv (see Sect. 2.1 for details on each case).
In addition, switching from GLEAM- to NARR-based PET when calculating fPET for AmeriFlux-based NMI(θs, fPET) and NMI(θv, fPET) does not qualitatively change results and produces only a very slight (∼6 %) increase in the median NMI(θs, fPET) ∕ NMI(θv, fPET) ratio.
3.3 Spatial distribution of NMI(θs, fPET) and NMI(θv, fPET)
Figure 3 plots the spatial distribution of NMI(θs, fPET) and NMI(θv, fPET) results for each of the individual 34 AmeriFlux sites listed in Table 1. The climatic regime is represented by AI (aridity index) values plotted as the background color in Fig. 3. It can be seen in Fig. 3 that NMI(θs, fPET) estimates from LSMs and GLEAM are spatially related to hydro-climatic conditions, as NOAHMP and CLSM predict that θs is moderately coupled with fPET (i.e., NMI(θS, fPET) of 0.3–0.5 [–]) in the arid southwestern USA (AI < 0.2) and only loosely coupled with fPET in the relatively humid eastern USA. A similar decreasing trend of NMI(θs, fPET) from the southwestern to eastern USA is also captured by GLEAM. However, as noted above, GLEAM generally overestimates NMI(θs, fPET) and NMI(θv, fPET) compared to NOAHMP, CLSM and AmeriFlux. In contrast, a relatively weaker spatial pattern emerges in AmeriFlux-based NMI(θs, fPET) results. In addition, spatial patterns for NMI(θs, fPET) are less defined than for NMI(θv, fPET) in all four datasets.
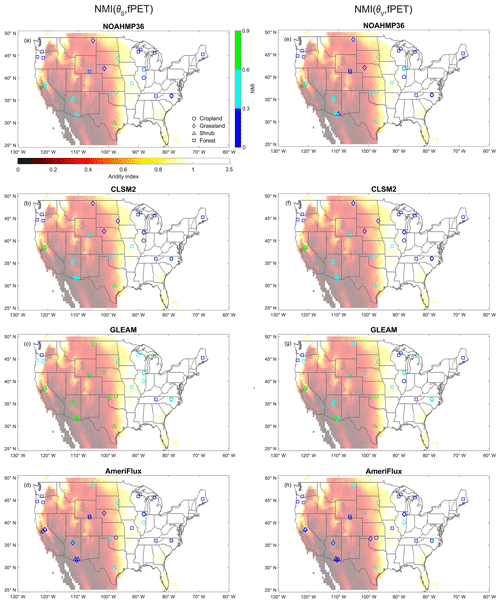
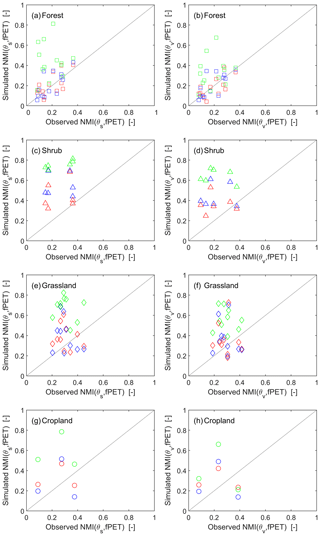
Figure 3NMI(θs, fPET) (left panels) and NMI(θv, fPET) (right panels) estimates at AmeriFlux sites for (a, e) NOAHMP, (b, f) CLSM, (c, g) GLEAM and (d, h) AmeriFlux. Marker color reflects NMI magnitudes and symbol type reflects local land-cover type at each site. Background color shading reflects aridity index (AI) values.
Scatterplots in Fig. 4 summarize the spatial relationship between LSM- and GLEAM-based NMI(θs, fPET) and NMI(θv, fPET) results versus AmeriFlux observations across different land use types. While observed levels of correlation in Fig. 4 are relatively modest, there is a significant level (p < 0.05) of spatial correspondence between modeled and observed NMI results only over forest sites, motivating the need to better understand processes responsible for spatial variations in NMI results. In addition, stratifying NMI(θs, fPET) ∕ NMI(θv, fPET) ratio results according to vegetation type (Fig. A1 in the Appendix) confirms that NMI(θs, fPET) slightly exceeds NMI(θv, fPET) across all vegetation types (and thus all rooting depths characterizing each vegetation type). This suggests that our analysis is not severely affected by variations in the depth of θ measurements. For further discussion on the impact of land cover on NMI results, please see Appendix A.
3.4 Sensitivity of NMI(θs, fPET) ∕ NMI(θv, fPET) ratio to climatic conditions
Figure 5 further summarizes the NMI(θs, fPET) ∕ NMI(θV, fPET) ratio as a function of AI for all four products (NOAHMP, CLSM, GLEAM and AmeriFlux). Error bars represent the standard deviation of sampling errors calculated from a 500-member bootstrapping analysis. With increasing AI, there is a significant decreasing trend in both NMI(θS, fPET) and NMI(θv, fPET) for all three simulations, with a goodness of fit above 0.5 (figure not shown). For all cases, the NMI(θs, fPET) ∕ NMI(θv, fPET) ratios are consistently greater than unity under all climatic conditions. However, the estimated NMI(θs, fPET) ∕ NMI(θv, fPET) ratios from all three simulations (NOAHMP, CLSM and GLEAM) exhibit quite different trends with respect to AI. The NMI(θs, fPET) ∕ NMI(θV, fPET) ratio for CLSM decreases with increasing AI, with a moderate goodness-of-fit value of 0.28, while GLEAM estimates of NMI(θs, fPET) ∕ NMI(θv, fPET) shows an opposite increasing trend with increasing AI. Conversely, there is relatively lower sensitivity of the NMI(θs, fPET) ∕ NMI(θv, fPET) ratio to AI captured in the AmeriFlux measurements.
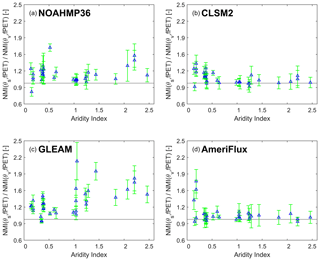
Figure 5For (a) NOAHMP, (b) CLSM, (c) GLEAM and (d) AmeriFlux estimates, the ratio of NMI(θs, fPET) and NMI(θv, fPET) as a function of AI across all AmeriFlux sites.
Connecting these findings to the spatial distribution of NMI(θs, fPET) and NMI(θv, fPET; Fig. 3) confirms that the relative magnitudes of NMI(θs, fPET) and NMI(θv, fPET) for both LSMs and GLEAM are spatially related to hydro-climatic regimes. In contrast, this link is weaker in the AmeriFlux measurements which, except for a small fraction of very low AI sites, do not appear to vary as a function of AI. These conclusions are not qualitatively impacted by looking at NMI(θs, fPET) and NMI(θv, fPET) differences, as opposed to their ratio as in Fig. 5, or by looking at R(θs, fPET) and R(θv, fPET) instead of NMI.
Since transpiration dominates the global ET (Jasechko et al., 2013), deep-layer soil water content (θv) is generally considered to contain more ET information than that of surface soil water content (θs), given that plant transpiration is balanced by root water uptake from deeper soils (Seneviratne et al., 2010). However, this assumption is rarely tested using models and/or observations. Here, we apply normalized mutual information (NMI) to examine how the vertical support of a soil water content product affects its relationship with concurrent surface ET.
Specifically, using AmeriFlux ground observations, we examine whether (NMI-based) estimates of LSMs and GLEAM θs versus ET and θv versus ET coupling strength accurately reflect observations acquired at a range of AmeriFlux sites. In general, compared to the baseline case of exponential filter extrapolated 40 cm bottom-layer θv, LSMs and GLEAM agree with AmeriFlux observations in that the overall fPET information contained in θs is slightly higher than that of θv (Fig. 1). However, the sensitivity analysis showed this difference between NMI(θs, fPET) and NMI(θv, fPET) diminishes when using different methods for calculating θv using AmeriFlux observations (Fig. 2). As a result, this result should be viewed with caution.
While NOAHMP- and CLSM-derived NMI(θs, fPET) and NMI(θV, fPET) results are generally consistent with the AmeriFlux observations, GLEAM overestimates NMI(θs, fPET), NMI(θV, fPET) and the ratio NMI(θs, fPET) ∕ NMI(θV, fPET) relative to observations. Although both LSMs and GLEAM are based on the same classical two-section (soil water content-limited and energy-limited) ET regimes framework (Sect. 2.2), they differ in two fundamental aspects. First, the evaporative stress factor S is represented as a more direct and strong function of soil water content in GLEAM – see Eqs. (4) and (5) – which leads to the overestimation of the θ ∕ ET coupling strength. This is consistent with our results that GLEAM generally overestimates NMI(θs, fPET) and NMI(θv, fPET) consistently across all land covers, compared to AmeriFlux-based estimates. On the other hand, NOAHMP and CLSM approximate ET in the manner of biophysical models, and expresses biophysical control on ET through the stomatal resistance rs, which is a function of multiple limiting factors including θ. Therefore, the more complex ET scheme employed by NOAHMP and CLSM would seem to mitigate the overestimation of NMI(θS, fPET) and NMI(θv, fPET), as other relevant factors besides θ (such as temperature, foliage nitrogen) are also considered in determining maximum carboxylation rate Vmax and stomatal resistance rs, and consequently more realistic actual ET.
Second, the stress factor β in both LSMs considers the cumulative effects of θconditions along different layers (Eq. 1), while the corresponding factor S in GLEAM only uses the wettest soil layer condition, which is top layer at most sites. This likely explains the overestimation of the NMI(θs, fPET) ∕ NMI(θv, fPET) ratio by GLEAM.
Nevertheless, we would like to stress that all approaches considered in our paper contain (at their core) a parameterized relationship between θ and ET. While the implications of mis-parameterizing this relationship are arguably more severe for a land surface model, we argue that the issue remains relevant for any approach (such as GLEAM) that utilizes a water balance (and/or data assimilation system) approach to estimate θ and, in turn, uses θ to constrain ET. Regardless of the complexity that a given approach employs, failing to accurately describe the relationship between ET and (large number of potential) environmental constraints should eventually degrade the robustness of the model, whether it is employed as a retrospective, diagnostic or predictive manner. To examine this issue directly, Fig. 6 plots the relationship between GLEAMS bias in NMI(θs, fPET) ∕ NMI(θv, fPET) ratio versus the RMSE of daily GLEAM ET simulations for a range of AmeriFlux sites. There is a positive correlation between the two quantities, which suggests that GLEAM overestimation of θ ∕ ET coupling during the summer may undermine the accuracy of its daily ET retrievals. It should be noted that GLEAM simultaneously overestimates both NMI(θs, fPET) and NMI(θv, fPET); however, the impact of this mis-parameterization impact on GLEAM ET accuracy is most obvious when plotted against the ratio NMI(θs, fPET) ∕ NMI(θv, fPET).
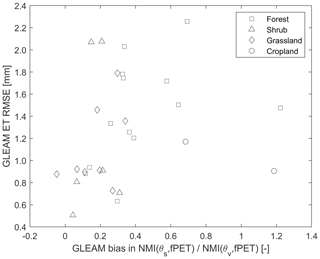
Figure 6Daily ET error in GLEAM as a function of GLEAM bias in NMI(θS, fPET) ∕ NMI(θv, fPET) ratio across 34 AmeriFlux sites.
Although the median values of NMI(θs, fPET) and NMI(θV, fPET) predicted by NOAHMP and CLSM are generally in line with AmeriFlux observations, they are more spatially related to hydro-climatic conditions (as summarized by AI) than their counter parts acquired from AmeriFlux measurements. Seen from the plot of NMI(θs, fPET) ∕ NMI(θv, fPET) ratio as a function of AI (Fig. 5), the modeled and observed median of NMI(θs, fPET) ∕ NMI(θV, fPET) ratio decreases with increasing AI, and the decreasing trend is particularly clear when AI is lower than 1.0 [–]. In contrast, there is relatively lower sensitivity to aridity exhibited in the AmeriFlux measurements.
These results provide several key insights into future land–atmosphere coupling analysis and LSMs, as well as ET algorithm development. First, all the datasets – both model-based and ground-observed – indicate that θs contains at least as much ET information as θv. Hence, remote-sensing land surface soil water content datasets are suitable, and should be considered, for analyzing the general interaction between land and atmosphere, e.g., soil water content–air temperature coupling (Dong and Crow, 2019) and the interplay of soil water content and precipitation (Yin et al., 2014). Additionally, future generations of GLEAM may consider more sophisticated evaporation stress functions, which may improve its accuracy in representing the soil's control on local ET. This may, in turn, improve the accuracy of the GLEAM ET product. Finally, our results demonstrate that modeled θ ∕ ET is more sensitive to hydro-climates than the observed relationship. Modifying the model structures to reduce such sensitivity might be necessary for accurately representing the interaction of land surface and atmosphere across different climate zones. This may lead to more realistic projections of future drought-induced heat waves, when coupled with general circulation models.
We performed an additional sensitivity analysis to explicitly demonstrate the effect of different vegetation land-cover types and consequently different rooting depths (or θv measurement depths) on the NMI(θS, fPET) ∕ NMI(θv, fPET) ratio, and plotted these results in Fig. A1. The figure confirms that, consistent with AmeriFlux, both LSMs and GLEAM predict that NMI(θs, fPET) is slightly higher than NMI(θv, fPET) over most vegetation types, and GLEAM overestimates NMI(θs, fPET) ∕ NMI(θv, fPET) for most vegetation types.
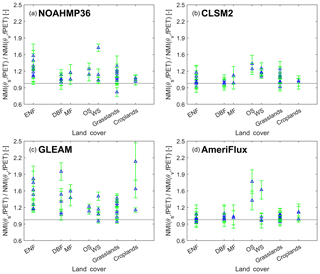
Figure A1For (a) NOAHMP, (b) CLSM, (c) GLEAM and (d) AmeriFlux estimates, the ratio of NMI(θs, fPET) and NMI(θv, fPET) as a function of vegetation types across all AmeriFlux sites. “ENF”, “DBF”, “MF”, “OS” and “WS” represent evergreen needleleaf forests, deciduous broadleaf forests, mixed forests, open shrubland, and woody savannas, respectively.
Ground-based soil water content and surface flux data are available from https://ameriflux.lbl.gov/login/?redirect_to=/data/download-data/ (last access: February 2020) (Raz-Yaseef et al., 2015). GLEAM dataset is available from https://www.gleam.eu/ (last access: February 2020). LSMs simulations of NOAHMP and CLSM used in this study are available by contacting the authors.
The supplement related to this article is available online at: https://doi.org/10.5194/hess-24-581-2020-supplement.
JQ and WTC conceptualized the study. JD helped preparing the LSMs simulation. GSN assisted in the mutual information analysis. JQ carried out the analysis and wrote the first draft manuscript and WTC refined the work. All authors contributed to the analysis, interpretation and writing.
The authors declare that they have no conflict of interest.
This research has been supported by the National Natural Science Foundation of China (grant nos. 41971031, 41501450 and 51779278), the Natural Science Foundation of Guangdong Province (grant no. 2016A030310154).
This paper was edited by Dominic Mazvimavi and reviewed by two anonymous referees.
Albergel, C., Rüdiger, C., Pellarin, T., Calvet, J.-C., Fritz, N., Froissard, F., Suquia, D., Petitpa, A., Piguet, B., and Martin, E.: From near-surface to root-zone soil moisture using an exponential filter: an assessment of the method based on in-situ observations and model simulations, Hydrol. Earth Syst. Sci., 12, 1323–1337, https://doi.org/10.5194/hess-12-1323-2008, 2008.
Basara, J. B. and Crawford, K. C.: Linear relationships between root-zone soil moisture and atmospheric processes in the planetary boundary layer, J. Geophys. Res., 107, 4274, https://doi.org/10.1029/2001JD000633, 2002.
Boden, T. A., Krassovski, M., and Yang, B.: The AmeriFlux data activity and data system: an evolving collection of data management techniques, tools, products and services, Geosci. Instrum. Method. Data Syst., 2, 165–176, https://doi.org/10.5194/gi-2-165-2013, 2013.
Cover, T. M. and Thomas, J. A.: Elements of information theory, John Wiley & Sons, New York, 1991.
Crow, W. T., Lei, F., Hain, C., Anderson, M. C., Scott, R. L., Billesbach, D., and Arkebauer, T.: Robust estimates of soil moisture and latent heat flux coupling strength obtained from triple collocation, Geophys. Res. Lett., 42, 8415–8423, https://doi.org/10.1002/2015GL065929, 2015.
Dong, J. and Crow, W. T.: Use of satellite soil moisture to diagnose climate model representations of European soil moisture – air temperature coupling strength, Geophys. Res. Lett., 45, 12884–12891, https://doi.org/10.1029/2018GL080547, 2018.
Dong, J. and Crow, W. T.: L-band remote-sensing increases sampled levels of global soil moisture – air temperature coupling strength, Remote Sens. Environ., 22, 51–58, https://doi.org/10.1016/j.rse.2018.10.024, 2019.
Ford, T. W. and Quiring, S. M.: In situ soil moisture coupled with extreme temperatures: A study based on the Oklahoma Mesonet, Geophys. Res. Lett., 41, 4727–4734, https://doi.org/10.1002/2014gl060949, 2014.
Ford, T. W., Wulff, C. O., and Quiring, S. M.: Assessment of observed and model-derived soil moisture-evaporative fraction relationships over the United States Southern Great Plains, J. Geophys. Res., 119, 6279–6291, https://doi.org/10.1002/2014JD021490, 2014.
Hirschi, M., Mueller, B., Dorigo, W., and Seneviratne, S. I.: Using remotely sensed soil moisture for land–atmosphere coupling diagnostics: The role of surface vs. root-zone soil moisture variability, Remote Sens. Environ., 154, 246–252, https://doi.org/10.1016/j.rse.2014.08.030, 2014.
Jasechko, S., Sharp, Z. D., and Gibson, J. J.: Terrestrial water fluxes dominated by transpiration, Nature, 496, 347–350, https://doi.org/10.1038/nature11983, 2013.
Koster, R. D., Suarez, M. J., Ducharne, A., Stieglitz, M., and Kumar, P.: A catchment-based approach to modeling land surface processes in a general circulation model: 1. Model structure, J. Geophys. Res., 105, 24809–24822, https://doi.org/10.1029/2000JD900327, 2000.
Koster, R. D., Schubert, S. D., and Suarez, M. J.: Analyzing the concurrence of meteorological droughts and warm periods, with implications for the determination of evaporative regime, J. Climate., 22, 3331–3341, https://doi.org/10.1175/2008JCLI2718.1, 2009.
Kullback, S. and Leibler, R. A.: On information and sufficiency, Ann. Math. Stat., 22, 79–86, https://doi.org/10.1214/aoms/1177729694, 1951.
Kumar, S. V., Peters-Lidard, C. D., Tian, Y., Houser, P. R., Geiger, J., Olden, S., Lighty, L., Eastman, J. L., Doty, B., Dirmeyer, P., Dams, J. A., Mitchell, K., Wood, E. F., and Sheffield, J.: Land information system: An interoperable framework for high resolution land surface modeling, Environ. Modmell. Softw., 21, 1402–1415, https://doi.org/10.1016/j.envsoft.2005.07.004, 2006.
Mahrt, L. and Ek, M.: The influence of atmospheric stability on potential evaporation, J. Clim. Appl. Meteorol., 23, 222–234, https://doi.org/10.1175/1520-0450(1984)023<0222:TIOASO>2.0.CO;2, 1984.
Martens, B., Miralles, D. G., Lievens, H., van der Schalie, R., de Jeu, R. A. M., Fernández-Prieto, D., Beck, H. E., Dorigo, W. A., and Verhoest, N. E. C.: GLEAM v3: satellite-based land evaporation and root-zone soil moisture, Geosci. Model Dev., 10, 1903–1925, https://doi.org/10.5194/gmd-10-1903-2017, 2017.
Miralles, D. G., Holmes, T. R. H., De Jeu, R. A. M., Gash, J. H., Meesters, A. G. C. A., and Dolman, A. J.: Global land-surface evaporation estimated from satellite-based observations, Hydrol. Earth Syst. Sci., 15, 453–469, https://doi.org/10.5194/hess-15-453-2011, 2011.
Nearing, G. S., Gupta, H. V. Crow, W. T., and Gong, W.: An approach to quantifying the efficiency of a Bayesian filter, Water Resour. Res., 49, 2164–2173, https://doi.org/10.1002/wrcr.20177 2013.
Nearing, G. S., Mocko, D. M., Peters-Lidard, C. D., Kumar, S. V., and Xia, Y.: Benchmarking NLDAS-2 Soil Moisture and Evapotranspiration to Separate Uncertainty Contributions, J. Hydrometeorol., 17, 745–759, https://doi.org/10.1175/JHM-D-15-0063.1, 2016.
Nearing, G. S., Yatheendradas, S., and Crow, W. T.: Nonparametric triple collocation, Water Resour. Res., 53, 5516–5530, https://doi.org/10.1002/2017WR020359, 2017.
Nearing, G. S., Ruddell, B. L., Clark, M. P., Nijssen, B., and Peters-Lidard, C. D.: Benchmarking and Process Diagnostics of Land Models, J. Hydrometeorol., 19, 1835–1852, https://doi.org/10.1175/JHM-D-17-0209.1, 2018.
Niu, G. Y., Yang, Z. L., Mitchell, K. E., Chen, F., Ek, M. B., Barlage, M., Kumar, A., Manning, K., Niyogi, D., Rosero, E., Tewari, M., and Xia, Y. L.: The community Noah land surface model with multiparameterization options (Noah-MP): 1. Model description and evaluation with local-scale measurements, J. Geophys. Res., 116, 1248–1256, https://doi.org/10.1029/2010jd015139, 2011.
Paninski, L.: Neural Computation, Estimation of Entropy and Mutual Information, 15, 1191–1253, https://doi.org/10.1162/089976603321780272, 2003.
Priestley, J. H. C. and Taylor, J.: On the assessment of surface heat flux and evaporation using large-scale parameters, Mon. Weather Rev., 100, 81–92, https://doi.org/10.1175/1520-0493(1972)100<0081:OTAOSH>2.3.CO;2, 1972.
Qiu, J., Crow, W. T., Nearing, G. S., Mo, X., and Liu, S.: The impact of vertical measurement depth on the information content of soil moisture time series data, Geophys. Res. Lett., 41, 4997–5004, https://doi.org/10.1002/2014GL060017, 2014.
Qiu, J., Crow, W. T., and Nearing, G. S.: The impact of vertical measurement depth on the information content of soil moisture for latent heat flux estimation, J. Hydrometeorol., 17, 2419–2430, https://doi.org/10.1175/JHM-D-16-0044.1, 2016.
Raz-Yaseef, N., Billesbach, D. P., Fischer, M. L., Biraud, S. C., Gunter, S. A., Bradford, J. A., and Torn, M. S.: Vulnerability of crops and native grasses to summer drying in the U.S. Southern Great Plains, Agr. Ecosyst. Environ., 213, 209–218, https://doi.org/10.1016/j.agee.2015.07.021, 2015.
Seneviratne, S. I., Corti, T., Davin, E. L., Hirschi, M., Jaeger, E. B., and Lehner, I.: Investigating soil moisture–climate interactions in a changing climate: A review, Earth-Sci. Rev., 99, 125–161, https://doi.org/10.1016/j.earscirev.2010.02.004, 2010.
Seneviratne, S. I., Wilhelm, M., Stanelle, T., Hurk, B., Hagemann, S., and Berg, A.: Impact of soil moisture-climate feedbacks on CMIP5 projections: First results from the GLACE-CMIP5 experiment, Geophys. Res. Lett., 40, 5212–5217, https://doi.org/10.1002/grl.50956, 2013.
Shannon, C. E.: A mathematical theory of communication, Bell Labs Tech. J., 27, 379–423, https://doi.org/10.1002/j.1538-7305.1948.tb00917.x, 1948.
Wagner, W., Lemoine, G., and Rott, H.: A method for estimating soil moisture from ERS scatterometer and soil data, Remote Sens. Environ., 70, 191–207, https://doi.org/10.1016/S0034-4257(99)00036-X, 1999.
Yin, J., Porporato, A., and Albertson, J., Interplay of climate seasonality and soil moisture-rainfall feedback, Water Resour. Res., 50, 6053–6066, https://doi.org/10.1002/2013WR014772, 2014.