the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Bathymetry and latitude modify lake warming under ice
Cintia L. Ramón
Hugo N. Ulloa
Tomy Doda
Kraig B. Winters
Damien Bouffard
In late winter, solar radiation is the main driver of water motion in ice-covered lakes. The resulting circulation and mixing determine the spatial distribution of heat within the lake and affect the heat budget of the ice cover. Although under-ice lake warming is often modeled as a one-dimensional (1D) vertical process, lake bathymetry induces a relative excess heating of shallow waters, creating horizontal density gradients. This study shows that the dynamic response to these gradients depends sensitively on lake size and latitude – Earth's rotation – and is controlled by the Rossby number. In the ageostrophic limit, horizontal density gradients drive cross-shore circulation that transports excess heat to the lake interior, accelerating the under-ice warming there. In the geostrophic regime, the circulation of the near- and off-shore waters decouples, and excess heat is retained in the shallows. The flow regime controls the fate of this excess heat and its contribution to water-induced ice melt.
- Article
(6286 KB) - Full-text XML
-
Supplement
(10308 KB) - BibTeX
- EndNote
Convection in rotating fluids is a ubiquitous process redistributing heat in planetary systems (Afanasyev and Zhang, 2018; Heimpel et al., 2016). In the case of the Earth, its spin controls the outer core convective flows responsible for the “geodynamo” (e.g., Buffett, 2000) as well as the thermohaline oceanic circulation and the large-scale atmospheric “cell” circulation (Vallis, 2017) and its climate (e.g., Cabré et al., 2017). Yet as we move from planetary to smaller-scale systems, the importance of rotation in affecting convective processes has drawn, comparatively, less attention. This is the case in lakes. The classical example of convection in lakes is the winter cooling that controls deep mixing (Schwefel et al., 2016), but field observations have been able to characterize other convective processes (e.g., Bouffard and Wüest, 2019). For example, the presence of sloping lateral boundaries sets up lateral convective flows that connect the usually shallow littoral region with the deep lake interior (Fer et al., 2002; Monismith et al., 1990; Wells and Sherman, 2001). Shallow littoral waters heat or cool more quickly than the deeper off-shore waters. This differential heating or cooling results in a cross-shore density gradient that triggers horizontal convection and downslope gravity currents. However, the influence of rotation on the distribution of heat is not well understood. The importance of Earth's rotation for horizontal flows can be parameterized with the Rossby number, . Here, f is the Coriolis frequency, which increases with latitude, and U and L are the characteristic velocity and length scales of the flow, respectively. Earth's rotation affects horizontal flows when Ro<1, and it is known, for example, to modify the pathways of rivers entering lakes (e.g., Davarpanah Jazi et al., 2020) to decelerate the off-shore progression of thermal bars (e.g., Holland et al., 2003) and to promote the formation of their associated basin-scale gyres (e.g., Huang, 1972). For the downslope gravity currents, the scales U and L correspond to the cross-shore velocity and the distance from the shore to the center of the lake basin, respectively. Gravity currents triggered by horizontal convection are usually “slow” (U of O (cm s−1), Fer et al., 2002; Monismith et al., 1990; Wells and Sherman, 2001), so their Rossby numbers are usually less than 1. Here we show that rotational effects on horizontal convection are especially relevant for ice-covered lakes in late winter since they modulate their warming regime.
Lake ice largely insulates the water column from the wind and from most of the atmospheric heat fluxes (Kirillin et al., 2012). Nevertheless, under thin snow cover conditions, solar radiation penetrates the ice and heats the water adjacent to it (Kirillin et al., 2012). In ice-covered freshwater lakes, water temperature typically increases from that of the freezing point at the ice–water interface to the temperature of maximum water density, Tmd (∼3.98 ∘C), near the bottom of the lake. The density of water can be estimated from its temperature through an equation of state. For temperature values below Tmd, an increase in temperature results in an increase in density. Thus, by heating the uppermost coldest water, it becomes denser, causing it to plunge, initiating convectively driven turbulence (Farmer, 1975). Radiatively driven convection tends to both homogenize and heat the upper portion of the water column. The latter can have important implications for winter lake ecology (Farmer et al., 2015) and biogeochemical processes (e.g., Hampton et al., 2017; Karlsson et al., 2013). In addition, lake warming enhances ice melting by increasing the diffusive heat flux from the lake water to the ice. Having a robust mechanistic understanding of the processes controlling the vertical heat transport and distribution is especially relevant to assessing the fate of lakes under climate change scenarios. Long-term predictions based on one-dimensional (1D, vertical) models indicate that up to 25 % of the current seasonally ice-covered lakes are projected to be permanently ice-free by the end of the 21st century (Woolway and Merchant, 2019). The latter might have broad impacts. However, such models and predictions do not integrate the effect of lateral boundaries into the vertical heat distribution.
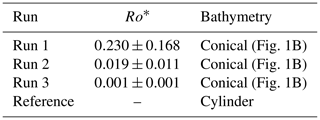
Lake warming under ice is often modeled as a 1D vertical process (Farmer, 1975; Mironov et al., 2002). In the 1D framework, convective plumes driven by solar radiation lead to the formation of a convective mixed layer (CML, Fig. 1a) above the relative quiescent stratified deep layers of the lake and below the diffusive layer at the ice–water interface (Farmer, 1975) (Fig. 1a). On a timescale of days to weeks during late winter, the cumulative insolation increases and the CML becomes warmer and deeper (e.g., Bouffard et al., 2019; Farmer, 1975), and, in shallow lakes, complete thermal mixing of the water column can occur before the end of the ice-on season (e.g., Huang et al., 2019; Salonen et al., 2014). However, even if the radiative flux through the ice remains spatially uniform over the lake area, the interaction of solar radiation and lake bathymetry can drive horizontal convection due to differential heating. Horizontal density gradients trigger gravity currents that propagate downslope and intrude into deep water at the base of the CML (Cortés and MacIntyre, 2020; Kirillin et al., 2015; Salonen et al., 2014; Stefanovic and Stefan, 2002) (Fig. 1b, c). Return flows towards the littoral regions develop at the top of the CML, leading to the formation of cross-shore circulation cells (Fig. 1b). Recently, it has been shown via 2D numerical experiments that horizontal advective fluxes of heat due to differential heating speed up the warming and deepening of the CML (Ulloa et al., 2019). The degree of departure from the 1D formulation increases as the fraction of the basin volume occupied by the littoral region – the region whose maximum depths are shallower than the CML depth – increases. By assuming that all the excess heat in the littoral region is effectively flushed into the lake interior, the underestimation of the contribution of advection and, thus, of the warming of the CML, can be quantified by a time-dependent geometrical factor G that accounts for a deepening mixed layer and the bulk hypsometry of the basin (Ulloa et al., 2019):
where the vertical bars refer to absolute values, Atotal and Ashallow are the surface areas of the lake and the littoral region (Figs. 1b and S1 in the Supplement), respectively, and and hcml are the average depth of the littoral region and that of the CML, respectively (Fig. 1d and details in Fig. S1). However, depending on the lake size – controlling the scale L in Ro – and location (latitude) – controlling f in Ro – lake dynamics can also be strongly affected by Earth's rotation, which affects the heat exchange between shallow and deep waters. There is field evidence of the influence of Coriolis in the circulation of lakes under ice (Forrest et al., 2013; Kirillin et al., 2015; Likens and Ragotzkie, 1966; Rizk et al., 2014), where the presence of horizontal cyclonic or anticyclonic gyres has been inferred or measured. These gyres can potentially modulate the advection of heat from the littoral region and modify lake warming.
Figure 1Schematic of the modeled lake forcing and under-ice differential heating. (a) Variation in depth of the radiative forcing (I) and the resulting temperature profile at the lake center, characterized by the formation of a convective mixed layer (CML) immediately below the thin diffusive layer (DL). (b) Daily cycle of the radiative heat flux and snapshot of the temperature field in a cross section showing gravity currents developing in the littoral region as a result of differential heating for Ro O (10−1). The isotherm spacing is 0.02 ∘C. (c) The signature of these gravity currents can also be detected by positive radial velocities (positive towards the lake interior) and positive horizontal density anomalies (deviations from the basin-average density profile). (d) Schematic of the mixed-layer heat balance at the lake interior and locations of profiles P1 and P2 (red lines), ∼91 m apart, used in Fig. 2.
Here we report, through 3D real-scale numerical simulations, that indeed for a fixed radiative heating, the resulting under-ice basin-scale heat distribution strongly depends on rotation and, thus, potentially on the bathymetry and latitudinal location of a given lake. We found two distinctive dynamical regimes, controlled by the Rossby number, that result in a remarkably divergent distribution of incoming heat beneath the ice. In the ageostrophic regime, Ro O(10−1–100), advection of heat from the littoral region effectively increases the deepening and warming rates of the CML in the lake interior. In the geostrophic regime, , the dynamics of the littoral and off-shore regions decouple: the excess heat is retained in the littoral region, while the deepening and warming of the CML in the lake interior is well approximated using the 1D framework.
2.1 Scenarios
For validation and comparison purposes, our scenarios extend the simulations presented in Ulloa et al. (2019). We specifically kept the same lake bathymetry as in their 2D spectral large-eddy simulations (LES) but expanded into three dimensions to obtain a basin with radial symmetry (Fig. 1b). The fluid was initially at rest and linearly stratified, with T=0 ∘C at the surface and T=Tmd at the maximum depth. We fix T at 0 ∘C at the ice–water boundary and subject the under-ice water to a laterally uniform but time- and depth-dependent radiative flux, I(t,z) (∘C m s−1). This is equivalent to a surface heat flux, (W m−2), with cp and ρ0 being the heat capacity and reference density of freshwater near its freezing point, respectively. The vertical distribution was modeled using Beer's law (Fig. 1a), whereas the time evolution was prescribed to roughly mimic the daily cycle of solar insolation (Fig. 1b and see Sect. 2.3). The forcing parameters reflect under-ice conditions in late winter. We investigate three scenarios ranging from weak (Ro O(10−1)) to stronger (Ro O(10−3)) rotational influence (Table 1 and see Sects. 2.4 and S1.1 for the Ro calculations). This range of Ro spans the expected range of values typical of the varying size and latitudinal distribution of ice-covered lakes on Earth (see Sect. 4). We focus on a rotational regime where convective-plume plunging and mixing occur on timescales much shorter than the inertial period (), but the temperature gradients that result from differentially heating the shallow littoral and deep interior regions give rise to slower motions that are affected by rotation over longer timescales.
2.2 Computational model
Simulations were conducted with RANS model MITgcm (MIT General Circulation Model, Marshall et al., 1997a, b, and details in http://mitgcm.org, last access: 5 December 2020). MITgcm is a 3D, non-hydrostatic, z-coordinate, finite-volume model that solves the Boussinesq form of the Navier–Stokes equations for incompressible fluids. The momentum equations are discretized on an Arakawa-C grid. The variables are advanced in time using a quasi-second-order Adams–Bashforth time-stepping scheme, and preconditioned conjugate-gradient methods are used in the 2D and 3D inversions of the hydrostatic and non-hydrostatic pressure, respectively. The advection terms in the transport equation for temperature were discretized with the nonlinear third-order DST (direct space–time) with a flux limiter. A modified nonlinear UNESCO equation of state (Jackett and Mcdougall, 1995) and the non-hydrostatic capabilities of MITgcm were used. Horizontal and vertical viscosities were parameterized with the isotropic 3D Smagorinsky approach (0.0005 coefficient). Background grid-dependent lateral viscosities were set to 0.002 (equivalent to a lateral eddy viscosity, υh, of m2 s−1 for grid resolution in the x direction, Δx, of 0.9 m and a time step, Δt=0.5 s). Background vertical viscosities, υz, were set to 10−6 m2 s−1. Background horizontal and vertical diffusivities for heat, Kh and Kz, were set to 10−5 and m2 s−1, respectively. No-slip conditions were applied at the lateral walls and the bottom. Though we could potentially have done this initial study using 3D LES, our interest extends to larger lakes over seasonal timescales, and this setup provides and validates a starting point for such studies. MITgcm was originally built for ocean modeling but has been applied satisfactorily to study lake hydrodynamics (e.g., Cimatoribus et al., 2018; Dorostkar et al., 2017). We further validate MITgcm against spectral LES (Ulloa et al., 2019) of radiatively heated ice-covered lakes (see Sect. S1.5).
2.3 Under ice hydrodynamic and transport model
The lake bathymetry is conical and axisymmetric (Fig. 1), with a radius R=114 m and depths, D, increasing towards the lake interior in the radial direction, r, as in Ulloa et al. (2019):
where H=27.1 m is the maximum height of the basin, dmin (=0.56 m) is the minimum depth in the littoral region, and r0 (=57.2 m) and β (=22.9 m) are topographic (slope) parameters. The physical domain was discretized using a horizontally uniform Cartesian grid ( m) with vertically variable thickness (Δz). Δz increases with depth from Δz=0.05 m within the first 2 m to a bottom cell of 0.3 m. In our simulations, temperature and pressure are the only scalars affecting density. The lake was initially quiescent with horizontal isotherms following a linear thermal stratification, with T= 0 ∘C at the ice–water interface and T=Tmd at the bottom. Boundaries are prescribed as no slip and adiabatic, except at the ice–water interface. The ice–water boundary is modeled as a rigid lid with a constant temperature of 0 ∘C. The radiative heat flux through the ice–water interface is specified as a sinusoidal daily cycle that attenuates with depth as in Ulloa et al. (2019):
Here the time t is expressed in days, I0 ( ∘C m s−1) is the water surface radiative forcing, F(t)=sin (2πt) during the day (t<0.5) and zero otherwise, and m−1) is the depth scale for light attenuation. The order of magnitude of I0 and the value for λ selected are representative of late-winter conditions in turbid waters (Bouffard et al., 2019; Leppäranta et al., 2003). The intensity of convection is expected to decrease as λ increases (e.g., Winters et al., 2019), but the effect of light attenuation on differential heating and on the magnitude of the radial velocities remains secondary compared to the magnitude of I0 and the geometry of the littoral region. For visualization purposes only, our results are shifted 0.25 d so the peak in the radiative heat flux matches midday (Fig. 1).
2.4 Rossby number and test cases
Since we are interested in evaluating the advection of heat from the littoral to the lake interior, the surface radius, R, was selected as the characteristic length scale in the calculations of Ro. Ro was calculated using the maximum radial velocity in the littoral region, Urs-max, as the characteristic velocity scale (see details in Sect. S1.1):
is the nominal time required for a gravity current at speed Urs-max to reach the center of the lake. When , gravity currents are affected by Earth's rotation (e.g., Davarpanah Jazi et al., 2020). While R could vary several orders of magnitude among the ice-covered lakes on Earth, f remains O(10−4) s−1. Thus, Ro depends predominantly on the horizontal dimensions of the lake. Still, the variability in f alone allows bigger lakes to lie within the same rotation regime as one moves towards lower latitudes. Note that for a given value of Urs-max, to obtain the same value of Ro, Eq. (4) shows that a lake at 30∘ N ( s−1) would still double the size of a lake at latitudes ≥70∘ N ( s−1).
The model was first used to simulate rotational effects as in Ulloa et al. (2019), with a characteristic Ro O(10−1). This corresponds to run 1 in Table 1. For a range of measured radial velocities of O(10−3–10−2) m s−1 under ice (Forrest et al., 2013; Kirillin et al., 2015; Rizk et al., 2014), a value of Ro O(10−1) could be representative of lakes of O(10−1–100) km in length (∼2L). To analyze the effect of rotation in the lake circulation and in the warming of the CML, two additional simulations were conducted where we increased rotational effects by decreasing Ro up to 2 orders of magnitude (runs 2 and 3 in Table 1). To analyze bathymetric effects (differential heating), an additional simulation was conducted (reference simulation) where forcing was kept as in run 1, but the bathymetry was modified to obtain a cylinder of depth D=H. Each run spans 12 radiative cycles (12 d). This number of cycles was long enough to expose and analyze the effect of rotation and bathymetry on lake warming under ice.
2.5 Differential heating, warming of the CML and heat balance
The magnitude of differential heating was quantified by comparing CML temperatures, Tcml, in the littoral region and at the lake center. We compared temperatures at 1 m depth (inside the CML in all runs and days >1) at profile P1 in the littoral region (at a distance β from the outer edge and ∼91 m from the lake center) and at profile P2 at the lake center (Fig. 1c). The average Tcml at the lake interior was calculated as the average mixed-layer temperature inside an interior control volume (Fig. 1d) of radius ∼25 m (as in Ulloa et al., 2019). This control volume was also used to calculate the importance of the advection of heat from the littoral region in the mixed-layer heat balance at the lake interior (see Sect. 3).
3.1 Mixed layer warming and differential heating for different Rossby numbers
Radiatively driven convection produces a CML with uniform temperature in each of the Ro scenarios simulated (see the temperature profiles in Fig. 2a–c). This CML warms and deepens during the 12 daily cycles simulated, with higher temperatures reached as Ro increases (red line in Fig. 2a–c). Figure 2d shows the time history of temperature in the CML, Tcml, in the lake interior (average value in the interior control volume CV, Fig. 1d) for the three Ro tested. The rate of warming of the interior mixing layer, dT dt, increases with increasing Ro, with the net warming rate for Ro O(10−1) 23 % higher on average than that for Ro O(10−3) (compare the red and blue lines in Fig. 2d).
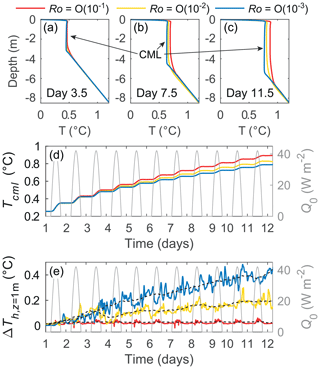
Figure 2Warming of the CML in the lake interior and differential heating. (a–c) Laterally averaged midday temperature profiles on given days in the lake interior (lake volume below the surface area of the control volume in Fig. 1d). (d–e) Time evolution of (d) temperature in the interior of the CML (average in the control volume in Fig. 1d) and (e) the horizontal temperature gradient at 1 m depth between the littoral region and the lake interior (profiles P1 and P2 in Fig. 1d). Black dotted lines in (e) show the 24 h moving averages.
The development and maintenance of a temperature contrast between the littoral and the lake interior is also affected by Ro. To quantify the differential heating, we compared the temperature difference at 1 m depth (inside the CML), , between two profiles, one in the littoral region (P1, Fig. 1d) and one at the lake center (P2, Fig. 1d). The temporal evolution of is remarkably sensitive to Ro (Fig. 2e). For Ro O(10−3) (blue line in Fig. 2e), increases with time over the entire simulation, reaching values up to 0.48 ∘C (). In contrast, for Ro O(10−1), the growth rate of (red line in Fig. 2e) is substantially lower owing to the daily flushing of the littoral region by gravity currents. Note that in this scenario follows the daily cycle of solar radiation, reaching its maximum of up to 0.05 ∘C () immediately after the peak in solar radiation.
For the intermediate Ro of O(10−2) (yellow line in Fig. 2e), both of these limiting behaviors are seen. At early times, heat is retained in the shallows and the cross-shore temperature contrast increases with time. Once a threshold contrast is reached ( ca. 0.1 ∘C, ), further heating of the shallows induces an off-shore transport and a quasi-steady state becomes established. For Ro O(10−3) (blue line in Fig. 2e), the rate of change of in time also decreases, which may also suggest the establishment of a quasi-steady state.
The simulations illustrate that horizontal temperature and density gradients increase by about an order of magnitude as Ro decreases from O(10−1) to O(10−3–10−2) and that the increasing cross-shore contrast over successive days indicates that excess heat is effectively retained in the littoral region. As a consequence, the horizontal lake circulation becomes modified by rotational effects.
3.2 Radial and azimuthal lake circulation
The characteristic signal of differential heating under ice, with temperature at a given depth increasing towards the littoral region and the formation of cross-shore circulation cells, is clearly observed for Ro O(10−1) (Figs. 1b and 3a, b). Because of rotation, however, the gravity currents and the return flows are deflected towards the right in the Northern Hemisphere. Driven by the off-shore-directed gravity currents, a cyclonic gyre develops in the lake interior (positive azimuthal velocities, uθ, in Fig. 3c), while the on-shore return flow drives an anticyclonic gyre in the littoral region (negative uθ in Fig. 3b). The gyres are governed by a three-way balance of horizontal pressure gradient, Coriolis and centripetal forces (cyclogeostrophic balance, Sect. S1.2). The signature of the double-gyre circulation is distinguishable from the CML-averaged azimuthal velocities shown in Fig. 3d. The strength of the gyres is maximal immediately after the peak in solar radiation, when gravity currents flush the littoral region. Although weaker in strength, the double gyre circulation does not fully dissipate at night (see video S1). The weakly dissipative nature of the gyres is in agreement with estimates of the Ekman damping timescale, , where is the Ekman number, υz is the vertical kinematic viscosity and hgyre is the gyre thickness. For m2 s−1 (see Sect. 2) and hgyre between 3 and 7 m (Fig. 3c), tEk ranges between 3 and 7 d, which is longer than the period of the radiative forcing (less than 1 d). Flow convergence in the lake interior in the radial direction and rotation upwell isotherms at the bottom of the CML. This is illustrated by the dome shape of the isotherms at the bottom of the CML in Figs. 1b and 3a and by the positive horizontal density anomaly at the center of the lake in Fig. 1c. Isotherm upwelling explains the presence of a weaker stratification immediately below the CML at the center of the lake (red profiles in Figs. 1a and 2a–c).
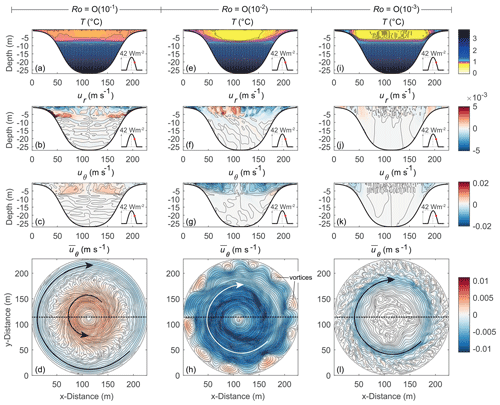
Figure 3Snapshots of the thermal and velocity structure for different Ro. Snapshots from day 11.6, just after peak insolation, showing the simulated cross-sectional (a, e, i) temperature (0.02 ∘C isotherm spacing) and (b, f, j) radial and (c, g, k) azimuthal velocities (0.002 m s−1 isovel spacing) and depth-averaged (d, h, l) azimuthal velocities and flow streamlines at depths ≤hcml. Radial and azimuthal velocities are positive towards the lake interior and for cyclonic circulation, respectively. Black dashed lines in (d, h, l) show the location of the cross section displayed in (a–c), (e–g) and (i–k). Results for runs with (a–d) Ro O(10−1), (e–h) Ro O(10−2) and (i–l) Ro O(10−3).
Decreasing Ro from O(10−1) to O(10−2) alters the circulation described above. The bowl shape of isotherms above 10 m depth in Fig. 3e shows that temperature increases towards the littoral region. However, the radial velocity in Fig. 3f shows that the downslope cross-shore gravity currents are strongly suppressed. There, a balance is set between the Coriolis force and the pressure gradient (geostrophic balance, Eq. S1 in Sect. S1.2). This geostrophic balance results in the formation of an anticyclonic gyre that dominates the circulation within the CML (Fig. 3g and h) and restricts the cross-shore transport. For Ro O(10−3), isotherms in the littoral region get closer together (Fig. 3i) and the cross-shore transport stops (see radial velocities in Fig. 3j). As the area where cross-shore density gradients develop becomes smaller, the spatial extension of the anticyclonic gyre becomes confined to the shallow littoral region (Fig. 3k and l). Thus, water circulation under ice is strongly affected by Earth's rotation. Once a geostrophic balance is set, the circulation in the CML evolves from a combination of radial (counter-rotating cells) and azimuthal (gyre) motions to a circulation that occurs preferentially in the azimuthal direction. This change in the lake circulation could have consequences for the heat balance of the lake interior.
3.3 Earth's rotation modifies the interior mixed-layer heat balance
We examine the impact of rotation on the heating rate of the interior mixed layer. For this, we consider an arbitrary control volume away from the littoral region (gray cylinder in Fig. 1d) with a surface area ACV and extending vertically from the ice–water interface to a depth hcml. Neglecting interior diffusive fluxes, the heat balance in this control volume is (Ulloa et al., 2019)
where Fext is the sum of the solar heating rate (yellow arrow in Fig. 1d) and the diffusive heat lost towards the ice (blue arrow in Fig. 1d), and Fadv is the sum of advective heat fluxes across the lateral and bottom boundaries of the control volume (red and orange arrows in Fig. 1d). The daily averaged Fext and Fadv are calculated as
and
Here, the angle brackets denote both a volume and a daily averaging in the CML, zcml is the height of the base of the CML, H is the total height of the basin (Figs. 1d and S1) and Kz is the vertical thermal diffusivity. Equation (7) integrates both vertical and radial advective fluxes, SCV being the surface of the control volume with an outward-facing unit normal vector and u being the vector velocity.
The relative contribution of advection to the total heat fluxes is, thus, . We compared this ratio, for the three Ro examined, as deviations from the contribution calculated in a reference numerical experiment where the 1D approach for deepening and warming of the CML applies, that is, Δδadv. This reference run is identical to run 1 in Table 1, except for the lake bathymetry: the conical shape in the reference run was replaced by a cylinder of height H and of surface area equal to Atotal. By choosing a cylinder, we eliminated the effect of differential heating. Figure 4a shows Δδadv for the three Ro tested. For Ro O(10−2-10−1), Δδadv increases over time, while for Ro O(10−3) the contribution of advection is close to zero or even takes negative values, which indicates that the net effect of advection is to export heat from the control volume towards shallower regions. Δδadv reaches the highest values in the simulations with the largest Ro tested. For example, from day 6 onwards, Δδadv with Ro O(10−1) consistently approximately triple that with Ro O(10−2). The increasing importance of advective heat transport with increasing Ro is consistent with efficient flushing of the shallows and enhanced warming of the interior CML (Fig. 2a–d), while the lack of advective flux at small Ro is further indication of heat retention in the littoral region (Fig. 2e).
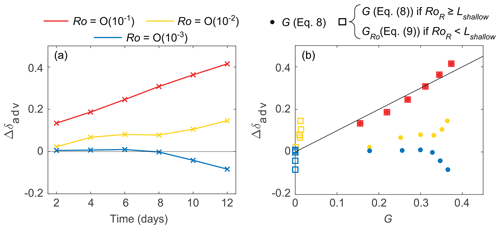
Figure 4Contribution of advection to the total heat fluxes into the lake interior. (a) Time evolution of the simulated Δδadv. (b) Simulated versus predicted contribution of advection based on the geometrical factors G (Eq. 8) and GRo (Eq. 9). Each point in (a–b) represents the average value over the previous 2 d. The black line in (b) shows the 1:1 relationship.
Advective fluxes, thus, depend on the rotation regime. This limits the applicability of the geometrical factor G (Eq. 1, Ulloa et al., 2019) to predict the extra warming of the CML due to differential heating as Ro decreases. To obtain G (Eq. 1), Ulloa et al. (2019) defined the length of the littoral region, Lshallow, as the distance from the lake perimeter to the location in the bathymetry where depths intersect hcml (Figs. 1d and S1). Adapted to a circular surface area, this corresponds to
Dots in Fig. 4b show that only the calculated Δδadv values for Ro O(10−1) are consistent with predictions using the G factor (red dots in Fig. 4b), while the contribution of advection to the heat balance at the lake interior would be strongly overpredicted for Ro O(10−3–10−2) (blue and yellow dots in Fig. 4b). Given that rotation controls the advection of heat to the lake interior, the characteristic length scale to define the littoral region is, however, better characterized by the Rossby radius (, Sect. S1.1) whenever RoR<Lshallow. This leads to a new definition of G, here called GRo, expressed as a function of the Rossby radius and, specifically for our bathymetry, as (see details in Fig. S1 and Sect. S1.3)
where is the average depth of the littoral region within a distance RoR from the lake interior (Fig. S1). Note that for RoR≥Lshallow, GRo=G. By using GRo when RoR<Lshallow, the trends in the contribution of advection of heat from the littoral region to the heat balance at the lake interior are better represented, especially for the scenario with the lowest Ro (blue squares in Fig. 4b).
4.1 Advection of heat from the littoral regions decreases with decreasing Ro (big lakes and/or high latitude lakes)
In this study, we show that, subjected to the same radiative forcing, the under-ice warming of lakes is strongly modulated by the combination of lake bathymetry and latitude (i.e., intensity of Earth's rotation). Once solar radiation is able to penetrate the ice and heat the water below it, under-ice convection becomes the main driver of lake circulation and mixing (Kirillin et al., 2012). Convective cells impinge on the stratified layer below, entraining water from below and deepening the CML. This process is often viewed as a 1D process (Farmer, 1975). However, the presence of a bathymetry with sloping boundaries implies that as the CML becomes deeper in the lake interior, convective deepening is constrained by the bottom in the shallower regions. With a smaller volume to heat up, these shallower areas warm more quickly than the lake interior, and a horizontal density gradient develops. If this excess heat is advected towards the lake interior, the warming and deepening of the CML in the lake interior speed up (Ulloa et al., 2019; Fig. 2a–d). The advection of heat from the littoral region to the lake interior is, however, constrained by Earth's rotation. Our findings show that the rotation regime plays a fundamental role in the heating rate of the CML and in the cross-shore and vertical heat distribution (Figs. 2–3). As the rotation increases, the vertical and radial heat exchanges are dramatically inhibited (Figs. 3–4a). In fact, the warming and deepening rates of the interior CML for the scenario with the smallest Rossby number (O(10−3)) examined match the results of the reference simulation, which lacks differential heating and lateral neat heat transport. For this scenario, the density difference between the littoral region and the lake interior increases over time until the end of the simulation (Fig. 2e). This indicates that heat is effectively retained in the littoral region (see also Fig. 3k). Consistent with the results of our simulations, the new GRo (Eq. 9) geometrical parameter that adopts RoR as the representative length scale when RoR<Lshallow predicts a decrease in the lateral advection of heat as Ro decreases.
4.2 Lake circulation
Differential heating and Earth's rotation set up a circulation characterized by the formation of gyres within the CML (Figs. 3 and 5). The double-gyre circulation (Fig. 5a) for Ro O(10−1–100) is consistent with past field-based work on ice-covered lakes. Forrest et al. (2013) conducted conductivity–temperature–depth (CTD) measurements mounted on an autonomous underwater vehicle and observed a density distribution in the interior of Pavilion Lake (50∘ N, R∼0.4 km and Atotal=5 km2) that suggested the existence of a cyclonic gyre for Ro O(10−1) (recalculated from Forrest et al., 2013, using L=R). Kirillin et al. (2015) conducted CTD profiles across Lake Kilpisjärvi (69∘ N, R∼1.5 km and Atotal=37 km2) and ADCP measurements in the littoral region when Ro was O(10−1). With the former data, they observed warm “upwelling” at the lake center, which could be indicative of a strong cyclonic gyre in the lake interior, and with the latter, they measured radial velocities of ∼3–5 cm s−1 and the presence of an anticyclonic gyre in the littoral region with azimuthal velocities of 2–4 cm s−1. A double-gyre circulation was also reproduced in numerical simulations (Huttula et al., 2010) of early winter conditions in Lake Pääjäarvi (61∘ N), when under-ice circulation was dominated by the input of heat from the sediment (Winter I, Kirillin et al., 2012) instead of by radiatively driven convection (Winter II, Kirillin et al., 2012). Also, when the input of heat from the sediment dominated lake circulation, Likens and Ragotzkie (1966) injected radioactive tracers near the center and in the littoral region in Tub Lake (45∘ N, R∼50 m and m2) and detected the presence of a double-gyre circulation when Ro∼0.1 (calculated with their reported horizontal velocities of – m s−1). The central cyclonic circulation had already been detected in this same lake by Likens and Hasler (1962) in a previous winter, suggesting that this azimuthal circulation pattern is recurrent during the ice-on season in the lake. Note, however, that for the ageostrophic regime to display a double-gyre circulation, the cross-shore cell circulation should exist over a significant fraction of an inertial period (). In our simulations, I0 is close to its daily maximum for ca. 6 h, but cloudiness or mountain shading could decrease this duration in real settings. When Ro≳10−1, the horizontal heat transport is then accomplished by the ageostrophic components of the flow (downslope gravity currents). This cross-shore circulation might be considered analogous to the atmospheric Hadley cells, as reproduced in laboratory rotating-tank experiments (e.g., Fultz et al., 1959).

Figure 5Conceptual model for under-ice circulation induced by differential heating. (a–c) Conceptual model for the ageostrophic and geostrophic regimes under ice. (d) Boxplot of Ro values and (e) distribution of lakes used for the calculations of Ro for latitude intervals of 2.5∘. The HydroLAKES database (Messager et al., 2016) was used to construct panels (d–e) (see details in Sect. S1.4). Latitude in (d–e) is expressed in absolute values. Red lines and gray rectangles in (d) show the median value and the interquartile range, respectively.
As Ro decreases, the circulation in the lake becomes geostrophic (Fig. S3), the daily cross-shore cells are rotationally suppressed and, because of the horizontal density gradient, an anticyclonic gyre (in the Northern Hemisphere) with velocities decreasing with depth must develop (Eq. S1 and Fig. 5b). With decreasing Ro, the spatial extent of this anticyclonic gyre is progressively confined to the littoral region (Fig. 5c). To our knowledge, this circulation has not been reported in the field at times of under-ice radiatively driven convection. The lake-wide anticyclonic circulation in Fig. 5b would be consistent with the inferred lake-wide anticyclonic gyre reported by Rizk et al. (2014) at a time when circulation in Lake Pääjäarvi was dominated by a lateral gradient in the heat flux from the sediment (Winter I) and Ro was O(10−3–10−2). Nonetheless, Welch and Bergmann (1985) reported radial velocities of m s−1 during Winter I in Methane Lake (63∘ N, R∼100 m and Atotal<0.1 km2) that would lead to estimates for Ro of O(10−3–10−2). By adding a dye (rhodamine) in a point in the littoral region and close to the lake bed, they detected the presence of density currents flowing off-shore and no sign of gyre formation. This would be contrary to the expected radiatively driven lake circulation in the geostrophic regime as presented in this study and suggests that (1) other processes could be at play during Winter I or that (2) the radial velocity magnitude, and thus Ro, was underestimated by the authors. The latter is possible given that Welch and Bergmann (1985) used dye concentrations to estimate O(10−4) m s−1 radial velocities in the lake. Due to a different distribution of the pressure field (decreasing towards the littoral region in the under-ice differential heating case), the sense of the azimuthal circulation in Fig. 3g, h and k, l is, for example, opposite to that observed in-shore of thermal bars (ice-free period), where a cyclonic gyre develops (e.g., Huang, 1972; Malm et al., 1993). The basin-scale gyre circulation in Fig. 3g, h and k, l and its sense of rotation are, however, consistent with the Rossby wave regime reported in laboratory studies (rotating cylinder and annulus) mimicking the mid- to high-latitude atmospheric circulation (e.g., Condie and Rhines, 1994; Fultz et al., 1959; Sommeria et al., 1989). Water temperature in the rotating tanks is above Tmd, and the sense of the gyre rotation is anticyclonic when the heating and cooling sources are provided at the center and the tank rim, respectively. The sense of rotation is reversed (cyclonic gyre) when the heating and cooling sources are exchanged. Within the Rossby regime, vortices and waves develop (Fig. 3h), and as Ro decreases, the wave lengths decrease and the gyre circulation is concentrated into jets that meander in the radial direction and could finally break (Condie and Rhines, 1994; Read et al., 2015; Smith et al., 2014). The presence of waves and/or vortices as in the scenario with Ro O(10−2) (Fig. 3h) is typical of a transitional regime (Fultz et al., 1959), and when they develop, the center of the anticyclonic gyre is not static in time but fluctuates laterally (video S1). This lateral displacement favors the existence of pulses of gravity currents from the littoral region to the lake interior, leading to a higher contribution of advection in the heat balance of the lake interior. The lateral fluctuations of the gyre cannot be accounted for in the geometrical factor GRo and explains the underprediction of the contribution of advection for Ro O (10−2) in Fig. 4b (note that the yellow squares in Fig. 4b are above the 1:1 line).
4.3 Implications
This study reveals that for a given radiative forcing and latitude, as a result of differential heating, a temperature mooring deployed at the deepest point of an ice-covered lake will record a higher warming rate if shallow regions contribute substantially to the lake volume. Thus, for a given lake surface area, a lake with more vertical walls would tend to warm at a slower rate than a bowl-shaped lake with gentle slopes. However, if we could virtually move these two same lakes to higher latitudes, that mooring could potentially record the same warming rate in the two lakes. That is because the contribution of the littoral region to the warming of the lake interior under ice is strongly dependent on its size and its latitudinal location, both of which condition the importance of Earth's rotation (parameterized by Ro) in driving lake water circulation. The range of Ro values investigated here lies within the natural range of variability of Ro that characterizes lake circulation driven by under-ice differential heating in lakes on Earth (Fig. 5d, e). This means we are covering ice-covered lakes from the Himalayas and the Tibet Plateau (∼30∘ N) to high-latitude polar regions. The bias in the distribution of lake size towards smaller lakes (more than 85 % of lakes on Earth have surface areas smaller than 1 km2, Messager et al., 2016), the bias in the potential for ice-cover formation (e.g., Sharma et al., 2019) and the distribution of lakes on Earth towards mid to high latitudes (>45∘ N, Fig. 5b) indicate that the ageostrophic regime with Ro O(10−1) should be common under ice, as shown by the mean (red lines) values in Fig. 5d. The geostrophic regime, Ro< O(10−1), lies outside the interquartile range (gray bars in Fig. 5d) but is also naturally occurring in lakes at almost all latitudes (Fig. 5d). The retention of heat in the littoral region in the geostrophic regime could potentially reinforce ice melting near the shoreline. This is suggested in our simulations, where with Ro O(10−3) the diffusive flux towards the ice is on average 23 % larger in the littoral region than at the center of the lake (profiles P1 and P2 in Fig. 1c). However, heat retention in the littoral region does not necessarily imply an increase in the diffusive flux towards the ice. The diffusive flux, , depends not only on the temperature in the shallow region, but also on the thickness of the diffusive boundary layer, which determines the value of . Due to the retention of heat in the littoral region, water temperature there could potentially reach values ≥Tmd. This would lead to the development of a stable stratification in the littoral region and to the suppression of convection that, in contrast, would continue in the lake interior. This could have implications for early formation of thermal bars and/or contribute to the formation of moats (e.g., Nolan et al., 2003).
The numerical experiments described herein intend to provide a general characterization of the respective contribution of lake bathymetry and rotation on the warming of lakes under the ice; however, site-specific conditions will determine the actual response of a given lake. For example, although basin or sub-basin-scale gyre formation has been reported to occur in lakes with bathymetries departing from the bowl-shaped one used in this study (e.g., Forrest et al., 2013; Kirillin et al., 2015), bathymetric effects could prevent gyre formation, or, by contrast, lead to the development of more complicated patterns (for example, multiple horizontal gyres, as in Huttula et al., 2010). Also, the initial conditions could vary among lakes (e.g., Yang et al., 2020). Although there are examples in the literature of lakes reaching values close to Tmd near the lake bottom (e.g.,Bengtsson and Svensson, 1996; Cortés and MacIntyre, 2020; Forrest et al., 2013; Malm et al., 1998), other lakes reach temperatures of only 2–3∘ at the bottom of the lake (e.g., Bouffard et al., 2016; Yang et al., 2021). The radiative forcing conditions could also depart from those in this study. The radiative flux could vary spatially (e.g., Malm et al., 1997) and the daily radiative cycle could vary over time (e.g., Bouffard et al., 2016). The initial and forcing conditions (magnitude and time evolution) will influence the deepening rate of the CML and/or the strength of differential heating and density currents and will also determine the magnitude of Ro.
Depending on the magnitude of the forcing and the thickness of the convective mixing layer hcml, the Rayleigh number, which quantifies the strength of buoyancy over diffusion, ), can easily reach magnitudes of ∼O(1015) or even higher if we consider the horizontal convective length to be the relevant scale. Here α is the thermal expansion coefficient. These magnitudes are difficult to achieve in laboratory and numerical experiments (King et al., 2009). There have been significant advances in in situ measurements over the last years that facilitate more robust measurement of turbulence and mixing properties (Bouffard et al., 2019). Thus, ice-covered lakes might provide unique observations to test theoretical advances on the heat and mass transfer in rapidly rotating convection in fluid systems of planetary scale (e.g., Julien et al., 2012; King et al., 2009). Large and high-latitude ice-covered lakes provide, therefore, unique opportunities to investigate strong convective regimes at low (≪1) Rossby and Ekman numbers and with Prandtl numbers ≈10.
Penetrative radiation affects the under-ice melting rate by regulating the water-to-ice heat transfer and is often modeled as a 1D process. Our results show, however, that lake bathymetry and latitudinal location also affect the rate of warming of ice-covered lakes. Lake bathymetry induces a relative excess heating of shallow waters. The transport of this excess heat to the lake interior depends on the intensity of Earth's rotation and determines lake warming rates and the horizontal distribution of heat. This study stresses that accounting for the shape and size of the lake's basin and its latitudinal location is essential for global estimations of lake ice cover that take into account the warming rates and the distribution of heat in the water column.
The MITgcm code is publicly available at http://mitgcm.org (MITgcm, 2020).
The data displayed in the figures, temperature profiles at P1 and P2, time series of cross-sectional data and the input files to run the simulations are available for download at Zenodo (https://doi.org/10.5281/zenodo.4027393, Ramón et al., 2020). The complete time series of the 3D model outputs used in this study can be requested from the corresponding author.
The supplement related to this article is available online at: https://doi.org/10.5194/hess-25-1813-2021-supplement.
CLR ran the simulations, conducted the bulk analysis and led the writing of the manuscript. The other co-authors contributed equally to the study design, interpretation of the data and editing of the manuscript.
The authors declare that they have no conflict of interest.
This work was supported by the Swiss National Science Foundation (project Buoyancy driven nearshore transport in lakes, HYPOlimnetic THErmal SIphonS, HYPOTHESIS). KBW is grateful for support from the U.S. National Science Foundation, Physical Oceanography.
We thank the two anonymous reviewers for their thorough comments and suggestions.
This research has been supported by the Swiss National Science Foundation (grant no. 175919) and the U.S. National Science Foundation (grant no. OCE-1657791).
This paper was edited by Bettina Schaefli and reviewed by two anonymous referees.
Afanasyev, Y. D. and Zhang, Y.: Cyclonic circulation of Saturn's atmosphere due to tilted convection, Nat. Geosci., 11, 164–167, https://doi.org/10.1038/s41561-018-0070-3, 2018.
Bengtsson, L. and Svensson, T.: Thermal regime of ice covered Swedish lakes, Nord. Hydrol., 27, 39–56, https://doi.org/10.2166/nh.1996.0018, 1996.
Bouffard, D. and Wüest, A.: Convection in Lakes, Annu. Rev. Fluid Mech., 51, 189–215, https://doi.org/10.1146/annurev-fluid-010518-040506, 2019.
Bouffard, D., Zdorovennov, R. E., Zdorovennova, G. E., Pasche, N., Wüest, A., and Terzhevik, A. Y.: Ice-covered Lake Onega: effects of radiation on convection and internal waves, Hydrobiologia, 780, 21–36, https://doi.org/10.1007/s10750-016-2915-3, 2016.
Bouffard, D., Zdorovennova, G., Bogdanov, S., Efremova, T., Lavanchy, S., Palshin, N., Terzhevik, A., Vinnå, L. R., Volkov, S., Wüest, A., Zdorovennov, R., and Ulloa, H. N.: Under-ice convection dynamics in a boreal lake, Inl. Waters, 9, 142–161, https://doi.org/10.1080/20442041.2018.1533356, 2019.
Buffett, B. A.: Earth's core and the geodynamo, Science, 288, 2007–2012, https://doi.org/10.1126/science.288.5473.2007, 2000.
Cabré, A., Marinov, I., and Gnanadesikan, A.: Global atmospheric teleconnections and multidecadal climate oscillations driven by Southern Ocean convection, J. Climate, 30, 8107–8126, https://doi.org/10.1175/JCLI-D-16-0741.1, 2017.
Cimatoribus, A. A., Lemmin, U., Bouffard, D., and Barry, D. A.: Nonlinear Dynamics of the Nearshore Boundary Layer of a Large Lake (Lake Geneva), J. Geophys. Res.-Oceans, 123, 1016–1031, https://doi.org/10.1002/2017JC013531, 2018.
Condie, S. A. and Rhines, P. B.: Topographic Hadley cells, J. Fluid Mech., 280, 349–368, https://doi.org/10.1017/S002211209400296X, 1994.
Cortés, A. and MacIntyre, S.: Mixing processes in small arctic lakes during spring, Limnol. Oceanogr., 65, 260–288, https://doi.org/10.1002/lno.11296, 2020.
Davarpanah Jazi, S., Wells, M. G., Peakall, J., Dorrell, R. M., Thomas, R. E., Keevil, G. M., Darby, S. E., Sommeria, J., Viboud, S., and Valran, T.: Influence of Coriolis Force Upon Bottom Boundary Layers in a Large-Scale Gravity Current Experiment: Implications for Evolution of Sinuous Deep-Water Channel Systems, J. Geophys. Res.-Oceans, 125, e2019JC015284, https://doi.org/10.1029/2019JC015284, 2020.
Dorostkar, A., Boegman, L., and Pollard, A.: Three-dimensional simulation of high-frequency nonlinear internal wave dynamics in Cayuga Lake, J. Geophys. Res.-Oceans, 122, 2183–2204, https://doi.org/10.1002/2016JC011862, 2017.
Farmer, D. M.: Penetrative convection in the absence of mean shear, Q. J. Roy. Meteor. Soc., 101, 869–891, https://doi.org/10.1002/qj.49710143011, 1975.
Farmer, T. M., Marschall, E. A., Dabrowski, K., and Ludsin, S. A.: Short winters threaten temperate fish populations., Nat. Commun., 6, 7724, https://doi.org/10.1038/ncomms8724, 2015.
Fer, I., Lemmin, U., and Thorpe, S. A.: Winter cascading of cold water in Lake Geneva, J. Geophys. Res., 107, 3060, https://doi.org/10.1029/2001JC000828, 2002.
Forrest, A. L., Laval, B. E., Pieters, R., and Lim, D. S. S.: A cyclonic gyre in an ice-covered lake, Limnol. Oceanogr., 58, 363–375, https://doi.org/10.4319/lo.2013.58.1.0363, 2013.
Fultz, D., Long, R. R., Owens, G. V., Bohan, W., Kaylor, R., and Weil, J.: Studies of Thermal Convection in a Rotating Cylinder with Some Implications for Large-Scale Atmospheric Motions, in: Studies of Thermal Convection in a Rotating Cylinder with Some Implications for Large-Scale Atmospheric Motions, Meteorological Monographs, vol 4., American Meteorological Society, Boston, MA, https://doi.org/10.1007/978-1-940033-37-2_1, 1959.
Hampton, S. E., Galloway, A. W. E., Powers, S. M., Ozersky, T., Woo, K. H., Batt, R. D., Labou, S. G., O'Reilly, C. M., Sharma, S., Lottig, N. R., Stanley, E. H., North, R. L., Stockwell, J. D., Adrian, R., Weyhenmeyer, G. A., Arvola, L., Baulch, H. M., Bertani, I., Bowman, L. L., Carey, C. C., Catalan, J., Colom-Montero, W., Domine, L. M., Felip, M., Granados, I., Gries, C., Grossart, H.-P., Haberman, J., Haldna, M., Hayden, B., Higgins, S. N., Jolley, J. C., Kahilainen, K. K., Kaup, E., Kehoe, M. J., MacIntyre, S., Mackay, A. W., Mariash, H. L., McKay, R. M., Nixdorf, B., Nõges, P., Nõges, T., Palmer, M., Pierson, D. C., Post, D. M., Pruett, M. J., Rautio, M., Read, J. S., Roberts, S. L., Rücker, J., Sadro, S., Silow, E. A., Smith, D. E., Sterner, R. W., Swann, G. E. A., Timofeyev, M. A., Toro, M., Twiss, M. R., Vogt, R. J., Watson, S. B., Whiteford, E. J., and Xenopoulos, M. A.: Ecology under lake ice, Ecol. Lett., 20, 98–111, https://doi.org/10.1111/ele.12699, 2017.
Heimpel, M., Gastine, T., and Wicht, J.: Simulation of deep-seated zonal jets and shallow vortices in gas giant atmospheres, Nat. Geosci., 9, 19–23, https://doi.org/10.1038/ngeo2601, 2016.
Holland, P. R., Kay, A., and Botte, V.: Numerical modelling of the thermal bar and its ecological consequences in a river-dominated lake, J. Mar. Syst., 43, 61–81, https://doi.org/10.1016/S0924-7963(03)00089-7, 2003.
Huang, J. C. K.: The thermal bar, Geophys. Fluid Dyn., 3, 1–25, https://doi.org/10.1080/03091927208236071, 1972.
Huang, W., Zhang, J., Leppäranta, M., Li, Z., Cheng, B., and Lin, Z.: Thermal structure and water-ice heat transfer in a shallow ice-covered thermokarst lake in central Qinghai-Tibet Plateau, J. Hydrol., 578, 124122, https://doi.org/10.1016/J.JHYDROL.2019.124122, 2019.
Huttula, T., Pulkkanen, M., Arkhipov, B., Leppäranta, M., Solbakov, V., Shirasawa, K., and Salonen, K.: Modelling circulation in an ice-covered lake, Est. J. Earth Sci., 59, 298, https://doi.org/10.3176/earth.2010.4.06, 2010.
Jackett, D. R. and Mcdougall, T. J.: Minimal Adjustment of Hydrographic Profiles to Achieve Static Stability, J. Atmos. Ocean. Tech., 12, 381–389, https://doi.org/10.1175/1520-0426(1995)012<0381:maohpt>2.0.co;2, 1995.
Julien, K., Knobloch, E., Rubio, A. M., and Vasil, G. M.: Heat transport in low-Rossby-number Rayleigh-Bénard convection, Phys. Rev. Lett., 109, 254503, https://doi.org/10.1103/PhysRevLett.109.254503, 2012.
Karlsson, J., Giesler, R., Persson, J., and Lundin, E.: High emission of carbon dioxide and methane during ice thaw in high latitude lakes, Geophys. Res. Lett., 40, 1123–1127, https://doi.org/10.1002/grl.50152, 2013.
King, E. M., Stellmach, S., Noir, J., Hansen, U., and Aurnou, J. M.: Boundary layer control of rotating convection systems, Nature, 457, 301–304, https://doi.org/10.1038/nature07647, 2009.
Kirillin, G., Leppäranta, M., Terzhevik, A., Granin, N., Bernhardt, J., Engelhardt, C., Efremova, T., Golosov, S., Palshin, N., Sherstyankin, P., Zdorovennova, G., and Zdorovennov, R.: Physics of seasonally ice-covered lakes: a review, Aquat. Sci., 74, 659–682, https://doi.org/10.1007/s00027-012-0279-y, 2012.
Kirillin, G. B., Forrest, A. L., Graves, K. E., Fischer, A., Engelhardt, C., and Laval, B. E.: Axisymmetric circulation driven by marginal heating in ice-covered lakes, Geophys. Res. Lett., 42, 2893–2900, https://doi.org/10.1002/2014GL062180, 2015.
Leppäranta, M., Reinart, A., Erm, A., Arst, H., Hussainov, M., and Sipelgas, L.: Investigation of ice and water properties and under-ice light fields in fresh and Brackish water bodies, Hydrol. Res., 34, 245–266,https://doi.org/10.2166/nh.2003.0006, 2003.
Likens, G. E. and Hasler, A. D.: Movements of radiosodium (Na 24) within an ice-covered lake, Limnol. Oceanogr., 7, 48–56, https://doi.org/10.4319/lo.1962.7.1.0048, 1962.
Likens, G. E. and Ragotzkie, R. A.: Rotary circulation of water in an ice-covered lake, SIL Proceedings, 16, 126–133, https://doi.org/10.1080/03680770.1965.11895674, 1966.
Malm, J., Grahn, L., Mironov, D., and Terzhevik, A.: Field investigation of the thermal bar in Lake Ladoga, spring 1991, Nord. Hydrol., 24, 339–358, https://doi.org/10.2166/nh.1993.12, 1993.
Malm, J., Terzhevik, A., Bengtsson, L., Boyarinov, P., Glinsky, A., Palshin, N., and Petrov, M.: Temperature and salt content regimes in three shallow ice-covered lakes: 1. Temperature, salt content, and density structure, Nord. Hydrol., 28, 99–128, https://doi.org/10.2166/nh.1997.0007, 1997.
Malm, J., Bengtsson, L., Terzhevik, A., Boyarinov, P., Glinsky, A., Palshin, N., and Petrov, M.: Field study on currents in a shallow, ice-covered lake, Limnol. Oceanogr., 43, 1669–1679, https://doi.org/10.4319/lo.1998.43.7.1669, 1998.
Marshall, J., Adcroft, A., Hill, C., Perelman, L., and Heisey, C.: A finite-volume, incompressible Navier Stokes model for studies of the ocean on parallel computers, J. Geophys. Res.-Oceans, 102, 5753–5766, https://doi.org/10.1029/96JC02775, 1997a.
Marshall, J., Hill, C., Perelman, L. and Adcroft, A.: Hydrostatic, quasi-hydrostatic, and nonhydrostatic ocean modeling, J. Geophys. Res.-Oceans, 102, 5733–5752, https://doi.org/10.1029/96JC02776, 1997b.
Messager, M. L., Lehner, B., Grill, G., Nedeva, I., and Schmitt, O.: Estimating the volume and age of water stored in global lakes using a geo-statistical approach, Nat. Commun., 7, 1–11, https://doi.org/10.1038/ncomms13603, 2016.
Mironov, D., Terzhevik, A., Kirillin, G., Jonas, T., Malm, J., and Farmer, D.: Radiatively driven convection in ice-covered lakes: Observations, scaling, and a mixed layer model, J. Geophys. Res., 107, 3032, https://doi.org/10.1029/2001JC000892, 2002.
MITgcm Massachusetts Institute of Technology General Circulation Model: available at: https://mitgcm.org/, last access: 5 December 2020.
Monismith, S. G., Imberger, J., and Morison, M. L.: Convective motions in the sidearm of a small reservoir, Limnol. Oceanogr., 35, 1676–1702, https://doi.org/10.4319/lo.1990.35.8.1676, 1990.
Nolan, M., Liston, G., Prokein, P., Brigham-Grette, J., Sharpton, V. L., and Huntzinger, R.: Analysis of lake ice dynamics and morphology on Lake El'gygytgyn, NE Siberia, using synthetic aperture radar (SAR) and Landsat, J. Geophys. Res. Atmos., 108, ALT 3-1–ALT-3-12, https://doi.org/10.1029/2001jd000934, 2003.
Ramón, C. L., Ulloa, H. N., Doda, T., Winters, K., and Bouffard, D.: Bathymetry and latitude modify lake warming under ice, Data set, Zenodo, https://doi.org/10.5281/zenodo.4027393, 2020.
Read, P. L., Jacoby, T. N. L., Rogberg, P. H. T., Wordsworth, R. D., Yamazaki, Y. H., Miki-Yamazaki, K., Young, R. M. B., Sommeria, J., Didelle, H., and Viboud, S.: An experimental study of multiple zonal jet formation in rotating, thermally driven convective flows on a topographic beta-plane, Phys. Fluids, 27, 085111, https://doi.org/10.1063/1.4928697, 2015.
Rizk, W., Kirillin, G., and Leppäranta, M.: Basin-scale circulation and heat fluxes in ice-covered lakes, Limnol. Oceanogr., 59, 445–464, https://doi.org/10.4319/lo.2014.59.2.0445, 2014.
Salonen, K., Pulkkanen, M., Salmi, P., and Griffiths, R. W.: Interannual variability of circulation under spring ice in a boreal lake, Limnol. Oceanogr., 59, 2121–2132, https://doi.org/10.4319/lo.2014.59.6.2121, 2014.
Schwefel, R., Gaudard, A., Wüest, A., and Bouffard, D.: Effects of climate change on deepwater oxygen and winter mixing in a deep lake (Lake Geneva): Comparing observational findings and modeling, Water Resour. Res., 52, 8811–8826, https://doi.org/10.1002/2016WR019194, 2016.
Sharma, S., Blagrave, K., Magnuson, J. J., O'Reilly, C. M., Oliver, S., Batt, R. D., Magee, M. R., Straile, D., Weyhenmeyer, G. A., Winslow, L., and Woolway, R. I.: Widespread loss of lake ice around the Northern Hemisphere in a warming world, Nat. Clim. Chang., 9, 227–231, https://doi.org/10.1038/s41558-018-0393-5, 2019.
Smith, C. A., Speer, K. G., and Griffiths, R. W.: Multiple Zonal Jets in a Differentially Heated Rotating Annulus, J. Phys. Oceanogr., 44, 2273–2291, https://doi.org/10.1175/JPO-D-13-0255.1, 2014.
Sommeria, J., Meyers, S. D., and Swinney, H. L.: Laboratory model of a planetary eastward jet, Nature, 337, 58–61, https://doi.org/10.1038/337058a0, 1989.
Stefanovic, D. L. and Stefan, H. G.: Two-dimensional temperature and dissolved oxygen dynamics in the littoral region of an ice-covered lake, Cold Reg. Sci. Technol., 34, 159–178, https://doi.org/10.1016/S0165-232X(02)00003-4, 2002.
Ulloa, H. N., Winters, K. B., Wüest, A., and Bouffard, D.: Differential Heating Drives Downslope Flows that Accelerate Mixed-Layer Warming in Ice-Covered Waters, Geophys. Res. Lett., 46, 13872–13882, https://doi.org/10.1029/2019GL085258, 2019.
Vallis, G. K.: Atmospheric and oceanic fluid dynamics: Fundamentals and large-scale circulation, second edn., Cambridge University Press, Cambridge, UK, 2017.
Welch, H. E. and Bergmann, M. A.: Water circulation in small Arctic lakes in winter., Can. J. Fish. Aquat. Sci., 42, 506–520, https://doi.org/10.1139/f85-068, 1985.
Wells, M. G. and Sherman, B.: Stratification produced by surface cooling in lakes with significant shallow regions, Limnol. Oceanogr., 46, 1747–1759, https://doi.org/10.4319/lo.2001.46.7.1747, 2001.
Winters, K. B., Ulloa, H. N., Wüest, A., and Bouffard, D.: Energetics of Radiatively Heated Ice-Covered Lakes, Geophys. Res. Lett., 46, 8913–8925, https://doi.org/10.1029/2019GL084182, 2019.
Woolway, R. I. and Merchant, C. J.: Worldwide alteration of lake mixing regimes in response to climate change, Nat. Geosci., 12, 271–276, https://doi.org/10.1038/s41561-019-0322-x, 2019.
Yang, B., Wells, M. G., McMeans, B. C., Dugan, H. A., Rusak, J. A., Weyhenmeyer, G. A., et al.: A new thermal categorization of ice‐covered lakes, Geophys. Res. Lett., 48, e2020GL091374, https://doi.org/10.1029/2020GL091374, 2021.
Yang, B., Wells, M. G., Li, J., and Young, J.: Mixing, stratification, and plankton under lake-ice during winter in a large lake: Implications for spring dissolved oxygen levels, Limnol. Oceanogr., 65, 2713–2729, https://doi.org/10.1002/lno.11543, 2020.