the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Quantifying new water fractions and transit time distributions using ensemble hydrograph separation: theory and benchmark tests
Decades of hydrograph separation studies have estimated the proportions of recent precipitation in streamflow using end-member mixing of chemical or isotopic tracers. Here I propose an ensemble approach to hydrograph separation that uses regressions between tracer fluctuations in precipitation and discharge to estimate the average fraction of new water (e.g., same-day or same-week precipitation) in streamflow across an ensemble of time steps. The points comprising this ensemble can be selected to isolate conditions of particular interest, making it possible to study how the new water fraction varies as a function of catchment and storm characteristics. Even when new water fractions are highly variable over time, one can show mathematically (and confirm with benchmark tests) that ensemble hydrograph separation will accurately estimate their average. Because ensemble hydrograph separation is based on correlations between tracer fluctuations rather than on tracer mass balances, it does not require that the end-member signatures are constant over time, or that all the end-members are sampled or even known, and it is relatively unaffected by evaporative isotopic fractionation.
Ensemble hydrograph separation can also be extended to a multiple regression that estimates the average (or “marginal”) transit time distribution (TTD) directly from observational data. This approach can estimate both “backward” transit time distributions (the fraction of streamflow that originated as rainfall at different lag times) and “forward” transit time distributions (the fraction of rainfall that will become future streamflow at different lag times), with and without volume-weighting, up to a user-determined maximum time lag. The approach makes no assumption about the shapes of the transit time distributions, nor does it assume that they are time-invariant, and it does not require continuous time series of tracer measurements. Benchmark tests with a nonlinear, nonstationary catchment model confirm that ensemble hydrograph separation reliably quantifies both new water fractions and transit time distributions across widely varying catchment behaviors, using either daily or weekly tracer concentrations as input. Numerical experiments with the benchmark model also illustrate how ensemble hydrograph separation can be used to quantify the effects of rainfall intensity, flow regime, and antecedent wetness on new water fractions and transit time distributions.
Please read the corrigendum first before continuing.
-
Notice on corrigendum
The requested paper has a corresponding corrigendum published. Please read the corrigendum first before downloading the article.
-
Article
(7794 KB)
- Corrigendum
-
Supplement
(180 KB)
-
The requested paper has a corresponding corrigendum published. Please read the corrigendum first before downloading the article.
- Article
(7794 KB) - Full-text XML
- Corrigendum
-
Supplement
(180 KB) - BibTeX
- EndNote
For nearly 50 years, chemical and isotopic tracers have been used to quantify the relative contributions of different water sources to streamflow following precipitation events (Pinder and Jones, 1969; Hubert et al., 1969); see also reviews by Buttle (1994) and Klaus and McDonnell (2013), and references therein. As reviewed by Klaus and McDonnell (2013), chemical and isotopic hydrograph separation studies have led to many important insights into runoff generation. Foremost among these has been the realization that even at stormflow peaks, stream discharge is often composed primarily of “old” catchment storage rather than “new” recent precipitation (Sklash et al., 1976; Sklash, 1990; Neal and Rosier, 1990; Buttle, 1994). The previous dominant paradigm, based on little more than intuition, had held that because streamflow responds promptly to rainfall, the storm hydrograph must consist primarily of precipitation that reaches the channel quickly. Isotope hydrograph separations showed that this intuition is often wrong, because the isotopic signatures of stormflow often resemble baseflow or groundwater rather than recent precipitation. These observations have not only overthrown the previous dominant paradigm, but also launched decades of research aimed at unraveling the paradox of how catchments store water for weeks or months, but release it within minutes following the onset of rainfall (Kirchner, 2003).
The foundations of conventional two-component hydrograph separation are straightforward. If one assumes that streamflow is a mixture of two end-members of fixed composition, which I will call for simplicity “new” and “old” water, then at any time j the mass balance for the water itself is
and the mass balance for a conservative tracer is
where Q denotes water flux and C denotes the concentration of a passive chemical tracer or the δ value of 18O or 2H. One can straightforwardly solve Eqs. (1) and (2) to express the fraction of new water in streamflow at any time j as
In typical applications, the new water is recent precipitation and the tracer signature of the old water is obtained from pre-event baseflow, which is generally assumed to originate from long-term groundwater storage.
The assumptions underlying conventional hydrograph separation can be summarized as follows:
-
Streamflow is a mixture formed entirely from the sampled end-members; contributions from other possible streamflow sources (such as vadose zone water or surface storage) are negligible.
-
The samples of the end-members are representative (e.g., the sampled precipitation accurately reflects all precipitation, and the sampled baseflow reflects all pre-event water).
-
The tracer signatures of the end-members are constant through time, or their variations can be taken into account.
-
The tracer signatures of the end-members are significantly different from one another.
As reviewed by Rodhe (1987), Sklash (1990), Buttle (1994), and Klaus and McDonnell (2013), each of these assumptions can be problematic in practice:
-
Hydrograph separation studies often lead to implausible (including negative) inferred contributions of new water, and such anomalous results are sometimes attributed to contributions from un-sampled end-members (e.g., von Freyberg et al., 2017). In such cases, assumption no. 1 is clearly not met.
-
The isotopic composition of precipitation can vary considerably within an event, both spatially and temporally, even in small catchments (e.g., McDonnell et al., 1990; McGuire et al., 2005; Fischer et al., 2017; von Freyberg et al., 2017). Likewise, the isotopic signature of the baseflow or groundwater end-member has been shown to vary in space and time during snowmelt and rainfall events (e.g., Hooper and Shoemaker, 1986; Rodhe, 1987; Bishop, 1991; McDonnell et al., 1991). In these cases, assumptions no. 2 and 3 are not met. Various schemes have been proposed to address this spatial and temporal variability by weighting the isotopic compositions of individual samples, but the validity of these schemes typically rests on strong assumptions about the nature of the runoff generation process and the heterogeneity to be averaged over.
-
When the difference between Cnew and Cold is not large compared to their uncertainties, Eq. (3) becomes unstable and the resulting hydrograph separations become unreliable. This problem can be detected using Gaussian error propagation (Genereux, 1998), but Bansah and Ali (2017) report that less than 20 % of the hydrograph separation studies they reviewed have used it.
One can agree with Buttle (1994) that “despite frequent violations of some of its underlying assumptions, the isotopic hydrograph separation approach has proven to be sufficiently robust to be applied to the study of runoff generation in an increasing number of basins,” at least as a characterization of the community's widespread acceptance of the technique. Nonetheless, there is clearly room for new and different ways to quantify stormflow generation. In addition, weekly or even daily isotope measurements are now becoming available for many catchments, sometimes spanning periods of many years, and despite their many uses (particularly for calibrating hydrological models) there is an obvious need for new ways to extract hydrological insights from such time series.
Here I propose a new method for using isotopes and other conservative tracers to quantify the origins of streamflow. This method is based on statistical correlations among tracer fluctuations in streamflow and one or more candidate water sources, rather than mass balances. As such, it exploits the temporal variability in candidate end-members, rather than requiring them to be constant. It also does not require strict mass balance and thus is relatively insensitive to the presence of unmeasured end-members. Because this method quantifies the average proportions of source waters in streamflow across an ensemble of events or time steps, it does not answer the same question that traditional hydrograph separation does (namely, how fractions of new and old water change over time during individual storm events). Instead, it can answer new and different questions, such as how the average fractions of new and old water vary with stream discharge or precipitation intensity, antecedent moisture, etc. The proposed method is designed to provide insights into stormflow generation from regularly sampled time series, even if those time series have gaps and even if they are sampled at frequencies much lower than the storm response timescale of the catchment.
The purpose of this paper is to describe the method, document its mathematical foundations, and test it against a benchmark model, in which the method's results can be verified by age tracking. Applications to real-world catchments will follow in future papers. Because the proposed method is new and thus must be fully documented, several parts of the presentation (most notably Sect. 4.2–4.4 and Appendix B) necessarily contain strong doses of math. The math can be skipped, or lightly skimmed, by those who only need a general sense of the analysis. A table of symbols is provided at the end of the text.
Here I propose a new type of hydrograph separation based on correlations between tracer fluctuations in streamflow and in one or more end-members. This new approach to hydrograph separation does not have the same goal as conventional hydrograph separation. It does not estimate the contributions of end-members to streamflow for each time step (as in Eq. 3). Instead, it estimates the average end-member contributions to streamflow over an ensemble of time steps – hence its name, ensemble hydrograph separation. The ensemble of time steps may be chosen to reflect different catchment conditions and thus used to map out how those catchment conditions influence end-member contributions to streamflow.
2.1 Basic equations
I will first illustrate this approach with a simple example of a time-varying mixing model. Let us assume that we have measured tracer concentrations in streamflow, and in at least one contributing end-member, over an ensemble of time intervals j. The simplest possible mass balance for the water that makes up streamflow would be
where Qnew represents the water flux in streamflow Q that originates from recent precipitation (or, potentially, any other end-member in which tracers can be measured) during time interval j. All other contributions to streamflow are lumped together as Qold. Conservative mixing implies that
where CQ and Cnew are the tracer concentrations in the stream and the new water, and Cold is the tracer signature of all other sources that contribute to streamflow. Combining Eqs. (4) and (5), we directly obtain
where is the fractional contribution of Qnew to streamflow Q. Equation (6) can be rewritten as
which in turn could be rearranged as a conventional mixing model (Eq. 3), with the important difference that the new and old water concentrations are time-varying rather than constant. If we represent the old water composition using the streamwater concentration during the previous time step, Eq. (7) becomes
The lagged concentration serves as a reference level for measuring fluctuations in precipitation and streamflow tracer concentrations and the correlations between them. Thus, it is not necessary that consists entirely of old water as defined in conventional hydrograph separations (i.e., groundwater or baseflow water). It is only necessary that contains no new water (that is, no precipitation that fell during time step j), and this condition is automatically met because is measured during the previous time step. The net effect of is to factor out the legacy effects of previous tracer inputs and to filter out long-term variations in CQ that could otherwise lead to spurious correlations with Cnew.
The ensemble hydrograph separation approach is based on the observation that Eq. (8) is almost equivalent to the conventional linear regression equation,
where the intercept α and the error term εj can be viewed as subsuming any bias or random error introduced by measurement noise, evapoconcentration effects, and so forth. The analogy between Eqs. (9) and (8) suggests that it may be possible to estimate the average value of from the regression slope of a scatterplot of the streamflow concentration against the new water concentration , both expressed relative to the lagged streamflow concentration .
However, astute readers will notice an important difference between Eqs. (8) and (9): in Eq. (9), the regression slope β is a constant, whereas in Eq. (8) varies from one time step to the next. It is not obvious how an estimate of the (constant) slope β will be related to the (non-constant) or whether this relationship could be affected by the other variables in Eq. (8). The answer to this question can be derived analytically and tested using numerical experiments (see Appendix A). As explained in Appendix A, the regression slope in a scatterplot of versus (Fig. A1d) will closely approximate the average value of (averaged over the ensemble of time steps j), under rather general conditions:
-
The slope of the relationship between and , times the mean of , should be small compared to the average Fnew. This will usually be true for conservative tracers, for two reasons. First, because all streamflow is ultimately derived from new water, mass conservation implies that the mean of should usually be small. Second, unless there is a correlation between storm size and tracer concentration (not just between storm size and tracer variance), the slope of the relationship between and should also be small. Thus the product of these two small terms should be small.
-
Points with large leverage in the scatterplot (i.e., with values far above and below the mean) should not be systematically associated with either high or low values of . Such a systematic association is unlikely unless large storms (which are likely to generate large new water fractions) are also associated with both very high and very low tracer concentrations.
-
As expected for typical sampling and measurement errors, the error term εj should not be strongly correlated with .
Thus the analysis in Appendix A shows that a reasonable estimate of the ensemble average of Fnew should, under typical conditions, be obtainable from the regression slope of a plot of versus (i.e., Eq. 9; Fig. A1d).
The least-squares solution of Eq. (9) can be expressed in several equivalent ways. For consistency with the analysis that will be developed in Sect. 4 below, I will use the following formulation, which is mathematically equivalent to those more commonly seen:
where is the least-squares estimate of β, and Fnew is the average of the over the ensemble of points j. Values of yj that lack a corresponding xj, or vice versa (due to sampling gaps, for example, or lack of precipitation), are omitted.
2.2 Uncertainties
The uncertainty in Fnew, expressed as a standard error, can be written as
where sx and sy are the standard deviations of x and y, rxy is the correlation between them, and neff is the effective sample size, which can be adjusted to account for serial correlation in the residuals (Bayley and Hammersley, 1946; Brooks and Carruthers, 1953; Matalas and Langbein, 1962):
where nxy is the number of pairs of xj and yj, and rsc is the lag-1 serial correlation in the regression residuals . For large nxy, Eq. (12) can be approximated as (Mitchell et al., 1966)
where for all positive rsc, Eq. (13) is conservative (it underestimates neff from Eq. 12), and for rsc=0.5 and nxy>50, for example, Eqs. (12) and (13) differ by less than 3 %. If the scatterplot of versus contains outliers, a robust fitting technique such as iteratively reweighted least squares (IRLS) may yield more reliable estimates of Fnew than ordinary least-squares regression. However, the analyses presented here are based on outlier-free synthetic data generated from a benchmark model (see Sect. 3), so in this paper I have used conventional least squares (Eqs. 10–11) instead.
2.3 New water fraction for time steps with precipitation
The meaning of the new water fraction Fnew depends on how the new water and streamwater are sampled. For example, if the new water concentrations Cnew are measured in daily bulk precipitation samples and the stream water concentrations CQ are measured in instantaneous grab samples taken at the end of each 24 h precipitation sampling period, then Fnew will estimate the average fraction of streamflow that is composed of precipitation from the preceding 24 h. If the sampling interval is weekly instead of daily, then Fnew will estimate the average fraction of streamflow that consists of precipitation from the preceding week. This will generally be larger than the Fnew calculated from daily sampling, for the obvious reason that on average more precipitation will have fallen during the previous week than during the previous 24 h, so this precipitation will comprise a larger fraction of streamflow. Also, if the weekly streamflow concentrations are measured in integrated composite samples rather than instantaneous grab samples, then Fnew will estimate the fraction of same-week precipitation in average weekly streamflow rather than in the instantaneous end-of-week streamflow. The general rule is: Fnew should generally estimate whatever new water has been sampled as Cnew, expressed as a fraction of whatever streamflow has been sampled as CQ.
In all of these cases, from Eq. (10) estimates the average fraction of new water in streamflow during time steps with precipitation, because time steps without precipitation lack a new water tracer concentration and thus must be left out from the regression in Eq. (9). Using Qp to denote discharge during periods with precipitation, we can represent this event new water fraction as .
2.4 New water fraction for all time steps
Periods without precipitation will inherently lack same-day (or same-week) precipitation in streamflow. Thus we can calculate the average fraction of new water in streamflow during all time steps, including those without precipitation, as
where QFnew is the new water fraction of all discharge, is the new water fraction of discharge during time steps with precipitation (as estimated by the regression slope , from Eq. 10), and np∕n is the fraction of time steps that have precipitation. The ratio np∕n in Eq. (14) accounts for the fact that during time steps without rain, the new water contribution to streamflow is inherently zero. The same ratio is also used to estimate the uncertainty in QFnew:
2.5 Volume-weighted new water fractions
The regression derived through Eqs. (4)–(9) gives each time interval j equal weight. As a result, from Eq. (10) can be interpreted as estimating the time-weighted average new water fraction. Alternatively, one can estimate the volume-weighted new water fraction,
where and are the volume-weighted means of x and y (averaged over all j for which xj and yj are not missing),
and the notation j∈(xy) indicates sums taken over all j for which xj and yj are not missing. Equations (16)–(17) yield the slope coefficient for linear regressions like Eq. (9), but with each point weighted by the discharge Qj. We can denote the weighted regression slope as , the volume-weighted new water fraction of time intervals with precipitation, where the asterisk indicates volume-weighting.
If, instead, one wants to estimate the new water fraction in all discharge (during periods with and without precipitation), following the approach in Sect. 2.4 one simply rescales this regression slope by the sum of discharge during time steps with precipitation, divided by total discharge:
where is the volume-weighted new water fraction of all discharge, is the fitted regression slope from Eq. (16), is the average discharge for time steps with precipitation, is the average discharge for all time steps (including during rainless periods), and np∕n is the fraction of time steps with rain.
Because the volume-weighting will typically be uneven, the effective sample size will typically be smaller than n; for example, in the extreme case that one sample had nearly all the weight and the other samples had nearly none, the effective sample size would be roughly 1 instead of nxy. Thus, uncertainty estimates for these volume-weighted new water fractions should take account of the unevenness of the weighting. One can account for uneven weighting by calculating the effective sample size, following Kish (1995), as
where the notation Qj(xy) indicates discharge at time steps j for which pairs of xj and yj exist. Equation (19) evaluates to nxy (as it should) in the case of evenly weighted samples and declines toward 1 (as it should) if a single sample has much greater weight than the others. To obtain an estimate of the effective sample size that accounts for both serial correlation and uneven weighting, one can multiply the expressions in Eqs. (19) and (12) or (13). Combining these approaches, one can estimate the standard error of as
where is the fitted regression slope from Eq. (16).
2.6 New water fraction of precipitation
One can also express the flux of new water as a fraction of precipitation rather than discharge. Recently, von Freyberg et al. (2018) have noted, in the context of conventional hydrograph separation, that expressing event water as a proportion of precipitation rather than discharge may lead to different insights into catchment storm response. Analogously, within the ensemble hydrograph separation framework we can estimate the new water fraction of precipitation, denoted PFnew, as
where is the new water fraction of discharge during time steps with precipitation (as estimated by the regression slope , from Eq. 10), and and are the average discharge and precipitation during these time steps. An alternative strategy is to recast Eq. (8) by multiplying both sides by Qj∕Pj, such that the Fnew on the right-hand side now expresses new water as a fraction of precipitation,
This yields a linear regression similar to Eq. (9), but with yj rescaled,
where the regression slope , which can be calculated from Eq. (10) with the new values yj, should approximate the average new water fraction of precipitation PFnew.
The approaches represented by Eqs. (21) and (22)–(23) are not equivalent. Equation (21) is based on the ad hoc assumption – which is verified by the benchmark tests in Sect. 3.3–3.5 – that the average of (new water in streamflow, as a fraction of precipitation) should approximate the average (new water in streamflow, as a fraction of discharge), rescaled by the ratio of average discharge to average precipitation . This is only an approximation, of course; it relies on the approximation that appears in the middle of the following chain of expressions:
where the “p” subscripts on the angled brackets indicate averages taken only over time intervals with precipitation. Whether this is a good approximation will depend on how Pj, Qj, and are distributed, and how they are correlated with one another. By contrast, the approach outlined in Eqs. (22)–(23) is based on the exact substitution of for , which requires no approximations. The same substitution also leads to two other algebraically equivalent formulations of Eq. (22),
and
But although Eqs. (22), (25), and (26) are algebraically equivalent, their statistical behavior is different when they are used as regression equations to estimate the average value of PFnew. The regression estimate of PFnew depends on the distributions of Pj, Qj, and and their correlations with each other, and benchmark testing shows that Eq. (22) yields reasonably accurate estimates of PFnew, but Eqs. (25) and (26) do not. One can also note that the approach outlined in Eq. (21) – the other approach that is successful in benchmark tests – represents an ad hoc time averaging of Pj and Qj in Eq. (22), because it is formally equivalent to
The precise interpretation of PFnew depends on how streamflow is sampled. If the streamflow tracer concentrations come from integrated composite samples over each day or week, then PFnew can be interpreted as the fraction of precipitation that becomes same-day or same-week streamflow. If the streamflow tracer concentrations instead come from instantaneous grab samples (as is more typical), then PFnew can be interpreted as the rate of new water discharge at that time (typically the end of the precipitation sampling interval), as a fraction of the average rate of precipitation. Adapting terminology from the literature of transit time distributions (TTDs), we can call PFnew the “forward” new water fraction because it represents the fraction of precipitation that will exit as streamflow soon (during the same time step), and call and QFnew “backward” new water fractions because they represent the fraction of streamflow that entered the catchment a short time ago. Although the backward new water fraction of discharge comes in two forms ( or QFnew), depending on whether one includes or excludes rainless periods, the forward new water fraction PFnew can only be defined for time steps with precipitation (otherwise PFnew represents the ratio between zero new water and zero precipitation and thus is undefined).
Readers should keep in mind that although PFnew represents the fraction of precipitation that becomes same-day (or same-week) streamflow, different fractions of precipitation may leave the catchment the same day (or week) by other pathways, most notably by evapotranspiration. One could also estimate PFnew for water that leaves the catchment by evapotranspiration if one had tracer time series for evapotranspiration fluxes, but at present such time series are not available. Thus, to echo the principle outlined in Sect. 2.3 above, the new water fraction of precipitation does not represent the forward new water fraction for all possible pathways, but only whatever pathway has been sampled.
2.7 Volume-weighted new water fraction of precipitation
The new water fraction of precipitation as estimated by Eq. (21) is a time-weighted average, in which each day with precipitation counts equally. One may also want to estimate the volume-weighted new water fraction of precipitation, which we can denote as , in keeping with the naming conventions used above. We can estimate at least two different ways. The first method involves recognizing that we are seeking the ratio between the total volume of new water – that is, same-day precipitation reaching streamflow – and the total volume of precipitation. This will equal the volume-weighted new water fraction of discharge (total new water divided by total discharge, which has already been derived in Sect. 2.5 above), rescaled by the ratio of total discharge to total precipitation:
where and are the average rates of discharge and precipitation (averaged over all time steps), is the average discharge on days with rain, and np∕n is the fraction of time steps with rain. An alternative strategy, which yields nearly equivalent results in benchmark tests, precipitation-weights the regression for PFnew (Eq. 22), yielding
where and are the precipitation-weighted means of x and y (averaged over all j for which xj and yj are not missing),
and where the regression slope approximates the precipitation-weighted average forward new water fraction .
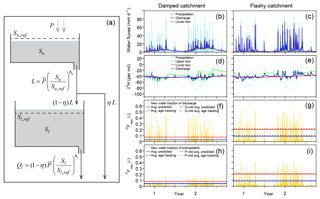
Figure 1Schematic diagram of the benchmark model (a), with 2-year excerpts from illustrative simulations of its behavior (b–i). Model parameters for simulations of damped catchment response (b, d, f, h) are mm, mm, bu=10, bl=3, and η=0.3. For simulations of flashy catchment response (c, e, g, i), all but one of the parameters are the same; only η is changed to 0.8 and a different random realization of precipitation isotopes is used. The same daily precipitation time series (Smith River, Mediterranean climate) is used in both cases. The isotopic composition of streamflow exhibits complex dynamics over multiple timescales (blue line in d, e), as dominance shifts between the upper and lower boxes (green and orange lines, respectively, in d, e). Like the discharge and its isotopic composition, the fraction of discharge comprised of same-day precipitation (the new water fraction of discharge, QFnew, f, g) exhibits complex nonstationary dynamics. Nonetheless, its long-term average (dashed blue line) is well predicted by ensemble hydrograph separation (solid blue line); the same is true of the discharge-weighted average (dashed and solid red lines). The fraction of precipitation appearing in same-day discharge (the forward new water fraction, PFnew, h, i) is somewhat less variable, but both its average and precipitation-weighted average are also well predicted by ensemble hydrograph separation (solid and dashed blue and red lines). In several cases the dashed and solid lines cannot be distinguished because they overlap.
3.1 Benchmark model
To test the methods outlined in Sect. 2 above, I use synthetic data generated by a simple two-box lumped-parameter catchment model. This model is documented in greater detail in Kirchner (2016a) and will be described only briefly here. As shown in Fig. 1a, drainage L from the upper box is a power function of the storage Su within the box; a fraction η of this drainage flows directly to streamflow, and the complementary fraction 1−η recharges the lower box, which drains to streamflow at a rate Ql that is a power function of its storage Sl. The model's behavior is determined by five parameters: the equilibrium storage levels Su, ref and Sl, ref in the upper and lower boxes, their drainage exponents bu and bl, and the drainage partitioning coefficient η. For simplicity, evapotranspiration is not explicitly simulated; instead, the precipitation inputs can be considered to be effective precipitation, net of evapotranspiration losses. Discharge from both boxes is assumed to be non-age selective, meaning that discharge is taken proportionally from each part of the age distribution. Tracer concentrations and mean ages are tracked under the assumption that the boxes are each well mixed but also distinct from one another, so their tracer concentrations and water ages will differ. Water ages and tracer concentrations are also tracked in daily age bins up to an age of 70 days, and mean water ages are tracked in both the upper and lower boxes.
The model operates at a daily time step, with the storage evolution of the lower box calculated by a weighted combination of the partly implicit trapezoidal method (for greater accuracy) and the fully implicit backward Euler method (for guaranteed stability). Unlike in Kirchner (2016a), here the storage evolution of the upper box is calculated by forward Euler integration at 50 sub-daily time steps of 0.02 days (roughly 30 min) each. At this time step, forward Euler integration is stable across the entire parameter ranges used in this paper and is more accurate than daily time steps of trapezoidal or backward Euler integration (which are still adequate for the lower box, where storage volumes change more slowly). Following Kirchner (2016a), the model is driven with three different real-world daily rainfall time series, representing a range of climatic regimes: a humid maritime climate with frequent rainfall and moderate seasonality (Plynlimon, Wales; Köppen climate zone Cfb), a Mediterranean climate marked by wet winters and very dry summers (Smith River, California, USA; Köppen climate zone Csb), and a humid temperate climate with very little seasonal variation in average rainfall (Broad River, Georgia, USA; Köppen climate zone Cfa). Synthetic daily precipitation tracer (deuterium) concentrations are generated randomly from a normal distribution with a standard deviation of 20 ‰ and a lag-1 serial correlation of 0.5, superimposed on a seasonal cycle with an amplitude of 10 ‰. The model is initialized at the equilibrium storage levels Su, ref and Sl, ref, with age distributions and tracer concentrations corresponding to steady-state equilibrium values at the mean input fluxes of water and tracer. The model is then run for a 1-year spin-up period; the results reported here are from 5-year simulations following this spin-up period.
For the simulations shown here, the drainage exponents bu and bl are randomly chosen from uniform distributions of logarithms spanning the range of 1–20, and the partitioning coefficient η is randomly chosen from a uniform distribution ranging from 0.1 to 0.9. The reference storage levels Su,ref and Sl, ref are randomly chosen from a uniform distribution of logarithms spanning the ranges of 50–200 mm and 200–2000 mm, respectively. These parameter distributions encompass a wide range of possible behaviors, including both strong and damped response to rainfall inputs.
I illustrate the behavior of the model using two particular parameter sets, one that gives damped response to precipitation ( mm, mm, bu=10, bl=3, and η=0.3) and one that gives a more rapid response (the same parameters, except η=0.8). These parameter values are not preferable to others in any particular way; they simply generate strongly contrasting streamflow and tracer responses that look plausible as examples of small catchment behavior. They can be interpreted as the behavior of two contrasting model catchments, which for simplicity (but with some linguistic imprecision) I will call the “damped catchment” and the “flashy catchment”, as shorthand for “model catchment with parameters giving more damped response” and “model catchment with parameters giving more flashy response”.
The model also simulates the sampling process and its associated errors. I assume that tracer concentrations cannot be measured when precipitation rates are below a threshold of Pthreshold=1 mm day−1, such that tracer samples below this threshold will be missing. I further assume that 5 % of all other precipitation tracer measurements, and 5 % of all streamflow tracer measurements, will be lost at random times due to sampling or analysis failures. I have also added Gaussian random errors (with a standard deviation of 1 ‰) to all tracer measurements.
3.2 Benchmark model behavior
Panels b–i of Fig. 1 show 2 years of simulated daily behavior driven by the Smith River daily precipitation record applied to the damped and flashy catchment parameter sets. The simulated stream discharge responds promptly to rainfall inputs, and unsurprisingly the discharge response is larger in the flashy catchment (Fig. 1b, c). The streamflow isotopic response is strongly damped in both catchments, with isotope ratios between events returning to a relatively stable baseline value composed mostly of discharge from the lower box (Fig. 1d, e). Like the stream discharge and the isotope tracer time series, the instantaneous new water fractions (determined by age tracking within the model) also exhibit complex nonstationary dynamics (Fig. 1f–i). Despite the complexity of the modeled time-series behavior, ensemble hydrograph separation (Eqs. 14, 18, 21, and 28) accurately predicts the averages of these new water fractions, both unweighted and time-weighted, as can be seen by comparing the dashed and solid lines (which sometimes overlap) in Fig. 1f–i.
It should be emphasized that the ensemble hydrograph separation and the benchmark model are completely independent of one another. The ensemble hydrograph separation does not know (or assume) anything about the internal workings of the benchmark model; it knows only the input and output water fluxes and their isotope signatures. This is crucial for it to work in the real world, where any particular assumptions about the processes driving runoff could potentially be violated. Likewise, the benchmark model is not designed to conform to the assumptions underlying the ensemble hydrograph separation method. It would be relatively trivial to model a tracer time series assuming that new water constituted a fixed fraction of discharge, and then demonstrate that this fraction can be retrieved from the tracer behavior. What Fig. 1 demonstrates is much less obvious, and more important: that even when the new water fraction is highly dynamic and nonstationary, an appropriate analysis of tracer behavior can accurately estimate its mean.
3.3 Benchmark tests: random parameter sets
This result holds not just for the two parameter sets shown in Fig. 1, but throughout the parameter ranges that are tested in the benchmark model. The scatterplots shown in Fig. 2 show new water fractions estimated by ensemble hydrograph separation, compared to the true average new water fractions determined by age tracking in the benchmark model, for 1000 random parameter sets spanning the parameter ranges described in Sect. 3.1. Figure 2 shows that ensemble hydrograph separation yields reasonably accurate estimates of average event new water fractions (Fig. 2a, b), new water fractions of discharge (Fig. 2c) and precipitation (Fig. 2d), and volume-weighted new water fractions (Fig. 2e, f). Estimates derived from single years of data (Fig. 2b) understandably exhibit greater scatter than those derived from 5 years of data (Fig. 2a), but in all of the plots shown in Fig. 2 there is no evidence of significant bias (the data clouds cluster around the 1:1 lines). The scatter of the points around the 1:1 line generally agrees with the standard errors estimated from Eqs. (11), (15), and (20), suggesting that these uncertainty estimates are also reliable.
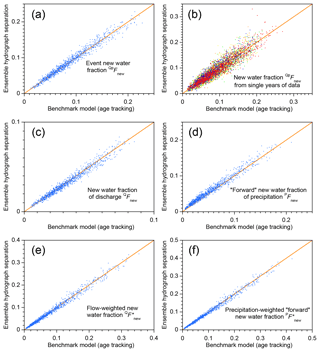
Figure 2New water fractions predicted from tracer dynamics using ensemble hydrograph separation, compared to averages of time-varying new water fractions determined from age tracking in the benchmark model. Diagonal lines show perfect agreement. Each scatterplot shows 1000 points, each of which represents an individual catchment, with its own individual random set of model parameters (i.e., catchment characteristics), randomly generated precipitation tracer time series, and random set of measurement errors and missing values (see Sect. 3.1). The daily precipitation amounts are the same (Smith River time series; Mediterranean climate) in each case. The event new water fraction (a, b) is the average fraction of new (same-day) water in streamflow during time steps with precipitation, as described in Sect. 2.3. Panel (a) shows event new water fractions estimated from 5 years of simulated tracer data; panel (b) shows the same quantity estimated from single years (each year is denoted by a different color). Averaging over the 5 years reduces both the range and the scatter, compared to the single-year estimates. The new water fraction of discharge (c) is the fraction of same-day precipitation in streamflow, averaged over all time steps including rainless periods (Eq. 14, Sect. 2.4); its flow-weighted counterpart (e) is calculated using Eqs. (16)–(18) of Sect. 2.5. The forward new water fraction (the fraction of precipitation that becomes same-day streamflow; d) is calculated using Eq. (21), and its precipitation-weighted counterpart (f) is calculated using Eq. (28). In all cases there is little evidence of bias, and the scatter around the 1:1 line is relatively small.
Mean transit times have often been estimated in the catchment hydrology literature, often under the assumption that they should also be correlated with other timescales of catchment transport and mixing as well. This naturally leads to the question, in the context of the present study, of whether there is a systematic relationship between mean transit times and new water fractions, such that they could potentially be predicted from one another. The benchmark model allows a direct test of this conjecture, because it tracks mean water ages as well as new water fractions. Figure 3a shows that, across the 1000 random parameter sets from Fig. 2, the relationship between new water fractions and mean transit times is a nearly perfect shotgun blast: mean transit times vary from about 40 to 400 days and new water fractions vary from nearly zero to nearly 0.1, with almost no correlation between them. Both of these quantities are estimated from age tracking in the benchmark model, so their lack of any systematic relationship does not arise from difficulties in estimating either of them from tracer data. It instead arises because the upper tails of transit time distributions (reflecting the amounts of streamflow with very old ages) exert strong influence on mean transit times, but have no effect on new water fractions (reflecting same-day streamflow).
I have recently proposed the “young water fraction”, the fraction of streamflow younger than about 2.3 months, as a more robust metric of water age than the mean transit time (Kirchner, 2016b). Figure 3b shows that, like the mean transit time, the young water fraction is also a poor predictor of the new water fraction, beyond the obvious constraint that new water (≤1 day old) must be a small fraction of young water (≤69 days old). The new water fraction will only be correlated with the young water fraction or mean transit time if the shape of the underlying transit time distribution is held constant, which is not the case for the 1000 random parameter sets considered here and is not likely to be true in real-world catchments either.
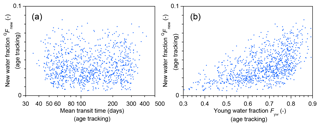
Figure 3Average new water fractions (same-day precipitation in streamflow) for the 1000 simulated catchments (i.e., 1000 model parameter sets) shown in Fig. 2, compared to the catchment mean transit time and the young water fraction Fyw (the fraction of streamflow younger than 2.3 months). All values plotted here are determined from age tracking within the benchmark model, and thus are true values, without any errors associated with estimating these quantities from tracer data. Neither mean transit time nor the young water fraction can reliably predict the fraction of new water in streamflow.
3.4 Benchmark tests: weekly tracer sampling
Many long-term water isotope time series have been sampled at weekly intervals. Can new water fractions be estimated reliably from such sparsely sampled records? To find out, I aggregated the benchmark model's daily time series to weekly intervals, volume-weighting the isotopic composition of precipitation to simulate the effects of weekly bulk precipitation sampling, and subsampling streamflow isotopes every seventh day to simulate weekly grab sampling. I then performed ensemble hydrograph separation on the aggregated weekly data, using the methods presented in Sect. 2.
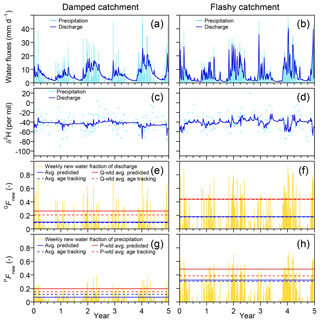
Figure 4Illustrative simulations of weekly water fluxes, deuterium concentrations, and new water fractions. The benchmark model, precipitation forcing, and parameter values are identical to those in Fig. 1. Although the isotope tracer concentrations and new water fractions exhibit complex nonstationary dynamics, ensemble hydrograph separation yields reasonable estimates of the average backward and forward weekly new water fractions, as shown in (e, f) and (g, h), respectively. Panels (a) and (b) show weekly average rates of precipitation and discharge. Panels (c) and (d) show the weekly volume-weighted isotopic composition of precipitation (mimicking what would be collected in a weekly rain sample) and the instantaneous composition of discharge at the end of each week (mimicking what would be collected in a weekly grab sample). Panels (e) and (f) show the fraction of discharge that is composed of same-week precipitation (the weekly new water fraction; yellow lines), as determined from model age tracking, and its long-term average (dashed blue line), compared to the new water fraction predicted by ensemble hydrograph separation (solid blue line) from the weekly samples shown in (b). Panels (g) and (h) show the fraction of precipitation that becomes same-week discharge (the weekly new water fraction of precipitation, or forward new water fraction, yellow lines), as determined from model age tracking, and its long-term average (dashed blue line), compared to the new water fraction predicted by ensemble hydrograph separation (solid blue line). Discharge-weighted and precipitation-weighted average new water fractions, and their predicted values, are shown by red solid and dashed lines.
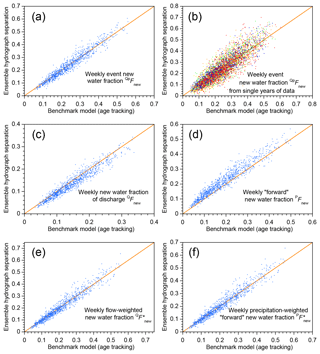
Figure 5New water fractions estimated from weekly tracer dynamics using ensemble hydrograph separation, compared to averages of time-varying new water fractions determined from age tracking in the benchmark model. Plots are similar to those in Fig. 2, except here they are derived from simulated weekly sampling of tracer concentrations in precipitation and streamflow. Diagonal lines show perfect agreement. Each scatterplot shows 1000 points, each representing an individual random set of parameters, a randomly generated precipitation tracer time series, and a random set of measurement errors and missing values (see Sect. 3.1). The daily precipitation amounts are the same (Smith River time series) in each case. The event new water fraction (a, b) is the average fraction of new (same-day) water in streamflow during time steps with precipitation, as described in Sect. 2.3. Panel (a) shows event new water fractions estimated from 5 years of simulated weekly tracer data; panel (b) shows the same quantity estimated from single years of simulated weekly tracer data (each year is denoted by a different color). Averaging over the 5 years reduces scatter compared to the individual-year estimates. The new water fraction of discharge (c) is the fraction of same-day precipitation in streamflow, averaged over all time steps including rainless periods (Eq. 14, Sect. 2.4); its flow-weighted counterpart (e) is calculated using Eqs. (16)–(18) of Sect. 2.5. The forward new water fraction (the fraction of precipitation that becomes same-day streamflow; d) is calculated using Eq. (21), and its precipitation-weighted counterpart (f) is calculated using Eq. (28). There is only slight visual evidence of bias, and the scatter around the 1:1 line is small compared to the range spanned by the new water fractions.
Figure 4 shows the behavior of the benchmark model at weekly resolution for both the damped and flashy catchments. At the weekly timescale, the benchmark model exhibits complex nonstationary dynamics in discharge (panels a, b), water isotopes (panels c, d), and new water fractions (panels e, h). Nonetheless – and even though the weekly sampling timescale is much longer than the timescales of hydrologic response in the system – ensemble hydrograph separation yields reasonable estimates for the mean new water fractions of both precipitation and discharge (both unweighted and flow-weighted), as one can see by comparing the dashed and solid lines in Fig. 4e–h.
A comparison of Figs. 1 and 4 shows that the isotopic signature of precipitation is less variable among the weekly samples than among the daily samples, reflecting the fact that the weekly bulk samples of precipitation will inherently average over the sub-weekly variability in daily rainfall. By contrast, the weekly grab samples of streamflow lose all information about what is happening on shorter timescales. The new water fractions calculated from the weekly data are distinctly higher than those calculated from the daily data, owing to the fact that the definition of new water depends on the sampling frequency: the proportion of water ≤7 days old (new under weekly sampling) can never be less than the proportion ≤1 day old (new under daily sampling).
Figure 5 shows scatterplots comparing new water fractions estimated by ensemble hydrograph separation and those determined by age tracking in the benchmark model, analogous to Fig. 2 but for weekly instead of daily sampling. The weekly new water fractions are larger than the daily ones, for the reasons described above, and exhibit more scatter because they are based on fewer data points than their daily counterparts are. A small overestimation bias is visually evident in Fig. 2d and an even smaller underestimation bias is evident in Fig. 2c. These reservations notwithstanding, Fig. 5 shows that ensemble hydrograph separation can reliably predict new water fractions of both discharge and precipitation, with and without volume-weighting, based on weekly tracer samples.
3.5 Variations in new water fractions with discharge, precipitation, and seasonality
Ensemble hydrograph separation does not require continuous data as input, so it can be used to estimate Fnew values for (potentially discontinuous) subsets of a time series that reflect conditions of particular interest. For example, if we split the time series shown in Fig. 1 into several discharge ranges, we can see that at higher flows, tracer fluctuations in the stream are more strongly correlated with tracer fluctuations in precipitation (Fig. 6a, b). Each of the regression slopes in Fig. 6a, b defines the event new water fraction for the corresponding discharge range. Repeating this analysis for each 10 % interval of the discharge distribution (0th–10th percentile, 10th–20th percentile, etc.), plus the 95th–100th percentile, yields the profiles of as functions of discharge, as shown by the blue dots in Fig. 6c–h. The green squares show the corresponding forward new water fractions PFnew for comparison. The light blue and light green lines show the corresponding true new water fractions determined by age tracking in the benchmark model.
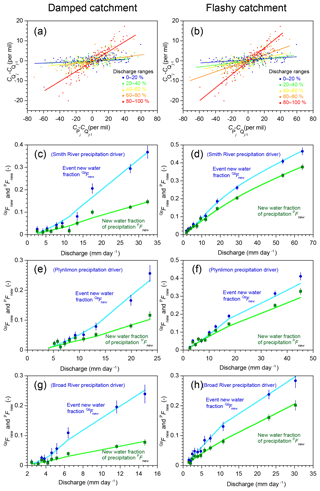
Figure 6Variations in new water fractions across ranges of discharge. (a, b) Relationship between tracer concentrations in precipitation and streamflow in the benchmark model run shown in Fig. 1, stratified by percentiles of the frequency distribution of discharge, for damped and rapid response parameter sets. In these coordinates, the slopes of the regression lines through the ensembles of points estimate their average event new water fractions (Eq. 10; Sect. 2.3). (c–h) Variation in new water fractions across discharge bins in the benchmark model. Dark blue and green symbols show estimates of the event new water fraction of discharge ( and the forward new water fraction (fraction of precipitation appearing in same-day streamflow, PFnew, Eq. 21) for each decile of the daily discharge distribution (the leftmost 10 points) and the uppermost 5 % (the rightmost point). Error bars show standard errors, where these are larger than the plotting symbols. Light blue and light green lines show the corresponding true new water fractions measured by age tracking in the benchmark model. The three rows (c–d, e–f, and g–h) show catchment response to three different precipitation climatologies (Smith River, Plynlimon, and Broad River), for both the damped response parameter set (c, e, g) and the flashy response parameter set (d, f, h). The new water fractions and PFnew vary strongly with discharge. Ensemble hydrograph separation accurately estimates both QpFnew and PFnew across the full range of discharge for all three forcings and both parameter sets.
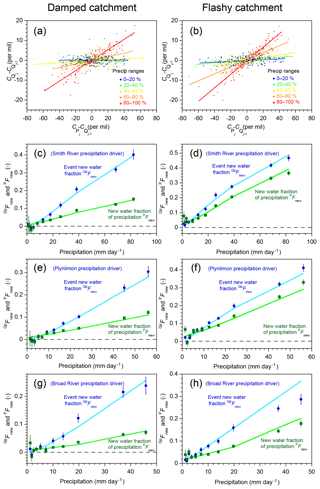
Figure 7Variations in new water fractions across ranges of precipitation. (a, b) Relationship between tracer concentrations in precipitation and streamflow in the benchmark model run shown in Fig. 1, stratified by percentiles of the frequency distribution of precipitation, for damped and rapid response parameter sets. In these coordinates, the slope of the regression line through each ensemble of points estimates its average event new water fraction QpFnew (Eq. 10; Sect. 2.3). (c–h) Variation in new water fractions across precipitation bins in the benchmark model. Dark blue and green symbols show estimates of the event new water fraction of discharge (QpFnew) and the forward new water fraction (PFnew, the fraction of precipitation appearing in same-day streamflow; Eq. 21). Average QpFnew and PFnew values are plotted for each decile of the daily precipitation distribution (the leftmost 10 points) and the uppermost 5 % (the rightmost point), excluding precipitation amounts less than 1 mm day−1 (see text). Error bars show standard errors, where these are larger than the plotting symbols. Light blue and light green lines show the corresponding true new water fractions measured by age tracking in the benchmark model. The three rows (c–d, e–f, and g–h) show catchment response to three different precipitation climatologies (Smith River, Plynlimon, and Broad River), for both the damped response parameter set (c, e, g) and the flashy response parameter set (d, f, h). The new water fractions QpFnew and PFnew vary strongly with daily precipitation. Ensemble hydrograph separation accurately estimates both and PFnew across the full range of precipitation for all three forcings and both parameter sets.
If, instead, we split the time series shown in Fig. 1 into subsets reflecting ranges of precipitation rates rather than discharge, we obtain Fig. 7. Figure 7 is a counterpart to Fig. 6, but with and PFnew plotted as functions of rainfall rates rather than discharge. The two figures exhibit broadly similar behavior. Unsurprisingly, new water fractions are higher at higher discharges and rainfall rates, because under these conditions a higher fraction of discharge comes from the upper box, which has younger water. Forward new water fractions are typically smaller than event new water fractions, because during storms the rainfall rate is higher than the streamflow rate, so the ratio between same-day streamflow and the total rainfall rate (PFnew) will necessarily be smaller than the ratio between same-day streamflow and the total streamflow rate (). Exceptions to this rule arise when rainfall rates are lower than discharge rates, such as during periods of light rainfall while streamflow is still undergoing recession from previous heavy rain. Thus the green and blue curves cross over one another at the left-hand edges of Fig. 7c–h, whereas in Fig. 6c–h they do not.
Three conclusions can be drawn from Figs. 6 and 7. First, in these model catchments, new water fractions vary dramatically between low flows and high flows, and between low and high precipitation rates, with the event new water fraction and the forward new water fraction PFnew diverging from one another more at higher flows and higher rainfall forcing. Second, different catchment parameters (different columns in Fig. 6) and different precipitation forcings (different rows in Fig. 6) yield different patterns in the relationships between the new water fractions and PFnew on the one hand and precipitation and discharge on the other. And third, these patterns are accurately quantified by ensemble hydrograph separation, which matches the age-tracking results (shown by the solid lines) within the estimated standard errors in most cases.
Thus the patterns describing how new water fractions change with precipitation and discharge may be useful as signatures of catchment transport behavior and can be estimated directly from tracer time series using ensemble hydrograph separation. These observations raise the question of whether any of these signatures of behavior, as inferred from the patterns in these plots (if not the individual numerical values), might imply something useful about the characteristics of the catchments themselves, ideally in a way that is not substantially confounded by precipitation climatology. A comprehensive answer is not possible within the scope of this paper, since it focuses mostly on just two parameter sets and three precipitation records. But as a first approach, one can try superimposing the results in Figs. 6 and 7 on consistent axes (note that the axes in these figures' various panels differ from one another in order to show the full range of behavior). Doing so yields Fig. 8, which overlays the age-tracking results from Figs. 6c–h and 7c–h in its left- and right-hand panels, respectively. In Fig. 8, catchments with the damped and flashy parameter sets are denoted by green and blue curves, respectively, with different levels of brightness corresponding to the three different precipitation climatologies. The key question is: are there patterns in or PFnew that clearly distinguish the flashy catchment from the damped catchment, regardless of the precipitation forcing? Figure 8a shows an example where this is not the case; instead, the two catchments' behaviors largely overlap in a tangle of blue and green lines. In the other three panels, however (and particularly for the trends in PFnew as a function of precipitation rates, as shown in Fig. 8d), the blue and green curves are relatively distinct from one another, but the different climatologies largely overlap for each catchment. This result suggests that these traces may be useful as diagnostic signatures of catchment characteristics, which are relatively insensitive to precipitation climatology. However, Fig. 8 can only be considered a preliminary indication of what might be possible, rather than a definitive demonstration.
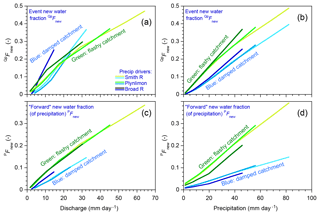
Figure 8Effects of precipitation climatology and catchment properties on discharge dependence and precipitation dependence of new water fractions. The lines plotted here superimpose the model age-tracking results (solid lines) from Figs. 6 and 7. Panels (a) and (d) show how event new water fractions (QpFnew, Sect. 2.3) and forward new water fractions (PFnew, Sect. 2.6) vary as functions of discharge and precipitation, respectively. Green and blue lines show benchmark model behavior under the flashy and damped parameter sets, with three levels of brightness corresponding to the three different precipitation climatologies: Mediterranean climate (Smith River, lightest colors), humid maritime climate (Plynlimon, intermediate colors), and humid temperate climate (Broad River, darkest colors). When event new water fractions are plotted as functions of discharge (a), different catchments and precipitation climatologies overlap. By contrast, in the other three panels (and particularly in d, which shows forward new water fractions as functions of precipitation), the lines for the flashy catchment and the damped catchment are clearly distinct from one another, regardless of precipitation climatology. This suggests that these patterns may be diagnostic of the internal workings of the catchment, but relatively insensitive to the particular rainfall forcing.
The behavior summarized in Figs. 6–8 shows that, in general, new water fractions are functions of both catchment characteristics and precipitation climatology. Moreover, new water fractions will depend on the sequence of precipitation events, not just on their frequency distribution, because they will depend on antecedent wetness. Thus although the ensemble hydrograph separation approach does not require continuous data, and thus can be applied to time series with data gaps, any inferred new water fractions will obviously represent only the particular time intervals that are included in the analysis.
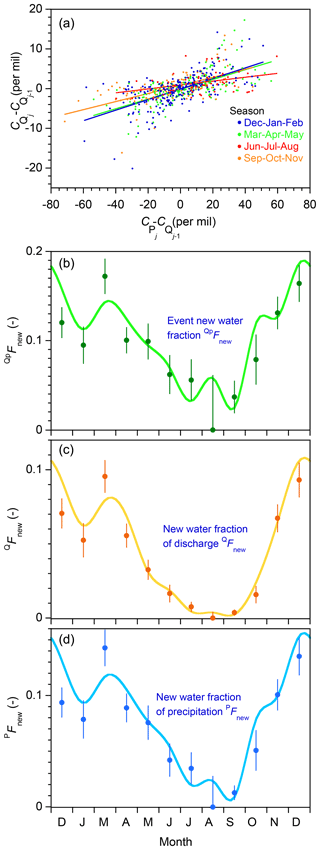
Figure 9Seasonality in new water fractions under Mediterranean climate precipitation forcing. (a) Relationship between tracer concentrations in precipitation and streamflow in the flashy benchmark model run shown in Fig. 1, stratified by season. Each season's event new water fraction can be estimated from the slope of the regression line fitted to the corresponding set of points. (b, c, d) Average event new water fractions (, new water fractions of discharge (QFnew), and forward new water fractions of precipitation (PFnew) calculated from ensembles of all points within each month, across the 5 years of benchmark model simulations. Error bars show standard errors, where these are larger than the plotting symbols. Curves are drawn through true monthly average new water fractions, as determined by age tracking in the benchmark model. Ensemble hydrograph separation reproduces this seasonal pattern in new water fractions reasonably well. The uncertainty estimates also realistically predict the average deviation of the ensemble hydrograph separation estimates from the true age-tracking determinations. Values shown here are generated by the benchmark model with the flashy catchment parameter set and Smith River (Mediterranean climate) precipitation forcing. The new water fractions would exhibit less pronounced seasonality if the rainfall forcing were less strongly seasonal or the catchment response were less flashy.
One implication of the forgoing considerations is that seasonal differences in storm size and frequency should also be reflected in seasonal variations in new water fractions. Figure 9a shows a scatterplot of tracer fluctuations in streamflow and precipitation, color-coded by season, for the flashy catchment simulation shown in Fig. 1. The regression lines (whose slopes define the event new water fractions for the corresponding seasons) show that tracer concentrations in streamflow and precipitation are more tightly coupled in winter and spring than in summer and autumn. Panels b–d of Fig. 9 demonstrate large variations in the event new water fraction , the new water fraction of discharge QFnew, and the forward new water fraction of precipitation PFnew from month to month, with a broad seasonal trend towards larger new water fractions in winter and spring. The month-to-month variations in the age-tracking results (the smooth curves) are usually quantified by the ensemble hydrograph separation estimates (the solid dots) within their calculated uncertainties (as shown by the error bars). Thus Fig. 9 suggests that ensemble hydrograph separation can be used to quantify how catchment transport behavior is shaped by seasonal patterns in precipitation forcing.
3.6 Effects of evaporative fractionation
Any analysis based on water isotopes must deal with the potential effects of isotopic fractionation due to evaporation (e.g., Laudon et al., 2002; Taylor et al., 2002; Sprenger et al., 2017; Benettin et al., 2018). A detailed treatment of evaporative fractionation would necessarily be site-specific and thus beyond the scope of this paper. Nonetheless, it is possible to make a simple first estimate of how much evaporative fractionation could affect new water fractions estimated from ensemble hydrograph separation. The benchmark model does not explicitly simulate evapotranspiration and its effects on the catchment mass balance, but the issue to be addressed here is different: how much could evaporative fractionation alter the isotope values measured in streamflow, and how could this affect the resulting estimates of new water fractions?
To explore this question, I first adjusted the isotope values of infiltration entering the model in Fig. 1 to mimic the effects of seasonally varying evaporative fractionation. I assumed that evaporative fractionation was a sinusoidal function of the time of year, ranging from zero in midwinter to 20 ‰ in midsummer. Thus I assumed that evaporative fractionation effectively doubled the seasonal isotopic cycle in the water entering the model catchment (but not in the sampled rainfall itself, since any fractionation that occurs before the rainfall is sampled will not distort the ensemble hydrograph separation). I then calculated new water fractions based on the time series of sampled precipitation tracer concentrations and of streamflow tracer concentrations (altered by the lagged and mixed effects of evaporative fractionation), and compared these to the true new water fractions calculated by age tracking within the model.
The results are shown in Fig. 10, which compares 1000 Monte Carlo trials with evaporative fractionation (the blue dots) and another 1000 Monte Carlo trials without evaporative fractionation (the gray dots). One can see that, in these simulations, evaporative fractionation leads to a slight tendency to underestimate new water fractions. Nonetheless, the blue and gray dots largely overlap, and both generally follow the 1:1 lines. These results are reassuring, because the modeled fractionation effects were designed to be a worst-case scenario, in the following sense. Because ensemble hydrograph separation is based on patterns of fluctuations in precipitation and streamflow tracers, any fractionation process that created a constant offset between inputs and outputs would introduce no bias. For the same reason, any fractionation process that was uncorrelated to the input isotopic signature would also introduce no bias; thus, for example, the modeled seasonal fractionation cycle would have had no effect if there were no seasonal pattern in the precipitation isotopes themselves. But because the seasonal fractionation cycle is correlated with the seasonal pattern in the precipitation isotopes, it can potentially bias the resulting estimates of new water fractions. The fact that these biases are small, as shown in Fig. 10, suggests that ensemble hydrograph separation should yield realistic estimates of new water fractions, even with substantial confounding by evaporative fractionation.
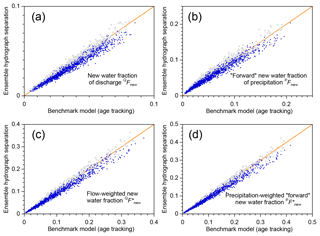
Figure 10Effects of seasonally varying evaporative fractionation on new water fractions estimated by ensemble hydrograph separation. Points show new water fractions predicted from tracer fluctuations in precipitation and streamflow (on the vertical axis), compared to averages of time-varying new water fractions determined by age tracking in the benchmark model (on the horizontal axis). Blue points show 1000 model runs in which precipitation undergoes seasonally varying evaporative fractionation ranging from zero in winter to 20 ‰ in summer. Gray background points show 1000 model runs without evaporative fractionation (analogous to Fig. 2). Each model run has a different random set of model parameters, measurement errors, and missing values, but the precipitation driver (Smith River daily precipitation) is the same in all cases. The blue data clouds closely follow the 1:1 line, indicating that ensemble hydrograph separation can reliably estimate new water fractions even in the presence of substantial evaporative fractionation.
A natural extension of the approach outlined in Sect. 2 would be to quantify the contributions of precipitation to streamflow over a range of lag times: to quantify, in other words, the catchment transit time distribution. In principle this should be straightforward, although in practice several challenges must be overcome. Below, I describe these issues and outline techniques for addressing them. Readers who are not interested in the methodological details can proceed directly from Sect. 4.1 to 4.5, skipping over Sect. 4.2–4.4.
4.1 Definitions
I assume that catchment inputs and outputs are sampled at the same fixed time interval Δt and define the time that a parcel of water enters the catchment (via rainfall, snowmelt, etc.) as ti and the time that it exits via streamflow as tj. The lag interval between precipitation and streamflow is indexed as . Pi is the rate that precipitation or snowmelt (net of evaporative losses) enters the catchment at time ti, and Qj is the rate of discharge that exits the catchment at time tj. and are the tracer concentrations in precipitation and streamflow, respectively. The water flux that enters as precipitation at time ti and leaves as streamflow k time steps later (at time is represented as qj+k. The sum of qjk over all lag times k (corresponding to all previous entry times ) is the total discharge Qj. Each of the qjk will be a fraction of the total precipitation falling at time and a (typically different) fraction of the total discharge at time tj. The fraction of discharge exiting at time tj that entered k time steps earlier is qjk∕Qj, and the distribution of qjk∕Qj over lag time k yields the transit time distribution conditioned on the exit time tj (also called the “backward” transit time distribution). The fraction of precipitation entering at time ti that subsequently leaves as streamflow k time steps later is , and the distribution of over lag time k yields the transit time distribution conditioned on the entry time ti (also called the “forward” transit time distribution).
In practice, precipitation fluxes are typically measured as averages over discrete time intervals, and tracer concentrations in precipitation are likewise volume-averaged over discrete intervals (such as a day or a week) during which the sample accumulates in the precipitation collector. By contrast, discharge fluxes are typically measured instantaneously, and discharge tracer concentrations are typically measured in instantaneous grab samples. In most of what follows, I will assume that Pi and are averages over the interval , and Qj and are instantaneous values at t=tj. However, in a few catchment studies, discharge concentrations have instead been measured in time-integrated samples. The analysis presented below is the same, whether the discharge tracer concentrations are instantaneous at t=tj or are integrated over each time interval . The interpretation is slightly different, however, because the average lag time corresponding to a given lag interval k will depend on how precipitation and streamflow are sampled. Usually, streamwater samples are collected more or less instantaneously (grab sampling), and precipitation samples are integrated over the time interval that the sampler is open. A typical daily sampling scheme, for example, might involve collecting a precipitation sample at noon (which integrates precipitation that fell over the previous 24 h) and also collecting a grab sample of streamflow at noon. In this case, the average lag time between a raindrop falling as precipitation and being sampled in the same day's streamflow (i.e., k=0) would be 12 h, assuming that, on average, the probability of rainfall is independent of the time of day. Thus in this conventional sampling scheme, the average lag time will be (k+0.5)Δt, where Δt is the sampling interval. If, instead, the stream samples were daily composites, then (for example) the same-day raindrops appearing in the first hour's subsample of streamflow would have an average lag time of 30 min, the second hour's would be 60 min, and so forth, and therefore the daily average lag time would be 6 h. Thus if stream samples are time-integrated composites, the average lag time will be (k+0.25)Δt.
I now outline the fundamentals of the ensemble hydrograph separation approach to estimating transit time distributions. Conservation of water mass requires that the discharge at time step j equals the contributions from all lag times k (corresponding to all previous entry times ):
Because tracing contributions to streamflow from all previous time steps would be impractical, it will be necessary to truncate the summation in Eq. (31) at some maximum lag, which I will denote as m, and to combine the unmeasured older contributions in a water flux :
Conservation of tracer mass requires that the tracer fluxes add up similarly, again with a catch-all flux :
Dividing Eq. (33) by Qj and rearranging terms directly yields
which readers will recognize as the multi-lag counterpart of Eq. (7).
Analogous to the approach in Sect. 2, here I account for the concentration of older inputs using the streamflow concentration at lag m+1, just beyond the longest lag m, with the goal of filtering out long-term patterns that could otherwise distort the correlations between and . Thus serves as a reference level for measuring fluctuations in precipitation and streamflow tracer concentrations, analogous to in Eq. (8). Adding a bias term α and an error term εj yields
which almost looks like a conventional multiple linear regression equation,
where
with the difference that the coefficients βk in Eq. (36) are constant over all exit times j and differ only as a function of the lag time k, whereas the qjk∕Qj terms in Eq. (35) can differ among both lag times k and exit times j. Nonetheless, by analogy with the mathematical arguments in Appendix A and those at the end of Appendix B, one can expect that βk will closely approximate the average of the time-varying contributions qjk∕Qj to streamflow over the ensemble of exit times j (please note that this is not the same as assuming that the transit time distribution is time-invariant). Substituting βk as an ensemble estimate of qjk∕Qj, one obtains the ensemble hydrograph separation equation for estimating transit time distributions,
When appropriately rescaled as described in Sect. 4.5–4.7 below, the coefficients βk in Eq. (38) – or more precisely, their regression estimates – can be used to estimate the time-averaged (also sometimes called “marginal”) transit time distribution.
4.2 Solution method
Using Y to represent the vector of reference-corrected streamflow tracer concentrations and X to represent the matrix of reference-corrected input tracer concentrations , we can rewrite Eq. (38) in the array form of a multiple regression equation:
where Xk is the kth column vector of X, and ε is the vector of the errors εj. The least-squares solution for multiple regressions like Eq. (39) can be expressed in matrix form as
where the regression coefficients are the least-squares estimators of the true (but unknowable) coefficients βk. Equation (40) is the multidimensional counterpart to Eq. (10). The first term on the right-hand side of Eq. (40) is the inverse of the matrix of the covariances of the Xk at each lag with each other lag, and the second term is a vector of the covariances between Y and the Xk at each lag. Equation (40) is equivalent to the more widely known “normal equation” for solving multiple regressions,
if one first normalizes Y and each of the Xk by subtracting their respective means; doing so has no effect on the estimates of the regression coefficients . (The elements of the square matrix XTX are the covariances between the Xk's at each pair of lags, multiplied by the number of samples; likewise the elements of the column matrix XTY are the covariances between each of the Xk's and Y, multiplied by the number of samples.)
Astute readers will immediately notice a fundamental problem with applying Eqs. (40) or (41) in practice, namely that they require precipitation tracer concentrations for all time steps j=1 … n and lags k=0 … m. In every practical case, many precipitation tracer concentrations will be missing, for two reasons. Some tracer concentrations will be missing due to sampling or measurement failures, and many more will be inherently missing because precipitation tracer concentrations cannot exist for time steps without precipitation. As we will see shortly, missing measurements that arise for these two different reasons must be handled in two different ways. But regardless of its origins, each missing tracer concentration at time step i will create a diagonal line of missing values xj, k in the matrix X, causing a missing value in the first column (k=0) at j=i, and another in the second column (k=1) at , and so on up to the last column (k=m) at .
So-called “missing data problems” arise frequently in the statistical literature, and several approaches have been proposed for handling them (Little, 1992). One approach, termed “listwise deletion” or “complete-case analysis”, involves discarding all cases (meaning all rows j in the matrix X) in which any variables are missing and analyzing only the remaining (complete) cases. In our situation, this would mean analyzing only exit times tj that are preceded by unbroken series of rainy periods, up to the maximum lag m for which we want to estimate the coefficients . Such ensembles of points would be mathematically convenient, but they would also be very strongly biased in a hydrological sense, because they would represent periods of unusually consistent rainfall (and thus unusually wet catchment conditions). Furthermore, if the maximum lag m is sufficiently long, records with continuous rainfall over all m+1 lags (k=0 … m) will become impossible to find. For these reasons, complete-case analysis is not a feasible approach to our problem.
A second class of approaches to the missing data problem involves imputing values to the missing data (Little, 1992). In our case, however, many of the missing data are not simply unmeasured, but cannot exist at all (because rainless days have no rainfall concentrations), so it is not obvious how to impute the missing values.
A third approach, termed “pairwise deletion” or “available-case analysis”, first proposed by Glasser (1964), entails evaluating each of the covariances in Eq. (40) using any cases for which the necessary pairs of observations exist. Thus the covariances in Eq. (40) are replaced by
and
where the notation (kℓ) indicates terms that are evaluated over all cases j for which both xjk and xjℓ exist (e.g., is the mean of the column vector Xk for rows j where neither xjk nor xjℓ is missing, and n(kℓ) is the number of such cases), and (ky) indicates terms that are evaluated over all cases j for which xjk and yj exist.
Glasser's approach can potentially handle the problem of tracer measurements that are missing at random due to sampling or analysis failures. However, it will not correctly handle the problem of tracer concentrations that are missing due to a lack of sufficient precipitation, because it assumes that the missing values occur randomly and therefore that Eqs. (42)–(43) are unbiased estimators of the covariances that one would obtain if no samples were missing. But when little or no precipitation falls on the catchment, it delivers little or no tracer to subsequent streamflow, and thus its contribution to the covariance between precipitation and streamflow concentrations will be nearly zero. Therefore different handling is required for precipitation tracer concentrations that are missing because they were not measured, versus those that are missing because they never existed at all (because no rain fell). As shown in Appendix B, periods without precipitation must be taken into account with weighting factors on the off-diagonal elements of the covariance matrix (because the tracer covariances will be less strongly coupled to one another, the less frequently precipitation falls). When the approach outlined in Appendix B is combined with Glasser's method for estimating each of the covariances, the end result is
where the covariance terms are defined by Eqs. (42)–(43), is the number of time steps j for which precipitation fell at time (whether or not that precipitation was sampled and analyzed), and is the number of time steps j for which precipitation fell at both j−k and j−ℓ (again, whether or not those precipitation events were sampled and analyzed). As explained in Appendix B, the estimated coefficients will closely approximate the average of the time-varying coefficients , averaged over times j for which precipitation fell at times (but not over rainless periods, from which no streamflow can originate and thus must be zero). In practice, a single droplet of mist does not make a rainstorm, so there will be some threshold rate of precipitation below which there will be too little water to have any detectable effect on streamflow (and too little water to analyze). Thus and will be determined by counting the time steps that exceed this precipitation threshold:
In the calculations presented here, I have assumed a precipitation threshold of 1 mm day−1, but expert judgment may lead to other values of Pthreshold in real-world situations. Note that some measurements will usually also be missing due to sampling or measurement failures in addition to precipitation intermittency. Thus n(ky) and n(kℓ) in Eqs. (42)–(43), which account for both types of missing data, will typically be smaller than and in Eq. (44).
4.3 Tikhonov–Phillips regularization
Gaps in the underlying data imply that, unlike covariance matrices in conventional multiple regressions, the covariance matrix in Eq. (40) is not guaranteed to be positive definite (and thus may not be invertible). Even when the covariance matrix is invertible, it may be ill-conditioned, making its inversion unstable. This issue arises frequently in inversion problems whenever different combinations of lagged inputs will have nearly equivalent effects on the output, making it difficult for the inversion to decide among them (this is the multidimensional analogue to nearly dividing by zero in Eq. 10). In minimizing the sum of squared deviations from the observations, inversions like Eq. (40) can potentially yield wildly oscillating solutions, with huge negative values of at some lags delicately balancing huge positive values at other lags. Such results are not just unrealistic; they are also unstable, with tiny differences in the underlying data potentially having huge effects on the estimates.
A standard therapy for this disease is Tikhonov–Phillips regularization (Phillips, 1962; Tikhonov, 1963). This technique (also known by many other names, including Tikhonov regularization, Tikhonov–Miller regularization, and the Phillips–Twomey method) is commonly used to solve ill-conditioned geophysical inversion problems (Zhadanov, 2015) but is less widely known in hydrology. Whereas conventional least-squares inversion finds the set of parameters that will minimize the misfit between the predicted and observed yj, no matter how strange those values may be, Tikhonov–Phillips regularization adds a second criterion that quantifies the strangeness of the values themselves and finds the set of parameters that will minimize the sum of both criteria. Phillips (1962) first showed how this joint minimization could be formulated as a simple extension of the normal matrix approach to solving linear inversion problems. This formulation, applied to our problem, is
where C is the matrix of covariance terms in Eq. (44), and the parameter λ controls the relative weight given to the two criteria, namely the mean squared deviations of the predicted and observed yj values (controlled by the covariance matrix C) and the deviations from ideal behavior of the values (controlled by the matrix H).
The form of H is determined by the criterion of reasonableness that is applied to the . One possible criterion (among many that can be found in the literature) can be called “parsimony”: minimize the mean square of the , thus penalizing solutions with large values. Minimizing the functional yields the identity matrix for H (Tikhonov, 1963):
This approach, also called “ridge regression” because it adds a “ridge” of extra weight along the diagonal of the covariance matrix, was Tikhonov's original regularization criterion and is widely used in geophysical inversions (including unit hydrograph estimation). In our case, however, it would have the undesirable effect of creating a systematic underestimation bias in our estimates of recent contributions to streamflow, by always making the smaller than they would be otherwise.
A second possible criterion is consistency: minimize the variance of the , thus penalizing solutions with individual values that differ greatly from the mean of all the . Minimizing the functional , where angled brackets indicate averages from k=0 to k=m, leads to an H matrix of the form (Press et al., 1992)
Like Eq. (47), this minimum-variance criterion is also widely used and has the advantage that, unlike Eq. (47), it does not lead to systematic biases in the average values. However, if the transit time distribution is strongly skewed, with large contributions to streamflow at short lags, minimizing the variance of the will tend to suppress this short-lag peak in the transit time distribution. This distortion of the transit time distribution is undesirable when one seeks to quantify recent contributions to streamflow.
A third possible criterion is smoothness: minimize the mean square of the second derivatives of the , thus penalizing values that deviate greatly from their neighbors. Minimizing the second derivative functional , where the angled brackets indicate an average from k=1 to , leads to an H matrix of the form (Phillips, 1962; Press et al., 1992)
This criterion, first used by Phillips (1962), has the advantage of strongly suppressing rapid oscillations in the while barely affecting the larger-scale structure of the inferred transit time distribution. Therefore this will be the regularization criterion employed here.
The solution to Eq. (46) will depend on the value of the parameter λ, which determines the relative weight given to the regularization criterion versus the goodness-of-fit criterion. How should the value of λ be chosen? One can first note that, for λH to be dimensionally consistent with the covariance matrix, λ must have the same dimensions as the variance of Xk. The second point to note is that the regularization criterion and the goodness-of-fit criterion will have roughly equal weight in determining the if the trace of λH equals the trace of the covariance matrix C (Press et al., 1992). Combining these two considerations, we can define a dimensionless parameter ν that ranges between 0 and 1 and expresses the fractional weight given to the regularization criterion, and then calculate the corresponding value of λ as
As one can see from Eq. (50), when ν=0.5, the trace of λH will equal the trace of the covariance matrix C, and the two criteria will have roughly equal weight in determining the . As ν grows toward 1, the solution will be increasingly dominated by the regularization criterion; conversely, if ν=0 the regularization criterion will be ignored, and Eq. (46) will become equivalent to Eq. (40).
The question remains as to what the most appropriate value of ν (or λ) would be for any particular situation. An appropriate degree of regularization will prevent the predicted values of yj from fitting the data more closely than they should (that is, it will prevent “fitting the noise” with unrealistic values of . Thus a theoretically optimal value of ν or λ would be one that makes the variance of the prediction errors of the yj similar to the expected variance of the εj (Press et al., 1992). This approach will not work for our problem, for three reasons. First, the variance of the εj is not known a priori. Second, directly calculating the predicted yj, and thus the prediction errors, is impossible if many values of xjk are missing, as will usually be the case. Third, and perhaps most importantly, Eq. (39) is, strictly speaking, structurally incorrect for our system, because is only an approximation to the time-varying qjk∕Qj. Therefore in our case a more pragmatic approach (which is also taken in many geophysical applications of regularization methods) is to follow the advice of Phillips (1962) that
in practice several values … should be tried and the best value should be the one that appears to take out the oscillation without appreciably smoothing the [solution],
while keeping in mind that an element of subjectivity is inevitably introduced. In the analyses presented here, ν=0.5 and thus the regularization criterion and the least-squares criterion have roughly equal weight in determining the values of the . Regularization usually has little effect on the estimated transit time distributions presented below, but it can serve as a safeguard against obtaining wildly unrealistic results, particularly with large fractions of missing measurements.
4.4 Uncertainties
In conventional multiple regression analysis, calculating the uncertainties in the requires estimating the variance of the prediction errors εj:
It may seem that calculating Eq. (51) is impossible in our case, because values of are missing for all days without rain. However, as noted in Sect. 4.2 above, for those points the true value of βj, k is known to be zero, so the rainless terms can simply be ignored because they will have no effect on the predicted yj. Thus if sampling and measurement failures account for only a small fraction of the missing tracer concentrations, Eq. (51) may yield adequate estimates of . Where there are many sampling and measurement failures, we can use the error variance formula of Glasser (1964), adapted to our problem as
which is the mean square error of the estimated yj values. The factor accounts for the fact that there are n values of yj, but only of them are affected by ; for the other , xjk is missing and has no influence on yj. In both Eqs. (51) and (52), the factor corrects for degrees of freedom. If one removes this degree-of-freedom correction, one gets the population mean square error (i.e., the error variance of the fit to these particular data). With the degree-of-freedom correction, one gets the sample mean square error (i.e., an estimate of the prediction error for data drawn from the same population, but not used to fit the model in the first place). When applied to complete data sets (without missing values and without regularization), Eq. (52) equals the conventional error variance for multiple regression, and it usually works reasonably well with missing values and with unbiased regularization, e.g., with the consistency criterion of Eq. (48) or the smoothness criterion of Eq. (49). However, unlike in conventional multiple regression, there is no absolute guarantee that the variance of the predicted values (the summation in Eq. 52) will be smaller than the variance of the observed values of yj. Users should therefore be aware that Eq. (52) could potentially yield nonsensical negative values (or unrealistically small positive values) for the error variance in particular cases.
In conventional multiple regression, the covariance matrix of the coefficients equals the inverse of the covariance matrix C, scaled by the error variance divided by the sample size n. This approach must be adapted to account for the effects of regularization, yielding the following expression for the covariances of the :
where is the error variance as estimated in Eqs. (51) or (52), and neff is the sample size n, adjusted to account for serial correlation in the residuals using Eq. (13). (Where there are so many measurement or analysis failures that residuals cannot be calculated reliably, it is better to guess a reasonable value for their serial correlation than to assume it is zero, which will typically lead to overestimates of neff and thus underestimates of the associated uncertainties.) The standard errors of the will be the square roots of the diagonal elements of the matrix defined by Eq. (53),
Benchmark data sets verify that Eqs. (53) and (54) perform as they should: the root-mean-square averages of the calculated are close to the root-mean-square averages, over many replicate data sets, of the deviation of the fitted coefficients from the true βk used to generate the synthetic data. This result holds both with and without substantial fractions of missing values, strong correlations among the Xk, and substantial additive noise.
There is one important caveat to this generalization, however: it holds only if the assumptions underlying the regularization criterion are actually true. For example, if the true βk vary smoothly with k, then regularization using Eq. (49) will retrieve a set of smoothly varying coefficients that deviate from the true βk by amounts that are well approximated by the calculated standard errors . But if (say) the true βk oscillate wildly from one k to the next, regularization using Eq. (49) will generate a smoothly varying set of which will deviate from the true (wildly oscillating) βk by much more than the calculated standard errors as calculated from Eq. (54). Regularization methods are forced to assume that the βk obey the regularization criterion (with the strength of this assumption determined by the parameter λ), and thus they cannot be used to test whether this assumption is true. Thus what the calculated standard errors tell us is that, if the true βk vary smoothly over k, then the estimation errors of the should be on the order of .
4.5 Transit time distribution of discharge
The coefficients determined by Eqs. (40)–(54) estimate the average contribution to discharge Qj that originated as precipitation k time steps earlier; that is, they estimate the average of qjk∕Qj for combinations of times j and k for which precipitation occurred at . They do not account for times i when no precipitation occurred and thus for which qjk=0 at the corresponding time steps .
To estimate the average contribution qjk∕Qj of precipitation to discharge across all time steps, both with and without precipitation, we need to include values of qjk=0 for times without precipitation (and thus without any contribution of precipitation to discharge). This is done by rescaling the coefficients and their uncertainties by , the ratio of event time steps (those with precipitation) to all time steps. We also need to divide by the time step length Δt to obtain the transit time distribution in the correct dimensions (fraction per unit time). With these normalizations, the coefficients yield the transit time distribution of discharge QTTDk (also termed the backward transit time distribution, or the transit time distribution conditioned on exit time):
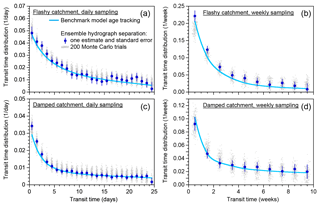
Figure 11Transit time distributions of discharge estimated by ensemble hydrograph separation based on both daily and weekly tracer sampling, versus true transit time distributions determined by benchmark model age tracking (light blue curves). Panels (a–d) show TTDs for the modeled flashy and damped catchments, both driven by Smith River (Mediterranean climate) precipitation. Dark blue symbols show transit time distributions estimated from one time series. Data clouds show ensemble hydrograph separation results (slightly jittered on the horizontal axis) from 200 different realizations of random precipitation tracer values, random missing data, and random measurement errors. Ensemble hydrograph separation correctly reveals the shapes of the transit time distributions and also quantifies their values, within the calculated uncertainties, at most lags. It can clearly distinguish the transit time distributions of the two catchments under either daily or weekly tracer sampling.
These transit time distributions can be tested by comparing them to time-averaged streamwater age distributions calculated by age tracking in the benchmark model (Sect. 3.1). Figure 11 shows the results of several such tests, using both daily and weekly tracer data as input (left and right columns, respectively). The light blue curves indicate the true time-averaged transit time distribution (determined from age tracking in the benchmark model), the dark blue symbols show transit time distributions estimated from one tracer time series, and the gray data clouds show 200 more transit time distributions from the same model with different realizations of the random inputs. The weekly TTDs are larger, in absolute terms, than the daily TTDs, because streamflow will always contain at least as much water that originated as precipitation during the previous week as during the previous day (for the simple reason that the previous day is part of the previous week). Figure 11 shows that ensemble hydrograph separation correctly estimates the general shapes of the TTDs and their quantitative values. Furthermore, the gray data clouds show that no TTD estimates deviate too wildly from the age-tracking curves.
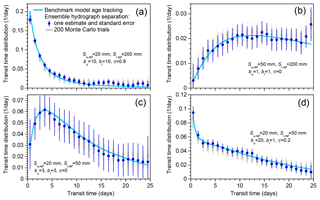
Figure 12Transit time distributions (TTDs) of discharge estimated by ensemble hydrograph separation based on daily sampling, compared to true TTDs determined by benchmark model age tracking (light blue curves), for four model parameter sets yielding diverse patterns of transport behavior. Dark blue symbols show transit time distributions estimated from one time series. Data clouds show ensemble hydrograph separation results (slightly jittered on the horizontal axis) from 200 different realizations of random precipitation tracer values, random missing data, and random measurement errors. Vertical axis scales differ greatly. Ensemble hydrograph separation correctly reveals the shapes of the TTDs and also quantifies their values at most lags. However, panels (b) and (c) show that standard errors are overestimated for TTDs that result in strong serial correlation in the modeled time series (see text).
Real-world transit time distributions could potentially have different shapes from those shown in Fig. 11. To test whether ensemble hydrograph separation can correctly estimate transit time distributions with more widely varying shapes, I explored the benchmark model's parameter space, in some cases venturing beyond the nominal parameter ranges outlined in Sect. 3.1. As Fig. 12 illustrates, widely differing time-averaged (or marginal) transit time distributions generated by the benchmark model (solid lines) are well approximated by the ensemble hydrograph separation estimates (blue dots) calculated from the tracer time series. The standard errors are overestimated for humped TTDs, which generate strongly autocorrelated time series. The reason appears to be that when the benchmark model's parameters generate a strongly autocorrelated tracer time series, the residuals will also be strongly autocorrelated; thus the effective sample size neff will be small (Eq. 13) and the resulting uncertainties SE(QTTDk) will be correspondingly large (Eqs. 54–55). One can also see that in some TTDs the last few lags can exhibit substantial deviations from the age-tracking results (e.g., Figs. 11c and 12b). This may be an aliasing effect that arises when does not adequately capture the effects of the unmeasured older fluxes (see Eqs. 32–35), in which case one would expect it to be strongest when the TTD does not approach zero at the longest measured lags (such as in Fig. 12b). It may also arise for other unknown reasons. In any case, a pragmatic solution is to estimate the TTD over a few more lags than desired, and then to simply ignore the last few lags of the estimated TTD. These caveats notwithstanding, Figs. 11 and 12 demonstrate that ensemble hydrograph separation can reliably quantify transit time distributions with widely varying shapes.
4.6 Volume-weighted transit time distribution
The transit time distributions defined in Eq. (55) are ensemble averages in which each day counts equally; that is, for a given lag k, QTTDk estimates the average of the ratio qjk∕Qj across all time steps, including zeroes at time steps for which there was no precipitation at the corresponding time step . Thus Eq. (55) estimates time-weighted average TTDs, which quantify the distribution of temporal origins of an average day of discharge.
For many purposes, it would be useful to estimate the temporal origins of an average liter of discharge instead, that is, the volume-weighted TTD, which we can denote (where, following the convention in Sect. 2, the asterisk indicates volume-weighting). Instead of estimating the average of the ratio qjk∕Qj (the time-weighted average), a volume-weighted TTD approximates the ratio of the average qjk to the average Qj across all time steps (the ratio of the averages rather than the average of the ratios). This is the multidimensional analogue to the volume-weighted new water fraction presented in Sect. 2.4 and is handled similarly. The multiple regression in Eq. (36) can be volume-weighted by replacing the covariances in Eqs. (42)–(43) with volume-weighted covariances (Galassi et al., 2016) instead:
and
where
are the volume-weighted means of the Xk′s, Xℓ′s, and Y′s, and x's and y's, and where the notations j∈(kℓ) and j∈(ky) indicate sums taken over all j for which xjk and xjℓ (or, respectively, xjk and yj) are not missing. With these volume-weighted covariances in place of the unweighted covariances from Eqs. (42)–(43), the volume-weighted regression can be solved by the same procedures described in Sect. 4.2–4.4, yielding volume-weighted estimates of the coefficients (where, as above, the asterisk indicates volume-weighting). Following the approach of Sect. 2.5, one should account for the unevenness of the weighting when calculating the effective sample size neff to be used in Eq. (54) to estimate the uncertainties in the ,
where is the effective sample size at lag k, and Qj(ky) denotes discharge during time steps j for which pairs of yj and xjk exist (for a given lag k).
To estimate the volume-weighted TTD, we must average over all discharge (including discharge after time steps with no precipitation). Thus the coefficients and their uncertainties should be rescaled, following the approach in Sect. 2.5, as follows:
where is the average discharge during the time steps j for which precipitation fell at , is the average discharge over all time steps (including rainless periods), is the fraction of time steps with precipitation, and and are estimated from the multiple regression in Eq. (54), with the effective sample size defined in Eq. (59). The ratio corrects for any differences in average discharge during sampled and un-sampled time steps, and the ratio corrects for rain-free periods, which contribute no new water to streamflow.
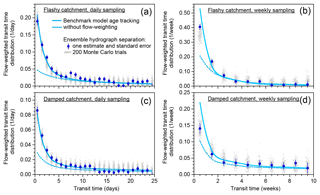
Figure 13Volume-weighted transit time distributions (TTDs) of discharge estimated by ensemble hydrograph separation (Eq. 60) compared to benchmark model age tracking. Panels (a, b) and (c, d) show TTDs for rapid and damped response parameters, respectively; model is driven by Smith River precipitation in both cases. Ensemble hydrograph separation estimates from tracer fluctuations (dark blue symbols) are broadly consistent with true TTD from age tracking in the benchmark model (solid curve). Data clouds show ensemble hydrograph separation results (slightly jittered on the horizontal axis) from 200 different realizations of random precipitation tracer values, random missing data, and random measurement errors. Dashed curve is the unweighted benchmark model TTD from Fig. 11 for comparison.
4.7 Forward transit time distribution
In addition to the backward transit time distributions qjk∕Qj, which estimate the fraction of streamflow that originated as precipitation k time steps earlier, it may also be useful to estimate forward transit time distributions , which estimate the fraction of precipitation that becomes streamflow k time steps later. Instantaneous, time-varying forward and backward transit time distributions can differ markedly at any point in time. For example, today's backward transit time distribution strongly depends on the timing and magnitude of previous precipitation supplying today's streamflow, whereas the forward transit time distribution strongly depends on how future precipitation mobilizes water stored from today's rainfall. These individual differences become less prominent when averaged over a large ensemble of events. Systematic differences nonetheless persist, because forward transit time distributions are defined only during periods with precipitation (otherwise both qjk and Pj−k are both zero and their ratio is undefined), and during these periods precipitation must be higher, on average, than discharge (otherwise there can be no recharge of the storages that supply discharge during rainless periods).
Forward transit time distributions are less straightforward to estimate from tracers than backward distributions are, for the simple reason that although streamflow is a mixture of contributions from previous precipitation events, the converse does not hold: that is, precipitation cannot be expressed as a mixture of subsequent streamflows. Although it is algebraically straightforward to rewrite Eq. (35) as either
or
Regressions based on these equations do not reliably predict the average of when applied to synthetic data from the benchmark model. (Note that these are the multidimensional counterparts to Eqs. 25 and 26, which likewise fail benchmark tests. Although Eqs. 35, 61, and 62 are algebraically equivalent, they behave differently as TTD estimators because the variance introduced by Qj will affect the results differently when it appears on right-hand side versus the left-hand side).
Instead, by analogy to Eq. (21), we can estimate the forward transit time distribution from the regression coefficients of Eq. (44), rescaled as
where
is the average precipitation rate during time steps with precipitation, and
is the average of the discharges that occur k time steps after each of these precipitation intervals. Figure 14 shows that forward transit time distributions estimated with Eq. (63) are broadly consistent with true forward TTDs calculated by age tracking in the benchmark model.
It should be emphasized that PTTDk represents the forward transit time distribution of water that enters the catchment as precipitation and subsequently exits as streamflow, because these are the entry and exit fluxes in which the tracers are measured. The forward transit time distribution of water that exits by other pathways (such as evapotranspiration) may be different. That distribution will be unmeasurable without catchment-scale tracer data from those other pathways, which are not available at present. Thus, echoing the principle outlined in Sect. 2.3 and 2.6, one should not interpret PTTDk as the forward transit time distribution of all precipitation entering the catchment, but only of the precipitation that exits as streamflow.
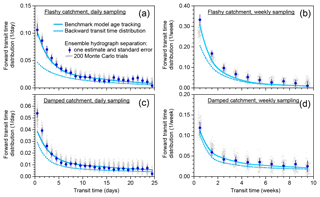
Figure 14Forward transit time distributions (the fraction of precipitation that leaves the catchment within one time step, two time steps, and so on) estimated by ensemble hydrograph separation (Eq. 63) compared to benchmark model age tracking. Panels (a, b) and (c, d) show TTDs for flashy and damped catchments, respectively; the model is driven by Smith River (Mediterranean climate) precipitation in both cases. Ensemble hydrograph separation estimates from tracer fluctuations (dark blue symbols) are broadly consistent with true TTDs from age tracking in the benchmark model (solid curve). Data clouds show ensemble hydrograph separation results (slightly jittered on the horizontal axis) from 200 different realizations of random precipitation tracer values, random missing data, and random measurement errors. Dashed curve is the benchmark model backward TTD from Fig. 11 for comparison.
The volume-weighted forward transit time distribution can also be calculated by rescaling arguments, analogous to the approach in Sect. 2.7. The key is to recognize that we are seeking the ratio between the total volume of precipitation that will leave the catchment k days after falling as precipitation (the sum of qjk over all j) and the total volume of precipitation that fell on the catchment during the corresponding rainy days. The numerator of this ratio is identical to the numerator of the volume-weighted backward transit time distribution , but the denominator is total precipitation rather than total discharge. Thus the precipitation-weighted forward transit time distribution can be estimated as
Because the benchmark model in Fig. 1 has no evaporative losses and thus , benchmark tests of the precipitation-weighted forward TTD () and the discharge-weighted backward TTD will yield identical results; thus the benchmark test of (Fig. 13) will not be repeated here as a test of .
4.8 Variations in transit time distributions with discharge, precipitation, antecedent moisture, and seasonality
Like the new water fraction Fnew, estimating the transit time distribution QTTDk does not require unbroken time series. Thus, using approaches similar to those outlined in Sect. 3.5, one can estimate transit time distributions for subsets (including discontinuous subsets) of the precipitation and streamflow time series that reflect conditions of particular interest. In the case of new water fractions, subdividing the source data is relatively simple, because new water fractions are estimated from precipitation and streamflow tracers at the same time steps; thus when one subdivides the streamflow time series one also subdivides the precipitation time series, and vice versa. Transit time distributions are not so simple, because each discharge time j is potentially affected by k=0 … m precipitation time steps ; thus the precipitation and streamflow time series can be subdivided differently, according to different criteria.
For example, we can choose to subdivide the data set according to the discharge time j, thus evaluating Eq. (36) only for time steps j that meet particular criteria (for example, to analyze time steps with high or low flows separately). Doing so has the effect of creating blank rows in the vector Y and matrix X in Eq. (39) for each excluded value of j. Figure 15 shows the results of estimating transit time distributions QTTDk using only the highest 20 % of discharges (the corresponding QTTDk's calculated from the entire time series are also shown for comparison). Because large inputs of recent precipitation are likely to result in high flows, one would intuitively expect that high flows should contain larger contributions from recent precipitation. But how much larger? As Fig. 15 shows, this question can be answered, at least on average, by examining the transit time distributions of high-flow discharges. Figure 15 shows that ensemble hydrograph separation can accurately estimate the transit time distributions of both high flows and normal flows, and thus can accurately quantify how transport behavior is different under high-flow conditions.
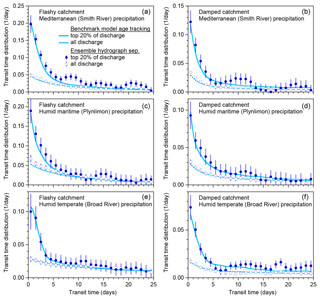
Figure 15Transit time distributions QTTDk for high flows (the highest 20 % of daily discharges; solid curve and solid circles), compared to transit time distributions for all flows (dashed curve and open squares). Solid circles and open squares show QTTDk estimates from ensemble hydrograph separation (Eq. 55); solid and dashed curves show true QTTDk determined by age tracking in the benchmark model. Panels (a, c, e) and (b, d, f) show TTDs for flashy and damped catchments, respectively; the three rows of panels represent three different precipitation drivers. Note that vertical axis scales differ substantially. High flows have much larger contributions of recent precipitation than average flows do. Ensemble hydrograph separation quantitatively captures this behavior across flashy and damped model catchments with all three precipitation drivers.
In a Mediterranean climate (as depicted by, for example, the Smith River precipitation record shown in Fig. 1), one would intuitively expect rainy-season streamflow to have larger contributions from recent precipitation. Conversely, one would expect that dry-season streamflow will have much smaller contributions from recent rainfall (because there is so little of it, among other reasons). But how big are the differences between rainy-season and dry-season transit time distributions? As an illustration of what may be possible with real-world data, I took the 5-year daily and weekly time series for the benchmark model driven by the Mediterranean climate (Smith River) precipitation record, separated them into summer (dry) and winter (wet) seasons, and analyzed the two seasons separately. Figure 16 shows that, as expected, the contributions of recent precipitation to streamflow are much larger during the wet season than the dry season. But more importantly, Fig. 16 also shows that these differences can be accurately quantified, directly from data.
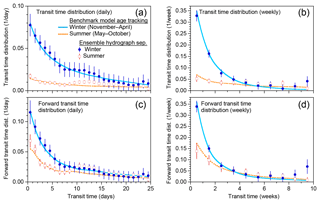
Figure 16Backward and forward transit time distributions (a, b and c, d, respectively) compared for summer (May–October) and winter (November–April) months, from the benchmark model with Mediterranean (Smith River) precipitation climatology and flashy catchment parameters. Solid circles and open squares show estimates from ensemble hydrograph separation (Eqs. 55 and 63); solid and dashed curves show the true TTDs determined by age tracking in the benchmark model. Panels (a, c) and (b, d) show TTDs estimated from daily and weekly sampling, respectively. Owing to larger and more frequent rainfalls during winter (see Fig. 1), transit time distributions calculated for the winter months show a much larger contribution of recent rainfall to current streamflow (a, b) and a much larger fraction of current precipitation becoming streamflow in the near future (c, d). Ensemble hydrograph separation quantitatively captures the seasonal differences in the benchmark model's transit time distributions.
The examples above are based on subdividing the data set according to the discharge time j. It is also possible to subdivide the data according to precipitation times that meet particular criteria (for example, to analyze time steps with large and small rainstorms separately). Doing so has the effect of creating diagonal stripes of blanks in the matrix X in Eq. (39) at for each excluded value of i. These are in addition to the diagonal stripes of missing values that arise because of sampling and measurement failures, or more commonly because no rain fell. Thus they pose no new mathematical challenges and can be handled by the methods outlined in Sect. 4.2.
One question that can be explored by subdividing the time series according to precipitation is whether larger rainfall events propagate faster through catchments. Intuition suggests that intense rainfall should lead to larger contributions to streamflow from faster flow paths. But how much larger? Figure 17 illustrates how this kind of question could potentially be explored. In Fig. 17, the forward transit time distributions of the highest 20 % of precipitation are compared to the average transit time distributions of all precipitation events, for the damped and flashy parameter sets and all three precipitation climatologies. One can see that large rain events are associated with much larger amounts of water reaching the stream quickly, but this effect largely disappears after about 2–3 days. Moreover, the magnitude and timing of this effect are nearly the same in the estimates derived from ensemble hydrograph separation and benchmark model age tracking, suggesting that they could also be reliably estimated from real-world data.
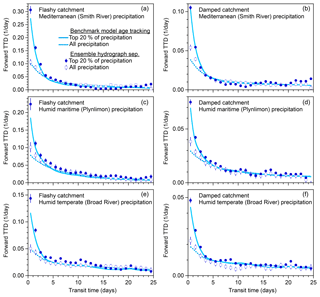
Figure 17Forward transit time distributions PTTDk for intense precipitation (the highest 20 % of daily precipitation totals; solid curve and solid circles), compared to forward transit time distributions for all precipitation (dashed curve and open squares). Solid circles and open squares show PTTDk estimates from ensemble hydrograph separation (Eq. 63); solid and dashed curves show the true PTTDk determined by age tracking in the benchmark model. Panels (a, c, e) and (b, d, f) show TTDs for flashy and damped catchments, respectively; the three rows of panels represent three different precipitation drivers. Note that vertical axis scales differ greatly. Despite a tendency for ensemble hydrograph separation to over-predict PTTDk for short lag times, the differences between the ensemble hydrograph separation estimates for intense precipitation and normal precipitation (open squares and solid circles) closely mirror the differences between the solid and dashed curves. Thus ensemble hydrograph separation can estimate the relative effect of intense precipitation on forward transit times, across widely differing precipitation drivers and catchment characteristics.
Antecedent wetness has been recognized as a controlling factor in catchment storm response (e.g., Detty and McGuire, 2010; Merz et al., 2006; Penna et al., 2011), but its effects on solute transport at the catchment scale have rarely been quantified, outside of the context of calibrated simulation models (e.g., van der Velde et al., 2012; Heidbüchel et al., 2012; Harman, 2015; Rodriguez et al., 2018). To assess whether the antecedent moisture dependence of solute transport might be measurable directly from field data, I binned the benchmark model time series into ranges of antecedent moisture (as measured by the upper-box storage values Su at the end of the previous day) and estimated the new water fractions QFnew and PFnew using ensemble hydrograph separation. I used the upper-box storage as a proxy for measurements of soil moisture or shallow groundwater levels, which are commonly used as indicators of antecedent wetness in catchment studies (one could use antecedent discharge as a proxy instead; this would yield nearly equivalent results). As Fig. 18a and c show, ensemble hydrograph separation accurately predicts how both backward and forward new water fractions increase as functions of antecedent moisture.
To visualize how high antecedent moisture affects transit time distributions, I isolated the discharge times tj associated with the highest 10 % of antecedent moisture values and calculated the corresponding backward transit time distribution QTTDk (Fig. 18b). This TTD shows that high antecedent moisture is associated with large contributions of recent rainfall to streamflow, up to lags of about 3–4 days. The peak of the transit time distribution does not come at the shortest possible lag (same-day precipitation), but instead at a lag of 1.5 days (i.e., previous-day precipitation). This is the inevitable result of selecting points with high previous-day moisture, which are likely to be associated with high previous-day precipitation (and thus high contributions of that previous-day precipitation to current streamflow). Storms typically last about 2–3 days in the Smith River precipitation record underlying the simulations in Fig. 18, so much of the backward TTD could potentially just reflect the pattern of precipitation, combined with the fact that points with high antecedent moisture have been selected.
One can even question why one would expect a backward TTD to help in understanding the effects of antecedent moisture at all, given that the backward TTD will mostly reflect precipitation inputs that came before and, in some cases, created the antecedent moisture conditions themselves. A forward TTD, on the other hand, might help in quantifying how antecedent moisture affects the transmission of future precipitation to streamflow. I therefore isolated the precipitation times associated with the highest 10 % of antecedent moisture values (thus, as explained above, filtering the matrix X in Eq. 39 along diagonal lines) and calculated the corresponding forward transit time distribution PTTDk (Fig. 18d). As Fig. 18d shows, in this model system, high antecedent moisture roughly doubles the proportion of precipitation that reaches the stream, but only out to lags of approximately 2 days, beyond which there is no clearly detectable effect. Naturally, these inferences pertain only to the model system, and do not tell us how real-world catchments might behave. However, because Fig. 18 shows that new water fractions and transit time distributions could be accurately quantified across a range of antecedent moisture conditions directly from field data, it illustrates how ensemble hydrograph separation could be used to explore the effects of antecedent moisture in real-world catchments.
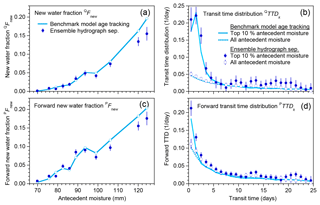
Figure 18Effects of antecedent moisture on new water fractions and transit time distributions (a, b) and their forward counterparts (c, d). Panels (a) and (c) show new water fractions from benchmark model age tracking (solid curves) and ensemble hydrograph separation (solid circles) stratified by percentiles of antecedent moisture (previous-day storage Su in the benchmark model's upper box). Panels (b) and (d) show transit time distributions for high antecedent moisture conditions (the highest 10 % of previous-day storage levels in the upper box of the benchmark model; solid curve and solid circles), compared to transit time distributions for all antecedent moisture levels (dashed curve and open squares). All panels are derived from simulations with the flashy catchment parameter set driven by Smith River (Mediterranean climate) precipitation time series. Error bars are 1 standard error.
Over 20 years ago, Rodhe et al. (1996) wrote that transit times, despite their importance to modeling discharge, were “impractical to determine experimentally except in rare manipulative experiments where catchment inputs can be adequately controlled.” Despite over two decades of effort, including increasingly elaborate theoretical discussions of transit time distributions, the problem identified by Rodhe et al. remains: how can we measure transit times, and transit time distributions, of real-world catchments under real-world conditions? And how can we verify whether the estimates we get are realistic ones? The theory and benchmark tests presented in Sects. 2–4 aim to provide a partial answer.
5.1 Comparisons with other approaches
Particularly because their names are similar, it is important to recognize how ensemble hydrograph separation contrasts with conventional hydrograph separation. Although one could view Eq. (9) as an algebraic rearrangement of the conventional hydrograph separation equation (Eq. 3), with both sides multiplied by (Cnew−Cold) and substituted in place of Cold, there are important differences between the two approaches:
-
Conventional hydrograph separation estimates the time-varying new water fraction at each individual point in time. By contrast, ensemble hydrograph separation estimates the average new water fraction Fnew over an ensemble of points (hence the name).
-
Conventional hydrograph separation assumes that the end-member tracer signatures are constant, but ensemble hydrograph separation assumes them to be time-varying; indeed, it exploits their variability through time as its main source of information.
-
Conventional hydrograph separation requires that all end-members that contribute to streamflow must be identified, sampled, and measured. Ensemble hydrograph separation, by contrast, requires tracer measurements only from streamflow and any end-members whose contributions to streamflow are to be estimated. There is no need to assume that all end-members have been identified and measured, just that tracer fluctuations in any unmeasured end-members are not strongly correlated with those in measured end-members and in streamflow.
-
Conventional hydrograph separation requires that the end-members' tracer concentrations are distinct from one another; otherwise the solution to Eq. (3) becomes unstable because the denominator is nearly zero. By contrast, ensemble hydrograph separation estimates the new water fraction by regression, and points where the new water and old water concentrations overlap will have almost no leverage on the regression slope (they correspond to points near zero on the x axes of Figs. 6a, b, 7a, b, 9a, or A1d, for example).
-
Conventional hydrograph separation is vulnerable to biases in tracer measurements, such as could arise from isotopic evaporative fractionation. By contrast, these same biases should have relatively little effect on ensemble hydrograph separation (e.g., Sect. 3.6), because it is based on regressions between tracer fluctuations, and regression slopes are unaffected by constant offsets on either the x or y axes.
It is also useful to contrast ensemble hydrograph separation with other methods for estimating transit time distributions from conservative tracers. As reviewed by McGuire and McDonnell (2006), these approaches typically convolve the precipitation tracer time series with an assumed transit time distribution, and then adjust the parameters of that distribution to achieve a best fit with the streamflow tracer time series. This convolution approach differs from ensemble hydrograph separation in several important respects:
-
In the convolution approach, the functional form of the transit time distribution must be assumed (although shape parameters often allow the shape of the TTD to be fitted, within a given family of distributions). By contrast, the ensemble hydrograph separation approach makes no assumption about the shape of the distribution; instead, the TTD values at each lag k are estimated directly from data.
-
Ensemble hydrograph separation quantifies the transit time distribution out to a maximum lag m, beyond which it makes no assumptions (and draws no inferences) about the behavior of the TTD. By contrast, because convolution approaches assume a shape for the entire TTD, their results include the long tails that are missing from TTDs estimated from ensemble hydrograph separation. However, these long tails will typically be poorly constrained by data in any case, because the long-timescale signal of conservative tracers is typically so weak that it cannot be reliably separated from the noise (DeWalle et al., 1997; Stewart et al., 2010; Seeger and Weiler, 2014; Kirchner, 2016b). This is not an algorithmic problem and it does not have an algorithmic solution; instead it arises from the limited information content of conservative tracer time series on these long timescales. Although convolution approaches seek to get around this problem by assuming a (potentially parameterized) shape for the TTD, the long tails will largely reflect the underlying assumptions that are made, rather than any substantial influence of the tracer data themselves.
-
Convolution approaches are based on convolution integrals, and thus errors in the input terms accumulate over time. By contrast, the ensemble hydrograph separation approach is based on local derivatives of the stream tracer concentrations and their covariances with fluctuations in the input tracer concentrations at various lags; as a result, errors in the input terms do not accumulate.
-
Missing input data pose a fundamental problem for convolution integrals, whereas they can be readily accommodated in the ensemble hydrograph separation approach (Sect. 4.2).
These considerations also generally apply to approaches that use tracer concentrations in rainfall and streamflow to calibrate storage selection (SAS) functions, instead of time-invariant transit time distributions (e.g., van der Velde et al., 2012; Harman, 2015). SAS function estimation also faces the additional difficulty that the SAS functions for streamflow and evapotranspiration are interrelated, because they both depend on, and jointly determine, the age distribution of catchment storage (e.g., Eqs. 2–8 of Botter, 2012; Rigon et al., 2016). Because we currently have no practical way to determine the age distributions of catchment storage or evapotranspiration, estimating SAS functions for streamflow requires making unverifiable assumptions concerning evapotranspiration ages, and the effects of these assumptions have not been quantified. By contrast, ensemble hydrograph separation directly quantifies the forward and backward transit time distributions of precipitation that subsequently leaves the catchment as streamflow, without needing to estimate, or to make any assumption about, the ages of waters that leave the catchment by other pathways.
Another approach that is coming into more frequent use is to calibrate a conceptual or physically based model to reproduce, as closely as possible, the observed hydrograph and streamflow tracer time series, and then infer the catchment transit time distribution or SAS function from particle tracking within the model (e.g., Benettin et al., 2013, 2015; Remondi et al., 2018). For these inferences to be valid, the model must not only be a good predictor of the calibration data, but its underlying processes must also be the correct ones. In other words, the model must get the right answers for the right reasons, and it will generally be difficult to verify whether this is the case. Thus it will be difficult to know how much the inferred transit times are determined by the tracer data or by the structural assumptions of the underlying model. Nor does a good fit to the observational data verify the correctness of the model and the inferences drawn from it, because a good fit can imply either that the model is doing everything correctly or that it is doing multiple things wrong, in offsetting ways.
One can argue that every data analysis approach also implies some underlying model, and one might argue that ensemble hydrograph separation is based on the (implausible) assumption that the transit time distribution is time-invariant. Such an argument would be mistaken. As I have shown, ensemble hydrograph separation neither assumes nor requires that the transit time distribution is stationary (see Appendices A and B). Instead, ensemble hydrograph separation quantifies the ensemble average of a catchment's time-varying transit time distribution, even when that distribution is highly dynamic.
5.2 Benchmark testing
Considerable effort has been devoted to benchmark tests of the methods proposed in Sects. 2 and 4. One may naturally ask: why bother? Why not just describe how ensemble hydrograph separation works, and apply it to several field data sets, and see whether it gives reasonable results? One answer is that whether the results seem reasonable only reflects whether they agree with our preconceptions, not whether they (or our preconceptions) are correct. A second answer is that only through properly designed benchmark tests can we assess how accurate the method is, and what factors might affect its accuracy. Yet another answer is that the benchmark model gives the analysis method a precise target to hit, thus better revealing its strengths and weaknesses.
Benchmark tests also have a role to play in the day-to-day application of data analysis methods like those proposed here. Users may wonder: will this approach work with data from my catchment? Given the data I have, how accurately can I estimate the ensemble average transit time distribution? What kinds of tracer data will be needed to distinguish between two different conceptualizations of catchment-scale storage and transport? Carefully designed benchmark tests with synthetic data can be helpful in addressing questions such as these.
It should be emphasized that, in the tests presented here, the benchmark model knows nothing about how the analysis method works; in fact, its nonlinearity and nonstationarity rather badly violate the assumptions underlying the analysis. Conversely, the analysis method knows nothing about the inner workings of the benchmark model. It knows the model inputs and outputs (the water fluxes and tracer concentrations in rainfall and streamflow), but it does not know – and, importantly, it does not need to know – how those outputs were generated. This is important because, for ensemble hydrograph separation to be useful in real-world catchments, its validity must not depend on the particular mechanisms that regulate flow and transport at the catchment scale.
Likewise, its validity must not depend on having unrealistically accurate or complete data. For this reason, the benchmark tests include substantial measurement errors and substantial numbers of missing values (Sect. 3.1).
Thus these benchmark tests are much stricter than many in the literature. For example, some benchmark tests generate the benchmark data set using the same assumptions that underlie the analysis method itself (e.g., Klaus et al., 2015). Such tests usually generate very nice-looking results, but they are guaranteed to succeed because they are performing the same calculations twice (first forwards, then backwards). At the same time, such tests are not realistic, because they would only be relevant to real-world cases where all of the assumptions underlying the analysis method were exactly true. Such cases are unlikely to exist.
One could argue that the benchmark model presented here would be more realistic if it were (for example) a spatially distributed three-dimensional model based on Richards' equation, calibrated to a particular research watershed. However, the benchmark model's purpose is to generate a wide variety of targets for the analysis method to hit, with each target precisely defined, rather than to realistically mimic any particular catchment. All that is essential is that it must generate realistically complex patterns of behavior and exactly compute the true new water fractions and transit time distributions by age tracking. The relatively simple two-box conceptual model that has been used here was chosen because it fulfills both criteria, not because it embodies a particular mechanistic view of flow and transport. Likewise, consistency with the assumptions underlying ensemble hydrograph separation was not one of the criteria, nor should it be.
For the same reason, it should be clear that real-world catchments may not necessarily exhibit similar patterns of behavior to those of the benchmark model, as shown in Figs. 6–9 and 15–18. Thus the analyses presented here do not necessarily mean, for example, that we should expect new water fractions in real-world catchments to be roughly linear functions of discharge (Fig. 6), precipitation (Fig. 7), or antecedent moisture (Fig. 18). These patterns of behavior reflect the properties of the benchmark model and its precipitation forcing. Whether real-world catchments behave similarly or differently is an open question. The benchmark tests demonstrate that these analyses are reliable (which cannot be demonstrated with real-world data because we cannot know independently what the right answer is), but they should not be taken as examples of what the real-world results would necessarily look like.
5.3 Errors, biases, and uncertainties
The analysis methods outlined in Sects. 2 and 4 include explicit procedures for estimating the uncertainties (as quantified by standard errors) in both new water fractions (Eqs. 11, 15, and 20) and transit time distributions (Eqs. 54, 55, 60, 69, and 66). These uncertainties are generally realistic predictors of how much the ensemble hydrograph separation estimates deviate from the true benchmark values determined from age tracking: the scatter in Figs. 2 and 5, for example, is consistent with the estimated standard errors, and the error bars in Figs. 6, 7, 9, and 11–18 (1 standard error in all cases) are usually reasonable estimates of the deviations from the benchmark values (exceptions include the humped transit time distributions in Fig. 12, where the uncertainties are overestimated).
Unsurprisingly, the standard errors scale with the scatter (error variance) in the data and inversely with the square root of the effective number of degrees of freedom. Thus the uncertainties will be larger when the data set is sparse and noisy, and when the new water fraction and/or transit time distribution explains only a small fraction of its variance. It should also be noted that the relative standard error can be large, for example when the TTD is small at long lags.
Because ensemble hydrograph separation does not require continuous input data, it can facilitate comparisons among various subsets of a catchment time series, as demonstrated in Sects. 3.5 and 4.7. However, it should be kept in mind that, as one cuts the data set into more (and thus smaller) pieces, the statistical sampling variability among the data points remaining in each piece will become more and more influential, and the inferences drawn on each piece will become correspondingly more uncertain. Thus there will be practical limits to the granularity of the subsampling that can be applied in real-world cases.
One should also keep these considerations in mind when choosing m, the largest TTD lag to be estimated. Although m can be any value that the user chooses, as m increases, the uncertainties in TTDk at each lag also increase, in essence because the user is choosing to distribute the (limited) information contained in the tracer time series among a larger number of TTDk values. Conversely, if one sets m to zero and thus estimates only the amount of same-day or same-week water in streamflow (whereupon the approaches outlined in Sects. 2 and 4 become equivalent), one brings all the available information to bear on estimating that one quantity. The tradeoff between TTD length and precision will depend on the length of the time series and the gaps that it contains, as well as the characteristic storage times of the catchment and the noise characteristics of the data (which will often be unknown). Thus it is difficult to give general guidance on appropriate values of m, but benchmark tests with synthetic data could be used to illustrate the tradeoffs involved.
In some TTDs, the last few lags exhibit unusually large deviations from the true TTD curves derived from age tracking (e.g., Figs. 12b, 13a, c, 14c, 16b, d, and 17b, d; in several of these cases the last point is below zero and thus does not appear on the plot). As noted in Sect. 4.5, I suspect (but cannot prove) that this is an aliasing effect that arises when the effects of fluxes beyond the longest measured lag are not adequately accounted for by the reference concentration . In practice this means that TTD values for the last few lags should not be taken too literally, particularly if they deviate from the trend in the previous lags.
Because ensemble hydrograph separation is based on correlations among tracer fluctuations, it is relatively insensitive to systematic biases that produce persistent offsets in the underlying data. For example, isotope ratios in precipitation often vary with altitude, leading to potential biases in precipitation tracer samples (depending on the sampling location). To the extent that these biases are constant, however, they should not alter regression slopes between tracer fluctuations in precipitation and streamflow (e.g., Figs. A1d, 6a, b, and 7a, b), or their multidimensional counterparts that determine the TTD. The same applies to randomly fluctuating precipitation tracer biases, unless they are large compared to the standard deviation of the tracer concentrations themselves – i.e., unless the fluctuating biases account for most of the variability in the precipitation tracer measurements. Likewise, confounding by any unmeasured end-members should be small, unless the unmeasured end-members are correlated with the measured ones, and have a strong influence on stream tracer concentrations.
The uncertainties calculated here, like all error propagation results, depend on the assumptions underlying the analysis (in this case, ensemble hydrograph separation). Under different assumptions, the errors in estimating the average Fnew by regression could be larger. For example, if the means of and differed by much more than their pooled standard deviations, then variations in would mostly be driven by variations in Fnew rather than variations in . This highlights the important contrast between conventional and ensemble methods of hydrograph separation. Conventional hydrograph separation is based on comparing stream tracer values to constant end-members and therefore works best when the end-members have widely separated means and small variability. By contrast, ensemble hydrograph separation works best when the variations in the end-members are large compared to the differences among their means, because it relies on correlating tracer fluctuations in streamflow with fluctuations in measured end-members.
5.4 Potential applications and extensions
The techniques proposed here quantify the timescales over which catchments store and transport water, and quantify how those timescales change with precipitation, discharge, and antecedent moisture. Such descriptive methods are often grouped under the heading of “catchment characterization”. One should keep in mind, however, that a catchment's storage and transport behavior also depends on its external forcing. If its precipitation climatology were wetter (or drier), for example, its timescales of storage and transport would decrease (or increase) accordingly. Thus transport and storage timescales are not characteristics of the catchment alone, but rather of the catchment and its particular precipitation climatology. By mapping out how a catchment's storage and transport behavior changes with hydrologic forcing (e.g., Figs. 6, 7, 15, 17, and 18), however, ensemble hydrograph separation can contribute to a more complete picture of catchment response. Alternatively, these patterns of response to hydrologic forcing can be considered as catchment characteristics in their own right.
Because new water fractions and transit time distributions from ensemble hydrograph separation closely match benchmark model age tracking, one might consider using them as a model for catchment transport processes. This will usually be a bad idea. One must remember that ensemble hydrograph separation quantifies ensemble averages, which will not be good models of catchment processes unless the real-world transit time distribution is approximately time-invariant. That is unlikely to be the case.
This observation raises an important point. Ensemble hydrograph separation yields inferences that are phenomenological, not mechanistic. It quantifies how catchments behave, but does not, by itself, explain how they work. It can nonetheless contribute to mechanistic understanding by precisely quantifying catchment transport behavior, and thus facilitating more incisive comparisons with models. Examples of possible comparisons include
-
Do the model and the real-world catchment have similar new water fractions and forward new water fractions (Figs. 2 and 5)?
-
Do these new water fractions change similarly as functions of precipitation and discharge (Figs. 6 and 7)?
-
Do they exhibit similar seasonal patterns (Fig. 9)?
-
Do the model and the real-world catchment have similar transit time distributions, including forward transit time distributions (Figs. 11–14)?
-
Do these transit time distributions change similarly as functions of precipitation, discharge, antecedent moisture, and seasonality (Figs. 15–18)?
In this approach to hypothesis testing, key signatures of behavior are extracted from both the model and the data before they are compared (Kirchner et al., 1996; Kirchner, 2006). This approach stands in contrast to the conventional model-testing paradigm in which model predictions are compared with observational time series through standard goodness-of-fit statistics. The conventional approach ignores the important question of in what ways the model predictions deviate from the data. Exploring this question requires diagnostic signatures of catchment behavior like those presented here and is essential to improving models of catchment processes.
The analysis methods developed here can potentially be extended in several ways. For example, these methods could potentially be applied to infer transit times in other catchment fluxes, such as groundwater seepage or evapotranspiration. They could also be applied to other systems where transit times could be inferred from the propagation of fluctuating tracer inputs; potential examples include not only lakes, oceans, and aquifers, but also the atmosphere and perhaps even organisms.
The multiple regression analysis presented in Sect. 4 demonstrates that one can quantify the contributions of multiple end-members using a single conservative tracer. This is not possible in conventional end-member mixing analysis, which assumes that the end-members are constant and consequently requires that the number of end-members cannot exceed the number of tracers plus one. But because ensemble hydrograph separation is based on correlations of tracer fluctuations, one tracer can potentially identify many end-members as long as their fluctuations are not too tightly correlated. This is potentially useful, because hydrologists typically have very few truly conservative tracers to work with (arguably only one, in the case of stable isotopes, because 18O and 2H are strongly correlated with one another). In the analysis in Sect. 4, the TTDs can be considered to represent 25 different end-members (which are all precipitation, at different lags). However the same approach could be used to analyze (for example) precipitation and snowmelt as sources of streamflow, if tracer time series are available in both candidate end-members and they are not too strongly correlated with one another. Similarly, in large river basins one could potentially quantify the contributions (and transit time distributions) of waters sourced from precipitation in different parts of the catchment – if, again, tracer time series are available for these multiple precipitation sources and are not too strongly correlated with one another.
Last but not least, the approach presented here can also, with some modifications, be applied to rainfall and streamflow rates in order to quantify the time lags in catchments' hydraulic response to precipitation (reflecting the celerity of hydraulic potentials, as distinct from the velocity of water transport). A follow-up paper describing this “ensemble unit hydrograph” analysis is currently in preparation.
The analysis codes and benchmark model used here will be published separately in more user-friendly form. The Plynlimon rain gauge data were provided by the Centre for Ecology and Hydrology (UK), and the Smith River and Broad River precipitation data are reanalysis products from the MOPEX (Model Parameter Estimation Experiment) project (Duan et al., 2006; ftp://hydrology.nws.noaa.gov/pub/gcip/mopex/US_Data/, last access: 1 December 2018).
A conventional linear regression equation has the form
where yj and xj are response and explanatory variables, respectively, measured for individual cases j, where α and β are (unknown) constants, and where εj is a random (and unknown) additive error term with mean of zero (alternatively, one can consider α+εj to represent all of the unmeasured factors that influence yj). Under the assumption that these unmeasured factors are uncorrelated with xj, linear regression obtains unbiased estimates of β from any of several functionally equivalent formulas, including
where denotes the conventional least-squares estimator of β, primes denote deviations from means, and means over all j may be denoted by either angled brackets or overbars, depending on context.
In many practical situations, the unknown constant β may not in fact be constant, but instead may differ among the cases j. In such situations, the true relationship among the variables is not Eq. (A1), but instead
where the small but important difference between Eqs. (A1) and (A3) is the subscript j on β. It may be unclear a priori whether β is a constant or not, and therefore whether Eqs. (A1) or (A3) applies. In other words, Eq. (A1) represents a special case of the more general relationship represented by Eq. (A3), and it may be unclear whether we are dealing with the special case or the general one.
Thus, in environmental work, regression equations are often used to estimate “constants” that are not known to be constant, or, even more pointedly, “constants” that we know are not constant. Regression equations are nonetheless used, under the assumption that the result will provide a useful estimate of some central tendency of the non-constant “constant”. The basis for this assumption and its range of validity are unclear.
The problem at hand can be stated like this: if the unknown coefficient βj differs among the cases j, as in Eq. (A3), but one nonetheless calculates a conventional least-squares estimator using Eq. (A2), how will the calculated value of depend on the properties of the (unknown) βj, including their possible relationships with the values xj of the explanatory variable? The answer can be obtained straightforwardly by substituting yj from Eq. (A3) into (A2) and solving for . The math is streamlined somewhat if one separates x, y, β, and ε into their (sample) means and deviations (replacing xj with , and similarly for y, β, and ε), where primed quantities indicate deviations from means. One can begin by expressing Eq. (A3) in terms of deviations from means,
and then by multiplying the terms in parentheses, yielding
The single-underlined terms in Eq. (A5) cancel each other, and the double-underlined terms are zero because primed quantities will always average to zero (although products of two or more primed quantities usually will not). Removing all underlined terms, multiplying by , averaging over all j, and dividing by the variance of x yields directly
The double-underlined term in the numerator of Eq. (A6) is zero, because the inner average is a constant and therefore just rescales , which in turn averages to zero. Simplifying the remaining terms, one obtains
Equation (A7) cannot be evaluated in practice, because the true coefficients βj and the errors εj will not be known. Nonetheless it can be useful to understand how their properties influence so that regression results can be properly interpreted. In this regard, each of the four terms of Eq. (A7) has a story to tell. The first term of Eq. (A7) says that the linear regression coefficient will be a good approximation to the (sample) mean of the βj, if the other terms are negligible.
The second term says that the linear regression coefficient can also be affected by correlations between βj and xj. The magnitude of this effect will be the average value of x, multiplied by the regression slope of the relationship between x and β. This second term will vanish if is zero or if there is no correlation between xj and βj.
The third term can be viewed as a weighted average of the deviations of the βj from their mean, where the weighting factors are the squared deviations of the xj from their mean (in statistical terms, these weighting factors are called leverages). Thus the third term of Eq. (A7) expresses the effect of a cup-shaped relationship between βj and xj; for example, if xj values with greater leverage on (because they lie farther from ) are also associated with higher values of βj (and thus a steeper relationship between xj and yj), the estimate of will be biased upward. Note in particular that the third term could be nonzero even if the correlation between βj and xj is zero (that is, the relationship between βj and xj could be cup-shaped even if it has a slope of zero overall). Conversely, the third term is insensitive to linear correlations (even strong ones) between βj and xj.
The fourth term says that could also be biased by correlations between the error term and the explanatory variable; the magnitude of this possible bias equals the regression slope of εj as a function of xj. This is the well-known problem of artifactual correlation (also called the “third variable problem” or “hidden variable problem”): if hidden (unmeasured) variables are correlated with the measured explanatory (x) variable, their effects on the response (y) variable will be falsely attributed to the x variable instead, distorting its regression coefficient.
It should be noted that the means, variances, and covariances in Eqs. (A2)–(A7) are sample statistics calculated over the sample cases j, which may differ from the true means, variances, and covariances of the underlying distributions. Thus there will be additional uncertainty resulting from sampling variability (in addition to the biases quantified by the second, third, and fourth terms in Eq. A7), if one interprets the regression slope as an estimate of the true mean of β rather than the sample mean of the βj for the particular cases j that have been sampled.
To illustrate the analysis outlined above, I conducted a simple numerical experiment based on ensemble hydrograph separation. I created a synthetic data set based on the mixing equation
where , the concentration in the stream, is a volume-weighted average of the (measured) new water concentration and the old water concentration from the previous time step, weighted by the new water fraction and its complement . Values of for each time step j are randomly chosen from a beta distribution,
where x is a random variable that, appropriately for a fraction, ranges from 0 to 1, the beta function is a normalization constant that ensures that the cumulative probability is 1, and α and β are shape parameters that are related to the mean (μ) by , or equivalently . In the simulations shown here (Fig. A1a–e), the α parameter is fixed at 1.
Values of for each point in time j are randomly chosen from a normal distribution with a standard deviation of 10 (Fig. A1b). Values of are calculated for the whole time series using Eq. (A8), and measurement errors (normally distributed, with a standard deviation of 1) are added to both Cnew and CQ. Then an ensemble estimate of the average Fnew is obtained by linear regression of on , following Eq. (9) in the main text. A plot of such a regression is shown in Fig. A1d. In this particular ensemble, the individual values for each time step varied between 0.0001 and 0.71, with a mean of 0.20 and a standard deviation of 0.16. The ensemble hydrograph separation estimate of the average Fnew was 0.205±0.009 (mean ± standard error), deviating from the true mean value by roughly its standard error, as one would expect. This analysis was repeated 1000 times for mean Fnew values randomly chosen between 0.025 and 0.975. The results are summarized in Fig. A1e, which compares the regression estimates of the average Fnew against the true means of the Fnew values in each sample. Although the individual values that make up each mean vary widely (as indicated by the horizontal width of the shading in Fig. A1e), the regression estimates of the average Fnew cluster tightly around the 1:1 line, with a root-mean-square deviation of less than 0.02 across the full range of average Fnew (this root-mean-square deviation scales, as one would expect, inversely with the square root of the number of data points in the simulated time series).
In the simulations shown in Fig. A1, is independent of , , and the measurement errors; therefore the biases quantified in Eq. (A7) are expected to be small. Nonetheless, one should be aware that in the specific case of Eq. (A8) there could be two additional sources of bias that Eq. (A7) does not account for. Large measurement errors in Cnew (meaning measurement errors that are not small compared to the standard deviation of Cnew itself) could potentially create negative biases in estimates of the average Fnew, because they would add spurious variation to the x axis of regressions like Fig. A1d. Conversely, large measurement errors in CQ – which again means errors that are not small compared to the standard deviation of Cnew (not CQ) – could potentially create positive biases in estimates of the average Fnew, because appears on both axes of the regression in Fig. A1d, so large errors in would spuriously increase the correlation between the x and y axes of regressions like Fig. A1d. Both of these biases should be negligible in real-world cases, however, because the measurement uncertainties in Cnew and CQ are typically much smaller than the variability in Cnew.
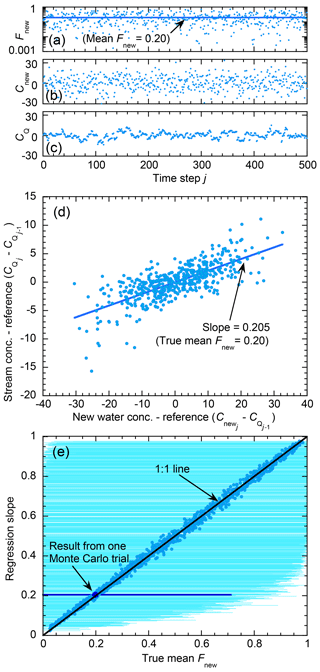
Figure A1Benchmark test of regression estimates of mean new water fractions, using data from a simple two-component mixing model. In that mixing model (Eq. A8), a randomly varying new water fraction Fnew (a) determines the relative proportions of new and old water ( and , respectively) which are combined to yield a mixture with concentration (c). Among the 500-point time series shown in (a–c), the new water fraction Fnew varies between 0.0001 and 0.71, with a mean of 0.20 and a standard deviation of 0.15. Plotting the concentration of the mixture in the stream as a function of the concentration in the new water end-member (e) yields a regression slope of 0.205±0.009, which agrees within error with the true average of Fnew of μ=0.20. Repeating this analysis 1000 times, with mean values of Fnew ranging from nearly zero to nearly one, yields regression slopes that agree with the means of the Fnew for each Monte Carlo trial with an RMSE of only 0.02 (e). In (e), the circles show the regression slopes and mean Fnew, and the horizontal light blue lines show the range of Fnew, for each Monte Carlo trial. The dark circle and dark line show the results for the individual Monte Carlo trial shown in (a–d).
Assume a multiple linear regression equation with non-constant unknown coefficients,
which can be more explicitly represented for a series of sampling times j=1…n as
For simplicity, and without loss of generality, assume that the yj's and xj, k's have means of zero. Assume further that, for each k, the coefficients βj, k either have a constant value of βk (when precipitation is present at time step ), or have a value of 0 (when precipitation in missing at time step ). In the latter case the value of xj, k will be undefined, but it will also be irrelevant because it is multiplied by zero. The resulting system of equations will then have the following form, with missing values along diagonal stripes (this illustration shows just one possible set of missing values):
Multiplying the left and right sides of Eq. (B3) by the transpose of X0 (to take one example) yields
where the constant α and the error term εj drop out because their sums of cross products with the xj, 0 are zero. One can see that each of the summations of cross products equals the covariance of the respective vectors, multiplied by the number of points in the summation. In contrast to a typical multiple regression, these numbers of points are not the same. For the left-hand side of Eq. (B4), the summation is taken over the non-missing members of X0; if we use to express the number of such members, this summation equals . The first term on the right-hand side can also be evaluated for all non-missing members of X0; there are of these, so this term becomes . The second term on the left-hand side, on the other hand, can only be evaluated when both X0 and X1 are non-missing. If we denote the number of such cases as , the second term equals , the third term equals , and so forth. Thus when re-expressed as covariances, Eq. (B3) becomes
Dividing through by the terms on the left-hand side, one directly obtains the following system of m equations in m unknowns:
which can be solved by the usual matrix inversion approach, yielding
One can see that Eq. (B7) is identical in form to Eq. (40), with the addition of weighting factors on the off-diagonal elements of the covariance matrix. One consequence of these leading terms is that the weighted covariance matrix will usually not be completely symmetrical, because (for example) will often differ from .
It bears emphasis that Eq. (B7) accounts for gaps in precipitation, but not for precipitation or streamflow samples that are missing due to sampling and measurement failures. A gap in precipitation means that the corresponding tracer values never existed at all and had no effect on streamflow, whereas tracer values that are missing due to sampling and measurement failures actually did affect streamflow, but are unknown. Equation (B7) accounts for the fact that the tracer covariances will necessarily be less strongly coupled to one another, the less frequently precipitation falls. Glasser's method, by contrast, estimates the covariances themselves from all available pairs of observations, but says nothing about how they are related to one another. Therefore we can account for both kinds of missing data using Eq. (B7), with the covariances between pairs of variables estimated using Glasser's method (Eqs. 42–43). That approach results in Eq. (44).
Astute readers may notice that Eq. (B3) is equivalent to the normal equations of conventional multiple regression, with the cases of missing precipitation replaced by (instead of . This provides a simple procedure for estimating the βk if tracer values are only missing due to lack of precipitation, with no sampling or measurement failures. This method proceeds as follows:
-
Normalize Y and each of the Xk to zero by subtracting the mean from each vector (excluding any missing values from these means).
-
Replace any values that are missing due to lack of precipitation with zeroes.
-
Solve for the βk using conventional multiple regression.
-
Multiply the standard errors of the βk (not the βk themselves) by to account for the fact that the zeroes that have been used to infill the missing values are not measured values and thus do not contribute information to constrain the βk.
This method is unlikely to be useful in most practical cases, in which occasional sampling and measurement failures are virtually guaranteed. However, it can provide a useful consistency check for implementations of the more complex approach developed here (Eqs. B7 and 44).
There remains one last important detail. In transitioning from Eq. (B2) to (B3), I made the simplifying assumption that all of the coefficients βj, k for a given k were either equal to zero or had a constant value of βk instead. The same assumption is made in the derivation presented in Sect. 4. One could naturally ask what happens if the βj, k vary individually across the time steps j. Is there is a (nearly) equivalent constant βk and, if so, how does it relate to the values of the βj, k?
If we have a variable βj, k rather than a constant βk, each of the terms of Eq. (B4) will be of the form instead of , and each of the terms of Eq. (B5) will be of the form instead of . Thus the effect of a variable vs. constant β depends on how differs from . Following the approach in Appendix A, I begin by expanding the three variables into their means and deviations, replacing βj, k with , xj, k with , and xj, ℓ with . Each covariance on the right-hand side of Eq. (B5) would thus become instead
where angled brackets and overbars indicate averages over j. The final result can thus be written as
where the first term on the right-hand side expresses the approximation on which the covariance matrices in Eqs. (B7) and (44) are based; if the second and third terms vanish, then this approximation is exact. The second term on the right-hand side should be small, unless there is a strong correlation between βj, k and xj, ℓ (which is unlikely unless storm size is correlated with tracer concentrations, as explained in Sect. 2.1), and is large (which is unlikely because , see Eq. (37), and mass conservation implies that the averages of CP and CQ should be similar). The third term on the right-hand side is a three-way cross product, technically termed a co-skewness, that bears the same relation to skewness that covariance does to variance. It has the interesting property that its expected value is zero if the three variables have symmetrical distributions, even if they are strongly correlated (either positively or negatively, in any combination) with one another. This behavior arises because the odd number of terms means that, for symmetrical distributions, the product is equally likely to be positive or negative for any j, and thus the positive and negative values of will tend to average out when one averages over all j. If the last two terms of Eq. (B9) are small compared to the first one, Eq. (B9) says that the covariance matrices in Eqs. (B5)–(B6) will be nearly the same whether β is constant or variable, whenever the constant βk is the average of the variable βj, k. This in turn implies that the analysis presented in Sect. 4 should result in estimated coefficients that closely approximate the average of the time-varying βj, k, as is confirmed by the benchmark tests of Sect. 4.6–4.8.
More readable versions of Eqs. (40), (44), and (B7) are available in the supplement. The supplement related to this article is available online at: https://doi.org/10.5194/hess-23-303-2019-supplement.
The author declares that there is no conflict of interest.
This work was motivated by discussions with Chris Soulsby and Doerthe
Tetzlaff during long walks in the Scottish countryside. I also thank Jana
von Freyberg, Andrea Rücker, Julia Knapp, Wouter Berghuijs, Paolo
Benettin, and Greg Quenell for helpful discussions; Riccardo Rigon, Nicolas
Rodriguez, and an anonymous reviewer for their comments; and Melissa Heyer
for proofreading assistance.
Edited by: Thom Bogaard
Reviewed by: Riccardo Rigon and one anonymous referee
Bansah, S. and Ali, G.: Evaluating the effects of tracer choice and end-member definitions on hydrograph separation results across nested, seasonally cold watersheds, Water Resour. Res., 53, 8851–8871, https://doi.org/10.1002/2016WR020252, 2017.
Bayley, G. V. and Hammersley, J. M.: The effective number of independent observations in an autocorrelated time series, J. R. Stat. Soc., 8, 184–197, https://doi.org/10.2307/2983560, 1946.
Benettin, P., van der Velde, Y., van der Zee, S., Rinaldo, A., and Botter, G.: Chloride circulation in a lowland catchment and the formulation of transport by travel time distributions, Water Resour. Res., 49, 4619–4632, https://doi.org/10.1002/wrcr.20309, 2013.
Benettin, P., Kirchner, J., Rinaldo, A., and Botter, G.: Modeling chloride transport using travel-time distributions at Plynlimon, Wales, Water Resour. Res., 51, 3259–3276, https://doi.org/10.1002/2014WR016600, 2015.
Benettin, P., Volkmann, T. H. M., von Freyberg, J., Frentress, J., Penna, D., Dawson, T. E., and Kirchner, J. W.: Effects of climatic seasonality on the isotopic composition of evaporating soil waters, Hydrol. Earth Syst. Sci., 22, 2881–2890, https://doi.org/10.5194/hess-22-2881-2018, 2018.
Bishop, K. H.: Episodic increases in stream acidity, catchment flow pathways and hydrograph separation, PhD dissertation, Department of Geography, University of Cambridge, Cambridge, 1991.
Botter, G.: Catchment mixing processes and travel time distributions, Water Resour. Res., 48, W05545, https://doi.org/10.1029/2011wr011160, 2012.
Brooks, C. E. P. and Carruthers, N. B.: Handbook of Statistical Methods in Meteorology, Meteorological Office, London, 412 pp., 1953.
Buttle, J. M.: Isotope hydrograph separations and rapid delivery of pre-event water from drainage basins, Prog. Phys. Geog., 18, 16–41, https://doi.org/10.1177/030913339401800102, 1994.
Detty, J. M. and McGuire, K. J.: Topographic controls on shallow groundwater dynamics: implications of hydrologic connectivity between hillslopes and riparian zones in a till mantled catchment, Hydrol. Process., 24, 2222–2236, https://doi.org/10.1002/hyp.7656, 2010.
DeWalle, D. R., Edwards, P. J., Swistock, B. R., Aravena, R., and Drimmie, R. J.: Seasonal isotope hydrology of three Appalachian forest catchments, Hydrol. Process., 11, 1895–1906, https://doi.org/10.1002/(SICI)1099-1085(199712)11:15<1895::AID-HYP538>3.0.CO;2-%23, 1997.
Duan, Q., Schaake, J., Andreassian, V., Franks, S., Goteti, G., Gupta, H. V., Gusev, Y. M., Habets, F., Hall, A., Hay, L., Hogue, T., Huang, M., Leavesley, G., Liang, X., Nasonova, O. N., Noilhan, J., Oudin, L., Sorooshian, S., Wagener, T., and Wood, E. F.: Model Parameter Estimation Experiment (MOPEX): An overview of science strategy and major results from the second and third workshops, J. Hydrol., 320, 3–17, https://doi.org/10.1016/j.jhydrol.2005.07.031, 2006.
Fischer, B. M. C., van Meerveld, H. J., and Seibert, J.: Spatial variability in the isotopic composition of rainfall in a small headwater catchment and its effect on hydrograph separation, J. Hydrol., 547, 755–769, https://doi.org/10.1016/j.jhydrol.2017.01.045, 2017.
Galassi, M., Davies, J., Theiler, J., Gough, B., Jungman, G., Alken, P., Booth, M., Rossi, F., and Ulerich, R.: GNU Scientific Library Reference Manual v. 2.3, available at: https://www.gnu.org/software/gsl/manual/gsl-ref.pdf (last access: 1 December 2018), 2016.
Genereux, D.: Quantifying uncertainty in tracer-based hydrograph separations, Water Resour. Res., 34, 915–919, https://doi.org/10.1029/98WR00010, 1998.
Glasser, M.: Linear regression analysis with missing observations among the independent variables, J. Am. Stat. Assoc., 59, 834–844, https://doi.org/10.1080/01621459.1964.10480730, 1964.
Harman, C. J.: Time-variable transit time distributions and transport: Theory and application to storage-dependent transport of chloride in a watershed, Water Resour. Res., 51, 1–30, https://doi.org/10.1002/2014WR015707, 2015.
Heidbüchel, I., Troch, P. A., Lyon, S. W., and Weiler, M.: The master transit time distribution of variable flow systems, Water Resour. Res., 48, W06520, https://doi.org/10.1029/2011WR011293, 2012.
Hooper, R. P. and Shoemaker, C. A.: A comparison of chemical and isotopic hydrograph separation, Water Resour. Res., 22, 1444–1454, https://doi.org/10.1029/WR022i010p01444, 1986.
Hubert, P., Marin, E., Meybeck, M., Olive, P., and Siwertz, E.: Aspects hydrologique, gèochimique et sèdimentologique de la crue exceptionnelle de la Dranse du Chablais du 22 septembre 1968, Archives des Sciences (Genève), 22, 581–604, 1969.
Kirchner, J. W.: A double paradox in catchment hydrology and geochemistry, Hydrol. Process., 17, 871–874, https://doi.org/10.1002/hyp.5108, 2003.
Kirchner, J. W.: Getting the right answers for the right reasons: Linking measurements, analyses, and models to advance the science of hydrology, Water Resour. Res., 42, W03S04, https://doi.org/10.1029/2005WR004362, 2006.
Kirchner, J. W.: Aggregation in environmental systems – Part 2: Catchment mean transit times and young water fractions under hydrologic nonstationarity, Hydrol. Earth Syst. Sci., 20, 299–328, https://doi.org/10.5194/hess-20-299-2016, 2016a.
Kirchner, J. W.: Aggregation in environmental systems – Part 1: Seasonal tracer cycles quantify young water fractions, but not mean transit times, in spatially heterogeneous catchments, Hydrol. Earth Syst. Sci., 20, 279–297, https://doi.org/10.5194/hess-20-279-2016, 2016b.
Kirchner, J. W., Hooper, R. P., Kendall, C., Neal, C., and Leavesley, G.: Testing and validating environmental models, Sci. Total Environ., 183, 33–47, https://doi.org/10.1016/0048-9697(95)04971-1, 1996.
Kish, L.: Survey Sampling, Wiley Classics Library, Wiley, New York, 643 pp., 1995.
Klaus, J. and McDonnell, J. J.: Hydrograph separation using stable isotopes: Review and evaluation, J. Hydrol., 505, 47–64, https://doi.org/10.1016/j.jhydrol.2013.09.006, 2013.
Klaus, J., Chun, K. P., McGuire, K. J., and McDonnell, J. J.: Temporal dynamics of catchment transit times from stable isotope data, Water Resour. Res., 51, 4208–4223, https://doi.org/10.1002/2014wr016247, 2015.
Laudon, H., Hemond, H. F., Krouse, R., and Bishop, K. H.: Oxygen 18 fractionation during snowmelt: Implications for spring flood hydrograph separation, Water Resour. Res., 38, 1258, https://doi.org/10.1029/2002wr001510, 2002.
Little, R. J. A.: Regression with missing X's: A review, J. Am. Stat. Assoc., 87, 1227–1237, https://doi.org/10.2307/2290664, 1992.
Matalas, N. C. and Langbein, W. B.: Information content of the mean, J. Geophys. Res., 67, 3441–1448, https://doi.org/10.1029/JZ067i009p03441, 1962.
McDonnell, J. J., Bonell, M., Stewart, M. K., and Pearce, A. J.: Deuterium variations in storm rainfall – Implications for stream hydrograph separation, Water Resour. Res., 26, 455–458, https://doi.org/10.1029/WR026i003p00455, 1990.
McDonnell, J. J., Stewart, M. K., and Owens, I. F.: Effect of catchment-scale subsurface mixing on stream isotopic response, Water Resour. Res., 27, 3065–3073, https://doi.org/10.1029/91WR02025, 1991.
McGuire, K. J., McDonnell, J. J., Weiler, M., Kendall, C., McGlynn, B. L., Welker, J. M., and Seibert, J.: The role of topography on catchment-scale water residence time, Water Resour. Res., 41, W05002, https://doi.org/10.1029/2004WR003657, 2005.
McGuire, K. J. and McDonnell, J. J.: A review and evaluation of catchment transit time modeling, J. Hydrol., 330, 543–563, https://doi.org/10.1016/j.jhydrol.2006.04.020, 2006.
Merz, R., Bloschl, G., and Parajka, J.: Spatio-temporal variability of event runoff coefficients, J. Hydrol., 331, 591–604, https://doi.org/10.1016/j.jhydrol.2006.06.008, 2006.
Mitchell, J. M., Dzerdzeevskii, B., Flohn, H., Hofmeyr, W. L., Lamb, H. H., Rao, K. N., and Waleen, C. C.: Climatic change: report of a working group of the Commission for Climatology, WMO Technical note No. 79, World Meteorological Organization, Geneva, 79 pp., 1966.
Neal, C. and Rosier, P. T. W.: Chemical studies of chloride and stable oxygen isotopes in 2 conifer afforested and moorland sites in the British uplands, J. Hydrol., 115, 269–283, https://doi.org/10.1016/0022-1694(90)90209-G, 1990.
Penna, D., Tromp-van Meerveld, H. J., Gobbi, A., Borga, M., and Dalla Fontana, G.: The influence of soil moisture on threshold runoff generation processes in an alpine headwater catchment, Hydrol. Earth Syst. Sci., 15, 689–702, https://doi.org/10.5194/hess-15-689-2011, 2011.
Phillips, D. L.: A technique for the numerical solution of certain integral equations of the first kind, J. ACM, 9, 84–97, https://doi.org/10.1145/321105.321114, 1962.
Pinder, G. F. and Jones, J. F.: Determination of the groundwater component of peak discharge form the chemistry of total runoff, Water Resour. Res., 5, 438–445, https://doi.org/10.1029/WR005i002p00438, 1969.
Press, W. H., Flannery, B. P., Teukolsky, S. A., and Vetterling, W. T.: Numerical Recipes in C: the Art of Scientific Computing, 2nd edn., Cambridge University Press, New York, 994 pp., 1992.
Remondi, F., Kirchner, J. W., Burlando, P., and Fatichi, S.: Water flux tracking with a distributed hydrological model to quantify controls on the spatiotemporal variability of transit time distributions, Water Resour. Res., 54, 3081–3099, https://doi.org/10.1002/2017WR021689, 2018.
Rigon, R., Bancheri, M., and Green, T. R.: Age-ranked hydrological budgets and a travel time description of catchment hydrology, Hydrol. Earth Syst. Sci., 20, 4929–4947, https://doi.org/10.5194/hess-20-4929-2016, 2016.
Rodhe, A.: The origin of streamwater traced by oxygen-18, PhD dissertation, Department of Physical Geography, Uppsala University, Uppsala, 1987.
Rodhe, A., Nyberg, L., and Bishop, K.: Transit times for water in a small till catchment from a step shift in the oxygen-18 content of the water input, Water Resour. Res., 32, 3497–3511, https://doi.org/10.1029/95WR01806, 1996.
Rodriguez, N. B., Mcguire, K. J., and Klaus, J.: Time-varying storage-water age relationships in a catchment with a Mediterranean climate, Water Resour. Res., 54, 3988–4008, https://doi.org/10.1029/2017WR021964, 2018.
Seeger, S. and Weiler, M.: Reevaluation of transit time distributions, mean transit times and their relation to catchment topography, Hydrol. Earth Syst. Sci., 18, 4751–4771, https://doi.org/10.5194/hess-18-4751-2014, 2014.
Sklash, M. G.: Environmental isotope studies of storm and snowmelt runoff generation, in: Process Studies in Hillslope Hydrology, edited by: Anderson, M. G. and Burt, T. P., Wiley, Chichester, 401–435, 1990.
Sklash, M. G., Farvolden, R. N., and Fritz, P.: A conceptual model of watershed response to rainfall, developed though the use of oxygen-18 as a natural tracer, Can. J. Earth Sci., 13, 271–283, https://doi.org/10.1139/e76-029, 1976.
Sprenger, M., Tetzlaff, D., Tunaley, C., Dick, J., and Soulsby, C.: Evaporation fractionation in a peatland drainage network affects stream water isotope composition, Water Resour. Res., 53, 851–866, https://doi.org/10.1002/2016wr019258, 2017.
Stewart, M. K., Morgenstern, U., and McDonnell, J. J.: Truncation of stream residence time: how the use of stable isotopes has skewed our concept of streamwater age and origin, Hydrol. Process., 24, 1646–1659, https://doi.org/10.1002/hyp.7576, 2010.
Taylor, S., Feng, X. H., Williams, M., and McNamara, J.: How isotopic fractionation of snowmelt affects hydrograph separation, Hydrol. Process., 16, 3683–3690, https://doi.org/10.1002/hyp.1232, 2002.
Tikhonov, A. N.: Solution of incorrectly formulated problems and the regularization method, Soviet Mathematics, 4, 1035–1038, 1963.
van der Velde, Y., Torfs, P. J. J. F., van der Zee, S. E. A. T. M., and Uijlenhoet, R.: Quantifying catchment-scale mixing and its effect on time-varying travel time distributions, Water Resour. Res., 48, W06536, https://doi.org/10.1029/2011WR011310, 2012.
von Freyberg, J., Studer, B., and Kirchner, J. W.: A lab in the field: high-frequency analysis of water quality and stable isotopes in stream water and precipitation, Hydrol. Earth Syst. Sci., 21, 1721–1739, https://doi.org/10.5194/hess-21-1721-2017, 2017.
von Freyberg, J., Studer, B., Rinderer, M., and Kirchner, J. W.: Studying catchment storm response using event- and pre-event-water volumes as fractions of precipitation rather than discharge, Hydrol. Earth Syst. Sci., 22, 5847–5865, https://doi.org/10.5194/hess-22-5847-2018, 2018.
Zhadanov, M. S.: Inverse Theory and Applications in Geophysics, Elsevier, Amsterdam, 704 pp., 2015.
- Abstract
- Introduction
- Estimating new water fractions by ensemble hydrograph separation
- Testing ensemble hydrograph separation with a simple non-stationary benchmark model
- Estimating transit time distributions by ensemble hydrograph separation
- Discussion
- Data availability
- Appendix A: Estimating non-constant “constants” via regression
- Appendix B: Accounting for rain-free periods, and estimating non-constant “constants” by multiple regression
- Appendix C
- Competing interests
- Acknowledgements
- References
- Supplement
The requested paper has a corresponding corrigendum published. Please read the corrigendum first before downloading the article.
- Article
(7794 KB) - Full-text XML
- Corrigendum
-
Supplement
(180 KB) - BibTeX
- EndNote
- Abstract
- Introduction
- Estimating new water fractions by ensemble hydrograph separation
- Testing ensemble hydrograph separation with a simple non-stationary benchmark model
- Estimating transit time distributions by ensemble hydrograph separation
- Discussion
- Data availability
- Appendix A: Estimating non-constant “constants” via regression
- Appendix B: Accounting for rain-free periods, and estimating non-constant “constants” by multiple regression
- Appendix C
- Competing interests
- Acknowledgements
- References
- Supplement






