Multi-site calibration and validation of SWAT with satellite-based evapotranspiration in a data-sparse catchment in southwestern Nigeria

The main objective of this study was to calibrate and validate the eco-hydrological model Soil and Water Assessment Tool (SWAT) with satellite-based actual evapotranspiration (AET) data from the Global Land Evaporation Amsterdam Model (GLEAM_v3.0a) and from the Moderate Resolution Imaging Spectroradiometer Global Evaporation (MOD16) for the Ogun River Basin (20 292 km²) located in southwestern Nigeria. Three potential evapotranspiration (PET) equations (Hargreaves, Priestley–Taylor and Penman–Monteith) were used for the SWAT simulation of AET. The reference simulations were the three AET variables simulated with SWAT before model calibration took place. The sequential uncertainty fitting technique (SUFI-2) was used for the SWAT model sensitivity analysis, calibration, validation and uncertainty analysis. The GLEAM_v3.0a and MOD16 products were subsequently used to calibrate the three SWAT-simulated AET variables, thereby obtaining six calibrations–validations at a monthly timescale. The model performance for the three SWAT model runs was evaluated for each of the 53 subbasins against the GLEAM_v3.0a and MOD16 products, which enabled the best model run with the highest-performing satellite-based AET product to be chosen. A verification of the simulated AET variable was carried out by (i) comparing the simulated AET of the calibrated model to GLEAM_v3.0b AET, which is a product that has different forcing data than the version of GLEAM used for the calibration, and (ii) assessing the long-term average annual and average monthly water balances at the outlet of the watershed. Overall, the SWAT model, composed of the Hargreaves PET equation and calibrated using the GLEAM_v3.0a data (GS1), performed well for the simulation of AET and provided a good level of confidence for using the SWAT model as a decision support tool. The 95 % uncertainty of the SWAT-simulated variable bracketed most of the satellite-based AET data in each subbasin. A validation of the simulated soil moisture dynamics for GS1 was carried out using satellite-retrieved soil moisture data, which revealed good agreement. The SWAT model (GS1) also captured the seasonal variability of the water balance components at the outlet of the watershed.

This study demonstrated the potential to use remotely sensed evapotranspiration data for hydrological model calibration and validation in a sparsely gauged large river basin with reasonable accuracy. The novelty of the study is the use of these freely available satellite-derived AET datasets to effectively calibrate and validate an eco-hydrological model for a data-scarce catchment.

1 Introduction

Hydrological modelling in data-sparse catchments has always been a challenging task due to the lack of ground observations and insufficient or poor-quality data. Data scarcity is the main limitation in tropical regions for setting up hydrological models for watershed simulations, which could be used as significant decision support tools for sustainable water resources management. Water resources globally are becoming increasingly vulnerable as a result of escalating water demand arising from population growth, expanding industrialisation, increased food production and pollution due to various anthropogenic activities, climate and land use change impacts (Carroll et al., 2013; McDonald et al., 2014; Goonetilleke et al., 2016). The situation is more evident and critical in many developing countries where no water resources monitoring plans or water management strategies are in place for the future. Like many developing countries, Nigeria cannot satisfy its domestic water needs as only 47 % of the total population has access to water from improved sources (Ishaku et al., 2012).

The Ogun River is the main source of public water supply for the people living in the states of Lagos and Ogun in southwestern Nigeria. The prevalent situation of insufficient hydrological data associated with a lack of up-to-date streamflow data (Sobowale and Oyedepo, 2013) and the poor level of data quality in this watershed can be attributed to a gradual decline in the number of hydrological stations and their management. Water management planners are facing considerable uncertainties in terms of future availability and quality of water resources. Therefore, a clear understanding of the ongoing challenges and innovative management approaches are needed. One of the many ways to tackle this task is by using hydrological models as tools coupled with the use of increasingly available global and regional datasets to run the models.

Numerous physically based distributed (PBD), continuous models that aim to describe which driving processes are present in a system and are able to make detailed predictions in both time and space are available to simulate water quantity and quality variables. These include, among others, the Soil and Water Assessment Tool (SWAT; Arnold et al., 1998), which is able to represent detailed agricultural management practices and simulate water quantity and quality variables, the Hydrologic Simulation Program Fortran (HSPF; Bicknell et al., 1997) used in predicting hydrology with in-stream nutrient transport processes and SHETRAN (Ewen et al., 2000), which has capabilities for modelling subsurface flow and transport. These PBD models attempt to explain hydrological phenomena through their underlying physical mechanisms and explicitly represent (through mathematical equations) the biological, chemical and physical processes of a basin.

Schuol et al. (2008) have successfully applied the hydrological model SWAT to quantify freshwater availability for the whole of Africa at a detailed subbasin level and on a monthly timescale. Using the SUFI-2 (sequential uncertainty fitting algorithm) programme with three different objective functions, the model was calibrated and validated at 207 discharge stations. They reported the model inability to simulate runoff adequately in some areas in eastern and southern Africa, but also reported that the model results were quite satisfactory for such a large-scale application despite containing large prediction uncertainties in some areas. Many of the limitations reported within this continental modelling study in Africa were data related. Abaho et al. (2012) applied an uncalibrated SWAT model to evaluate the impacts of climate change on river flows and groundwater recharge in the Sezibwa catchment, Uganda. They observed a 40 % increase in groundwater recharge for the period of 2070–2100 and a 47 % increase in average river flow. However, there are high levels of uncertainty associated with the model predictions since the model was not calibrated due to insufficient data.

In West Africa, the SWAT model has been widely applied to different river basins with satisfactory results. For example, Schuol and Abbaspour (2006) applied SWAT to model a 4×10⁶ km² area, mainly in the basins of the Niger, Volta and Senegal, addressing calibration and uncertainty issues. Measured river discharges at 64 stations, at many of which the available data do not cover the whole simulation period, were used for annual and monthly calibration with the SUFI-2 algorithm. Although the results obtained are preliminary with a basis for discussion and further improvement, Schuol and Abbaspour (2006) reported that the annual and monthly simulations with the calibrated SWAT model for West Africa showed promising results for freshwater quantification despite the modelling shortcomings, which include a lacking long-term dataset for dam management and operation. They also pointed out the importance of evaluating the conceptual model uncertainty as well as the parameter uncertainty. Laurent and Ruelland (2010) successfully calibrated SWAT for the Bani catchment (1×10⁶ km²) in Mali, a major tributary of the upper Niger River. The calibration and validation results were satisfactory at the catchment outlet and also in various gauging stations located in tributaries. They showed the model performance by reporting discharge and biomass calibration results but did not assess the model prediction uncertainty.

In northwestern Nigeria, Xie et al. (2010) evaluated the SWAT model performance in a large watershed (30 300 km²). Due to the short data period available, all the data obtained were used for calibration. In their study, the model parameters were first optimised with a genetic algorithm, and the uncertainty in the calibration was further analysed using the generalised likelihood uncertainty estimation (GLUE) method; the study presented a reasonably good calibrated model performance without validation. Adeogun et al. (2014) successfully calibrated and validated the SWAT model for the prediction of streamflow at the upstream watershed of Jebba reservoir (area: 12 992 km²) located in north-central Nigeria. The model results obtained were good, with a Nash–Sutcliffe efficiency (NSE) of 0.72 and coefficient of determination (R²) of 0.76 for the calibration period, an R² of 0.71 for the validation period, and NSE of 0.78 for monthly average streamflow, but the model prediction uncertainty was not quantified.

The findings from these past studies call for continued improvement in the hydrological model performances in Africa, especially in data-sparse regions. One solution is to use freely available global datasets to improve the model performance.

In the context of large-scale hydrological model simulation in data-scarce areas, López López et al. (2017) investigated alternative ways to calibrate the large-scale hydrological model PCRaster GLOBAL Water Balance (PCR-GLOBWB) using satellite-based evapotranspiration (GLEAM) and surface soil moisture (ESA CCI) for the data-poor catchment Oum Er-Rbia in Morocco with the aim of improving discharge estimates. In their study, different calibration scenarios are inter-compared. The results show that GLEAM evapotranspiration and ESA CCI soil moisture used for model calibration resulted in reasonable discharge estimates (NSE ranges from −0.22 to 0.68 and −0.31 to 0.66, respectively). Better model performance was achieved when the model was calibrated with in situ streamflow observations, resulting in NSE values from −0.15 to 0.75. Their results showed the possibility of using globally available Earth observation datasets in large-scale hydrological models to estimate discharge at a river basin scale. Abera et al. (2017) developed a methodology that can improve the state of the art by using available, but sparse, hydrometeorological data and satellite products to obtain the estimates of all the components of the hydrological cycle (precipitation, evapotranspiration, discharge and storage) in the upper Blue Nile basin. To obtain a water-budget closure, Abera et al. (2017) used the JGrass-NewAge hydrological model calibrated with observed discharge (1994–1999) using particle swarm optimisation. The simulation of each hydrological component by JGrass-NewAge was verified using available in situ and remote sensing data. GLEAM (Miralles et al., 2011a) and MOD16 AET were used as independent datasets to assess the JGrass-NewAge estimated AET. Overall, the AET simulations showed that the correlation and PBIAS obtained between JGrass-NewAge and GLEAM AET had a better agreement (very low bias and acceptable correlation) compared to JGrass-NewAge and MOD16.

Recently, Ha et al. (2018) used remotely sensed precipitation, actual evapotranspiration (AET) and leaf area index (LAI) from open-access data sources to calibrate the SWAT model for the Day Basin, a tributary of the Red River in Vietnam. The calibration was performed in SWAT-CUP using the sequential uncertainty fitting algorithm (SUFI-2). In this study simulated monthly AET correlations with remote sensing estimates showed an R² of 0.71. Pomeon et al. (2018) set up a hydrological modelling framework for sparsely gauged catchments in West Africa using the SWAT model whilst largely relied on remote sensing and reanalysis inputs. In their study, validation of the model was conducted to further investigate its performance, whereby simulated actual evapotranspiration, soil moisture and total water storage were evaluated using remote sensing data. The validation result reveals good agreement between predictions and the remotely sensed data (R² calibration: 0.52 and 0.51; R² validation: 0.63 and 0.61)

Remote sensing technologies offer large-scale spatially distributed observations and have opened up new opportunities for calibrating and validating hydrologic models. This advancement enables several global evapotranspiration products to be used. Extensive reviews of Earth-observation-based methods for deriving AET have been carried out by several research groups (Anderson et al., 2012; Bateni et al., 2013; Li et al., 2013; Savoca et al., 2013; Senay et al., 2013; Nouri et al., 2015; Wang-Erlandsson et al., 2016).

Two global-scale AET products derived from satellite observation have become available, and these two AET products were used in this study: the Global Land Evaporation Amsterdam Model (GLEAM; http://www.gleam.eu, last access: 12 July 2017) and Moderate Resolution Imaging Spectroradiometer Global Evaporation (MOD16). GLEAM is an evapotranspiration product developed by the VU University of Amsterdam (Miralles et al., 2011a, b) and contains a set of algorithms that separately estimate the different components of terrestrial evaporation (i.e. transpiration, interception loss, bare soil evaporation, snow sublimation and open water evaporation), as well as variables such as the evaporative stress factor, potential evaporation, root-zone soil moisture and surface soil moisture by using satellite-based climatic and environmental observations (Miralles et al., 2011a; Martens et al., 2017). Recently, the GLEAM_v3.0 AET has been validated against measurements from 64 eddy-covariance towers and 2338 soil moisture sensors across a broad range of ecosystems with varying levels of success (Martens et al., 2017). In this study, GLEAM_v3.0a and v3.0b were used. These two datasets differ only in their forcing variables and spatial–temporal coverage. GLEAM_v3.0a is a dataset spanning the 35-year period 1980–2014 and is based on reanalysis net radiation and air temperature, a combination of gauged-based, reanalysis and satellite-based precipitation and satellite-based vegetation optical depth. GLEAM_v3.0b is a dataset spanning the 13-year period 2003–2015 and is derived by satellite data only (Miralles et al., 2011a; Martens et al., 2017).

The MOD16 global evapotranspiration data are based on a 1 km² grid of land surface AET that was developed with an energy balance model using satellite data as input (Mu et al., 2011). The MOD16 product estimates evapotranspiration using a moderate-resolution imaging spectroradiometer, land cover, albedo, LAI, an enhanced vegetation index (EVI) and a daily meteorological reanalysis dataset from NASA's Global Modelling and Assimilation Office (GMAO). The non-satellite input data are NASA's MERRA GMAO (GEOS-5) daily meteorological reanalysis data. MOD16 has been validated using measurements from eddy-covariance stations at different tropical sites (Ruhoff et al., 2013; Ramoelo et al., 2014). Ruhoff et al. (2013) validated MOD16 AET using ground-based measurements of energy fluxes obtained from eddy-covariance sites in tropical regions in the Rio Grande basin, Brazil. Likewise, Ramoelo et al. (2014) validated MOD16 using data from two eddy-covariance flux towers installed in a savannah and woodland ecosystem within the Kruger National Park, South Africa.

The objective of our study was to obtain a high-performing eco-hydrological model for the Ogun River Basin in southwestern Nigeria that can be used as a decision support tool. To this effect, the specific objectives were (i) to calibrate and validate the SWAT model with remotely sensed actual evapotranspiration products, namely GLEAM_v3.0a and MOD16, and (ii) to use further independent products to validate the simulated soil moisture and verify the simulated water balance components.

Although the three PET equations and the corresponding AET simulations from SWAT have been tested for their performance before (Wang et al., 2006; Franco and Bonumá, 2017; Samadi, 2017; Ha et al., 2018), calibrating each of the three SWAT-simulated AET variables with two remotely sensed AET products for each delineated subbasin to determine the highest-performing model in a catchment has not been undertaken.

Hence, the contribution of this study includes the following: (i) the calibration and validation of simulated AET from the three SWAT models using satellite-derived AET data; (ii) the use of satellite-based AET data for calibration and validation of the SWAT model in each of the SWAT-delineated subbasins; and (iii) the validation of simulated soil moisture dynamics of the highest-performing SWAT model run using European Space Agency Climate Change Initiative soil moisture (ESA CCI SM) in each of the SWAT-delineated subbasins.

2 Materials and methods

2.1 Description of the study site

The study area is a sub-watershed (20 292 km²) of the Ogun River Basin (23 700 km²) located in southwestern Nigeria (Fig. 1), bordered geographically by latitudes 7^∘7^′ and 8^∘59^′ N and longitudes 2^∘4^′ and 4^∘9^′ E. About 2 % of the catchment area is located in the Benin Republic. The study area encompasses the Sepeteri, Iseyin, Olokemeji, Oyan and Abeokuta catchments and cuts across the Oyo and Ogun state administrative boundaries. The Ogun River, which literarily means the River of Medicine, springs from the Igaran Hills in Oyo state, near Saki, at an elevation of about 624 m above mean sea level. The elevation ranges from 624 to 23 m. The mean annual rainfall (1984–2012) obtained from measured data in Ogun watershed is 1224 mm yr⁻¹ and the mean annual temperature (1984–2012) obtained from measured data is about 27 ^∘C. Mean annual potential evapotranspiration (PET) estimated by the Hargreaves method (Hargreaves and Samani, 1985) from measured minimum and maximum temperature is 1720 mm yr⁻¹ and the mean AET obtained from SWAT output (1989–2012) for this study area is 692 mm yr⁻¹. Two seasons are distinguishable in the watershed: a dry season from November to March and a wet season between April and October. The watershed area is characterised by strong climatic variation and irregular rainfall (Eruola et al., 2012). The geology of the study area can be described as a rock sequence that starts with a Precambrian basement, which consists of quartzites and biotite schist, hornblende–biotite, granite and gneisses (Bhattacharya and Bolaji, 2010). The major soils of the basin are sandy clayey loam, sandy loam, clayey loam and silt loam. The land use in the watershed is primarily forest (75 %), cropland (24 %) and urban (1 %).

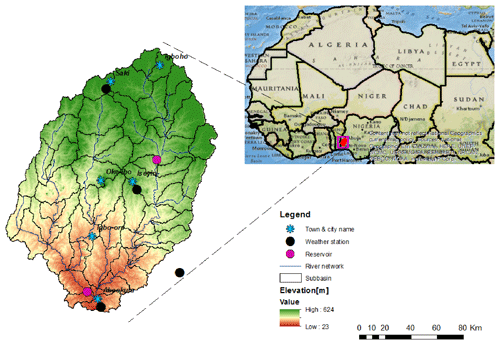
Figure 1 The Ogun River Basin located in Nigeria showing the SWAT-delineated subbasins, weather stations and river network.

The basin, in which two large dams (Oyan and Ikere Gorge dams) are located, is of great importance for economic advancement both at the federal and state level. The dams are the principal provider of water to Lagos and Ogun State Water Corporation for municipal drinking water production. The Oyan reservoir is located at the confluence of the Oyan and Ofiki rivers at an elevation of 43.3 m above mean sea level and was built in 1984; it has a surface area of 40 km² and a catchment area of 9×10³ km², with a dead storage capacity of 16×10⁶ m³, a gross storage capacity of 270×10⁶ m³, an embankment crest length of 1044 m, a height of 30.4 m, four spillway gates (each 15 m wide and 7 m high) and three outlet valves (each 1.8 m in diameter). The Ikere Gorge is an uncontrolled dam, which started operation in 1991. The dam crosses the Ogun River in the Iseyin local government area of Oyo state. Ikere Gorge has a capacity of 690×10⁶ m³. The reservoir is adjacent to the Old Oyo National Park, providing recreational facilities for tourists, and the river flows through the park (Oyegoke and Sojobi, 2012). A total of 25 local government areas fall within the study area. In densely populated areas, the Ogun River is used for bathing, washing and drinking.

2.2 SWAT model description

SWAT (Arnold et al., 1998) is an open-source eco-hydrological model developed for the USDA Agricultural Research Services. SWAT is a semi-distributed, process-based, continuous model that uses weather, soil, topography and land use for the hydrologic modelling of a basin and runs at a daily time step. It was developed to predict the impact of agricultural land management practices on discharge, sediments, nutrients, bacteria, pesticides and biomass in large complex watersheds with varying soils, land use and management conditions over long periods of time. The SWAT model uses at its core the plant growth model EPIC (Williams et al., 1989) to simulate the growth (including nutrient and water uptake) of many types of crops and trees as land cover. SWAT categorises plants into seven different types: warm season annual legume, cold season annual legume, perennial legume, warm season annual, cold season annual, perennial and trees. Plant growth is modelled by simulating leaf area development, light interception and the conversion of intercepted light into biomass assuming a plant species-specific radiation use efficiency. Hence, in SWAT, phenological plant development is based on daily accumulated heat units. The plant growth model is used to assess the removal of water and nutrients from the root zone, transpiration and biomass–yield production.

For modelling purposes in SWAT, the watershed is divided into subbasins which are then further subdivided into hydrologic response units (HRUs) that consist of homogeneous land use, soil types and slope (Arnold et al., 1998). Soil water balance (WB) is calculated for each HRU; the equation comprises six variables and is estimated in SWAT using the following (Eq. 1):

$$\begin{array}{ll}{\displaystyle }{\mathrm{SW}}_t=& {\displaystyle }{\mathrm{SW}}_{\mathrm{0}}+{\sum }_{i=\mathrm{1}}^t\left(R_{\mathrm{day}}-Q_{\mathrm{surf}}-E_{\mathrm{a}}-W_{\mathrm{seep}}\right.\\ \text{(1)}& {\displaystyle }& {\displaystyle }\left.-Q_{\mathrm{gw}}\right),\end{array}$$

where SW_t is the final soil water content (mm of water), SW₀ is the initial soil water content on day i (mm of water), t is the time (days), R_day is the amount of precipitation on day i (mm of water), Q_surf the amount of surface runoff on day i (mm of water), E_a the amount of evapotranspiration on day i (mm of water), W_seep the amount of water entering the vadose zone from the soil profile on day i (mm of water) and Q_gw the amount of return flow on day i (mm of water).

Evaporation estimation in SWAT

Evapotranspiration is a key process in water balance and one of the more difficult components to determine. Although different empirical methods for the estimation of PET are widely adopted, AET is difficult to quantify and it usually requires the reduction of PET through a factor that describes the level of stress experienced by plants. This relationship has been described in detail by several research papers (e.g. Morton, 1986; Hobbins et al., 1999; Wang et al., 2006). Numerous methods have been developed to estimate PET (Lu et al., 2005) and SWAT offers three PET estimation options from which the user can choose depending on e.g. the data availability: the Penman–Monteith method (P–M), the Priestley–Taylor method (P–T) or the Hargreaves method (HG). Any one of these three PET equations can be chosen to run in SWAT, but they vary in the amount of input data required. The Hargreaves method (Hargreaves and Samani, 1985) is temperature based and requires only average daily air temperature as input in Eq. (2):

$$\begin{array}{}\text{(2)}& \mathit{\lambda }{E}_{\mathrm{0}}=\mathrm{0.0023}\times H_{\mathrm{0}}\times {\left(T_{max}-T_{min}\right)}^{\mathrm{0.5}}\times \left(T_{\mathrm{mean}}+\mathrm{17.8}\right),\end{array}$$

where λ is the latent heat of vaporisation (MJ kg⁻¹), E₀ is the potential evapotranspiration (mm day⁻¹), H₀ is the extraterrestrial radiation (MJ m⁻² day⁻¹) , T_max is the maximum air temperature for a given day (^∘C), T_min is the maximum air temperature for a given day (^∘C) and T_mean is the mean air temperature for a given day (^∘C).

The Penman–Monteith method (Monteith, 1965; Allen, 1986; Allen et al., 1989) requires air temperature, solar radiation, relative humidity and wind speed as input in Eq. (3):

$$\begin{array}{}\text{(3)}& \mathit{\lambda }E={\displaystyle \frac{\mathrm{\Delta }\times \left(H_{\mathrm{net}}-G\right)+{\mathit{\rho }}_{\mathrm{air}}\times C_P\times \left(e_z^o-e_z\right)/r_{\mathrm{a}}}{\mathrm{\Delta }+\mathit{\gamma }\times \left(\mathrm{1}+r_{\mathrm{c}}/r_{\mathrm{a}}\right)}},\end{array}$$

where λE is the latent heat flux density (MJ m⁻² day⁻¹), E is the depth rate evaporation (mm day⁻¹), Δ is the slope of the saturation vapour pressure–temperature curve, de∕dT (kPa ^∘C⁻¹), H_net is the net radiation (MJ m⁻² day⁻¹), G is the heat flux density to the ground (MJ m⁻² day⁻¹), ρ_air is the air density (kg m⁻³), C_p is the specific heat at constant pressure (MJ kg^−1 ∘C⁻¹), $e_z^o$ is the saturation vapour pressure of air at height z (kPa), e_z is the water vapour pressure of air at height z (kPa), γ is the psychrometric constant (kPa ^∘C⁻¹), r_c is the plant canopy resistance (s m⁻¹) and r_a is the aerodynamic resistance (s m⁻¹).

The Priestley–Taylor equation (Priestley and Taylor, 1972) is a radiation-based method and it provides PET estimates for low advective conditions. The P–T method requires solar radiation, air temperature and relative humidity as input (Eq. 4):

$$\begin{array}{}\text{(4)}& \mathit{\lambda }{E}_o={\mathit{\alpha }}_{\mathrm{pet}}\times {\displaystyle \frac{\mathrm{\Delta }}{\mathrm{\Delta }+\mathit{\gamma }}}\times \left(H_{\mathrm{net}}-G\right),\end{array}$$

where α_pet is a coefficient, Δ is the slope of the saturation vapour pressure–temperature curve, de∕dT (kPa ^∘C⁻¹), γ is the psychometric constant (kPa ^∘C⁻¹), H_net is the net radiation (MJ m⁻² day⁻¹) and G is the heat flux density to the ground (MJ m⁻² day⁻¹).

Once PET is determined, AET is estimated in SWAT, whereby SWAT first evaporates any rainfall intercepted by the plant canopy. Second, it calculates the maximum amount of transpiration, sublimation and/or soil evaporation. Finally, the actual amount of sublimation and evaporation from the soil surface is calculated. If snow is presented in the HRU, sublimation can occur. When there is no snow (such as in this case study), only evaporation from the soil surface is calculated. A complete description of the SWAT model and the model equations can be found in Neitsch et al. (2002, 2005) and Arnold et al. (1998).

2.3 Model set-up

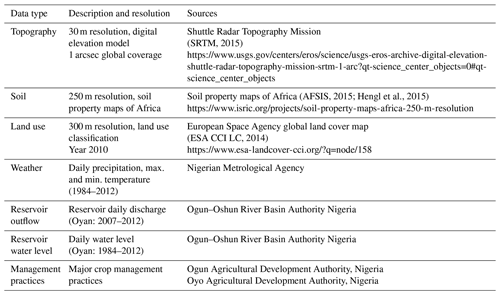
The ArcView GIS interface for SWAT2012 (Winchell et al., 2013) was used to configure and parameterise the SWAT model. SWAT model inputs included a 30 m spatial resolution digital elevation model (DEM) with minimum, maximum and mean values of 23, 624 and 289.1 m, respectively (Fig. 1), 17 soil classes, 17 land use classes, 3 slope categories, meteorological data and land use with its management (Table 1).

Table 1 Description and sources of input data used to configure the SWAT model for the Ogun River Basin.

For the SWAT model set-up, the watershed was delineated into 53 subbasins, with the main outlet in Abeokuta. The minimum and maximum subbasin areas are 72.4 and 853.1 km², respectively, while the mean is 382.8 km². Daily precipitation data (1984–2012) and minimum and maximum temperature data (1984–2012) were obtained from the Nigerian Meteorological Agency for four weather stations (Fig. 1) and used as observed input data. The weather stations are more or less evenly distributed in or around the watershed, and the weather data obtained from stations located in the same proximity show the same rise-and-fall dynamics. No orographic effect correction is needed for correcting the precipitation values.

The missing values of daily measured precipitation and minimum and maximum temperatures were simulated by the WGEN_CFSR_World. The WGEN_CFSR_World weather database is an input into SWAT (ArcSWAT CSFR_World weather generator) containing long-term monthly weather statistics covering the entire globe and developed using the National Centres for Environmental Prediction (NCEP) Climate Forecast System Reanalysis (CFSR) global dataset. The ArcSWAT CSFR_World weather generator was used to simulate daily solar radiation, relative humidity and wind speed. The simulated variables were used as input variables into the Penman–Monteith and Priestley–Taylor equations for obtaining the different PET estimates from SWAT.

The topHRU programme (Strauch et al., 2017) was used to determine the optimum number of HRUs in the watershed. The topHRU programme allows for the identification of a Pareto-optimal threshold which minimises the spatial error to 0.01 ha for a given number of HRUs and thereby minimises the trade-off between SWAT computation time and the number of HRUs. In this case, topHRU determined the optimum number of HRUs to be 1397 for the Ogun River Basin. Thresholds of 150 ha for soil and 250 ha for slope were used in the SWAT set-up. The physical consequences of the thresholds include improving the computational efficiency of simulations while keeping key landscape features and information on the watershed in the hydrologic modelling. Not selecting a threshold for land use was based on our desire to retain all of the land use classes for future land use change research needs. The surface runoff in SWAT was estimated using the modified Soil Conservation Society curve number method. The SWATfarmR programme (Schürz et al., 2017) was used to write the management files in SWAT. All SWAT simulations included a warm-up period of 5 years for the simulation period from 1984 to 2012.

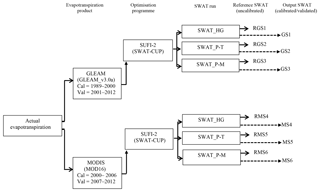
Figure 2 Schematic diagram showing the set-up of the SWAT model, the two global AET products, the resulting six SWAT reference runs, and calibration and validation procedures for the Ogun River Basin.

The SWAT model was set up once for the entire Ogun River Basin and then run three times, whereby each model run is composed of a different PET equation available in SWAT (HG, P–M or P–T). Figure 2 shows the framework in which the three SWAT model runs (SWAT_HG, SWAT_P-T and SWAT_P-M) were used to evaluate the model performance by (i) comparing the three uncalibrated SWAT simulations of AET with the two global AET products (GLEAM and MOD16), thus allowing for six reference runs of SWAT (RGS1 through RMS6). SWAT_HG represents the SWAT run using the Hargreaves PET equation to simulate uncalibrated AET, and these results were compared with the AET from GLEAM_V3.0a (RGS1) and MOD16 (RMS4). SWAT_P-T represents the SWAT run using the Priestley–Taylor PET equation to simulate uncalibrated AET, and the results were compared with the AET from GLEAM_V3.0a (RGS2) and MOD16 (RMS5). SWAT_P-M represents the SWAT run using the Penman–Monteith PET equation to simulate uncalibrated AET, and the results were compared with GLEAM_v3.0a (RGS3) and MOD16 (RMS6). (ii) The calibrations and validations implemented with two global AET products (GLEAM and MOD16) were also compared, thus allowing for six calibration results of SWAT (GS1 through MS6). SWAT_HG represents the SWAT run using the Hargreaves PET equation to simulate AET, and that was calibrated and validated with the AET from GLEAM_v3.0a (GS1) and MOD16 (MS4). SWAT_P-T represents the SWAT run using the Priestley–Taylor PET equation to simulate AET, and that was calibrated and validated with the AET from GLEAM_v3.0a (GS2) and MOD16 (MS5). SWAT_P-M represents the SWAT run using the Penman–Monteith PET equation to simulate AET, and that was calibrated and validated with the AET from GLEAM_v3.0a (GS3) and MOD16 (MS6). This procedure enabled the SWAT model run with the highest-performing simulated AET to be chosen for further use.

2.4 Satellite-derived datasets

Due to unavailability of discharge measurements in the watershed, two satellite-based AET products (GLEAM_v3.0a and MOD16) were used for the SWAT calibration and validation. The criteria for choosing GLEAM and MOD16 products are based on their temporal and spatial resolution, the fact that they are freely available, and because these two AET datasets have been validated in several countries in Africa. To further assess the model performance in simulating other components of the water balance (e.g. soil moisture), a remotely sensed ESA CCI soil moisture v3.2 dataset was used to validate SWAT-simulated soil moisture dynamics.

2.4.1 GLEAM

GLEAM combines a wide range of remote sensing observations from different satellites to separately estimate the different components of terrestrial evaporation and surface soil moisture through a process-based methodology (Martens et al., 2017). GLEAM was developed in 2011 and has been continuously revised and updated. The Priestley and Taylor (1972) equation used in GLEAM calculates the potential evaporation (mm day⁻¹) based on remotely sensed observations of surface net radiation and near-surface air temperature (Eq. 4). Since GLEAM separately derives the different components of terrestrial evaporation (Eq. 5), the estimates of potential evaporation for the land fractions of bare soil, open water, tall canopy and short canopy are converted into actual evaporation using a multiplicative evaporative stress factor (Eq. 6) obtained from observations of microwave vegetation optical depth (VOD) used as a proxy for vegetation water content and simulations of root-zone soil moisture. Interception loss is estimated separately based on the Gash analytical model of rainfall interception driven by observations of precipitation and both vegetation and rainfall characteristics.

Two of the three versions of the datasets produced in 2016 using GLEAM_v3.0 were downloaded for this study (GLEAM_v3.0a and GLEAM_v3.0b). In this study, GLEAM_v3.0a was used for SWAT calibration and validation, while GLEAM_v3.0b was used for the verification of the SWAT-simulated AET.

$$\begin{array}{}\text{(5)}& {\displaystyle }& {\displaystyle }E=\mathrm{Et}+\mathrm{Eb}+\mathrm{Ew}+\mathrm{Ei}+\mathrm{Es}\text{(6)}& {\displaystyle }& {\displaystyle }S={\displaystyle \frac{(E-\mathrm{Ei})}{\mathrm{Ep}}}\end{array}$$

E is the actual evaporation (mm day⁻¹), Et is the transpiration (mm day⁻¹), Eb is bare soil evaporation (mm day⁻¹), Ew is the open water evaporation (mm day⁻¹), Ei is the interception loss (mm day⁻¹), Es is the snow sublimation (mm day⁻¹), S is the evaporative stress factor (–) and Ep is potential evaporation (mm day⁻¹).

The datasets are provided on a 0.25^∘ by 0.25^∘ regular grid. For more information on GLEAM, its different forcing variables, and the satellite data used in the GLEAM_v3.0a and GLEAM_v3.0b datasets, the reader is referred to Miralles et al. (2011b) and Martens et al. (2017).

2.4.2 MOD16

The MOD16 retrieval algorithm (Mu et al., 2007, 2011) is based on the Penman–Monteith framework (Monteith, 1965) with modifications to account for parameters not readily available from space (Cleugh et al., 2007). Terrestrial evapotranspiration includes evaporation from wet and moist soil, evaporation from rainwater intercepted by the canopy before it reaches the ground, the sublimation of water vapour from ice and snow, and transpiration through stomata on plant leaves and stems (Mu et al., 2011). Mu et al. (2007) derived actual evaporation from potential evaporation data by using multipliers to halt soil evaporation and plant transpiration through transpiration flow that was limited by water stress and low temperatures with a complementary relationship which defines land–atmosphere interactions from relative humidity and vapour pressure deficit (Mu et al., 2007). Mu et al. (2011) apply the P–M equation (Eq. 3) to calculate PET on a global scale by using variables and parameters needed from Vis–NIR remote sensing (land cover, LAI, albedo, FPAR) and from daily meteorological reanalysis data from NASA's Global Modelling and Assimilation Office (radiation, T_air, pressure, relative humidity). In principle, the surface resistance (r_s) parameter in the P–M equation accounts for any direct effect on evapotranspiration due to limitations in available water. The way r_s is derived in the MOD16 evapotranspiration scheme only considers an indirect effect via a non-linear dependency of r_s with the water vapour pressure deficit (VPD) in the atmosphere. VPD under daytime conditions often represents a proxy for soil moisture conditions and therefore r_s. MOD16 AET is described in detail by Mu et al. (2007, 2011).

2.4.3 ESA CCI soil moisture

The European Space Agency Climate Change Initiative soil moisture data were generated by merging various available active and passive microwave-based soil moisture datasets (Gruber et al., 2017; Wagner et al., 2012). The combined product used is ESA CCI SM v3.2 that was released in 2017 and was generated by blending passive and active microwave soil moisture retrieval generated by C-band scatterometers (ERS-1/2 AMS WS; TU Wien, WARP 5.5) various additional scatterometers (ERS-2 AMI WS; TU Wien, WARP 5.4; MetOp A and B ASCAT, H – SAF H109–H110–WARP 5.6) and multi-frequency radiometer data (from SMMR, SSM/I, TMI, WinSat, all VUA/NASA LPRM v5; AMSR-E, AMSR2, SMOS, all VanderSat LPRM v6; Dorigo et al., 2017). The blending scheme of this product used a weighted average of measurements from all sensors that are available at a certain point in time to compute the merged soil moisture estimate (Dorigo et al., 2017). Since all input datasets used in generating the data have different dynamic ranges, they are rescaled through CDF matching into a common climatology. Specifically, the soil moisture retrievals from multi-frequency radiometer products (SMMR, SSM/I, TMI and AMSR-E) were rescaled and merged on a pixel basis (Liu et al., 2012). ESA CCI SM v3.2 data are available at a daily resolution from 1978 to 2015, at a spatial resolution of 0.25^∘ and representing the upper soil depth from 0.5–2 cm. For more detailed information on ESA CCI SM, the reader is referred to Wagner et al. (2012), Liu et al. (2012), Dorigo et al. (2014, 2017) and Gruber et al. (2017). The ESA CCI SM has been evaluated in West Africa using in situ soil moisture data (Dorigo et al., 2014).

2.5 SWAT calibration, validation and uncertainty analysis

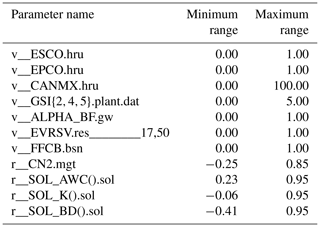
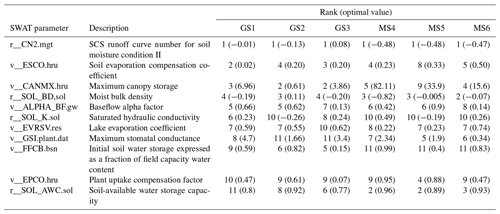
A multi-objective calibration and validation of SWAT-simulated AET using satellite-derived AET from GLEAM_v3.0a and MOD16 was implemented in SWAT-CUP (Abbaspour, 2015). SWAT-CUP is a package used to carry out sensitivity analysis, calibration and validation of the SWAT model. SUFI-2 (Abbaspour et al., 2004) is one of the programmes available in SWAT-CUP that is a multi-site, semi-automated, inverse modelling procedure used for calibrating parameters. SUFI-2 is based on a stochastic procedure for drawing independent parameter sets using Latin hypercube sampling (LHS). In this paper, we followed the split-sample test as presented by Klemes (1986) and Gan et al. (1997) using a model calibration and validation approach that consists of equally splitting the available data, when the record is sufficiently long, to represent different climatic conditions, i.e. wet, moderate and dry years in both periods. An initial pre-selection of parameters based on literature research (Bicknell et al., 1997; Wang et al., 2006; Rafiei Emam et al., 2016; Ha et al., 2018; López López et al., 2017) was undertaken to choose the most sensitive parameters to AET and make sure that each of the hydrological processes (runoff, evaporation, interception, transpiration and percolation) is represented in the 50 parameters of the global sensitivity analysis. The initial parameter ranges were based on Neitsch et al. (2002, 2005, 2011). A global sensitivity analysis based on the multiple regression method (Abbaspour, 2015) was carried out in which parameter sensitivities were determined by numerous rounds of LHS to obtain the most sensitive parameters by examining the resulting p value and the t stat value. The p value determines the significance of the sensitivity (a value close to zero has more significance) and the t stat provides a measure of parameter sensitivity (a larger absolute value is more sensitive). Based on the sensitivity analysis, 11 of the most sensitive parameters were selected and altered during the calibration process using SUFI-2. The ranking and the calibrated values of the 11 parameters for each of the six calibration procedures are listed in Table 2. The equations written in SWAT theoretical documentation (Neitsch et al., 2011) showing the selected 11 sensitive parameters are presented in Appendix C.

Table 2 Sensitivity rank and calibrated parameters with their optimal value for the three SWAT model runs through the six calibrations.

“v_” means a replacement (initial or existing parameter value is to be replaced by a given value); “r_” means a relative change (initial or existing parameter value is multiplied by
1+ given value within the range).

In this study, the first three calibrations and validations GS1, GS2 and GS3 use the AET from GLEAM_v3.0a for SWAT calibration (1989–2000) and validation (2001–2012). To compare SWAT-simulated AET in each subbasin to the GLEAM_v3.0a and GLEAM_v3.0b AET pixel values and compute their NSE, R², PBIAS and KGE for each subbasin, a NetCDF raster layer was created in ArcGIS to view how many pixels of GLEAM covered each Ogun River subbasin polygon (Fig. D1). A GLEAM AET pixel value (daily resolution) was extracted for each subbasin by using the “convert raster to points” and “make NetCDF table view” tools in ArcGIS. The extracted daily data were aggregated to monthly data for each subbasin for easy comparison with the monthly AET output from SWAT. We preferred and selected GLEAM_v3.0a AET for the calibration and validation because of its long-term availability that allows for reasonable selection and splitting of calibration and validation periods, which are not substantially different in climatic conditions, i.e. wet, moderate and dry years in both periods, and which cover our SWAT simulation output period (1989–2012). The GLEAM_v3.0a dataset spanning a 24-year period 1989–2012 was used because the SWAT simulation output was from 1989–2012. The splitting of the calibration period (1989–2000) and validation period (2001–2012) for GLEAM_v3.0a AET followed the split-sample test as presented by Klemes (1986) and Gan et al. (1997).

The last three calibrations and validations MS4, MS5 and MS6 use the MOD16 AET for SWAT calibration (2000–2006) and validation (2007–2012). Considering the MOD16 AET available time series period, the splitting of calibration and validation periods also followed the split-sample test as presented by Klemes (1986). Since MOD16 AET is a raster in geotiff format, to compare the AET pixel value to SWAT-simulated monthly AET values for each subbasin, an area-weighted averaging scheme was performed in ArcGIS to create aggregated monthly time series of MODIS AET for each subbasin (Fig. D2).

The three model runs were calibrated (GS1 through MS6) by adjusting the 11 most sensitive parameters found in SUFI-2. In the calibration of SWAT with the AET from GLEAM, a sample size of 1000 was chosen for the first iteration and a sample size of 500 for the second iteration, resulting in 1500 simulations. In the calibration of SWAT with AET from MOD16, a sample size of 1000 was chosen for two iterations of LHS, resulting in 2000 simulations. The validation process involved running the model using parameter values that were determined during the calibration process and comparing the SWAT AET simulations to satellite-based AET data.

In this study, we do not consider runoff-measured data for an independent validation because they are not available for the study basin, and this is the main reason we considered AET derived from satellite products as an alternative option for the SWAT model calibration and validation. We believe using available AET products (GLEAM and MOD16), which have been tested in the past in various calibration and validation studies undertaken by a number of scientists (Roy et al., 2017; Herman et al., 2017; López López et al., 2017; Ha et al., 2018; Poméon et al., 2018), is one solution to setting up a hydrological model that will be used as a decision support tool in such a data-scarce region.

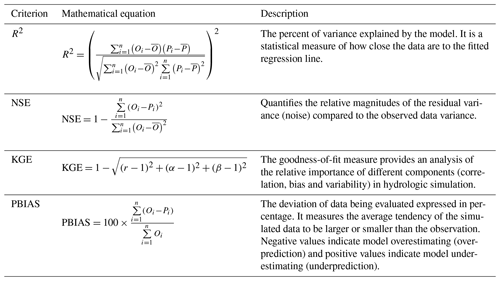
The three SWAT model runs calibrated and validated using GLEAM and MOD16 AET (GS1 through MS6) were evaluated with four objective functions, and their mathematical formulations are presented in Appendix A. It should be noted again that the AET in the GLEAM and MOD16 products does not stem from measured data obtained from eddy-covariance instruments, but instead is based on global Earth observation products (satellite).

Presently, the general hydrologic model performance ratings for recommended statistics (NSE, PBIAS, R²) performed at a monthly time step and mentioned by Moriasi et al. (2007, 2015) are mostly relevant for runoff, sediment and nutrients. For this study, the literature was searched on model evaluation methods for hydrologic model calibration using satellite- or non-satellite-derived evapotranspiration. The reviewed literature (Djaman et al., 2016; Samadi, 2017; López López et al., 2017; Ha et al., 2018) showed that these studies also set their performance ratings for recommended statistics (NSE, PBIAS and, R²) based on the Moriasi et al. (2007, 2015) guidelines. In this study, we followed López López et al. (2017) and others as the basis of our performance rating criteria for judging the SWAT model performance (GS1 to MS6) by using Nash–Sutcliffe efficiency (NSE; Nash and Sutcliffe, 1970), Kling–Gupta efficiency (KGE, Gupta et al., 2009), the percent bias (PBIAS) and the coefficient of determination (R²). NSE ranges from −∞ to 1, where NSE >0.5 indicates a good agreement (Moriasi et al., 2007, 2015) between simulated and satellite-based evapotranspiration with an NSE of 1 being the optimal value. R² ranges from 0 to 1 with higher values indicating less error variance and 1 being the optimal value. KGE ranges from −∞ to 1, where a KGE of 1 is the optimal value. PBIAS ranges from −∞ to ∞, where low-magnitude values indicate better simulation. The optimum value of PBIAS is 0. In this paper, NSE is the selected objective function that was optimised during the calibration process.

The recommended statistics for a monthly time step based on Kouchi et al. (2017) and Moriasi et al. (2007, 2015) stipulate that NSE >0.50, R²>0.60, KGE ≥0.50 and PBIAS $\le \pm \mathrm{25}$ % are the required satisfactory thresholds. SUFI-2 was also used for the uncertainty analysis of the AET modelling process. In this step, the procedure depicts the 95 % prediction uncertainty (95PPU) of the model compared with satellite-based AET. The 95PPU was estimated at the 2.5 % and 97.5 % levels of the cumulative distribution of the AET-simulated output variable derived through LHS. The uncertainties were quantified by two indices referred to as P factor and R factor (Abbaspour et al., 2004). The P factor represents the percentage of observed data plus the error bracketed by the 95 % predictive uncertainty (95PPU) band and varies from 0 to 1, where 1 indicates 100 % bracketing of the observed data within model simulations. While the R factor is the ratio of the average width of the 95PPU and the standard deviation of the observed variable, this value ranges between 0 and infinity. These two indices were also used to judge the strength of the calibration and validation in which the ideal situation would be to account for 100 % of the satellite AET data in the 95PPU while at the same time having an R factor close to 0.

2.6 SWAT model verification

In some modelling studies (EPA, 2018; Faramarzi et al., 2017), the term model verification is used to refer to the examination of the numerical technique and computer code to ascertain whether it truly represents the conceptual model and confirm that there are no inherent numerical problems with obtaining a solution. In this study, to further examine the accuracy of the calibrated SWAT model, a verification of the simulated variables was carried out through (i) a graphical comparison of calibrated SWAT-simulated AET to the GLEAM_v3.0b AET time series (2003–2012). We considered the GLEAM_v3.0b dataset for the verification of SWAT-simulated AET because there are no ground-truth AET data in the study area and because of its different forcing variable, which categorises it as an independent dataset not considered in the calibration and validation. (ii) An assessment of the long-term average annual and monthly water balances at the outlet of the watershed was also performed. The long-term average monthly and annual water balance assessment was based on SWAT-simulated output with only precipitation and temperature as measured input data. The SWAT water balance equations used for the assessment are

$$\begin{array}{}\text{(7)}& {\displaystyle }& {\displaystyle }\mathrm{WYLD}=\mathrm{SURQ}+\mathrm{LAT}\mathrm{\_}\mathrm{Q}+\mathrm{GW}\mathrm{\_}\mathrm{Q}-\mathrm{Q}\mathrm{\_}\mathrm{TLOSS},\text{(8)}& {\displaystyle }& {\displaystyle }\mathrm{PRECIP}=\mathrm{WYLD}+\mathrm{AET}+\mathrm{\Delta }\mathrm{SW}+\mathrm{PERC}-\mathrm{GW}\mathrm{\_}\mathrm{Q},\end{array}$$

where PRECIP (mm) is the observed precipitation; AET (mm) is the actual evapotranspiration; WYLD (mm) is the net amount of water that leaves the subbasin and contributes to streamflow in the reach; SURQ (mm) is the surface runoff contribution to streamflow; GW_Q (mm) is the groundwater contribution to streamflow; ΔSW (mm) is the change in soil water content; PERC (mm) is the water percolating past the root zone; LAT_Q (mm) is the lateral flow contribution to streamflow; and Q_TLOSS (mm) is the transmission loss. The soil water content for both monthly and annual output is the average soil water content for the time period. Hence, the initial soil water content is the average for the time period of 25 years.

2.7 SWAT soil moisture validation

Soil moisture is a key driver for runoff, evaporation and infiltration processes in a catchment. The ESA CCI SM v3.2 was used for validation because it has a similar spatial resolution to the satellite-based AET products used for model calibration, the available time period (1978–2015) fits the period of interest and the product has achieved reasonable accuracy when evaluated at various sites in West Africa (Dorigo et al., 2014). The SWAT-simulated soil moisture was validated using SUFI-2 against ESA CCI SM v3.2 for each of the Ogun River subbasins using 500 simulations in one iteration from the period 2001 to 2012. The R² statistics were computed between SWAT-simulated soil moisture and ESA CCCI SM v3.2 for each pixel (Fig. E1) using the same approach described for GLEAM extraction in Sect. 2.5. The ESA CCI SM product provides volumetric moisture in the shallow soil depth (0.5–2 cm), whereas SWAT provides plant-available soil moisture for the total soil layer (0–200 cm); therefore, a direct comparison was not possible. Hence, the proportion of the variance was considered to be an important criterion for evaluating the dynamics of the soil moisture simulated rather than evaluating the absolute values (Fig. 14).

3 Results

The results of the global sensitivity analysis revealed that the SCS runoff curve number (CN2.mgt) is the most sensitive parameter to SWAT simulations of AET for all six calibrations (Table 2). The sensitivity ranking of the remaining 10 parameters varies significantly.

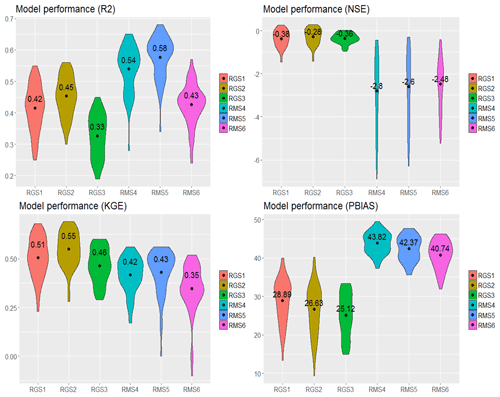
Figure 3 Plots of the performance results for the uncalibrated SWAT in simulating actual evapotranspiration. The values and the black dot symbols (•) depict the average value of R², NSE, KGE and PBIAS obtained for each of the reference runs.

Figure 3 show the performance of the uncalibrated SWAT (RGS1, RGS2, RGS3, RMS4, RMS5 and RSM6), which represents the reference runs. Results indicate that the uncalibrated SWAT model underestimated AET (positive PBIAS) and has a high percentage of deviation from GLEAM and MOD16 AET. The NSE, KGE, PBIAS and R² all depict a low model performance. Interestingly, the reference runs with MOD16 tend to have higher R² compared to reference runs with GLEAM. The results from all six reference runs justify the need to further improve the SWAT model performance.

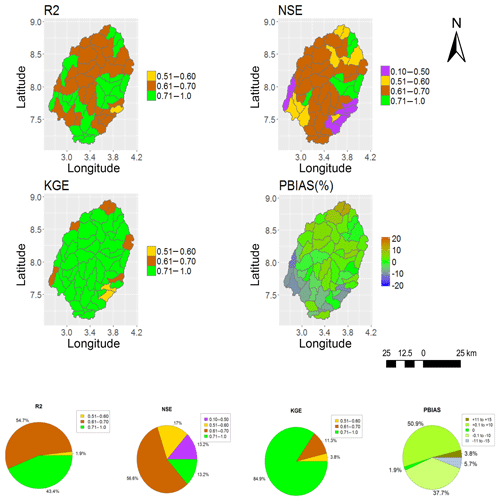
Figure 4 Performance metrics (NSE, KGE, R² and PBIAS) of SWAT (SWAT_HG) when calibrated with GLEAM_v3.0a (GS1).

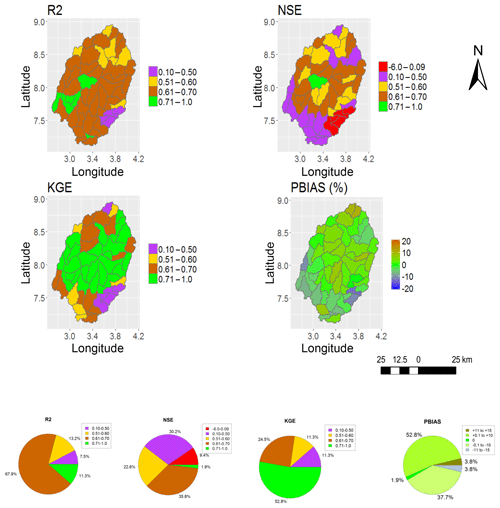
Figure 5 Performance metrics (NSE, KGE, R² and PBIAS) of SWAT (SWAT_HG) when validated with GLEAM_v.3.0a (GS1).

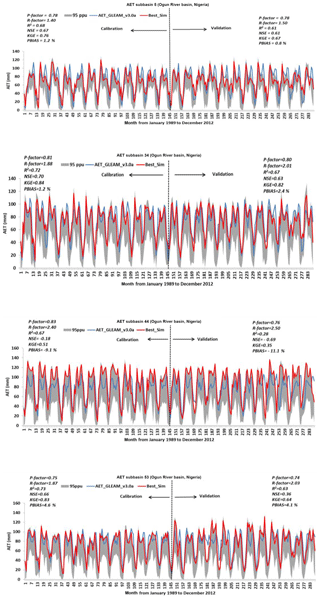
In this paper, only the spatial representations of SWAT_HG with the highest (GS1) and the lowest (MS6) model performance are included for the purpose of showing the two extreme results obtained (Figs. 4, 5, 6 and 7). The calibration and validation results for GS1 show a model performance of NSE >0.50, KGE >0.50 and R²>0.6 in more than half of the 53 subbasins and a PBIAS $<\pm \mathrm{15}$ % in all 53 subbasins (Figs. 4 and 5). The calibration and validation results for MS6 (Figs. 6 and 7) show the lowest model performance.

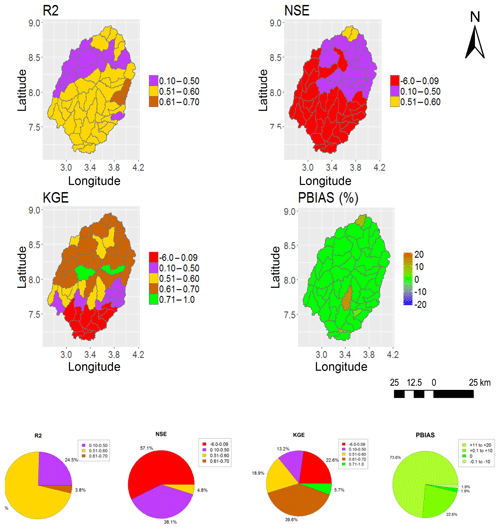
Figure 6 Performance metrics (NSE, KGE, R² and PBIAS) of SWAT (SWAT_P-M) when calibrated with MOD16 (MS6).

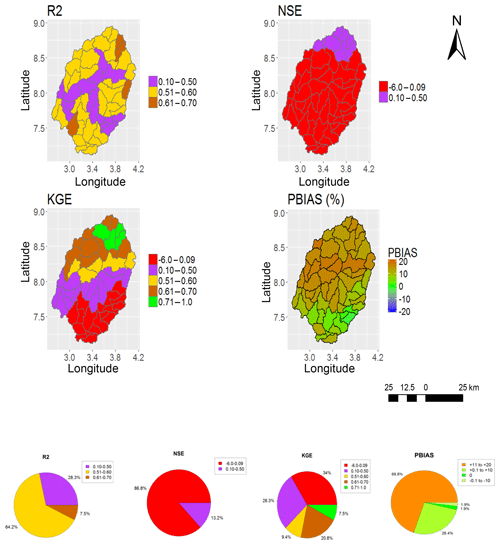
Figure 7 Performance metric (NSE, KGE, R² and PBIAS) results of SWAT (SWAT_P-M) when validated with MOD16 (MS6).

The remaining calibration and validation results of GS2, GS3, MS4 and MS5 (Figs. S1, S2, S3, S4, S5, S6, S7 and S8 in the Supplement) show a lower model performance than GS1.

Figures 8 and 9 summarise the model performance results of the SWAT model runs when calibrated and validated with GLEAM_v3.0a (GS1, GS2 and GS3) and MOD16 AET (MS4, MS5 and MS6). Overall, results indicate that the calibration and validation of GS1 (Figs. 8 and 9) exhibits a model performance superior to the remaining two model runs for AET simulation (through GS1 to MS6) judging by the four objective functions except for the validation period, during which a lower NSE (average value of 0.45) was obtained (GS1, Fig. 9). NSE >0.50 was achieved in 32 out of 53 subbasins during the model validation (GS1), meaning that more than half of the 53 subbasins have a satisfactory model performance, and therefore the average NSE value of 0.45 can be considered acceptable.

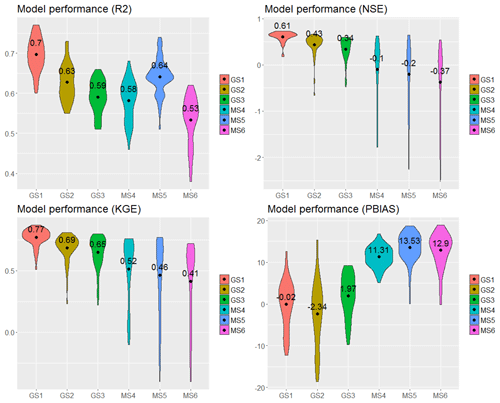
Figure 8 Plots of the performance result of SWAT in simulating actual evapotranspiration. The values and the black dot symbols (•) depict the average value of R², NSE, KGE and PBIAS obtained for each calibration.

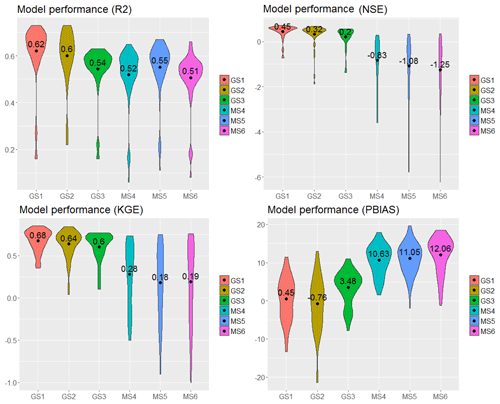
Figure 9 Plots of the performance result of SWAT in simulating actual evapotranspiration. The values and the black dot symbols (•) depict the average value of R², NSE, KGE and PBIAS obtained for each validation.

3.1 Uncertainty analysis of SWAT model

The SWAT model performance results of SWAT-HG when calibrated and validated with the AET from GLEAM_v3.0a (GS1) proved to be the most efficient of the three model runs (through GS1 to MS6); therefore, it was used to further predict the uncertainty associated with the AET simulations for each of the 53 subbasins to map error sources. In the calibration period, the values of the P factor were between 0.50 and 0.90, and the values of the R factor were between 1.40 and 2.4. In the validation period, the values of the P factor were between 0.6 and 0.88, and those of the R factor were between 1.43 and 2.5. The P factor values revealed that more than half of the Earth-observation-derived AET plus its error are bracketed by the 95 % predictive uncertainty. The predictive uncertainties were adequate in the 53 subbasins and had a satisfactory performance for monthly AET simulations using the Hargreaves equation, though the R factor was quite large in all 53 subbasins, indicating large model uncertainties. Extracts of the monthly calibration and validation results showing the 95 % prediction uncertainty intervals, along with the satellite-based AET (GLEAM_v3.0a), are presented in Fig. 10.

Figure 10 Extracts of the monthly calibration and validation results (GSI) showing the 95 % prediction uncertainty interval along with the best SWAT-simulated actual evapotranspiration and satellite-based actual evapotranspiration (GLEAM-v3.0a).

3.2 Model verification result

It was found that the AET from GLEAM_v3.0b was bracketed within the 95 % uncertainty prediction (Fig. 11). The long-term average monthly water balance assessment performed at the outlet of the watershed shows a seasonal fluctuation, which agrees with previous water balance studies conducted at the outlet of the study area located in Abeokuta (Ufoegbune et al., 2011, 2012; Eruola et al., 2012; Sobowale and Oyedepo, 2013). (i) The study area is characterised by a bimodal rainfall pattern, (ii) the AET increases in February from 55 to 76 mm as the wet season approaches and decreases in October from 72 to 54 mm as the dry season approaches (Ufoegbune et al., 2011), (iii) rainfall commences in March (66 mm) and is plentiful in June (165 mm) and September (167 mm), (iv) in August there is a decrease in precipitation to 96 mm and a decrease in AET to 94 mm, and the dry spell often experienced in August is termed the “August break” (Ufoegbune et al., 2011). (v) The dry period extends from November to March, the months of low rainfall, AET and soil moisture values (Ufoegbune et al., 2011), (vi) with moderate rain in March (soil water increases from 83 to 200 mm in July; Ufoegbune et al., 2011), (vii) and as the dry season commences, the soil water gradually declines.

Table 3 Average annual water balance at the outlet of the watershed in Abeokuta based on SWAT-simulated output.

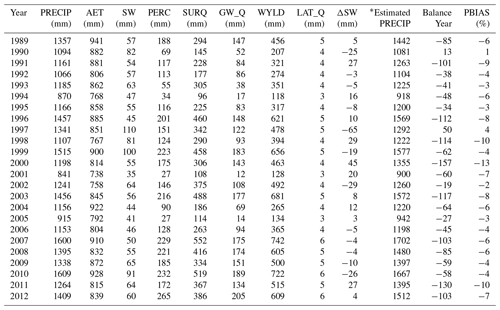
PRECIP: precipitation; AET: actual evapotranspiration; SW: soil water; PERC: percolation; SURQ: surface runoff; GW_Q: groundwater recharge; WYLD: water yield; LAT_Q: lateral flow; SW: change in soil moisture; ^∗ Estimated PRECIP is WYLD + AET + ΔS + PERC-GW_Q expressed in millimetres.

The differences in the long-term mean monthly water balance values obtained in past studies conducted within the catchment are due to variation in the number of years considered. Also, Eruola et al. (2012) revealed that two rainfall peaks in July and September agree with the current study, while Ufoegbune et al. (2011) showed the two rainfall peaks to be in the months of June and September. All these previous studies and the current study water balance results are in the same range. Figure 12 shows the seasonal fluctuation of the SWAT-estimated water balance components at the outlet of watershed, located in Abeokuta. Our results show the average long-term annual water balance estimated by SWAT to be within a reasonable percentage error of closure of ±15 % (Table 3).

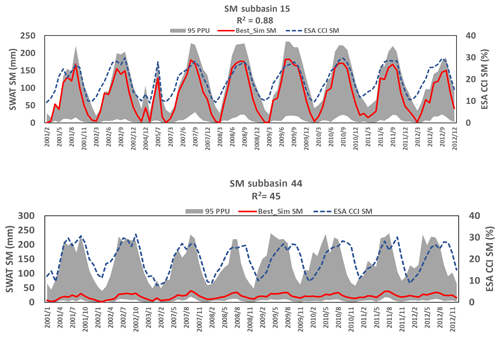
3.3 SWAT soil moisture validation result

Only the spatial representation of SWAT_HG with the highest AET calibration model result was validated against the ESA CCI SM. Overall, the average R² value obtained for the Ogun River Basin is 0.76 (Fig. 13). The results show that 88.6 % of the basin has R²>0.60 and 11.3 % of the basin has R²<0.60. A graphical representation of the soil moisture dynamics from the highest and the lowest R² results obtained is presented in Fig. 14.

4 Discussion

The global sensitivity analysis revealed that for the three SWAT model set-up calibrations (GS1 to MS6), the same 11 SWAT hydrologic parameters governing AET were sensitive (Table 2). When different PET equations were tested in SWAT, different simulated AET values were obtained and the overall sensitivity ranking of the parameters varied significantly. Since parameters represent processes, the significant variation in the sensitivity ranking of the parameters implies that the impact of the selected PET methods in simulating the AET in the study area is relatively high. The SCS runoff curve number for moisture condition II (CN2.mgt), which is one of the parameters that controls the overland processes and is a function of the soil permeability, land use and antecedent soil water, was used to determine the surface runoff generation in the basin. CN2.mgt is found to be the most sensitive parameter of the three model runs (through GS1 to MS6), indicating that it is also the dominant parameter controlling the AET processes in SWAT for the Ogun River Basin (Table 2). The soil evaporation compensation coefficient (ESCO.hru) controls soil evaporation and depends on soil characteristics. As the value of ESCO is reduced, more water is extracted from the lower layers to meet evaporative demand. ESCO is the second-most-sensitive parameter for GS1, with a very low value of 0.02, but for other runs (GS2 to MS6), the sensitivity ranking varies. The maximum canopy storage (CANMAX.hru) accounts for the amount of water that can be trapped in the canopy when fully developed and affects infiltration, surface runoff and evapotranspiration processes. It was more sensitive when the model was calibrated with GLEAM than when the model was calibrated with MOD16 AET. The soil bulk density (SOL_BD.sol) defines the relative amount of pore space and its overall sensitivity ranking is between 2 and 4 (GS1 through MS6). It was more sensitive when SWAT was calibrated with MOD16 than when SWAT was calibrated with GLEAM AET. The baseflow alpha factor (ALPHA_BF.gw) is the index of groundwater flow response to changes in recharge; it influences the baseflow simulation and its sensitivity varies (GS1 to MS6). The saturated hydraulic conductivity (SOL_K.sol) determines the shallow subsurface flow and groundwater recharge, and it affects the surface runoff response. In order to correctly account for the volume of water lost to evaporation from the two reservoirs (Oyan dam and Ikere George dam), the evaporation coefficient (EVRSV.res) was calibrated. Interestingly, we observed that GS1, GS3 and MS6 have higher EVRSV.res values that agree with the expected values in such a humid tropical region compared to EVRSV.res values obtained from GS2, MS4 and MS5. It is observed that GS1 tends to have the highest (4.7) maximum stomatal conductance (GSI.plant.dat), which denotes the maximum conductance of a leaf when the canopy resistance term is modified to reflect the impact of high vapour pressure deficit, during the calibration. MS4 has the highest value (0.99) of initial soil water storage expressed as a fraction of field capacity water content (FFCB). MS4 also obtained the highest value (0.95) of the plant uptake compensation factor (EPCO.hru), meaning that the calibration procedure makes the model allow more of the water uptake demand to be met by lower layers in the soil and as EPCO approaches 0 (GS3 with the value 0.07). The soil-available storage capacity (SOL_AWC.sol) values for GS1 to MS6 were allowed to vary by a factor of 0.8 to 0.96, meaning there is an increase in SOL_AWC for the soil in the model set-up for the Ogun River Basin.

Assessing the model performance with the objective functions and their satisfactory threshold values used in this study, the calibration and validation with the AET from GLEAM_v3.0a showed an overall satisfactory SWAT model performance when the Hargreaves PET equation was used in SWAT to simulate AET (GS1) compared to the other model calibration results (GS2 to MS6). The calibration and validation with the AET from MOD16 yielded a lower SWAT model performance regardless of which of the three PET equations was tested in SWAT.

Using the guidelines in Moriasi et al. (2007, 2015) and Kouchi et al. (2017) for evaluating the SWAT model performance at a monthly time step, the PBIAS values showed a satisfactory model performance (PBIAS $\le \pm \mathrm{25}$) in the six calibrations and validations of the three SWAT model runs (Figs. 8 and 9). The positive PBIAS obtained in the calibration and validation of the three SWAT model runs using the AET from MOD16 (MS4, MS5 and MS6) indicated a tendency for the SWAT model to underestimate monthly AET at the Ogun River Basin. An intuitive reason for this may be due to transient water stress occurring in the basin; however, transient water stress is not the main challenge in the study area, which is located in the humid region of southwestern Nigeria with a mean aridity index of 0.75 (for the period 1989–2012). The careful consideration of equal wet and dry years in the calibration and validation years has accounted for similar climatic conditions in both periods.

The positive PBIAS obtained using MOD16 for calibration agrees with previous studies conducted at sites in tropical regions. Ruhoff et al. (2013) validated MOD16 AET using ground-based measurements of energy fluxes obtained from eddy-covariance sites in tropical regions in the Rio Grande basin, Brazil, from a hydrological model (MGB-IPH) at both local and regional scales and found that at the natural savannah vegetation site, the annual AET estimate derived by the MOD16 algorithm was 19 % higher than the measured amount. Ruhoff et al. (2013) found that misclassification of land use and land cover was identified as the largest contributor to error from the MOD16 algorithm. Ramoelo et al. (2014) validated MOD16 using data from two eddy-covariance flux towers installed in a savannah and woodland ecosystem within the Kruger National Park, South Africa, and found that one flux tower result showed inconsistent comparisons with MOD16 AET and the other site achieved a poor comparison with MOD16 ET. In their study, they found that the inconsistent comparison of MOD16 and flux-tower-based AET can be attributed to the parameterisation of the Penman–Monteith model, flux tower measurement errors and flux tower footprint vs. MODIS pixels. Also, Trambauer et al. (2014) compared different evaporation products in Africa and found that MOD16 evaporation does not show a good agreement with other products in most parts of Africa, while other evaporation datasets (GLEAM, ECMWF reanalysis ERA-LAND and PCR-GLOBWB hydrological-model-simulated AET) are more consistent. From our results, we found that when the SWAT model was calibrated with MOD16 AET, the SWAT simulations tend to underestimate AET.

A satisfactory SWAT model GS1 performance was achieved for all objective functions, except for the average NSE value of 0.45 in the validation period; however, NSE values >0.50 were obtained in 60 % of the subbasins. The KGE result revealed the SWAT-HG model validation (GS1) to be satisfactory (Fig. 9). Also, the low PBIAS result of −0.02 % and 0.45 % (GS1, Figs. 8 and 9) corresponded to a performance rating of “very good”, indicating predictive capability for accurate model simulation. The better SWAT model performance in GS1 is attributed to the selection of the Hargreaves equation, which is based on available observed precipitation and maximum and minimum temperature to obtain AET, while the Penman–Monteith and Priestly–Taylor equations are driven by simulated variables (wind speed, relative humidity and solar radiation) in this study. Also, the complex water balance algorithm of GLEAM takes into account soil water balance, bare soil evaporation, open water evaporation, evaporative stress factor and rainfall interception, all of which assist in simulating dynamic hydrological components, especially the AET.

The differences in GLEAM and MOD16 products are due to their input and forcing data (Trambauer et al., 2014). Our results agree with another study in which AET from GLEAM performed satisfactorily for the calibration of a large-scale hydrological model set-up in Morocco (López López et al., 2017). The 95 % predictive uncertainty of the highest SWAT model performance (GS1) was quantified, and the 95 % predictive uncertainty bracketed most of the satellite-based AET, although the R factor was quite large in all of the subbasins, signifying a large model uncertainty which can be ascribed to the uncertainty in satellite-derived AET, the forcing climate data, the conceptual model and the model parameters. The 95PPUs are the combined outcome of the uncertainties. These uncertainty sources are not separately evaluated in SUFI-2 but attributed as a total model uncertainty to the parameters, which are visualised through the simulated model output ranges. A first verification of the SWAT model run with the best model performance (GS1) was carried out using GLEAM_v3.0b as an independent dataset, and the results were bracketed within the 95PPU of GS1 (Fig. 11). The second verification of the SWAT model structure with the best model performance (GS1) was carried out by assessing the output of SWAT water balance components (Table 3 and Fig. 12). The results obtained from the long-term mean monthly water balance agree with previous water balance studies conducted within the study area. The differences in the water balance component values of past and the current study are due to variation in the number of years considered. The average long-term water balance at the outlet of the study area shows a satisfactory percentage error of closure of ±15 % (Table 3).

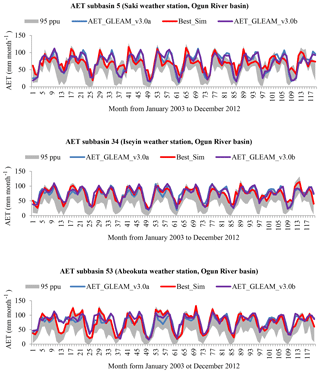
Figure 11 SWAT model verification results showing the satellite-based AET GLEAM_v3.0a used for the model calibration and validation, the best SWAT-simulated actual evapotranspiration (GS1) and an independent GLEAM_v3.0b time series bracketed by 95 % predictive uncertainty.

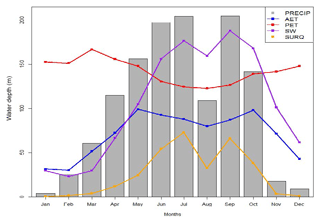
Figure 12 Seasonal fluctuation of water balance components at the outlet of the watershed located in Abeokuta.

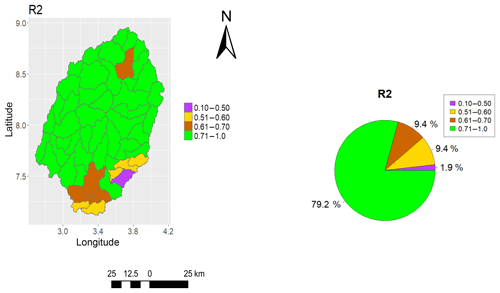
Figure 13 Performance metric (R²) of SWAT-simulated soil moisture when validated with ESA CCI soil moisture v3.2.

At a monthly time step, the dynamics of the SWAT-simulated soil moisture (mm) for the whole soil profile compared to the ESA CCI SM (%) in the upper few centimetres of the soil profile fit very well in most of the basin. The lowest R² of 0.45 obtained in subbasin 44 of the Ogun River Basin (Fig. 14) also corresponded to the lowest result (R²=0.28) obtained in subbasin 44 when the model was validated with AET from GLEAM_v3.0a (Fig. 10). Nevertheless, the high overall average soil moisture validation R² agrees with a previous study that validated a hydrological model with ESA CCI SM in West Africa (Poméon et al., 2018). The multi-calibration and validation results show the SWAT model to perform satisfactorily in the study area.

Figure 14 Extracts of R² results for SWAT monthly simulated soil moisture validation against ESA CCI SM v3.2 and a graphical representation of the SWAT SM 95 % prediction uncertainty band.

5 Conclusion

This study examined an alternative method to calibrate and validate the SWAT eco-hydrological model using available satellite-based AET products for the data-sparse Ogun River Basin in southwestern Nigeria. The approach opens up a new direction for the calibration and validation of hydrological models in ungauged basins. Due to the different retrieval algorithms of both the satellite-based AET and SWAT-simulated AET, two global evaporation products (GLEAM and MOD16) were used to calibrate the three SWAT-simulated AETs on a monthly timescale. The use of the Hargreaves, Priestley–Taylor and Penman–Monteith equations in SWAT cause the different AET values obtained. Six different calibrations were implemented for the global AET products with the aim of obtaining a high-performing model for the Ogun River Basin. Overall, the results are promising and show that global satellite-based AET data can be used as an alternative method to calibrate and validate the SWAT model in a tropical sparsely gauged basin. Specifically, when the SWAT model was used with the Hargreaves PET equation and was calibrated using the GLEAM_v3.0a AET product, the highest model performance was obtained with an acceptable predictive uncertainty.

Statistical analysis of the model performance shows that global AET datasets used for the calibration were significantly different from each other, which was expected because of their different retrieval algorithms. Our findings suggest that the SWAT model run using the Hargreaves equation can be used as a potential decision support tool for further studies and predictions on basin hydrology in the Ogun River Basin.

There is still a need for further research on (i) improving the model calibration performance in subbasins where the performances are unsatisfactory and (ii) the validation of other simulated variables (e.g. streamflow) of the calibrated SWAT model using observed datasets when these are available.

The results from this research contribute to a better understanding of the ease and suitability of using freely available satellite-based AET datasets for model calibration in tropical ungauged basins where the main limitation of setting up hydrological models for discharge simulations is the lack of measured streamflow data. Furthermore, a new contribution of this study is the better understanding of the calibration of the three different estimated AETs in SWAT to derive the model with the best goodness of fit and a satisfactory predictive capability.

We recommend testing the three PET equations in SWAT to simulate AET whenever SWAT calibration is carried out with any satellite-based AET products and to independently validate other water balance components. The work presented here is a first step in hydrological modelling that will establish a basis for future modelling applications within the study basin.

Appendix A: Performance metrics and their equations

Table A1 Table showing the performance metrics and their equations used to evaluate the model performance in this study.

O_i represents satellite-based AET values; P_i represents simulated AET values; $\stackrel{\mathrm{‾}}{O}$ represents mean satellite-based AET values; $\stackrel{\mathrm{‾}}{P}$ represents mean simulated AET values; r is the Pearson product correlation coefficient between satellite-based AET and the simulated AET; α is the standard deviation of the simulated AET over the standard deviation of the satellite-based AET; and β is the ratio of the mean simulated AET to the satellite-based AET.

Appendix B: SWAT model calibrated parameters

Table B1 The 11 parameters and their minimum and maximum range used in this study for the first iteration (1000 simulations) of all six calibrations.

Appendix C: Equations (taken from SWAT theoretical documentation; Neitsch et al., 2011) showing the selected 11 most sensitive SWAT parameters used in this study

C1 Maximum stomata conductance

The canopy resistance term is modified to reflect the impact of high vapour pressure deficit on leaf conductance when calculating actual evapotranspiration (Stockle et al., 1992). The adjusted leaf conductance in which parameter GSI appears is calculated in SWAT using Eqs. (C1) and (C2):

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }{g}_e=g_{e,\mathrm{mx}}\times \left[\mathrm{1}-\mathrm{\Delta }{g}_{e,\mathrm{dcl}}\left(\mathrm{vpd}-{\mathrm{vpd}}_{\mathrm{thr}}\right)\right]\\ \text{(C1)}& {\displaystyle }& {\displaystyle }\mathrm{if}\mathrm{vpd}>{\mathrm{vpd}}_{\mathrm{thr}},\text{(C2)}& {\displaystyle }& {\displaystyle }{g}_e=g_{e,\mathrm{mx}}\mathrm{if}\mathrm{vpd}\le {\mathrm{vpd}}_{\mathrm{thr}},\end{array}$$

where g_e is the conductance of a single leaf (m s⁻¹), g_e,mx is the parameter GS1, which is the maximum stomatal conductance of a single leaf (m s⁻¹), Δg_e,dcl is the rate of decline in leaf conductance per unit increase in vapour pressure deficit (m s⁻¹ kPa⁻¹), VPD is the vapour pressure deficit (kPa) and vpd_thr is the threshold vapour pressure deficit above which a plant will exhibit reduced leaf conductance (kPa). The rate of decline in leaf conductance per unit increase in vapour pressure is calculated by solving equation C1.

C2 The SCS curve number for soil moisture condition II

Three antecedent moisture conditions are defined by SCS curve number: I – dry (wilting point), II – average moisture and III – wet (field capacity). The SCS curve number II is calculated from either SCS moisture condition I or from SCS moisture III in Eqs. (C3) and (C4):

$$\begin{array}{ll}\text{(C3)}& {\displaystyle }& {\displaystyle }{\mathrm{CN}}_{\mathrm{1}}={\mathrm{CN}}_{\mathrm{2}},{\displaystyle }& {\displaystyle }-{\displaystyle \frac{\mathrm{20}\times \left(\mathrm{100}-{\mathrm{CN}}_{\mathrm{2}}\right)}{\left(\mathrm{100}-{\mathrm{CN}}_{\mathrm{2}}+\exp \left[\mathrm{2.533}-\mathrm{0.0636}\times \left(\mathrm{100}-{\mathrm{CN}}_{\mathrm{2}}\right)\right]\right)}}\\ \text{(C4)}& {\displaystyle }& {\displaystyle }{\mathrm{CN}}_{\mathrm{3}}={\mathrm{CN}}_{\mathrm{2}}\times \exp \left[\mathrm{0.00673}\times \left(\mathrm{100}-{\mathrm{CN}}_{\mathrm{2}}\right)\right],\end{array}$$

where CN₁ is the moisture condition I curve number, CN₂ is the moisture condition II curve number and CN₃ is the moisture condition III curve number.

C3 Maximum canopy storage

The maximum amount of water that can be held in canopy storage varies from day to day as a function of the leaf area index in the SWAT model and is estimated with Eq. (C5) in which the CANMAX parameter appears:

$$\begin{array}{}\text{(C5)}& {\displaystyle }{\mathrm{can}}_{\mathrm{day}}={\mathrm{can}}_{\mathrm{mx}}\times {\displaystyle \frac{\mathrm{LAI}}{{\mathrm{LAI}}_{\mathrm{mx}}}},\end{array}$$

where can_day is the maximum amount of water that can be trapped in the canopy on a given day (mm H₂O), can_mx is the CANMAX parameter and is the maximum amount of water than can be trapped in the canopy when the canopy is fully developed (mm H₂O), LAI is the leaf area index for a given day, and LAI_mx is the maximum leaf area index for the plant.

C4 Bulk density

Bulk density is calculated using Eq. (C6):

$$\begin{array}{}\text{(C6)}& {\displaystyle }{\mathit{\rho }}_{\mathrm{b}}={\displaystyle \frac{M_{\mathrm{s}}}{V_{\mathrm{T}}}},\end{array}$$

where ρ_b is the bulk density (Mg m⁻³), M_s is the mass of solids (Mg) and V_T is the total volume (m³). The total volume is calculated as

$$\begin{array}{}\text{(C7)}& {\displaystyle }{V}_{\mathrm{T}}=V_{\mathrm{A}}+V_{\mathrm{W}}+V_{\mathrm{S}},\end{array}$$

where V_A is the volume of air (m³), V_W is the volume of water (m³) and V_S is the volume of solids (m³).

C5 Soil-available water storage capacity

Soil-available water storage capacity is calculated by subtracting the fraction of water present at the permanent wilting point from that present at field capacity:

$$\begin{array}{}\text{(C8)}& {\displaystyle }\mathrm{AWC}=\mathrm{FC}-\mathrm{WP},\end{array}$$

where AWC is the plant-available water content, FC is the water content at field capacity and WP is the water content at the permanent wilting point.

C6 Saturated hydraulic conductivity

The equation in which the parameter saturated hydraulic conductivity (SOL_K) appears is given in Eq. (C9):

$$\begin{array}{}\text{(C9)}& {\displaystyle }{\mathrm{TT}}_{\mathrm{perc}}={\displaystyle \frac{{\mathrm{SAT}}_{\mathrm{ly}}-{\mathrm{FC}}_{\mathrm{ly}}}{K_{\mathrm{sat}}}},\end{array}$$

where TT_perc is the travel time for percolation (h), SAT_ly is the amount of water in the soil layer when completely saturated (mm H₂O), FC_ly is the water content of the soil layer at field capacity (mm H₂O) and K_sat is the saturated hydraulic conductivity for the layer (mm h⁻¹).

C7 Baseflow alpha factor

The baseflow recession constant (baseflow alpha factor) is α_gw. The α_gw is calculated using Eq. (C10):

$$\begin{array}{}\text{(C10)}& {\displaystyle }{\mathit{\alpha }}_{\mathrm{gw}}={\displaystyle \frac{\mathrm{1}}{N}}\times ln⌊{\displaystyle \frac{Q_{\mathrm{gw},N}}{Q_{\mathrm{gw},\mathrm{0}}}}⌋,\end{array}$$

where α_gw is the ALPHA_BF parameter, N is the time lapsed since the start of the recession (days), Q_gw,N is the groundwater flow on day N (mm H₂O) and Q_gw,0 is the groundwater flow at the of the start of the recession (mm H₂O).

C8 Lake evaporation coefficient

The equation in which the reservoir evaporation coefficient (EVRSV.res) appears is shown in Eq. (C11):

$$\begin{array}{}\text{(C11)}& {\displaystyle }{V}_{\mathrm{evap}}=\mathrm{10}\times \mathit{\eta }\times E_{\mathrm{0}}\times \mathrm{SA},\end{array}$$

where V_evap is the volume of water removed from the water body by evaporation during the day (m³ H₂O), η is an evaporation coefficient with a default value of 0.6 (EVRSV), E₀ is the potential evapotranspiration for a given day (mm H₂O) and SA is the surface area of the water body (ha).

C9 Plant uptake compensation factor

The equation in which the plant uptake compensation factor (EPCO) appears (Eq. C13) is used to calculate the adjusted potential water uptake when the upper layers in the soil profile do not contain enough water to meet the potential water uptake (Eq. C12):

$$\begin{array}{}\text{(C12)}& {\displaystyle }{W}_{\mathrm{up},\mathrm{ly}}=W_{\mathrm{up},\mathrm{zl}}-E_{\mathrm{up},\mathrm{zu}},\end{array}$$

where W_up,ly is the potential water uptake for layer ly (mm H₂O), W_up,zl is the potential water uptake for the profile to the lower boundary of the soil layer (mm H₂O) and E_up,zu is the potential water uptake for the profile to the upper boundary of the soil layer (mm H₂O).

$$\begin{array}{}\text{(C13)}& {\displaystyle }{W}_{\mathrm{up},\mathrm{ly}}^{\prime }=W_{\mathrm{up},\mathrm{ly}}+W_{\mathrm{demand}}\times \mathrm{EPCO},\end{array}$$

where $W_{\mathrm{up},\mathrm{ly}}^{\prime }$ is the adjusted potential water uptake for layer ly (mm H₂O), W_demand is the water uptake demand not met by overlying soil layers (mm H₂O) and EPCO is the plant uptake compensation factor.

C10 Soil evaporation compensation coefficient

The modified equation for the amount of evaporative demand for a soil layer, which is determined by taking the difference between the evaporative demands calculated at the upper and lower boundaries of the soil layer, incorporates a coefficient called ESCO for depth distribution modification. The modified equation is

$$\begin{array}{}\text{(C14)}& {\displaystyle }{E}_{\mathrm{soil},\mathrm{ly}}=E_{\mathrm{soil},\mathrm{zl}}-E_{\mathrm{soil},\mathrm{zu}}\times \mathrm{ESCO},\end{array}$$

where E_soil,ly is the evaporative demand for layer ly (mm H₂O), E_soil,zl is the evaporative demand at the lower boundary of the soil layer (mm H₂O), E_soil,zu is the evaporative demand at the upper boundary of the soil (mm H₂O) and ESCO is the soil evaporative compensation coefficient.

C11 Initial soil water storage expressed a fraction of field capacity water content

The estimation of field capacity water content is the equation in which the initial soil water storage expressed as a fraction of field capacity water content (FFCB) appears (Eq. C15):

$$\begin{array}{}\text{(C15)}& {\displaystyle }{\mathrm{FC}}_{\mathrm{ly}}={\mathrm{WP}}_{\mathrm{ly}}+{\mathrm{AWC}}_{\mathrm{ly}},\end{array}$$

where FC_ly is the water content at field capacity expressed as a fraction of the total soil volume (FFCB), WP_ly is the water content at the wilting point expressed as a fraction of the total soil volume and AWC_ly is the available water capacity of the soil layer expressed as a fraction of the total soil volume.

Appendix D: Ogun River Basin with its 53 subbasins intersected by the satellite-based AET pixels

Figure D1 Mean monthly actual evapotranspiration of GLEAM_v3.0a over the entire Ogun River Basin for 1989–2012.

Figure D2 Mean monthly actual evapotranspiration of MOD16 over the entire Ogun River Basin for 2000–2012.

Appendix E: Ogun River Basin with its 53 subbasins intersected by the ESA CCI soil moisture pixels

Figure E1 Mean monthly soil moisture of ESA CCI over the entire Ogun River Basin for 2001–2012.