Advancing measurements and representations of subsurface heterogeneity and dynamic processes: towards 4D hydrogeology

Essentially all hydrogeological processes are strongly influenced by the subsurface spatial heterogeneity and the temporal variation of environmental conditions, hydraulic properties, and solute concentrations. This spatial and temporal variability generally leads to effective behaviors and emerging phenomena that cannot be predicted from conventional approaches based on homogeneous assumptions and models. However, it is not always clear when, why, how, and at what scale the 4D (3D + time) nature of the subsurface needs to be considered in hydrogeological monitoring, modeling, and applications. In this paper, we discuss the interest and potential for the monitoring and characterization of spatial and temporal variability, including 4D imaging, in a series of hydrogeological processes: (1) groundwater fluxes, (2) solute transport and reaction, (3) vadose zone dynamics, and (4) surface–subsurface water interactions. We first identify the main challenges related to the coupling of spatial and temporal fluctuations for these processes. We then highlight recent innovations that have led to significant breakthroughs in high-resolution space–time imaging and modeling the characterization, monitoring, and modeling of these spatial and temporal fluctuations. We finally propose a classification of processes and applications at different scales according to their need and potential for high-resolution space–time imaging. We thus advocate a more systematic characterization of the dynamic and 3D nature of the subsurface for a series of critical processes and emerging applications. This calls for the validation of 4D imaging techniques at highly instrumented observatories and the harmonization of open databases to share hydrogeological data sets in their 4D components.

1 Introduction

While the surface components of continental water, such as streams, lakes, and glaciers, are a very familiar part of our landscape, the vast majority of continental water resources resides and flows in the subsurface and is thus generally inaccessible to direct observation (McDonnell, 2017). Growing societal needs imply that subsurface environments, which form part of the critical zone of the Earth (Brantley et al., 2007; Fan et al., 2019), are increasingly subject to pressure and multiple (possibly competing) uses for water resources, such as groundwater abstraction, artificial recharge and storage (Dillon et al., 2019; Russo and Lall, 2017; Aeschbach-Hertig and Gleeson, 2012), nuclear waste storage (e.g., Ewing, 2015; Butler, 2010), geothermal energy (Rivera et al., 2017; Fleuchaus et al., 2018; Lu, 2018), oil and gas extraction (e.g., Wang et al., 2014), and climate change mitigation, such as energy storage (Arbabzadeh et al., 2019) and CO₂ sequestration (Hamza et al., 2021; Kumar et al., 2020), while being threatened by anthropogenic contamination (e.g., Riedel and Weber, 2020). As a result, subsurface systems are experiencing profound modifications that affect their basic environmental functions and ecosystem services (Erostate et al., 2020; Fattorini et al., 2020; Luijendijk et al., 2020). These modifications include, both at the local and the catchment scales, water level depletion (Jasechko et al., 2021), which affects baseflow of many rivers and associated ecosystem services (Conant et al., 2019), a growing input of chemicals and pathogens, which threatens water quality (e.g., Szymczycha et al., 2020), seawater intrusion (Werner et al., 2013) and soil salinization (Litalien and Zeeb, 2020; Singh, 2021), threatening soil and water resources as well as food security in many arid and semi-arid regions of the world, and massive fluid injections at depth, related to CO₂ sequestration or gas extraction, which may lead to increased seismicity (Rathnaweera et al., 2020; Schultz et al., 2020; Keranen and Weingarten, 2018).

The last decade has seen great advances in stochastic subsurface hydrology (e.g., Scheidt et al., 2018), microscale imaging (e.g., Gouze et al., 2008; Blunt et al., 2013; Heyman et al., 2020), and geophysical characterization (e.g., Binley at al., 2015; Singha et al., 2015). Although geological heterogeneity has been long recognized, these advances have made it even more clear that the subsurface is highly heterogeneous at multiple scales and that this heterogeneity substantially controls many flow, transport, and biochemical processes (e.g., Hartmann et al., 2017; Comte et al., 2019; Zamrsky et al., 2020). Recent efforts have led to an improved ability for monitoring surface-water dynamics or characterizing the state of aquatic systems, but this has not been matched by a significant increase in our ability to quantify the dynamics of fluxes and processes in the subsurface (e.g., Schilling et al., 2018). A wide gap between common modeling approaches (e.g., homogeneous or multi-Gaussian representations of parameters, steady-state or transient simulations, upscaling approaches) and field reality prevails. On the one hand, data sets often have a very limited 3D spatial extent and are characterized by a low sampling density, preventing a full description of the complex nature of the aquifer (e.g., Xu and Valocchi, 2015). On the other hand, studies concerning the temporal dynamics of hydrological processes and structures are generally based on point data typically acquired in wells, potentially missing the underlying spatial variability (e.g., Johnson et al., 2012).

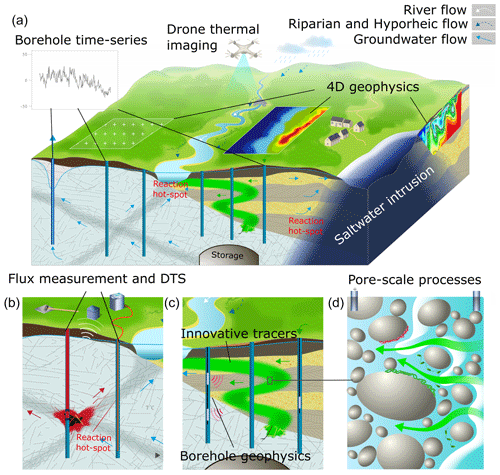
Figure 1 Illustration of the 4D nature of hydrogeological processes inaccessible from punctual data only: (a) imaging subsurface fluxes and their contribution to surface fluxes through the combination of borehole and surface imaging; (b) monitoring water content and temperature fluctuations for quantifying preferential flows and heat transfer; (c) characterizing tracer motion to elucidate transport processes and related parameters; and (d) analyzing and upscaling pore-scale signals produced by microscale reactive transport processes.

The persistent observation gap between data points contributes significantly to the current lack of understanding of subsurface processes and our (in)ability to accurately predict the evolution of subsurface systems. It limits our ability to answer critical scientific questions of significant societal and industrial impacts, such as the management of water quantity, quality, and ecology at the interface between the surface and the subsurface (Fleckenstein et al., 2006, 2010; Brunner et al., 2017; Conant et al., 2019), the fate of contaminant through mixing, reactions, and the development of biogeochemical hotspots (e.g., Wallis et al., 2020; Pannecoucke et al., 2020; Robinson and Hasenmueller, 2017; Bailey, 2017), or understand the contribution of subsurface processes to global cycles of carbon (Zhang and Planavsky, 2020; Liu et al., 2014) and nitrogen (Marzadri et al., 2012) (Fig. 1). The potential of characterization for coupled spatio-temporal monitoring of parameters and state variables and their temporal evolution, including 4D imaging, to understand these processes remains largely unexplored. This temporal component should not only include the evolution of state variables under transient conditions, but also the evolution of system properties because of coupled processes, such as hydromechanical effects impacting the pore space or fracture apertures (Davy et al., 2018), clogging and erosion processes in streambeds (Partington et al., 2017), or reactive transport inducing changes in the pore space (Izumoto et al., 2020).

A grand challenge of subsurface imaging methods for dynamic hydrogeological processes (Fig. 1) is to deal with systems characterized by pronounced structure and process heterogeneity, including preferential flow paths, evolving properties or geometry, unsaturated flow processes, fluctuating redox conditions, and multifunctional microbial communities. Recent breakthroughs in hydrogeophysical imaging techniques (e.g., Binley et al., 2015; Singha et al., 2015) and the emergence of interdisciplinary approaches combining new sensors such as fiber optics (Bense et al., 2016; Zhan, 2020), new experimental methodologies like ambient seismic noise correlation (Garambois et al., 2019), and coupled modeling techniques (e.g., Hinnell et al., 2010; Jardani et al., 2013; Linde and Doetsch, 2016) may profoundly change our vision and representation of the dynamics of processes that take place in these environments (Binley et al., 2015; St. Clair et al., 2015). However, monitoring and characterizing dynamical fluxes, transport, reactions, and hydromechanical processes that evolve spatially in 3D with geophysical imaging is still in its infancy in environmental sciences and engineering. The efficiency of those new methods and the full complexity that emerges from their coupling can only be revealed through in situ exploration with interdisciplinary approaches. In that sense, field observatories and case studies constitute a key component of the current research effort (e.g., Folch et al., 2020; Palacios et al., 2020, Table 2B6).

Table 1 Classification of processes according to their need for high-resolution space–time imaging.

The objective of this review paper is to identify and discuss when, why, and for which processes and applications the characterization of dynamic hydrogeological processes is crucial. Although heterogeneity influences all the processes occurring in the subsurface, an exhaustive characterization of the subsurface is not always necessary and strongly depends on the objective of the studies, the scale, and the available budget. We identify three categories of processes according to their need for coupled temporal and spatial monitoring, including 4D imaging (see Table 1 and Fig. 8): (A) processes that require high-resolution space–time imaging to develop accurate upscaled models applicable to less instrumented sites; (B) applications for which spatial and temporal monitoring is critical and desirable; and (C) applications for which limited hydrogeological data are often sufficient for a first approximation. Specifically, we discuss the potential and value of high-resolution space–time imaging in hydrogeology for monitoring and modeling groundwater fluxes, transport and reactions processes, soil moisture dynamics in the vadose zone, and surface–subsurface water interactions (Fig. 1). Based on a non-exhaustive overview of recent advances, we identify key scientific challenges and their relation to the heterogeneous and dynamic nature of the subsurface for each of the abovementioned processes. We then highlight some recent breakthroughs which allowed to advance our understanding of these processes. We also discuss the feasibility, advances, and challenges of numerical modeling of the identified processes in terms of 4D complexity. We finally highlight the central role of instrumented field observatories and corresponding case studies to tackle the scientific challenges and evaluate the performance and scope of recent innovations.

2 Key processes in hydrogeology and their 4D nature

In this section, we highlight hydrogeological processes for which the considerations of coupled spatial heterogeneity and temporal dynamics are important, present the main challenges related to the representation and inference of spatial and temporal variability, and point towards a few recent innovations that could help to address these challenges in the future (Fig. 1).

2.1 Groundwater fluxes

Inferring and modeling groundwater Darcy fluxes and fluid velocities is crucial in most hydrogeological processes and related applications, both for water quantity (e.g., water storage, groundwater discharge, transit time distribution) and quality (e.g., contaminant transport, reaction and mixing processes, see also Sect. 2.3) purposes (Fig. 1). Pore-scale advection flow, along with the other transport processes and the influence of the macro-scale geological heterogeneity, controls propagation and spreading of natural or contaminant solutes, from fast transfers to late time tailings (e.g., Dentz et al., 2011; Hoffmann et al., 2020; Table 2E2; Kang et al., 2015). In the context of risk assessment, measuring natural solutes or contaminant concentrations may be of limited value if not supported by quantitative flux rates allowing to estimate solute mass transfers (Brouyère et al., 2008). Groundwater fluxes drive mixing processes prevailing at aquifer interfaces such as subsurface–surface interactions in hyporheic zones (see also Sect. 2.4) or transition zones along coastal saltwater intrusion (e.g., Werner et al., 2013; Hester et al., 2017; Nogueira et al., 2019). They also influence hydrogeochemical and biogeochemical reactions by transporting reactants, such as nutrients, to these interfaces. They impact the feasibility of storage applications, including the injection and recovery of heat or CO₂ in the subsurface (Niemi et al., 2017; Fleuchaus et al., 2018), and control transit times distributions across watersheds (Goderniaux et al., 2013).

Table 2 Selection of datasets available online for multidimensional hydrogeological system characterization and monitoring. Datasets were selected based on their online availability, their link with a dynamic component of the subsurface, and their relevance for illustrating the paper. This table will be available online at https://hplus.ore.fr/en/database/4d-hydrogeology-dataset (last access: 15 August 2022), with the possibility to contribute to enrich the datasets with new data.

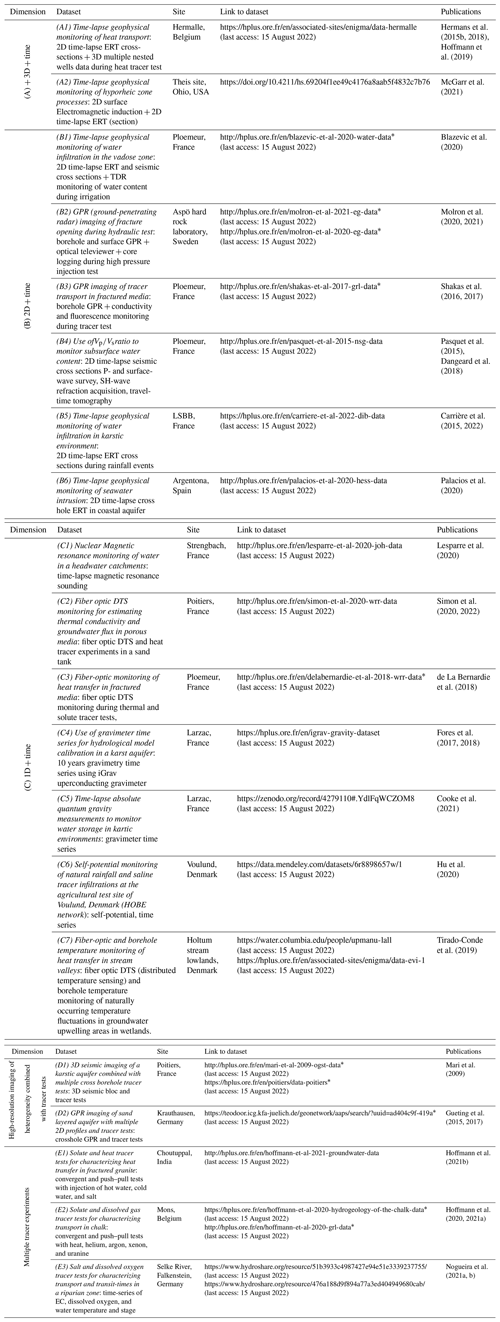
^* with login and password provided upon request.

The range of variation of expected groundwater fluxes may be very large, making them difficult to image, with their spatial and temporal variation. For decades, the basic approach consisted in first measuring the hydraulic conductivity and then predict fluxes, based on the hydraulic gradient. This approach however presents the serious disadvantage to average local variations and offers a limited understanding of the groundwater flux spatial distribution in heterogeneous media (Palmer, 1993; Brouyère et al., 2008; Jamin et al., 2015). In addition, many subsurface processes are time-dependent and exhibit an inherent periodicity. If deep systems are not expected to vary rapidly, shallow aquifers can exhibit fluctuations ranging from lower (e.g., multi-annual or seasonal recharge fluctuations) to higher frequencies (e.g., tide-dependent saltwater intrusion, aquifer exploitation or artificial storage applications, reaction to rainfall). The accurate quantification of groundwater flux rates including their spatial distribution and transient conditions is therefore needed to understand and manage these processes. This should be performed at the relevant scale(s), with the appropriate resolution, in adequation with the objectives of the study and the geological context (Jiménez-Martínez et al., 2013).

Recent research efforts have focused on the development of direct or indirect methods allowing for a more accurate assessment of groundwater fluxes, including their amplitude, spatial distribution, and temporal dynamics, with applications in highly heterogeneous media. Specific approaches, based on thermal methods for instance, have been developed for certain contexts, such as surface–subsurface interactions (Sect. 2.4), while approaches based on solute transport (e.g., tracer experiments), are allowing only indirect quantification of the fluxes (Popp et al., 2021, see Sect. 2.2). Other techniques are more general and available to directly and accurately measure local groundwater fluxes (e.g., Jamin et al., 2015; Le Borgne et al., 2006; Brouyère et al., 2008; Burnett et al., 2006). For instance, point measurements of Darcy fluxes are classically done from dilution methods (Drost et al., 1968; Klotz et al., 1980; Pitrak et al., 2007; Novakowski et al., 2006; Jamin et al., 2015). Well-points velocity probes have also been recently developed (Labaky et al., 2009; Devlin, 2020) to provide promising and complementary velocity measurements, although ranges of measurements are still limited. A key aspect of some recent approaches is to allow the monitoring of groundwater fluxes dynamics (Jamin and Brouyère, 2018).

Important challenges, also depending on the media type, however remain. The number of available methods for direct measurement is limited and most methods are suited for porous media rather than fractured aquifers where fluxes are expected to show stronger spatial variations (Pouladi et al., 2021). Current methods are still deficient in providing high-resolution 3D datasets, as they must be performed in wells. Current geophysical imaging techniques are still unable to directly estimate fluxes, as they are mostly based on the contrast in water properties induced through tracers or natural concentration variations (e.g., Robert et al., 2012; Paepen et al., 2022). Nevertheless, very promising results were obtained combining ambient noise surface wave tomography and self-potential (SP) measurements to image the hydrogeological structure and associated groundwater flow paths (Grobbe et al., 2021). Despite these improvements, monitoring the dynamics of fluxes remains resource expensive. Accurate measurements, which often imply complex experimental needs and designs, must be repeated regularly, with an adequate time resolution, for example to understand cyclic process evolution. Passive flux methods (e.g., Hatfield et al., 2004) integrate flux measurements over specific periods, providing mean representative value while avoiding repetitive field operations, but do not capture the dynamics.

Fiber optic distributed temperature sensing (DTS) allows for the measurement of temperature with high spatial and temporal resolution over large distances from a few meters up to several kilometers, using buried or borehole cables (Selker et al., 2006; Bense et al., 2016; Simon et al., 2020, see Table 2C2). By estimating the rates of temperature change along the cable, this kind of system allows an indirect estimation of groundwater fluxes intercepting the cable, provided that conditions are changing fast enough and that the temperature change is large enough to be detected (Read et al., 2013). Long-term changes can also be detected by using DTS systems as permanent monitoring tools (Susanto et al., 2017; McCobb et al., 2018). A new generation of active fiber optics with heated cables designed for hydrogeological investigations is currently being developed and is a promising approach for inferring borehole or in situ groundwater fluxes (Read et al., 2014; des Tombes et al., 2019; Maldaner et al., 2019; Simon et al., 2021; Del Val et al., 2021). The thermal response during the active heating of the cable and the subsequent cooling period is monitored, as it depends strongly on the water fluxes intercepting the cable, allowing an accurate groundwater flux assessment (Simon et al., 2021). Although challenges still remain to deploy such setups on the field, possible DTS applications extend to various domains, including 3D hydraulic tomography (Pouladi et al., 2021) or groundwater–surface water interactions (see Sect. 2.4).

In summary, the development of innovative in situ methods to characterize the spatial and temporal variability of groundwater flow opens a range of new opportunities for understanding, modeling, and monitoring hydrogeological systems. These advances may provide much more accurate estimation of subsurface velocity statistics in space and time in a highly instrumented site to establish upscaled transport models, for porous and fracture media, at the decameter scale that capture these dynamics (see next section and Table 1A and Fig. 8). In critical applications such as subsurface energy (thermal affected zone, induced seismicity related to fluid injection) or waste storage, these novel methods will likely be increasingly used to reduce the risks involved (Table 1B and Fig. 8). Finally, in more standard hydrogeological applications, such as water balance studies, aquifer recharge, or average residence time estimation, such a level of characterization is generally not required (Table 1C and Fig. 8).

2.2 Transport, mixing, and reaction

Three-dimensional heterogeneity and temporal fluctuations of fluxes have a first-order impact on transport and reaction processes (e.g., Dentz et al., 2011; Rolle and Le Borgne, 2019; Valocchi et al., 2019, Fig. 1). The inherent heterogeneity of subsurface environments leads to dispersion dynamics, which do not follow the conventional macrodispersion framework based on Fickian dispersion (e.g., Berkowitz et al., 2006; Neuman and Tartakovsky, 2009). Furthermore, mixing rates in 3D systems can be fundamentally different than predicted from 2D or steady representations of the subsurface (Lester et al., 2013). At the pore scale, recent 3D imaging techniques (Fig. 2) have shown that 3D flow topologies driven by pore-scale flow patterns lead to chaotic flows that strongly enhance mixing rates (Heyman et al., 2020; Souzy et al., 2020). At the Darcy scale, anisotropic permeability fields can generate helical flow that play a similar role (Ye et al., 2015). In fractured media, intersection of fractures with fluids of different chemical compositions can create microbial hot spots with intermittent activity (Bochet et al., 2020). In coastal aquifers, mixing between freshwater and saline water trigger reactions, including rock dissolution that leads to increased permeability and karst formation, which develop as hot spots due to medium heterogeneity (De Vriendt et al., 2020). Modeling and laboratory investigations have shown that these transport and reaction rates can be further altered by temporal fluctuations in head levels (Pool and Dentz, 2018) and variable water content (Jiménez-Martínez et al., 2017). Modeling studies have provided evidence that heterogeneity and temporal fluctuations can exert a strong control on biogeochemical reaction rates (Li et al., 2010; Sanz-Prat et al., 2016). However, there is increasing evidence that reactive transport processes are not well captured by the macrodispersion framework (Gramling et al., 2002; de Anna et al., 2014). Yet, in the absence of an alternative upscaling framework, it is still the main reference for field applications.

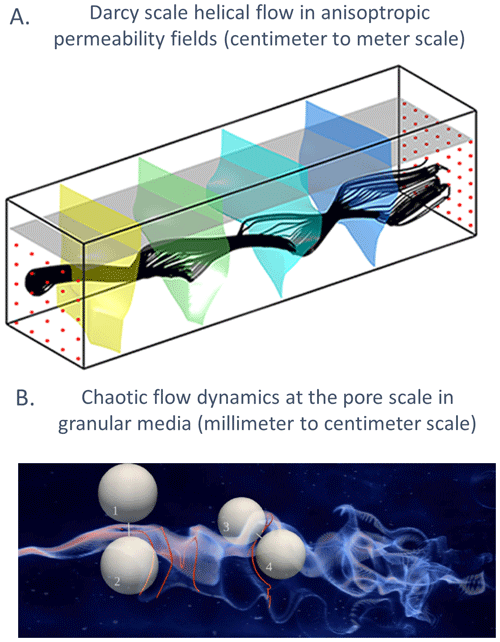
Figure 2 (a) Experimental evidence of helical flow at Darcy scale (top, modified from Ye et al., 2015): the black lines show simulated streamlines, the colored surfaces iso-pressure surfaces, and the red dots are experimental sampling points. (b) Experimental evidence of chaotic mixing at the pore scale in 3D porous media (bottom, modified from Heyman et al., 2020): the color field shows the concentration of a continuously injected fluorescent dye, the red line is the intersection of the plume with a 2D plane transverse to the mean flow, which shows the stretching and folding patterns that produce chaotic mixing, and the gray spheres represent selected grains in the bead pack that create the first successive folding of the plume.

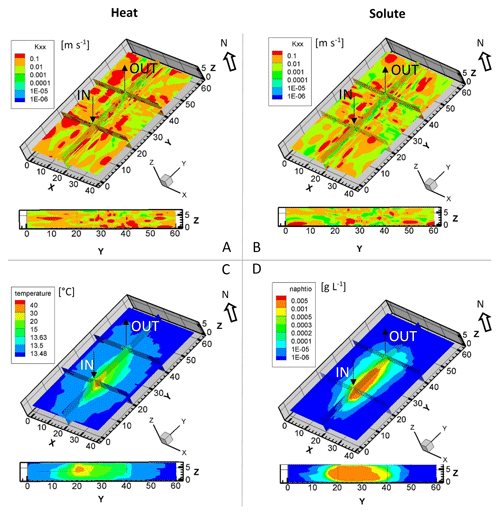
Figure 3 Hydraulic conductivity fields (a, b) and related simulations (c, d) obtained by inversion of temperature (a–c) and solute tracer concentration data (b–d) from heat and solute tracer experiments (modified from Hoffmann et al., 2019, Table 2A1).

Characterizing and imaging transport and reaction dynamics in the field is a critical challenge for a range of fundamental and applied questions, such as designing efficient remediation strategies for contaminated sites (Kitanidis and McCarty, 2012) or characterizing transport and reaction dynamics in mixing zones (Rolle and Le Borgne, 2019). Reactive hot spots that concentrate a disproportionate amount of reaction relative to their size tend to develop at the interfaces between surface and subsurface compartments (McClain et al., 2003), which include the vadose zone (Jiménez-Martiínez et al., 2017, see Sect. 2.3), the hyporheic zone (Hester et al., 2017; Nogueira et al., 2022, see Sect. 2.4), or the groundwater–seawater interface (Pool and Dentz, 2018; Duque et al., 2019).

Classical artificial tracer tests are commonly used to estimate solute transport properties and related parameters. Their use in highly heterogeneous media is, however, challenging due to the difficulty of positioning a limited amount of recovering points leading to low mass recovery (Kemna et al., 2002; Sanford et al., 2006). When interpreting or inverting tracer breakthrough data, with little information on the spatial heterogeneity, the range of possible interpretation in terms of parameter values can be quite large or misleading (e.g., Hoffmann et al., 2019, Table 2A1). Combining tracer test recovery with other monitoring methods, such as geophysics (e.g., Robert et al., 2012; Hermans et al., 2015b, Table 2A1) and model inversion, provides complementary information that can narrow down the uncertainty in the interpretation. Combining multiple tracers (Klepikova et al., 2016; Hoffmann et al., 2019, 2021a, b, Fig. 3, Table 2A1, and E) or tracers with flux measurements such as seepage meters (Tirado-Conde et al., 2019, Table 2C7; Duque et al., 2019) can also provide more constraints on tracer test interpretation, exchanges fluxes estimation, or heterogeneity. DTS fiber optics techniques provide the opportunity for spatial monitoring of thermal tracers (de La Bernardie et al., 2018; Klepikova et al., 2016, see also Sect. 2.1 and Tables 2C3 and 1C7). The combination of tracer experiments under different configurations (convergent, push pull, etc.) provides new constraints on transport models, providing the opportunity to capture the effect of complex 3D fracture networks architectures in effective transport models (Kang et al., 2015; Guihéneuf et al., 2017).

New mobile mass spectrometers have opened up new opportunities to use dissolved gas as tracers and measure them continuously in the field (Brennwald et al., 2016; Chatton et al., 2017; Popp et al., 2021). Dissolved gases, such as helium, argon and xenon, are conservative tracers with larger diffusivity compared to solute tracers, thus allowing the exploration of diffusive processes such as fracture–matrix or mobile–immobile water interactions (Hoffmann et al., 2020, Table 2E2). Reactive tracers have offered new methods for characterizing transport dynamics, including hyporheic exchange (Knapp et al., 2017, see also Sect. 2.4).

The use of time-lapse geophysical techniques provides a promising avenue to characterize the spatial distribution and temporal evolution of transport and reaction processes, at scale up to a few hundred meters (e.g., Binley et al., 2015, Table 2). Extensive geophysical imaging of transport processes has mainly been performed using electrical resistivity tomography (ERT) and ground-penetrating radar (GPR), even if immediate successes have often been hampered by issues of mass recovery due to unresolved concentration gradients (Slater et al., 2002; Singha and Gorelick, 2005; Müller et al., 2010; Doetsch et al., 2012; Dorn et al., 2012b; Fernandez-Visentini et al., 2020). A major challenge is thus to upscale the non-stationary and non-ergodic solute concentration fields as well as the macroscopic heterogeneity unresolved by geophysics (Gueting et al., 2015, 2017, Table 2D2) to derive relevant petrophysical relationships. Accounting for realistic heterogeneity patterns in inversion remains difficult (both flow and transport) and upscaling is not straightforward (Singha et al., 2015). In smoothness-constrained tomography inversion, there is usually underprediction of magnitudes and overprediction of target sizes (Day-Lewis et al., 2006). Overcoming this challenge requires advanced hydrogeophysical imaging (e.g., Hermans et al., 2016b, 2018; Oware et al., 2019), adapted regularization consistent with the studied process (e.g., Karaoulis et al., 2014; Hermans et al., 2016a; Nguyen et al., 2016; Lopez-Alvis et al., 2021), geostatistical post-processing (Moysey et al., 2005; Nussbaumer et al., 2019), or coupled inversion (e.g., Hinnel et al., 2010). Recent modeling results suggest that key geostatisical properties of permeability fields may be inferred from time-lapse ERT imaging (Fernandez Visentini et al., 2020). New geophysically sensitive tracers, allowing density matching with the resident fluid (Shakas et al., 2017, Table 2B3), provide images of tracer pathways that are not influenced by density effects. Theoretical work has suggested that tracers that change their electrical conductivity when reacting could be imaged by electrical methods, providing new opportunities to characterize mixing processes in situ (Ghosh et al., 2018). This idea remains to be tested in the laboratory and field.

Geophysical techniques that have the potential to map and monitor reactive processes, such as spectral induced polarization (SIP), which consists of measuring the phase shift of an alternating electrical signal occurring because of polarization phenomena in the electrical double layer, by mineral precipitation (Leroy et al., 2017) or by the activity of microorganisms (Kessouri et al., 2019), are highly sensitive to pore-scale processes and concentration distributions (Izumoto et al., 2020, 2022). This makes their interpretation challenging but potentially very rewarding. The coupling of geophysical techniques with pore-scale imaging techniques, including micro and millifluidics (Jougnot et al., 2018; Fernandez Visentini et al., 2021; Izumoto et al., 2022) and X-ray computed tomography (Johansson et al., 2019), represents a new avenue of research to understand and quantify the geophysical signature of unresolved pore-scale processes. Geophysical methods are thus increasingly used for mapping biogeochemical processes (Atekwana and Slater, 2009; Knight et al., 2010). Self-potential (SP) signals are sensitive to redox conditions in contaminated groundwater (Naudet et al., 2003; Revil et al., 2009; Arora et al., 2007). Laboratory studies have shown the correlation between SIP and bacteria activity using column experiments (Davis et al., 2006; Abdel Aal et al., 2010; Zhang et al., 2014), and the SIP method has been applied to detect biogeochemical reactions or root activities in the field (Wainwright et al., 2016; Flores Orozco et al., 2012; Ehosioke et al., 2020). However, current interpretations are largely qualitative or empirical through correlation. It remains challenging to mechanistically relate the SIP signal to biological and physiological processes or simply to the biomass itself. For many applications, the underlying mechanisms of the observed polarization are still the subject of active research and debate (see e.g., Leroy et al., 2017; Ehosioke et al., 2020), while field applications remain limited (Flores Orozco et al., 2021).

The coupling of heterogeneity, transport, and reaction often leads to scale effects influencing effective reactive transport parameters (Dentz et al., 2011; Salehikhoo et al., 2013), leading to a major upscaling challenge in transport characterization and reactive transport modeling at the catchment scale (Li et al., 2017). Improved time and space resolution of geophysical and inversion techniques, and the development of systems capable of surveying large areas repeatedly with multiple hydrogeophysical methods, open new perspectives for mapping and monitoring these dynamics in the field (Folch et al., 2020; Palacios et al., 2020, Table 2B6). As discussed above, hydrogeophysical imaging of transport and reaction processes is very attractive, but it requires upscaling the effects of sub-scale transport dynamics to the scales resolved by geophysical techniques (Fernandez Visentini et al., 2020). Processes occurring at unresolved scales require imaging by combining multiple methods across scales, different tracers, and use of integrating data with geostatistics, modeling, and inversion (Linde and Doetsch, 2016). Similar challenges occur when imaging the water content distribution in the vadose zone, as discussed in Sect. 2.3.

In summary, there is increasing evidence that conventional monitoring techniques and models are not able to capture the 3D heterogeneity and temporal fluctuations controlling transport and reaction processes. Four-dimensional imaging of transport and reaction at laboratory and field scale is critical to define new effective models able to upscale these dynamics and predict them in less instrumented sites (Table 1A and Fig. 8). Furthermore, recent advances in 4D imaging discussed here will open new opportunities for monitoring the fate of contaminants when risk management requires it (e.g., contamination remediation and monitoring, nuclear waste storage, Table 1B and Fig. 8). Current monitoring techniques and models may be sufficient only in applications where accurate predictions of transport dynamics are less critical (Table 1C and Fig. 8).

2.3 Water content dynamics in the vadose zone

The vadose or unsaturated zone is the upper part of the critical zone. The distribution of fluid phases and their evolution with time makes it a very complex media, where root systems and soil micro-organisms further complexify this dynamic environment (Fig. 1). Understanding, monitoring, and predicting the quantity (i.e., water content) and movement (i.e., water flow) of water are needed to address water quality and availability issues (e.g., Vereecken et al., 2015). Vadose zone hydrology usually relies on punctual measurements of physical variables with established sensors: TDR (time domain reflectometry, to infer the water content from dielectric permittivity) or tensiometers (to determine the matric potential). Vadose zone hydrology is still too often viewed by hydrogeologists as a vertical 1D transit compartment with homogeneous sources (rainwater infiltration) and sinks (evaporation or evapotranspiration) on the way to the aquifer. If such an approach might be sufficient to estimate average aquifer recharge rate, punctual measurements and 1D modeling approaches provide limited information for the characterization of this strongly 3D environment and its dynamics; thus it is not sufficient for applications such as precision agriculture. The varying water content (in time and space) and biological interactions (e.g., with the roots) are adding a layer of complexity compared to the saturated zone, making its spatial and dynamical characterization even more challenging.

While geophysical methods can provide fast and integrated measurements to characterize the spatial heterogeneity of the vadose zone and imaging the water content distribution (within the limitation of their resolution, e.g., Day-Lewis et al., 2005), the quantifications of dynamic processes related to water flow and (reactive) transport still remain an important challenge.

In vadose zone hydrogeophysics, the most promising approaches to tackle these challenges rely on using multiple methods and integrating the measured data in 4D numerical simulations with joint inversion strategies together with appropriate petrophysical knowledge (e.g., Hubbard and Linde, 2011, Table 2). Surface-based and cross-borehole imaging of the water content in the vadose zone through measurements of the electrical conductivity or dielectric permittivity distribution is well established (e.g., Carrière et al., 2015, 2022, Table 2B5). The electrical conductivity can be obtained using low-frequency electrical and electromagnetic methods such as electrical resistivity tomography and induced polarization (e.g., Kemna et al., 2012; Revil et al., 2012). Higher frequency methods such as the time domain or frequency domain electromagnetics can also be employed from the surface (e.g., Pellerin, 2002) or the air (Auken et al., 2020), allowing to cover large areas in a limited amount of time, but show generally a poor vertical resolution at the scale of the vadose zone. Electrical and electromagnetic methods are well established in static conditions but also in monitoring applications (e.g., Singha et al., 2015). The main limitation of these methods is the limited resolution that masks heterogeneities and can mislead quantitative estimation of water content or solute concentration using petrophysical relationships established in the laboratory (Day-Lewis et al., 2005; Jougnot et al., 2018), as already discussed in Sect. 2.2. Combining several methods (e.g., Blazevic et al., 2020, Table 2B1) and improving the petrophysical-based approaches (e.g., Day-Lewis et al., 2017a) is needed to move towards a more quantitative use of electrical and electromagnetic methods.

Ground-penetrating radar (GPR) is the most developed geophysical method to obtain the water content at high spatio-temporal resolution through the dielectric permittivity (e.g., Huisman et al., 2003; Roth et al., 1990; Klotzsche et al., 2018; Looms et al., 2008). Time-lapse studies using GPR to monitor water infiltration can provide insights about the hydrodynamic (e.g., Léger et al., 2014; Klotzsche et al., 2019a) and transport properties (e.g., Haarder et al., 2015) of the vadose zone, and reveal the 3D nature of flow processes, including lateral flow (Scholer et al., 2012).

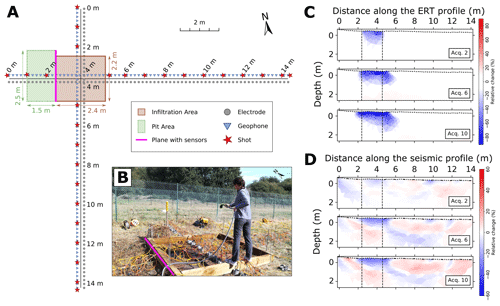
Figure 4 (a) Acquisition setup used by Blazevic et al. (2020) to jointly monitor the infiltration of water with ERT and seismic lines cross in the infiltration area. (b) Picture of the infiltration test, above a pit instrumented with TDR. Temporal evolution of relative change in properties inferred from (c) the ERT and (d) the seismic data along the North–South profile at different times (i.e., successive acquisitions) during the infiltration, respectively (modified after Blazevic et al., 2020, Table 2B1). One can see the preferential water flow from North to South, indicating lateral flow in the vadose zone.

Nuclear magnetic resonance (NMR) is sensitive to the quantity of water in the subsurface. It is based on the resonance of the magnetic moment of the protons from water molecules. NMR can be used from the surface or boreholes to infer the water content in the vadose zone (e.g., Schmidt and Rempe, 2020). Recent works have also shown its value for monitoring the water dynamics through time-lapse measurements (e.g., Mazzilli et al., 2020; Lesparre et al., 2020, Table 2C1).

From established P-wave velocity tomography (e.g., Bradford, 2002) to more recent imaging of surface wave velocities and Poisson ratios (e.g., Pasquet et al., 2015, Table 2B4), active seismic methods are developing toward a much more quantitative characterization of the water content distribution (e.g., Pride, 2005). Surface waves appear promising for monitoring of water content dynamics (Dangeard et al., 2018, Table 2B4), and combining time-lapse imaging of seismic tomography and ERT will allow providing a more quantitative imaging (Blazevic et al., 2020, Fig. 4 Table 2B1). This use of complementary methods, in terms of resolution and sensitivity to properties (electrical conductivity and mechanical properties), opens up new perspective such as joint inversion (e.g., Doetsch et al., 2010) and petrophysical-based inversion (e.g., Wagner et al., 2019). Passive seismic is also receiving increasing attention, as ambient noise can be used as a source to monitor hydrosystems. Recent works on seismic noise monitoring have been conducted using ballistic waves to monitor water table variations (Garambois et al., 2019). The development of distributed acoustic sensing will allow the acquisition of denser and larger-scale monitoring data in this direction (e.g., Zhan, 2020).

Another passive method that is increasingly used in the vadose zone is the self-potential method (e.g., Revil and Jardani, 2013). It consists of measuring naturally occurring electrical voltages that result from various coupling mechanisms, for instance, electrokinetic coupling when water flows in a porous medium or in a fractured system (e.g., Jougnot et al., 2020; Robert et al., 2011). A promising approach is to implant the SP electrodes in the ground at different locations and depths, and the measured signal is then integrated over the volume delimited by the electrodes, allowing vertical and lateral monitoring. Recent works of SP monitoring have shown the usefulness of SP to monitor infiltration (Jougnot et al., 2015; Hu et al., 2020, see Table 2C6) and root water uptake (Voytek et al., 2019). These works have shown the need for further improving petrophysical models to shift the use of SP towards a more quantitative paradigm.

Lastly, gravity is a well-established passive geophysical method that is suitable to monitor water movement (Fores et al., 2017, 2018, Table 2C4). Due to its very large footprint that integrates the density distribution from the center of the Earth, there is a crucial need for more accurate and sensitive gravimeters, e.g., quantum absolute gravimeters (Cooke et al., 2021, Table 2C5). The non-uniqueness of gravity signals requires the inclusion of complementary information (e.g., geodetic or hydrological data) for signal separation. Time-lapse gravimetry has been used to identify and constrain subsurface water storage changes, e.g., in artificial recharge facilities (Kennedy et al., 2016), to separate precipitation and groundwater mass signals (Delobbe et al., 2019), to locate karst storage dynamics (Pivetta et al., 2021), and identify evapotranspiration patterns (Carrière et al., 2022). Time-lapse gravity data have also been successfully used to improve the calibration of groundwater models (Christiansen et al., 2011a, b). Further data acquisition procedures and treatments that enhance sensitivity to local processes (e.g., gravity gradients and hydrological modeling coupled with gravity measurements; Cooke et al., 2020, Table 2C5) are needed to provide more quantitative interpretations.

In summary, the 3D nature of the subsurface is made even more complex in the vadose zone by its partial saturation and the evolution of the water phase, both in terms of saturation and spatial distribution, as well as by the presence of root systems and microorganisms. Detailed studies of processes in the vadose zone at highly instrumented sites open new opportunities for the quantification of transport and reaction processes from lab to field scales (Table 1A and Fig. 8). At a more intermediate scale, 4D imaging unveils preferential flow paths for infiltration or contaminant transport processes and water availability for plants through their root system, allowing to optimize irrigation systems (Table 1B and Fig. 8). At a much larger scale, such precise imaging is rendered impossible due to the subsurface complexity, in which case simple 1D hypothesis can lead to quantitatively reliable results (e.g., for quantitative assessment of mass balance or aquifer recharge, Table 1C and Fig. 8).

2.4 Groundwater–surface water interactions

The interface between groundwater (GW) and surface water (SW) is a structurally complex, dynamic transition zone that modulates fluxes of water, solutes, and heat between the two adjoining compartments (Lewandowski et al., 2019, Fig. 1). These fluxes in turn affect several processes that are relevant for the management of water quantity (e.g., water supply via bank filtration, groundwater recharge), quality (e.g., pollutant attenuation, nutrient transformations – eutrophication), and aquatic ecology (e.g., environmental flows, habitat, and refugia) (Fig. 5).

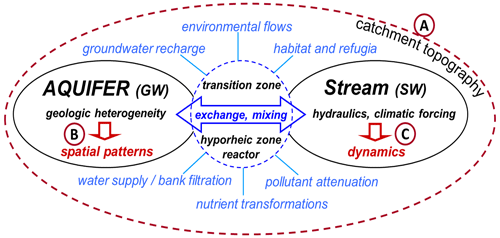
Figure 5 Conceptual depiction of the GW–SW interface and the nested controls of spatio-temporal patterns of exchange and solute turnover in the transition zone between GW and SW (using a river–aquifer system as an example). (a) Primary spatial controls defined by regional topography and geology, (b) secondary spatial controls defined by local aquifer and stream bed geologic heterogeneities as well as streambed morphology, and (c) temporal controls caused by river flow dynamics. Processes and management aspects that are affected by these exchange and turnover patterns are shown in light blue.

Exchange and turnover patterns in the GW–SW transition zone are defined by nested spatial controls ranging from regional topography and geology (Winter, 1999) to local variability of streambed permeability (Kalbus et al., 2009; Irvine et al., 2012; Tang et al., 2017) and morphology evolution (Trauth et al. 2015; Partington et al., 2017), the spatial arrangement of subsurface hydrofacies (Fleckenstein et al., 2006; Frei et al., 2009; Carlier et al., 2018), and their anisotropy (Gianni et al., 2018) and reactive zones (Frei et al., 2012; Loschko et al., 2016). Temporal dynamics are mainly imposed by the surface water system (Dudley-Southern and Binley, 2015; Trauth and Fleckenstein, 2017; Song et al., 2020), as SW heads can change significantly over short – event – timescales, while head changes in GW occur more gradually (e.g., at seasonal timescales). The resulting fluctuations in hydraulic gradients affect subsurface mixing (Hester et al., 2017; Bandopadhyay et al., 2018; Nogueira et al., 2022) as well as transit times and reactive turnover (Zarnetske et al., 2012; Trauth and Fleckenstein, 2017).

While a sufficient, mechanistic understanding of the links and feedbacks between flow and turnover processes at small spatial and temporal scales will clearly be needed for a sound management of water quality and ecosystem services in coupled GW–SW systems (Hester and Gooseff, 2010; Morén et al., 2017; Hester et al., 2018), the same level of process detail may not be required to evaluate conjunctive use of GW and SW for the management of larger-scale water quantity (Scanlon et al., 2016). In other words, the level of detail needed will also depend on the scale of the problem and the questions asked.

Recent years have seen significant advances in methods and technologies for the small-scale characterization and simulation of coupled GW–SW systems. Methods particularly suited for the study of GW–SW interactions, to name a few, include in situ and high-resolution sensing of temperatures (Constantz, 2008; Vogt et al., 2010) and solute concentrations (Blaen et al., 2016; Brandt et al., 2017), tracer techniques to characterize exchange flows (Mallard et al., 2014; Schilling et al., 2017a; Popp et al., 2021), transit times, and reactions (Schmidt et al., 2012; Knapp and Cirpka, 2017), and process-based, integrated modeling of coupled GW–SW systems (Schilling et al., 2017b; Trauth and Fleckenstein, 2017; Broecker et al., 2019; Nogueira et al., 2021b, Table 2E3) and geophysics (McGarr et al., 2021, Table 2A2). Here, we briefly discuss some key research fields related to the heterogeneous and dynamical nature of GW–SW systems, which have and likely will continue to contribute to an improved understanding of GW–SW interactions.

The use of heat as a natural tracer has become a popular tool to characterize GW–SW exchange patterns due to the natural temperature differences between GW and SW and the relative ease and accuracy of temperature measurements using standard sensors. This field has evolved significantly since some of the earlier seminal works (Stonestrom and Constantz, 2003; Schmidt et al., 2006) and has embraced novel technologies such as DTS (Krause et al., 2012; Rose et al., 2013) and hand-held (Glaser et al., 2016; Marruedo Arricibita et al., 2018) or airborne infrared imagery (Lewandowski et al., 2013). The suite of methods available today allows for high-resolution assessment of temperatures in space and time for a qualitative mapping of GW–SW exchange patterns (Anibas et al., 2011; Krause et al., 2012) or a quantification of exchange fluxes (Schornberg et al., 2010; Munz and Schmidt, 2017). Temperature data can constrain and improve numerical models of coupled GW–SW systems (Munz et al., 2017). Due to their relative ease of use, heat-based methods have become a robust and standard tool to characterize GW–SW exchange patterns. New opportunities may arise from a smart combination of different techniques (Tirado-Conde et al., 2019, Table 2C7) or the use of actively heated fiber optics (Simon et al., 2021), a technique (see also Sect. 2.1) that has been used punctually to quantify streambed flow dynamics in zones of groundwater upwelling (Briggs et al., 2016) and which is in current development for quantifying GW–SW exchange patterns along stream sections (Simon et al., 2022, Table 2C2).

The concentration of oxygen is a key variable that defines the redox state of the transition zone between GW and SW and with that the potential for important reactions like denitrification (Zarnetske et al., 2012). Understanding the dynamics of oxygen consumption is therefore important for evaluating nutrient turnover in hyporheic and riparian zones (Marzadri et al., 2012; Trauth et al., 2015, 2018). A key reaction consuming oxygen in these zones is aerobic respiration, which has been shown to depend on transit times (Zarnetzke et al., 2011a; Diem et al., 2014) and the availability of labile organic carbon as the main electron donor (Zarnetske et al., 2011b). Field deployable optode-based oxygen sensors have enabled high-resolution measurements of oxygen concentrations in time (Diem et al., 2014; Vieweg et al., 2016) and space (Brandt et al., 2017), allowing for robust assessments of respiration dynamics at the GW–SW interface (Vieweg et al., 2016). Based on such data, the strong temperature dependence of aerobic respiration rates has been demonstrated (Diem et al., 2014), which may dominate turnover rates compared to the effects of variable transit times (Nogueira et al., 2021a, Table 2E3). Similar effects were found to affect complex spatio-temporal patterns of riparian denitrification, which seem to be jointly controlled by hydraulically-driven variability in exchange fluxes and transit times, supply of organic carbon as an electron donor from stream water and riparian sediments, and seasonal temperature variations (Trauth et al., 2018; Lutz et al., 2020; Nogueira et al., 2021b, Table 2E3). Besides high-resolution data sets of key variables like oxygen concentration, it is often the combination of these rich data sets with innovative methods for analysis and modeling (e.g., Diem et al., 2014; Lutz et al., 2020; Nogueira et al., 2021a, b, Table 2E3) that advances our mechanistic understanding of the processes and feedbacks that define the functionality of GW–SW interfaces.

Another promising and still evolving field in the area of GW–SW interactions has been the use of mechanistic models in explorative mode to test hypotheses and to investigate process interactions and feedbacks (Fleckenstein et al., 2010; Brunner et al., 2017). Important insights into physics of flow, transport, and turnover processes in the hyporheic zone (HZ) have been gained based on such modeling studies. This includes the effects of ambient groundwater flow on hyporheic exchange (Cardenas and Wilson, 2007; Trauth et al., 2013, 2015), intermeander and parafluvial flows (Boano et al., 2006), reactions and turnover in the HZ (Boano et al., 2010; Trauth et al., 2014, 2015), effects of geologic heterogeneity on hyporheic flows and reactions (Laube et al., 2018; Bardini et al., 2013), and the influence of stream flow dynamics on hyporheic exchange and turnover (Trauth and Fleckenstein, 2017; Singh et al., 2020). Similar modeling studies have been conducted for riparian zones and river corridors, addressing aspects such as the effects of streamflow variations on riparian solute turnover (Gu et al., 2012), effects of bank filtration processes on solute mobilization from riparian zones (Mahmood et al., 2019), the effects of riverbed heterogeneity on GW–SW exchange patterns (Tang et al., 2017), or the presence and dynamics of unsaturated conditions at the stream–aquifer interface (Schilling et al., 2017b). Some studies have also used modeling experiments to address mixing processes at GW–SW interfaces, which are important for mixing-dependent reactions (Hester et al., 2017). These studies have addressed effects of flow geometries and hydraulics on mixing in hyporheic and riparian zones (Bandopadhyay et al., 2018; Lee et al., 2021; Nogueira et al., 2022) or effects of geologic heterogeneity at the groundwater–seawater interface on calcite dissolution and karstification (De Vriendt et al., 2020), as discussed in more detail in Sect. 2.2. Advances in modeling capabilities, including a seamless, integral simulation of flow and reactive transport in GW–SW systems (Broeker et al., 2019; Li et al., 2020), together with rich data sets from highly instrumented field sites to test these models, will help to improve our mechanistic understanding of small-scale GW–SW interactions.

In summary, many functionalities of the GW–SW interface related to water quality (e.g., hyporheic attenuation of nutrients and pollutants) and aquatic ecology (provision of habitat and refugia for aquatic organisms) are clearly defined by small-scale processes operating in 4D and need to be characterized and evaluated accordingly. A suite of field methods and modeling tools exists to characterize the relevant process patterns and dynamics in sufficient detail to develop new conceptual ideas about system functioning or to advise solutions to site-specific problems (Table 1A and Fig. 8). Although the heterogeneity of the SW–GW interface leads to a large variability in the exchange fluxes at (deca)metric scale (e.g., Ghysels et al., 2021, Table 1B and Fig. 8), larger-scale assessments of GW–SW exchange for water quantity (e.g., conjunctive use scenarios) or base flow management (e.g., environmental flows) can often be achieved with much simpler, integral approaches (Table 1C and Fig. 8).

3 Numerical methods development for 4D data integration and inversion

Numerical representation methods and numerical techniques have become essential tools in both understanding and forecasting subsurface models (e.g., Karatzas, 2017). Most common software suites in hydrogeology allow to model the subsurface using properties distributed in 3D. The temporal derivatives being an essential component of underlying physical equations, the transient character of hydrogeological processes is most often already included. When a mathematical formulation of the process exists, numerical methods allow simulating the response to any scenarios as long as the distribution of the involved hydrogeological parameters is provided. Specific models can handle non-linearity related to time-varying properties as illustrated by coupled models for unsaturated flow or geomechanics (Šimůnek et al., 2018; Davy et al., 2018). However, next to accuracy related to solvers and their parameterization (numerical dispersion, instability, non-convergence), numerical models remain dependent on the accuracy of the underlying mathematical representation of the modeled process. Previous sections have highlighted that experimental work remains necessary to characterize complex processes such as mixing and transport or GW–SW interactions (Heyman et al., 2020).

Nevertheless, several challenges remain to properly simulate heterogeneous groundwater reservoirs and their dynamics with numerical models. A key aspect is to feed the models with the appropriate data input (e.g., Schilling et al., 2018). Subsurface processes are influenced by the heterogeneity in subsurface properties. If the latter is essential for the purpose of the model, this should be reflected in the data input through sufficiently dense spatially distributed data (e.g., Guillaume et al., 2019). Even with powerful computers, simulating the transient response of a catchment-scale model with limited resolution might still take several hours, days, or even weeks (e.g., Hayley et al., 2014). The same is true for high-resolution geophysical models such as full-waveform GPR or 3D electromagnetics (e.g., Oldenburg et al., 2013; Klotzsche et al., 2019b; Zhou et al., 2020; Haruzi et al., 2022) and coupled approaches (Coulon et al., 2021). Including geophysical data in hydrogeological models is thus even more challenging. Surrogate models can be used to speed up simulation processes, but their accuracy remains dependent on the training process, which can be problematic in highly heterogeneous media (Linde et al., 2017; Köpke et al., 2018; Mo et al., 2020). Small-scale heterogeneity is present in many geological contexts (e.g., Bayer et al., 2011). Even if it is relevant for the objective of the model, it must thus often be neglected due to limited computational resources. This sometimes leads to unrealistic outputs, in particular for transport processes (e.g., Hoffmann et al., 2019, Table 2A1). This may be addressed by upscaling heterogeneous systems and defining equivalent properties at larger scale, but this is very challenging for transport processes with multiple physical scales and non-equilibrium phenomena (Li et al., 2017; Icardi et al., 2019).

Even if simulating small-scale heterogeneity would become possible, the actual distribution of properties is always unknown. The limited amount of noise-contaminated data do not allow to unequivocally recover this distribution through inverse modeling (Zhou et al., 2014), even when distributed geophysical data are available (Hermans et al., 2015a; Mari et al., 2009, Table 2D1). On the one hand, deterministic approaches have to simplify the parameter estimation problem to make it well-posed (e.g., smoothing, zonation or pilot-points) and are therefore limited for tackling uncertainty related to 4D processes. On the other hand, stochastic approaches such as Markov Chain Monte Carlo (MCMC) methods (e.g., Vrugt et al., 2013), using more or less complex and realistic geostatistical representations of the heterogeneity and more or less wide prior distribution (Linde et al., 2015b), often require thousands to millions of simulations to converge, especially when spatial uncertainty is included (e.g., de Pasquale et al., 2019). The transient aspects are also commonly simplified, due to a lack of data or the simplification of boundary conditions. In most applications, numerically resolving a time-dependent system of partial derivative equations based on spatially distributed parameters in 3D with a high spatial and temporal resolution remains utopic. It is therefore of uttermost importance to understand which simplifying assumptions can be applied without degrading the predictive capability of the model (Schilling et al., 2018).

Fractured aquifers are even more complicated to model. Fracture networks have complex 3D geometries and are therefore difficult to characterize from mostly 1D or 2D data (Le Goc et al., 2017; Day-Lewis et al., 2017b). Modeling flow in fractures occurs at a smaller scale, which brings additional challenges in terms of gridding (Schädle et al., 2019) and inversion (Ringel et al., 2019). Combined with a higher degree of heterogeneity and uncertainty than in porous media, it increases the abovementioned issues preventing efficient modeling.

Nevertheless, recent advances shed light on some innovative solutions to tackle those problems. For fractured aquifers, recent studies in fracture modeling such as realistic flow characterization and mechanical coupling using discrete fracture networks (Davy et al., 2018; Maillot et al., 2016; Lei et al., 2017), innovative inverse methodologies (Pieraccini, 2020), and characterization techniques (Dorn et al., 2011, 2012a, 2013; Shakas and Linde, 2017; Molron et al., 2020, 2021, Table 2B2) pushed forward our ability to account for the complexity of fractured media. More generally, cloud computing combined with increasing computational power is one avenue to allow modeling the subsurface at a higher 4D resolution for an increasing number of applications in the future (Hayley, 2017; Kurtz et al., 2017). The ongoing efforts for coupling different simulators, both in hydrogeology and hydrogeophysics, will also favor the incorporation of larger, more informative data sets (e.g., Commer et al., 2020). The incorporation of geophysical data, especially at the large scale, has remained limited for a long time by the use of empirical and local petrophysical relationship (Rubin and Hubbard, 2005). The combination of large-scale airborne electromagnetic data combined with advanced machine learning approaches for their integration will likely contribute to the broader use of 3D and 4D data sets in hydrogeology accounting for the inherent uncertainty at that scale (e.g., Vilhelmsen et al., 2019; Gottschalk and Knight, 2022).

Although Bayesian methods such as MCMC are widely recognized in the scientific literature for inversion, prediction, and uncertainty quantification (Ferre, 2020), they have not been widely adopted by practitioners because of their computational burdens, especially for complex geometries. Recent developments in machine learning such as deep neural networks (DNNs) have shown that complex spatial patterns can be efficiently reduced to a manageable number of dimensions. DNNs allow to simplify complex subsurface models with millions of cells to a few tens of dimensions while maintaining their geometrical complexity represented by a prior parameter distribution. This opens the possibility to apply McMC or global optimization methods at a reasonable cost, as recently demonstrated by Laloy et al. (2018) and Lopez-Alvis et al. (2021) (see Fig. 6). Since the parameterization of the prior is a key to obtain realistic solutions, the identification of realistic geological scenarios through falsification techniques (e.g., Hermans et al., 2015a; Linde et al., 2015a; Lopez-Alvis et al., 2019) or assembled prior (Lopez-Alvis et al., 2022) can further improve stochastic inversion by reducing the range of the prior.

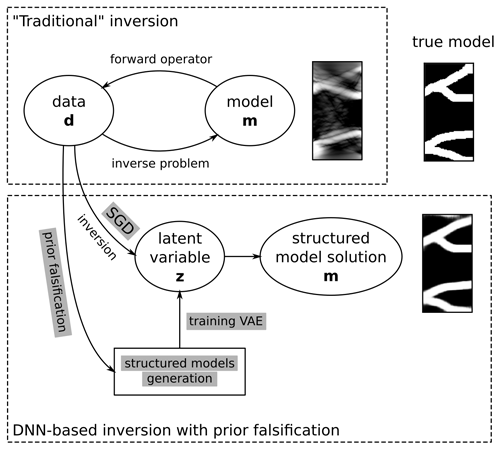
Figure 6 Adapted deep neural network-based (DNN) inversion scheme using a variational autoencoder (VAE) to represent complex geological structure in a latent space represented by sparse variable in which a stochastic gradient descent (SGD) can be applied to converge towards a more geologically realistic solution, modified from Lopez-Alvis et al. (2022).

Another recent innovation is to propose physically-based geostatistical upscaling, allowing to translate the small-scale spatial uncertainty at a larger scale (Benoit et al., 2021). Combining those recent advances with accurate fast approximations of the forward model (Linde et al., 2017) should allow for more accurate representations of spatial variability within affordable computational time. As an alternative, approximations of the inverse problems using ensemble Kalman generator (e.g., Nowak, 2009; Bobe et al., 2020; Tso et al., 2021) or normalization and linearization approaches (e.g., Holm-Jensen and Hansen, 2019) can also provide a relatively fast, though realistic, approximation of the solution to the inverse problem.

Alternatively, recent studies have proposed to investigate more prediction-oriented strategies to simulate complex hydrogeological systems (Sun and Sun, 2015; Ferre, 2017; Scheidt et al., 2018). For example, Bayesian Evidential Learning (BEL) proposes to use a set of simulations from realistic numerical models including the 4D complexity to learn a statistical relationship between a predictor (data set) and a target (model output, see Fig. 7), making it a model-driven machine learning approach, circumventing the challenges of non-linear inversion while providing a proxy for global sensitivity analysis (Hermans et al., 2018). The statistical learning requires reducing the dimensionality of the problem so that part of the complexity may remain unresolved (Park and Caers, 2020). If such a statistical relationship exists, this approach has the advantage to require only a limited amount of simulations to derive the posterior distribution of the prediction, typically only a few hundreds to a few thousands. The latter are independent and can be fully parallelized. Propagating noise in the statistical relationship is also straightforward (Hermans et al., 2016b). Such direct forecasting is possible because predictions often have a much lower dimensionality than models. The efficiency of such an approach makes it particularly interesting for experimental and optimum design studies under uncertainty (Thibaut et al., 2021, 2022). Nevertheless, when the data–prediction relationship is complex and highly non-linear, BEL might overestimate uncertainty (Michel et al., 2020), for instance when the prior uncertainty is large (Hermans et al., 2019). In such a case, classical inversion might still be needed (Scheidt et al., 2018). Recent advances have shown that BEL can also estimate the model parameter distributions and be used as a more traditional inversion technique (Yin et al., 2020; Michel et al., 2020). However, such more advanced applications require further development of appropriate tools to identify highly non-linear relationships (Park and Caers, 2020) which will inevitably come at a larger computational cost (Michel et al., 2023).

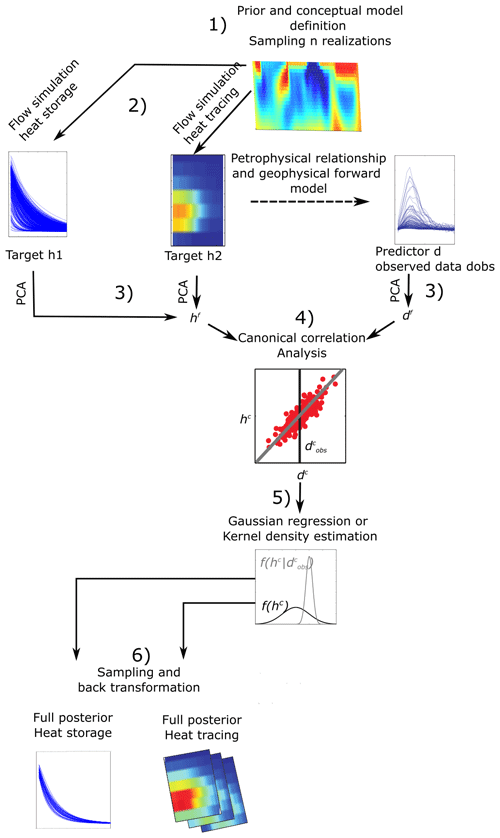
Figure 7 Framework of Bayesian Evidential Learning applied to the prediction of heat storage in an aquifer from a tracer experiment monitored by geophysics. (1) A prior model of the spatial heterogeneity is defined and sampled. (2) Both the predictor (data set such as a tracer experiment) and the target (prediction of heat storage) are simulated. For the predictor, a petrophysical transform is used to generate the corresponding geophysical data. (3) Dimension reduction techniques are applied to both data and prediction. (4) A statistical relationship between data and prediction is learned. (5) The posterior distribution of the prediction for field observed data is generated using the statistical relationship. (6) The posterior is back-transformed in the physical space (modified from Hermans et al., 2018).

Although these recent developments are promising solutions to integrate large 4D data sets within efficient simulation and inversion framework to forecast the behavior of aquifers, they still need to be more widely evaluated and used, including for complex field cases. New mechanistic models developed based on 4D data sets will need to be integrated in numerical models. The validation with case studies in different contexts will demonstrate if new inversion and prediction methods, including machine learning approaches, are adapted to the incorporation of the 4D complexity of hydrogeological processes. Synthetic numerical studies and global sensitivity analysis should help us to identify which simplifications can be reasonably made in applications at the large scale and/or with limited budget preventing the acquisition of dense data sets.

4 When is a coupled spatial and temporal characterization needed?

Although spatial heterogeneity and temporal variations by default influence all the processes occurring in the subsurface, a full 4D characterization coupled with a numerical model is not always necessary. Throughout the paper, we identified three levels of applications requiring a decreasing amount of resolution. Table 1 and Fig. 8 summarize and classify the different scales and processes according to their requirement for spatio-temporal monitoring, including 4D imaging.

Figure 8 Indicative temporal and spatial scales of some processes in hydrogeology for which accurate mechanistic models are still lacking (in reddish colors), for which 4D monitoring might be crucial (blueish and greenish colors), and for which 4D might be unnecessary (grayish colors), see also Table 1.

• A.

  Processes for which high-resolution space–time data are needed to improve mechanistic models. Previous sections have discussed how the acquisition of spatially and temporally distributed data is crucial for hydrological processes understanding. Observation gaps severely impede our ability to understand, model, and predict a series of critical subsurface processes (see Table 1A and Fig. 8). The acquisition of dense 4D data sets is needed to obtain new insights into internal mechanisms and process hierarchies, identify the dominant processes,which govern a specific response of the system, and ultimately develop upscaled models that capture these dynamics. High-resolution space–time data can thus help us to characterize the influence of heterogeneity and temporal dynamics, and thus understand and quantify how the small-scale processes must be upscaled to larger scales or to which level they can be simplified. This is crucial to develop new conceptual ideas about system functioning, to advise on solutions to site-specific problems, or to design accurate numerical models.

• B.

  Processes for which high-resolution space–time monitoring is desirable at the scale of individual sites. This is for example the case for precision agriculture for which knowing the spatio-temporal distribution of the soil moisture is a central element to implement efficient irrigation solutions or for site-risk management to avoid the spreading of contaminations. The oil industry has been aware of the importance of the spatio-temporal variations of their reservoirs for decades, and related research has been supported by economic interests. It has less been the case for hydrogeology, except for the characterization of storage site for nuclear waste or more recently induced seismicity related to geothermal exploitations. An increase in the number of applications include 4D investigations and monitoring is expected (see Table 1B and Fig. 8). Hydrology has been using remote sensing data for decades and a similar trend is now visible with airborne electromagnetic data in hydrogeology. This is a first step towards the generalization of the integration, to some extent, of 3D and 4D data in groundwater models, even at the catchment scale and beyond. A key challenge will be to determine which resolution and which sampling rate is necessary to properly account for the underlying subsurface complexity, which requires testing and validating these methods at highly instrumented observatories and sharing the produced space–time datasets.

• C.

  Processes for which 4D data may not be necessary. In some cases, the principle of parsimony applies and simple models can be calibrated explaining sparse data (see Table 1C and Fig. 8). For example, the management of water resources based on meteorological and production data using simple water balance approaches has been applied successfully in many contexts for decades. We may obtain reasonable estimates of groundwater volumes and fluxes from sparse hydrogeological data, so that a fine-scale characterization of the heterogeneity might not be needed or working in steady-state conditions might be sufficient. Estimating an average recharge rate for bypassing the complex processes occurring in the vadose zone has been proved to be efficient in many contexts.

In summary, although a few large-scale applications do not require a high level of spatial characterization and temporal monitoring, a large spectrum of processes are highly sensitive to 4D dynamics. We identify two complementary strategies to deal with this challenge. The first consists of developing upscaled models that capture the effect of spatial and temporal fluctuations. This requires first acquiring and sharing high-resolution space–time datasets at highly instrumented observatories (see Sect. 5). The second is to implement a site-specific 4D imaging strategy in critical applications that require it and have the corresponding budget. This requires as a first step to validate recent 4D imaging techniques in some dedicated observatories, where the degree of knowledge is sufficient to establish the relevant space–time resolution depending on the targeted process and application (see Sect. 5).

It is not evident to know a priori if 4D imaging is desirable. If a more systematic use of global sensitivity analysis and the multiplication of case studies should help the community to reveal when this is actually necessary, we also propose to consider some key elements when evaluating the need for a thorough spatio-temporal characterization of the reservoir at the three envisaged scales:

• Is there evidence for small-scale heterogeneity influencing the considered phenomenon?

• Are there any existing mechanistic models explaining the observed phenomena? Are these effective models in agreement with available observations at highly instrumented sites?

• Is there a technology available to monitor the desired 4D variations?

• Do transient phenomena have an influence on the results?

• Does the lack of data have an influence on the decision to ignore spatial heterogeneity or temporal variations?

• Is there evidence in the literature (e.g., global sensitivity analysis) that the processes at hand are not sensitive to the heterogeneity?

5 The need for highly instrumented and long-term hydrogeological observatories

Over the last decades, highly instrumented field sites have been equipped to explore, monitor, and model subsurface processes (e.g., Bogena et al., 2018). Long-term observations of subsurface environments, typically more than 10 years, are motivated by the broad range of responses and transit times of these systems that provide resilience to hydrological systems to environmental changes. When characterizing processes beyond the laboratory scales, the exhaustive 4D characterization of processes becomes a challenging task. While it is illusory and not necessary to equip all subsurface systems with 4D imaging techniques, the use of high spatial and temporal resolution techniques in few highly instrumented field observatories during passive monitoring and active experiments is a key step to establish effective models that capture the effect of 3D heterogeneity and temporal dynamics and can be used and parameterized in other less instrumented sites. The insights gained at these sites is thus a basis for simplifications and generalizations, which can be used to improve modeling concepts for management beyond the specific field sites. In particular, these datasets should allow unraveling the importance of 4D dynamics and the influence of different processes on hydrogeophysical signals. Furthermore, these field observatories provide platforms to test and validate emerging 4D imaging techniques, evaluate their accuracy and potential, and establish the required space–time resolution depending on the targeted process. We thus argue that hydrogeological observatories provide a key step between theory and laboratory experiments on one side and practical field applications on the other side.

Available datasets related to such sites often combine fixed geophysical and hydrogeological sensing systems for the short-term monitoring of experimental campaigns, but also for the long-term monitoring of natural systems required to characterize physical and chemical heterogeneity and target hotspots, which cannot be easily accessed by classical observations. Related studies often provide parameterized hydrological models for the interpretation.

A non-exhaustive list of time-lapse hydrogeological and hydrogeophysical datasets, selected based on their online availability and space–time resolution, is given in Table 2. As can be seen, 4D data openly available are still scarce given the large variability of geological systems and applications. Because such extensive spatially and temporally resolved imaging can only be achieved on few sites, we argue that it is important to archive and share such datasets in open databases. In particular, these data are critical to (i) test and validate model hypotheses and predictive capabilities, (ii) to develop appropriate inverse modeling approaches adapted to the high level of heterogeneity of subsurface environments, and (iii) evaluate the added value of different imaging techniques in order to optimize the design of monitoring strategies on other sites. Table 2 will be made available through the website at https://hplus.ore.fr/en/database/4d-hydrogeology-dataset (last access: 15 August 2022), which will be open to contributions to enrich the datasets with new data.

6 Concluding remarks

In this paper, we have illustrated that advances in our understanding of complex subsurface processes hinge on our ability to observe/image key parameters and state variables with the relevant spatial and temporal resolution. Key applications where the coupling of spatial heterogeneity and temporal fluctuations might be essential include flow heterogeneity and dynamics, transport and reaction, unsaturated flow and transport, and surface–groundwater interactions. In specific applications, data availability is always limited due to budget, time, and space constraints, and conceptual simplifications are required. In this context, field observatories linked to open database and techniques dedicated to the acquisition of spatially and temporally resolved data sets are essential to (i) build appropriate models based on spatially and temporally resolved measurements and (ii) test and validate relevant sensors and methodologies.

New technologies are advancing our ability to close observation gaps and image the subsurface heterogeneity and dynamics for processes of relevance in hydrogeology. Such data collected across scales and with dense networks could lead to a better description of the processes and the development of new mechanistic models as well as the proper definition of effective parameters and upscaling approaches to do away with the complexity at larger scales. Considering the spatial heterogeneity of the subsurface quickly requires the use of efficient and reliable numerical models. Including small-scale heterogeneity automatically calls for high-resolution models with refined grids leading to high if not unacceptable computation times. In addition, the uncertainty inherent to subsurface systems can only be properly dealt with by stochastic approaches that require many simulations to characterize the ensemble of possible outcomes. The current computational power available for the scientific community, and for practitioners in the industry, is not sufficient to systematically tackle groundwater reservoirs with their full 4D complexity. Simplifications, such as ignoring the small-scale heterogeneity or ignoring some transient processes, are always needed and can in many cases provide useful results for groundwater management.

Nevertheless, the hydrogeological community is still often facing model predictive outcomes that are not consistent when validation data become available. Even though the 4D complexity is not always the cause, it can probably explain why some models have poor predictive capability. Ideally, hydrogeological conceptual models should initially consider the 4D complexity of the system and only deviate from this rigorous description when there is no significant effect on the prediction or decision-making process. Such conceptual simplifications of hydrogeological systems should be based on strong experimental or numerical evidences and should not constitute the default hypothesis because of lack of data or computational power.

High-resolution space–time observations are needed to improve mechanistic models of hydrological processes and for their upscaling, as well as for the monitoring at the field scale when significant risks for humans or the environment are associated. Although 4D data are less needed at larger scales for which averaging models are often satisfactory, we expect they will become more crucial at this scale as well in the future to tackle the challenges of sustainable development linked to water availability. In that sense, the existence of large 4D data sets linked to field observatories and models can only be beneficial for the community. Similarly, the more systematic use of Monte Carlo simulations, prediction-oriented approaches, or global sensitivity analyses, although computationally expensive, can provide the necessary background information, at least for processes that can be properly characterized by mathematical models.