Technical note: The CREDIBLE Uncertainty Estimation (CURE) toolbox: facilitating the communication of epistemic uncertainty

There is a general trend toward the increasing inclusion of uncertainty estimation in the environmental modelling domain. We present the Consortium on Risk in the Environment: Diagnostics, Integration, Benchmarking, Learning and Elicitation (CREDIBLE) Uncertainty Estimation (CURE) toolbox, an open-source MATLAB^TM toolbox for uncertainty estimation aimed at scientists and practitioners who are not necessarily experts in uncertainty estimation. The toolbox focusses on environmental simulation models and, hence, employs a range of different Monte Carlo methods for forward and conditioned uncertainty estimation. The methods included span both formal statistical and informal approaches, which are demonstrated using a range of modelling applications set up as workflow scripts. The workflow scripts provide examples of how to utilize toolbox functions for a variety of modelling applications and, hence, aid the user in defining their own workflow; additional help is provided by extensively commented code. The toolbox implementation aims to increase the uptake of uncertainty estimation methods within a framework designed to be open and explicit in a way that tries to represent best practice with respect to applying the methods included. Best practice with respect to the evaluation of modelling assumptions and choices, specifically including epistemic uncertainties, is also included by the incorporation of a condition tree that allows users to record assumptions and choices made as an audit trail log.

1 Introduction

Environmental simulation models are used extensively for research and environmental management. There is a general trend toward the increasing inclusion of uncertainty estimation (UE) in the environmental modelling domain, including applications used in decision-making (Alexandrov et al., 2011; Ascough et al., 2008). Effective use of model estimates in decision-making requires a level of confidence to be established (Bennett et al., 2013), and UE is one element of determining this. Another required element is an assessment of the conditionality of any UE, i.e. the conditionality associated with the implicit and explicit choices and assumptions made during the modelling and UE process, given the information available (e.g. Rougier and Beven, 2013).

Here, we present the Consortium on Risk in the Environment: Diagnostics, Integration, Benchmarking, Learning and Elicitation (CREDIBLE) Uncertainty Estimation (CURE) toolbox, an open-source MATLAB^TM toolbox for UE associated with environmental simulation models. It is aimed at scientists and practitioners with some modelling experience who are not necessarily experts in UE. The toolbox structure is similar to that of the SAFE (Sensitivity Analysis For Everybody) toolbox (Pianosi et al., 2016) in that it allows more experienced users to modify and enhance the code and to add new UE methods. The implementation of the toolbox also aims to increase the uptake of UE methods within a framework designed to be open and explicit in a way that tries to represent best practice; more specifically, we refer to best practice with respect to applying the various UE methods included as well as best practice with respect to being explicit about modelling choices and assumptions.

As the focus of the toolbox is UE for simulation models, often with relatively complex structures and many model parameters, the toolbox employs a range of different Monte Carlo methods. These are used for the forward propagation of uncertainties by sampling from input and parameter distributions defined a priori, for forward UE, or for the estimation of refined model structures and/or associated posterior parameter distributions when conditioned on observations (conditioned UE). The methods included span both formal statistical and informal approaches to UE, which are demonstrated using a range of modelling applications set up as workflow scripts that provide examples of how to utilize toolbox functions. As noted in the comments in the code, many of the workflows can be linked to the description of methods in Beven (2009).

Formal statistical and informal methods are included because there are no commonly agreed upon techniques for UE in environmental modelling applications, as evidenced by continuing debates and disputes in the literature (e.g. Clark et al., 2011; Beven et al., 2012; Beven, 2016; Nearing et al., 2016). The lack of a consensus on the most appropriate UE method is to be expected given that the sources of uncertainty associated with environmental modelling applications are dominated by a lack of knowledge (epistemic uncertainties; e.g. Refsgaard et al., 2007; Beven, 2009, 2016; Beven and Lane, 2022) rather than solely by random variability (aleatory uncertainties). Rigorous statistical inference applies to the latter, but it might lead to unwarranted confidence if applied to the former, especially where some data might be disinformative in model evaluation (e.g. Beven and Westerberg, 2011; Beven and Smith, 2015; Beven, 2019; Beven and Lane, 2022).

Assessing the impact of epistemic uncertainties for environmental modelling requires assumptions about their nature (which are difficult to define); thus, the output from any UE will be conditional upon these assumptions. This poses the question of what is good practice with respect to evaluating assumptions and choices made during the modelling process and what is good practice with respect to communicating the meaning of any subsequent analyses (Walker et al., 2003; Sutherland et al., 2013; Beven et al., 2018b; see also the TRACE (TRAnsparent and Comprehensive Ecological model documentation) framework of Grimm et al., 2014, for documentation on the modelling process). Beven and Alcock (2012) suggest a condition tree approach that records the modelling choices and assumptions made during analyses and, thus, provides a clear audit trail (e.g. Beven et al., 2014; Beven and Lane, 2022). The audit trail consequently provides a vehicle that promotes transparency, best practice and communication with stakeholders (Refsgaard et al., 2007; Beven and Alcock, 2012). To encourage best practice, the process of defining a condition tree and recording an audit trail has been made an integral part of the CURE toolbox via a condition tree graphical user interface (GUI).

Other freely available toolboxes for forward UE include the Data Uncertainty Engine (DUE; http://harmonirib.geus.info/due_download/index.html, last access: 2 July 2023; Brown and Heuvelink, 2007) and the SIMLAB toolbox (https://ec.europa.eu/jrc/en/samo/simlab, last access: 2 July 2023; Saltelli et al., 2004). For conditioned UE, the following freely available toolboxes are accessible: GLUEWIN (https://joint-research-centre.ec.europa.eu/macro-econometric-and-statistical-software/econometric-software/gluewin_en, last access: 2 July 2023; Ratto and Saltelli, 2001), UCODE 2014 (http://igwmc.mines.edu/freeware/ucode, last access: 2 July 2023; Poeter et al., 2014), the MATLAB^TM Framework for Uncertainty Quantification (UQLAB; http://www.uqlab.com, last access: 2 July 2023; Wagener and Kollat, 2007), the Interactive Probabilistic Predictions software (http://www.probabilisticpredictions.org, last access: 2 July 2023; McInerney et al., 2018) and the DREAM toolbox (http://faculty.sites.uci.edu/jasper/files/2015/03/manual_DREAM.pdf, last access: 2 July 2023; Vrugt et al., 2008, 2009; Vrugt, 2016). The reader is also referred to the broader review of uncertainty tools undertaken by the Uncertainty Enabled Model Web (UNCERTWEB) European research project (Bastin et al., 2013), which includes tools supporting elicitation, visualization, uncertainty and sensitivity analysis. While links exist for these toolboxes, it is not clear if all continue to be maintained and supported. The CURE toolbox presented here is open source and brings together formal and informal modelling methodologies, underpinned by different philosophies, that users are encouraged to explore via the example workflows (Table 1). It also offers a method not included in previous toolboxes (i.e. the coupled generalized likelihood uncertainty estimation and limits of acceptability, GLUE-LoA, method; Beven, 2006; Blazkova and Beven, 2009; Hollaway et al., 2018; Beven et al., 2022) and explicitly sets out to encourage best practice regarding the conditionality of modelling results using the condition tree approach.

Table 1 Toolbox workflow examples and the uncertainty estimation methods employed.

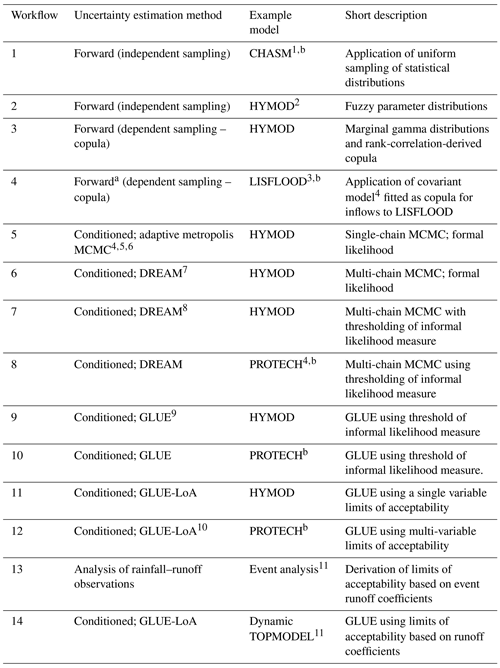
^a In this example, the input was sampled in a forward uncertainty analysis, but the LISFLOOD model was conditioned in a prior analysis. ¹ Almeida et al. (2017). ² Wagener et al. (2001). ³ Neal et al. (2013). ⁴ Haario et al. (2001). ⁵ Roberts and Rosenthal (2001). ⁶ Roberts and Rosenthal (2009). ⁷ Differential evolution adaptive metropolis (Vrugt, 2016). ⁸ Sadegh and Vrugt (2014). ⁹ Generalized likelihood uncertainty estimation (GLUE; Beven and Binley, 1992). ¹⁰ Blazkova and Beven (2009). ^b Owing to long model run times, this example uses pre-run simulation output. ¹¹ Beven et al. (2022).

Figure 1 The decision tree guiding users towards different methodologies and workflows.

2 Choosing a workflow

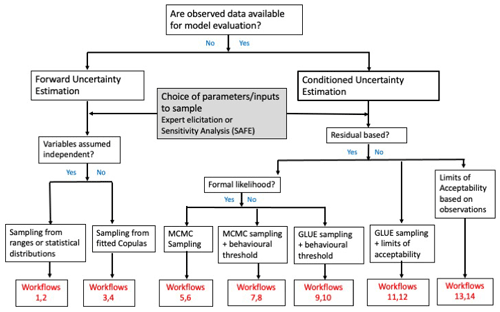
Table 1 lists the example workflows included in the first release of the CURE toolbox and the methods employed, with references to published papers where the methods have been applied. A variety of workflows covering forward UE and both formal statistical and informal methods of conditioned UE are given. Figure 1 provides an illustration of the choices that might be made in deciding on a workflow within the CURE toolbox (see also the earlier decision trees of this type in Pappenberger et al., 2006, and Beven, 2009). Forward UE methods (workflows 1 and 2) must be used when there are no observational data with which to condition the model output. The outcomes will then be directly dependent on the assumptions about the prior distributions and covariation of parameters and input variables. Copula methods are used to sample covariates (workflows 3 and 4). In the case of both forward and conditioned UE workflows, input uncertainties are parameterized to be applied as ranges or distributions, for example, as multipliers or an additive bias applied when the model is run.

When observational data are available, formal statistical likelihood methods (workflows 5 and 6) will be most appropriate in cases where any model residuals can be assumed to be aleatory and represented by a simple stochastic model. Where such assumptions are difficult to justify because of epistemic sources of uncertainty, there is a choice between approximate Bayesian estimation (ABC) using Markov chain Monte Carlo (MCMC) sampling and GLUE methods. Within ABC, a threshold of acceptability for some informal summary measure of performance is chosen. MCMC sampling is implemented using the DREAM code described in Vrugt (2015); the reader is also referred to Vrugt (2016) for a more recent description. This aims to produce an ensemble of model parameter sets comprising the samples from the final iterations of the DREAM algorithm (defined by the user) that are considered to be equally probable (workflows 7 and 8). Convergence of the sampling can be tested using the Gelman and Rubin (1992) diagnostic statistic.

Within GLUE each model is associated with a likelihood measure that initially reflects sampling of the assumed prior distributions and is then modified during the conditioning process. GLUE allows for different ways of updating the likelihood measure, including both Bayesian multiplication and fuzzy operators (Beven and Binley, 1992, 2014). Uniform independent priors across specified ranges are often assumed when there is a lack of robust knowledge about the parameters but, as in the options for the forward UE workflows, other prior distributions can be used. Deciding on whether a model is acceptable or behavioural can again be based on some informal summary measure of performance (workflows 9 and 10) or some predefined limits of acceptability (workflows 11 and 12). A particular case of defining limits of acceptability for rainfall–runoff models based on historical event runoff coefficients as a way of reflecting epistemic uncertainties in observed input and output is included (workflows 13 and 14). Vrugt and Beven (2018) demonstrated an adaptive sampling methodology for applying the limits of acceptability (DREAM_(LoA)) that aims to find feasible samples that satisfy all of the limits applied. The DREAM algorithm used in workflows 7 and 8 can be adapted to be used in this way.

It should be noted that the examples associated with each workflow are intended to be illustrative. They cannot all be described in detail in this publication, which is intended to introduce the toolbox. However, the MATLAB^TM code is freely available and can be easily adapted by users for their own application. Extensive comments are included in each workflow to aid this process.

3 The CURE toolbox, version 1.0, structure

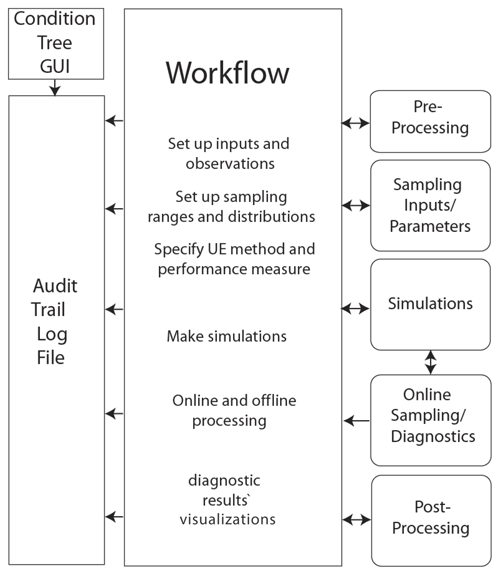
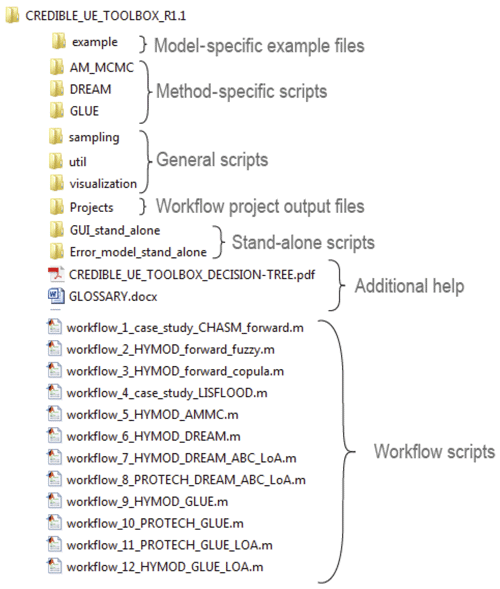
The CURE toolbox essentially has two linked structures. There is an overall structure with which the user interacts throughout the analysis (Fig. 2) and an underlying folder structure (Fig. 3) containing the toolbox functions and example model-specific files. The toolbox folder structure has specific folders for the UE methods where method-specific functions are collated (e.g. method-specific sampling and diagnostics and visualization) and for the individual example modelling applications (i.e. the model functions and input files as well as any links to any “external models”, such as models not coded as a MATLAB^TM function but which can be executed from the command line). Folders also exist for general (i.e. not method-specific) sampling methods, visualizations and utility functions. Additionally, there are project folders for each example workflow where audit trail logs, diagnostics and results are written.

Figure 2 Overall structure of the CURE toolbox.

The functions for general sampling of parameter distributions (e.g. uniform, low-discrepancy or Latin hypercube sampling of the large number of supported distributions) are common with the SAFE toolbox of Pianosi et al. (2016). In addition, and of particular importance for forward uncertainty analysis, the sampling functions have been extended to represent parameter and forcing-input dependencies using copulas (e.g. Workflow 3 in Table 1 uses copula sampling based on results from previous analyses to describe parameter dependencies for forward uncertainty propagation). Other specific sampling functions are associated with the adaptive sampling (“online” sampling) for Markov chain Monte Carlo (MCMC) approaches, implemented using the DREAM algorithm of Vrugt (2016), where distributions and correlation structures are modified as the chain(s) evolve. Modelling diagnostics, both numerical and graphical, are provided for both online adaptive sampling and “offline” methods (i.e. those that are not adaptively sampled within a given method). In the case of online MCMC methods, visualization of the evolution of the states of the chain(s) and tests for convergence to stationary distributions are included (e.g. Fig. 4a, b).

Figure 3 Outline of the folder structure of the CURE toolbox.

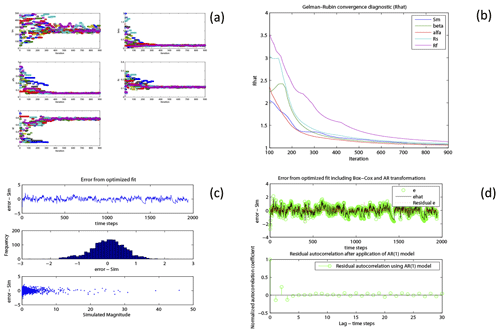
Figure 4 Visualization of simulation diagnostics in conditioning of HYMOD parameters in Workflow 5 using DREAM with a formal likelihood: (a) the evolution of 12 chains using DREAM, (b) the evolution of the Gelman–Rubin convergence statistic for five parameters and (c, d) the visualization of structural parameters during residual model fitting.

In the case of formal statistical likelihood methods (e.g. Evin et al., 2013, 2014, and the recent “universal likelihood” of Vrugt et al., 2022), residual model fitting can be carried out interactively, using command line prompts, and can form part of a workflow (or can be used in a stand-alone manner). The approach uses Box–Cox transformations, which provide flexibility in transforming the data to remove heteroscedasticity and non-normality (Box and Cox, 1964), and also provides for fitting an autoregressive model of suitable order in an iterative way, as proposed by Beven et al. (2008). Figure 4c and d, for example, show the use of the residual model-fitting visualizations in Workflow 5. The visualizations also serve as an approximate check of the residual model assumptions when analysing posterior simulations.

For the GLUE methods (see Beven and Binley, 1992, 2014; Beven and Freer, 2001; Beven et al., 2008; Beven and Lane, 2022), diagnostics are included for the exploration of the acceptable parameter space and which criterion (or criteria) and at which time steps (or locations) simulations were rejected. There are also method-specific and generic toolbox functions for the visualization and presentation of simulation results and associated uncertainties (e.g. see Fig. 5 for the application in Workflow 1). Results are both alphanumerical and graphical; alphanumerical results (including those from diagnostic statistics and summary variables where appropriate) can be automatically written to the audit trail log, and plots are saved to the project folder.

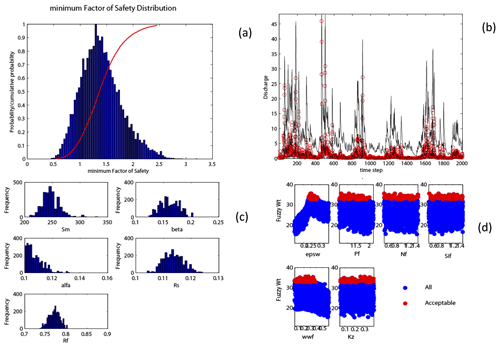
Figure 5 Visualization of results: (a) the distribution of the simulated minimum factor of safety from a forward UE using the CHASM landslide model in Workflow 1; (b) the 5th, 50th and 95th percentiles of simulated discharge (black lines) and observed discharge (red circles) from an MCMC-conditioned UE method using HYMOD; and (c) the posterior parameter distributions for the same CHASM example and (d), both showing all and acceptable parameter sets from a GLUE analysis using the PROTECH model (Workflow 10).

4 Condition tree implementation within CURE

An important part of any CURE toolbox application is the way that users can explore and document modelling choices, assumptions and uncertainties using the condition tree GUI (e.g. Fig. 6). The GUI aids in the elicitation of primary modelling uncertainties, their likely sources and how they are to be treated during the analysis. It is also designed to elicit other important choices and assumptions, including those regarding elements of the analysis assumed to be associated with insignificant uncertainties and perhaps treated deterministically; for example, where only one model structure is considered or where uncertainties are assumed negligible for certain elements or are perhaps subsumed into other uncertain elements. Similar to the incorporation of UE, the condition tree would be completed, ideally, as an integral part of any modelling application and can help in the definition of an appropriate workflow structure. This is particularly important in considering epistemic sources of uncertainty. We fully understand that non-probabilistic approaches to UE remain controversial (e.g. Nearing et al., 2016) but have, in the past, demonstrated that the assumptions required to use formal statistical methods (e.g. the recent paper of Vrugt et al., 2022) may lead to overconfidence in the resulting inference when epistemic uncertainties are important (Beven and Smith, 2015; Beven, 2016). Because epistemic uncertainties are the result of a lack of knowledge, their nature and impacts cannot be defined easily. That means that, effectively, there can be no right answer (e.g. Beven et al., 2018a, b; Beven and Lane, 2022); therefore, the recording of assumptions in the audit trail for analysis should be a requisite of any analysis to allow for later evaluation by others.

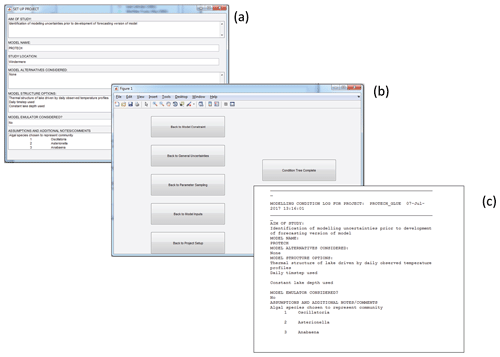
Figure 6 Condition tree example: GUI dialogue box for (a) the project set-up, (b) the condition tree navigation pane and (c) part of an example audit trail log.

The GUI takes the form of a number of simple, sequential dialogue boxes in which the user is asked to enter text. In the initial release of the toolbox there are five primary dialogue boxes covering the following:

1. project aims and model(s)/model structures considered;

2. modelling uncertainties – overview, covering the model structure, parameters, input and observations for model conditioning;

3. uncertainties – observations for model conditioning – specific, covering the associated uncertainties and basis for assessing simulation performance;

4. uncertainties – input – specific, covering the sampling strategy, distributions and dependencies;

5. uncertainties – parameters – specific, covering the choice of parameters, sampling strategy, distributions and dependencies.

The information, elicited using the dialogue boxes, can be automatically written to the project audit trail log during the initial phase of entry; the audit trail log remains editable as the user defines their own workflow and during any subsequent modifications to the analysis contained within a workflow.

5 Defining a workflow

An a priori consideration of modelling uncertainties via the condition tree is an optional first step to help choose and structure an appropriate workflow. The decision tree in Fig. 1 can also be used as a guide in this respect. These are complemented by the toolbox documentation and help text, which are available via the workflows and functions. Documentation and help are in the form of targeted comments within the code, and function header text is available by typing the help “function name” in the command line (e.g. headers may include a definition of function variables and references for a specific UE method). Each workflow is also linked, where possible, to the relevant chapters of Beven (2009); these are specified in the header text of each workflow script. Clarification of the terminology used in the help and documentation is provided by a glossary of terms included as part of the toolbox.

Table 2 Parameters and uniform distribution sampling ranges for the application of the PROTECH model to Lake Windermere (Workflow 12 application).

It is assumed that the user has completed any necessary pre-processing analyses such as forcing-input uncertainty assessment and disinformation screening (e.g. Beven and Smith, 2015) as well as an assessment of uncertainties associated with conditioning observations, where used. An exception is the interactive toolbox facility for fitting residual models mentioned earlier, where formal statistical likelihoods are to be used.

The example workflows have been chosen to span the UE methods included in the toolbox and, in some cases, provide comparison of different UE methods for similar modelling applications. The structure of the workflows themselves includes the primary steps to be “populated” that are outlined in the following.

The condition tree GUI project set-up and interactive dialogue boxes are as follows:

1. set up input and observations;

2. set up parameter ranges, distributions and sampling strategy;

3. define performance measure (if conditioned UE);

4. simulations (online or offline; MATLAB^TM function or external model);

5. post-processing, including diagnostics, results, propagation and visualization of uncertainty.

Associated with these main steps, example workflows include automatic “text writes” that are appended to the audit trail log for each analysis. These include specific choices that are made when implementing steps 1–5 above, such as the ranges of parameter values used and their distributions, the sampling strategy employed, and diagnostic and simulation results.

In general, users will not need to modify any toolbox functions; they will only need to build a workflow. However, given the requirement for online simulation performance to be assessed for MCMC methods as well as the many permutations of performance measures and ways of combining them where multiple criteria are used, users are also required to specify the function that returns an overall measure of individual simulation performance. In addition, where external models are to be used for online approaches, additional modifications may be required for modification of input/parameter files using some form of wrapper code.

Figure 7 PROTECH application to the Lake Windermere example in Workflow 12: observed chlorophyll data (red circles), limits of acceptability (green circles), and predictions of models that satisfy all of the chlorophyll, R-type and CS-type algae limits.

6 An example workflow

The CURE workflows can be applied to a wide range of geoscience applications, including the water science examples set out in Table 1. In particular, CURE is well suited to the specification of assumptions about epistemic uncertainties, to conditioning using uncertain observational data and to rejectionist approaches to model evaluation (see also Beven et al., 2018a, b, 2022; Beven and Lane, 2022). Here, we provide some more detail on the application of the PROTECH model within such a multi-variable rejectionist conditioning framework (Workflow 12 in Table 1). The full workflow and output are given in the Supplement.

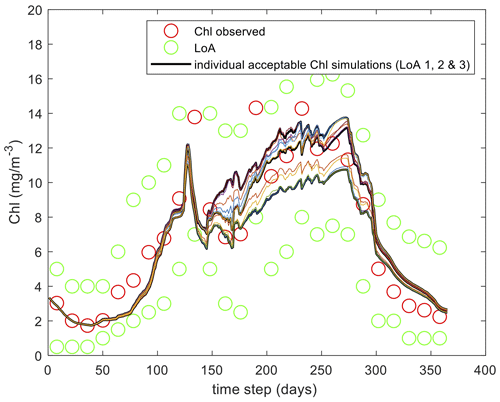
PROTECH is a lake algal community model that has been applied to predict concentrations for functional classes of algae in Lake Windermere in Cumbria, UK (Page et al., 2017 ). It is a 1D model with water volumes related to the lake bathymetry and runs with a daily time step. In this case, the model is provided in an executable form and was run offline for randomly sampled parameter sets; thus, the workflow takes the simulated output files as input. The model requires flow, weather and nutrient information as input. A reduced set of six parameters was sampled, as in Table 2 (see Page et al., 2017, for a more complete analysis). Model evaluation is based on limits of acceptability for three variables: chlorophyll and the concentrations of R-type and CS-type algae. Figure 7 shows the resulting chlorophyll output for the surviving models from the analysis after evaluation against all three sets of limits of acceptability. The full workflow and resulting audit trail and output figures are presented in the Supplement.

7 Toolbox evolution

The toolbox structure is such that new methods can be easily added, and it will be subject to ongoing development and augmentation with additional workflow examples. It is hoped that the CURE toolbox will contribute to the ongoing development and testing of UE methods and good practice with respect to their application. In particular, the condition tree approach could be further developed via feedback from toolbox users and end users of the conditional uncertainty estimates. The toolbox is freely available for non-commercial research and education from https://www.lancaster.ac.uk/lec/sites/qnfm/credible (Page et al., 2021).