Linking the complementary evaporation relationship with the Budyko framework for ungauged areas in Australia

While the calibration-free complementary relationship (CR) has performed excellently in predicting terrestrial evapotranspiration (ET_a), how to determine the Priestley–Taylor coefficient (α_e) is a remaining question. In this work, we evaluated this highly utilizable method, which only requires atmospheric data, with in situ flux observations and basin-scale water-balance estimates (ET_wb) in Australia, proposing how to constrain it with a traditional Budyko equation for ungauged locations. We found that the CR method with a constant α_e transferred from fractional wet areas performed poorly in reproducing the mean annual ET_wb in unregulated river basins, and it underperformed advanced physical, machine-learning, and land surface models in closing grid-scale water balance. This problem was remedied by linking the CR method with a traditional Budyko equation that allowed for an upscaling of the optimal α_e from gauged basins to ungauged locations. The combined CR–Budyko framework enabled us to reflect climate conditions in α_e, leading to more plausible ET_a estimates in ungauged areas. The spatially varying α_e conditioned by local climates enabled the CR method to outperform the three ET_a models in reproducing the grid-scale ET_wb across the Australian continent. We argued here that the polynomial CR with a constant α_e could result in biased ET_a, and it can be constrained by a traditional Budyko equation for improvement.

1 Introduction

Evapotranspiration (ET_a) plays a pivotal role in water and energy exchanges between the land and the atmosphere. On the global scale, more than 60 % of terrestrial precipitation (P) returns to the atmosphere through plants' vascular systems and soil pores while consuming over 70 % of surface net radiation (Trenberth et al., 2007, 2009). Since it is tightly coupled with carbon cycles, abnormally low ET_a would indicate food insecurity and low ecosystem sustainability (Jasechko, 2018; Kyatengerwa et al., 2020; Pareek et al., 2020; Swann et al., 2016). In severe cases, ET_a limited by deficient soil moisture can lead to extreme heatwaves that further propagate the water deficit in space and time (Miralles et al., 2014; Mueller and Seneviratne, 2012; Schumacher et al., 2022).

Despite great community efforts for sharing in situ observations (e.g., Baldocchi, 2020; Novick et al., 2018), ET_a gauging networks are unevenly established over land surfaces and often subjected to error sources (e.g., unclosed energy balance) and limited data lengths (Ma et al., 2021). Inevitably, modeling approaches are needed to predict ET_a in ungauged or poorly gauged areas or to characterize it on a long timescale in a large area. Hence, various approaches have been proposed, including physical models (e.g., Martens et al., 2017; Zhang et al., 2016), machine-learning techniques (e.g., Jung et al., 2019; Tramontana et al., 2016), and conceptual land surface schemes (e.g., Guimberteau et al., 2018; Haverd et al., 2018).

Those modeling approaches typically require P data and land surface information (e.g., remote-sensing vegetation indices) to quantify available soil moisture to the vaporization process. However, due in part to uncertainty associated with P data (Sun et al., 2018) and model structures (Samaniego et al., 2017; Zhang et al., 2019), resulting ET_a estimates have shown substantial disparities. In the comprehensive intercomparison by Pan et al. (2020), for example, the 14 advanced land surface models generated the global mean ET_a varying widely between 450 and 700 mm a⁻¹. Such a large incongruity in modeled ET_a was also found by the earlier Global Soil Wetness Project (Schlosser and Gao, 2010), suggesting that an alternative method is necessary to circumvent the uncertainty sources.

A practical method to simulate ET_a without P data and land surface schemes is the complementary relationship (CR) of evaporation (Bouchet, 1963). It uses the evident fact that the air over a water-limited surface amplifies its vapor pressure deficit (VPD), while this effect disappears when the same surface is amply wet (Chen and Buchberger, 2018; Ramírez et al., 2005; Zhou et al., 2019). Based on the atmospheric self-adjustment, numerous equations have been formulated to predict ET_a only using routine meteorological data (e.g., Anayah and Kaluarachchi, 2014; Crago and Crowley, 2005; Crago and Qualls, 2013; Hobbins et al., 2004; Huntington et al., 2011; Kahler and Brutsaert, 2006 among others). In particular, the definitive derivation by Brutsaert (2015) and the following modifications (Crago et al., 2016; Crago and Qualls, 2021; Szilagyi, 2021; Szilagyi et al., 2017) provided strong physical foundations to the early principle of Bouchet (1963). They have excellently predicted ET_a at various spatial and temporal scales (e.g., Brutsaert et al., 2017, 2020; Crago and Qualls, 2018; Ma et al., 2019, 2021; Ma and Szilagyi, 2019) and allowed users to assess vegetation droughts over national and continental areas (e.g., Kim et al., 2019, 2021; Kyatengerwa et al., 2020).

Nevertheless, definitive CRs still require at least some ET_a data to calibrate the parameters that determine the hypothetical wet-surface evaporation (ET_w; Qualls and Crago, 2020); thus, they are not fully free of P data or parameterization. For instance, Brutsaert et al. (2020) calibrated the single parameter of the CR of Brutsaert (2015) with flux observations and basin-scale P and runoff (Q) data to estimate mean annual ET_a across the globe. For evaluating four definitive CRs from the derivation of Brutseart (2015), Crago et al. (2022) also calibrated their parameters against eddy-covariance flux observations. To date, Szilagyi et al. (2017) have proposed the only CR formulation that purely uses routine meteorological data; however, it depends on a questionable assumption that the parameter for ET_w is constant over a large continental area, being counterfactual to experimental studies on the Priestley and Taylor (1972) coefficient (e.g., Assouline et al., 2016; Baldocchi et al., 2016; Parlange and Katul, 1992; Wang et al., 2014). Given the complex space–time links between climate, soil, and vegetation (Hagedorn et al., 2019; Mekonnen et al., 2019; Rodriguez-Iturbe, 2000), the aerodynamic component of ET_w is unlikely represented by a fixed fraction of the net radiation.

Owing to the data required for parameter calibration, the state-of-the-art CR formulations might not be applicable in ungauged locations. In part, this problem can be mended by an additional constraint for determining the essential parameters, and the traditional Budyko framework can come into play. A Budyko function (e.g., Fu, 1981; Yang et al., 2008) explains the mean ratio of ET_a to P (i.e., surface water balance) simply by climatological aridity and a few implicit parameters, simultaneously closing the surface energy budget (Mianabadi et al., 2020). Although Bouchet's principle has often been linked with the water balance described by Budyko functions (e.g., Carmona et al., 2016; Chen and Buchberger, 2018; Lhomme and Moussa, 2016; Zhang and Brutsaert, 2021), this theoretical link has been ignored when predicting ET_a by the definitive CRs. Kim and Chun (2021) explicitly showed that the atmospheric self-adjustment is tightly coupled with the climatological aridity within a Budyko function. This implies that the optimal parameter for a definitive CR should vary with climates rather than staying constant.

In this work, we showed that a Budyko equation could become an important physical constraint when predicting ET_a by a definitive CR over a continental area. Here, a practical approach was proposed to determine the parameter reasonably in ungauged locations via a case study for the Australian continent, where the performance of the CR method remained unknown in many parts. Based on the analytical relationship between the CR and the Budyko framework, we showed why the parameter of the CR is not independent of local climate conditions and addressed how to reflect spatially varying climates in its essential parameter.

2 Methodology and data

2.1 The polynomial CR by Szilagyi et al. (2017)

For the case study, we employed the calibration-free CR formulated by Szilagyi et al. (2017). It describes the atmospheric self-adjustment to surface moisture conditions using three evaporation rates, namely, ET_a, ET_w, and the potential evaporation (ET_p). ET_a is the actual moisture flux from a land surface to the atmosphere, and ET_w is the hypothetical ET_a rate that should occur with ample water availability. ET_p is the atmospheric capacity to receive water vapor that responds actively to soil moisture conditions. By defining the two dimensionless variables as $x\equiv {\text{ET}}_{\text{w}}/{\text{ET}}_{\text{p}}$ and $y\equiv {\text{ET}}_{\text{a}}/{\text{ET}}_{\text{p}}$, Szilagyi et al. (2017) derived a polynomial function from four definitive boundary conditions.

Under ample water conditions, ET_p does not deviate from ET_w and ET_a (i.e., ET_p = ET_w = ET_a); hence, the corresponding zero-order boundary condition is (i) y=1 for x=1. In contrast, ET_a must be nil over a desiccated surface (i.e., y=0), and by energy balance, the surface net radiation should be fully transformed to the sensible heat flux. Then, the atmospheric VPD would be amplified at the maximum level with the same net radiation and wind speed. Defining the maximum ET_p rate as E_pmax, another zero-order boundary condition is given as (ii) y=0 for $x=x_{\text{min}}\equiv {\text{ET}}_{\text{w}}/E_{\text{pmax}}$. When x=1 (i.e., ample water), changes in ET_a would be controlled by changes in ET_w, yielding a first-order boundary condition as (iii) $\mathrm{d}y/\mathrm{d}x=\mathrm{1}$ for x=1. Over a desiccated surface, ET_a stays at zero, even when ET_w changes; thus, another first-order boundary condition becomes (iv) $\mathrm{d}y/\mathrm{d}x=\mathrm{0}$ for x=x_min. The simplest polynomial equation satisfying the four boundary conditions is

$$\begin{array}{}\text{(1)}& y=\mathrm{2}{X}^{\mathrm{2}}-X^{\mathrm{3}},\end{array}$$

where X rescales the variable x into [0, 1] as

$$\begin{array}{}\text{(2)}& X={\displaystyle \frac{x-x_{\min }}{\mathrm{1}-x_{\min }}}={\displaystyle \frac{E_{\mathrm{pmax}}-{\mathrm{ET}}_{\mathrm{p}}}{E_{\mathrm{pmax}}-{\mathrm{ET}}_{\mathrm{w}}}}{\displaystyle \frac{{\mathrm{ET}}_{\mathrm{w}}}{{\mathrm{ET}}_{\mathrm{p}}}}.\end{array}$$

Equation (1) allows users to estimate ET_a with no land surface information because ET_p, ET_w, and E_pmax are all obtainable from a set of net radiation, air temperature, dew-point temperature, and wind speed data. ET_p and E_pmax can be estimated by the Penman (1948) equation:

$$\begin{array}{}\text{(3)}& {\displaystyle }{\mathrm{ET}}_{\mathrm{p}}={\displaystyle \frac{\mathrm{\Delta }\left(T_{\mathrm{a}}\right)}{\mathrm{\Delta }\left(T_{\mathrm{a}}\right)+\mathit{\gamma }}}{\displaystyle \frac{R_{\mathrm{n}}}{{\mathit{\lambda }}_{\mathrm{v}}}}+{\displaystyle \frac{\mathit{\gamma }}{\mathrm{\Delta }\left(T_{\mathrm{a}}\right)+\mathit{\gamma }}}{f}_{\mathrm{u}}\mathrm{VPD},\text{(4)}& {\displaystyle }{E}_{\mathrm{pmax}}={\displaystyle \frac{\mathrm{\Delta }\left(T_{\mathrm{dry}}\right)}{\mathrm{\Delta }\left(T_{\mathrm{dry}}\right)+\mathit{\gamma }}}{\displaystyle \frac{R_{\mathrm{n}}}{{\mathit{\lambda }}_{\mathrm{v}}}}+{\displaystyle \frac{\mathit{\gamma }}{\mathrm{\Delta }\left(T_{\mathrm{dry}}\right)+\mathit{\gamma }}}{f}_{\mathrm{u}}{e}_{\mathrm{s}}\left(T_{\mathrm{dry}}\right),\end{array}$$

where Δ(⋅) is the slope of the saturation vapor pressure curve (kPa ^∘C⁻¹); T_a is the mean air temperature (^∘C); γ is the psychrometric constant (kPa ^∘C⁻¹); R_n is the surface net radiation less the soil heat flux (MJ m⁻² d⁻¹); λ_v is the latent heat of vaporization (MJ kg⁻¹); f_u=2.6 (1+0.54 u₂) is the Rome wind function (mm d⁻¹ kPa⁻¹), where u₂ is the 2 m wind speed (m s⁻¹); and VPD is calculated by e_s (T_a) minus e_s (T_dew), where e_s(⋅) is the saturation vapor pressure (kPa), and T_dew is the dew-point temperature (^∘C).

T_dry in Eq. (4) is the air temperature (^∘C) at which the lower atmosphere is devoid of humidity presumably by the adiabatic drying process:

$$\begin{array}{}\text{(5)}& T_{\mathrm{dry}}=T_{\mathrm{wb}}+{\displaystyle \frac{e_{\mathrm{s}}\left(T_{\mathrm{wb}}\right)}{\mathit{\gamma }}}=T_{\mathrm{a}}+{\displaystyle \frac{e_{\mathrm{s}}\left(T_{\mathrm{dew}}\right)}{\mathit{\gamma }}},\end{array}$$

where T_wb is the wet-bulb temperature (^∘C) at which the saturation vapor pressure curve intersects with the adiabatic wetting line. Thus, it is obtained by

$$\begin{array}{}\text{(6)}& \mathit{\gamma }{\displaystyle \frac{T_{\mathrm{wb}}-T_{\mathrm{avg}}}{e_{\mathrm{s}}\left(T_{\mathrm{wb}}\right)-e_{\mathrm{s}}\left(T_{\text{dew}}\right)}}=-\mathrm{1}.\end{array}$$

To estimate ET_w in Eq. (2), the Priestley–Taylor (1972) equation has been a typical choice (e.g., Brutsaert, 2015; Crago et al., 2016; Han and Tian, 2018; Szilagyi et al., 2017):

$$\begin{array}{}\text{(7)}& {\mathrm{ET}}_{\mathrm{w}}={\mathit{\alpha }}_{\mathrm{e}}{\displaystyle \frac{\mathrm{\Delta }\left(T_{\mathrm{w}}\right)}{\mathrm{\Delta }\left(T_{\mathrm{w}}\right)+\mathit{\gamma }}}{\displaystyle \frac{R_{\mathrm{n}}}{{\mathit{\lambda }}_{\mathrm{v}}}},\end{array}$$

where α_e is the Priestley–Taylor coefficient ranging usually within [1.10, 1.32] (Szilagyi et al., 2017), and T_w is the wet-environment air temperature (^∘C). T_w can be approximated with the wet-surface temperature (T_ws) because the vertical air temperature gradient is negligible under a wet environment. Given its independence on areal extent (Szilagyi and Schepers, 2014), T_ws can be approximated by the implicit Bowen ratio (β) of a small wet patch:

$$\begin{array}{}\text{(8)}& \mathit{\beta }={\displaystyle \frac{R_{\mathrm{n}}-{\mathrm{ET}}_{\mathrm{p}}}{{\mathrm{ET}}_{\mathrm{p}}}}\approx \mathit{\gamma }{\displaystyle \frac{T_{\mathrm{ws}}-T_{\mathrm{a}}}{e_{\mathrm{s}}\left(T_{\mathrm{ws}}\right)-e_{\mathrm{s}}\left(T_{\mathrm{dew}}\right)}}.\end{array}$$

Equation (8) assumes that the available radiation for the wet patch is close to that of the drying surface (Szilagyi et al., 2017). T_ws might be higher than T_a when the air is close to saturation. In such a case, T_ws should be capped by T_a when calculating ET_w.

The single parameter of the polynomial CR, i.e., α_e, is analytically obtainable by inserting the Priestley–Taylor equation into the Bowen ratio of a wet environment (Szilagyi et al., 2017) as

$$\begin{array}{}\text{(9)}& {\mathit{\alpha }}_{\mathrm{e}}={\displaystyle \frac{\left[\mathrm{\Delta }\left(T_{\mathrm{a}}\right)+\mathit{\gamma }\right]\left[e_{\mathrm{s}}\left(T_{\mathrm{ws}}\right)-e_{\mathrm{s}}\left(T_{\mathrm{dew}}\right)\right]}{\mathrm{\Delta }\left(T_{\mathrm{a}}\right)\left\{\left[e_{\mathrm{s}}\left(T_{\mathrm{ws}}\right)-e_{\mathrm{s}}\left(T_{\mathrm{dew}}\right)\right]+\mathit{\gamma }\left[T_{\mathrm{ws}}-T_{\mathrm{a}}\right]\right\}}},\end{array}$$

where α_e must fall within the theoretical limit of [1, $\mathrm{1}+\mathit{\gamma }/\mathrm{\Delta }\left(T_{\text{a}}\right)]$ (Priestley and Taylor, 1972).

2.2 The analytical relationship between the polynomial CR and a Budyko function

Since Eq. (9) is only applicable in a wet environment, Szilagyi et al. (2017) identified wet locations in a continental area based on the fact that the air close to saturation should have high relative humidity (RH) with T_ws>T_a. Thus, they calculated α_e values at locations with RH > 90 % and $T_{\text{ws}}>T_{\text{a}}+\mathrm{2}$ ^∘C, and the average value was used to predict ET_a for a continental area. However, the spatially constant α_e is unlikely suitable in such a large area under diverse climates because the equilibrium between the atmosphere and the underlying surface is intertwined with the partitioning of P to ET_a and Q over the surface.

Kim and Chun (2021) analytically related Eq. (1) with the traditional Turc–Mezentsev equation and found that the self-adjustment of ET_p (i.e., x) is tightly linked with climatological aridity and land properties. For the independence between P and “the possible maximum ET_a” of the Budyko framework, Kim and Chun (2021) reformulated the traditional equation with ${\mathrm{\Phi }}_{\mathrm{0}}\equiv {\text{ET}}_{\text{w}}/P$ instead of the commonly used aridity index ($\mathrm{\Phi }\equiv {\text{ET}}_{\text{p}}/P$) as

$$\begin{array}{}\text{(10)}& {\displaystyle \frac{{\mathrm{ET}}_{\mathrm{a}}}{P}}={\displaystyle \frac{{\mathrm{ET}}_{\mathrm{w}}}{P}}{\left[{\displaystyle \frac{\mathrm{1}}{\mathrm{1}+{\left(\frac{{\mathrm{ET}}_{\mathrm{w}}}{P}\right)}^n}}\right]}^{\frac{\mathrm{1}}{n}}={\displaystyle \frac{x{\mathrm{ET}}_{\mathrm{p}}}{\mathrm{P}}}{\left[{\displaystyle \frac{\mathrm{1}}{\mathrm{1}+{\left(\frac{{\mathrm{xET}}_{\mathrm{p}}}{\mathrm{P}}\right)}^n}}\right]}^{\frac{\mathrm{1}}{n}},\end{array}$$

where the parameter n implicitly represents the factors affecting the P partitioning other than the climatic drivers. When dividing Eq. (10) by Φ, it is found that the Budyko Eq. (10) is intertwined with the Eq. (1) of the CR:

$$\begin{array}{}\text{(11)}& y={\displaystyle \frac{{\mathrm{ET}}_{\mathrm{a}}}{{\mathrm{ET}}_{\mathrm{p}}}}=\mathrm{2}{X}^{\mathrm{2}}-X^{\mathrm{3}}={\left[{\displaystyle \frac{x^n}{\mathrm{1}+x^n{\mathrm{\Phi }}^n}}\right]}^{\frac{\mathrm{1}}{n}}.\end{array}$$

Equation (11) implies that the self-adjustment of ET_p (i.e., x) is tightly related with the climatic condition (i.e., Φ) and the implicit land property (i.e., n).

While the x and n can be achievable from a set of ET_a, ET_p, E_pmax, and P values by inverting Eq. (11), such an approach is not applicable in locations with no ET_a data. To quantify x values only using ET_p, E_pmax, and P, Kim and Chun (2021) developed a regression equation between x and Φ, x_min, and n values from 513 gauged river basins around the world. We used the same regression-based regionalization. Considering $x_{\text{min}}=x{\text{ET}}_{\text{p}}/E_{\text{pmax}}$, the nonlinear expression in Eq. (11) can be approximated by a multiple regression as

$$\begin{array}{}\text{(12)}& \stackrel{\mathrm{̃}}{x}=b_{\mathrm{0}}+b_{\mathrm{1}}\ln \left(\mathrm{\Phi }\right)+b_{\mathrm{2}}\ln \left({\mathrm{ET}}_{\mathrm{p}}/E_{\mathrm{pmax}}\right)+{\mathrm{b}}_{\mathrm{2}}\ln \left(n\right),\end{array}$$

where $\stackrel{\mathrm{̃}}{x}$ is the approximate ratio of ET_w to ET_p, and b₀, b₁, and b₂ are the intercept and the regression coefficients. Since the implicit parameter n is unavailable in ungauged locations, Eq. (12) needs to be further simplified by neglecting the last term:

$$\begin{array}{}\text{(13)}& \stackrel{\mathrm{̃}}{x}\approx c_{\mathrm{0}}+c_{\mathrm{1}}\ln \left(\mathrm{\Phi }\right)+c_{\mathrm{2}}\ln \left({\mathrm{ET}}_{\mathrm{p}}/{\mathrm{E}}_{\mathrm{pmax}}\right),\end{array}$$

where c₀, c₁, and c₂ are the intercept and the coefficients of the approximated regression.

If $\stackrel{\mathrm{̃}}{x}$ is known by the regression by Eq. (13), the parameter α_e can be estimated using the Priestley–Taylor equation as

$$\begin{array}{}\text{(14)}& {\displaystyle }{\stackrel{\mathrm{̃}}{\mathit{\alpha }}}_{\mathrm{e}}=\stackrel{\mathrm{̃}}{x}{\displaystyle \frac{{\mathrm{ET}}_{\mathrm{p}}}{{\mathrm{ET}}_{\mathrm{eq}}}}\text{(15)}& {\displaystyle }{\mathrm{ET}}_{\mathrm{eq}}={\displaystyle \frac{\mathrm{\Delta }\left(T_{\mathrm{w}}\right)}{\mathrm{\Delta }\left(T_{\mathrm{w}}\right)+\mathit{\gamma }}}{\displaystyle \frac{R_{\mathrm{n}}}{{\mathit{\lambda }}_{\mathrm{v}}}},\end{array}$$

where ${\stackrel{\mathrm{̃}}{\mathit{\alpha }}}_{\mathrm{e}}$ is the Priestley–Taylor coefficient that approximately satisfies the CR and the Budyko equations together, and ET_eq is the equilibrium ET_a (mm d⁻¹) at which VPD is nil under a wet environment. It should be noted that P, ET_p, E_pmax, and ET_eq within Eqs. (10)–(13) must be on a timescale where the Turc–Mezentsev equation is valid (typically longer than a year), and ${\stackrel{\mathrm{̃}}{\mathit{\alpha }}}_{\mathrm{e}}$ is still bounded within [1, $\mathrm{1}+\mathit{\gamma }/\mathrm{\Delta }\left(T_{\text{a}}\right)]$.

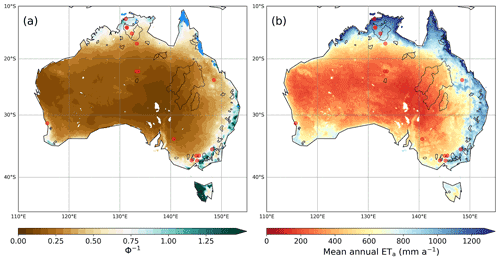
Figure 1 Spatial distributions of (a) the reciprocals of aridity index and (b) the mean annual ET_a for 1998–2014 predicted by the CR with α_e=1.15. The red circles and the gray polygons are the locations of 15 flux towers and the boundaries of 71 CAMELS basins. The blue-colored points in (a) indicate the wet cells with RH > 90 % and $T_{\text{ws}}>T_{\text{a}}+\mathrm{2}$ ^∘C. CR ET_a was calculated at the grid cells where the land fraction was larger than 50 %.

2.3 Atmospheric forcing, eddy-covariance, and runoff data

We examined the CR–Budyko combined framework in the Australian continent lying within (10–45^∘ S, 113–155^∘ E). The required atmospheric forcing data (R_n, T_a, T_dew, and u₂) were collected from the advanced ERA5-Land reanalysis archive (Muñoz-Sabater et al., 2021) of the European Centre for Medium-Range Weather Forecasts (https://cds.climate.copernicus.eu; last access: 10 December 2021). The monthly averages of surface latent and sensible heat fluxes, 2 m air temperature, 2 m dew-point temperature, and 10 m U and V wind speed components at ${\mathrm{0.1}}^{\circ }\times {\mathrm{0.1}}^{\circ }$ were downloaded for 1981–2020. R_n was calculated by summing the two heat fluxes, and the 10 m wind speed components were converted to u₂ using the logarithmic wind profile (Allen et al., 1998).

We also collected the Australian edition of the Catchment Attributes and Meteorology for Large sample Studies (CAMELS; Fowler et al., 2021) series of datasets (https://doi.org/10.1594/PANGAEA.921850). The CAMELS datasets comprise daily time series of 19 hydrometeorological variables at 222 unregulated river basins in Australia up to 2014, and we selected the 71 basins larger than 500 km² to contain at least five CR ET_a estimates within the boundaries. The water-balance ET_a (ET_wb) (i.e., ET${}_{\text{wb}}\approx \sum P-\sum Q)$ of each basin was calculated for the two periods of 1981–1997 and 1998–2014. The mean annual ET_wb for the former period was used for the regressions with Eqs. (12) and (13), and the predicted ET_a was evaluated against the latter.

Table 1 List of the chosen FLUXNET2015 sites.

As a point-scale evaluation dataset, the annual flux observations were taken from the 15 eddy-covariance stations (Table 1) included in the FLUXNET2015 archive (https://fluxnet.org/; last access: 1 July 2021). We chose the flux towers with two or more annual means and adopted the energy-balance-corrected latent heat flux observations with the quality measures “LE_F_MDSQC” higher than 0.70. Given the fine resolution of the ERA5-Land forcing data, we believed that the ET_a estimates by CR could be directly compared with the point-scale observations.

In addition, as a grid-scale evaluation reference, the SILO P data at ${\mathrm{0.01}}^{\circ }\times {\mathrm{0.01}}^{\circ }$ were collected from the Queensland government (https://www.longpaddock.qld.gov.au/silo/gridded-data; last access: 1 June 2021) together with the Global RUNoff (GRUN) ENSEMBLE (Ghiggi et al., 2021) (https://doi.org/10.6084/m9.figshare.12794075; last access: 1 October 2021). The global Q data were produced at ${\mathrm{0.5}}^{\circ }\times {\mathrm{0.5}}^{\circ }$ using a machine-learning algorithm trained by in situ streamflow observations, and potential biases were reduced by simulations with 21 sets of atmospheric forcing (Ghiggi et al., 2021). The SILO P was used to calculate Φ at each grid of the forcing data. After bilinearly unifying the resolutions of SILO P and GRUN Q data, we also calculated the mean annual ET_wb for 1998–2014 at ${\mathrm{0.5}}^{\circ }\times {\mathrm{0.5}}^{\circ }$ over the entire Australian continent.

Against the grid-scale ET_wb estimates, performance of the polynomial CR was also compared with three ET_a products from a physical, a machine-learning, and a land surface model. The physical model was the Global Land Evaporation Amsterdam Model (GLEAM) v3.2 (Martens et al., 2017; https://www.gleam.eu; last access: 3 June 2020) based on the Priestley–Taylor equation constrained by microwave-derived soil moisture, surface temperature, and vegetation optical depth. The machine-learning ET_a product was the FluxCom (http://www.fluxcom.org/; last access: 18 March 2019) that upscaled in situ observations at 224 eddy-covariance towers using 11 algorithms (Jung et al., 2019). We used the version forced by the CRUNCEPv8 that has the longest data length from 1950 to 2016. The land surface model product was the ERA5-Land monthly ET_a (https://cds.climate.copernicus.eu; last access: 7 July 2021) simulated by the advanced Hydrology Tiled ECMWF Scheme for Surface Exchanges over Land (Balsamo et al., 2015). All the modeled ET_a datasets were bilinearly regridded to ${\mathrm{0.5}}^{\circ }\times {\mathrm{0.5}}^{\circ }$ for 1998–2014 to be compared with the grid-scale ET_wb data.

Figure 2 The 1:1 comparison between the CR ET_a estimates with α_e=1.15 and (a) the annual FLUXNET2015 observations and (b) the mean annual ET_wb of the 71 CAMELS basins for 1998–2014.

Figure 3 Same as Fig. 2 except α_e=1.10.

3 Results

3.1 Performance of the calibration-free CR in Australia

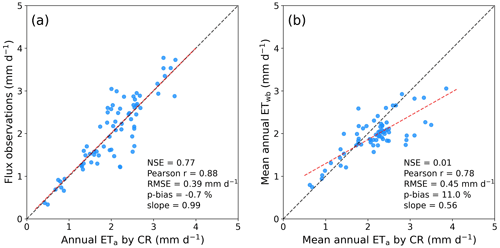
Figure 1a depicts the spatial distribution of the inverted aridity index (${\mathrm{\Phi }}^{-\mathrm{1}}=P/{\text{ET}}_{\text{p}})$ that can traditionally categorize climate conditions. The mean ratios between SILO P and ET_p for 1998–2014 indicated that 83 % of the Australian land surfaces were under arid ($\mathrm{0.05}<{\mathrm{\Phi }}^{-\mathrm{1}}<\mathrm{0.2}$) and semi-arid climates ($\mathrm{0.2}<{\mathrm{\Phi }}^{-\mathrm{1}}<\mathrm{0.5}$). Semi-humid ($\mathrm{0.5}<{\mathrm{\Phi }}^{-\mathrm{1}}<\mathrm{0.65}$) and humid climates (${\mathrm{\Phi }}^{-\mathrm{1}}>\mathrm{0.65}$) were only found in the northern and southeastern coastal areas and the southwestern edge where major cities and agricultural lands have developed. Despite the high aridity, hyper-arid climates (${\mathrm{\Phi }}^{-\mathrm{1}}>\mathrm{0.05}$) were not found in Australia.

We first examined the calibration-free approach by Szilagyi et al. (2017) that only uses the meteorological forcing inputs. The blue-colored points in Fig. 1a are the locations with RH > 90 % and T_ws > T_a+2 ^∘C, at which the α_e values from Eq. (9) were within 1.15 ± 0.047 (mean ± standard deviation). Though the two conditions were met in some mountainous areas in the southeastern part, we excluded them because unexpectedly high α_e values were obtained. The mean α_e=1.15 fell within the theoretical limits and was equal to the value used in the prior studies in China (Ma et al., 2019) and the conterminous United States (Ma and Szilagyi, 2019).

Using the CR with α_e=1.15, we predicted ET_a over the entire Australian continent (Fig. 1b). The distribution of the resulting mean ET_a for 1998–2014 was coherent with that of Φ⁻¹. The mean CR ET_a ranged in 262 ± 85.3 and 547 ± 173 mm a⁻¹ under arid and semi-arid climates, respectively. On the other hand, CR ET_a in semi-humid and humid locations was much higher, at 886 ± 187 mm a⁻¹ and 1010 ± 213 mm a⁻¹, respectively. The calibration-free CR predicted the continental mean ET_a to be as high as 489 mm a⁻¹ for 1981–2012, and it was about 11.3 % higher than the estimate for the same period (439 mm a⁻¹) by Zhang et al. (2016). The mean fraction of ET_a to P for 1998–2014 (97 %) was larger than the typical ET_a value in Australia (∼90 %; Glenn et al., 2011), implicating that the constant α_e=1.15 seemed to make the CR overrate ET_a.

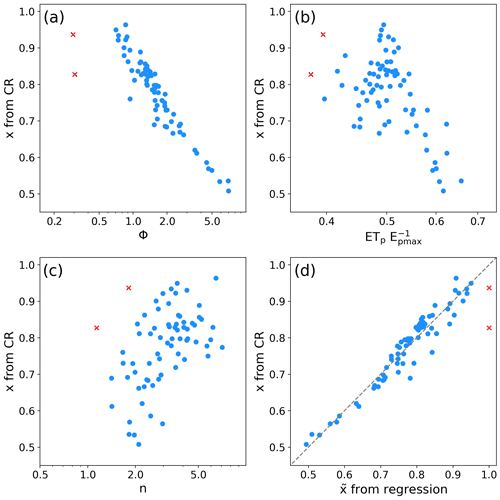
Figure 4 The scatter plots between the x estimated by CR with ET_wb for 1981–1997 and the corresponding (a) Φ, (b) ET${}_{\text{p}}/E_{\text{pmax}}$, and (c) n values and (d) the 1:1 plot between the x from CR and the $\stackrel{\mathrm{̃}}{x}$ predicted by Eq. (17). The red x symbols are the outliers excluded from the regression analysis.

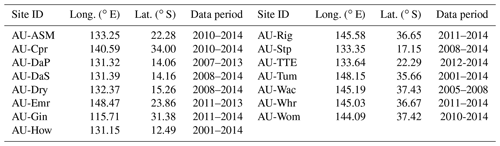
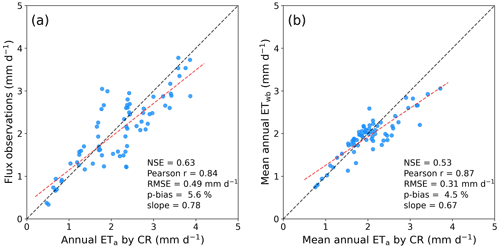
The overestimation of the calibration-free CR was confirmed by the flux observations and the basin-scale ET_wb (Fig. 2). The percent bias (p-bias) of CR ET_a to the point-scale annual ET_a was +10.4 %, while it became more than doubled when compared to the basin-scale ET_wb. Though the Pearson correlation coefficients (Pearson r) were significantly high between the CR ET_a and the two evaluation references, the low Nash–Sutcliffe efficiency (NSE) to ET_wb implies that the CR method could perform poorly in wet river basins. The regression slopes in Fig. 2 also indicate that the calibration-free CR tends to increasingly overestimate as climate becomes wetter. The root mean square error (RMSE) of CR ET_a to ET_wb was higher than to the point observations. Although it appeared to perform acceptably at the 15 flux towers, the CR method produced considerable biases in the 71 CAMELS basins. The performance measures were not as excellent as the same CR method had shown in the United States (Ma et al., 2021; Ma and Szilagyi, 2019; Kim et al., 2019) and in China (Ma et al., 2019).

One may argue that the mean α_e derived from fractional wet areas is unlikely representative of the large Australian continent, and this might introduce the biases to CR ET_a estimates. Hence, we re-simulated CR ET_a with the estimate by Ma et al. (2021) (α_e=1.10) from a global-scale analysis. Figure 3a shows that the predicted ET_a became nearly unbiased at the 15 flux tower locations and seemingly suggests that the decreased α_e could become a solution to improving the CR method. Nevertheless, the fixed α_e still made the CR overestimate ET_a in the CAMELS basins under (semi-)humid climates, albeit slightly ameliorated (Fig. 3b).

Figure 5 Distributions of (a) the ${\stackrel{\mathrm{̃}}{\mathit{\alpha }}}_{\mathrm{e}}$ values from Eq. (17) and (b) the mean annual ET_a for 1998–2014 by the CR method with the ${\stackrel{\mathrm{̃}}{\mathit{\alpha }}}_{\mathrm{e}}$ values.

3.2 The empirical relationship between $\stackrel{\mathrm{̃}}{x}$ and climate conditions

Figures 2 and 3 imply that the calibration-free CR with a fixed α_e was unlikely good at closing the local water balance in (semi-)humid river basins. To resolve this problem with the CR–Budyko framework, first we estimated the climatological x and the parameter n of the CAMELS basins using Eq. (11) with the mean annual ET_wb, P, ET_p, and E_pmax for 1981–1997. Figure 4a–c illustrate the scatter plots between the resultant x and corresponding Φ, ET${}_{\text{p}}/E_{\text{pmax}}$, and n values. Pearson r values between the x and the other three variables were −0.88, −0.59, and 0.44, respectively (significant at the 1 % level), suggesting that the self-adjustment of ET_p is not only correlated with climate conditions, but with land surface properties at least in part. By regressing between the x values and the log-transformed Φ, ET_p/E_pmax and n, we obtained an empirical relationship that enables us to spatially predict the mean annual ratio of ET_w to ET_p as

$$\begin{array}{}\text{(16)}& \begin{array}{rl}\stackrel{\mathrm{̃}}{x}=& \mathrm{0.949}-\mathrm{0.204}\ln \left(\mathrm{\Phi }\right)+\mathrm{0.231}\ln \left({\mathrm{ET}}_{\mathrm{p}}/E_{\mathrm{pmax}}\right)\\ +& \mathrm{0.0712}\ln \left(n\right).\end{array}\end{array}$$

The regression coefficients were all significant at the 1 % level, and the coefficient of determination (R²) was 0.98. The regression equation was further approximated by discarding n from the explanatory variables:

$$\begin{array}{}\text{(17)}& \stackrel{\mathrm{̃}}{x}=\mathrm{1.023}-\mathrm{0.220}\ln \left(\mathrm{\Phi }\right)+\mathrm{0.210}\ln \left({\mathrm{ET}}_{\mathrm{p}}/E_{\mathrm{pmax}}\right).\end{array}$$

The R² value of Eq. (17) declined to 0.93. We found that the simple regression between x and Φ further reduced R² to 0.90. While the heterogeneous land properties exert non-negligible influences, the regression analyses indicate that the climatic condition dominantly explains the spatial variation of the atmospheric self-adjustment.

Equation (17) performed excellently in reproducing the x values from CR with Φ and ET${}_{\text{p}}/E_{\text{pmax}}$ (Fig. 4d). The NSE, RMSE, Pearson r, and p-bias between the predicted $\stackrel{\mathrm{̃}}{x}$ and the x from CR were 0.93, 0.03, 0.96, and 0.0 %, respectively.

3.3 Evaluation of the CR and the advanced models against the grid ET_wb

By multiplying $\stackrel{\mathrm{̃}}{x}$ by the mean annual ratio between ET_p and ET_eq, we determined ${\stackrel{\mathrm{̃}}{\mathit{\alpha }}}_{\mathrm{e}}$ across the Australian land surfaces. The resulting ${\stackrel{\mathrm{̃}}{\mathit{\alpha }}}_{\mathrm{e}}$ values ranged within 1.13 ± 0.114, and the median value was almost equal to the global estimate (1.10) by Ma et al. (2021). They were relatively high in the northwestern and the northern part while being below the mean in the southern and the eastern parts (Fig. 5a). On 19 % of the surfaces, ${\stackrel{\mathrm{̃}}{\mathit{\alpha }}}_{\mathrm{e}}$ values were unity, and thus they might become below the theoretical limit unless bounded.

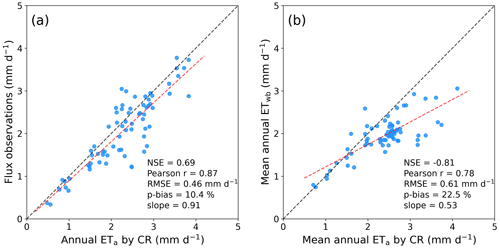
We again generated CR ET_a using the spatially varying ${\stackrel{\mathrm{̃}}{\mathit{\alpha }}}_{\mathrm{e}}$ values (Fig. 5b). The mean CR ET_a for 1998–2014 ranged in 249 ± 78.8 and 530 ± 172.0 mm a⁻¹ under arid and semi-arid climates, while it decreased to 805.2 ± 209 and 932 ± 239 mm a⁻¹ in semi-humid and humid regions, respectively. The flux observations were still acceptably regenerated with the less biases than in the case of α_e=1.15 (Fig. 6a). The ${\stackrel{\mathrm{̃}}{\mathit{\alpha }}}_{\mathrm{e}}$ based on the Budyko framework significantly reduced the biases introduced by the constant α_e in (semi-)humid basins. Albeit some biases remained, the water-balance ET_wb for 1998–2014 in the CAMELS basins were better reproduced by the spatially varying ${\stackrel{\mathrm{̃}}{\mathit{\alpha }}}_{\mathrm{e}}$ (Fig. 6b).

To confirm the improved performance of the combined CR–Budyko method across Australia, we resampled the new CR ET_a estimates to ${\mathrm{0.5}}^{\circ }\times {\mathrm{0.5}}^{\circ }$ and compared them with the grid ET_wb data. The ET_a products by GLEAM, FluxCom, and ERA5-Land were evaluated with the grid evaluation reference. As shown, the CR method with a constant α_e=1.15 overrated the mean annual ET_a along the eastern and the northern coastlines (Fig. 7b), underperforming the physical, the machine-learning, and the land surface models (Figure 8a). Although the smaller α_e=1.10 made the CR method perform better, its predictability was still poorer than the three advanced models, and the residual variance was as large as in the case of α_e=1.15 (Fig. 8b).

Figure 6 Same as Fig. 2 except that the ${\stackrel{\mathrm{̃}}{\mathit{\alpha }}}_{\mathrm{e}}$ values from Eq. (17) were used for CR ET_a.

In contrast, when employing the ${\stackrel{\mathrm{̃}}{\mathit{\alpha }}}_{\mathrm{e}}$ conditioned by local climate conditions, the same CR formulation could alleviate the overestimation along the coastlines (Fig. 7c). The Budyko-function-based ${\stackrel{\mathrm{̃}}{\mathit{\alpha }}}_{\mathrm{e}}$ led the CR ET_a estimates to neatly agree with the grid ET_wb, and the residual variance was much smaller than in the case of α_e=1.10 (Fig. 8c). The CR method with ${\stackrel{\mathrm{̃}}{\mathit{\alpha }}}_{\mathrm{e}}$ clearly outperformed the three advanced models in reproducing the grid ET_wb estimates (Fig. 8d–f). Although the referenced grid ET_wb has some error sources associated with the upscaling of P and Q, our comparative evaluation suggests that conditioning α_e with local climate conditions could substantially reduce the uncertainty of CR ET_a estimates in ungauged areas.

4 Discussion

4.1 Constraining the CR with the Budyko framework for ungauged areas

The CR explains the dynamic equilibrium between the atmospheric ET_p and the underlying moisture conditions, while the Budyko framework describes the steady-state water balance with climatic controls (i.e., P and ET_w). The analytical link between the CR and the Budyko equations, hence, implies that the atmospheric self-adjustment needs to be conditioned by the long-term climate conditions. Constraining the Turc–Mezentsev equation by the polynomial CR, Kim and Chun (2021) found that Q changes would be more sensitive to climatic changes than when they were not linked. In the opposite direction, the CR can be constrained by the Budyko equation to determine its essential parameter.

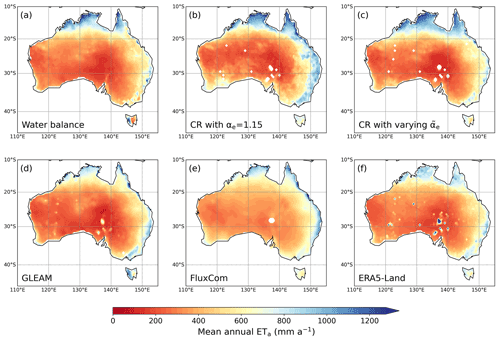
Figure 7 Distributions of (a) the mean annual water-balance ET_wb for 1998–2014 and the predictions by (b) CR with α_e=1.15, (c) CR with spatially varying ${\stackrel{\mathrm{̃}}{\mathit{\alpha }}}_{\mathbf{e}}$, (d) GLEAM, (e) FluxCom, and (f) ERA5-Land.

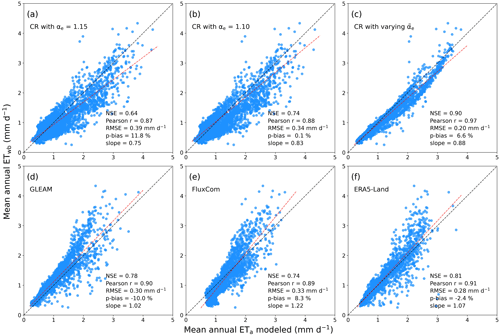
Figure 8 Scatter plots between the mean annual ET_wb for 1998–2014 at $\mathrm{0.5}{}^{\circ }\times {\mathrm{0.5}}^{\circ }$ and the predictions by (a) CR with α_e=1.15, (b) CR with α_e=1.10, (c) CR with spatially varying ${\stackrel{\mathrm{̃}}{\mathit{\alpha }}}_{\mathbf{e}}$, (d) GLEAM, (e) FluxCom, and (f) ERA5-Land.

In Crago and Qualls (2018), the optimal α_e for the linear CR of Crago et al. (2016) varied largely between 1.00 and 1.43. This point-scale experiment has already suggested that a constant α_e is unlikely suitable for definitive CRs to predict ET_a in Australia. The ratio between the aerodynamic and the radiation components of ET_w is evidently affected by the heat entrainment from the top of the boundary layer (Baldocchi et al., 2016), the dissimilarity between heat and water vapor sources (Assouline et al., 2016), the large-scale synoptic changes (Guo et al., 2015), and the horizontal advection of dry-air mass (Jury and Tanner, 1975). More recently, Han et al. (2021) proved the nonlinear dependence of ET_w on ET_eq, and Yang and Roderick (2019) showed α_e changing with R_n over ocean surfaces. Hence, the constant α_e assumption underpinning the calibration-free CR is counterintuitive to the theoretical and empirical evidence. Although Ma et al. (2021) found some global applicability of the calibration-free CR, its performance remains unknown in most of the Australian surfaces and in many ungauged basins over the world.

Since ET_a plays a pivotal role in the terrestrial water and energy balances, the partitioning of R_n into the latent and the sensible heat fluxes cannot be independent of the partitioning of P into ET_a and Q. On a mean annual scale, P and ET_w are the major determinants of the P partitioning, and thus the parameter α_e might not be independent of P. Given the large variability of P, assuming a fixed α_e across a continental area may introduce considerable biases to CR ET_a estimates. Thus, discarding available P data may not be a good choice when predicting ET_a by the CR method in ungauged areas. It is noteworthy that Φ dominantly explained the spatial variation of the mean annual x of the 71 CAMELS basins, and the ${\stackrel{\mathrm{̃}}{\mathit{\alpha }}}_{\mathrm{e}}$ values conditioned by local climates were of a large spatial variation. This suggests that the CR with a constant α_e may produce unreliable ET_a estimates in ungauged locations.

Nonetheless, the low performance with a constant α_e does not indicate that the CR method underperforms the sophisticated ET_a models. The simple polynomial CR seemed to outperform the advanced the advanced physical, machine-learning, and land surface models, when its parameter was conditioned by local climates. The proposed CR–Budyko framework enabled us to regionalize the optimal α_e for the CR method from gauged basins to ungauged locations in an empirical manner. It should be highlighted that the CR with spatially varying ${\stackrel{\mathrm{̃}}{\mathit{\alpha }}}_{\mathrm{e}}$ produced much smaller residual variance than the three advanced models.

4.2 Remaining issues and caveats

In seven Australian eddy-covariance flux towers, Crago et al. (2022) found that the optimal α_e for the polynomial CR was 1.35 for predicting daily ET_a in the dimensionless form (i.e., $y={\text{ET}}_{\text{a}}/{\text{ET}}_{\text{p}})$. However, it was increased to 1.42, 1.45, 1.47, and 1.50 to simulate the dimensional latent heat fluxes at daily, weekly, monthly, and annual timescales, respectively. This implies that the timescale would largely affect the optimal α_e for the definitive CRs. Though the stationary Budyko equation can become a constraint at a mean-annual scale, how to capture the scale dependence of α_e is a remaining question.

Further questions can arise as to how to quantify ET_p and E_pmax. For example, the α_e values from ET_p with the Rome wind function rely upon an unrealistic assumption that the aerodynamic resistance on a vegetated surface is equivalent to that of an open-water surface. It is still unknown if this assumption is practically valid because the Penman equation with the Rome wind function may result in unrealistically high ET_p, even on a large wet area (McMahon et al., 2013). Given the importance of the aerodynamic resistance in modulating surface temperature (Chen et al., 2020), ignoring its variability may become a significant error source for the CR method at both annual and subannual timescales.

In addition, there are some caveats in our case study. We employed the meteorological data different from those used in Ma et al. (2021). The ERA5-Land dataset is a downscaled version of the ERA5 data (Hersbach et al., 2020) by which Ma et al. (2021) predicted ET_a globally. Ma et al. (2021) incorporated remotely sensed albedo and emissivity together with a correction factor when calculating R_n, whereas we used the sum of the ERA5-Land latent and sensible heat fluxes. Those input differences may lead to differences in CR ET_a estimates.

The gridded GRUN Q, too, has some uncertainty sources, though it is the ensemble of many runoff simulations from 21 different atmospheric forcing inputs. In the machine-leaning process by Ghiggi et al. (2021), some Q observations affected by human activities (e.g., dam regulation and return flows from groundwater abstraction) might not be excluded, potentially disrupting the empirical relationship between atmospheric forcing and natural flows. In addition, the uncertainty of SILO P might be non-negligible in areas with limited weather stations and in mountainous areas (Fu et al., 2022). Though we reduced the potential biases of the gridded P and Q datasets by temporal averaging, the grid-scale ET_wb estimates should be treated as plausible values rather than exact observations.

5 Summary

Via a case study in Australia, we showed that the polynomial CR by Szilagyi et al. (2017) is unlikely to perform well when local climate conditions are neglected. The assumption of a constant Priestley–Taylor coefficient cannot reflect the long-term water balance; thereby, CR ET_a estimates can be biased. We resolved this problem by conditioning the CR with the traditional Budyko equation, and it allowed for a reasonable determination of the essential parameter in ungauged locations. The following conclusions are worth emphasizing:

1. The constant Priestley–Taylor coefficient transferred from fractional wet locations could make the CR method perform poorly in closing the local water balance. The unrealistic assumption could make the CR method underperform the advanced physical, machine-learning, and land surface models.

2. The Budyko framework can play a role in determining the degree of ET_p adjustment at the mean annual scale. It allows for upscaling of the Priestley–Taylor coefficients from gauged to ungauged locations.

3. The Priestley–Taylor coefficients conditioned by local climates made the CR better close the basin-scale water balance. The spatially varying Priestley–Taylor coefficients seemed to make the CR method outperform the advanced ET_a models.