Low and contrasting impacts of vegetation CO₂ fertilization on global terrestrial runoff over 1982–2010: accounting for aboveground and belowground vegetation–CO₂ effects

Elevation in atmospheric carbon dioxide concentration (eCO₂) affects vegetation water use, with consequent impacts on terrestrial runoff (Q). However, the sign and magnitude of the eCO₂ effect on Q are still contentious. This is partly due to eCO₂-induced changes in vegetation water use having opposing responses at the leaf scale (i.e., water-saving effect caused by partially stomatal closure) and the canopy scale (i.e., water-consuming induced by foliage cover increase), leading to highly debated conclusions among existing studies. In addition, none of the existing studies explicitly account for eCO₂-induced changes to plant rooting depth that is overwhelmingly found in experimental observations. Here we develop an analytical ecohydrological framework that includes the effects of eCO₂ on plant leaf, canopy density, and rooting characteristics to attribute changes in Q and to detect the eCO₂ signal on Q via vegetation feedbacks over 1982–2010. Globally, we detect a very small decrease of Q induced by eCO₂ during 1982–2010 (−1.7 %). Locally, we find a small positive trend (p < 0.01) in the Q–eCO₂ response along a resource availability (β) gradient. Specifically, the Q–eCO₂ response is found to be negative (i.e., eCO₂ reduces Q) in low-β regions (typically dry and/or cold) and gradually changes to a small positive response (i.e., eCO₂ increases Q) in high-β areas (typically warm and humid). Our findings suggest a minor role of eCO₂ on changes in global Q over 1982–2010, yet we highlight that a negative Q–eCO₂ response in semiarid and arid regions may further reduce the limited water resource there.

1 Introduction

Runoff (Q) is the flow of water over the Earth's surface, forming streamflow, and represents one of the most important water resources for irrigation, hydropower, and other human needs (Oki, 2006). Anthropogenic climate change is expected to alter the global hydrological cycle, with greenhouse-gas-induced climate warming intensifying the hydrological cycle (Huntington, 2006). Besides climate, terrestrial vegetation also affects the water cycle (Brown et al., 2005). It is well documented that elevated atmospheric CO₂ concentration (eCO₂) reduces stomatal opening, which in turn suppresses leaf-level transpiration (Field et al., 1995). If this were the only mechanism, i.e., that eCO₂ changed vegetation, this would increase runoff (Q) (Gedney et al., 2006). However, eCO₂ increases vegetation foliage cover (Donohue et al., 2013; Zhu et al., 2016), leading to enhanced canopy-level transpiration and consequently reductions of Q (Piao et al., 2007). These two opposing responses of vegetation water use to eCO₂ complicate the landscape-scale net effect of eCO₂ on Q, and existing modeling results are highly debated since they focus on different aspects (i.e., physiological functioning and/or structural change) of how eCO₂ affects the plants and thus the water cycle (Fatichi et al., 2016; Gedney et al., 2006; Huntington, 2008; Piao et al., 2007; Yang et al., 2016a, b). Moreover, observational and evaluation studies of eCO₂ effects on Q remain limited, particularly at regional to global scales.

In addition to stomatal and aboveground vegetation structure responding to eCO₂, the belowground vegetation structure (e.g., rooting depth) is also affected by eCO₂, with eCO₂ increasing rooting depth overwhelmingly found in experimental observations (Nie et al., 2013) (Supplement Tables S1 and S2). Deeper rooting depth increases plant-available water storage capacity by allowing vegetation to access deeper soil moisture, which potentially increases transpiration water loss and reduces Q, especially during dry spells (Trancoso et al., 2017; Yang et al., 2016b). To date, no previous eCO₂–Q modeling attempts have explicitly considered the belowground eCO₂-induced feedback simultaneously with the two previously mentioned aboveground feedbacks; this paper fills that niche.

Here we use a parsimonious, analytical ecohydrological model based on the Budyko framework (i.e., the Budyko–Choudhury–Porporato (BCP) model; Donohue et al., 2012), in combination with an analytical rooting depth model based on ecosystem optimality theory (Guswa, 2008), an analytical CO₂ fertilization model for steady-state vegetation (Donohue et al., 2017), and observed plant stomatal response to eCO₂ (Ainsworth and Rogers, 2007), to detect the impact of eCO₂ on Q changes (dQ) via vegetation feedbacks over global vegetated lands for 1982–2010. The Budyko framework describes the steady-state (i.e., mean annual scale) hydrological partitioning as a functional balance between atmospheric water supply (i.e., precipitation, P) and demand (i.e., potential evapotranspiration, E_P) and a model parameter that modifies the climate–hydrology relationship (Choudhury, 1999; Donohue et al., 2012). In this framework, both E_P and the model parameter are affected by the response of vegetation to eCO₂ (see Methods section). The “top-down” (Sivapalan et al., 2003) developed framework allows for analytical and transparent attribution of dQ changes, which overcomes the uncertainty raised from nonlinear interactions among numerous processes when attributing dQ numerically by using “bottom-up” Earth system models (Yang et al., 2015). To examine the long-term eCO₂ impact and to minimize year-to-year “transient” effects (i.e., water storage changes), we performed our analyses using sequential 5-year periods (Yang et al., 2016a; Han et al., 2020), resulting in six 5-year means during 1982–2010, with the first period containing 4 years. Additionally, since vegetation response to eCO₂ can be greatly mediated by the availability of other resources (e.g., water, light, and nutrients) (Donohue et al., 2013, 2017; Nemani et al., 2003; Yang et al., 2016a; Norby et al., 2010), we examine the impact of eCO₂ on Q along a resource availability gradient (Donohue et al., 2017; Friedlingstein et al., 1999) (see Methods section). Resource availability is typically low in dry (and/or cold) environments and increases as the climate becomes more humid, which enables us to detect the signal of eCO₂ on Q across a dry–wet gradient.

2 Material and methods

2.1 Methods

The Budyko–Choudhury–Porporato (BCP) model was adopted here to simulate Q and to attribute changes in Q (Yang et al., 2016b; Donohue et al., 2012). The BCP model uses the formulation by Choudhury (1999) of the Budyko curve to estimate Q (Eq. 1 below), in which the model parameter is estimated based on the relationship between Choudhury's model parameter and Porporato's model parameter (Eq. 2 below). The required rooting depth (Z_r) in estimating Porporato's parameter is calculated using the rooting depth model by Guswa (2008) (Eqs. 3–5 below). To quantify the response of Q to eCO₂ via vegetation feedbacks, the stomatal response of vegetation to eCO₂ is determined by upscaling the observed response at the site level to the biome level (Sect. 2.1.4), and the leaf area index (L) response to eCO₂ is quantified based on the response of water use efficiency (WUE) to eCO₂ adjusted by the local resource availability following Donohue et al. (2017) (Sect. 2.1.5). The effects of eCO₂ on both stoma and L also affect rooting depth in the model by Guswa (2008). A flowchart of our modeling approach is summarized in Fig. 1, and detailed calculation procedures are described in Sect. 2.1.1 to 2.1.5.

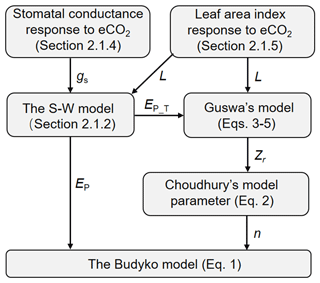
Figure 1 Flowchart of using the analytical models to detect the eCO₂ impact on Q. The terminologies used are explained in the following text (Sect. 2.1.1 through to 2.1.5).

2.1.1 Runoff simulation

The BCP model adopts the formulation of the Budyko curve by Choudhury (1999), which is given as

$$\begin{array}{}\text{(1)}& E={\displaystyle \frac{P{E}_{\mathrm{P}}}{(P^n+E_{\mathrm{P}}^n{)}^{\mathrm{1}/n}}},\end{array}$$

where E is the annual average actual evapotranspiration (mm yr⁻¹). P is the annual average precipitation (mm yr⁻¹). E_P is the annual average potential evapotranspiration (mm yr⁻¹) here estimated using the Shuttleworth–Wallace two-source evapotranspiration model (Shuttleworth and Wallace, 1985; see Sect. 2.1.2). n is a unitless model parameter that encodes all factors other than mean climate conditions and modifies the partitioning of P between E and Q. For assumed steady-state conditions, Q is calculated by subtracting E from P as a result of catchment water balance.

The probabilistic steady-state solution to the stochastic dynamic soil moisture model by Porporato (2004) shares a similar form with the Budyko curve (Porporato et al., 2004). Porporato's parameter ω is a dimensionless parameter, which is a function of effective rooting depth (Z_r, mm), mean rainfall intensity (α, mm per event), and soil water holding capacity (WHC, mm³ mm⁻³), and it exhibits a close relationship with Choudhury's parameter n (Yang et al., 2016b; Porporato et al., 2004). A relationship between Porporato's ω parameter and Choudhury's n parameter was built following three steps. Firstly, we obtained the numerical solution of Porporato's model for the corresponding $E/P$ for every 0.1 increment in $E_{\mathrm{P}}/P$ for six separate ω curves. Secondly, by numerically solving Choudhury's formulation of the Budyko curve, we determined the values of Choudhury's parameter (n) that correspond to the $E/P$ values of each of the six ω curves. Thirdly and finally, we pooled all n–ω pairs together and deduced the relationship between n and ω (R²=0.96, p < 0.001; Supplement Fig. S1) as

$$\begin{array}{}\text{(2)}& n=\mathrm{0.82}\ln \left(\mathit{\omega }\right)+\mathrm{0.636}=\mathrm{0.82}\ln \left({\displaystyle \frac{Z_{\mathrm{r}}\times \mathrm{WHC}}{\mathit{\alpha }}}\right)+\mathrm{0.636}.\end{array}$$

Effective rooting depth (Z_r) was determined using an analytical carbon cost-benefit model based on ecosystem optimality theory proposed by Guswa (2008). The Z_r model is given as

$$\begin{array}{}\text{(3)}& {\displaystyle }{Z}_{\mathrm{r}}={\displaystyle \frac{\mathit{\alpha }}{\mathrm{WHC}(\mathrm{1}-W)}}\ln \left(X\right);\text{(4)}& {\displaystyle }X=\left\{\begin{array}{c}W\left[\mathrm{1}+\frac{\mathrm{WHC}}{\mathit{\alpha }}\frac{(\mathrm{1}-W{)}^{\mathrm{2}}}{\mathrm{2}A}-\sqrt{\frac{\mathrm{WHC}}{\mathit{\alpha }}\frac{(\mathrm{1}-W{)}^{\mathrm{2}}}{A}+{\left(\frac{\mathrm{WHC}}{\mathit{\alpha }}\frac{(\mathrm{1}-W{)}^{\mathrm{2}}}{\mathrm{2}A}\right)}^{\mathrm{2}}}\right]\begin{array}{ccc}& \mathrm{if}& W>\mathrm{1},\end{array}\\ W\left[\mathrm{1}+\frac{\mathrm{WHC}}{\mathit{\alpha }}\frac{(\mathrm{1}-W{)}^{\mathrm{2}}}{\mathrm{2}A}+\sqrt{\frac{\mathrm{WHC}}{\mathit{\alpha }}\frac{(\mathrm{1}-W{)}^{\mathrm{2}}}{A}+{\left(\frac{\mathrm{WHC}}{\mathit{\alpha }}\frac{(\mathrm{1}-W{)}^{\mathrm{2}}}{\mathrm{2}A}\right)}^{\mathrm{2}}}\right]\begin{array}{ccc}& \mathrm{if}& W<\mathrm{1},\end{array}\end{array}\right.\text{(5)}& {\displaystyle }A={\displaystyle \frac{{\mathit{\gamma }}_{\mathrm{r}}\times \mathrm{RLD}}{\mathrm{SRL}\times \mathrm{WUE}}}\times {\displaystyle \frac{\mathrm{1}}{E_{P\mathit{\_}\mathrm{T}}\times f_{\mathrm{GS}}}};\end{array}$$

where W is the ratio of the multiyear growing season mean P over potential transpiration, E_{P_T}; γ_r is the root respiration rate (g C g⁻¹ roots d⁻¹), which is quantified using the standard Q₁₀ theory (Lloyd and Taylor, 1994; Ryan, 1991) with a fixed Q₁₀ coefficient of 2.0 (Zhao et al., 2011). The base respiration rate at 20 ^∘C for each biome type is determined following Heinsch (2003). RLD is the root length density (cm roots cm⁻³ soil), and SRL is the specific root length (cm roots g⁻¹ roots). We fixed RLD to be 0.1 cm roots cm⁻³ soil and SRL to be 1500 cm roots g⁻¹, representing the median value of these two parameters reported in the literature (Caldwell, 1994; Eissenstat, 1997; Fitter and Hay, 2002; Pregitzer et al., 2002). f_GS is the fraction of the growing season within a year, with the growing season length quantified according to Zhu et al. (2016). WUE is the photosynthetic water use efficiency (g C cm⁻³ H₂O), which is determined for the first period (i.e., 1982–1985) from the ensemble mean from eight ecosystem models (see Data section) of annual gross primary production (GPP) and transpiration (E_T) estimates (i.e., WUE = GPP $/$ E_T). For the following periods, WUE was estimated by considering the effects of changes in atmospheric CO₂ concentration (C_a) and vapor pressure deficit (v) on WUE (Donohue et al., 2013; Wong et al., 1979; Farquhar et al., 1993) as

$$\begin{array}{}\text{(6)}& {\mathrm{WUE}}_{t+\mathrm{1}}={\mathrm{WUE}}_t+{\mathrm{WUE}}_t\left({\displaystyle \frac{C_{\mathrm{a},t+\mathrm{1}}}{-C_{\mathrm{a},t}}}{C}_{\mathrm{a},t}-{\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}{\displaystyle \frac{v_{t+\mathrm{1}}-v_t}{v_t}}\right),\end{array}$$

where t is time in year. Note that the above equation implicitly assumes the same upscaling factor when converting the leaf-level assimilation and transpiration to the canopy level for a given location (Donohue et al., 2017). The spatial pattern of mean annual Z_r is shown in Supplement Fig. S2.

2.1.2 The Shuttleworth–Wallace model

The Shuttleworth–Wallace two-source evapotranspiration model (the S–W model) was used to estimate E_P and its two components (potential transpiration, E_{P_T}, and potential evaporation, E_{P_S}) (Shuttleworth and Wallace, 1985). The S–W model estimates evapotranspiration as

$$\begin{array}{}\text{(7)}& {\displaystyle }\mathit{\lambda }{E}_{\mathrm{P}}=\mathit{\lambda }{E}_{P\mathit{\_}\mathrm{T}}+\mathit{\lambda }{E}_{P\mathit{\_}S}=C_{T}P{M}_T+C_{S}P{M}_S,\text{(8)}& {\displaystyle }P{M}_T={\displaystyle \frac{\mathrm{\Delta }A+(\mathit{\rho }{c}_{p}v-\mathrm{\Delta }{r}_{\mathrm{a}}^{\mathrm{c}}{A}_{\mathrm{s}})/(r_{\mathrm{a}}^{\mathrm{a}}+r_{\mathrm{a}}^{\mathrm{c}})}{\mathrm{\Delta }+\mathit{\gamma }[\mathrm{1}+r_{\mathrm{s}}^{\mathrm{c}}/(r_{\mathrm{a}}^{\mathrm{a}}+r_{\mathrm{a}}^{\mathrm{c}}\left)\right]}},\text{(9)}& {\displaystyle }P{M}_{\mathrm{S}}={\displaystyle \frac{\mathrm{\Delta }A+[\mathit{\rho }{c}_{\mathrm{p}}v-\mathrm{\Delta }{r}_{\mathrm{a}}^{\mathrm{s}}(A-A_{\mathrm{s}}\left)\right]/(r_{\mathrm{a}}^{\mathrm{a}}+r_{\mathrm{a}}^{\mathrm{s}})}{\mathrm{\Delta }+\mathit{\gamma }[\mathrm{1}+r_{\mathrm{s}}^{\mathrm{s}}/(r_{\mathrm{a}}^{\mathrm{a}}+r_{\mathrm{s}}^{\mathrm{c}}\left)\right]}},\text{(10)}& {\displaystyle }{C}_{\mathrm{T}}=[\mathrm{1}+R_{\mathrm{c}}{R}_{\mathrm{a}}/R_{\mathrm{s}}(R_{\mathrm{c}}+R_{\mathrm{a}}){]}^{-\mathrm{1}},\text{(11)}& {\displaystyle }{C}_{\mathrm{S}}=[\mathrm{1}+R_{\mathrm{s}}{R}_{\mathrm{a}}/R_{\mathrm{c}}(R_{\mathrm{s}}+R_{\mathrm{a}}){]}^{-\mathrm{1}},\text{(12)}& {\displaystyle }{R}_{\mathrm{a}}=(\mathrm{\Delta }+\mathit{\gamma })r_{\mathrm{a}}^{\mathrm{a}},\text{(13)}& {\displaystyle }{R}_{\mathrm{s}}=(\mathrm{\Delta }+\mathit{\gamma })r_{\mathrm{a}}^{\mathrm{s}}+\mathit{\gamma }{r}_{\mathrm{s}}^{\mathrm{s}},\text{(14)}& {\displaystyle }{R}_{\mathrm{c}}=(\mathrm{\Delta }+\mathit{\gamma })r_{\mathrm{a}}^{\mathrm{c}}+\mathit{\gamma }{r}_{\mathrm{s}}^{\mathrm{c}},\end{array}$$

where λ is the latent heat for vaporization (MJ kg⁻¹), Δ is the gradient of the saturation vapor pressure with respect to temperature (kPa K⁻¹), ρ is the air density (kg m⁻³), c_p is the specific heat of air at constant pressure (MJ kg⁻¹ K⁻¹), γ is the psychrometric constant (kPa K⁻¹). $r_{\mathrm{a}}^{\mathrm{a}}$, $r_{\mathrm{a}}^{\mathrm{c}}$, and $r_{\mathrm{a}}^{\mathrm{s}}$ are the aerodynamic resistance (s m⁻¹) to heat and vapor transfer between the canopy–air space and the atmosphere, between the leaf and the canopy–air space, and between the soil surface and the canopy–air space, respectively. These three aerodynamic resistance terms are estimated following Sánchez et al. (2008). $r_{\mathrm{s}}^{\mathrm{s}}$ and $r_{\mathrm{s}}^{\mathrm{c}}$ are soil surface resistance and stomatal resistance (the reciprocal of stomatal conductance), respectively. To estimate E_P using the S–W model, $r_{\mathrm{s}}^{\mathrm{s}}$ is set to zero, and $r_{\mathrm{s}}^{\mathrm{c}}$ is set to its non-water-stressed value (Milly and Dunne, 2016). The non-water-stressed values of $r_{\mathrm{s}}^{\mathrm{c}}$ for each biome type are provided in Mu et al. (2007). A is the available energy (equal to net radiation minus ground heat flux, W m⁻²), and A_s is the available energy at the soil surface, which is estimated as a function of L following Beer's law (Campbell and Norman, 1998; Yang and Shang, 2013). As a result, A – A_s is the available energy absorbed by the plant canopy. The impacts of eCO₂ on E_P and its two components are obtained by allowing L and $r_{\mathrm{s}}^{\mathrm{c}}$ to vary with C_a. Recently, Milly and Dunne (2016) showed that the S–W model could most satisfactorily reproduce evapotranspiration estimates under non-water-limited conditions from climate models under eCO₂.

2.1.3 Attribution of runoff changes

We used the BCP model to attribute changes in Q (dQ) due to different influencing factors following Roderick and Farquhar (2011). To a first-order approximation, the change in Q (dQ) is

$$\begin{array}{}\text{(15)}& \mathrm{d}Q={\displaystyle \frac{\partial Q}{\partial P}}\mathrm{d}P+{\displaystyle \frac{\partial Q}{\partial E_{\mathrm{P}}}}\mathrm{d}{E}_{\mathrm{P}}+{\displaystyle \frac{\partial Q}{\partial n}}\mathrm{d}n,\end{array}$$

where $\partial Q/\partial P$, $\partial Q/\partial E_{\mathrm{P}}$, and $\partial Q/\partial n$ represent the sensitivity of Q to changes in P, E_P, and n, respectively, and can be expressed as

$$\begin{array}{}\text{(16)}& {\displaystyle \frac{\partial Q}{\partial P}}=\mathrm{1}-{\displaystyle \frac{E}{P}}\left({\displaystyle \frac{E_{\mathrm{P}}^n}{P^n+E_{\mathrm{P}}^n}}\right),\text{(17)}& {\displaystyle \frac{\partial Q}{\partial E_{\mathrm{P}}}}=-{\displaystyle \frac{E}{E_{\mathrm{P}}}}\left({\displaystyle \frac{P^n}{P^n+E_{\mathrm{P}}^n}}\right),\text{(18)}& {\displaystyle \frac{\partial Q}{\partial n}}=-{\displaystyle \frac{E}{n}}\left[{\displaystyle \frac{\ln (P^n+E_{\mathrm{P}}^n)}{n}}-{\displaystyle \frac{P^n\ln P+E_{\mathrm{P}}^n\ln E_{\mathrm{P}}}{P^n+E_{\mathrm{P}}^n}}\right].\end{array}$$

The physiological (stomatal conductance, g_s) and structural (leaf area index, L, and effective rooting depth, Z_r) parameters impact both E_P and n. More specifically, decreases in g_s lower the transpiration rate per leaf area, whereas increases in L and Z_r enhance the canopy-level transpiration rate. Additionally, increases in L also reduce soil evaporation by shading the soil surface (Shuttleworth and Wallace, 1985). The impact of eCO₂ on parameter n is expressed through its impact on Z_r. On the one hand, increases in WUE induced by eCO₂ permit a larger vegetation carbon uptake per amount of water loss, potentially leading to more carbon allocated to roots and thus a deeper Z_r. Conversely, increases in plant water demand (as quantified by potential transpiration) require vegetation to develop deeper roots to access deeper soil moisture and vice versa (Guswa, 2008). As a result, we write the functional dependencies of E_P and Z_r as

$$\begin{array}{}\text{(19)}& {\displaystyle }{E}_{\mathrm{P}}=f(C_{\mathrm{a}},E_{P\mathit{\_}M}),\text{(20)}& {\displaystyle }{Z}_{\mathrm{r}}=g(C_{\mathrm{a}},O),\end{array}$$

where E_{P_M} is the meteorological component of E_P (without considering the increases in C_a). O represents factors other than eCO₂ that affect Z_r, which effectively encode the climate-change-induced vegetation change. Functions f and g describe these relationships. Changes in E_P and Z_r are given by

$$\begin{array}{}\text{(21)}& {\displaystyle }\mathrm{d}{E}_{\mathrm{P}}={\displaystyle \frac{\partial E_{\mathrm{P}}}{\partial C_{\mathrm{a}}}}\mathrm{d}{C}_{\mathrm{a}}+{\displaystyle \frac{\partial E_{\mathrm{P}}}{\partial E_{P\mathit{\_}\mathrm{M}}}}\mathrm{d}{E}_{P\mathit{\_}\mathrm{M}},\text{(22)}& {\displaystyle }\mathrm{d}{Z}_{\mathrm{r}}={\displaystyle \frac{\partial Z_{\mathrm{r}}}{\partial C_{\mathrm{a}}}}\mathrm{d}{C}_{\mathrm{a}}+{\displaystyle \frac{\partial Z_{\mathrm{r}}}{\partial O}}\mathrm{d}O.\end{array}$$

Combining Eqs. (2), (15), (21), and (22), we have

$$\begin{array}{}\text{(23)}& \begin{array}{rl}\mathrm{d}Q& ={\displaystyle \frac{\partial Q}{\partial P}}\mathrm{d}P+\left({\displaystyle \frac{\partial Q}{\partial E_{\mathrm{P}}}}{\displaystyle \frac{\partial E_{\mathrm{P}}}{\partial C_{\mathrm{a}}}}+{\displaystyle \frac{\mathrm{0.82}}{Z_{\mathrm{r}}}}{\displaystyle \frac{\partial Q}{\partial n}}{\displaystyle \frac{\partial Z_{\mathrm{r}}}{\partial C_{\mathrm{a}}}}\right)\mathrm{d}{C}_{\mathrm{a}}\\ & +{\displaystyle \frac{\partial Q}{\partial E_{\mathrm{P}}}}{\displaystyle \frac{\partial E_{\mathrm{P}}}{\partial E_{P\mathit{\_}\mathrm{M}}}}\mathrm{d}{E}_{P\mathit{\_}\mathrm{M}}+{\displaystyle \frac{\mathrm{0.82}}{\mathit{\alpha }}}{\displaystyle \frac{\partial Q}{\partial n}}\mathrm{d}\mathit{\alpha }\\ & +{\displaystyle \frac{\mathrm{0.82}}{Z_{\mathrm{r}}}}{\displaystyle \frac{\partial Q}{\partial n}}{\displaystyle \frac{\partial Z_{\mathrm{r}}}{\partial O}}O.\end{array}\end{array}$$

The first term on the right-hand side of Eq. (23) represents dQ caused by P change, and the second term represents dQ caused by eCO₂. The third term calculates dQ induced by changes in E_{P_M} and is calculated as $\frac{\partial Q}{\partial E_{\mathrm{P}}}\mathrm{d}{E}_{\mathrm{P}}-\frac{\partial Q}{\partial E_{\mathrm{P}}}\frac{\partial E_{\mathrm{P}}}{\partial C_{\mathrm{a}}}\mathrm{d}{C}_{\mathrm{a}}$. The fourth and fifth terms on the right-hand side of Eq. (23) represent dQ caused by changes in rainfall intensity and climate-change-induced vegetation change, respectively, and we group them as one factor in the attribution of dQ. Since our primary focus was to examine how eCO₂ affects vegetation and the consequent impact on Q, as well as its relative importance to changes in P and E_{P_M}, the other factors driving dQ were estimated as the residual of Eq. (23) (i.e., total dQ minus the sum of dQ induced by dP, dE_{P_M}, and eCO₂). By introducing Eqs. (17) and (18) into Eq. (23), the sensitivity of Q to eCO₂ (S_{Q_to_eCO2}, mm yr⁻¹ ppm⁻¹) is written as

$$\begin{array}{}\text{(24)}& \begin{array}{rl}& S_{\mathrm{Q}\mathrm{\_}\mathrm{to}\mathrm{\_}\mathrm{eCO}\mathrm{2}}=-{\displaystyle \frac{E}{E_{\mathrm{P}}}}\left({\displaystyle \frac{P^n}{P^n+E_{\mathrm{P}}^n}}\right){\displaystyle \frac{\partial E_{\mathrm{P}}}{\partial C_{\mathrm{a}}}}-{\displaystyle \frac{E}{n}}{\displaystyle \frac{\mathrm{0.82}}{Z_{\mathrm{r}}}}\\ & \left[{\displaystyle \frac{\ln (P^n+E_{\mathrm{P}}^n)}{n}}-{\displaystyle \frac{P^n\ln P+E_{\mathrm{P}}^n\ln E_{\mathrm{P}}}{P^n+E_{\mathrm{P}}^n}}\right]{\displaystyle \frac{\partial Z_{\mathrm{r}}}{\partial C_{\mathrm{a}}}}.\end{array}\end{array}$$

The sensitivities of E_P and Z_r to eCO₂ (i.e., $\frac{\partial E_{\mathrm{P}}}{\partial C_{\mathrm{a}}}$ and $\frac{\partial Z_{\mathrm{r}}}{\partial C_{\mathrm{a}}}$) are quantified by numerically running the E_P model and Z_r model with and without changes in C_a, respectively. The difference between the two simulations under the two C_a scenarios is considered the net effect of eCO₂ on Q.

2.1.4 Stomatal conductance response to eCO₂

The response of leaf-level stomatal conductance (g_s) response to eCO₂ was determined using 244 field experiments with artificially elevated CO₂ across a broad range of bioclimates (Ainsworth and Rogers, 2007). We linearly rescaled the reported change in g_s for the magnitude of eCO₂ in each of the 244 studies to obtain the sensitivity of g_s to eCO₂, that is, the percentage change in g_s per 1 % increase in C_a. We then classified the 244 observations based on their biome type to construct a biome-type-based look-up table of g_s sensitivity to eCO₂.

2.1.5 Resource availability index and L response to eCO₂

The response of L to eCO₂ was predicted based on the response of WUE to eCO₂ adjusted by the local resource availability. We define a site resource availability index (β) based on growing season mean L following Donohue et al. (2017). This is because observed L at a site is the net response to the local growing conditions and provides an effective proxy of the growing conditions experienced by vegetation (Donohue et al., 2017). Another advantage of this approach is that L can be readily measured directly or remotely. We calculated β as

$$\begin{array}{}\text{(25)}& \mathit{\beta }=\mathrm{1}-{\mathrm{e}}^{-\mathit{\tau }L},\end{array}$$

where τ is an exponential extinction coefficient, which typically varies from 0.3 to 1.2 (Campbell and Norman, 1998) and is set to be 0.7 herein. Broadly across the globe, β also corresponds well with climate aridity. The calculated β increases from 0.0 with low resource availability (typically dry and/or cold) to 1.0 with high resource availability (typically warm and humid) (Fig. 2). This suggests a predominant role of the climate in shaping the global vegetation pattern (Budyko, 1974; Nemani et al., 2003; Yang et al., 2015). This also implies that the resource limitations on plant growth are mainly exerted by climate, which is consistent with the framework of climate limitation on vegetation proposed in previous studies (Nemani et al., 2003; Budyko, 1974; Yang et al., 2015). Then following Norby and Zak (2011), who showed that the observed response of L to eCO₂ was a nonlinear function of L, we estimated the relative change in L induced by eCO₂ as per Donohue et al. (2017):

$$\begin{array}{}\text{(26)}& {\displaystyle \frac{\mathrm{d}L}{L}}={\displaystyle \frac{\mathrm{dWUE}}{\mathrm{WUE}}}(\mathrm{1}-\mathit{\beta }{)}^{\mathrm{2}}=\left({\displaystyle \frac{\mathrm{d}{C}_{\mathrm{a}}}{C_{\mathrm{a}}}}-{\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}{\displaystyle \frac{\mathrm{d}v}{v}}\right)e^{-\mathrm{2}\mathit{\tau }L}.\end{array}$$

Figure 2 Spatial distributions of (a) resource availability index categories and (b) climate aridity zones over global vegetated lands for 1982–2010. For the land surface, blank areas are non-vegetated regions. Respectively, there are 2536, 8194, 10316, 12930, and 9093 $\mathrm{0.5}{}^{\circ }\times \mathrm{0.5}{}^{\circ }$ resolution grid cells in the 0.0–0.2, 0.2–0.4, 0.4–0.6, 0.6–0.8, and 0.8–1.0 resource availability index categories.

2.2 Data

The BCP model is validated against observed Q in 2268 strictly selected unimpaired catchments located across the globe that cover a broad range of bioclimates (Fig. 3). Originally, daily and/or monthly Q observations were collected from more than 22 000 catchments globally (Beck et al., 2019). Three selection criteria were implemented to ensure that only catchments with continuous Q records that are negligibly affected by humans were used. First, catchments with > 5 % missing data during the entire study period (1982–2010) were removed. Linear interpolation was applied to fill the gaps in the remaining Q series. Second, catchments smaller than 100 km² were excluded. This is to ensure that at least one precipitation pixel (i.e., 0.1^∘ × 0.1^∘ or ∼ 100 km²) is included for a catchment. Third, we excluded catchments where observed Q is likely to be affected by human interventions, including catchments with (i) significant forest gain or loss (> 2 % of the total catchment area) (Hansen et al., 2013), (ii) irrigated areas larger than 2 % (Siebert et al., 2005), (iii) urban areas (https://www.edenextdata.com/?q=content/esa-globcover-version-23-2009-300m-resolution-land-cover-map-0, last access: 17 June 2019) larger than 2 %, and (iv) the presence of large dams (Lehner et al., 2011) (i.e., where the reservoir's capacity in a catchment is larger than 10 % of the catchment mean annual Q). Exactly 2268 catchments pass these selection criteria (Fig. 3).

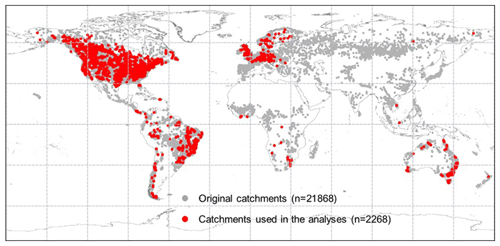
Figure 3 Locations of the catchments across the globe. The grey dots show the locations of the original 21 856 catchments, and red dots are the 2268 catchments that pass the selection criteria and are used herein.

Precipitation from 1981 through 2010 was sourced from the Multi-Source Weighted-Ensemble Precipitation (MSWEP) version 2 dataset, which has a 3 h temporal resolution and 0.1^∘ spatial resolution (Beck et al., 2019). The mean rainfall intensity was calculated as the ratio of annual total precipitation over the number of wet days (with daily precipitation higher than 1 mm; Hartmann et al., 2013). Other climate variables, including net radiation, air temperature, relative humidity, air pressure, and wind speed were obtained from the Multi-scale Synthesis and Terrestrial Model Intercomparison Project (MsTMIP; Wei et al., 2014). To obtain a spatial pattern of WUE, global monthly GPP and E_T estimates over 1982–1985 were obtained from eight ecosystem models from MsTMIP (Huntzinger et al., 2013), including (i) CLM (Mao et al., 2012), (ii) CLM4-VIC (Li et al., 2011), (iii) ISAM (Jain et al., 1996), (iv) TRIPLEX (Peng et al., 2002), (v) LPJ-wsl (Sitch et al., 2003), (vi) ORCHIDEE-LSCE (Krinner et al., 2005), (vii) SiBCASA (Schaefer et al., 2008), and (viii) VISIT (Ito, 2010). Monthly C_a from 1982–2010 was obtained from the Hawaiian Mauna Loa Observatory (http://www.esrl.noaa.gov/gmd/obop/mlo/, last access: 30 June 2019), and we assume a uniform C_a concentration across the globe at the mean annual scale (i.e., 5 years). Monthly L for 1982–2010 was derived from Zhu et al. (2013) based on AVHRR GIMMS-3g NDVI data (Pinzon and Tucker, 2014). Land cover classification in the year 2001 was acquired from the Moderate Resolution Imaging Spectroradiometer (MODIS) land use map (MOD12Q1) available from the NASA Data Center (Friedl et al., 2010). The global C₄ vegetation fraction was obtained from the International Satellite Land Surface Climatology Project (ISLSCP) Initiative II C4 Vegetation Percentage dataset (Still et al., 2009; http://webmap.ornl.gov/ogcdown/dataset.jsp?ds_id=932, last access: 24 June 2018). Soil texture data at 30^′′ spatial resolution was acquired from the Harmonized World Soil Database (HWSD) (Nachtergaele et al., 2009), which was used to determine WHC according to the US Department of Agriculture (USDA) soil classification (Saxton and Rawls, 2006). For catchment-scale calculations, these gridded data were further aggregated for individual catchments at a mean annual scale (i.e., 5 years). For grid cell analyses, all gridded datasets were resampled to a 0.5^∘ resolution.

3 Results

3.1 Validation of the BCP model in runoff estimation

The validity of the BCP model is tested by comparing the estimated Q with observed Q, in terms of both spatial and temporal variability, at the 2268 unimpaired catchments (Fig. 4). Spatially, the BCP model well captures the observed spatial variability in Q at the mean annual scale, with a coefficient of determination (R²) of 0.93, root-mean-squared error (RMSE) of 87.9 mm yr⁻¹, and mean bias (estimated Q minus observed Q) of −11.4 mm yr⁻¹ (Fig. 4a). Temporally, trends in mean annual Q are also reasonably reproduced by the BCP model, having an R² of 0.71, RMSE of 0.71 mm yr⁻², and mean bias of −0.05 mm yr⁻² (Fig. 4b). Additionally, we also perform a sensitivity analysis by comparing the simulated Q using the BCP model with and without considering eCO₂. Results show that the BCP model, when considering eCO₂, performed better in estimating Q trends than the BCP model without considering eCO₂, as evidenced by an improvement of R² by 0.02, a reduction of RMSE by 0.03 mm yr⁻², and a decrease of mean bias by 0.11 mm yr⁻², averaged over all 2268 catchments (Fig. 4d). More apparent improvements of the BCP model performance with the consideration of eCO₂ are found in regions having a relatively higher resource availability index. For β of 0.4–0.6, 0.6–0.8, and 0.8–1.0, the mean bias of simulated Q trends with eCO₂ is −0.02, 0.06, or −0.36 mm yr⁻² but increased to 0.24, 0.20, or −0.53 mm yr⁻², respectively, when eCO₂ is not considered (Fig. 4d). These results suggest that the analytical framework developed herein captures the eCO₂ signal on the observed Q changes.

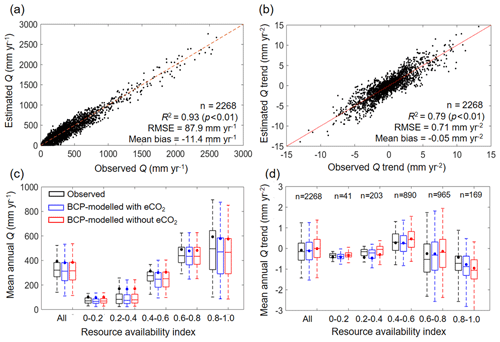
Figure 4 Validation of estimated Q at catchments. (a) Model performance in predicting mean annual Q in 2268 catchments over 1982–2010. (b) Model performance in predicting Q trend in 2268 catchments during 1982–2010. (c) Model performance in predicting mean annual Q in 2268 catchments over 1982–2010 stratified by resource availability index category. (d) Model performance in predicting Q trend in 2268 catchments over 1982–2010 stratified by resource availability index category. The number of catchments in each resource availability index category are provided at the top of each subplot. The legend from (c) applies to (d). In (c) and (d), the upper and lower box edges represent the quartile division, the inner horizontal line is the median, the dots indicate the mean, and the dashed lines represent the 5th and 95th percentiles.

3.2 Plant physiological and structural responses to eCO₂

The physiological response of plants to eCO₂, that is, the response of g_s to eCO₂, is directly compiled from field experiments and summarized for each plant functional type in Ainsworth and Rogers (2007) (also see Supplement Fig. S3). All those field experiments report a reduction of g_s in response to eCO₂, with the largest g_s reduction found in C₄ crops and lowest in shrubs for the same level of eCO₂. On average, for a 1 % increase in C_a, g_s decreases by 0.47 % ± 0.12 % (mean ± 1 standard deviation), which means that g_s decreases by 5.67 % ± 1.47 % under a 12.1 % increase in C_a over 1982–2010 (i.e., from ∼343.7 ppm in 1982–1985 to 385.2 ppm in 2006–2010; Keeling et al., 2001). This result is consistent with a recent isotope-based study (i.e., ∼ 5 % reduction of g_s during the past 3 decades; Frank et al., 2015).

For structural response, averaged across global vegetated lands, our model reveals that elevated C_a has caused an increase of L by 2.12 % (0.14 % and 3.88 % for 5th and 95th percentiles) over 1982–2010 (Fig. 5a and b). Despite this relatively small fertilization effect of eCO₂ on L at the global scale, an evident gradient is found in the L–eCO₂ response: a larger eCO₂-induced relative L increase is found in low resource availability regions (smaller β value in Fig. 2a) and vice versa (Fig. 5b). This modeled pattern of L–eCO₂ response agrees very well with observations at the Free-Air CO₂ Enrichment (FACE) observations (R²= 0.96, p < 0.01; Fig. 5c) and is also consistent with large-scale satellite-based observations (Donohue et al., 2013; Zhu et al., 2016; Yang et al., 2016a).

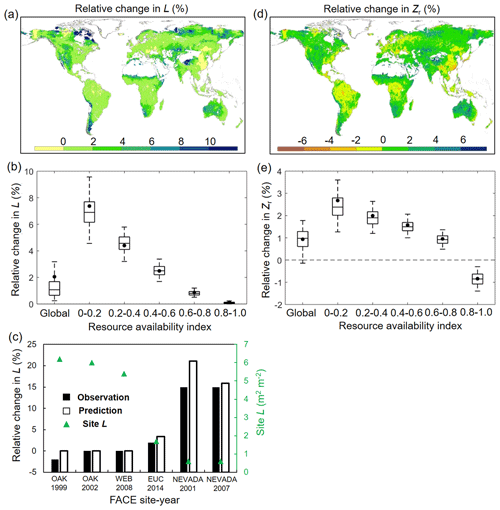
Figure 5 Modeled relative changes in L and Z_r caused by eCO₂. (a) Spatial distribution of relative change in L induced by eCO₂ during 1982–2010. (b) Same as (a) but for each resource availability index category. (c) Validation of predicted L change against in situ measurement during six Free-Air CO₂ Enrichment (FACE) experiments. Note that only FACE sites with undisturbed vegetation are used (see Donohue et al., 2017). (d) Spatial distribution of relative change in Z_r induced by eCO₂ during 1982–2010. (e) Same as (d) but for each resource availability index category. In panels (b) and (e) the upper and lower box edges represent the quartile divisions, the inner horizontal line is the median, the dots indicate the mean, and the dashed lines represent the 5th and 95th percentiles. The number of grid cells in each resource availability index category is provided in Fig. 2.

In terms of Z_r, our modeling results show that elevated C_a over 1982–2010 has resulted in a very minor (0.93 %, −0.12 % and 1.85 % for 5th and 95th percentiles) overall increase of Z_r averaged across the globe (Fig. 5e). Since large-scale observations of Z_r in response to eCO₂ are not available, we are not able to quantitatively validate the estimated response of Z_r to eCO₂. Nevertheless, the modeled result that eCO₂ increases Z_r is overwhelmingly found in site- and/or plant-level experiments (Nie et al., 2013) (Tables S1 and S2). Moreover, similar to L, the response of Z_r to eCO₂ also exhibits a notable difference along the resource availability gradient (Fig. 5d and e). The positive response of Z_r to eCO₂ is larger in low-β regions and gradually decreases as the resource availability becomes higher. In high-β regions (e.g., tropical rainforest and Southeast Asia), Z_r even shows a slight decrease in response to eCO₂, suggesting a reduced plant water need given the range of C_a over 1982–2010 in those regions.

3.3 Attribution of runoff changes over 1982–2010

Over 1982–2010, C_a increased by ∼ 12.1 %. For the same period, the BCP model detected a very small reduction in Q of ∼ 1.7 % (or 2.2 mm yr⁻¹) induced by eCO₂ via vegetation feedbacks across the entire global vegetated lands (Figs. 6b and 7d). This 1.7 % reduction in Q, under the context of 12.1 % increases in C_a, demonstrates a muted response of Q to eCO₂. In addition, the overall negative effect of eCO₂ on Q suggests that the structural forcing of eCO₂ on vegetation water consumption (both aboveground and belowground) outweighs the physiological effect of eCO₂ driving leaf-level water saving. Across the global vegetated lands and for the same period, the physiological response of vegetation to eCO₂ has led to an increased Q by 0.7 % (or 0.9 mm yr⁻¹), with the simulated Q increases being increasingly larger as β increases (Fig. 6d). By contrast, the structural response of vegetation to eCO₂ has resulted in an overall Q reduction by 2.4 % (or 3.1 mm yr⁻¹), with the decreases in Q being increasingly smaller as β increases (Fig. 6e). These two opposite responses of vegetation water use to eCO₂ along the resource availability gradient have led to a significant positive trend (p < 0.01) in the Q–eCO₂ response along the resource availability gradient, from a negative response in low-β landscapes to a positive response in high-β landscapes (Fig. 6b). Nevertheless, an exception is found in extreme arid zones (i.e., when β < 0.1; Fig. 6b). This is because, in extremely dry areas, the availability of water defines the outcome, and the sensitivity of Q to any changes in land surface properties is very small (Donohue et al., 2013; Roderick et al., 2014).

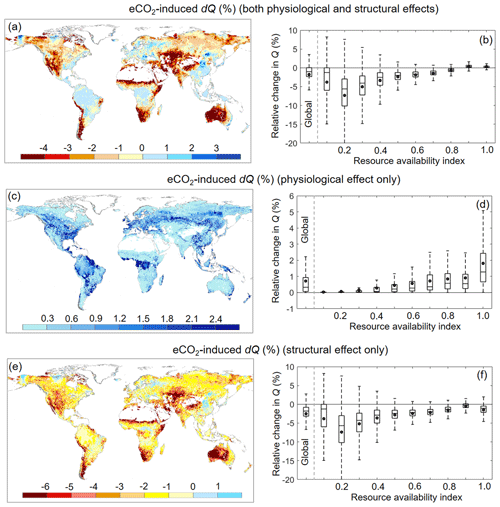
Figure 6 Relative Q change induced by eCO₂ during 1982–2010 across the global vegetated lands. (a) Spatial distribution of relative change in Q induced by eCO₂. (b) Boxplot of relative change in Q induced by eCO₂ for each resource availability index category. (c) Spatial distribution of relative change in Q induced by eCO₂ when only the physiological effect is considered. (d) Boxplot of relative change in Q induced by eCO₂ when only the physiological effect is considered for each resource availability index category. (e) Spatial distribution of relative change in Q induced by eCO₂ when only the aboveground and belowground structural effects are considered. (f) Boxplot of relative change in Q induced by eCO₂ when only the aboveground and belowground structural effects are considered for each resource availability index category. In (b), (d), and (f) the upper and lower box edges represent the quartile divisions, the inner horizontal line is the median, the dots indicate the mean, and the dashed lines represent the 5th and 95th percentiles. The number of grid cells in each resource availability index category is provided in Fig. 2.

We then attribute dQ to different forcing factors between 1982–1985 and 2006–2010 over the global vegetated lands (Figs. 7 and 8). Compared with the early 1980s (i.e., 1982–1985), mean observed Q over the global vegetated lands in the late 2010s (i.e., 2006–2010) increased by 29.7 mm yr⁻¹, and the observed pattern with comparable magnitude in dQ is well captured by the BCP model (Fig. 4b and d). Consistent with relative Q changes (in %; Fig. 6), the impacts of eCO₂ on the absolute Q change (in mm yr⁻¹) also exhibit a significant upward trend as β increases (0.53 mm yr⁻¹ per 0.1 increase in β, p < 0.01). Compared to that, increases in P led to a 43.9 mm yr⁻¹ increase in Q, and enhanced E_{P_M} has resulted in a decreased Q by 5.3 mm yr⁻¹ (Fig. 7f). For the entire vegetated lands and each resource availability category, the impact of dP on Q generally dominates dQ and is often much higher than that of eCO₂ (Fig. 7). An exception is the low-β regions (β < 0.2), where the impact of eCO₂ on Q outweighs the impact of dP on Q (Fig. 8a). As for the impact E_{P_M} on Q, it also shows a notable gradient with changes in β as detected for the eCO₂ effect, with the impact of E_{P_M} on Q being increasingly negative as β increases (Fig. 8b-e). The combined influence of other factors including changes in rainfall intensity (Porporato et al., 2004; Westra et al., 2013) and climate-change-induced vegetation change (e.g., higher L) have, in general, exerted a negative impact on Q.

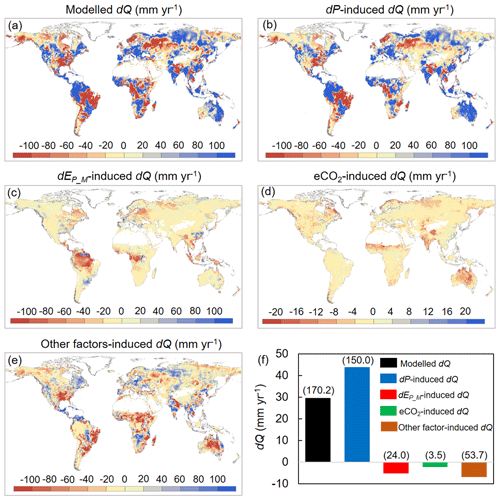
Figure 7 Attribution of changes in Q between 1982–1985 and 2006–2010 across global vegetated lands. (a) Spatial distribution of changes in Q. (b–e) Spatial distributions of changes in Q induced by (b) changes in P, (c) changes in E_{P_M}, (d) eCO₂, and (e) changes in other factors (mainly rainfall intensity and climate-change-induced vegetation change). (f) Attribution of changes in Q between 1982–1985 and 2006–2010 averaged over the entire global vegetated lands. Values in parentheses represent 1 standard deviation of each response among all vegetated grid cells.

Figure 8 Attribution of changes in Q between 1982–1985 and 2006–2010 at grid boxes within each resource availability index (β) category. Values in parentheses represent 1 standard deviation of each response among grid cells within each resource availability index category. The number of grid cells in each resource availability index category is provided in Fig. 2.

Since changes in meteorological factors (P and E_{P_M}) are often considered to dominate changes in Q and have been extensively examined previously (e.g., Roderick and Farquhar, 2011; Yang et al., 2018; Zhang et al., 2018), we next examine the sensitivity of Q to eCO₂ (S_{Q_to_eCO2}) and compare it with the sensitivity of Q to changes in P and E_{P_M}. Because C_a has different units from P and E_{P_M}, we use relative units to better compare the three sensitivities (Fig. 9). Globally, an increase in C_a by 1 % only leads to a decrease of Q by ∼ 0.14 % (equivalent to ∼ 1.7 % for the range of eCO₂ experienced over 1982–2010). Similar to the attribution results shown above (Fig. 6a and b), S_{Q_to_eCO2} is generally more negative in global arid ecosystems where β is low (Fig. 9a and b). The negative S_{Q_to_eCO2} diminishes quickly as β increases and becomes positive S_{Q_to_eCO2} in high-β regions. The overall small S_{Q_to_eCO2} is further manifested when comparing S_{Q_to_eCO2} with the sensitivities of Q to P and E_{P_M}. Averaged across the global vegetated lands, the same relative change in P and E_P would, respectively, lead to an ∼ 10 times and ∼ 4 times stronger impact on Q than eCO₂ does. This highlights the predominant role of climate in shaping the global Q regime (Figs. 9c–f and S4).

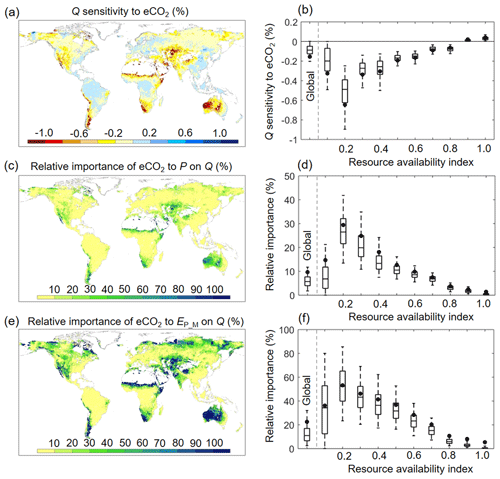
Figure 9 Sensitivity of Q to eCO₂ and its relative importance to P and E_{P_M} across the globe. (a) Spatial distribution of Q sensitivity to eCO₂ (percent change in Q per 1 % change in C_a). (b) Boxplot of Q sensitivity to eCO₂ for each resource availability index category. (c) Relative importance of eCO₂ to Q compared to changes in P on Q (percent change in Q per 1 % change in C_a compared to percent change in Q per 1 % change in P). (d) Boxplot of the relative importance of eCO₂ to Q compared to changes in P on Q for each resource availability category. (e) Relative importance of eCO₂ toQ compared to changes in E_{P_M} on Q (percent change in Q per 1 % change in C_a compared to percent change in Q per 1 % change in E_P). (f) Boxplot of the relative importance of eCO₂ to Q compared to changes in E_{P_M} on Q for each resource availability category. In (b), (d), and (f), the upper and lower box edges represent the quartile divisions, the inner horizontal line is the median, the dots indicate the mean value, and the dashed lines represent the 5th and 95th percentiles. The number of grid cells in each resource availability index category is provided in Fig. 2.

4 Discussion and concluding remarks

Elevation in atmospheric CO₂ concentration (and other greenhouses gases) is regarded as the ultimate driver of anthropogenic climate change, with consequent impacts on Q. Although the impacts of climate change on Q have been extensively studied, the response of Q to eCO₂ through vegetation feedbacks is less understood and remains controversial (Gedney et al., 2006; Piao et al., 2007; Huntington, 2008; Cheng et al., 2014; Trancoso et al., 2017; Yang et al., 2016a; Ukkola et al., 2016a, b). Here, by developing an analytical attribution framework, we detected a very small response of global Q to eCO₂-induced changes in vegetation structural (both aboveground and belowground) and physiological functioning (Figs. 6–8), suggesting that the eCO₂ vegetation feedback only exerts a minor impact on water resources (partly due to the two opposing water effects between the structural and physiological responses to eCO₂) for the range of eCO₂ experienced over 1982–2010.

The overall negative impact of eCO₂ on Q detected herein suggests that increased vegetation water consumption driven by the structural response of vegetation (i.e., increases in L and Z_r) to eCO₂ outweighs the functional change of leaf-level water saving caused by the physiological effect of eCO₂ (i.e., decreases in g_s). This result is consistent with previous findings by Cheng et al. (2014), Trancoso et al. (2017), and Ukkola et al. (2016a). In addition, we also detected a significant positive trend (p < 0.01) in the Q–eCO₂ response along the resource availability gradient (Figs. 6–9). This Q–eCO₂ response pattern suggests that the structural response of vegetation (i.e., increases in L and Z_r) to eCO₂ is larger in areas with lower resource availability and gradually decreases as resources become less limiting on plant growth (Fig. 5). The positive response of Q to eCO₂ in high-β catchments (primarily located in tropical rainforests; Fig. 6a) implies a dominant effect of eCO₂-induced partial stomatal closure over increases in L and Z_r on E in these environments (Fig. 6). This is reasonable, as both theoretical predictions and in situ observations have consistently reported a negligible response of L to eCO₂ in humid and closed-canopy environments (Donohue et al., 2017; Yang et al., 2016a; Norby and Zak, 2011; Körner and Arnone, 1992). In such environments, water is generally abundant with light and/or nutrient availability limiting vegetation growth (Nemani et al., 2003; Yang et al., 2015), and vegetation has evolved to efficiently capture light by maximizing its aboveground structure (i.e., L). As a result, in these high-L regions, vegetation has already absorbed most of the incident light, and any extra leaves would not materially increase the light absorption (Yang et al., 2016a). By contrast, in dry regions, an eCO₂-induced increase in vegetation water use efficiency (so less transpiration for the same amount of carbon assimilation at the leaf level) would lead to an increase in L that is directly proportional to an increase in water use efficiency which would increase canopy-level carbon fixation (Fig. 5b). This finding is consistent with satellite observations (Donohue et al., 2013) and in situ FACE experiments (Norby and Zak, 2011).

Our findings have important implications for an improved understanding of the global hydrological cycle and managing the world's water resources in a changing climate. Climate models have predicted an increased Q that is primarily driven by an increased P for the 21st century (Lian et al., 2021; Milly and Dunne, 2016; Swann et al., 2016; Yang et al., 2018). Here we show that eCO₂-induced vegetation feedbacks would mitigate this positive impact of climate change on Q in relatively dry regions and exacerbate the Q increase in relatively wet regions. In addition, higher C_a and increased P enhance the availability of resources for vegetation growth, which increases vegetation coverage or L (Piao et al., 2020; Zhang et al., 2020a, b). As the vegetation aboveground structural responses to eCO₂ decrease with the increase of L, the predicted future L increases suggest that the structural response of vegetation to eCO₂ may eventually decrease, and the physiological effect of vegetation on eCO₂ may become increasingly dominant in the overall response of vegetation water use to eCO₂, leading to an increasing water-saving effect of vegetation in response to eCO₂ under future climate change (Zhang et al., 2020b). Analyses of the state-of-the-art climate model outputs already consistently show this water-saving effect of eCO₂ globally, especially in relatively warm and humid environments where L is high (Yang et al., 2019). Nevertheless, this may partly be because only some climate models consider the physiological effect while ignoring structural responses of vegetation to eCO₂. In addition, the impacts of eCO₂ on Q in relatively dry regions are still highly uncertain and show a great diversity between climate models (Zhang et al., 2020b).

Finally, it is worthwhile noting that there are several limitations in the developed modeling framework. First, the rooting depth model by Guswa (2008) adopted herein employs an intensive root water uptake strategy, which assumes that root water uptake occurs at a potential rate (i.e., E_{P_T}) until soil moisture reaches the wilting point when transpiration is completely suppressed (Guswa, 2008). This intensive root water uptake strategy differs from the root water uptake strategy employed in the stochastic soil water balance model by Porporato et al. (2004), which is a more conservative strategy under which root water uptake linearly decreases with the decrease of soil moisture (Porporato et al., 2004). Combining the two strategies into one modeling framework potentially leads to inconsistency in the theoretical aspect of the approach. In fact, a later study by Guswa (2010) incorporated the soil water balance model by Porporato et al. (2004) into Guswa's cost-benefit framework for rooting depth (referred to as the Guswa-2010 approach herein). However, the Guswa-2010 approach could not provide an explicit solution for Z_r, because the solution for transpiration in Porporato's model is an incomplete gamma function of Z_r (Guswa, 2010; Porporato et al., 2004). As a result, to allow an analytical solution to be derived, we used Guswa (2008) for Z_r in our modeling framework. According to Guswa (2010), using the conservative root water uptake strategy resulted in a slightly deeper Z_r compared to when the intensive strategy was used. Despite that, the response of Z_r to changes in C_a under the two strategies should be similar, as the effects of eCO₂ on Z_r are expressed via water use efficiency and E_{P_T} in our parameterization, which are independent of Z_r parameterizations. This means that adopting different root water uptake strategies would only lead to differences in the resultant absolute magnitude of runoff (Q) but unlikely to result in differences in the response of Q to eCO₂, especially when the relative magnitude is used (Figs. 5d, e and 6a, b, e and f). Alternatively, Rodríguez-Iturbe and Porporato (2004) incorporated the intensive root water uptake strategy into a stochastic soil water balance model and obtained a steady-state solution that has a simper form than the one by Porporato et al. (2004) and also mimics the Budyko curve. This approach deserves further investigation. Second, if interpreted strictly from a theoretical perspective, the model by Porporato et al. (2004) is more suitable to estimate hydrological partitioning during growing seasons instead of over the entire year as it assumes a constant evaporative demand and precipitation regimes and does not account for snow processes. Expanding all these simplifications and acknowledging imperfect knowledge and parameterization would require further analyses to better understand how they might affect the results shown here. Nevertheless, the uncertainties caused by these simplifications in the model by Porporato et al. (2004) might be partly overcome during the empirical connection made here between Porporato's model and Choudhury's formulation of the Budyko curve, as evidenced by the overall good performance of the developed BCP model in capturing the observed Q (Fig. 4). The third limitation of the current study lies in the steady-state assumption of the modeling framework. More specifically, the steady-state assumption is made in (i) catchment water balance and (ii) vegetation functioning. For point (i), a 5-year period does not necessarily guarantee zero-storage change. Nevertheless, the imbalance in water balance calculation under a steady-state assumption at a 5-year scale is generally very small (i.e., typically less than 6 % of P in arid regions and less than 3 % of P in humid regions) (Han et al., 2020). For point (ii), both Guswa's model for Z_r and Donohue's model for L (see Sect. 2.1.5) adopted herein were developed for steady-state vegetation (i.e., mature and undisturbed vegetation). Applying these two models to immature (e.g., seedlings) and/or disturbed vegetation can be problematic, because immature and/or disturbed vegetation may have very different water use and carbon allocation strategies compared to steady-state vegetation (Donohue et al., 2017; Kuczera, 1987). However, the issues of vegetation age and disturbances are extremely complex and are well beyond our scope. Moreover, global datasets of vegetation age and disturbances are currently lacking. In this light, our modeled response of Q to eCO₂ should be regarded as if all vegetation was mature and undisturbed. Further efforts are needed to better quantify the age and disturbances of vegetation and to better understand the water use and carbon allocation strategies through the entire vegetation life cycle and under various types of disturbances.