the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Interpretation of multi-scale permeability data through an information theory perspective
Aronne Dell'Oca
Alberto Guadagnini
Monica Riva
We employ elements of information theory to quantify (i) the information content related to data collected at given measurement scales within the
same porous medium domain and (ii) the relationships among information contents of datasets associated with differing scales. We focus on gas permeability data collected over Berea Sandstone and Topopah Spring Tuff
blocks, considering four measurement scales. We quantify the way information
is shared across these scales through (i) the Shannon entropy of the data
associated with each support scale, (ii) mutual information shared between
data taken at increasing support scales, and (iii) multivariate mutual
information shared within triplets of datasets, each associated with a given
scale. We also assess the level of uniqueness, redundancy and synergy
(rendering, i.e., information partitioning) of information content that the
data associated with the intermediate and largest scales provide with
respect to the information embedded in the data collected at the smallest
support scale in a triplet.
Highlights.
-
Information theory allows characterization of the information content of permeability data related to differing measurement scales.
-
An increase in the measurement scale is associated with quantifiable loss of information about permeability.
-
Redundant, unique and synergetic contributions of information are evaluated for triplets of permeability datasets, each taken at a given scale.
- Article
(1736 KB) - Full-text XML
-
Supplement
(460 KB) - BibTeX
- EndNote
Characterization of permeability of porous media plays a major role in a variety of hydrological settings. There are abundant studies documenting that permeability values and their associated statistics depend on a variety of scales, i.e., the measurement support (or data support), the sampling window (domain of investigation), the spatial correlation (degree of structural coherence) and the spatial resolution (rendering the degree of the descriptive detail associated with the characterization of a porous system) (see, e.g., Brace, 1984; Clauser, 1992; Neuman, 1994; Schad and Teutsch, 1994; Rovey and Cherkauer, 1995; Sanchez-Villa et al., 1996; Schulze-Makuch and Cherkauer, 1998; Schulze-Makuch et al., 1999; Tidwell and Wilson, 1999a, b, 2000; Vesselinov et al., 2001a, b; Winter and Tartakovsky, 2001; Hyun et al., 2002; Neuman and Di Federico, 2003; Maréchal et al., 2004; Illman, 2004; Cintoli et al., 2005; Riva et al., 2013; Guadagnini et al., 2013, 2018, and references therein). Among these scales, we focus here on the characteristic length associated with data collection (i.e., support scale).
In this context, experimental evidence at the laboratory scale (observation scale on the order 0.1–1.0 m) suggests that the mean value and the correlation length of the permeability field tend to increase with the size of the data support, the opposite trend being documented for the variance (e.g., Tidwell and Wilson, 1999a, b, 2000). Similar observations, albeit with some discrepancies, are also tied to investigations at larger scales (i.e., 10–1000 m) (Andersson et al., 1988; Guzman et al., 1994, 1996; Neumann, 1994; Schulze-Makuch and Cherkauer, 1998; Zlotnik et al., 2000). We consider here laboratory-scale permeability datasets which are associated with various measurement scales.

Figure 1Examples of spatial distributions of the natural logarithm of normalized gas permeability, , for two faces of a cubic block of Berea Sandstone (first and second rows) and Topopah Spring Tuff (third and fourth rows) taken with four increasing support scales (columns, left to right).
The above-mentioned documented pattern suggests that the spatial distribution of permeability tends to be characterized by an increased degree of homogeneity (as evidenced by a decreased variance and an increased spatial correlation) as the support/measurement scale increases. At the same time, increasing the measurement scale somehow hampers the ability to detect locally low permeability values, as reflected by the observed increased mean value of the data. As an example of the kind of data we consider in this study to clearly document these features, Fig. 1 depicts the spatial distribution of the natural logarithm of (normalized) gas permeabilities, i.e., (where is gas permeability and is the mean value of the data), collected across two faces of a laboratory-scale block of (i) a Berea Sandstone (Tidwell and Wilson, 1999a) and (ii) a Topopah Spring Tuff (Tidwell and Wilson, 1999b) at four support scales ri (see Sect. 2 for a detailed description). As a preliminary observation, one can note that increasing the measurement scale ri yields a decreased level of descriptive detail of the heterogeneous spatial distribution of the system properties. It is important to note that a reduced level of detail in the description of the system properties (e.g., ) could hinder reliability and accuracy of further predictions of system behavior (in terms of, e.g., flow and solute transport patterns). It is therefore relevant to quantify the amount of loss (or of preservation) of the information about the system properties associated with a fine scale(s) of reference as the data support increases.
Our study aims at providing an assessment and a firm quantification of these aspects upon relying on information theory (IT) (e.g., Stone, 2015) and the multi-scale collection of data described above. We consider such a framework of analysis as it provides the elements to quantify (i) the information content associated with a dataset collected at a given scale as well as (ii) the information shared between pairs or triplets of data, each associated with a unique scale (while preserving the design of the measurement device). In this context, IT represents a convenient theoretical framework to properly assist the characterization of the way the information content is distributed across sets of measurements, without being confined to a linear analysis (relying, e.g., on analyses of linear correlation coefficients) or invoking some tailored assumption(s) about the nature of the heterogeneity of permeability (e.g., the characterization of the datasets through a Gaussian model).
To the best of our knowledge, as compared to surface hydrology systems only a limited set of works consider relying on IT concepts to analyze scenarios related to processes taking place in subsurface porous media. Nevertheless, we note a great variety in the topics covered in these works, reflecting the broad potential for applicability of IT concepts. These studies include, e.g., the works of Woodbury and Ulrych (1993, 1996, 2000), who apply the principle of minimum relative entropy to tackle uncertainty propagation and inverse modeling in a groundwater system. The principle of maximum entropy is employed by Gotovac et al. (2010) to characterize the probability distribution function of travel time of a solute migrating across a heterogeneous porous formation. Within the same context, Kitanidis (1994) leverages the definition of entropy and introduces the concept of a dilution index to quantify the dilution state of a solute cloud migrating within an aquifer. Mishra et al. (2009) and Zeng et al. (2012) evaluate the mutual information shared between pairs of (uncertain) model input(s) and output(s) of interest and view this metric as a measure of global sensitivity. Nowak and Guthke (2016) focus on sorption of metals onto soil and the identification of an optimal experimental design procedure in the presence of multiple models to describe sorption. Boso and Tartakovsky (2018) illustrate an IT approach to upscale/downscale equations of flow in synthetic settings mimicking heterogeneous porous media. Relying on IT metrics, Butera et al. (2018) assess the relevance of non-linear effects for the characterization of the spatial dependence of flow and solute transport related observables. Bianchi and Pedretti (2017, 2018) developed novel concepts, mutuated by IT, for the characterization of heterogeneity within a porous system and its links to salient solute transport features. Wellman and Regenaur-Lieb (2012) and Wellman (2013) leverage IT concepts to quantify uncertainty and its reduction about the spatial arrangement of geological units of a subsurface formation. Recently, Mälicke et al. (2020) combined geostatistics and IT to analyze soil moisture data (representative of a given measurement scale) to assess the persistence over time of the spatial organization the soil moisture under diverse hydrological regimes.
Here, we focus on the aforementioned datasets of Tidwell and Wilson (1999a, b), who conducted extensive measurement campaigns collecting air permeability data across the faces of Berea Sandstone and Topopah Spring Tuff blocks, considering four different support/measurement scales (see Sect. 2 for details). While our study does not tackle directly issues associated with the way one can upscale (flow or transport) attributes of porous media, we leverage such unique and truly multi-scale datasets to address research questions such as “How much information about the natural logarithm of (normalized) gas permeabilities is lost as the support scale increases?” and “How informative are data taken at a coarser support scale(s) with respect to those associated with a finer support scale?” (see Sect. 3). In this sense, our study yields a unique perspective of the assessment of the value of hydrogeological information collected at differing scales.
We consider the datasets provided by Tidwell and Wilson (1999a, b), who rely on a multisupport permeameter (MSP) to evaluate spatial distributions of air permeabilities across the faces of a cubic block of Berea Sandstone (hereafter denoted as Berea) and Topopah Spring Tuff (hereafter denoted as Topopah). Data are collected at uniform intervals with spacing Δ=0.85 cm across a grid of 24×24 and 36×36 nodes along each face (of uniform side equal to 19.5 and 29.75 cm, to avoid boundary effects) of the Berea and Topopah blocks, respectively. Four measurement campaigns are conducted, each characterized by the use of a MSP with a tip seal of inner radius ri (i=1, 2, 3, 4) = (0.15, 0.31, 0.63, 1.27) cm and outer radius 2ri (interested readers can find additional details about the MSP design and functioning in Tidwell and Wilson, 1997). While the precise nature and size of the support/measurement scale associated with a MSP are still under study for heterogeneous media (e.g., Goggin et al., 1988; Molz et al., 2003; Tartakovsky et al., 2000; Beckie, 2001), hereafter we denote data associated with a given support/measurement scale by referring these to the associated value of ri. The ensuing dataset is then composed of 3456 and 6480 data points for each measurement scale, ri, for the Berea and Topopah blocks, respectively (we exclude data for one of the faces of the Topopah block, due to some anomalies with respect to the other faces). We consider here the quantity , i.e., the natural logarithm of the air permeability normalized by the mean value (i.e., of the data of the corresponding sample.
The two types of rocks analyzed display distinct features. The Berea sample may be classified as a very fine-grained, well-sorted quartz sandstone. Following Tidwell and Wilson (1999a), visual inspection of the spatial distributions of (see, e.g., Fig. 1) shows that the Berea sample exhibits a generally uniform spatial organization of permeabilities, devoid of particular features, with the exception of a mild stratification, thus allowing us to consider this sample a fairly homogenous system. Otherwise, the Topopah rock sample clearly exhibits a heterogenous structure, whereas pumice fragments (∼23 % of the sample) are embedded in the surrounding matrix (see Fig. 1). In general, the pumice is characterized by higher permeability values than the surrounding matrix. As such, the Topopah sample can be considered a fairly heterogenous system, with a tendency to display a bimodal distribution of permeability values (see also Sect. 4.2). In this sense, the two rock samples analyzed provide two clearly distinct scenarios for the analysis of the interplay of the information contained in datasets collected at diverse measurement scales.
We note that the IT elements described in Sect. 3 refer to discrete variables. While corresponding definitions are available also for continuous variables (i.e., summation(s) and probability mass function(s) are replaced by integral(s) and probability density function(s), respectively), these are characterized by a less intuitive and immediate interpretation (e.g., entropy could be negative, infinite or could not be evaluated in case of probability density function(s) involving a Dirac delta; see, e.g., Kaiser and Schreiber, 2002; Cover and Thomas, 2006). Moreover, in case the probability density functions of the analyzed continuous variables cannot be associated with an analytical expression, it is necessary to subject these variables to quantization, and the IT metrics related to the continuous variables are estimated through their quantized counterparts (see Cover and Thomas, 2006). In general, the quality of these estimates increases (in a way which depends on the specific metric) with the level of quantization of the continuous variables (see, e.g., Kaiser and Schreiber, 2002). This leads us to treat as a discrete variable, a modeling choice which is consistent with several previous studies (see, e.g., Ruddell and Kumar, 2009; Goodwell and Kumar, 2017; Nearing et al., 2018, and references therein).
3.1 Information theory
Considering a discrete random variable, X, one can quantify the associated uncertainty through the Shannon entropy
where N is the number of bins used to analyze the outcomes of X; and pi is the probability mass function and is the (so-called) information (or degree of surprise) associated with the ith bin (see, e.g., Shannon, 1948). We employ base two logarithms in (1), thus leading to bits as a unit of measure for entropy and for the IT metrics we describe in the following. While other choices (relying, e.g., on the natural logarithm) are admissible, the nature and meaning of the metrics we illustrate remain unaffected. The Shannon entropy can be interpreted as a measure of the uncertainty associated with X; i.e., H(X) is largest and equal to log 2(N) in case pi is uniform across all bins (i.e., ), while it is zero when outcomes of X reside only within a single bin. Moreover, one can note that Shannon entropy in (1) is directly linked to the average number of binary questions (i.e., questions with a yes or no answer) one needs to ask to infer the state in which X is. In our study, samples drawn from the population of the random variable X are identified with values and Shannon entropy can also be interpreted as a measure of the degree of heterogeneity of the system. In this sense, considering a support scale ri, if the collected data (which are spatially distributed over the system) would cluster into one (or only a few) bin(s), one could interpret the system as homogeneous (or nearly homogeneous) at such a scale.
The information content shared by two random variables, i.e., X1 and X2, is termed bivariate mutual information and is defined as
where N and M represent the number of bins associated with X1 and X2, respectively; pi and pj are marginal probability mass functions associated with X1 and X2, respectively; and pi,j is the joint probability mass function of X1 and X2. The bivariate mutual information measures the average reduction in the uncertainty (as quantified through the Shannon entropy) about one random variable that one can obtain by knowledge of the other variable (Gong et al., 2013, and references therein). As such, the bivariate mutual information (a) vanishes for two independent variables and (b) coincides with the entropy of either of the two variables when one variable fully explains the other one, i.e., ; X2). In light of the latter observations, it is clear that the bivariate mutual information can also be interpreted as a measure of the degree of dependence between X1 and X2.
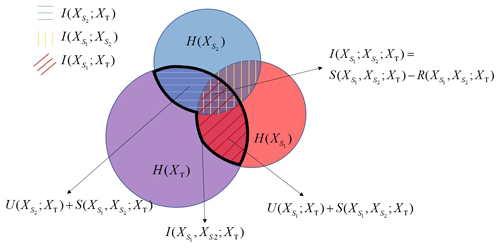
Figure 2Venn diagram representation of the information theory concepts considering two sources, i.e., and , and a target variable, XT. Areas of the circles are proportional to Shannon entropy (i.e., , and H(XT)); overlaps of pairs of circles reflect bivariate mutual information (i.e., ; XT), ; XT), and ; ); and the strength of the multivariate mutual information (i.e., , ; XT)) corresponds to the region delimited by the thick black curve. Unique (i.e., ; XT) and ; XT)), synergetic (i.e., , ; XT)), and redundant (i.e., , ; XT)) components are also highlighted, as well as the interaction information (i.e., ; ; XT)).
When considering three discrete random variables, it is possible to quantify the amount of information that two of these (termed sources, i.e., and ) share with the third one (termed the target variable, i.e., XT) upon evaluating the following multivariate mutual information:
Here, N, M, and W represent the number of bins associated with , , and XT, respectively; pk is the probability mass function of XT; pi,j is the joint probability mass function of and ; and is the joint probability mass function of , , and XT. Relying on the partial information decomposition or information partitioning (Williams and Beer, 2010), the multivariate mutual information in Eq. (3) can be partitioned into unique, redundant, and synergetic contributions, i.e.,
Here, ; XT) and ; XT) represent the amount of information that is uniquely provided to the target XT by and , respectively (i.e., the information ; XT) cannot be provided to XT by knowledge of , a corresponding observation holding for ; XT)); the redundant contribution , ; XT) is the information that both source variables provide to the target (i.e., it is the amount of information transferable to XT that is contained in both and ); and the synergetic contribution , ; XT) is the information about XT that knowledge of and brings in a synergic way. Note that the latter contribution corresponds to the amount of information that (possibly) emerges by simultaneous knowledge of the two sources and through an analysis of their joint relationship with XT; i.e., it would not appear by knowing both and while analyzing their individual relationship with XT separately. All components in Eq. (4) are positive (Williams and Beer, 2010). Figure 2 provides a graphical depiction in terms of Venn diagrams of the above information components in a system characterized by two sources and a target variable.
The bivariate mutual information shared by the target and each source can be written as
Note that Eq. (5) reflects the nature of the information that is shared by the target and each of the sources, when these are taken separately; i.e., no synergy can be detected here. We also remark that one should expect the emergence of some redundancy of information when the two sources are correlated.
An additional element of relevance for the aim of our study is the interaction information
Here, ; is the bivariate mutual information shared by source (i=1, 2) and the target, conditional to the knowledge of source (j=2, 1). Note that ; can be evaluated in a way similar to Eq. (2) upon relying on the conditional probability for XT. Williams and Beer (2010) show that
According to Eq. (7), the bivariate interaction information could be either positive, i.e., when synergetic interactions prevail over redundant contribution, or negative, i.e., when the degree of redundancy overcomes the synergetic effects.
Inspection of Eqs. (4)–(7) reveals that an additional equation is required to evaluate all components in Eq. (4). Various strategies have been proposed in this context (e.g., Williams and Beer, 2010; Harder et al., 2013; Bertschinger et al., 2014; Griffith and Koch, 2014; Olbrich et al., 2015; Griffith and Ho, 2015). We rest here on the recent partitioning strategy formalized by Goodwell and Kumar (2017), due to its capability of accounting for the (possible) dependences between sources when evaluating the unique and redundant contributions. The rationale underpinning this strategy is that (i) each of the two sources can provide a unique contribution of information to the target even as these are correlated, and (ii) redundancy should be lowest in case of independent sources. The redundant contribution can then be evaluated as (Goodwell and Kumar, 2017)
with
Goodwell and Kumar (2017) termed Eq. (8) as a rescaled measure of redundancy, whereas (a) , ; XT) represents the lowest bound for redundancy, which is set on the basis of the rationale that the minimum value of redundancy must at least be equal to ; ; XT) in case ; ; XT)<0 (thus also ensuring positiveness of the synergy; see Eq. 7); (b), ; XT) is an upper bound, consistent with the rationale that all information from the weakest source is redundant; and (c) Is accounts for the degree of dependence between the sources, i.e., Is=0 and , ; , ; XT) for independent sources, while Is=1 and redundancy in Eq. (8) attains its upper limit value, , ; XT), in case of a complete dependency (i.e., or vice versa) between the sources. Once the redundancy has been evaluated, all of the other components in Eq. (4) can be determined.
We emphasize that, despite some additional complexities, analyzing the partitioning of the multivariate mutual information provides valuable insights into the way information is shared across three variables, these being here permeability data associated with three diverse support scales. In summary, addressing information partitioning enables us to (i) quantify and (ii) characterize the nature of the information that two variables (sources) provide to a third one (target) as a whole, i.e., considering the entire triplet. Doing so overcomes the limitation of depicting the system as a simple sum of parts, as based on solely inspecting the corresponding pairwise bivariate mutual information, which allows quantification of just the amount of information that pairs of variables (i.e., the first source and the target, and the second source and the target) share (without being able to define redundant or unique contributions; see Eq. 9). In the context of our work, this implies that information partitioning enables us to characterize the nature of the information that permeability data collected at two support scales provide to/share with permeability data taken at a third one.
3.2 Implementation aspects
Evaluation of the quantities introduced in Sect. 3.1 is accomplished according to three main steps. We employ the Kernel Density Estimator (KDE) routines in Matlab2018© to estimate the continuous counterparts of the probability mass functions pi, pj, pi,j, and and assess the associated probability density functions, i.e., pdfs. This step enables us to smooth and regularize the available finite datasets. We then discretize the ensuing pdfs to evaluate the associated probability mass functions. Note that this two-step procedure allows us to obtain results that are more stable (with respect to the number of bins employed) than those that one could obtain upon discretizing directly the available finite datasets. As a final step, we evaluate the metrics detailed in Sect. 3 by treating separately the multi-scale measurements on each face and then averaging the ensuing face-related results for each of the two rock samples. The benefit of resting on this approach is especially critical when considering the Topopah rock, whereas pooling the data of all faces as a unique sample hindered the emergence of the bimodal behavior (i.e., the permeability values corresponding to the peaks of the bimodal distributions are slightly different depending on the face considered, and the joint treatment of the data from all faces yielded a nearly unimodal distribution). We employ a binning scheme corresponding to a uniform discretization of the range delimited by the lowest and largest values detected considering all datasets associated with both rocks (i.e., we employ the same specific binning for the Berea and Topopah rock samples to assist quantitative comparison of the results). We observe that within an IT approach the selection of a bin size is an a priori choice (see, e.g., Gong et al., 2014; Loritz et al., 2018), the influence of which should be properly assessed (see Sect. 4 and Supplement). We inspect how the IT metrics described in Sect. 2 vary as a function of (i) the number of bins (i.e., we consider a number of 50, 75, 100, and 125 bins for the discretization of the range of data variability) and (ii) the size of the kernel bandwidth (which is varied within the range 0.1–0.4) employed in the KDE routine (see Figs. S1–S3 in the Supplement for additional details). This analysis highlights a weak dependence of the values of the investigate IT metrics on the number of bins and on the size of the bandwidth employed in the KDE procedure, the overall patterns of these metrics remaining substantially unaffected. This leads us to use 100 bins and a kernel bandwidth equal to 0.3. Note that we consistently employ this binning for the evaluation of all metrics introduced in Sect. 2.
We remark that the bivariate and multivariate mutual information metrics are evaluated by focusing on the joint probability mass function based on the multi-scale data collected at the same location on the sampling grids.
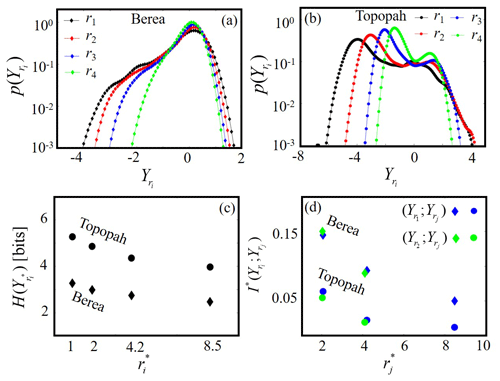
Figure 3Probability mass function of the logarithm of normalized gas permeability, , for various support scales, ri (i=1 (black), 2 (red), 3 (blue), and 4 (green)) for (a) the Berea and (b) Topopah samples; (c) Shannon entropy versus for the Topopah (circles) and Berea (diamonds) samples; (d) bivariate normalized mutual information between data at a reference support scale, , and data at larger support scales, , for i=1 (blue symbols) and 2 (green symbols) against , considering the Berea (diamonds) and Topopah (circles) rock samples.
Figure 3 depicts the probability mass function for i=1 (r1; black symbols), 2 (r2; red symbols), 3 (r3; blue symbols), and 4 (r4; green symbols) for the (a) Berea and (b) Topopah rock samples. For both rocks the associated with only one face is depicted (similar patterns are noted for all of the remaining faces). Figure 3c depicts the Shannon entropy as a function of the MSP support scale normalized by the smallest one, i.e., , for the Berea (diamonds) and Topopah (circles) samples. Figure 3d depicts the bivariate mutual information between data collected at two distinct support scales normalized by the entropy of the data associated with the smaller support scale, i.e., ; ; with j>i, for i=1 (blue symbols) and 2 (green symbols). The latter is plotted against the ratio between the larger and the smallest support scales considering those associated with each pair of datasets i.e., (blue symbols) or (green symbols). Results for the Berea (diamonds) and Topopah (circles) samples are reported.
Inspection of Fig. 3a and b reveals that distributions related to increasing values of ri tend not to encompass extreme values (in particular the low ones) of Y. This observation supports the fact that increasing ri favors a homogenization of the permeability values and suggests that the response of the MSP tends to be only weakly sensitive to the less permeable portions of the rock that are encompassed within a given measurement scale. As a consequence, the associated with increasing ri are characterized by a reduced number of populated bins, this feature being in turn reflected in the observed reduction of with increasing (Fig. 3c) for both rock samples. This result can be interpreted as a signature (see also the discussion about (1) in Sect. 3.1) of the effect of increasing ri, which yields a decrease in (i) the uncertainty about the spatial distribution of the values of and (ii) the ability to capture the degree of spatial heterogeneity of Y. Note that Fig. 3c suggests that the value of , given , associated with the Topopah sample is always higher than its counterpart associated with the Berea rock. This outcome is consistent with the higher heterogeneity displayed by the former sample, where the spatial distribution of is affected by an increased level of uncertainty as compared to its Berea-based counterpart.
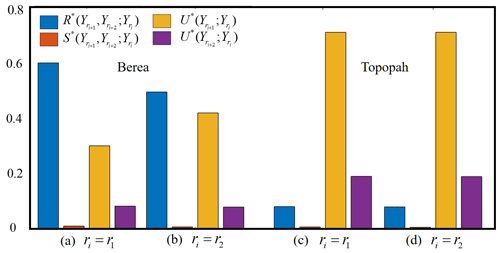
Figure 4Information partitioning of the multivariate mutual information, , ; , considering two triplets of data and ri = (a) r1 and (b) r2 for the Berea sample and ri = (c) r1 and (d) r2 for the Topopah sample. For ease of comparison, we show the redundant, unique, and synergetic contributions normalized by , ; .
Otherwise, two distinct behaviors emerge with regard to the location of the peak(s) of the distributions: (i) the location of the peak of the distributions is virtually insensitive to ri for the Berea sample, while (ii) the two peaks of the bimodal distributions of the Topopah sample display a clear tendency to migrate towards higher permeability values as ri increases. These observations are consistent with the homogeneous nature of the Berea sample and the two-material (pumice and matrix being high and low permeable, respectively) type of heterogeneity displayed by the Topopah sample. It is also in line with the previously noted weak sensitivity of the MSP measurements to regions of low permeability. With reference to the Berea sample, if a measurement taken at a given location with a small ri is close to the average value (i.e., is close to zero in our setting), it is likely that the same behavior is observed also for larger ri due to the homogeneity of the sample. Otherwise, in the case of the Topopah sample there are more chances that increasing ri (hence involving larger volumes of the rock) yields a shift of the ensuing measurements toward higher values.
Inspection of Fig. 3d reveals that, given a reference support scale ri, the mutual information shared with measurements taken at larger support scales rj decreases with an increasing ratio for both rock samples. In other words, the representativeness for system characterization of the sets of data associated with increasingly coarse support scale diminishes, as compared to the data collected at the given reference scale. At the same time, we note that the way in which ; decreases with is very similar for (i) the two analyzed reference support scales, i.e., r1 and r2, and (ii) for the two considered rock types. We interpret this result as a sign of (at least qualitative) consistency in the way information is shared between datasets of measurements associated with increasing size of ri, despite the different geological nature of the two types of samples analyzed. Otherwise, Fig. 3d indicates that the (normalized) mutual information ; ) is always lower in the Topopah system than in the Berea system. This result provides a quantification of the qualitative observation that there is an overall decrease in the representativeness of the datasets associated with increasing data support (with respect to data collected with smaller ri) as the system heterogeneity becomes stronger.
Figure 4 depicts the results of the information partitioning procedure detailed in Sect. 2.3 considering the Berea sample and two triplets of datasets , ; ), with ri = (a) r1 and (b) r2. Corresponding results for the Topopah sample are depicted in (c) for ri=r1 and (d) for ri=r2. For ease of comparison between the results, we normalize the unique, synergetic and redundant contributions in Eq. (4) by the multivariate mutual information of the corresponding triplet, e.g., ; ; , ; , ; ; , ; ; , ; , ; , ; , , ; , ; , ; . Results in Fig. 4a and b suggest that, for the Berea sample, (i) most of the multivariate information is redundant, a finding that can be linked to the dependence detected between the sets of data associated with the two coarser support scales (see, e.g., Fig. 3d); (ii) the synergetic information is practically zero for both triplets considered; i.e., the simultaneous knowledge of the system at two coarser scales does not provide any additional information; (iii) data associated with the middle (in the triplets) support scale provide a non-negligible unique information content, the latter being less pronounced for the data referring to the coarsest support (in the triples). These results (i.e., high redundancy and high/low uniqueness for the middle/largest support scale) suggest that, considering the depiction of the system rendered at the finest support scale, the information provided by the investigations at the coarsest support scale is mostly contained by the information provided by the data collected at the intermediate scale. This element suggests a nested nature of the information linked to data collected at progressively increasing scales with respect to the information contained in the data associated with the smallest support scale. This finding can be linked to the homogeneous nature of the Berea sample, whereas the characterization at diverse scales does not change dramatically (e.g., note the similarities in the spatial patterns of in Fig. 1 for the Berea sample as a function of ri), thus promoting (a) the redundancy of information associated with measurements at the intermediate and larger scales and (b) the uniqueness of information revealed for the intermediate scale.
Otherwise, inspection of Fig. 4c and d reveals that, for the Topopah rock sample, (i) most of the multivariate information coincides with the unique information associated with the intermediate scale; (ii) the redundant and unique contributions associated with the largest scale are still non-negligible yet substantially smaller than the uniqueness contribution provided by the intermediate scale; and (iii) there is practically no synergetic information. This set of results derives from the moderate or marked discrepancies displayed by data as ri increases by one or two sizes, respectively (e.g., see the faces depicted in Fig. 1 for the Topopah sample). In other words, relying on a device such as the MSP to obtain permeability data enables sampling of a volume of the rock according to which the majority of the multivariate information in a triplet is associated with a significant unique contribution of the intermediate scale, the information related to the largest scale still being weakly unique and weakly redundant.
We recall that the focus of the present study is the quantification of the information content and information shared between pairs and triplets of datasets of air permeability observations associated with diverse sizes of the measurement/support scale. We exemplify our analysis by relying on data collected across two different types of rocks, i.e., a Berea and a Topopah sample, that are characterized by different degrees of heterogeneity.
These datasets (or part of these) have been considered in some prior studies. Tidwell and Wilson (1999a, b) and Lowry and Tidwell (2005) assess the impact of the size of the support/measurement scale on key summary one-point (i.e., mean and variance) and two-point (i.e., variogram) statistics within the context of classical geostatistical methods and evaluate kriging-based estimates of the underlying random fields. Siena et al. (2012) and Riva et al. (2013) analyze the scaling behavior of the main statistics of the log permeability data and of their increments (i.e., sample structure functions of various orders), with emphasis on the assessment of power-law scaling behavior. On these bases, Riva et al. (2013) conclude that the data related to the Berea sample can be interpreted as observations from a sub-Gaussian random field subordinated to truncated fractional Brownian motion or Gaussian noise. All of these studies focus on (a) the geostatistical interpretation of the behavior displayed by the probability density function (and key moments) of the data and their spatial increments and (b) the analysis of the skill of selected models to interpret the observed behavior of the main statistical descriptors evaluated upon considering separately data associated with diverse measurement/support scales. Furthermore, Tidwell and Wilson (2002) analyzed the Berea and Topopah datasets (considering separately data characterized by diverse support scales) to assess possible correspondences between the permeability field and some attributes of the rock samples determined visually through digital imaging and conclude that image analysis can assist delineation of spatial patterns of permeability.
We remark that in all of the studies mentioned above the datasets associated with a given support (or measurement) scale are analyzed separately. Otherwise, we leverage elements of IT, which allow a unique opportunity to circumvent limitations of linear metrics (e.g., Pearson correlation) and analyze the relationships (in terms of shared amount of information) between pairs (i.e., bivariate mutual information) or triplets (i.e., multivariate mutual information) of variables. We also note that, even as visual inspection of associated with diverse sizes of the support scale ri (see Fig. 3a and b for the Berea and Topopah samples, respectively) can show that these probability densities can be intuitively linked to the documented decrease in the corresponding Shannon entropies with increasing ri (see Fig. 3c and Sect. 4), it would be hard to readily infer from such a visual comparative inspection the behavior of the bivariate (see Fig. 3d) and multivariate (see Fig. 4) mutual information because these require (see Eqs. 2–8) the evaluation of the joint probability mass functions.
Considering an operational context, including, e.g., groundwater resource management or (conventional/unconventional) oil recovery, we observe that it is common to have at our disposal permeability data associated with diverse support scales. These can be inferred from, e.g., large-scale pumping tests, downhole impeller flowmeter measurements, core flood experiments at the laboratory scale, geophysical investigations, or particle-size curves (see, e.g., Paillet, 1989; Oliver, 1990; Dykaar and Kitanidis, 1992a, b; Harvey, 1992; Deutsch and Journel, 1994; Zhang and Winter, 2000; Attinger, 2003; Pavelic et al., 2006; Neuman et al., 2008; Riva et al., 2013; Barahona-Palomo et al., 2011; Quinn et al., 2012; Shapiro et al., 2015; Galvão et al., 2016; Menafoglio et al., 2016; Medici et al., 2018; Dausse et al., 2019, and reference therein). Assessing (i) the information content and (ii) the amount of information shared between permeability data associated with differing support scales (and/or diverse measuring devices/techniques) along the lines illustrated in the present study can be beneficial for obtaining a quantitative appraisal of possible feedbacks among diverse approaches employed for aquifer/reservoir characterization. Results of such an analysis can potentially serve as a guidance for the screening of datasets which are most informative to provide a comprehensive description of the spatially heterogeneous distribution of permeability. While the methodology detailed in Sect. 3 is readily transferable to scenarios where multi-scale permeability is available, the appraisal of the general nature of some specific findings of the present study (e.g., decrease in the Shannon entropy as the support scale increases, regularity in the trends displayed by the normalized bivariate mutual information) still remains an open issue which will be the subject of future works.
We rely on elements of information theory to interpret multi-scale permeability data collected over blocks of Berea Sandstone and a Topopah Spring Tuff, representing a nearly homogeneous and a heterogeneous porous medium composed of a two-material mixture, respectively. The unique multi-scale nature of the data enables us to quantify the way information is shared across measurement scales, clearly identifying information losses and/or redundancies that can be associated with the joint use of permeability data collected at differing scales. Our study leads to the following major conclusions.
-
An increase in the characteristic length associated with the scale at which the laboratory-scale (normalized) gas permeability data are collected corresponds to a quantifiable decrease in the Shannon entropy of the associated probability mass function. This result is consistent with the qualitative observation that the ability to capture the degree of spatial heterogeneity of the system decreases as the data support scale increases.
-
The (normalized) bivariate mutual information shared between pairs of permeability datasets collected at (i) a fixed fine scale (taken as the reference) and (ii) larger scales decreases in a mostly regular fashion independent of the size of the reference scale, once the bivariate mutual information is normalized by the Shannon entropy of the data taken at the reference scale. This result highlights a consistency in the way information associated with data at diverse scales is shared for the instrument and the porous systems here analyzed.
-
As the degree of heterogeneity of the system increases, we document a corresponding increase in the Shannon entropy (given a support scale) and a decrease in the values of the normalized bivariate mutual information (given two support scales) between permeability data collected at the differing measurement scales.
-
Results of the information partitioning of the multivariate mutual information shared by permeability data collected at three increasing support scales for the Berea Sandstone sample exhibit a marked level of redundancy and high/low uniqueness for the data collected at the intermediate/coarser scale in the triplets with respect to the data associated with the finest scale. This result can be linked to the fairly homogeneous nature of the sample that is also reflected in the moderate variation of the observed (normalized) gas permeability values with increasing size of the support scale.
-
Information partitioning for the Topopah tuff sample indicates the occurrence of a still significant amount of unique information associated with the data collected at the intermediate scale, while the redundant portion and the unique contribution linked to the largest scale in a triplet are clearly diminished. This result descends from the heterogeneous structure of the Topopah porous system, where the recorded (normalized) gas permeabilities display moderate or marked discrepancies as ri increases by one or two sizes, respectively.
-
For both rock samples considered, the simultaneous knowledge of permeability data taken at the intermediate and coarser support scales in a triplet does not provide significant additional information with respect to that already contained in the data taken at the fine scale; i.e., the synergic contribution in the resulting datasets is virtually zero.
Given the nature of the approach we employ, the latter is potentially amenable to being transferred to analyze settings involving other kinds of datasets associated with diverse hydrogeological quantities (including, e.g., porosity or sorption/desorption parameters) or considering measurement/sampling devices of a diverse design. Future developments could also include exploring the possibility of embedding the approach within the workflow of optimal experimental design and/or data-worth analysis strategies.
Data employed were graciously provided by Tidwell, VC, and are available online (https://data.mendeley.com/datasets/ygcgv32nw5/1 (last access: 26 August 2019) (Dell'Oca, 2019).
The supplement related to this article is available online at: https://doi.org/10.5194/hess-24-3097-2020-supplement.
The methodology was developed by AD and supervised by and discussed with AG and MR. All codes were developed by AD. The manuscript was drafted by AD. Structure, narrative and language of the manuscript were revised and significantly improved by AG and MR.
The authors declare that they have no conflict of interest.
The authors would like to thank the EU and MIUR for funding in the framework of the collaborative international consortium (WE-NEED) financed under the ERA-NET WaterWorks2014 Cofunded Call. This ERA-NET is an integral part of the 2015 Joint Activities developed by the Water Challenges for a Changing World Joint Programme Initiative (Water JPI). Alberto Guadagnini is grateful for funding from Région Grand-Est and Strasbourg-Eurométropole through “Chair Gutenberg”.
This research has been supported by the EU and MIUR (grant no. ERA-NET WaterWorks2014).
This paper was edited by Erwin Zehe and reviewed by Ralf Loritz and one anonymous referee.
Andersson, J. E., Ekman, L., Gustafsson, E., Nordqvist, R., and Tiren, S.: Hydraulic interference tests and tracer tests within the Brändöan area, Finnsjon study site, the fracture zone project-Phase 3, Technical Report 89-12, Sweden Nuclear Fuel and Waste Management Company, Stockholm, 1988.
Attinger, S.: Generalized coarse graining procedures for flow in porous media, Comput. Geosci., 7, 253–273, https://doi.org/10.1023/B:COMG.0000005243.73381.e3, 2003.
Barahona-Palomo, M., Riva, M., Sanchez-Vila, X., Vazquez-Sune, E., and Guadagnini, A.: Quantitative comparison of impeller flowmeter and particle-size distribution techniques for the characterization of hydraulic conductivity variability, Hydrogeol. J., 19, 603–612, https://doi.org/10.1007/s10040-011-0706-5, 2011.
Beckie, R.: A comparison of methods to determine measurement support volumes, Water Resour. Res., 37, 925–936, https://doi.org/10.1029/2000WR900366, 2001.
Bertschinger, N., Rauh, J., Olbrich, E., Jost, J., and Ay, N.: Quantifying unique information, Entropy, 16, 2161–2183, https://doi.org/10.3390/e16042161, 2014.
Bianchi, M. and Pedretti, D.: Geological entropy and solute transport in heterogeneous porous media, Water Resour. Res., 53, 4691–4708, https://doi.org/10.1002/2016WR020195, 2017.
Bianchi, M. and Pedretti, D.: An entrogram-based approach to describe spatial heterogeneity with applications to solute transport in porous media, Water Resour. Res., 54, 4432–4448, https://doi.org/10.1029/2018WR022827, 2018.
Boso, F. and Tartakovsky, D. M.: Information-theoretic approach to bidirectional scaling, Water Resour. Res., 54, 4916–4928, https://doi.org/10.1029/2017WR021993, 2018.
Brace, W. F.: Permeability of crystalline rocks: New in situ measurements, J. Geophys. Res., 89, 4327–4330, https://doi.org/10.1029/JB089iB06p04327, 1984.
Butera, I., Vallivero, L., and Rodolfi, L.: Mutual information analysis to approach nonlinearity in groundwater stochastic fields, Stoch. Environ. Res. Risk Assess., 32, 2933–2942, https://doi.org/10.1007/s00477-018-1591-4, 2018.
Cintoli, S., Neuman, S. P., and Di Federico, V.: Generating and scaling fractional Brownian motion on finite domains, Geophys. Res. Lett., 32, 925–936, https://doi.org/10.1029/2005GL022608, 2005
Clauser, C.: Permeability of crystalline rocks, Eos Trans. AGU, 73, 233–238, 1992.
Cover, T. M. and Thomas, J. A.: Elements of Information Theory, John Wiley, Hoboken, NJ, 2006.
Dausse, A., Leonardi, V., and Jourde, H.: Hydraulic characterization and identification of flow-bearing structures based on multiscale investigations applied to the Lez karst aquifer, J. Hydrol.: Reg. Stud., 26, 100627, https://doi.org/10.1016/j.ejrh.2019.100627, 2019.
Dell'Oca, A.: Berea Permeabilities, available at: https://data.mendeley.com/datasets/ygcgv32nw5/1, last access: 26 August 2019.
Deutsch, C. V. and Journel, A. G.: Integrating well test derived effective absolute conductivities in geostatistical reservoir modeling, in: Stochastic Modeling and Geostatistics: Principles, Methods and Case Studies, AAPG Computer Applications in Geology, No. 3, edited by: Yarus, J. and Chambers, R., Amer. Assoc. of Petrol. Geol., Tulsa, 131–142, 1994.
Dykaar, B. B. and Kitanidis, P. K.: Determination of the effective hydraulic conductivity for heterogeneous porous media using a numerical spectral approach, 1. Methods, Water Resour. Res., 28, 1155–1166, https://doi.org/10.1029/91WR03084, 1992a.
Dykaar, B. B. and Kitanidis, P. K.: Determination of the effective hydraulic conductivity for heterogeneous porous media using a numerical spectral approach, 2. Results, Water Resour. Res., 28, 1167–1178, https://doi.org/10.1029/91WR03083, 1992b.
Galvão, P., Halihan, T., and Hirata, R.: The karst permeability scale effect of Sete Lagos, MG, Brazil, J. Hydrol., 532, 149–162, https://doi.org/10.1016/j.jhydrol.2015.11.026, 2016.
Goggin, D. J., Thrasher, R. L., and Lake, L. W.: A theoretical and experimental analysis of minipermeameter response including gas slippage and high velocity flow effects, In Situ, 12, 79–116, 1988.
Gong, W., Gupta, H. V., Yang, D., Sricharan, K., and Hero III, A. O.: Estimating epistemic and aleatory uncertainties during hydrologic modeling: An information theoretic approach, Water Resour. Res., 49, 2253–2273, https://doi.org/10.1002/wrcr.20161, 2013.
Gong, W., Yang, D., Gupta, H. V., and Nearing, G.: Estimating information entropy for hydrological data: One-dimensional case, Water Resour. Res., 50, 5003–5018, https://doi.org/10.1002/2014WR015874, 2014.
Goodwell, A. E. and Kumar, P.: Temporal information partitioning: Characterizing synergy, uniqueness, and redundancy in interacting environmental variables, Water Resour. Res., 53, 5920–5942, https://doi.org/10.1002/2016WR020216, 2017.
Gotovac, H., Cvetkovic, V., and Andrievic, R.: Significance of higher moments for complete characterization of the travel time probability density function in heterogeneous porous media using the maximum entropy principle, Water Resour. Res., 46, W05502, https://doi.org/10.1029/2009WR008220, 2010.
Griffith, V. and Ho, T.: Quantifying redundant information in predicting a target random variable, Entropy, 17, 4644–4653, https://doi.org/10.3390/e17074644, 2015.
Griffith, V. and Koch, C.: Quantifying synergistic mutual information, Guided Self-Organization: Inception, edited by: Prokopenko, Springer-Verlag, Berlin, Germany, 159–190, 2014.
Guadagnini, A., Neuman, S. P., Schaap, M. G., and Riva, M.: Anisotropic statistical scaling of vadose zone hydraulic property estimates near Maricopa, Arizona, Water Resour. Res., 49, 1–17, https://doi.org/10.1002/2013WR014286, 2013.
Guadagnini, A., Riva, M., and Neuman, S. P.: Recent advances in scalable non-Gaussian geostatistics: the generalized sub-Gaussian model, J. Hydrol., 562, 685–691, https://doi.org/10.1016/j.jhydrol.2018.05.001, 2018.
Guzman, A., Neuman, S. P., Lohrstorfer, C., and Bassett, R. L.: Validation studies for assessing flow and transport through unsaturated fractured rocks, in: Rep. NUREG/CR-6203, chap. 4, edited by: Bassett, R. L., Neuman, S. P., Rasmussen, T. C., Guzman, A., Davidson, G. R., and Lohrstorfer, C. E., US Nuclear Regulatory Commission, Washington, D.C., 1994.
Guzman, A. G., Geddis, A. M., Henrich, M. J., Lohrstorfer, C. F., and Neuman, S. P.: Summary of air permeability data from single-hole injection tests in unsaturated fractured tuffs at the Apache Leap research site: Results of steady state test interpretation, Rep. NUREG/CR-6360, US Nuclear Regulatory Commission, Washington, D.C., 1996.
Harder, M., Salge, C., and Polani, D.: Bivariate measure of redundant information, Phys. Rev. E, 87, 012130, https://doi.org/10.1103/PhysRevE.87.012130, 2013.
Harvey, C. F.: Interpreting parameter estimates obtained from slug tests in heterogeneous aquifers, MS thesis, Appl. Earth Science Department, Stanford University, Stanford, 1992.
Hyun, Y., Neuman, S. P., Vesselinov, V. V., Illman, W. A., Tartakovsky, D. M., and Di Federico, V.: Theoretical interpretation of a pronounced permeability scale effect in unsaturated fractured tuff, Water Resour. Res., 38, 1092, https://doi.org/10.1029/2001WR000658, 2002.
Illman, W. A.: Analysis of permeability scaling within single boreholes, Geophys. Res. Lett., 31, L06503, https://doi.org/10.1029/2003GL019303, 2004.
Kaiser, A. and Schreiber, T.: Information transfer in continuous processes, Physica D, 166, 43–62, https://doi.org/10.1016/S0167-2789(02)00432-3, 2002.
Kitanidis, P. K.: The concept of the dilution index, Water Resour. Res., 30, 2011–2016, https://doi.org/10.1029/94WR00762, 1994.
Loritz, R., Gupta, H., Jackisch, C., Westhoff, M., Kleidon, A., Ehret, U., and Zehe, E.: On the dynamic nature of hydrological similarity, Hydrol. Earth Syst. Sci., 22, 3663–3684, https://doi.org/10.5194/hess-22-3663-2018, 2018.
Lowry, T. S. and Tidwell, V. C.: Investigation of permeability upscaling experiments using deterministic modeling and monte carlo analysis, in: World Water and Environmental Resources Congress 2005, 15–19 May 2005, Anchorage, Alaska, USA, https://doi.org/10.1061/40792(173)372, 2005.
Mälicke, M., Hassler, S. K., Blume, T., Weiler, M., and Zehe, E.: Soil moisture: variable in space but redundant in time, Hydrol. Earth Syst. Sci., 24, 2633–2653, https://doi.org/10.5194/hess-24-2633-2020, 2020.
Maréchal, J. C., Dewandel, B., and Subrahmanyam, K.: Use of hydraulic tests at different scales to characterize fracture network properties in the weathered-fractured layer of a hard rock aquifer, Water Resour. Res., 40, W11508, https://doi.org/10.1029/2004WR003137, 2004.
Medici, G., West, L. J., and Mountney, N. P.: Characterization of a fluvial aquifer at a range of depths and scales: the Triassic St. Bees sandstone formation, Cumbria, UK, Hydrogelog. J., 26, 565–591, https://doi.org/10.1007/s10040-017-1676-z, 2018.
Menafoglio, A., Guadagnini, A., and Secchi, P.: A Class-Kriging predictor for functional compositions with application to particle-size curves in heterogeneous aquifers, Math. Geosci., 48, 463–485, https://doi.org/10.1007/s11004-015-9625-7, 2016.
Mishra, S., Deeds, N., and Ruskauff, G.: Global sensitivity analysis techniques for probabilistic ground water modeling, Ground Water, 47, 730–747, https://doi.org/10.1111/j.1745-6584.2009.00604.x, 2009.
Molz, F., Dinwiddie, C. L., and Wilson, J. L.: A physical basis for calculating instrument spatial weighting functions in homogeneous systems, Water Resour. Res., 39, 1096, https://doi.org/10.1029/2001WR001220, 2003.
Nearing, G. S., Ruddell, B. J., Clark, P. M., Nijssen, B., and Peters-Lidard, C. D.: Benchmarking and process diagnostic of land models, J. Hydrometeorol., 19, 1835–1852, https://doi.org/10.1175/JHM-D-17-0209.1, 2018.
Neuman, S. P.: Generalized scaling of permeabilities: Validation and effect of support scale, Geophys. Res. Lett., 21, 349–352, https://doi.org/10.1029/94GL00308, 1994.
Neuman, S. P. and Di Federico, V.: Multifaceted nature of hydrogeologic scaling and its interpretation, Rev. Geophys., 41, 1014, https://doi.org/10.1029/2003RG000130, 2003.
Neuman, S. P., Riva, M., and Guadagnini, A.: On the geostatistical characterization of hierarchical media, Water Resour. Res., 44, W02403, https://doi.org/10.1029/2007WR006228, 2008.
Nowak, W. and Guthke, A.: Entropy-based experimental design for optimal model discrimination in the geosciences, Entropy, 18, 409, https://doi.org/10.3390/e18110409, 2016.
Olbrich, E., Bertschinger, N., and Rauh, J.: Information decomposition and synergy, Entropy, 11, 3501–3517, https://doi.org/10.3390/e17053501, 2015.
Oliver, D. S.: The averaging process in permeability estimation from well-test data, SPE Form Eval., 5, 319–324, https://doi.org/10.2118/19845-PA, 1990.
Paillet, P. L.: Analysis of geophysical well logs and flowmeter measurements in borehole penetrating subhorizontal fracture zones, Lac du Bonnet Batholith, Manitoba, Canada, Water-Resources investigation report 89, US Geological Survey, Lakewood, Colorado, 30 pp., 1989.
Pavelic, P., Dillon, P., and Simmons, C. T.: Multiscale characterization of a heterogeneous aquifer using an ASR operation, Ground Water, 44, 155–164, https://doi.org/10.1111/j.1745-6584.2005.00135.x, 2006.
Quinn, P., Cherry, J. A., and Parker, B. L.: Hydraulic testing using a versatile straddle packer system for improved transmissivity estimation in fractured-rock boreholes, Hydrogeol. J., 20, 1529–1547, 2012.
Riva, M., Neuman, S. P., Guadagnini, A., and Siena, S.: Anisotropic scaling of Berea sandstone log air permeability statistics, Vadose Zone J., 12, 1–15, https://doi.org/10.2136/vzj2012.0153, 2013.
Rovey, C. W. and Cherkauer, D. S.: Scale dependency of hydraulic conductivity measurements, Ground Water, 33, 769–780, https://doi.org/10.1111/j.1745-6584.1995.tb00023.x, 1995.
Ruddell, B. L. and Kumar, P.: Ecohydrologic process networks: 1. Identification, Water Resour. Res., 45, W03419, https://doi.org/10.1029/2008WR007279, 2009.
Sanchez-Vila, X., Carrera, J., and Girardi, J. P.: Scale effects in transmissivity, J. Hydrol., 183, 1–22, https://doi.org/10.1016/S0022-1694(96)80031-X, 1996.
Schad, H. and Teutsch, G.: Effects of the investigation scale on pumping test results in heterogeneous porous aquifers, J. Hydrol., 159, 61–77, https://doi.org/10.1016/0022-1694(94)90249-6, 1994.
Schulze-Makuch, D. and Cherkauer, D. S.: Variations in hydraulic conductivity with scale of measurements during aquifer tests in heterogenous, porous carbonate rock, Hydrogeol. J., 6, 204–215, https://doi.org/10.1007/s100400050145, 1998.
Schulze-Makuch, D., Carlson, D. A., Cherkauer, D. S., and Malik, P.: Scale dependency of hydraulic conductivity in heterogeneous media, Ground Water, 37, 904–919, https://doi.org/10.1111/j.1745-6584.1999.tb01190.x, 1999.
Shannon, C.: A mathematical theory of communication, Bell Syst. Tech. J., 27, 379–423, https://doi.org/10.1002/j.1538-7305.1948.tb01338.x, 1948.
Shapiro, A. M., Ladderud, J. A., and Yager, R. M.: Interpretation of hydraulic conductivity in a fractured-rock aquifer over increasingly larger length dimensions, Hydrogeol. J., 23, 1319–1339, https://doi.org/10.1007/s10040-015-1285-7, 2015.
Siena, M., Guadagnini, A., Riva, M., and Neuman, S. P.: Extended power-law scaling of air permeabilities measured on a block of tuff, Hydrol. Earth Syst. Sci., 16, 29–42, https://doi.org/10.5194/hess-16-29-2012, 2012.
Stone, J. V.: Information Theory: A Tutorial Introduction, Sebtel Press, preprint: arXiv:1802.05968, 2015.
Tartakovsky, D. M., Moulton, J. D., and Zlotnik, V. A.: Kinematic structure of minipermeameter flow, Water Resour. Res., 36, 2433–2442, https://doi.org/10.1029/2000WR900178, 2000.
Tidwell, V. C. and Wilson, J. L.: Laboratory method for investigating permeability upscaling, Water Resour. Res., 33, 1607–1616, https://doi.org/10.1029/97WR00804, 1997.
Tidwell, V. C. and Wilson, J. L.: Permeability upscaling measured on a block of Berea Sandstone: Results and interpretation, Math. Geol., 31, 749–769, https://doi.org/10.1023/A:1007568632217, 1999a.
Tidwell, V. C. and Wilson, J. L.: Upscaling experiments conducted on a block of volcanic tuff: Results for a bimodal permeability distribution, Water Resour. Res., 35, 3375–3387, https://doi.org/10.1029/1999WR900161, 1999b.
Tidwell, V. C. and Wilson, J. L.: Heterogeneity, permeability patterns, and permeability upscaling: Physical characterization of a block of Massillon Sandstone exhibiting nested scales of heterogeneity, SPE Reser. Eval. Eng., 3, 283–291, https://doi.org/10.2118/65282-PA, 2000.
Tidwell, V. C. and Wilson, J. L.: Visual attributes of a rock and their relationship to permeability: A comparison of digital image and minipermeameter data, Water Resour. Res., 38, 1261, https://doi.org/10.1029/2001WR000932, 2002.
Vesselinov, V. V., Neuman, S. P., and Illman, W. A.: Three-dimensional numerical inversion of pneumatic cross-hole tests in unsaturated fractured tuff: 1. Methodology and borehole effects, Water Resour. Res., 37, 3001–3018, https://doi.org/10.1029/2000WR000133, 2001a.
Vesselinov, V. V., Neuman, S. P., and Illman, W. A.: Three-dimensional numerical inversion of pneumatic cross-hole tests in unsaturated fractured tuff: 2. Equivalent parameters, high-resolution stochastic imaging and scale effects, Water Resour. Res., 37, 3019–3042, https://doi.org/10.1029/2000WR000135, 2001b.
Wellman, F. J. and Regenaur-Lieb, K.: Uncertainties have a meaning: Information entropy as a quality measure for 3-D geological models, Tectonophysics, 526–529, 207–216, https://doi.org/10.1016/j.tecto.2011.05.001, 2012.
Wellman, F. J.: Information theory for correlation analysis and estimation of uncertainty reduction in maps and models, Entropy, 15, 1464–1485, https://doi.org/10.3390/e15041464, 2013.
Williams, P. L. and Beer, R. D.: Nonnegative decomposition of multivariate information, CoRR, available at: http://arxiv.org/abs/1004.2515, last access: 14 April 2010.
Winter, C. L. and Tartakovsky, D. M.: Theoretical foundation for conductivity scaling, Geophys. Res. Lett., 28, 4367–4369, https://doi.org/10.1029/2001GL013680, 2001.
Woodbury, A. D. and Ulrych, T. J.: Minimum relative entropy: forward probabilistic modeling, Water Resour. Res., 29, 2847–2860, https://doi.org/10.1029/93WR00923, 1993.
Woodbury, A. D. and Ulrych, T. J.: Minimum relative entropy inversion: theory and application to recovering the release history of a groundwater contaminant, Water Resour. Res. 32, 2671–2681, https://doi.org/10.1029/95WR03818, 1996.
Woodbury, A. D. and Ulrych, T. J.: A full-Bayesian approach to the groundwater inverse problem for steady state flow, Water Resour. Res., 36, 2081–2093, https://doi.org/10.1029/2000WR900086, 2000.
Zeng, X. K., Wan, D., and Wu, J. C.: Sensitivity analysis of the probability distribution of groundwater level series based on information entropy, Stoch. Environ. Res. Risk. Assess., 26, 345–356, https://doi.org/10.1007/s00477-012-0556-2, 2012.
Zhang, D. and Winter, C. L.: Theory, modeling and field investigation in Hydrogeology: A special volume in honor of Shlomo P. Neuman's 60th birthday, Special paper, Geological Society of America, Boulder, Colorado, 2000.
Zlotnik, V. A., Zurbuchen, B. R., Ptak, T., and Teutsch, G.: Support volume and scale effect in hydraulic conductivity: experimental aspects, in: Theory, Modeling, and Field Investigation in Hydrogeology: A Special Volume in Honor of Shlomo P. Neuman's 60th Birthday, Geological Society of America Special Paper 348, edited by: Zhang, D. and Winter, C. L., Geological Society of America, Boulder, CO, 191–213, 2000.





