Nonstationary stochastic rain type generation: accounting for climate drivers

At subdaily resolution, rain intensity exhibits a strong variability in space and time, which is favorably modeled using stochastic approaches. This strong variability is further enhanced because of the diversity of processes that produce rain (e.g., frontal storms, mesoscale convective systems and local convection), which results in a multiplicity of space–time patterns embedded into rain fields and in turn leads to the nonstationarity of rain statistics. To account for this nonstationarity in the context of stochastic weather generators and therefore preserve the relationships between rainfall properties and climatic drivers, we propose to resort to rain type simulation.

In this paper, we develop a new approach based on multiple-point statistics to simulate rain type time series conditional to meteorological covariates. The rain type simulation method is tested by a cross-validation procedure using a 17-year-long rain type time series defined over central Germany. Evaluation results indicate that the proposed approach successfully captures the relationships between rain types and meteorological covariates. This leads to a proper simulation of rain type occurrence, persistence and transitions. After validation, the proposed approach is applied to generate rain type time series conditional to meteorological covariates simulated by a regional climate model under an RCP8.5 (Representative Concentration Pathway) emission scenario. Results indicate that, by the end of the century, the distribution of rain types could be modified over the area of interest, with an increased frequency of convective- and frontal-like rains at the expense of more stratiform events.

1 Introduction

Stochastic weather generators are statistical models designed to simulate realistic random sequences of atmospheric variables (e.g., temperature, rain and wind). Their main target is to reproduce both the internal variability of each variable of interest and the relationships between these variables (Wilks and Wilby, 1999; Furrer and Katz, 2007; Ailliot et al., 2015). These features make stochastic weather generators particularly well suited for producing synthetic climate histories for the purpose of impact studies (Mavromatis and Hansen, 2001; Verdin et al., 2015; Paschalis et al., 2014), as well as for stochastic downscaling of climate projections (Burton et al., 2010; Wilks, 2010; Volosciuk et al., 2017). Within stochastic weather generators, rainfall has long been recognized as a critical variable, in particular because of the strong intermittency (Pardo-Igúzquiza et al., 2006; Schleiss et al., 2011) and variability (Smith et al., 2009; Gires et al., 2014) of the rain process. The apparent intermittency and variability of rainfall increase with the time resolution of interest (Krajewski et al, 2003; Mascaro et al., 2013), and if resolutions of the order of 1 h (or finer) are considered, it appears that storms caused by different generation processes (e.g., frontal storms, mesoscale convective systems and local convection) result in different rain field organizations and temporal patterns (Emmanuel et al., 2012; Marra and Morin, 2018).

Such changes in rainfall characteristics make rain statistics time-varying. In terms of stochastic modeling, this implies that the stochastic process used to model rainfall is nonstationary through time; i.e., the parameters of the stochastic model change over time. The most common way to deal with the nonstationarity of rain statistics is to define a priori (i.e., prior to model calibration) the time periods during which stationarity is assumed. Afterwards, a piecewise-stationary modeling is applied; i.e., model parameters are kept constant within a single stationary period but are allowed to vary between stationary periods. The temporal scale at which nonstationarity occurs is defined by the modeler according to prior knowledge and assumptions about the rain process at hand and ranges from seasons (Paschalis et al., 2013; Bárdossy and Pegram, 2016; Peleg et al., 2017) to a single rainstorm (Caseri et al., 2016; Benoit et al., 2018a). However, several empirical studies have shown that at the subdaily scale, rain statistics can change at a higher rate than alleged in most piecewise-stationary stochastic rainfall models. More precisely, rain statistics have been shown to abruptly change within a single day (Emmanuel et al., 2012) and even within a single rainstorm (Kumar et al, 2011; Ghada et al., 2019). To model rain nonstationarity on a more data-driven basis and thereby account for the subdaily nonstationarities reported above, it has recently been proposed to classify rain fields into rain types (e.g., based on weather radar images) prior to the stochastic modeling of rain intensity (Lagrange et al., 2018; Benoit et al., 2018b). Rain fields belonging to the same rain type are then deemed statistically similar, and periods with a constant rain type can be regarded as stationary periods for the simulation of rain intensity.

In this context, the main goal of this paper is to propose a new approach to leverage the use of rain types for encoding nonstationarity in the framework of stochastic weather generators. However, the finality differs from that of classical weather generators (Richardson, 1981; Wilks and Wilby, 1999; Peleg et al., 2017), since we aim at simulating rainfall conditional to meteorological covariates that are already known, instead of simulating jointly the whole weather (i.e., all variables). More precisely, we develop a method for stochastic simulation of rain type time series conditional to the current state of the atmosphere, i.e., conditional to meteorological variables such as pressure, temperature, humidity or wind (Fig. 1a). These meteorological covariates are assumed to be known beforehand, either from observations, numerical weather model outputs or other stochastic simulations. The advantage of the proposed approach is twofold: firstly, using a stochastic simulation to generate rain types allows for properly reproducing the natural variability of rain type occurrence and thereby to indirectly model the nonstationarity of rain statistics observed in historical datasets. Secondly, the conditioning of the stochastic rain type model to the state of the atmosphere preserves the relationships between rain type occurrence and climatological drivers. Once realistic rain type time series have been simulated (i.e., the core of this study; Fig. 1a), high-resolution rain fields can be generated conditional to rain types using any high-resolution stochastic rainfall generator (Vischel et al., 2011; Leblois and Creutin, 2013; Paschalis et al., 2013; Nerini et al., 2017; Benoit et al., 2018a) as illustrated in Fig. 1b. Using rain types to guide the stochastic generation of synthetic rains has been shown to improve the realism of the resulting high-resolution space–time simulations (Benoit et al., 2018b).

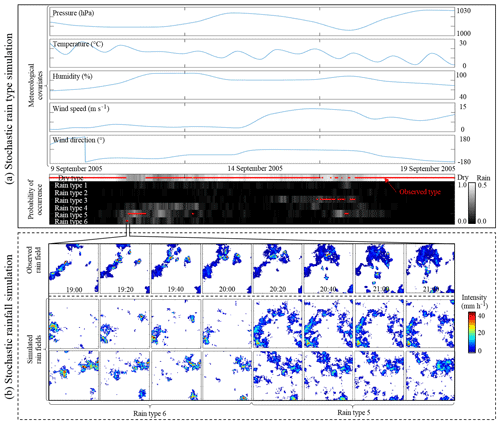
Figure 1 Overview of stochastic rain type generation (core of this study) and its application to simulate high-resolution synthetic rain fields whose statistical properties depend on meteorological conditions. (a) Rain type simulation framework developed in this study. (b) Illustration of stochastic rainfall simulation conditioned to changing rain types. In the bottom row of (a), the observed rain types are in red, and the gray-shaded background denotes the probability of rain type occurrence derived from stochastic rain type simulations conditioned to the meteorological covariates displayed in the four top lines. In (b), the upper row displays actual rain fields observed by radar imagery, and the two bottom rows display two stochastic simulations of synthetic rain fields for the same period generated using the approach of Benoit et al. (2018a).

The remainder of the paper is structured as follows. First, Sect. 2 presents an example of subdaily rain type time series, and Sect. 3 proposes a stochastic model able to capture the main statistical features of this dataset. Next, Sect. 4 assesses the performance of the model through a cross-validation procedure, and Sect. 5 illustrates the application of the proposed approach to the downscaling of EURO-CORDEX (European Coordinated Regional Climate Downscaling Experiment) RCM (regional climate model) precipitation future projections. Finally, Sect. 6 provides some conclusions about stochastic rain type modeling.

2 Example dataset of rain type time series and related meteorological covariates

Before proposing a stochastic model able to mimic the rain type occurrence process (Sect. 3), the present section explains how rain type time series are derived from weather radar observations and investigates the main features of rain type occurrence in a mid-latitude climate.

2.1 Rain type time series

We focus hereafter on a 100 km × 100 km squared area centered in the city of Jena in the federal state of Thuringia, Germany (Fig. 2a). This area has been chosen because its flat topography, and its location far from coastlines or major topographic barriers ensures spatially homogeneous rain fields, allowing for focusing on the temporal component of rainfall nonstationarity. Over this area, data used for rain typing consist of radar images extracted from the RADOLAN (RAdar-OnLine-ANeichung) dataset (Winterrath et al., 2012; Kaspar et al., 2013), which are provided in an open-access way by the German meteorological agency (Deutscher Wetterdienst – DWD). It consists of raw (i.e., not adjusted on rain gauges) radar image composites over all of Germany from 1 January 2001 to present. The RADOLAN radar image resolution is 1 km × 1 km in space and 5 min in time. In practice, however, we resampled radar images at a 10 min resolution and restricted our study to the period 1 January 2001–31 December 2017. The RADOLAN dataset is used as baseline information for rain typing, following a space–time classification approach (Benoit et al., 2018b). Using raw radar images can lead to biases in estimated rain intensities, but the impact of such biases on the classification are deemed negligible, since the adopted approach focuses on rainfall space–time behavior rather than rainfall intensity. A problematic source of errors would be the change of radar biases along time, which could alter the interannual frequency of rain types. To alleviate this problem, uniformly reprocessed radar images are used as the basis for the classification, which ensures a consistent data cube throughout the period of interest. In practice, no adverse trend is noted in the observed rain type distribution (Fig. 3).

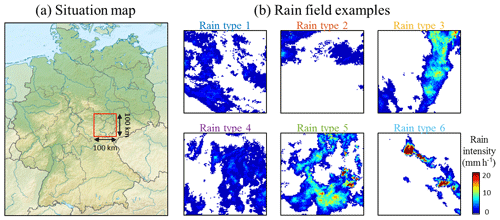
Figure 2 Radar dataset used for rain typing. (a) Study area. The red square denotes the area of interest, centered on Jena, Thuringia, Germany. (Background map from https://www.wikipedia.org/, last access: 27 May 2020, licensed under CC BY 3.0.) (b) Example of RADOLAN radar images (cropped over the area of interest) for each rain type.

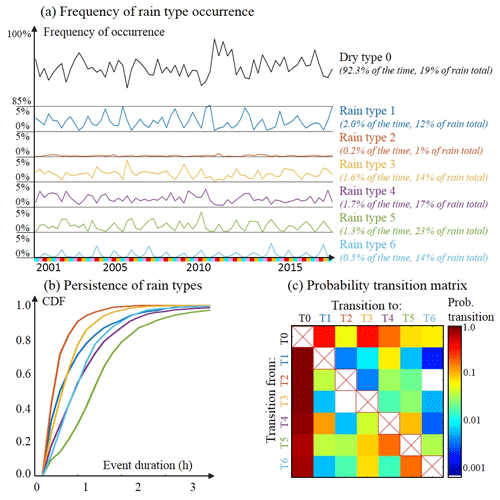
Figure 3 Main features of a rain type time series (2001–2017) observed over central Germany. (a) Frequency of rain type occurrence computed at a seasonal basis (seasons are December, January and February – DJF – in light blue; March, April and May – MAM – in pink; June, July and August – JJA – in red; and September, October and November – SON – in yellow). (b) CDF of event duration stratified by rain type. (c) Empirical matrix of transition probability between rain types.

In a nutshell, the classification method proposed by Benoit et al. (2018b) and used hereafter for rain typing consists of the following. First, rainy time steps are defined as periods with more than 10 % radar pixels measuring rain. The other time steps are classified as dry and are not considered for rain typing. For classification, 10 statistical metrics are computed for each rainy radar image in order to assess the space–time intensity behavior of the rain field observed in the image. Among these metrics, three relate to the statistical distribution of rain intensity observed in the radar image; three characterize the spatial arrangement of rain patterns within the image; and four evaluate the temporal evolution of the rain field due to rain advection and diffusion between consecutive periods. Then, the 10 metrics are used as a basis for classification using a Gaussian mixture model (GMM). All details about the 10 metrics and the clustering approach with a GMM can be found in Benoit et al. (2018b). The resulting clusters correspond to rain fields with similar space–time behaviors. The number of rain types is selected as a compromise between the goodness of fit to rain field statistics and model parsimony. In the present case, the parsimony is favored in order to allow for a physical interpretation of the resulting rain types. As a result, six rain types are identified in the example dataset (Fig. 2b). Among them, rain types 1 and 4 correspond to rather stratiform and spread rain events; rain type 3 corresponds to frontal rainstorms; and rain types 5 and 6 can be associated with rather convective rains. Rain type 2 cannot be associated to a specific rain behavior but rather gathers rain fields that are not classified otherwise and often correspond to partial rain coverage.

Using only radar images with more than 10 % wet pixels to define rain types ensures a reliable classification but at the cost of a dry bias (in the present dataset, 32 % of the images have a rain fraction between 0 % and 10 % and encompass 19 % of the rain total; cf. Fig. 3). To deal with images with less than 10 % wet pixels, Benoit et al. (2018b) proposed classifying images with a small rain fraction (i.e., 0 % < rain fraction < 10 %) in a second step by assigning them the type of the closest classified image (i.e., nearest neighbor interpolation in time). This postprocessing scheme is not directly transferable to the context of simulation because no information about images with low rain coverage is available in simulation outputs. Two options can be considered to alleviate this problem. First, the rain type model defined in Sect. 3 can be calibrated on the final classification (i.e., including images with low rain coverage), which results in simulations that preserve the actual rain proportion. However, using a classification that includes the onset and the end of rainstorms leads to less clear relationships between climate covariates and rain type occurrence, which may degrade simulation results. Hence the second option, which we follow in this paper, which consists of (1) calibrating and running the rain type model for rain types defined only from radar images with more than 10 % rain coverage and then (2) readjusting the dry–wet balance by postprocessing. The dry bias is corrected assuming the ratio $R=\frac{N_{\mathrm{s}}}{N_{\mathrm{l}}}$ between the number N_s of images with low rain coverage and the number N_l of images with large rain coverage as a constant in observations and simulations. Subsequently, the number of epochs for which rain is simulated is increased by propagating the closest rain type to the R×N_l dry epochs located at the beginning and at the end of rainstorms. Section S1 in the Supplement shows that such postprocessing performs well to mitigate the dry bias originating from the use of a 10 % rain coverage threshold to define a wet image. However, since the present study focuses on climate–rain-type relationships, which are better defined when considering only the first step of the classification, the aforementioned postprocessing is not applied in the remainder of this paper. Hence, one should keep in mind that in the following the dry type also includes epochs with a low rain coverage (under 10 %) and that postprocessing is required if the end-use application involves the stochastic simulation of actual rain fields.

Figure 3 investigates the occurrence of rain types through time and highlights some features. Figure 3a displays the frequency of each rain type at the seasonal scale. It appears from Fig. 3a that the frequency of occurrence of individual rain types is strongly variable across the year. For example, stratiform rain types 1 and 4 occur mostly in winter, while convective rain types 5 and 6 are most common in summer. In addition, one can notice a strong interannual variability in rain occurrence, with summers 2003 and 2011 having a low occurrence of rain, while rain occurrence is particularly high during winters 2006 and 2011. Figure 3b displays the cumulative distribution function (CDF) of the duration of each rain type. Here rain type duration is defined as the duration (i.e., length along the time axis) of a segment of constant rain type. Each curve in Fig. 3b therefore corresponds to the probability that a rain event of a given type does not exceed the duration given in abscissa. This figure shows that all rain types are persistent in time with durations ranging from a few minutes to more than 3 h and that some types (e.g., rain types 4 and 5) are more persistent than others (e.g., rain types 2 and 3). Finally, Fig. 3c displays the empirical transition matrix between rain types and focuses on inter-type transitions (i.e., transitions to the same type are ignored and denoted by red crosses). This figure shows that the patterns of transition between rain types are complex and that the transitions involving type 0 (i.e., no rain) are largely dominant.

Figure 4 Statistics of meteorological covariates for each rain type. The meteorological data were extracted from the ERA5 reanalysis dataset.

2.2 Meteorological covariates

The strong seasonality and interannual variability of rain type occurrence emerging from Fig. 3a can be explained to a large extent by regional meteorological conditions. Hereafter, we investigate the links between rain type occurrence and a set of five meteorological covariates that are deemed to influence rainfall behavior (Vrac et al., 2007; Willems, 2001; Rust et al., 2013), namely sea level pressure, temperature at 2 m, relative humidity, and the direction and intensity of synoptic wind at 850 hPa. The actual values of the meteorological covariates used in this study are extracted from the ERA5 reanalyzes (Hersbach et al., 2018) and averaged over the whole area of interest before further use. Only parameters provided at daily resolution are used hereafter in order to be compatible with the temporal resolution of RCM projections used for the illustration of our framework (see Sect. 5). To match the resolution of rain type data, the above daily resolution meteorological covariates are disaggregated to a 10 min resolution. To this end, the mean daily pressure, humidity, wind direction and wind intensity are assumed to occur at 00:00 LT (local time) and are then interpolated at a 10 min resolution using a polynomial interpolation. For temperature, the daily minimum is assumed to occur at 05:00 LT, and the daily maximum is assumed to occur at 15:00 LT; the diurnal cycle is captured by spline interpolation. This disaggregation framework leads to 10 min resolution meteorological covariates in good agreement with actual 10 min resolution observations carried out by a weather station located close to the center of the area of interest, and rain type simulations conditioned to these two sets of covariates (in situ observations and disaggregated reanalysis data) give very similar results (Sect. S2; Fig. S3).

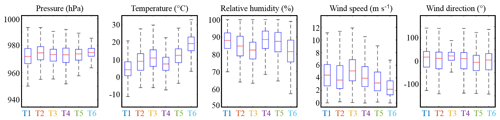
Figure 4 displays the relationships between meteorological covariates and rain type occurrence and confirms the strong influence of temperature and wind speed on rain types. Indeed, stratiform rain types 1 and 4 occur at lower temperatures than convective types 5 and 6 and co-occur with stronger winds. The frontal rain type 3 is characterized by strong westerlies but occurs for a broad range of temperatures. In contrast to temperature and wind speed, the standalone knowledge of pressure, relative humidity or wind direction does not allow for discriminating between all rain types. However, when considered jointly (Sect. S2; Fig. S4), all meteorological covariates bring information about rain type occurrence. In particular, pressure and humidity are key drivers for rain occurrence (no matter the type) and are therefore useful to predict dry and wet spells. Furthermore, wind direction informs the occurrence of rain type 3 and helps to discriminate between rain types 5 and 6.

3 Stochastic rain type model

Daily resolution stochastic weather generators do not distinguish between rain types and typically resort to Markov chain models to simulate rain occurrence (Richardson, 1981; Wilby, 1994; Wilks and Wilby, 1999). Within Markov chain models, semi-Markov models are often favored when the persistence of dry and wet spells is of prime importance (Foufoula-Georgiou and Lettenmaier, 1987; Bárdossy and Plate, 1991), and nonhomogeneous Markov models are preferred when the dry–wet sequence has to be conditioned to meteorological covariates (Hughes and Guttorp, 1999; Vrac et al., 2007). An easy option to deal with rain type simulation conditional to meteorological covariates would therefore be to extend one of these Markov-chain-based frameworks by simply increasing the number of states of the Markov chain in order to account for the diversity of rain types. However, both rain type persistence and conditioning to covariates are equally important for the targeted application, which led us to combine both frameworks to build a nonhomogeneous semi-Markov model. Unfortunately, semi-Markov models do not allow for an easy conditioning to continuous-time covariates, and our attempt to build a nonhomogeneous semi-Markov model led to a significant dry bias in rain type simulations (Sect. S3). Hence, it appeared that even relatively sophisticated parametric models are challenged by the complexity of rainfall at subdaily resolution (Oriani et al., 2018).

One alternative to account for such complexity is to consider high-order properties through a nonparametric approach based on the resampling of historical datasets (Oriani et al., 2014). For the simulation of rain types conditional to meteorological covariates, we therefore adopt the framework of a multiple-point simulation (MPS). MPS consists of using a training dataset (here a past rain type record) to estimate empirically the probability distribution of the variable of interest (here rain type occurrence at a given time step) conditionally to the values already simulated in its temporal neighborhood (Fig. 5a). In the specific MPS algorithm we use (Gravey and Mariethoz, 2018, 2019), the conditional probability density function (PDF) is indirectly assessed by making a random sampling of the training dataset that aims at finding a pattern that is similar to the local conditioning neighborhood (Fig. 5b). In practice, we use a 100 h neighborhood for the present application. Once a match is found (i.e., a pattern in the training image that minimizes the Hamming distance with the target pattern), the corresponding value is imported in the simulation grid (Fig. 5c), and the procedure is iterated until the full simulation grid is filled. In the MPS framework, the dependence of rain type occurrence to meteorological covariates can be handled by multivariate-MPS simulation (Mariethoz et al., 2010). It consists of stacking time series of meteorological covariates with the time series of rain type occurrence and evaluating the conditioning neighborhood on the time series of the resulting vector variable. Here we use a simplified version of a multivariate-MPS simulation where only the co-located covariates (i.e., the values of the covariates observed at the exact time step to simulate) are accounted for during the matching procedure.

Figure 5 Schematic view of the MPS algorithm used for the nonparametric resampling of historical rain type time series.

Since MPS is a nonparametric approach, it does not require model calibration strictly speaking. Instead, it requires a training dataset to resample, which should include both the variable of interest (here a rain type time series) and optional covariates (here meteorological covariates). To produce reliable results and, in particular, meaningful uncertainty estimates, MPS requires large training datasets (Emery and Lantuéjoul, 2014). In the present case, the training dataset is the historical record of joint rain types and meteorological covariates observations available over the target area (17 years). After the selection of a training dataset, simulations are obtained by resampling the training dataset using the MPS algorithm described above.

4 Model assessment

4.1 Cross-validation procedure

Model performance is assessed by a cross-validation procedure, using the dataset introduced in Sect. 2. In practice, we adopt a procedure of leaving 1 year out. For a given simulation year, the rain type model is first trained using data from the 2001–2017 period, excluding the year to simulate. Next, 50 realizations of rain type time series are generated for the year of interest by MPS simulation and conditioned to observations of the meteorological covariates derived from the ERA5 reanalysis as described in Sect. 2. Finally, the same procedure is iterated for each year of the test period (i.e., 2001–2017), and 50 realizations of 17-year-long rain type time series are obtained by concatenating in time the 17 yearly simulations.

The 50 simulations are compared to the reference rain type time series in Fig. 6. Focusing first on the ability of the model to simulate dry and wet conditions (i.e., without distinction between rain types), the first panel of Fig. 6a compares the observed and simulated frequencies of dry occurrence for each season of the validation period 2001–2017. The results show that our model properly simulates the overall proportion of rain (ratio of simulated to observed rain frequency is 0.93). In addition, the chronology of dry–wet occurrence at the seasonal scale is reasonably simulated (correlation between observed and simulated dry type occurrence is 0.6).

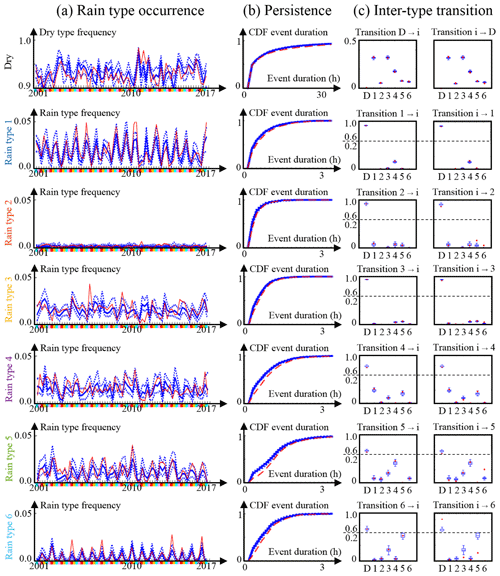
Figure 6 Results of the cross-validation experiment. (a) Seasonality of rain (and dry) type occurrence (seasons are DJF in light blue, MAM in pink, JJA in red and SON in yellow), (b) rain type persistence and (c) probability of transition between rain types. Observations are in red, and simulations are in blue. In simulations, continuous lines represent the median of the simulated ensembles (50 realizations), and dashed lines represent the Q₁₀ and Q₉₀ quantiles.

Focusing next on the simulation of rain types, Fig. 6 (lines 2–7) assesses the ability of the model to reproduce the typical features of rain type occurrence highlighted in Sect. 2, namely seasonality, persistence and transition. Figure 6a assesses rain type seasonality and shows that for strongly seasonal rain types (types 1, 5 and 6) the annual cycle of rain type occurrence is properly simulated. It is also worth noting that the interannual variability of the annual cycle is reasonably well simulated, as well as the interannual variability of weakly seasonal rain types (types 3 and 4). This shows that the proposed approach not only reproduces the annual cycle of rain type occurrence driven by monthly scale variations of the covariates but also captures the impact of short-term fluctuations of meteorological conditions that trigger rainstorms of types 3 and 4. However, when scrutinizing the minima and maxima in Fig. 6a, one can notice that peaks in observations are smoothed out in simulations, which traduces the difficulty of the model to simulate extreme cases. This is a known drawback of MPS simulations (Mariethoz and Caers, 2015), and it constitutes the main limitation of the present approach for the simulation of future climates in which unusual climatic conditions are deemed to become more frequent. Regarding rain type persistence, Fig. 6b shows that this feature is in general very well reproduced, except for the long-lasting types 4 and 5, for which persistence is slightly underestimated. Finally Fig. 6c assesses inter-type transitions. One can notice that the transition patterns are almost perfectly reproduced, except for the transition from dry (and to a lesser extent from type 5) to rain type 6 that is underestimated (overestimated, respectively).

Overall, the proposed stochastic rain type model properly reproduces the main features of observed rain type time series. This good performance is linked to the ability of MPS to accurately reproduce high-order statistics of rain type time series.

4.2 Sensitivity to climate variability

To ensure that the proposed rain type model is able to capture the impact of climatic signals on rain type occurrence, the results of the cross-validation procedure are stratified according to annual climatic signatures. To this end, Fig. 7 compares simulated and observed rain type occurrences at the monthly scale for four sub-datasets: the 5 coldest years of the 2001–2017 period (Fig. 7a), the 5 warmest years (Fig. 7b), the 5 driest years (Fig. 7c) and finally the 5 wettest years (Fig. 7d). Observations (red curves in Fig. 7) show that years with different climatic signatures indeed develop distinct dry ∕ wet ratios and rain type distributions. Simulation results (blue curves in Fig. 7) show that the proposed model properly reproduces these climatically driven differences in rain type distribution.

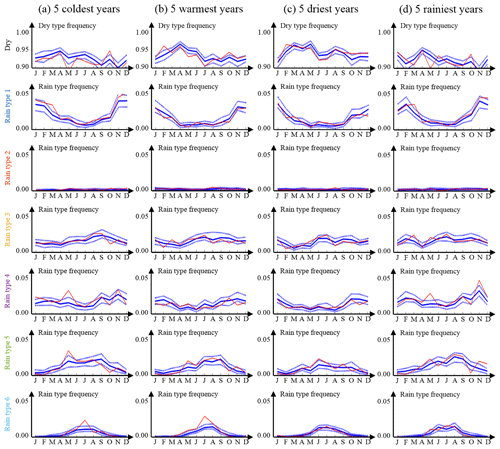
Figure 7 Monthly rain type occurrence stratified according to climate forcing: (a) 5 coldest years of the 2001–2017 period (2001, 2004, 2005, 2010 and 2013), (b) 5 warmest years (2007, 2011, 2014, 2015 and 2017), (c) 5 driest years (2003, 2011, 2012, 2015 and 2016) and (d) 5 wettest years (2001, 2002, 2007, 2009 and 2010). Observations are in red, and simulations are in blue. In simulations, continuous lines represent the median of the simulated ensembles (50 realizations), and dashed lines represent the Q₁₀ and Q₉₀ quantiles.

Figure 7 therefore allows for a detailed investigation of the impact of climatic signals on local rain type distribution over central Germany. Comparing first cold and warm years (Fig. 7a and b), one can notice that warm years tend to be drier, in particular in late winter and spring. This is mostly caused by a deficit of type 1 precipitation during warm years, which corresponds to less snow (type 1 occurs mostly at low temperatures; cf. Fig. 4). Drier springs during warm years are also caused by a deficit of type 5 (slightly convective), which probably corresponds for this time of the year to rain and sleet showers. Finally, one can notice an increased occurrence of type 6 (strongly convective) during warm years, which is captured by the model despite a slight underestimation of this type for both cold and warm years. Comparing dry and wet years (Fig. 7c and d), one can notice that all months contribute to the rain imbalance but that the rain deficit is more pronounced in spring and autumn. In terms of rain type distribution, this is mostly caused by a deficit of rain types 1 and 4 (stratiform) as well as 5 (slightly convective) during dry years. It is also worth noting that rain type 3 (frontal) tends to be slightly more common during rainy years, but in contrast to other types, its increased occurrence is spread along the whole year.

Overall, the proposed approach properly captures the impact of climatic signals on rain type occurrence. This property is essential to preserve the relationships between rain types and climatological drivers and paves the way to RCM precipitation downscaling.

5 Application to RCM precipitation downscaling

For illustration purposes, the stochastic rain type model developed in Sect. 3 is used to simulate the evolution of rain type occurrence in a changing climate simulated by one RCM run extracted from the EURO-CORDEX climate downscaling experiment (Jacob et al., 2014). To drive the simulation of rain types in a changing climate, the same set of meteorological covariates as the one used in the cross-validation procedure is derived from one RCM run, more precisely from the Regional Atmospheric Climate MOdel of the Dutch national weather service (RACMO-KNMI; Van Meijgaard et al., 2008) driven by the CNRM-CM5 (Centre National de Recherches Météorologiques Coupled global climate Model, version 5) Earth system model (Voldoire et al., 2013) forced according to the RCP8.5 (Representative Concentration Pathway) emission scenario. Three intervals of 20 years each are selected to investigate the evolution of rain type occurrence over the 21st century: 1997–2017 (reference period that encompasses the 2001–2017 calibration period for which rain type observations are available), 2037–2057 and 2077–2097. For each period, the meteorological covariates are extracted from the RCM simulation, averaged over the area of interest and disaggregated at a 10 min resolution as described in Sect. 2. In addition, RCM outputs are bias-corrected using the CDF-t (cumulative distribution function transform) method for each variable separately (Vrac et al., 2012). After the bias correction of RCM data, the performance of the model to simulate rain types in the present climate is almost identical for meteorological covariates derived from the RACMO-KNMI RCM and the ones derived from the ERA5 reanalysis (Sect. S4).

For each 20-year period, 50 realizations are simulated conditional to bias-corrected RCM-derived meteorological covariates. To evaluate the projected changes in rain type distribution, Fig. 8 displays the evolution of the monthly frequency of rain type occurrence between the reference period 1997–2017 and the two future periods 2037–2057 and 2077–2097. Observed changes in rain type occurrence frequency are considered as significant if they exceed the uncertainty of the projection that is defined as the Q₁₀–Q₉₀ interval of the 50 realizations. It should be noted that in contrast to rain type occurrence, the simulated persistence and transition behavior of rain types remain constant over the whole test period (not shown). Results in Fig. 8 show that the frequency of rain occurrence slightly decreases in summer and increases in winter, spring and autumn. Among these changes, only the increase of rain occurrence during autumn and winter is significant. The distribution of rain types conditional to the presence of rain is more significantly modified than rain occurrence. More precisely, during winter, rain type 1 (stratiform) significantly declines, while the frequency of rain types 3 (frontal) and 5 (moderately convective) significantly increases. During spring and autumn, rain type 1 (stratiform) significantly declines, while rain types 5 and 6 (convective) tend to increase but not significantly. Finally, during summer, rain types 1, 4 (stratiform) and 5 (moderately convective) decrease, while rain types 3 (frontal) and 6 (strongly convective) increase, with most of these changes being significant. Overall, it appears from this exploratory study that under the assumption of the specific RCM run used to simulate the meteorological covariates, convective and frontal rains could become more frequent at the expense of stratiform rains by the end of the 21st century. The most significant changes are obtained during winter and summer. It is worth mentioning that the evolution of rain behavior along the 21st century simulated in the present study is qualitatively in line with results obtained over western Europe by studies using physical models, which anticipate more frequent heavy rains driven by convection or active fronts (Molnar et al., 2013; Faranda et al., 2019) at the expense of low-intensity stratiform precipitations.

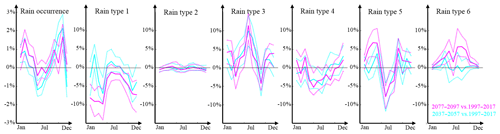
Figure 8 Changes in rain occurrence frequency (left panel) and rain type distribution conditional to the presence of rain (other panels) simulated using the stochastic rain type model developed in Sect. 3: 2037–2057 vs. 1997–2017 (light blue) and 2077–2097 vs. 1997–2017 (purple). Continuous lines represent the median of the simulated ensembles (50 realizations), and dashed lines represent the Q₁₀ and Q₉₀ quantiles.

6 Concluding remarks

6.1 Discussion

By introducing a step of rain type simulation in the framework of stochastic rainfall generators, we suggest that for high-temporal-resolution applications, the simulation of rain can be split in two steps (Fig. 1). In a first instance, rain types are simulated conditional to meteorological covariates to account for the diversity of rainstorms at the regional scale. This first step is the main focus of the present paper. For subsequent applications, we assume that the rain intensity can be simulated conditional to rain types. This is the classical aim of space–time-distributed stochastic rainfall generators, which are becoming more and more common to address the needs of high-resolution hydrometeorological impact studies (Vischel et al., 2011; Leblois and Creutin, 2013; Paschalis et al., 2013; Nerini et al., 2017; Benoit et al., 2018a).

Hence, two main applications can be considered for stochastic rain type simulation. The first one, briefly illustrated in Sect. 5, consists of assessing the evolution of the statistical signature of rainfall in a changing climate simulated by RCMs. It is worth noting that if one wants to carefully evaluate the change in rain type occurrence that may emerge in the future, one should rely on a large ensemble of emission scenario, general circulation model and regional climate model combinations to properly capture the uncertainty on meteorological covariates. In addition, one should keep in mind that the present approach only accounts for changes in the distribution of existing rain types and therefore ignores the possible emergence of new rain types in response to climate conditions that have never been observed over the area of interest. Such new rain types could potentially be modeled by reparametrizing the stochastic rainfall model used to simulate local rain fields (Peleg et al., 2019), by using rain analogs from areas that today experience the climate that is simulated in the future over the area of interest (Hallegatte et al., 2007; Fitzpatrick and Dunn, 2019) or by running a convection-permitting climate model (Prein et al., 2015) for the newly emerging climate conditions. The development of a framework to model emerging rain types is however left for future research.

The second application is the simulation of rain intensity at high space–time resolution while preserving consistency with climatological drivers such as temperature, pressure, humidity and wind. As mentioned in the Introduction, simulating rain intensity would require setting up and calibrating a high-resolution stochastic rainfall model for each rain type over the area of interest and was therefore not considered in the present study except in Fig. 1b for illustration purposes. However, two advantages are expected to emerge from adding a rain type simulation step into stochastic rainfall modeling: first, a relatively low number of rain types can be specified, which implies that the model of rain intensity has to be calibrated a limited number of times. This ensures that enough observations are available to calibrate the rain intensity model for each rain type and therefore prevents model overfitting. The second advantage is the added flexibility to simulate rainstorm dynamics, which allows for generating intra-storm variations of the space–time rainfall statistics.

6.2 Outlook

In this paper, a nonparametric approach based on the resampling of historical records using multiple-point statistics has been proposed and thoroughly tested for the simulation of rain type time series conditional to meteorological covariates. Evaluation results based on a 17-year-long rain type dataset in a mid-latitude climate (central Germany) show that MPS simulations are able to reproduce both the internal variability of rain type time series, as well as relationships with meteorological covariates. After validation, stochastic rain type simulation is applied to the downscaling of RCM projections over the 21st century. Rain type simulations conditioned to meteorological covariates simulated by a regional climate model under an RCP8.5 emission scenario indicate a possible change in rain type distribution by the end of the century, with an increased frequency of heavy rains driven by convection or active fronts, and a decline of low-intensity stratiform precipitations.

The ability of stochastic simulations to generate realistic rain type time series when conditioned to meteorological covariates advocates for including stochastic rain type simulation into rainfall generators in order to (1) reproduce the internal variability or rain type occurrence, in particular interannual variability, seasonality, persistence and inter-type transitions, and (2) preserve the relationships between rain statistics and meteorological covariates, in the present case temperature, pressure, humidity and wind. The above features make stochastic rain type simulation a convenient tool to account for the nonstationarity of rain statistics driven by meteorological conditions. This opens the door to the subdaily stochastic downscaling of climate projections and to improved stochastic rainfall simulations.