A novel regional irrigation water productivity model coupling irrigation- and drainage-driven soil hydrology and salinity dynamics and shallow groundwater movement in arid regions in China

The temporal and spatial distributions of regional irrigation water productivity (RIWP) are crucial for making decisions related to agriculture, especially in arid irrigated areas with complex cropping patterns. Thus, in this study, we developed a new RIWP model for an irrigated agricultural area with complex cropping patterns. The model couples the irrigation- and drainage-driven soil water and salinity dynamics and shallow groundwater movement in order to quantify the temporal and spatial distributions of the target hydrological and biophysical variables. We divided the study area into 1 km × 1 km hydrological response units (HRUs). In each HRU, we considered four land use types: sunflower fields, wheat fields, maize fields, and uncultivated lands (bare soil). We coupled the regional soil hydrological processes and groundwater flow by taking a weighted average of the water exchange between unsaturated soil and groundwater under different land use types. The RIWP model was calibrated and validated using 8 years of hydrological variables obtained from regional observation sites in a typical arid irrigation area in North China, the Hetao Irrigation District. The model simulated soil moisture and salinity reasonably well as well as groundwater table depths and salinity. However, overestimations of groundwater discharge were detected in both the calibration and validation due to the assumption of well-operated drainage ditch conditions; regional evapotranspiration (ET) was reasonably estimated, whereas ET in the uncultivated area was slightly underestimated in the RIWP model. A sensitivity analysis indicated that the soil evaporation coefficient and the specific yield were the key parameters for the RIWP simulation. The results showed that the RIWP decreased from maize to sunflower to wheat from 2006 to 2013. It was also found that the maximum RIWP was reached when the groundwater table depth was between 2 and 4 m, regardless of the irrigation water depth applied. This implies the importance of groundwater table control on the RIWP. Overall, our distributed RIWP model can effectively simulate the temporal and spatial distribution of the RIWP and provide critical water allocation suggestions for decision-makers.

1 Introduction

An increasing food demand currently exists due to global population growth, and water resources are limiting food production in many areas (Kijne et al., 2003; Fraiture and Wichelns, 2010). Especially in arid and semiarid regions of the world, where irrigated agriculture accounts for about 70 % to 90 % of the total water use (Jiang et al., 2015; Gao et al., 2017; Dubois, 2011), this water deficit and the related land salinity are the two major limitations on agricultural production (Williams, 1999; Xue et al., 2018). To maximize agricultural production, the improvement of irrigation water productivity (IWP) is vital (Bessembinder et al., 2005; Surendran et al., 2016). IWP is defined as the crop yield per cubic meter of irrigation water supplied, and it is expressed in kilograms per cubic meter (Singh et al., 2004).

Furthermore, by changing hydrological processes, irrigation and drainage affect water and salt dynamics in the crop root zone, the groundwater, and, eventually, crop production (Morison et al., 2008; Bouman, 2007). Specifically, in arid regions, irrigation-induced deep seepage is the main groundwater recharge mechanism. Shallow groundwater can also move upward and contribute to crop water use by capillary action, which means that the abovementioned irrigation seepage can be reused by the crop to improve the IWP. Thus, the RIWP analysis requires the quantification of complex agro-hydrological processes, including soil water and salt dynamics, groundwater movement, crop water use, and crop production.

Various methods have been used to evaluate the IWP, such as field measurements (Talebnejad and Sepaskhah, 2015; Gowing et al., 2009), remote sensing (Zwart and Bastiaanssen, 2007), and distributed hydrological models (Singh, 2005; Jiang et al., 2015; Steduto et al., 2009). Field experiments have also been widely used to evaluate the effect of water management on the IWP (Talebnejad and Sepaskhah, 2015; Gowing et al., 2009); however, field experiments are expensive and time-consuming, making them unsuitable for the regional evaluation of IWP. Therefore, remote sensing is commonly used to quantify regional IWP, as it can reveal temporal and spatial distributions of ET and crop yields (Biradar et al., 2008). Nevertheless, this method only reports the past IWP distribution and cannot readily predict the impacts of water management practices on the IWP.

Recently, distributed integrated crop and hydrological models have been widely used to simulate the complex agro-hydrological processes coupled with salt dynamics and crop production (Aghdam et al., 2013; Noory et al., 2011; Van Dam et al., 2008; Vanuytrecht et al., 2014). Taking advantage of geographic information systems (GIS), distributed integrated crop and hydrological models provide precise simulations of regional hydrological processes and crop growth by incorporating the heterogeneity of soil moisture, salinity, and texture, the groundwater table depth and salinity, and cropping patterns (Amor et al., 2002; Bastiaanssen et al., 2003a; Jiang et al., 2015; Nazarifar et al., 2012; Xue et al., 2017).

There are two types of distributed hydrological models that are used to monitor complex regional hydrological processes: numerical distributed models, such as SWAT and MODFLOW, and simplified distributed models, such as FARME (Kumar and Singh, 2003) and HEC-HMS (USACE, 1999), the latter of which are based on water balance equations. Numerical, process-based models consider the entire complexity and heterogeneity of regional hydrological systems. MODFLOW is commonly used for the simulation of groundwater dynamics (Kim et al., 2008), but it is limited in well-monitored large irrigation areas due to the large number of parameters and input data required. SWAT is used to simulate land surface hydrological and crop growth processes. It relies on a digital elevation model (DEM) to delineate surface water flow pathways. However, many irrigation areas are quite flat, and surface water flow pathways are controlled by irrigation and drainage systems instead of terrain elevation differences.

Simplified distributed models often employ mass balance equations to describe the soil water and salt dynamics (Sharma, 1999; Sivapalan et al., 1996), which means fewer input parameters as well as larger spatial grids and temporal steps. However, the large spatial grids poorly reflect the regional complex cropping pattern heterogeneity, and the large temporal steps cannot capture daily soil water and salt dynamics, which are essential for crop growth simulation. SWAT alone does not describe the complex interactions between groundwater and soil water, which are fundamental in arid and semiarid areas with shallow groundwater.

Therefore, there are still two big challenges with respect to developing distributed integrated irrigation water productivity models in irrigated areas. First, the networks of irrigation canals and drainage ditches cause spatial heterogeneity in irrigation, drainage, deep percolation, canal seepage, and groundwater table depth within the irrigation area; however, previous studies have overlooked the important role of the networks of irrigation canals and drainage ditches in RIWP evaluations. Second, the multi-scale matching problem arises when coupling the unsaturated and saturated zones in irrigation areas with complex cropping patterns, as the spatial heterogeneity of cropping patterns is much stronger than that of the groundwater table depth. However, most of the existing distributed hydrological models simulated the hydrological processes within the same hydrological response unit (HRU) between the unsaturated and saturated zones independently but overlooked the lateral exchange of groundwater between adjacent HRUs.

Therefore, the main objectives of our study are (1) to develop a RIWP model framework coupling the irrigation and drainage processes, soil water and salt dynamics, crop water and salt response processes, and lateral movement of groundwater and salt; and (2) to analyze the distributed RIWP of the study area and establish the effects of crop type, irrigation water depth applied, and groundwater table depth on the RIWP.

2 Methods

We will present a four-module integrated RIWP model, the coupling between the modules, and one case study evaluating the model performance.

2.1 Regional irrigation water productivity model

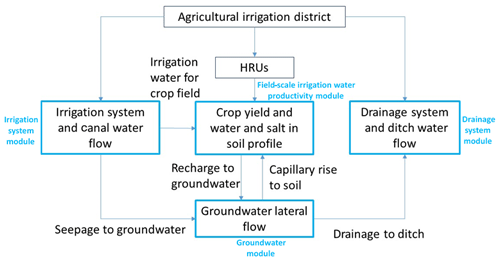
General descriptions will be given for the four modules and their integration, the division and connections of HRUs, and the boundary conditions of the model. Detailed descriptions will then be given for each of the four modules: the irrigation system module, the drainage system module, the groundwater module, and the field-scale IWP module.

2.1.1 General descriptions

A four-module integrated RIWP model was developed in order to simulate the complex system, including water supply from irrigation open canals, field crop water consumption, groundwater drainage into open ditches, and groundwater lateral flow.

The four modules and their integration

The RIWP model developed in this study couples an irrigation system module, a drainage system module, a groundwater module, and a field-scale IWP evaluation module (Fig. 1). The irrigation system module simulates the water flow along canals and the canal seepage to groundwater (the recharge of the groundwater module), and it provides the amount of water available for field-scale irrigation. The drainage system module simulates the drainage to the main drainage ditches from groundwater, and this is the discharge of the groundwater module. The groundwater module is used to simulate the groundwater lateral movement, the groundwater boundary for the field-scale water–salt balance processes, and the groundwater level dynamics for the drainage module. In the field-scale IWP module, the vertical movement of water and salt in the soil profile is simulated in order to obtain the soil moisture and salinity of the crop root zone and to calculate the field-scale irrigation water productivity. This module provides deep percolation to the groundwater module and obtains capillary rise to soil from the groundwater module. The four abovementioned modules will be described comprehensively in Sect. 2.1.2–2.1.5.

Figure 1 Schematic diagram of the conceptual RIWP model and the coupling between its sub-modules.

Hydrological response units

The irrigation area is spatially heterogeneous in terms of soil, land use, meteorology, and groundwater. To include the spatial heterogeneities in the simulation of regional water and salt dynamics and its impact on crop growth, the irrigation district was divided into hydrological response units (HRUs; Kalcic et al., 2015). The HRU is an abstract artifact created by a hydrological developer and is like the smallest spatial unit of the model, which provides an efficient way to discretize large watersheds where simulation at the field scale may not be computationally feasible. In each HRU, soil texture and groundwater conditions are assumed to be homogeneous, but different cropping patterns can exist, e.g., sunflower fields, wheat fields, maize fields, and uncultivated lands. As the irrigation quota is different for different cropping patterns, the model first runs the field IWP model for each cropping pattern independently in each HRU in order to obtain the soil water and salt dynamics, the IWP, and groundwater recharge. The groundwater levels and salinity of each HRU can then be updated according to the area proportions of different cropping patterns in each HRU. The groundwater flow is determined by the pressure head gradient between adjacent HRUs.

Boundary conditions

The upper boundary of the model is the atmospheric boundary layer above the plant canopy, which determines reference ET and precipitation. The main irrigation canals and drainage ditches directly connect with groundwater and can be considered as the side boundaries in the model. With the canal conveyance water loss deducted from the gross water supplied, the amount of water diverted into the field can be calculated as the actual amount of irrigation. The local irrigation schedules of different crops and the actual time of canal water supply are both considered to determine the actual irrigation time and irrigation amounts. The lower boundary is the confining bed at the bottom of phreatic layer. The phreatic layer is vitally important due to its vertical exchange with the unsaturated soil zone in each HRU and its lateral exchange with adjacent HRUs to bond the whole region together.

2.1.2 Irrigation system module

When irrigation water passes through canals, regardless of if they are lined or unlined, seepage loss occurs and recharges groundwater. In a large irrigation area, there are many main, submain, lateral, and field canals, which are categorized as the first-, second-, third-, and fourth-order canals, respectively. During the water allocation period, canal seepage loss from different levels of canals can be divided into two parts: the seepage loss from the main and submain canals, which are permanently filled with water and recharge directly into groundwater along the route; and the seepage loss from lateral and field canals, which are intermittently filled with water and only recharge the groundwater units within their control area. Each HRU has its corresponding groundwater unit, which is used when calculating lateral exchange of groundwater between adjacent HRUs.

We calculated the decreasing water flow along the canal and water losses in the main and submain canals as follows (Men, 2000):

$$\begin{array}{}\text{(1)}& {\displaystyle }& {\displaystyle }\mathit{\sigma }={\displaystyle \frac{A}{\mathrm{100}{Q}^m}}\text{(2)}& {\displaystyle }& {\displaystyle }\mathit{\sigma }={\displaystyle \frac{dQ}{Qdl}},\end{array}$$

where σ represents the water loss coefficient per unit length per unit flow in the canal (m⁻¹); A is the soil permeability coefficient of the canal bed (m^3m−1 d^−m), m is the soil permeability exponent of the canal bed (–), and their values depend on the soil type of the canal bed (please refer to Guo, 1997, for the values). Q represents the daily net flow in the canal (m³ d⁻¹), and dQ represents the daily flow loss of the water conveyance within dl distance in the canal (m³ d⁻¹).

Thus, Eq. (1) is equal to Eq. (2), and they can be transformed into

$$\begin{array}{}\text{(3)}& Q^{m-\mathrm{1}}dQ=Adl.\end{array}$$

Integrations of both sides of Eq. (3) give

$$\begin{array}{}\text{(4)}& {\displaystyle }& {\displaystyle }\underset{Q_L}{\overset{Q_{\mathrm{g}}}{\int }}{Q}^{m-\mathrm{1}}dQ=\underset{\mathrm{0}}{\overset{L}{\int }}Adl\text{(5)}& {\displaystyle }& {\displaystyle }{Q}_L={\left(Q_{\mathrm{g}}^m-ALm\right)}^{\mathrm{1}/m},\end{array}$$

where Q_g is the daily gross flow in the head of the canal (m³ d⁻¹), and Q_L is the daily net flow in the canal at L distance from the canal head (m³ d⁻¹). Thus, flow loss in water conveyance process can be calculated as follows:

$$\begin{array}{}\text{(6)}& {\displaystyle }& {\displaystyle }{Q}_{\mathrm{Ls}}={\displaystyle \frac{A}{\mathrm{100}}}{\left(Q_{\mathrm{g}}^m-ALm\right)}^{(\mathrm{1}-m)/m}\text{(7)}& {\displaystyle }& {\displaystyle }{W}_{\mathrm{ls}}=Q_{\mathrm{ls}}/\left(n_{\mathrm{1}}\times A_{\mathrm{su}}\right),\end{array}$$

where Q_Ls is the daily groundwater recharge due to water conveyance loss in the main and submain canals (m³ d⁻¹), W_ls is the daily groundwater recharge per unit area due to water conveyance loss in the main and submain canals (m d⁻¹), n represents the total number of HRUs along selected main and submain canals (–), and A_HRU is the area of each HRU (m²).

Lateral and field canals are densely distributed in the irrigated area, and they are intermittently filled with low water flow. Thus, it is assumed that seepage from these canals uniformly recharges groundwater units within their control area. The canal seepage is estimated by the following empirical formula:

$$\begin{array}{}\text{(8)}& \begin{array}{rl}{W}_{\mathrm{as}}& =I_n\cdot {\mathit{\eta }}_{\mathrm{mc}}\cdot \left(\mathrm{1}-{\mathit{\eta }}_{\mathrm{sbmc}}\right)+I_n\cdot {\mathit{\eta }}_{\mathrm{mc}}\cdot {\mathit{\eta }}_{\mathrm{sbmc}}\cdot \left(\mathrm{1}-{\mathit{\eta }}_{\mathrm{lc}}\right)\\ & +I_n\cdot {\mathit{\eta }}_{\mathrm{mc}}\cdot {\mathit{\eta }}_{\mathrm{sbmc}}\cdot {\mathit{\eta }}_{\mathrm{lc}}\cdot \left(\mathrm{1}-{\mathit{\eta }}_{\mathrm{fc}}\right),\end{array}\end{array}$$

where W_as represents daily groundwater recharge per unit area due to water conveyance loss in the lateral and field canals (m d⁻¹), and I_n is the daily irrigation water depth applied per unit area (m d⁻¹). η_mc, η_sbmc, η_lc, and η_fc are the utilization coefficients of the main, submain, lateral, and field canals, respectively (–).

2.1.3 Drainage system module

In the drainage system module, only the groundwater draining into ditches is considered, as the precipitation directly on ditches is negligible in arid and semiarid areas. The drainage processes are simulated based on the spatial distributions of the main, submain, and lateral ditches, which are grouped into the first-, second-, and third-order ditches, respectively. Drainage is estimated by comparing local groundwater levels and ditch bottom elevation. According to Tang et al. (2007), the groundwater drainage was calculated as follows:

$$\begin{array}{}\text{(9)}& D_{\mathrm{g}}=\left\{\begin{array}{lc}{\mathit{\gamma }}_{\mathrm{d}}\times \left(h_{\mathrm{db}}-h_{\mathrm{g}}\right);& h_{\mathrm{db}}>h_{\mathrm{g}}\\ \mathrm{0};& h_{\mathrm{db}}<h_{\mathrm{g}},\end{array}\right.\end{array}$$

where D_g is the daily groundwater drainage per unit area (m d⁻¹). γ_d is the drainage coefficient (–), which describes the groundwater table decline caused by the elevation difference between the groundwater table and the streambed of the drainage ditch, and it depends on the underlying soil conductivity and the average distance between the drainage ditches. h_g represents the daily groundwater table depth (m d⁻¹), and h_db is the daily streambed depth of the drainage ditch (m d⁻¹).

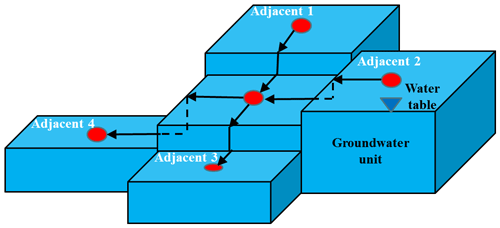
2.1.4 Groundwater module

For a plain irrigation area, groundwater levels are usually relatively flat on the large scale. In our model, it is assumed that groundwater lateral flow exists between one HRU and its four adjacent HRUs (Fig. 2). Using the water table gradient, groundwater flow between the current HRU and its adjacent HRUs can be calculated as follows:

$$\begin{array}{}\text{(10)}& W_{\mathrm{gr}}=\left(K\times h\times B{\displaystyle \frac{L_{\mathrm{ga}}-L_{\mathrm{g}}}{D}}\right)/B^{\mathrm{2}},\end{array}$$

where W_gr is the daily groundwater inflow of the current HRU from adjacent HRUs (m d⁻¹), and K is the daily permeability coefficient of unconfined aquifers in the current HRU (m d⁻¹). h represents the thickness of the unconfined aquifers, which is the difference between the water table and the upper confined bed and varies with water table changes (m). B is the length of the groundwater unit (m) – here the value is 1 km. L_ga and L_g represent the water table level of adjacent HRUs and the current HRU, respectively (m). D is the distance between the center of the current HRU and the centers of its adjacent HRUs (m). There are three types of groundwater boundary conditions: river head (when the boundary HRU, including the irrigation canal and the daily river flux, equals to the daily canal flux), river flux (when the boundary HRU, including the drainage ditches and the water heads in ditches, is assumed constant and equal to the river head), and constant flux (when the boundary HRU is mainly barren area and no irrigation is applied); thus, in our study, zero flux is assumed.

Figure 2 Schematic diagram of groundwater lateral runoff exchange between HRUs.

Based on the field-scale simulation, groundwater lateral exchange, canal seepage, and groundwater drainage are added in the daily water and salt balance calculations of each groundwater unit at the regional scale:

$$\begin{array}{}\text{(11)}& {\displaystyle }\begin{array}{rl}{\mathrm{hg}}_i& ={\mathrm{hg}}_{i-\mathrm{1}}-\left(\mathrm{1}/S_{\mathrm{y}}\right)\left(P_{{\mathrm{wg}}_{i-\mathrm{1}}}-G_{{\mathrm{wg}}_{i-\mathrm{1}}}-{\mathrm{ext}}_{i-\mathrm{1}}\right.\\ & +W_{\mathrm{grup}i-\mathrm{1}}+W_{\mathrm{grdown}i-\mathrm{1}}+W_{\mathrm{grleft}i-\mathrm{1}}+W_{\mathrm{grright}i-\mathrm{1}}\\ & \left.+W_{\mathrm{ls}i-\mathrm{1}}+W_{\mathrm{as}i-\mathrm{1}}-D_{\mathrm{g}i-\mathrm{1}}\right)\end{array}\text{(12)}& {\displaystyle }\begin{array}{rl}{\mathrm{SCa}}_i& =Z_a\times {\mathrm{Sa}}_{i-\mathrm{1}}+W_{\mathrm{grup}i-\mathrm{1}}\times {\mathrm{Sa}}_{\mathrm{up}i-\mathrm{1}}+W_{\mathrm{grdown}i-\mathrm{1}}\\ & \times {\mathrm{Sa}}_{\mathrm{down}i-\mathrm{1}}+W_{\mathrm{grleft}i-\mathrm{1}}\times {\mathrm{Sa}}_{\mathrm{left}i-\mathrm{1}}+W_{\mathrm{grright}i-\mathrm{1}}\\ & \times {\mathrm{Sa}}_{\mathrm{right}i-\mathrm{1}}+\left(W_{\mathrm{ls}i-\mathrm{1}}+W_{\mathrm{as}i-\mathrm{1}}\right)\times {\mathrm{Is}}_{i-\mathrm{1}}-D_{\mathrm{g}i-\mathrm{1}}\\ & \times {\mathrm{Sa}}_{i-\mathrm{1}}+P_{{\mathrm{sg}}_{i-\mathrm{1}}}-G_{{\mathrm{sg}}_{i-\mathrm{1}}},\end{array}\end{array}$$

where W_grup, W_grdown, W_grleft, and W_grright represent the daily groundwater lateral runoff per unit area into the current groundwater unit from the up, down, left, and right adjacent groundwater units, respectively (m d⁻¹). SCa is the daily soluble salt content in the saturated zone below the transmission soil profile (mg m⁻² d⁻¹). Z_a is the thickness of the saturated zone, which is the difference between the groundwater table depth and the depth that groundwater table fluctuations largely cannot reach (m). Z_a only affects the soluble salt concentration in the groundwater salt balance, while it has no effect on the water balance and groundwater fluctuation simulation. Sa, Sa_up, Sa_down, Sa_left, and Sa_right represent the salt concentration of the current groundwater unit and the up, down, left, and right adjacent groundwater units, respectively (mg m⁻³). “Is” represents the salt concentration of the irrigation water (mg m⁻³). S_y represents the specific yield (–), which is the ratio of the volume of water that can be drained by gravity to the total volume of the saturated soil/aquifer. “ext” is the daily groundwater extraction per unit area (m d⁻¹). P_wg is the daily percolation water depth to groundwater from the potential root zone (m d⁻¹), and G_wg is the daily water depth supplied to the potential root zone from shallow groundwater due to the rising capillary action (m d⁻¹). P_sg and G_sg are the quantity of soluble salt in P_wg and G_wg, respectively (mg m⁻² d⁻¹). The detailed calculations of the water and salt exchange components between unsaturated soil and groundwater, such as P_wg and G_wg, were described in our previous field-scale water productivity model (Xue et al., 2018).

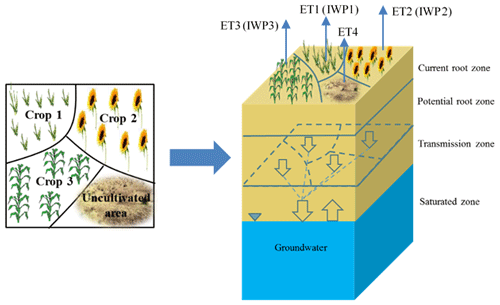
2.1.5 Field-scale irrigation water productivity module

Cropping patterns are complex for each HRU, and sometimes HRUs include uncultivated land, forest land, and other nonagricultural land. In our model, using a high-resolution land use map, different cropping patterns can be separated to simulate soil water and salt processes as well as the responses of ET and crop yields to the water and salt content of root zone. Here, we employed our previously developed field IWP model to simulate field water, salt, ET, and crop yield under shallow groundwater conditions (Xue et al., 2018). The soil profile is vertically divided into four soil zones: the current root zone, the potential root zone, the transmission zone, and the saturated zone. In each HRU, the soil water and salt balance processes and the water productivity are independently simulated for each cropping pattern under its corresponding groundwater unit condition. For uncultivated lands, only water and salt balance are simulated, and the IWP is zero. The water and salt exchange between unsaturated soil and groundwater of different cropping patterns are then weight-averaged by area proportion. Finally, the weighted averages are used to update the daily groundwater table and salinity (Fig. 3).

Figure 3 Schematic diagram of coupling soil water and salt dynamics and groundwater level and salinity. The IWP evaluation in each HRU is also shown.

2.2 Module coupling and flowchart calculation

The simulation was run using a daily temporal step and a HRU spatial step. The irrigation system module simulates the canal seepage to the groundwater and the field irrigation water amount; the canal seepage to the groundwater is the recharge of the groundwater module, whereas the field irrigation water amount is the input of the field IWP module. The drainage system module simulates the groundwater drainage to drainage ditches, which is the discharge from the groundwater module. The groundwater module is used to simulate the groundwater table depth, which is the input for the field IWP module and also the input for the drainage module. In the field-scale IWP module, the deep percolation to groundwater under different cropping patterns is simulated independently, and the weighted average value is the recharge of the groundwater module. The salt exchange is simulated along with the water exchange. The groundwater module is used to simulate the groundwater lateral movement between the current HRU and its adjacent HRUs to update the groundwater level at the next time step. By coupling the irrigation system module, the drainage system module, and the groundwater module with the field IWP model, this RIWP model simulates the temporal and spatial distribution of the IWP over the whole irrigation area from the beginning to the end of the growing season.

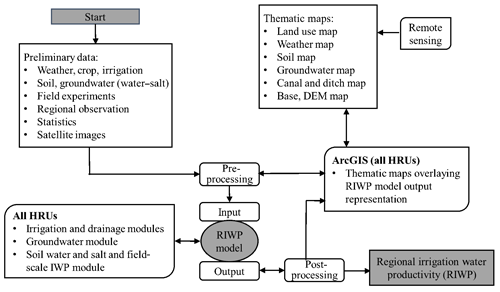
The model was implemented using a combination of ArcGIS, MATLAB, and Microsoft Excel (Fig. 4). The HRUs were created in ArcGIS using Create Fishnet, with each grid numbered. In MATLAB, the HRUs were represented using a matrix, and the daily time step was represented using a vector. At each time step, all of the HRUs were traversed by a nested loop. The updated information for the current time step was then used to calculate the next time step. Microsoft Excel stored the ArcGIS vector layer and its attribute data for MATLAB modeling, and it also stored MATLAB output results for ArcGIS analysis and visualization.

Figure 4 Procedure chart for the regional irrigation water productivity simulation.

Considering the high spatial heterogeneity, meteorological data need to be collected from all of the weather stations within or close to the study area. The distribution of soil physical properties, moisture, and salinity in unsaturated soil, and the groundwater table depth and salinity need to be collected from many observation sites, which are uniformly or randomly spread over the study area. Each data set can then be interpolated in ArcGIS using inverse distance weighting to obtain a spatial distribution vector layer. For each layer, the average value in each HRU is calculated by ArcGIS using geometric division statistics. The vector layer of the irrigation control zones and the vector layer of drainage control zones are overlaid with the HRU division layer in ArcGIS, respectively, to obtain the HRU numbers controlled by each irrigation control zone and each drainage control zone, respectively. The HRU numbers controlled by the same zone are stored in the same matrix for batch simulation in MATLAB. In MATLAB, the soil water and salt balances and the field-scale IWP for main crops are simulated simultaneously for each HRU, whereas groundwater lateral exchange is simulated between adjacent HRUs. At the end of the model simulation, soil moisture and salinity, groundwater table depth and salinity, ET, crop yield, and IWP for different land use types in each HRU can be obtained. The area proportion-weighted average in each HRU can then be imported into ArcGIS to visualize the spatial distribution.

2.3 Model evaluation

We will provide a case study using the abovementioned new RIWP model in order to test its applicability; we will also provide a sensitivity analysis of the parameters.

Figure 5 Location of the Jiefangzha Irrigation District.

2.3.1 Description of study area and data

As a typical subdistrict of the Hetao Irrigation District, the Jiefangzha Irrigation District (JFID) is a typical arid irrigated area with shallow groundwater that has resulted from its arid continental climate, years of flood irrigation, and poor drainage systems (Fig. 5). Located on the Hetao Plain, the JFID is very flat with an average slope of 0.02 % from southeast to northwest (Xu, 2011). The mean annual precipitation is only 155 mm, 70 % of which occurs between July to September, and the mean annual potential evaporation is 1938 mm. The mean annual temperature is 7^∘, with the respective lowest and highest monthly average being −10.1 and 23.8^∘ in January and July. The JFID covers an area of 22×10⁴ ha, 66 % of which is irrigated farmland area. Wheat, maize, and sunflower are the main crops in this region, comprising more than 90 % of the irrigated farmland area. The 12×10⁸ m³ yr⁻¹ of irrigation water is diverted from the Yellow River. Due to the poor maintenance of drainage ditches, it is quite common for poor drainage situations to exist in this area. Therefore, the annual average groundwater table depth ranges from 1.5 to 3.0 m during the crop growing season. Soils in the JFID are spatially heterogeneous and are primarily composed of silt loam in the northern region and sandy loam in the southern region. The shallow groundwater table and strong evaporation makes soil salinization a very serious problem in this area, and salinization is becoming the main constraint on crop production.

An irrigation and drainage network includes 4 main irrigation canals, 16 submain irrigation canals, 5 main drainage ditches, and 12 submain drainage ditches that control the water movement in the JFID (Fig. 5). The streambed depths of the regional main, submain, and lateral ditches were collected by a regional survey in 2016. Daily water flow data from the main and submain irrigation canals and monthly data from the five main drainage ditches were obtained from the local irrigation administration bureau. A total of 55 groundwater observation wells are installed in the JFID (Fig. 5). The groundwater level was measured on the 1st, 6th, 11th, 16th, 21st, and 26th of each month, and groundwater salinity was measured three times each month. Near the groundwater observation wells, soil moisture was measured four times, and soil electrical conductivity was measured once before wheat sowing and once before autumn irrigation. Due to the spatially homogeneous climate in the JFID, daily meteorological data (air temperature, humidity, wind speed, and precipitation) were obtained from the Hangjinghouqi weather station for the calculation of the regional reference ET.

HJ-1A, HJ-1B, and Landsat NDVI images from 2006 to 2013 with a 30 m resolution were downloaded from the official website of the CERSDA (2013) and the USGS (2013) in order to determine the annual cropping pattern distributions. Due to the lack of measured ET values, the ET values estimated by the SEBAL model using MODIS images from NASA (2013) were utilized as a reference for comparison with the simulated ET values (Bastiaanssen et al., 2003b).

2.3.2 Parameterization of the distributed RIWP model

The JFID was divided into 2485 1 km × 1 km HRUs (Fig. S1a in the Supplement). In terms of boundary conditions, the upper Quaternary aquifer layer was regarded as the phreatic layer in the model. It was modeled as an aquitard with loamy soil. From north to south, the thickness of the aquifer in the JFID varied from 2 to 20 m with an average of 7.4 m (Bai and Xu, 2008). Thus, the initial value of the average thickness of unconfined aquifer was set as 7.4 m. The water level contour maps of the JFID from 1997 to 2002 from Bai (2008) were used to determine the direction of water flow near the groundwater boundary. Based on the topography conditions, land use types, the locations of the main canals and ditches, and the directions of water flow, the regional phreatic layer was divided into five zones with river, drainage, and impervious boundary conditions (Fig. S1b).

The JFID was divided into four irrigation control sections and five drainage control sections, and each section was controlled by one main irrigation canal or one main drainage ditch. These sections were further divided into 48 irrigation control subareas and 17 drainage control subareas, and each subarea was controlled by one submain irrigation canal or one submain drainage ditch (Fig. S2). Sunflower fields, wheat fields, maize fields, and uncultivated lands were the four cropping patterns, i.e., land use types, in the RIWP model. When considering the irrigation schedule applied, many other studies on distributed hydrological models simply set the sowing and irrigation of a particular crop as occurring on the same day over the whole study area, which may be a simplification of actual conditions (Singh, 2005). In our study, the irrigation time and the amount of irrigation water for each HRU were co-determined by both the local irrigation schedule of the three main crops and the actual water amount flowing into the fields.

The simulation period was from 1 April to 20 September, which covers the growing seasons of all of the three main crops. The initial crop parameters were set as the default values suggested for sunflower, wheat, and maize by Allen et al. (1998). The empirical values of the regional canal utilization and the ditch drainage coefficient were obtained from the Jiefangzha administration.

2.3.3 Model calibration and validation

To comprehensively evaluate the accuracy and reliability of the model, the data from 2010 to 2013 and from 2006 to 2009 were used as the calibration and validation datasets, respectively. The daily measured soil moisture content of the crop root zone (θ), the electrical conductivity of soil water (EC), and the groundwater table depth (h_g) and groundwater salinity, were calibrated using measured data from the 22 soil water and salt observation sites and 55 groundwater observation sites (Fig. 5) mentioned in Sect.  2.3.1. The regional ET simulated by RIWP for each HRU was calibrated using the remote-sensing-based ET images obtained once every 8 d. The regional drainage processes was calibrated using the monthly groundwater drainage data from main ditches, in which the simulated drainage of each main ditch was the sum of the drainage of its controlling HRUs. Overall, the soil hydraulic parameters, the crop water productivity-related coefficient, and the canal conveyance and ditch drainage parameters were all calibrated using observed data from 2010 to 2013 and then validated with observed data from 2006 to 2009.

To quantify the model performance, the root-mean-square error (RMSE), the Nash and Sutcliffe model efficiency (NSE), and the coefficient of determination (R²) were used as the indicators. The RMSE was used to measure the deviation of simulated values from measured values, the NSE is commonly used to verify the credibility of the hydrological model, and R² represented the degree of linear correlation. The indicators were calculated as follows:

$$\begin{array}{}\text{(13)}& {\displaystyle }\mathrm{RMSE}={\left[{\displaystyle \frac{\sum _{i=\mathrm{1}}^n{\left({\mathrm{Output}}_{\mathrm{s}}-{\mathrm{Output}}_{\mathrm{o}}\right)}^{\mathrm{2}}}{n}}\right]}^{\mathrm{0.5}}\text{(14)}& {\displaystyle }\mathrm{NSE}=\mathrm{1}-{\displaystyle \frac{\sum _{i=\mathrm{1}}^n{\left({\mathrm{Output}}_{\mathrm{s}}-{\mathrm{Output}}_{\mathrm{o}}\right)}^{\mathrm{2}}}{\sum _{i=\mathrm{1}}^n{\left({\mathrm{Output}}_{\mathrm{o}}-{\mathrm{Output}}_{\mathrm{m}}\right)}^{\mathrm{2}}}}\text{(15)}& {\displaystyle }\begin{array}{rl}& R^{\mathrm{2}}=\mathrm{1}-\\ & {\displaystyle \frac{\sum _{i=\mathrm{1}}^n\left({\mathrm{Output}}_{\mathrm{o}}-\stackrel{\mathrm{‾}}{{\mathrm{Output}}_{\mathrm{o}}}\right)\left({\mathrm{Output}}_{\mathrm{s}}-\stackrel{\mathrm{‾}}{{\mathrm{Output}}_{\mathrm{s}}}\right)}{\sqrt{\sum _{i=\mathrm{1}}^n{\left({\mathrm{Output}}_{\mathrm{o}}-\stackrel{\mathrm{‾}}{{\mathrm{Output}}_{\mathrm{o}}}\right)}^{\mathrm{2}}}\sqrt{\sum _{i=\mathrm{1}}^n{\left({\mathrm{Output}}_{\mathrm{s}}-\stackrel{\mathrm{‾}}{{\mathrm{Output}}_{\mathrm{s}}}\right)}^{\mathrm{2}}}}},\end{array}\end{array}$$

where n is the number of simulations; Output_s and Output_o are the simulated and observed values of model outputs, respectively; and $\stackrel{\mathrm{‾}}{{\mathrm{Output}}_{\mathrm{s}}}$ and $\stackrel{\mathrm{‾}}{{\mathrm{Output}}_{\mathrm{o}}}$ are the average values of the simulated and observed model outputs, respectively. The RMSE indicates a perfect match between observation and simulation values when it equals 0, and increasing RMSE values indicate an increasingly poor match. Singh et al. (2005) stated that RMSE values less than 50 % of the standard deviation of the observed data could be considered low enough to be an indicator of a good model prediction. With a range between −∞ and 1, the NSE indicates a perfect match between observed and predicted values when it is equal to 1. Values between 0 and 1 are generally considered to be an acceptable level of performance, whereas values less than 0.0 indicate that the simulation is worse than taking an average of the observation values, which indicates unacceptable performance. The R², which ranges between 0 and 1, describes the proportion of the variance in the observed data, and higher values indicate less error variance. Typically, an R² value higher than 0.5 is considered acceptable (Santhi et al., 2001).

2.3.4 Global sensitivity analysis

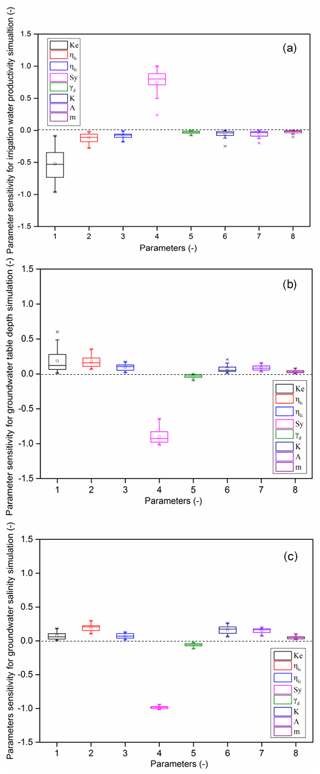
To find the key parameters significantly impacting the model output, a global sensitivity analysis was conducted. The analysis related the changes in three output variables – RIWP, the groundwater table depth, and the groundwater salinity – to eight parameters in the RIWP model. Latin hypercube sampling (LHS; please see Mckay et al., 1979; Muleta and Nicklow, 2005; Wang et al., 2008 for detailed descriptions of the sampling method), which is a typical sampling method for sensitivity and uncertainty analysis, was used to sample the parameter space. Following Dai (2011), the test number was set as 20, more than double the parameter number (which was 8), in order to ensure that the test points were evenly distributed in space and to guarantee the accuracy of the test. For uniform distributions, the parameter range was subdivided into 20 equal intervals. Each interval was sampled only once to generate random values of the possible parameter sets. The possible parameter value ranges referred to the local measurements, the survey data, and relevant research papers. Additionally, considering the spatial heterogeneity of the three output variables, 22 evenly distributed groundwater observation sites in the JFID were selected for the global sensitivity analysis. Based on the LHS method, 20 groups of parameter combinations were obtained, and the simulation was run 20 times. Finally, the sensitivity of the three output variables to the eight parameters were determined in SPSS Statistics. The absolute values of the standardized regression coefficients (SRCs) obtained quantified the significance of each parameter to each output variable (Table 1; Cannavó, 2012), and the plus or minus sign of the SRCs indicated the positive or negative correlations between the corresponding parameter and output variable pairs.

Table 1 The significance level of the input parameter to the model output variables.

3 Results and discussion

3.1 Model performance

Good agreement was obtained by the RIWP model in simulating the IWP and hydrological components during the calibration and validation periods. Table 2 shows the calibrated parameters describing crop growth and water usage, and Table 3 shows the possible variation ranges and calibrated values of the parameters describing the soil hydraulic characteristics and the irrigation and drainage system. The agreement between the observed and simulated soil moisture content in the crop root zone in both the calibration (Fig. 6a; RMSE of 2.867 cm³ cm⁻³, NSE of 0.330, and R² of 0.502) and validation (Fig. 6b; RMSE of 2.989 cm³ cm⁻³, NSE of 0.232, and R² of 0.548) indicates the reasonable performance of the RIWP model. The good performance of the RIWP model was also indicated by the simulation of the soil salt content in both the calibration (Fig. 6c; RMSE of 1.108 dS m⁻¹, NSE of 0.612, and R² of 0.657) and validation (Fig. 6d; RMSE of 1.205 dS m⁻¹, NSE of 0.525, and R² of 0.590). The simulated and observed groundwater table depth (Fig. 6e: RMSE of 0.786 m, NSE of 0.424, and R² of 0.509 in calibration; Fig. 6f: RMSE of 0.667 m, NSE of 0.637, and R² of 0.504 in validation) and groundwater salinity (Fig. 6g: RMSE of less than 10 %, NSE of 0.813, and R² of 0.815 in calibration; Fig. 6h: RMSE of less than 10 %, NSE of 0.604, and R² of 0.730 in validation) at 55 observation sites are also in good agreement.

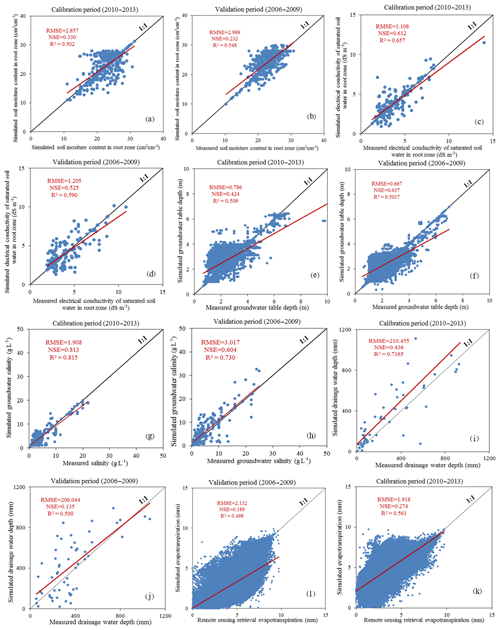
Figure 6 Relationship between the simulated and measured values during the crop growing season in the calibration and validation periods, respectively.

The model did not perform very well with respect to simulating groundwater drainage. The overestimated drainage (Fig. 6i, j) was due to the different operating conditions of the drainage ditches of different orders. The reader may recall that we classified the main, submain, and lateral drainage ditches into first-, second-, and third-order ditches, respectively. In the model, for each year, we adopt the same drainage coefficient for all of the ditches of the different orders, assuming well-operated conditions. However, the actual operating conditions of the ditches of the different orders cannot be the same, resulting in the simulation discrepancy.

The ET simulated by the RIWP model (ET_IWP) and the ET estimated by the SEBAL model using MODIS images (ET_RS) agree well both in calibration (RMSE of 1.918 mm, NSE of 0.274, and R² of 0.561) and in validation (RMSE of 2.132 mm, NSE of 0.189, and R² of 0.498) (Fig. 6l). Furthermore, the comparison of the spatial distribution of cumulative ET_IWP and ET_RS during the crop growth season showed that ET_IWP was lower than ET_RS in the uncultivated area, while they agreed well in farmland (Fig. S3). The uncultivated area, which was merely bare soil, accounted for about 34 % of the JFID, and the ET_IWP of the uncultivated area was merely soil evaporation; this resulted in the underestimation of actual ET in the uncultivated area compared with the ET acquired by remote sensing images, which was consistent with previous studies (Singh, 2005; Tian et al., 2015). Moreover, the cumulative ET_RS was calculated based on eight images of daily ET on eight satellite acquisition dates; thus, using the non-representative ET_RS above the average daily value may also result in the underestimation of ET_IWP.

To test the model performance under different cropping patterns, one representative site was selected for each cropping pattern to compare the observed and simulated time series of the groundwater table depth (Fig. 7). Results indicated that the model can adequately capture the groundwater dynamics at the four representative sites. Occasionally, the simulated groundwater table depth declined quickly, while the observed value rose. This was most likely due to the fact that we ignored the time lag between groundwater recharge from soil and deep percolation. In the uncultivated area (Fig. 7a), the simulated groundwater table level presented a slower and more flat decreasing trend than the measured value. By assuming a completely nonvegetated coverage condition in the uncultivated area, although this is not actually the case, the estimated groundwater evapotranspiration driven by capillarity action will become lower than its actual value; small vegetation, in comparison, transpires amounts of water from the soil, and soil moisture is relatively low, meaning that groundwater evapotranspiration is higher.

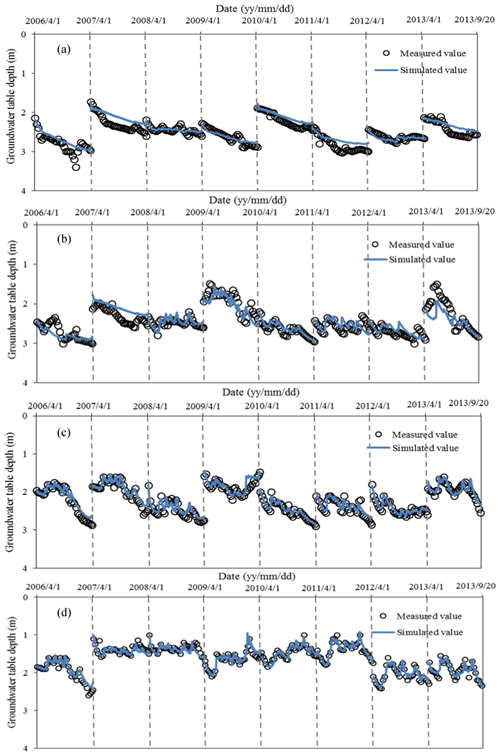
Figure 7 The comparison of the simulated and measured groundwater table depth for four typical sites during the crop growing season from 2006 to 2013. Panel (a) shows the uncultivated area from 2006 to 2013; panel (b) shows the uncultivated area from 2006 to 2008 and the sunflower field and maize field from 2009 to 2013; panels (c) and (d)  show the sunflower, wheat, and maize fields from 2006 to 2013.

Figure 8 Parameter sensitivity analysis results of the model for the three output variables: (a) irrigation water productivity, (b) groundwater table depth, and (c) groundwater salinity.

3.2 Global sensitivity analysis

Recall that a global sensitivity analysis was carried out to determine the sensitivity of the three output variables to the eight parameters. The three output variables were RIWP, groundwater table depth, and groundwater salinity, and the eight parameters were those parameters describing soil hydraulic characteristics and irrigation and drainage system, as shown in Table 3. The specific yield (S_y) and the soil evaporation coefficient (K_e) were the two key parameters influencing the RIWP (Fig. 8a). The specific yield indicated the readily available soil moisture released to the crop root zone from the shallow aquifer under capillary action for crop consumption. Thus, its significant positive influence on the RIWP was explained. The soil evaporation coefficient indicated the proportion of water that was transferred into the atmosphere but was not used by crops. Therefore, a significant negative impact on the RIWP was expected from this parameter. We concluded that the effect of the groundwater contribution on the IWP would sometimes be greater than that of the irrigation water depth applied for a shallow groundwater area such as the JFID. Applying lots of shallow irrigation to crops may reduce the deep percolation and decrease unbeneficial water use due to evaporation. Applying less and deeper irrigation water will result in deeper percolation, while a greater groundwater contribution will be beneficial for crop water use. Thus, compared with applying lots of shallow irrigation, a deeper irrigation schedule involving less water may have greater affect on the IWP in arid regions with shallow groundwater. For both groundwater table depth (Fig. 8b) and groundwater salinity (Fig. 8c), specific yield was the only key parameter. Canal seepage was expected be the cause of the variation in the groundwater table depth around the canal at the local scale. However, the results indicated that the variation in the groundwater table depth was more susceptible to the local groundwater properties, i.e., the specific yield, than to canal seepage at the regional scale. We speculate that lateral groundwater movement might compensate for the variation in the groundwater table depth caused by the canal seepage. Moreover, salt moves with water; thus, the variation in groundwater salinity was also dominated by the specific yield. Due to the high sensitivity of the IWP, the groundwater table depth, and the salinity to the specific yield, it is highly recommended to use spatially variable values of the specific yield rather than a constant value as a model input if it is available. This could greatly enhance the evaluation accuracy of the RIWP model. Furthermore, it is indicated that the permeability coefficient of unconfined aquifers (K) did not significantly affect the IWP, groundwater table depth, or salinity. Due to the lack of measurement data in our study, we adopted a unified K value for the whole study area, which also make the model simulations reasonable, as they are insensitive to this parameter.

3.3 Regional irrigation water productivity

3.3.1 The spatial distribution of irrigation water productivity

Validated by the measured soil moisture and salinity, the groundwater table depth and salinity, and the drainage water depth and ET, specifically the 2006–2013 time series of the groundwater table depth under the four cropping patterns, the RIWP model developed can be used to estimate the spatial distribution of IWP for the three main crops over the period from 2006 to 2013 (Fig. 9). Note that these IWP values were based on the simulated water balance and crop yields of individual HRUs, which may deviate to a certain extent from the real values. However, the values can still represent the utilization of water resources at the regional scale. We note that there are “red HRUs” in Fig. 9 that change with time and space due to the different irrigation water depths applied under different groundwater conditions. Even different crop species can result in a big difference in the IWP. As we mentioned previously, the spatial distribution of these three crops is very complex in the JFID, and the field plot is small; thus, we use remote sensing data to obtain the cropping pattern map with a 30 m × 30 m resolution. Every HRU has these three crops; therefore, we can simulate the IWP for each main crop in every HRU. The RIWP of the three main crops showed a declining trend during the period from 2006 to 2010 (Fig. 9a, b, c, d, e).This was mainly attributed to the increasing irrigation quota, as the excess water lowered the IWP. During the period from 2011 to 2013 (Fig. 9f, g, h), in contrast, the RIWP of the three main crops showed an increasing trend. This was because the irrigation quota was reduced over this period, and the contribution of groundwater compensated for the crop yield losses. When less irrigation water is applied, the number of red HRUs will increase.

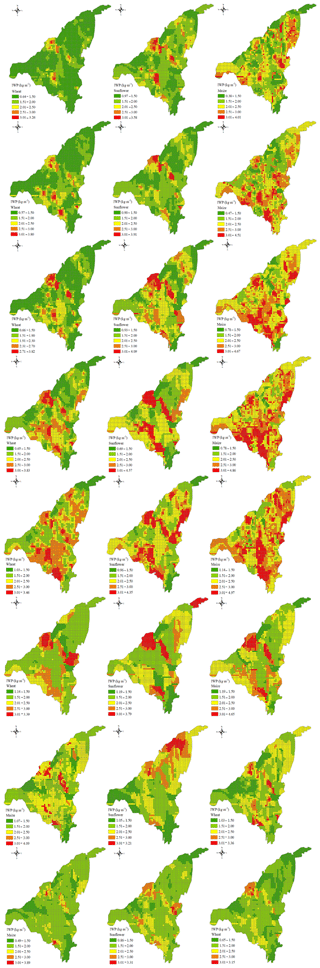
Figure 9 Spatial distribution of irrigation water productivity for the three main crops from 2006 to 2013. Each line shows the RIWP for each year in ascending order. The left, middle, and right columns show the RIWP of wheat, sunflower, and maize, respectively.

Table 2 Calibrated crop parameters for wheat, sunflower, and maize for the regional irrigation water productivity model.

Table 3 The possible parameter variation ranges and calibrated values of the parameters that were collected to describe the soil hydraulic characteristics (K_e, S_y, K) and the irrigation and drainage system (η_lc, η_fc, γ_d, A, m).

Note: The parameter value ranges were collected from local measurements, survey data, and relevant research results. The soil texture of canal bed was silty sandy loam for depths of 0–1 and 2–3 m below the ground and sandy loam for a depth of 1–2 m. For silty sandy loam soil, the bulk density and saturated soil water conductivity were 502.3 mm d⁻¹ and 1.42 g cm⁻³, respectively. For sandy loam soil, the bulk density and saturated soil water conductivity were 1.49 g cm⁻³ and 592.6 mm d⁻¹, respectively. There was fine sand and sandy soil in the phreatic layer.

Under a given irrigation water distribution, the spatial distribution of ET was the key factor controlling the RIWP distribution. The spatial distribution of ET was also fundamentally determined by the solar energy as well as the water and salt dynamics of soil. Recall that the climate and, therefore, the solar energy, was homogeneous in the JFID. The spatial heterogeneity of RIWP must then be attributed to the water and salt heterogeneity caused by the spatial heterogeneity of the cropping pattern, the groundwater table depth, and the irrigation and drainage networks. Particularly, when the farmlands had a limited supply of irrigation water, the groundwater table depth and salinity played an important role with respect to the IWP. Groundwater could drain both water and salt out of the field through the drainage ditches; thus, groundwater evapotranspiration decreased, and the soluble salt content involved in groundwater evapotranspiration also decreased as well. Despite the negative effect of draining water on the IWP, draining salt out of the field will positively affect the IWP. As we see from Fig. 9, the simulated IWP values for three crops were lower in the south, west, north, and northwest of the JFID than in the other regions. The south of the JFID is the main canal for water diversion, which provides a higher irrigation quota than other regions and results in a lower IWP. The west of the JFID, in contrast, is mainly uncultivated area; thus, the IWP is lower than in the other regions. In the northwest of the JFID, the main drainage ditch received the drainage water with a high saline content from the four submain ditches and drained all the way to the north of the region. Ditch seepage water with high salinity resulted in severe soil salinization in the north and northwest of the JFID, which will restrict the crop growth and lower the IWP. Thus, appropriate groundwater drainage management and dealing with salt accumulation at the end of main drainage ditches in irrigated areas is also a pressing and unsolved problem with respect to increasing the red HRUs, which needs to be solved by irrigation managers.

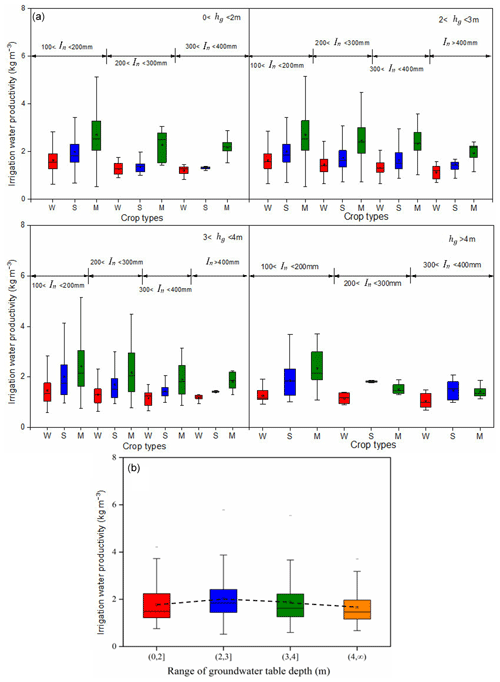
Figure 10 (a) Simulated regional irrigation water productivity under various groundwater table depth (h_g) conditions with the application of different irrigation water amounts (I_n); (b) the results of the statistical analysis. In Fig.10a, W, S, and M represent wheat, sunflower, and maize, respectively.

As the JFID is the major food-producing region of China, improving water productivity means greater food crop yields with less water usage, based on local or regional potential. With declining access to water resources, farmers will need to grow different crops to maintain or increase crop production profitability in the future. A comparison of the RIWP values of different crops (comparison of the three columns in Fig. 9) showed that maize had the highest IWP, wheat had the lowest IWP, and the IWP of sunflower was in between. Therefore, modestly increasing the planting area of maize will improve the crop production per unit of irrigation water. In addition, the RIWP of sunflower is a little higher than that of wheat, and the salt tolerance of sunflower is much higher than that of wheat. Thus, planting sunflowers should be promoted in the JFID if the amount of irrigation water available declines in the future; this practice will definitely increase the red HRUs.

3.3.2 The impact of the irrigation water depth applied and the groundwater table depth on the irrigation water productivity

In arid shallow groundwater areas, the irrigation water productivity (IWP) is affected by the irrigation water depth (IWD) applied and the groundwater table depth (h_g). In all of the four simulated h_g ranges, the IWP decreased when the IWD increased (Fig. 10a), which are findings consistent with Huang et al. (2005). Moreover, the magnitude of the IWP decrease per unit increase of IWD was different for different h_g ranges. The magnitude of the IWP decrease for a shallower h_g was smaller than that for a deeper h_g. This effect of increasing h_g on the relationship between IWP and IWD was consistent with Gao et al. (2017). The above results indicate that groundwater can help meet the crop water demand when irrigation water is insufficient. However, when irrigation water is excessive, a large proportion will eventually drain through the drainage ditches, and the IWP will decrease. Additionally, among the four h_g ranges, the highest IWP was obtained between 2 and 3 m (Fig. 10b), which was consistent with Xue et al. (2018). This indicates that a h_g deeper than the abovementioned depth provides insufficient water for crop growth, whereas a h_g shallower than 2–3 m will increase the root zone soil salinity and the salt stress of crops. The negative effect of shallow groundwater salinity can also be seen in Fig. 10a when h_g is less than 2 m; this indicates that when the amount of irrigation applied decreases from 300 < IWD< 400 mm to 200 < IWD < 300 mm, it leads to decreases in the IWP, which is caused by the faster reduction of ET than the irrigation applied. The shallow groundwater contribution will make up for the ET reduction when a smaller amount of irrigation water is applied; thus, another reason exists to accelerate the reduction of ET. We deduced that less irrigation water will weaken the role of irrigation on salt leaching and result in more severe salinization in the crop root zone. The negative effect of salt stress on the crop water use is greater than the positive effect of the shallow groundwater contribution on the crop water use in this situation. Thus, keeping the groundwater table depth within the optimal range and sustainable is of great importance to reach a higher crop IWP at the regional scale, and irrigation managers may need to reasonably determine the irrigation quota and constantly maintain the drainage system. Groundwater sustainability includes spacing withdrawals to avoid excessive depletion and taking measures to safeguard or improve groundwater quality. To achieve this, regional irrigation managers may need to undertake monitoring efforts to establish historic and current conditions, carry out research to model groundwater systems, forecast future variation, and create policy to manage activities influencing the groundwater table and groundwater quality.

4 Conclusions

In view of the heterogeneous conditions of irrigated areas, and fully considering the supply, consumption, and drainage processes of irrigation water and groundwater, a distributed RIWP model was developed to couple the irrigation water flow processes along main canals and the drainage processes, the water and salt transport processes in soil profile, the groundwater water and salt lateral transport, and the agricultural water productivity module. In particular, a new method was designed and incorporated to couple regional soil hydrology process and groundwater flow with the spatial difference of the cropping pattern. Taking advantage of remote sensing and GIS tools, the quantitative distributed RIWP model requires fewer soil and groundwater hydraulic parameters and crop growing parameters, and it needs only readily available data from several observation sites at the regional scale; moreover, regional water and salt process can be simulated on a daily time step. Despite the simplifications involved, the proposed methods of irrigation canal and drainage ditch digitization and groundwater–runoff lateral exchange simulation between grids means that the spatial IWP is simulated in a real distributed way, instead of using a field-scale model applied in a distributed mode to simulate all simulation units independently. The calibration and validation results indicate good RIWP model performance in this typical study area, and the spatial distribution of IWP for different crops can be produced.

As it was programmed in MATLAB (Mathworks Inc., 2011), the RIWP model can be run on different operating systems. Furthermore, the model includes the capability for the parallelization of simulations to reduce batch run times when conducting simulations over large areas, conditions, and/or time periods. In the near future, enabling the code to be linked quickly with other disciplinary models to support integrated water resource management could be a great improvement over the current RIWP model. Furthermore, we plan to develop a website that can be used for the long-term distribution of the RIWP model and associated documentation. Finally, the RIWP model could improve the knowledge of best practices to enhance water productivity for key irrigation decision-makers. The simplicity of the RIWP model with respect to its required minimum input data, which are readily available or can easily be collected, also makes it user-friendly. Furthermore, it is a very useful model for scenario simulations and for planning purposes, and it can be used by economists, water administrators, and managers working in arid irrigated areas with shallow groundwater.