the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Managing uncertainty in flood protection planning with climate projections
Olga Špačková
Lukas Schoppa
Daniel Straub
Technical flood protection is a necessary part of integrated strategies to protect riverine settlements from extreme floods. Many technical flood protection measures, such as dikes and protection walls, are costly to adapt after their initial construction. This poses a challenge to decision makers as there is large uncertainty in how the required protection level will change during the measure lifetime, which is typically many decades long. Flood protection requirements should account for multiple future uncertain factors: socioeconomic, e.g., whether the population and with it the damage potential grows or falls; technological, e.g., possible advancements in flood protection; and climatic, e.g., whether extreme discharge will become more frequent or not. This paper focuses on climatic uncertainty. Specifically, we devise methodology to account for uncertainty associated with the use of discharge projections, ultimately leading to planning implications. For planning purposes, we categorize uncertainties as either “visible”, if they can be quantified from available catchment data, or “hidden”, if they cannot be quantified from catchment data and must be estimated, e.g., from the literature. It is vital to consider the “hidden uncertainty”, since in practical applications only a limited amount of information (e.g., a finite projection ensemble) is available. We use a Bayesian approach to quantify the “visible uncertainties” and combine them with an estimate of the hidden uncertainties to learn a joint probability distribution of the parameters of extreme discharge. The methodology is integrated into an optimization framework and applied to a pre-alpine case study to give a quantitative, cost-optimal recommendation on the required amount of flood protection. The results show that hidden uncertainty ought to be considered in planning, but the larger the uncertainty already present, the smaller the impact of adding more. The recommended planning is robust to moderate changes in uncertainty as well as in trend. In contrast, planning without consideration of bias and dependencies in and between uncertainty components leads to strongly suboptimal planning recommendations.
- Article
(10940 KB) - Full-text XML
-
Supplement
(475 KB) - BibTeX
- EndNote
The frequency of large fluvial flood events is expected to increase in Europe due to climate change (Alfieri et al., 2015). Therefore, planning authorities increasingly incorporate discharge projections into the assessment of future flood protection needs, rather than considering past observations alone. However, projections differ widely in terms of the level and trend of extreme discharge that they forecast. Future discharge extremes therefore should be modeled probabilistically for flood protection planning (Aghakouchak et al., 2013). This raises two main questions: (1) how does one quantify a relevant uncertainty spectrum and (2) how is this then further used to identify a protection strategy?
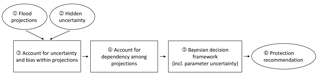
Figure 1Process of finding the recommended planning margin from projections and hidden uncertainty estimate.
Recent studies have aimed at quantifying individual uncertainties in (extreme) discharge (Bosshard et al., 2013; Hawkins and Sutton, 2011; Sunyer, 2014). Sunyer (2014) has pointed out the usefulness of finding a methodology to combine uncertainties for flood protection planning. In the first part of this paper we present such a methodology for deriving a probabilistic model of extreme discharge; it is a pragmatic approach to handling the limited available data in practical problems. We quantitatively incorporate climate uncertainty from multiple information sources as well as an estimate of the “hidden uncertainty” into learning the probability distribution of parameters of extreme discharge. The term hidden uncertainty refers to uncertainty components that cannot be quantified from the given projections and data. For example, if the same hydrological model has been used for all projections, then the hydrological model uncertainty is “hidden”, since one effectively has only a single sample of hydrological model output. It is vital to consider the hidden uncertainty since in practical applications only a limited amount of information and models is available and hidden uncertainty will always be present.
Once established, the question is then how to deal with the uncertainty in flood risk estimates when conducting flood protection planning. Multiple approaches have been proposed (Hallegatte, 2009; Kwakkel et al., 2010), including the addition of a planning margin to the initial design. The planning margin is the protection capacity implemented in excess of the capacity that would be selected without taking into account the uncertainties. Such reserves are used in practice; for example, in Bavaria, a planning margin of 15 % is applied to the design of new protection measures to account for climate change (Pohl, 2013; Wiedemann and Slowacek, 2013). Planning margins are typically implemented based on rule-of-thumb estimates rather than a rigorous quantitative analysis (KLIWA, 2005, 2006; De Kok et al., 2008).
We have previously proposed a fully quantitative Bayesian decision-making framework for flood protection (Dittes et al., 2018). Bayesian techniques are a natural way to model discharge probabilistically (Coles et al., 2003; Tebaldi et al., 2004). They also make it easy to combine several sources of information (Viglione et al., 2013). Furthermore, Bayesian methods support updating the discharge distribution in the future, when new information becomes available (Graf et al., 2007). Our framework probabilistically updates the distribution of extreme discharge with hypothetical observations of future discharge, which are modeled probabilistically. This is an instance of a sequential (or “preposterior”) decision analysis (Benjamin and Cornell, 1970; Davis et al., 1972; Kochendorfer, 2015; Raiffa and Schlaifer, 1961). This enables a sequential planning process, where it is taken into consideration that the measure design may be revised in the future. Furthermore, it naturally takes into account the uncertainty in the parameters of extreme discharge. The output of the framework is a cost-optimal capacity recommendation of flood protection measures, given a fixed protection criterion (such as the 100-year flood). To protect for the 100-year flood is common European practice (Central European Flood Risk Assessment and Management in CENTROPE, 2013) and is also the requirement in the case study.
In this paper, we show how to incorporate into the flood planning process the “visible uncertainty” from an ensemble of climate projections as well as hidden uncertainties that cannot be quantified from the ensemble itself but may be estimated from the literature. In the process of combining these uncertainties, we account for uncertainty and bias in projections as well as for dependencies among different projections. We provide reasoned estimates of climatic uncertainties for a pre-alpine catchment, followed by an application of the previously proposed Bayesian decision framework, sensitivity and robustness analysis. The process is shown in Fig. 1: (1) projections of annual maximum discharges (see Sect. 2.2) and (2) an estimate of the shares of various uncertainties that are not covered by the projection ensemble (see Sect. 2.5) form the inputs to the analysis. (3) For each projection individually, a likelihood function of annual maximum discharge is computed. This is done such that bias is integrated out and projections later on the horizon are assigned diminishing weights, making use of the hidden uncertainty shares (see Sect. 3.2). (4) The likelihoods of individual projections are combined using the method of effective projections (Pennell and Reichler, 2011; Sunyer et al., 2013b) in order to account for dependencies among them (see Sect. 3.3). (5) The Bayesian decision framework of Dittes et al. (2018) is used to obtain (6) a protection recommendation based on the likelihood of extreme discharge. The qualitative basis of the framework is outlined in Sect. 3.4.
It is stressed that this paper focusses on the engineering aspect of planning flood protection under climate change. We aim to demonstrate how different sources of uncertainty can be combined probabilistically to make decisions, taking into account future developments. This is to aid decision making under climate uncertainty, when there are limited data and models available. Some authors advocate not using a probabilistic approach when the uncertainty is very large. This is because of the potential of surprises under large uncertainty (Hall and Solomatine, 2008; Merz et al., 2015; Paté-Cornell, 2011). Instead, they recommend an approach focussed on robustness: the ability of the protection system to work well under a wide range of scenarios. We consider our approach to be complementary: rather than prescribing a protection system for the study site, it gives a recommendation for the optimal protection capacity. Expert judgement remains central for identifying robust protection systems to provide the recommended protection, e.g., by implementing a protection system that consists of several different, possibly spatially distributed, measures. Such an approach leads to more robust protection in which floods in excess of the design flood do not quickly lead to very high damages or even failure (Blöschl et al., 2013b; Custer and Nishijima, 2013).
The paper is structured as follows: in Sect. 2, we introduce the pre-alpine case study catchment together with the available data and relevant uncertainties, concluding in an estimate of the hidden uncertainties. In Sect. 3, we show how to combine the different sources of uncertainty to use in the decision framework of Dittes et al. (2018). The resulting recommendations are presented and discussed in Sect. 4, together with the sensitivity analysis. Finally, a discussion is given in Sect. 5 and conclusions in Sect. 6.
In this section, we introduce individual components of uncertainty in estimates of extreme future discharge. This is done on the example of a pre-alpine catchment with a short historic record and a limited set of available climate projections, which do not exhaustively cover the spectrum of climate uncertainties. The resulting problem of planning under uncertainty is typical in practice. We introduce the case study catchment in Sect. 2.1, followed by the available discharge projections in Sect. 2.2. We then move on to describe climatic uncertainties in Sect. 2.3 and 2.4 and give an estimate of their magnitude for our analysis in Sect. 2.5. We end by introducing the mathematical modeling of uncertainties and the respective uncertainty of model parametrization in Sect. 2.6.
2.1 The Mangfall catchment in Rosenheim
Our case study site is the river Mangfall at gauge Rosenheim, shortly before it flows into the Inn river. Rosenheim is a city in Bavaria that has suffered severe flood losses from Mangfall flooding in the past (Wasserwirtschaftsamt Rosenheim, 2014). With an area of 1102 km2, the Mangfall is a medium-sized catchment exhibiting a highly heterogeneous topography. Elevations within the catchment range from 443 to 1988 m a.s.l. with a mean value of approximately 1000 m a.s.l., indicating the pre-alpine nature of the river basin. Southern sub-catchments in the Mangfall mountains are steep and rocky, resulting in a rapid runoff response. On the contrary, northern regions in the Alpine foothills show a more moderate discharge behavior due to gentle slopes. Thus, the discharge pattern of the Mangfall combines both characteristics of mountainous and lowland areas (Kunstmann and Stadler, 2005; RMD Consult, 2016; Magdali, 2015).
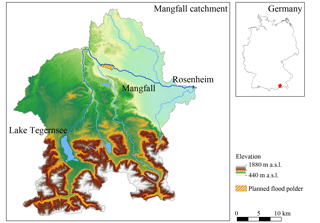
Figure 2Digital elevation model of the pre-alpine Mangfall catchment with its river network. The catchment is characterized by its highly heterogeneous topography leading to different discharge behavior between the northern and southern regions of the river basin (Geobasisdaten© Bayerische Vermessungsverwaltung).
Precipitation in the catchment is strongly affected by the adjacent Alpine arch leading to annual mean amounts of 1800 mm in mountainous and 1000 mm in low-altitude zones. The watershed receives most precipitation in July, often in form of convective, high-intensity precipitation (Magdali, 2015; Deutscher Wetterdienst, 2018). Therefore, this study focusses on the uncertainty analysis for summer discharge, since it poses the greatest threat to the city of Rosenheim. Planning authorities give the 100-year design discharge at the Rosenheim gauge as 480 m3 s−1 (RMD Consult, 2016). Figure 2 shows the topography of the Mangfall catchment alongside its river network. The available historic record at the Mangfall gauge in Rosenheim is reproduced in Supplement S1.
2.2 Available ensemble of discharge projections
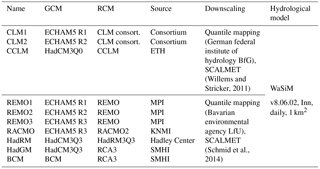
Table 1 lists the projections available at the case study gauge. Several projections have identical modeling chains and differ only in the model run; 6 of the 10 regional climate models (RCMs) are nested in the same global climate model (GCM), ECHAM5; and all GCM–RCMs are based on the same IPCC SRES (Special Report on Emissions Scenarios) emission scenario, A1B. Furthermore, all climate models are coupled to the same hydrological model (WaSiM) and same downscaling technique (quantile mapping). The ensemble is limited in that it does not cover a wide range of modeling uncertainties, and it is imperfect in that the projections of the ensemble are not independent. Such a set of available projections is quite typical of what is encountered in flood protection planning. The projections are reproduced in Supplement S2.
2.3 Internal variability
The term “internal variability” describes the irreducible uncertainty component in extreme discharge: even with perfect knowledge, it cannot be predicted deterministically what the annual maximum discharge of a year will be, and thus how the design flood estimate will change. This is because discharge realizations occur spontaneously, due to interactions of components within the climate system (IPCC, 2013). In the available projections, the absolute amount of internal variability did not change in time significantly and is thus modeled as stationary. In projections of future discharge, however, the relative importance of internal variability decreases with time as climatic uncertainties increase with increasing projection horizon. In a small pre-alpine catchment, such as considered in our case studies, the internal variability is large and dominates the uncertainty spectrum, potentially masking existing trend signals in heavy precipitation (and thus extreme discharge) for the entire projection horizon up to the year 2100 (Maraun, 2013). Alternative terms for the internal variability are “inherent randomness” or “noise”.
2.4 Uncertainties in the climate modeling chain
Discharge projections are the result of a complex multistep climate modeling process. In the literature, this is often termed the climate modeling “chain”, which, as new uncertainties are introduced at each modeling step, leads to the “uncertainty cascade” (Mitchell and Hulme, 1999; Foley, 2010). It is worth pointing out that the uncertainty cascade does not necessarily lead to an increase in uncertainty at each step, as the modeling steps depend on each other in a nonlinear fashion. Just as uncertainties can add up, it is conceivable that they may not be relevant for future steps in the modeling chain (Refsgaard et al., 2013). In the following, we briefly introduce the individual modeling steps required to obtain projections of (extreme) discharge. The uncertainty from the interaction of consecutive steps in the modeling chain is called “interaction uncertainty” (Bosshard et al., 2013). The uncertainties in the climate modeling chain are in principle epistemic, yet it is debatable whether they can and will be reduced in the foreseeable future (Hawkins and Sutton, 2009).
The forcing of the climate through greenhouse gas emissions (GHGs) is the first element in the climate modeling chain. The future socioeconomic, political and technological development determines the amount of GHGs emitted. The SRES scenarios – first introduced by the IPCC in 2000 (IPCC, 2000) – were recently substituted by representative concentration pathways (RCPs), which directly refer to the amount of GHGs emitted rather than complex scenarios (Moss et al., 2010). For our case study, only projections based on SRES scenario A1B, a widely used scenario with moderate socioeconomic and technological changes, are available. Thus, we have to take into account the uncertainty of what the projection results might have been under other forcing scenarios. However, in Europe, forcing uncertainty only becomes relevant in the far future and is of particularly low significance for local extreme precipitation (Hawkins and Sutton, 2011; Maraun, 2013; Tebaldi et al., 2015).
For climate change impact studies, it is customary to use ensembles of multiple combinations of global and regional climate models (GCMs–RCMs) (Huang et al., 2014; Muerth et al., 2012; Rajczak et al., 2013). The differences in GCM–RCM output when driven by the same emission forcing are termed “model response uncertainty” or “model spread” (IPCC, 2013). Multi-model ensembles (MMEs) such as the one available for the case study reproduce part of this spread. They do not reproduce it completely because they consist of a finite number of possibly biased and dependent models that typically have to be chosen based on availability rather than on statistical considerations (Knutti et al., 2013; Tebaldi and Knutti, 2007). To mitigate this problem, some researchers assign weights to individual models, but there is an ongoing debate about this: some researchers are making a general case for the benefits of weighting (Ylhäisi et al., 2015) or its drawbacks (Aghakouchak et al., 2013), some are detailing when it may make sense on the basis of model performance (Refsgaard et al., 2014; Rodwell and Palmer, 2007) or genealogy (Masson and Knutti, 2011), but all approaches are disputed. The relative importance of model response increases with projection lead time and is particularly significant for extreme summer precipitation (Bosshard et al., 2013). Since flooding in the case study catchment is dominated by extreme summer precipitation, we expect model response to form the second most important uncertainty contribution (after internal variability).
The available projections underwent statistical downscaling using quantile mapping, which is often recommended for extreme events (Bosshard et al., 2011; Dobler et al., 2012; Hall et al., 2014; Themeßl et al., 2010). Statistical downscaling is frequently used to align GCM–RCM outputs with historic records, but its use is still controversial (Chen et al., 2015; Ehret et al., 2012; Huang et al., 2014; Maurer and Pierce, 2014). The uncertainty contribution of the downscaling is likely to be large (Hundecha et al., 2016; Sunyer et al., 2015b). It would be beneficial to use not one but several downscaling techniques, similarly to how one uses an ensemble of GCM–RCMs (Arnbjerg-Nielsen et al., 2013; Sunyer et al., 2015a), as well as several calibration datasets (Sunyer et al., 2013a).
Up to and including statistical downscaling, the climate modeling chain produces not discharge but various other climatic variables that are translated to discharge in a specific catchment through a hydrological model. Catchment parameters (such as surface roughness) are typically found in an elaborate calibration procedure (Labarthe et al., 2014; Li et al., 2012). The parameters are usually assumed to be stationary, but they might in fact be non-stationary (Merz et al., 2011). Furthermore, the calibration might mask model errors by tuning the catchment parameters to balance them. Thus, the parameter estimates strongly depend on the calibration period (Brigode et al., 2013). Several approaches exist to quantify the uncertainty stemming from the hydrological model (Götzinger and Bárdossy, 2008; Velázquez et al., 2013). Overall, however, the error from the choice of hydrological model is small, in particular for high-flow indicators (Velázquez et al., 2013). It is likely smaller than or comparable to forcing uncertainty (Wilby, 2005).
2.5 Estimate of climatic uncertainty shares in extreme discharge for case study
In this section, we estimate the relative contribution of climatic uncertainties, using internal variability as a reference. Note that this is done as a rough estimate, since uncertainty quantification is not the focus of this paper. As will become clear in Sects. 4.2 and 5; an exact quantification is also not necessary for the proposed decision-making process. To summarize the previous two sections, the following qualitative statements can be made about the contribution of relevant sources of uncertainty in the considered midsize pre-alpine catchments with floods driven by summer precipitation:
-
internal variability is dominant throughout most of the coming century;
-
model response is the second largest source of uncertainty, growing with lead time;
-
the impact of downscaling is also considerable, again particularly later in the projection horizon;
-
the role of forcing uncertainty and hydrological model is minor; the former becomes relevant only very late in the projection horizon;
-
uncertainty from interaction of the individual components may be of some significance.
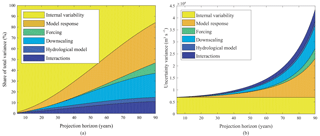
Figure 3(a) Share of different uncertainty components (variance) for extreme discharge in Rosenheim. (b) Resulting absolute uncertainties for CCLM. Uncertainties that are “visible” in our case study are shaded yellow–orange and “hidden” ones blue–green.
A methodology to quantify the size of the internal variability, model response and forcing uncertainty in mean precipitation and corresponding results for different regions and seasons has been presented in Hawkins and Sutton (2009, 2011). We base our estimate of these components on equivalent results for summer precipitation in Europe obtained from Ed Hawkins (email communication, 17 February 2017). We consider precipitation results to be transferable to discharge in the given catchment since extreme summer precipitation has in the past been the dominant trigger of high discharge in the Mangfall. A comparison of uncertainty shares for mean versus extreme discharge is available in Bosshard et al. (2013) and is used to adapt the results. Quantitative estimates of the shares of model response, downscaling, hydrological model and interactions for a different pre-alpine catchment are also provided in Bosshard et al. (2013). We combine the quantitative results with the catchment-specific qualitative knowledge to produce the estimate. The uncertainty spectrum is shifted towards the later projection horizon to account for the longer dominance of internal variability in a pre-alpine catchment with small-scale, extreme summer precipitation as the flood-triggering process. This results in a near-term contribution of the internal variability of at least 80 % of total uncertainty, as expected. The shift also reduces the uncertainty share attributed to model response and emission forcing, which, following Ed Hawkins (email communication, 17 February 2017), explained over 90 % of total uncertainty by the end of the century. The shares are adjusted to better represent the particular modeling and topography: the share of model response is set to peak at around 40 %. For downscaling, shares of up to 25 % are expected. Uncertainties stemming from interactions are anticipated to lie on the order of 10 %. Contributions attributed to hydrological modeling are set to remain below 5 % over the whole time horizon. The results of the estimation are shown in Fig. 3. Figure 3a shows the resulting relative uncertainty shares and Fig. 3b the resulting absolute uncertainties for the projection CCLM. Forcing, downscaling, hydrological model and interaction components are hidden uncertainties in the case study. As will be shown in Sect. 3, the sum of hidden uncertainties rather than individual components is used in the Bayesian estimation. Thus, it does not matter if the share of any one of these uncertainties has been slightly over- or underestimated. The question of sensitivity will be discussed further in Sect. 4. The estimated variance shares of the hidden uncertainty components and internal variability with respect to total uncertainty for Rosenheim are given in Supplement S3.
2.6 Parameter uncertainty
Statistical modeling of extreme discharge Q is commonly based on fitting a suitable extreme value distribution to the available data, e.g., a Gumbel or a generalized extreme value (GEV) distribution. These are described by their probability density function (PDF), fQ|θ(q|θ), in which θ is the set of parameters of the distribution function that are estimated from the data. Estimating θ from finite data will result in a probability distribution over θ, which describes parameter uncertainty (Kennedy and O'Hagan, 2001).
The discharge q(T) of a design flood associated with a return period T is defined as a function of θ as
where FQ(t)|θ is the cumulative distribution function (CDF) and is the inverse CDF of the annual maximum discharge Q(t). In a Bayesian setting, the posterior joint PDF of the parameters θ can be estimated from N years of annual maximum discharges q = [q1, …, qN] (from historic record or projections) as follows:
where fθ(θ) is the prior distribution of the parameters and L(θ|q) is the likelihood describing the discharge data q. The discharge maxima can be assumed to be independent between individual years (Coles, 2004). Neglecting measurement error, the likelihood function in Eq. (2) can hence be formulated as
With increasing number of records of annual maximum discharges qt, the uncertainty in the parameters θ is reduced.
The Bayesian method requires the selection of a prior distribution fθ(θ) in Eq. (2). For the application to flood protection planning, one may wish to select a prior distribution that is only weakly informative in q(T). We propose to use the following distribution for this purpose (dropping the time dependence t for readability):
where is the PDF of q(T) based on a prior distribution that is uniform in θ and Eq. (1) has been applied in the equality.
In this section, we propose an approach for combining different uncertainty components when using projections to estimate the parameters θ of the time-variant distribution fQ(t)|Θ(q|θ) of annual maximum discharge Q(t) in year t (see Sect. 2.6). This distribution is first estimated for each projection of extreme discharges individually. For projection, we increase the distribution spread in a time-dependent manner using the estimate of hidden uncertainty from Sect. 2.5. Since the uncertainty increases with time, projections late on the horizon are naturally assigned less information value. We then combine the distributions from different projections.
In Sect. 3.1, we categorize uncertainties in such a way that it is conducive for our application. We then combine these uncertainties within a Bayesian approach. In Sect. 3.2, we show how the likelihood L(θ|q) for the joint parameter PDF is estimated for any individual projection, taking into account uncertainty estimates from the literature. In Sect. 3.3, we show how to combine the likelihoods of the projection ensemble. Finally, we give a summary of planning and decision making under uncertainty in Sect. 3.4.
3.1 Uncertainty categorization
Different categorizations of uncertainty have been proposed in the literature. In Sect. 2.3–2.6 for example, we have presented the uncertainties in extreme discharge by source. Another common way to categorize uncertainties is the distinction between aleatory (irreducible) and epistemic (reducible) uncertainties (Der Kiureghian and Ditlevsen, 2009; Refsgaard et al., 2013). This categorization is useful in that it underlines in which areas future research could lead to uncertainty reduction. Other authors focus their categorization on the different effects of uncertainties (Merz et al., 2015).
In the context of estimating flood extremes under climate change with limited information, we distinguish between the following:
-
Visible uncertainty, which is known and can be quantified. For an ensemble of discharge projections, this would, for example, be the internal variability, the model response uncertainty and parameter uncertainty. Parameter uncertainty is also visible in that it is straightforward to quantify, but it is not a climatic uncertainty.
-
Hidden uncertainty, which is the remaining uncertainty and can, at best, be estimated. For example, in the projection ensemble of the case study, forcing uncertainty is hidden since all projections are based on the same emission scenario. In real planning situations, hidden uncertainty is typically significant because of limited and imperfect projections and data; it can therefore not be neglected.
In the following sections, a methodology will be presented to estimate the distribution of parameters of annual maximum discharge using these uncertainties.
3.2 Accounting for uncertainty and bias in projections
When using discharge projections, it is important to account for uncertainty and bias within them. As discussed in Sect. 2, climatic uncertainties increase with the projection horizon and thus the information value of a projection made late on the horizon is smaller than that of an earlier one. For example, a projection for the year 2100 is associated with higher uncertainty than one that is made for the coming year and should have less weight when estimating the parameters θ of the distribution of annual maximum discharge from climate projections. In the following, we develop a methodology that accounts for this.
We introduce the standard deviation , in which the superscript (u) describes which type of uncertainty is considered (internal or hidden), the subscript i denotes the projection and the subscript t the time dependence. The internal variability in a projection, , can be quantified following Hawkins and Sutton (2009). Note that the subscript t is excluded here since internal variability is assumed to be independent of time. Relative variance shares of the individual uncertainties, including hidden ones, can be estimated using literature (Bosshard et al., 2013; Hawkins and Sutton, 2011) and expert judgement, as was done in Sect. 2.5. The share of an individual uncertainty component in the total variance is here labeled , with the indexing as for σ. The uncertainty shares are assumed to be general for a given location, independent of the projection. Thus, the absolute value of the hidden uncertainty can be found from the absolute internal variability and the uncertainty variance shares of Sect. 2.5 (reproduced numerically in Supplement S3) as
For estimating the joint PDF of the parameters θ of the annual maximum discharge distribution, we treat the i = 1, …, M discharge projections pi = [, …, ] as samples of the true future discharge τt with a bias Δi,t: τt = pi,t − Δi,t. We express the likelihood , Δi,t) describing the annual maximum discharge of projection i in year t as
where fQ(t)|Θ is the PDF of the extreme value distribution describing Q(t). The likelihood , Δi,t) determines the estimation of the PDF of parameters θ from projections, similar to Eq. (2).
The bias Δi,t is modeled as a normal random variable with zero mean and standard deviation :
with z being a standard normal random variable. By modeling all Δi,t as a function of the same z, it is assumed that the Δi,t are fully dependent within one projection i. This treatment is conservative, since it minimizes the amount of learning from projected discharges. Due to the large impact of the projection on the bias, it is a better depiction of reality than the assumption of independent Δi,t within one projection i. From this follows the likelihood for a complete projection time series pi as
where ν is the standard normal PDF. Internal variability is included in Eq. (8) naturally via pi,t, as is parameter uncertainty, which is a function of the length of projections. The estimate of hidden uncertainty, as from Sect. 2.5, is included via . While we are focussing on climate uncertainty here, in principle, any kind of additional uncertainty can be incorporated via the hidden uncertainty parameter in Eq. (8). Model response uncertainty is included in the combination of the likelihoods Li(θ|pi) from different projections i, as described in the following section.
3.3 Accounting for dependency among projections
Individual projections are not independent. Hence, one cannot combine Li(θ|pi) into a joint likelihood L(θ|p) via a simple product over projections pi. Dependence among multiple projections is due to common model biases, be it because they, for example, share code from the same institution or because our understanding of climate processes is not perfect (Knutti et al., 2013; Tebaldi and Knutti, 2007). Consequently, confidence in the prediction variance should not increase linearly with the number of projections in an ensemble. Instead, the ensemble should be seen as consisting of an effective number I of quasi-independent projections (adding independent pieces of knowledge) that is smaller than the ensemble size M (Pennell and Reichler, 2011; Sunyer et al., 2013b). We thus partition the ensemble into J sets of I projections, where J is the integer quotient of . For each of these sets, the likelihood function can then be formulated as the product of the likelihoods ) of the set members, since they are assumed to contain independent information:
Climatological rationale is applied to determine the division of the ensemble into sets: in line with the concept of effective projections, the projections in each set should be as distinct as possible, adding a maximum of additional information.
Based on their genealogy, we partition the available projections (Table 1) as follows.
-
When using two sets of five effective projections:
-
Set 1: CLM1, CCLM, REMO2, HadGM, RACMO.
-
Set 2: CLM2, REMO1, REMO3, HadRM, BCM.
-
-
When using three sets of three effective projections (dropping REMO3):
-
Set 1: CLM1, REMO2, HadRM.
-
Set 2: CLM2, REMO1, HadGM.
-
Set 3: CCLM, RACMO, BCM.
-
The set likelihood L(j)(θ|p) from Eq. (9) is used to compute the joint set posterior of parameters, , similar to Eq. (2). The set posteriors are then averaged to result in an overall posterior fΘ|Q(t)(θ|p) of learning from projections under climate uncertainty. The averaging over posteriors expresses that we place equal trust in distributions estimated from the different sets.
3.4 Planning under uncertainty
Protection requirements (“criterions”) are based on the T-year discharge q(T) (see Eq. 1), most commonly the 100 year discharge. Since the estimate of q(T) – the peak of the PDF – changes as new data become available, the capacity of the flood protection system will be re-evaluated in the future and possibly be adjusted. The probability that adjustment becomes necessary is determined by the level of uncertainty: the higher the uncertainty in the future extreme discharges, the more likely it is that an adjustment of the protection system will become necessary in the future. To understand why this is, consider Fig. 4: after initial planning, new discharges are observed (lilac dots). If, as pictured here, the observed discharges are higher than expected, the design flood estimate q(T) will increase. (We show the estimate of q(1) to be able to display observations on the same scale. Note that the 99th percentile of the shown PDF does not correspond to q(100).) If the uncertainty is large at the time of initial planning – as is the case here, visualized with the blue, original PDF – then the additional information from the new observation has a larger weight in predicting future extreme discharges. The change in q(T) is larger than if the distribution of extreme discharges had been more informative (i.e., more “certain”, less “spread out”). In practice, the protection will only be adjusted when a significant change in q(T) has occurred that cannot be compensated by the freeboard and planning margin present (represented by the protection level boundary from which onward adjustment is needed). To avoid the need for frequent adjustments and increase robustness, the optimization framework of Dittes et al. (2018) thus recommends a higher planning margin when the system is constructed under higher uncertainty initially, as will become apparent in the results.

Figure 4Original and updated PDF based on a period of high new observations of annual maximum discharge. Because the original PDF is so broad, the period of extreme observations results in a strongly shifted updated PDF, the peak of which (corresponding to the estimate of q(1)) crosses the protection boundary level. Thus, the protection system must be adjusted.
Because the – as yet uncertain – future discharge realizations determine future decisions, they have an impact on the optimality of the initial decision. Therefore, it is sensible to model protection planning as sequential, with probabilistic future discharge observations, updating of the discharge PDF and corresponding decisions on adjustment in regular time intervals. A Bayesian network approach doing so for decisions on adapting infrastructure to a changing climate has been presented by Nishijima (2015) and a POMDP (partially observable Markov decision process) approach applied to flood protection, using climate scenarios, has been described by Špačková and Straub (2016). An alternative sampling-based approach, which takes the full joint parameter PDF into account, has been proposed by Dittes et al. (2018). The planning horizon is divided into a number of time periods. After each period, the current protection level is re-evaluated and possibly adjusted based on the annual maximum discharges that have been observed during that period or – more precisely – based on the q(100) as resulting from the updated distribution of annual maximum discharges. To probabilistically model this future updating (before these data are actually available), future realizations of annual maximum discharge q are sampled from the discharge distribution fQ(t)|Θ(q|θ) estimated initially. Optimal decisions are then identified via backwards induction optimization (Raiffa and Schlaifer, 1961), which works by first determining the system that should be installed at the last adjustment, conditional on the existing protection and discharges observed by then. The obtained recommendation is then used to find the system that should be installed at the second to last adjustment and so forth until arriving at a recommendation for the system that should be installed initially. We employ this optimization framework in the following case study.
Note that, since there is often a discrepancy between the level of observed past discharge at a specific gauge and the corresponding regional climate projections, we take the commonly used approach (Fatichi et al., 2013; Pöhler et al., 2012) of computing relative rather than absolute values from the climate projections. Here, this means that we find a planning margin γ based on the projection ensemble and uncertainty estimates from the literature, which may then be applied to the absolute protection (100-year flood) as estimated from historic records.
We present the integration of the uncertainty quantification of extreme discharge in the pre-alpine Mangfall gauge at Rosenheim as shown in Sect. 2 with the uncertainty combination methodology of Sect. 3 and the decision framework of Dittes et al. (2018). Section 4.1 gives details of the implementation, followed by the protection recommendation and sensitivity results in Sect. 4.2.
4.1 Implementation
We conduct our case study for the Mangfall river in Rosenheim, which has been introduced in Sect. 2.1. We consider the designed flood protection systems to have a lifetime of 90 years and to be designed in such a way as to protect from the 100-year flood, with design discharge q(100). The decision on the protection capacity will be revised every 30 years, taking into account the discharge records that will be available at these points in time. When estimating climate parameters – especially trends – from a time step, 30 years is an often used compromise between the desire to minimize statistical uncertainty and that to capture recent climate developments (IPCC, 2013; Kerkhoff et al., 2015; Laprise, 2014; Pöhler et al., 2012). The protection requirement corresponds to the maximal required protection during the time step in question. As in Dittes et al. (2018), a square root function describes the cost of the construction/extension of the protection system and a discounting rate of 2 % annually is employed. In Dittes et al. (2018), we considered a measure of flexibility which describes how costly it is to adapt measures later in their lifetime. In this contribution, we give results for the non-flexible case only, which implies that future adjustments to the system are expensive. Introducing some flexibility into the protection system would lead to lower planning margin results than those obtained here.
Table 2Recommended planning margin when using the historic record versus differing numbers of effective projections for estimating the initial parameter space.

Following model plausibility testing on the projections (MacKay, 1992), a GEV distribution is chosen to model the annual maximum discharges. It is described by shape parameter k, scale parameter β>0 and location parameter μ. We employ a linear trend in the scale and location parameters, which is common practice in the literature (Coles, 2004; Delgado et al., 2010; Hanel and Buishand, 2011; Maraun, 2013). The scale is expressed as β = β0 + β1t and the location as μ = μ0 + μ1t (Coles, 2004; Hanel and Buishand, 2011). Thus, θ = (kβ0μ0, β1μ1).
The joint PDF of parameters of annual maximum discharge estimated from the climate projections is used as the basis for future updating with discharge realizations. To obtain this PDF, the climate projections are estimated on a prior distribution that is weakly informative in the 100-year design discharge of the first time step (years 1–30) as by Eq. (4). Computationally, the prior distribution is constructed by uniform sampling of parameters over a large space, computing the respective 100-year flood estimate for the first time step for each sampled parameter vector, and performing rejection sampling to obtain samples on the order of 6 × 105 following Eq. (4).
To find the optimal flood protection considering the full sequential decision process, it is necessary to simulate future discharge data, from which new flood estimates will be estimated (see Sect. 3.4). For this purpose, we used 300 samples of annual maximum discharge in the period 1–30 years and 70 samples of annual maximum discharge in the period 31–60 years. Using fewer discharge samples in later periods is computationally preferable and still comes with a high accuracy, as the absolute number of samples in the second period overall is 300 × 70 = 21 000. This choice of number of samples leads to a relative error of less than 4 % in the protection recommendation.
4.2 Protection recommendation and sensitivity
Figure 5 shows the 100-year discharge PDF (weighted mean) from the initial parameter distribution for the first 30 years of planning when estimated from the 39-year-long historic record versus 10, 5, 3 and 1 effective projections of 90-year length. Ten effective projections correspond to multiplying all posteriors and one effective projection corresponds to averaging all posteriors. For five and three effective projections, we split the projections into sets as given in Sect. 3.3.
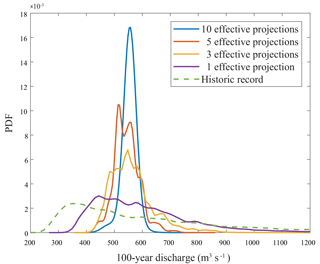
Figure 5The 100-year discharge PDF from initial parameter distribution when estimated based on the historic record (dashed) versus different numbers of effective projections, for years 1–30.
The PDFs shown in Fig. 5 are used as input to the optimization framework of Dittes et al. (2018) to obtain recommendations for the planning margin. Section 3.4 gave an intuitive understanding of how these relate to the 100-year PDF. The planning margin that is recommended when estimating based on the historic record only is 111.8 %, versus 81.9, 16.5, 12.5 and 2.6 % for 1, 3, 5 and 10 effective projections, respectively. These results are summarized in Table 2.
Using a similar ensemble of climate projections over Denmark, Sunyer et al. (2013b) established that an ensemble of 10 projections corresponds to 5 effective projections for 20-year heavy summer precipitation. Despite some issues with transferability – as will be discussed in Sect. 5 – we thus use five effective projections and hence a planning reserve of 12.5 % as the recommended protection margin from the extreme summer precipitation floods observed at the Mangfall in Rosenheim.
To investigate the effect of hidden uncertainty on the protection recommendation, we repeated the optimization, once using no hidden uncertainty and once doubling the hidden uncertainty variance shares estimated in Sect. 2.5 (reproduced numerically in Supplement S3), with an effective model number of five. The recommended planning margins lay in the expected order, with the “no uncertainty” recommendation the smallest at 8.1 % and the “double uncertainty” recommendation the largest at 13.8 %. Finally, we studied the effect of changing the trend in the projections of annual maximum discharge. Detrending the projected annual maxima lead to a recommendation of 12.2 %. We then used the projected annual maxima with doubled trend: from the observed average of 0.25 m3 s−1 per year (corresponding to an 11 % rise in mean annual maximum discharge during the 90-year lifetime) to 0.5 m3 s−1 per year. The recommended planning margin increased only very slightly, from 12.5 to 12.7 %. The results are summarized in Table 3.
It is apparent from the results that the number of effective projections has a large impact on the recommended planning margin. Hence, we recommend that planners make use of the concept of effective projections and partition ensembles accordingly, rather than just average over all members of a projection ensemble. Our assumption that five effective projections are applicable for the 10-member ensemble at Rosenheim can be questioned. The transferability of the corresponding results of Sunyer et al. (2013b) might be hindered by the difference in considered location (a southern German catchment versus an averaging over Denmark), ensemble (some members differ) and extreme index (100-year event versus 20-year event). From other results presented in Sunyer et al. (2013b) using an alternative measure of projection dependence as well as higher extreme indices, we believe that the 12.5 % recommendation given here is conservative and a slightly lower recommendation for the planning margin (based on a slightly higher number of effective projections) may be applicable. However, the transferability remains questionable for the location and ensemble and thus the study ideally ought to be repeated for the given catchment and ensemble, in particular with respect to the large impact of the number of effective projections on the protection recommendation.
It is striking that the recommended planning margin from the historic record alone is very large. A main reason is that we use a GEV distribution with two trend parameters (i.e., five parameters overall) to pick up climate signals in the projections. We are using the same distribution for the historic record for comparability. In reality, one should not attempt to estimate such a high number of parameters from such a small set of data (38 annual maxima in the historic record); instead, one would assume stationarity or a fixed trend. We repeated the analysis for a stationary GEV (no trend parameters), resulting in a planning margin recommendation of 75.1 %. This is still high, confirming that it is not recommendable to plan based on a short historic record alone. Additional information should always be used, e.g., climate projections (as in this study), tools from runoff prediction in ungauged basins and climate analogues (Arnbjerg-Nielsen et al., 2015; Blöschl et al., 2013a).
Table 3Recommended planning margin (%) when using five effective projections and varying hidden uncertainty and trend.

We turn to the sensitivity analysis. First, the trend: the fact that signals that emerge late on the planning horizon are masked by noise and rendered less relevant by discounting explains why changing the trend signal leads to only insignificant changes in recommended planning margin. This is compounded by the fact that the trend signal is weak, which is to be expected from the location of the case study catchment (Madsen et al., 2014; Maraun, 2013) and is potentially amplified by projections underestimating trends in extreme precipitation (Haren et al., 2013). It should be added that not all scientists are comfortable with linear trend projections in extreme precipitation and discharge and that there is also an argument to be made for cyclical components (Gregersen et al., 2014) or “flood-rich” versus “flood-poor” periods (Hall et al., 2014; Merz et al., 2014), though these may not be applicable to floods of large return periods such as studied here (Merz et al., 2016). We assumed a linear trend in the case study for simplicity, but the proposed methodology is general. To use a different trend representation, one just has to change the definition of θ (see Sect. 4.1) accordingly.
Finally, we discuss the impact of varying size of uncertainty on planning. To investigate this, we evaluated the recommended planning margin when not adding any hidden uncertainty, when using the estimated amount and when using double the estimated amount of hidden uncertainty (see Sect. 4.2). The effect was small, in particular between adding the estimate versus double the estimate of hidden uncertainty. The share of hidden uncertainty is larger in the farther future, where its effect is limited because of discounting. We conclude that hidden uncertainty should be considered in decision making, yet the sensitivity to its exact amount is low and, when there is already a considerable level of uncertainty, including more has little effect. This is why we do not engage in detailed discussion on whether the size of the hidden uncertainty has been gauged correctly and whether additional uncertainty components should be included, despite this certainly being debatable (Grundmann, 2010; Refsgaard et al., 2013; Seifert, 2012; Sunyer, 2014; Velázquez et al., 2013). We believe that the low sensitivity of the protection recommendation to the size of the hidden uncertainty in the presented case study can be explained by the considerable visible uncertainty present: the capacity to project the future extreme discharge is already extremely limited and can barely be reduced by adding more uncertainty. While this may appear disheartening, it can also be a wake-up call to stop waiting for (doubtful) uncertainty reductions in climate modeling and start making (robust) decisions (Arnbjerg-Nielsen et al., 2013; Curry and Webster, 2011; Hawkins and Sutton, 2011).
Estimates of future extreme discharge are fraught with significant uncertainties that need to be accounted for in flood protection planning. In particular, the following points must be considered when estimating the parameters of future extreme discharge distributions:
-
an estimate of the uncertainty that cannot be quantified from the available data (the hidden uncertainty) must be included, since projections and data at hand cover only a limited range of the uncertainty spectrum (the visible uncertainty);
-
the time development of the uncertainty, so as to give less weight to projections far on the projection horizon;
-
dependency between projections, since projection ensembles often include several projections sharing code or assumptions.
In the proposed methodology, we quantitatively include these aspects in estimating the probabilistic distribution of flood discharge. Both “visible” and hidden uncertainty are included in a time-dependent Bayesian likelihood function. Dependence between projections is accounted for by using the concept of effective projection number. The uncertainty analysis proposed in this paper was used with the optimization framework of Dittes et al. (2018) to find protection recommendations for a pre-alpine case study catchment. The results show that when there is sizable visible uncertainty, the protection recommendation is robust to further uncertainty and moderate changes in trend. However, hidden uncertainty should not be neglected in planning as this would lead to insufficient protection recommendations.
The code is available upon request.
Data are available in the Supplement.
The supplement related to this article is available online at: https://doi.org/10.5194/hess-22-2511-2018-supplement.
BD developed the concepts of this paper under the guidance of OŠ and DS. BD wrote the code and performed the simulations. The results presented in Sect. 2 were obtained by LS. BD prepared the manuscript with contributions from all co-authors.
The authors declare that they have no conflict of interest.
We would like to thank Holger Komischke of Bayerisches Landesamt für
Umwelt (LfU) for fruitful discussions. The LfU also provided the discharge
records and projections used in the case study. The discharge projections
were modeled within the cooperation KLIWA and the Interreg IVB project
AdaptAlp. They were based either on ENSEMBLES data funded by the EU FP6
Integrated Project ENSEMBLES (contract number 505539), whose support is
gratefully acknowledged, or additional available climate projections. These
are REMO1 (“UBA”) and REMO2 (“BfG”) (Umweltbundesamt, 2018), as well as CLM1
and CLM2 (Hollweg et al., 2008). This work was supported by Deutsche Forschungsgemeinschaft (DFG)
through the TUM International Graduate School of Science and
Engineering (IGSSE).
This work was supported
by the German Research
Foundation (DFG) and the Technische
Universität
München within the funding programme
Open Access Publishing.
Edited by: Uwe Ehret
Reviewed by: two anonymous referees
Aghakouchak, A., Easterling, D., Hsu, K., Schubert, S., and Sorooshian, S. (Eds.): Extremes in a Changing Climate, Springer, Dordrecht, 2013.
Alfieri, L., Burek, P., Feyen, L., and Forzieri, G.: Global warming increases the frequency of river floods in Europe, Hydrol. Earth Syst. Sci., 19, 2247–2260, https://doi.org/10.5194/hess-19-2247-2015, 2015.
Arnbjerg-Nielsen, K., Willems, P., Olsson, J., Beecham, S., Pathirana, A., Bülow Gregersen, I., Madsen, H., and Nguyen, V. T. V: Impacts of climate change on rainfall extremes and urban drainage systems: A review, Water Sci. Technol., 68, 16–28, https://doi.org/10.2166/wst.2013.251, 2013.
Arnbjerg-Nielsen, K., Funder, S. G., and Madsen, H.: Identifying climate analogues for precipitation extremes for Denmark based on RCM simulations from the ENSEMBLES database, Water Sci. Technol., 71, 418–425, https://doi.org/10.2166/wst.2015.001, 2015.
Benjamin, J. R. and Cornell, C. A.: Probability, Statistics and Decisions for Civil Engineers, Mc Graw – Hill Book Company, New York City, 1970.
Blöschl, G., Sivapalan, M., Wagener, T., Viglione, A., and Savenije, H.: Runoff Prediction in Ungauged Basins: Synthesis Across Processes, in: Places and Scales, Cambridge University Press, Cambridge, 2013a.
Blöschl, G., Nester, T., Komma, J., Parajka, J., and Perdigão, R. A. P.: The June 2013 flood in the Upper Danube Basin, and comparisons with the 2002, 1954 and 1899 floods, Hydrol. Earth Syst. Sci., 17, 5197–5212, https://doi.org/10.5194/hess-17-5197-2013, 2013b.
Bosshard, T., Kotlarski, S., Ewen, T., and Schär, C.: Spectral representation of the annual cycle in the climate change signal, Hydrol. Earth Syst. Sci., 15, 2777–2788, https://doi.org/10.5194/hess-15-2777-2011, 2011.
Bosshard, T., Carambia, M., Goergen, K., Kotlarski, S., Krahe, P., Zappa, M., and Schär, C.: Quantifying uncertainty sources in an ensemble of hydrological climate-impact projections, Water Resour. Res., 49, 1523–1536, https://doi.org/10.1029/2011WR011533, 2013.
Brigode, P., Oudin, L., and Perrin, C.: Hydrological model parameter instability: A source of additional uncertainty in estimating the hydrological impacts of climate change?, J. Hydrol., 476, 410–425, https://doi.org/10.1016/j.jhydrol.2012.11.012, 2013.
Central European Flood Risk Assessment and Management in CENTROPE: Current standards for flood protection, available at: http://www.floodcba2.eu/site/wp-content/uploads/CEframe_363_Current_standards_for_flood_protection.pdf (last access: 22 April 2018), 2013.
Chen, J., Brissette, F. P., and Lucas-picher, P.: Assessing the limits of bias-correcting climatemodel outputs for climate change impact studies, J. Geophys. Res.-Atmos., 120, 1123–1136, https://doi.org/10.1002/2014JD022635, 2015.
Coles, S.: An Introduction to Statistical Modeling of Extreme Values, Springer, London, 2004.
Coles, S., Pericchi, L. R., and Sisson, S.: A fully probabilistic approach to extreme rainfall modelling, J. Hydrol., 273, 35–50, https://doi.org/10.1016/S0022-1694(02)00353-0, 2003.
Curry, J. A. and Webster, P. J.: Climate science and the uncertainty monster, B. Am. Meteorol. Soc., 92, 1667–1682, https://doi.org/10.1175/2011BAMS3139.1, 2011.
Custer, R. and Nishijima, K.: Hierarchical decision making for flood risk reduction, in: 11th International Conference on Structural Safety & Reliability, ICOSSAR, New York, 4865–4872, 2013.
Davis, D. R., Kisiel, C. C., and Duckstein, L.: Bayesian decision theory applied to design in hydrology, Water Resour. Res., 8, 33–41, 1972.
De Kok, J. L., Hoekstra, A. Y., Defence, F., and Change, C.: Living with peak discharge uncertainty: The self-learning dike, in 4th Biennial Meeting of the International Congress on Environmental Modelling and Software, iEMSs, Barcelona, 1542–1549, 2008.
Delgado, J. M., Apel, H., and Merz, B.: Flood trends and variability in the Mekong river, Hydrol. Earth Syst. Sci., 14, 407–418, https://doi.org/10.5194/hess-14-407-2010, 2010.
Deutscher Wetterdienst: Deutscher Klimaatlas, available at: https://www.dwd.de/DE/klimaumwelt/klimaatlas/klimaatlas_node.html, last access: 22 April 2018.
Dittes, B., Špačková, O., and Straub, D.: Managing uncertainty in design flood magnitude: Flexible protection strategies vs. safety factors, J. Flood Risk Manage., accepted, 2018.
Dobler, C., Hagemann, S., Wilby, R. L., and Stätter, J.: Quantifying different sources of uncertainty in hydrological projections in an Alpine watershed, Hydrol. Earth Syst. Sci., 16, 4343–4360, https://doi.org/10.5194/hess-16-4343-2012, 2012.
Ehret, U., Zehe, E., Wulfmeyer, V., Warrach-Sagi, K., and Liebert, J.: Should we apply bias correction to global and regional climate model data?, Hydrol. Earth Syst. Sci., 16, 3391–3404, https://doi.org/10.5194/hess-16-3391-2012, 2012.
Fatichi, S., Rimkus, S., Burlando, P., Bordoy, R., and Molnar, P.: Elevational dependence of climate change impacts on water resources in an Alpine catchment, Hydrol. Earth Syst. Sci. Discuss., 10, 3743–3794, https://doi.org/10.5194/hessd-10-3743-2013, 2013.
Foley, A. M.: Uncertainty in regional climate modelling: A review, Progress in Physical Geography, 34(5), 647–670, doi:10.1177/0309133310375654, 2010.
Götzinger, J. and Bárdossy, A.: Generic error model for calibration and uncertainty estimation of hydrological models, Water Resour. Res., 44, W00B07, https://doi.org/10.1029/2007WR006691, 2008.
Graf, M., Nishijima, K., and Faber, M.: Bayesian updating in natural hazard risk assessment, Aust. J. Struct. Eng., 9, 35–44, https://doi.org/10.1080/13287982.2009.11465008, 2007.
Gregersen, I. B., Madsen, H., Rosbjerg, D., and Arnbjerg-Nielsen, K.: Long term variations of extreme rainfall in Denmark and southern Sweden, Clim. Dynam., 44, 3155–3169, https://doi.org/10.1007/s00382-014-2276-4, 2014.
Grundmann, J.: Analyse und Simulation von Unsicherheiten in der Flächendifferenzierten Niederschlags-Abfluss-Modellierung, in: Dresdner Schriften zur Hydrologie, PhD Thesis, 165 pp., https://d-nb.info/1008804363/34 (last access: 22 April 2018), 2010.
Hall, J. and Solomatine, D.: A framework for uncertainty analysis in flood risk management decisions, Int. J. River Basin Manage., 6, 85–98, https://doi.org/10.1080/15715124.2008.9635339, 2008.
Hall, J., Arheimer, B., Borga, M., Brázdil, R., Claps, P., Kiss, A., Kjeldsen, T. R., Kriaucuniene, J., Kundzewicz, Z. W., Lang, M., Llasat, M. C., Macdonald, N., McIntyre, N., Mediero, L., Merz, B., Merz, R., Molnar, P., Montanari, A., Neuhold, C., Parajka, J., Perdigão, R. A. P., Plavcová, L., Rogger, M., Salinas, J. L., Sauquet, E., Schär, C., Szolgay, J., Viglione, A., and Blöschl, G.: Understanding flood regime changes in Europe: A state-of-the-art assessment, Hydrol. Earth Syst. Sci., 18, 2735–2772, https://doi.org/10.5194/hess-18-2735-2014, 2014.
Hallegatte, S.: Strategies to adapt to an uncertain climate change, Global Environ. Change, 19, 240–247, https://doi.org/10.1016/j.gloenvcha.2008.12.003, 2009.
Hanel, M. and Buishand, T. A.: Analysis of precipitation extremes in an ensemble of transient regional climate model simulations for the Rhine basin, Clim. Dynam., 36, 1135–1153, https://doi.org/10.1007/s00382-010-0822-2, 2011.
Hawkins, E. and Sutton, R.: The potential to narrow uncertainty in regional climate predictions, B. Am. Meteorol. Soc., 90, 1095–1107, https://doi.org/10.1175/2009BAMS2607.1, 2009.
Hawkins, E. and Sutton, R.: The potential to narrow uncertainty in projections of regional precipitation change, Clim. Dynam., 37, 407–418, 2011.
Hollweg, H.-D., Böhm, U., Fast, I., Hennemuth, B., Keuler, K., Keup-Thiel, E., Lautenschlager, M., Legutke, S., Radtke, K., Rockel, B., Schubert, M., Will, A., and Michael Woldt, C. W.: Ensemble Simulations over Europe with the Regional Climate Model CLM forced with IPCC AR4 Global Scenarios, CLM Technical Report, 20, 857–861, https://doi.org/10.1089/lap.2010.0351, 2008.
Huang, S., Krysanova, V., and Hattermann, F.: Projections of climate change impacts on floods and droughts in Germany using an ensemble of climate change scenarios, Reg. Environ. Change, 15, 461–473, https://doi.org/10.1007/s10113-014-0606-z, 2014.
Hundecha, Y., Sunyer, M. A., Lawrence, D., Madsen, H., Willems, P., Martinkova, M., Vormoor, K., Bürger, G., Hanel, M., Kriaučiuniene, J., Loukas, A., Osuch, M., and Yücel, I.: Inter-comparison of statistical downscaling methods for projection of extreme flow indices across Europe, Hydrol. Earth Syst. Sci., 19, 1827–1847, https://doi.org/10.5194/hess-19-1827-2015, 2016.
IPCC: IPCC Special Report – Emission Scenarios, edited by: Nakicenovic, N. and Swart, R., Cambridge University Press, Cambridge, England, 2000.
IPCC: Climate Change 2013: The Physical Science Basis, Cambridge University Press, Cambridge, 2013.
Kennedy, M. C. and O'Hagan, A.: Bayesian calibration of computer models, J. Roy. Stat. Soc. B, 63, 425–464, https://doi.org/10.1111/1467-9868.00294, 2001.
Kerkhoff, C., Künsch, H. R., and Schär, C.: A Bayesian hierarchical model for heterogeneous RCM-GCM multimodel ensembles, J. Climate, 28, 6249–6266, https://doi.org/10.1175/JCLI-D-14-00606.1, 2015.
KLIWA: Der Klimawandel in Bayern für den Zeitraum 2021–2050, Arbeitskreis KLIWA, Mannheim, 2005.
KLIWA: Heft 9 – Regionale Klimaszenarien für Süddeutschland, Arbeitskreis KLIWA, Mannheim, 2006.
Knutti, R., Masson, D., and Gettelman, A.: Climate model genealogy: Generation CMIP5 and how we got there, Geophys. Res. Lett., 40, 1194–1199, https://doi.org/10.1002/grl.50256, 2013.
Kochendorfer, M. J.: Decision Making Under Uncertainty, The MIT Press, Cambridge, Massachusetts, 2015.
Kunstmann, H. and Stadler, C.: High resolution distributed atmospheric–hydrological modelling for Alpine catchments, J. Hydrol., 314, 105–124, https://doi.org/10.1016/j.jhydrol.2005.03.033, 2005.
Kwakkel, J., Walker, W., and Marchau, V.: Grappling with uncertainty in the long-term development of infrastructure systems, in: 3rd International Conference on Infrastructure Systems and Services: Next Generation Infrastructure Systems for Eco-Cities, INFRA, Shenzhen, 2010.
Labarthe, B., Abasq, L., de Fouquet, C., and Flipo, N.: Stepwise calibration procedure for regional coupled hydrological-hydrogeological models, in: EGU General Assembly Conference Abstracts (Vol. 16), May 2014, Vienna, Austria, 2014.
Laprise, R.: Comment on “The added value to global model projections of climate change by dynamical downscaling: A case study over the continental U.S. using the GISS-ModelE2 nad WRF models” by Racherla et al., J. Geophys. Res.-Atmos., 119, 3877–3881, https://doi.org/10.1002/2013JD019945, 2014.
Li, M., Yang, D., Chen, J., and Hubbard, S. S.: Calibration of a distributed flood forecasting model with input uncertainty using a Bayesian framework, Water Resour. Res., 48, W08510, https://doi.org/10.1029/2010WR010062, 2012.
MacKay, D. J. C.: Bayesian interpolation, Neural Computation, 4, 415–447, https://doi.org/10.1162/neco.1992.4.3.415, 1992.
Madsen, H., Lawrence, D., Lang, M., Martinkova, M., and Kjeldsen, T. R.: Review of trend analysis and climate change projections of extreme precipitation and floods in Europe, J. Hydrol., 519, 3634–3650, https://doi.org/10.1016/j.jhydrol.2014.11.003, 2014.
Magdali, M.: Calibration of the hydrological model WaSiM for the Mangfall, MS Thesis, Technical University of Munich, Munich, 2015.
Maraun, D.: When will trends in European mean and heavy daily precipitation emerge?, Environ. Res. Lett., 8, 14004, https://doi.org/10.1088/1748-9326/8/1/014004, 2013.
Masson, D. and Knutti, R.: Climate model genealogy, Geophys. Res. Lett., 38, L08703, https://doi.org/10.1029/2011GL046864, 2011.
Maurer, E. P. and Pierce, D. W.: Bias correction can modify climate model simulated precipitation changes without adverse effect on the ensemble mean, Hydrol. Earth Syst. Sci., 18, 915–925, https://doi.org/10.5194/hess-18-915-2014, 2014.
Merz, B., Aerts, J., Arnbjerg-Nielsen, K., Baldi, M., Becker, A., Bichet, A., Blöschl, G., Bouwer, L. M., Brauer, A., Cioffi, F., Delgado, J. M., Gocht, M., Guzzetti, F., Harrigan, S., Hirschboeck, K., Kilsby, C., Kron, W., Kwon, H. H., Lall, U., Merz, R., Nissen, K., Salvatti, P., Swierczynski, T., Ulbrich, U., Viglione, A., Ward, P. J., Weiler, M., Wilhelm, B., and Nied, M.: Floods and climate: Emerging perspectives for flood risk assessment and management, Nat. Hazards Earth Syst. Sci., 14, 1921–1942, https://doi.org/10.5194/nhess-14-1921-2014, 2014.
Merz, B., Vorogushyn, S., Lall, U., Viglione, A, and Blöschl, G.: Charting unknown water – on the role of surprise in flood risk assessment and management, Water Resour. Res., 51, 6399–6416, https://doi.org/10.1002/2014WR016259, 2015.
Merz, B., Dung, N. V., and Vorogushyn, S.: Temporal clustering of floods in Germany: Do flood-rich and flood-poor periods exist?, J. Hydrol., 541, 824–838, https://doi.org/10.1016/j.jhydrol.2016.07.041, 2016.
Merz, R., Parajka, J., and Blöschl, G.: Time stability of catchment model parameters: Implications for climate impact analyses, Water Resour. Res., 47, 6119, https://doi.org/10.1029/2010WR009505, 2011.
Mitchell, T. D. and Hulme, M.: Predicting regional climate change: living with uncertainty, Prog. Phys. Geogr., 23, 57–78, https://doi.org/10.1191/030913399672023346, 1999.
Moss, R. H., Edmonds, J. a, Hibbard, K. a, Manning, M. R., Rose, S. K., van Vuuren, D. P., Carter, T. R., Emori, S., Kainuma, M., Kram, T., Meehl, G. A., Mitchell, J. F. B., Nakicenovic, N., Riahi, K., Smith, S. J., Stouffer, R. J., Thomson, A. M., Weyant, J. P., and Wilbanks, T. J.: The next generation of scenarios for climate change research and assessment, Nature, 463, 747–756, https://doi.org/10.1038/nature08823, 2010.
Muerth, M., St.-Denis, B. G., Ludwig, R., and Caya, D.: Evaluation of different sources of uncertainty in climate change impact research using a hydro-climatic model ensemble, in: 6th Biennial Meeting of the International Congress on Environmental Modelling and Software, iEMSs, Leipzig, 2012.
Nishijima, K.: Concept of decision graphical framework for optimising adaptation of civil infrastructure to a changing climate, Struct. Infrastruct. Eng., 12, 477–483, https://doi.org/10.1080/15732479.2015.1020496, 2015.
Paté-Cornell, E.: On “Black swans” and “Perfect storms”: Risk analysis and management when statistics are not enough, Risk Analysis, 32, 1823–1833, 2011.
Pennell, C. and Reichler, T.: On the effective number of climate models, J. Climate, 24, 2358–2367, https://doi.org/10.1175/2010JCLI3814.1, 2011.
Pohl, R.: Freibordbemessung an Hochwasserschutzanlagen, 36 Dresdner Wasserbaukolloquium “Technischer und organisatorischer Hochwasserschutz”, Technische Universität Dresden, Institut für Wasserbau und technische Hydromechanik, Dresden, 2013.
Pöhler, H., Schultze, B., and Scherzer, J.: KLIWA: Vergleichende Analyse der neuen globalen Klimaprojektionen aus CMIP5 für Süddeutschland, Abschlussbericht, Arbeitskreis KLIWA, Mannheim, 2012.
Raiffa, H. and Schlaifer, R.: Applied Statistical Decision Theory, 5th Edn., The Colonial Press, Boston, 1961.
Rajczak, J., Pall, P., and Schär, C.: Projections of extreme precipitation events in regional climate simulations for Europe and the Alpine Region, J. Geophys. Res.-Atmos., 118, 3610–3626, https://doi.org/10.1002/jgrd.50297, 2013.
Refsgaard, J. C., Arnbjerg-Nielsen, K., Drews, M., Halsnæs, K., Jeppesen, E., Madsen, H., Markandya, A., Olesen, J. E., Porter, J. R., and Christensen, J. H.: The role of uncertainty in climate change adaptation strategies – A Danish water management example, Mitig. Adapt. Strat. Global Change, 18, 337–359, https://doi.org/10.1007/s11027-012-9366-6, 2013.
Refsgaard, J. C., Madsen, H., Andréassian, V., Arnbjerg-Nielsen, K., Davidson, T. A., Drews, M., Hamilton, D. P., Jeppesen, E., Kjellström, E., Olesen, J. E., Sonnenborg, T. O., Trolle, D., Willems, P., and Christensen, J. H.: A framework for testing the ability of models to project climate change and its impacts, Climatic Change, 122, 271–282, https://doi.org/10.1007/s10584-013-0990-2, 2014.
RMD Consult: Erläuterungsbericht – Hochwasserrückhaltebecken Feldolling, Munich, Germany, 2016.
Rodwell, M. J. and Palmer, T. N.: Using numerical weather prediction to assess climate models, Q. J. Roy. Meteorol. Soc., 133, 937–948, https://doi.org/10.1002/qj.23, 2007.
Schmid, F. J., Willkofer, F., and Ludwig, R.: Endbericht Einfluss der Biaskorrektur dynamischer regionaler Klimamodelldaten auf die Wasserhaushaltsmodellierung und Klimafolgeabschätzung in Bayerischen Flussgebieten – Erstellung eines Klimamodell-Audits und ergänzende Untersuchungen (BI-KLIM-2014), Ludwig Maximilian Universität, München, 2014.
Seifert, P.: Mit Sicherheit wächst der Schaden. Überlegungen zum Umgang mit Hochwasser in der räumlichen Planung, Geschäftsstelle des Regionalen Planungsverbandes Oberes Elbtal/Osterzgebirge, Meissen, 2012.
Špačková, O. and Straub, D.: Long-term adaption decisions via fully and partially observable Markov decision processes, Sustain. Resil. Infrastruct., 2, 37–58, 2017.
Sunyer, M. A.: Uncertainties in extreme precipitation under climate change conditions, Technical University of Denmark, available at: http://www.orbit.dtu.dk Copenhagen, 2014.
Sunyer, M. A., Sørup, H. J. D., Christensen, O. B., Madsen, H., Rosbjerg, D., Mikkelsen, P. S., and Arnbjerg-Nielsen, K.: On the importance of observational data properties when assessing regional climate model performance of extreme precipitation, Hydrol. Earth Syst. Sci., 17, 4323–4337, https://doi.org/10.5194/hess-17-4323-2013, 2013a.
Sunyer, M. A., Madsen, H., Rosbjerg, D., and Arnbjerg-Nielsen, K.: Regional interdependency of precipitation indices across Denmark in two ensembles of high-resolution RCMs, J. Climate, 26, 7912–7928, https://doi.org/10.1175/JCLI-D-12-00707.1, 2013b.
Sunyer, M. A., Gregersen, I. B., Rosbjerg, D., Madsen, H., Luchner, J., and Arnbjerg-Nielsen, K.: Comparison of different statistical downscaling methods to estimate changes in hourly extreme precipitation using RCM projections from ENSEMBLES, Int. J. Climatol., 35, 2528–2539, https://doi.org/10.1002/joc.4138, 2015a.
Sunyer, M. A., Hundecha, Y., Lawrence, D., Madsen, H., Willems, P., Martinkova, M., Vormoor, K., Bürger, G., Hanel, M., Kriaučiūnienė, J., Loukas, A., Osuch, M., Yücel, I., Kriaučiuniene, J., Loukas, A., Osuch, M., Yücel, I., Kriaučiūnienė, J., Loukas, A., Osuch, M., and Yücel, I.: Inter-comparison of statistical downscaling methods for projection of extreme precipitation in Europe, Hydrol. Earth Syst. Sci., 19, 1827–1847, https://doi.org/10.5194/hess-19-1827-2015, 2015b.
Tebaldi, C. and Knutti, R.: The use of the multi-model ensemble in probabilistic climate projections, Philos. T. Roy. Soc. A, 365, 2053–2075, https://doi.org/10.1098/rsta.2007.2076, 2007.
Tebaldi, C., Smith, R., Nychka, D., and Mearns, L.: Quantifying uncertainty in projections of regional climate change: a Bayesian approach to the analysis of multimodel ensembles, J. Climate, 18, 1524–1540, 2004.
Tebaldi, C., O'Neill, B., and Lamarque, J.-F.: Sensitivity of regional climate to global temperature and forcing, Environ. Res. Lett., 10, 74001, https://doi.org/10.1088/1748-9326/10/7/074001, 2015.
Themeßl, J., Gobiet, A., and Leuprecht, A.: Empirical-statistical downscaling and error correction of daily precipitation from regional climate models, Int. J. Climatol., 31, 1530–1544, https://doi.org/10.1002/joc.2168, 2010.
Umweltbundesamt: Einführung in Klimaprojektionen, available at: https://www.umweltbundesamt.de/themen/klima-energie/klimafolgen-anpassung/folgen-des-klimawandels/klimamodelle-szenarien/einfuehrung-in-klimaprojektionen#textpart-1, last access: 22 April 2018.
Van Haren, R., Van Oldenborgh, G. J., Lenderink, G., and Hazeleger, W.: Evaluation of modeled changes in extreme precipitation in Europe and the Rhine basin, Environ. Res. Lett., 8, 14053, https://doi.org/10.1088/1748-9326/8/1/014053, 2013.
Velázquez, J. A., Schmid, J., Ricard, S., Muerth, M. J., Gauvin St-Denis, B., Minville, M., Chaumont, D., Caya, D., Ludwig, R., and Turcotte, R.: An ensemble approach to assess hydrological models' contribution to uncertainties in the analysis of climate change impact on water resources, Hydrol. Earth Syst. Sci., 17, 565–578, https://doi.org/10.5194/hess-17-565-2013, 2013.
Viglione, A., Merz, R., Salinas, J. L., and Blöschl, G.: Flood frequency hydrology: 3. A Bayesian analysis, Water Resour. Res., 49, 675–692, https://doi.org/10.1029/2011WR010782, 2013.
Wasserwirtschaftsamt Rosenheim: Das Hochwasser vom Juni 2013, Wasserwirtschaftsamt Rosenheim, Rosenheim, 2014.
Wiedemann, C. and Slowacek, W.: Hochwasserrückhaltebecken Feldolling: Zweck, Betrieb Bemessung und Funktionsweise, Wasserwirtschaftsamt Rosenheim, Rosenheim, available at: http://www.wwa-ro.bayern.de/hochwasser/hochwasserschutzprojekte/mangfalltal/doc/hrb_feldolling/funktion_hrb_feldolling.pdf (last access: 22 April 2018), 2013.
Wilby, R. L.: Uncertainty in water resource model parameters used for climate change impact assessment, Hydrol. Process., 19, 3201–3219, 2005.
Willems, W. and Stricker, K.: Klimawandel und Wasserhaushalt: AdaptAlp – Untersuchung zum Einfluss des Klimawandels auf Wasserbilanzen und Abflüsse für das Inneinzugsgebiet mittels verschiedener Klimaszenarien. Endbericht, Bayerisches Landesamt für Umwelt, Hof, 2011.
Ylhäisi, J. S., Räisänen, J., Masson, D., Räty, O., and Järvinen, H.: How does model development affect climate projections?, Atmos. Sci. Lett., 16.3, 414–419, https://doi.org/10.1002/asl2.577, 2015.