the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Active heat pulse sensing of 3-D-flow fields in streambeds
Eddie W. Banks
Margaret A. Shanafield
Saskia Noorduijn
James McCallum
Jörg Lewandowski
Okke Batelaan
Profiles of temperature time series are commonly used to determine hyporheic flow patterns and hydraulic dynamics in the streambed sediments. Although hyporheic flows are 3-D, past research has focused on determining the magnitude of the vertical flow component and how this varies spatially. This study used a portable 56-sensor, 3-D temperature array with three heat pulse sources to measure the flow direction and magnitude up to 200 mm below the water–sediment interface. Short, 1 min heat pulses were injected at one of the three heat sources and the temperature response was monitored over a period of 30 min. Breakthrough curves from each of the sensors were analysed using a heat transport equation. Parameter estimation and uncertainty analysis was undertaken using the differential evolution adaptive metropolis (DREAM) algorithm, an adaption of the Markov chain Monte Carlo method, to estimate the flux and its orientation. Measurements were conducted in the field and in a sand tank under an extensive range of controlled hydraulic conditions to validate the method. The use of short-duration heat pulses provided a rapid, accurate assessment technique for determining dynamic and multi-directional flow patterns in the hyporheic zone and is a basis for improved understanding of biogeochemical processes at the water–streambed interface.
- Article
(4584 KB) - Full-text XML
-
Supplement
(586 KB) - BibTeX
- EndNote
Application of heat as a tracer to hydrological studies has rapidly progressed in recent decades, driven by the simplicity of the methodology and low cost of sensor technology (Anderson, 2005; Rau et al., 2014). Using this method, spatial and temporal flow dynamics within the hyporheic zone, particularly hyporheic transport and exchange (e.g. longer attenuation), have been shown to enhance stream denitrification (Harvey et al., 2013; Gomez-Velez et al., 2015; Zarnetske et al., 2011), degradation of mine-pollutants (Gandy et al., 2007) and the degradation of wastewater micro-pollutants (Engelhardt et al., 2013). It is also widely used by other disciplines, e.g. ecology, where the thermal regime in river systems plays an important role in ecosystem health (Caissie, 2006; Harvey and Wagner, 2000; Brunke and Gonser, 1997; Boulton et al., 1998).
The majority of streambed heat tracer studies use vertical, ambient temperature profiles and a one-dimensional analytical solution of the heat diffusion–advection equation to estimate streambed exchange fluxes and infer hyporheic flow patterns (Constantz et al., 2002; Naranjo and Turcotte, 2015; Rau et al., 2010; Vogt et al., 2010). Series of vertical temperature profile sticks installed along transects have also be used in other studies to examine 2-D flow fields in the streambed (Constantz et al., 2013, 2016; Shanafield et al., 2010). When using ambient temperature fluctuations and one-dimensional heat transport models, several days of data are required to estimate the vertical flux. In addition, an assumption is made that the dominant exchange process is in the vertical direction only and the horizontal or lateral component of flow is considered to be negligible. There are very few investigations which have tried to capture both the vertical and horizontal component of flow, as the determination of the non-vertical component is challenging with the physical installation of sensors to measure the flow field as well as the mathematical framework to process the data (Munz et al., 2016; Briggs et al., 2012; Shanafield et al., 2016).
More recently, the suitability of active temperature sensing has been explored as an approach to characterise streambed spatial and temporal exchange dynamics in three dimensions. The injection of heat as a tracer is not new, with a number of studies using the active temperature-sensing technique to evaluate groundwater flow within wells (Sellwood et al., 2016; Read et al., 2014; Banks et al., 2014), flow in sediments (Greswell et al., 2009; Ballard, 1996; Bakker et al., 2015), surface water–groundwater exchange processes (Kurth et al., 2015) and hyporheic exchange flows in the hyporheic zone (Angermann et al., 2012a, b; Lewandowski et al., 2011).
The aim of the present study was to develop an active heat-pulse-sensing (HPS) instrument to conduct rapid assessments of the three-dimensional (3-D) flow field in the streambed from fine silt to coarse gravels across different geomorphological structures. It builds upon previous studies by Lewandowski et al. (2011) and Angermann (2012a, b), who developed an active heat pulse sensor to determine the flow direction and flow velocity in shallow sandy stream environments. In the present study we have developed a more robust field instrument and advanced the analysis of the temperature breakthrough data using the analytical solution of the heat transport equation for a 3-D array. Parameter estimation and uncertainty analysis was implemented using the differential evolution adaptive metropolis (DREAM) algorithm (Vrugt et al., 2009c), an adaption of the standard Markov chain Monte Carlo method, to determine the direction and magnitude of flow velocity patterns in the streambed at multiple depths. Laboratory tests were conducted in a sand tank using an extensive range of flow scenarios with tightly controlled hydraulic conditions to evaluate the methodology. Field tests demonstrated the active heat pulse instrument in different geomorphological structures in a small stream in the Mount Lofty Ranges, South Australia.
2.1 General design and operating principles
A 56-sensor, 3-D temperature array with three heat pulse sources (also known as the Hot Rod) was developed to measure the flow direction and magnitude up to 200 mm below the water–sediment interface in the streambed (Fig. 1). The central carbon-fibre rod (260 mm long with a diameter of 12 mm) has three equally spaced, 60 W heating elements along its length at positions of 65, 140 and 215 mm below the base plate and are referred to as heat injection depth R1, R2 and R3, respectively (Fig. 1). Eight stainless steel rods (6 mm diameter and 298 mm long) housing seven equally spaced (38 mm apart) temperature thermistors (Maxim DS18B20; precision 0.06∘) are arranged cylindrically around the carbon-fibre rod and at two fixed spacings of 28 and 47 mm (Table S1 in the Supplement). The central rod and thermistor sticks are fixed to a rigid circular aluminium base plate which is attached to a collapsible handle. The material, dimensions and spacing of the rods to the base plate were designed to reduce flexibility and minimise disturbance to the sediment material on insertion, as this was a limitation in previous studies. A critical design feature was to ensure that the rods stayed parallel to one another and that the spacing did not vary during installation, as it was designed to be used in a range of sedimentary environments from fine silt to coarse gravels.
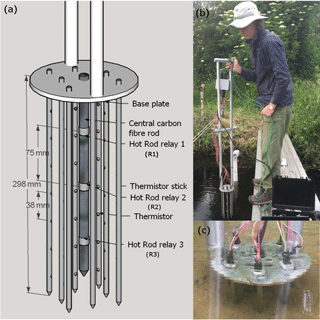
Figure 1(a) Detailed design of the active HPS Hot Rod with three heating elements (R1, R2 and R3) on the central carbon-fibre rod surrounded by 56 temperature sensors at two distances from the central heat source (28 and 47 mm). (b) and (c) Installation of the Hot Rod in a small stream characterised by shallow bedforms.
A terminal program is used to communicate with the data logger and to control the sampling routine of the Hot Rod (e.g. sampling frequency, duration and power output of the active heat pulse, selected heating element used and logging period). A sealed 12 V lead acid battery together with a power supply regulator is used to maintain a constant 12 V output to the heating elements. The power delivered to the three heating elements can be adjusted in the logger program from 0 to 100 % to provide greater flexibility to the required active heat pulse. The input current from the power supply regulator is also recorded each time the temperature is measured to ensure a tight control on the actual power being delivered through the heating elements to the surrounding material and therefore reducing uncertainty in the analysis routine.
An important aspect of the design was that it could be rapidly and easily deployed to capture large spatial data sets along a reach of stream or across a pool–riffle sequence. Installation requires gently pushing (or lightly tapping with a shockless impact hammer) the device into the streambed ensuring that there is a sufficient gap between the top of the sediment and the underside of the base plate to prevent streamflow constriction (the top thermistor is set at 44 mm below the baseplate so a gap of ∼30 mm puts the first thermistor just below the sediment–water interface). The impact of the installed device on flow velocity and direction is expected to be minimal given that the volume of the device relative to the volume of the measurement area is less than 4 %.
Once installed and equilibrated with the surrounding sediment, the logger program is executed and the ambient temperature is measured at each thermistor (T0), directly followed by activation of the selected heat element for the chosen duration. The data logger records the temperature differential () at the chosen sample frequency to clearly discern the timing and location of the breakthrough curve at each of the thermistors. Field and laboratory tests showed that short, 1 min heat pulse injections and a 20–30 min temperature response monitoring period are appropriate for estimating the dominant direction and flux magnitude in sandy streambeds. Specific details of the analysis routine that was used are described in the following section.
2.2 Data analysis and routine outputs
2.2.1 Heat transport simulation
The magnitude and direction of the water velocity at the observation point based on the measured temperature breakthrough curves at the 56 sensors were determined using a modified version of the heat transport equation:
where T is temperature (∘C) and Dt is the thermal dispersion coefficient given as (de Marsily, 1986)
where κ0 is the bulk thermal conductivity of the water-saturated sediments (), ρc is the volumetric heat capacity of the water-saturated sediments (), βn is the thermal dispersivity where the subscript n is T for the transverse direction and L for the longitudinal direction, ρwcw is the volumetric heat capacity of water (4.1 ) and q is the Darcy velocity (or Darcy flux) of water (m s−1). Where , Eq. (2) can be simplified to .
An analogy can be made to the solute transport equation where the mean water velocity is replaced with and the dispersion tensor can be replaced with Dt. Assuming that these components are constant in space and time, Eq. (1) can be reduced to
An instantaneous injection of a thermal mass into an infinite three-dimensional sediment volume where there is only an x component of velocities can be defined as follows (Domenico and Schwartz, 1998):
where M0 is the thermal mass (J).
The thermal mass input was not considered in previous studies as a known parameter (Angermann et al., 2012b). The Hot Rod, however, uses a known wattage, and the thermal mass term is given as
where F is the heat flux and dt is the duration of application. The thermal mass input, M0, is measured by the data logger such that at full power the theoretical output of the 60 W heating element provides 5 A of current and an injection period of 60 s equals an energy input of 3600 J.
The requirement of Eq. (4) is that the flow component is only in the x direction, removing the non-diagonal components of the dispersion tensor. The aim of this paper is to define a flow direction and magnitude using a fixed sensor array, allowing the use of multiple sensors to constrain the thermal transport and flow properties. It is not always the case that the fluxes are oriented with the sensor array and therefore the location of the observations can be converted through rotation of the coordinate system, aligning the measurements relative to the flow direction. In this application we assume that the vector of Darcy fluxes in the x, y and z direction is defined as
The coordinate system is first rotated such that the points are orientated around the z axis and we define the angle θ (Fig. 2), where
The rotational Jacobian matrix is then defined as
the coordinates as
and the flux as
Secondly, we rotate the points around the y axis. To do this we define the angle ϕ, where
The rotational Jacobian matrix is then defined as
the coordinates as
and the flux as
The transformation results in the representation of the Darcy fluxes as (the magnitude of the non-transformed flow vector) and . The distances of the sensors are oriented relative to this new flow vector. The main advantage over previous approaches is that all sensors can be included rather than a single sensor from the array accounting for a single transverse distance (Lewandowski et al., 2011).
We then substitute these new dimensions into Eq. (4) to get
Equation (15) represents an impulse response function. The tests implemented used a finite pulse that did not meet this condition. As we assume that the properties are not temperature dependent, we can treat the contribution of multiple impulse responses as additive. Hence, Eq. (15) was implemented for a series of discrete, lagged pulses to represent the actual addition of thermal mass to the system. The use of discrete pulses is implemented as
where Ttot is the total temperature response, ton is the time at which the heating element was turned on and toff is the time when the heating element was turned off. The operator τ represents the time lags, and for each discrete pulse . The summed T term on the right-hand side is evaluated using Eq. (15) for t≥τ and is zero otherwise. This method allows for the representation of a non-Dirac heat pulse and also for variations in the input flux from the heating elements. The interval dτ was 3 s; hence, the Dirac representation was valid on a small scale.
2.2.2 Parameter estimation
Parameter estimation and uncertainty analysis was undertaken using the DREAM algorithm (Vrugt et al., 2009a, b). The fit of the data was performed by assessing the likelihood of each individual model run. The likelihood is defined as
where Tmod and Tobs represent the modelled and observed temperatures, respectively; σ2 represents the error of the temperature observation squared; pobs represents the probability of the modelled observation, assuming a normal distribution and a mean of Tobs and a variance of σ2; and ppar represents the probability of the parameter X. We assume that the parameters are uniformly distributed; hence, ppar(X)=1 when the parameters are in bounds and zero elsewhere.
Table 1Initial parameter values for ∥q∥, θ, ϕ, κ0 and ρc used in the analysis routine. A uniform distribution of the five parameters was used.

The DREAM method is an adaption of the standard Markov chain Monte Carlo method. The technique is initialised by specifying a number of chains. Each chain receives starting parameters by randomly sampling the parameter ranges (Table 1). After calculating an initial likelihood for the starting parameters, the algorithm selects proposed parameter values using the other chains, and the likelihood of these model parameters are also calculated. If the likelihood of these parameters is greater than the current parameters, the new parameters are accepted; however, if the likelihood of the new parameters is lower, the transition probability is calculated using a ratio of the likelihoods, and the transition is determined by generating a random number. The method is explained in greater detail in Vrugt et al. (2009c). The general outcome is that the chains spend a greater amount of time in locations of more favourable parameters, and the distribution of these parameters represents the posterior distribution of the parameter probabilities, given the model, the data and the prior knowledge of the parameter distributions.
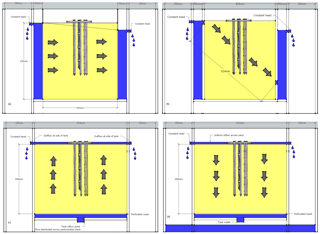
Figure 3Laboratory sand tank dimensions for each of the flow scenarios: (a) horizontal flow, (b) diagonal flow, (c) upward flow and (d) downward flow.
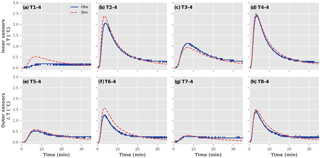
Figure 4Breakthrough curves shown of the fourth vertical thermistor (158 mm depth) from each radial sensor location for the horizontal flow scenario from heat injection depth at relay 2. Solid lines are observed and dashed lines are modelled.
The optimisation was undertaken using five parameters: ∥q∥, θ, ϕ, κ0 and ρc. All of the parameters in the thermal dispersion term (Eq. 2) cannot be identified simultaneously in the optimisation, resulting in non-convergence of the Markov Chain approach because of the correlation between the thermal dispersivity flow term and the thermal conductivity. In the experiments that we conducted we found that the longitudinal and transverse dispersion terms, and therefore Eq. (2) can be simplified to . Hence, κ0 was included as an optimisation parameter and it was also physically measured in the experiments. The default parameter likelihoods and initial distributions were taken from the ranges presented in Table 1. The error of the temperature observations (σ) was taken to be 0.06 ∘C, the precision of the temperature sensors. Whilst the model parameters are estimated using angle and the flow magnitude, the actual flow vector can be recovered as
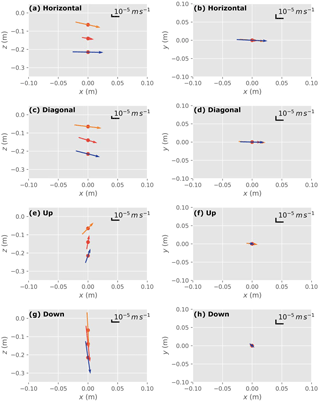
Figure 5Calculated fluxes and directions for the four flow scenarios at each of the heat injection depths: (a, b) horizontal, (c, d) diagonal, (e, f) upward and (g, h) downward flow scenarios.
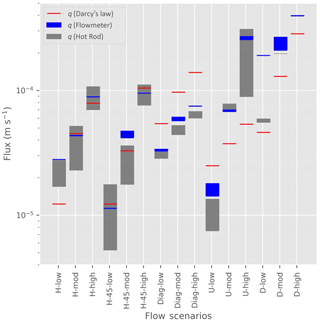
Figure 6Fluxes of the different flow scenarios, listed along the x axis, and different flow intensities calculated based on different heat injection depths of the HPS (grey bars) compared to fluxes determined based on Darcy's law (hydraulic gradient and hydraulic conductivity – red dashes) and the flux calculated from the measured discharge from the tank using an ultrasonic flowmeter and the cross-sectional area of the tank (blue dashes).
2.3 Laboratory sand tank
A laboratory sand tank was used to provide a controlled environment on the hydraulic regime to test the performance of the Hot Rod and so that the different flux calculation methods could be compared. A total of 36 combinations of flow direction, magnitude and depth of heat pulse were used. The dimensions of the sand tank for each of the scenarios varied slightly according to the fixed boundary conditions (Fig. 3). Four flow scenarios were tested: (1) horizontal flow from left to right (inflow and outflow occurred over the entire saturated cross-sectional area of the sediment volume on the left and right boundaries of the tank), (2) diagonal flow from the top left to bottom right (inflow was through a 20 mm horizontal inlet slit on the top left boundary and outflow through a 20 mm horizontal slit, 85 mm above the base of the right boundary), (3) upward flow (inflow occurred over the cross-sectional area of the base of the tank and outflow at the top of the sediment at overflow points above the sediment on the left and right boundaries), and (4) downward flow (inflow was distributed over the cross-sectional area of the sediment surface and outflow via the cross-sectional area of the tank base). A steady state flow regime for each scenario was maintained by constant heads at the inflow and outflow ports of the tank and the use of a peristaltic pump with a highly accurate ultrasonic flowmeter (Atrato ultrasonic flowmeter; 0.05 % linearity on flow less than 5 L min−1) to ensure a constant discharge rate. The flowmeter data were also used to determine the Darcy flux for the different flow conditions. Fine perforated mesh was used to contain the sediment and to provide the necessary flow conditions along each of the tank boundaries. The hydraulic conductivity and thermal hydraulic conductivity of the graded, saturated sand were measured using a KSAT meter (UMS GmbH, Munich, Germany) and KD2 Pro (Decagon, Washington, USA), respectively. Three different hydraulic gradients and discharge rates for the four flow scenarios were conducted to capture low- ( m s−1), moderate- ( m s−1) and high-flow conditions ( m s−1). The Hot Rod was positioned in the middle of the sand tank with thermistor stick sensor number one orientated perpendicular (90∘) to the flow direction for all of the scenarios. To validate the spatial arrangement of the sensors, the horizontal flow scenario was repeated with thermistor stick sensor number one rotated to be 45∘ to the direction of flow. In addition to these flow scenarios, a no-flow experiment was conducted to evaluate the analysis routine, where the boundary conditions meant that there was stagnant water.
2.4 Experimental field site
The Sturt River, Adelaide, Australia, is a perennial river system receiving the majority of its input from a wastewater treatment facility. The geomorphology of the river was characterised by a narrow channel, no more than 3 m wide with 0.3–0.5 m deep sediment ranging from fine silt to coarse gravels overlying a tight, low-permeability clay. The selection of this field site was part of another ongoing investigation looking at attenuation of micro-pollutants in the hyporheic zone. The residence time in the hyporheic zone was critical in evaluating the stream attenuation modelling.
3.1 Laboratory sand tank
Overall, the modelled breakthrough curves closely fit the observed data from the 56-sensor array with the modelled curves capturing the rising limb, peak and tail of the measured temperature data over the sample period (Fig. 3). The variance of each parameter is included in the modelled temperature breakthrough curves; however, the uncertainty is so small that it cannot be seen without zooming in on the individual curves. Selected breakthrough curve plots are shown of the fourth vertical thermistor (158 mm depth) from each radial sensor location. Four flow scenarios are presented: (a) horizontal (Fig. 4), (b) diagonal (Fig. S1-ii in the Supplement), (c) upwards (Fig. S1-iii) and (d) downwards (Fig. S1-iv). The tests presented were conducted at a moderate flow rate. Thermistor 4 was 158 mm below the base plate and at a greater depth than the heat injection depth (R2; at 140 mm). Temperature increases associated with the heat pulse were observed at the inner sensor sticks (28 mm) more quickly than at the outer (47 mm) sensor sticks in the horizontal flow scenario (see Fig. 4d and h). The inner sensors also displayed a steeper rising and falling limb compared to the outer sensors. The temperature response reflected the sensor position relative to the dominant flow direction. For example, sensor T3–4 (Fig. 4c) was directly in line and down-gradient of the heat pulse, whilst sensor T7–4 (Fig. 4g) was in line but up-gradient of the heat pulse and therefore showed a smaller response. The breakthrough curves from the diagonal flow scenario showed a similar response in those sensors up- and down-gradient of the heat pulse (Fig. S1a). In the upward and downward flow scenarios there was very little response in the outer thermistor sensors due to the dominant vertical component of flow (Fig. S1b–c). This low response of the outer sensors was even more pronounced under higher flow conditions in the upward and downward flow scenarios. The 3-D time series videos showed clearly the migration of the heated plume vertically and highlighted the complexity of fitting multiple breakthrough curves to the most likely solution (refer to the video file in https://doi.org/10.4226/86/5aab1b67337bb).
Overall, the 3-D flow fields calculated from the HPS Hot Rod in the laboratory sand tank for the four flux scenarios and heat injection depths (65, 140 and 215 mm) were consistent with the flow conditions established in the tank (Fig. 5). Under left to right horizontal flow conditions (Fig. 5a and b), the modelled direction of flow from each of the heat injection depths is very similar with some slight offset to the observed flow in the y direction, which was perpendicular to thermistor stick sensor 1 (90∘ to the flow direction). There was also a slight deviation downwards in the z direction, particularly for the shallowest heat injection depth. To refute any bias in the optimisation routine and the array configuration, the Hot Rod was rotated by 45∘ for the horizontal flow scenario and it showed a very similar output to when it was orientated 90∘ to the flow direction.
Results from the other three scenarios showed that the modelled flux direction is close to parallel to the flow conditions established in the tank and the magnitude of the flux was similar at each of the heat injection depths (Fig. 5c–h). Reviewing the time series data in the 3-D plots (Supplement), the spreading of the heat pulse from the heat injection depth can be clearly detected, indicating how the heat pulse moves along the established flow line. The thermistor highlighted in blue in the 3-D plot was the sensor that showed the maximum temperature breakthrough curve and clearly shows a different orientation to the most likely flux direction (black arrow) as determined by the DREAM algorithm.
Some discrepancies in the direction of the modelled flow and differences in flux magnitude at each heat injection depth may be attributed to (1) placement orientation and the angle of the sensor positions of the Hot Rod relative to the flow conditions established in the tank, (2) boundary conditions in the tank to establish flow and (3) the fact that the optimisation routine determines the best fit of all the observed data in a 3-D volume around the heat injection depth rather than at a specific point.
The difference in flux magnitude at each heat injection depth may be attributed to the number of sensors that were used in the optimisation routine. For example, at the heat injection depth R2 (140 mm) there are three sensor arrays (an array being eight sensors positioned horizontally around the central carbon-fibre rod) vertically above R2 and four sensor arrays vertically below R2. In comparison, at heat injection depth R1 (65 mm) there is only one sensor array vertically above R1 and six sensor arrays below R2, which may limit the optimisation routines for particular flow conditions i.e. strongly upwards flow.
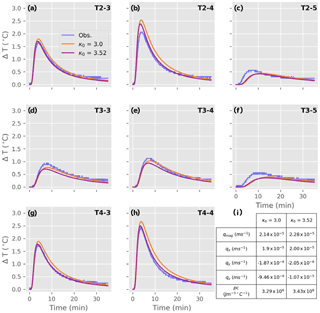
Figure 7Comparison of the observed (blue line) and modelled breakthrough curves for selected temperature sensors (Tx−x) when the thermal conductivity, κ0, of the sediment has a known value of 3 (orange graph) and when the model is provided with a range of plausible values from 2.5 to 4.5 resulting in 3.52 (red graph).
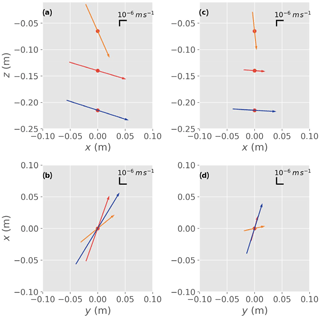
Figure 8Calculated fluxes and flux directions at the three heat injection depths from two of the stations at the experimental field site. (a, b) Station 1 and (c, d) Station 2. The x axis in the figures is positive in the direction of streamflow.
In the case of no-flow conditions established in the sand tank (Fig. S2), the optimisation routine fitted the measured temperature breakthrough data; however, on closer inspection of the 3-D time series plot it was evident based on the uniform heat plume around the heat injection point during the injection period that heat transport was by conduction only. Absence of clear advective movement of the heat pulse and a calculated flux less than about m s−1 indicated the lower limit of the active heat pulse sensor.
The flux magnitude (∥q∥) of the different flow scenarios and different flow intensities calculated based on different heat injection depths of the HPS (grey bars) compared to the fluxes determined based on Darcy's law (hydraulic gradient and hydraulic conductivity) and the measured discharge from the tank using an ultrasonic flowmeter is shown in Fig. 6 and Table S2.
The measured saturated hydraulic conductivity according to the KSAT meter for the sand tank sand was m s−1. The measured saturated thermal conductivity of the sand was 3 (using the Decagon KD2 Pro), whilst the average modelled κ0 from all of the flow scenarios in the sand tank was 3.8 . The thermal conductivity is strongly influenced by the porosity, and therefore some differences can be expected due to changes to the particle density with the packing of the sediment, where by thermal conductivity increases with decreasing porosity (Smits et al., 2010).
Histograms of the flux magnitude (∥q∥) and flux components in the x, y and z direction for the combination of most likely parameter values used in the DREAM algorithm were generated for each measurement. The results from heat injection depth R2 for the horizontal flow scenario is shown in Fig. S3, which shows that the distribution is tightly constrained. This is also evident in cross correlation plots of the flux magnitude, thermal conductivity and the specific heat capacity (Fig. S4).
Constraining the range of the thermal conductivity values used in the optimisation routine to the known measured thermal conductivity of the sand from the KD2 Pro instrument showed little impact on the calculated flux magnitude. However, comparing the modelled breakthrough curves from two optimisations when the range in thermal conductivity was limited to the measured known thermal conductivity (3 ) in one model and in the other model it used a value of 3.52 (for a best fit from a range of values from 2.5 to 4.5 ) showed there were subtle differences between the modelled breakthrough curve peak and falling limbs (Fig. 7).
Our study found that the inclusion of longitudinal and transverse thermal dispersion had less than a 2 % difference on the mean calculated fluxes. The study by Rau et al. (2012) determined Darcy velocities derived from heat experimentation that included the thermal dispersivity term differed by up to 20 % when compared to solute experimentation. However, other studies in the literature have shown that there is considerable uncertainty on the magnitude of the thermal dispersivity (Anderson, 2005). Thermal dispersivity has also been found not to be scale-dependent such as solute dispersivity because heat transport happens through the pore water and through the sediment matrix (Vandenbohede et al., 2009). Therefore, given the scale that we are working at (few centimetres) and also the low velocities, the effect on the calculated flux is likely to be negligible.
3.2 Experimental field site
The measured 3-D flow fields at the experimental site showed considerable variability in the direction of flow and flux magnitude over ∼0.20 m depth of the streambed. The flux magnitude at the six stations along the river at the three heat injection depths (0.065, 0.140 and 0.215 m) ranged from to m s−1 (mean: m s−1). At each of the stations, the component of horizontal flow compared to vertical flow within the streambed was dominant. It was only at the shallowest heat injection depth, just below the stream bed surface, that there was a greater component of vertical flow. The results from two of the six stations are shown in Fig. 8, where the Hot Rod was positioned in the streambed such that the x axis of the figure was aligned to the direction of stream flow. In such environments the flow direction is driven by the surface flow and the geomorphological features of the streambed. Small bed structures such as ripples will only impact the hyporheic flow field in the uppermost centimetres of the sediment, which is a plausible explanation as to what was observed from the outputs of the Hot Rod.
Measured κ0 values for the sediment collected at the six stations from 0 to 0.2 m depth ranged from 0.9 to 2.84 , (mean: 2.07 ) compared to the values that were determined by the optimisation routine, which ranged from 1.0 to 3.74 (mean: 2.91 ). Physical observation of the sediments collected at the experimental site stations showed that the streambed material was quite heterogeneous and also contained varying proportions of organic matter. Higher clay content and organic matter in the sediment would cause a higher volumetric heat capacity compared to sandy sediments. The volumetric heat capacity also increases with increasing moisture content and particle density (Abu-Hamdeh, 2003; Barry-Macaulay et al., 2013; Jury and Horton, 2004). The assumption of uniform thermal properties of the 3-D volume around the heat injection point is likely to contribute to the uncertainty in the flow direction. For example, Su et al. (2006) used numerical simulations to show that differences in the thermal properties of the sediment around a flow sensor can lead to incorrect velocity estimates and in particular differences in the horizontal and vertical flux components. Additional measurements of the streambed sediments would provide a tighter constraint on the parameter set used in the optimisation; however, the parameter estimation and uncertainty analysis routine does successfully fit the measured data to provide a reliable estimate of the flux and its direction. Refer to Banks et al. (2017) for all of the temperature data files from the sand tank and experimental site, available at https://doi.org/10.4226/86/5aab1b67337bb.
Despite the early pioneering work of Lewandowski et al. (2011) and Angermann et al. (2012b) for the concept of a 3-D active heat pulse sensor to determine flux and direction in the shallow streambed, their studies experienced a number of shortcomings that are related to the design of the instrument and the analysis of the data. This included (1) a limited number of sensors and spatial positions around the heating element; (2) weakness with the sensor sticks wobbling and therefore poorly constrained sensor positions in relation to the heating element; (3) limited constraint on the input functions to the heat transport equation, i.e. not knowing the current input; and (4) lack of a suitable optimisation routine to determine the most likely set of parameters to constrain the data and an uncertainty analysis on the flux magnitude and its direction.
The rigidity and robustness of the Hot Rod and use of heating elements at three different vertical positions provided a method to examine how the flux and its direction varied vertically with depth beneath the streambed interface at individual locations in a range of different environmental settings and sediment types. The use of two horizontal spacings between the heating elements and thermistors as well as additional thermistors at multiple angles to the heating elements increased confidence in the measurement of heat transport processes and tightened the optimisation routine of the temperature data. The addition of the measured input of energy at the heating element in the heat transport equation as a series of discrete heat pulses over the injection period provided one less unknown variable to calibrate against. In many of the experiments conducted in the sand tank and at the experimental site, the optimisation routine using the DREAM algorithm showed that the most likely flux direction from the heat injection depth was not towards the sensor that showed the maximum temperature breakthrough because it uses all of the sensor temperature breakthrough curves in the analysis. The 3-D time series plot was a valuable tool in assessing this result and it also showed whether heat transport was dominated by diffusion and/or conduction with radial symmetry around the heating element or whether there was convective heat flow. This interrogation process was found to be critical in the data assessment to ensure that the model did not overfit the measured data with unrealistic physical values for the sediment and heat transport conditions.
The laboratory and experimental field site applications using the DREAM algorithm for parameter estimation and uncertainty analysis demonstrated the performance of the active heat-pulse-sensing instrument (the Hot Rod) to measure the multi-directional 3-D-flow fields and fluxes in the near-surface streambed. Active heat pulse sensing provides a number of advantages over other approaches that have investigated hyporheic exchange, including the low cost of data collection and the rapid assessment of small physical processes that can be undertaken on a reach scale. Marzadri et al. (2013) showed that the hyporheic residence time, which is influenced by the streambed physical morphology and in-stream flow discharge, ultimately determines the spatially complex patterns of the time-varying thermal regime within the hyporheic zone. The short-duration active heat pulse sensing helped overcome some of the challenges in measuring the water temperatures because of the stronger signal from the heat pulse.
Most other studies that use heat as a tracer assume 1-D flow only and the lateral or horizontal component is not considered. Studies that have identified the geometry of the subsurface flow field using a polynomial model fitted to the amplitude ratio of the vertical temperature profiles were only able to determine the deviation from one-dimensional vertical flow (Munz et al., 2016). Errors in the vertical component of flow have been shown to progressively increase with the magnitude of the horizontal flow component (Lautz, 2010). The 3-D analysis routine and sensor arrangement applied in this study were able to capture all three components of the flow field around the point of observation. The importance of capturing the multi-directional flow field was clearly demonstrated in the sand tank under an extensive range of flow conditions that would be anticipated in a dynamic stream environment. Measurements of the hydraulic gradient and characterising the physical properties of the streambed sediment are also important in understanding the dynamic exchange processes within the hyporheic zone and the very transient nature of such environments.
The concept and design of the active heat-pulse-sensing instrument could also be adapted to other hydrological research areas, including the measurement of shallow interflow along hillslopes and discharge from groundwater seeps and springs.
Data are available at https://doi.org/10.4226/ 86/5aab1b67337bb (Banks, 2017).
The supplement related to this article is available online at: https://doi.org/10.5194/hess-22-1917-2018-supplement.
The authors declare that they have no conflict of interest.
We are grateful to Flinders University South Australia for a small grant to develop the HPS Hot Rod and all Faculty of Science and
Engineering technical workshop staff for their assistance in hardware development and construction. Funding support from the
Australian Research Council (ARC) Linkage Project LP150100588 is acknowledged. Additional funding through the Australia–Germany Joint
Research Cooperation Scheme of Universities Australia and the German Academic Exchange Service (DAAD, grant no. 57216806) provided
support for fieldwork collaboration between the research institutes.
Edited by: Thom Bogaard
Reviewed by: Jim Constantz and Bas des Tombe
Abu-Hamdeh, N. H.: Thermal properties of soils as affected by density and water content, Biosyst. Eng., 86, 97–102, https://doi.org/10.1016/S1537-5110(03)00112-0, 2003.
Anderson, M. P.: Heat as a ground water tracer, Ground Water, 43, 951–968, 2005.
Angermann, L., Krause, S., and Lewandowski, J.: Application of heat pulse injections for investigating shallow hyporheic flow in a lowland river, Water Resour. Res., 48, W00P02, https://doi.org/10.1029/2012WR012564, 2012a.
Angermann, L., Lewandowski, J., Fleckenstein, J. H., and Nützmann, G.: A 3D analysis algorithm to improve interpretation of heat pulse sensor results for the determination of small-scale flow directions and velocities in the hyporheic zone, J. Hydrol., 475, 1–11, https://doi.org/10.1016/j.jhydrol.2012.06.050, 2012b.
Bakker, M., Caljé, R., Schaars, F., van der Made, K.-J., and de Haas, S.: An active heat tracer experiment to determine groundwater velocities using fiber optic cables installed with direct push equipment, Water Resour. Res., 51, 2760–2772, https://doi.org/10.1002/2014WR016632, 2015.
Ballard, S.: The in situ permeable flow sensor: a ground-water flow velocity meter, Ground Water, 34, 231–240, https://doi.org/10.1111/j.1745-6584.1996.tb01883.x, 1996.
Banks, E. W., Shanafield, M. A., and Cook, P. G.: Induced temperature gradients to examine groundwater flowpaths in open boreholes, Groundwater, 52, 943–951, https://doi.org/10.1111/gwat.12157, 2014.
Banks, E.: Temperature time series data for active HPS Hot Rod, Flinders University, https://doi.org/10.4226/86/5aab1b67337bb, 2017.
Barry-Macaulay, D., Bouazza, A., Singh, R. M., Wang, B., and Ranjith, P. G.: Thermal conductivity of soils and rocks from the Melbourne (Australia) region, Eng. Geol., 164, 131–138, https://doi.org/10.1016/j.enggeo.2013.06.014, 2013.
Boulton, A. J., Findlay, S., Marmonier, P., Stanley, E. H., and Valett, H. M.: The functional significance of the hyporheic zone in streams and rivers, Annu. Rev. Ecol. Syst., 29, 59–81, 1998.
Briggs, M. A., Lautz, L. K., McKenzie, J. M., Gordon, R. P., and Hare, D. K.: Using high-resolution distributed temperature sensing to quantify spatial and temporal variability in vertical hyporheic flux, Water Resour. Res., 48, W02527, https://doi.org/10.1029/2011WR011227, 2012.
Brunke, M. and Gonser, T.: The ecological significance of exchange processes between rivers and groundwater, Freshwater Biol., 37, 1–33, 1997.
Caissie, D.: The thermal regime of rivers: a review, Freshwater Biol., 51, 1389–1406, https://doi.org/10.1111/j.1365-2427.2006.01597.x, 2006.
Constantz, J., Stewart, A. E., Niswonger, R., and Sarma, L.: Analysis of temperature profiles for investigating stream losses beneath ephemeral channels, Water Resour. Res., 38, 1–13, https://doi.org/10.1029/2001WR001221, 2002.
Constantz, J., Eddy-Miller, C. A., Wheeler, J. D., and Essaid, H. I.: Streambed exchanges along tributary streams in humid watersheds, Water Resour. Res., 49, 2197–2204, https://doi.org/10.1002/wrcr.20194, 2013.
Constantz, J., Naranjo, R., Niswonger, R., Allander, K., Neilson, B., Rosenberry, D., Smith, D., Rosecrans, C., and Stonestrom, D.: Groundwater exchanges near a channelized versus unmodified stream mouth discharging to a subalpine lake, Water Resour. Res., 52, 2157–2177, https://doi.org/10.1002/2015WR017013, 2016.
de Marsily, G.: Quantitative Hydrogeology: Groundwater Hydrology for Engineers, Academic Press, Cambridge, Massachusetts, United States, 1986.
Domenico, P. A. and Schwartz, F. W.: Physical and Chemical Hydrogeology, vol. 1, Wiley, New Jersey, United States, 1998.
Engelhardt, I., Prommer, H., Moore, C., Schulz, M., Schüth, C., and Ternes, T. A.: Suitability of temperature, hydraulic heads, and acesulfame to quantify wastewater-related fluxes in the hyporheic and riparian zone, Water Resour. Res., 49, 426–440, https://doi.org/10.1029/2012WR012604, 2013.
Gandy, C. J., Smith, J. W. N., and Jarvis, A. P.: Attenuation of mining-derived pollutants in the hyporheic zone: a review, Sci. Total Environ., 373, 435–446, 2007.
Gomez-Velez, J. D., Harvey, J. W., Cardenas, M. B., and Kiel, B.: Denitrification in the Mississippi River network controlled by flow through river bedforms, Nat. Geosci., 8, 941–945, https://doi.org/10.1038/ngeo2567, 2015.
Greswell, R. B., Riley, M. S., Alves, P. F., and Tellam, J. H.: A heat perturbation flow meter for application in soft sediments, J. Hydrol., 370, 73–82, https://doi.org/10.1016/j.jhydrol.2009.02.054, 2009.
Harvey, J. W., Böhlke, J. K., Voytek, M. A., Scott, D., and Tobias, C. R.: Hyporheic zone denitrification: controls on effective reaction depth and contribution to whole-stream mass balance, Water Resour. Res., 49, 6298–6316, https://doi.org/10.1002/wrcr.20492, 2013.
Harvey, W. H. and Wagner, B. J.: Quantifying hydrologic interactions between streams and their subsurface hyporheic zones, in: Streams and Ground Waters, edited by: Jones, J. B. and Mulholland, P. J., Academic Press, San Diego, 3–44, 2000.
Jury, W. A. and Horton, R.: Soil Physics, 6th Edn., John Wiley, New Jersey, United States, 2004.
Kurth, A.-M., Weber, C., and Schirmer, M.: How effective is river restoration in re-establishing groundwater–surface water interactions? – A case study, Hydrol. Earth Syst. Sci., 19, 2663–2672, https://doi.org/10.5194/hess-19-2663-2015, 2015.
Lautz, L. K.: Impacts of nonideal field conditions on vertical water velocity estimates from streambed temperature time series, Water Resour. Res., 46, 1–14, https://doi.org/10.1029/2009WR007917, 2010.
Lewandowski, J., Angermann, L., Nützmann, G., and Fleckenstein, J. H.: A heat pulse technique for the determination of small-scale flow directions and flow velocities in the streambed of sand-bed streams, Hydrol. Process., 25, 3244–3255, https://doi.org/10.1002/hyp.8062, 2011.
Marzadri, A., Tonina, D., and Bellin, A.: Effects of stream morphodynamics on hyporheic zone thermal regime, Water Resour. Res., 49, 2287–2302, https://doi.org/10.1002/wrcr.20199, 2013.
Munz, M., Oswald, S. E., and Schmidt, C.: Analysis of riverbed temperatures to determine the geometry of subsurface water flow around in-stream geomorphological structures, J. Hydrol., 539, 74–87, https://doi.org/10.1016/j.jhydrol.2016.05.012, 2016.
Naranjo, R. C. and Turcotte, R.: A new temperature profiling probe for investigating groundwater-surface water interaction, Water Resour. Res., 51, 7790–7797, https://doi.org/10.1002/2015WR017574, 2015.
Rau, G. C., Andersen, M. S., McCallum, A. M., and Acworth, R.: Analytical methods that use natural heat as a tracer to quantify surface water–groundwater exchange, evaluated using field temperature records, Hydrogeol. J., 18, 1093–1110, https://doi.org/10.1007/s10040-010-0586-0, 2010.
Rau, G. C., Andersen, M. S., and Acworth, R. I.: Experimental investigation of the thermal dispersivity term and its significance in the heat transport equation for flow in sediments, Water Resour. Res., 48, 1–21, https://doi.org/10.1029/2011WR011038, 2012.
Rau, G. C., Andersen, M. S., McCallum, A. M., Roshan, H., and Acworth, R. I.: Heat as a tracer to quantify water flow in near-surface sediments, Earth-Sci. Rev., 129, 40–58, https://doi.org/10.1016/j.earscirev.2013.10.015, 2014.
Read, T., Bour, O., Selker, J. S., Bense, V. F., Le Borgne, T., Hochreutener, R., and Lavenant, N.: Active-distributed temperature sensing to continuously quantify vertical flow in boreholes, Water Resour. Res., 50, 3706–3713, https://doi.org/10.1002/2014wr015273, 2014.
Sellwood, S. M., Bahr, J. M., and Hart, D. J.: Evaluation of a discrete-depth heat dissipation test for thermal characterization of the subsurface, Geol. Soc. Am. Spec. Pap., 519, 67–79, https://doi.org/10.1130/2016.2519(05), 2016.
Shanafield, M., Pohll, G., and Susfalk, R.: Use of heat-based vertical fluxes to approximate total flux in simple channels, Water Resour. Res., 46, W03508, https://doi.org/10.1029/2009wr007956, 2010.
Shanafield, M., McCallum, J. L., Cook, P. G., and Noorduijn, S.: Variations on thermal transport modelling of subsurface temperatures using high resolution data, Adv. Water Resour., 89, 1–9, https://doi.org/10.1016/j.advwatres.2015.12.018, 2016.
Smits, K. M., Sakaki, T., Limsuwat, A., and Illangasekare, T. H.: Thermal conductivity of sands under varying moisture and porosity in drainage–wetting cycles, Vadose Zone J., 9, 172–180, https://doi.org/10.2136/vzj2009.0095, 2010.
Su, G., Freifeld, B., Oldenburg, C., Jordan, P., and Daley, P.: Interpreting Velocities from Heat-Based Flow Sensors by Numerical Simulation, Ground Water, 44, 386–393, https://doi.org/10.1111/j.1745-6584.2005.00147.x, 2006.
Vandenbohede, A., Louwyck, A., and Lebbe, L.: Conservative solute versus heat transport porous media during push-pull tests, Transport Porous Med., 76, 265–287, https://doi.org/10.1007/s11242-008-9246-4, 2009.
Vogt, T., Schneider, P., Hahn-Woernle, L., and Cirpka, O. A.: Estimation of seepage rates in a losing stream by means of fiber-optic high-resolution vertical temperature profiling, J. Hydrol., 380, 154–164, https://doi.org/10.1016/j.jhydrol.2009.10.033, 2010.
Vrugt, J. A., Robinson, B. A., and Hyman, J. M.: Self-adaptive multimethod search for global optimization in real-parameter spaces, IEEE T. Evolut. Comput., 13, 243–259, https://doi.org/10.1109/TEVC.2008.924428, 2009a.
Vrugt, J. A., ter Braak, C. J. F., Diks, C. G. H., Robinson, B. A., Hyman, J. M., and Higdon, D.: Accelerating Markov Chain Monte Carlo Simulation by differential evolution with self-adaptive randomized subspace sampling, Int. J. Nonlinear Sci., 3, 273–290, 2009b.
Vrugt, J. A., ter Braak, C. J. F., Gupta, H. V., and Robinson, B. A.: Equifinality of formal (DREAM) and informal (GLUE) Bayesian approaches in hydrologic modeling?, Stoch. Env. Res. Risk A., 23, 1011–1026, https://doi.org/10.1007/s00477-008-0274-y, 2009c.
Zarnetske, J. P., Haggerty, R., Wondzell, S. M., and Baker, M. A.: Dynamics of nitrate production and removal as a function of residence time in the hyporheic zone, J. Geophys. Res.-Biogeo., 116, 1–15, https://doi.org/10.1029/2010JG001356, 2011.





