the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
A review of current best practices and future directions in assimilating GRACE/-FO terrestrial water storage data into numerical models
Gabriëlle De Lannoy
Matthew Rodell
Yorck Ewerdwalbesloh
Helena Gerdener
Mehdi Khaki
Bailing Li
Fupeng Li
Maike Schumacher
Natthachet Tangdamrongsub
Mohammad J. Tourian
Wanshu Nie
Jürgen Kusche
Water cycle reanalyses, generated by integrating observations into hydrological and land surface models, provide long-term and consistent estimates of key water cycle components. Reanalyses are essential to understand hydrological variability, extreme events such as droughts and floods, and to improve water resource management. Over the past two decades, the assimilation of terrestrial water storage anomaly data from the GRACE and GRACE Follow-On (GRACE/-FO) missions has significantly enhanced these reanalyses, as GRACE/-FO observations uniquely constrain total water storage variability across all terrestrial compartments. Incorporating GRACE/-FO data has led to major advances in representing trends in key hydrological variables, climate-driven changes in the water cycle, and anthropogenic influences such as irrigation-induced groundwater depletion – factors often poorly captured in models. With processing pipelines now being developed for low-latency short-term data products from the upcoming next-generation gravity missions, we expect that low-latency periodically updated reanalyses and analyses from assimilation will become more relevant.
However, challenges remain, particularly in resolving mismatches in spatial and temporal resolution between GRACE/-FO observations and high-resolution models, and there is no consensus yet on the optimal approach for assimilating GRACE/-FO data. In light of the upcoming launches of next-generation gravity missions and the development of increasingly sophisticated Earth system modeling frameworks, this review synthesizes insights from approximately 60 GRACE/-FO data assimilation studies in an attempt to converge to best practices. The review reveals that the most effective assimilation strategies leverage (robust modifications of) the classical ensemble Kalman filter and localization techniques, explicitly account for correlated observation errors, and address biases contained in the observations as well as those arising from model perturbations. Unmodeled processes must be carefully handled through signal separation, multi-source assimilation, or removal prior to assimilation. Future directions include developing low-latency products for near-real-time assimilation, integrating enhanced and combined satellite observations, and employing machine-learning approaches for downscaling and hybrid assimilation. Collectively, these strategies provide a pathway toward more accurate, physically consistent, and operationally useful water cycle reanalyses.
- Article
(3215 KB) - Full-text XML
- BibTeX
- EndNote
The distribution of water on Earth shapes the daily lives of individuals and societies and is, in turn, influenced by human activities. Quantifying and monitoring water resources is critical to ensuring water availability for human consumption, supporting agriculture, predicting natural hazards, and addressing climate change through mitigation and adaptation strategies. Continental freshwater resources are stored in groundwater aquifers, soils ranging from the surface through the root zone to deeper layers, surface water bodies, snow or ice sheets, and plants. These water storage compartments are inextricably linked to both global and regional water, carbon and energy cycles and interact with various components of our Earth system, such as the biosphere. The dynamics of water storage and fluxes undergo significant changes due to human activities, and shifts in the frequency and patterns of hydrological extremes driven by climate change.
Our current understanding of water storage dynamics across different terrestrial compartments relies on global and regional hydrological and land surface models, remote sensing, and in situ observations. However, global numerical models often underestimate long-term trends in terrestrial water storage (TWS), do not accurately capture extremes of wet and dry conditions (Scanlon et al., 2018; Forootan et al., 2024), often do not account for human impacts, and struggle to represent the seasonal cycle of TWS variations effectively (Scanlon et al., 2019). On the other hand, most in situ and remote sensing data only provide insight into water storage in specific land surface compartments.
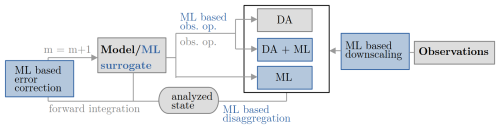
Satellite gravimetry is the only remote sensing technique that provides information on the vertically integrated variations of TWS, based on observations from the Gravity Recovery and Climate Experiment (GRACE) and its successor, GRACE Follow-On (GRACE-FO). However, their use at subregional scales and in operational applications is limited by their coarse spatial resolution of a few hundred kilometers and their monthly temporal resolution. Integrating GRACE/-FO observations into hydrological and land surface models allows us to update all sub-monthly simulated water storage compartments, which typically include groundwater, soil moisture at different depths, surface water and snow, while simultaneously downscaling the coarse GRACE/-FO observations to the higher resolution model grid (Fig. 1). Several approaches exist for merging GRACE/-FO observations with numerical models including Bayesian Model Averaging (BMA), machine learning (ML) – including deep learning (DL) – and data assimilation (DA) algorithms (Sect. 3). DA offers the significant advantage of updating not only the target state variables such as groundwater and soil moisture, but also related hydrological fluxes, including evapotranspiration, snowmelt, river discharge, surface and subsurface runoff, infiltration, and groundwater recharge and discharge, in a physically consistent way (Fig. 1). DA can be used to produce long-term reanalysis estimates of TWS to support land system understanding (Baatz et al., 2021), or to obtain the best current state estimate for operational forecasting, as is needed for early warning systems (e.g. drought). Given the monthly resolution of GRACE/-FO observations, the line between both is vague, and we loosely use the term reanalysis for both.
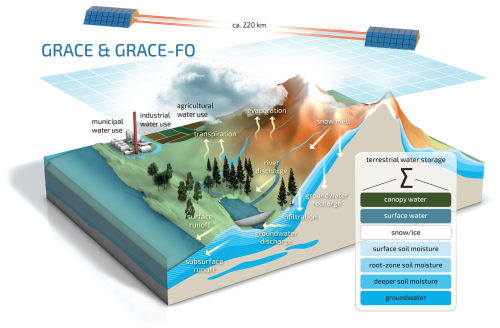
Figure 1The GRACE and GRACE Follow-On (GRACE/-FO) data assimilation (DA) concept: A numerical model simulates daily or even subdaily individual water storage components and fluxes on a user-defined grid. In contrast, the GRACE/-FO satellites observe the total variation in monthly TWS aggregated over large footprints and over all storage compartments. During DA, the model's individual storage compartments are updated towards the GRACE/-FO observations. These updates influence water fluxes – illustrated by the arrows in the figure – as well as other related model variables such as soil temperature, energy fluxes, and plant growth.
In their seminal paper, Zaitchik et al. (2008) introduced a Kalman smoother algorithm for assimilating GRACE data into the Catchment Land Surface Model (CLSM, Koster et al., 2000) over the Mississippi river basin. Two key takeaways from this pioneering work are as follows: first, the demonstrated potential of DA to downscale coarse-scale GRACE observations, and second, the success of vertical disaggregation of TWS to updates in groundwater, soil moisture and snow, with a particular enhancement of groundwater and also river discharge modeling. Several subsequent studies applied GRACE/-FO DA to other hydrological and land surface models.
A key variable of interest in GRACE/-FO DA studies is groundwater, as it remains challenging to observe directly at large scales and is significantly influenced by human activities (Döll et al., 2012; Girotto et al., 2017; Li et al., 2019). Yin et al. (2020) validated GRACE DA results against more than 150 in situ groundwater wells across the North China Plain, demonstrating a substantial improvement in correlation. Likewise, Tangdamrongsub et al. (2017) found that GRACE DA enhanced the correlation between groundwater storage estimates and well observations in the Hexi Corridor in northern China, where a rapid groundwater decline was identified and attributed to agricultural activities. Similarly, Tangdamrongsub et al. (2018) reported that GRACE DA improved estimates of groundwater depletion in the North China Plain and Australia compared to global hydrological models. Over Iran, Khaki et al. (2018c) showed that GRACE DA more effectively captured the extensive groundwater extraction occurring in the region compared to a standard model run. Aiming at applications for local water management, Stampoulis et al. (2019) set up a high-resolution model over California and integrated GRACE data to determine water table dynamics.
Snow-dominated catchments contribute a large seasonal component to TWS variations, and GRACE/-FO DA shows great potential for constraining snow cover fraction and depth in land surface or hydrological models, especially with multi-sensor approaches (Su et al., 2010; Zhao and Yang, 2018; Girotto et al., 2020; De Lannoy et al., 2022). Forman et al. (2012) demonstrated improved snowpack estimation over the Mackenzie River Basin using GRACE DA. Subsequently, Bahrami et al. (2021) showed improvements in grid-scale snow estimates and highlighted their relationship to improved flood simulations. Finally, Wang et al. (2021) discussed the potential conflicts in snow compartment updates resulting from multi-sensor DA.
Long-term water cycle reanalyses using GRACE/-FO DA have been shown to be effective in constraining trends not only in TWS but also in other key hydrological variables (van Dijk et al., 2014; Gerdener et al., 2022, 2023; Chi et al., 2024). For instance, Chi et al. (2024) found that GRACE DA amplified negative TWS and evapotranspiration (ET) trends over Northern India and attributed these trends to high irrigation rates. Jung et al. (2019) reported improved surface soil moisture simulations resulting from GRACE DA in humid West African regions characterized by large TWS amplitudes.
The impact of GRACE/-FO DA on streamflow simulations varies considerably by region. For example, Tangdamrongsub et al. (2015) reported only minor improvements in streamflow simulations compared to gauging station observations in the Rhine catchment. In contrast, Getirana et al. (2020a) demonstrated that updating groundwater and soil moisture storage with GRACE DA led to significant improvements in streamflow forecasts over the Niger River basin. Furthermore, Wu et al. (2022) conducted a global GRACE DA study and found that streamflow estimates were notably enhanced in snow-dominated catchments.
The downscaling and disaggregation of GRACE/-FO data through DA also improves drought monitoring and contributes to water-related disaster warning systems. TWS-based drought indices can be computed at the resolution of the model grid and are available in near-real-time applications, such as NASA's GRACE-based Drought Indicators (https://nasagrace.unl.edu/, last access: 10 December 2025; Houborg et al., 2012; Li et al., 2019; Getirana et al., 2020b). Moreover, DA enables improved attribution of droughts to individual water storage components, such as soil moisture drought and groundwater drought, as demonstrated for regions like the Murray-Darling Basin (Schumacher et al., 2018), over Europe (Li et al., 2012), and Mexiko (Arciniega-Esparza et al., 2025). On the other hand, GRACE/-FO DA also improves the simulation of wet extreme events, as shown by Reager et al. (2015) for the Missouri River Basin, where updated groundwater and snow water data helped constraining flood potential in the region.
In recent years, GRACE/-FO DA has been increasingly integrated into multi-sensor DA systems, mainly in combination with remotely sensed surface soil moisture data. An attempt by Tian et al. (2017) demonstrated improved estimates of surface soil moisture, root-zone soil moisture and groundwater – compared to in situ observations – by joint assimilation of GRACE and SMOS data over Australia. These results have been confirmed by Girotto et al. (2019) over the United States, by Khaki and Awange (2019) over South America, and by Khaki et al. (2019) for the Murray-Darling and Mississippi River basins. Building on this work, Khaki et al. (2020) further incorporated leaf area index to investigate the impact of individual observational datasets on DA results, model parameter estimation and model prediction. The study found that while single-sensor DA led to greater improvements for individual variables, the multi-sensor approach produced the most consistent improvements across all variable estimates, consistent with the findings of Tangdamrongsub et al. (2020). More recently, Mehrnegar et al. (2023) reported similar results using different Bayesian and Markov chain Monte Carlo merging algorithms. Schulze et al. (2024) demonstrated that the degradation of simulated streamflow through GRACE DA could be mitigated to some extent by additionally assimilating streamflow observations. Another multi-sensor DA framework was developed by Wongchuig et al. (2024) over the Amazon River Basin. This framework integrated observations of water surface elevation, TWS, flood extent, and soil moisture, demonstrating that multi-sensor DA consistently outperformed single-sensor DA experiments.
In other applications, GRACE/-FO DA output has demonstrated potential in removing hydrology-induced deformation from Global Navigation Satellite System (GNSS) vertical deformation time series, which could help reveal underlying geophysical signals (Springer et al., 2019). Similarly, but with a different objective, Tangdamrongsub and Šprlák (2021) showed that GRACE/-FO DA effectively captures hydrology-induced loading deformation of the land surface, offering promising applications, particularly in data-sparse regions. Furthermore, Jensen et al. (2024) utilized GRACE/-FO DA results to evaluate long-term drying and wetting trends in TWS within CMIP6 models. Recently, Khaki et al. (2023) assimilated GRACE-FO data based on along-orbit line-of-sight gravity differences into a land surface model, enhancing its ability to capture high-frequency water storage variations. This method is particularly valuable for simulating wet extremes. Moreover, Soltani et al. (2024) were the first to assimilate GRACE data into a land surface model coupled with a dedicated subsurface model with three-dimensional groundwater flow within a multi-sensor framework. Furthermore, the integration of DA frameworks with machine learning techniques, as demonstrated by Liu et al. (2021), has shown promise in improving groundwater level predictions at lead times of several months. Finally, the impact of human activities, such as groundwater pumping and irrigation – often not represented in land surface models but potentially corrected through GRACE/-FO DA – has gained increasing attention (Girotto et al., 2017; Nie et al., 2019; Getirana et al., 2020b). However, this remains a challenging task, as assimilation increments are not always allocated to the correct storage compartments, highlighting the need for further research.
The above studies use a variety of different hydrological and land surface models and different GRACE/-FO observation products and differ significantly in their assimilation algorithms. Developing an assimilation framework requires several methodological choices, including (i) the selection of the observation grid (Forman and Reichle, 2013), (ii) the handling of observation error correlations (Eicker et al., 2014; Khaki et al., 2017c), (iii) the choice among various sequential DA techniques, including localization methods and emerging DA algorithms (Khaki et al., 2017b, 2018a; Shokri et al., 2018, 2019), (iv) adopting strategies for applying analysis increments and updating the model (Girotto et al., 2016), and (v) selecting other observables within multi-sensor DA (Girotto et al., 2019; Tangdamrongsub et al., 2020).
Previous review papers have focused on providing an overview of methods for assimilating GRACE data into hydrological models, with an emphasis on error modeling and data assimilation algorithms (e.g. Soltani et al., 2021). This paper aims to provide a thorough synthesis of existing studies, highlighting the various application areas and offering a systematic analysis of the common settings within current DA frameworks. Additionally, we synthesize the current state of research, evaluate the present lack of consensus within the community regarding DA strategies, and outline directions that may support convergence and open up perspectives on new directions.
In Sect. 2, we start with the representation of simulated TWS in hydrological and land surface models and establish the link to observed TWS from GRACE/-FO. We also examine possible choices for GRACE/-FO data products, the handling of observation errors, and necessary post-processing steps. Section 3 provides a comprehensive review of existing GRACE/-FO DA frameworks, analyzing key methodological choices, technical aspects, and the advantages and limitations of different approaches. This is followed by a discussion of validation strategies for DA experiments in Sect. 4. A major point of this paper is to identify current challenges and open issues in GRACE/-FO DA frameworks, which we explore in Sect. 5. Finally, we conclude in Sect. 6 with perspectives on future research directions and in Sect. 7 with a synthesis of best practice recommendations and key next steps for the community.
Remote sensing observations and numerical models provide complementary insights into TWS, but they have significant differences in spatial and temporal resolution, sources of error, and correction requirements. Most hydrological and land surface models simulate TWS as the sum of the individual storage compartments, while GRACE/-FO products provide only TWS anomalies (TWSA), i.e., the deviation of TWS from a long-term mean. This section outlines the challenges associated with deriving TWSA from hydrological and land surface models. It also presents the currently available GRACE/-FO products along with the commonly applied geophysical corrections and downscaling techniques.
2.1 Modeling terrestrial water storage
Numerical models simulate increasingly complex processes that control water storage and fluxes, while they disregard others depending on the intended application of the model. Models used in GRACE/-FO analyses are generally classified into Global Hydrological Models (GHMs, Sood and Smakhtin, 2015), and Land Surface Models (LSMs, Overgaard et al., 2006), with some hybrid models incorporating features of both types. Each model category emphasizes different aspects of the water cycle. GHMs typically focus on large-scale hydrological processes and often account for anthropogenic influences such as water abstraction, irrigation, and reservoir management. In contrast, LSMs simulate land-atmosphere interactions, prioritizing energy and water exchanges and often allowing the incorporation of the carbon cycle. While GHMs primarily rely on simplified hydrological equations that emphasize water movement, LSMs use more detailed, process-based equations to model energy, water, and carbon exchanges, but often with a poor representation of anthropogenic processes.
A key aspect of TWS modeling is the representation of changes in individual water storage components. Common GHMs and LSMs differ in how these individual storages are simulated. For example, some models include detailed representations of groundwater flow and aquifer dynamics, whereas others treat groundwater more simplistically or omit it altogether (Scanlon et al., 2018; Condon et al., 2021). It is important to note that this hinders a quantitative comparison of individual storages across different models or even different versions of the same model; e.g. soil water storage may refer to vastly different soil depths in differing models (Jensen et al., 2024). Similarly, processes such as river routing, snowmelt, and evaporation are handled with varying degrees of complexity. Most models struggle with accurately capturing the interactions between individual storage components and the temporal and spatial variability of these processes (Telteu et al., 2021).
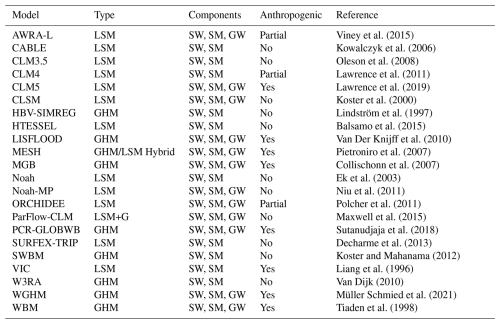
Table 1 provides a summary of models that generate TWS data at the global or continental scale. These models are categorized by type into GHM, LSM, or hybrids thereof, and their original capability to include anthropogenic influences (e.g., water management, land use changes). Most global models are run at resolutions ranging between 0.5 and 0.25°, but continental-scale applications are available at much higher resolutions down to a few kilometers.
Viney et al. (2015)Kowalczyk et al. (2006)Oleson et al. (2008)Lawrence et al. (2011)Lawrence et al. (2019)Koster et al. (2000)Lindström et al. (1997)Balsamo et al. (2015)Van Der Knijff et al. (2010)Pietroniro et al. (2007)Collischonn et al. (2007)Ek et al. (2003)Niu et al. (2011)Polcher et al. (2011)Maxwell et al. (2015)Sutanudjaja et al. (2018)Decharme et al. (2013)Koster and Mahanama (2012)Liang et al. (1996)Van Dijk (2010)Müller Schmied et al. (2021)Tiaden et al. (1998)Table 1Summary of some models that have been used to estimate total water storage anomalies. GHM: Global Hydrological Model; LSM: Land Surface Model; G: Groundwater Model. AWRA: Australian Water Resources Assessment; CABLE: CSIRO Atmosphere Biosphere Land Exchange; CLM: Community Land Model; HBV: Hydrologiska Byråns Vattenbalansavdelning (Hydrological Bureau Water Balance Section); CLSM: Catchment Land Surface Model; CRUNCEP: Climate Research Unit National Centers for Environmental Prediction; GSWP: Global Soil Wetness Project; HTESSEL: Hydrology-Tiled ECMWF Scheme for Surface Exchanges over Land; LISFLOOD: Lisflood-Flood Forecasting System; MESH: Modélisation Environmentale Communautaire (Community Environmental Modeling); MGB: Modelo de Grandes Bacias (Large Basin Model); ORCHIDEE: ORganizing Carbon and Hydrology In Dynamic EcosystEms; PARFLOW: Parallel Flow Model; PCR-GLOBWB: PCRaster Global Water Balance; SWBM: Simplified Water Balance Model; SURFEX-TRIP: Surface Externalisée (SURFEX) with Total Runoff Integrating Pathways; VIC: Variable Infiltration Capacity; W3RA: World Wide Water Resources Assessment model; WGHM: WaterGAP Global Hydrology Model; WBM: Water Balance Model. The components available for each model are indicated by SW: Surface Water, SM: Soil Moisture and GW: Groundwater.
2.2 GRACE-/FO products
The GRACE satellite mission (Wahr et al., 1998; Tapley et al., 2004) monitored global TWS changes from 2002 to 2017, with its follow-on mission GRACE-FO, launched in 2018 (Landerer et al., 2020), continuing these observations. TWS changes are an essential climate variable reflecting the impact of global climate change on water resources (Rodell and Reager, 2023). Three official analysis centers process the GRACE/-FO observations, including the Center for Space Research (CSR), the Jet Propulsion Laboratory (JPL), and the Helmholtz Centre for Geosciences (GFZ). However, other research institutions and universities also provide GRACE/-FO-derived datasets, e.g., NASA Goddard Space Flight Center (GSFC), Space Geodesy Research Group at the French National Centre for Space Studies (GRGS/CNES), the Ohio State University, the Technical University of Graz, and Tongji University. Besides, combined solutions are available from the European Gravity Service for Improved Emergency Management (EGSIEM, http://egsiem.eu/tools, last access: 10 December 2025). The most commonly used GRACE/-FO data products are based on the two main processing strategies of spherical harmonics (SH) and mass concentration (mascon) methods that are usually provided with monthly temporal resolution and a few hundred km spatial resolution. These monthly gravity field estimates are typically accompanied by an error estimate of the measurement noise, provided either as formal errors or as full covariance matrices (Chen et al., 2022). Estimating monthly gravity fields involves reducing tidal and non-tidal high-frequency mass changes in the atmosphere and ocean (e.g., by applying Atmosphere and Ocean De-Aliasing (AOD1B) background model corrections, Shihora et al., 2022). Recently, the estimation of daily SH-based products (such as Mayer-Gürr et al., 2018) and five-daily mascon-based products (Retab et al., 2024) is gaining growing attention.
Post-processing of the GRACE/-FO SH coefficients (provided as Level-2 data products) includes replacing the degree-1 (geocenter; e.g., Sun et al., 2016) and C20 and C30 coefficients by solutions from Satellite Laser Ranging (Loomis et al., 2019, 2020; Cheng and Ries, 2023) and applying corrections to account for glacial isostatic adjustment (GIA, see Sect. 2.3). Furthermore, spatial filtering is essential to reduce noise from higher-order coefficients. This can be achieved using an anisotropic filter (e.g., Kusche, 2007; Klees et al., 2008b), which also helps to mitigate correlated errors, or an isotropic filter (e.g., the Gaussian filter introduced by Jekeli, 1981), which is often combined with a destriping filter to further reduces the impact of correlated errors (Swenson and Wahr, 2006). To account for spatial leakage effects, several methods have been developed that attempt to restore the lost signal in GRACE/-FO data. Commonly used approaches that depend on hydrological model outputs are the multiplicative approach by Longuevergne et al. (2010), the additive approach by Klees et al. (2007), the grid factor scaling approach by Landerer and Swenson (2012), and the unconstrained forward modeling approach by Chen et al. (2015). Vishwakarma et al. (2017) developed a data-driven approach to overcome the dependency on hydrological models and their associated uncertainties. All provided Level-2 datasets are anomalies relative to a specified temporal baseline. As a result, expert knowledge is required for making appropriate decisions for the individual post-processing steps.
Gridded Level-3 datasets, i.e. TWSA grid values obtained from SH, or mascon solutions that also provide a global TWSA grid, might be more user-friendly for a wider community. The mascon approach applies similar corrections compared to the SH approach but uses equal-area spherical cap mascons placed on the surface of an elliptical Earth to derive global TWSA grids (see, e.g., Watkins et al., 2015). It is important to distinguish between the native spatial resolution of the GRACE/-FO data of approximately 300 km (Kim et al., 2024) and the spatial sampling used to provide Level-3 TWSA grids, e.g., on 0.5 or 1° global grids. Some studies have compared the SH and mascon solutions for selected river basins, e.g., Jing et al. (2019); Novák et al. (2021), where statistically significant differences are observed for several of the selected regions. A comparison with GNSS vertical deformations for the Amazon basin showed slightly better agreement with mascon solutions (Wang et al., 2023). However, the authors also report larger differences between different mascon solutions compared to differences between different SH solutions (Wang et al., 2023). In orbit K-band range-rate residuals (derived from Level-1B data products) and along-orbit line-of-sight gravity difference measurements from the GRACE-FO laser ranging interferometer can also be used to study hydrological processes (e.g., Eicker and Springer, 2016; Ghobadi‐Far et al., 2022).
Although GRACE and GRACE-FO provide a largely continuous record of TWSA, there is an observational gap between the missions of almost one year. Several studies have addressed this gap using different methods, including physically based hydrological models (Zhang et al., 2022), interpolation and statistical approaches such as singular spectrum analysis (SSA) and autoregressive (AR) models (Lecomte et al., 2024; Lenczuk et al., 2022), and machine learning techniques including convolutional or recurrent neural networks (Uz et al., 2022; Mo et al., 2022). Dynamic mode decomposition (Libero and Ciriello, 2025) of GRACE/-FO data to extract essential spatial and temporal patterns could also support these efforts. These techniques allow reconstruction of TWSA during the gap while preserving both seasonal cycles and long-term trends.
The GRACE/-FO data products are commonly accompanied by uncertainty estimations. These might be provided as standard deviations of SH or gridded TWSA or as fully propagated error-covariance matrices (Sect. 3.3). Only full error-covariance matrices reflect spatial correlations between TWSA grid cells, which are particularly strong in the north–south direction (e.g., Kvas et al., 2019). However, formal error covariances (or variances, if only standard deviations are provided) reflect only instrument and orbital errors but not errors in background models, and calibrated error covariances should be preferred in DA applications (Klees et al., 2008a).
2.3 Geophysical corrections
Since GRACE/-FO observations contain signals that are not representative of hydrological processes, geophysical corrections are essential to extract the water storage changes of interest. Glacial isostatic adjustment (GIA) is the effect of ice unloading in response to the ice masses covering the Earth during the ice ages, which is still present and thus sensed nowadays, approximately 20 000 years after the last glacial maximum. The effect of GIA in GRACE/-FO TWSA is most prominent in areas that are still covered by ice, e.g., Greenland but also far-distance regions can be affected albeit with a smaller magnitude. Typically, GIA is removed from the GRACE/-FO TWSA by using models that incorporate ice history and viscosity of the mantle to compute GIA mass rates (Peltier, 2004; A et al., 2012; Caron et al., 2018). However, these GIA models are subject to considerable uncertainties that inevitably create false trends in TWSA estimates (Vishwakarma et al., 2021a).
Earthquakes are another source of mass redistribution that are included in the GRACE/-FO data biasing the correct analysis of other hydrological signatures and events such as linear trends or droughts (Deggim et al., 2021). A temporal model can be fitted to the data (e.g., Einarsson et al., 2010; Deggim et al., 2021) that contains a co-seismic jump and a post-seismic relaxation. In this way, large earthquakes can be removed from the data, for example, the Sumatra-Andaman earthquake in 2004. However, Gerdener (2024) found that the removal of two earthquakes from GRACE/-FO TWSA prior to DA did not significantly alter the results. Yet, the higher spatial resolution which will be achieved with future gravity missions might lead the earthquake correction to be a necessary processing step prior to DA (Kusche et al., 2025).
Due to the mission constellation and background model errors, the GRACE/-FO gravity fields provided as SH are affected by high-frequency noise and correlated errors, requiring filtering (e.g., Wahr et al., 1998; Jekeli, 1981; Kusche, 2007). As the filters cannot distinguish between signal and noise, the signal magnitude is changed as well, which is known as leakage. Leakage is especially dominant for those locations with large water bodies or at the coast. For example for lakes, the signal within the lake is reduced by the filter and smears into the surrounding land area. To account for leakage before DA, approaches based on hydrological model output or data-driven estimates are available, but these could in turn also create another source of uncertainty (see Sect. 2.2 for details). Another possibility is the RECOG (REgional COrrections for GRACE) dataset (Deggim et al., 2021) that allows the removal of signals from large lakes and reservoirs from GRACE TWSA and the relocation to its spatial origin within the lakes/reservoir outlines. The dataset was computed from forward-modeling of surface water volume estimates of major lakes sensed by altimetry and optical remote sensing.
2.4 Downscaling
The coarse resolution of GRACE/-FO-derived TWSA maps prohibits the monitoring of fine-scale hydrological signals. For example, TWSA error matrices are typically affected by inversion problems when provided on lower spatial resolution, e.g., for a 1° grid of global land TWSA (Eicker et al., 2014; Gerdener et al., 2023). This limitation necessitates the consideration of downscaling techniques before or along with DA, with careful attention to error propagation during the process. Downscaling not only aims to improve the spatial resolution of GRACE/-FO-derived TWSA but also to deal with issues such as leakage correction.
Various approaches have been proposed for downscaling GRACE/-FO data. A purely statistical approach to downscaling relies on multivariate or bivariate linear relationships between coarse- and fine-scale datasets to generate downscaled products. For instance, Yin et al. (2018) used the linear relationship between GRACE data and high-resolution evapotranspiration data to enhance the spatial detail of GRACE-derived groundwater storage anomalies. Similarly, Vishwakarma et al. (2021b) applied multivariate linear regression to downscale GRACE TWSA, leveraging relationships with water storage fields from WGHM, multiple precipitation datasets, evapotranspiration, and two distinct runoff models.
However, although the water-balance equation and spatial averaging are linear operations in theory, the empirical relationships between GRACE TWSA and fine-scale hydrological variables are often nonlinear in practice. GRACE does not observe many short-timescale fluxes or individual storage components; it only measures the net mass change integrated over large regions. Consequently, while GRACE captures the integrated mass-change signal resulting from processes such as soil-moisture dynamics, infiltration, recharge, runoff generation, groundwater–surface-water interactions, and anthropogenic water use, it does not directly observe these processes individually; their effects are embedded collectively in the coarse-scale TWS signal, resulting in nonlinear empirical relationships between GRACE TWSA and fine-scale data, including model-derived TWSA. So generally, linear statistical methods face two key limitations: (i) they cannot represent such nonlinear dependencies between coarse- and fine-scale variables, and (ii) they produce downscaled estimates without accounting for marginal or joint uncertainty distributions.
While the first challenge remains difficult to address, a Bayesian framework offers a solution to the second challenge by providing a posterior distribution for the target variable. It even allows the posterior distribution to be defined indirectly using sampling techniques like Markov Chain Monte Carlo (MCMC). Recent work has employed MCMC to downscale GRACE water storage changes, producing groundwater and soil moisture estimates at approximately 12.5 km resolution (Mehrnegar et al., 2021).
Although the Bayesian framework addresses uncertainty estimates and can be used to downscale GRACE/-FO data, it struggles to deal with the first challenge. To tackle this, nonlinear Machine Learning (ML) algorithms have been used in GRACE/-FO downscaling, including Artificial Neural Networks (ANN) (Miro and Famiglietti, 2018), Boosted Regression Trees (BRT) (Seyoum et al., 2019), Random Forest (RF) (Jyolsna et al., 2021), Long Short-Term Memory (LSTM) networks (Gorugantula and Kambhammettu, 2022) and more recently, Convolutional Neural Networks (CNN) (Gou and Soja, 2024). However, despite their strengths, ML methods typically lack physical interpretability and fail to provide comprehensive uncertainty estimates, suggesting that alternative or complementary methods may be needed.
Recently, Tourian et al. (2023) proposed a copula-supported Bayesian framework to tackle the two key challenges in statistical downscaling: modeling nonlinear dependencies and quantifying uncertainty. This approach is supposed to capture both linear and nonlinear dependencies between random variables without requiring explicit knowledge of their marginal distributions. Using this method, the posterior distribution is obtained directly, enabling the derivation of the Maximum A Posteriori (MAP) solution as the downscaled product and the posterior dispersion as an uncertainty estimate for the downscaled result.
In contrast to the above mentioned techniques, DA methods take care of the horizontal and vertical downscaling by design. This is discussed in Sect. 3.5. Prior to DA, it has to be ensured that the GRACE/-FO data coverage matches with the modeling domain.
2.5 Bias correction
As has been mentioned before, the GRACE/-FO data are heavily processed to obtain TWSA estimates (Sect. 2.2, 2.3) that would be representative of hydrological processes. This processing involves smoothing which inevitably results in signal loss. To restore the lost signal, some GRACE/-FO products are accompanied by multiplicative gain factors, which are applied to the gridded TWSA estimates (Landerer and Swenson, 2012). Furthermore, to combine GRACE/-FO TWSA observations and TWS simulated by models, the TWSA observations need to be converted to TWS by adding a long-term climatology, or conversely, the model climatology needs to be removed from TWS simulations before computing bias-free observation-minus-forecast differences, or innovations.
As a first order correction, the long-term mean can be either removed from the model within the observation operator (see below) – matching the GRACE/-FO reference period – or added to the GRACE/-FO time series prior to DA. It is also possible to match the higher order statistical moments of the observations to those of the model, which is often done in the case when assimilating remotely sensed soil moisture observations, to improve physical consistency and numerical stability (Drusch et al., 2005; Kumar et al., 2009; Albergel et al., 2017). To this end, Reichle and Koster (2004) introduced the concept of Cumulative Distribution Function (CDF) matching, and recent studies developed more sophisticated methods including neural network-based approaches (Kumar et al., 2012; Fairbairn et al., 2024). For TWSA DA, the differences in the observed and simulated dynamic range are often related to differences in amplitudes or trends (Scanlon et al., 2018, 2019). Some GRACE/-FO DA frameworks adjust both the mean and the standard deviation to match those of the model (Girotto et al., 2017; Khaki et al., 2020), which can potentially absorb all of the product scaling efforts above (Girotto et al., 2016) but sacrifice information contained in the measurements. Other GRACE/-FO DA frameworks prefer to retain the full information content of the GRACE/-FO time series and only adjust the long-term mean (Tangdamrongsub et al., 2020; Gerdener et al., 2023).
Ideally, any differences in trends should be reconciled to have a theoretically optimal DA system, but in most cases, the trend of the GRACE/-FO observations is kept to correct missing trends in the model (due to missing processes). The GRACE/-FO trend errors are in many regions between 5 %–30 % (or higher in regions strongly affected by GIA, e.g., Rodell et al. (2018); Zhao and Li (2017)) and are then implicitly (suboptimally) considered in the DA framework by weighting both observation and model forecast error. The choice of bias correction will eventually influence the nature of the remaining observation and forecast error covariances (Dee, 2005; Eyre, 2016), which are discussed in Sect. 3.3 and 3.4.
The assimilation of GRACE/-FO-derived TWSA into GHMs and LSMs is typically conducted on a monthly timescale as illustrated in Fig. 2. Throughout the month, an ensemble of model states ( in Fig. 2) is simulated, representing individual water storage compartments. These state variables are translated into observation space, i.e., into TWSA, via an observation operator (ℋ in Fig. 2, Sect. 3.5). The DA algorithm – most commonly variants of the Ensemble Kalman Filter (EnKF) or Ensemble Kalman Smoother (EnKS) – integrates model predictions with observations (y in Fig. 2) while accounting for their respective uncertainties. For monthly TWSA DA, the distinction between a filter and smoother is somewhat vague in the literature, and we will refer to EnKF and EnKS interchangeably, as will be discussed in Sect. 3.2. In any case, a monthly TWSA innovation (di in Fig. 2) is computed and usually translated into a monthly increment, or else into a daily increment (δxi in Fig. 2), using the error cross correlations between daily and monthly TWSA forecasts. The increment is then applied to the first or final day of the month, providing the initial condition for the next model run, or it is distributed across all days of the current month by rewinding the model and integrating the model for the entire month again (Fig. 2). All currently available continental to global-scale land reanalysis products typically use this “filter-like” approach, i.e. using a filter or a smoother with non-overlapping short one-month windows, for computational efficiency and because TWS varies at timescales of less than a month. For long-term reanalysis, longer or moving smoothing windows could be explored in the future, as is done for atmospheric or oceanographic reanalyses. Note that, in contrast to the above described approaches, some studies combine GRACE/-FO observations and model output after the model has been run over the entire study period, without incorporating new information into the model after each update step (van Dijk et al., 2014; Mehrnegar et al., 2023). The following sections provide a detailed discussion of each step outlined in Fig. 2. For ease of reference, key DA terminology is summarized in the glossary (Appendix A).
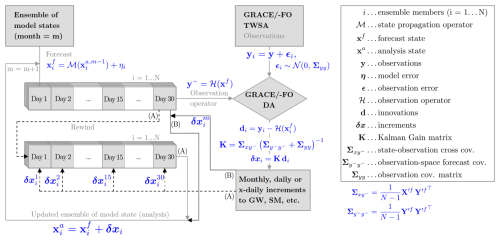
Figure 2General concept for assimilating monthly GRACE/-FO-derived TWSA into GHMs and LSMs along with most relevant Ensemble Kalman Filter (EnKF) equations showing two options for applying the assimilation increments: After computing the increments, the model is either (A) rewound and re-run over the month with the increments distributed across all days, or (B) updated by applying the full monthly increment at the end of the month. Please note that the equations provided refer to the EnKF and are expressed for each ensemble member i. The Kalman Gain matrix determines the update weights based on the state and observation error covariance matrices. and are matrices of forecast state anomalies and forecast state observation-space anomalies, respectively. Each column represents the deviation of one ensemble member from the ensemble mean. For further details on the equations for other DA algorithms, refer to the literature cited in Sect. 3.2.
3.1 Review of existing GRACE/-FO DA frameworks
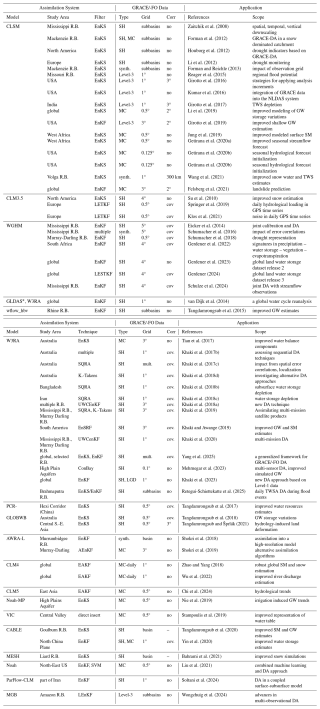
Table 2 provides a detailed overview of existing GRACE/-FO DA frameworks and their characteristics, along with an evolution of these frameworks. The frameworks exhibit notable differences in terms of filter algorithms, perturbation processes, model update strategies, selected GRACE/-FO solutions, and approaches to dealing with observation errors.
Zaitchik et al. (2008)Forman et al. (2012)Houborg et al. (2012)Li et al. (2012)Forman and Reichle (2013)Reager et al. (2015)Girotto et al. (2016)Kumar et al. (2016)Girotto et al. (2017)Li et al. (2019)Girotto et al. (2019)Jung et al. (2019)Getirana et al. (2020a)Getirana et al. (2020b)Getirana et al. (2020b)Wang et al. (2021)Felsberg et al. (2021)Su et al. (2010)Springer et al. (2019)Klos et al. (2021)Eicker et al. (2014)Schumacher et al. (2016)Schumacher et al. (2018)Gerdener et al. (2022)Gerdener et al. (2023)Gerdener (2024)Schulze et al. (2024)van Dijk et al. (2014)Tangdamrongsub et al. (2015)Tian et al. (2017)Khaki et al. (2017b)Khaki et al. (2017c)Khaki et al. (2018d)Khaki et al. (2018b)Khaki et al. (2018c)Khaki et al. (2018a)Khaki et al. (2019)Khaki and Awange (2019)Khaki et al. (2020)Yang et al. (2025)Mehrnegar et al. (2023)Khaki et al. (2023)Retegui-Schiettekatte et al. (2025)Tangdamrongsub et al. (2017)Tangdamrongsub et al. (2018)Tangdamrongsub and Šprlák (2021)Shokri et al. (2018)Shokri et al. (2019)Zhao and Yang (2018)Wu et al. (2022)Chi et al. (2024)Nie et al. (2019)Stampoulis et al. (2019)Tangdamrongsub et al. (2020)Yin et al. (2020)Bahrami et al. (2021)Liu et al. (2021)Soltani et al. (2024)Wongchuig et al. (2024)Table 2Overview on GRACE/-FO DA frameworks and conducted studies (Status as of November 2024). Please refer to Table 1 for details on the models in the first column. Abbrevations: R.B.: River Basin, MC: mascon, SH: Spherical Harmonics, no: not available, EnKS: Ensemble Kalman Smoother, EnKF: Ensemble Kalman Filter, LETKF: Local Ensemble Transform Kalman Filter, LGD: line-of-sight gravity difference, SQRA: Square root Analysis, K.-Takens: Kalman Takens, EnSRF: Ensemble Square Root Filter, UWCenKF: Unsupervised Weak Constrained ensemble Kalman Filter, AEnKF: Adaptive Ensemble Kalman Filter, EAKF: Ensemble Adjustment Kalman Filter, SVM: Support Vector Machine, LEnKF: Localized Ensemble Kalman Filter, * includes several GLDAS models (CLM, Mosaic, NOAH, VIC), GLDAS: Global Land Data Assimilation System (Rodell et al., 2004), SM: soil moisture, GW: groundwater, Corr: correlation.
In their seminal paper, Zaitchik et al. (2008) utilized three years of GRACE data, which were incorporated into the CLSM model as catchment-averaged time series for four subbasins of the Mississippi river basin. Later, this framework has been extended and applied for exploring technical aspects of the DA process, such as strategies for applying analysis increments (Girotto et al., 2016). Concurrently, various GRACE/-FO frameworks based on different models have been developed. For instance, the WGHM model was integrated within a joint calibration and DA framework (Eicker et al., 2014), a W3RA-based DA framework was employed to investigate water balance components over Australia (Tian et al., 2017), and DA schemes for different LSMs were developed for investigating trends in different water storage compartments (Springer et al., 2019; Nie et al., 2019; Zhao and Yang, 2018; Stampoulis et al., 2019). Today, there are at least 12 GRACE/-FO DA frameworks based on different GHMs and LSMs, and most of the studies to date have been conducted for CLSM and W3RA (Fig. 3a). These frameworks have been primarily developed and tested for individual river basins rather than globally, the majority of which are located on the North American continent, while only a small number of GRACE/-FO studies have been conducted for the South American and African continents (Fig. 3b).
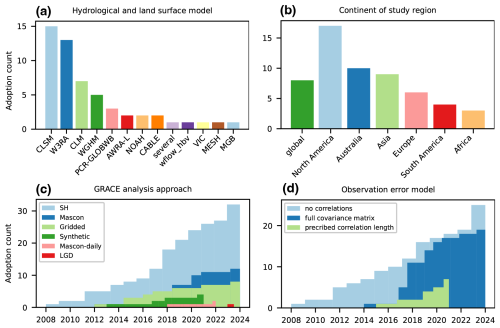
Figure 3Statistics of common settings in GRACE/-FO DA experiments, including the (a) hydrological model used, (b) continent of study, (c) GRACE/-FO observation product (analysis approach), and (d) observation error model (Status as of October 2024).
Table 2 highlights that most GRACE/-FO DA frameworks use the classical EnKF or EnKS approaches, but the effectiveness of other sequential DA algorithms has also been evaluated (Schumacher et al., 2016; Khaki et al., 2017b) along with non-parametric alternatives (Khaki et al., 2018d). Initially, GRACE/-FO data was assimilated at the basin or subbasin scale, but later studies explored a range of grid sizes, typically from 0.5 to 4° (Khaki et al., 2017c). So far, no cross-framework consensus has been reached regarding the optimal choice for the observation grid. It is crucial to consider that for higher-resolution observation grids, obtained after downscaling (Sect. 2.4), the examination of spatial correlations is a logical approach (Khaki et al., 2017c; Springer, 2019), given the inherent limitations in the spatial resolution of GRACE/-FO data, but this is not done as a standard so far (Fig. 3d). At the time of the initial GRACE-DA studies, only GRACE solutions in the form of SH coefficients were available. However, subsequent studies have employed not only mascon solutions but also Level-3 TWSA products derived from SH solutions, which require less preprocessing efforts (Fig. 3c, Sect. 2.2). As spatial filtering is employed in the processing of SH solutions, which attenuates signals, approximately half of the studies utilize a rescaling procedure to restore filtered signals (see Sect. 2.2 for further details). To date, the majority of studies have been conducted using SH solutions, which permit the consideration of spatial correlations via the full error covariance matrices of the coefficients, which can then be propagated onto the observation grid. In contrast, studies utilizing mascon solutions or Level-3 data may alternatively assume a fixed correlation length (Fig. 3d). The latest research developments have begun to explore the direct incorporation of GRACE/-FO Level-1b data, represented by along-orbit line-of-sight gravity difference (LGD) measurements (Khaki et al., 2023). This approach overcomes the limitations of the conventional method, offering enhanced performance in capturing high-frequency TWSA observations, including at submonthly time scales (Sect. 6.3).
In recent years, multi-sensor DA frameworks have gained popularity, through a combination of GRACE/-FO data with other satellite data to better constrain the DA (see Sect. 1). To the best of our knowledge, only the CLSM-based GRACE/-FO DA framework has been used operationally, i.e. for the NASA drought monitor for groundwater and soil moisture conditions https://nasagrace.unl.edu/ (last access: 10 December 2025; Houborg et al., 2012; Li et al., 2019; Getirana et al., 2020b). Recently, the groundwater storage changes from the GLWS2.0 dataset developed at the University of Bonn via assimilating GRACE/-FO TWSA data into the WaterGAP model have been integrated into the operational water and biodiversity risk assessment tools of the WWF (World Wide Fund for Nature, 2024).
3.2 DA algorithms
Most TWSA DA studies use a variant of the sequential EnKF or EnKS (Evensen, 1994, 2009; Lorenz et al., 2015). For monthly GRACE/-FO TWSA DA, the line between the EnKF and EnKS is vague in literature. Whereas a filter typically assimilates observations at one instant, a smoother would assimilate observations at multiple time steps over a longer observation window. One can state that the assimilation of a single monthly GRACE/-FO TWSA observation at one instant is done through an EnKF. However, since the TWSA is a monthly aggregate, it is often used to update an entire time window of state variables in a retrospective analysis and this process is then often referred to as an EnKS (e.g., Zaitchik et al., 2008; Li et al., 2012; Forman et al., 2012; Kumar et al., 2016; Tian et al., 2017; Li et al., 2019; Getirana et al., 2020b; Wang et al., 2021; Bahrami et al., 2021; Tangdamrongsub and Šprlák, 2021). In any case, the EnKF and EnKS represent the probability distribution of the system state using a dynamic ensemble of model simulations (see Eqs. 27 to 39 in Nerger et al., 2005), and thereby overcome the need for a linear(ized) model to analytically propagate the forecast uncertainty in a traditional (extended) Kalman filter or smoother. The ensemble approach is computationally efficient, making it suitable for large-scale systems and real-time applications, and can further provide uncertainty estimates for both state variables and parameters. Nevertheless, all ensemble techniques are sensitive to the choice of ensemble size, which can lead to sampling errors, especially with small ensemble sizes or in highly nonlinear systems. In such cases, the ensemble may fail to capture the true variability of the system, and it is particularly prone to collapse, meaning that all ensemble members converge to the same state (Mitchell et al., 2002). Furthermore, strictly speaking the EnKF and EnKS are optimal and unbiased only when errors are Gaussian (Sect. 3.4), however unless strong nonlinearities lead to violations of this assumption they usually work in a satisfactory way. This is a known limitation and can result in biased estimates. In the context of GRACE/-FO DA, recent advancements have sought to address these issues through techniques such as localization (Hunt et al., 2007), covariance inflation (Anderson and Anderson, 1999), and modifications of the EnKF or EnKS, including square root filters (Tippett et al., 2003) and alternative methods like particle filters (Crisan, 2001).
Localization is supposed to mitigate spurious long-range correlations, restrict the influence of observations on nearby grid cells, and improve performance with limited ensemble sizes. This can be achieved either through covariance localization, which modifies the forecast error covariance matrix ( in Fig. 2) using a distance-dependent tapering function, or through domain-based localization, where the analysis is performed independently for local regions or grid points (Kirchgessner et al., 2014; Evensen et al., 2022), or a combination of both. These two approaches imply that long-range correlations in the forecast error covariance matrix are damped or removed, respectively. In the case of covariance localization, the influence of distant observations on model state updates is reduced by damping error cross-covariances between state variables and observation predictions. The covariance localization scale is typically set to a multiple of the spatial autocorrelation length in the forecast errors. Meanwhile, via domain localization, the state update is restricted to the assimilation of nearby observations within an influence radius, as illustrated in Fig. 2 of De Lannoy et al. (2016) for the case of soil moisture DA. Most often, both approaches are used together. Thus, both localization approaches mitigate the impact of spurious error correlations in GRACE/-FO TWSA data and have proven highly beneficial for GRACE/-FO DA (Schumacher, 2016; Khaki et al., 2017c). Additionally, covariance inflation methods, which prevent filter divergence by artificially increasing the ensemble forecast spread, are commonly applied in GRACE/-FO DA frameworks (Khaki et al., 2020; Gerdener et al., 2023).
Square root filters, such as the Ensemble Transform Kalman Filter and the Ensemble Adjustment Kalman Filter, were designed for improved numerical stability and reduced sampling errors compared to the standard EnKF (Schumacher et al., 2016; Khaki et al., 2017b). Particle filters and smoothers, also known as Sequential Monte Carlo methods, are another class of sequential DA techniques that have been applied for GRACE/-FO DA (e.g., Khaki et al., 2017b, 2018d). These techniques utilize a set of particles to represent the probability distribution of the system state, propagating these particles through the model and weighting them based on their agreement with the observations. However, particle filters and smoothers are computationally more demanding, especially for high-dimensional systems.
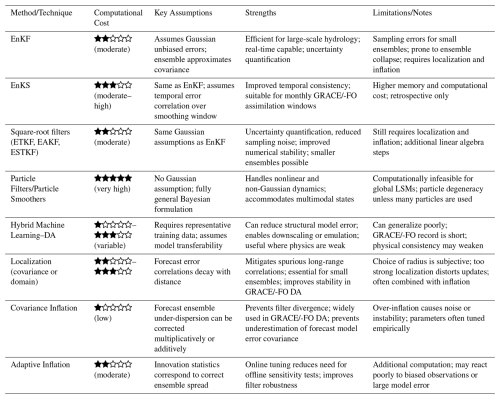
More recently, machine learning algorithms in conjunction with traditional DA methods have been put forward to assimilate GRACE/-FO data. For instance, Liu et al. (2021) proposed a support vector machine framework integrated with DA for groundwater level forecasting using GRACE/-FO data. The effectiveness of such hybrid approaches depends on the availability of high-quality training data and the ability to generalize across different hydrological contexts. Such data-driven methods have also been extensively applied to reconstruct past (Humphrey et al., 2017) and forecast future (Li et al., 2024) GRACE-like TWSA. To clarify the relative strengths and limitations of the DA methods discussed in this part, Table 3 provides a structured comparison of their computational requirements, underlying assumptions, advantages, and known challenges in the context of GRACE/-FO TWSA assimilation.
3.3 Observation errors
After bias correction (Sect. 2.5), GRACE/-FO data still contains inherent errors that, if not adequately accounted for, can propagate through the assimilation process and affect the accuracy and reliability of the assimilated model version. In traditional EnKF and EnKS approaches, observations are perturbed with additive noise to represent the random error.
The first GRACE/-FO DA studies assumed spatially uniform and uncorrelated errors in the range of 10 to 30 mm equivalent water height (Zaitchik et al., 2008). However, in reality the observation errors may not be uniformly distributed across the observed area (Sect. 2.2) and Eicker et al. (2014) highlighted the importance of understanding the impact of anisotropically correlated TWSA observation errors on state estimates. Since then, three major strategies have emerged to address this issue, which are applied either individually or in combination. First, the grid spacing can be chosen to match the native resolution of the TWSA maps, resulting in either thinning or aggregation of the grid, typically to 3 or 4° spacing (Eicker et al., 2014; Khaki et al., 2017c; Girotto et al., 2019; Gerdener et al., 2023). However, this means that some possible signal loss is accepted. Second, spatial correlations between observation grid cells may be taken into account either by prescribing a fixed correlation length, typically 3°, or by taking into account full error covariance matrices (Shokri et al., 2019; Tangdamrongsub and Šprlák, 2021; Wang et al., 2021). Third, researchers have proposed localization techniques that account for spatial correlation errors in the DA process (Tangdamrongsub et al., 2017; Gerdener, 2024). By ensuring that the influence of observations is appropriately weighted based on their spatial proximity to model grid points, these techniques can enhance the reliability of GRACE/-FO data integration into numerical models by limiting in particular the impact of spurious long-range correlations (Khaki et al., 2017c).
3.4 Forecast errors
In ensemble-based DA approaches, the forecast uncertainty is estimated by perturbing key components such as forcing data, state variables, and model parameters (Table 4). The perturbation scheme is designed based on the assumption that model uncertainties are unknown and are propagated from model inputs (e.g., forcing data), configuration (such as number of soil layers and static parameters), and model physics. However, due to the finite ensemble size, the perturbation process can introduce unrealistic long-range correlations within the ensemble. In high-dimensional systems, a small ensemble struggles to represent the true error structures accurately.
Shokri et al. (2018)Tang et al. (2020)Su et al. (2010)Springer et al. (2019)Soltani et al. (2024)Reichle et al. (2007)Girotto et al. (2016)Bahrami et al. (2021)Wongchuig et al. (2024)Liu et al. (2021)Nie et al. (2019)Tangdamrongsub et al. (2017)Tangdamrongsub et al. (2015)Eicker et al. (2014)Schumacher et al. (2016)Tian et al. (2017)Table 4Summary of perturbations applied in various hydrological and land surface models for GRACE/-FO DA, including the types of state variables, meteorological forcing variables, and calibrated parameters perturbed. CD: Catchment deficit, SE: Surface excess, SMC: soil moisture; SWE: snow water equivalent; GW: groundwater storage; PCP: precipitation; SWR: shortwave radiation; LWR: longwave radiation; RAD: radiation; TEMP: air temperature; minT/maxT: minimum/maximum air temperature; PET: potential evapotranspiration; infR: infrared surface temperature; SysE: systematic error; radE: random error; TRMM: Tropical Rainfall Measuring Mission; maxDrain: maximum subsurface drainage rate; DrainRt: drainage rate; TWS: terrestrial water storage, see Table 1 for model abbreviations.
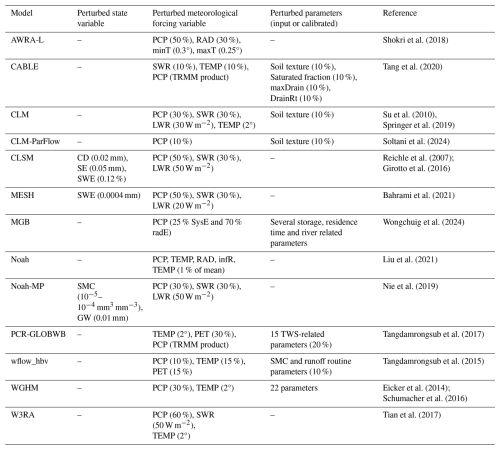
Forcing data such as precipitation, temperature, and solar radiation are usually obtained from global atmospheric reanalyses and often perturbed by adding or multiplying random noise to represent uncertainties in these variables. Spatial correlation errors are often introduced during the perturbation process, to reflect the reality that reanalysis errors are often spatially correlated, e.g., due to topography influences. Additionally, correlations among variables can be accounted for to preserve the proper interactions between forcing variables during DA (Reichle et al., 2007).
Perturbing state variables – such as soil moisture or snow, which define the current condition of the system – ensures that the ensemble represents a range of possible states. This becomes especially important when the perturbation from forcing data is small or does not impact all state variables that contribute to TWS. In GRACE/-FO DA, state variables typically include all components of TWS, such as soil moisture, groundwater, and snow. However, the choice of which state variables to perturb depends on the design of the DA scheme and the model employed. While perturbing all variables contributing to TWS is one option, another approach is to perturb only a few selected state variables, or alternatively, to use only parameter perturbation, as described below (Nie et al., 2019; Tangdamrongsub et al., 2018; Springer et al., 2019). Introducing correlations among TWS variables can also help maintain realistic interactions and behavior in the TWS estimates (Kumar et al., 2016). This ensures that the ensemble better reflects the system's actual dynamics during the DA process. Challenges may arise from non-Gaussian behaviour of variables contributing to TWS (Sect. 5.3).
Finally, parameters that govern hydrological processes and/or describe soil properties can be perturbed to reflect uncertainties in the physical or empirical relationships within the model. In real-world applications, many parameters are either estimated from limited data, or based on assumptions that may not be valid under all conditions. Perturbing these parameters allows the ensemble to explore a range of possible model behaviors, which is crucial for accurately estimating the true state of the system, especially when certain model processes are poorly formulated. The implementation of parameter perturbation may be simpler in models where parameters are pre-calculated (Tangdamrongsub et al., 2017), but it becomes more complex in models where parameters are determined dynamically, such as through look-up tables (Peters-Lidard et al., 2007). Dedicated studies are often required to determine the sensitivity of model parameters and uncertainty ranges, ensuring that the perturbations adequately capture the variability (Benke et al., 2008; Herrera et al., 2022).
The above perturbations may create an unintended bias in the forecast errors. To address this, the ensemble can be readjusted after each perturbation step to better fit a Gaussian distribution, using an unperturbed model run in parallel with the ensemble to correct the mean perturbation bias (Ryu et al., 2009). Furthermore, modern DA systems also provide opportunities to calibrate forecast uncertainties automatically during runtime, rather than relying solely on offline perturbation design. Techniques such as adaptive covariance inflation (Anderson, 2007) and relaxation-to-prior-spread (RTPS) or relaxation-to-prior-perturbations (RTPP) (Whitaker and Hamill, 2012) dynamically adjust ensemble spread using innovation statistics to compensate for under- or over-dispersive ensembles. In addition, stochastic model error estimation and hierarchical Bayesian approaches allow perturbation magnitudes or model error parameters to be updated online (Ruiz et al., 2013; Berry and Harlim, 2017). These automated strategies reduce the reliance on extensive offline sensitivity analyses and enable forecast uncertainties to evolve consistently with model–observation discrepancies.
3.5 Innovations and increments
When assimilating GRACE/-FO data into models, key considerations include the mismatch in spatial and temporal resolution, along with the decision of whether to compute innovations and increments at the observation or model resolution (in space and time). Today, the most common approach for assimilating GRACE/-FO data is to use monthly TWSA maps, which have a coarse spatial resolution (∼ 300 km), capturing large-scale changes in TWS. In contrast, GHMs or LSMs operate at much finer spatial (order of km) and temporal (daily or subdaily) scales. This discrepancy creates a challenge, as localized water storage dynamics (such as small-scale groundwater variations or snow in complex terrains) may be smoothed out in the GRACE/-FO observations (Sect. 5.2.2). Recent research has also explored submonthly assimilation intervals using weekly or daily observation datasets (Khaki et al., 2017c; Wu et al., 2022; Khaki et al., 2023; Retegui-Schiettekatte et al., 2025), which is discussed in detail in Sect. 6.2.
Depending on the temporal and spatial scale at which model simulations and observations are compared, GRACE/-FO DA can be categorized into two types: DA with TWSA innovations computed at the spatial and temporal resolution of GRACE/-FO observations, and DA with TWSA innovations calculated at the model’s spatial resolution which is generally finer than that of GRACE/-FO data. The latter choice is unique to GRACE/-FO DA – see Sect. 5.2 for a discussion of the specific challenges associated with each approach. In most GRACE/-FO DA frameworks, TWSA forecasts (also called observation predictions) are computed at the resolution of the GRACE/-FO observations. The daily or subdaily model state variables (groundwater, soil moisture, …) at the pixel scale are mapped to monthly coarser-scale TWSA observation predictions. TWSA innovations are formed by taking the difference between observation predictions and GRACE/-FO observations, and these TWSA innovations are then projected to model state increments via error cross covariances between these state variables and their associated TWSA observation predictions (Fig. 2). This process involves several steps that are implemented in the observation operator (Reichle et al., 2014): (i) computing TWS(A) for each model grid cell by summing individual storage compartments (and possibly removing the climatology), (ii) spatially aggregating model grid cells to match the GRACE/-FO observation grid, and (iii) temporally aggregating the modeled observation predictions to the monthly GRACE/-FO observation frequency, by averaging all or select days within the month. The second approach takes on a simplified strategy by interpolating or downscaling GRACE/-FO data directly onto the model’s finer grid, where innovations are then computed independently at each model grid cell (Tangdamrongsub et al., 2015; Nie et al., 2024; Chi et al., 2024).
Assimilation increments are computed for each entry of the state vector. Typically, the state vector is filled with water storage in individual compartments, such as root-zone soil moisture, snow, and groundwater of considered model grids, allowing for the disaggregation of TWSA updates during the DA process (Khaki et al., 2017b; Gerdener et al., 2023). However, storage compartments with a small contribution to the overall TWS variability, such as canopy water, are often excluded from the state vector to prevent instabilities and spurious updates in these variables. For monthly GRACE/-FO DA, monthly increments are computed using the state error covariances on the last day of the month, or the monthly increment is computed as an average of daily resolved increments (Girotto et al., 2016). This monthly increment is then applied either to the first day or the last day of the month or distributed across all days by iterating through the entire month again.
In addition to updating model state variables, model parameters can also be adjusted during DA by augmenting the state vector with parameters sensitive to TWSA observations (Schumacher et al., 2016). This approach requires a prior sensitivity study to identify the most relevant parameters.
This section discusses the validation of GRACE/-FO DA experiments using independent observation-based datasets, where different metrics are applied and tailored to the variables of interest and the specific applications. Key challenges such as data sparsity, scale mismatches, and uncertainty quantification are addressed.
4.1 Commonly used validating variables and metrics
Hydrological applications often use GRACE/-FO TWSA observations to benchmark GHMs or LSMs (Scanlon et al., 2018; Jensen et al., 2019). However, once GRACE/-FO data is assimilated, it can obviously no longer serve as an independent validation dataset. Since direct TWS measurements are rare, the performance is typically evaluated using independent observations corresponding to the model's storage components (e.g., soil moisture, groundwater, snow water equivalent (SWE)) or to fluxes impacted by the assimilation (such as runoff, streamflow, river water levels, and evapotranspiration (ET)). Recently, GPS measurements of vertical land motion have also been used as a reference dataset for validation. It is important to note that datasets used as model inputs, or observational constraints for assimilation in addition to GRACE/-FO TWSA, are not independent.
Validation metrics can be broadly categorized into bias and variance dimensions. Bias metrics assess systematic errors between model and reference targets, including bias, Mean Absolute Error (MAE), Root Mean Square Error (RMSE), trends, and climatology (seasonal amplitude and phase). Root Mean Square Difference (RMSD) is sometimes used in place of RMSE when the reference dataset is not considered as a definitive “ground truth” to highlight discrepancies between datasets without implying that one is entirely accurate. Besides, because models, satellite retrievals, and in situ measurements involve different assumptions that may reflect real-world dynamics differently, they typically exhibit very different mean values and variability, therefore, absolute bias evaluations are not always meaningful (Reichle and Koster, 2004). Instead, unbiased RMSE or RMSD (ubRMSE or ubRMSD) can be used to isolate variance-related errors by removing bias (Girotto et al., 2016).
Variance metrics focus on capturing how much the model outputs vary from their expected values or fluctuate over time. Common metrics include Pearson or rank correlation (on raw, deseasonalized, or detrended data), or more integrated metrics such as Nash-Sutcliffe Efficiency (NSE) and Kling-Gupta Efficiency (KGE) coefficients. However, deseasonalizing and detrending rely on assumptions, like a fixed seasonal cycle or linear trend. These assumptions can introduce errors, especially in complex, nonlinear, or non-stationary systems (Nie et al., 2024). Removing information based on such assumptions effectively inserts distortions into the data, which can significantly affect the validation results. For instance, nonstationary TWS changes, driven by climate change and human activities, are increasingly prevalent (Rodell et al., 2018; Humphrey et al., 2016; Nie et al., 2024). In such a context, validation strategies may consider robustness and flexibility on data distribution assumptions. For instance, some studies (Kumar et al., 2018) apply information theory (Shannon, 1948) to assess whether the model captures inherent variability and randomness in observations without assuming linearity or stationarity.
Another emerging focus is evaluating whether GRACE/-FO DA enhances the representation of extreme events like droughts and floods (Houborg et al., 2012; Reager et al., 2015; Li et al., 2019; Jung et al., 2019; Khaki et al., 2023). However, validating drought performance is challenging due to differences in propagation times and speeds across indicators. For example, validating a TWS-based drought indicator using a vegetation or precipitation-based drought indicator is difficult, as each responds differently to drought conditions over space and time. Furthermore, establishing a consistent ground truth for droughts is complicated due to human activities. For instance, during a severe drought, responding with increased irrigation may maintain soil moisture levels, making soil moisture-based drought indicators less representative of actual drought conditions.
Overall, the design of validation depends on the goal of the application, reasonable assumptions regarding the properties of the variable of interest, and the availability of reliable observational data. A non-exhaustive list of commonly used datasets, variables, and metrics in GRACE/-FO assimilation validation can be found in Table 5.
Houborg et al. (2012)Girotto et al. (2019)Tian et al. (2017)Kumar et al. (2016)Khaki et al. (2023)Zhao and Yang (2018)Nie et al. (2019)Jung et al. (2019)Soltani et al. (2024)Zaitchik et al. (2008)Houborg et al. (2012)Reager et al. (2015)Girotto et al. (2017)Kumar et al. (2016)Tian et al. (2017)Li et al. (2019)Getirana et al. (2020b)Su et al. (2010)Forman et al. (2012)van Dijk et al. (2014)Kumar et al. (2016)Zhao and Yang (2018)Bahrami et al. (2021)Khaki et al. (2023)Forman et al. (2012)Li et al. (2012)Bahrami et al. (2021)Wu et al. (2022)Khaki et al. (2023)van Dijk et al. (2014)Kumar et al. (2016)Tian et al. (2017)Girotto et al. (2017)Nie et al. (2019)Khaki and Awange (2019)Houborg et al. (2012)Li et al. (2012)Li et al. (2019)Tangdamrongsub and Šprlák (2021)Klos et al. (2021)Gerdener et al. (2023)Table 5Non-exhaustive list of commonly used datasets, variables, metrics, and exemplary references in GRACE/-FO assimilation validation. Abbreviations: SCAN: Soil Climate Analysis Network, USCRN: United States Climate Reference Network, ISMN: International Soil Moisture Network, NASMD: North American Soil Moisture Database, ESA CCI: European Space Agency Climate Change Initiative, ASCAT: Advanced Scatterometer, SMOS: Soil Moisture and Ocean Salinity, SMAP: Soil Moisture Active Passive, USGS: United States Geological Survey, NSW: New South Wales, CMC: Canadian Meteorological Centre, GHCN: Global Historical Climatology Network, SNODAS: Snow Data Assimilation System, GRDC: Global Runoff Data Centre, LEGOS: Laboratoire d'Etudes en Géophysique et Océanographie Spatiales, ALEXI: Atmosphere-Land Exchange Inverse model, MODIS: Moderate-resolution Imaging Spectroradiometer, GLEAM: Global Land Evaporation Amsterdam Model, USDM: United States Drought Monitor, NDVI: Normalized Difference Vegetation Index, FDM: Flood and Drought Monitor, SPI: Standardized Precipitation Index, GNSS: Global Navigation Satellite System, R: Correlation, ubRMSD: unbiased Root Mean Square Difference, RMSE: Root Mean Square Error, MAE: Mean Absolute Error, RMSD: Root Mean Square Difference, NSE: Nash-Sutcliffe Efficiency, KGE: Kling–Gupta Efficiency.
4.2 Impact of GRACE/-FO DA on model variables
The impact of GRACE/-FO DA on hydrological processes varies with spatial scales, simulated storage components, and external factors on water storage dynamics such as human impacts. An improved performance is especially present in large river basins where natural variability dominates (Humphrey et al., 2023). Challenges in model-only simulations include underestimated amplitudes and seasonal dynamics of TWS due to model parametrization (Schellekens et al., 2017) and underestimated trends and variability due to uncertainties in meteorological forcings (Tang et al., 2020). GRACE/-FO DA has proven effective in addressing these issues, improving correlation and long-term trends in storage components such as groundwater and soil moisture with respect to observation-based datasets across various basins (Zaitchik et al., 2008; Li et al., 2012; Li et al., 2019; Kumar et al., 2016; Schumacher et al., 2018; Tangdamrongsub et al., 2018). These improvements underscore the value of GRACE/-FO in capturing large-scale hydrological variability. However, the impact on other storage components, such as SWE, is often mixed. SWE performance, for example, may degrade, as GRACE/-FO lacks the resolution to capture local snow dynamics for reliable spatiotemporal scaling and mass redistribution. Mass tends to shift incorrectly from SWE into other water components, dampening runoff responses and misrepresenting hydrological flows (Su et al., 2010; Forman and Reichle, 2013; Zhao and Yang, 2018). Beyond storage components, the effects of GRACE/-FO DA on fluxes like ET and runoff remain less consistent (Springer, 2019; Nie et al., 2019; Chen et al., 2021). For example, a model might overestimate groundwater storage but underestimate baseflow; when GRACE/-FO DA decreases groundwater, it exacerbates the baseflow deficiency. Or a model might not simulate groundwater pumping for irrigation; GRACE/-FO DA will decrease groundwater and thereby erroneously decrease ET (Girotto et al., 2017). In potential applications of GRACE/-FO DA for surface and/or subsurface components in coupled Earth System Models, such misrepresentations could degrade land-atmosphere or land-ocean feedbacks.
GRACE/-FO DA has also proven effective in capturing large-scale droughts (Li et al., 2019; Rodell and Li, 2023) and floods (Reager et al., 2015; Khaki et al., 2023). It has been effectively utilized in drought monitoring systems, such as the U.S. Drought Monitor (Houborg et al., 2012). However, GRACE/-FO DA still tends to underestimate extreme intensities and is limited in representing events that occur rapidly with short duration, such as flash floods, due to its coarse temporal and spatial resolution (Sect. 5).
In regions with intensive human water management practices, such as those relying on groundwater pumping for irrigation, assimilating GRACE/-FO can improve groundwater trends but may degrade other variables such as ET (Girotto et al., 2017; Li et al., 2019) and degrade storage forecast skill (Getirana et al., 2020b) if such human impact is not explicitly represented by the model. Nevertheless, the potential of GRACE/-FO DA for improving groundwater monitoring and informing decision-making processes has been indicated by several studies (Zaitchik et al., 2008; Li et al., 2019).
4.3 Validation challenges and best practices
It is essential that spatial scale mismatch is resolved for meaningful validation. While in situ stations provide measurements of storage changes or fluxes at point scale, model simulations are conducted on much broader scales. Additionally, given the coarse temporal and spatial resolution of GRACE/-FO TWSA, improvements or degradations due to the assimilation compared to in situ station data have to be interpreted cautiously. Strategies such as averaging or interpolating could be used when in situ measurements are densely available to obtain a broader representation of measured storage changes and fluxes.
Alternatively, many studies also set certain criteria to select representative sites to approximate basin or grid-level variability (De Lannoy et al., 2007). Careful assumptions need to be made when key data is missing or limited. For instance, groundwater observations are usually available as groundwater level changes. Specific yield needs to be used to convert it into groundwater storage in order to be able to compare it with model simulation. The information on specific yield is often only available at sparse sites or even unavailable, introducing further uncertainties into the validation (Khaki et al., 2017a). Additionally, quality control and data cleaning are recommended for validation as in situ data is also prone to missing periods or poor-quality measurements (van Dijk et al., 2014). If scale mismatches cannot be fully addressed, point-scale comparisons should be interpreted cautiously.
Remotely sensed hydrological products are now widely used to validate GRACE/-FO DA simulations (Kumar et al., 2016; Zhao and Yang, 2018; Khaki et al., 2019; Jung et al., 2019). However, these datasets often differ in accuracy and consistency, making robust comparisons challenging (van Dijk et al., 2014). When multiple independent datasets are available for the same hydrological variable, triple collocation provides a way to assess the quality of each dataset without assuming that any of them is error-free (Stoffelen, 1998; Gruber et al., 2016). The method separates unpredictable measurement noise (random errors) from systematic offsets or scaling differences (calibration biases) based solely on the mutual agreement among the datasets. As such, triple collocation offers a practical solution for validation when more than two datasets are collocated in space and time and should therefore be considered a standard option.
When GRACE/-FO DA is applied in regions with significant human water management, model state variables that are directly updated through assimilation such as soil moisture and groundwater tend to improve remarkably (Girotto et al., 2019; Tangdamrongsub et al., 2020), but the impact on other processes like runoff or ET remains challenging. Among these processes, runoff and streamflow have received considerably more attention than vegetation-related processes like ET and carbon fluxes. Including them in evaluations is equally important to ensure a more comprehensive understanding of model behavior and to better reflect the interconnected nature of hydrological and ecological processes.
Moreover, any preprocessing operations applied to the data (for example deseasonalizing, detrending, spatial averaging, or temporal aggregation) introduce additional uncertainty which must be propagated into the final validation metrics. Error propagation models can be used to quantify the uncertainty of observational datasets by estimating how input measurement errors or retrieval assumptions propagate into derived variables. Such approaches can provide spatially explicit uncertainty estimates for each observation, thereby offering a more comprehensive view of dataset reliability than local in situ validations alone (Dorigo et al., 2010). Neglecting these aspects can lead to overconfidence in skill estimates or misinterpretation of variance metrics, particularly when multiple data sources or preprocessing steps are involved.
An additional challenge is that both the model state distributions and even the retrieval error distributions may depart significantly from Gaussian assumptions. If validation metrics assume Gaussian error or linear relationships (e.g. RMSE, linear regression), the non-Gaussian nature of the underlying distributions may skew results or invalidate confidence statements. We therefore recommend assessing the distributional characteristics of the errors (e.g., skewness) and, where needed, applying non-Gaussian or rank-based metrics (e.g., information-theoretic scores (Kumar et al., 2018; Maina et al., 2024)) to ensure robust validation.
In multi-sensor assimilation settings, the role of GRACE becomes less straightforward by only comparing the hydrological states and fluxes. Analyses of the Kalman Gain matrix (K in Fig. 2) or assimilation increments offer deeper insights into how mass moves within the system. For example, Girotto et al. (2019) observed that storage increments from GRACE TWSA and SMOS soil moisture were negatively correlated.
Lastly, because neighboring grid cells are spatially correlated for GRACE/-FO data, this dependency propagates through DA outputs. Therefore, validation strategies must avoid treating adjacent grid cells as independent and carefully interpret regional behavior in a spatially coherent manner (Humphrey et al., 2023).
TWS processes possess unique dynamics and characteristics such as their lagged responses to atmospheric effects (precipitation and ET). These properties present challenges to DA techniques which were originally designed for linear processes. Here, we discuss a wide range of issues and challenges, most of them are unique to GRACE/-FO DA, and have not been fully explored in past studies.
5.1 Unmodeled TWS processes
GRACE/-FO observes the entire sum of TWS changes, but models do not simulate all relevant storage compartments; for example, some models do not simulate reservoirs, lakes and glaciers (Sect. 2.1). As a result, DA may inadvertently integrate these mass change signals into the TWS compartments that are simulated. It is therefore crucial to correct GRACE/-FO observations for these signals before DA (Sect. 2.3 and 2.5). We hope that with improving remote sensing capabilities, e.g., from the SWOT mission, the data base for such corrections will grow significantly. Future versions of hydrological models and LSMs might also take into account improved representation of other processes, e.g., in soil hydraulics (Vereecken et al., 2022).
In regions with significant human impacts on the water cycle, explicitly representing human water use in models helps to ensure realistic distribution of observed mass changes among the storage components (Nie et al., 2019). However, representing human water use in models is limited by the availability, and the spatial and temporal resolution of water use data. Another possible strategy is to assimilate GRACE/-FO data simultaneously with other observational datasets to better constrain the human-affected water budget (Tian et al., 2017; Zhao and Yang, 2018; Girotto et al., 2019; Tangdamrongsub et al., 2020; Khaki et al., 2020; Nie et al., 2024; Schulze et al., 2024). However, efforts are still needed to understand and resolve signal conflicts and improve the quantification of uncertainties.
5.2 Computation of innovations
Innovations – the differences between model predictions and observations – can be computed either at the resolution of the observations or at the resolution of the model. Both approaches are used in current GRACE/-FO DA frameworks, each with its own advantages and challenges.
5.2.1 DA with innovations at the observation resolution
When computing innovations at the spatial and temporal resolution of the GRACE/-FO TWSA observations, all relevant storage compartments within the model grid cells corresponding to a given observation grid cell are aggregated (Sect. 3.5). When applying an EnKF without applying any localization for the entire globe, where a single high-dimensional state vector represents the entire model domain, DA at the resolution of the observations would be an ill-posed problem. The combination of limited observational constraints and the high dimensionality of the forecast state vector leads to a rank-deficient system, making it difficult to derive unique and stable state updates. Incorporating full observation error covariance matrices (Σyy in Fig. 2) can introduce further numerical instability (Eicker et al., 2014; Gerdener et al., 2023). Therefore, many studies parallelize the problem into updates to individual state vectors for each local model domain or grid cell (Khaki et al., 2017c; Girotto et al., 2019; Springer et al., 2019; Wang et al., 2021) – thereby improving overall system stability by removing spurious long-range correlations. This strategy is also discussed in the context of domain localization in Sect. 3.2.
Assimilation at the observation resolution enables the DA algorithm to disaggregate information from the observations onto the finer model grid, effectively using DA as a downscaling approach in which the finer-scale patterns are informed by the model. For large study areas, especially in high-resolution and highly parallelized models, this downscaling can involve quite some communication between processes.
5.2.2 DA with innovations at the model resolution
After a priori interpolation of observations to the model grid, they can be assimilated directly for each model grid cell, which reduces computational complexity (Nie et al., 2019). With a one-to-one relationship between an observation and the state vector of a single model grid cell, this approach can be considered as an extreme case of localization, where all spatial correlations between model grid cells and between model and observations are suppressed. This approach also allows easy code parallelization and efficient GRACE/-FO DA in an operational setting.
However, this approach has its own drawbacks. When coarse-scale GRACE/-FO observations are applied directly to finer model grid cells without any pre-spatial downscaling and without applying variable observation errors, the spatial details of simulated TWS are inevitably smoothed out; in regions with complex terrains, this may suppress the dynamic range of TWS at high-elevations while amplifying it in adjacent low-elevation grid cells as shown in Fig. 4.
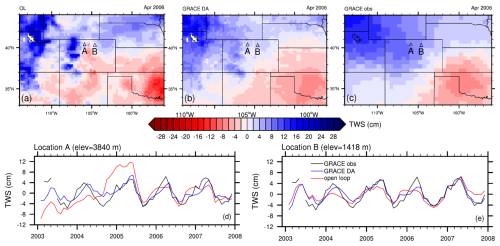
Figure 4Spatial maps of TWSA from the CLSM model only (open loop), GRACE DA into CLSM and GRACE for a US western region centered around Colorado in April 2006 (panels a, b and c); TWSA time series during 2003–2007 for locations A and B (panels d and e). CLSM refers to the NASA Catchment LSM. Further details on CLSM and this GRACE DA simulation can be found in Li et al. (2019).
More importantly, GRACE/-FO DA at the model resolution can lead to GRACE/-FO observed mass changes leaking into unintended areas. For instance, mass change signals related to seasonal snowpack in the Rocky Mountains of the U.S. may incorrectly spread eastward into the plains with this DA approach, while the reverse is also true, resulting in underestimated TWS amplitude in the front range (Fig. 4). Similarly, mass change signals from large surface water bodies such as lakes and reservoirs can be inadvertently distributed to surrounding areas if these signals are not properly managed prior to GRACE/-FO DA.
5.3 Non-Gaussian behaviors of TWS processes
A fundamental assumption for the EnKF and EnKS is that forecast errors are Gaussian, which is needed to achieve optimal output, i.e., minimized estimation errors. However, this assumption is frequently violated by TWS processes (soil moisture, groundwater and snow), degrading the effectiveness of GRACE/-FO DA for constraining these processes. Soil moisture typically exhibits a skewed distribution near its two bounds, the wilting point and saturation (Li and Rodell, 2013). As a result, ensemble spreads must be kept small in both dry and wet soil moisture ranges, limiting the ability of GRACE/-FO DA to improve soil moisture in extreme conditions.
SWE is known to follow a log-normal distribution and thus, perturbation errors added to SWE states are generated in log-normal space. When these errors are transformed back to normal space, the zero-mean errors become biased, with greater biases for larger SWE estimates. While reducing perturbation errors can mitigate biases, it also limits the usefulness of GRACE/-FO DA in improving SWE estimates, especially in high mountain regions (Li et al., 2019).
Groundwater storage is practically unbounded and is expected to behave as a Gaussian process (Li et al., 2015). However, non-linear model physics can introduce biases to simulated groundwater. In particular, groundwater recharge is often calculated as a power function of soil moisture (Niu et al., 2011). Since power functions are highly skewed, the ensemble recharge is inevitably biased even with an unbiased soil moisture ensemble, resulting in a biased groundwater ensemble (Ryu et al., 2009). Ensemble biases in groundwater can persist for months due to groundwater’s long memory, especially in models that simulate limited two-way interactions between soil moisture and groundwater and during prolonged dry seasons.
Since groundwater controls baseflow generation, biases in groundwater can propagate into simulated runoff similar to that from soil moisture to moisture fluxes (Ryu et al., 2009). While soil moisture, groundwater and snow estimates are still constrained by GRACE/-FO observations despite their respective biases, ensemble biases in runoff can go unchecked because runoff is not constrained by any observations in a typical GRACE/-FO DA framework, potentially leading to erroneous conclusions. For example, in a model that underestimates baseflow, increases in baseflow from GRACE/-FO DA may give an appearance that the improvement is due to GRACE/-FO DA, while, in fact, the increased runoff is caused by ensemble biases. Therefore, it is crucial to evaluate ensemble biases in fluxes, particularly when they are the primary focus for improvement.
5.4 Others
The effects of the issues described above are unevenly distributed across different climates and regions, often with larger impacts in wet climates than in dry climates (Li et al., 2019). This is likely since ensemble spreads in wetter conditions can be increased through perturbation errors added to precipitation while they remain small in dry climates due to lack of rainfall (Sect. 3.4). Ensemble spreads may be strongly affected by model physics as well. For a model with a strong tendency for ET, ensemble spreads may not be able to sustain in a dry climate where all available soil moisture is used for ET quickly. Conversely, when a modeled state has minimal interaction with other processes, ensemble spreads may grow unchecked with time if perturbation errors are added continuously. This is especially true for groundwater in a dry climate where baseflow and the capillary rise is naturally low, leading to weak groundwater dynamics.
In addition to the non-Gaussian behaviors discussed above, GRACE/-FO DA (and most other DA) for state updating violates the water balance (Li et al., 2012; Schumacher, 2016) to some extent, which is the price to be paid to nudging a model run closer to real observations. Techniques exist to mitigate this effect. Furthermore, model skill (e.g., bias) in simulating fluxes may be anti-correlated with skill in simulating states (Sect. 4.2), because GRACE/-FO DA updates may push TWS in a direction opposite to what would have been needed to treat the underlying errors in the simulated fluxes (Schulze et al., 2024). This is a motivation for developing new DA techniques that adjust TWS while maintaining water balance by adjusting the fluxes instead of the states (Girotto et al., 2021).
All DA frameworks require a faithful representation of forecast and observation errors. For GRACE/-FO DA this means estimates of the error variances and spatial covariances for TWSA maps (Sects. 2.2 and 3.4). However, even after two decades of analyzing GRACE/-FO observations, the error structure of Level-2 SH data products is not well understood, and in particular, error correlations due to mis-modeled short-term mass variations (i.e. aliasing errors) are not represented in current approaches. The reason for this is that on one hand we have only few independent datasets to calibrate GRACE/-FO error representations, and on the other hand it appears challenging to quantify the errors in Level-2 and -3 data (including mascon representations) that are injected via incorrect atmospheric and oceanic non-tidal and tidal background models (Shihora et al., 2024), and that seem to dominate over satellite instrument errors. We suggest that for future missions full error covariance matrix representations becomes part of the official products, even if it would represent only the dominating patterns of error correlation in space. We notice that several groups have assessed the propagation of background model errors through Monte Carlo simulation (Flechtner et al., 2016); however it would be desirable if (i) background model ensembles used in these approaches would seek to span complete understanding of model errors (i.e. rely on independent datasets and reanalyses), and (ii) such efforts aim to provide full-rank error variance-covariance matrices to the community instead of the rank-defect sample covariance matrices.
Recent research discussed in Sect. 3 primarily focuses on current DA strategies, whereas Sect. 5 highlights the associated challenges with some suggestions to advance DA algorithms via e.g. multi-sensor DA and better water balance closure. This section focuses on potential future directions that can open up through new satellite gravimetry observations or data products.
6.1 Key strategies to increase the DA value of gravity data
To address the challenges in GRACE/-FO DA using currently available tools and data, we propose two key strategies. First, further enhancing the spatial resolution of GRACE/-FO products prior to DA could greatly benefit the use of TWSA retrievals. Beyond relying on future higher-resolution gravity missions, the most intuitive approaches remain to downscale GRACE/-FO products within dynamic DA schemes (Girotto et al., 2021; Forman and Reichle, 2013; Reichle et al., 2014), using auxiliary datasets and advanced statistical methods (Vishwakarma et al., 2021b; Tourian et al., 2023) or deep learning techniques (Seyoum et al., 2019; Foroumandi et al., 2023; Gou and Soja, 2024). Perhaps a combination of deep learning and dynamic downscaling in a hybrid DA scheme offers new perspectives. Second, improving the hydrological consistency in GRACE/-FO DA is essential. On the one hand, further development of DA systems is needed, including refined error assumptions that better describe the relevant variables, enforced physical constraints on water balance closure, improved representation of uncertainties, and reduced bias for both model and observations. For instance, Gou and Soja (2024) introduced a self-supervised DA workflow that ensures water balance closure in small basins while preserving large-scale accuracy inherited from the GRACE/-FO measurements. On the other hand, domain knowledge of the underlying drivers of GRACE/-FO signals can help in parameterizing relevant processes in models, enabling more accurate water redistribution across storage components, which in turn enhances the estimates of relevant fluxes. This includes better representation of lake, reservoir, and glacier dynamics as well as anthropogenic water activities. Alternatively, regularly updated correction datasets can be developed to remove signals in TWSA observations that cannot be represented by GHMs or LSMs.
To mitigate ensemble biases associated with non-Gaussian behaviors of hydrological variables, we recommend tuning the model prior to GRACE/-FO DA so that simulated TWS is better aligned with GRACE/-FO observations. This step reduces the need for large perturbation errors, and consequently, minimizes ensemble biases. Tuning model parameters to reduce systematic errors is also critical for improving the performance of EnKF based approaches, which are designed to correct random errors rather than systematic errors; in addition, it helps reduce mass imbalances caused by large DA updates. As noted earlier, the particle filtering method (Crisan, 2001) is not restricted to specific statistical distributions and therefore can address the non-Gaussian issue; however, a large ensemble size is needed to effectively represent a highly skewed distribution. Similarly, transforming functions have been used for non-Gaussian data assimilation within a 3-D variational method (Van Loon and Fletcher, 2023) and their application in variants of the EnKF warrants future investigation.
Recent years have seen substantial progress in applying ML within DA systems for numerical models, particularly in geophysical applications such as improving regional climate simulations (Bocquet, 2023; He et al., 2023; Keller and Potthast, 2024). GRACE/-FO DA frameworks can benefit from ML at several stages of the assimilation workflow (Fig. 5). As described above, ML can support observation preprocessing, including gap filling and spatial downscaling of coarse TWSA fields. ML can potentially act as a surrogate observation operator and might also support the model update step by learning hydrologically meaningful distributions of DA increments across storage compartments. More intrusive uses involve learning from the state corrections produced during assimilation, enabling targeted model-error correction at each forecast step (Arcucci et al., 2021). Finally, the DA algorithms themselves (e.g., EnKF variants) can benefit from ML – for instance, by automatically correcting the ensemble spread through ML-based adaptive inflation or improving covariance structure by ML-based localization schemes – and may even be replaced by ML architectures designed to emulate full sequential filtering. However, these potential benefits need to be balanced against the substantial computational cost of training such models. In several meteorological applications, the training effort can exceed the runtime savings unless transfer learning strategies are used to adapt pre-trained models to new domains or conditions. Similar considerations are expected for GRACE/-FO DA, where the limited length of the observational record poses additional challenges for generating suitable training data.
6.2 Low latency TWSA product DA
As noted previously, assimilating standard GRACE/-FO products, which are delivered weeks to months after observation, limits their value for near-real-time DA applications. Low-latency gravity products would offer a solution despite higher errors from automated processing. Latency is influenced by the observational averaging window, with a monthly mean product having a minimum latency of two weeks, assuming an effective date at mid-month. Alternatives, such as 21 d rolling window products updated daily or weekly (Sakumura et al., 2016), reduce latency to as little as 11 d while enabling more frequent updates in the DA scheme. However, since each rolling window field shares data with previous and subsequent fields, assimilating all fields without properly increasing observational uncertainty may over-constrain the model (i.e., put too much weight on the observations relative to the simulated states). Additionally, shorter averaging windows improve latency but degrade the effective spatial resolution of TWSA retrievals, which can negatively impact DA accuracy (Sect. 3.3). Gouweleeuw et al. (2018) and Retegui-Schiettekatte et al. (2025) demonstrated that daily GRACE solutions from a Kalman filter approach could resolve major flood events in the Ganges-Brahmaputra delta, but these are among the largest signals that we observe worldwide. Low latency products will be essential for optimizing the value of satellite gravimetry DA for operational applications, but only if these issues are carefully managed. One option could be integrating TWSA forecast approaches on the basis of ML with data assimilation (Li et al., 2024, 2025).
6.3 Line-of-sight gravity measurement DA
Another approach to addressing the limited spatial resolution is the direct DA of higher-frequency LGD data into GHMs and LSMs (Soltani et al., 2021). This approach offers the potential for improved temporal resolution and a deeper understanding of rapid mass transport processes such as floods, droughts and human water management activities (Han et al., 2005, 2006; Banerjee and Kumar, 2019). In contrast to monthly Level-2 or -3 products, LGD measurements capture instantaneous changes in gravitational acceleration between the two GRACE/-FO satellites as they orbit Earth (Khaki et al., 2023). Thus, LGD data provide information on gravity variations at much higher frequencies, potentially revealing submonthly mass changes. Directly assimilating LGD measurements also reduces temporal aliasing, leading to a more accurate representation of hydrological processes in models. Furthermore, the high temporal resolution of LGD measurements opens up possibilities for near-real-time applications, such as flood forecasting and drought monitoring. In a recent study, Khaki et al. (2023) presented a new methodology based on the direct assimilation of LGD measurements from the GRACE-FO laser ranging interferometer (LRI) into an LSM using the EnKF. They showed that the new approach not only offers improved accuracy when compared to independent measurements but also performs better in capturing high-frequency water storage variations imposed by submonthly climatic events due to its higher number of DA cycles within a month.
Despite the potential benefits, assimilating LGD measurements presents challenges, for example, these measurements are inherently noisier. Data processing and noise reduction are crucial to extracting meaningful geophysical signals and efficiently incorporating GRACE/-FO daily products into the models (Khaki et al., 2023). Additionally, assimilating high-frequency LGD measurements demands significant computational resources, necessitating efficient DA algorithms. Furthermore, GHMs and LSMs need to be sophisticated enough to represent the relevant processes at those scales, potentially requiring refined model structures, improved parameterizations, and the incorporation of additional data sources. Nevertheless, there have been recent attempts that have demonstrated the potential of assimilating LGD measurements for various applications, including hydrological modeling and ongoing research for ice mass balance assessment, and earthquake and volcano monitoring.
6.4 GRACE-C, NGGM and future gravimetry missions
GRACE-FO, which launched in 2018, is unlikely to equal GRACE in providing useful observations for 15 years. Errors associated with the accelerometer data transplant (which mitigates the impact of a faulty accelerometer on one of the two GRACE-FO spacecraft) will be exacerbated as the satellites’ altitudes decay during the current solar maximum (Wiese et al., 2022; Harvey et al., 2022). Larger errors will pose a new challenge for DA. Fortunately, the NASA/German GRACE Continuity (GRACE-C) mission, with observational capability nearly identical to its predecessors (Wiese et al., 2022), is planned to launch in 2029. This should enable continuity of satellite gravimetry observations through at least 2034 (given a 5-year design lifetime) or up to a decade longer.
Further, ESA's Next Generation gravity Mission (NGGM, Haagmans et al., 2020; Massotti et al., 2021; Cesare et al., 2022) is currently in phase B development and foreseen for launch in 2032, most likely in an inclined orbit, complementing GRACE-C’s polar orbit to what is known as “Bender constellation”. NGGM will be again equipped with a laser ranging instrument and electrostatic accelerometers.
Combining measurements from the two missions, as proposed by the ESA/NASA MAss Change and Geosciences International Constellation (MAGIC) Working Group (Daras et al., 2024), would enable substantial improvements in spatial and/or temporal resolution relative to a single pair gravimetry mission with an equivalent level of uncertainty (Heller-Kaikov et al., 2023; Daras et al., 2024; Kusche et al., 2025). This is expected due to potentially reduced effects of temporal aliasing in the Level-2 data generation, and thus potentially being less reliant on background models and post-processing methods. If MAGIC comes to fruition, it could thus help to overcome some of the DA issues described earlier, including tradeoffs between latency and accuracy and degradation of model output where high-resolution TWS signals exist. Experiments will be needed to confirm that assimilating a single MAGIC product generates better results than separately assimilating GRACE-C and NGGM products.
6.5 SLR-based TWSA product DA
GRACE was the first satellite mission dedicated to measuring the time-varying gravity field (Wahr et al., 1998), but ground-to-satellite laser ranging (SLR) measurements captured low-degree temporal variations in the gravity field as far back as 1975 (Cox and Chao, 2002; Flechtner et al., 2021). By 1993, SLR satellites and observations were sufficient to derive mass change time series with subcontinental scale resolution. At continental to global scales, SLR based TWSA time series compare favorably with those from GRACE/-FO (Rodell et al., 2024). Assimilating SLR data into a LSM would entail the same challenges as GRACE/-FO DA but greatly magnified due to the extremely coarse spatial resolution.
Simulations suggest (Najder et al., 2023) that adding new SLR satellites could help in improving the accuracy of low-degree spherical harmonic solutions and remove error correlation with Earth Orientation Parameters (EOP) and site coordinates, however, this would likely not dramatically improve resolution. Also, alternative approaches such as fitting GRACE/-FO-derived TWSA Empirical Orthogonal Functions (EOFs) directly to SLR ranges showed a promising effect on resolution (Löcher and Kusche, 2021; Cheng and Ries, 2023), but they rely on the hypothesis that the main spatial patterns of TWSA variability did not change significantly during past decades. Nevertheless, considering that most models struggle to simulate large-scale TWS changes accurately and consistently across global, multi-decadal timescales (Scanlon et al., 2018), the effort may be worthwhile if done properly.
6.6 TWS products based on inversion of GNSS time series
Time series of GNSS vertical land motion have been used for validating GRACE/-FO-derived TWSA products as well as DA-derived TWSA maps (Springer et al., 2019; Gerdener et al., 2023). Observed vertical land motion can be related to mass redistribution data through elastic loading theory and assumptions on reference frame realization (van Dam and Wahr, 1998; Blewitt, 2003). Various regional and global TWSA datasets have been derived experimentally from GNSS network or Precise Point Positioning (PPP) timeseries (see review in White et al., 2022), but this approach suffers usually from heterogeneous station density and it is challenging to resolve loading signals beyond the seasonal cycle (Rietbroek et al., 2014). It has been further suggested that combining GNSS vertical land motion with InSAR and GRACE/-FO data enables one to isolate groundwater decline and recharge from TWSA (Carlson et al., 2024) in an inverse approach. Investigations would be required to understand if GNSS and InSAR data could be useful in joint GRACE/-FO DA systems.
The growing number of GRACE/-FO DA studies reflects the increasing interest in these frameworks for a wide range of applications, but it also reveals a variety of methodological choices and a lack of coordinated direction. This paper compiled insights from existing studies and discussed the strengths and limitations of different approaches, with the aim of providing best practice recommendations for GRACE/-FO DA. In summary, we have identified key methodological components that require further standardization and community consensus:
-
Model and process description including error modeling. Successful GRACE/-FO DA depends, to some extent, on the physical realism of the underlying model. Although GRACE/-FO DA can introduce water storage signals that are not explicitly represented by numerical models – such as those from groundwater abstraction – doing so without corresponding process representation may lead to imbalances or degradation of other model variables. Therefore, it is essential to explicitly incorporate key anthropogenic processes into the model in order to fully exploit the information provided by GRACE/-FO observations. Additionally, providing a realistic representation of model forecast uncertainty, ideally informed by prior sensitivity studies, is crucial, particularly for the vertical disaggregation of GRACE/-FO signals across storage compartments. Most current GRACE–FO DA systems rely on Gaussian assumptions, which can restrict the representation of skewed or heavy tailed uncertainties in water storage dynamics, so future work should develop more flexible assimilation approaches that allow advanced statistical descriptions of errors, including non Gaussian methods.
-
GRACE/-FO postprocessing. Gridded TWSA observations obtained from either SH or mascon solutions need to be carefully corrected for geophysical signals that are not represented in the GHMs and LSMs prior to DA – a standard correction dataset is still missing. All GRACE/-FO products require bias correction, at least by aligning the long-term mean with the model. Depending on the application, this may also involve matching higher-order statistical moments or applying multiplicative gain factors to restore signal loss introduced during post-processing. Where possible, spatially distributed observation errors – ideally derived from full covariance matrices – should be accounted for. With upcoming missions such as GRACE-C and NGGM, the availability of standardized Level-3 products and reliable error estimates is expected to enhance consistency in postprocessing.
-
DA strategy including algorithms and tuning. In terms of the assimilation algorithm, EnKF and EnKS are typically used, and square root variants are generally preferred due to their enhanced numerical robustness. Localization remains essential in GRACE/-FO DA, particularly for higher-resolution observation grids. Furthermore, spatial correlations between observations should be explicitly considered. In order to preserve spatial detail and enable effective horizontal disaggregation, it is preferable to compute innovations at the resolution of the observations. The state vector should include all storage compartments targeted for the vertical disaggregation of GRACE/-FO observations. Currently, it is standard practice to assimilate monthly products. When temporally downscaled products are used for specific applications, careful attention should be paid to error propagation and to potential issues arising from strong temporal correlations in the downscaled fields. Finally, assimilation increments are best applied by rewinding and reintegrating the model over the same month again to maintain temporal consistency – though this may become less critical with the improved temporal resolution of future mission products.
While past studies offer valuable insights, future work should focus on establishing a set of standards to make GRACE/-FO DA experiments more comparable, reproducible and interpretable, so that DA results can clearly be attributed to signals in the water cycle rather than to differences in methodology. Firstly, we propose defining a standardized benchmark experiment for GRACE/-FO DA. This benchmark should specify the GRACE/-FO data products and associated error assumptions, study area(s), meteorological forcing data, LSMs or GHMs, error modeling approaches, and assimilation strategies. It should be designed to isolate and quantify the impact of each of these components on the DA results. Second, the community must agree on a core set of performance metrics and validation data sets. This includes not only comparison to in situ observations but also ensemble spread diagnostics, water balance checks, and analysis of assimilation increments. This could be supported by community diagnostics following the example of the Earth System Model Evaluation Tool (ESMValToo). Third, we urge the formation of an intercomparison initiative similar to the Land Surface, Snow and Soil Moisture Model Intercomparison Project (LS3MIP), to systematically test and compare GRACE/-FO DA systems. Such an effort, potentially hosted under the umbrella of, e.g, the Global Energy and Water Exchanges (GEWEX) program, would provide a controlled, transparent framework for evaluating the influence of key choices in data, models, and methods through multi-group collaboration.
| Term/Acronym | Definition |
| 3D-Var | Three-dimensional variational data assimilation: adjusts the model state at a single time step by minimizing a cost function combining background and observations. |
| 4D-Var | Four-dimensional variational data assimilation: adjusts initial conditions over a time window to match observations distributed in time, minimizing a cost function subject to model dynamics. |
| Analysis state | The model state after assimilation, obtained by optimally combining the background state and observations. |
| Background state | The model state prior to assimilation, representing the best estimate of the system before incorporating observations. |
| Bias correction | Adjustments applied to model or observations to remove systematic differences. |
| DA | Data Assimilation: combining model predictions and observations while accounting for uncertainties. |
| EnKF | Ensemble Kalman Filter: sequential DA using an ensemble to estimate state and error covariances. |
| EnKS | Ensemble Kalman Smoother: updates states over a time window using past and future observations to improve earlier estimates. For GRACE/GRACE-FO TWSA assimilation, the smoothing window is typically one month, meaning the monthly observation is used to redistribute the increment across the days of that month for improved temporal consistency. |
| Error covariance matrix | Represents uncertainties in the background model and/or observations; used to weight contributions in DA. |
| Filter | Sequential DA method updating the state at observation times. |
| Hybrid methods | Data assimilation approaches combining ensemble-based and variational techniques to leverage the advantages of both. |
| Increment | Adjustment applied to the model state computed by the DA algorithm. |
| Innovation | Difference between observations and model-predicted observations. |
| Inflation | A technique to artificially increase the ensemble spread in sequential DA, compensating for underestimation of uncertainties due to finite ensemble size or model errors. |
| Localization | Limits the influence of observations to nearby model grid points to reduce spurious correlations. |
| Observation operator (ℋ) | Maps model state variables to observation space for comparison with observations. |
| Particle Filter | Nonlinear, non-Gaussian DA method using a weighted ensemble (particles) to represent the probability distribution of the state. |
| Rewind/Re-run | Strategy distributing monthly increments across previous days to improve temporal consistency. |
No data sets were used in this article.
A.S. developed the paper structure and organized the writing process. All co-authors contributed to the shaping of the paper's contents and the writing and editing of the paper. Final editing was performed by G.DL., J.K., M.R., and A.S. All authors contributed to the article and approved the submitted version.
The contact author has declared that none of the authors has any competing interests.
Publisher's note: Copernicus Publications remains neutral with regard to jurisdictional claims made in the text, published maps, institutional affiliations, or any other geographical representation in this paper. The authors bear the ultimate responsibility for providing appropriate place names. Views expressed in the text are those of the authors and do not necessarily reflect the views of the publisher.
Y.E., J.K., and A.S. acknowledge funding by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) within the CRC DETECT (DFG – SFB 1502/1-2022 – Projektnummer: 450058266). J.K and H.G. acknowledges funding from DFG within the research unit GlobalCDA (KU1207/26-1) and from the “NGGM and MAGIC Science and Applications Impact Study” ESA Contract No. 4000145265/24/NL/SC, funded by the European Space Agency. G.D.L. acknowledges Belspo EO4Peat (SR/00/414). M.R. and B.L. acknowledge funding from NASA's GRACE-FO Science Team. M.S. acknowledges funding by VILLUM FONDEN under research grant number VIL60779. We are deeply grateful to Armin Corbin and Bernd Uebbing for providing an external perspective on our manuscript and offering valuable, constructive feedback. We also sincerely thank the two anonymous reviewers for their valuable feedback, which greatly improved this paper. This manuscript originated from a technical workshop on GRACE/GRACE-FO data assimilation into land surface and hydrological models, held online in January 2024. The workshop brought together several research groups working on this topic to foster a shared understanding (https://sfb1502.de/news-events/events/events-archive/grace-fo-workshop-org, last access: 10 December 2025).
This research has been supported by the Deutsche Forschungsgemeinschaft (CRC DETECT (grant no. DFG – SFB 1502/1-2022 – Projektnummer: 450058266) and research unit GlobalCDA (KU1207/26-1)), the European Space Agency (grant no. 4000145265/24/NL/SC), the National Aeronautics and Space Administration (GRACE-FO Science Team), the Villum Fonden (grant no. VIL60779), and Belspo EO4Peat (grant no. SR/00/414).
This paper was edited by Markus Hrachowitz and reviewed by two anonymous referees.
A, G., Wahr, J., and Zhong, S.: Computations of the viscoelastic response of a 3-D compressible Earth to surface loading: an application to Glacial Isostatic Adjustment in Antarctica and Canada, Geophysical Journal International, 192, 557–572, https://doi.org/10.1093/gji/ggs030, 2012. a
Albergel, C., Munier, S., Leroux, D. J., Dewaele, H., Fairbairn, D., Barbu, A. L., Gelati, E., Dorigo, W., Faroux, S., Meurey, C., Le Moigne, P., Decharme, B., Mahfouf, J.-F., and Calvet, J.-C.: Sequential assimilation of satellite-derived vegetation and soil moisture products using SURFEX_v8.0: LDAS-Monde assessment over the Euro-Mediterranean area, Geoscientific Model Development, 10, 3889–3912, https://doi.org/10.5194/gmd-10-3889-2017, 2017. a
Anderson, J. L.: An adaptive covariance inflation error correction algorithm for ensemble filters, Tellus A: Dynamic Meteorology and Oceanography, 59, 210–224, https://doi.org/10.1111/j.1600-0870.2006.00216.x, 2007. a
Anderson, J. L. and Anderson, S. L.: A Monte Carlo Implementation of the Nonlinear Filtering Problem to Produce Ensemble Assimilations and Forecasts, Monthly Weather Review, 127, 2741–2758, https://doi.org/10.1175/1520-0493(1999)127<2741:AMCIOT>2.0.CO;2, 1999. a
Arciniega-Esparza, S., Hernández-Espriú, J. A., Salinas-Calleros, G., Birkel, C., and Sanchez, R.: Assessing hydrological drought propagation through assimilation of GRACE for groundwater storage anomalies modelling in northeastern Mexico, Journal of Hydrology, 661, 133826, https://doi.org/10.1016/j.jhydrol.2025.133826, 2025. a
Arcucci, R., Zhu, J., Hu, S., and Guo, Y.-K.: Deep Data Assimilation: Integrating Deep Learning with Data Assimilation, Applied Sciences, 11, 1114, https://doi.org/10.3390/app11031114, 2021. a
Baatz, R., Hendricks Franssen, H. J., Euskirchen, E., Sihi, D., Dietze, M., Ciavatta, S., Fennel, K., Beck, H., De Lannoy, G., Pauwels, V. R. N., Raiho, A., Montzka, C., Williams, M., Mishra, U., Poppe, C., Zacharias, S., Lausch, A., Samaniego, L., Van Looy, K., Bogena, H., Adamescu, M., Mirtl, M., Fox, A., Goergen, K., Naz, B. S., Zeng, Y., and Vereecken, H.: Reanalysis in Earth System Science: Toward Terrestrial Ecosystem Reanalysis, Reviews of Geophysics, 59, e2020RG000715, https://doi.org/10.1029/2020RG000715, 2021. a
Bahrami, A., Goïta, K., Magagi, R., Davison, B., Razavi, S., Elshamy, M., and Princz, D.: Data assimilation of satellite-based terrestrial water storage changes into a hydrology land-surface model, Journal of Hydrology, 597, 125744, https://doi.org/10.1016/j.jhydrol.2020.125744, 2021. a, b, c, d, e, f
Balsamo, G., Albergel, C., Beljaars, A., Boussetta, S., Brun, E., Cloke, H., Dee, D., Dutra, E., Muñoz-Sabater, J., Pappenberger, F., de Rosnay, P., Stockdale, T., and Vitart, F.: ERA-Interim/Land: a global land surface reanalysis data set, Hydrology and Earth System Sciences, 19, 389–407, https://doi.org/10.5194/hess-19-389-2015, 2015. a
Banerjee, C. and Kumar, D. N.: Integration of GRACE Data for Improvement of Hydrological Models, in: Hydrology in a Changing World: Challenges in Modeling, edited by Singh, S. K. and Dhanya, C., Springer Water, Springer International Publishing, Cham, 1–22, ISBN 978-3-030-02197-9, https://doi.org/10.1007/978-3-030-02197-9_1, 2019. a
Benke, K. K., Lowell, K. E., and Hamilton, A. J.: Parameter uncertainty, sensitivity analysis and prediction error in a water-balance hydrological model, Mathematical and Computer Modelling, 47, 1134–1149, https://doi.org/10.1016/j.mcm.2007.05.017, 2008. a
Berry, T. and Harlim, J.: Correcting biased observation model error in data assimilation, Monthly Weather Review, 145, 2833–2853, https://doi.org/10.1175/MWR-D-16-0428.1, 2017. a
Blewitt, G.: Self-consistency in reference frames, geocenter definition, and surface loading of the solid Earth, Journal of Geophysical Research: Solid Earth, 108, https://doi.org/10.1029/2002JB002082, 2003. a
Bocquet, M.: Surrogate modeling for the climate sciences dynamics with machine learning and data assimilation, Frontiers in Applied Mathematics and Statistics, 9, https://doi.org/10.3389/fams.2023.1133226, 2023. a
Carlson, G., Werth, S., and Shirzaei, M.: A novel hybrid GNSS, GRACE, and InSAR joint inversion approach to constrain water loss during a record-setting drought in California, Remote Sensing of Environment, 311, 114303, https://doi.org/10.1016/j.rse.2024.114303, 2024. a
Caron, L., Ivins, E., Larour, E., Adhikari, S., Nilsson, J., and Blewitt, G.: GIA model statistics for GRACE hydrology, cryosphere, and ocean science, Geophysical Research Letters, 45, 2203–2212, https://doi.org/10.1002/2017GL076644, 2018. a
Cesare, S., Dionisio, S., Saponara, M., Bravo-Berguño, D., Massotti, L., Teixeira da Encarnação, J., and Christophe, B.: Drag and Attitude Control for the Next Generation Gravity Mission, Remote Sensing, 14, https://doi.org/10.3390/rs14122916, 2022. a
Chen, J., Wilson, C., Li, J., and Zhang, Z.: Reducing leakage error in GRACE-observed long-term ice mass change: a case study in West Antarctica, Journal of Geodesy, 89, 925–940, https://doi.org/10.1007/s00190-015-0824-2, 2015. a
Chen, J., Cazenave, A., Dahle, C., Llovel, W., Panet, I., Pfeffer, J., and Moreira, L.: Applications and Challenges of GRACE and GRACE Follow-On Satellite Gravimetry, Surveys in Geophysics, 43, 305–345, https://doi.org/10.1007/s10712-021-09685-x, 2022. a
Chen, W., Huang, C., and Yang, Z.-L.: More severe drought detected by the assimilation of brightness temperature and terrestrial water storage anomalies in Texas during 2010–2013, Journal of Hydrology, 603, 126802, https://doi.org/10.1016/j.jhydrol.2021.126802, 2021. a
Cheng, M. and Ries, J.: C20 and C30 Variations From SLR for GRACE/GRACE-FO Science Applications, Journal of Geophysical Research: Solid Earth, 128, e2022JB025459, https://doi.org/10.1029/2022JB025459, 2023. a, b
Chi, H., Seo, H., and Kim, Y.: Hydrological trends captured by assimilating GRACE total water storage data into the CLM5-BGC model, Journal of Hydrology, 629, 130527, https://doi.org/10.1016/j.jhydrol.2023.130527, 2024. a, b, c, d
Collischonn, W., Allasia, D., Da Silva, B. C., and Tucci, C. E.: The MGB-IPH model for large-scale rainfall–runoff modelling, Hydrological Sciences Journal, 52, 878–895, 2007. a
Condon, L. E., Kollet, S., Bierkens, M. F. P., Fogg, G. E., Maxwell, R. M., Hill, M. C., Fransen, H. H., Verhoef, A., Van Loon, A. F., Sulis, M., and Abesser, C.: Global Groundwater Modeling and Monitoring: Opportunities and Challenges, Water Resources Research, 57, e2020WR029500, https://doi.org/10.1029/2020WR029500, 2021. a
Cox, C. M. and Chao, B. F.: Detection of a Large-Scale Mass Redistribution in the Terrestrial System Since 1998, Science, https://doi.org/10.1126/science.1072188, 2002. a
Crisan, D.: Particle Filters– A Theoretical Perspective, in: Sequential Monte Carlo Methods in Practice, edited by Doucet, A., Freitas, N., and Gordon, N., Springer New York, New York, NY, 17–41, ISBN 9781441928870, 9781475734379, https://doi.org/10.1007/978-1-4757-3437-9_2, 2001. a, b
Daras, I., March, G., Pail, R., Hughes, C. W., Braitenberg, C., Güntner, A., Eicker, A., Wouters, B., Heller-Kaikov, B., Pivetta, T., and Pastorutti, A.: Mass-change And Geosciences International Constellation (MAGIC) expected impact on science and applications, Geophysical Journal International, 236, 1288–1308, https://doi.org/10.1093/gji/ggad472, 2024. a, b
De Lannoy, G. J. M., Houser, P. R., Verhoest, N. E. C., Pauwels, V. R. N., and Gish, T. J.: Upscaling of point soil moisture measurements to field averages at the OPE3 test site, Journal of Hydrology, 343, 1–11, https://doi.org/10.1016/j.jhydrol.2007.06.004, 2007. a
De Lannoy, G. J. M., de Rosnay, P., and Reichle, R. H.: Soil Moisture Data Assimilation, in: Handbook of Hydrometeorological Ensemble Forecasting, edited by Duan, Q., Pappenberger, F., Thielen, J., Wood, A., Cloke, H. L., and Schaake, J. C., Springer, Berlin, Heidelberg, 1–43, ISBN 9783642404573, https://doi.org/10.1007/978-3-642-40457-3_32-1, 2016. a
De Lannoy, G. J. M., Bechtold, M., Albergel, C., Brocca, L., Calvet, J.-C., Carrassi, A., Crow, W. T., de Rosnay, P., Durand, M., Forman, B., Geppert, G., Girotto, M., Hendricks Franssen, H.-J., Jonas, T., Kumar, S., Lievens, H., Lu, Y., Massari, C., Pauwels, V. R. N., Reichle, R. H., and Steele-Dunne, S.: Perspective on satellite-based land data assimilation to estimate water cycle components in an era of advanced data availability and model sophistication, Frontiers in Water, 4, https://doi.org/10.3389/frwa.2022.981745, 2022. a
Decharme, B., Martin, E., and Faroux, S.: Reconciling soil thermal and hydrological lower boundary conditions in land surface models, Journal of Geophysical Research: Atmospheres, 118, 7819–7834, 2013. a
Dee, D. P.: Bias and data assimilation, Quarterly Journal of the Royal Meteorological Society, 131, 3323–3343, https://doi.org/10.1256/qj.05.137, 2005. a
Deggim, S., Eicker, A., Schawohl, L., Gerdener, H., Schulze, K., Engels, O., Kusche, J., Saraswati, A. T., van Dam, T., Ellenbeck, L., Dettmering, D., Schwatke, C., Mayr, S., Klein, I., and Longuevergne, L.: RECOG RL01: correcting GRACE total water storage estimates for global lakes/reservoirs and earthquakes, Earth Syst. Sci. Data, 13, 2227–2244, https://doi.org/10.5194/essd-13-2227-2021, 2021. a, b, c
Dorigo, W. A., Scipal, K., Parinussa, R. M., Liu, Y. Y., Wagner, W., de Jeu, R. A. M., and Naeimi, V.: Error characterisation of global active and passive microwave soil moisture datasets, Hydrology and Earth System Sciences, 14, 2605–2616, https://doi.org/10.5194/hess-14-2605-2010, 2010. a
Drusch, M., Wood, E. F., and Gao, H.: Observation operators for the direct assimilation of TRMM microwave imager retrieved soil moisture, Geophysical Research Letters, 32, 2005GL023623, https://doi.org/10.1029/2005GL023623, 2005. a
Döll, P., Hoffmann-Dobrev, H., Portmann, F., Siebert, S., Eicker, A., Rodell, M., Strassberg, G., and Scanlon, B.: Impact of water withdrawals from groundwater and surface water on continental water storage variations, Journal of Geodynamics, 59–60, 143–156, https://doi.org/10.1016/j.jog.2011.05.001, 2012. a
Eicker, A. and Springer, A.: Monthly and sub-monthly hydrological variability: in-orbit validation by GRACE level 1B observations, Journal of Geodesy, 90, 573–584, 2016. a
Eicker, A., Schumacher, M., Kusche, J., Döll, P., and Schmied, H. M.: Calibration/data assimilation approach for integrating GRACE data into the WaterGAP Global Hydrology Model (WGHM) using an ensemble Kalman filter: First results, Surveys in Geophysics, 35, 1285–1309, 2014. a, b, c, d, e, f, g, h
Einarsson, I., Hoechner, A., Wang, R., and Kusche, J.: Gravity changes due to the Sumatra-Andaman and Nias earthquakes as detected by the GRACE satellites: a reexamination, Geophysical Journal International, 183, 733–747, https://doi.org/10.1111/j.1365-246X.2010.04756.x, 2010. a
Ek, M., Mitchell, K., Lin, Y., Rogers, E., Grunmann, P., Koren, V., Gayno, G., and Tarpley, J.: Implementation of Noah land surface model advances in the National Centers for Environmental Prediction operational mesoscale Eta model, Journal of Geophysical Research: Atmospheres, 108, https://doi.org/10.1029/2002JD003296, 2003. a
Evensen, G.: Sequential data assimilation with a nonlinear quasi‐geostrophic model using Monte Carlo methods to forecast error statistics, Journal of Geophysical Research: Oceans, 99, 10143–10162, https://doi.org/10.1029/94JC00572, 1994. a
Evensen, G.: Data Assimilation: The Ensemble Kalman Filter, Springer Berlin Heidelberg, Berlin, Heidelberg, ISBN 9783642037108, 9783642037115, https://doi.org/10.1007/978-3-642-03711-5, 2009. a
Evensen, G., Vossepoel, F. C., and van Leeuwen, P. J.: Localization and Inflation, in: Data Assimilation Fundamentals: A Unified Formulation of the State and Parameter Estimation Problem, edited by Evensen, G., Vossepoel, F. C., and van Leeuwen, P. J., Springer International Publishing, Cham, 111–122, ISBN 9783030967093, https://doi.org/10.1007/978-3-030-96709-3_10, 2022. a
Eyre, J. R.: Observation bias correction schemes in data assimilation systems: a theoretical study of some of their properties, Quarterly Journal of the Royal Meteorological Society, 142, 2284–2291, https://doi.org/10.1002/qj.2819, 2016. a
Fairbairn, D., De Rosnay, P., and Weston, P.: Evaluation of an Adaptive Soil Moisture Bias Correction Approach in the ECMWF Land Data Assimilation System, Remote Sensing, 16, 493, https://doi.org/10.3390/rs16030493, 2024. a
Felsberg, A., Lannoy, G. J. M. D., Girotto, M., Poesen, J., Reichle, R. H., and Stanley, T.: Global Soil Water Estimates as Landslide Predictor: The Effectiveness of SMOS, SMAP, and GRACE Observations, Land Surface Simulations, and Data Assimilation, Journal of Hydrometeorology, 22, 1065–1084, https://doi.org/10.1175/JHM-D-20-0228.1, 2021. a
Flechtner, F., Neumayer, K.-H., Dahle, C., Dobslaw, H., Fagiolini, E., Raimondo, J.-C., and Güntner, A.: What Can be Expected from the GRACE-FO Laser Ranging Interferometer for Earth Science Applications?, Surveys in Geophysics, 37, 453–470, https://doi.org/10.1007/s10712-015-9338-y, 2016. a
Flechtner, F., Reigber, C., Rummel, R., and Balmino, G.: Satellite Gravimetry: A Review of Its Realization, Surveys in Geophysics, 42, 1029–1074, https://doi.org/10.1007/s10712-021-09658-0, 2021. a
Forman, B. A. and Reichle, R. H.: The spatial scale of model errors and assimilated retrievals in a terrestrial water storage assimilation system, Water Resources Research, 49, 7457–7468, https://doi.org/10.1002/2012WR012885, 2013. a, b, c, d
Forman, B. A., Reichle, R. H., and Rodell, M.: Assimilation of terrestrial water storage from GRACE in a snow‐dominated basin, Water Resources Research, 48, 2011WR011239, https://doi.org/10.1029/2011WR011239, 2012. a, b, c, d, e
Forootan, E., Mehrnegar, N., Schumacher, M., Schiettekatte, L. A. R., Jagdhuber, T., Farzaneh, S., Van Dijk, A. I., Shamsudduha, M., and Shum, C.: Global groundwater droughts are more severe than they appear in hydrological models: An investigation through a Bayesian merging of GRACE and GRACE-FO data with a water balance model, Science of The Total Environment, 912, 169476, https://doi.org/10.1016/j.scitotenv.2023.169476, 2024. a
Foroumandi, E., Nourani, V., Jeanne Huang, J., and Moradkhani, H.: Drought monitoring by downscaling GRACE-derived terrestrial water storage anomalies: A deep learning approach, Journal of Hydrology, 616, 128838, https://doi.org/10.1016/j.jhydrol.2022.128838, 2023. a
Gerdener, H.: A global drought monitoring framework using GRACE/-FO data assimilation, Dissertation, Rheinische Friedrich-Wilhelms-Universität Bonn, https://doi.org/10.48565/BONNDOC-438, 2024. a, b, c
Gerdener, H., Kusche, J., Schulze, K., Ghazaryan, G., and Dubovyk, O.: Revising precipitation – water storages – vegetation signatures with GRACE-based data assimilation, Journal of Hydrology, 612, 128096, https://doi.org/10.1016/j.jhydrol.2022.128096, 2022. a, b
Gerdener, H., Kusche, J., Schulze, K., Döll, P., and Klos, A.: The global land water storage data set release 2 (GLWS2.0) derived via assimilating GRACE and GRACE-FO data into a global hydrological model, Journal of Geodesy, 97, 73, https://doi.org/10.1007/s00190-023-01763-9, 2023. a, b, c, d, e, f, g, h, i, j
Getirana, A., Jung, H. C., Arsenault, K., Shukla, S., Kumar, S., Peters‐Lidard, C., Maigari, I., and Mamane, B.: Satellite Gravimetry Improves Seasonal Streamflow Forecast Initialization in Africa, Water Resources Research, 56, e2019WR026259, https://doi.org/10.1029/2019WR026259, 2020a. a, b
Getirana, A., Rodell, M., Kumar, S., Beaudoing, H. K., Arsenault, K., Zaitchik, B., Save, H., and Bettadpur, S.: GRACE Improves Seasonal Groundwater Forecast Initialization over the United States, Journal of Hydrometeorology, 21, 59–71, https://doi.org/10.1175/JHM-D-19-0096.1, 2020b. a, b, c, d, e, f, g, h
Ghobadi‐Far, K., Han, S., McCullough, C. M., Wiese, D. N., Ray, R. D., Sauber, J., Shihora, L., and Dobslaw, H.: Along‐Orbit Analysis of GRACE Follow‐On Inter‐Satellite Laser Ranging Measurements for Sub‐Monthly Surface Mass Variations, Journal of Geophysical Research: Solid Earth, 127, e2021JB022983, https://doi.org/10.1029/2021JB022983, 2022. a
Girotto, M., De Lannoy, G. J., Reichle, R. H., and Rodell, M.: Assimilation of gridded terrestrial water storage observations from GRACE into a land surface model, Water Resources Research, 52, 4164–4183, 2016. a, b, c, d, e, f, g
Girotto, M., De Lannoy, G. J. M., Reichle, R. H., Rodell, M., Draper, C., Bhanja, S. N., and Mukherjee, A.: Benefits and pitfalls of GRACE data assimilation: A case study of terrestrial water storage depletion in India, Geophysical Research Letters, 44, 4107–4115, https://doi.org/10.1002/2017GL072994, 2017. a, b, c, d, e, f, g, h
Girotto, M., Reichle, R. H., Rodell, M., Liu, Q., Mahanama, S., and De Lannoy, G. J. M.: Multi-sensor assimilation of SMOS brightness temperature and GRACE terrestrial water storage observations for soil moisture and shallow groundwater estimation, Remote Sensing of Environment, 227, 12–27, https://doi.org/10.1016/j.rse.2019.04.001, 2019. a, b, c, d, e, f, g, h, i
Girotto, M., Musselman, K. N., and Essery, R. L. H.: Data Assimilation Improves Estimates of Climate-Sensitive Seasonal Snow, Current Climate Change Reports, 6, 81–94, https://doi.org/10.1007/s40641-020-00159-7, 2020. a
Girotto, M., Reichle, R., Rodell, M., and Maggioni, V.: Data Assimilation of Terrestrial Water Storage Observations to Estimate Precipitation Fluxes: A Synthetic Experiment, Remote Sensing, 13, 1223, https://doi.org/10.3390/rs13061223, 2021. a, b
Gorugantula, S. S. and Kambhammettu, B. P.: Sequential downscaling of GRACE products to map groundwater level changes in Krishna river basin, Hydrological Sciences Journal, 1846–1859, https://doi.org/10.1080/02626667.2022.2106142, 2022. a
Gou, J. and Soja, B.: Global high-resolution total water storage anomalies from self-supervised data assimilation using deep learning algorithms, Nature Water, 2, 139–150, https://doi.org/10.1038/s44221-024-00194-w, 2024. a, b, c
Gouweleeuw, B. T., Kvas, A., Gruber, C., Gain, A. K., Mayer-Gürr, T., Flechtner, F., and Güntner, A.: Daily GRACE gravity field solutions track major flood events in the Ganges–Brahmaputra Delta, Hydrology and Earth System Sciences, 22, 2867–2880, https://doi.org/10.5194/hess-22-2867-2018, 2018. a
Gruber, A., Su, C. H., Zwieback, S., Crow, W., Dorigo, W., and Wagner, W.: Recent advances in (soil moisture) triple collocation analysis, International Journal of Applied Earth Observation and Geoinformation, 45, 200–211, https://doi.org/10.1016/j.jag.2015.09.002, 2016. a
Haagmans, R., Siemes, C., Massotti, L., Carraz, O., and Silvestrin, P.: ESA’s next-generation gravity mission concepts, Rendiconti Lincei. Scienze Fisiche e Naturali, 31, S15–S25, 2020. a
Han, S., Shum, C. K., Jekeli, C., and Alsdorf, D.: Improved estimation of terrestrial water storage changes from GRACE, Geophysical Research Letters, 32, 2005GL022382, https://doi.org/10.1029/2005GL022382, 2005. a
Han, S., Shum, C. K., and Jekeli, C.: Precise estimation of in situ geopotential differences from GRACE low‐low satellite‐to‐satellite tracking and accelerometer data, Journal of Geophysical Research: Solid Earth, 111, 2005JB003719, https://doi.org/10.1029/2005JB003719, 2006. a
Harvey, N., McCullough, C. M., and Save, H.: Modeling GRACE-FO accelerometer data for the version 04 release, Advances in Space Research, 69, 1393–1407, https://doi.org/10.1016/j.asr.2021.10.056, 2022. a
He, X., Li, Y., Liu, S., Xu, T., Chen, F., Li, Z., Zhang, Z., Liu, R., Song, L., Xu, Z., Peng, Z., and Zheng, C.: Improving regional climate simulations based on a hybrid data assimilation and machine learning method, Hydrology and Earth System Sciences, 27, 1583–1606, https://doi.org/10.5194/hess-27-1583-2023, 2023. a
Heller-Kaikov, B., Pail, R., and Daras, I.: Mission design aspects for the mass change and geoscience international constellation (MAGIC), Geophysical Journal International, 235, 718–735, https://doi.org/10.1093/gji/ggad266, 2023. a
Herrera, P. A., Marazuela, M. A., and Hofmann, T.: Parameter estimation and uncertainty analysis in hydrological modeling, WIREs Water, 9, e1569, https://doi.org/10.1002/wat2.1569, 2022. a
Houborg, R., Rodell, M., Li, B., Reichle, R., and Zaitchik, B. F.: Drought indicators based on model‐assimilated Gravity Recovery and Climate Experiment (GRACE) terrestrial water storage observations, Water Resources Research, 48, 2011WR011291, https://doi.org/10.1029/2011WR011291, 2012. a, b, c, d, e, f, g, h
Humphrey, V., Gudmundsson, L., and Seneviratne, S. I.: Assessing Global Water Storage Variability from GRACE: Trends, Seasonal Cycle, Subseasonal Anomalies and Extremes, Surveys in Geophysics, 37, 357–395, https://doi.org/10.1007/s10712-016-9367-1, 2016. a
Humphrey, V., Gudmundsson, L., and Seneviratne, S. I.: A global reconstruction of climate-driven subdecadal water storage variability, Geophysical Research Letters, 44, 2300–2309, 2017. a
Humphrey, V., Rodell, M., and Eicker, A.: Using Satellite-Based Terrestrial Water Storage Data: A Review, Surveys in Geophysics, 44, 1489–1517, https://doi.org/10.1007/s10712-022-09754-9, 2023. a, b
Hunt, B. R., Kostelich, E. J., and Szunyogh, I.: Efficient data assimilation for spatiotemporal chaos: A local ensemble transform Kalman filter, Physica D: Nonlinear Phenomena, 230, 112–126, https://doi.org/10.1016/j.physd.2006.11.008, 2007. a
Jekeli, C.: Alternative methods to smooth the Earth's gravity field, Report No. 327, Reports of the Department of Geodetic Science and Surveying, Ohio State Univ. Columbus, OH, United States, https://ntrs.nasa.gov/citations/19820014947 (last access: 28 January 2026), 1981. a, b
Jensen, L., Eicker, A., Dobslaw, H., Stacke, T., and Humphrey, V.: Long-Term Wetting and Drying Trends in Land Water Storage Derived From GRACE and CMIP5 Models, Journal of Geophysical Research: Atmospheres, 124, 9808–9823, https://doi.org/10.1029/2018JD029989, 2019. a
Jensen, L., Gerdener, H., Eicker, A., Kusche, J., and Fiedler, S.: Observations indicate regionally misleading wetting and drying trends in CMIP6, npj Climate and Atmospheric Science, 7, 1–12, https://doi.org/10.1038/s41612-024-00788-x, 2024. a, b
Jing, W., Zhang, P., and Zhao, X.: A comparison of different GRACE solutions in terrestrial water storage trend estimation over Tibetan Plateau, Scientific Reports, 9, 1765, https://doi.org/10.1038/s41598-018-38337-1, 2019. a
Jung, H. C., Getirana, A., Arsenault, K. R., Kumar, S., and Maigary, I.: Improving surface soil moisture estimates in West Africa through GRACE data assimilation, Journal of Hydrology, 575, 192–201, https://doi.org/10.1016/j.jhydrol.2019.05.042, 2019. a, b, c, d, e
Jyolsna, P., Kambhammettu, B., and Gorugantula, S.: Application of random forest and multi-linear regression methods in downscaling GRACE derived groundwater storage changes, Hydrological Sciences Journal, 66, 874–887, 2021. a
Keller, J. D. and Potthast, R.: AI-based data assimilation: Learning the functional of analysis estimation, arXiv [preprint], https://doi.org/10.48550/arxiv.2406.00390, 2024. a
Khaki, M. and Awange, J.: The application of multi-mission satellite data assimilation for studying water storage changes over South America, Science of The Total Environment, 647, 1557–1572, https://doi.org/10.1016/j.scitotenv.2018.08.079, 2019. a, b, c
Khaki, M., Ait-El-Fquih, B., Hoteit, I., Forootan, E., Awange, J., and Kuhn, M.: A two-update ensemble Kalman filter for land hydrological data assimilation with an uncertain constraint, Journal of Hydrology, 555, 447–462, https://doi.org/10.1016/j.jhydrol.2017.10.032, 2017a. a
Khaki, M., Hoteit, I., Kuhn, M., Awange, J., Forootan, E., van Dijk, A. I. J. M., Schumacher, M., and Pattiaratchi, C.: Assessing sequential data assimilation techniques for integrating GRACE data into a hydrological model, Advances in Water Resources, 107, 301–316, https://doi.org/10.1016/j.advwatres.2017.07.001, 2017b. a, b, c, d, e, f
Khaki, M., Schumacher, M., Forootan, E., Kuhn, M., Awange, J. L., and van Dijk, A. I. J. M.: Accounting for spatial correlation errors in the assimilation of GRACE into hydrological models through localization, Advances in Water Resources, 108, 99–112, https://doi.org/10.1016/j.advwatres.2017.07.024, 2017c. a, b, c, d, e, f, g, h, i
Khaki, M., Ait-El-Fquih, B., Hoteit, I., Forootan, E., Awange, J., and Kuhn, M.: Unsupervised ensemble Kalman filtering with an uncertain constraint for land hydrological data assimilation, Journal of Hydrology, 564, 175–190, https://doi.org/10.1016/j.jhydrol.2018.06.080, 2018a. a, b
Khaki, M., Forootan, E., Kuhn, M., Awange, J., Papa, F., and Shum, C. K.: A study of Bangladesh's sub-surface water storages using satellite products and data assimilation scheme, Science of The Total Environment, 625, 963–977, https://doi.org/10.1016/j.scitotenv.2017.12.289, 2018b. a
Khaki, M., Forootan, E., Kuhn, M., Awange, J., van Dijk, A. I. J. M., Schumacher, M., and Sharifi, M. A.: Determining water storage depletion within Iran by assimilating GRACE data into the W3RA hydrological model, Advances in Water Resources, 114, 1–18, https://doi.org/10.1016/j.advwatres.2018.02.008, 2018c. a, b
Khaki, M., Hamilton, F., Forootan, E., Hoteit, I., Awange, J., and Kuhn, M.: Nonparametric Data Assimilation Scheme for Land Hydrological Applications, Water Resources Research, 54, 4946–4964, https://doi.org/10.1029/2018WR022854, 2018d. a, b, c
Khaki, M., Hoteit, I., Kuhn, M., Forootan, E., and Awange, J.: Assessing data assimilation frameworks for using multi-mission satellite products in a hydrological context, Science of The Total Environment, 647, 1031–1043, https://doi.org/10.1016/j.scitotenv.2018.08.032, 2019. a, b, c
Khaki, M., Hendricks Franssen, H.-J., and Han, S. C.: Multi-mission satellite remote sensing data for improving land hydrological models via data assimilation, Scientific Reports, 10, 18791, https://doi.org/10.1038/s41598-020-75710-5, 2020. a, b, c, d, e
Khaki, M., Han, S., Ghobadi‐Far, K., Yeo, I., and Tangdamrongsub, N.: Assimilation of GRACE Follow‐On Inter‐Satellite Laser Ranging Measurements Into Land Surface Models, Water Resources Research, 59, e2022WR032432, https://doi.org/10.1029/2022WR032432, 2023. a, b, c, d, e, f, g, h, i, j, k, l
Kim, J.-S., Seo, K.-W., Kim, B.-H., Ryu, D., Chen, J., and Wilson, C.: High-Resolution Terrestrial Water Storage Estimates From GRACE and Land Surface Models, Water Resources Research, 60, e2023WR035483, https://doi.org/10.1029/2023WR035483, 2024. a
Kirchgessner, P., Nerger, L., and Bunse-Gerstner, A.: On the Choice of an Optimal Localization Radius in Ensemble Kalman Filter Methods, Monthly Weather Review, 142, 2165–2175, https://doi.org/10.1175/MWR-D-13-00246.1, 2014. a
Klees, R., Zapreeva, E. A., Winsemius, H. C., and Savenije, H. H. G.: The bias in GRACE estimates of continental water storage variations, Hydrology and Earth System Sciences, 11, 1227–1241, https://doi.org/10.5194/hess-11-1227-2007, 2007. a
Klees, R., Liu, X., Wittwer, T., Gunter, B., Revtova, E., Tenzer, R., Ditmar, P., Winsemius, H., and Savenije, H.: A comparison of global and regional GRACE models for land hydrology, Surveys in Geophysics, 29, 335–359, 2008a. a
Klees, R., Revtova, E. A., Gunter, B. C., Ditmar, P., Oudman, E., Winsemius, H. C., and Savenije, H. H. G.: The design of an optimal filter for monthly GRACE gravity models, Geophysical Journal International, 175, 417–432, https://doi.org/10.1111/j.1365-246X.2008.03922.x, 2008b. a
Klos, A., Karegar, M. A., Kusche, J., and Springer, A.: Quantifying Noise in Daily GPS Height Time Series: Harmonic Function Versus GRACE-Assimilating Modeling Approaches, IEEE Geoscience and Remote Sensing Letters, 18, 627–631, https://doi.org/10.1109/LGRS.2020.2983045, 2021. a, b
Koster, R. D. and Mahanama, S. P.: Land surface controls on hydroclimatic means and variability, Journal of Hydrometeorology, 13, 1604–1620, https://doi.org/10.1175/JHM-D-12-050.1, 2012. a
Koster, R. D., Suarez, M. J., Ducharne, A., Stieglitz, M., and Kumar, P.: A catchment‐based approach to modeling land surface processes in a general circulation model: 1. Model structure, Journal of Geophysical Research: Atmospheres, 105, 24809–24822, https://doi.org/10.1029/2000JD900327, 2000. a, b
Kowalczyk, E., Wang, Y., Law, R., Davies, H., McGregor, J., and Abramowitz, G.: The CSIRO Atmosphere Biosphere Land Exchange (CABLE) model for use in climate models and as an offline model, CSIRO Marine and Atmospheric Research Paper, 13, 42, https://doi.org/10.4225/08/58615c6a9a51d, 2006. a
Kumar, S. V., Reichle, R. H., Koster, R. D., Crow, W. T., and Peters-Lidard, C. D.: Role of Subsurface Physics in the Assimilation of Surface Soil Moisture Observations, Journal of Hydrometeorology, 10, 1534–1547, https://doi.org/10.1175/2009JHM1134.1, 2009. a
Kumar, S. V., Reichle, R. H., Harrison, K. W., Peters‐Lidard, C. D., Yatheendradas, S., and Santanello, J. A.: A comparison of methods for a priori bias correction in soil moisture data assimilation, Water Resources Research, 48, 2010WR010261, https://doi.org/10.1029/2010WR010261, 2012. a
Kumar, S. V., Zaitchik, B. F., Peters-Lidard, C. D., Rodell, M., Reichle, R., Li, B., Jasinski, M., Mocko, D., Getirana, A., De Lannoy, G., Cosh, M. H., Hain, C. R., Anderson, M., Arsenault, K. R., Xia, Y., and Ek, M.: Assimilation of Gridded GRACE Terrestrial Water Storage Estimates in the North American Land Data Assimilation System, Journal of Hydrometeorology, 17, 1951–1972, https://doi.org/10.1175/JHM-D-15-0157.1, 2016. a, b, c, d, e, f, g, h, i
Kumar, S. V., Dirmeyer, P. A., Peters-Lidard, C. D., Bindlish, R., and Bolten, J.: Information theoretic evaluation of satellite soil moisture retrievals, Remote Sensing of Environment, 204, 392–400, https://doi.org/10.1016/j.rse.2017.10.016, 2018. a, b
Kusche, J.: Approximate decorrelation and non-isotropic smoothing of time-variable GRACE-type gravity field models, Journal of Geodesy, 81, 733–749, https://doi.org/10.1007/s00190-007-0143-3, 2007. a, b
Kusche, J., Strohmenger, C., Gerdener, H., Uebbing, B., Springer, A., Ewerdwalbesloh, Y., Eicker, A., Braitenberg, C., Pastorutti, A., Pail, R., Zingerle, P., Schlaak, M., Reguzzoni, M., Rossi, L., Migliaccio, F., and Daras, I.: Benefit of MAGIC and multipair quantum satellite gravity missions in Earth science applications, Geophysical Journal International, 242, ggaf195, https://doi.org/10.1093/gji/ggaf195, 2025. a, b
Kvas, A., Behzadpour, S., Ellmer, M., Klinger, B., Strasser, S., Zehentner, N., and Mayer-Gürr, T.: ITSG-Grace2018: Overview and evaluation of a new GRACE-only gravity field time series, Journal of Geophysical Research: Solid Earth, 124, 9332–9344, https://doi.org/10.1029/2019JB017415, 2019. a
Landerer, F. W. and Swenson, S. C.: Accuracy of scaled GRACE terrestrial water storage estimates, Water Resources Research, 48, https://doi.org/10.1029/2011WR011453, 2012. a, b
Landerer, F. W., Flechtner, F. M., Save, H., Webb, F. H., Bandikova, T., Bertiger, W. I., Bettadpur, S. V., Byun, S. H., Dahle, C., Dobslaw, H., Fahnestock, E., Harvey, N., Kang, Z., Kruizinga, G. L. H., Loomis, B. D., McCullough, C., Murböck, M., Nagel, P., Paik, M., Pie, N., Poole, S., Strekalov, D., Tamisiea, M. E., Wang, F., Watkins, M. M., Wen, H.-Y., Wiese, D. N., and Yuan, D.-N.: Extending the Global Mass Change Data Record: GRACE Follow-On Instrument and Science Data Performance, Geophysical Research Letters, 47, https://doi.org/10.1029/2020GL088306, 2020. a
Lawrence, D. M., Oleson, K. W., Flanner, M. G., Thornton, P. E., Swenson, S. C., Lawrence, P. J., Zeng, X., Yang, Z.-L., Levis, S., Sakaguchi, K., Bonan, G. B., and Slater, A. G.: Parameterization improvements and functional and structural advances in version 4 of the Community Land Model, Journal of Advances in Modeling Earth Systems, 3, https://doi.org/10.1029/2011MS00045, 2011. a
Lawrence, D. M., Fisher, R. A., Koven, C. D., Oleson, K. W., Swenson, S. C., Bonan, G., Collier, N., Ghimire, B., Van Kampenhout, L., Kennedy, D., Kluzek, E., Lawrence, P. J., Li, F., Li, H., Lombardozzi, D., Riley, W. J., Sacks, W. J., Shi, M., Vertenstein, M., Wieder, W. R., Xu, C., Ali, A. A., Badger, A. M., Bisht, G., Van Den Broeke, M., Brunke, M. A., Burns, S. P., Buzan, J., Clark, M., Craig, A., Dahlin, K., Drewniak, B., Fisher, J. B., Flanner, M., Fox, A. M., Gentine, P., Hoffman, F., Keppel‐Aleks, G., Knox, R., Kumar, S., Lenaerts, J., Leung, L. R., Lipscomb, W. H., Lu, Y., Pandey, A., Pelletier, J. D., Perket, J., Randerson, J. T., Ricciuto, D. M., Sanderson, B. M., Slater, A., Subin, Z. M., Tang, J., Thomas, R. Q., Val Martin, M., and Zeng, X.: The Community Land Model version 5: Description of new features, benchmarking, and impact of forcing uncertainty, Journal of Advances in Modeling Earth Systems, 11, 4245–4287, 2019. a
Lecomte, H., Rosat, S., and Mandea, M.: Gap filling between GRACE and GRACE-FO missions: assessment of interpolation techniques, Journal of Geodesy, 98, 107, https://doi.org/10.1007/s00190-024-01917-3, 2024. a
Lenczuk, A., Weigelt, M., Kosek, W., and Mikocki, J.: Autoregressive Reconstruction of Total Water Storage within GRACE and GRACE Follow-On Gap Period, Energies, 15, 4827, https://doi.org/10.3390/en15134827, 2022. a
Li, B. and Rodell: Spatial variability and its scale dependency of observed and modeled soil moisture over different climate regions, Hydrology and Earth System Science, 17, 1177–1188, https://doi.org/10.5194/hess-17-1177-2013, 2013. a
Li, B., Rodell, M., Zaitchik, B. F., Reichle, R. H., Koster, R. D., and van Dam, T. M.: Assimilation of GRACE terrestrial water storage into a land surface model: Evaluation and potential value for drought monitoring in western and central Europe, Journal of Hydrology, 446–447, 103–115, https://doi.org/10.1016/j.jhydrol.2012.04.035, 2012. a, b, c, d, e, f, g
Li, B., Rodell, M., and Famiglietti, J. S.: Groundwater variability across temporal and spatial scales in the central and northeastern U.S., Journal of Hydrology, 525, 769–780, https://doi.org/10.1016/j.jhydrol.2015.04.033, 2015. a
Li, B., Rodell, M., Kumar, S., Beaudoing, H. K., Getirana, A., Zaitchik, B. F., De Goncalves, L. G., Cossetin, C., Bhanja, S., Mukherjee, A., Tian, S., Tangdamrongsub, N., Long, D., Nanteza, J., Lee, J., Policelli, F., Goni, I. B., Daira, D., Bila, M., De Lannoy, G., Mocko, D., Steele‐Dunne, S. C., Save, H., and Bettadpur, S.: Global GRACE Data Assimilation for Groundwater and Drought Monitoring: Advances and Challenges, Water Resources Research, 55, 7564–7586, https://doi.org/10.1029/2018WR024618, 2019. a, b, c, d, e, f, g, h, i, j, k, l, m, n, o
Li, F., Kusche, J., Sneeuw, N., Siebert, S., Gerdener, H., Wang, Z., Chao, N., Chen, G., and Tian, K.: Forecasting next year's global land water storage using GRACE data, Geophysical Research Letters, 51, e2024GL109101, https://doi.org/10.1029/2024GL109101, 2024. a, b
Li, F., Springer, A., Kusche, J., Gutknecht, B. D., and Ewerdwalbesloh, Y.: Reanalysis and Forecasting of Total Water Storage and Hydrological States by Combining Machine Learning With CLM Model Simulations and GRACE Data Assimilation, Water Resources Research, 61, e2024WR037926, https://doi.org/10.1029/2024WR037926, 2025. a
Liang, X., Wood, E. F., and Lettenmaier, D. P.: Surface soil moisture parameterization of the VIC-2L model: Evaluation and modification, Global and Planetary Change, 13, 195–206, 1996. a
Libero, G. and Ciriello, V.: Dominant spatiotemporal structures in total water storage anomalies, Advances in Water Resources, 203, 105015, https://doi.org/10.1016/j.advwatres.2025.105015, 2025. a
Lindström, G., Johansson, B., Persson, M., Gardelin, M., and Bergström, S.: Development and test of the distributed HBV-96 hydrological model, Journal of Hydrology, 201, 272–288, 1997. a
Liu, D., Mishra, A. K., Yu, Z., Lü, H., and Li, Y.: Support vector machine and data assimilation framework for Groundwater Level Forecasting using GRACE satellite data, Journal of Hydrology, 603, 126929, https://doi.org/10.1016/j.jhydrol.2021.126929, 2021. a, b, c, d
Longuevergne, L., Scanlon, B. R., and Wilson, C. R.: GRACE Hydrological estimates for small basins: Evaluating processing approaches on the High Plains Aquifer, USA, Water Resources Research, 46, https://doi.org/10.1029/2009WR008564, 2010. a
Loomis, B. D., Rachlin, K. E., and Luthcke, S. B.: Improved Earth Oblateness Rate Reveals Increased Ice Sheet Losses and Mass-Driven Sea Level Rise, Geophysical Research Letters, 46, 6910–6917, https://doi.org/10.1029/2019GL082929, 2019. a
Loomis, B. D., Rachlin, K. E., Wiese, D. N., Landerer, F. W., and Luthcke, S. B.: Replacing GRACE/GRACE‐FO With Satellite Laser Ranging: Impacts on Antarctic Ice Sheet Mass Change, Geophysical Research Letters, 47, e2019GL085488, https://doi.org/10.1029/2019GL085488, 2020. a
Lorenz, C., Tourian, M. J., Devaraju, B., Sneeuw, N., and Kunstmann, H.: Basin-scale runoff prediction: An Ensemble Kalman Filter framework based on global hydrometeorological data sets, Water Resources Research, 51, https://doi.org/10.1002/2014WR016794, 2015. a
Löcher, A. and Kusche, J.: A hybrid approach for recovering high-resolution temporal gravity fields from satellite laser ranging, Journal of Geodesy, 95, 6, https://doi.org/10.1007/s00190-020-01460-x, 2021. a
Maina, F. Z., Xue, Y., Kumar, S. V., Getirana, A., McLarty, S., Appana, R., Forman, B., Zaitchik, B., Loomis, B., Maggioni, V., and Zhou, Y.: Development of a multidecadal land reanalysis over High Mountain Asia, Scientific Data, 11, 827, https://doi.org/10.1038/s41597-024-03643-z, 2024. a
Massotti, L., Siemes, C., March, G., Haagmans, R., and Silvestrin, P.: Next Generation Gravity Mission Elements of the Mass Change and Geoscience International Constellation: From Orbit Selection to Instrument and Mission Design, Remote Sensing, 13, https://doi.org/10.3390/rs13193935, 2021. a
Maxwell, R. M., Condon, L. E., and Kollet, S. J.: A high-resolution simulation of groundwater and surface water over most of the continental US with the integrated hydrologic model ParFlow v3, Geoscientific Model Development, 8, 923–937, https://doi.org/10.5194/gmd-8-923-2015, 2015. a
Mayer-Gürr, T., Behzadpur, S., Ellmer, M., Kvas, A., Klinger, B., Strasser, S., and Zehentner, N.: ITSG-Grace2018-monthly, daily and static gravity field solutions from GRACE, GFZ Data Services [data set], https://doi.org/10.5880/ICGEM.2018.003, 2018. a
Mehrnegar, N., Jones, O., Singer, M. B., Schumacher, M., Jagdhuber, T., Scanlon, B. R., Rateb, A., and Forootan, E.: Exploring groundwater and soil water storage changes across the CONUS at 12.5 km resolution by a Bayesian integration of GRACE data into W3RA, Science of the Total Environment, 758, 143579, https://doi.org/10.1016/j.scitotenv.2020.143579, 2021. a
Mehrnegar, N., Schumacher, M., Jagdhuber, T., and Forootan, E.: Making the Best Use of GRACE, GRACE‐FO and SMAP Data Through a Constrained Bayesian Data‐Model Integration, Water Resources Research, 59, e2023WR034544, https://doi.org/10.1029/2023WR034544, 2023. a, b, c
Miro, M. E. and Famiglietti, J. S.: Downscaling GRACE remote sensing datasets to high-resolution groundwater storage change maps of California’s Central Valley, Remote Sensing, 10, 143, https://doi.org/10.3390/rs10010143, 2018. a
Mitchell, H. L., Houtekamer, P. L., and Pellerin, G.: Ensemble Size, Balance, and Model-Error Representation in an Ensemble Kalman Filter, Monthly Weather Review, 130, 2791–2808, https://doi.org/10.1175/1520-0493(2002)130<2791:ESBAME>2.0.CO;2, 2002. a
Mo, S., Zhong, Y., Forootan, E., Mehrnegar, N., Yin, X., Wu, J., Feng, W., and Shi, X.: Bayesian convolutional neural networks for predicting the terrestrial water storage anomalies during GRACE and GRACE-FO gap, Journal of Hydrology, 604, 127244, https://doi.org/10.1016/j.jhydrol.2021.127244, 2022. a
Müller Schmied, H., Cáceres, D., Eisner, S., Flörke, M., Herbert, C., Niemann, C., Peiris, T. A., Popat, E., Portmann, F. T., Reinecke, R., Schumacher, M., Shadkam, S., Telteu, C.-E., Trautmann, T., and Döll, P.: The global water resources and use model WaterGAP v2.2d: model description and evaluation, Geoscientific Model Development, 14, 1037–1079, https://doi.org/10.5194/gmd-14-1037-2021, 2021. a
Najder, J., Sośnica, K., Strugarek, D., and Zajdel, R.: A Simulation Study for Future Geodetic Satellites Tracked by Satellite Laser Ranging, Journal of Geophysical Research: Solid Earth, 128, e2022JB026192, https://doi.org/10.1029/2022JB026192, 2023. a
Nerger, L., Hiller, W., and Schröter, J.: A comparison of error subspace Kalman filters, Tellus A: Dynamic Meteorology and Oceanography, 57, https://doi.org/10.3402/tellusa.v57i5.14732, 2005. a
Nie, W., Zaitchik, B. F., Rodell, M., Kumar, S. V., Arsenault, K. R., Li, B., and Getirana, A.: Assimilating GRACE into a land surface model in the presence of an irrigation-induced groundwater trend, Water Resources Research, 55, 11274–11294, 2019. a, b, c, d, e, f, g, h, i, j
Nie, W., Kumar, S. V., Getirana, A., Zhao, L., Wrzesien, M. L., Konapala, G., Ahmad, S. K., Locke, K. A., Holmes, T. R., Loomis, B. D., and Rodell, M.: Nonstationarity in the global terrestrial water cycle and its interlinkages in the Anthropocene, Proceedings of the National Academy of Sciences, 121, e2403707121, https://doi.org/10.1073/pnas.2403707121, 2024. a, b, c, d
Niu, G.-Y., Yang, Z.-L., Mitchell, K. E., Chen, F., Ek, M. B., Barlage, M., Kumar, A., Manning, K., Niyogi, D., Rosero, E., Tewari, M., and Xia, Y.: The community Noah land surface model with multiparameterization options (Noah-MP): 1. Model description and evaluation with local-scale measurements, Journal of Geophysical Research: Atmospheres, 116, D12109, https://doi.org/10.1029/2010JD015139, 2011. a, b
Novák, A., Janák, J., and Korekáčová, B.: Joint analysis of selected GRACE monthly spherical harmonic solutions and monthly MASCON solutions, Contributions to Geophysics and Geodesy, 51, 47–61, https://doi.org/10.31577/congeo.2021.51.1.3, 2021. a
Oleson, K. W., Niu, G. ‐Y., Yang, Z. ‐L., Lawrence, D. M., Thornton, P. E., Lawrence, P. J., Stöckli, R., Dickinson, R. E., Bonan, G. B., Levis, S., Dai, A., and Qian, T.: Improvements to the Community Land Model and their impact on the hydrological cycle, Journal of Geophysical Research: Biogeosciences, 113, 2007JG000563, https://doi.org/10.1029/2007JG000563, 2008. a
Overgaard, J., Rosbjerg, D., and Butts, M. B.: Land-surface modelling in hydrological perspective – a review, Biogeosciences, 3, 229–241, https://doi.org/10.5194/bg-3-229-2006, 2006. a
Peltier, W. R.: Global glacial isostasy and the surface of the ice-age Earth: the ICE-5G (VM2) model and GRACE, Annual Review of Earth and Planetary Sciences., 32, 111–149, https://doi.org/10.1146/annurev.earth.32.082503.144359, 2004. a
Peters-Lidard, C. D., Houser, P. R., Tian, Y., Kumar, S. V., Geiger, J., Olden, S., Lighty, L., Doty, B., Dirmeyer, P., Adams, J., Mitchell, K., Wood, E. F., and Sheffield, J.: High-performance Earth system modeling with NASA/GSFC’s Land Information System, Innovations in Systems and Software Engineering, 3, 157–165, 2007. a
Pietroniro, A., Fortin, V., Kouwen, N., Neal, C., Turcotte, R., Davison, B., Verseghy, D., Soulis, E. D., Caldwell, R., Evora, N., and Pellerin, P.: Development of the MESH modelling system for hydrological ensemble forecasting of the Laurentian Great Lakes at the regional scale, Hydrology and Earth System Sciences, 11, 1279–1294, https://doi.org/10.5194/hess-11-1279-2007, 2007. a
Polcher, J., Bertrand, N., Biemans, H., Clark, D. B., Floerke, M., Gedney, N., Gerten, D., Stacke, T., van Vliet, M., and Voss, F.: Improvements in hydrological processes in general hydrological models and land surface models within WATCH, WATCH – European Commission, https://nora.nerc.ac.uk/id/eprint/16487/ (last access: 28 January 2026), 2011. a
Reager, J. T., Thomas, A. C., Sproles, E. A., Rodell, M., Beaudoing, H. K., Li, B., and Famiglietti, J. S.: Assimilation of GRACE Terrestrial Water Storage Observations into a Land Surface Model for the Assessment of Regional Flood Potential, Remote Sensing, 7, 14663–14679, https://doi.org/10.3390/rs71114663, 2015. a, b, c, d, e
Reichle, R., De Lannoy, G., Forman, B., Draper, C., and Liu, Q.: Connecting satellite observations with water cycle variables through land data assimilation: Examples using the NASA GEOS-5 LDAS, Surveys of Geophysics, 35, 577–606, 2014. a, b
Reichle, R. H. and Koster, R. D.: Bias Reduction in Short Records of Satellite Soil Moisture, https://ntrs.nasa.gov/citations/20040172040 (last access: 28 January 2026), 2004. a, b
Reichle, R. H., Koster, R. D., Liu, P., Mahanama, S. P. P., Njoku, E. G., and Owe, M.: Comparison and assimilation of global soil moisture retrievals from the Advanced Microwave Scanning Radiometer for the Earth Observing System (AMSR‐E) and the Scanning Multichannel Microwave Radiometer (SMMR), Journal of Geophysical Research: Atmospheres, 112, 2006JD008033, https://doi.org/10.1029/2006JD008033, 2007. a, b
Retab, A., Save, H., Sun, A., and Scanlon, B.: Rapid mapping of global flood precursors and impacts using novel five-day GRACE solutions, Scientific Reports, 14, 13841, https://doi.org/10.1038/s41598-024-64491-w, 2024. a
Retegui-Schiettekatte, L., Schumacher, M., Madsen, H., and Forootan, E.: Assessing daily GRACE Data Assimilation during flood events of the Brahmaputra River Basin, Science of The Total Environment, 975, 179181, https://doi.org/10.1016/j.scitotenv.2025.179181, 2025. a, b, c
Rietbroek, R., Fritsche, M., Dahle, C., Brunnabend, S.-E., Behnisch, M., Kusche, J., Flechtner, F., Schröter, J., and Dietrich, R.: Can GPS-Derived Surface Loading Bridge a GRACE Mission Gap?, Surveys in Geophysics, 35, 1267–1283, https://doi.org/10.1007/s10712-013-9276-5, 2014. a
Rodell, M. and Reager, J. T.: Water cycle science enabled by the GRACE and GRACE-FO satellite missions, Nature Water, 1, 47–59, https://doi.org/10.1038/s44221-022-00005-0, 2023. a
Rodell, M. and Li, B.: Changing intensity of hydroclimatic extreme events revealed by GRACE and GRACE-FO, Nature Water, 1, 241–248, https://doi.org/10.1038/s44221-023-00040-5, 2023. a
Rodell, M., Houser, P. R., Jambor, U., Gottschalck, J., Mitchell, K., Meng, C.-J., Arsenault, K., Cosgrove, B., Radakovich, J., Bosilovich, M., Entin, J. K., Walker, J. P., Lohmann, D., and Toll, D.: The Global Land Data Assimilation System, Bulletin of the American Meteorological Society, 85, 381–394, https://doi.org/10.1175/BAMS-85-3-381, 2004. a
Rodell, M., Famiglietti, J. S., Wiese, D. N., Reager, J. T., Beaudoing, H. K., Landerer, F. W., and Lo, M.-H.: Emerging trends in global freshwater availability, Nature, 557, 651–659, https://doi.org/10.1038/s41586-018-0123-1, 2018. a, b
Rodell, M., Barnoud, A., Robertson, F. R., Allan, R. P., Bellas-Manley, A., Bosilovich, M. G., Chambers, D., Landerer, F., Loomis, B., Nerem, R. S., O’Neill, M. M., Wiese, D., and Seneviratne, S. I.: An Abrupt Decline in Global Terrestrial Water Storage and Its Relationship with Sea Level Change, Surveys in Geophysics, 45, 1875–1902, https://doi.org/10.1007/s10712-024-09860-w, 2024. a
Ruiz, J. J., Pulido, M., and Miyoshi, T.: Estimating model parameters with ensemble-based data assimilation: A review, Journal of the Meteorological Society of Japan Series II, 91, 79–99, https://doi.org/10.2151/jmsj.2013-201, 2013. a
Ryu, D., Crow, W. T., Zhan, X., and Jackson, T. J.: Correcting unintended perturbation biases in hydrologic data assimilation, Journal of Hydrometeorology, 10, 734–750, 2009. a, b, c
Sakumura, C., Bettadpur, S., Save, H., and McCullough, C.: High‐frequency terrestrial water storage signal capture via a regularized sliding window mascon product from GRACE, Journal of Geophysical Research: Solid Earth, 121, 4014–4030, https://doi.org/10.1002/2016JB012843, 2016. a
Scanlon, B. R., Zhang, Z., Save, H., Sun, A. Y., Schmied, H. M., van Beek, L. P. H., Wiese, D. N., Wada, Y., Long, D., Reedy, R. C., Longuevergne, L., Döll, P., and Bierkens, M. F. P.: Global models underestimate large decadal declining and rising water storage trends relative to GRACE satellite data, Proceedings of the National Academy of Sciences, 115, E1080–E1089, https://doi.org/10.1073/pnas.1704665115, 2018. a, b, c, d, e
Scanlon, B. R., Zhang, Z., Rateb, A., Sun, A., Wiese, D., Save, H., Beaudoing, H., Lo, M. H., Müller‐Schmied, H., Döll, P., Van Beek, R., Swenson, S., Lawrence, D., Croteau, M., and Reedy, R. C.: Tracking Seasonal Fluctuations in Land Water Storage Using Global Models and GRACE Satellites, Geophysical Research Letters, 46, 5254–5264, https://doi.org/10.1029/2018GL081836, 2019. a, b
Schellekens, J., Dutra, E., Martínez-de la Torre, A., Balsamo, G., van Dijk, A., Sperna Weiland, F., Minvielle, M., Calvet, J.-C., Decharme, B., Eisner, S., Fink, G., Flörke, M., Peßenteiner, S., van Beek, R., Polcher, J., Beck, H., Orth, R., Calton, B., Burke, S., Dorigo, W., and Weedon, G. P.: A global water resources ensemble of hydrological models: the eartH2Observe Tier-1 dataset, Earth Syst. Sci. Data, 9, 389–413, https://doi.org/10.5194/essd-9-389-2017, 2017. a
Schulze, K., Kusche, J., Gerdener, H., Döll, P., and Schmied, H. M.: Benefits and pitfalls of GRACE and streamflow assimilation for improving the streamflow simulations of the WaterGAP Global Hydrology Model, Journal of Advances in Modeling Earth Systems, 16, e2023MS004092, https://doi.org/10.1029/2023MS004092, 2024. a, b, c, d
Schumacher, M.: Methods for assimilating remotely-sensed water storage changes into hydrological models, Thesis, Universitäts- und Landesbibliothek Bonn, https://bonndoc.ulb.uni-bonn.de/xmlui/handle/20.500.11811/6630 (last access: 21 April 2020), 2016. a, b
Schumacher, M., Kusche, J., and Döll, P.: A systematic impact assessment of GRACE error correlation on data assimilation in hydrological models, Journal of Geodesy, 90, 537–559, https://doi.org/10.1007/s00190-016-0892-y, 2016. a, b, c, d, e
Schumacher, M., Forootan, E., van Dijk, A. I. J. M., Müller Schmied, H., Crosbie, R. S., Kusche, J., and Döll, P.: Improving drought simulations within the Murray-Darling Basin by combined calibration/assimilation of GRACE data into the WaterGAP Global Hydrology Model, Remote Sensing of Environment, 204, 212–228, https://doi.org/10.1016/j.rse.2017.10.029, 2018. a, b, c
Seyoum, W. M., Kwon, D., and Milewski, A. M.: Downscaling GRACE TWSA Data into High-Resolution Groundwater Level Anomaly Using Machine Learning-Based Models in a Glacial Aquifer System, Remote Sensing, 11, https://doi.org/10.3390/rs11070824, 2019. a, b
Shannon, C. E.: A Mathematical Theory of Communication, Bell System Technical Journal, 27, 379–423, https://doi.org/10.1002/j.1538-7305.1948.tb01338.x, 1948. a
Shihora, L., Balidakis, K., Dill, R., Dahle, C., Ghobadi‐Far, K., Bonin, J., and Dobslaw, H.: Non‐Tidal Background Modeling for Satellite Gravimetry Based on Operational ECWMF and ERA5 Reanalysis Data: AOD1B RL07, Journal of Geophysical Research: Solid Earth, 127, e2022JB024360, https://doi.org/10.1029/2022JB024360, 2022. a
Shihora, L., Liu, Z., Balidakis, K., Wilms, J., Dahle, C., Flechtner, F., Dill, R., and Dobslaw, H.: Accounting for residual errors in atmosphere–ocean background models applied in satellite gravimetry, Journal of Geodesy, 98, https://doi.org/10.1007/s00190-024-01832-7, 2024. a
Shokri, A., Walker, J. P., Van Dijk, A. I. J. M., and Pauwels, V. R. N.: Performance of Different Ensemble Kalman Filter Structures to Assimilate GRACE Terrestrial Water Storage Estimates Into a High‐Resolution Hydrological Model: A Synthetic Study, Water Resources Research, 54, 8931–8951, https://doi.org/10.1029/2018WR022785, 2018. a, b, c
Shokri, A., Walker, J. P., Van Dijk, A. I. J. M., and Pauwels, V. R. N.: On the Use of Adaptive Ensemble Kalman Filtering to Mitigate Error Misspecifications in GRACE Data Assimilation, Water Resources Research, 55, 7622–7637, https://doi.org/10.1029/2018WR024670, 2019. a, b, c
Soltani, S. S., Ataie-Ashtiani, B., and Simmons, C. T.: Review of assimilating GRACE terrestrial water storage data into hydrological models: Advances, challenges and opportunities, Earth-Science Reviews, 213, 103487, https://doi.org/10.1016/j.earscirev.2020.103487, 2021. a
Soltani, S. S., Ataie-Ashtiani, B., Al Bitar, A., Simmons, C. T., Younes, A., and Fahs, M.: Assimilating multivariate remote sensing data into a fully coupled subsurface-land surface hydrological model, Journal of Hydrology, 641, 131 812, https://doi.org/10.1016/j.jhydrol.2024.131812, 2024. a, b, c, d
Sood, A. and Smakhtin, V.: Global hydrological models: a review, Hydrological Sciences Journal, 60, 549–565, 2015. a
Springer, A.: A water storage reanalysis over the European continent: assimilation of GRACE data into a high-resolution hydrological model and validation, Thesis, Universitäts- und Landesbibliothek Bonn, https://bonndoc.ulb.uni-bonn.de/xmlui/handle/20.500.11811/7987 (last access: 10 December 2025), 2019. a, b
Springer, A., Karegar, M. A., Kusche, J., Keune, J., Kurtz, W., and Kollet, S.: Evidence of daily hydrological loading in GPS time series over Europe, Journal of Geodesy, 93, 2145–2153, https://doi.org/10.1007/s00190-019-01295-1, 2019. a, b, c, d, e, f, g
Stampoulis, D., Reager, J. T., David, C. H., Andreadis, K. M., Famiglietti, J. S., Farr, T. G., Trangsrud, A. R., Basilio, R. R., Sabo, J. L., Osterman, G. B., Lundgren, P. R., and Liu, Z.: Model-data fusion of hydrologic simulations and GRACE terrestrial water storage observations to estimate changes in water table depth, Advances in Water Resources, 128, 13–27, https://doi.org/10.1016/j.advwatres.2019.04.004, 2019. a, b, c
Stoffelen, A.: Toward the true near-surface wind speed: Error modeling and calibration using triple collocation, Journal of Geophysical Research: Oceans, 103, 7755–7766, https://doi.org/10.1029/97JC03180, 1998. a
Su, H., Yang, Z., Dickinson, R. E., Wilson, C. R., and Niu, G.: Multisensor snow data assimilation at the continental scale: The value of Gravity Recovery and Climate Experiment terrestrial water storage information, Journal of Geophysical Research: Atmospheres, 115, 2009JD013035, https://doi.org/10.1029/2009JD013035, 2010. a, b, c, d, e
Sun, Y., Riva, R., and Ditmar, P.: Optimizing estimates of annual variations and trends in geocenter motion and J2 from a combination of GRACE data and geophysical models, Journal of Geophysical Research: Solid Earth, 121, 8352–8370, https://doi.org/10.1002/2016JB013073, 2016. a
Sutanudjaja, E. H., van Beek, R., Wanders, N., Wada, Y., Bosmans, J. H. C., Drost, N., van der Ent, R. J., de Graaf, I. E. M., Hoch, J. M., de Jong, K., Karssenberg, D., López López, P., Peßenteiner, S., Schmitz, O., Straatsma, M. W., Vannametee, E., Wisser, D., and Bierkens, M. F. P.: PCR-GLOBWB 2: a 5 arcmin global hydrological and water resources model, Geoscientific Model Development, 11, 2429–2453, https://doi.org/10.5194/gmd-11-2429-2018, 2018. a
Swenson, S. and Wahr, J.: Post-processing removal of correlated errors in GRACE data, Geophysical Research Letters, 33, https://doi.org/10.1029/2005GL025285, 2006. a
Tang, G., Clark, M. P., Papalexiou, S. M., Ma, Z., and Hong, Y.: Have satellite precipitation products improved over last two decades? A comprehensive comparison of GPM IMERG with nine satellite and reanalysis datasets, Remote Sensing of Environment, 240, 111697, https://doi.org/10.1016/j.rse.2020.111697, 2020. a, b
Tangdamrongsub, N., Steele-Dunne, S. C., Gunter, B. C., Ditmar, P. G., and Weerts, A. H.: Data assimilation of GRACE terrestrial water storage estimates into a regional hydrological model of the Rhine River basin,Hydrology and Earth System Sciences, 19, 2079–2100, https://doi.org/10.5194/hess-19-2079-2015, 2015. a, b, c, d
Tangdamrongsub, N., Steele-Dunne, S. C., Gunter, B. C., Ditmar, P. G., Sutanudjaja, E. H., Sun, Y., Xia, T., and Wang, Z.: Improving estimates of water resources in a semi-arid region by assimilating GRACE data into the PCR-GLOBWB hydrological model, Hydrology and Earth System Sciences, 21, 2053–2074, https://doi.org/10.5194/hess-21-2053-2017, 2017. a, b, c, d, e
Tangdamrongsub, N., Han, S.-C., Tian, S., Müller Schmied, H., Sutanudjaja, E. H., Ran, J., and Feng, W.: Evaluation of Groundwater Storage Variations Estimated from GRACE Data Assimilation and State-of-the-Art Land Surface Models in Australia and the North China Plain, Remote Sensing, 10, 483, https://doi.org/10.3390/rs10030483, 2018. a, b, c, d
Tangdamrongsub, N., Han, S.-C., Yeo, I.-Y., Dong, J., Steele-Dunne, S. C., Willgoose, G., and Walker, J. P.: Multivariate data assimilation of GRACE, SMOS, SMAP measurements for improved regional soil moisture and groundwater storage estimates, Advances in Water Resources, 135, 103477, https://doi.org/10.1016/j.advwatres.2019.103477, 2020. a, b, c, d, e, f
Tangdamrongsub, N. and Šprlák, M.: The Assessment of Hydrologic- and Flood-Induced Land Deformation in Data-Sparse Regions Using GRACE/GRACE-FO Data Assimilation, Remote Sensing, 13, 235, https://doi.org/10.3390/rs13020235, 2021. a, b, c, d, e
Tapley, B. D., Bettadpur, S., Watkins, M., and Reigber, C.: The gravity recovery and climate experiment: Mission overview and early results, Geophysical Research Letters, 31, https://doi.org/10.1029/2004GL019779, 2004. a
Telteu, C.-E., Müller Schmied, H., Thiery, W., Leng, G., Burek, P., Liu, X., Boulange, J. E. S., Andersen, L. S., Grillakis, M., Gosling, S. N., Satoh, Y., Rakovec, O., Stacke, T., Chang, J., Wanders, N., Shah, H. L., Trautmann, T., Mao, G., Hanasaki, N., Koutroulis, A., Pokhrel, Y., Samaniego, L., Wada, Y., Mishra, V., Liu, J., Döll, P., Zhao, F., Gädeke, A., Rabin, S. S., and Herz, F.: Understanding each other's models: an introduction and a standard representation of 16 global water models to support intercomparison, improvement, and communication, Geoscientific Model Development, 14, 3843–3878, https://doi.org/10.5194/gmd-14-3843-2021, 2021. a
Tiaden, J., Nestler, B., Diepers, H.-J., and Steinbach, I.: The multiphase-field model with an integrated concept for modelling solute diffusion, Physica D: Nonlinear Phenomena, 115, 73–86, 1998. a
Tian, S., Tregoning, P., Renzullo, L. J., Van Dijk, A. I., Walker, J. P., Pauwels, V. R., and Allgeyer, S.: Improved water balance component estimates through joint assimilation of GRACE water storage and SMOS soil moisture retrievals, Water Resources Research, 53, 1820–1840, 2017. a, b, c, d, e, f, g, h, i
Tippett, M. K., Anderson, J. L., Bishop, C. H., Hamill, T. M., and Whitaker, J. S.: Ensemble Square Root Filters, Monthly Weather Review, 131, 1485–1490, https://doi.org/10.1175/1520-0493(2003)131<1485:ESRF>2.0.CO;2, 2003. a
Tourian, M. J., Saemian, P., Ferreira, V. G., Sneeuw, N., Frappart, F., and Papa, F.: A copula-supported Bayesian framework for spatial downscaling of GRACE-derived terrestrial water storage flux, Remote Sensing of Environment, 295, 113685, https://doi.org/10.1016/j.rse.2023.113685, 2023. a, b
Uz, M., Atman, K. G., Akyilmaz, O., Shum, C., Keleş, M., Ay, T., Tandoğdu, B., Zhang, Y., and Mercan, H.: Bridging the gap between GRACE and GRACE-FO missions with deep learning aided water storage simulations, Science of The Total Environment, 830, 154701, https://doi.org/10.1016/j.scitotenv.2022.154701, 2022. a
van Dam, T. and Wahr, J.: Modeling environment loading effects: a review, Physics and Chemistry of the Earth, 23, 1077–1087, https://doi.org/10.1016/S0079-1946(98)00147-5, 1998. a
Van Der Knijff, J., Younis, J., and De Roo, A.: LISFLOOD: a GIS-based distributed model for river basin scale water balance and flood simulation, International Journal of Geographical Information Science, 24, 189–212, 2010. a
Van Dijk, A.: The Australian Water Resources Assessment System Technical Report 3. Landscape Model (version 0.5) Technical Description, CSIRO: Water for a Healthy Country National Research Flagship, https://awo.bom.gov.au/assets/notes/publications/Van_Dijk_AWRA05_TechReport3.pdf (last access: 28 January 2026), 2010. a
van Dijk, A. I. J. M., Renzullo, L. J., Wada, Y., and Tregoning, P.: A global water cycle reanalysis (2003–2012) merging satellite gravimetry and altimetry observations with a hydrological multi-model ensemble, Hydrology and Earth System Sciences, 18, 2955–2973, https://doi.org/10.5194/hess-18-2955-2014, 2014. a, b, c, d, e, f, g
Van Loon, S. and Fletcher, S. J.: Foundations for Universal Non-Gaussian Data Assimilation, Geophysical Research Letters, 50, e2023GL105148, https://doi.org/10.1029/2023GL105148, 2023. a
Vereecken, H., Amelung, W., Bauke, S. L., Bogena, H., Brüggemann, N., Montzka, C., Vanderborght, J., Bechtold, M., Blöschl, G., Carminati, A., Javaux, M., Konings, A. G., Kusche, J., Neuweiler, I., Or, D., Steele-Dunne, S., Verhoef, A., Young, M., and Zhang, Y.: Soil hydrology in the Earth system, Nature Reviews Earth & Environment, 3, 573–587, https://doi.org/10.1038/s43017-022-00324-6, 2022. a
Viney, N., Vaze, J., Crosbie, R., Wang, B., Dawes, W., and Frost, A.: AWRA-L v4. 5: technical description of model algorithms and inputs, CSIRO: Water for a Healthy Country National Research Flagship, https://discovery.csiro.au/discovery/fulldisplay/alma9910243329401981/61CSIRO_INST:CSIRO (last access: 28 January 2026), 2015. a
Vishwakarma, B. D., Horwath, M., Devaraju, B., Groh, A., and Sneeuw, N.: A Data-Driven Approach for Repairing the Hydrological Catchment Signal Damage Due to Filtering of GRACE Products, Water Resources Research, 53, 9824–9844, https://doi.org/10.1002/2017WR021150, 2017. a
Vishwakarma, B. D., Horwath, M., Groh, A., and Bamber, J. L.: Accounting for GIA signal in GRACE products, Geophysical Journal International, 228, 2056–2060, https://doi.org/10.1093/gji/ggab464, 2021a. a
Vishwakarma, B. D., Zhang, J., and Sneeuw, N.: Downscaling GRACE total water storage change using partial least squares regression, Scientific Data, 8, 1–13, 2021b. a, b
Wahr, J., Molenaar, M., and Bryan, F.: Time variability of the Earth's gravity field: Hydrological and oceanic effects and their possible detection using GRACE, Journal of Geophysical Research: Solid Earth, 103, 30205–30229, https://doi.org/10.1029/98JB02844, 1998. a, b
Wang, J., Forman, B. A., Girotto, M., and Reichle, R. H.: Estimating Terrestrial Snow Mass via Multi‐Sensor Assimilation of Synthetic AMSR‐E Brightness Temperature Spectral Differences and Synthetic GRACE Terrestrial Water Storage Retrievals, Water Resources Research, 57, e2021WR029880, https://doi.org/10.1029/2021WR029880, 2021. a, b, c, d, e
Wang, P., Wang, S.-Y., Li, J., Chen, J., and Qi, Z.: Comparison of GRACE/GRACE-FO Spherical Harmonic and Mascon Products in Interpreting GNSS Vertical Loading Deformations over the Amazon Basin, Remote Sensing, 15, 252, https://doi.org/10.3390/rs15010252, 2023. a, b
Watkins, M. M., Wiese, D. N., Yuan, D.-N., Boening, C., and Landerer, F. W.: Improved methods for observing Earth's time variable mass distribution with GRACE using spherical cap mascons, Journal of Geophysical Research: Solid Earth, 120, 2648–2671, https://doi.org/10.1002/2014JB011547, 2015. a
Whitaker, J. S. and Hamill, T. M.: Evaluating methods to account for system errors in ensemble data assimilation, Monthly Weather Review, 140, 3078–3089, https://doi.org/10.1175/MWR-D-11-00276.1, 2012. a
White, A. M., Gardner, W. P., Borsa, A. A., Argus, D. F., and Martens, H. R.: A Review of GNSS/GPS in Hydrogeodesy: Hydrologic Loading Applications and Their Implications for Water Resource Research, Water Resources Research, 58, e2022WR032078, https://doi.org/10.1029/2022WR032078, 2022. a
Wiese, D. N., Bienstock, B., Blackwood, C., Chrone, J., Loomis, B. D., Sauber, J., Rodell, M., Baize, R., Bearden, D., Case, K., Horner, S., Luthcke, S., Reager, J. T., Srinivasan, M., Tsaoussi, L., Webb, F., Whitehurst, A., and Zlotnicki, V.: The Mass Change Designated Observable Study: Overview and Results, Earth and Space Science, 9, e2022EA002311, https://doi.org/10.1029/2022EA002311, 2022. a, b
Wongchuig, S., Paiva, R., Siqueira, V., Papa, F., Fleischmann, A., Biancamaria, S., Paris, A., Parrens, M., and Al Bitar, A.: Multi‐Satellite Data Assimilation for Large‐Scale Hydrological‐Hydrodynamic Prediction: Proof of Concept in the Amazon Basin, Water Resources Research, 60, e2024WR037155, https://doi.org/10.1029/2024WR037155, 2024. a, b, c
Wu, W.-Y., Yang, Z.-L., Zhao, L., and Lin, P.: The impact of multi-sensor land data assimilation on river discharge estimation, Remote Sensing of Environment, 279, 113138, https://doi.org/10.1016/j.rse.2022.113138, 2022. a, b, c, d
World Wide Fund for Nature: WWF Water Risk Filter Indicator & Scenario Documentation (2.0), Zenodo, https://doi.org/10.5281/zenodo.13693590, 2024. a
Yang, F., Schumacher, M., Retegui-Schiettekatte, L., van Dijk, A. I. J. M., and Forootan, E.: PyGLDA: a fine-scale python-based global land data assimilation system for integrating satellite gravity data into hydrological models, Geoscientific Model Development, 18, 6195–6217, https://doi.org/10.5194/gmd-18-6195-2025, 2025. a
Yin, W., Hu, L., Zhang, M., Wang, J., and Han, S.-C.: Statistical Downscaling of GRACE-Derived Groundwater Storage Using ET Data in the North China Plain, Journal of Geophysical Research: Atmospheres, 123, 5973–5987, https://doi.org/10.1029/2017JD027468, 2018. a
Yin, W., Han, S.-C., Zheng, W., Yeo, I.-Y., Hu, L., Tangdamrongsub, N., and Ghobadi-Far, K.: Improved water storage estimates within the North China Plain by assimilating GRACE data into the CABLE model, Journal of Hydrology, 590, 125348, https://doi.org/10.1016/j.jhydrol.2020.125348, 2020. a, b
Zaitchik, B. F., Rodell, M., and Reichle, R. H.: Assimilation of GRACE Terrestrial Water Storage Data into a Land Surface Model: Results for the Mississippi River Basin, Journal of Hydrometeorology, 9, 535–548, https://doi.org/10.1175/2007JHM951.1, 2008. a, b, c, d, e, f, g, h
Zhang, X., Li, J., Dong, Q., Wang, Z., Zhang, H., and Liu, X.: Bridging the gap between GRACE and GRACE-FO using a hydrological model, Science of The Total Environment, 822, 153659, https://doi.org/10.1016/j.scitotenv.2022.153659, 2022. a
Zhao, K. and Li, X.: Estimating terrestrial water storage changes in the Tarim River Basin using GRACE data, Geophysical Journal International, 211, 1449–1460, 2017. a
Zhao, L. and Yang, Z.-L.: Multi-sensor land data assimilation: Toward a robust global soil moisture and snow estimation, Remote Sensing of Environment, 216, 13–27, https://doi.org/10.1016/j.rse.2018.06.033, 2018. a, b, c, d, e, f, g, h
- Abstract
- Introduction
- Modeling and remote sensing of terrestrial water storage changes
- Status of current GRACE/-FO DA frameworks
- Validation of DA experiments
- Current challenges and open issues
- Future directions
- Synthesis
- Appendix A
- Data availability
- Author contributions
- Competing interests
- Disclaimer
- Acknowledgements
- Financial support
- Review statement
- References
- Abstract
- Introduction
- Modeling and remote sensing of terrestrial water storage changes
- Status of current GRACE/-FO DA frameworks
- Validation of DA experiments
- Current challenges and open issues
- Future directions
- Synthesis
- Appendix A
- Data availability
- Author contributions
- Competing interests
- Disclaimer
- Acknowledgements
- Financial support
- Review statement
- References