A mathematical model to improve water storage of glacial lake prediction towards addressing glacial lake outburst floods

Moraine-dammed glacial lakes (MDLs) are not only vital sources of freshwater but also a hazard to mountain communities if they drain in sudden glacial lake outburst floods (GLOFs). Accurately measuring the water storage of these lakes is crucial to ensure sustainable use and safeguard mountain communities downstream. However, thousands of glacial lakes still lack a robust estimate of their water storages because bathymetric surveys in remote regions are difficult and expensive. Here we geometrically approximate the shape and depths of moraine-dammed lakes and provide a cost-effective model to improve lake water storage estimation. Our model uses the outline and the terrain surrounding a glacier lake as input data, assuming a parabolic lake bottom and constant hillslope angles. We initially validate our model using data from four newly surveyed glacial lakes on the Qinghai–Tibet Plateau. Subsequently, we incorporate data from 40 additional measured lakes as a sample set to compare and evaluate the model's performance against other existing models. Our model overcomes the autocorrelation issue inherent in earlier area/depth–water storage relationships and incorporates an automated calculation process based on the topography and geometrical parameters specific to moraine-dammed lakes. Compared to other models, our model achieved the lowest average relative error of approximately 14 % when analyzing a dataset of 44 observed lakes, surpassing the > 44 % average relative error from alternative models. Finally, the model is used to calculate the water storage change in moraine-dammed lakes in the past 30 years in High-mountain Asia. The model has been proven to be robust and can be utilized to update the water storage of lake water for conducting further management of glacial lakes with the potential for outburst floods in the world.

1 Introduction

Moraine-dammed glacial lakes (MDLs) trap meltwater from snow, ice, and liquid precipitation within basins behind dams at or near the termini of glaciers (Westoby et al., 2014; Yao et al., 2018; Veh et al., 2019a). As glaciers have been retreating in past decades in most mountain regions worldwide, new MDLs have been forming, and existing ones have been growing in size and water storage (Bolch et al., 2012; Carrivick and Tweed, 2013; Cook et al., 2018; Shugar et al., 2020; Zhang et al., 2023). During the period from 1990 to 2018, High-mountain Asia witnessed a remarkable 52 % and 54 % increase in the number and area of MDLs, respectively (Wang et al., 2020). Notably, the eastern Himalayas experienced the most significant growth, leading in both the number and area of MDLs during this period. MDLs are vital water reservoirs for communities in glaciated high mountains, but were also repeatedly sources for glacial lake outburst floods (GLOFs) (Westoby et al., 2014; Wu et al., 2019; Gao et al., 2021; Fischer et al., 2021; Zheng et al., 2021a; Veh et al., 2019b). According to a report by Lützow et al. (2023), a total of 630 GLOFs have been linked to MDLs occurring in 27 countries between 850 and 2022 CE. A recent study indicates that multiple GLOFs documented from 1964 to 2022 caused damage to infrastructure in High-mountain Asia (Nie et al., 2023).

MDLs are prone to sudden failure due to the instability of the dam structure, releasing parts of the impounded water storage in catastrophic floods (Westoby et al., 2014; Zheng et al., 2021b). MDLs can grow towards steep slopes, where debris or ice could fall into the lakes, causing the barriers to overflow (Emmer and Vilímek, 2014; Carrivick and Tweed, 2013; Liu et al., 2020). Due to their high altitude and potential energy, these flood waves can attain runout distances of many tens of kilometers, transporting and entraining large amounts of sediment from moraines and riverbanks (Westoby et al., 2014). Many GLOFs have transformed into debris flows, and their coarse debris rapidly filled hydropower reservoirs and further destroyed infrastructure along the flow path (Westoby et al., 2014; Zheng et al., 2021b; Veh et al., 2022). For example, GLOFs descending from the mountains with high kinetic energy have recently damaged transport and power infrastructure such as the upper Bhote Koshi hydropower plant, with a reconstruction cost of USD 57 million (Cook et al., 2018). Future flash floods are a potential threat to major new infrastructure, such as hundreds more hydropower projects (Nie et al., 2023). GLOFs may also undercut hillslopes along mountain rivers, which may fail, impound river runoff, and form potentially unstable lakes (Zheng et al., 2021a). Thus, MDLs have become a major glacier-related hazard in high mountains and will likely remain so as glaciers could lose more than a third of their mass by the end of the 21st century (Rounce et al., 2023). Appraising the water storage of glacial lakes is key to allowing for sustainable development along river channels originating in glaciated headwaters (Yao et al., 2018; Harrison et al., 2018; Shugar et al., 2020; Liu et al., 2020).

Effective management of GLOF hazards hinges on the ability to assess both the likelihood and magnitude of such events (Clague and Evans, 2000). This typically requires understanding several critical factors, including the water storage of MDLs, the structural integrity and stability of the dam, the potential external triggers, and the flood's anticipated flow path (e.g. Richardson and Reynolds, 2000; Westoby et al., 2014; Mergili et al., 2020; Sattar et al., 2021; Qi et al., 2023). Estimating glacial lake volume, however, presents significant challenges. Many glacial lakes are situated in remote, physically demanding, and hazardous environments, complicating bathymetric surveys of the lake basins (Cook and Quincey, 2015; Qi et al., 2022; Duan et al., 2023). Therefore, in situ measurements of lake depth are available only for a few dozen cases in the Himalayas, while the water storage remains unknown for the other thousands of lakes in this region. Current optical or radar-based satellite missions, while useful for mapping lakes, are limited in measuring lake bathymetry due to the strong attenuation of electromagnetic waves in glacial lakes (Zhu et al., 2019). As such, there has been an ongoing effort to refine empirical scaling relationships from the few available worldwide samples that relate glacial lake depth and/or area to lake water storage (Fujita et al., 2013; Carrivick and Quincey, 2014; Cook and Quincey, 2015; Veh et al., 2019a; Shugar et al., 2020; Qi et al., 2022). However, these equations may yield significant errors in orders of magnitude for a given lake area due to the the autocorrelation issue inherent in earlier area/depth–volume relationships. Although there are models that consider the specific geometric shapes and topography surrounding lakes, they are limited to estimating the water storage of larger-sized plateau tectonic lakes (Zhou et al., 2020; Zhu et al., 2019). After numerous experiments, we have found that the aforementioned models do not apply to estimating the water storage of glacier lakes due to the lack of consideration for glacial lake and related parameters. Given the critical role of glacial lake water storage in assessing hazard risk and providing early warning information, the development of a mathematically robust yet cost-effective model is urgently needed.

Our goal is to introduce a novel approach for accurately estimating water storage by incorporating its geometry and surrounding terrain. To this end, we propose a three-dimensional model to approximate the basin morphology of MDLs and derive its analytical equation. We assess the performance of this model against field-measured underwater topography data and further compare the model error against other available empirical scaling relationships. Finally, we discuss the uncertainty and rationality of the new model and apply the model to estimate the water storage of the MDLs in High-mountain Asia.

2 MDL types and their geometric approximation

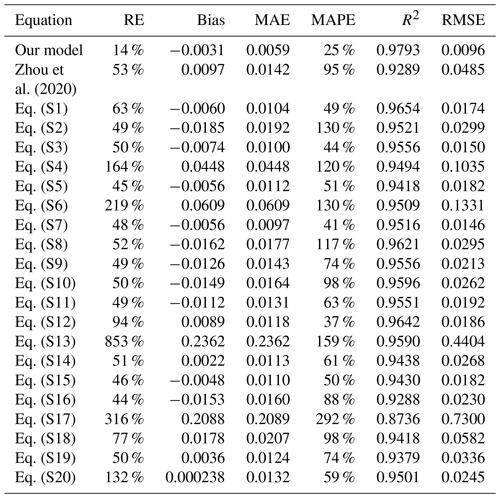
MDLs can be classified into glacier-contacted lakes (GCLs) and glacier-uncontacted lakes (GULs). GCLs are supraglacial ponds on top of debris-covered glaciers or lakes at the termini of glaciers (Richardson and Reynolds, 2000; Bennett et al., 2000). We term GCLs as MDLs in direct contact with the glacier terminus (Fig. 1a). By contrast, GULs are separated from the present glaciers but impound substantial parts of the meltwater from the glacier upstream (Fig. 1b). The bottom of an MDL may be a sediment-covered bedrock depression that was eroded and deepened by the parent glacier during earlier advances. As glaciers retreat, they provide space for lakes to grow between the glacier terminus, with the abandoned moraine trapping excess meltwater from the parent glacier (Nie et al., 2023).

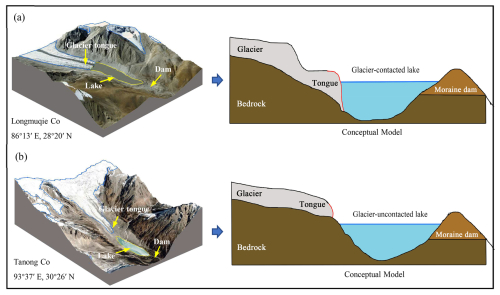
Figure 1 Longitudinal cross sections along a glacier-contacted (a) and glacier-uncontacted lake (b). (The base images are from Google Earth imagery; © Google Earth.) Sketches are idealized and do not represent measured elevations.

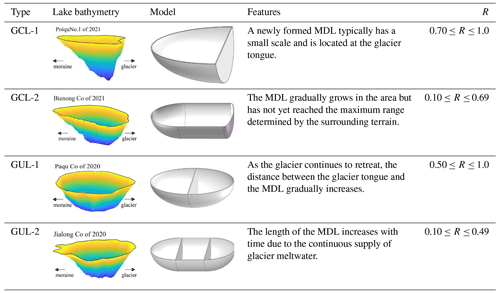
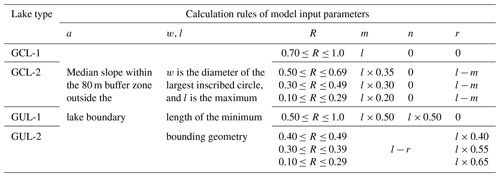
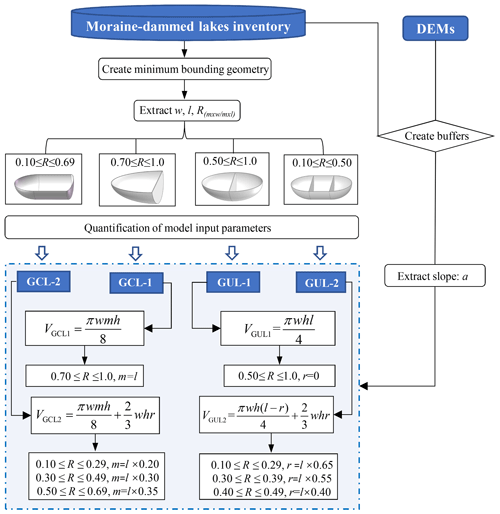
We use the glacial lake inventory of High-mountain Asia by Wang et al. (2020) to differentiate between these two types of MDLs. In general, glacial lakes grow in area largely because they become longer. Lower values of the ratio (R) between the maximum width and maximum length indicate that the shape of the lake is elongated; R equals 1 if the lake is perfectly circular or square (Qi et al., 2022). According to the glacial lake inventory, the R value for glacial lakes in High-mountain Asia ranges from 0.1 to 1.0. If R is lower than 0.1, it may indicate the presence of glacial lakes with lengths exceeding 10 m but widths of approximately 1 m. However, in reality, glacial lakes with such dimensions are practically non-existent. Therefore, thresholds of R allow us to divide glacial lakes into four subclasses (Table 1). We find that newly formed GCLs typically have small surface areas and high values of R. We classified GCLs with R between 0.70 and 1.0 as GCL-1 and those with R of less than 0.69 as GCL-2. Examples of these two types are Poiqu No. 1 Lake (28.14° N, 85.92° E) and Bienong Co (30°31^′ N, 93°26^′ E) (Table 1). With ongoing glacier recession, lakes might become decoupled from their parent glacier, switching from a lake-terminating to a land-terminating glacier. We termed lakes GUL-1 if R ranged between 0.5 and 1.0 and GUL-2 if R<0.49. Paqu Co (28°30^′ N, 86°15^′ E) and Jialong Co in 2020 are the examples of these two classes (Table 1). It is noteworthy that the establishment of the R threshold in this study is grounded in the glacial lake catalog dataset developed by Wang et al. (2020). Initially, the glacial lakes were divided into two major categories, GCL and GUL. Subsequently, R values for each glacial lake were calculated, and all co-authors classified the geometric shapes based on different types and sizes of glacial lakes. Ultimately, through statistical analysis of glacial lake sizes for different types, we defined the threshold for R. This allows the model to automatically categorize glacial lakes based on this value.

Table 1 Examples of a glacier-contacted lake and a glacier-uncontacted lake. The ratio R represents the maximum width (m) divided by the maximum length (m) of the glacial lake. The vertical scale is exaggerated.

3 Model development

3.1 Input data

We suggest specific geometric models for the four subclasses (Table 1) to approximate the water storages of MDLs. Our models are fed with data from a digital elevation model (DEM) and from the outline of a glacial lake. We used the 12.5 m ALOS PALSAR DEM, which is freely available from the Japan Aerospace Exploration Agency (JAXA, https://www.eorc.jaxa.jp, last access: 11 Octoeber 2023).

3.2 Analytical equations

We surmise that an ideal cross section of an MDL (Fig. 2) can be partitioned into three distinct portions, V₁, V₂, and V₃, representing the water storage of the lake stored adjacent to the moraine dam, at the center of the lake, and near the glacier (or bedrock if the lake is disconnected from the glacier). The corresponding lengths of these three portions along the maximum length of the lake are denoted by m, r, and n. The lake has its maximum depth, h₁ and h₂, on either side of r. Points g and f represent the positions of a sediment layer at the lake bottom, and a and β are the slopes near the water surface.

The core assumptions of our geometric model can be summarized as follows: (1) an MDL has a parabolic longitudinal bottom profile with a uniform sediment layer at the bottom of the lake to keep h₁=h₂ and a parabolic cross section P_S (Figs. 2 and 3), (2) the lake surface shape can be approximated by ellipses at both ends and a rectangle in between, and (3) the glacier surface and the moraine dam dip towards the lake with the same slope.

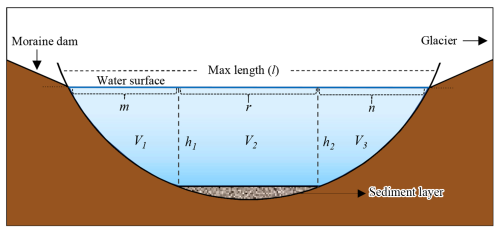
Figure 2 Longitudinal cross section through an MDL. The horizontal blue line (l) is the maximum length on the lake surface, subdivided by m, r, and n. The solid black line is the hypothetical bottom of the lake, and the textured gray area represents a sediment layer covering the lake bottom. The maximum water depth is $h=h_{\mathrm{1}}=h_{\mathrm{2}}$, and points g and f are at equal depths.

In three-dimensional form, the MDL basin can be divided into three parts, with each having a water storage of V₁, V₂, and V₃ (Fig. 3a). V₁ and V₃ can be considered the water storages of elliptical semi-paraboloids controlled by the water depth h (Fig. 3b and c). Significantly, V₁ and V₃ may or may not be equal, depending on the values of m and n. V₂ is a semi-parabolic cylinder (Fig. 3d) that has height r, diameter w, and parabolic cross section P_s (Fig. 3e). Thus, the total water storage of the MDL is $V=V_{\mathrm{1}}+V_{\mathrm{2}}+V_{\mathrm{3}}$.

Figure 3 Definition diagram for the geometry of the MDL. (a) Hypothetical three-dimensional model of the MDL. (b) Model for V₁ describing the lake water storage adjacent to the moraine dam. (c) Model for V₁ describing the lake water storage adjacent to the glacier. (d) Model for V₃ describing the lake water storage stored in the center part of the lake. (e) Cross section of the column P_s. The parameters m and n are the semi-major axes of the elliptical paraboloid near the MDL inlet and outlet, respectively; r is the length of the parabolic cylinder in the middle of MDL; w and l represent the largest width and length of the MDL, respectively; and h is the lake depth.

To obtain the individual lake water storages, we define the elliptical paraboloids for V₁ and V₂ (Eqs. 1–2) in a Cartesian coordinate system (x, y, z) as

$$\begin{array}{}\text{(1)}& {\displaystyle }{V}_{\mathrm{1}}=\left\{(x,y,z)\mathrm{|}{\displaystyle \frac{x^{\mathrm{2}}}{a_{\mathrm{1}}^{\mathrm{2}}}}+{\displaystyle \frac{y^{\mathrm{2}}}{b_{\mathrm{1}}^{\mathrm{2}}}}\le z,y\ge \mathrm{0},\mathrm{0}\le z\le h\right\},\text{(2)}& {\displaystyle }{V}_{\mathrm{3}}=\left\{(x,y,z)\mathrm{|}{\displaystyle \frac{x^{\mathrm{2}}}{a_{\mathrm{2}}^{\mathrm{2}}}}+{\displaystyle \frac{y^{\mathrm{2}}}{b_{\mathrm{2}}^{\mathrm{2}}}}\le z,y\ge \mathrm{0},\mathrm{0}\le z\le h\right\},\end{array}$$

and the parabolic cylinder for V₂ (Eq. 3) as

$$\begin{array}{}\text{(3)}& V_{\mathrm{2}}=\left\{(x,y,z)\mathrm{|}k{x}^{\mathrm{2}}\le z\le h,\mathrm{0}\le y\le r\right\},\end{array}$$

where a₁> 0, b₁> 0, a₂> 0, and b₂> 0 are the lengths of the semi-axes of upper surfaces of V₁ and V₃; h> 0 is the height of V₁,V₂, and V₃; and r> 0 is the length of V₂.

Considering the four types of MDLs, GCL-1 corresponds to the case where r=0 and n=0. In this study, m represents the part of the lake area closer to the moraine dam, and in most cases, m is not equal to zero. However, in certain special cases, such as lake Zhasuo Co (30.31° N, 93.25° E) in southeastern Tibet, $m=n=\mathrm{0}$ because the surface morphology of this lake is rectangular. In most scenarios, the water storage of the GCL-1 can be represented as

$$\begin{array}{}\text{(4)}& V_{\mathrm{GCL}\mathrm{1}}={\displaystyle \frac{\mathit{\pi }wmh}{\mathrm{8}}}.\end{array}$$

When n=0, the model of MDL corresponds to GCL-2, and its water storage can be represented as

$$\begin{array}{}\text{(5)}& V_{\mathrm{GCL}\mathrm{2}}={\displaystyle \frac{\mathit{\pi }wmh}{\mathrm{8}}}+{\displaystyle \frac{\mathrm{2}}{\mathrm{3}}}whr.\end{array}$$

When r=0, the model of MDL conforms to GUL-1, and its water storage can be expressed as

$$\begin{array}{}\text{(6)}& V_{\mathrm{GUL}\mathrm{1}}={\displaystyle \frac{\mathit{\pi }whl}{\mathrm{4}}}.\end{array}$$

When the type of MDL corresponds to GUL-2, its water storage can be expressed as

$$\begin{array}{}\text{(7)}& V_{\mathrm{GUL}\mathrm{2}}={\displaystyle \frac{\mathit{\pi }wh(l-r)}{\mathrm{4}}}+{\displaystyle \frac{\mathrm{2}}{\mathrm{3}}}whr.\end{array}$$

Finally, the water depth (h) can be derived from the w and slope angle (a) of the glacial lake:

$$\begin{array}{}\text{(8)}& h={\displaystyle \frac{w\tan \left(a\right)}{\mathrm{4}}}.\end{array}$$

The Supplement elaborates more on the derivation of these analytical equations, and Table 2 shows the definition of the abbreviations in the model procedure.

Table 2 The definition of the abbreviations in the geometric model.

3.3 Determination of model parameters

We determined the parameters in Eqs. (4)–(8), namely, w, l, a, m, n, and r, using the lake boundary and the DEM. We measured w and l by drawing a minimum rectangle bounding box with length l encompassing the MDL (Fig. 4a). If the width w^′ of the bounding box of the MDL exceeds the actual width (w) of the lake, as in the case of the tortuous boundary of Lake Longmuqie Co (28.35° N, 86.23° E) (Fig. 4b), we label the diameter of the maximum inscribed circle within the MDL as w in Fig. 4c.

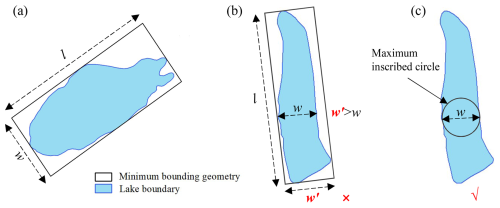
Figure 4 Schematic illustration of the method for extracting the maximum length (l) and width (w) of the MDL. The outline in panel (a) represents the geometric boundary of Lake Jialong Co (28.21° N, 86.85° E), while the outlines in panels (b) and (c) depict the geometric boundaries of Lake Longmuqie Co (28.35° N, 86.23° E).

To determine the value of slope a surrounding the MDL, we use a DEM with a spatial resolution of 12.5 m in the model computation. We tested buffer sizes of 30, 50, 80, and 100 m width beyond the MDL boundary and extracted the mean and median value of a within each buffer. By comparing the simulated results with the measured data (lakes Bienong Co, Maqiong Co, Tanong Co, and Jialong Co), we found that the water storage estimation using the median value within the 80 m external buffer zone had a lower relative error and higher overall accuracy. Therefore, we defined the value of a as the median slope within the 80 m buffer zone surrounding the MDL boundary. The choice of buffer zone distance can be adjusted based on the specific terrain characteristics of the research area, allowing researchers to adapt the methodology to their data accuracy.

Determining the appropriate thresholds for m, n, and r of different MDL types is challenging as methods for extracting these parameters vary depending on the MDL types. In other words, due to the different types of glacial lakes, the values of m, n, and r vary. Additionally, these values change with the size of the glacial lake. To enable the model to automatically identify and calculate the corresponding m, n, and r for each glacial lake, we need to define a threshold. Based on the geometry of the glacial lake, we established a proportional relationship between m, n, r, and the glacier lake length (l). This proportional relationship is empirically defined and essentially represents a geometric segmentation of the glacial lake. The lake is divided into three sections, and the volume of each section is calculated separately. The total water storage of the lake is then obtained by summing the volumes of these three sections. Relying on R, the lake boundary from Wang et al. (2020), and DEM, m and n were estimated for GUL-1 and GUL-2 as shown in Table 3. In the case of GCL-1, l=m due to its small area of water surface. For GCL-2, m was determined to be 35 % of l for lakes with $\mathrm{0.50}<R<\mathrm{0.69}$, 30 % of l for lakes with $\mathrm{0.30}<R<\mathrm{0.49}$, and 20 % of l for lakes with R<0.30 (Table 3).

For GUL-1, R ranges from 0.50 to 0.10, and both m and n are considered equal to half of l. On the other hand, for GUL-2, it is possible to estimate the MDL water storage solely based on r, as described in Eq. (7). Accordingly, r values were statistically set to 0.4, 0.55, and 0.65l, respectively, with three R levels (Table 3). Figure 5 illustrates several representative cases of MDLs.

The above quantitative question about m, n, and r is not based on subjective judgment. First, we computed the R values for all glacial lakes utilizing catalog data and then categorized them by glacial lake type, and finally, we provided a definition by statistically assessing the shape of glacial lakes. This definition pertains to the proportionality of m, n, and r concerning the l of the glacial lake. Consequently, our model is capable of autonomously classifying each glacial lake type through boundary data analysis. It further computes various parameters for each lake, encompassing m, n, r, and h, ultimately culminating in the determination of the water storage for each lake.

Table 3 Quantification of model input parameters.

Figure 5 Example for the extraction of input parameters for different types of MDLs. The base map is a Google Earth image (© Google Earth).

We executed our workflow (Fig. 6) on 44 MDLs in High-mountain Asia that have known depths and water storages. For each lake, we checked whether its outline was in contact with the parent glacier. We automatically fitted a rectangular bounding box to calculate R and then automatically assigned each lake to one of the four types of MDLs based on R thresholds (Table 1). Finally, we estimated their water storages using our and traditional empirical relationships. Our model requires the MDL boundary and DEM data as inputs, and it automatically quantifies each parameter while selecting the optimal model for water storage estimation.

Finally, we applied our model to more than 10 000 glacial lakes with unknown bathymetry in High-mountain Asia. This region had one of the highest rates of MDL growth in the world in the past few decades.

Figure 6 The flowchart of the model procedure derivation.

3.4 Model validation and application

In this study, we initially validated our parameterization using bathymetric measurements from four representative glacial lakes surveyed between 2020 and 2021. Subsequently, we combined the data from these four lakes with the remaining six glacier lakes we measured along with water storage data from 34 MDLs obtained from relevant literature sources (see Table S1 in the Supplement for details). This resulted in a dataset of 44 lakes, which was used to compare and validate the performance of our model against other existing methods.

A glacier lake inventory of the High-mountain Asia region, published by Wang et al. (2020), was used as input data for the model application to assess the water storage of moraine-dammed lakes in this region. Notably, Wang et al. (2020)'s glacier lake inventory provides a detailed classification of GCL and GUL, which has been internationally recognized. It is important to note that in their dataset, GUL refers specifically to glacier lakes that do not come in contact with glaciers, which may not necessarily all be moraine-dammed lakes. To ensure the accuracy of our analysis, we conducted a thorough review based on the classification criteria proposed by Yao et al. (2018), who identify three types of moraine-dammed lakes: (1) lakes situated between the end moraine ridge and the glacier terminus, (2) lakes beside the lateral moraine ridge, and (3) lakes on the moraine ridge. Each GUL in the dataset was individually assessed against these criteria, and only those meeting the classification as moraine-dammed lakes were retained for further analysis.

4 Results

4.1 Model validation

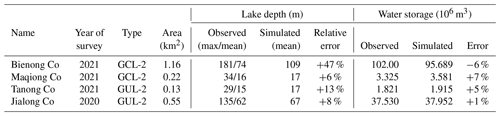
We validated our parameterization using bathymetry measurements from four representative glacial lakes, namely, Bienong Co, Maqiong Co, Tanong Co, and Jialong Co, located in the Qinghai–Tibet Plateau. These lakes represent the four types of glacier lakes, with depths measured through bathymetric surveying (Fig. 7). By comparing estimated with measured water storages (Table 4), we find that Jialong Co has the highest accuracy, with a relative error of only 1 %. Maqiong Co and Tanong Co are overestimated by approximately 5 % and 7 %, respectively. The largest lake, Bienong Co, had an underestimated water storage of 6 %.

In addition, our model is designed to approximate the mean depth of MDLs and therefore underestimates the maximum measured lake depth by about 50 % (Table 4). Modeled mean water depths only deviate by 18 % (mean) from the measured mean water depths. Except for a notable prediction error for Bienong Co (+47 %), errors for Jialong Co, Tanong Co, and Maqiong Co range from 6 % to 13 % relative to the measured values.

In summary, our model has a high degree of concordance with observed glacial lake water storages and provides better estimations of water depth compared to the measured average depths. This suggests that our proposed model can be used in glacial lake water storage estimation and the management of GLOF hazards.

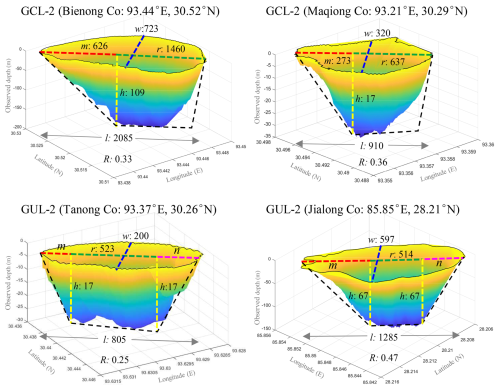
Figure 7 Subaqueous glacial lake morphology based on bathymetric surveys. The dashed black line represents the hypothetical longitudinal profile of the glacial lake; l and w are measured from the lake boundary, h is simulated lake depth, and the remaining parameters (m, n, and r) are calculated by the rules in Table 3. Lake depth is exaggerated.

Table 4 Validation results of the mathematical model.

4.2 Comparison with other methods

Table 5 displays the dataset of glacial lake bathymetry used in this study to validate the model. We compare our model with another model that employed the lake geometry (Zhou et al., 2020) and with 20 additional formulas (Eqs. S1–S20) collated by Qi et al. (2022) in Table S1. In the estimation of a single MDL, Eqs. (S4), (S6), (S13), (S17), and (S20) displayed significant inaccuracies (132 %–853 %). For instance, Eq. (S13) shows an average error of 853 %. Consequently, we have refrained from conducting a comparative analysis of these five formulas in the subsequent discussions.

Table 5 The glacial lake bathymetry dataset used in this study. The lake bathymetry data are shown in bold if provided by this study, and the rest were obtained from references; see Table S1 for details.

Our assessment (Table 6) involves the relative error (RE, absolute value), bias, root mean square error (RMSE), mean absolute percentage error (MAPE), and mean absolute error (MAE) to quantify the uncertainty of the new model. We use the coefficient of determination (R²) to describe the goodness of fit between the model-derived data series and the measured data. Accordingly, our model had an R² value of approximately 0.98, indicating a strong correlation between observed and predicted lake water storages (Fig. 8). Moreover, our model has the lowest variance, according to the bias (−0.0031 km³), MAE (0.0059 km³), RMSE (0.0096 km³), and MAPE (25 %). Also, our model has the lowest average relative error at around 14 %. The average relative error in Eqs. (S2), (S3), (S5), (S7), (S9), (S11), (S15), and (S16) ranged from 44 % to 50 %, while the remaining formulas display average relative errors exceeding 50 %. Although all equations achieved R²>0.93, the predicted values have a high variance and tend to either overestimate or underestimate the water storage of glacial lakes. Compared with our method, their bias, MAE, RMSE, and MAPE were all 55 %, 64 %, 52 %, and 64 %, respectively, and thus higher than ours. Eq. (S7) had a better prediction accuracy. However, their bias, MAE, and RMSE values are 82 %, 64 %, and 52 % higher than those of our model, respectively. This indicates a significant estimation error for specific glacial lakes, and both RMSE and MAE are sensitive to outliers. Overall, most of the equations tend to underestimate glacial lake water storages, with the underestimation becoming more pronounced for larger water storages. Nevertheless, we consider the accuracy level of our method to be acceptable due to the lower uncertainty compared to other models, providing an alternative for predicting the water storage of MDLs.

Figure 8 Comparison of the overall performance in glacial lake water storage estimation between our and previous models (a) and comparison of measured and estimated water storage by our model (b).

Table 6 Comparison of all empirical scaling relationships (Eqs. S1–S20) in terms of bias, mean absolute error (MAE), and root mean square error (RMSE), measured in cubic kilometers. See Tables S2 and S3 for details.

4.3 Application of the new model

Considering the frequent occurrence of GLOF events in High-mountain Asia, posing threats to downstream infrastructure and the safety of the lives and properties of the local communities, assessing the water storage of glacial lakes is crucial for the management of potentially hazardous ones (Nie et al., 2023). Therefore, this study employs our model to provide preliminary estimates of glacial lake water storages in the study area.

Glacial lake inventory data (Wang et al., 2020) reveal that in 2018, there were a total of 13 166 glacial lakes (≥0.01 km²) distributed in High-mountain Asia. The dataset highlights a significant increase in both the number and area of GCLs from 1990 to 2018, experiencing remarkable growth of 52 % and 54 %, respectively. Model estimation results indicate that the total glacial lake water storage in the study area was 37.18 km³ in 2018. Over the past 3 decades, the overall MDL water storage increased by 8.94 km³ from 28.24 km³ in 1990, representing growth of approximately 32 %. The expansion rates of glacial lakes varied significantly across different regions (Fig. 9). Notably, the Hindu Kush–Karakoram and the central and eastern parts of the Himalayas to the Hengduan Mountains witnessed the fastest increases in both glacial lake area and water storage.

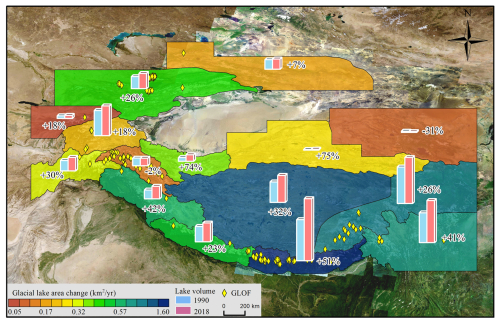
Figure 9 Changes in the area and water storage of glacial lakes from 1990 to 2018 in High-mountain Asia. The base map is a Google Earth image (© Google Earth).

The eastern Himalayas had the largest gain in both the area and the water storage of glacial lakes, concurrently establishing it as a hotspot for frequent GLOFs (Fig. 9). The results indicate that the water storage of 1410 MDLs (≥0.01 km²) within the study area was 9337 ± 990 × 10⁶ m³ in 2022. Among these, GCLs and GULs account for 70 % and 30 % of the total water storage, respectively. Between 1990 and 2022, the total water storage in glacial lakes experienced substantial growth of 162 %. Notably, GCLs contributed 134 %, with an average annual growth rate of 8.8 % a⁻¹, indicating an overall increase of 280 %. In contrast, the change in the water storage of unconnected lakes remained relatively stable, experiencing modest growth of 52 % over the past 32 years, which is considerably lower than that of GCLs.

5 Discussion

5.1 Justification and uncertainty of model assumptions

In this study, we discuss the rationality and uncertainty of the model in three respects. We first assumed that the MDL features a parabolic longitudinal bottom profile and a uniformly distributed sediment layer. The basin morphology of glacial lakes is a result of glacial erosion during the glacier retreat process. Glacier erosion involves certain lateral shear stress, leading to the formation of U-shaped valleys. Glacial lakes develop on these U-shaped valley terrains (Seddik et al., 2009). Therefore, based on the lake bathymetry and the longitudinal bottom profile of the MDLs (Fig. 10), the variations in the underwater morphology of MDLs can be fitted with a parabolic curve. However, when observing trends in underwater topography, it is evident that some large and deep lakes (depth > 100 m), such as Jialong Co and Bienong Co, exhibit relatively flat underwater terrain, while others do not (Fig. 7). This finding aligns with the research conducted by Carrivick and Tweed (2013), who proposed that most proglacial lake basins have flat landforms resulting from extensive sedimentation. These flat terrains, which were previously subdued and smoothed by glaciation, can become covered and obscured by thin layers of silts and clays. Furthermore, it has been suggested by some scholars that in large and deep proglacial lakes, the instability of the glacier margin and the increased likelihood of wave erosion can lead to the erosion of moraine ridges at the lake bottom (Murton and Murton, 2012).

The underwater landforms of some MDLs are not always a smooth parabolic shape. As depicted in Fig. 11, the bottom topography of most glacial lakes exhibits a fluctuating parabolic trend. Golledge and Phillips (2008) and Bennett et al. (2000) revealed that subaqueous moraines in glacial lakes often have linear or sinuous crests and their ridges frequently exhibit heavily glacitectonized sediment structures indicative of compression. Although the presence of subaqueous moraines is uncertain, this perspective offers a plausible explanation for the fluctuations in underwater topography. In conclusion, concerning the formation process of subglacial geomorphology in MDLs and lake bathymetry, both aspects substantiate our postulation that the MDL features a parabolic longitudinal bottom profile. Furthermore, we hypothesize the presence of uniform sediment surface to keep h₁=h₂, although sediment distribution may be non-uniform due to factors such as the position of the ice margin and water density (Carrivick and Tweed, 2013). As a result, the uneven terrain at the bottom of some glacial lakes or the non-uniform distribution of sediments therein constitutes one of the sources of uncertainty in the model.

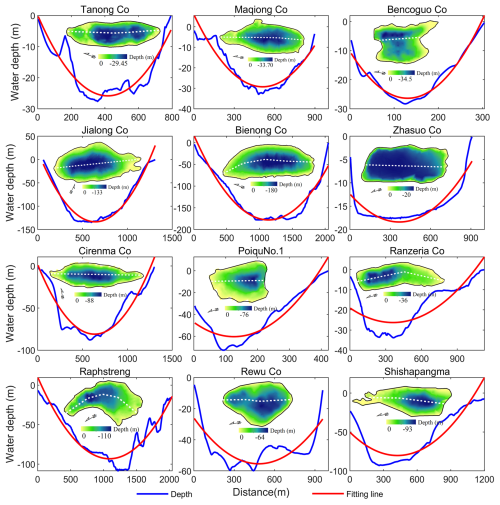
Figure 10 The longitudinal bottom profile underwater topography of the MDLs obtained by bathymetry and the fitting lines of the terrain change trend. (The dotted white line is the longitudinal profile line of the lake.)

The second source of uncertainty in the model arises from the assumption regarding the lake surface of the MDL. Here, we assumed that the MDL surface shape is characterized by an ellipse at both ends and a rectangle in between. MDLs develop on parabolic or U-shaped glacial troughs. A mature MDL, characterized by a relatively stable surface morphology, tends to exhibit an elliptical shape due to its geological characteristics (e.g. GUL lake type in Fig. 5). Similar trends in the boundaries of MDLs are observed in different lake catalog datasets. Furthermore, in this study, MDLs are classified into four types based on their geometric shapes (see Table 1). Treating the complete geometric shape of an MDL as an ellipse allows the model to automatically partition the lake basin structure (e.g. V₁, V₂, and V₃ in Fig. 2) based on the lake's shape coefficient, facilitating the calculation of the water storage for MDLs with different morphologies. However, in reality, as suggested by Rubensdotter and Rosqvist (2009), factors such as the position of the glacier margin, surrounding landscape elevation and topography, and the location and elevation of lake overflow channels can affect the basin morphology of MDLs. For instance, Bencoguo Co and Raphstreng in Fig. 10 do not exhibit the characteristic elliptical shape on the lake surface. This uncertainty in the geometric shape of the lakes may lead to an overestimation of lake water storage in the model, as the maximum width of the lake significantly influences the model results.

Finally, assuming the slope angle near the lake remains constant (a=β) is another aspect contributing to the uncertainty in the model. In actuality, the slopes surrounding the lake exhibit variations influenced by factors such as the glacier tongue's position, the surrounding topography, and the presence of moraine ridges. This variability in slope angles can further contribute to the uncertainty when estimating the model's maximum water depth and water storage.

5.2 Sensitivity of model input parameters

Additionally, our model requires key parameters, namely, w, l, a, m, n, and r, with the relationship between m, n, r, and l defined as $l=m+n+r$. Thus, we only investigated the sensitivity of our model to l, w, and a. Since water depth is closely related to w and a (see Eq. S13), we also conducted parameter sensitivity tests on the estimated water depth using our model. In this study, we employed Jialong Co and Bienong Co as representatives of GUL and GCL of MDLs, respectively, to assess the sensitivity of the model to various parameters across different types of glacial lakes. Figure 11a–f demonstrate the sensitivity of volume (v) and water depth (h) in our model to variations in the maximum length (l), maximum width (w), and slope (a) of glacial lakes. Overall, there was a linear increase in glacial lake volume with changes in length (Fig. 11a and d). As shown in Fig. 11b and e, variations in maximum width exhibited a consistent power-law relationship with volume, where volume increased exponentially with width. The water depth of glacial lakes demonstrated a linear increase with changes in width. The slope of the lake's edge showed a power-law relationship with estimated both water depth and volume (Fig. 11e and f). In summary, when estimating volume using our model, glacial lake width and slope were found to be the most sensitive parameters, followed by the lake's length. Regarding water depth, the model was most sensitive to the slope, followed by the width.

Figure 11 Parameter sensitivity analysis for glacial lake volume estimation using the new model. (Note that the shaded part represents the confidence interval and the definition of parameters in the figure is as shown in Table 2.)

6 Conclusions

Water storage plays a crucial role in predicting peak discharge of GLOFs. This study proposed a mathematically robust and cost-effective approach for estimating lake water storage in regions where field measurements of bathymetry are limited. The new model utilized lake geometry and DEMs to estimate lake water storage. By parameterizing the model based on assumptions such as a parabolic longitudinal bottom profile and consistent slope angles, it offers a reliable estimation of lake water storage.

We validated our parameterization using bathymetry measurements from four representative glacial lakes, namely, Bienong Co, Maqiong Co, Tanong Co, and Jialong Co, located on the Qinghai–Tibet Plateau. Additionally, we applied the new model to 10 glacial lakes with depth measurements conducted during 2020–2021, and we included bathymetry data from 34 other glacial lakes sourced from the published literature. Our model overcomes the autocorrelation issue inherent in earlier area/depth–water storage relationships and incorporates an automated calculation process based on the topography and geometrical parameters specific to MDLs. Compared to other models, our model achieved the lowest average relative error of approximately 14 % when analyzing a dataset of 44 observed lakes, surpassing the > 44 % average relative error from alternative models. This study model will allow researchers and practitioners to better predict potential outburst water storages and peak discharge of MDLs.