A new approach for joint assimilation of cosmic-ray neutron soil moisture and groundwater level data into an integrated terrestrial model

Uncertainties in hydrological simulations can be quantified and reduced through data assimilation (DA). This study explores strategies for assimilating soil moisture (SM) data from Cosmic-Ray Neutron Sensors (CRNS) and groundwater level (GWL) data into the Terrestrial System Modeling Platform (TSMP), which integrates both land surface and subsurface processes. DA experiments incorporating both state and parameter estimation were performed using the localized Ensemble Kalman Filter (LEnKF) within a representative catchment in Germany over the period 2016 to 2018, with cross-validation conducted on non-overlapping years. Univariate assimilation of SM reduced the unbiased root mean square error (ubRMSE) by approximately 50 %, while univariate assimilation of GWL achieved up to a 70 % reduction in ubRMSE at assimilation sites. Improvements in GWL estimates extended up to 5 km from the assimilation points, with ubRMSE reductions ranging between 2 % and 50 %. However, assimilating GWL independently had a negative effect on SM representation, and similarly, assimilating SM alone degraded GWL predictions. To address these issues, a novel multivariate DA framework was developed, enabling SM and GWL to be assimilated independently through separate modules. Groundwater data were used to constrain the water table position, thereby improving the estimation of the boundary between unsaturated and saturated zones and allowing updates to hydraulic conditions within the saturated zone. Meanwhile, SM data improved the representation of hydrological processes in the unsaturated zone. The multivariate assimilation approach resulted in comparable improvements in GWL, SM, and evapotranspiration (ET) at the assimilation sites. Moreover, including parameter estimation alongside state updating further reduced the ubRMSE by up to 17 %.

1 Introduction

Subsurface hydrologic states such as root zone soil moisture (RZSM) and groundwater level (GWL) are critical in regulating surface-subsurface water interactions in hydrologic and land modeling frameworks (Zhang et al., 2016; Maxwell and Condon, 2016). Shallow groundwater controls fluxes between saturated and unsaturated zones, directly influencing soil moisture (SM) dynamics and evapotranspiration (ET) (Chen and Hu, 2004; Scanlon et al., 2023). Accurate representation of RZSM and GWL is crucial for quantifying coupled water-energy exchanges across the soil-plant-atmosphere continuum (Sehgal et al., 2024). However, conventional land surface models often neglect groundwater-surface interactions and their impact on land-atmosphere exchanges (Gleeson et al., 2021; Maxwell et al., 2007; Maxwell and Condon, 2016). Integrated frameworks like the Terrestrial System Modeling Platform (TSMP) (Shrestha et al., 2014) simulate complex interactions among subsurface hydrology, soil processes, vegetation, and atmosphere, effectively capturing spatiotemporal GWL dynamics and their influence on terrestrial ecosystems (Gasper et al., 2014; Kollet et al., 2018; Shams Eddin and Gall, 2024).

Complicated coupled models often involve many parameters, introducing uncertainty and reducing forecast reliability. In groundwater modeling, parameterization simplifications and assumptions cause significant uncertainties due to spatial variability in hydraulic properties and limited in-situ data (Xu et al., 2017). Additional uncertainties stem from input forcings, initial states, and model structure (Beven, 2006; Herrera et al., 2022). Data assimilation (DA) reduces uncertainties in model parameters and states by integrating observations to improve predictions (Liu et al., 2012). The Ensemble Kalman Filter (EnKF) is a widely used sequential DA method that effectively handles complex, high-dimensional nonlinear hydrologic and terrestrial system dynamics (Evensen, 2009; Houtekamer and Zhang, 2016; Evensen, 2003). EnKF has been shown to enhance SM prediction in land surface models (Dan et al., 2020; De Lannoy et al., 2007) and improve groundwater table simulations in subsurface hydrological models (Chen and Zhang, 2006; Tang et al., 2024).

Terrestrial SM can be estimated across various spatial scales using in-situ and remotely sensed (RS) data, which are often assimilated into land surface models to enhance simulation accuracy (Han et al., 2015; Gebler et al., 2019; Strebel et al., 2022). However, in-situ measurements have limited spatial coverage and temporal continuity (Nicolai-Shaw et al., 2015), while RS products like Soil Moisture Active Passive (SMAP) (Kwon et al., 2024; Zhou et al., 2022; Seo et al., 2021) and Soil Moisture Ocean Salinity (SMOS) (Tangdamrongsub et al., 2022; Hostache et al., 2020) offer broader coverage but with coarser resolution, shallow sensing depth, and greater uncertainty. These limitations hinder effective DA, particularly in high-resolution modeling (Zhou et al., 2020; Shen et al., 2024). As an alternative, Cosmic-Ray Neutron Sensors (CRNS) (Zreda et al., 2008) provide reliable, non-invasive SM estimates at the field scale (∼ 18 ha), with deeper penetration (∼ 80 cm) and reduced bias compared to RS products (Zreda et al., 2012; Köhli et al., 2015; Bogena et al., 2022). Recent advances in CRNS techniques, including improved footprint characterization and revised calibration strategies, have substantially enhanced its robustness (Franz et al., 2013; Köhli et al., 2015; Schrön et al., 2017). As a result, CRNS data have been adopted in diverse applications such as hydrology, snow and vegetation monitoring, and land surface modeling (Fersch et al., 2020; Dimitrova-Petrova et al., 2021; Bogena et al., 2022). With the establishment of long-term monitoring networks, CRNS data have also been increasingly integrated into DA frameworks (Baatz et al., 2017; Cooper et al., 2021; Patil et al., 2021). By bridging the scale gap between point measurements and model grids, CRNS serves an effective data source in DA frameworks, thereby reducing model uncertainties and enhancing the reliability of terrestrial hydrology simulations (Shuttleworth et al., 2013; Han et al., 2015; Baatz et al., 2017; Mwangi et al., 2020).

Groundwater table depth is typically monitored via observation wells. Most groundwater DA studies have relied on synthetic experiments. For example, Chen and Zhang (2006) showed that EnKF can reconstruct hydraulic conductivity using synthetic head data. Subsequent studies (Hendricks Franssen and Kinzelbach, 2008; Tong et al., 2011) highlighted the benefits of localization in LEnKF to mitigate filter divergence and improve parameter estimation. Panzeri et al. (2013, 2014) introduced EnKF variants tailored to groundwater DA by solving ensemble-based flow dynamics. These efforts demonstrate EnKF's effectiveness in handling nonlinear, high-dimensional groundwater systems. However, even with synthetic data, EnKF requires careful adaptation-such as localization-to avoid filter instability. Real-world applications pose greater challenges, demanding further modifications to enhance DA performance.

Most DA research has focused on single Earth system components, typically assimilating one variable. However, groundwater and SM are strongly interconnected, and multivariate DA is essential to capture their interactions. Previous studies have applied multivariate EnKF within coupled models like CATHY and Flux-PIHM to jointly assimilate multiple observations, including SM, groundwater, discharge, and land surface fluxes, demonstrating improved estimates of hydrologic states and parameters (Camporese et al., 2009a; Shi et al., 2014; Botto et al., 2018; Shi et al., 2015). Despite being tested primarily on small experimental catchments, these multivariate DA frameworks remain computationally intensive and may involve trade-offs among variables. Some parameters can only be identified under specific hydrological conditions, particularly in strongly nonlinear problems involving the unsaturated zones. To overcome these challenges, some studies have explored alternative multivariate DA strategies within coupled models. Using MIKE-SHE, Zhang et al. (2016) highlighted the importance of spatial and variable-based localization in jointly assimilating SM and groundwater head. Yet, its unsaturated flow is still modeled in one dimension, limiting full system representation. More recently, Zafarmomen et al. (2024) demonstrated that a multivariate particle filter framework assimilating Sentinel-based leaf area index (LAI) and streamflow in a coupled SWAT-MODFLOW model improved estimates of vegetation and hydrologic states. However, the loosely coupled model, in which surface and groundwater components interact via data exchange, may not fully capture integrated dynamics of saturated and unsaturated zones.

The coupled modeling system TSMP integrated with Parallel Data Assimilation Framework (PDAF) (Nerger et al., 2005) has also been utilized for the assimilation of both synthetic and observed SM or groundwater data across various spatial scales. Kurtz et al. (2016) showed its capability in simulating terrestrial states and quantifying uncertainties. Subsequent studies (Gebler et al., 2019; Li et al., 2023a) demonstrated improved SM estimates through assimilation of in-situ and CRNS-derived SM. Brandhorst and Neuweiler (2023) found that jointly updating van Genuchten parameters, porosity, and saturated conductivity optimized SM forecasts. Li et al. (2023b) improved GWL estimates using LEnKF with real GWL data. While most TSMP studies focused on single-variable assimilation, Zhang et al. (2018) and Hung et al. (2022) explored joint assimilation of SM and groundwater in synthetic domains, highlighting the benefits of weakly coupled approach (only updates the saturated subsurface states) in more complex domain. Further research is needed on multivariate assimilation in real-world settings.

Given the challenges of jointly assimilating SM and GWL data into the integrated TSMP framework under realistic conditions in the German Rur catchment, we propose a novel multivariate assimilation method. This study aims to: (i) evaluate the effectiveness of simultaneously assimilating CRNS-based SM and GWL observations using the new method; (ii) compare assimilation performance across different multivariate DA strategies; and (iii) demonstrate the advantages of the proposed approach over conventional single-variable assimilation in improving SM, GWL, and ET predictions. To our knowledge, this study represents the first attempt to simultaneously assimilate in-situ CRNS SM and observed GWL data within TSMP at the catchment scale.

2 Data and Methodology

2.1 Rur catchment

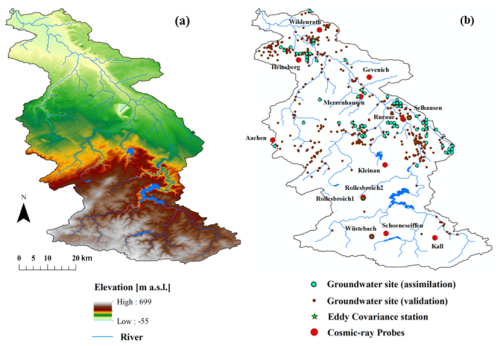
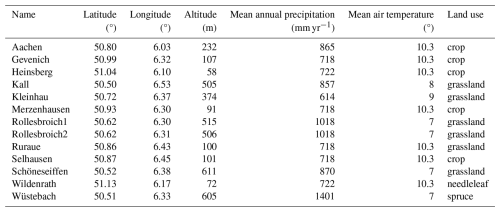
This study focuses on the Rur catchment (Fig. 1), which covers approximately 2354 km² and is mainly located in western Germany, with a small portion extending into the Netherlands and Belgium. The Rur River originates in the southern highlands and flows northward, descending gradually in elevation from about 690 to 15 m above sea level. Elevation strongly influences the regional climate: mean annual temperature decreases from around 10 °C in the northern lowlands to approximately 7 °C in the southern mountains, while precipitation increases from 650 mm to nearly 1300 mm (Bogena et al., 2018). Potential evapotranspiration declines with altitude, ranging from 850 mm in the north to 450 mm in the south (Montzka et al., 2008). Land use varies spatially; the northern lowlands are primarily dominated by agricultural fields, mainly maize and wheat, and extensive grasslands. In contrast, the southern mountainous zone is predominantly forested, featuring both coniferous and broadleaf vegetation types (Waldhoff and Lussem, 2015; Shukla et al., 2023). Additionally, lignite extraction through open-pit mining and urban infrastructure constitute significant components of the land use pattern (Shukla et al., 2023). Hydrogeological characteristics also differ markedly across the catchment: the southern mountainous area is dominated by consolidated bedrock that limits aquifer permeability and groundwater recharge, whereas the northern lowlands, composed of loose sediments, enable higher rates of groundwater recharge (Bogena et al., 2018).

Figure 1 (a) Elevation map of the study area, accompanied by (b) the spatial distribution of hydrological monitoring infrastructure, including groundwater wells, cosmic-ray neutron probes, and flux measurement towers.

2.2 Terrestrial System Modeling Platform (TSMP)

The TSMP framework was developed as a fully coupled land-energy-hydrology model to simulate vertical and lateral exchanges of water and heat across the surface-subsurface continuum (Shrestha et al., 2014). In this study, only the Community Land Model (CLM, version 3.5) (Oleson et al., 2004; Oleson et al., 2008) was employed to simulate terrestrial surface dynamics, while ParFlow (Kollet and Maxwell, 2006, 2008; Kollet et al., 2010), a three-dimensional simulator of groundwater dynamics under variable saturation conditions, was used for subsurface modeling. These two models are coupled through a two-way interaction using the Ocean Atmosphere Sea Ice Soil Model Coupling Toolkit (OASIS-MCT) (Valcke, 2013), which enables the exchange of variables and fluxes between them. Within TSMP, CLM primarily simulates water and energy exchanges, including ET from soil and vegetation, as well as processes such as snow accumulation and melting (Oleson et al., 2004; Oleson et al., 2008). The terrestrial surface heterogeneity is represented in CLM via a hierarchical subgrid system, where individual grid cells are subdivided into distinct land units such as glaciers, lakes, wetlands, urban areas, and vegetated areas. Each land unit may consist of multiple soil or snow columns, within which different plant functional types (PFTs) with unique physiological characteristics can be specified (Oleson et al., 2008). Subsurface hydrology and the representation of surface and groundwater dynamics are handled by ParFlow within the TSMP framework, which takes over soil water movement, overland flow, and aquifer interactions from CLM (Ashby and Falgout, 1996; Jones and Woodward, 2001; Maxwell, 2013). ParFlow couples a two-dimensional surface flow module with a high-performance three-dimensional solver for saturated-unsaturated subsurface flow (Kollet and Maxwell, 2006). It employs the Newton-Krylov iterative algorithm (Jones and Woodward, 2001) to solve the coupled partial differential equations governing interactions between surface and subsurface hydrological systems, including the three-dimensional form of Richards' equation (Richards, 1931) for saturated and unsaturated flow, and the kinematic wave formulation (Lighthill and Whitham, 1955) to simulate surface runoff. Designed for parallel computing, ParFlow efficiently manages large-scale, high-resolution, and highly heterogeneous problems. Further details on the coupling mechanism between CLM and ParFlow are provided in Kollet and Maxwell (2008).

2.3 Model Forcing Data and Observations

2.3.1 Forcing Data from Atmospheric Reanalysis

The TSMP model utilized atmospheric forcing derived from the COSMO-REA6 reanalysis dataset, which provides high spatial resolution of approximately 6 km (0.055°) and hourly temporal frequency (Bollmeyer et al., 2015). This dataset, produced by the German Meteorological Service (DWD), was generated through simulations of the COSMO numerical weather prediction system (Baldauf et al., 2011; Borsche et al., 2016). The primary meteorological variables used to drive TSMP include precipitation, air pressure, specific humidity, air temperature, wind speed, as well as incoming longwave and shortwave radiation.

2.3.2 Terrestrial and Subsurface Data

The Shuttle Radar Topography Mission (SRTM) version 4 dataset with 90 m resolution (Jarvis et al., 2008) provided the digital terrain for the Rur catchment (Fig. 1). Land cover classification was based on Sentinel-2 imagery (Phiri et al., 2020; Drusch et al., 2012) and mapped to PFTs in CLM following Montzka et al. (2021). Monthly LAI data for 2016–2018 were retrieved per PFT using the Sentinel-2 Level 2 Prototype Processor (SL2P) within SNAP (Weiss and Baret, 2020). SL2P employs an artificial neural network trained on global LAI and biophysical data, including PROSAIL-simulated canopy reflectance (Chander et al., 2009; Verrelst et al., 2016; Poulter et al., 2023). For pixel-level LAI estimation, the model inputs include Sentinel-2 canopy-top reflectance and geometric factors such as solar illumination and viewing angles derived from satellite orbit data.

Figure 2 shows the distribution of soil sand and clay fractions derived from the BK50 soil map of North Rhine-Westphalia, which has a mapping scale of 1 : 50 000 (Geologischer Dienst NRW, 2009). Bulk density information was obtained from the European Soil Database (Pano, 2006). These soil texture and density datasets were then used to estimate soil hydraulic properties via the Rosetta pedotransfer functions, as described by Schaap et al. (2001) and Zhang and Schaap (2017). Furthermore, the HK100 subsurface geology map, produced at a scale of 1 : 100 000 by Geologischer Dienst NRW (2011), supplied the data necessary to define the hydraulic conductivity (K_s) for the aquifer layers.

Figure 2 Spatial distribution of sand (a) and clay (b) fractions, along with hydraulic conductivity of aquifer layers (c) within the Rur catchment.

2.3.3 Field Measurements of Soil Moisture, Groundwater, and Evapotranspiration

Soil moisture observations were obtained from 13 CRNS sites (Bogena and Ney, 2021) (see Table 1) distributed across the Rur catchment within the TERrestrial Environmental Observatories (TERENO) framework (Bogena et al., 2018), with preprocessing carried out through the COSMOS-Europe project (Bogena et al., 2022). To prevent redundancy caused by spatial proximity, measurements from Rollesbroich1 and Rollesbroich2 were aggregated into a single representative value, resulting in 12 effective CRNS sites used for DA.

Table 1 Key site-specific information for the CRNS stations.

Groundwater table depth data for assimilation and independent validation were obtained from the Geoportal NRW platform (http://www.geoportal.nrw, last access: 2 May 2025). Given the weak hydraulic connectivity between the RZSM and the deep confined aquifer, this study focused on assimilating data from the unconfined upper aquifer. Wells selected exhibited observation depths between 0 to 20 m and supplied records with at least monthly observations. In total, 616 wells met these criteria during the 2016–2018 period (Fig. 1). Due to the 500 m model resolution and the spatial clustering of observation wells near rivers, multiple wells were often located within a single grid cell or within river cells. To ensure representative observations for assimilation, the median GWL was chosen among multiple wells within a grid cell to minimize potential biases from unusually high or low groundwater levels. Additionally, grid cells adjacent to stream networks were excluded from the assimilation process, as persistent saturation in these areas caused large discrepancies with observed values. Accordingly, wells situated in river grid cells were excluded from the assimilation. Following these screening procedures, 78 wells were selected for DA, while the remaining 465 wells were reserved for independent validation.

Evapotranspiration estimations from various DA experiments were assessed against flux measurements obtained from three eddy covariance monitoring sites located at Selhausen, Rollesbroich, and Wüstebach. These datasets were made available through the TERENO infrastructure (https://www.tereno.net/, last access: 26 August 2024). The eddy covariance-based ET data were quality-controlled, gap-filled, and energy-balance corrected following the procedures outlined in Bogena et al. (2018).

2.4 Localized Ensemble Kalman Filter for Data Assimilation

Data assimilation consists of two main phases: the prediction phase and the correction phase (Carrassi et al., 2018). During the prediction phase, system state estimates are generated solely based on prior historical information. In the correction phase, these predictions are updated by integrating current observational data, which refines the estimates of states and/or parameters and subsequently updates their probability distributions (McLaughlin, 2002).

Hendricks Franssen et al. (2011) developed a method using an augmented state vector to enable the simultaneous assimilation of multiple variables and model parameters. In this study, the focus is on updating soil water content (θ) and groundwater levels, represented by the piezometric head (h). To address parameter uncertainty, hydraulic conductivity (K_s) is also included in the update process. These variables and parameters are combined into a single vector within the EnKF framework, structured as follows:

$$\begin{array}{}\text{(1)}& \mathit{\psi }=\left(\begin{array}{l}\mathit{x}\\ {\log }_{\mathrm{10}}\left(K_s\right)\end{array}\right)=\left(\begin{array}{l}h\\ \mathit{\theta }\\ {\log }_{\mathrm{10}}\left(K_s\right)\end{array}\right)\end{array}$$

State and parameter updates are carried out by integrating observations from SM and GWL (represented as h) into a unified observation vector.

The update formula for ψ is computed individually for each member j (j=1, …, N) of the ensemble as outlined in Evensen (2003). To generate the ensembles, this study considered the uncertainties from both atmospheric inputs and model parameters (e.g., K_s and porosity). The update equation for each realization is as follows:

$$\begin{array}{}\text{(2)}& {\mathit{\psi }}_j^a={\mathit{\psi }}_j^f+\mathit{\alpha }\mathbf{K}\left({\widehat{y}}_j-\mathbf{H}{\mathit{\psi }}_j^f\right)\end{array}$$

where ${\mathit{\psi }}_j^f$ and ${\mathit{\psi }}_j^a$ represent the prior and posterior state-parameter vectors for the jth realization, y_j denotes the measurement vector (e.g., θ and h), K stands for the Kalman gain matrix, and α is a relaxation coefficient (or called damping factor) for parameter (log₁₀K_s) update, with values ranging from 0 to 1. This step is essential to prevent covariance underestimation, a phenomenon that may arise when the ensemble Kalman filter is employed iteratively with limited realizations, leading to a reduced estimate of the ensemble spread (Hendricks Franssen and Kinzelbach, 2008).

The K matrix is defined by the following equation:

$$\begin{array}{}\text{(3)}& \mathbf{K}={\mathbf{PH}}^T{\left({\mathbf{HPH}}^T+\mathbf{R}\right)}^{-\mathrm{1}}\end{array}$$

The observation operator H links the observation vector to the state vector. The matrix P represents the covariance of the model states and uncertain parameters, while R denotes the covariance matrix for measurement error. The performance of the filter relies on the state-error covariance matrix P, which is estimated based on the members of ensemble (Evensen, 2003; Houtekamer and Mitchell, 1998).

Due to the small ensemble size, spurious correlations may arise between distant model grid points, potentially distorting the covariance estimation. To address this, we employed the localized EnKF approach introduced by Houtekamer and Mitchell (1998), which incorporates spatial localization to confine observational influence within a specified radius (Hamill et al., 2001). This is achieved by modifying PH^T to ρ∘PH^T in Eq. (3), where the Schur product involves a localization matrix ρ and the original cross-covariance. The localization weights in ρ are computed using a compactly supported fifth-order function proposed by Gaspari and Cohn (1999), ensuring smooth spatial falloff of influence.

The correlation ω, representing an element in ρ that links a grid point to an observation, can be approximated as follows:

$$\begin{array}{}\text{(4)}& \begin{array}{rl}& \mathit{\omega }(l,e)\\ & =\left\{\begin{array}{ll}\mathrm{1}-\frac{\mathrm{1}}{\mathrm{4}}{\left(\frac{e}{l}\right)}^{\mathrm{5}}+\frac{\mathrm{1}}{\mathrm{2}}{\left(\frac{e}{l}\right)}^{\mathrm{4}}+\frac{\mathrm{5}}{\mathrm{8}}{\left(\frac{e}{l}\right)}^{\mathrm{3}}-\frac{\mathrm{5}}{\mathrm{3}},& \mathrm{0}\le e\le l\\ \frac{\mathrm{1}}{\mathrm{12}}{\left(\frac{e}{l}\right)}^{\mathrm{5}}-\frac{\mathrm{1}}{\mathrm{2}}{\left(\frac{e}{l}\right)}^{\mathrm{4}}+\frac{\mathrm{5}}{\mathrm{8}}{\left(\frac{e}{l}\right)}^{\mathrm{3}}+\frac{\mathrm{5}}{\mathrm{3}}{\left(\frac{e}{l}\right)}^{\mathrm{2}}-\mathrm{5}\left(\frac{e}{l}\right)+\mathrm{4}-\frac{\mathrm{2}}{\mathrm{3}}{\left(\frac{e}{l}\right)}^{-\mathrm{1}},& l<e\le \mathrm{2}l\\ \mathrm{0},& e>\mathrm{2}l\end{array}\right.\end{array}\end{array}$$

Here, l refers to the chosen localization radius, while e indicates the direct distance from the measurement location to the particular grid cell being analyzed. The correlation value ω varies with this distance, attaining a maximum of 1 directly at the observation point and gradually decreasing to zero once the distance exceeds twice the radius l.

In this study, SM observations for assimilation were obtained from CRNS. As CRNS measurement depth depends on SM conditions, it was first estimated following Schrön et al. (2017). The PDAF framework then mapped CRNS data to soil layers within the estimated penetration depth (Fig. 3), allowing updates to the simulated SM profiles. After assimilation, modeled SM was aggregated using a weighted average and compared to CRNS data for validation, as detailed in Schrön et al. (2017). The Rur catchment model consists of 100 × 162 grid cells with a resolution of 500 m × 500 m. Following previous EnKF studies using 12 CRNS stations (Baatz et al., 2017; Li et al., 2023a), we set the localization radius to ∼ 100 km to ensure that assimilation effects cover the entire study area. In the LEnKF framework, a fifth-order polynomial (Eq. 4) is applied to gradually reduce update magnitudes with distance, distinguishing it from the standard EnKF approach.

Figure 3 Conceptual diagram illustrating the assimilation of CRNS-based soil moisture and groundwater level (pressure head) observations into the TSMP system (CLM-ParFlow) using the PDAF framework. Here, θ^f and θ^a represent the predicted and updated states of soil moisture in the unsaturated zone, respectively, while h^f and h^a denote the predicted and updated pressure heads in the saturated zone. Groundwater level measurements are converted into pressure head values to serve as input data.

Within the TSMP-PDAF framework, GWL observations were converted to pressure head values for saturated layers based on hydrostatic equilibrium (Zhang et al., 2018). The saturated zone was defined using the shallowest water table values from the ensemble. An update range was constrained using a horizontal localization radius of 5 km, derived from spatial correlation patterns of GWL.

Earlier research by Zhang et al. (2018) showed that in TSMP, assimilating SM and/or GWL enables updates to all relevant subsurface states via DA. In this fully coupled DA configuration of Zhang et al. (2018), cross-variable covariances ensured that observations of one variable (e.g., SM) could directly adjust others (e.g., GWL). Later, Hung et al. (2022) applied GWL assimilation restricted to the saturated zones and demonstrated that this approach outperformed the fully coupled strategy of Zhang et al. (2018). In this study, we develop a new weakly coupled DA scheme that introduces separate update restrictions for each observation type: GWL observations are used to update only saturated cells, while SM observations are used to update only unsaturated zones. This design minimizes potential spurious cross-variable correlations and enhances the robustness of multivariate assimilation. Additionally, updates are applied asynchronously to account for the different temporal dynamics of the variables: SM, which changes more rapidly, is typically updated daily, whereas groundwater, with slower dynamics, is updated weekly. Furthermore, unlike previous DA studies of TSMP, which generally used the same localization radius for joint GWL and SM assimilation, our approach applies different localization radii for the two variables, accounting for their distinct spatial correlation characteristics.

3 Setup of Model and Experiments

3.1 Generation of Ensemble Members

To represent input uncertainty, the CLM-ParFlow system was perturbed by modifying atmospheric forcings and subsurface properties, including saturated hydraulic conductivity and soil porosity, resulting in 128 ensemble realizations. Table 2 summarizes the statistical metrics of meteorological perturbations. Precipitation, air temperature, and shortwave and longwave radiation were stochastically perturbed using a multivariate normal framework with temporal dependencies. A first-order autoregressive model was applied to capture temporal structure (Han et al., 2015). Standard deviations and time-series dependencies were informed by previous regional-scale DA studies (Reichle et al., 2010; Baatz et al., 2017). To preserve mass-energy balance, lognormally distributed noise with correction was added to shortwave radiation and precipitation (Yamamoto, 2007).

Table 2 Statistics of atmospheric variable perturbations. The last column presents their cross-correlations, arranged in the same order as the variables listed in the first column of the table.

The model domain is discretized at 500 m resolution horizontally and extends 100 m vertically with 25 layers of increasing thickness. The top 10 layers (to 3 m depth) align with CLM-defined soil layers, while deeper layers represent bedrock. Porosity and hydraulic conductivity were perturbed separately in soil and aquifer zones. Soil hydraulic parameters for the Mualem-Van Genuchten model were derived using Rosetta (Schaap et al., 2001; Zhang and Schaap, 2017), based on geostatistically simulated sand and clay content using a spherical variogram (mean 0, variance 50 %², range 12.5 km). Silt was calculated as the residual. Soil textures were constrained to 0 %–100 %, and Rosetta estimated spatially variable porosity and K_s. Aquifer K_s values were taken from a hydrogeological map (Fig. 2) and perturbed by spatially uniform noise on log₁₀K_s (range: −0.5 to 0.5), while aquifer porosity was fixed at 0.15.

3.2 Configuration of Data Assimilation Experiments

Each ensemble member underwent a spin-up to achieve hydrologic equilibrium specific to its realization. This involved two phases: first, ParFlow was run for 100 years using initial groundwater depths averaged from Bogena et al. (2005), driven by 30-year average recharge derived from climatological inputs (precipitation and actual evapotranspiration) provided by the German Meteorological Service. Second, the steady-state output from ParFlow initialized the coupled CLM-ParFlow model, which was then repeatedly forced with 2015 atmospheric inputs for ten years. Following spin-up, DA experiments were conducted over three years (1 January 2016–31 December 2018), assimilating GWL from 78 wells and SM from 12 CRNS sites using LEnKF.

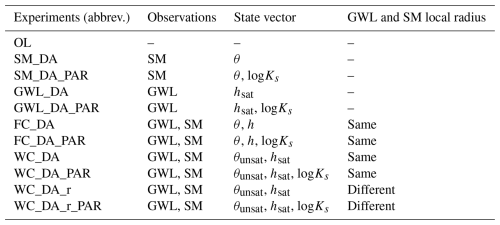
11 DA experiments (Table 3) were conducted to assess assimilation performance, differing in observation type, state vector composition, and localization strategy. The open loop (OL) experiment, performed without assimilation, served as the reference for DA comparisons. SM_DA assimilated daily SM observations from CRNS (observation error of 0.03 cm³ cm⁻³) with 100 km localization radius. GWL_DA assimilated weekly GWL observations, with an observational error of 0.05 m, using a 5 km localization radius, updating only hydraulic head (h) in the saturated zone. FC_DA assimilated both SM and GWL using the fully coupled DA strategy, with the state vector including h and θ in all subsurface layers. θ and h were updated daily and weekly, respectively, both with a 5 km localization radius. WC_DA used the weakly coupled scheme, with h updated only in the saturated zone and θ only in the unsaturated zone; all other settings were the same as FC_DA. Moreover, WC_DA_r followed the same setup as WC_DA, except that the localization radius differed between the two variables: 5 km for GWL and 100 km for SM. For all DA experiments, the suffix _PAR indicates that, in addition to state updates, the saturated hydraulic conductivity (logK_s) was updated every seven days using a damping factor of 0.1. The _PAR runs were initialized from the same spun-up equilibrium state as their corresponding state-update experiments, and the gradual parameter updates ensured that changes remained small and did not disturb the equilibrium state too much, thereby avoiding the need for additional spin-ups. Furthermore, parameter validation involved applying K_s updated from one year to OL simulations in other years (e.g., using updated K_s from 2016 in 2017–2018).

Table 3 Summary of the data assimilation experiments conducted. Observational data include groundwater levels (GWL) and soil moisture (SM). Key variables consist of pressure head (h), soil water content (θ), and hydraulic conductivity (K_s). The terms “unsat” and “sat” distinguish between the unsaturated and saturated domains, respectively. Experiments FC_DA and FC_DA_PAR were performed using the fully coupled framework, following the methodology described by Hung et al. (2022).

3.3 Model Performance Assessment

Simulation outputs from the OL run along with multiple assimilation experiments were evaluated against daily observed data for GWL, SM, and ET. The assessment employed statistical indicators including the root mean square error (RMSE), unbiased RMSE (ubRMSE), and Pearson's correlation coefficient (R). Among these, ubRMSE was emphasized in our analysis because it is widely applied in DA research and facilitates comparison with previous studies. To avoid redundancy, detailed results for RMSE and R are presented in the Supplement tables to ensure a comprehensive evaluation of model performance.

The RMSE at a given time step t was computed using the following formula:

$$\begin{array}{}\text{(5)}& {\mathrm{RMSE}}_t=\sqrt{{\displaystyle \frac{{\sum }_{i=\mathrm{1}}^{N_{\mathrm{obs}}}{\left(y_t^{\mathrm{sim}}-y_t^{\mathrm{obs}}\right)}^{\mathrm{2}}}{N_{\mathrm{obs}}}}},\end{array}$$

The ubRMSE at each time step t was computed using:

$$\begin{array}{}\text{(6)}& {\mathrm{ubRMSE}}_t=\sqrt{{\displaystyle \frac{{\sum }_{i=\mathrm{1}}^{N_{\mathrm{obs}}}{\left[\left(y_t^{\mathrm{sim}}-\stackrel{\mathrm{‾}}{y^{\mathrm{sim}}}\right)-\left(y_t^{\mathrm{obs}}-\stackrel{\mathrm{‾}}{y^{\mathrm{obs}}}\right)\right]}^{\mathrm{2}}}{N_{\mathrm{obs}}}}},\end{array}$$

Calculation of R is based on the following expression:

$$\begin{array}{}\text{(7)}& R={\displaystyle \frac{{\sum }_{t=\mathrm{1}}^n\left(y_t^{\mathrm{obs}}-\stackrel{\mathrm{‾}}{y^{\mathrm{obs}}}\right)\left(y_t^{\mathrm{sim}}-\stackrel{\mathrm{‾}}{y^{\mathrm{sim}}}\right)}{\sqrt{{\sum }_{t=\mathrm{1}}^n{\left(y_t^{\mathrm{obs}}-\stackrel{\mathrm{‾}}{y^{\mathrm{obs}}}\right)}^{\mathrm{2}}{\sum }_{t=\mathrm{1}}^n{\left(y_t^{\mathrm{sim}}-\stackrel{\mathrm{‾}}{y^{\mathrm{sim}}}\right)}^{\mathrm{2}}}}},\end{array}$$

Here, $y_t^{\mathrm{sim}}$ denotes the ensemble-mean simulation for the target variable (SM, GWL, or ET) at a given time step t, originating from either an OL or DA experiment, while $y_t^{\mathrm{obs}}$ refers to the matching observation. N_obs represents the count of available observations at time t, and n indicates the overall count of evaluated temporal intervals.

4 Results

4.1 Univariate Soil Moisture Assimilation

Table 4 compares the ubRMSE of SM, ET, and GWL between the baseline OL simulation and the SM only assimilation scenarios (SM_DA and SM_DA_PAR), while additional metrics including RMSE and R for SM and ET are provided in Table S1 in the Supplement. Assimilating CRNS SM observations significantly improved SM prediction accuracy at monitored sites during 2016–2018, as shown in Supplement Figs. S1–S3. In the SM_DA scenario, SM ubRMSE and RMSE decreased by over 45 % and 50 %, respectively. Joint updates of states and parameters (SM_DA_ PAR) outperformed state-only assimilation. Correlation coefficients for SM improved notably in DA runs (R= 0.85–0.90) versus OL (R= 0.61–0.63) (Table S1). However, SM assimilation had limited impact on ET, with RMSE reduced by less than 3 % compared to OL. However, GWL ubRMSE metric showed variable changes when only SM was assimilated, ranging from −7 % to 15 % across individual years, where positive values indicate a deterioration in performance. Over the 2016–2018 period, the average change in ubRMSE was small, corresponding to 3.87 % for SM_DA and −0.41 % for SM_DA_PAR. Overall, SM assimilation had a minor negative effect on GWL, with some annual variability.

Table 4 Annual unbiased root mean square error of volumetric soil moisture, evapotranspiration, and groundwater level during 2016-2018 for the open-loop (OL) and univariate soil moisture data assimilation experiments (SM_DA and SM_DA_PAR).

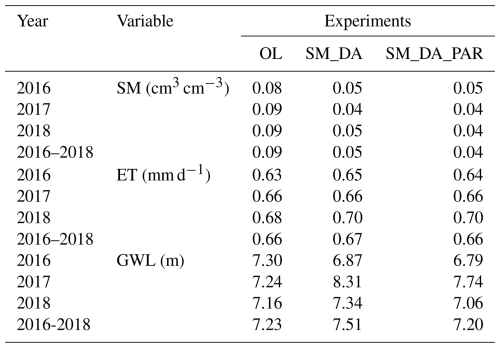
Figure 4 illustrates the differences in SM, ET, and GWL between the OL simulation and the univariate SM assimilation scenarios for the year 2018, with corresponding findings for 2016 and 2017 shown in Figs. S4 and S5. In the scenarios involving only state estimation and those involving simultaneous parameter estimation, assimilation led to distinct spatial changes in SM distribution across the catchment-marked by increased moisture in the northern areas and a drying trend in the south. For 2018, the spatial distribution in annual SM was similar for both the state-only and joint state-parameter update runs, indicating a limited parameter influence that year. In contrast, the impact of parameter updates on SM was more pronounced in 2016 and 2017, likely due to differing hydrological conditions. Specifically, under the wetter conditions of 2016, elevated SM levels enhanced spatial coherence, thereby increasing sensitivity to parameter adjustments (Li et al., 2023a).

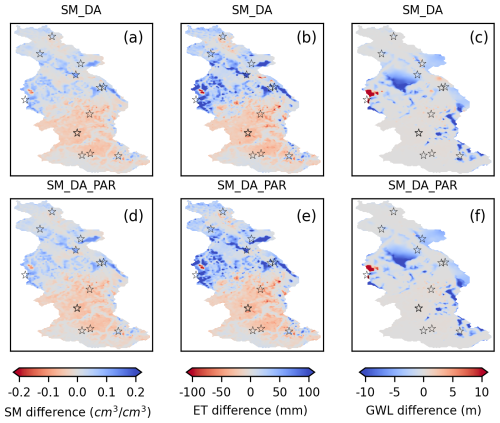
Figure 4 Spatial variations in annual soil moisture (0–80 cm), evapotranspiration, and groundwater level for 2018 are shown in panels (a)–(c), depicting the differences between SM_DA and OL simulations (SM_DA minus OL). Panels (d)–(f) present similar contrasts between SM_DA_PAR and OL (SM_DA_PAR minus OL). Black pentagrams mark the locations of the CRNS monitoring stations.

The regional distribution of ET changes closely followed the corresponding SM patterns, indicating a direct influence of SM assimilation on ET dynamics. Within the southern region of the catchment, both SM_DA and SM_DA_PAR simulations exhibited reduced ET compared to the OL simulation, consistent with lower SM levels. In contrast, the northern catchment showed increased ET linked to higher SM following assimilation. The impact of SM assimilation on ET in the southern region was relatively limited, with changes generally below 50 mm yr⁻¹, as ET there was primarily constrained by available energy. However, in the northern Rur subregion-characterized by lower precipitation-ET responded more strongly to assimilation, with increases exceeding 100 mm yr⁻¹ following the rise in SM. Notable spatial variations in GWL also emerged across certain areas of the catchment after assimilation. Since TSMP is a comprehensive system, assimilation of SM alone also influenced GWL dynamics. Additionally, due to the SM localization radius covering the entire basin and the inclusion of lateral groundwater flow in TSMP, changes in GWL were not confined to areas near CRNS locations. While GWL spatial patterns showed some alignment with those of SM, they were less consistently matched than the patterns observed in ET.

4.2 Univariate Groundwater Level Assimilation

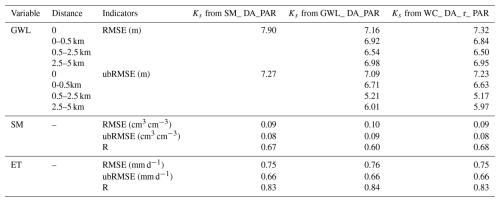
Table 5 provides an overview of simulation results for GWL, SM, and ET across multiple years, comparing outputs from the OL and univariate GWL assimilation experiments. The unbiased RMSE of GWL was evaluated at update points and at validation sites categorized by their distance from these points, with consistent patterns observed across all distance groups. A more detailed assessment of GWL performance, including RMSE metrics, is available in Table S2. Temporal dynamics of GWL in response to assimilation are illustrated in Fig. S6, which depicts GWL evolution at 12 monitoring locations. Substantial improvements in GWL simulations were observed at assimilation sites in the GWL_DA experiment, where the annual ubRMSE was reduced by approximately 60 % relative to the OL run. When both states and parameters were jointly updated in the GWL_DA_PAR experiment, the ubRMSE further decreased to 2.04 m, corresponding to a ∼ 72 % reduction compared to OL. While notable improvements were evident near assimilation wells, the performance gains declined with increasing distance from these locations. Joint updating of states and parameters (GWL_DA_PAR) consistently outperformed state-only updates (GWL_DA). Within the 0–0.5 km ranges from assimilation points, GWL ubRMSE decreased from 6.96 to 3.78 m, reflecting a 46 % improvement. Beyond 0.5 km, ubRMSE in the GWL_DA_PAR experiment remained at least 10 % lower than in OL. In contrast to the large improvements in GWL, univariate GWL assimilation generally had a limited negative impact on SM, with interannual variability. Over the 2016–2018 period, the average SM ubRMSE was 0.09 cm³ cm⁻³ in GWL_DA and 0.11 cm³ cm⁻³ in GWL_DA_PAR, compared with 0.09 cm³ cm⁻³ in OL. In individual years, SM ubRMSE ranged from 0.09 to 0.10 cm³ cm⁻³ in GWL_DA, corresponding to annual changes of 0 %–25 % compared with OL value in each respective year. In GWL_DA_PAR, SM ubRMSE further increased to 0.10–0.11 cm³ cm⁻³, reflecting annual rises of over 20 % relative to OL values of the corresponding year. This absence of enhancement in SM was likewise observed in ET, since univariate GWL assimilation did not improve SM simulations. Consequently, ET simulations exhibited minimal change, with ubRMSE, RMSE, and R metrics showing negligible differences, as summarized in Table S1.

Table 5 Annual unbiased root mean square error of groundwater level, volumetric soil moisture, and evapotranspiration for 2016–2018, evaluated for the open-loop (OL) and univariate groundwater level assimilation scenarios (GWL_DA and GWL_DA_PAR). Note: “0” refers to assimilation points; validation sites are grouped by their distance from these points into three categories: less than 0.5 km, between 0.5 and 2.5 km, and between 2.5 and 5 km.

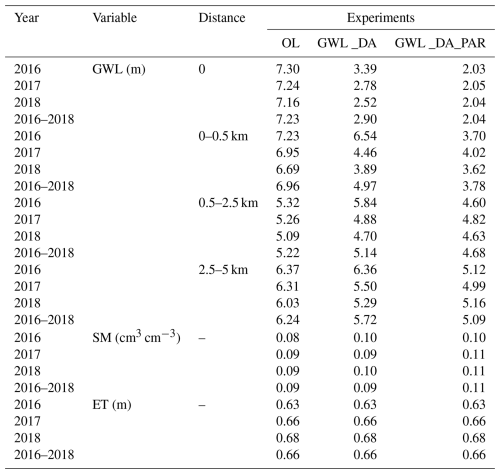
Figure 5 illustrates the annual variations in multiple variables by comparing the univariate GWL assimilation scenarios with the OL simulation for 2018, while corresponding results for 2016 and 2017 are provided in Figs. S7 and S8. A 5 km localization radius was applied during groundwater assimilation, leading to notable GWL variations primarily in the vicinity of the assimilation points. In contrast, the hilly southern region-characterized by sparse measurement locations-exhibited minimal GWL changes. Although spatial differences in GWL between the state-only and state-parameter update runs were generally small, several areas in the central catchment experienced distinct GWL adjustments resulting from parameter updates. Groundwater assimilation also influenced SM estimates, particularly near assimilation locations where changes in SM closely corresponded to GWL variations. However, since most CRNS sites were located at greater distances from the assimilated groundwater wells, SM simulations at those CRNS locations remained largely unaffected. Furthermore, annual SM estimates exhibited only minor differences between the state-only and state-parameter GWL assimilation runs. The influence on ET was similarly limited to areas surrounding the GWL update points due to the applied localization radius. It is worth highlighting that the distributions of variations in SM and ET showed strong consistency across space.

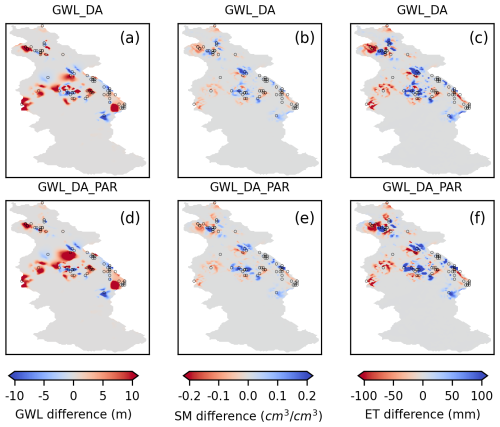
Figure 5 Spatial variations in annual groundwater level, soil moisture (0–80 cm), and evapotranspiration for 2018 are shown in panels (a)–(c), illustrating the differences between GWL_DA and OL simulations (GWL_DA minus OL). Panels (d)–(f) present similar contrasts between GWL_DA_PAR and OL (GWL_DA_PAR minus OL). Black hollow circles indicate the locations of groundwater monitoring wells.

4.3 Multivariate Data Assimilation of Soil Moisture and Groundwater Level

Table 6 summarizes the ubRMSE values of GWL, SM, and ET from various multivariate assimilation scenarios between 2016 and 2018. Additional RMSE results for groundwater table depth are provided in Table S3. Among all experiments, the WC_DA_PAR scenario produced the best-performing groundwater estimates at the assimilated sites, lowering the ubRMSE substantially-dropping it from 7.23 to 2.05 m, representing a reduction of nearly three-quarters. A similar level of accuracy was attained by the GWL_DA_PAR run, yielding a ubRMSE of 2.04 m. At validation sites within 0 to 0.5 km of assimilation points, the multivariate assimilation of SM and GWL slightly underperformed compared to the standalone groundwater update in predicting GWL, although the difference was not statistically significant. Across all single- and multi-variable assimilation scenarios, WC_DA_r_PAR achieved the minimum ubRMSE (4.56 m) for GWL predictions within the 0.5–2.5 km range from assimilation sites. In comparison, the FC_DA_PAR experiment yielded the lowest ubRMSE value (4.91 m) at sites 2.5 to 5 km away from the assimilation points.

Table 6 Annual unbiased root mean square error of groundwater level, soil moisture, and evapotranspiration during 2016–2018, evaluated for the open-loop (OL) and multivariate assimilation scenarios (FC_DA, FC_DA_PAR, WC_DA, WC_DA_PAR, WC_DA_r, and WC_DA_r_PAR). Note: “0” denotes assimilation locations; validation sites are grouped by their distance from these points into three ranges: less than 0.5, 0.5 to 2.5, and 2.5 to 5 km.

In the multivariate DA experiments, SM depiction showed a significant improvement, with WC_DA_PAR and WC_DA_r_PAR yielding the greatest ubRMSE decrease of 50 %. Detailed RMSE and R statistics for SM and ET are provided in Table S4. However, SM evaluation results under fully coupled joint SM and groundwater assimilation scenarios (FC_DA or FC_DA_PAR) failed to surpass the outcomes from SM-only assimilation runs (SM_DA or SM_DA_PAR), suggesting that incorporating groundwater data did not improve SM representation in the fully coupled system. Multivariate assimilation produced a slight enhancement in ET simulation accuracy, reflected by an approximate 3 % decrease in RMSE, though this was not evident in ubRMSE values. Furthermore, applying parameter updates had minimal impact on ET simulation results across these experiments.

To facilitate comparison, Fig. 6 presents the ubRMSE values from both univariate and multivariate assimilation runs. In contrast with the OL simulation, the FC_DA and FC_DA_PAR experiments showed improved ability to reproduce SM and groundwater dynamics. Nonetheless, the results were inferior to those obtained through individual assimilation of SM or GWL for their corresponding hydrological variables. Alternatively, the weakly integrated schemes (WC_DA and WC_DA_PAR) yielded improved estimates of SM and GWL relative to the fully coupled configuration. According to Fig. 6, WC_DA_r and WC_DA_r_PAR demonstrated superior capability in replicating GWL and SM at observation sites relative to the remaining multivariate assimilation approaches. Within the 2.5 to 5 km range from assimilation locations, predictive accuracy declined slightly compared to the fully coupled configuration, possibly attributed to the broader localization radius applied during SM assimilation, which imposed a more pronounced effect on groundwater estimation. By way of reference, assimilating SM alone showed that updating SM led to decreased accuracy in GWL estimates.

Figure 6 Comparison of unbiased root mean square error (ubRMSE) for groundwater level (GWL, m) at different distances from assimilation points, alongside soil moisture (SM, cm³ cm⁻³) results from both univariate and multivariate assimilation runs. Groundwater level metrics are shown on the left y-axis, while soil moisture values correspond to the right y-axis.

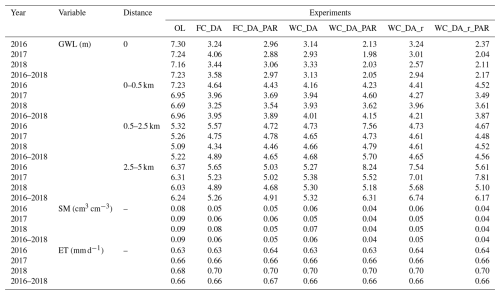
Figure 7 illustrates the annual changes in GWL, SM, and ET for the Rur catchment in 2018, comparing various multivariate assimilation experiments with the OL simulation. Since the results from combined state-parameter updates closely matched those from state-only updates, only the joint state-parameter updating results are presented. Outcomes for 2016 and 2017 are presented in Figs. S9 and S10, respectively. In the WC_DA_PAR scenario, changes in GWL estimates were highly consistent with those from the GWL-only DA runs. This consistency arises from using the same groundwater updating approach, specifically updating only the hydraulic pressure confined to the saturated zone. Notable GWL variations were also observed in areas without direct groundwater assimilation points. These changes likely resulted from SM updates within the multivariate assimilation scenarios, particularly in the FC_DA_PAR and WC_DA_r_PAR experiments. The spatial distribution of SM in the WC_DA_r_PAR run was very similar to that of the univariate SM assimilation, since both used the identical assimilation localization radius. Due to the smaller 5 km assimilation radius applied in the FC_DA_PAR and WC_DA_PAR runs, SM changes remained largely limited to areas close to assimilation sites. Significant variations in annual SM were also detected near groundwater monitoring points in the northern catchment, indicating that combined assimilation of SM and groundwater influences SM prediction accuracy. The spatial pattern of ET aligned closely with SM, reflecting ET's primary control by SM variability. Moreover, in the multivariate assimilation runs, SM at certain locations adjacent to groundwater assimilation points was influenced by GWL adjustments, resulting in ET fluctuations that might contrast with those observed in univariate SM assimilation.

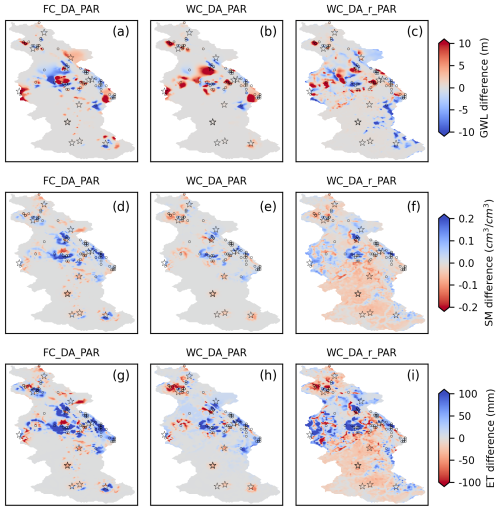
Figure 7 Spatial variations in the 2018 annual differences of groundwater level, 0–80 cm soil moisture, and evapotranspiration are presented in panels (a), (d), (g), showing comparisons between the multivariate data assimilation scenario FC_DA_PAR and the open-loop (OL) run. Panels (b), (e), (h) and (c), (f), (i) display the corresponding differences for the WC_DA_PAR and WC_DA_r_PAR scenarios, respectively. The locations of CRNS stations and assimilated groundwater wells are marked by black pentagrams and circles.

To enable a comprehensive comparison between single-variable and multivariate assimilation approaches, Fig. 8 presents the time-series variations of SM and GWL recorded at a CRNS site and a monitoring well throughout all assimilation scenarios. The simulated SM patterns from the state-only (GWL_DA) and state-parameter (GWL_DA_PAR) groundwater assimilation runs closely follow those of the OL simulation, indicating that assimilating GWL data has little impact on SM estimates for these scenarios. Likewise, assimilating SM alone produced only minor changes in GWL. When GWL data were assimilated, the modeled GWL progressively converged toward the observed values gradually. Within the multivariate assimilation runs, the fully coupled setups (FC_DA and FC_DA_PAR) showed the largest discrepancies in GWL and SM compared to observations. In general, differences in modeled SM and GWL were small when comparing assimilation experiments updating both states and parameters to those updating states alone.

Figure 8 Temporal dynamics of volumetric soil moisture at the Kall CRNS site and groundwater levels at a selected observation well throughout 2018 are shown for the open-loop (OL) simulation alongside various assimilation scenarios. Panels (a)–(b) present results for the SM_DA and SM_DA_PAR scenarios; panels (c)–(d) correspond to GWL_DA and GWL_DA_PAR; panels (e)–(f) display FC_DA and FC_DA_PAR outcomes; panels (g)–(h) illustrate WC_DA and WC_DA_PAR; and panels (i)–(j) show results for the WC_DA_r and WC_DA_r_PAR configurations.

4.4 Impact of ParameterK_s Updates on Model Performance

Across all DA experiments, incorporating parameter updates consistently outperformed relying solely on state updates. To assess the performance of the adjusted parameters, they were implemented in OL simulations for independent years and evaluated against results obtained using the initial parameter set. Table 7 summarizes evaluation metrics-RMSE, ubRMSE, and R, which serve as indicators of model performance for various variables during the K_s validation period. Improvements in SM estimates were attributed to the updated K_s derived from the SM_DA_PAR scenarios, as reflected by enhanced results across all evaluation metrics. Applying K_s values estimated from SM_DA_PAR reduced the SM ubRMSE from 0.09 to 0.08 cm³ cm⁻³ in the OL validation runs. Nevertheless, the updated K_s did not improve GWL predictions, nor were significant enhancements observed in ET simulations.

Table 7 Summary of performance metrics for simulated groundwater level, volumetric soil moisture, and evapotranspiration across all validation runs during the 2016–2018 period. Note: “0” refers to groundwater assimilation locations; validation sites are categorized by their distance from these points as follows: less than 0.5, 0.5 to 2.5, and 2.5 to 5 km.

Applying the K_s values updated through the GWL_DA_PAR experiments in OL runs for other independent years resulted in a slight reduction (less than 2 %) in the overall RMSE and ubRMSE of GWL compared to simulations using the original K_s. Additionally, enhanced GWL modeling was observed in unassimilated areas following the incorporation of the revised K_s. Specifically, within a range of 2.5–5 km from the assimilation points, the modeled GWL improved by approximately 4 %, indicated by a decrease in ubRMSE from 6.24 to 6.01 m. However, no evident improvements were found in SM and ET estimates after applying the revised K_s derived through the univariate GWL assimilation (GWL_DA_PAR) experiments.

No noticeable improvement in simulated GWL was observed at the assimilation points during the OL validation using the revised K_s derived from the WC_DA_r_PAR scenario. Compared to the GWL_DA_PAR experiment, the K_s values estimated from WC_DA_r_PAR produced more accurate GWL predictions at unassimilated grid locations. Within the 0–0.5 km and 2.5–5 km ranges from assimilation points, the GWL ubRMSE decreased by over 4 %. Furthermore, the revised K_s enhanced SM simulation performance, demonstrated by a reduction in SM ubRMSE from 0.09 cm³ cm⁻³ with the original K_s to 0.08 cm³ cm⁻³ following the WC_DA_r_PAR assimilation. Although the revised K_s obtained from the WC_DA_r_PAR scenario brought some improvements, its impact on ET simulation remained minimal.

Figure 9 illustrates the differences in the mean spatial values of log₁₀K_s at soil depths of 2 cm and 10 m for the SM_DA_ PAR, GWL_DA_PAR, and WC_DA_r_PAR scenarios compared with the reference OL simulation. The outcomes illustrated correspond to the year 2018, with supplementary outcomes for 2016 and 2017 provided in Figures S11 and S12. The spatial patterns of K_s modifications were consistent across all three years. In the SM_DA_PAR experiment, changes in K_s occurred both within the root zone and, indirectly, extended to the saturated zone at 10 m depth. Such modifications in K_s may have a significant influence on the accuracy of GWL estimation. Conversely, during the GWL_DA_PAR run, state modifications were limited to the saturated layers, producing pronounced changes in K_s primarily at the groundwater assimilation points in that zone. No significant impact on K_s was observed in the unsaturated zone due to these updates.

Figure 9 Spatial comparison of ensemble mean log₁₀K_s between the open-loop simulation and various data assimilation schemes for the year 2018. Panels (a) and (d) show results for the SM_DA_PAR scenario; panels (b) and (e) present outputs for GWL_DA_PAR; panels (c) and (f) depict results for WC_DA_r_PAR. The upper row corresponds to estimates at 2 cm soil depth, while the lower row represents values at 10 m depth. Locations of CRNS sites and assimilated groundwater wells are marked by red pentagrams and black circles, respectively.

Within the WC_DA_r_PAR scenario, the assimilation processes for SM and GWL were conducted separately. Consequently, modifications in K_s within the unsaturated zone were projected to mirror the patterns identified in the SM_DA_PAR experiment, whereas variations in the saturated layers were anticipated to correspond to those seen in the GWL_DA_PAR experiment. These findings indicate that the distribution of K_s modifications across the affected regions closely match those from the individual assimilation runs. Nevertheless, due to the interdependence between SM and GWL updates in the joint assimilation, the resulting K_s modifications exhibit more intricate and integrated system behavior, rather than merely a straightforward combination of changes seen in the separate univariate runs. As a result, certain areas of the study region exhibited greater variations in K_s at different subsurface depths.

5 Discussions

5.1 Benefits and Challenges of the New Multivariate Data Assimilation Framework

In this research, we propose an innovative joint DA framework that improves the accuracy of both SM and GWL estimations. When assimilation is limited to a single variable, either SM or GWL, it generally enhances the assimilated variable but frequently decreases the reliability of the non-assimilated one. The observed deterioration may stem from spurious inter-variable covariances generated during the state estimation process. These covariances can modify the natural trade-offs between SM and GWL that arise from their physical coupling through soil water retention and pressure head relationships. Specifically, changes in shallow groundwater directly affect SM in the unsaturated zone, while SM dynamics control recharge and thus influence GWL. Importantly, the strength of this connection is not spatially uniform. In areas with shallow groundwater tables, SM and GWL are tightly coupled, so assimilating one variable has stronger impacts on the other. In contrast, with deeper groundwater, the hydraulic link between SM and GWL weakens, and under such conditions this connection can be functionally disconnected, resulting in assimilating one variable having little or no effect on the other, and in some cases, minor degradations may occur. Such degradations may be partially caused by small ensemble sizes, which make estimated covariances less reliable, especially for weaker correlations. In addition, non-Gaussianity related to drier soil conditions may impair the effectiveness of assimilating one variable on improving the estimates of the other. This effect particularly impacts the upper soil states when GWL is assimilated, or the deeper subsurface states when SM is assimilated from dry soils. This issue can also be partly attributed to the use of point-scale observations, given that neutron sensing stations and groundwater monitoring wells are unevenly distributed across the study area. When assimilation targets only one state component (e.g., GWL), it is difficult to reduce uncertainties in hydrologically connected states (such as SM) at non-adjacent spatial locations. Such spatial heterogeneity and statistical limitation explain why assimilation of a single variable can improve its own estimates while occasionally causing small degradations in the other, depending on local hydrogeological settings. However, the observed reductions in the non-assimilated variable are relatively small compared with the improvements in the assimilated variable, suggesting that univariate assimilation still provides substantial benefits for the targeted state. These limitations of univariate assimilation underscore the value of multivariate approaches, which may better account for the coupled dynamics of SM and GWL and improve the accuracy of both states simultaneously.

Building on earlier TSMP-PDAF studies of multivariate DA, Hung et al. (2022) used a detailed synthetic modeling scenario for a southwestern German domain. They showed that updating only the saturated layers improved GWL estimation compared to fully coupled DA, in contrast to earlier studies based on highly simplified synthetic frameworks (Zhang et al., 2018). However, in Hung et al. (2022), the synthetic GWL and SM data for assimilated locations were situated within a single grid cell. In contrast, this research was carried out within an actual watershed, where the majority of CRNS SM and groundwater monitoring sites are located on different grid cells, allowing for a more precise spatial mapping of SM and GWL measurements. The results of this research indicate that the novel multivariate assimilation technique introduced here outperforms the fully coupled DA approach employed by Hung et al. (2022) in predicting system states.

In multivariate DA, previous studies have shown that challenges persist despite methodological advances. Shi et al. (2015) combined model states and global calibration coefficients into a high-dimensional joint vector, requiring covariance relaxation, conditional covariance inflation, and quality control to prevent filter divergence and ensure physical plausibility. Zhang et al. (2016) employed distance and variable localization to control spurious correlations in joint SM and groundwater head assimilation, but this approach relies on manually defined rules and may lose physically meaningful cross-variable information. Botto et al. (2018) applied normalization to measurement error covariance matrices and addressed simulated data anomalies and innovation vectors to prevent ill-conditioning of the Kalman gain. While these measures ensure numerical stability, they require careful manual scaling of each variable.

In contrast, the weakly coupled DA scheme adopted in this study updates states and parameters sequentially, with each variable employing its own spatial localization and independent updates. This allows saturated zone pressure to be updated using GWL observations, while SM estimates in the unsaturated zone are adjusted based on CRNS-derived measurements. The use of variable-specific localization parameters further improves the representation of their distinct spatial characteristics, reduces the influence of spatially distant uncertainties, and limits unphysical information propagation. Importantly, this framework achieves these benefits without requiring extensive manual tuning or high-dimensional corrective procedures, which are often needed in traditional multivariate DA approaches. Additionally, asynchronous assimilation enables different update intervals for each variable: SM, which varies rapidly, is typically updated daily, whereas groundwater, with slower dynamics, is updated weekly. This approach allows coupled models to better accommodate the differing timescales of fast-evolving and slowly changing processes and to assimilate multiple variables from diverse data inputs. These characteristics enhance the robustness and reliability of the assimilation framework in real-world catchments, where observations are spatially heterogeneous and hydrological processes operate across multiple timescales.

Beyond improving state estimates, the impact of independent updates on water balance needs to be considered. During assimilation, SM and groundwater states are modified directly, which can temporarily disturb the local water balance. These imbalances may persist for a period depending on site-specific conditions. Such local imbalances are common in data assimilation, but the tight coupling between CLM and ParFlow ensures that surface and subsurface fluxes redistribute these adjustments through the model's physical processes. Consequently, at the catchment scale, independent updates do not induce systematic water balance errors, as they only alter storage states and local imbalances are mitigated by the coupled land-subsurface dynamics. Compared to uncoupled models, these local imbalances are not necessarily larger, but in coupled systems they are redistributed differently due to interactions between surface and subsurface processes.

To evaluate the robustness of this framework, experiments were conducted over the 2016–2018 period, capturing hydrological variability. Despite interannual fluctuations, the results demonstrated stability and reliability throughout the study period, with improved forecasting accuracy for diverse elements across the coupled surface-subsurface system. Nonetheless, it is noteworthy that the ubRMSE for GWL within the 2.5 to 5 km range was higher under the multivariate assimilation scheme than in univariate groundwater assimilation experiments (6.17 m versus 5.09 m). Consequently, although multivariate assimilation integrates a wider variety of observations than univariate assimilation, it is unable to consistently yield enhanced performance. The findings align with those of Botto et al. (2018), who used the CATHY model to investigate an artificial hillslope and showed that including more variables in the assimilation framework can negatively impact the prediction accuracy of certain other model variables. They suggested that the filter's effectiveness was constrained by the poor precision of pressure head measurements. Similarly, Zhang et al. (2016) attributed the unreliable model outputs observed during joint assimilation of SM and GWL primarily to unrealistic inter-variable correlations arising from a small number of ensemble members. Overall, the factors limiting the advantages of multivariate assimilation relative to single-variable assimilation can vary depending on the model used.

Beyond the assimilated state variables, the coupled model's related ET output was also assessed. Nonetheless, findings showed that groundwater assimilation failed to enhance ET simulation accuracy, primarily owing to the insufficient improvement in representing SM. In regions with deeper groundwater table depth, assimilating GWL had a diminished influence on near-surface SM and ET dynamics. This study found that assimilating SM data into the integrated models led to some improvements in ET predictions, although these gains were relatively minor. Moreover, multivariate DA did not provide further improvements in ET simulation accuracy compared to univariate SM assimilation, with the positive impact on ET estimates remaining comparable.

5.2 Uncertainty Analysis and Enhancement Strategies

This research presents novel strategies for applying multivariate assimilation techniques within integrated hydrological modeling frameworks. While advancements have been made, the assimilation results still indicate unresolved uncertainties that should be addressed in future work. Part of this uncertainty arises from the model's use of coarse spatial discretization. Coarser spatial resolution typically smooths terrain features, which reduces gradients in both surface and groundwater flows and likely contributes to persistent discrepancies in simulated GWL. Moreover, DA tends to be less effective in the presence of such systematic biases. For example, Xue et al. (2021) systematically evaluated hydrological simulations over High Mountain Asia using models at different spatial resolutions, and found that coarse model resolution introduced systematic biases in runoff, particularly over complex terrain, thereby limiting the effectiveness of DA. Future research could explore finer spatial resolutions (e.g., 100 m) to more accurately represent groundwater systems linked to narrow valleys, thereby minimizing biases caused by coarse spatial discretization and improving DA performance. Furthermore, the performance of assimilation tends to decline with increasing distance from observation wells, as localized updates have weaker influence on more remote areas. Potential strategies to mitigate this issue include applying adaptive localization radii, assimilating spatially distributed datasets (e.g., RS products), or increasing the number of groundwater wells to enhance spatial coverage. Employing higher spatial resolution reduces the likelihood of multiple observation wells being located within a single grid cell, thereby allowing a larger number of wells to be effectively assimilated. It also reduces wet biases in simulated GWL, decreasing the probability of wells falling within river or near-river grid cells and thereby increasing the number of observations that can be reliably assimilated. Additionally, this study does not consider possible systematic err in the observational datasets. In real-world scenarios, multiple approaches are employed to handle observational biases during DA, including adjustments for scale mismatches and the use of long-term normalization techniques, as highlighted in earlier research (Zhang et al., 2016; Reichle et al., 2002; Crow and van den Berg, 2010).

The study took place in the Rur catchment, which features a comprehensive and accurate network of field measurements, including CRNS and groundwater observation sites. These comprehensive datasets provide a unique opportunity to evaluate the performance of the novel multivariate assimilation approach within the catchment area. Based on existing information, no other hydrological region offers such a reliable and extensive observation network. To broaden the applicability of this approach, future studies could focus on integrating more widely accessible datasets, such as terrestrial water storage variations derived from GRACE/GRACE-FO (Tapley et al., 2019; Khaki et al., 2017) or RS-based SM products (Bayat et al., 2021). Such spatially distributed observations could also help to reduce the decline in assimilation performance with distance from individual ground-based observations, thereby providing additional constraints across larger areas. However, these data products are unfortunately too coarse to resolve hydrological processes in our study area, highlighting the need for higher-resolution observations for effective local-scale assimilation.

Beyond spatial resolution and observation distribution, structural deficiencies in the model may contribute to persistent uncertainties and further complicate the effective application of DA with real-world observations. This study performs GWL assimilation under the simplifying assumption of hydrostatic equilibrium, even though real-world conditions are considerably more complex. Multiple aquifers can coexist in a vertically layered system, separated by intervening aquitards. Additionally, fault lines may act as horizontal barriers that disrupt aquifer continuity, potentially altering groundwater flow patterns and their spatial distribution. Anthropogenic groundwater withdrawal also significantly affects aquifers. This is particularly evident in the Rur catchment, where hydrogeological conditions are strongly influenced by water management practices aimed at preventing water accumulation in open-cast lignite mines (Bogena et al., 2018). These processes are insufficiently represented in the current model, which contributes to systematic biases and makes updating necessary. By assimilating GWL data, the model can be better calibrated and its parameters fine-tuned to reflect observed conditions, thereby improving prediction accuracy while effectively accounting for the complexities of layered aquifer systems, groundwater withdrawals, and mining-related disturbances. Nonetheless, the impact of structural model uncertainties on assimilation performance should be carefully addressed in future research.

This study employs SM data derived from CRNS measurements for assimilation. The effectiveness of DA relies on the proper calibration of CRNS data and the use of the weighting function for CRNS data (see Schrön et al., 2017). The COSMIC operator (Shuttleworth et al., 2013) allows for the direct assimilation of neutron intensity data from CRNS. Currently under development within TSMP-PDAF, this approach is expected to support future DA applications.

The EnKF, originally developed to address nonlinearity in dynamic modeling systems, has demonstrated effectiveness in coupled terrestrial simulations. This nonlinearity primarily arises from the complex interdependencies among state variables, such as the coupling between SM and GWL through pressure head dynamics (Camporese et al., 2009b). This inherent nonlinearity complicates the design of multivariate assimilation schemes. As a result, determining the most suitable observational inputs and evaluating the compromises associated with integrating diverse variables continue to pose major obstacles for upcoming investigations. Potential strategies to enhance multivariate DA include using different variants of EnKF, combining EnKF with other filtering methods, or implementing bias-aware filters.

The primary objective of multivariate DA is to enhance the accuracy of both state variables and associated parameter estimates. This research focused on updating K_s, identified as a critical parameter for the subsurface groundwater system. Although the temporal evolution of assimilated states may not show large differences between experiments with and without K_s updates, this does not imply that parameter updating is ineffective. For example, in our experiments, K_s updates led to reductions in ubRMSE of more than 10 % for both GWL and SM compared with state-only assimilation. However, the immediate temporal impact of K_s updates may be limited, partly due to the constrained adjustment range applied by the fixed damping factor (0.1) and the slow response of groundwater states. Moreover, model biases are also influenced by other factors, including forcing uncertainty and structural model errors, which may play a dominant role in the temporal evolution of SM and groundwater states. Nevertheless, parameter-updating experiments improved performance metrics and long-term mean states, demonstrating their value in correcting systematic model biases that cannot be fully addressed by state assimilation alone. Independent validations using the revised K_s confirmed enhanced predictions of both GWL and SM. These results highlight the importance of considering both state and parameter updates in multivariate assimilation frameworks to achieve more reliable hydrologic predictions.

Even though estimating a larger set of parameters is theoretically possible, Brandhorst and Neuweiler (2023) reported computational stability issues in idealized scenarios when assimilating SM to estimate subsurface hydraulic properties. As a result, updating the full set of van Genuchten parameters in practical applications remains challenging. Similarly, Shi et al. (2015) demonstrated through synthetic experiments that simultaneously estimating multiple soil hydraulic parameters using EnKF becomes increasingly difficult as the number of parameters grows. Their findings also indicated that incorporating a broader range of data types can improve the accuracy of subsurface hydraulic parameter estimation. Therefore, future studies will need to integrate diverse datasets within multivariate assimilation frameworks to effectively update key parameters in coupled surface-subsurface models, ultimately enhancing overall model predictive performance.

6 Conclusions

This study investigated various strategies for assimilating groundwater and CRNS SM data collected from an extensive observation network into the integrated land surface and subsurface model (CLM-ParFlow) within a German watershed. The benefits and limitations of using these datasets independently were compared with those of multivariate DA methods. A novel multivariate DA technique is introduced, in which GWL and SM are weakly coupled through separate phases using the LEnKF, thereby improving update stability. Assimilating groundwater data adjusts the transition boundary between the vadose and phreatic zones and updates the hydrological states (and potentially parameters) within the saturated domain. CRNS-derived SM data is used to modify vadose zone conditions and may also influence its parameterization. A set of 128 realizations was created by varying both meteorological inputs and subsurface hydraulic parameters. DA simulations were conducted over the 2016–2018 period. ET data from eddy covariance stations, alongside GWL and SM observations, served to assess the impact of both univariate and multivariate assimilation on predicting GWL, SM, and ET. Improvements in model predictions varied across the different DA experiments and years. Generally, univariate assimilation yielded better accuracy for the assimilated variable; for example, assimilating SM data reduced the ubRMSE for SM by 50 % at measurement sites, while assimilating GWL data decreased the ubRMSE for GWL by 70 % at observation points, nearly 50 % at 500 m, and approximately 20 % at 5 km. However, assimilating GWL data alone negatively affected SM prediction accuracy, with the 2016–2018 average ubRMSE increasing by approximately 20 %. Similarly, assimilating SM data alone reduced the accuracy of GWL estimates, leading to a less than 4 % rise in the 2016–2018 average ubRMSE. Overall, the improvements in the targeted state clearly exceeded the limited deteriorations in the non-assimilated state, demonstrating the benefit of univariate assimilation. This also highlights the importance of multivariate approaches for achieving simultaneous improvements in both variables.

The simultaneous assimilation of CRNS SM and GWL observations using the conventional integrated model framework fails to provide additional benefits beyond those achieved by single-variable assimilation and, in fact, is considerably less efficient. However, the newly developed multivariate assimilation method successfully integrates the strengths of individual univariate assimilation models, thereby enhancing their respective advantages. As a result, the accuracy of variables estimated under the multivariate scheme closely matches that obtained from single-variable assimilation. In summary, the combined assimilation of GWL and SM through the novel method offers a clear improvement over univariate assimilation. Furthermore, improvements in ET estimation are observed only when SM is included in the assimilation process, whether in univariate or multivariate form. This study highlights the benefits of jointly assimilating CRNS and groundwater data from observation networks, aiming to advance terrestrial hydrology modeling within physically based coupled frameworks. Future research should focus on developing multivariate DA techniques that integrate diverse data sources, such as RS products and ground-based measurements, to enhance the representation of terrestrial system components at finer spatial scales. Achieving this requires exploring the interrelationships among various variables within coupled modeling frameworks during joint assimilation and designing improved assimilation strategies to prevent degradation in the accuracy of non-assimilated states.