The benefits and trade-offs of multi-variable calibration of the WaterGAP global hydrological model (WGHM) in the Ganges and Brahmaputra basins

While global hydrological models (GHMs) are affected by large uncertainties regarding model structure, forcing and calibration data, and parameters, observations of model output variables are rarely used to calibrate the model. Pareto-dominance-based multi-objective calibration, often referred to as Pareto-optimal calibration (POC), may serve to estimate model parameter sets and analyse trade-offs among different objectives during calibration. Within a POC framework, we determined optimal parameter sets for the WaterGAP global hydrological model (WGHM) in the two largest basins of the Indian subcontinent – the Ganges and the Brahmaputra, collectively supporting nearly 580 million inhabitants. The selected model parameters, determined through a multi-variable, multi-signature sensitivity analysis, were estimated using up to four types of observations: in situ streamflow (Q), GRACE and GRACE Follow-On terrestrial water storage anomaly (TWSA), LandFlux evapotranspiration (ET), and surface water storage anomaly (SWSA) derived from multi-satellite observations. While our sensitivity analysis ensured that the model parameters that are most influential for the four variables were identified in a transparent and comprehensive way, the rather large number of calibration parameters, 10 for the Ganges and 16 for the Brahmaputra, had a negative impact on parameter identifiability during the calibration process. Calibration against observed Q was crucial for reasonable streamflow simulations, while additional calibration against TWSA was crucial for the Ganges basin and helpful for the Brahmaputra basin to obtain a reasonable simulation of both Q and TWSA. Additionally calibrating against ET and SWSA enhanced the overall model performance slightly. We identified several trade-offs among the calibration objectives, with the nature of these trade-offs closely tied to the physiographic and hydrologic characteristics of the study basins. The trade-offs were particularly pronounced in the Ganges basin, in particular between Q and SWSA, as well as between Q and ET. When considering the observational uncertainty of the calibration data, model performance decreases in most cases. This indicates an overfitting to the singular observation time series by the calibration algorithm. We therefore propose a transparent algorithm to identify high-performing Pareto solutions under consideration of observational uncertainties of the calibration data.

1 Introduction

Global hydrological models (GHMs), which quantify water fluxes and storage changes on the continents, are essential tools for understanding large-scale water dynamics (Grogan et al., 2022; Gudmundsson et al., 2012), for analysing the impact of humans on freshwater systems (Huang et al., 2015; Döll and Zhang, 2010), for developing scenarios of the future (Gu et al., 2022; Zheng et al., 2018; Giuntoli et al., 2015), and for supporting a sustainable water management (Ai and Hanasaki, 2023; Banda et al., 2022) in a globalized world. Even more than local to regional hydrological models, GHMs suffer from high predictive uncertainties that stem from input data and climate forcing uncertainties, incomplete knowledge about hydrological processes and their imprecise mathematical description, unknown initial and boundary conditions, and uncertain parameters (Moges et al., 2021). It is state-of-the-art to decrease predictive uncertainties of local to regional hydrological models by estimating model parameters through model calibration, i.e. by comparing the model output to observations and then identifying model parameters that lead to an optimal fit to observations. This is not yet general practice for global hydrological models (Yoshida et al., 2022).

There are many practical challenges of parameter calibration for GHMs. First, a GHM contains thousands of spatially distributed parameters. For example, the WaterGAP global hydrological model (WGHM; Müller Schmied et al., 2021) has more than 30 parameters for each of its 68 420 grid cells. Second, commensurable observations of most hydrological variables are scarce. While streamflow observations aggregate over the upstream drainage areas, streamflow records are lacking in many regions of the Earth. Other observations, such as groundwater recharge, are mostly point estimates that are difficult to relate to the behaviour in 0.5° grid cells that cover about 2000 km² (depending on the geographic latitude). In addition, observations may suffer from substantial uncertainties that are challenging to quantify (Di Baldassarre and Montanari, 2009). Third, despite the increase in computational power over the last few decades and the availability of high-capacity supercomputing facilities, the high runtimes of current GHMs do not allow most optimization algorithms to explore the high-dimensional decision space (i.e. parameter space) in sufficient detail, which results in premature termination in most cases before true convergence can be reached (Cheng et al., 2005). Due to these difficulties, GHMs are rarely calibrated at all or are calibrated against streamflow only. In its standard version, the WGHM is calibrated in a simple manner against mean annual streamflow observed at more than 1300 gauging stations, by adjusting one to three parameters (Müller Schmied et al., 2021). For most GHMs, the estimation of distributed parameters is accomplished by transferring knowledge from gauged to ungauged basins through parameter regionalization (Beck et al., 2016; Hrachowitz et al., 2013). For example, Arheimer et al. (2020) used daily and monthly streamflow observations at more than 5000 gauging stations in a stepwise calibration approach for the GHM World-wide HYPE (WWH; HYPE – Hydrological Predictions for the Environment), where process-specific parameters for representative catchments of different physiographic categories were calibrated in each step, and the parameters were transferred to similar catchments worldwide. Similarly, Beck et al. (2020) performed global-scale parameter regionalization for the hydrological model HVB using streamflow observations of over 4000 catchments.

The equifinality thesis proposed by Beven (1993) challenges the notion of a singular optimal model – whether in terms of structure, input, or parameters – particularly in the presence of multifaceted uncertainties. Instead, it suggests that there can be alternative models that exhibit comparable predictive capabilities while differing in their specific configurations. The fundamental causes of equifinality of model parameter sets are the uncertain model structure and inputs (e.g. climate or soil data) as well as the observations (and their errors) that are used to estimate model parameters or evaluate model outputs (Beven, 2006). It is common knowledge that different “optimal” parameter sets would be obtained from calibrations against observations of different periods or if a different model evaluation criterion were used, even though the calibration technique remains unchanged (Beven and Binley, 1992; Kirchner, 2006). Given all these uncertainties, a large number of model parameter sets can be optimal; it is expected that the number of optimal parameter sets increases with the number of parameters that are adjusted. In addition, individual parameters can vary strongly among the optimal parameter sets due to balancing effects among the parameters. For example, in a humid basin, a high soil water storage capacity may decrease streamflow, while a low value for a parameter in the equation for potential evapotranspiration may increase it in a similar way; then, the values of each parameter in two equally optimal parameter sets can differ strongly, and an optimal parameter value cannot be identified. Nevertheless, non-identifiability can also arise when input parameters have little or no impact on the output variable of a model when compared to observations (Herrera et al., 2022). It is assumed that the identifiability of model parameters is enhanced by (1) adjusting only a small number of parameters, those to which model output is most sensitive, and (2) increasing the information content of observations, either by taking into account multiple characteristics (signatures) of the same observation time series or by using observations of more than one model output variable (Bai et al., 2018; Hosseini-Moghari et al., 2020). Jakeman and Hornberger (1993) demonstrated that conventional rainfall-runoff data provide sufficient information to constrain a simple hydrological model with a maximum of four free parameters. Gupta et al. (1998) recognized that parameter estimation for any hydrological model is inherently a multi-objective problem. Observations in addition to streamflow provide information on the behaviour of specific fluxes or storages and constrain parameters better than just streamflow observations.

The basis of any hydrological model is the water balance equation $P=\mathrm{ET}+R+\mathrm{\Delta }\mathrm{TWS}$. That is, the only system input precipitation (P) has to be partitioned into evapotranspiration (ET), runoff (R), and terrestrial water storage change (ΔTWS) during a specific period. Clearly, the prediction accuracy of such a model may be significantly improved if the model could be constrained using observations of all three response variables of the water balance equation. Historically, the streamflow observations alone, i.e. aggregated and routed R from the upstream catchment area, have been used in most model calibration experiments. In the context of multi-objective calibration, Efstratiadis and Koutsoyiannis (2010) recommended a 1:5 or 1:6 ratio between the number of objectives and the number of calibration parameters to optimize parameter identifiability and to facilitate the search algorithm to find a robust solution of the given optimization problem. Developing criteria based on different features of the same observations could potentially increase the ratio of objectives to the number of parameters. However, this approach is not favoured, as the overall information content within any observation dataset is inherently limited. Thus, observations of multiple model output variables become essential to successful calibration (e.g. Denager et al., 2023). Advances in remote sensing technologies and the related generation of data products provide more large-scale information that often is the only source of observation for many data-scarce regions of the world. The Gravity Recovery and Climate Experiment (GRACE) mission and its successor GRACE Follow-On, for example, provide global observations of terrestrial water storage anomaly (TWSA) starting from April 2002 onwards. Following these ideas of multi-variable parameter estimation, a more detailed calibration of six to eight parameters of the WGHM was done by Werth and Güntner (2010) for 28 large basins worldwide using monthly time series of streamflow (Q) and TWSA observations following the multi-objective calibration methodology proposed by Werth et al. (2009). Hosseini-Moghari et al. (2020) performed a multi-objective calibration of WGHM parameters for the Lake Urmia basin using three observation variables, streamflow, TWSA, and groundwater storage, after adjusting the model input of human water use using observational data in the first step. More than three observation types have rarely been used for hydrological model calibrations (Meyer Oliveira et al., 2021).

Since TWSA from the GRACE mission has become available, TWSA observations have been added to in situ streamflow observations as the measure of storage change (ΔS) in GHM calibration studies (Dembélé et al., 2020; Hosseini-Moghari et al., 2020; Demirel et al., 2019; Bai et al., 2018; Schumacher et al., 2018; Nijzink et al., 2018; Kittel et al., 2018; Rakovec et al., 2016; Milzow et al., 2011; Lo et al., 2010; Werth and Güntner, 2010; Werth et al., 2009). Döll et al. (2024) also used observations of Q and TWSA to calibrate the WGHM alternatively for determining Pareto-optimal parameter sets for the Mississippi basin as a whole or individually for each of five sub-basins. The whole-basin approach improved the fit to sub-basin observations in all sub-basins as compared to the uncalibrated model (with the exception of one sub-basin for Q). It did not degrade the fit to TWSA for three sub-basins compared to the computationally more demanding sub-basin approach, but this was only the case in one sub-basin regarding Q. In contrast, only a few studies have attempted to incorporate global-scale ET products into hydrological model calibration, primarily because of their low reliability and high errors (Liu et al., 2022; Meyer Oliveira et al., 2021; Huang et al., 2020; Nijzink et al., 2018; López López et al., 2017). Demirel et al. (2018) demonstrated successful enhancement of spatial pattern performance in a distributed hydrological model through multi-objective calibration using discharge and remote-sensing-based ET observations. Additionally, Demirel et al. (2024) provide a discussion on the trade-offs between temporal and spatial pattern calibration of the same distributed model using discharge and ET observations. To the best of our knowledge, only a few studies have attempted to simultaneously use all three variables on the right-hand side of the water balance equation to condition a hydrological model (Yang et al., 2022; Dembélé et al., 2020; Livneh and Lettenmaier, 2012). While the study by Huang et al. (2020) employed streamflow data for bias correction of the ET dataset, they utilized the bias-corrected ET and TWSA for parameterization of a hydrological model, aiming to establish a streamflow-independent calibration scheme. Similarly, in a study by Nijzink et al. (2018), in situ streamflow observations were utilized to benchmark the performance of five hydrological models across 27 very small European catchments (area < 1600 km²). In that study, 10 remote sensing data products, including TWSA and ET, were employed for model calibration, with the exclusion of streamflow observations. In their study, Meyer Oliveira et al. (2021) calibrated a hydrological model using several remote sensing products, including terrestrial water storage anomaly and evapotranspiration, while employing streamflow observations solely for benchmarking. Hulsman et al. (2021) utilized in situ discharge, satellite-based evapotranspiration (ET), and GRACE TWSA data to calibrate a process-based distributed hydrological model in a large semi-arid basin in Africa, aiming to incrementally improve the process representation of the model. Also, Liu et al. (2022) calibrated 59 large basins worldwide using ET and TWSA observations, with streamflow observations exclusively utilized for validating the calibration results. Trautmann et al. (2018, 2022) calibrated a global model at the scale of selected grid cells with TWSA, ET, and a gridded runoff product, instead of using streamflow at the basin scale. For a slightly different purpose, Pellet et al. (2020) utilized observations of all the variables in the water balance equation to derive terrestrial water storage changes by reconstructing the water cycle in five southern Asian basins, including the Ganges and the Brahmaputra river basins.

The terms “multi-objective” and “multi-variable” are not always interchangeable, as multiple objectives can stem from the same variable and multiple variables can contribute to a single composite objective. We use these terms contextually based on their literal meanings. Our multi-objective calibration analyses involve multiple objectives and multiple variables, with one objective corresponding to each variable. A “signature” of a data series consists of quantitative metrics or indices that describe its statistical or dynamic properties (McMillan, 2021). In this context, the term “multi-signature” refers to a scenario where multiple quantitative properties of a data series are considered simultaneously.

In this study, we present a comprehensive multi-objective calibration framework for estimating optimal basin-specific parameter values for a global hydrological model by taking into account observations of multiple model output variables. The framework consists of (1) an approach for selecting model parameters that is based on a global sensitivity analysis and considers multiple signatures of each variable and (2) a multi-objective parameter optimization that includes multiple variables. We apply the framework to the WGHM and estimate, for the Ganges and the Brahmaputra basins of the Indian subcontinent, the most important model parameters using multi-variable, multi-signature sensitivity analysis and multi-variable parameter optimization. We then analysed the calibration outcome to answer the following scientific questions.

• How does a multi-variable, multi-signature sensitivity analysis enhance the identification of important model parameters?

• Does the inclusion of observations of multiple variables in model calibration increase parameter identifiability and thus reduce model equifinality?

• To what degree does the inclusion of TWSA, ET, and surface water storage anomaly (SWSA) observations, in addition to Q observations, improve the simulation of important hydrologic variables by a GHM such as the WGHM, and what is the value of streamflow observations?

• What is the impact of uncertainties on the calibration outcome? Can we integrate knowledge about observation uncertainties when selecting the so-called compromise solution?

2 Study area

The transboundary basins of the Ganges and Brahmaputra (Fig. 1) exert significant socio-economic, geo-political, and ecological influence in the region. These two basins are home to approximately 580 million human inhabitants and cover an aggregated area of 1.63×10⁶ km² shared among India, China, Bangladesh, Nepal, and Bhutan (India-WRIS, 2014a, b; FAO, 2011). With a population density of 355 inhabitants per square kilometre and the necessity to irrigate crops outside the monsoon period, the basins and their inhabitants experience significant water stress. As a result of climate change and the rapid pace of economic growth aimed at lifting a large population out of poverty, the region's water scarcity is expected to intensify rapidly in the coming decades (Gain and Wada, 2014). The Ganges and Brahmaputra rivers collectively account for over 40 % of the total freshwater discharge into the Bay of Bengal, which constitutes approximately 25 % of the total freshwater inflow received by the Bay of Bengal (Papa et al., 2010). Streamflow in both rivers significantly influences delta formation, sediment deposition, and salinity dynamics in the coastal region (Becker et al., 2020; Akhil et al., 2014).

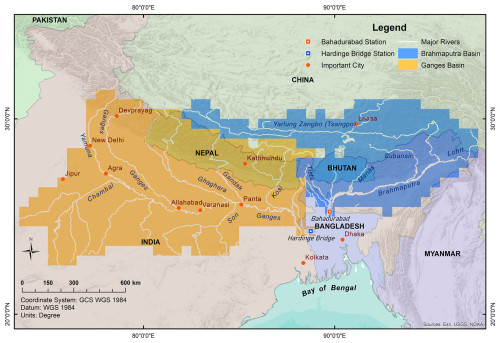
Figure 1 Spatial extent of the two calibration units: the Ganges and the Brahmaputra river basins, delineated as the upstream of the two streamflow gauging stations Hardinge Bridge (Ganges) and Bahadurabad (Brahmaputra).

In the current study, the Ganges and Brahmaputra basins were treated as two distinct calibration units, with calibration parameters adjusted uniformly within each unit. Drainage basins were defined as the upstream areas from the gauging stations at Hardinge Bridge and Bahadurabad, respectively, for the Ganges and Brahmaputra units (Fig. 1). This delineation was based on the drainage direction map DDM30 of Döll and Lehner (2002). A detailed description of the basin's physiographic properties is provided in Sect. S1 in the Supplement. Table 1 presents key characteristics of the two basins.

Table 1 Key characteristics of the study basins Granges and Brahmaputra.

¹ April–October considered summer months and November–March considered winter months. ² Calculated with data from 1969 to 2004. Sources: (a) Immerzeel (2008), (b) FAO (2011), (c) India-WRIS (2014b), (d) India-WRIS (2014a), (e) Masood et al. (2015), (f) Khan et al. (2015), (g) Ray et al. (2015), and (h) Wang et al. (2023).

3 Data and methods

3.1 WaterGAP global hydrological model (WGHM) and forcing data

The WaterGAP global hydrological model (WGHM; Müller Schmied et al., 2021, 2014) simulates the continental water cycle to estimate water storage dynamics in 10 different storage compartments and water fluxes (ET and streamflow) for all continents (except Antarctica) at 0.5° spatial and daily temporal resolution. In this study, we consider the sum of water storage in lakes, wetlands, human-made reservoirs, and rivers as surface water storage (SWS) and the sum of SWS, canopy, snow, soil, and groundwater storage as terrestrial water storage (TWS). Glacier dynamics could not be taken into account in the WGHM version that was available for this study. For some storage compartments such as lakes and groundwater, the WGHM does not simulate absolute values of storage but only storage anomalies such that SWSA and TWSA with respect to a temporal mean over a reference period are analysed, consistent with observations of TWSA and SWSA. The conceptual framework of the model is based on solving the vertical water balance of precipitation, snow accumulation and melt, interception by the vegetation canopy, evapotranspiration, soil water storage and groundwater recharge, and the lateral water movement of generated surface runoff and groundwater outflow through the surface water bodies until it reaches the ocean or inland sinks. The vertical water balance and the horizontal water movement depend on various geomorphological and physiographic characteristics including soil storage capacity, land-cover-specific interception capacity and root depth, area of surface water bodies, and drainage directions. The WGHM accounts for the impact of human-made reservoirs and human water use on water flows and storages. It is driven by potential net abstractions from groundwater and surface water bodies that are computed by other modules of WaterGAP. For a detailed description of the WGHM, see Müller Schmied et al. (2021).

The WGHM in its standard version is calibrated for one parameter (the runoff coefficient, SL-RC) against river discharge observations of 1319 gauging stations worldwide such that the simulated long-term mean annual river discharge of the corresponding river basin is within a 10 % error range of the observed mean. Upon failure of the above calibration target, two additional correction factors (i.e. the areal correction factor – CFA, and the station correction factor – CFS) are introduced in the standard model version for synthetic runoff adjustment (Müller Schmied et al., 2021). To suppress these corrections for the calibration experiments in this study, we set both correction factors to 1.0 in all cells. A total of 24 model parameters, including the runoff coefficient SL-RC, were considered in this study (Table 2). The spatial distribution of parameter values is according to one of the following schemes:

• U. This is the uniform parameter value in all 0.5° cells of a river basin.

• S. Parameter values are specific to sub-areas of the river basin; e.g. in the case of the Priestley–Taylor coefficients, all cells in the arid or humid part of the river basin have the same parameter value, respectively.

• M. Multiplier parameters are uniform throughout the river basin but multiply the spatially distributed cell-specific values of their base parameter.

For example, a value of 1.5 of the river roughness coefficient multiplier (SW-RRM) parameter increases the cell-specific roughness coefficient values by 50 % in all cells in a basin. Out of the 24 parameters, two multipliers – the net radiation multiplier (EP-NM) and the precipitation multiplier (P-PM) – alter the climate input variables radiation and precipitation, respectively. They were excluded from the sensitivity analysis because of their predominating influence on the target model variables which masks the relative importance of the rest of the parameters. Nevertheless, P-PM was selected as an additional calibration parameter because precipitation forcing data, in contrast to radiation data, contain high uncertainties and biases which need to be corrected during model calibration, if possible. Recently, Goteti and Famiglietti (2024) pointed out the underestimation of precipitation in datasets of India that need to be corrected (here by P-PM) to avoid non-physical or process-based compensation by calibration of other parameters.

Table 2 WGHM parameters with a priori parameter ranges; spatial scheme U (uniform), M (multiplier), S (sub-area specific) (see text for details). The parameters are categorized according to the storage compartments or processes that they directly affect. P: precipitation. EP: potential evapotranspiration. CA: canopy. SN: snow. SL: soil. SW: surface water. GW: groundwater. NA: net abstraction of water by humans.

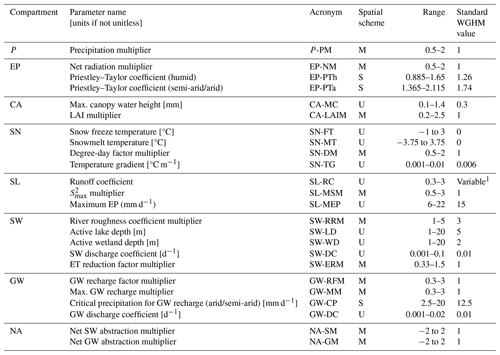
¹ Spatially variable among grid cells. ² Maximum soil water storage in the effective root zone.

The WGHM is driven by a climate forcing dataset which is a homogenized combination of WFD (WATCH Forcing Data based on ERA40; Weedon et al., 2011) for 1901–1978 and WFDE5 (WATCH Forcing Data methodology applied to ERA5 reanalysis data; Cucchi et al., 2020) for 1979–2019, with precipitation data being bias-corrected using monthly precipitation from GPCC (Global Precipitation Climatology Centre) according to Schneider et al. (2015). The climate forcing dataset includes precipitation, air temperature, downward shortwave radiation, and downward longwave radiation.

3.2 Observations

3.2.1 Surface water storage anomaly (SWSA)

Based on multi-satellite observations of surface water extent and water level, Salameh et al. (2017) produced a 15-year dataset of SWSA for the Ganges and the Brahmaputra basins by analysing pixel-wise hypsographic curves that represent area–volume relationships. A detailed description of the method can be found in Papa et al. (2013) and Papa and Frappart (2021). Two different global digital elevation models (GDEMs) were used: (i) ASTER (Advance Spaceborne Thermal Emission and Reflection Radiometer) and (ii) HyMAP (Hydrological Modelling and Analysis Platform) based on SRTM30 (Shuttle Radar Topography Mission). Thus, two SWSA observation products were produced for the period 1993–2007 on an equal area (773 km²) grid of 0.25° resolution at the Equator. We used the basin-scale monthly mean values of the two products in our analysis. As we considered the river basin area upstream of the last gauging station only, our SWSA basin-scale values for Ganges and Brahmaputra are substantially smaller than those presented in Salameh et al. (2017).

The uncertainties in data products like the one of Salameh et al. (2017) are difficult to assess. Nevertheless, we provide a maximum error estimate from other similar SWS products combining GIEMS and radar altimetry. Frappart et al. (2012) estimated SWS uncertainty of 23 % over the Amazon, and Papa et al. (2015) estimated the uncertainty to be 24 % over the Ganges–Brahmaputra. Based on these two similar estimates, we used an error estimate of 25 % for the basin-average monthly SWS data in our study.

3.2.2 Actual evapotranspiration (ET)

We used the benchmark ET product LandFlux-EVAL of Mueller et al. (2013), which is a merged synthesis of available global ET products covering observation-based estimations, estimations from several land surface models (LSMs), and estimations from atmospheric reanalyses. Many studies have used or compared this product in recent years (Lienert and Joos, 2018; Nanteza et al., 2016; Orth and Seneviratne, 2015; Tsarouchi et al., 2014; Liu et al., 2014). Here, we used the LandFlux-EVAL product that was merged from 14 datasets for the period  9 to 2005. We used the ensemble mean as monthly ET observation. The standard deviation (σ with N=14) of the mean is also provided in the dataset as an estimate of the monthly observation error; we used 2σ range as the uncertainty of the ET observations in our analysis. The errors are provided in absolute terms with the unit of millimetres of water equivalent for each month, which in equivalent relative terms corresponds to 25 % in the Ganges basin and 24 % in the Brahmaputra basin.

3.2.3 Terrestrial water storage anomaly (TWSA)

The TWSA dataset is based on Level-2 data (spherical harmonic coefficient, SHC) of the GRACE and GRACE Follow-On of TU Graz monthly solutions (Mayer-Gürr et al., 2018) up to degree and order 96 and by applying the anisotropic DDK3 filter (Kusche et al., 2009) to correct the degree-related correlated noise. Further corrections were necessary to eliminate errors related to low-degree effects such as glacial isostatic adjustment (Gerdener et al., 2020). The residual geoid changes due to two large earthquake signals with magnitude over 9.0 (west coast of northern Sumatra, Indonesia on 24 December 2004 and near the east coast of Honshu, off Tohoku, Japan, on 11 March 2011) were removed according to the estimated values following Einarsson et al. (2010). The TWSA data were aggregated to area-average monthly time series from 2003–2019 for the two study basins. The anomalies were computed by using the mean of the period 2003–2009 as the reference mean.

2σ errors based on the full variance–covariance matrix of the TU Graz data, which accounts for orbital effects and the meridional behaviour of errors, were propagated to estimate the uncertainty of the TWSA data. The resultant time series of propagated errors is used to bracket the monthly uncertainty of TWSA observations.

3.2.4 Streamflow (Q)

We use monthly river discharge from 1980–2012 at the Hardinge Bridge and the Bahadurabad gauging stations (Fig. 1) derived by Masood et al. (2015), using daily water level observations acquired from the Hydrology Department of the Bangladesh Water Development Board (BWDB) and rating curves developed by the Institute of Water Modelling, Bangladesh (IWM). We assume an error of monthly discharge values of 20 % following McMillan et al. (2012), who compared reported streamflow uncertainties and concluded that the uncertainty varies between 10 %–20 % for medium to high in-bank flows, 50 %–100 % for low flows, and over 40 % for out-of-bank flows. Considering the large average streamflow in the two study basins (11 300 m³ s⁻¹ in the Ganges and 20 000 m³ s⁻¹ in the Brahmaputra basin), we took a pessimistic range of error of 20 %, which aligns with the estimate of Sir William Halocrow and Partners Ltd. (1991, cited in Mirza, 2003), who reported that uncertainty of streamflow could reach 20 % in those stations due to the method of velocity measurement from non-anchored boats and inaccurate measurement of depths of current meters.

3.2.5 Water balance closure of observations

To avoid an ill-posed calibration problem in particular when using all major terms of the water balance equation as forcing (P) or calibration variables (Q, ET, ΔTWS), it is important to check to what extent the water balance is closed in the observations. For this purpose, we calculated the water balance ($P-\mathrm{ET}-Q-\mathrm{\Delta }\mathrm{TWS}$) of the observation data using annual mean values over the available data period. ΔS from the GRACE TWSA was computed as the difference between the December values of consecutive years. Observation gaps were filled for all variables through linear regressions for individual months, accounting for seasonality and trends. It is worth noting that the water balance of the WGHM is closed at all time intervals.

The mean values of annual precipitation, streamflow, ET, and ΔS for the Ganges basin used in this study as observation data are 1119, 402, 621, and −14 mm, respectively. This results in an annual mean non-closure of the water balance of +109 mm. While reconciling the water budget for the whole of India, Narasimhan (2008) argued that ET estimation in India is significantly underestimated. However, in a recent study, Kushwaha et al. (2021) estimated ET for the Ganges basin to be in the range of 511–622 mm yr⁻¹, which closely aligns with our observed mean. In the Brahmaputra basin, the discrepancy is even more pronounced (−436.6 mm). The mean values of P, Q, ET, and ΔS from GRACE for the Brahmaputra basin are 1490, 1361, 564, and −11 mm, respectively. In the case of the Brahmaputra basin, input precipitation is significantly underestimated (Schneider et al., 2017; Michailovsky et al., 2013), a phenomenon attributed to convective rainfall (Bookhagen and Burbank, 2006), resulting from pronounced differences in basin topology. In their study, Schneider et al. (2017) used a scaling factor of 1.4 to correct the input precipitation and achieve a reasonable water balance closure, while Michailovsky et al. (2013) applied a factor of 1.25 to scale the TRMM 3B42 precipitation data for the Brahmaputra basin in their work. This also underscores the importance of using the WGHM parameter P-PM, a multiplicative factor to adjust the precipitation amount of the forcing data, in the calibration experiments.

It is important to note that mismatches in water balance can also occur in data-rich regions. For example, Rakovec et al. (2016) reported water balance closure errors ($P-Q-\mathrm{ET}$ in some European basins, ranging from −200 to 100 mm yr⁻¹ for most of the 179 considered basins.

3.3 Sensitivity analysis

We used the multi-start perturbation sensitivity analysis (SA) method of Morris (1991), also known as the elementary effect test (EET). The elementary effect (EE) is expressed as the derivative of a response variable with respect to change in a parameter. The EET method measures the sensitivity to a parameter as the average of EEs at many locations of the parameter space. The sensitivity index (SI) of ith parameter ($i\in \mathit{\{}\mathrm{1},\mathrm{2},\mathrm{\dots }m\mathit{\}}$, where m denotes total number of parameters) is calculated as

$$\begin{array}{}\text{(1)}& \begin{array}{rl}{\mathrm{SI}}_i=& {\displaystyle \frac{\mathrm{1}}{r}}\sum _{j=\mathrm{1}}^r{\displaystyle \frac{f\left({\mathit{\theta }}_{\mathrm{per},j}\right)-f\left({\mathit{\theta }}_{\mathrm{ref},j}\right)}{{\mathrm{\Delta }}_i^j}}\times C_i={\displaystyle \frac{\mathrm{1}}{r}}\sum _{j=\mathrm{1}}^r\\ & {\displaystyle \frac{f\left({\mathit{\theta }}_{\mathrm{1}j},{\mathit{\theta }}_{\mathrm{2}j},\mathrm{\dots }{\mathit{\theta }}_{ij}+{\mathrm{\Delta }}_i^j,\mathrm{\dots }{\mathit{\theta }}_{mj}\right)-f\left({\mathit{\theta }}_{\mathrm{1}j},{\mathit{\theta }}_{\mathrm{2}}j,\mathrm{\dots }{\mathit{\theta }}_{ij},\mathrm{\dots }{\mathit{\theta }}_{mj}\right)}{{\mathrm{\Delta }}_i^j}}\\ & \times C_i,\end{array}\end{array}$$

where r is the total number of EEs at random locations of the parameter space; θ_ref and θ_per (θ_ref∈R^m; θ_per∈R^m) are, respectively, a reference parameter set and a perturbed parameter set where only the ith parameter is perturbed from the reference parameter set; ${\mathrm{\Delta }}_i^j$ ($j\in \mathit{\{}\mathrm{1},\mathrm{2},\mathrm{\dots }r\mathit{\}}$) is the amount of change in the ith parameter at the jth location ($j\in \mathit{\{}\mathrm{1},\mathrm{2},\mathrm{\dots }r\mathit{\}}$); f(θ) is the model response of parameter set θ (θ∈R^m); and C_i is the scaling factor of the ith parameter. The scaling factors (C_i) correspond to the range of the respective parameter values (Table 2) and facilitate inter-parameter comparisons in parameter ranking, for instance, as the parameters mostly have differing units and ranges. While the Morris method does not explicitly show interaction terms, it produces a variance term for the elementary effect that accounts for parameter interactions and the functional non-linearity of the model response. We computed the standard error of the sensitivity index from this variance term and used it for parameter selection (Algorithm 4 in Sect. S2).

As a measure of change in the model response (i.e. f(θ_per)−f(θ_ref)), we used the root mean squared deviation (RMSD) between simulated values of a response variable using a reference parameter set (θ_ref) and simulated values of that variable using the perturbed parameter set (θ_per). The sensitivity index of the EET method averages out the local influences by taking samples from many locations in the parameter space, making it a global sensitivity analysis method (Pianosi et al., 2016). The method is computationally inexpensive and recommended for ranking and screening purposes by Pianosi et al. (2016). A total of 1000 random reference samples were taken using Latin hypercube sampling (LHS) which were then perturbed one at a time based on radial design (Campolongo et al., 2011). We used the SAFE MATLAB Toolbox developed by Pianosi et al. (2015) for sampling and later computing the sensitivity index. We included 22 WGHM parameters during the SA from Table 2 (excluding EP-NM and P-PM as stated earlier). During the SA, a total of 23 000 samples were analysed for each of the river basins. Model simulations were conducted for the period 1990–2019, with the spin-up period from 1985 to 1989. The initial year of the spin-up was run five times to allow water storages to reach an equilibrium state.

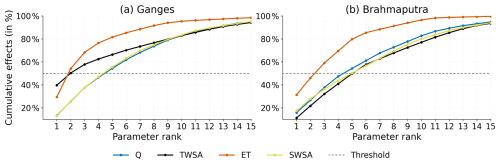
Figure 2 Cumulative effect in percent of the total effect (sum of all effects of all parameters) of top-ranked parameters up to different cut-off ranks. The function of the cumulative effect and the cut-off level differ among the four response variables Q, TWSA, ET, and SWSA in the two basins – Ganges (a) and Brahmaputra (b). Sensitivity to parameters in this example was for the monthly time series (MTS) of the four target response variables. The grey line indicates the cut-off threshold at 50 % of the total effect that must be surpassed by the top-ranked parameters for each variable and for each signature. For example, the cumulative effect of the three highest-ranked parameters on the TWSA in the Ganges basin accounts for 58 % of the total combined effects of all parameters on this variable, while the cumulative effect of the top-three parameters on Q is only 38 % of the total combined effects of all parameters in the basin.

Parameter sensitivity differs among the response variables and their statistics, i.e. hydrological signatures. To identify parameters that are important for characterizing different features of the target response variables, i.e. those against which the model will be calibrated, we performed a multi-variable, multi-signature sensitivity analysis on the four variables with available observations (Q, ET, TWSA, SWSA), considering four signatures, (1) the continuous monthly time series (MTS); (2) the “climatology” or seasonality, i.e. the 12 mean monthly values, averaged over the study period (MM); (3) the time series of annual means (ATS); and (4) the time series of the seasonal amplitudes computed as the difference between the largest and the smallest monthly values of a year (SNA). The sensitivity indices for each signature were computed separately. We observed that the sensitivities of the four response variables to the individual parameters as well as the share of cumulative effect of top-ranking parameters to the “total effect” (sum of sensitivity indices for all parameters) vary considerably among the response variables (Fig. 2). Thus, we decided to select, for each response variable, those top-ranking parameters that together contribute at least 50 % of the combined total effect. Application of this threshold ensures that (i) only the most influential parameters for a given signature of a given variable are selected, and (ii) the total number of selected parameters does not become very large.

3.4 Calibration

We used the Borg Multiobjective Evolutionary Algorithm (Borg-MOEA; Hadka and Reed, 2013) to identify non-dominated Pareto-optimal parameter sets of the WGHM against one to a maximum of four objectives. A parameter set is considered non-dominated if it outperforms all other competing sets in at least one objective.

The Borg-MOEA has been successfully used for hydrological model calibration in many studies (Fernandez-Palomino et al., 2020; Chilkoti et al., 2018) because of its superior performance over many state-of-the-art multi-objective algorithms (Reed et al., 2013; Hadka and Reed, 2013). The critical features of the Borg-MOEA include amalgamation of multiple (six) search operators and strategies from benchmark optimization algorithms (e.g. NSGA-II of Deb et al. (2002), ε-MOEA of Deb et al. (2005), ε-NSGA-II of Kollat and Reed (2006), and GDE3 of Kukkonen and Lampinen (2005)), an auto-adaptive recombination mechanism for search operators based on operators' success rates of producing non-dominated solutions over time, a restart mechanism upon detection of a search stagnation, and straightforward adaptation of the algorithm in a parallel computation framework (Reed and Hadka, 2014). Except for the initial population size, all algorithmic parameters were kept to their recommended values of Hadka and Reed (2013). The ε-precision level for all objectives was set to 0.005 to obtain a detailed Pareto front consisting of a high number of solutions. We deployed a master–worker parallel implementation of the Borg-MOEA and ran the algorithm on 401 processors of a cluster machine operating in a Scientific Linux 7 environment. Related to this configuration, the initial population size 400 was used, which was equal to the number of worker processes.

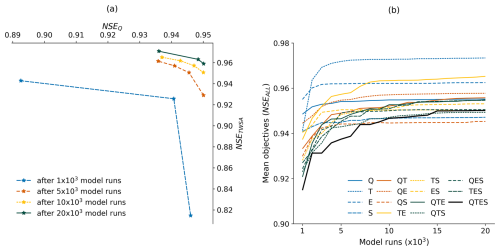
Figure 3 Convergence of single- and multi-objective calibrations of the Brahmaputra basin. (a) Pareto fronts of a two-objective calibration experiment (Experiment-QT with objectives NSE_Q and NSE_TWSA) after 1000, 5000, 10 000, and 20 000 model evaluations. (b) The mean objective value (NSE) of the compromise solution of all calibration experiments as a function of no. of model evaluations. The Pareto fronts and the compromise solutions have been determined after merging all solutions in all replications.

The objectives are to maximize values of the Nash–Sutcliffe efficiency (NSE; Eq. 2; Nash and Sutcliffe, 1970) of streamflow (NSE_Q), terrestrial water storage anomaly (NSE_TWSA), evapotranspiration (NSE_ET), and surface water storage anomaly (NSE_SWSA).

$$\begin{array}{}\text{(2)}& \mathrm{NSE}=\mathrm{1}-{\displaystyle \frac{\sum _{t=\mathrm{1}}^T{\left({\mathrm{sim}}_{\left(t\right)}-{\mathrm{obs}}_{\left(t\right)}\right)}^{\mathrm{2}}}{\sum _{t=\mathrm{1}}^T{\left({\mathrm{obs}}_{\left(t\right)}-{\mathit{\mu }}_{\mathrm{obs}}\right)}^{\mathrm{2}}}}=\mathrm{1}-{\displaystyle \frac{\mathrm{MSE}}{{\mathit{\sigma }}_{\mathrm{obs}}^{\mathrm{2}}}},\end{array}$$

where sim_(t) and obs_(t) are the simulated and observed monthly values at time step t, respectively; μ_obs is the mean of the observations; σ_obs is the standard deviation of observations; and MSE is the mean squared error. NSE serves as a good indicator for inter-basin comparison since it normalizes the MSE by the observed variance (Livneh and Lettenmaier, 2012). While four signatures (MTS, ATS, MM, and SATS) were analysed by the SA, we restricted the parameter estimation to using the monthly time series data (MTS) as observations, which has the least aggregation of temporal information among the four.

A total of 15 calibration experiments were carried out for each of the two basins, covering all possible combinations of objectives. Each experiment was repeated eight times with different initial populations generated by varying random seeds. The experiments and their objective(s) are listed in Table 4. The maximum number of model runs was limited to 20 000, which proved sufficient for approximating the Pareto front (PF), representing the frontier formed by the set of non-dominated parameter sets. This adequacy is evident from the relatively small difference in PFs between 10 000 and 20 000 model runs (as shown in Fig. 3a for a two-objective case) and the stabilization of the mean objective value of the compromise solution occurring well before reaching 20 000 runs in most experiments (Fig. 3b).

The “compromise” solution or parameter set is said to have the “best” overall performance among the non-dominated solutions, and it is determined by finding the solution with the lowest Euclidian distance (ED; Eq. 3) in the objective space from the point of theoretical best values of the objectives, known as the “utopia” point. Separate compromise solutions were determined for each replication of an experiment, and an “overall compromise solution”, after merging all solutions from the eight replications, was also determined.

$$\begin{array}{}\text{(3)}& \mathrm{ED}=\sqrt{\sum _{i=\mathrm{1}}^n{\left(U_i-O_i\right)}^{\mathrm{2}}},\end{array}$$

where n is the number of objectives, and U_i and O_i represent, respectively, the best value of the ith objective and the ith objective of a solution parameter set.

The observation datasets available for this study cover different periods (Table 3). The only overlapping period of all four observables is the 3 years of 2003 to 2005. We considered this period insufficiently short for calibration. Thus, we used observations in partly non-overlapping periods for model calibration while still trying to include overlapping datasets as far as possible. The calibration period was set to 1980–2009. Like in the sensitivity analysis, the model run started 5 years before the start of the calibration period; additionally, the first year was repeated five times. The initial 5 years (1975–1979) was considered the spin-up period.

Table 3 Availability of observation variables and their error estimates.

^* Personal communication with the Astronomical, Physical and Mathematical Geodesy Group, Institute of Geodesy and Geoinformation, University of Bonn, Germany (2022).

3.5 Validation

The validation period was set to 2010–2012, while using the same start time (year 1975) of model runs as for calibration. Validation covered Q and TWSA only as no observations for validating ET and SWSA were available for this period. For validation, we also used several performance metrics including root mean squared error (RMSE), mean absolute deviation (MAD), Pearson correlation coefficient (r), and the Nash and Sutcliffe efficiency (NSE) for the four signatures MTS, MM, ATS, and SNA. Furthermore, a thorough visual inspection of the simulation results was also performed.

3.6 Uncertainty estimation

To account for the uncertainty of the observation data in the calibration results in its entirety, we would need to repeat the calibration multiple times with alternative realizations of the observation time series. This is not feasible given its high computational demand. Alternatively, Werth and Güntner (2010) defined an error ellipse around the compromise solution after the regular calibration against the original observation time series. For defining the length of one axis of the ellipse, they generated 5000 perturbed observation time series of the observable according to its assumed error characteristics and calculated the performance indices of the simulated time series for each of them. The axis length was then determined by the standard deviation of the performance indices. We recognized that the method of Werth and Güntner (2010) does not consider the uncertainty of the compromise solution itself given the fact that a different solution will probably result as the compromise solution if the parameter search by the algorithm starts from a different starting location, a different initial population is used, or simply a different realization of the observational time series is used in the calibration. With the change of the compromise solution, the axis lengths of the error ellipse are also expected to change. In our analysis, we employed a Monte Carlo process to generate 1000 realizations of observation time series for each variable, taking into account the given uncertainty range. Subsequently, we computed the objective values (NSE) for all variables using the 1000 observation time series for each variable, separately for each of the eight compromise solutions (with one compromise solution per replication). We established thresholds for each objective to extract high-performing solutions from the combined set of solutions across all replications and referred to them as “acceptable” Pareto solutions, accounting for observation uncertainty. These solutions can be viewed as “equivalent” to the compromise solution in the context of uncertain observations. By applying thresholds to subset solutions, we effectively delineate a hyperrectangle in the objective space, which is conceptually similar to the error ellipsoid used by Werth and Güntner (2010).

4 Results and discussion

4.1 Parameter importance

The sensitivity to parameters varies among the response variables in the two river basins, and in many cases, it also varies among the different signatures of a response variable (Fig. 4). The response variables, especially streamflow (Q) and TWSA, represent an aggregate response of many complex processes over various temporal and spatial scales. Thus, they are often sensitive to parameters associated with many storage compartments or processes (Table 2) such as ET, soil (SL), surface water (SW), groundwater (GW), snow (SN) (predominantly in the Brahmaputra basin), and net abstraction (NA) by human water use (mainly in the Ganges basin). In addition to the SW parameters, the SWSA is highly sensitive to one soil parameter (SL-MSM); a few groundwater-related parameters (GW-RFM, GW-MM, and GW-DC), with varying importance depending on the considered signature; two snow parameters (SN-MT, SN-TG); and the ET parameter EP-PTh, only in the Brahmaputra basin. ET is computed as the sum of evaporation and transpiration from canopy, snow, soil, and surface water bodies. However, the soil component dominates total ET, and ET is highly sensitive to the parameter SL-MSM, which governs the soil water storage capacity. ET is also sensitive to the snowmelt (SN-SM) in the Brahmaputra basin as apparently sublimation in the basin contributes substantially to total ET. Apart from these storage parameters, the EP-PTh, which scales potential ET in the humid zone, highly influences the simulated actual ET.

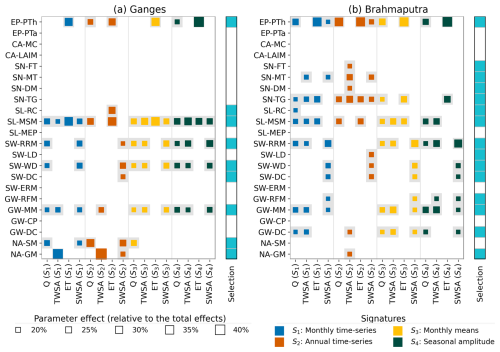
Figure 4 Most influential parameters for the Ganges (a) and the Brahmaputra (b) river basin based on the sensitivity of four signatures S₁ to S₄ – monthly time series (MTS; blue), monthly means (MM; gold), annual time series (ATS; orange), and seasonal amplitude (SNA; dark green) of simulated Q, TWSA, ET, and SWSA. The size of each box represents the effect of a parameter relative to the total effect, i.e. the sum of the effects of all parameters. The final set of calibration parameters with a significant impact on any signature of the four variables is shown on the right of each plot (cyan boxes). For parameter abbreviations, see Table 2.

Several parameters influence most or all response variables across various signatures. However, certain parameters affect only one or two signatures of the response variables. For instance, the runoff coefficient (SL-RC) – which is one of the parameters considered in the standard WGHM calibration – significantly influences monthly means (MM) of ET in the Ganges basin and MTS of streamflow. Similarly, the snowmelt temperature (SN-MT) is important for some cases in snow-dominated catchments in the Brahmaputra basin. These parameters may also affect other response variables and signatures to some extent but do not meet the defined threshold for parameter selection (Fig. 4). The relative contributions of all parameters to all response variables and signatures are presented in Tables S2 and S3.

Based solely on sensitivity to streamflow and TWSA, we identified 7 influential parameters in the Ganges basin and 12 influential parameters in the Brahmaputra basin (Fig. 4). Additionally, 3 SW parameters in the Brahmaputra basin and 1 in the Ganges basin were selected due to their significant impact on SWSA. Furthermore, 1 additional parameter in the Ganges basin was found to be sufficiently influential on ET and was included as a calibration parameter. After including the P-PM parameter for both basins, we selected 10 WGHM parameters for calibration in the Ganges basin and 16 parameters in the Brahmaputra basin.

The use of multiple signatures from various variables ensures that key parameters governing all critical hydrological processes in the model are identified. For instance, if only one signature were considered, 5–9 parameters in the Ganges basin and 9–12 parameters in the Brahmaputra basin would have been selected for calibration. Similarly, if parameter sensitivity was assessed based on Q or TWSA only, influential parameters governing other important observables could have been overlooked. However, the method of parameter selection is not without challenges. Parameters with significant impacts may be excluded if the cut-off threshold (e.g. 50 % of the total effect, as used in this study) is surpassed by only a few top-ranked parameters. For example, in the Brahmaputra basin, despite contributing a substantial 12 % to the total impact, the parameter SL-RC is deemed non-influential for ET according to this threshold (Table S3). Raising the threshold would result in the selection of a larger number of parameters, potentially leading to an unnecessary expansion of the decision space. This could increase computational demand and exacerbate issues of equifinality (Sect. 4.2.3).

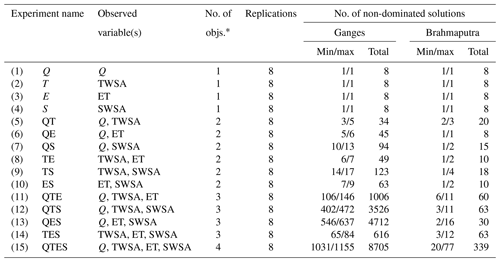
Table 4 Configuration of the 15 calibration experiments, with the observed variable(s), number of objectives, number of replications, minimum and maximum number of non-dominated (Pareto-optimal) solutions (i.e. estimated parameter sets) obtained among the 8 replications, and the total number of non-dominated solutions over all eight replications.

^* NSE used as calibration objective.

4.2 Model calibration

Calibration experiments with all 15 possible combinations of the four objectives (NSE_Q, NSE_TWSA, NSE_ET, and NSE_SWSA) were carried out for the two study basins. Furthermore, each of the experiments was repeated eight times with random seeds, resulting a total number of 240 calibrations. Overall, the study involved the evaluation of 4.8 million samples, requiring approximately 3.2¹ million CPU hours of model runtime.

4.2.1 Added value of multi-objective calibration and trade-offs among objectives

A high cardinality, i.e. a high number of solutions in the non-dominated Pareto solution set, was obtained in most multi-objective calibrations (Table 4). The cardinality depends on the shape of the Pareto frontier (PF) and the allowed crowding distance, which was constant (0.005) for all objectives in all experiments. A wider PF resulting in high cardinality reflects a high trade-off between the objectives. The high cardinality observed in the Ganges experiments indicates marked trade-offs among objectives, especially between NSE_Q and NSE_SWSA, as well as between NSE_SWSA and NSE_TWSA. This observation is further supported by the experiments involving solely those objective pairs, which yielded a larger number of solutions. The three-objective calibration TES has a lower cardinality than the other three-objective cases, which indicates the simulation of Q is in rather strong conflict with the simulation of the three other variables. This is supported by the poor fits to streamflow observations of the TES calibration variant for both basins (Tables 5 and 6). As expected, the four-objective calibration produced the highest number of non-dominated solutions.

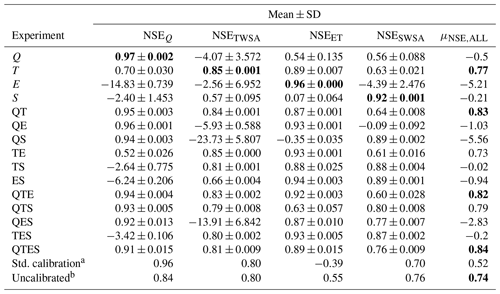
Table 5 Mean and standard deviation of model performance indicator NSE for the compromise solutions (N=8) of the calibration experiments in the Ganges river basin during the calibration period. The WGHM was rerun using parameters from the compromise solutions to compute NSEs of all variables. The μ_NSE,ALL represents the mean NSE across all objectives over all eight compromise solutions per experiment. The highest NSE for each objective is highlighted using bold face; the highlighted mean across objectives (μ_NSE,ALL) also shows the highest value in each group (single-objective, two-objective, three-objective, and four-objective). The objective obtained in the standard calibration and in the uncalibrated model is also shown.

^a SL-RC and two correction factors are calibrated by adjusting mean annual streamflow, which was calibrated against observed values (Müller Schmied et al., 2021). ^b SL-RC is set to the default 2.0, and correction factors were set to 1.

The single-objective calibration experiments obtained the best NSE values for the specific objective under consideration (Tables 5 and 6). The mean NSE of all four objectives (μ_NSE,ALL) was used as a simple indicator of the overall performance of an experiment. In multi-objective calibrations, although the objective values for each individual objective decrease slightly, the overall performance tends to increase when more objectives are included. In the Brahmaputra basin, the highest μ_NSE,ALL increases from 0.84 for single-objective calibration to 0.90 for two-objective calibrations, to 0.93 for three-objective calibration, and to 0.95 for four-objective calibration. In the Ganges basin, the highest μ_NSE,ALL is slightly smaller in three-objective calibrations than in two-objective calibrations. Nevertheless, the four-objective calibration experiments achieved the highest overall performances in the basin. In their study, Livneh and Lettenmaier (2012) demonstrated that the overall performance of the calibrated model improved with the inclusion of ET and TWSA observations in addition to streamflow observations. In contrast, Mei et al. (2023) observed a reduction in the overall performance of a three-objective calibration, including observations of Q, soil moisture, and ET, when compared to single- and two-objective calibrations. This reduction was attributed to suspected model structural errors and/or erroneous observations.

Different from the Brahmaputra, calibration against only Q in the Ganges basin resulted in worse fits to all three other variables as compared to the uncalibrated model version. Multi-variable calibration, however, works best if streamflow observations are included. Excluding NSE_Q as an objective in any calibration resulted in significantly poorer performance in streamflow simulation (Tables 5 and 6). The importance of streamflow observations in model calibration is well documented in the literature, with a particular focus on multi-variable calibration scenarios (Dembélé et al., 2020; Livneh and Lettenmaier, 2012). Liu et al. (2022) reported that calibrating a model with ET and TWSA observations can occasionally produce reasonable streamflow simulations in certain basin. In their study, Livneh and Lettenmaier (2012) concluded that calibrating the model with either ET or TWSA alone was insufficient to achieve good performance in streamflow simulation. We also discovered that calibrating with these two variables only resulted in high NSE_Q (>0.8) in a few replications in the Brahmaputra basin.

Table 6 Mean and standard deviation of model performance for the compromise solutions (N=8) of the calibration experiments of the Brahmaputra basin. μ_NSE,ALL represents the mean across the four objectives. The highest objective values in all experiments and in each group are highlighted in bold. Objectives of the standard calibration and uncalibrated model is also shown.

In comparison to the standard calibration, the four-objective calibration resulted in better performance in the Brahmaputra for all four response variables and in all variables except streamflow in the Ganges basin, where the standard calibration leads to a very high NSE_Q of 0.96 (Table 6). As the streamflow simulation for the single-objective calibration with Q only is better in the two basins than the standard calibration, this suggests that the slight decrease in streamflow performance in four-objective calibration in the Ganges basin is due to some trade-offs among the objectives. The improvement in ET by the four-objective calibration was much higher than the improvement in other variables which underpins the need to include ET as a calibration variable. This is corroborated by the observation that the standard calibration procedure of Müller Schmied et al. (2021) with Q only degrades the ET simulation, even in comparison to the uncalibrated WGHM. This, in fact, contradicts the conclusion of the study by Nijzink et al. (2018), in which they analysed the potential of several remote sensing products to constrain hydrological models and calibrated five hydrological models for 27 small catchments in Europe. They concluded that remote-sensing-based ET observations were less effective at adequately constraining the posterior parameter distribution compared to other observations such as soil moisture, TWSA, and snow. One probable cause could be the fact that the catchment size in that study was too small (<1600 km²) for the ET products to be effective; in our study, the catchment size is significantly larger.

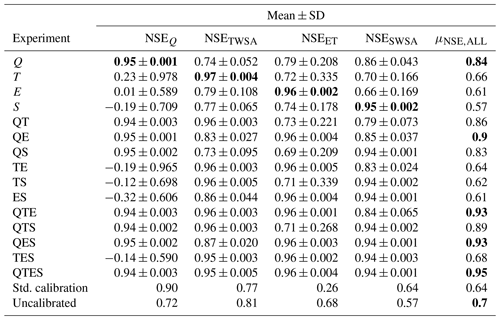
As mentioned above, multi-objective calibration enhances the overall model performance at the expense of a slight decrease in the performance of individual variables, which is common and often expected. Many studies have reported a reduction in the performance of streamflow simulation when the model is calibrated with streamflow and TWSA observations, as compared to models calibrated solely with streamflow data (Li et al., 2018; Bai et al., 2018; Yassin et al., 2017; Rakovec et al., 2016; Livneh and Lettenmaier, 2012). The trade-offs among other variables are not well documented in the literature. Mei et al. (2023) compiled a list of the previous studies that incorporated streamflow observations and observations of some additional variables in model calibration. They documented changes in performance in four target variables – streamflow, ET, soil moisture, and TWS – as a result of incorporating additional variables in those studies. In addition to the trade-offs between streamflow and TWSA, we also observed substantial trade-offs between NSE_Q and NSE_SWSA, between NSE_TWSA and NSE_SWSA, and NSE_SWSA and NSE_ET (Fig. 5). The trade-offs among the objectives behave differently in the two basins as the shape of the Pareto front (PF) of non-dominated solutions differs significantly between the basins. In general, PFs of the Ganges experiments have a smooth curvature with extended spread near the theoretical optimum of the objectives, while the Pareto fronts in the Brahmaputra basin are mostly very steep resembling right angles (Fig. 5). Due to the conflicts among objectives, the number of non-dominated solutions in the Ganges basin became much larger than in the Brahmaputra where the trade-offs are much smaller.

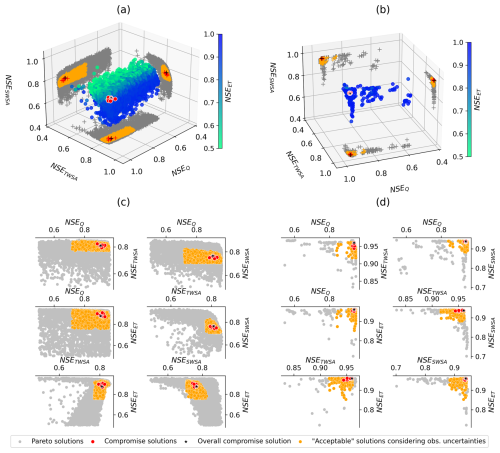
Figure 5 The Pareto front of four-objective calibration experiments of the Ganges basin and for the Brahmaputra basin. The 3-D view of the 4-D PF of Ganges (a) and Brahmaputra (b) is shown, while the fourth dimension is colour-coded. Only solutions with NSEs greater than 0.5 are shown. The 2-D projection is shown with crosses. The bottom row shows the 2-D view of each pair of objectives for the Ganges (c) and the Brahmaputra basin (d). All non-dominated solutions are shown in grey, the compromise solution of each replication in red, the overall compromise solution in black, and the acceptable solutions considering observation uncertainties in orange.

The substantial variations of the performance values of the compromise solutions across the calibration repetitions, which can be regarded as the “uncertainty” of the calibration method itself, further complicates the assessment of trade-offs among objectives. Bai et al. (2018) observed inconsistent conclusions in the literature regarding the impact on streamflow simulations when incorporating GRACE data for model calibration in addition to streamflow observations. Some studies reported a “positive” impact, while others reported a “negative” impact. We argue that the source of such inconsistency could be attributed to (i) the failure to account for the uncertainty in the calibration method; (ii) the lack of convergence to the Pareto front; and (iii) an ill-posed problem formulation resulting from the choice of an inappropriate model, non-identifiable parameters, or inadequate data. Thus, the uncertainty of the calibration outcome should be considered whenever possible when discussing trade-offs. While we consider the impact of observational uncertainty in the next chapter of this study, we found here that the uncertainty stemming from the calibration method differed significantly between the two basins. In the Ganges basin, the highest uncertainties were observed in single-objective calibration cases involving only NSE_Q and only NSE_ET. Among the three-objective calibrations, the highest level of uncertainty was observed in calibrations without NSE_TWSA and without NSE_Q. High variations were observed in those objectives that were not used in the calibration. In the Brahmaputra basin, among the single-objective calibration cases, calibrations with only NSE_TWSA and with only NSE_ET exhibited the highest level of variation. When one object is omitted from calibration, the calibrations without NSE_Q and without NSE_ET generated the highest degree of uncertainty in the objectives NSE_Q and NSE_ET, respectively. Probably the most important calibration cases for trade-off analysis are the bivariate cases with two objectives, which in our case exhibit an insignificant level of uncertainty resulting from the calibration method itself.

In the Ganges, calibrating against ET leads to negative NSE values for TWSA and SWSA. This conflict between ET and TWSA results in the only positive NSE_Q value that was obtained in two-objective calibrations without Q. In a single-objective calibration against ET, the calibration algorithm aims at keeping storage as high as possible to ensure that there is enough water for evaporation and there is no penalty for overestimating storage. However, including TWSA forces the algorithm to release some of the storage to achieve a good fit for TWSA, which leads to a better simulation of Q compared to a single calibration against ET. Calibration against ET and SWSA does not improve Q in the Ganges, suggesting that the adjustment of TWSA is likely related to soil storage. In the Brahmaputra basin, the trade-off between ET and TWSA is very small, and the two-objective calibration against ET and TWSA does not improve Q.

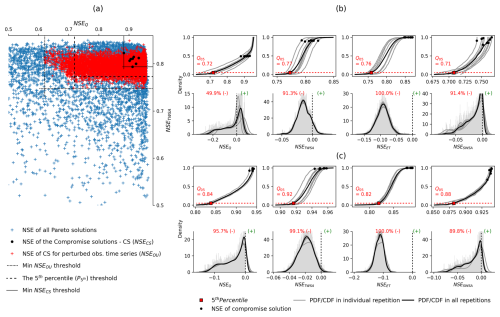
Figure 6 Uncertainty in NSE of the compromise solutions (CSs) in the repeated experiments of four-objective calibration, obtained by propagation of observational uncertainties into objectives. (a) Scatter plot of objective values (NSE) of (i) all Pareto solutions, (ii) the compromise solutions (NSE_CS), and (iii) the compromise solutions computed for 1000 perturbed observation time series (NSE_OU) for the Ganges basin. Three thresholds (M2, M3, M4) are visualized as options to delineate the space of compromise solutions under consideration of observational uncertainties (see text for details). Density functions (CDFs and PDFs) of NSE_OU in the Ganges basin (b) and in the Brahmaputra basin (c). PDFs represent the deviations NSE_OU–NSE_CS. The dashed black vertical lines in the density plots delineate the zones of NSE decrease and NSE increase. Densities of NSE_OU for each compromise solution of a single repetition are plotted in grey, and the density functions of NSE_OU of all compromise solutions are in black. The black dots show the objective values of the compromise solutions.

4.2.2 Impact of observation uncertainty on the calibration outcome

The uncertainties associated with individual data points in the observation time series alter the values of the performance criteria. We conducted an assessment of this effect by perturbing all observations using their respective uncertainties through a Monte Carlo simulation, resulting in 1000 perturbed time series for each variable. Subsequently, we calculated the objective (NSE) values for the compromise solutions across all eight replications of the four-objective calibration. The largest deviations of NSE from the reference values, i.e. the values of the compromise solutions with the original observation time series, were found in streamflow for both the Ganges and the Brahmaputra basins (on average 0.26 and 0.12, respectively), followed by ET (0.12 and 0.10) (Fig. 6b and c). Low deviation in the range of 0.05–0.07 was observed for both storage variables (TWSA and SWSA) for which the means are always zero in both the simulation values and observation data. The changes of the objective function values with the perturbed time series may result in different Pareto solutions. For this reason, we propose a mechanism to objectively identify a group of solutions that could be considered alternatives to the compromise solution.

Table 7 Metrics related to the spread of the objectives of the compromise solutions (CSs) for two sources of uncertainties – observation uncertainty and uncertainty due to the calibration method, i.e. random starting population used during the parameter search. Observation uncertainty is propagated by perturbation of the observation with a Monte Carlo process within the estimated uncertainty bound of an observable and then computing objectives for those perturbed observation time series (NSE_OU) (N=1000).

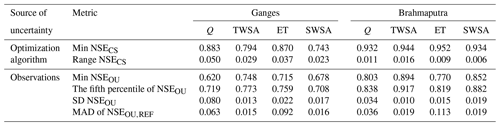
We tested several objective thresholding methods to delineate the space of solutions that can be considered equivalent to the compromise solution in view of the observation uncertainties. In the following, we name them “acceptable Pareto solutions considering observation uncertainties”. The minimum NSE value of all compromise solutions (Min NSE_CS) in the repeated experiments is discarded as a threshold (M1) as it represents the uncertainty due to the random start of the parameter search in the calibration algorithm only but not the observation uncertainties themselves (Table 7). The second threshold (M2) is computed by subtracting the standard deviation of all the objective values obtained with perturbed observation time series (SD NSE_OU) from Min NSE_CS. The third threshold (M3) is computed by subtracting the mean absolute deviation of objective values with perturbed time series from the reference values (MAD NSE_OU,REF; the objectives of compromise solutions are used as reference values); the threshold is set at Min NSE_CS − MAD NSE_OU,REF. Threshold M4 is the fifth percentile of NSE_OU, which ensures 95 % of NSE_OU remain above the threshold. For the most unrestricted option (M5), the minimum value of NSE_OU is taken as the threshold.

In some instances, we found that the standard deviations of NSE_OU (SD NSE_OU) and MAD NSE_OU are smaller than the range of objectives in the compromise solutions of the repeated experiments. For this reason, we argue M2 and M3 are incapable of distinguishing the objective uncertainty attributed to the observational uncertainty from other sources of uncertainty like the randomness in the calibration method itself. Thus, we rejected them as appropriate thresholds for identifying acceptable solutions considering observation uncertainties, although they could find a reasonable number of good solutions (Tables S5 and 7). It is worth noting that Werth and Güntner (2010) used a similar strategy to M2 for identifying the uncertainty in objectives. We also rejected the least restrictive threshold M5 as a singular extreme low value of an objective can extremely limit the efficacy of the threshold. Conversely, the threshold M4 holds a balance between restrictedness and efficacy. While it excludes the poor extremes, 95 % of good objective values are kept in the final set. Using M4, we obtained over 1400 solutions (16 % of the total number) in the Ganges basin and 221 solutions (65 %) in the Brahmaputra basin having model performance above the threshold. Overall, the performance of the acceptable Pareto solutions considering observation uncertainties is seen generally higher with smaller dispersion in the Brahmaputra basin than those of the Ganges basin.

Any perturbation of the ET observation time series within its uncertainty ranges leads to a lower NSE than the reference value in both basins (Fig. 6). In all cases, NSE_OU is worse than the objectives of the compromise solutions. A similar performance decrease was observed in NSE_OU for all variables, except for streamflow in the Ganges basin where only about half of the uncertainty-perturbed time series leads to a decrease in NSE_OU, while the rest causes NSE_OU to increase. The aforementioned indicates that during calibration the parameters are so finely tuned to the (undisturbed) observation time series that any modification of the time series leads to a deterioration of the objective values. On the one hand, this corroborates the strength of the optimization algorithm. On the other hand, it clearly indicates overfitting of the parameters. This raises questions about their usability in scenarios where variations in observations are anticipated such as model predictions in a different time period or when extrapolating parameters for uncalibrated basins (parameter regionalization). The reason that streamflow in the Ganges behaves differently in this regard is not very clear; one probable cause could be that during the choice of the compromise solutions, most high-performing solutions for the streamflow variable were rejected due to low performance in other variables (the maximum NSE_Q in all solutions is 0.97, but max. NSE_Q in the compromise solutions is 0.93).

It is also noteworthy to observe that the shape of the density function for changes in objectives (Fig. 6b and c) is closely associated with the error structure of observations. An average percentage bias was considered the error of the streamflow and SWSA observables, whereas for TWSA and ET absolute errors were assumed. When converted to the percentage error, it was observed that the TWSA and ET observation error has a sinusoidal seasonal structure. In contrast, the constant percent bias in streamflow and SWSA causes high errors in the monsoon season in the perturbed observations and added only very small bias in the dry winter season. This ultimately causes a left skewness to the distribution of deviations of NSE_OU for streamflow and SWSA (Fig. 6b and c).

When comparing the parameter values of the eight compromise solutions (group 1) to those of the acceptable Pareto solutions considering observation uncertainties (group 2) (Fig. 7), the parameter distributions of these two groups are very similar in most cases, although the total number of solutions in group 2 is very high. Mostly, we observed flattening and widening of the density curves for the parameter values in the solutions of group 2. The peak of the density curves of two groups matches most of the time, with a few exceptions with slight horizontal shifts. The overall compromise solution, which is the compromise solution among all outcomes of all replications, does however not always coincide with the peak of the density distributions. The standard WGHM parameter values significantly differ from the calibrated values for most parameters in the two basins.

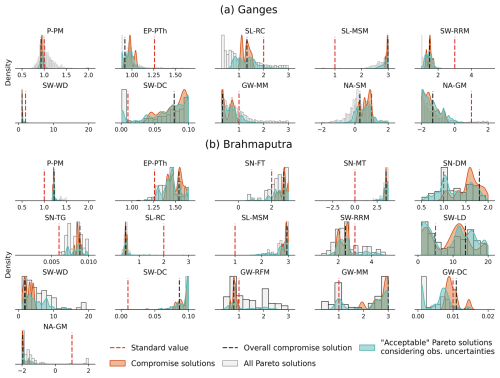
Figure 7 The distribution of parameters of the compromise solutions in the eight repeated four-objective calibration experiments (dark orange), the acceptable Pareto solutions considering observation uncertainties (cyan), and all Pareto solutions in all replications (grey). The overall compromise solution (dashed black vertical line) represents the compromise solution among all solutions in all replications. The parameter value of the standard WGHM is shown with the dashed red vertical line.

The impact of observation uncertainty is often overlooked in hydrological model calibrations, largely due to the lack of strategies for incorporating this uncertainty into the calibration framework. These uncertainties can severely limit the applicability of calibrated models, as they are often overfitted to mean or single observation values. Even small fluctuations in the observations can degrade the performance of the model, potentially disqualifying it as a non-dominated solution. This, in turn, reduces the reliability of what is considered a compromise solution. Conversely, identifying solutions similar to the compromise solution that account for observation uncertainty, while maintaining an acceptable level of performance, could enhance the reliability of the calibration outcomes. However, scrutinizing these “acceptable solutions considering observation uncertainties” comes with challenges. The influence of observational uncertainties varies across variables and depends on the objective functions used in calibration as well as the nature of the data uncertainties.

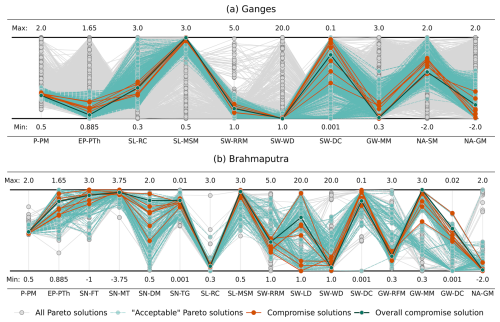
Figure 8 Parallel coordinate plot of all Pareto solutions (grey), the compromise parameter sets (N=8, dark orange), the overall compromise solution (solid cyan), and the set of “acceptable Pareto solutions considering observation uncertainty” (dark green) of the four-objective calibration in the Ganges basin (a) and the Brahmaputra basin (b).

4.2.3 Parameter identifiability and equifinality

Figure 8 illustrates that the four-objective calibration effectively reduced the parameter space substantially in the two basins for most parameters, particularly when comparing the compromise solutions across repeated experiments. Even when we consider the acceptable Pareto solutions considering observation uncertainties, a significant reduction in the a priori parameter range was achieved for most cases, except two parameters in the Ganges and five in the Brahmaputra basin. This already indicates that a good level of identifiability has been achieved. A parameter is considered identifiable for a given set of observations if the true value of the parameter can be inferred with confidence (Wu et al., 2019). The degree of identifiability is usually measured by the posterior standard deviation for individual parameters and posterior covariance matrix for multiple parameters (Wu et al., 2019; Arendt et al., 2012a, b). Cibin et al. (2010) determined parameter identifiability in the Soil and Water Assessment Tool (SWAT) model through visual inspection of scatter plots of model parameters against their corresponding performance metric, considering a parameter identifiable if a distinct performance metric maximum was observable in the scatter plot. In the absence of a posterior distribution, we measured the degree of identifiability as the ratio of the parameter range in the compromise solutions of the eight replications to the a priori parameter range (Tables S8 and S9, Fig. 7).

Due to the fewer parameters involved in the Ganges calibration experiments, better parameter identifiability is observed within the basin compared to experiments in the Brahmaputra basin. We investigated how individual observations influence parameter identifiability during calibration and explored the impact of sensitivity on parameter identifiability. The least satisfactory result was obtained for the calibration with Q only where the ranges of only two parameters (P-PM and SL-RC) in the compromise solutions are less than 15 % of the a priori range. Five parameters (P-PM, EP-PTh, SL-MSM, SL-RC, and SW-RRM) are better constrained by the calibration with TWSA alone. Two sets of six parameters are best constrained by the ET and the SWSA variables, respectively. For ET, they are P-PM, EP-PTh, SL-MSM, SL-RC, GW-MM, and SW-DC, and for SWSA the parameters are SL-MSM, SL-RC, SW-RRM, SW-WD, NA-GM, and NA-SM. Compared to the sensitivity indices (mean EET, Table S2, Fig. 7), the parameters that are better identified in the SWSA-only calibration are those with the highest sensitivity for this variable. Wu et al. (2019) demonstrated that identifiability is largely related to the sensitivity or significance of the calibration parameters with respect to response variables. For ET, however, SW-DC and GW-MM are well constrained by the calibration but are not among the influential parameters for any signature of ET in the SA. For TWSA and Q the relationships between parameter identifiability based on the range ratio and the most sensitive signatures from SA are more diverse. In their study, Soares and Calijuri (2021) also observed a clear disparity between the results of their identifiability analysis and sensitivity analysis, although the majority of the results in the two analyses were similar. One should keep in mind, though, that the objective function used in calibration is only one of the signatures that was used to measure sensitivity in the SA. Nevertheless, we usually observe high correlations among the objectives and the parameters for at least one of the variables (Table S4, Fig. 7).

In calibrations with two or more objectives in the Ganges basin, the degree of parameter identifiability varies with the participating variables. Interestingly, parameters are best identifiable in the experiment ES in which the range of all parameters after calibration is less than 2.2 % of the a priori range except one for which the range ratio is only 11 %. In the case of the four-objective calibration, most parameter range ratios are below or around 20 %; only two parameters have a range ratio of more than 30 %. Arendt et al. (2012a) demonstrated that employing multiple responses, which exhibit mutual dependencies on a common set of parameters, can enhance the identifiability of those parameters. However, if the dependencies among themselves exhibit inverse relationships, parameter identifiability may worsen, as observed in the case of the four-objective calibration.

In the Brahmaputra basin, four parameters (P-PM, SN-MT, SN-TG, and SL-RC) are constrained well (i.e. they have low coverage of their a priori range in the compromise solution sets) with the variable Q, two parameters (SN-MT and SL-MSM) by the ET variable, and two (SN-TG and SW-RRM) by the SWSA observations. However, the TWSA seems to have no discernible control on any of the parameters in the basin. Parameters with a strong inverse correlation, such as GW-MM and GW-RFM (correlation of −0.90, Table S7, Fig. 7), leading to reduced identifiability in both the parameters in Brahmaputra basin (Fig. 8), may become more easily identifiable if one parameter is omitted from the calibration process.

Non-uniqueness, or equifinality, arises from the fact that a singular set of parameters is incapable of generating a unique set of model responses. This occurs because there are numerous pathways to achieve the same target (Beven and Binley, 1992), or the capacity for uniqueness is compromised, whether observation data are absent or present, often as a consequence of summarizing the response variable (Wagener et al., 2003). In the presence of input and data uncertainties, the degree of equifinality increases, even if the structural discrepancies within the model remain unchanged. As the non-uniqueness problem intensifies, it is expected that non-identifiability also rises. If, however, the equifinality arises from an inverse correlation among parameters, a parameter can still be identifiable if the opposing parameter is omitted. For example, GW-MM exhibits a strong negative correlation (−0.90, Table S7, Fig. 8) with the parameter GW-RFM among the acceptable Pareto solutions considering observation uncertainties, which reduced identifiability in both the parameters in Brahmaputra basin (Fig. 8). If one of them is omitted from the calibration process, the other may become identifiable.

The analysis of parameter identifiability does not provide clear evidence that including additional observables in the calibration process necessarily enhances identifiability, particularly in the presence of strong correlations among parameters. On the contrary, interactions among highly sensitive parameters must be carefully considered when selecting parameters for calibration, especially in multi-variable calibration scenarios. However, a strong relationship was observed between parameter identifiability and the number of parameters being optimized. Specifically, in almost all single- and multi-objective calibrations within the Ganges basin, the parameter ranges were significantly reduced compared to the calibration experiments conducted in the Brahmaputra basin (Tables S8 and S9).

4.2.4 Validation

We compare the simulations of the four variables of the overall compromise solution and the ensemble of the acceptable Pareto solutions considering observation uncertainties (Sect. 4.2.2) of the four-objective calibration experiment with the observations. Except in 1 to 2 months during monsoon, the simulation with the overall compromise solution overestimates monthly streamflow in the Ganges basin (Fig. 9). This led to an overestimation of monthly means for all months. The annual streamflow amplitudes are also overestimated in all years except one (2002). In comparison, the standard WGHM calibration with only streamflow observation resulted in a better fit in streamflow simulations, with a lower magnitude of under- and overestimations of monthly means, annual amplitudes, and annual means. Surprisingly, the uncalibrated model simulates the streamflow in the basin better than the compromise solutions in all signatures except in the seasonal amplitude (Table 8). The uncalibrated model mostly performed well to represent the low flows.

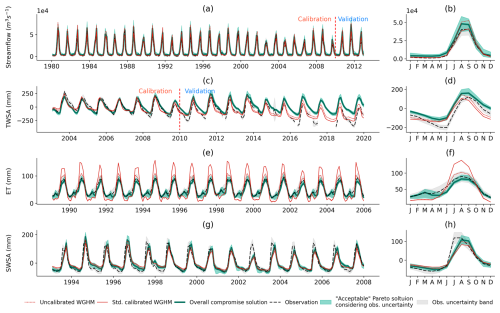
Figure 9 Simulations of streamflow (a, b), TWSA (c, d), ET (e, f), and SWSA (g, h) in the Ganges basin with the overall compromise solution of the four-objective calibration. The simulation results with the acceptable Pareto solutions considering observation uncertainties (dark green), with uncalibrated WGHM (dotted red line) and with the calibrated model with standard approach (solid red), are also shown. Monthly time series (a, c, e, g) and monthly mean values (b, d, f, h). The mean was computed over the entire period with available observations.

Table 8 Comparing the overall compromise solution of the four-objective calibration, standard calibration, and uncalibrated model across four signatures: monthly time series (MTS), monthly means (MM), annual time series (ATS), and seasonal amplitude (SNA). The mean absolute deviation (MAD) was computed by comparing observations and simulations across the entire observation period, expressed as a percentage of the observation mean. Observation gaps were filled using linear regressions ($\mathit{\gamma }={\mathit{\beta }}_{\mathrm{0}}+{\mathit{\beta }}_{\mathrm{1}}\mathit{\chi }$) for individual months, accounting for seasonality and trends.

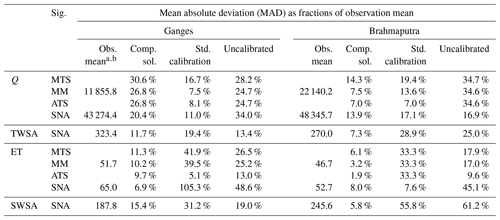
^a The unit for Q is m³ s⁻¹ and for all other variables millimetres (mm). ^b Means of seasonal amplitude are in mm yr⁻¹.

In the Brahmaputra basin, the simulation with the compromise solution underestimates streamflow for the monthly time series and annual averages (Fig. 10a). However, except for few high rainfall years, the seasonal amplitude was mostly overestimated (Fig. 10b). In comparison to the model that was calibrated with the standard approach, the compromise solution in this basin performed better, with lower mean absolute deviation in all aspects of streamflow simulation (Table 8).

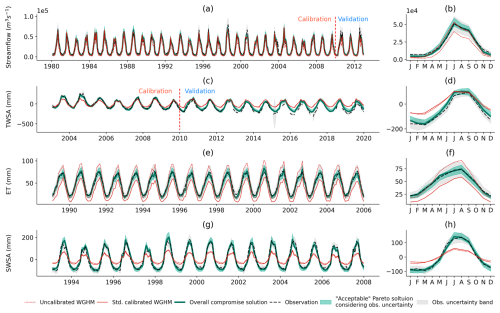
Figure 10 Simulations of streamflow (a, b), TWSA (c, d), ET (e, f), and SWSA (g, h) in the Brahmaputra basin with different solutions. See description of Fig. 9.

Negative trends of TWSA are clearly visible in observations of both the Ganges and the Brahmaputra basins (Figs. 9c and 10c). Because we used only few years of TWSA data in calibration (2003–2009) and within this period the trend was not very obvious, all calibrations fail to represent the TWSA decrease in the two basins. Nevertheless, beyond the calibration period, the seasonality and peaks are correctly represented (with high correlation coefficients between observation and simulation in 2010–2019; Table 9) by the simulations with the compromise solutions of the two basins. Also, the mean deviation of the TWSA is 11.7 % and only 7.3 % of mean annual amplitude in the Ganges and the Brahmaputra basin, respectively. The model's inability to produce the negative TWSA trends causes an overestimation of the TWSA in the later years of the simulation time series. The performance of the calibrated model with standard calibration in simulating the TWSA is worse than that of the compromise solution and even worse than the uncalibrated model.

Table 9 Performance metrics of the overall compromise solution of the four-objective calibration of the Ganges and Brahmaputra basin for all observables and for four signatures: monthly time series (MTS), annual average time series (ATS), monthly mean (MM), and seasonal amplitude (SNA). Calibration period is until 2009 from the start of observation availability, and validation period starts from 2010 till the last observation year.

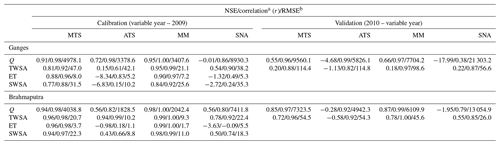
^a Pearson correlation coefficient. ^b The unit of RMSE for Q is m³ s⁻¹ and for the rest of the variables millimetres (mm).

ET simulation with the compromise solution in the Ganges basin mostly underestimates the observed values, except for a few winter months. It should be noted that the interannual variability of amplitude is very small in the ET observation in the two basins (13.6 mm in the Ganges and 11 mm in the Brahmaputra). The seasonal amplitude is underestimated by the compromise solution in most years in the Ganges basin, whereas it is slightly overestimated in the Brahmaputra basin in most years. The monthly means in the Ganges are underestimated for all months except March. In the Brahmaputra basin the monthly means match well with the observations with only 3 % of mean absolute deviation; the annual mean in the basin also has a very small deviation from the observations.

For SWSA, the simulation with the compromise solutions is limited in accurately reproducing the mean seasonality of the observed SWSA: the seasonal peak of the simulated SWSA is on average 1 month delayed relative to the observations. The earlier increase in the SWSA by 1 month as compared to the simulations could be explained by the detection of rice paddies or wet soil signal by the satellite method (Papa et al., 2006), which is not captured by the model.

The seasonal amplitude is slightly underestimated by the simulations, especially in the later observational years (2002–2007) (Fig. 9h). In contrast, in the Brahmaputra basin, the compromise solution simulates the SWSA dynamics very well (Fig. 10g and h).

The simulation results with the ensemble of compromise solutions obtained by consideration of observation uncertainties (group 2) usually show similar dynamics to the compromise solution itself. The uncertainty of the group 2 simulation results, i.e. the bandwidth around the compromise solution, is smaller than the observation uncertainty bandwidth (Table S13, Fig. 10) except for streamflow and SWSA simulations in the Ganges basin. The bandwidth of ET in the group 2 solutions is the lowest (32.2 % and 23.8 % of the observed mean in the Ganges and Brahmaputra basins, respectively, in comparison to observation average uncertainty band width of 53.4 % and 50.5 % in the two basins). In the Brahmaputra basin, the monthly streamflow simulations with the group 2 solutions fall mostly within the observation, while in the Ganges basin the monthly streamflow peaks are mostly overestimated and pass beyond the upper limit of observation uncertainty. Although the group 2 simulation bandwidth was smaller for TWSA for the two basins than the observation uncertainty bands, the simulation bandwidth follows the observation uncertainty band only in the Brahmaputra basin. In the Ganges basin, with the exception of a few years, the group 2 simulation uncertainty band misses the observation uncertainty band even in the calibration period. The group 2 uncertainty of ET simulations falls within the observation uncertainty band in both basins. For SWSA, due to the better representation of its seasonality in Brahmaputra, the uncertainty of SWSA simulations is also better covered by the observation uncertainty than in the Ganges basin.

As discussed before, due to the unavailability of observation data in ET and SWSA in the validation period, model validation was only possible for the Q and TWSA simulations of the compromise solution (Table 9). The simulation error (RMSE) in the validation period increased by factors of 2 to 5 relative to the calibration in most cases, indicating strong degradation of model performance in the validation period. The performance in monthly values (MTS) and mean monthly values (MM) is slightly better than the annual means (ATS) and seasonal amplitudes (SNA) in both basins because the calibration objectives were monthly time series. The performance with respect to these last two signatures is also worse in the calibration period. However, all the signatures stay with high correlations in the validation period, which implies the timing and the seasonal dynamics were well captured by the simulations with the compromise solutions. The validation metrics should be carefully interpreted as the number of validation data is small.

5 Conclusions

In this study, we introduced a multi-objective calibration framework for estimating basin-specific optimal parameter sets for large-scale hydrological models. The framework can make use of observations for multiple model output variables as well as for multiple signatures of each variable. Applying this approach to the Ganges and Brahmaputra basins with the global hydrological model WGHM, we analysed the impacts, benefits, and challenges of multi-variable, multi-signature sensitivity analysis and multi-variable calibration.

The multi-variable, multi-signature sensitivity analysis facilitates the identification of important parameters that would remain unidentified if not all variables or signatures were considered. Due to the different hydrological characteristics of the modelling units to be calibrated, the sensitivity analysis has to be carried out individually for each unit, resulting in identification of different influential parameters and in different numbers of parameters to be calibrated. The proposed parameter selection method is based on the relative impact of individual parameters compared to all parameters. The method can be adjusted with respect to the impact thresholds and by weighting variables and signatures depending on the modelling purpose and is thus an approach that can be used in a flexible way in other studies.

The results of this study show that parameter identifiability is inversely related to the number of parameters that were selected for calibration. Although a reasonably good level of parameter identifiability in the multi-variable calibrations was achieved, the results do not provide evidence that using multiple observational variables generally enhances parameter identifiability. Certain combinations of observations used for calibration resulted in a high parameter identifiability, e.g. calibration with ET and SWSA or with TWSA, ET, and SWSA in the Ganges basin, but this is not the case of the Brahmaputra basin. While in the Ganges basin, all two-variable calibrations lead to a better identifiability than all one-variable calibrations, calibration against Q only results in a better identifiability than all the two-variable calibration except calibration with Q and SWSA. Thus it depends on the basin as well as on the selected calibration parameters to what degree the inclusion of observations of multiple variable in the model calibration increases parameter identifiability.

Including additional observations in the calibration consistently improved the overall model performance. The highest overall performance is achieved by the calibration that takes into account all four output variables. The value of calibrating with Q and TWSA observations for the overall model performance was higher than that of ET and SWSA observations. The degree of improvements depends on basin characteristics as well as on the trade-offs and interactions among the objectives. This, in turn, depends on the capability of the model to represent the relevant hydrological processes in the basin. In line with Döll et al. (2024), we found that using streamflow observations in the calibration is essential for achieving good streamflow simulations, which are the primary target for most hydrological model applications. In contrast, good simulation results for TWSA could also be achieved in the Brahmaputra basin even when the TWSA was not used for calibration but Q and ET.

In this study, we considered two sources of uncertainty in the calibration process: (i) those arising from the search algorithm used to identify the non-dominated Pareto-optimal parameter sets and (ii) those stemming from observational errors. As the random seeds used in the BORG algorithm lead to non-negligible variations in the calibration results and model performances, in particular for the variables that were not used for calibration, a sufficient number of replications of the calibration runs with different initial parameter sets is vital. The results show that a large part of the variations of optimal parameter sets can be attributed to observational uncertainties, a factor often overlooked in calibration exercises. We demonstrated that in the presence of observational uncertainty, relying solely on a “best solution” or a compromise solution can become unreliable, leading to decreased overall efficiency. To address this challenge, we propose a method to select an ensemble of acceptable solutions from the Pareto solutions derived by the search algorithm, taking into account uncertainties in the observation data used for calibration.

The multi-variable, multi-signature parameter selection and calibration methodology presented in this study is suggested for other calibration studies with GHMs or other large-scale hydrological models for all large river basins of the globe where diverse observations of model output variables are available. While the methodology also allows for considering the effect of observational uncertainties on the multi-criteria calibration results, it is imperative to further explore how accounting for observation uncertainties can enhance the robustness of calibration outcomes. Developing uncertainty-based performance metrics would represent a significant advancement in this direction. In regions with limited data availability, leveraging remote-sensing-based streamflow observations such as HydroSAT (http://hydrosat.gis.uni-stuttgart.de, last access: 20 January 2025) or SWOT can provide new insights, complementing TWSA data from GRACE, GRACE-FO, and GRACE-C (GRACE-Continuity). Given the availability of numerous contemporary ET products, future calibration efforts should explore the benefits of considering these ET data sources.