Revealing joint evolutions and causal interactions in complex ecohydrological systems by a network-based framework

There is evidence that climate change and human activities are changing ecohydrological systems, yet the complex relationships among ecological (normalized difference vegetation index, gross primary productivity, and water use efficiency) and hydrological variables (runoff, soil water storage, groundwater storage, etc.) remain understudied. This study develops a novel framework based on network analysis alongside satellite data and in situ observations to delineate the joint evolutions (phenomena) and causal interactions (mechanisms) in complex systems. The former employs correlations, and the latter uses physically constrained causality analysis to construct network relationships. This framework is applied to the Yellow River basin, a region undergoing profound ecohydrological changes. Results suggest that joint evolutions are controlled by compound drivers and direct causality. Different types of network relationships are found – namely, joint evolution with weak causality, joint evolution with high causality, and asynchronous evolution with high causality. The upstream alpine subregions, for example, where the ecological subsystem is more influenced by temperature, while the hydrological one is more driven by precipitation, show relatively high synchronization but with weak and lagged causality between two subsystems. On the other hand, ecohydrological causality can be masked by intensive human activities (revegetation, water withdrawals, and reservoir regulation), leading to distinct evolution trends. Other mechanisms can also be deduced. Reductions in water use efficiency in the growing season are directly caused by the control of evapotranspiration, and the strength of control decreases with the greening land surface in some subregions. Overall, the proposed framework provides useful insight into the complex interactions within the ecohydrological systems for the Yellow River basin and has applicability to broader geographical contexts.

1 Introduction

The hydrosphere and biosphere are intrinsically coupled subsystems of the Earth. Hydrological conditions shape the distribution, structure, and function of terrestrial ecosystems, which, in turn, affect the hydrological components via modulations of land–atmosphere water and energy fluxes (Pappas et al., 2017). Hence, ecohydrological systems are complex, with time-dependent interactions occurring between and within the atmosphere, vegetation, soil, and waterbodies (Yan et al., 2023). These interactions contain intensifying and mitigating mechanisms, e.g., vegetation coverage can be enhanced by warmer temperatures, increased water availability, and afforestation and can be further reduced by the decrease in water storage through root uptake. Together, these interactions among multiple components dictate a collective behavior of the ecohydrological system (Goodwell et al., 2018). In the context of climate change and increasing human activities, ecohydrological processes have undergone substantial changes. Therefore, there is a pressing need for a comprehensive understanding of how the system behaves (phenomenon) and unraveling the multivariate interactions (mechanisms) that drive such behaviors at the system level.

A comprehensive understanding of a system requires finding as many patterns and associations within it, which is a major challenge (Runge et al., 2019a). Network analysis is a powerful tool to study the relationships between elements in complex systems with a clear visualization (Watts and Strogatz, 1998; Barabási and Albert, 1999). This approach generates undirected or directed networks, where links between pairwise variables are assigned varying weights (typically measured by correlations). Such weights between variables are often used as a proxy to deduce the underlying physical relationships, which can be either direct or indirect. Recently, network analysis has received growing attention in the field of hydrology, primarily for identifying hydrologically homogeneous sites or basins based on spatial precipitation and streamflow networks (e.g., Sivakumar and Woldemeskel, 2014; Jha et al., 2015; Fang et al., 2017; Yasmin and Sivakumar, 2018) and for analyzing temporal co-occurrence of hydrological extreme events such as floods and droughts (e.g., Boers et al., 2013; Han et al., 2020; Brunner and Gilleland, 2021; Mondal and Mishra, 2021; Fan et al., 2022; Liu et al., 2022). However, beyond spatial network analysis, this methodology can also be applied to other types of systems, such as exploring relationships among multiple hydrological, meteorological, and ecological variables in a certain region (Goodwell et al., 2018; Jiang and Kumar, 2019; Terán et al., 2023). Recent advancements in ground-based data, remote sensing data, and outputs from various Earth system models provide unprecedented opportunities to simultaneously characterize complex process dynamics across different scales.

In the literature, correlation relationships remain prevalent for modeling ecohydrological systems in the form of networks (Chauhan and Ghosh, 2020; Runge et al., 2023). In these studies, networks are referred to as correlation-based networks. Correlation is useful for measuring the scalar similarity in dynamic behaviors among variables (Aslam, 2015; Su et al., 2023). However, networks defined solely based on correlations cannot infer causal relationships (Altman and Krzywinski, 2015; Yasmin and Sivakumar, 2018). Ecohydrological interactions are inherently causal as changes in one variable are caused by changes in other system variables (Jiang and Kumar, 2019). Additionally, information on the directionality and lagged effects is also useful (Chen et al., 2024). Causal detection has been proven to enhance the understanding of physical mechanisms and contribute to improved model construction (Wang et al., 2018a). To capture causal interdependencies within the system, causal inference techniques are essential. Obtained causal links can form causality-based networks, which is beneficial for discovering the path followed by a perturbation introduced in an ecohydrological variable.

In recent decades, theories and algorithms for causal inference based on observations have been developed, including structural causal modeling (SCM; Peters et al., 2017), transfer entropy (TE; Schreiber, 2000), graph-based methods such as Peter and Clark's (PC) algorithm and Bayesian networks (Pearl, 1988; Darwiche, 2009; Dechter, 2013), Granger causality (GC; Granger, 1969), and convergent cross mapping (CCM; Sugihara et al., 2012). These methods have also been applied in several hydrology studies. For instance, Jiang and Kumar (2019) used an information-flow-based method to investigate the information flows in a long-memory observed stream chemistry dynamics. Singh and Borrok (2019) conducted the Granger causality analysis to identify the causes of groundwater patterns. Shi et al. (2022) used the convergent cross mapping (CCM) method to study drought propagation. Terán et al. (2023) used Peter and Clark's momentary conditional independence framework (PCMCI+) to investigate drivers of three water use efficiency indices in Europe.

However, capturing causality remains challenging in handling high-dimensional datasets with limited sample sizes, like other generic problems. The ecohydrological system is intricate, highly interconnected, and dynamic, necessitating the consideration of multiple variables to better depict the system (Su et al., 2023). From a computational and statistical perspective, this complexity significantly impacts the reliability of statistical inference. Previous studies have noted that causal inference techniques can encounter issues such as high false–positive rates or low recall rates when identifying causal relationships (Rinderer et al., 2018; Delforge et al., 2022). In addition, considering confounding factors and feedback loops, the results should be interpreted cautiously due to potential spurious links (Deyle et al., 2016; Peng and Susan, 2022). To improve reliability, hybrid approaches should be developed by reintroducing the physical aspects of the problem to exclude or control for the risk of physically irrelevant results (Delforge et al., 2022). Causality results may also be context-specific, so conclusions may not generalize well to different settings or time periods. Ensuring the robustness and applicability of causal findings across different conditions is also challenging (Runge et al., 2019a).

In these regards, this study develops a network-based framework that aims to comprehensively improve our understanding of ecohydrological systems from the observed evolutions (phenomena) to the underlying complex causal interactions (mechanisms). More precisely, a wide range of variables, mainly related to different types of water storage, streamflow, vegetation growth, and ecosystem functioning, are used to represent the characteristics of our systems. Climatic forcings and human activities are considered potential drivers outside the system. To capture system-level variations, the evolutionary dynamics of each variable are linked to form correlation-based networks. The joint evolution modules are then detected by clustering and network metrics are used to assess the network properties. To capture system-level mechanisms, physically possible and plausible links between the variables are constructed to constrain the core structure of causality-based networks, and significant contemporaneous and lagged causal links are portrayed quantitatively. Overall, this study contributes to the understanding of ecohydrological processes and extends the network analysis application within the realm of ecohydrology. An important ecological corridor in China, the Yellow River basin (YRB), which has been undergoing significant changes in ecohydrological processes, is taken as the study case. The YRB is vast with different climatic conditions, land use types, and human disturbances, providing various types of ecohydrological regimes for investigation (Luan et al., 2021; Wang et al., 2021; Yin et al., 2021). Our framework has the potential to be generalized and applied to the analysis in different regions of the world as well.

The paper is structured as follows. Section 2 describes the framework developed. Section 3 introduces the study area and the data used. Section 4 presents the results for each subregion of the YRB, followed by a discussion of the findings in Sect. 5, including the significance of the study, comparisons with other studies, limitations, and future outlooks. Finally, some conclusions are drawn in Sect. 6.

2 Methodology

The general framework for investigating ecohydrological systems consists of the following main steps, as shown in Fig. 1. Relationships between ecohydrological processes vary within the year, so we focus on the most active growing season (April to September).

Step I selects variables describing key characteristics/components of the ecohydrological system and processes the data. Based on Fig. 1a, regional runoff (R_modulus) and terrestrial water storage (TWSA) together with its components (soil moisture storage anomalies, SMSA, and groundwater storage anomalies, GWSA) are chosen as the main hydrological variables. Regional sediment load (SL_modulus) is also selected since the Yellow River is known for high sediment loads. Besides, snow cover (SCA) of the source region is considered due to its location on the Tibetan Plateau. Vegetation coverage (normalized difference vegetation index, NDVI) and physiological activities (gross primary productivity, GPP) are selected as main ecological variables. In addition, ecosystem water use efficiency (WUE; quantified as the ratio of GPP to actual evapotranspiration) is employed to characterize the trade-off between carbon and water cycles. Due to the difficulty of accurate quantification, more detailed processes such as infiltration and interception are not considered. External climate forcings include precipitation (P) and air temperature (T), and human impacts contain reservoirs (RSC) and human water withdrawals (WW).

Step II identifies the evolution of each variable using the Mann–Kendall (M–K) test, providing an overview of how the ecohydrological variables change individually.

Step III detects which variables exhibit joint changes. SMSA and GWSA are the two principal components of TWSA, and we therefore remove TWSA to reduce redundant correlations. A correlation-based network is constructed for each subregion, and module clustering is employed for the analysis of positive correlations. Modularity and the degree of synchronization between hydrological and ecological subsystems are constructed as network metrics.

Step IV further investigates the causality between variables. Potential drivers, including climatic forcings and human activities, are considered here to fulfill the causal sufficiency. Since multiple variables (more than 10) can generate a large number of causal links with different time lags and some of them may be spurious, empirical knowledge is incorporated into the causality analysis (Peter–Clark momentary conditional independence, PCMCI) to reduce the uncertainty. As the causality can be strongly influenced by the input data, such as the presence of outliers, data length, and interannual variability in causality, representative subregions are selected to check the robustness of the results.

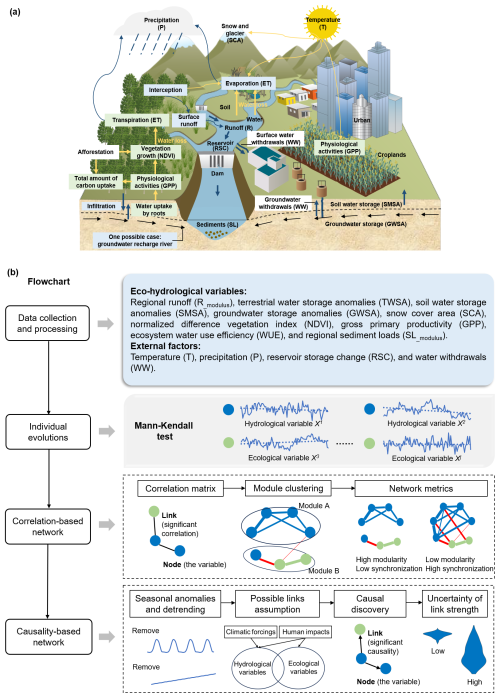
Figure 1 The general framework for investigating ecohydrological systems. (a) The conceptual diagram of ecohydrological processes in a basin. (b) The detailed flowchart. The blue circles denote the hydrological variables and the green circles represent the ecological variables. The blue lines stand for the connection between hydrological variables, the green lines represent the connections between ecological variables, and the red lines are the connections between hydrological and ecological variables.

2.1 Trend analysis for individual ecohydrological variables

The interannual trend analysis for ecohydrological variables is conducted using the commonly applied nonparametric M–K test (Mann, 1945; Kendall, 1975). The positive and negative values of Z statistic indicate the increasing and decreasing tendencies, respectively (Sect. S1 in the Supplement). When the absolute value of Z is larger than 1.96, there is a statistically significant trend at the 95 % confidence level.

2.2 Correlation network analysis

2.2.1 Construction of the network

Correlation networks are undirected with no ordering in the nodes defining a link. The nodes represent the ecohydrological variables, and the links between nodes are their correlations. The commonly used Pearson correlation coefficient (PCC; Pearson, 1895) is used to calculate the strength of connections. A positive PCC indicates a joint evolution between a pair of variables, while a negative value denotes their opposite evolution trends. PCC is calculated as follows:

$$\begin{array}{}\text{(1)}& \mathrm{PCC}(X_i,X_j)={\displaystyle \frac{\mathrm{Cov}(X_i,X_j)}{\sqrt{\mathrm{Var}\left(X_i\right)\mathrm{Var}\left(X_j\right)}}},\end{array}$$

where X_i and X_j are the time series data of two variables; Cov(X_i, X_j) is the covariance of X_i and X_j; and Var(X_i) and Var(X_j) are the variances of X_i and X_j, respectively. PCC ranges from −1 to 1, and the correlation is stronger when its absolute value is closer to 1.

Networks for each subregion are constructed using the adjacent matrix A, where the links satisfy the significance level of P<0.05.

$$\begin{array}{}\text{(2)}& A_{ij}=\left\{\begin{array}{l}{\mathrm{PCC}}_{\mathrm{ij}}\mathrm{if}P<\mathrm{0.05},i\ne \mathrm{j}\\ \mathrm{0}\mathrm{otherwise}\end{array},\right.\end{array}$$

where A_ij is the weight of the link between variables i and j and is the element of the weighted adjacency matrix A. The threshold of P<0.05 is determined to include substantial correlations without excluding too many potential relationships. In addition, the positively correlated ecohydrological variables are more densely connected, and we further separate them into several modules using the “cluster walktrap” algorithm in the R package (Pons and Latapy, 2005; Csardi and Nepusz, 2006). The walktrap approach has been widely used and reported to obtain better results on average (Rocha and Filho et al., 2023). Each module represents a group of variables that are more highly correlated among themselves and loosely correlated to others.

2.2.2 Network metrics

Modularity (M) represents the ability to partition a network into modules, and the modules are detected according to the concentration of links. In this study, this metric is used to measure whether the variables in the system tend to change together or evolve separately. It is defined as follows:

$$\begin{array}{}\text{(3)}& {\displaystyle }m={\displaystyle \frac{{\sum }_{i,j}\left|A_{ij}\right|}{\mathrm{2}}},\text{(4)}& {\displaystyle }M={\displaystyle \frac{{\sum }_{ij}(A_{ij}-\frac{k_i{k}_j}{\mathrm{2}m})\mathit{\delta }(c_i,c_j)}{\mathrm{2}m}},\end{array}$$

where m is the total weighted existing connections; M is the modularity, ranging from 0 to 1; A_ij is the element of the adjacent matrix; k_i and k_j are the degrees of variable i and variable j, respectively; and c_i and c_j are the modules that variable i and variable j belong to, respectively. If variables i and j belong to the same module, the function δ (c_i, c_j) returns 1 and otherwise returns 0 (Newman, 2004).

A new metric S representing the degree of synchronization between hydrological and ecological subsystems is proposed. It is the ratio of total positive correlations to all the potential links between ecological and hydrological variables:

$$\begin{array}{}\text{(5)}& S={\displaystyle \frac{{\sum }_{ij}{A}_{ij}\mathit{\delta }{}^{\prime }(\mathrm{hs},\mathrm{es})}{\mathrm{2}p\ast q}},\end{array}$$

where p is the number of variables in the hydrological subsystem; q is the number of variables in the ecological subsystem. hs represents the hydrological subsystem, and es represents the ecological subsystem, respectively. δ^′ (hs, es) returns 1 when the two variables i and j are correlated and are in hs and es respectively; otherwise returns 0.

2.3 Causal network analysis

2.3.1 Causal discovery method

Causality is estimated based on the PCMCI method (Runge et al., 2019a, b). PCMCI is a graphical-based method for linear and nonlinear causal discovery from multivariate time series datasets. This method is used because it is able to address the challenges regarding autocorrelated, high-dimensional time series data by first using a condition–selection step (PC; Colombo and Maathuis, 2014) and then applying a momentary conditional independence (MCI) test. Compared to other causal inference methods (such as GC and CCM), PCMCI is more efficient in dealing with high dimensionality, reports significant contemporaneous dependencies, and provides causal relationships with link strengths and different time lags (Runge et al., 2019b).

Specifically, in an underlying time-dependent system with N variables $X_t^j\in (X_t^{\mathrm{1}},\mathrm{\dots },X_t^N)$ varying in time t, the link $X_{t-\mathit{\tau }}^i\to X_t^j$ (where τ is a positive time lag) exists if the lagged variable $X_{t-\mathit{\tau }}^i$ has a significant dependence or predictive power over $X_t^j$ while removing the influence of all other potential variables that affect $X_{t-\mathit{\tau }}^i$ or $X_t^j$, except $X_{t-\mathit{\tau }}^i$. These potential variables are parents, denoted as $P\left(X_{t-\mathit{\tau }}^i\right)$ and $P\left(X_t^j\right)\mathit{\left\{}{X}_{t-\mathit{\iota }}^i\mathit{\right\}}$ (an example is shown in Fig. 2a). In the PC step, the preliminary parents $\widehat{P}\left(X_t^j\right)=(X_{t-\mathrm{1}},X_{t-\mathrm{2}},\mathrm{\dots },X_{t-\mathit{\tau }max})$ of each variable $X_t^j$ are initialized. The null hypothesis is set that $X_{t-\mathit{\tau }}^i$ and $X_t^j$ are conditional independence. In the first iteration, p=0, unconditional independence tests are conducted, and $X_{t-\mathit{\tau }}^i$ will be removed from $\widehat{P}\left(X_t^j\right)$ if the null hypothesis cannot be rejected at the significance level of α_pc. In each next iteration, $p\to p+\mathrm{1}$, the preliminary parents are sorted according to their absolute statistic value and then conduct conditional independence tests. After each iteration, irrelevant parents are removed from $\widehat{P}\left(X_t^j\right)$, and the algorithm converges if no more conditions can be tested. In the second step, the MCI test uses a much smaller set of conditions (generated in the PC stage) to identify cause links for various time delays. MCI is defined as follows:

$$\begin{array}{}\text{(6)}& \mathrm{MCI}:X_{t-\mathit{\tau }}^i\perp X_t^j\mathrm{|}\widehat{P}\left(X_t^j\right)\mathit{\left\{}{X}_{t-\mathit{\tau }}^i\mathit{\right\}},\widehat{P}\left(X_{t-\mathit{\tau }}^i\right),\end{array}$$

where ⊥ denotes (conditional) independence.

Both PC and MCI stages use conditional independence tests to measure the strength and the statistical significance of links. The significance level, α_pc, and maximum time delay, τ_max, are two parameters governing the allowable amount of false–positive link discovery. The linear test statistic is based on partial correlation (ParCorr) and the nonlinear connections can be estimated by conditional mutual information using the k-nearest-neighbor approach (CMI-knn). For more details about the method, please refer to Runge et al. (2019a, 2020).

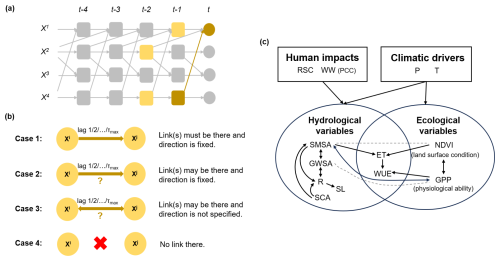
Figure 2 Overview of the causal inference method. (a) An example of causality that a lagged variable $X_{t-\mathrm{1}}^{\mathrm{4}}$ (the brown square) is said to be a cause of $X_t^{\mathrm{1}}$ (the brown circle) if $X_{t-\mathrm{1}}^{\mathrm{4}}$ has a significant dependence or predictive power over $X_t^{\mathrm{1}}$ while removing the effect of all other potential variables influencing $X_{t-\mathrm{1}}^{\mathrm{4}}$ or $X_t^{\mathrm{1}}$ (the yellow squares), except $X_{t-\mathrm{1}}^{\mathrm{4}}$. (b) Four types of assumptions to construct physically possible and plausible links. τ_max represents the maximum lag time. (c) The network with physically possible and plausible links between the included variables in the PCMCI analysis. PCMCI will test shown links for significant causality and yield the final causal network as a subset of this. The dashed lines represent the causality considered to be spurious, but we do not remove it from the test as in Case 4 as it might help illustrate ecohydrological mechanisms in this study.

Although ecohydrological relationships are nonlinear, our study uses ParCorr to capture significant links. This is because the nonlinear CMI-knn is unstable in the real case study, especially when the data sample is limited (Delforge et al., 2022). Besides, the CMI-knn test is more likely to miss the effective connections and the linear ParCorr test has been reported to detect small nonlinearities as well (Terán et al., 2023). Furthermore, to avoid the penalty of high dimensionality and to maintain high statistical power in conditional independence tests, the maximum time lag, τ_max, is set to 3 months. We believe that this time delay is sufficient to detect the majority of significant cause–effect relationships during the growing season. We set a strict significance level of 99 % for both condition selection and condition independence tests.

2.3.2 Satisfaction of causal assumptions

Faithfulness, causal Markov condition, causal sufficiency, and stationarity of variables are the main assumptions of PCMCI (Runge et al., 2019a). Causal sufficiency refers to the included variables being sufficient to capture the causal relationships between them. However, it always depends on subjective judgment and is difficult to handle due to no boundaries in the system (Chauhan et al., 2023). We account for common influencing factors while controlling high dimensionality. Climatic forcings, i.e., temperature (T) and precipitation (P), as well as reservoir storage change (RSC), are added as potential influencing factors. The actual evapotranspiration (ET) is also added to fulfill causal processes as it governs the ecosystem water use efficiency (WUE) according to the definition. To satisfy the stationarity assumption, the time series of each variable is masked according to the growing-season months. The series are further detrended and use seasonal anomalies based on the additive model (Ombadi et al., 2020; Terán et al., 2023):

$$\begin{array}{}\text{(7)}& X_t=T_t+S_t+a_t,\end{array}$$

where X_t is the original time series, T_t is the trend, S_t is the seasonality, a_t is the remainder, and t denotes time. We first remove the multi-year monthly mean values to obtain seasonal anomalies. The remaining time series are tested for long-term trends using the M–K test. When the null hypothesis of no trend is rejected at a significance level of 0.05, the linear trend is removed from the time series.

2.3.3 Using prior knowledge as physical constraints

Ecohydrological systems present highly interdependent time series (or functional connections), favoring a high false–positive rate. Uncertainties in causality analysis are therefore minimized with the aid of prior knowledge. As illustrated in Fig. 2b, there are four types of link assumptions, and they are that (1) the causal link must exist and its direction is fixed (Case 1), (2) the causal link may exist and its direction is fixed (Case 2), (3) the causal link may exist but its direction is not specified (the direction is then given by the time order; Case 3), and (4) the causal link is physically inappropriate and will not be tested (Case 4). In this study, the second case is designed to specify the direction of potential contemporaneous links, and the third case is used for potential bidirectional interactions. Such knowledge is incorporated by utilizing the link_assumptions function in the Python package tigramite (https://github.com/jakobrunge/tigramite, last access: 18 October 2024). As a result, physically possible and plausible links between the included variables are hypothesized as a constrained structure (Fig. 2c). Then, PCMCI tests possible links and provides the final results as a subset of the total possible network, showing causal links, directions, strengths, and time lags.

Since this study focuses mainly on the ecohydrological feedback occurring at the land surface, climate forcings are considered external system factors, as are human impacts. The effects of ecohydrological variables in turn on climatic drivers and human activities are not considered. The interactions can be separated into the processes of hydrological→hydrological variables, hydrological→ecological variables, ecological→ecological variables, and ecological→hydrological variables. Some interactions are potentially bidirectional; for example, GWSA and SMSA can complement each other. Afforestation, i.e., the increase in vegetation coverage (NDVI), improves the total GPP of a region, while the enhanced physiological ability (GPP) also facilitates leaf growth (NDVI). Vegetation productivity (GPP) is directly supported by soil water supply (SMSA), while enhanced GPP in turn influences SMSA. Note that water withdrawal (WW) is an important anthropogenic influence, but due to the lack of monthly data, the correlation coefficient (PCC) is used to characterize its general association with other variables in the system.

3 Study area and data

3.1 Study area

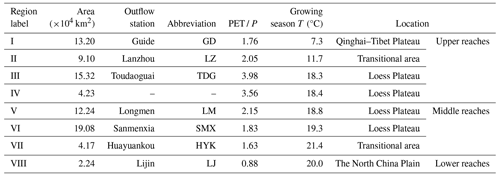
The Yellow River (Fig. 3) is the second-longest river in China (Wang et al., 2020). It originates from the northeastern Qinghai–Tibet Plateau, flowing through the Loess Plateau and the North China Plain, and finally enters the Bohai Sea. The YRB is an important ecological corridor, hosting more than 12 % of the population and creating about 14 % of the gross domestic product (GDP) of China. In general, the YRB is dominated by the arid and semi-arid continental monsoon with a long-term mean annual PET / P ratio of 2.1 (Xie et al., 2019). Summer serves as the primary rainy season, with precipitation from June to September comprising approximately 70 % of the annual total (Ni et al., 2022).

In this study, the YRB is divided into eight subregions labeled Region I to Region VIII from the upstream to the downstream (Fig. 3 and Table 1). The upper reaches include Regions I–IV, covering part of the Qinghai–Tibet Plateau and part of the Loess Plateau. The source region (Region I) has a cold and vulnerable eco-environment where the climate is inland alpine semi-humid, generating 35 % of the total annual runoff for the entire basin (Zhan et al., 2024). From west to east, the altitude gradually decreases, the temperature rises, and the climate becomes drier. Region II is the transitional zone between the source (Region I) and the Loess Plateau (Regions III and IV). Regions III and IV are the driest parts of the YRB, characterized by low precipitation, high evapotranspiration, and sparse vegetation coverage. The dominant land use type in the upper reaches is grassland (Cao et al., 2022).

The middle reaches are Regions V–VII, and the lower reaches are Region VIII, with a temperate monsoon climate. From Region V to Region VIII, climatic conditions become warmer and wetter, and vegetation cover increases. The main land use types are cropland and forests. Compared to the upper reaches, these regions have experienced more intensive human activities, including the change of agricultural land back to forest and excessive water withdrawals for large populations, agricultural irrigation, and industrial production (Xie et al., 2019; Zhou et al., 2024).

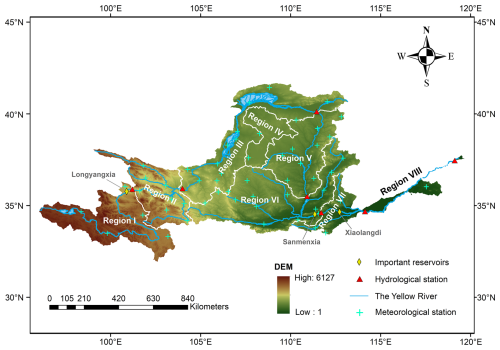
Figure 3 Location of the Yellow River basin and its topography, with the basin divided into eight subregions based on the secondary basin boundary in China. Distributions of meteorological stations and hydrological stations are also shown in this figure. Region I: above the Guide, Region II: Guide to Lanzhou, Region III: Lanzhou to Toudaoguai, Region IV: Endorheic Basin, Region V: Toudaoguai to Longmen, Region VI: Longmen to Sanmenxia, Region VII: Sanmenxia to Huayuankou, Region VIII: the downstream part of Huayuankou.

Table 1 Summarized information on eight subregions in the YRB.

Note: PET / P is the long-term dryness index based on Xie et al. (2019). PET is potential evapotranspiration, and P is precipitation.

3.2 Data sources and processing

3.2.1 Hydrological data

The monthly runoff observations from 2003 to 2019 at GD, LZ, TDG, LM, SMX, HYK, and LJ main-stem hydrological stations are collected from the National Hydrological Yearbook. Since the Yellow River is one of the most heavily loaded rivers in the world, we collect the sediment loads from the National Hydrological Yearbook as well. Gauged streamflow and sediment are not suitable for regional investigation, so we calculate the increments in flow (R_modulus) and sediment loads (SL_modulus) for each subregion, i.e., the difference in flow/sediment loads between two gauged stations that are standardized as modulus by area (Xu et al., 2022).

The MODIS-based snow cover product is used to obtain the variation in snow cover area (SCA; Hao et al., 2022) in the source region. Terrestrial water storage (TWS) data are derived from three monthly gridded GRACE products, which are the GRACE mascon data from the Center for Space Research (CSR, at the University of Texas, Austin) (Save et al., 2016), the GRACE mascon data from the Jet Propulsion Laboratory (JPL, at NASA and the California Institute of Technology, California) (Swenson and Wahr, 2006; Landerer and Swenson, 2012), and the GRACE mascon data from the Goddard Space Flight Center (GSFC, at NASA) (Awange et al., 2011; Luthcke et al., 2017). The three GRACE products are used by taking their ensemble mean values. A few months of data missing during the study period due to battery management are interpolated by averaging the values of adjacent months. All GRACE data used are anomalies relative to a 2004–2009 time-mean baseline – namely, terrestrial water storage anomalies (TWSA). Monthly data simulated by the Noah model of the Global Land Data Assimilation System (GLDAS-v2.1; http://disc.sci.gsfc.nasa.gov/services/grads-gds/gldas, last access: last access: 18 October 2024) are utilized to collect the surface water storage (SWS) and the soil (moisture) water storage (SMS). SWS contains snow water equivalent and canopy water storage from the Noah model, as well as the volume of water stored in reservoirs and lakes. SMS is calculated as the total soil moisture content from four different soil layers (0–10, 10–40, 40–100, and 100–200 cm). Their values are also processed into the anomaly values as surface water storage anomalies (SWSA) and soil moisture storage anomalies (SMSA). Groundwater storage anomalies (GWSA) are calculated by subtracting SWSA and SMSA from TWSA (Scanlon et al., 2018; Yao et al., 2019).

3.2.2 Ecological data

Normalized difference vegetation index (NDVI) and gross primary productivity (GPP) are used as proxies for vegetation growth and photosynthetic activity, respectively. The time series of NDVI at 1 km is obtained from the Terra Moderate-Resolution Imaging Spectroradiometer (MODIS) Vegetation Indices Monthly (MOD13A3) product (Didan, 2021) (https://lpdaac.usgs.gov/products/mod13a3v061/, last access: 18 October 2024). The GPP dataset is obtained from the MOD17A2H product (Running et al., 2021a), available at a 500 m spatial resolution and 8 d temporal resolution. Ecosystem water use efficiency (WUE) is the ratio of GPP to actual evapotranspiration (ET) (Beer et al., 2007; Cooley et al., 2022), where ET is available from the MOD16A2 product (Running et al., 2021b) (https://lpdaac.usgs.gov/products/mod16a2v061/, last access: 18 October 2024). All the time series are processed to monthly data.

3.2.3 Auxiliary data

Monthly average air temperature (T) and precipitation (P) during the period of 2003–2019 at 76 National Meteorological Observatory stations (Fig. 3) are derived from the China Meteorological Administration (http://data.cma.cn/, last access: 18 October 2024). For each subregion, meteorological values are calculated using the Thiessen polygon method based on gauged values. Longyangxia (LYX), Sanmenxia (SMX), and Xiaolangdi (XLD) are important reservoirs engaged in the water-sediment regulation scheme of the Yellow River (Xie et al., 2022). In Region I, we use the data above the reservoir due to concerns within the research community, and we consider reservoir storage changes (RSC) in Regions VI and VII. Water storage changes in the reservoirs are captured based on runoff records from the National Hydrological Yearbook. Water withdrawal (WW) data are obtained from the Water Resources Bulletin of the Yellow River (http://yrcc.gov.cn/gzfw/szygb/index.html, last access: 18 October 2024). Table S1 in the Supplement is the lookup table for all the data used in this study.

4 Results

4.1 Evolutions of individual variables

The evolutions of ecohydrological variables during the growing season across eight subregions are presented in Fig. 4a–h. The corresponding M–K test results are plotted in Fig. 4i. The multi-year mean values of the variables are listed in Table S2. At the basin scale, TWSA of the growing season significantly reduced (with a decreasing rate of −5.12 mm yr⁻¹), and GWSA also had a significant downward trend (with a rate of −6.66 mm yr⁻¹), but the evolution trends of SMSA, R_modulus, and SL_modulus are not significant. The spatial heterogeneity of hydrological evolutions was as follows. In the source regions (Regions I–II), the water resources were relatively abundant with high R_modulus, and most of the hydrological variables exhibited increasing trends (significant or insignificant) except for GWSA. The trend in snow cover area in the source region was not significant. However, the snow cover for melting (April) increased, and the onset of melting shifted earlier from June to May (Fig. S1 in the Supplement). In Regions III–VI on the Loess Plateau, R_modulus became much lower compared to the source regions and showed a decreasing trend, except for Region VI (which is disturbed by the reservoir). TWSA and GWSA all showed significant downward trends, with depletion increasing from the upstream to the downstream region, while SMSA displayed non-significant upward trends. In the lower reaches (Region VIII), all the hydrological variables showed scarcity and declined substantially from 2003 to 2019. Regarding the regional sediment loads (SL_modulus), their evolution seemed to be irregular across the basin, with significant trends only in Regions VII (with the XLD reservoir) and VIII (with severe water withdrawals).

Ecological conditions differed from hydrological conditions a lot. The poorest areas in terms of vegetation coverage (NDVI) and productivity (GPP) were the driest regions, Regions III–IV, while for WUE, the poorest part of the YRB was the source region where the temperature is low. NDVI and GPP of the growing season increased by 31.16 % and 35.70 % for the entire YRB, respectively. It indicated that the large-scale vegetation restoration undertaken over the last 2 decades was effective (Yu et al., 2023). However, the ecosystem water use efficiency (WUE) of the growing season decreased significantly in most subregions (except in Regions I and VIII) from 2003 to 2019.

Figure 4 Ecohydrological variables of the growing season, where the horizontal axis represents the year and the vertical axis is different subregions: (a) terrestrial water storage anomalies (TWSA), (b) soil water storage anomalies (SMSA), (c) groundwater storage anomalies (GWSA), (d) runoff increment modulus (R_modulus), (e) normalized difference vegetation index (NDVI), (f) gross primary productivity (GPP), (g) ecosystem water use efficiency (WUE), (h) sediment load increment modulus (SL_modulus), and (i) Z-statistic values of the M–K test for each ecohydrological variable. The significance level is taken to be 0.05. A gray box denotes no data, a red box represents a positive trend, a blue box represents a negative trend, and the symbol ^∗ means the trend is significant.

4.2 Correlation-based networks and module detection

Networks were constructed for each subregion in which evolutions of ecohydrological variables were linked by correlations (if significant). The correlations in each network can be found in Fig. 5a. GWSA played a significant role in the formation of negative correlations in most subregions (Fig. 5a). Positive correlations were further clustered into different modules due to their complexity (Fig. 5b).

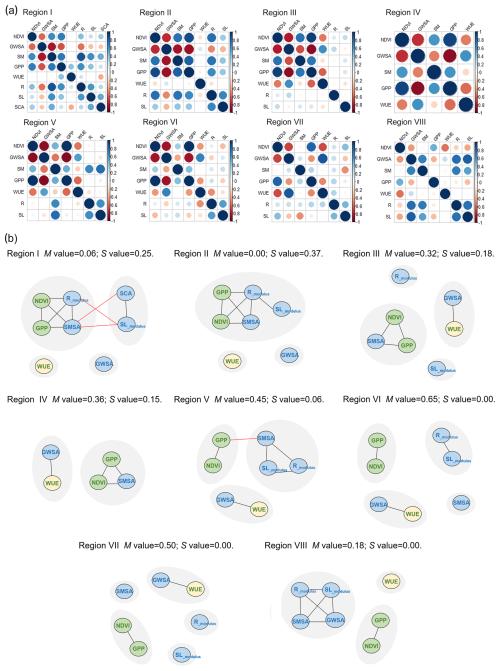
Figure 5 (a) Correlation metrics for each subregion. (b) Module composition of positively correlated networks in different subregions. Different gray circles in the background represent different modules. Black lines represent correlations in the same module, and red lines represent correlations in different modules. Blue circles indicate variables of the hydrological subsystem, and green circles indicate variables of the ecological subsystem. WUE is a special ecological indicator represented in yellow circles as it is the coupling of hydrological (ET) and ecological (GPP) processes.

From Fig. 5b, we recognized which parts of the system behaved similarly during the growing season from 2003 to 2019. The modularity was found to be low in the upper two reaches (Regions I and II), meaning that positive correlations were highly connected and were difficult to separate. In particular, the ecological variables in the green circles were correlated with the hydrological variables in the blue circles, and they formed a big module. The S values (synchronization between the two subsystems) for these two regions were 0.25 and 0.37, respectively. This raised the question of whether there was strong feedback between vegetation and water resources that promoted their joint increases. However, the remaining regions, Regions III–VIII, had relatively high modularity, ranging from 0.18–0.65. In Regions III and IV, some variables in the ecological (NDVI and GPP) and hydrological (SMSA) subsystems still evolved together, with the decoupling of R_modulus and SL_modulus. The synchronization of the two subsystems was reduced to 0.18 and 0.15, respectively. WUE and GWSA were divided into the same module, both showing downward trends. In Regions V–VIII, which were more affected by intensive human activities (Zhang et al., 2023; Yin et al., 2023), the hydrological subsystems in blue and the ecological subsystems in green were found to be decoupled, indicating the two different evolution directions. In the downstream of the basin (Region VIII), the modularity decreased due to the synchronized decreases in all hydrological components. Given that the network structure and metrics can be influenced using different thresholds, PCC > 0.4 and PCC > 0.5 were also employed to construct networks for validation (Figs. S2 and S3). The mechanisms behind decoupling correlations of the ecological and hydrological subsystems from the upper to the lower reaches required further investigation.

4.3 Causality-based networks

Figure 6 presents the significant contemporaneous and lagged causal links within the complex ecohydrological systems. The resulting networks display the drivers of small timescale changes as the maximum time lag is 3 months. If a pair of variables exhibits significant causality at multiple time lags and in the same direction, only the strongest lagged link is shown. The most important causal processes typically took place in the current month and with a lag of 1 month. The self-dependencies of the variables are shown in Table S3.

4.3.1 Causal links between water components and vegetation

In alpine regions, Regions I–II, NDVI and GPP were found to positively evolve together with R_modulus and SMSA during the growing season. Figure 6 uncovered the only weak and lagged causal link between the ecological (green circles) and hydrological subsystems (blue circles) – namely, SMSA→GPP at a 1-month lag. It suggested less water demand for vegetation and the delayed vegetation response to changes in the water supply. Instead, increased T (Fig. 4) was the dominant factor stimulating GPP since the contemporaneous T→ GPP links with the strengths of 0.78 (Region I) and 0.52 (Region II) were detected. It can be interpreted that these alpine areas are heat-limited and have a certain number of water resources, resulting in a higher sensitivity of biological photosynthesis, such as carbon allocation and biomass accumulation, to temperature. Meanwhile, P was the crucial driver of the increases in the hydrological subsystem, evidenced by strong contemporaneous and lagged links of P→ SMSA, P→R_modulus and P→ SL_modulus in the networks. T and P also affected snow melting (SCA) and further impacted R_modulus positively, with a 3-month lag. In general, the exhibiting “joint evolution” between water components and vegetation was more attributed to their respective drivers instead of direct causality.

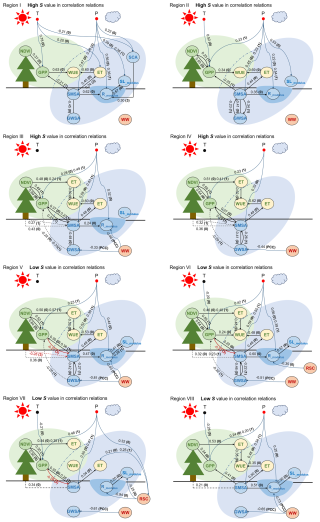
Figure 6 Causal process networks of ecohydrological variables in the growing season (April to September) for Regions I–VIII. A link is only shown if found statistically significant at a 99 % confidence level. Link labels in (1), (2), or (3) indicate the lag at which the connection is found, and only the strongest one is shown in the graph for clarity. (0) means a contemporaneous link, and a dashed line (–) indicates a contemporaneous link with uncertain direction. All links regarding WW are special as they are determined by correlations marked by PCC. Links between SMSA and NDVI as well as GWSA and GPP are regarded as spurious ones and are denoted in dashed lines. The red circle under P or (and) T indicates its dominance in controlling the local ecohydrological system.

In Regions III–IV, joint evolutions in NDVI, GPP, and SMSA were observed. These are water-limited areas with a PET / P over 3.0 (Table 1), where water availability, rather than heat supply, is the primary factor stimulating the ecological subsystem. The positive contemporaneous/lagged links of P → GPP and SMSA → GPP were evidence of this. The results indicated a relatively strong and rapid vegetation response to changes in the water supply, and the contribution of vegetation to the conservation of soil water storage was also found (GPP → SMSA with a 1-month lag). Similar links between NDVI and SMSA were detected although they were treated as “spurious” ones (Sect. 2.3.3). The direct causal interactions and the common driver P mainly contributed to the joint increases. Compared to Regions I–II, R_modulus was decoupled from the module. It was found that human water withdrawals exerted a significant influence on regional runoff (WW →R_modulus), and thus WW was regarded as a significant contributor to the decoupling of R_modulus from NDVI, GPP, and SMSA.

In Regions V–VIII, water availability was still important for NDVI and GPP. However, ecological and hydrological variables evolved in a non-synchronous manner. This could be attributed to the disturbance from human activities. WW negatively affected GWSA with magnitudes of −0.81, −0.51, −0.61, and −0.65, respectively. It could further influence soil water storage via the causality between GWSA and SMSA. WW also decreased R_modulus, and WW → R_modulus with strengths of −0.43 and −0.73 was found in Regions V and VIII, respectively. Reservoir regulation posed strong influences on R_modulus and SL_modulus as well as strong links with respect to RSC were observed from the networks of Region VI (with the SMX reservoir) and Region VII (with the XLD reservoir). These led to great differences between natural and human-induced evolutions, disrupting the correlations between not only ecological and hydrological variables, but also hydrological variables. On the other hand, revegetation measures represented by the Grain for Green project have been active since 1999 (Zhou et al., 2022). The greening of the land surface (NDVI) contributed to the rapid growth of GPP (strong NDVI → GPP links). However, excessive vegetation required a lot of extra water to support physiological activities, which had lagged negative impacts on SMSA (Fig. 6). This could also result in different trends in GPP or NDVI and SMSA. A more detailed insight into this is given in the Discussion section.

4.3.2 Drivers of WUE variability

As an integrated product of ecological and hydrological processes, WUE was observed to co-evolve with GWSA in Regions III–VII according to correlation networks, and it remained isolated in the other regions. Conceptually, WUE and GWSA do not have a direct causality. The causal networks indicated two potential pathways through which GWSA might indirectly influence WUE so that groundwater could replenish soil water storage, thereby influencing GPP and ET and further increasing/decreasing the value of WUE. However, the decline in GWSA was also driven by WW, and WUE decreased directly due to the control of ET (Fig. 7).

Either GPP or ET, or both, is directly responsible for WUE changes. In Regions I–II, the control of WUE was exerted by both GPP and ET. The distinction was that the two types of controls exhibited comparable strengths in Region I (with an insignificant WUE decrease), whereas ET was more dominant in Region II (with a significant WUE decrease). In Regions III–VI (the Loess Plateau), the growing-season WUE had a more significant decrease, and causality analysis revealed the control of ET over WUE. Therefore, the observed decline was attributed to the increases in ET (direct causality) originating from increased vegetation coverage (NDVI) and soil water storage (SMSA). The increases in NDVI were largely due to afforestation, and changes in SMSA were mainly determined by a combination of vegetation condition, precipitation, and groundwater. Generally, the increase in NDVI was more significant than SMSA (Fig. 4). The influence of NDVI on ET was also pronounced, with evident contemporaneous and lagged effects (Fig. 6). Hence, revegetation contributed significantly to GPP, but it also enhanced ET. As the increase rate of ET exceeded that of GPP, the WUE value was threatened. Interestingly, we found the control of ET gradually decreased over time in these regions, illustrating that the decreasing trends in WUE were alleviated.

One special thing was that the GPP → WUE and ET → WUE links were weak in Regions VII–VIII, particularly in Region VII, where both links were insignificant. This was due to the high synchronization of monthly ET and GPP (Fig. S4), which almost canceled out their respective contributions to WUE. Consequently, the decreasing trends of WUE in these two regions were relatively small.

Figure 7 Link strengths of GPP versus ET to WUE during the growing season. The bar chart is derived from Fig. 6, representing the overall link strength during 2003–2019. The line graph represents time-varying link strengths (absolute value), with a sliding window of 8 years.

5 Discussion

5.1 Network perspective for understanding complex systems

A correlation network links the individual evolutions of multiple variables in the system and separates tightly correlated ones into different modules. The joint increases and decreases in variables within and across the subsystems can therefore be recognized. However, using correlations alone makes it difficult to explore the underlying causes. Sometimes intuitively irrelevant variables had similar evolution trends, such as WUE and GWSA, declining together in some cases. Causality is valuable for uncovering underlying mechanisms but has limited applications in ecohydrology, particularly when multiple variables complicate the cause-and-effect relationships. Theoretically, it is possible to trace the compound causes of changes regarding any variable, contributing to the understanding of ecohydrological processes. The exhibited joint increases and decreases were found to be controlled by a combination of common drivers, respective drivers, and causality. Correlation and causality both make sense, representing phenomena and mechanisms, respectively, while causality-based networks uncover more details. On the other side, ecohydrological models are also important tools to help understand processes of the system or subsystem, but our observation- and network-based approach (1) is more directly linked to physical processes and avoids large uncertainties raised from model structure deficiencies and equifinality in parameterizations (Kelleher et al., 2017), (2) is more convenient and more flexible to select variables and temporal scales to be studied, and (3) better incorporates processes that are difficult to be considered and parameterized in the models (e.g., human activities). The results revealed by our network approach are further discussed below, taking the YRB as the case study.

5.1.1 Climatic forcings can be important to drive joint evolutions

Climatic forcings are critical drivers of variations in the ecohydrological system, but the effects vary due to the heterogeneous characteristics of the subregions. Due to such external drivers, synchronous increases/decreases or the similar bivariate “causality” between ecohydrological variables are ambiguous in mechanism interpretation and may lead to incorrect conclusions. Bonotto et al. (2022) identified relationships between streamflow and groundwater using CCM. They pointed out that streamflow and groundwater were forced by rainfall and potential evapotranspiration, and hence the identified relationships might be the result of a third (or further) strong common forcing. A synthetic study also showed that the common meteorological forcing could always make streamflow and subsurface flow show CCM convergence (Delforge et al., 2022).

Our study presented good examples to illustrate this as well. The source region of the YRB (Region I) experienced a warmer and wetter climate in the past decades (Wang et al., 2018b; Yang et al., 2023), and we found different drivers and influencing pathways ultimately led to synchronized growth of the variables. Results showed that T was important for variables regarding vegetation growth and physiological activity in this subregion. A similar conclusion was also drawn by Bo et al. (2022). P was discovered to dominate the evolutions of hydrological components in the source region, just as Li et al. (2024) reported. However, increasing T had minor influences on the hydrological subsystem. This is due to the relatively small proportion of snow and glaciers (about 6 % of the area; Table S2) and the insignificant contribution of the frozen-ground thawing process to soil moisture and runoff during the growing season (Qin et al., 2017; Yang et al., 2023). A similar result was also found in Region II, a transitional area between the Tibetan and Loess plateaus. In the remaining subregions, P was the common driver of both hydrological and ecological subsystems. P regulated GPP mainly by influencing soil water for uptake and was also the main source for replenishing local water resources.

5.1.2 Asynchronous evolutions attributed to human activities

Large-scale ecological restoration has been undertaken under the Grain for Green policy, particularly in Regions III–VII. Previous studies have highlighted the negative relationship between water storage and vegetation greenness due to revegetation (e.g., Liu et al., 2023). However, some studies (e.g., Zhang et al., 2022a, and Zhou et al., 2022) have challenged this conclusion, finding that a large part of the Loess Plateau has experienced robust upward trends of surface water yield since the implementation of vegetation restoration. In our study, SMSA did not show significant downward trends during 2003–2019 in core areas of vegetation restoration (especially in the upper reaches) although GWSA decreased substantially. On the one hand, the greening of the land surface can contribute positively to soil water storage by allocating more precipitation to infiltration (Lan et al., 2024). The increase in regional P may also lead to increased SMSA, largely due to enhanced land–atmosphere interactions that accelerate local moisture recycling following revegetation (Zhang et al., 2022a). In Regions III and IV (mainly grassland), we found positive GPP (NDVI) → SMSA effects with a delay of 1 month. That is to say, although revegetation leads to water consumption from the soil (Lv et al., 2019; Ge et al., 2020; Li et al., 2020; Zhao et al., 2022), it is potentially beneficial for soil water storage in turn. Wang et al. (2024) also concluded that revegetation had a notably positive impact on root-zone soil moisture and terrestrial water storage in the upstream grasslands. In this case, the overall evolution trends of SMSA and GPP/NDVI showed similar upward trends in these regions.

On the other hand, revegetation was found to have significant adverse impacts on SMSA in Regions V–VII (Fig. 6), which was consistent with Cao et al. (2022). This was evidenced by the negative GPP (NDVI) → SMSA links with a lag of 3 months, which were more significant than the positive lagged links from GPP to SMSA. These regions are mainly croplands and forests, having a greater impact on water consumption than grasses due to higher canopy covers and more developed rooting systems (Zhang et al., 2022a). Indirect consumption of deep groundwater storage was also captured, but Region VII was special due to the less significant replenishment effect between GWSA and SMSA, which might be caused by groundwater overexploitation and resulting low water levels. Therefore, revegetation can, at least in part, lead to different trends in water components and vegetation indices.

In addition, direct water withdrawal and groundwater exploitation (WW) were reported to significantly influence both surface water and groundwater storage in the middle and lower reaches of the YRB (Yin et al., 2017; Zhang et al., 2023). However, such influences have not been considered as much when investigating the connections between revegetation and water resources (e.g., Liu et al., 2023; Wang et al., 2024). Our study also quantified the impacts of RSC and WW on regional water storage and runoff. The relevant links all showed strong strength, providing intuitive evidence of anthropogenic influences on decoupled ecohydrological evolutions in Regions V–VIII.

5.2 WUE in the growing season

In this study, WUE was considered an intersection of hydrological and ecological subsystems. Previous studies argued that vegetation restoration on the Loess Plateau led to an improvement in WUE on the annual scale, and the improvement was mainly driven by the increasing GPP (Zhang et al., 2022b; Jiao et al., 2022). Our study found similar upward trends in annual mean WUE (Fig. S5) but found decreases in growing-season WUE (Fig. 4). Thus, ecosystems may not have adapted well to environmental changes, with reduced functionality and performance in terms of the growing season (Terán et al., 2023). Causality-based networks indicated that the growing-season WUE of the YRB was generally controlled by ET (except in Region I), especially in the more arid areas (Regions III–V). This conclusion was consistent with Zhang et al. (2022b). Rapid revegetation increased the GPP; however, such measures also increased the ET. On a positive note, the influence of ET on WUE showed decreasing trends in many subregions, especially those with relatively low GPP. These trends suggested that the gap between ET and GPP growth rates narrowed as revegetation progressed. It also indicated that the composition of the control over WUE may continue to change in the future. In addition, as water consumption for carbon uptake varies between vegetation types (Naeem et al., 2023), vegetation structures in the YRB could be further adjusted. To further improve growing-season WUE, it is also necessary to minimize the use of water resources by promoting water-saving irrigation systems.

5.3 Temporal uncertainty of ecohydrological relationships

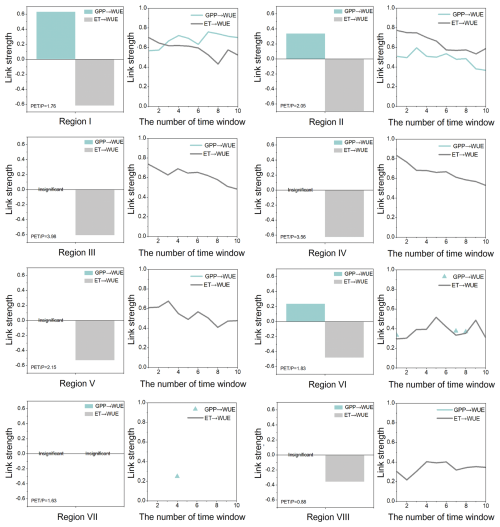
A violin plot is a graphical representation of data distribution. The presence of a flatter or multimodal violin plot indicates a higher degree of uncertainty regarding the causal relationships between variables (Lan et al., 2020). The uncertainty regarding the link strength was characterized using violin plots given the influence of potential outliers in the series, different data lengths, and non-stationarity of causality. Due to the requirement of sufficient sample data for causality analysis, sliding windows of 8–16 years were used to construct different networks and explore the uncertainty of network relationships. Regions I, V, and VII were taken as representative cases, standing for the typical alpine area, intensive revegetation area, and water-regulated area, respectively.

In Fig. 8, the relative dominance of different ecohydrological processes (i.e., the median strength represented by the white dots) is generally consistent with the results displayed in Fig. 6. This suggests that the relationships found to be significant (Fig. 6) are not coincidental but are generally robust from 2003 to 2019. Nevertheless, some processes show high levels of uncertainty, particularly those with lower link strengths, which may not exhibit significance at some times. Such uncertainty may arise from the random fluctuations in ecohydrological variables over time, or there may be ongoing evolutionary trends in system relationships. However, the whole study period of 2003–2019 is not a long time for studying the time-varying network relationships. Taking Region V as an example, only a small part of the link strengths, e.g., NDVI → ET, NDVI → ET (1), and ET → WUE in Fig. 8b, have obvious trends. Hence, we did not discuss the time-varying relationships too much in our study.

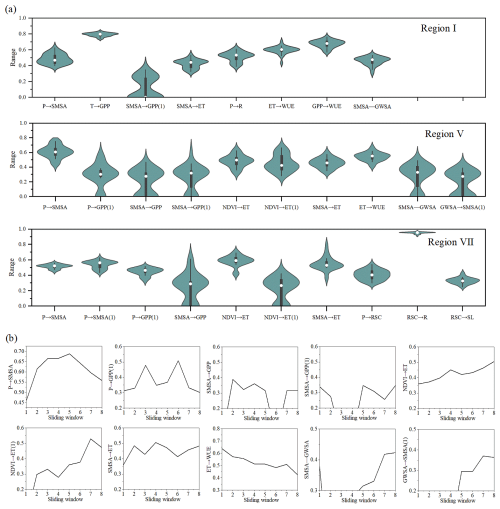
Figure 8 (a) Absolute values of causal relationships in three representative subregions of YRB. The important processes of each subregion are selected. If a link is not identified at the significance level, then the link strength is defined as 0. (b) Temporal uncertainty in causal link strength when the time window is 10 years (taking Region V as an example).

5.4 Limitations and future outlooks

This study adopted a significant amount of remote sensing and reanalysis data, which inevitably resulted in uncertainty in the findings. GRACE data were proven to be a useful tool to reflect the mass changes in TWS of the YRB (Xie et al., 2019), and we used the ensemble mean values of three products to reduce the uncertainty. NDVI, GPP, and WUE were derived from MODIS products, which were widely used to study the ecological environment of the YRB. For example, Zhang et al. (2022b) explored the spatial–temporal variations in WUE, GPP, and ET utilizing MODIS products across the Ordos Plateau. Liu et al. (2023) checked the accuracy of MODIS-derived GPP data on the Loess Plateau and demonstrated its capacity in ecology applications. SCA was derived from a MODIS-based dataset with good performance. Still, uncertainty can be reduced by comparing and fusing data from different datasets in the future.

In addition, we must acknowledge that our study only captured the most important interactions in the basin. We cannot observe everything, everywhere, or all the time. Depicting all real-world processes is also challenging due to difficulties in mathematical assumptions and algorithm performance. Nevertheless, we believe that our findings are important for understanding the general watershed functioning and could guide the development of more accurate and region-specific ecohydrological models. Models that are causally similar to observations (i.e., our causality results) may yield more reliable future projections (Runge et al., 2019a). For example, in the area where snowmelt contributes significantly to runoff, a snowmelt module considering the accurate influencing time is required in the model. In places where groundwater greatly contributes to the upper soil layers and the water uptake by roots, modules regarding groundwater and soil water movement should be carefully considered. We promote the use of network-based approaches and models together in the future to more formally address the perceptions of causality in hydrology and to better prepare for a broad range of possible futures.

6 Conclusions

To enhance our understanding of the complex interactions within ecohydrological systems, including which variables change similarly and potentially why, this study presented a developed framework based on a correlation analysis, a causality analysis, and a large amount of satellite data and in situ observations to create network perspectives. The YRB was taken as the study area, and the main conclusions are summarized as follows.

Ecohydrological dynamics in the YRB exhibited significant shifts from 2003 to 2019. During the growing season, TWSA generally decreased, primarily due to GWSA depletion. Meanwhile, NDVI and GPP showed notable increases, whereas WUE declined. Variables in ecological (represented by NDVI and GPP) and hydrological subsystems (represented by R_modulus, SMSA, etc.) displayed stronger correlations in Regions I–IV (upper reaches) compared to Regions V–VIII (middle and lower reaches). The joint changes in these variables were influenced by common drivers, respective factors, and causality.

Further analysis of causality revealed more detailed interactions within the system. Distinct interaction patterns between ecological and hydrological subsystems emerged across the basin: joint evolution with relatively weak causality (Regions I–II), joint evolution with relatively strong causality (Regions III–IV), and asynchronous evolution with relatively strong causality (Regions V–VIII). We concluded that joint increases observed in Regions I–II primarily resulted from the combined influence of warming and humidifying climate conditions, whereas in Regions III–IV, joint increases were driven by causality and a common driver, P. The divergent trends observed in Regions V–VIII were largely attributed to human activities.

Unexpectedly, a joint decline in growing-season WUE and GWSA was observed. The decrease in WUE was primarily regulated by increased ET (direct causality), originating from NDVI and SMSA. GWSA decreased due to WW and the replenishment to SMSA (which further supported GPP and ET). Interestingly, in some subregions, the influence of ET on WUE gradually decreased with the greening of land surface, indicating a mitigation of WUE decline during the growing season. However, optimizing local vegetation structure and water-saving irrigation remain crucial for further improving WUE.

To sum up, this study contributes to the scientific understanding of ecohydrological systems under a complicated context of climate change and intensive human activities. Furthermore, it demonstrates the potential of causality analysis in revealing complex dependable interactions among multiple variables. The proposed framework not only facilitates the exploration and interpretation of ecohydrological mechanisms in the YRB, but also holds promise for broader geographical applications.