Observation-driven model for calculating water-harvesting potential from advective fog in (semi-)arid coastal regions

Motivated by the need to find complementary water sources in (semi-)arid regions, we develop and assess an observation-driven model to calculate fog-harvesting water potential. We aim to integrate this model with routine meteorological data collected under complex meteorological and topographic conditions to characterize the advective fog phenomenon. Based on the mass balance principle, the Advective fog Model for (semi-)Arid Regions Under climate change (AMARU) offers insights into fog-water-harvesting volumes across temporal and spatial domains. The model is based on a simple thermodynamic approach to calculate the dependence of the liquid water content (r_l) on height. Based on climatological fog collection records, we introduce an empirical efficiency coefficient. When combined with r_l, this coefficient facilitates the estimation of fog-harvesting volumes (L m⁻²). AMARU's outputs are validated against in situ observations collected over Chile's coastal (semi-)arid regions at various elevations and during various years (2018–2023). The model's representations of the seasonal cycle of fog harvesting follow observations, with errors of ∼ 10 %. The model satisfactorily estimates the maximum r_l (∼ 0.8 g kg⁻¹) available for fog harvesting in the vertical column. To assess spatial variability, we combine the model with satellite-retrieved data, enabling the mapping of fog-harvesting potential along the Atacama coast. Our approach enables the application of the combined observation–AMARU model to other (semi-)arid regions worldwide that share similar conditions. Through the quantification of fog harvesting, our model contributes to water planning, ecosystem delimitation efforts, and the study of the climatological evolution of cloud water, among others.

1 Introduction

Water resources in (semi-)arid regions are of critical value for social, economic, and ecological development. However, in recent decades, climate change has enhanced drought periods, intensifying water stress in areas already facing scarcity. This has resulted in a worldwide dryland expansion (Koppa et al., 2023). For example, Chile's (semi-)arid and Mediterranean regions have suffered a 15-year drought, experiencing a nearly 40 % decrease in precipitation (Garreaud et al., 2021). Likewise, other dry regions, such as California, South Africa, Australia, Spain, and Morocco, are confronting similar challenges related to water scarcity, including new threats like increased fire risk, degradation of soil ecosystems, and impacts on food security (Goulden and Bales, 2019; Berbel and Esteban, 2019; Keeley and Syphard, 2021; Kogan and Kogan, 2019). Moreover, future Intergovernmental Panel on Climate Change (IPCC) climate scenarios are discouraging, projecting even drier conditions by 2050 (Masson-Delmotte et al., 2021). Under this escalating water scarcity scenario, the exploration of new water resources is imperative.

In this context, the collection of freshwater from fog presents itself as a viable alternative to face water scarcity, especially in (semi-)arid regions along the subtropical western coasts. Fog harvesting has long represented a significant untapped water potential in the world's dry regions (Klemm et al., 2012). For example, in the coastal Atacama Desert, fog and dew represent the sole water source across vast territories with almost null precipitation (Cereceda et al., 2008). However, quantifying this water potential represents a scientific challenge, requiring a deep understanding of the physical processes controlling the formation and dissipation of the marine stratocumulus (Sc) cloud deck over the ocean (Andersen et al., 2020; del Río et al., 2021b), its interaction with coastal topography (Lobos-Roco et al., 2018), and the effectiveness of fog collector designs (Verbrugghe and Khan, 2023). In addition, the lack of available and direct observations of the fog phenomenon, combined with the complexity of topography, makes it challenging to pinpoint where fog forms, identify optimal harvesting seasons, and determine potential yield. Consequently, advancing our knowledge to quantify harvestable water from fog clouds is imperative to develop this promising alternative water source. Estimating where, when, and how much water can be harvested from fog is socially relevant. Estimating fog water potential can facilitate the transition from experimental fog-harvesting practices to industrial ones (Lobos-Roco et al., 2024), potentially enhancing the development of overlooked desert territories and benefiting their local communities. Moreover, estimating potential fog water production can help us better understand the unique ecosystems sustained by fog (Koch et al., 2019; Muñoz-Schick et al., 2001; Moat et al., 2021), contributing to the assessment of their conservation status under a rapidly warming climate.

Fog is a meteorological phenomenon defined by a boundary layer cloud in permanent contact with the Earth’s surface (Roach, 1995; Stull, 2012). The origins of fog are influenced by different atmospheric boundary layer and local topographic conditions. However, in most of the (semi-)arid regions along the (sub)tropical western margins of continents, fog formation is driven by the ocean-to-land advection of Sc cloud. Sc cloud forms over the ocean in a vast deck controlled by a strong inversion layer resulting from an interaction between sea surface temperature and large-scale subsidence (Muñoz et al., 2011). Here, one of the main physical processes involved in Sc formation is the microphysical properties of cloud droplets, which are linked to cloud optical properties that have important climate effects (Wood, 2012). In the southeastern Pacific, cloud droplet sizes of 5–15 µm are often found; the concentration of these droplets is ≤ 50 cm⁻³, increasing to 200 cm⁻³ along coastal areas of Chile (Painemal and Zuidema, 2011). The droplet size and concentration determine the liquid water content (Gultepe et al., 2021), which is essentially the amount of water that can be harvested on land once Sc becomes fog. Moreover, the stability of the marine boundary layer (MBL) determines the formation, maintenance, and dissipation of Sc cloud. Formation and maintenance depend on how well mixed the MBL is in terms of potential temperature ($\partial \mathit{\theta }/\partial z$ < 3.1 × 10⁻³ K m⁻¹), while dissipation is influenced by the MBL's stratification ($\partial \mathit{\theta }/\partial z$ > 3.1 × 10⁻³ K m⁻¹) (Lobos-Roco et al., 2018). This cloud forms at the upper part of the MBL, exhibiting a clear vertical structure. This structure is characterized by an averaged cloud base ranging from 300 to 400 m (Lu et al., 2007), determined by the lifting condensation level. From the lifting condensation level upwards, the measured liquid water content progressively rises. Based on observations in the same region, we take ∼ 0.7 g kg⁻¹ at cloud top as the maximum value (Schween et al., 2022). The liquid water content abruptly drops to 0 g kg⁻¹ just above the cloud top, where the air becomes stratified and extremely dry. The Sc cloud is advected into the continent by the typical strong thermal-driven sea breeze of (semi-)arid regions (Lobos-Roco et al., 2021). Upon reaching land, the cloud deck is affected by local conditions that, together with high topography, lift it, forming fog belts (del Río et al., 2021b). Depending on latitude and topography, these fog belts vary in altitude; for example, in the Atacama region, they are found in the coastal mountains between 600 and 1200 m a.s.l. (meters above sea level) (Cereceda et al., 2008; Garreaud et al., 2008). This narrow belt represents the area in which fog can potentially be harvested.

The harvesting process is performed by nature through specialized plants that accumulate water in their leaves, spines, and branches, making it available for the soil and roots (Malik et al., 2014; García et al., 2021; Koch et al., 2019). However, fog can also be harvested artificially through passive collectors, which efficiently harvest fog water using meshes (Schemenauer and Cereceda, 1994). Numerous studies have reported promising fog-harvesting volumes worldwide in arid and semi-arid regions. For example, rates between 6 and 8 L m⁻² d⁻¹ have been reported in the hyperarid Atacama Desert in Chile (Cereceda et al., 2002; Larrain et al., 2002), rates between 1 and 5 L m⁻² d⁻¹ have been observed along the western coast of South Africa (Klemm et al., 2012), and a rate of 7 L m⁻² d⁻¹ has been reported for the Iberian Peninsula in Spain (Estrela et al., 2009).

In recent years, significant progress has been made in understanding the spatial variability in Sc cloud and fog (del Río et al., 2021b; Andersen et al., 2020), the vertical structure of fog clouds (García et al., 2021; Lobos-Roco et al., 2018), and the practical applications of fog and dew collection in water-stressed regions (Lobos-Roco et al., 2024; Baguskas et al., 2021). Despite these advancements, there remains a need to integrate these findings into a unified model that can address the questions of where, when, and how much water can be harvested from clouds. In this research, we present the Advective fog Model for (semi-)Arid Regions Under climate change (AMARU), a phenomenological model designed to estimate fog-harvesting potential volumes continuously in time and space.

2 Model formulation and evaluation

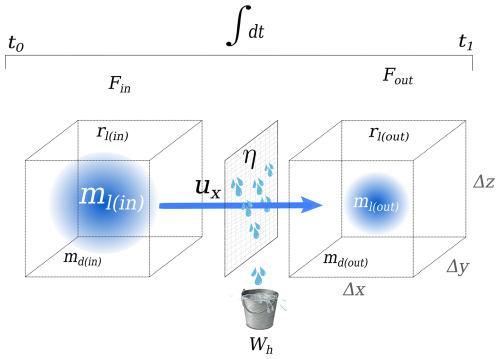
AMARU reproduces the fog that can be potentially harvested using standard fog collectors, estimating the liquid water content of the air. A particular aspect of AMARU is the application of the available routine meteorological observations to obtain this liquid water content. The model is based on the evolution of time and the height of marine Sc adiabatic liquid water content moving towards land characterized by complex topography. Figure 1 shows the physical assumptions and processes along with the respective variables and units. The model is derived from the mass conservation equation. The sequence of physical mechanisms is as follows:

• i.

  During a fog event, a certain amount of liquid water (W_h) is retained from the total fog inflow when passing through a passive collector. We assume that the harvested fog water results from the difference between fog inflow (F_in) and outflow (F_out) in grams per kilogram multiplied by meters per second (g kg⁻¹ m s⁻¹). This equation reads as

  $$\begin{array}{}\text{(1)}& W_{\mathrm{h}}=F_{\mathrm{in}}-F_{\mathrm{out}}.\end{array}$$
• ii.

  Fog inflow and outflow are described as fluxes of the mixing ratio as

  $$\begin{array}{}\text{(2)}& {\displaystyle }{F}_{\mathrm{in}}=r_{\mathrm{l}}{u}_x,\text{(3)}& {\displaystyle }{F}_{\mathrm{out}}=F_{\mathrm{in}}(\mathrm{1}-\mathit{\eta }).\end{array}$$

  Here, r_l is the liquid water mixing ratio, defined as the amount of liquid water (m_l in Fig. 1) per unit mass of dry air (m_d) that contains it, expressed in grams of water per kilogram of dry air (g kg⁻¹). To calculate the inflow, we use u_x, which represents the perpendicular (mean ± SD) wind speed (m s⁻¹) relative to the collector.

• iii.

  The term η is a dimensionless ratio representing the collector efficiency. This coefficient is described as

  $$\begin{array}{}\text{(4)}& \mathit{\eta }={\displaystyle \frac{W_{\mathrm{h}}}{F_{\mathrm{in}}}}.\end{array}$$

  Here, η corresponds to the percentage of water harvested out of the total water that can potentially pass through the collector (calculation in Sect. 2.2). Reordering the terms, we express Eq. (1) in net terms as

  $$\begin{array}{}\text{(5)}& W_h=r_{\mathrm{l}}{u}_x\mathit{\eta }.\end{array}$$

  The W_h units are then grams per kilogram multiplied by meters per second (g kg⁻¹ m s⁻¹). However, for the final output, we convert liters per square meter per second (L m⁻² s⁻¹; equivalent to mm) once grams are transformed to liters, and dry-air density (kg m⁻³) is included as

  $$\begin{array}{}\text{(6)}& W_h=r_{\mathrm{l}}{\mathit{\rho }}_a{u}_x\mathit{\eta }.\end{array}$$

  Finally, W_h is integrated over a period as

  $$\begin{array}{}\text{(7)}& {\stackrel{\mathrm{‾}}{W}}_h^{\mathrm{\Delta }t}=\underset{t_{\mathrm{0}}}{\overset{t_{\mathrm{1}}}{\int }}{W}_{\mathrm{h}}\mathrm{d}t.\end{array}$$

  Here, t₀ and t₁ correspond to the respective initial and ending times (in seconds). The model has three main assumptions. First, it assumes that F_in > F_out. Second, as the model aims to reproduce advective fog collection, it is assumed that condensation only occurs in the atmosphere under the condition r_l= r_v − r_s. Third, it assumes that the mixing ratio (r_v), which is 2 orders of magnitude higher than r_l, is nearly conserved.

  In Eq. (6), r_l and η depend on the location and condensation processes. Regarding location, r_l varies with respect to height (the vertical dimension of the model) and depends on the conditions of the marine Sc cloud over the ocean and its interaction with the topography. To estimate this variable using routine data, we assume that water vapor condenses once it reaches the thermodynamic conditions to reach saturation, This assumption implies that we do not consider microphysical properties such as droplet size, nucleation, or droplet concentration in the calculations. The second term, η, groups cloud microphysics, the collector design, and its material properties. To delve into the detailed calculation of r_l and η, we break down the analysis of Eq. (6) into two parts – the thermodynamic and water potential modules (Sect. 2.1 and 2.2). Additionally, we introduce a third module to represent the model's horizontal spatial variability in W_h via spatial interpolation, thereby creating a fog-harvesting potential map.

Figure 1 AMARU model physical interpretation, including terms from Eqs. (1)–(7).

2.1 Thermodynamic module: obtaining the liquid water mixing ratio (r_l)

The liquid water mixing ratio is a complex variable to estimate and measure. It can be obtained from complex and computationally expensive atmospheric models (e.g., the Weather Research and Forecasting, WRF, and large-eddy-simulation, LES, models) (Bergot, 2016) or by sophisticated and expensive instrumentation (fog measurements devices or microwave radiometers) (Kim et al., 2022; Gultepe and Milbrandt, 2007). However, our objective here is to estimate r_l using routine meteorological data. To achieve this, we propose employing the air parcel method (Wetzel, 1990), which calculates thermodynamic changes related to an air parcel as it is uplifted from the surface. The strategy here is to obtain the adiabatic liquid water mixing ratio including the mixing during the lifting. This method has been successfully tested in the Atacama region by Lobos-Roco et al. (2024, 2018), who averaged the meteorological conditions of two meteorological stations located at different heights (z₁ and z₂) along a topographic transect. This strategy allows for observation at two combined points within the MBL during advective fog events: z₁ represents near-surface marine meteorological conditions, whereas z₂ represents inland meteorological conditions close to the MBL top, where fog formation occurs. Figure 2a provides a schematic illustration of the strategy for estimating r_l using the parcel method. This estimation involves four steps, which are described and evaluated in the following subsections.

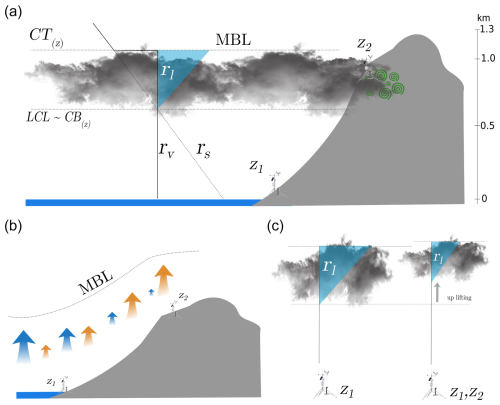
Figure 2 (a) Schematic vertical cross section representing the estimation of the liquid water content (r_l) using the air parcel method. (b) Physical representation of the topographic uplifting of Sc cloud and its interaction in the ocean–land transition. Blue (orange) arrows indicate latent heat flux (sensible heat flux) from the surface (c). Representation of the combined meteorological conditions from stations z₁ and z₂ at the cloud base and the cloud top and the r_l representation.

2.1.1 Fog frequency

AMARU is a phenomenological model that relies on the presence of advective fog, which typically occurs under a well-mixed MBL regime (Lobos-Roco et al., 2018). We define fog frequency as the number of counts when fog is present over a time step (1 h), expressed as a percentage. For example, a 50 % fog frequency means that fog occurred during 30 min over 1 h. Thus, we propose three criteria for estimating fog frequency using routine meteorological data. The first criterion posits fog frequency when air temperatures reach the dew temperature ($T_{\mathrm{a}}-T_{\mathrm{d}}=\mathrm{0}$). However, this condition has been rarely observed, particularly in the coastal Atacama region, even during fog formation. For this reason, we propose and test four alternative thresholds. For this estimation, we exclusively use data from station z₂. The second criterion is that MBL must be well mixed. Our criterion for fulfilling this assumption is that the potential temperature gradient ($\partial \mathit{\theta }/\partial z$) between ${\mathit{\theta }}_{\left(z_{\mathrm{1}}\right)}$ and ${\mathit{\theta }}_{\left(z_{\mathrm{2}}\right)}$ is minimal. Here, we propose and test four thresholds close to 0 K m⁻¹. The third criterion is similar to the second one but employs the specific humidity (assumed as a mixing ratio) vertical gradient ($\partial q/\partial z$) to assess MBL mixing. Similar to the first criterion, we propose and test four thresholds to determine how well mixed the MBL is in terms of potential temperature and specific humidity.

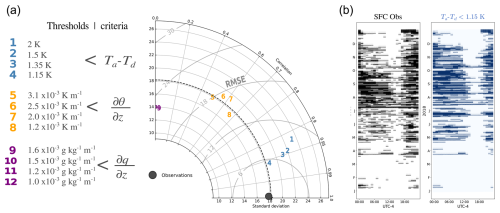
Figure 3 (a) Taylor diagram comparing the proposed criteria and thresholds for estimating fog frequency (FF, %). The diagram displays the correlation coefficient, standard deviation (in FF units, %), and root-mean-square error (RMSE, in FF units, %) between the criteria thresholds and observations. The number of data points used is 8760, corresponding to hourly data over a year. (b) Comparison of the annual diurnal cycle of fog frequency between observations (SFC; in blue) and the best-performing criteria (in black). Every black or blue mark represents the presence (100 % frequency) for every hour during 2018. Note that nos. 11 and 12 have a slightly negative correlation, placed behind (left) the Taylor diagram y axis.

Figure 3a shows a statistical comparison between the estimated fog frequency (in %) derived from the three proposed criteria and thresholds, while Fig. 3b presents a comparison of the annual diurnal cycle of fog frequency between observations from a standard fog collector (SFC) and the best-performing criteria (Schemenauer and Cereceda, 1994). The observations were conducted in the fog oases of Alto Patache (z₂) within the Atacama Desert during the year 2018 (20.82° S; 70.14° W; 850 m a.s.l.; 5 km from the coast). In addition, we also use data from the meteorological station at Diego Aracena Airport, z₁ (20.52° S; 70.15° W; 48 m a.s.l.), to calculate the vertical gradients.

In general terms, among the three proposed criteria, those based on T_a−T_d (marked using blue in Fig. 3a) show the strongest correlation with directly observed fog collection. Among these, the threshold T_a−T_d < 1.15 K (no. 4 in Fig. 3a) emerges as the most accurate, exhibiting a standard deviation aligned with observations (18 %), a correlation coefficient of 0.95, and a root-mean-square error (RMSE) of 6 %. However, the remaining thresholds yield similar results, suggesting that fog occurs when T_a−T_d spans from 2 to 1.15 K. The second and third criteria are based on the mixed-layer theory, which states that Sc cloud formation occurs under well-mixed MBL conditions. The chosen thresholds have been studied before in the coastal Atacama region by Lobos-Roco et al. (2018, 2024), del Río et al. (2021a), and García et al. (2021). The second criterion (depicted in orange in Fig. 3a) shows promising results when compared to observations, displaying a standard deviation ranging between 17 % and 20 %, a correlation coefficient value ranging from 0.5 to 0.7, and a RMSE of ∼ 17 %. These values suggest that the MBL tends to be thermally well mixed (exhibiting minimal vertical gradients) during fog presence. The last criterion (depicted in purple in Fig. 3a) demonstrates insufficient performance with respect to detecting fog frequency, exhibiting no correlation with observations. The disparity in the correlation between thermal and moisture vertical gradients with fog frequency can be attributed to the aridity of the observation location. On the one hand, the arid terrain thermally contributes less to the MBL during fog events (low radiation during the day over arid coastal zones), showing a well-mixed MBL. Conversely, when fog is absent (e.g., during the night), the arid slopes contributes to a stable stratified MBL. On the other hand, the arid landscape does not contribute moisture to the MBL during fog presence or when fog is absent, thereby showing no correlation with fog frequency. Figure 3b illustrates the diurnal cycle of fog frequency observed at the Alto Patache fog oasis throughout 2018, as measured by the standard fog collector (SFC) and estimated using the threshold with the best performance (no. 4). This threshold successfully estimates fog frequency using simple meteorological data for any day and time throughout the year.

2.1.2 Cloud base (CB)

Once fog frequency is estimated, we proceed to calculate the height of the fog-cloud base (CB). This process is summarized in Fig. 2. The calculation assumes that the lifting condensation level (LCL) in boundary layer clouds, such as Sc, is equivalent to the cloud base. To compute this, we adopt two approaches inspired by the parcel method of Wetzel (1990). The first approach solely considers data from the lowest station (z₁), representative of surface marine conditions, where the LCL corresponds to the height at which the mixing ratio equals the saturated mixing ratio: $r_{\mathrm{v}}-r_{\mathrm{s}}=\mathrm{0}$ (Fig. 2a). This LCL represents the CB over the ocean.

The second approach considers two physical processes involved in the Sc-to-fog transition: environmental mixing and topographic uplifting. Firstly, to represent the mixing with the environment experienced by an air parcel during adiabatic ascent, and based on Lobos-Roco et al. (2018), we combine the meteorological conditions measured at both transect stations (z₁, z₂) using a mixing parameter m as follows:

$$\begin{array}{}\text{(8)}& {\mathit{\psi }}_{\left(z\right)}^p=(\mathrm{1}-m{\displaystyle \frac{z}{z_{\mathrm{LCL}}}}){\mathit{\psi }}^s+m{\displaystyle \frac{z}{z_{\mathrm{LCL}}}}{\mathit{\psi }}^{\mathrm{ML}},\end{array}$$

where ψ is a scalar for potential temperature (θ) or specific humidity (q); superscript p represents the state of the air parcel; s indicates the conditions at the lowest station used (z₁); ML refers to the mixed layer, which is an average of conditions observed at the two stations; m is the mixing parameter ranging from 0 (no mixing) to 1 (maximum mixing); and z_LCL is the height at which the LCL is reached. Secondly, to account for the inland effect (observed at z₂ station), the LCL is calculated iteratively using an averaged θ and q (ψ^ML) from z₁ and z₂. This ψ^ML and LCL are used in Eq. (8) to estimate the air parcel state ${\mathit{\psi }}_{\left(z\right)}^p$, which is then used to calculate a new LCL. This calculation is repeated several times, with ψ^ML being re-averaged with the conditions at station z₂ in each iteration. This repetitive calculation ensures that the inland conditions (z₂) in the MBL's state are accurately represented. Our estimations show that the appropriate number of iterations is related to the distance in kilometers between z₁ and z₂. For example, if z₁ and z₂ are separated by 5 km, we iterate five times.

The physical interpretation of this topographic uplifting is depicted in Fig. 2b, where the initial iteration represents an equal (averaged) influence of marine (z₁) and inland (z₂) conditions. Subsequent iterations represent the dominance of inland conditions over marine conditions. Dominant marine conditions exhibit a higher latent heat flux (blue arrows in Fig. 2b) compared with sensible heat flux (orange arrows in Fig. 2b). Conversely, inland-dominant conditions showcase a prevalence of sensible heat flux over latent heat flux (Fig. 2b). The shift in surface energy partitioning toward dominant sensible heat flux (inland conditions) leads to the LCL being reached at a higher altitude, resulting in the uplifting of Sc cloud (Fig. 2c). This phenomenon is due to the warmer and drier conditions prevalent over land. It is important to note that the MBL remains well mixed during the advection of Sc cloud, thereby minimizing differences between marine (z₁) and inland conditions (z₂).

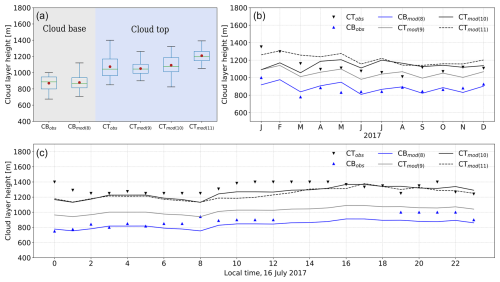
Figure 4 The (a) annual, (b) monthly averaged, and (c) typical diurnal cycle of CB and CT comparisons between the observations (obs) and model (mod). The subscript numbers refers to the equation numbers in Sect. 2.1.2 and 2.1.3.

To assess the accuracy of our CB estimations, Fig. 4 presents a multi-temporal comparison between CB estimations derived from the AMARU model and observations conducted in the Atacama Desert in 2017 as part of the Ground Optical Fog Observations (GOFOS) experiment (del Río et al., 2021a). The GOFOS experiment entails yearlong monitoring of cloud-base and cloud-top dynamics during an El Niño–Southern Oscillation (ENSO)-neutral year (2017), employing optical cameras placed across the terrain to record the vertical movement of Sc cloud and fog. The left-hand side of Fig. 4a illustrates that CB estimates generated by the model using Eq. (8) (CB_mod(8)) closely align with those observed in 2017. The mean values of the estimated CB stand at 879 m compared to the observed average of 870 m, with similar standard deviations of 88 and 93 m, respectively. This satisfactory performance of the model with respect to estimating CB is also observed on a monthly scale in Fig. 4b, where the estimated CB generally differs by ∼ 50 m from the observed values on a monthly basis. To assess the model’s capacity to replicate the diurnal cycle of CB, Fig. 4c shows a representative foggy day in the Atacama region. It is evident from the figure that the estimated CB closely tracks its diurnal cycle, with errors of ∼ 100 m observed during the afternoon.

2.1.3 Cloud top (CT)

The parcel method, upon which our CB calculations are founded, determines r_l from the LCL level upward, according to atmospheric pressure decreases. However, atmospheric pressure also decreases beyond the MBL, where Sc is located. Consequently, it becomes necessary to estimate the cloud top (CT, in m) in order to calculate the r_l within the cloud layer. Given the challenges associated with estimating CT using basic meteorological data and in order to take advantage of the homogeneity of Sc as a cloud layer, we propose estimating CT as the function of modeled CB using three simple linear regression models. These models are phenomenological expressions based on CT measurements obtained during the GOFOS experiment in 2017 (del Río et al., 2021a). The proposed linear regression models are as follows:

$$\begin{array}{}\text{(9)}& {\displaystyle }{\mathrm{CT}}_{\mathrm{mod}\left(\mathrm{9}\right)}=\mathrm{236.47}+\mathrm{0.9355}\left(\mathrm{CB}\right),\text{(10)}& {\displaystyle }{\mathrm{CT}}_{\mathrm{mod}\left(\mathrm{10}\right)}=\mathrm{CB}+\mathrm{CB}\sqrt{{\displaystyle \frac{\mathrm{FF}}{\mathrm{2}}}},\text{(11)}& {\displaystyle }{\mathrm{CT}}_{\mathrm{mod}\left(\mathrm{11}\right)}=\mathrm{236.47}+\mathrm{0.9355}\left(\mathrm{CB}\right)\left(\mathrm{1}-{\displaystyle \frac{\partial \mathit{\theta }}{\partial z}}\right)\mathrm{100}.\end{array}$$

Equation (9) shows a linear regression model in which CT (in m) solely depends on CB (in m), where constants are determined from the relation between observed CB and CT during the GOFOS experiment. Equations (10) and (11) correspond to linear regression models in which CT is determined by CB and fog frequency. The FF (fog frequency, in units of %; Sect. 2.1.1) in Eqs. (10) and the vertical potential temperature gradient ($\partial \mathit{\theta }/\partial z$, in units of K m⁻¹; Fig. 3a) in Eq. (11) are based on observations conducted during the GOFOS experiment, where CT demonstrates a negative correlation with fog frequency (del Río et al., 2021a). A comparable linear regression model, combining CB and fog frequency to estimate CT, has been tested in various locations within the coastal Atacama region by Lobos-Roco et al. (2024).

Figure 4 shows the effectiveness of linear regression models in predicting CT compared to observations obtained from the GOFOS experiment. The right-hand side of Fig. 4a shows the performance of the three linear regression models against observations for the year 2017. The annual means of the three models are similar to the observed value of (1073 m), with respective values of 1050, 1091, and 1209 m. However, the CT derived from Eq. (10) is the one that performs better, exhibiting a standard deviation of 142 m compared to the observed value of 124 m. At the monthly scale (Fig. 4b), the CT estimated by Eq. (11) overestimates observations by 150 m. However, the CT derived from Eqs. (9) and (10) remains within a 50 m range of the observed values. In Fig. 4c, showing a representative diurnal cycle during the foggy season, both observed and modeled CTs are presented. Here, it is evident that the CT estimated by Eqs. (10) and (11) demonstrates better performance, closely aligning with observations (black triangles). However, the CT estimated from Eq. (9) underestimates observations by over 200 m. These three linear regression models offer a statistical framework for estimating CT, with performance varying based on the temporal scale. Henceforth, in this paper, we adopt the CT derived from Eq. (10).

2.1.4 Liquid water mixing ratio (r_l)

Once we had estimated the fog frequency (FF) and the fog-cloud base (CB) and fog-cloud top (CT) using simple meteorological data from a topographic transect, we proceeded to determine the adiabatic liquid water mixing ratio (r_l, in units of g kg⁻¹) within the cloud layer (z: CT–CB). To achieve this, we utilize the following equation:

$$\begin{array}{}\text{(12)}& r_{l\left(z\right)}=r_{v\left(z\right)}-r_{s\left(z\right)};r_l\ge \mathrm{0},\end{array}$$

where r_v is the mixing ratio of the grams of water vapor mass over a kilogram of dry air, r_s is the saturated mixing ratio, and z represents the vertical level between CB and CT (Fig. 2a). Here, as r_v is very close to being a conserved variable (r_v ∼q_v), it is assumed to be constant over the cloud layer. Therefore, any excess of r_v with respect the change in r_s (T) will result in r_l. It is important to note that, using a combination of stations z₁ and z₂ (as in Eq. 8), the term r_v is assumed to be the specific humidity of the mixed MBL (q^ML), and r_s depends on absolute temperature; therefore, the latter term is influenced by θ^ML.

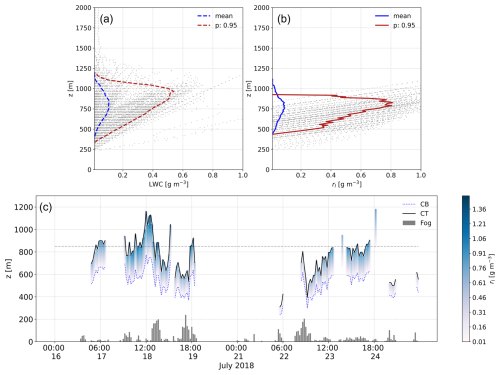
Figure 5 Vertical profiles of r_l (in g m⁻³) (a) derived from a microwave radiometer and Doppler lidar observations (Schween et al., 2022; CLU, 2024) and (b) estimated by the AMARU model over Diego Aracena Airport. Gray dots represent hourly averaged profiles filtered by the 0.99 percentile, red lines represent the 0.95 percentile, and the blue line represents the mean. (c) The evolution of the vertical profile simulated by the AMARU model for the Alto Patache site. Gray bars at the bottom represent fog collection measurements at 850 m (dashed line).

Figure 5a and b show the validation of the model-estimated adiabatic liquid water mixing ratio (r_l) against observations of the liquid water content (LWC) (CLU, 2024) derived from combined measurements of a microwave radiometer with a Doppler lidar (Schween et al., 2022), conducted at the Diego Aracena Airport in the coastal Atacama Desert during July 2018.

In general terms, Fig. 5a and b show a satisfactory comparison between our modeled estimations of the LWC and the measured values. The mean observed values peak at 0.1 g m⁻³ at 800 m altitude, while our mean estimations peak at 0.09 g m⁻³ at the same altitude (∼ 800 m), consistent with typical values found in marine Sc clouds. When analyzing the 0.95 percentile curve (red line in Fig. 5) the model follows the vertical distribution of observations, exhibiting peaks of 0.7 g m⁻³ between 700 and 900 m a.s.l., while observations show peaks of 0.5 g m⁻³. Upon comparing the modeled and observed 0.95 percentile values, we note that the model overestimates observations by ∼ 0.2 to 0.3 g m⁻³. Finally, upon integrating the vertical column of the LWC, we also observe similarities in the mean liquid water path (LWP), with values of 3.6 and 2.6 kg m⁻² for modeled and observed data, respectively. To validate the results obtained from the thermodynamic module of the AMARU model, Fig. 5c presents the temporal evolution of a simulated fog cloud during a fog event occurring at the Alto Patache site between 16 and 25 July 2018. The aforementioned figure illustrates the model's capability to accurately represent fog-cloud frequency, its vertical structure, and water density (r_l) over time. In terms of fog frequency, our model shows fog-cloud formation from 17 to 19 July and from the 22 to 24 July, aligning with the periods of highest fog collection rates (gray bars in Fig. 5c). From the 19 to 22 July, our model does not depict cloud formation, consistent with near-null fog water collection during this period. Likewise, we observe that changes in the vertical structure of the cloud (base and top) correspond to variations in the LWC and fog collection.

In summary, our straightforward methodology, employing a topographic transect of meteorological stations, effectively estimates the r_l within the MBL vertical column. This estimation is achieved by combining thermodynamic principles and statistical regressions, supported by climatological observations. Notably, our approach not only provides estimates of r_l but also estimates fog frequency and the vertical structure of the fog cloud, thereby enhancing our understanding of the fog phenomenon in arid coastal regions.

2.2 Water potential module: collector efficiency coefficient (η)

The second critical parameter in our proposed model is the collector efficiency coefficient (η). This variable is intricately linked with complex processes and factors such as wind flow, liquid water content, droplet size, collector positioning, material properties, mesh curvature, and porosity (Carvajal et al., 2020). To ensure that our assumptions align with climatological observations, we determine the collector efficiency using an empirical coefficient. This coefficient, previously defined in Eq. (4), is now redefined as the ratio between the observed fog collection (f_obs) and the fog inflow (F_in), where f_obs=W_h. As a ratio, η represents the percentage of the maximum water that a fog collector can potentially capture under given atmospheric conditions. It is calculated as follows:

$$\begin{array}{}\text{(13)}& \mathit{\eta }={\displaystyle \frac{f_{\mathrm{obs}}}{F_{\mathrm{in}}}}.\end{array}$$

Note that both F_in and f_obs are averaged per hour; therefore, both terms have the unit of liters per square meter per hour (L m⁻² h⁻¹). As η is calculated based on fog observations, its value depends on the type of collector used, providing flexibility to the model with respect to adapting to different collector types if observations are available.

Table 1 Descriptive statistics of the empirical efficiency coefficient η estimated at five fog collection stations along a 2000 km coastal strip in Chile. The 25 %, 50 %, and 75 % columns display the interquartile descriptive statistics.

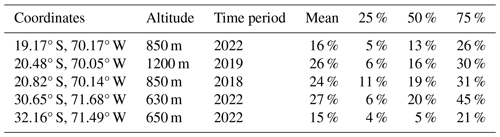
Table 1 shows the empirical collector efficiency coefficient (η) calculated for five fog collection stations located between 600 and 1200 m along a coastal strip of Chile. Overall, mean η varies from 15 % to 27 %, with variability ranging from 4 % to 45 %. Three factors contribute to this variability in the efficiency coefficient. Firstly, the model’s ability to accurately determine fog frequency (RMSE of 6 % in Fig. 3a) can lead to discrepancies, potentially resulting in very high (η∼ 100 %) or null (η∼ 0 %) efficiencies when fog collection is observed, thereby altering the averages. Secondly, wind speed may also play a significant role, as it is responsible for transporting r_l through the collector. Lastly, both the material of the mesh and its curvature during fog collection could impact mesh efficiency (Carvajal et al., 2020). Despite the variability in η across all sites, we find an average efficiency coefficient of 25 % ± 10 %, consistent with results in the literature. For instance, Montecinos et al. (2018) reported efficiencies ranging from 0 % to 36 % in large fog collectors. Similarly, using numerical simulations, Carvajal et al. (2020) reported a mean efficiency of 28 % with a theoretical maximum of 36 %. Finally, de Dios Rivera (2011) reported maximum fog collection efficiencies of between 20 % and 24 % using a simple numerical model approach for different mesh types.

For our study, we use an η of 0.25 (25 %). Once η is estimated, we can readily solve Eq. (6) to obtain an estimation of the fog-water-harvesting (W_h) potential. Given that r_l has a vertical dimension, assuming a constant wind speed (u) along the MBL, we can derive the vertical distribution of the fog-harvesting potential.

2.3 Spatial module: fog-harvesting maps

In addition to the thermodynamic module, we propose a spatial module for extrapolating the vertical variability in W_h into a horizontal spatial domain. To do this, we integrate the vertical domain (z) of W_h to an area of optimal fog-harvesting potential obtained from a combination of a digital elevation model (DEM) and GOES satellite images. We outline four steps to achieve this spatial variability.

The first step involves reclassifying the DEM grid cells based on the cloud layer height and removing all grid cells below the CB and above the CT elevation. This reclassification ensures that only the elevation range in which Sc cloud could potentially impact the topography is considered. In the second step, we create an aspect image (slope orientation) with the DEM and reclassify the pixels based on the angle range of the main wind direction (mean ± SD) when fog is collected (obtained from observations at the z₂ station). The third step involves calculating the fog and low-cloud (FLC) frequency using data from the GOES satellite (del Río et al., 2021b; Espinoza et al., 2024). This algorithm continuously calculates the presence and absence of FLC in every GOES grid cell. The third step serves as a geographical framework, delineating the area in which fog cloud interacts with topography. The spatial intersection of the three steps generates optimal areas for fog collection, physically representing the locations at which Sc cloud and its harvesting potential intersect with the surface. It is important to note that the values of grid cells in these optimal areas for fog collection represent elevations (m a.s.l.) in areas with a high FLC frequency. The final step involves replacing the elevation grid cell values of the optimal fog collection areas with the vertical distribution of potential fog harvesting (W_h). As W_h values are associated with a vertical domain (z), each W_h value can be mapped onto the resulting grid of optimal fog collection areas. The result of this last step yields a spatial distribution of potential fog harvesting.

3 Model applications to (semi-)arid study case sites

AMARU enables us to evaluate the spatiotemporal variability in fog harvesting using routine meteorological data and satellite products. In this section, we evaluate the application of the model (W_h) to three sites along the coastal strip of Chile, corresponding to hyper-arid, arid, and semi-arid ecosystems, between 2018 and 2023.

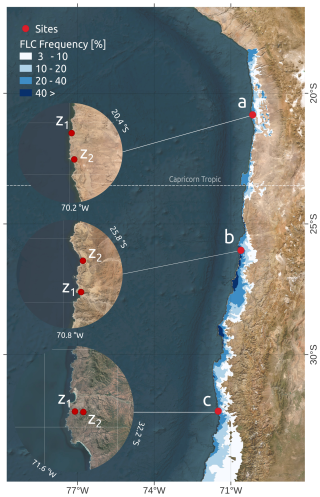
Figure 6 Location of the study sites and their meteorological stations. The areas shaded using blue colors represent the fog and low-cloud (FLC) frequency obtained by the GOES satellite (del Río et al., 2021b) between 2018 and 2023. z₁ and z₂ represent the meteorological stations forming the transect used for running the model according to our methodology.

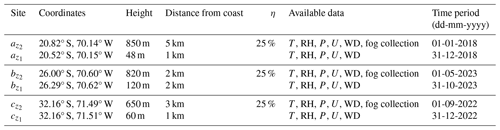
Figure 6 shows the geographical setting of the study sites, which correspond to hyperarid (Site a), arid (Site b), and semi-arid (Site c) fog ecosystems situated between 600 and 1200 m a.s.l., along the coastal mountains of Chile. Generally, these sites represent xeric ecosystems (Muñoz-Schick et al., 2001) sustained year-round by fog, with a frequency exceeding 40 % (Fig. 6). Each of these three sites is equipped with meteorological and fog collection instrumentation, managed by the Centro UC Desierto de Atacama of Pontificia Universidad Católica de Chile. The characteristics of these stations and their data and parameters used in the model are summarized in Table 2. In addition, to meet the model’s requirements, observations from these three sites (z₂) are complemented with data from near-sea-level observations (z₁), sourced from public datasets (https://www.agromet.cl/, last access: 10 October 2023), which are also detailed in Table 2.

Table 2 Geographic characteristics and available data of observational sites (z₂) and their corresponding stations at the coast (z₁). T represents air temperature at 2 m, RH denotes relative humidity, P represents air pressure, U is wind speed, and WD is wind direction.

3.1 Seasonal cycle of modeled and observed fog harvesting

AMARU satisfactorily reproduces the observations of fog harvesting with respect to both magnitude and variability over time. Figure 7 shows a comparison of monthly averaged daily rates of fog harvesting at the three analyzed sites. Overall, the model results (blue) follow the seasonal cycle of observed fog collection (gray) across latitudes, albeit showing annual disagreement with observations (by 0.5–1 L m⁻² d⁻¹). In the hyperarid environment of Site a (Fig. 7a), the model estimates an annual daily rate of 5.0 L m⁻² d⁻¹, which satisfactorily compares to the rate of 5.5 L m⁻² d⁻¹ obtained through observations. Likewise, the model can closely track the seasonal cycle of fog harvesting, exhibiting low rates in summer (January–March) and autumn (April–June) and higher rates in winter (July–September) and spring (October–December). Moreover, the model correctly estimates the frequency of fog events. For instance, during summer, the model estimates a very low (January and March) or null (February) fog collection, with mean errors of around 0.39 L m⁻² d⁻¹ in the season compared with observations. Similarly, during the optimal fog-harvesting season between winter and spring, the model correctly estimates the monthly magnitude of observed fog collection with errors of 2 L m⁻² d⁻¹. Finally, the model successfully replicates the variability in the monthly daily rates of fog collection, as indicated by the error bars in Fig. 7. For example, at Site a in spring, the observed mean variability rates (errors bars) range from 4 to 9 L m⁻² d⁻¹, while the model estimates spring mean rates ranging from 6 to 10 L m⁻² d⁻¹.

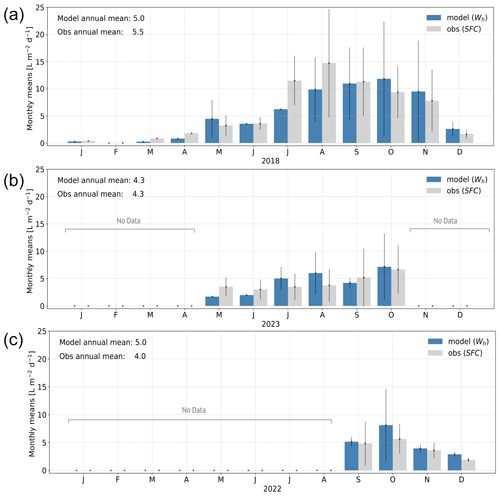
Figure 7 Comparison of monthly averaged daily fog collection rates between the model (blue) and observations (gray) in three fog ecosystems situated on the (a) hyperarid, (b) arid, and (c) semi-arid Chilean coast. The error bars show the data variability between the 25th and 75th percentiles.

For Site b, situated in an arid environment (Fig. 6), the amount of fog collection is notably lower compared with Site a (hyperarid). However, the model accurately reproduces the annually averaged daily rate of fog harvesting of 4.3 L m⁻² d⁻¹. Despite this overall good performance, the model still underestimates observations by approximately 1 L m⁻² d⁻¹ during winter in terms of magnitude and variability (as indicated by the error bars). Unfortunately, the annual cycle for Site b remains incomplete, as observations were only recorded from May to October 2023. For the semi-arid environment of Site c, the model shows annual daily rates of fog harvesting similar to those of Site b, albeit with an overestimation of 1 L m⁻² d⁻¹ compared with observations. During the months with the highest fog collection rates (September–December), the model overestimates observations by ∼ 0.7 L m⁻² d⁻¹ on average. It is worth mentioning that these discrepancies in estimation are not systematic and that, despite them, the model captures the same seasonal cycle obtained through observations at all three sites.

3.2 Vertical variability in fog-harvesting potential (W_h)

As the model estimates the LWC (r_l) in the vertical column of Sc cloud when it interacts with topography, and assuming constant wind at z₂ throughout the vertical, we can model the fog-harvesting potential at every height within the Sc cloud layer.

Figure 8 shows the vertical variability in W_h potential for the three analyzed sites. In the aforementioned figure, dots represent the total W_h per hour at each height within the fog-cloud layer over the course of 1 year. The red line depicts the annual average daily rate of W_h as a function of height, while the black dot shows the observed annual average daily rate. In addition, the dots are color-coded based on the corresponding r_l values. From Fig. 8, it is evident that fog-harvesting potential decreases from the hyperarid (north) to the semi-arid (south) regions for both W_h and r_l. Specifically, at the hyperarid site, a W_h of 10 L m⁻² d⁻¹ can be easily reached, whereas maximum W_h values of 5 and 3 L m⁻² d⁻¹ are observed at the arid and semi-arid sites, respectively. The same behavior is observed for r_l, which exhibits higher values (mean 0.95 percentile of up to 0.7 g kg⁻¹) at the hyperarid site compared with the arid and semi-arid sites, where the 0.95 percentile reaches up to 0.6 and 0.4 g kg⁻¹, respectively. The vertical variability in W_h also allows us to study the vertical liquid water capacity of the fog cloud. For instance, at the hyperarid site, the model estimates a fog-harvesting potential between 600 and 1350 m, whereas fog can be harvested from 500 to 1250 m and from 370 to 1050 m at the arid and semi-arid sites, respectively. These variations in r_l and the fog-cloud layer height are explained in Eq. (3) and Fig. 2b and c. In Eq. (3), we show that the calculation of CB (and consequently r_l) is influenced by the combined conditions of stations z₁ and z₂. For example, at the hyperarid site, situated within the tropics (Fig. 6), air temperature is higher at both z₁ and z₂ compared with the semi-arid site. This implies that the condensation of the air parcel at Site a will occur at a higher altitude than at Site b. Likewise, higher temperatures increase the air's capacity to hold humidity, resulting in a higher r_l observed at the hyperarid site compared with the semi-arid one. Another significant factor contributing to the difference in r_l and cloud layer height is the distance from the coast at which station z₂ is located. For instance, the hyperarid site is 5 km inland, compared with the arid and semi-arid sites that are located 2 and 3 km from the coast, respectively (Table 2). Consequently, inland conditions at the hyperarid site are hotter than at the other two sites, contributing to the formation of the cloud layer at higher altitudes.

Figure 8 also shows the annual average daily rates (red line) estimated by the model and observed by a standard fog collector (black dot). This red line indicates the vertical placement of the maximum annual W_h. For example, at the hyperarid site, the maximum W_h is located at a height of 900 m, while observations are situated at 850 m a.s.l., explaining the highest annual daily fog collection rates. In contrast, at the arid and semi-arid sites, the maximum W_h is not aligned with the height of the observations. For Site b, the maximum W_h is reached at ∼ 680 m, whereas observations are located at 820 m a.s.l. Similarly, for Site c, the maximum W_h is situated at 500 m, while observations are at 650 m a.s.l. The validation of annual average daily rates in Fig. 8 is determined by the proximity of the black dot to the red line at the observed height. For example, in Fig. 8a, we observe an underestimation by the model, which is also evident in Fig. 7a, although not in the vertical dimension, as the observations differ by ∼ 0.5 L m⁻² d⁻¹ from the modeling results. For sites (b) and (c) (Fig. 8b and c), the model accurately reproduces the annual daily rates, consistent with the observation, as also observed in Fig. 7b and c.

Figure 8 Vertical variability in the modeled fog harvesting (W_h) at the (a) hyperarid, (b) arid, and (c) semi-arid sites. Dispersed dots represent the total fog harvesting at every hour, the red line is the annual average daily rate of W_h, whereas the gray dot is the observed annually averaged daily rate of W_h. The dispersed dots are color-coded using a blue scale representing the liquid water content (r_l). The gray shading represents the topographic profile of each site. The right-hand panels show a photograph of each site during a fog event.

3.3 Spatial variability in W_h: fog-harvesting potential mapping

The combination of AMARU's results with satellite products enables us to interpolate the influence of Sc cloud over land and its potential harvesting in space. This subsection introduces two examples of AMARU's results with respect to spatial variability that can be utilized for fog ecosystem delimitation and water planning.

Figure 9a shows the optimal fog-harvesting areas (highlighted in red), corresponding to the region where Sc cloud interacts with the Earth's surface. For Site c, these areas are displayed near the summit of the coastal mountains, specifically ranging from 370 to 1050 m a.s.l. (Fig. 8c). In addition, based on data from the meteorological station (z₂) at this site, the fog-cloud flux originates from the south and southeast (110–300°), which is reflected in the model's depiction of the mountain slopes facing south and southeast. In the zoomed-out view in Fig. 9a, we observe that the extent of these optimal fog-harvesting areas spans the first ∼ 20 km from the coast, as determined by the frequency of FLC derived from the GOES satellite (Sect. 2.3).

Figure 9 (a) Optimal fog-harvesting areas (red line) resulting from the model for Site c compared to the normalized difference vegetation index (NDVI; ranging from 0.1 to 0.4) estimated using Sentinel satellite images for 2022. The yellow dot indicates the meteorological station (z₂). (b) Spatial variability in the annual average daily rates of W_h for Site a estimated during 2018. The red dot indicates the meteorological station (z₂).

To independently validate the spatial interpolation of AMARU's results, we compare the optimal fog-harvesting areas with fog-dependent vegetation. In Fig. 9a, areas highlighted in green represent the normalized difference vegetation index (NDVI) estimated using Sentinel satellite imagery. Overall, the optimal fog-harvesting areas align with areas exhibiting the highest NDVI values. For example, a concentration of NDVI is observed at the summit of the mountains and the southeast slopes, indicative of a forest ecosystem sustained by fog (Garreaud et al., 2008). Furthermore, the NDVI also concentrates at the bottom of small valleys downstream of the summits, suggesting that fog water that accumulates on the summits may potentially flow down, supplementing the precipitation input to the streams.

Figure 9b shows the spatial variability modeled from the intersection between the vertical profile annual average daily rate (red line; Fig. 8a) and the optimal fog-harvesting areas. In the aforementioned figure, we observe the spatial distribution of the fog water potential along the mountain, with maximum values observed around 900 m. The topography of the mountain favors altitudes around 900 m a.s.l. with southwestern slope orientations, leading the model to project large areas with fog-harvesting potential ranging from 4 to 5 L m⁻² d⁻¹. In the eastern areas of the meteorological station (red dot, z₂), fog-harvesting potential decreases to lower altitudes, consistent with the results presented in Fig. 8a. Likewise, fog-harvesting potential decreases towards regions southwest of the station at higher altitudes until it disappears. The area surrounding the station corresponds to the well-known fog oasis of Alto Patache (Muñoz-Schick et al., 2001), situated between 600 and 850 m, within the optimal fog-harvesting areas determined by the model.

This model application is further extrapolated to the entire region to determine optimal fog-harvesting zones within the area of influence of fog and low clouds, as determined using the GOES satellite. An example of these larger areas is shown in the zoomed-out view of Fig. 9b, where optimal fog-harvesting areas are situated within 10 km of the coast. As the model runs with simple meteorological time series, fog-harvesting potential maps can be generated for different temporal averages, enabling us to study and assess spatial changes in fog-harvesting potential over hours (events), days, seasons, and years.

4 Model limitations and challenges

Despite the versatility of the AMARU model with respect to representing the harvesting of the advective fog phenomenon in both time and space, it has several limitations worth describing.

Firstly, one of the most important variables in the model is the adiabatic liquid water mixing ratio (r_l), which is estimated assuming water vapor is condensed because it reaches saturation. Despite our simplistic approach and reliable results, we know that further model improvements must be made by including essential microphysical processes. Such processes are mean volume diameter, effective size, droplet concentration, and effective droplet size (Gultepe et al., 2021). To account for these processes, comprehensive observations must be performed to get a complete budget equation, thereby allowing more realistic modeling.

Secondly, the model's capability to represent fog harvesting in time is primarily limited by the empirical collector coefficient. However, this coefficient remains constant in the model, resulting in both underestimations and overestimations compared with observations. To improve our estimations of fog harvesting over time, further exploration into the collector efficiency is necessary, incorporating factors such as wind speed, collector material properties, and cloud droplet size into more complex functions.

Thirdly, the model’s capability to assess fog-harvesting potential in the vertical column of the MBL enables us to evaluate the maximum fog-harvesting potential beyond single point observations. However, this vertical W_h estimation is contingent upon accurately determining r_l, assuming that wind speed remains consistent at every level of the MBL. Although r_l estimations align with observations from microwave radiometers, our results must be validated with in situ observations of LWC during fog collection. In addition, relevant physical processes influencing CT, such as dry-air entrainment from the free troposphere, and thermal inversion are not included in its calculation. Instead, CT is statistically estimated, leading to uncertainties in a variable whose precision is crucial for estimating the maximum r_l and, consequently, W_h. Regarding wind speed, our assumption of a constant horizontal wind along the MBL is based on the mixed-layer theory, which posits that scalars such as potential temperature, mixing ratio, and wind speed remain constant if the MBL is well mixed. However, this theory does not consider topography, which may disturb this constant pattern when interacting with MBL winds. To improve the model’s estimation of r_l and better W_h potential, future research must incorporate accurate vertical profile observations of the temperature, mixing ratio, and wind speed.

Finally, the spatial extrapolation of W_h represents a preliminary approach for fog-harvesting-potential mapping. This is because its accuracy is limited by the availability of spatially distributed meteorological data. We spatially extrapolate the conditions determined by the model for the z₂ station to all surrounding areas that share the same geographic conditions. Nevertheless, this approach may overestimate several inland locations that meet the geographical characteristics of z₂ but not the atmospheric ones. Improving this spatial extrapolation of W_h can be addressed using two approaches. The first one involves utilizing gridded meteorological data that allow us to solve Eq. (6) at every grid point. Unfortunately, available gridded data are often too coarse to accurately represent the sub-kilometer fog-harvesting phenomenon. The second approach entails incorporating the FLC frequency determined by the GOES satellite (Fig. 6) into the spatial interpolation of W_h. For example, we can modify W_h spatially using a function based on the FLC frequency, where locations with similar geographical conditions to z₂ station may see their W_h reduced (increased) if their FLC frequency is higher (lower) than that observed at z₂ station.

5 Conclusions

We propose, formulate, and evaluate an observation-driven model, named AMARU, for estimating advective fog-water-harvesting potential in (semi-)arid regions. This model uses standard and routine meteorological observations to estimate where, when, and how much water can potentially be harvested from fog clouds. The proposed model employs a thermodynamic approach to estimate fog's adiabatic liquid water mixing ratio, incorporating key physical processes associated with the interaction between stratocumulus cloud and topography. This approach yields vertical profiles of the liquid water mixing ratio, from which the fog frequency, cloud base, and cloud top can be derived. In addition, by integrating estimations of the liquid water mixing ratio with climatological records of fog-harvesting observations, we derive an empirical collector efficiency coefficient to estimate vertical profiles of fog-harvesting potential. Finally, by combining vertical profiles of fog-harvesting potential with satellite products, we introduce a methodology for spatially extrapolating these results, thereby generating fog-harvesting-potential maps.

The main conclusions of our research are as follows:

• Despite the simple approach, this model correctly reproduces essential physical components involved in fog harvesting. Our model evaluation against available observations shows that model results reproduce the fog frequency (correlation coefficient of 0.95 and RMSE of 6 %), cloud-base and cloud-top height (errors < 50 m), liquid water content (errors ∼ 0.2 g m⁻³), and fog collector efficiency (errors ∼ 5 %). Overall, fog-harvesting observations are satisfactorily reproduced by the model, with mean errors of 10 % (< 1 L m⁻²).

• The simple approach takes advantage of using routine meteorological data, which is widely available worldwide in areas characterized by land–ocean contrast and complex topography.

• However, the model presents several limitations, and the improvement of these limitations will depend on comprehensive observations and further research. Among these limitations, microphysics observations of cloud droplet size, concentration, and actual water content must be incorporated to improve the model. Moreover, further research must be done on the empirical coefficient, which is constant in the model. However, our observations suggest a variability that depends mainly on wind speed but also on the materials. Finally, future research should incorporate accurate vertical profiles of the temperature, mixing ratio, and wind speed to corroborate our vertical modeling assumptions.

• Our model offers a versatile approach with multiple applications in massive fog-harvesting planning and ecosystem delimitation for conservation purposes, among others. As fog is a global meteorological phenomenon, this model holds potential for applicability in many coastal (semi-)arid regions, addressing data deficiencies in regions where fog harvesting represents a viable water source.

Finally, we expect this research to yield significant social benefits by providing decision-makers with valuable insights into new water sources, thus aiding in the mitigation of climate change impacts.