Multi-scale soil moisture data and process-based modeling reveal the importance of lateral groundwater flow in a subarctic catchment

Soil moisture plays a key role in soil nutrient and carbon cycling; plant productivity; and energy, water, and greenhouse gas exchanges between the land and the atmosphere. The knowledge on drivers of spatiotemporal soil moisture dynamics in subarctic landscapes is limited. In this study, we used the Spatial Forest Hydrology (SpaFHy) model, in situ soil moisture data, and Sentinel-1 synthetic aperture radar (SAR)-based soil moisture estimates to explore spatiotemporal controls of soil moisture in a subarctic headwater catchment in northwestern Finland. The role of groundwater dynamics and lateral flow in soil moisture was studied through three groundwater model conceptualizations: (i) omission of groundwater storage and lateral flow, (ii) conceptual TOPMODEL approach based on topographic wetness index, and (iii) explicit 2D lateral groundwater flow. The model simulations were compared against continuous point soil moisture measurements, distributed manual measurements, and novel SAR-based soil moisture estimates available at high spatial and temporal resolutions. Based on model scenarios and model–data comparisons, we assessed when and where the lateral groundwater flow shapes shallow soil moisture and under which conditions soil moisture variability is driven more by local ecohydrology, i.e., the balance of infiltration, drainage, and evapotranspiration. The choice of groundwater flow model was shown to have a strong impact on modeled soil moisture dynamics within the catchment. All model conceptualizations captured the observed soil moisture dynamics in the upland forests, but accounting for the lateral groundwater flow was necessary to reproduce the saturated conditions common in the peatlands and occasionally in lowland forest grid cells. We further highlight the potential of integrating multi-scale observations with land surface and hydrological models. The results have implications for ecohydrological and biogeochemical processes, as well as for modeling hydrology and Earth system feedbacks in subarctic and boreal environments.

1 Introduction

Soil moisture has a direct influence on land surface energy fluxes (Seneviratne et al., 2010; Ji et al., 2017), partitioning of precipitation into infiltration and runoff (Liu et al., 2019; Singh et al., 2021), and plant productivity and water use (Daly and Porporato, 2005; Lagergren and Lindroth, 2002). It is also a key variable controlling soil microbial activity and consequent greenhouse gas emissions (Bonan, 1990; Karhu et al., 2014; Lohila et al., 2016; Makhnykina et al., 2020) and soil carbon balances (Larson et al., 2023). In the boreal and subarctic regions, climate change is predicted to amplify seasonal variability of soil moisture due to longer and more frequent summer droughts, increased autumn and winter precipitation (Holmberg et al., 2014; Ruosteenoja et al., 2018), and changes in snow accumulation and melt (Räisänen, 2021). The altered soil moisture dynamics have an effect on the severity of abiotic stressors (e.g., water shortage, excess water, extreme temperatures) and biotic damages, affecting tree health, mortality, and forest productivity (Buermann et al., 2014; Muukkonen et al., 2015; Wang et al., 2023). The changes in soil moisture across the landscape can significantly impact vegetation dynamics and alter competition between species, shaping the structures of the ecosystem (Venäläinen et al., 2020; Junttila et al., 2022; Ameray et al., 2023). Moreover, northern peatlands are sources of methane (Huttunen et al., 2003; Schneider et al., 2016), and boreal upland forests can change from methane sinks to sources under long-lasting high-soil-moisture conditions (Korkiakoski et al., 2022; Lohila et al., 2016). Hence, accurate information on spatiotemporal soil moisture conditions has the potential to improve estimates of tree health, terrestrial carbon stocks, and greenhouse gas sinks and sources, as well as the lateral export of carbon and nutrients (Bond-Lamberty et al., 2016; Nakhavali et al., 2021). Soil moisture dynamics are also critical for weather and hydrological forecasting (Zhang et al., 2020a; Joo and Tian, 2021), climate change impact studies (Seneviratne et al., 2010; Kløve et al., 2014; IPCC, 2019), and developing sustainable forest management practices (Salmivaara et al., 2021; Kankare et al., 2019).

Soil moisture has strong spatiotemporal variability driven by hydrometeorological conditions, landscape heterogeneity, and hydrological connectivity through lateral groundwater flow (Corradini, 2014; Kemppinen et al., 2023; Kim and Mohanty, 2016; Ji et al., 2017). The unsaturated soil is bounded at the bottom by the water table, and exchanges between the saturated and unsaturated zone occur through upward capillary rise and downward percolation (Maxwell et al., 2007; Miguez-Macho et al., 2007; Vergnes et al., 2014). The lateral groundwater flow and consequent variation in the water table depth influence soil moisture, especially in areas with shallow water tables, such as riparian areas, floodplains, and peatlands (Krinner, 2003; Decharme et al., 2019; Kollet and Maxwell, 2008).

Information on soil moisture dynamics can be obtained via in situ measurements and remote sensing, as well as using numerical models (Robinson et al., 2008; Yu et al., 2021; Dobriyal et al., 2012). Continuous automatic in situ measurements are well-suited to capturing soil moisture patterns at high temporal resolutions at the point scale (Moreno et al., 2022; Kemppinen et al., 2023). However, distributing the observation network in space requires significant resources (Tyystjärvi et al., 2022) and is thus restricted to specific study areas (Kemppinen et al., 2023). Recent advances in satellite remote sensing have shown the potential to obtain soil moisture estimates at high spatial resolutions (e.g., Sentinel-1 synthetic aperture radar (SAR): Quast et al. (2023); Bauer-Marschallinger et al. (2019); Manninen et al. (2021)), but their accuracy for high-latitude forests is still limited (Celik et al., 2022). To predict soil moisture conditions under environmental change, process-based hydrological models are a prerequisite. However, their development also relies largely on observations (Panday and Huyakorn, 2004; Tyystjärvi et al., 2022), and it is widely accepted that the integration of in situ measurements, remote sensing, and process-based modeling is the best avenue forward (Crow and Yilmaz, 2014; Sidle, 2021; De Lannoy et al., 2022). To yield accurate predictions, it is essential that process-based models represent the most relevant local features and processes that affect soil moisture dynamics (Sidle, 2021; Ji et al., 2017; Kollet and Maxwell, 2008).

Due to the proliferation of geospatial data on land use, topography, vegetation, and soil characteristics, spatially distributed models can, to an increasing extent, incorporate spatial variability in their parameterizations and extend point-scale simulations to scales relevant for practical applications (Launiainen et al., 2019; Ma et al., 2016; Clark et al., 2015; Maneta and Silverman, 2013). To model soil moisture at high spatial resolutions, incorporating the effects of local soil texture and vegetation and the conceptualization of subsurface water storage and lateral flow become important. Integrated surface–groundwater models can explicitly represent these interactions in 3D (Ala-aho et al., 2017a; Thornton et al., 2022; Autio et al., 2023), but these are rarely used in ecosystem studies or large-scale applications due to their vast data needs and low computational efficiency. Attention to groundwater dynamics is rather recent in land surface models used in climate, weather, and hydrological modeling communities (Decharme et al., 2019; Zeng et al., 2018; Li et al., 2022; Maxwell and Condon, 2016; Ji et al., 2017; Niu et al., 2014). In catchment hydrological models, the lateral movement of groundwater is also rarely explicitly described, and the groundwater dynamics are often based on conceptual approaches such as the use of the topographic wetness index (TWI) (Beven and Kirkby, 1979) or grid cell-independent groundwater buckets (Bergström, 1992). These simplified approaches can efficiently link grid cell and catchment water budgets and simulate sufficient discharge dynamics (Launiainen et al., 2019). They can also accurately estimate soil moisture dynamics at locations where the water balance is mostly driven by local processes, i.e., infiltration, vertical water percolation, and evapotranspiration (ET), rather than lateral flows and capillary rise (Tyystjärvi et al., 2022). However, once the impacts of lateral groundwater flow and a shallow water table become more pronounced, models neglecting these processes encounter obvious challenges in accurately simulating soil moisture dynamics (Kollet and Maxwell, 2008). Consequently, they often exhibit dry biases that directly affect simulations of soil evaporation and plant transpiration (Maxwell and Condon, 2016).

Hydrological models are currently advancing towards incorporating more processes at higher spatial resolutions (Sidle, 2021; Wood et al., 2011), but model calibration and evaluation are still largely based on point-scale observations of soil moisture, ET, and stream discharge at the catchment outlet (Ala-aho et al., 2017b; Launiainen et al., 2019), creating uncertainties for spatiotemporal simulations (Koch et al., 2018). The persistent lack of spatial observations of hydrological fluxes and water storages (model state variables) prevents leveraging the full potential of distributed models and available data on landscape characteristics. Recent advances in remote sensing with regard to producing spatially explicit data of precipitation (Yu et al., 2022; Skofronick-Jackson et al., 2017) and ET (Bhattarai and Wagle, 2021), canopy and soil water content (Manninen et al., 2021; Zhang and Zhou, 2015), snow cover (Meriö et al., 2023), and water table depth (Toca et al., 2023; Räsänen et al., 2022; Isoaho et al., 2023) open new opportunities to evaluate (Niu et al., 2021) and, in some cases, calibrate (Koch et al., 2018) spatially distributed models. Such data are increasingly being included in hydrological model–data assimilation (Li et al., 2023; Deschamps-Berger et al., 2022).

In this study, we assess the controls of soil moisture dynamics at the subarctic Pallas Lompolonjängänoja headwater catchment in northern Finland. We combine the analysis of multi-scale observations, including in situ continuous and manual soil moisture measurements (Marttila et al., 2021; Aurela et al., 2015); SAR-based spatiotemporal estimates (Manninen et al., 2021); and process-based hydrological modeling. We use the Spatial Forest Hydrology model (SpaFHy; Launiainen et al., 2019) at high spatial resolution (16 × 16 m²) with three alternative conceptualizations for groundwater storage and dynamics. We focus particularly on the influence of a shallow water table and lateral groundwater flow, as well as vegetation heterogeneity, on spatiotemporal soil moisture dynamics through the following research questions:

1. Where does lateral groundwater flow affect the temporal variability of shallow soil moisture?

2. How does the role of lateral groundwater flow compare to the impact of vegetation heterogeneity in shaping soil moisture patterns?

3. How do SAR-based soil moisture estimates compare with the models and can they be useful in model evaluation?

To answer the research questions, we compare and contrast model predictions (i) between model conceptualizations, ii) against point-scale soil moisture data, and (iii) against SAR-based soil moisture estimates available from the study area.

2 Materials and methods

2.1 Study site

Our study area is located in the Pallas area (67°59^′ N, 24°13^′ E) in northwestern Finland (Fig. 1b, c). Pallas has over 85 years of meteorological observations (Lohila et al., 2015), and the area has been recently set up as an interdisciplinary platform for atmospheric, ecological, and hydrological research. It includes multiple eddy covariance (EC) stations measuring surface–atmosphere energy and greenhouse gas fluxes and both manual and automated ecohydrological monitoring over a range of ecosystem types (Marttila et al., 2021). The climate in the area is characterized as subarctic. The long-term annual (1991–2020) mean temperature and mean annual precipitation at the Muonio weather station, located approximately 25 km west of Pallas, are −0.6 °C and 532 mm, respectively (Jokinen et al., 2021). The proportion of precipitation falling as snow is approximately 42 % (Marttila et al., 2021), and the seasonal snow cover persists from about October until May (Aurela et al., 2015). Particularly, we consider the Lompolonjängänoja catchment (hereafter LJO, Fig. 1a), which has a total area of circa 4.5 km², with elevations varying between 268 and 364 m a.s.l. Soils in the upland parts of the catchment are mainly gravely sand and sandy tills, and vegetation cover varies from coniferous forests to various types of mires such as open fens, treed mires, and paludified forests. Except for a few small roads and ditches, the area has had little human influence and can be considered to be a mostly pristine subarctic headwater catchment. Figure 1a gives an overview of the landscape and the main measurement locations in the LJO catchment.

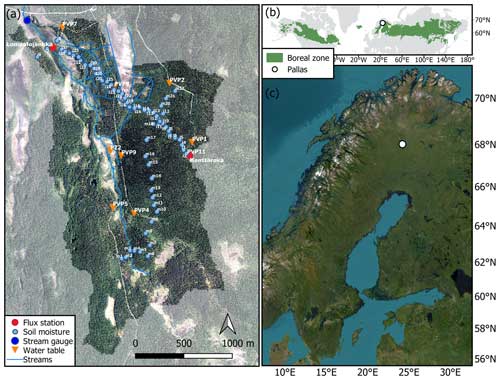
Figure 1 The Lompolonjängänoja (LJO) catchment and its hydrological measurement locations (a) (the aerial image by NLSF (2020)) are located in the northern boreal zone (b) (green area, Olson et al. (2001)) in northwestern Finland (c) (Esri (2023)). The ICOS flux stations Kenttärova (forest) and Lompolojänkkä (open mire) are presented in red circles, the stream gauge is presented in blue, soil moisture measurement locations are labeled and presented in light blue, and water table depth monitoring locations are labeled and presented in orange. Streams are shown as blue lines.

EC flux data and the meteorological data used in this paper were collected from two stations located in the catchment of Lompolonjängänoja (Fig. 1a). The forest site Kenttärova (ICOS Ecosystem associate site) is a Norway-spruce-dominated forest growing on podzol soil, with the age of the trees varying from 90 to 250 years. The number of trees, 643 and 68 stems per hectare for spruce and deciduous trees (mainly Betula pubescens), has stayed the same since a survey in 2011 (Aurela et al., 2015). The dominant tree height is currently about 15.5 and 11 m for spruce and Betula pubescens, respectively. In 2011, a mean one-sided leaf area index (LAI) for Norway spruce and Betula pubescens was 2.0 and 0.1 m² m⁻², respectively (Aurela et al., 2015).

The mire site Lompolojänkkä (ICOS Ecosystem Class-2 site) is an open, mesotrophic sedge fen (Zhang et al., 2020b) with a maximum peat thickness of about 2.5 m (Mathijssen et al., 2014). The Lompolonjängänoja stream flows through the long and narrow fen, draining into a nearby lake, Pallasjärvi. The dominant vascular species are Andromeda polifolia, Betula nana and B. pubescens, Carex spp., Equisetum spp., and Eriophorum spp. The dominant moss species are Sphagnum spp., whose coverage is about 50 %. In 2018, the mean one-sided LAI was 1.4 m² m⁻², and the mean vegetation height was 0.4 m.

2.2 Models

We used the Spatial Forest Hydrology model (SpaFHy; Launiainen et al., 2019), developed to predict spatial and temporal patterns of hydrological fluxes and state variables in the vegetation canopy, organic moss–humus layer, and topsoil (root zone). SpaFHy has been tested for 9 EC flux sites in Finland and Sweden (stand-scale; ET and soil moisture) and for 21 small boreal headwater catchments in Finland (catchment-scale; runoff dynamics and ET-to-precipitation ratio) in Launiainen et al. (2019). It has been adapted to drained peatland forests (Leppä et al., 2020; Stenberg et al., 2022), extended with nutrient balance and leaching modules (Laurén et al., 2021), applied to model forest drought risks (Launiainen et al., 2022), and used to predict soil moisture dynamics in arctic tundra (Tyystjärvi et al., 2022). Its aim is to provide a simple and practically applicable framework to study the effects of landscape heterogeneity, management, and macroclimatic change on catchment hydrology in boreal and subarctic landscapes.

The original SpaFHy includes two groundwater conceptualizations: a free-drainage approach (i.e., neglecting groundwater dynamics, SpaFHy-1D) and a TOPMODEL-based approach (i.e., groundwater return flow based on topographic wetness index, SpaFHy-TOP). In this study, we implemented a new submodel to represent the 2D lateral Darcy flow (SpaFHy-2D). The salient features of the three model versions are briefly described next and are summarized in Table 1. The general model parameters are given in Table 2.

Table 1 Geospatial data used by each submodel and submodel used by each model configuration.

2.2.1 SpaFHy-1D

SpaFHy-1D considers grid cells to be independent hydrological units (Launiainen et al., 2019). The hydrological processes in the vegetation canopy, snowpack, organic moss–humus layer, and root zone are explicitly simulated at a daily time step for each grid cell in the model domain. The aboveground fluxes and state variables are computed in the canopy submodel, including rainfall and snowfall interception and evaporation, throughfall, transpiration, and snow accumulation and snowmelt (see Sect. 2.2 in Launiainen et al. (2019)). Snowmelt is computed with a degree-day approach, while ET components are solved by the Penman–Monteith equation. For transpiration, the canopy conductance is derived from the stomatal optimality principle, accounting for an exponential attenuation of light in the canopy (Launiainen et al., 2019). The bucket submodel describes topsoil hydrology and soil moisture dynamics in two layers. The upper layer is the organic moss–humus layer, whose water budget is affected by throughfall and snowmelt interception and soil evaporation, as well as infiltration to the lower root zone layer, where drainage and transpiration take place. The lateral water flow between the grid cells is omitted, and drainage from the bucket submodel is removed from the model domain as stream discharge at the catchment outlet without a delay. Thus, SpaFHy-1D represents a situation where soil moisture variability within the catchment is driven solely by the heterogeneity of vegetation, soil characteristics, and meteorological forcing. Similar conceptualizations of soil hydrology are common for large-scale land surface and hydrological models (Smith et al., 2001; Seibert and Vis, 2012; Clark et al., 2008; Niu et al., 2011). The canopy and bucket submodels are common to all three SpaFHy versions.

2.2.2 SpaFHy-TOP

SpaFHy-TOP includes a conceptual description of the saturated zone using the TOPMODEL approach (Beven and Kirkby, 1979). Drainage from the bucket submodel feeds TOPMODEL's lumped catchment groundwater storage, which is then spatially distributed via the topographic wetness index (TWI). The TWI is defined as the natural logarithm of the flow accumulation area (i.e., upslope area draining through the grid cell) divided by the tangent of the local slope (Beven and Kirkby, 1979). The local saturation deficit is related to the TWI and catchment average saturation deficit, creating a higher probability for grid cells with greater TWI to become saturated. During a model time step, return flow from groundwater storage to the root zone and organic moss–humus layer occurs in grid cells where the local saturation deficit is zero (Launiainen et al., 2019). The return flow is routed through the root zone and the organic moss–humus layer, and their respective soil moisture values are updated, while potential excess water becomes surface runoff. Discharge at the catchment outlet is the sum of catchment average baseflow (predicted by TOPMODEL) and surface runoff without a delay. This version of SpaFHy-TOP is identical to the one used in Launiainen et al. (2019, 2022).

2.2.3 SpaFHy-2D

The SpaFHy-2D version was developed in this study to explicitly describe lateral groundwater flow within the catchment. The modeling domain consists of soil columns whose relative elevation compared to one another is defined by the digital elevation model. Each soil column extends to an impermeable layer (no-flow boundary) at a predefined depth, while the columns are characterized by their water retention characteristics (following the van Genuchten -model; van Genuchten, 1980) and saturated hydraulic conductivity based on the soil type.

Lateral flow in the saturated zone is solved using the 2D groundwater flow equation:

$$\begin{array}{}\text{(1)}& C{\displaystyle \frac{\partial h}{\partial t}}={\displaystyle \frac{\partial h}{\partial x}}\left(T{\displaystyle \frac{\partial h}{\partial x}}\right)+{\displaystyle \frac{\partial h}{\partial y}}\left(T{\displaystyle \frac{\partial h}{\partial y}}\right)+S,\end{array}$$

where t is time (d), x and y are the horizontal dimensions (m), C is the storage coefficient (m m⁻¹), T is transmissivity (m² d⁻¹), h is the hydraulic head (m), and S (m d⁻¹) is water drained from the overlaying bucket submodel. Lateral groundwater flow between grid cells takes place only in the saturated zone, and, thus, T is obtained by integrating the saturated hydraulic conductivity over the saturated layer depth. C describes the change in h relative to a change in the soil column water content W (m). The relation between h and W is solved based on the assumption that, in the unsaturated zone, the water content profile is set to hydraulic equilibrium (constant hydraulic head in vertical dimension; Skaggs, 1980). For numerical efficiency with regard to solving Eq. (1), interpolation functions for W(h), T(h), and C(h) were constructed prior to simulation for each soil column type (Laurén et al., 2021). When the soil column becomes oversaturated, i.e., when the groundwater level rises to the root zone, the excess water is routed as return flow to the bucket submodel, similarly to in SpaFHy-TOP.

Streams (and ditches) in the catchment were described as grid cells with constant h. The outflow to streams is computed from the local hydraulic head gradient when the surrounding water table level is above the stream h. No flow from streams to the soil is allowed. We do not consider temporal changes in stream water level and omit channel flow in the stream network; thus, the sum of the outflow into the stream cells and the surface runoff form the runoff at the catchment outlet without a delay. The assumption of a constant stream water level simplifies the modeling framework and should not significantly impact catchment soil moisture dynamics. Catchment borders are defined as no-flow boundaries, assuming that no significant water flows occur between the delineated catchment and its surroundings that impact shallow soil moisture.

2.3 Model input

2.3.1 Geospatial data

To set up SpaFHy for the LJO catchment, we used mainly open geospatial data that are available throughout Finland. The rasters used are presented in Fig. 2 and are summarized in Table 1.

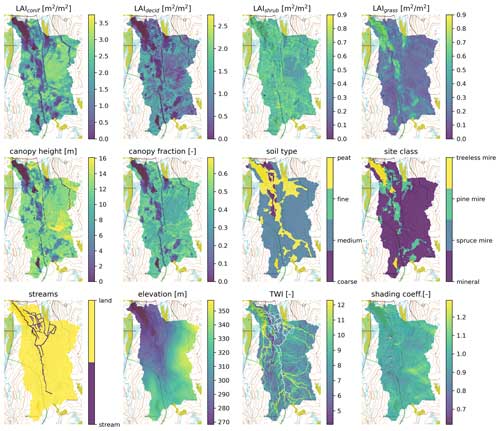
Figure 2 Set of geospatial rasters used to set up the model for the LJO catchment. Top row shows leaf area index (LAI) for different plant types. For each grid cell, the conifer and deciduous LAI forms the canopy LAI, and the understory LAI is the sum of shrubs and grasses. TWI is the topographic wetness index. The rasters overlay a topographic map (NLSF, 2020).

For canopy attributes and for distinguishing between forest soils and mires, we used the multi-source National Forest Inventory (mNFI;  Mäkisara et al., 2016) data at 16 m horizontal resolution. This was also chosen as the model grid resolution for the simulations, and other input rasters were aggregated accordingly, consistently with Launiainen et al. (2019). From mNFI data, needle and leaf mass rasters were used to derive the one-sided LAI of deciduous and coniferous trees. LAI values were estimated using specific one-sided leaf areas for pine, spruce, and birch (6.8, 4.7, and 12.0 m² kg⁻¹, respectively; Härkönen et al., 2015). LAI estimates of shrub and grass were adopted from local multi-source remote sensing data by Räsänen et al. (2021). The canopy fraction and prevailing site class (used for parameterizing the organic moss–humus layer) were also obtained from the mNFI data.

The soil type affects the hydraulic properties of the root zone and the SpaFHy-2D lateral groundwater flow module. A combined soil type raster was constructed by taking the peatland boundaries from the National Land Survey of Finland topographic map (NLSF, 2020) and the remaining soil characteristics from the Geological Survey of Finland soil texture map (GSF, 2020), similarly to Launiainen et al. (2019).

The catchment was delineated based on the digital elevation model (NLSF, 2020) with Whitebox Geospatial Analysis Tools (GAT) software (Lindsay, 2014). TWI was calculated using the slope and flow accumulation raster, with the flow accumulation determined through the D8 method (O'Callaghan and Mark, 1984). The stream network was obtained from NLSF (2020). Furthermore, topographic impacts for solar radiation were considered by computing a daily shading coefficient, calculated as the potential daily radiation input for each grid cell normalized by the potential input at the grid cell of the Kenttärova station, where the global radiation forcing was measured (see Sect. 2.3.2).

2.3.2 Meteorological forcing

All SpaFHy versions require the same daily meteorological forcings: mean air temperature T_a (°C), global radiation R_g (W m⁻²), relative humidity RH (%), wind speed U (m⁻¹), and daily accumulated precipitation P (mm). These data were compiled and made available by Nousu et al. (2023) and include in situ observations at Kenttärova station available from the Finnish Meteorological Institute (FMI) open database (FMI, 2021), supplemented by the FMI's R_g observations from the Kenttärova station (located at the hilltop, Fig. 1). The data gaps in R_g were first filled by data from contiguous sites and then by ERA5 reanalysis data (Hersbach et al., 2020). We multiplied the R_g forcing by the shading coefficient (see Sect. 2.3.1) for each day (Fig. 2) to account for the topographic effects on the radiation forcing at each grid cell. For the other meteorological variables, a spatially uniform forcing was applied.

2.4 Model parameterization

The canopy and bucket submodels were common to all model versions and were parameterized as in Launiainen et al. (2019). The only exception was the organic moss–humus layer, which was refined to allow for full or partial saturation in situations where upward return flow occurs from the root zone layer. Drainage from the organic moss–humus layer to the root zone layer is represented identically as the drainage from the root zone layer (Eq. 18 in Launiainen et al. (2019)). A depth of 0.05 m was assigned to the organic moss–humus layer (Table 2). To account for the different hydraulic properties of the organic moss–humus layer in mineral forest soils (dominated by feather mosses) and peatlands (mainly Sphagnum moss), the moss hydraulic parameters (porosity, field capacity, and relative available water) were derived from Williams and Flanagan (1996) and Elumeeva et al. (2011). The peatlands and mineral soils were separated based on mNFI site class (see Fig. 2); the site-class- and soil-type-specific parameters for the organic moss–humus, root zone, and deep soil layers are given in the Supplement (Tables S1–S3). The available literature was used to define the van Genuchten (1980) water retention parameters for the bucket and 2D flow submodels (Autio et al., 2023; Menberu et al., 2021). The root zone was assigned a depth of 0.30 m (Table 2). Due to a lack of reliable data on the depth to bedrock, a uniform thickness of 5 m was assigned for the deep soil layer of the 2D groundwater module throughout the model domain. This estimate corresponds approximately to the thickest peat layers and the shallowest mineral soil depths of the catchment (Autio et al., 2023). Canopy parameters for surface conductance and for evaporation from the wet forest floor (G_f), the canopy storage capacity for rain (w_max), and the TOPMODEL effective soil depth parameter were obtained from Launiainen et al. (2019). No further calibration or sensitivity tests of any model parameters were conducted in this study.

Model simulations with the three different treatments of groundwater dynamics (named 1D, TOP, and 2D) were run with identical meteorological forcings, geospatial inputs (Fig. 2), and canopy and bucket submodel parameterizations (Table 2). To study how spatially heterogeneous vegetation affects soil moisture, an additional 1D simulation was run with site-class-specific mean vegetation parameters. This experiment is referred to as 1D_homog.canopy, and vegetation characteristics at each grid cell belonging to a certain site class (Fig. 2) were set to the average of that particular site class (see Fig. S1 in the Supplement). All simulations cover the period from 1 January 2011 to 1 September 2021, of which the beginning until 1 September 2013 was considered to be a model spin-up period and was omitted from subsequent analysis.

2.5 Hydrological observations

This study benefits from the extensive hydrological monitoring of the LJO catchment (Marttila et al., 2021; Aurela et al., 2015). We further conducted several campaigns to measure the spatiotemporal variability of soil moisture (i.e., volumetric water content θ) during 2019–2021. In particular, during snow-free seasons, biweekly manual measurements at 15 different points (denoted as “i” in Fig. 1) were conducted using WET-2 and PR2 Profile Probe sensors with an HH2 readout unit (Delta-T Devices Ltd., Cambridge, UK), sampling the soil moisture profile at depths of 0, 10, 20, and 30 cm (from the soil surface). Additionally, we conducted two extended soil moisture measurement campaigns, including 56 additional locations (denoted as “l” and “m” in Fig. 1). The first (17 June 2021) represents wet conditions when the soil moisture was still highly impacted by the snowmelt. The second (1 September 2021) was conducted in early-autumn conditions after a precipitation event. Both these campaigns used the sensor ML3 ThetaProbe (Delta-T Devices Ltd., Cambridge UK) that measures soil moisture at 5 cm depth. For the ML3 ThetaProbe sensor, soil moisture values at locations with peat soils at full saturation were assigned directly to the assumed peat porosity (0.89).

In addition, we used data from continuous soil moisture sensors distributed in close proximity to the Kenttärova flux site. From 2013 to 2017, soil moisture was continuously measured by four ThetaProbe type ML2x sensors at 5 and 20 cm depths (two each) (Aurela et al., 2015). In 2017, more sensors were installed alongside the existing ones, among which we used two sensors (Soil Scout Oy, Helsinki, Finland) at depths of 5 and 30 cm (from the soil surface). The continuous soil moisture measurements were averaged into daily values. To overcome the inherent uncertainties in in situ measurements of soil moisture, stemming from different devices and measurement and installation procedures (Robinson et al., 2008; Dobriyal et al., 2012; Iwata et al., 2017), we present the means and variability ranges of continuous soil moisture sensors and address these uncertainties by averaging multiple manual probings within the area of interest within a radius of approximately 5 m. All soil moisture measurements from 0 to 30 cm depth correspond to the root zone layer of SpaFHy. As soil moisture of the organic moss–humus layer was not directly measured, we assume soil moisture measurements at the soil surface (0 cm depth) to best represent this layer.

ET was measured by the eddy covariance (EC) technique at the two flux stations, Kenttärova spruce forest and Lompolojänkkä peatland (Fig. 1a). The EC systems consist of USA-1 (METEK) 3D sonic anemometers and closed-path LI-7000 (LI-COR, Inc.) CO₂ $/$ H₂O analyzers (Aurela et al., 2015). EC data processing is described in detail in Aurela et al. (2015) and in Nousu et al. (2023).

The runoff was measured by the Finnish Environment Institute with a 120° V-notch weir at the outlet (stream gauge in Fig. 1a). Snow data consisted of automated snow depth observations at the Kenttärova flux station and approximately monthly manual snow water equivalent (SWE) measurements at Kenttärova and Lompolojänkkä stations (Marttila et al., 2021).

2.6 SAR-based soil moisture estimates

We used SAR-based surface soil moisture estimates from the study area. This newly derived research data set was developed by Manninen et al. (2021), who used Sentinel-1 synthetic aperture radar (SAR) ground-range-detected high-resolution data to produce high-resolution spatiotemporal soil moisture estimates. The soil moisture retrieval using SAR images is based on the gradient-boosting method, utilizing input variables of non-locally averaged VH (vertical–horizontal) and VV (vertical–vertical) backscattering coefficients, multitemporal SAR statistics, terrain data, effective LAI estimates based on SAR, SAR overpass information, and the time for the soil moisture estimate to be calculated. Distinct algorithms were developed for morning and evening flyovers, both relating soil moisture estimates to instantaneous midday. They were validated against discrete and continuous in situ soil moisture measurements at Pallas (Manninen et al., 2021). In particular, the gradient-boosted-tree methods were trained with manual surface soil moisture measurements (depth = 0 cm) and continuous soil moisture measurements at deeper soil layers that were converted to surface conditions via linear regression in order to correspond to the penetration depth of the C-band SAR signal in soil, which is in the range of 1–5 cm (Beale et al., 2021; Nolan and Fatland, 2003). Further details on the SAR data can be found in Manninen et al. (2021). In this study, the original irregular grids with approximately 10 m pixel spacing were averaged into a 16 m regular grid using subpixel area weights to be compared with the model outputs.

Launiainen et al. (2019)Launiainen et al. (2015)Lin et al. (2015)Launiainen et al. (2019)Launiainen et al. (2019)Lagergren and Lindroth (2002)Launiainen et al. (2019)Launiainen et al. (2019)Launiainen et al. (2019)Pomeroy et al. (1998)Essery et al. (2003)Kuusisto (1984)Koivusalo and Kokkonen (2002)Kolari et al. (2007)Kolari et al. (2007)Kolari et al. (2007)Launiainen et al. (2019)Kalliokoski et al. (2010)Launiainen et al. (2019)Launiainen et al. (2019)

Table 2 Parameters used by each submodel. Soil-type- and site-type-specific parameters are listed in the Supplement (Tables S1–S3).

2.7 Evaluation methods

Annual periods are defined as hydrological years starting from September (e.g., 2016 is from 1 September 2015 to 31 August 2016). We use performance metrics of mean absolute error (MAE), mean bias error (MBE), and coefficient of determination (R²) for model–data comparisons. Moreover, we use the Kling–Gupta efficiency (KGE) (Gupta et al., 2009) for comparing daily runoffs between simulations and observations. Mean differences (MDs) are computed to compare different simulations (i.e., the mean difference at each grid cell).

3 Results

3.1 Climatology and water budget dynamics

As is typical for high latitudes, the period with permanent snow cover and freezing temperatures is long (Fig. 3a, b), with nearly half of the annual precipitation falling as snow (250–350 mm, Fig. 3c), resulting in annual peak snow depths from approximately 0.9 to 1.3 m (Fig. 3b). The snowmelt period commonly spans roughly from late April to the beginning of June, resulting in the highest soil moisture during snowmelt (Fig. 3B). The summer is characterized by cool to warm temperatures and higher precipitation that typically peaks in July (Fig. 3a).

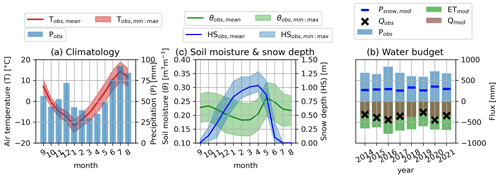
Figure 3 Hydrometeorological characteristics of Pallas. (a) Monthly observed climatology for the simulation period and (b) monthly observed volumetric soil moisture (θ) and snow depth (HS) at Kenttärova forest site. The air temperature (T) and θ envelopes represent minimum and maximum monthly averages during the simulation period, while the snow depth envelope shows the minimum and maximum of monthly maximum during the simulation period. (c) Annual water budget as observed (obs) and simulated (mod) with SpaFHy-2D, where Q is catchment runoff, ET is evapotranspiration, P_obs is observed precipitation, and P_snow,mod is modeled snow precipitation. The change in catchment water storage (including canopy water, soil water, and groundwater storage) dS $/$ dt =$P+\mathrm{ET}+Q$ is not shown. Due to gaps in measurements, Q_obs is not available for 2018.

Due to energy limitations for annual ET and a high peak SWE, runoff dominates the water balance, covering 49 % to 67 % of annual precipitation, while ET represents 34 % to 50 % depending on the year (Fig. 3c). SpaFHy-2D is able to closely capture the observed annual runoff during the simulated years (Fig. 3c). Also, daily runoff dynamics are reasonably well represented by both SpaFHy-TOP (KGE: 0.63) and SpaFHy-2D (KGE: 0.65; see Fig. S2). The summer runoff dynamics after precipitation events are better captured by the 2D approach, whereas the baseflow is better predicted by TOP (Fig. S2). The simulations of SWE also align relatively well with the observations at Kenttärova and Lompolojänkkä (Fig. S3). Although catchment-scale ET observations are not available, the good performance in reproducing the $Q/P$ ratio (Fig. 3c) means that annual ET is also well described. This is in accordance with the relatively good correspondence between simulated and EC-measured daily ET from the Lompolojänkkä mire and the Kenttärova spruce forest flux sites (Fig. S4). SpaFHy has also been shown in earlier studies to reproduce well the EC-based ET across the range of boreal and subarctic forests and peatlands (Launiainen et al., 2019).

3.2 Comparison of temporal soil moisture with in situ observations

Intra-seasonal continuous in situ data allow the analysis of temporal soil moisture dynamics and the evaluation of models and SAR data (Fig. 4). Soil moisture peaks during snowmelt, and the date of complete snow melt-out corresponds to the date when the modeled organic moss–humus layer moisture content begins to drop due to evaporative drying (Fig. 4). Later in the summer, the soil moisture dynamics are driven by intermittent precipitation events and more continuous drying by ET and drainage, with the general drying trend being dominant (Figs. 4 and 5).

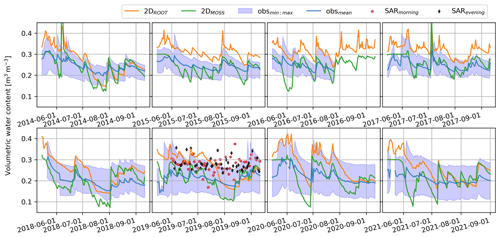
Figure 4 Temporal dynamics of soil moisture at Kenttärova spruce forest simulated by SpaFHy-2D (root zone and organic moss–humus layers), measured in situ and estimated from SAR for 2014–2021 during May–September period. Simulations and SAR-based estimates correspond to the mean of the nearby grid cells (64 × 64 m² grid northwest of Kenttärova). The SAR-based surface soil moisture estimates are only available in 2019.

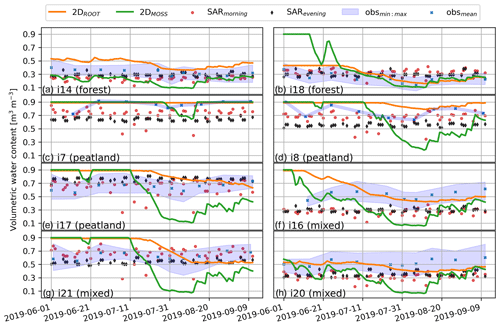
Figure 5 Temporal dynamics of SpaFHy-2D-simulated, SAR-estimated, and in situ-measured range of soil moisture (obs_min:max) at two forest, three peatland, and three mixed forested-peatland locations during June–September period in 2019.

At Kenttärova hilltop area (Fig. 1a), which contributes to groundwater recharge, the SpaFHy-1D and TOP predictions were nearly identical to SpaFHy-2D. The model captures well the seasonal trend but tends to overestimate both root zone soil moisture content and its temporal variability compared to the mean of point observations (Fig. 4, MBE: 0.05 m³ m⁻³). This mismatch could be corrected by calibrating the soil field capacity and wilting point. However, as the simulations mostly fall within the observed range (MBE: −0.01 m³ m⁻³ when compared to observed maximum) and because the comparison in Fig. 4 represents a single location, such a calibration was not considered to be meaningful for the aims of this study.

The SpaFHy-2D predicts reasonably well the root zone soil moisture differences between locations, especially in terms of ranking the locations between wet, intermediate, and dry (Fig. 5). Minor discrepancies between SpaFHy-2D-predicted root zone and in situ-measured shallow soil moisture content are likely due to uncertainties in soil hydraulic parameters (e.g., too-large field capacity in Fig. 5a). The moisture content of the organic moss–humus layer is more dynamic than the root zone moisture as evaporative losses exceed throughfall input, leading to drying of the organic moss–humus layer from mid-July to the end of August (Fig. 5). SpaFHy-2D does not include capillary rise to the organic moss–humus layer, and, therefore, simultaneous high evaporation and a high water table can create large differences between the moisture contents of the two layers (Fig. 5d, e, g). The largest differences between data and root zone simulations are found in mixed forested-peatland grid cells (Fig. 5f, g), mostly due to overestimation of the water table level in early summer. Considering the fact that no model calibration was conducted, the comparison of SpaFHy-2D-simulated and in situ-observed groundwater levels shows rather good model performance, and, in particular, the shallow water tables are well captured (see Fig. S5 and Table S4). As we aim to assess the influence of lateral flow on shallow soil moisture dynamics rather than fully replicate the observations, the performance of the 2D model is considered to be sufficient.

SAR-based shallow soil moisture values mostly fall within the observed range, and the SAR morning flyover captures the main temporal dynamics of the observations, particularly drying in June and wetting in late August (Figs. 4 and 5). However, the SAR-based estimates consistently fall short of the highest observed and simulated values, leading to an underestimation of soil moisture content (Fig. 5). There is also noticeable noise in the SAR-based soil moisture, and the level and temporal patterns of SAR morning and evening flyovers differ from each other. The comparison at different locations (Fig. 5: two forest, three peatland, and three mixed forested-peatland grid cells) shows a systematic shift (up to 0.2 m³ m⁻³) between SAR morning and evening flyover.

3.3 Effect of groundwater flow conceptualizations on soil moisture

The in situ soil moisture data are further used to compare the model conceptualizations and to assess the impact of groundwater flow on shallow soil moisture across the catchment (Fig. 6). The comparison shows that the observed soil moisture contents below ca. 0.55 m³ m⁻³ are rather well captured by all model conceptualizations (Fig. 6a, b, c), especially considering the uncertainties in soil hydraulic parameters based on geospatial data (Fig.  2: soil type). Most of the forest grid cells (i.e., grid cells with high canopy fraction) belong to this category. The results indicate that model performance improves when the lateral flows are accounted for, and only the 2D approach with explicit lateral groundwater flow can satisfactorily reproduce the wetter conditions above 0.55 m³ m⁻³, commonly found in open-peatland grid cells and occasionally in forest grid cells (Fig. 6). Conceptually, the SpaFHy-TOP should also be able to mimic groundwater dynamics via TWI. However, it was able to capture only one of the observed wet grid cells, and the overall goodness of fit is close to that of the SpaFHy-1D version. All evaluation metrics are considerably better for the 2D model, but this model variant tends to overestimate soil moisture on peatland grid cells, consistently with Fig. 5f and g.

Figure 6 Comparison of simulated root zone soil moisture content and SAR-based surface soil moisture estimates against spatiotemporal manual in situ soil moisture observations. The color of the points correspond to grid cell canopy fraction, ranging from open peatlands to forest grid cells.

The same comparison in Fig. S6c, but with colors classifying the points as either mineral soil or peat soil (based on Fig. 2: soil type), indicates that either many of the grid cells where the model overestimates soil moisture are faultily parameterized as peat soil or the model may exaggerate the impact of lateral flow at those locations.

Qualitative spatial evaluation of the model versions in Fig. 7 reveals that the large-scale spatial heterogeneity of shallow soil moisture is most strongly driven by the soil type (see Fig. 2) via the soil hydraulic properties. In particular, the differences in the 1D simulation arise almost solely from differences in soil types (coarse- and medium-texture mineral soil and peat), while the role of vegetation heterogeneity appears to be minimal (Fig. 10). The histograms of 1D simulations show that daily moisture values are distributed around field capacities of mineral and peat soils (Fig. 7), which is consistently the case in Fig. S7a, where all daily simulated distributions are shown. All model conceptualizations match the drier observations in the upland forest areas rather well, consistently with Fig. 6. However, as the 1D approach neglects groundwater storage and flow, the soil moisture estimates do not reach the observed high values as drainage rapidly removes water in excess of field capacity. Hence, the 1D simulation is biased low at wet locations (Figs. 6 and 7). Slightly more spatial variability can be seen in the TOP simulation, yet the cells where return flow from groundwater storage is activated remain rare (except close the stream network), even in wet conditions (17 June 2021, Fig. 7b), and almost non-existent in drier autumn conditions (1 September 2021, Fig. 7e).

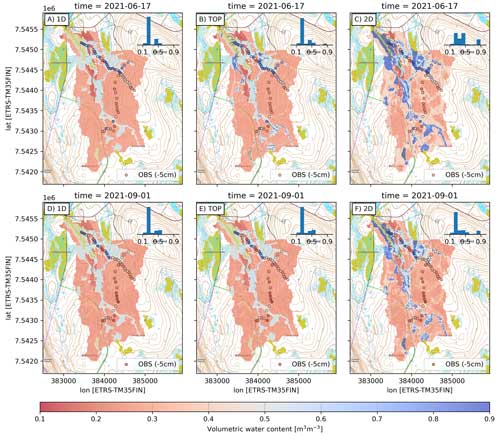
Figure 7 Spatial patterns of modeled root zone volumetric water content from the three model conceptualizations on 17 June 2021 (upper row, more moist) and 1 September 2021 (lower row, drier conditions). The bar plot shows binned distributions of simulated grid cell soil moisture across the whole catchment, and in situ measurements at 5 cm depth are shown as circles. The rasters overlay a topographic map (NLSF, 2020).

The SpaFHy-2D simulates larger saturated areas and matches most of the point observations well in Fig. 7. Nevertheless, there are still inaccuracies as saturated conditions adjacent to ditches are not well simulated and the observed variability in forests is not fully captured. The spatial variability of soil moisture in the 2D simulation depends strongly on the water table dynamics. Compared to other model variants, this creates stronger soil moisture variability within the catchment and yields better agreement with the observations. The histograms of Figs. 7c and f and S7c also show a higher frequency of grid cells being wet.

3.4 Comparison of spatial soil moisture

The previous section suggests that it is necessary to include the lateral groundwater flow to model the spatial patterns of soil moisture at the LJO catchment. However, comparison to point measurements can only capture a fraction of the simulated time steps and grid cells, and comparison with the spatially explicit SAR-based soil moisture is useful. In contrast to the model, SAR-based soil moisture values have poorer correspondence with the observations in grid cells where canopy fraction is high but provide a better match in open and wetter grid cells (i.e., peatlands, Figs. 6d and S6d). However, it is worth noting that the observations in Figs. 6d and S6d include all measurements in the root zone (0–30 cm), surpassing the assumed penetration depth of the SAR signal (1–5 cm).

A spatial comparison between SpaFHy-2D and spatially explicit SAR-based soil moisture is shown in Fig. 8. As already noted, the simulated spatial patterns mostly follow soil parameterizations, as well as water table dynamics affected by the lateral flow. The vegetation heterogeneity and consequent differences in rainfall interception and evaporation result in additional variability for simulated organic moss–humus layer moisture in dry conditions (Figs. 5 and 10). SAR and the SpaFHy-2D root zone simulations agree in terms of their main spatial patterns (i.e., drier forests and wetter peatlands). Spatiotemporal comparison metrics (Table S5) show that SAR generally predicts lower mean soil moisture and variance (mean, variance = 0.34, 0.02 m³ m⁻³) than SpaFHy-2D (mean, variance = 0.39, 0.04 m³ m⁻³) but higher mean soil moisture and variance compared to SpaFHy-1D (mean, variance = 0.29, 0.01 m³ m⁻³). It is also noticeable from Table S5 that the wet quantiles (0.9) of SpaFHy-2D root zone (0.82 m³ m⁻³) and SAR (0.65 m³ m⁻³) both suggest a major influence of lateral groundwater flow on soil moisture, consistently with earlier findings concerning peatlands (Fig. 8), throughout the season (Fig. 5c, d)

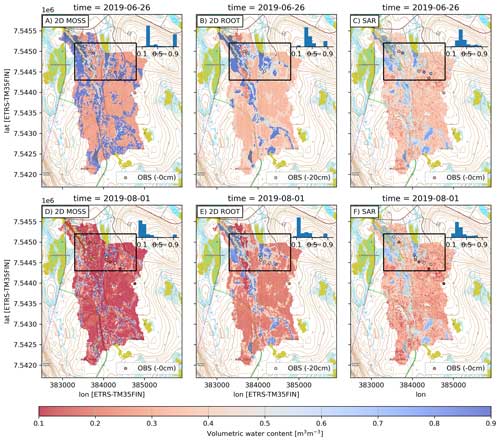
Figure 8 Spatial patterns of SpaFHy-2D modeled root zone and organic moss–humus moisture and SAR-based estimates on wet (26 June 2019, upper row) and dry days (1 August 2019, lower row). In situ measurements at 0 and 20 cm depths are shown as circles, and the bar plot shows binned distributions of simulated and SAR-estimated soil moisture across the whole catchment. The rectangular box shows an area that is presented in Fig. 9. The rasters overlay a topographic map (NLSF, 2020).

It is likely that SpaFHy-2D overestimates the organic moss–humus layer moisture content variability as there is a clear discrepancy between the SpaFHy-2D and the SAR-based estimates. The simulations provide too-high moisture content in wet (Fig. 8a) and are biased low in drier conditions (Fig. 8d). Compared to the simulations, SAR data show significantly more cell-to-cell variability, and the histogram appears to be nearly normally distributed, especially below 0.55 m³ m⁻³ (mainly mineral soils). Histograms of all daily soil moisture values in Fig. S7d confirm that the SAR data tend to be normally distributed between 0.1 and 0.5 m³ m⁻³. A closer look at the rectangular box shown in Fig. 8 further confirms the good agreement of SpaFHy-2D-simulated and SAR-estimated root zone moisture in both the dry and wet areas but also demonstrates the high cell-to-cell variability in SAR-based soil moisture (Fig. 9).

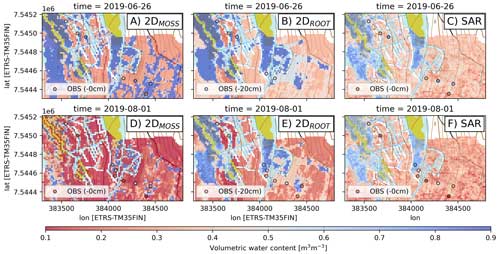
Figure 9 A zoomed-in distribution of 2D modeled root zone and organic moss–humus moisture and SAR-based estimates on wet (26 June 2019, upper row) and dry days (1 August 2019, lower row). In situ measurements at 0 and 20 cm depths are shown as circles. The rasters overlay a topographic map (NLSF, 2020).

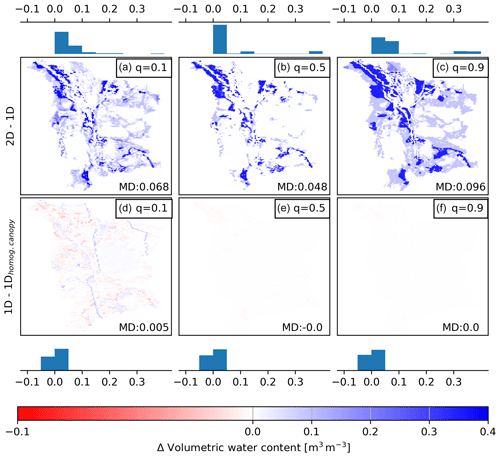
Figure 10 The impact of lateral groundwater flow (upper row) on root zone soil moisture expressed as simulated Δθ = 2D–1D and the impact of vegetation heterogeneity (bottom row) expressed as simulated Δθ = 1D–1D_homog.canopy in different catchment soil moisture states. The panels correspond to 0.1, 0.5, and 0.9 quantiles of grid cell soil moisture, and the bars show the distribution of binned differences. The mean difference (MD) is shown in each panel. Note that the blank panel refers to Δθ = 0.0 m³ m⁻³.

Considering the ability of SAR to predict relatively well the peatland soil moisture (Figs. 6d and S6d), the agreement of SpaFHy-2D and SAR provides support for our earlier findings that soil moisture predictions improve when the lateral groundwater flow is included (SpaFHy-2D). The agreement of SpaFHy-2D and SAR is further supported by a quantitative comparison in Fig. S8, where two clusters of soil moisture emerge in peatlands. The cluster of wet points corresponds to the grid cells with groundwater flow influence, while the other cluster is not impacted by the lateral flow. The consistency between the SAR and SpaFHy-2D is not as clear in mineral soil grid cells (Fig. S8), likely due to uncertainties in the model's soil hydraulic parameters, as well as limitations in SAR soil moisture detection in forests (Fig. 6).

3.5 Drivers of spatiotemporal soil moisture variability

To better separate the role of lateral groundwater flow from that of vegetation heterogeneity under different temporal soil moisture regimes, Fig. 10 shows the grid-cell-to-grid-cell differences (Δθ) between SpaFHy-2D and 1D simulations, as well as between 1D and 1D_homog.canopy runs. As expected, the difference between SpaFHy-2D and 1D simulations is highest in wet conditions (q = 0.9, Fig. 10c). In this case the lateral groundwater flow has a large impact on soil moisture (mean Δθ between 2D and 1D of ca. 0.1 m³ m⁻³) in major parts of the catchment, including parts of the forested areas. The difference between the models is smallest at periods with intermediate soil moisture (q = 0.5, mean difference of ca. 0.05 m³ m⁻³, Fig. 10b), during which the lateral flow has an effect almost only in peatland grid cells. Interestingly, the difference between the 2D and 1D predicted soil moisture also becomes significant in dry conditions (mean difference of ca. 0.07 m³ m⁻³, Fig. 10a), indicating a long-lasting effect of lateral groundwater flow from the upland to the lowland grid cells. The role of vegetation heterogeneity in soil moisture patterns is negligible at intermediate and wet conditions (Fig. 10e, f), and only minor differences are found in very dry conditions (Fig. 10d). The vegetation heterogeneity plays a larger role in the moisture content of the organic moss–humus layer, but the impact of lateral flow still remains stronger (Fig. S9).

4 Discussion

4.1 Insights into the role of lateral groundwater flow for shallow soil moisture

Our multi-scale data and high-resolution process-based simulations in the subarctic LJO catchment showed that, regardless of the catchment hydrologic state (from dry summer to very moist conditions after snowmelt), lateral groundwater flow plays a major role in shaping the spatial variability of soil moisture (Fig. 10). The results indicate that spatially resolved models which include groundwater flow are necessary to predict soil moisture variability at high-latitude catchments. Nevertheless, lateral groundwater flow is commonly neglected in current hydrological and land surface models that operate at a coarse resolution (Best et al., 2011; Lawrence et al., 2012; Niu et al., 2011; Noilhan and Mahfouf, 1996). Increasing the spatial resolution of hydrological and biogeochemical land surface models is the current trend; for instance, Wood et al. (2011) set the ambition for future hyper-resolution land surface models (LSMs) to 1 km for global-scale and 100 m for regional-scale simulations. When the models are adapted to finer grids, it becomes increasingly important to implement lateral groundwater dynamics (Ji et al., 2017; Kim and Mohanty, 2016; Decker et al., 2013). Our relatively simple 2D shallow groundwater Darcy flow model, incorporating only seven additional parameters (water retention parameters, depth-to-bedrock, and stream water level) determined using openly available digital elevation model, soil type, and stream network rasters, performed comparably to the state-of-the-art integrated surface–groundwater model HydroGeoSphere (Brunner and Simmons, 2012) in predicting observed groundwater levels at the LJO catchment (compare Fig. S6 and Table S4 and Fig. 6 and Table S6 in Autio et al. (2023)). Also, the groundwater-influenced areas in the catchment are in broad agreement with the simulations by Autio et al. (2023).

Regardless of the known sensitivity of ecohydrological fluxes (i.e., interception, evaporation, transpiration) to changes in LAI and plant type (Launiainen et al., 2019; Kozii et al., 2020; Launiainen et al., 2016), the impact of lateral groundwater flow outweighed the impact of vegetation heterogeneity on soil moisture dynamics throughout the year. However, the growing season in Pallas is short, and vegetation is rather sparse and not very heterogeneous within the site classes (Fig. 2). In addition, the impact of vegetation heterogeneity on soil moisture is attenuated due to the compensating processes; soil evaporation decreases while transpiration and interception evaporation increase with increasing LAI, resulting in less drastic changes in total ET (Leppä et al., 2020; Launiainen et al., 2019). Consistently with Kollet and Maxwell (2008), the impact of groundwater flow on shallow soil moisture also persisted in dry conditions, suggesting high resilience of lowlands to droughts due to long-lasting lateral flow from the upland part of the catchment. The simulations showed that, for large parts of the catchment, root zone moisture content was controlled by lateral groundwater flow, and the strength of this effect depends on the state of the groundwater storage. Ji et al. (2017) showed that the role of lateral water flow becomes crucial in high-resolution land surface simulations in a region dominated by a humid climate and coniferous forests in the western USA. At a resolution of 100 m, they showed that subsurface lateral flow transports moisture from high-elevation areas to valley bottoms, impacting local grid cell and catchment average ET, especially in dry conditions. Kollet and Maxwell (2008) coupled a groundwater and a land surface model and demonstrated that, when the water table depth was above 5 m, there was strong coupling between groundwater dynamics and land surface processes at the subhumid grassland-dominated watershed in the USA. Our results at the LJO catchment are in line with these studies regarding the importance of groundwater flow to shallow soil moisture.

The impact of lateral flow was found to be especially important for peatlands due to both the high porosity of peat (Menberu et al., 2021) and the location in the valley bottom (Figs. 2, 7, and 8). Mineral forest topsoils can also be (temporarily) impacted by lateral flow, especially soon after strong precipitation events and snowmelt. However, the difference between 1D and 2D models remained smaller due to the small difference in mineral soil field capacity and porosity (Fig. 10).

4.2 SAR-based soil moisture: potential and limitations

The Sentinel-1 SAR-based soil moisture estimates were useful in supplementing the point-scale in situ measurements and confirming the plausibility of the spatial soil moisture predicted by the SpaFHy-2D. To this date, model developments and evaluations of soil moisture predictions in boreal and subarctic forests and peatlands have typically been limited to point-scale studies, which fail to encompass the full spatiotemporal extent that distributed hydrological models simulate (Launiainen et al., 2015; Ala-aho et al., 2017b; Tyystjärvi et al., 2022). We found SAR estimates useful for spatial model–data comparison, and envision SAR to have further potential as, for instance, a proxy for water table depth assimilation or improved estimates of topographic wetness indices (TWIs, depth to water) in peatlands (Bechtold et al., 2020; Zhang et al., 2018).

The comparison between SAR-based estimates and modeled soil moisture was not straightforward and revealed limitations in using the SAR-based data as, for instance, ground-truth calibration data for hydrological models. A direct comparison is challenging due to the disparate penetration depth of SAR in soil (1–5 cm: Nolan and Fatland (2003)), contrasting with the model layering (root zone layer of 0–30 cm). Indeed, the correspondence of SAR-based estimates with in situ measurements in the root zone (0–30 cm, Fig. 6) was poorer than the original validation of SAR estimates in relation to in situ measurements at the surface soil (0 cm, Fig. 11 in Manninen et al. (2021)). This vertical mismatch is a common challenge (Shellito et al., 2020), and, hence, enhancing the comparability of in situ measurements, as well as of hydrological models, with SAR estimates would contribute to more effectively harnessing the SAR-based data. Another notable difference is that hydrological models such as SpaFHy neglect heterogeneity within the grid cells, while SAR estimates can integrate multiple backscattering signals for a given grid cell (Manninen et al., 2021). In turn, hydrological models can integrate temporal information, whereas SAR-based estimates are instantaneous.

We also emphasize the need for potential algorithm improvements in computing soil moisture from SAR signals. Given the homogeneity of the vegetation and soil texture, some of the spatial variability in the SAR-based data appeared more as noise than realistic soil moisture patterns. To a large extent, the different SAR incidence and view angles with respect to the topography cause the systematic difference in the soil moisture estimates from the morning and evening flyover times (Figs. 4 and 5). Indeed, topography-induced shading posed a significant challenge in the development of the evening soil moisture algorithm for SAR-based estimates (Manninen et al., 2021). Consequently, Manninen et al. (2021) reported higher RMSEs for the evening flyover (0.088 m³ m⁻³) than for the morning flyover (0.065 m³ m⁻³), while the maximum errors were relatively similar (0.341 m³ m⁻³ for morning flyover and 0.339 m³ m⁻³ for evening flyover). Further discussion on the differences between these SAR flyovers can be found in Manninen et al. (2021).

Although the SAR-based soil moisture fell mostly within the observed range, the temporal variability and seasonal patterns, especially from the evening flyovers, were small and followed neither the simulated nor in situ-observed shallow soil moisture (Fig. 5). The morning flyover occasionally captured some temporal dynamics observed and simulated (see, e.g., Fig. 5d). The SAR-based estimates do not reach the highest observed or simulated values, resulting in underestimation of the soil moisture content, likely because they integrate information from multiple signals within a given grid cell that have been averaged to correspond to the model grid. The presence of different vegetation characteristics and soil textures further complicates the interpretation of the backscattering signals, leading to uncertainties and noise in soil moisture estimates.

Overall, the capability of any remote-sensing-based soil moisture estimate to represent various meteorological and landscape conditions can only be as good as the training data. As acquiring high-quality and representative in situ soil moisture data is challenging and costly, we encourage deeper collaboration between hydrological measurement, modeling, and remote sensing communities.

4.3 Model limitations and outlook

The modularity of SpaFHy (Launiainen et al., 2019) was ideal for comparing the impact of different conceptualizations of the lateral groundwater flow. Nevertheless, there are potentially relevant hydrological processes that are not yet represented. For instance, overland flow and soil freezing and thawing are currently omitted, and this may influence soil moisture dynamics, particularly during and after snowmelt and in the autumn (Ala-Aho et al., 2021). Lateral overland flow has been found to distribute water from saturated grid cells to unsaturated areas (e.g., in subarctic tundra and boreal forests;  Tang et al., 2014). We suspect that it may be especially important after snowmelt and heavy-precipitation events over the low-lying flat peatlands of the catchment. The snowpack representation of SpaFHy successfully captured the snowmelt timing (Figs. S2 and S3) but relies on a simple degree-day approach, potentially limiting its ability to fully capture snowmelt dynamics. Moreover, the radiation conditions on the forest floor within a specific grid cell may be influenced by the forest canopy in the surroundings. Thus, employing 3D radiation transfer schemes that consider the shading from grid cell neighbors (Webster et al., 2023) or the demography of individual trees within a grid cell could be beneficial (Mazzotti et al., 2021).

Although the explicit 2D lateral groundwater flow module added process realism and improved shallow soil moisture predictions, the simulations were still far from perfect due to uncertainties in classifying soil types and because soil moisture data were not used to calibrate the model's hydraulic parameters. The improvement also comes with a computational cost: in terms of running time, SpaFHy-2D is approximately 60 times slower than TOP and 1D versions. For instance, a 1-year simulation with 1D and TOP was completed in 5.4 s, while 2D took 321.6 s. This can become a burden when applying the 2D model to large areas or when parameter calibration or ensemble simulations are done.

Uncertainties in model simulations and model evaluation accumulate from multiple sources: input data, model parameters, model structure, and errors in in situ measurements (Moges et al., 2021). The meteorological forcing time series was constructed from observations at the upland forest site, and radiation data gaps were filled with ERA5 data (Hersbach et al., 2020). It is known that there are intrinsic uncertainties in meteorological observations (Stuefer et al., 2020). Although data gaps were limited, those filled by ERA5 data further add uncertainties into the model–data comparison (Raleigh et al., 2015). In addition, we used spatially uniform meteorological forcings (excluding radiation where topographic shading was accounted for) measured at the forest site that may have been slightly different to those experienced on the lowland peatlands (Aurela et al., 2015).

The model was initiated and parameterized based on the best available open geospatial data on the landscape characteristics. As Härkönen et al. (2015) found a good agreement between the mNFI-based and ground-based LAI estimates and because soil moisture patterns were not majorly altered by vegetation characteristics (Fig. 10), we assume that vegetation parameters did not create marked biases in the soil moisture predictions. However, estimating soil hydraulic properties from available geospatial data sets is challenging (Launiainen et al., 2022) and can yield systematic uncertainties and biased local soil moisture. Modeling lateral groundwater flow by means of the proposed 2D Darcy scheme also requires distributed data on the depth to bedrock. As such information was not readily available, these parameters were assigned as estimates. Even with these limitations, the modeled groundwater level dynamics were relatively close to the observed levels (Fig. S5 and Table S4)

5 Conclusions

We explored the controls of high-resolution soil moisture dynamics, particularly the role of lateral groundwater flow, in the subarctic Lompolonjängänoja catchment in northwestern Finland. We combined soil moisture data from multiple sources, including in situ measurements and Sentinel-1 SAR-based estimates, and interpreted soil moisture variability with high-resolution (16 × 16 m²) process-based hydrological modeling. To accomplish this, we extended the Spatial Forest Hydrology (SpaFHy) model with an explicit lateral groundwater (2D Darcy flow) submodel and compared it to existing approaches where lateral groundwater flow was either neglected (free drainage) or based on a simple TOPMODEL conceptualization. The results showed the major impact of lateral groundwater flow on shaping soil moisture dynamics, particularly post snowmelt and after heavy rainfall. The inclusion of the lateral groundwater flow model notably improved soil moisture simulations in forested peatlands and open peatlands. The soil moisture simulations were affected by uncertainties in hydraulic parameters, which were assigned based on geospatial data on soil types. SAR-based soil moisture estimates were valuable in confirming modeled spatial patterns. Discrepancies in spatial resolutions, SAR penetration depth, and model layering, however, hampered direct comparison. Moreover, the noise in SAR-based data, particularly for forested areas, complicates the use of SAR as ground-truth evaluation data for hydrological models. Our study provides novel insights and tools for predicting soil moisture dynamics at a high resolution, necessary for ecohydrological, biogeochemical, and climate change adaptation studies, as well as for land use management and planning in high-latitude environments.