the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Estimating the sensitivity of the Priestley–Taylor coefficient to air temperature and humidity
Ziwei Liu
Changming Li
Taihua Wang
The Priestley–Taylor (PT) coefficient (α) is generally set as a constant value or is fitted as an empirical function of environmental variables, and it can bias the evaporation estimation or hydrological projections under global warming. By using an atmospheric boundary layer model, this study derives a theoretical and parameter-free equation for estimating α as a function of air temperature (T) and specific humidity (Q). With observations from several waterbodies and non-water-limited land sites, we demonstrate that, in addition to estimating the value of α well, the derived expressions can also capture the sensitivity of α to T and Q, that is, and . α is generally negatively associated with T and Q, in which regard T plays a more fundamental role in controlling α behaviors. Based on climate model data, we further show that this negative relationship between α and T is of great importance for long-term hydrological predictions. We also provide a lookup graph for practical and broad uses to directly find the values of and under specific conditions. Overall, the derived expression gives a physically clear and straightforward approach to quantify changes in α, which is essential for PT-based hydrological simulation and projections.
- Article
(2707 KB) - Full-text XML
- BibTeX
- EndNote
Evaporation from wet surfaces, including oceans, lakes, and reservoirs, is relevant to global hydrological cycles and water availability. There is a long history of developing theories and methods to estimate wet-surface evaporation (Bowen, 1926; Penman, 1948; Priestley and Taylor, 1972; Thornthwaite and Holzman, 1939; Yang and Roderick, 2019). Among the existing models, the Priestley–Taylor (PT) model or equation is known for its transparent structure and low input requirement (Priestley and Taylor, 1972). The PT equation is widely used in evaporation estimation across varied scales and is the basis for various hydrologic and land surface models. Specifically, the PT equation comes from the equilibrium evaporation (λEeq), and λEeq can be calculated as follows (Slatyer and McIlroy, 1961):
where λ (J kg−1) is the latent heat of water vaporization, , Δ (kPa K−1) is the slope of the saturated vapor pressure versus the temperature curve (a function of temperature), and γ is the psychrometric constant. εa is a function of air temperature (T). Rn−G (kPa K−1) is the available energy. The equilibrium evaporation indicates that the near-surface air is saturated, supposing the vapor pressure deficit (VPD) is zero. However, it does not exist in the real world (Brutsaert and Stricker, 1979; Lhomme, 1997a) due to the continuous exchanges of warm and dry air from the entrainment layer, although water is continuously transported from the bottom wet surface into the atmosphere through the evaporation process (Fig. 1).

Figure 1Atmospheric boundary layer box model describing the energy and water fluxes at the saturated surface and in the atmosphere above. The dotted line represents the removable upper boundary of the box. H and λE are the sensible and latent heat fluxes. Ta is the air temperature, and VPD is the vapor pressure deficit.
In this case, the PT equation introduced a parameter, α, known as the PT coefficient, to estimate wet-surface evaporation (Priestley and Taylor, 1972). α represents the effects of vertical mixing of dry and moist air and adjusts the equilibrium evaporation to the actual evaporation. So, qualitatively speaking, the α is impossibly lower than 1 because the air is always non-saturated and can only come infinitely close to a saturated condition, no matter how moist the near-surface air is. The PT equation is as follows:
In the original study of Priestley and Taylor (1972), the value of α was fitted as 1.26. While a fixed α value can reasonably estimate wet-surface evaporation (Yang and Roderick, 2019), some studies found that α varies across time and space; for example, α often shows a more prominent value under cold conditions and becomes lower as temperature increases (Xiao et al., 2020; De Bruin and Keijman, 1979). This indicates that α should be a variable rather than a constant (Assouline et al., 2016; Guo et al., 2015; Jury and Tanner, 1975; Lhomme, 1997b; Van Heerwaarden et al., 2009; Eichinger et al., 1996; McNaughton and Spriggs, 1986; Crago et al., 2023; Maes et al., 2019). However, the hydrology field predominantly employs the fixed value of α=1.26 despite those earlier findings being over 3 decades old.
A general method to quantify the changes in α is to invert it with observations based on Eq. (2) and then build relationships among α and investigated variables. Since the existence of a negative relationship between α and temperature (T) is the consensus from multi-scale observations (Assouline et al., 2016; Xiao et al., 2020), many attempts empirically fitted α as a function of T (Andreas and Cash, 1996; Hicks and Hess, 1977; Yang and Roderick, 2019). Recent work further showed that the air humidity state can also influence the spatiotemporal patterns of α (Su and Singh, 2023). While those methods promote our understanding of the potential variations in α, they lie more on the empirical side and pay less attention to the underlying process. Hence, various endeavors have been made to calculate α through physical means, but they are often constrained by the complexity of numerous parameters. For instance, in the research conducted by Lhomme (1997b), α was explicitly formulated utilizing the PM model in conjunction with boundary layer theory. Nevertheless, the formulation incorporates parameters that signify surface and aerodynamic resistances, making them hard to determine through direct measurements. Subsequently, by using a refined boundary layer model, Van Heerwaarden et al. (2009) introduced a mathematical expression for estimating α; however, the expression also involves a set of parameters necessitating that numerical experiments delineate a feasible range for α. Consequently, obtaining a precise α estimation using conventional observations has still remained a challenge.
Based on a recent study by Liu and Yang (2021), here, we aim to derive a physically clear, transparent, and calibration-free equation for estimating α by introducing a governing equation (potential vapor pressure deficit budget) into the conventional boundary layer model. In the following sections, we will first provide the theory for estimating α and its sensitivity to climate conditions: air temperature (T) and humidity (represented by the air specific humidity, Q). We further evaluate the theory based on measurements from the water and non-water-limited land surfaces, followed by the influences of α changes over long-term hydrologic projections.
2.1 Derivation of the Bowen ratio
Here, we use a model based on the atmospheric boundary layer (ABL) as the basis for the Bowen ratio (Bo, defined as the ratio of sensible heat fluxes to latent heat fluxes, ) derivation (Liu and Yang, 2021). The fundamental conservation equations for states of moisture and energy over the water surfaces are as follows (Raupach, 2001):
where θ (K) is the potential temperature, Q is the specific humidity, cp () is the specific heat capacity of air at constant pressure, ge (m s−1) is the entrainment flux velocity into the ABL box, and h (m) is the height of the ABL. The subscript e indicates that the variable is evaluated at the upper boundary of the ABL (see Fig. 1).
According to Eqs. (3) and (4), we can obtain a formula to calculate the rate of VPD (; see details in Liu and Yang, 2021):
where ΔD is calculated as
Under the state in which the air is saturated, the water vapor is continuously transported from the water surface to the atmosphere, keeping the air saturated. In this case, there is no vertical moisture gradient; that is, the air near the surface and the air at the upper boundary of the ABL should be saturated, and so VPD and VPDe are both equal to zero. With Eq. (6), we can know ΔD=0.
When air is not saturated, we can rewrite Eq. (6) as follows:
where Qe is much smaller than Q, and Qsat(θe)−Qsat(θ) is small (1 order of magnitude smaller than Q) so that the ΔD roughly equals Q (Raupach, 2001; Liu and Yang, 2021).
Under a relatively long-term period (monthly and/or longer), there is a potential VPD budget over water surfaces (Raupach, 2001), and ge can be estimated as the function of H and λE as follows:
where Λ is a constant (0.07), and γv is the potential virtual temperature gradient in the free atmosphere above the ABL. γvh can be set as a fixed value of 7 K (Liu and Yang, 2021). Combining Eqs. (5) and (8) with the VPD budget, we can obtain the expression for Bo:
where , a function of Q.
2.2 Theoretical formula for α
The surface energy balance is expressed as follows:
Combining Eqs. (2) and (10), α can be calculated as follows:
With Eqs. (9) and (11), we can derive the formula for α:
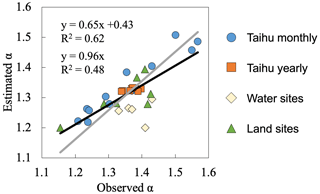
Equation (12) is one of the main results in this study, and it can estimate α well compared to a large number of observations (Fig. 2; please see the description of observed data in Sect. 3).
2.3 The sensitivity of α to air temperature and humidity
According to the above derivations, we can know that α is not a constant and that it changes with T and Q. The sensitivity of α to T and Q, and , determines the variation of α if the initial α value is given. In this section, we derive explicit equations to estimate and .
Firstly, we decompose α changes into those of T and Q with partial differential equations based on Eq. (11):
where partial differential terms of and can be estimated based on Eq. (9) as
where terms of and can be approximated as
where Δ can be calculated as
Combining Eqs. (13)–(18), we can obtain the following:
We can rewrite Eq. (20) as follows:
The total differentiation of α is
Thus, and can be written as follows:
With the above equations, we can get theoretical relationships among α, T, and Q. This derivation can provide a simple and physically clear estimation for α changes. We also obtained and values by fitting measured data using the linear regression model.
For practical use, we simplified Eqs. (20) and (21) as follows:
We further gave a numerical plot to show how α changes with T and Q (Fig. 3). We plot this figure by setting gradients from 0.0005, 0.0007, and 0.0009 K−1 to ensure coverage of most of the cases over water surfaces. The lookup graphs in Fig. 3 can be used to directly find and values. For example, for a water surface with equating to about 0.0007 K−1, the values of and can be found in the second column of Fig. 3.
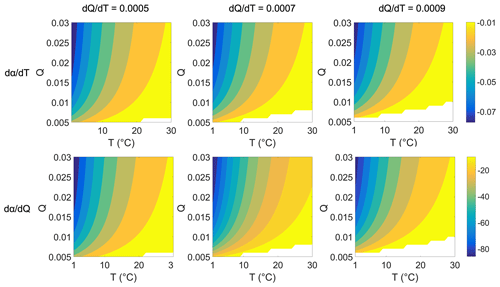
Figure 3Values of and under different T and Q. The first and second rows are and , respectively. The first to third columns are under different correlations between Q and T () at 0.0005, 0.0007, and 0.0009 K−1, respectively. The blank space in each subpanel refers to values of and that are negative, indicating situations that rarely happen in the real world (i.e., with a very high temperature, the specific humidity is hardly deficient over wet surfaces).
3.1 Data
We select data from eddy covariance measurements on several water surfaces (Han and Guo, 2023): (i) Lake Taihu, located in the Yangtze River Delta, China, with an area of ∼2400 km2 and an average depth of 1.9 m (Lee et al., 2014) – there are five sites over the Taihu surface, and the poor-quality data marked with quality flags are removed; (ii) Lake Poyang, located in the Yangtze Plain, China, with an area of ∼3000 km2 and an average depth of 8.4 m (Zhao and Liu, 2018); (iii) Erhai, located in the Yun-Gui Plateau of China, with an area of ∼250 km2 and an average depth of 10 m (Du et al., 2018); (iv) the Guandu ponds, located in Anhui Province, China, with an area of ∼0.05 km2 and an average depth of 0.8 m (Zhao et al., 2019); and (v) Lake Suwa, located in Nagano, Japan, with an area of ∼13 km2 and an average depth of 4 m (Taoka et al., 2020). Months with negative values in terms of sensible heat fluxes have not remained. Given the absence of observed heat storage (G) at some sites, we use the sum of latent heat flux and sensible heat flux (i.e., LE+H) instead of net radiation minus G (Rn−G) as the measure of available energy. Using either LE+H or Rn−G yields identical results as our objective is to use the available energy to invert parameter α from observations. The latitude, longitude, and available data periods of the five lakes and ponds are listed in Table 1. For α changes in time, we use data from Lake Taihu for our investigation due to its sufficient data length. For α changes in space, we calculate the average temperature, specific humidity, and α of each lake for comparison.
Table 1Location and date period of each waterbody.
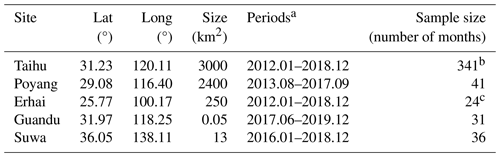
a The term “periods” refers to the date of the first measurement to the date of the last one, including months for which no data are available. b There are five eddy covariance sites over Lake Taihu. c Only climatology monthly data from two periods of 2012–2015 and 2015–2018 are available.
Observations from global flux sites (FluxNet2015 database) are also selected. We first examine days without water stress based on the following steps (Maes et al., 2019). At each site, the evaporative fraction (i.e., EF, latent heat flux over the sum of latent and sensible fluxes) is first calculated, and the days with an EF exceeding the 95th-percentile EF and with an EF larger than 0.8 remain. Secondly, the days with soil moisture lower than 50 % of the maximum soil moisture (taken as the 98th percentile of the soil moisture series) are removed. Days having rainfall and negative values of latent and sensible heat fluxes are also not included. As a result, a total of ∼700 non-water-stressed site days meet the criteria. Data are divided into seven vegetation types, including croplands (CRO), wetlands (WET), evergreen needleleaf and mixed forests (DNF_MF), evergreen broadleaf and deciduous broadleaf forests (EBF_DBF), grasslands (GRA), close shrublands (CSH), and woody savanna (WSA), to analyze α changes in space. It should be noted that we do not average the daily data to a monthly scale due to variations in data sizes across different months for a specific site. Instead, we organize the selected daily data by vegetation type as the primary objective of utilizing land flux data is to assess the derived relationship spatially rather than temporally.
We also collect ocean surface data from 11 CMIP6 models (under scenario SSP585, Table 2) from 2021 to 2100 to see the temporal changes in α. The calculation is limited to the latitudinal range 60° S to 60° N and takes all ocean surface grids as a whole (Roderick et al., 2014). We average the monthly data to the yearly scale and calculate α every 10 years from 2021 to 2100 (i.e., 2021–2030, 2031–2040, etc.).
Table 2CMIP6 models used in this study.
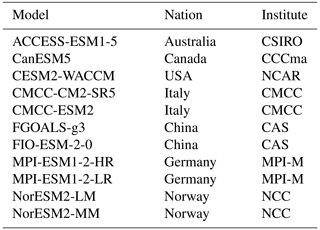
CSIRO is the Commonwealth Scientific and Industrial Research Organization, CCCma is the Canadian Centre for Climate Modelling and Analysis, NCAR is the National Center for Atmospheric Research, CMCC is the Euro-Mediterranean Center on Climate Change, CAS is the Chinese Academy of Sciences, MPI-M is the Max Planck Institute for Meteorology, and NCC is the Norwegian Climate Centre.
3.2 Results
3.2.1 Temporal and spatial changes in α
We used yearly and monthly (from January to December) climatology data from Lake Taihu to investigate the temporal variation in α. α is firstly inversed by the PT model and measurements, and then we found significant negative relationships of α with both T and Q (Fig. 4). On the yearly scale, the regressed values of and are −0.029 °C−1 and −47.42, and the values on the seasonal scale are −0.014 °C−1 and −20.75, respectively. on the seasonal scale is higher than that on the yearly scale because the variation range of α on the seasonal scale is more extensive. Theoretical derivations can roughly reproduce the sensitivity of α to T and Q, although there is some potential uncertainty from interannual variations (Table 3). We also analyzed the results on the 10 d scale and obtained similar findings (see Fig. A1 and Table A1 in the Appendix).
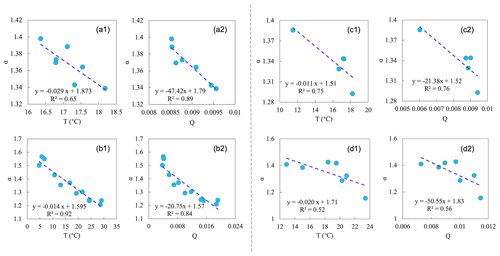
Figure 4Temporal and spatial relationships of α and temperature (T) and specific humidity (Q). (a, b) Temporal relationships based on Lake Taihu data: (a) yearly data and (b) monthly climatology data. (c, d) Spatial relationships: (c) data from five water surface sites and (d) land surface data from FluxNet2015, with each circle representing one vegetation type. The linear regression line and correlation coefficient (R2) are shown in each subpanel.
Table 3Sensitivity of α to temperature (T) and specific humidity (Q) by regression and theoretical derivation.

Spatial relationships of α with T and Q are similar to those in time; i.e., higher T and Q generally correspond to lower α, supported by measurements over both water and land surfaces (Fig. 4). For the water surfaces, the values of and are −0.011 °C−1 and −21.38, and the values for land surfaces are −0.020 °C−1 and The derived and roughly matched well with the regressed values, despite more or fewer errors (Table 3). The correlations (represented by R2 in Fig. 4) between α and T and between α and Q over water surfaces are higher than those over the land surfaces. This indicates that changes in α are more associated with T and Q over water surfaces, which may be because T and Q dominate the water surface evaporation process, while some other factors, like vegetation and wind speed, also play specific roles over land surfaces.
Based on Eqs. (20) to (22), is always a negative value, and is always positive. The regressed and derived and are both negative. Combined with Eqs. (24) and (25), considering the positive relationship between T and Q, the plays a more critical role in determining (the signs of) and , that is, and . Specifically, based on the data from Lake Taihu (for detecting α changes in time) and data from different water surface sites and land surface sites (for detecting α changes in space), we found the contribution of to dα is ∼70 %, which is much more significant than that of of ∼30 % (Table 4). Therefore, according to the evaporation process over the wet surface (Sect. 2.1) and the above analyses, we can conclude that α is fundamentally controlled by T and modulated by Q.
Table 4Contributions of changes in temperature (T) and specific humidity (Q) to changes in α.

Note that, since , the contribution of is calculated as , and the contribution of is calculated as . dα refers to the estimated variation of α from the lowest to highest T (also from the lowest to highest Q since T and Q are generally positively correlated).
Derived and have more or fewer errors compared to the regressed values. Several reasons can explain this: (i) there are errors in the measurements of eddy covariance systems; (ii) the additional factors other than T and Q, like wind speed, can also influence α; and (iii) the relationship of α and T (also of α and Q) cannot be well represented by the linear regression model. Besides, the water surface size effects on evaporation and α, reported by Han and Guo (2023), are not well considered in the presented derivation. Nevertheless, the derived expression can fairly match the observations of waterbodies with various sizes (Table 3).
3.2.2 Potential applications for global projections
Based on CMIP6 ocean surface data, we also detected significant negative relationships of α with T and Q (Fig. 5). and obtained by the linear regression are −0.009 °C−1 and −11.54, respectively. The derived and are close to the regressed values at −0.009 °C−1 and We further compared the changes in T, Q, and heat fluxes between the first and the last 10 years in 2021–2100 (Table 5). To the end of this century, CMIP6 models predict that ocean average available energy (Rn−G) and latent heat fluxes (also evaporation) will increase by ∼3.1 and ∼6.0 W m−2, respectively. Using the PT model with the fixed α (1.26), predicted evaporation shows an increase of ∼8.0 W m−2, which is far higher than climate models' direct outputs (with a relative bias of ∼30 %). Based on derived α, ocean evaporation shows a much smaller increase of ∼5.8 W m−2, with less than 5 % relative bias compared to CMIP6 values (Fig. 6). This indicates that changes in α should be well considered for the long-term projections. So, here, we suggest introducing the negative relationship between α and T, as proposed in this study, into the original PT model to correct for the overestimated sensitivity of evaporation to temperature (Liu et al., 2022), which could also improve the reliability of global long-term drought predictions (Greve et al., 2019).

Figure 5Temporal relationships of (a) α and temperature (T) and (b) α and specific humidity (Q) over global ocean surfaces. Each dot denotes the data in each 10-year window (2021–2030, 2031–2041, …, 2091–2100); from left to right is from 2021–2030 to 2091–2100.
Table 5Ocean surface temperature, specific humidity, and heat fluxes for the first 10 years (2021–2030) and for the end of the 21st century (2091–2100). T, Q, Rn−G, and LE are direct outputs of climate models. α-CMIP refers to α inversed by the PT model with CMIP data. LEPT is calculated by the PT model with fixed α at 1.26. α-ABL refers to α estimated by the ABL model. LEABL is calculated by the PT model with α-ABL.

In this study, we employed an open boundary layer model with a governing potential VPD budget (Raupach, 2001, 2000), originally integrated by Liu and Yang (2021), to formulate an expression for the Priestley–Taylor coefficient, α. Notably, the governing equation allows the derived expression to have no calibrated parameters and can estimate a precise α value with normal observations, rendering it superior to other methods that are also built with the boundary layer theory (Lhomme, 1997b; Van Heerwaarden et al., 2009). With the expression and a variety of measurements, we further demonstrated that temperature exerts a more significant influence over variations in α as opposed to specific humidity. We suggest that, for studies focusing on evaporation and/or drought projections, it is crucial to thoroughly characterize the negative correlation between α and temperature, a relationship easily determined using the derived expression.
It should be noted that, except for the PT model, the PM-based model can also be used to estimate wet-surface evaporation (Penman, 1948; Shuttleworth, 1993). While PM-based equations encapsulate all processes that possibly affect evaporation, the PT model, taking evaporation as a simple function of radiation and temperature, takes more account of the feedback and/or balance between the surface and near-atmosphere (Fig. 1). Besides, it has been noted that the PM-based models may fail at certain points and cannot capture the sensitivity of evaporation to temperature changes (Liu et al., 2022; McColl, 2020). So, in this case, also considering the fact that the PT model is currently one of the most popular equations due to its low input requirements, revisiting this classic model can greatly promote its adaption under the changing climate. Meanwhile, some revised PT equations can also be used to estimate the parameter α (Yang and Roderick, 2019; De Bruin and Holtslag, 1982). However, these modifications often exhibit significant deviations (Fig. A2). Specifically, the model developed by De Bruin and Holtslag (1982) is based on data from one specific site in the Netherlands, and the model built by Yang and Roderick (2019) comes from the fitness of global ocean surface data. These equations are primarily calibrated to match observed evaporation rates, while the underlying process is generally overlooked.
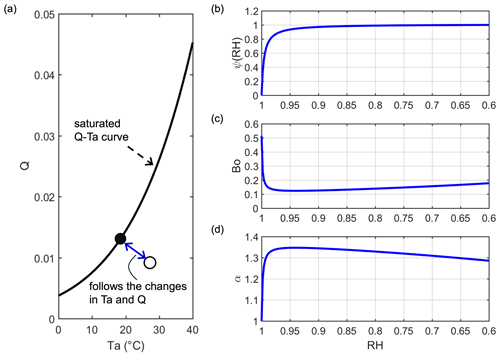
Figure 7(a) Transition between saturated and non-saturated air states. The filled circle represents one case in which the air is saturated (saturated state), and the open circle represents one case in which air is not saturated (non-saturated state). (b) Relationship between ψ(RH) and RH with Eq. (28). (c, d) Changes in Bo and α as a function of RH when air temperature is fixed at 18 °C.
In Sect. 2.1, it was suggested that ΔD=0 for the saturated air, while ΔD≈Q for the non-saturated air. In theory, it is expected that the transition track between saturated and non-saturated states should be continuous and smooth. That is, the changes in the value of ΔD between the saturated (0) and non-saturated (Q) states should follow the variations in air energy and moisture (Fig. 7). Since the relative humidity (RH) includes information on both air temperature and humidity, here, we introduce a possible track of ΔD depending on RH as follows: . As we expect, the value of ΔD approaches 0 when the air is very moist (i.e., very close to the saturated state and with RH close to 1), and so ψ should be a nonlinear and monotone convex function of RH. We give a possible expression of ψ(RH) as follows:
where, over the water surfaces, RHmax is 1, and RHmin is 0.6 (McColl and Tang, 2023). m and n are shape parameters. To make ψ(RH) simple, we fixed n at 1 and let m be 100. The relationship between ψ(RH) and RH can be viewed in Fig. 7b. For a specific case with T at 18 °C, we show the changes in Bo and α with RH in Fig. 7c and d. Although there is a dramatic shift in Bo and α, this appears when RH is at 0.95–1, which is outside the vast majority of actual cases (RH is generally smaller than 0.9 on a monthly or longer scale). After the shift point, with RH decreases, ψ(RH), Bo, and α remain roughly stable. It is worth noting that Eq. (28) (with specific parameters) is one possible case that connects the transition between saturated and non-saturated air states, and a fine determination may be affected by local conditions, but a ΔD value around Q is expected for most of the cases.
We recommend utilizing the derived model under warm conditions, for example, when the air temperature exceeds zero, to account for the prerequisite of a well-mixed boundary layer. In extremely cold regions or seasons, the water surface temperature can be lower than the air temperature, resulting in a downward sensible heat flux (De Bruin, 1982). Under such circumstances, the boundary layers exhibit relative stability and may not reach a well-mixed state. Additionally, we advise adopting a temporal scale ranging from weekly to monthly when applying the derived model. This is because the potential VPD budget (the governing equation) may not be rapidly achieved, such as on a diurnal or daily basis. Furthermore, over a longer term, the sensible heat flux typically manifests as upward in the majority of scenarios compared to a fine temporal scale.
The derived formula for α has important practical meanings. For example, it would be useful for estimating water surface evaporation and actual evapotranspiration based on the PT model (Miralles et al., 2011; Maes et al., 2019). It can also help to constrain the relationships among α, T, and Q in the complementary relationship, whose performance previously depended on the inversed α (Liu et al., 2016). Besides, considering the impacts of changing climate on α can significantly improve the performance of the hydrologic model in runoff simulations and predictions (Pimentel et al., 2023).
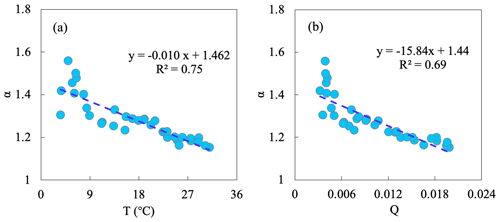
Figure A1Relationships of α with (a) temperature (T) and with (b) specific humidity (Q) on the 10 d scale using water surface observations collected over Lake Taihu.
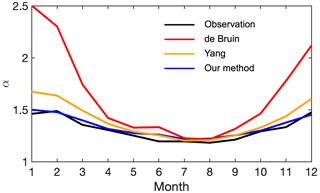
Figure A2Observed (black) and estimated α over Lake Taihu. The blue line is α estimated with our method, and the red and orange lines are with two revised PT equations. The red line represents (De Bruin and Holtslag, 1982), and the orange line represents (Yang and Roderick, 2019).
Data of Lake Taihu can be obtained from the Harvard Dataverse, https://doi.org/10.7910/DVN/HEWCWM (Zhang et al., 2020). The data of Poyang Lake can be obtained from Zhao and Liu (2018) (https://doi.org/10.6084/m9.figshare.5208595) and Gan and Liu (2020) (https://figshare.com/articles/figure/Heat_storage_data/13011917, last access: 27 September 2020). The data of Erhai can be obtained from Du et al. (2018). The data of Guandu can be obtained from Zhao et al. (2019). The data of Suwa Lake can be obtained from the AsiaFlux (http://asiaflux.net/index.php?page_id=1355, AsiaFlux, 2020). FluxNet 2015 data are available at https://fluxnet.fluxdata.org/data/download-data/ (last access: 1 September 2023). CMIP6 data can be obtained from the Earth System Grid Federation (https://esgf-node.llnl.gov, ESGF, 2022).
Conceptualization: ZL, HY. Data curation: ZL. Formal analysis: ZL. Funding acquisition: HY. Methodology: ZL, HY. Software: ZL. Supervision: HY. Writing – original draft: ZL. Writing – review and editing: CL, TW, HY.
The contact author has declared that none of the authors has any competing interests.
Publisher's note: Copernicus Publications remains neutral with regard to jurisdictional claims made in the text, published maps, institutional affiliations, or any other geographical representation in this paper. While Copernicus Publications makes every effort to include appropriate place names, the final responsibility lies with the authors.
This research has been supported by the National Natural Science Foundation of China (grant nos. 51979140 and 42041004).
This paper was edited by Bob Su and reviewed by two anonymous referees.
Andreas, E. L. and Cash, B. A.: A new formulation for the Bowen ratio over saturated surfaces, J. Appl. Meteorol., 35, 1279–1289, https://doi.org/10.1175/1520-0450(1996)035<1279:anfftb>2.0.co;2, 1996.
AsiaFlux: SWL:Suwa Lake Site, AsiaFlux [data set], http://asiaflux.net/index.php?page_id=1355, 2020.
Assouline, S., Li, D., Tyler, S., Tanny, J., Cohen, S., Bou-Zeid, E., Parlange, M., and Katul, G. G.: On the variability of the Priestley-Taylor coefficient over water bodies, Water Resour. Res., 52, 150–163, https://doi.org/10.1002/2015wr017504, 2016.
Bowen, I. S.: The ratio of heat losses by conduction and by evaporation from any water surface, Phys. Rev., 27, 779–787, https://doi.org/10.1103/PhysRev.27.779, 1926.
Brutsaert, W. and Stricker, H.: An advection-aridity approach to estimate actual regional evapotranspiration, Water Resour. Res., 15, 443–450, 1979.
Crago, R. D., Szilagyi, J., and Qualls, R. J.: What is the Priestley–Taylor wet-surface evaporation parameter? Testing four hypotheses, Hydrol. Earth Syst. Sci., 27, 3205–3220, https://doi.org/10.5194/hess-27-3205-2023, 2023.
De Bruin, H. and Holtslag, A.: A simple parameterization of the surface fluxes of sensible and latent heat during daytime compared with the Penman-Monteith concept, J. Appl. Meteorol. Clim., 21, 1610–1621, 1982.
De Bruin, H. A. R.: Temperature and energy balance of a water reservoir determined from standard weather data of a land station, J. Hydrol., 59, 261–274, https://doi.org/10.1016/0022-1694(82)90091-9, 1982.
De Bruin, H. A. R. and Keijman, J. Q.: Priestley-taylor evaporation model applied to a large, shallow lake in the netherlands, J. Appl. Meteorol., 18, 898–903, https://doi.org/10.1175/1520-0450(1979)018<0898:tptema>2.0.co;2, 1979.
Du, Q., Liu, H. Z., Liu, Y., Wang, L., Xu, L. J., Sun, J. H., and Xu, A. L.: Factors controlling evaporation and the CO2 flux over an open water lake in southwest of China on multiple temporal scales, Int. J. Climatol., 38, 4723–4739, https://doi.org/10.1002/joc.5692, 2018.
Eichinger, W. E., Parlange, M. B., and Stricker, H.: On the concept of equilibrium evaporation and the value of the Priestley-Taylor coefficient, Water Resour. Res., 32, 161–164, 1996.
ESGF: CMIP6 GCM data, ESGF [data set], https://esgf-node.llnl.gov, 2022.
Gan, G. and Liu, Y.: Heat Storage Effect on Evaporation Estimates of China's Largest Freshwater Lake, J. Geophys. Res.-Atmos. 125, e2019JD032334, https://doi.org/10.1029/2019JD032334, 2020 (data available at: https://figshare.com/articles/figure/Heat_storage_data/13011917).
Greve, P., Roderick, M. L., Ukkola, A. M., and Wada, Y.: The aridity Index under global warming, Environ. Res. Lett., 14, 124006, https://doi.org/10.1088/1748-9326/ab5046, 2019.
Guo, X., Liu, H., and Yang, K.: On the application of the Priestley–Taylor relation on sub-daily time scales, Bound.-Lay. Meteorol., 156, 489–499, 2015.
Han, S. and Guo, F.: Evaporation From Six Water Bodies of Various Sizes in East Asia: An Analysis on Size Dependency, Water Resour. Res., 59, e2022WR032650, https://doi.org/10.1029/2022wr032650, 2023.
Hicks, B. B. and Hess, G. D.: On the Bowen Ratio and Surface Temperature at Sea, J. Phys. Oceanogr., 7, 141–145, https://doi.org/10.1175/1520-0485(1977)007<0141:otbras>2.0.co;2, 1977.
Jury, W. and Tanner, C.: Advection Modification of the Priestley and Taylor Evapotranspiration Formula 1, Agron. J., 67, 840–842, 1975.
Lee, X., Liu, S., Xiao, W., Wang, W., Gao, Z., Cao, C., Hu, C., Hu, Z., Shen, S., Wang, Y., Wen, X., Xiao, Q., Xu, J., Yang, J., and Zhang, M.: THE TAIHU EDDY FLUX NETWORK An Observational Program on Energy, Water, and Greenhouse Gas Fluxes of a Large Freshwater Lake, B. Am. Meteorol. Soc., 95, 1583–1594, https://doi.org/10.1175/bams-d-13-00136.1, 2014.
Lhomme, J. P.: An examination of the Priestley-Taylor equation using a convective boundary layer model, Water Resour. Res., 33, 2571–2578, 1997a.
Lhomme, J. P.: A theoretical basis for the Priestley-Taylor coefficient, Bound.-Lay. Meteorol., 82, 179–191, 1997b.
Liu, X., Liu, C., and Brutsaert, W.: Regional evaporation estimates in the eastern monsoon region of China: Assessment of a nonlinear formulation of the complementary principle, Water Resour. Res., 52, 9511–9521, https://doi.org/10.1002/2016WR019340, 2016.
Liu, Z. and Yang, H.: Estimation of Water Surface Energy Partitioning With a Conceptual Atmospheric Boundary Layer Model, Geophys. Res. Lett., 48, e2021GL092643, https://doi.org/10.1029/2021GL092643, 2021.
Liu, Z., Han, J., and Yang, H.: Assessing the ability of potential evaporation models to capture the sensitivity to temperature, Agr. Forest Meteorol., 317, 108886, https://doi.org/10.1016/j.agrformet.2022.108886, 2022.
Maes, W. H., Gentine, P., Verhoest, N. E. C., and Miralles, D. G.: Potential evaporation at eddy-covariance sites across the globe, Hydrol. Earth Syst. Sci., 23, 925–948, https://doi.org/10.5194/hess-23-925-2019, 2019.
McColl, K. A.: Practical and theoretical benefits of an alternative to the Penman‐Monteith evapotranspiration equation, Water Resour. Res., 56, e2020WR027106, https://doi.org/10.1029/2020WR027106, 2020.
McColl, K. A. and Tang, L. I.: An analytic theory of near-surface relative humidity over land, J. Climate, 37, 1213–1230, https://doi.org/10.1175/JCLI-D-23-0342.1, 2023.
McNaughton, K. and Spriggs, T.: A Mixed-Layer Model for Regional Evaporation, Bound.-Lay. Meteorol., 34, 243–262, https://doi.org/10.1007/bf00122381, 1986.
Miralles, D. G., Holmes, T. R. H., De Jeu, R. A. M., Gash, J. H., Meesters, A. G. C. A., and Dolman, A. J.: Global land-surface evaporation estimated from satellite-based observations, Hydrol. Earth Syst. Sci., 15, 453–469, https://doi.org/10.5194/hess-15-453-2011, 2011.
Penman, H. L.: Natural evaporation from open water, bare soil and grass, P. Roy. Soc. Lond. A Mat., 193, 120–145, https://doi.org/10.1098/rspa.1948.0037, 1948.
Pimentel, R., Arheimer, B., Crochemore, L., Andersson, J. C. M., Pechlivanidis, I. G., and Gustafsson, D.: Which Potential Evapotranspiration Formula to Use in Hydrological Modeling World-Wide?, Water Resour. Res., 59, e2022WR033447, https://doi.org/10.1029/2022WR033447, 2023.
Priestley, C. H. B. and Taylor, R. J.: Assessment of surface heat-flux and evaporation using large-scale parameters, Mon. Weather Rev., 100, 81–92, https://doi.org/10.1175/1520-0493(1972)100<0081:otaosh>2.3.co;2, 1972.
Raupach, M. R.: Equilibrium evaporation and the convective boundary layer, Bound.-Lay. Meteorol., 96, 107–141, https://doi.org/10.1023/a:1002675729075, 2000.
Raupach, M. R.: Combination theory and equilibrium evaporation, Q. J. Roy. Meteor. Soc., 127, 1149–1181, https://doi.org/10.1002/qj.49712757402, 2001.
Roderick, M. L., Sun, F., Lim, W. H., and Farquhar, G. D.: A general framework for understanding the response of the water cycle to global warming over land and ocean, Hydrol. Earth Syst. Sci., 18, 1575–1589, https://doi.org/10.5194/hess-18-1575-2014, 2014.
Shuttleworth, W. J.: Evaporation, in: Handbook of hydrology, edited by: Maidment, D. R., Inc. New York, ISBN 0070397325, 1993.
Slatyer, R. O. and McIlroy, I. C.: Practical microclimatology: with special reference to the water factor in soil-plant-atmosphere relationships, Commonwealth Scientific and Industrial Research Organisation, Melbourne: CSIRO, 1961.
Su, Q. and Singh, V. P.: Calibration-Free Priestley-Taylor Method for Reference Evapotranspiration Estimation, 59, e2022WR033198, https://doi.org/10.1029/2022WR033198, 2023.
Taoka, T., Iwata, H., Hirata, R., Takahashi, Y., Miyabara, Y., and Itoh, M.: Environmental Controls of Diffusive and Ebullitive Methane Emissions at a Subdaily Time Scale in the Littoral Zone of a Midlatitude Shallow Lake, J. Geophys. Res.-Biogeo., 125, e2020JG005753, https://doi.org/10.1029/2020jg005753, 2020.
Thornthwaite, C. W. and Holzman, B.: Evaporation from land and water surfaces, Mon. Weather Rev., 67, 4–11, https://doi.org/10.1175/1520-0493(1939)67<4:tdoefl>2.0.co;2, 1939.
van Heerwaarden, C. C., de Arellano, J. V. G., Moene, A. F., and Holtslag, A. A. M.: Interactions between dry-air entrainment, surface evaporation and convective boundary-layer development, Q. J. Roy. Meteor. Soc., 135, 1277–1291, https://doi.org/10.1002/qj.431, 2009.
Xiao, W., Zhang, Z., Wang, W., Zhang, M., Liu, Q., Hu, Y., Huang, W., Liu, S., and Lee, X.: Radiation Controls the Interannual Variability of Evaporation of a Subtropical Lake, J. Geophys. Res.-Atmos., 125, e2019JD031264, https://doi.org/10.1029/2019jd031264, 2020.
Yang, Y. and Roderick, M. L.: Radiation, surface temperature and evaporation over wet surfaces, Q. J. Roy. Meteor. Soc., 145, 1118–1129, https://doi.org/10.1002/qj.3481, 2019.
Zhang, Z., Zhang, M., Cao, C., Wang, W., Xiao, W., Xie, C., Chu, H., Wang, J., Zhao, J., Jia, L., Liu, Q., Huang, W., Zhang, W., Lu, Y., Xie, Y., Wang, Y., Pu, Y., Hu, Y., Chen, Z., Qin, Z., and Lee, X.: A dataset of microclimate and radiation and energy fluxes from the Lake Taihu Eddy Flux Network, V2, Harvard Dataverse [data set], https://doi.org/10.7910/DVN/HEWCWM, 2020.
Zhao, J., Zhang, M., Xiao, W., Wang, W., Zhang, Z., Yu, Z., Xiao, Q., Cao, Z., Xu, J., Zhang, X., Liu, S., and Lee, X.: An evaluation of the flux-gradient and the eddy covariance method to measure CH4, CO2, and H2O fluxes from small ponds, Agr. Forest Meteorol., 275, 255–264, https://doi.org/10.1016/j.agrformet.2019.05.032, 2019.
Zhao, X. and Liu, Y.: Variability of Surface Heat Fluxes and Its Driving Forces at Different Time Scales Over a Large Ephemeral Lake in China, J. Geophys. Res.-Atmos., 123, 4939–4957, https://doi.org/10.1029/2017jd027437, 2018 (data available at: https://doi.org/10.6084/m9.figshare.5208595).