the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Changes in mean evapotranspiration dominate groundwater recharge in semi-arid regions
Tuvia Turkeltaub
Golan Bel
Groundwater is one of the most essential natural resources and is affected by climate variability. However, our understanding of the effects of climate on groundwater recharge (R), particularly in dry regions, is limited. Future climate projections suggest changes in many statistical characteristics of the potential evapotranspiration (Ep) and the rainfall that dictate the R. To better understand the relationship between climate statistics and R, we separately considered changes to the mean, standard deviation, and extreme statistics of the Ep and the precipitation (P). We simulated the R under different climate conditions in multiple semi-arid and arid locations worldwide. Obviously, lower precipitation is expected to result in lower groundwater recharge and vice versa. However, the relationship between R and P is non-linear. Examining the ratio is useful for revealing the underlying relation between R and P; therefore, we focus on this ratio. We find that changes in the average Ep have the most significant impact on . Interestingly, we find that changes in the extreme Ep statistics have much weaker effects on than changes in extreme P statistics. Contradictory results of previous studies and predictions of future groundwater recharge may be explained by the differences in the projected climate statistics.
- Article
(2117 KB) - Full-text XML
-
Supplement
(2002 KB) - BibTeX
- EndNote
Groundwater sustainability depends on balancing groundwater recharge (R) and groundwater abstraction (Hartmann et al., 2017; Wada et al., 2010; Collenteur et al., 2021; Singh et al., 2019; De Filippi and Sappa, 2024; Viaroli et al., 2018; Andualem et al., 2021). R is the amount of water infiltrating the soil deep enough such that it is not lost to evaporation, transpiration, or runoff. Note that this definition is not the same as the definition of some authors, who define it as the amount of water replenishing the aquifer (Healy and Scanlon, 2010) (the main difference is the travel time). Many areas across the globe show a growing dependence on groundwater resources, which will only increase in the future (Bierkens and Wada, 2019; Taylor et al., 2013a, b). Climate variability affects both the precipitation and the evapotranspiration statistics. Therefore, understanding the potential effects of these factors on R is of great importance. In order to improve groundwater resource management and reduce negative human effects (Taylor et al., 2013a; Vivek et al., 2024; Pino-Vargas et al., 2023; Sappa et al., 2019; Quandt et al., 2023), the direct influences of climate variability on R must be quantified.
In recent years, much effort has been devoted to the analysis of the sensitivity of groundwater systems to climate change (Meixner et al., 2016; Pulido-Velazquez et al., 2015; Touhami et al., 2015; Fu et al., 2019; Döll and Fiedler, 2008; Tillman et al., 2016; Reinecke et al., 2021; Huang et al., 2023; Berghuijs, 2024; Berghuijs et al., 2024; Lorenzi et al., 2024; Langman et al., 2022). However, no conclusive generic outcomes can be drawn regarding the relationship between changes in climate conditions and the resulting changes in R rates (Al Atawneh et al., 2021; Green et al., 2011). The main source of uncertainties in future R are the uncertainties in climate predictions. It is unclear whether the climate variability is amplified or smoothed in the R response (Taylor et al., 2013a; Field et al., 2012; Reinecke et al., 2021; Moeck et al., 2016). Moreover, even the trend of the R response is uncertain (Smerdon, 2017).
Climate variability may also change the seasonal distribution of the precipitation (P) (Allan and Soden, 2008; Field et al., 2012). Increasing temperatures are expected to increase evapotranspiration (Ea) (Condon et al., 2020), while the increased CO2 concentrations are expected to lower the Ea (Cao et al., 2010), and the overall effect is uncertain (Barnett et al., 2008). The future R uncertainties are even more dominant in arid and semi-arid regions, where the variability of the Ea affects the threshold values for R (Cuthbert et al., 2019b). Different studies have reached contradictory conclusions regarding the effects of climate change on R in arid and semi-arid regions (Crosbie et al., 2013). Some studies found that the changes in R are greater than the changes in climate conditions (Ng et al., 2010; McKenna and Sala, 2018), while others found a weak sensitivity of semi-arid regions to climate variability (Döll and Fiedler, 2008; Cuthbert et al., 2019a). Under future climate conditions, the precipitation and potential ET (Ep) statistics and, particularly, the frequency of extreme events (Myhre et al., 2019) may change. The effects of these extreme events may lead to an increase (Taylor et al., 2013b, a; Cuthbert et al., 2019b; Shamsudduha and Taylor, 2020; Goni et al., 2021) or a decrease (Cuthbert et al., 2019b) in R.
Previous studies investigated the R response to predicted future climate conditions using global climate models (GCMs) (Crosbie et al., 2013; Tillman et al., 2016) or regional GCM (Pulido-Velazquez et al., 2015) predictions. Pulido-Velazquez et al. (2015) also considered modifications of the mean and standard deviation (SD) of the P in the regional GCM predictions. However, these studies could not provide a conclusive understanding of the effects; in particular, changes in the Ep statistics were not directly considered.
The main objective of this study is to explore the changes in diffuse (rather than focused, agricultural, or mountain; see Meixner et al., 2016) R in semi-arid and arid regions due to changes in P and Ep statistics. In areas where R occurs predominantly through focused processes, additional factors dominate the overall recharge and are beyond the scope of this study. Here, R is defined as the accumulated water flux at a 5 m depth, assuming that this flux reaches the water table. To enhance our understanding of the R response to climate variability, we separately consider the changes in the (1) mean, (2) SD, and (3) extreme events of Ep and P statistics (relative to the measured statistics) in multiple locations across the globe. While we do not consider specific future climate projections, we identify and quantify the effects of changes in climate variable statistics on R in semi-arid and arid regions.
Groundwater recharge is a fraction of precipitation. Within the linear response regime, changes in precipitation would lead to a change in the recharge but not a change in the ratio between the groundwater recharge and the precipitation. To emphasize the non-linear response, we present the ratio between the recharge and the precipitation and the changes in these ratios. We use a numerical model to simulate the R under atmospheric boundary conditions. In what follows, we provide the details of the model, the independent data used for verification of the model, and the changes applied to the climate variable statistics.
2.1 Groundwater recharge data and modeling
To explore the impact of climate statistics on R, we identified 196 semi-arid and arid locations (see the Supplement) in which R was estimated using ground-based methods such as chloride mass balance, water isotopes, etc. (Taylor et al., 2013b; Scanlon et al., 2006; Moeck et al., 2020). These locations span both hemispheres and different continents (see Fig. 1a). Furthermore, they cover a wide range of soil types (Fig. 1b) and climate conditions, including various seasonal P distributions relative to temperature and other factors affecting evapotranspiration. The locations are characterized by bare soil or sparse vegetation, where transpiration is negligible relative to the evaporation. For locations where the model did not perform well, factors such as land use change may explain the discrepancies between simulated and reported R. In some locations, over the last decades, R may have changed substantially due to various human modifications of landscapes, such as changes in land use and land cover, as well as water conservation works (Turkeltaub et al., 2018; Favreau et al., 2009; Allison et al., 1990). Since the R fluxes estimated by the ground-based methods represent an integration over varying timescales, they are likely to reflect different stages of this evolution.
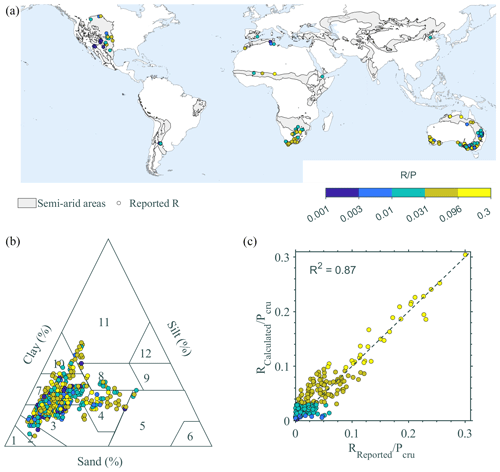
Figure 1(a) The geographic distribution of the locations considered. (b) The soil composition, in terms of sand, silt, and clay, for all the locations considered in this study. The data are based on Hengl et al. (2014) and represent the reported soil characteristics for 0–5, 5–15, and 15–30 cm depths. (c) The simulated and reported ratio between the precipitation and the groundwater recharge for all the locations (in addition to the R2 provided in the plot, other statistical indices for model performance evaluation are also provided: ; mean absolute error=0.016; root mean square error=0.02).
Diffuse R fluxes were simulated using unsaturated flow modeling for these locations by numerically solving the 1D vertical Richards equation:
where ψ is the matric potential head (L), θ is the volumetric water content (dimensionless), t is time (T), z is the vertical coordinate (L), and K(ψ) (L T−1) is the unsaturated hydraulic conductivity function. The Richards equation was numerically integrated using the Hydrus 1D (Šimŭnek et al., 2009). Knowledge regarding the soil hydraulic functions is essential in order to solve the Richards equation. The soil retention curves and the unsaturated hydraulic curves are commonly described according to the van Genuchten–Mualem (VGM) model (Mualem, 1976; Van Genuchten, 1980):
where Se is the degree of saturation (); θs and θr are the saturated and residual volumetric soil water contents, respectively; and α (L−1), n, and are shape parameters. Hydraulic conductivity is assumed to behave according to the following:
where Ks (L T−1) is the saturated hydraulic conductivity, and l is the pore connectivity parameter prescribed as 0.5.
Assuming that the unsaturated zone mainly consists of siliciclastic materials, the VGM parameters were determined using the pedo-transfer function ROSETTA (Zhang and Schaap, 2017), which uses a neural network to estimate the soil hydraulic parameters from soil attributes, such as soil texture and bulk density. Sand, silt, and clay contents and the bulk density were extracted at the considered locations from global soil maps reported by Hengl et al. (2014). Note that the data are divided into seven layers, but for the current study, only information from the top three layers was used (0–5, 5–15, and 15–30 cm; the VGM parameters are provided in the Supplement). We assume that evaporation is mostly limited to the topsoil (Or et al., 2013); therefore, we only considered the heterogeneity of these levels. Furthermore, the water table depths at the investigated locations, which were extracted from the global map presented by Fan et al. (2013), indicated that, in most locations, groundwater is below 0.8 m depth, and no phreatic evaporation is expected (see the Supplement; Chengcheng et al., 2020; Hellwig, 1973).
The water flow simulations were carried out using atmospheric-boundary conditions with surface runoff. Daily precipitation and Ep (potential ET) values were specified at the upper boundary. The minimum allowed pressure head at the soil surface was constant (hCritA=100 000 cm). Lower-boundary conditions were prescribed as free drainage, where the water flux across this boundary is considered to be the R. The depth of the simulated soil column was 500 cm, and it was discretized into 101 grid cells. A finer node spacing was implemented at the upper boundary, where the top node was 3 times thinner than the bottom node. Water content at field capacity was prescribed as the initial condition at the start of each simulation. Each simulation was run for 146 100 d, and the calculated daily R fluxes between days 73 050 and 146 100 were used for the analyses to avoid the influence of the initial conditions. In all the locations considered, the differences between the estimated and the reported ratios were below 5 %, illustrating the suitability of the model.
2.2 Climate data and generation of P and Ep time series
The CRU TS 3.2 climate dataset (Harris et al., 2014), including daily values of precipitation and potential evapotranspiration (Ep), was used for the analyses presented in the current study. The datasets were temporally downscaled, following van Beek (2008), to daily values using ERA40 (1958–1978, Uppala et al., 2005) and ERA-Interim (1979–2015, Dee et al., 2011). The daily Ep values were calculated according to the Penman–Monteith method using climate variables such as mean, maximum, and minimum temperatures; vapor pressure; cloud cover; and wind speed (Harris et al., 2014). Stochastic P and Ep time series spanning 400 years (146 100 d) were synthesized based on these 58 year-long CRU TS 3.2 records of daily precipitation and potential evapotranspiration (Ep). P time series were established based on the empirical histograms of the number of rainy days and the daily P amount distributions (see the Supplement; Turkeltaub and Bel, 2023). The Ep time series were established by random sampling of Ep empirical distributions for each calendar month separately (Turkeltaub and Bel, 2023). Furthermore, it was shown by the authors (Turkeltaub and Bel, 2023) that the best synthesis method involves a correction of the synthesized climate to match the observed monthly statistics. Thus, the P and Ep time series were corrected accordingly (see the examples in Figs. S1 and S2 in the Supplement for the effects of the correction on the monthly P and Ep statistics).
2.3 Modification of the mean (μ) and the standard deviation (SD, σ)
To examine the effects of changes in the statistics of the P and the Ep time series on groundwater recharge (R), the yearly mean, μ, and SD, σ, of these series were modified. Note that, when we modify the average of a time series, the SD is conserved and vice versa. The modification of μ is simply conducted by adding to each value (in the P series, only to non-zero values) in the original time series the difference between the original and modified yearly average divided by the number of relevant days in that year. Note that this correction could possibly have resulted in negative daily P and Ep amounts when considering a reduction in the yearly averages. Therefore, for the Ep, only days with amounts above the correction were modified in order to ensure non-negative values of Ep for all days. For the P series, we further wanted to conserve the statistics of the number of rainy days. Therefore, the maximal allowed reduction in P sets the value to 1 mm d−1 (Turkeltaub and Bel, 2023). The modification of the SD is done in two stages. Firstly, each value in the original time series is multiplied by the ratio between the original SD, σorg, of the total yearly P or the Ep and the modified SD, σmf. Subsequently, the differences between the averages of the original and the modified time series are corrected according to the procedure described above to preserve the original mean. Mathematically, the correction method for the annual μ of a time series is described as follows:
where MTSμ and OTS are the modified mean and the original time series, respectively. Δ is the difference between the modified and the original annual P or Ep averages (, and 〈.〉a is the annual average of the variable represented in the time series). Na(t) is the number of days in the year of time t with P or Ep values larger than the threshold. The threshold is defined as for the Ep and as for the P. Na(t) is found recursively.
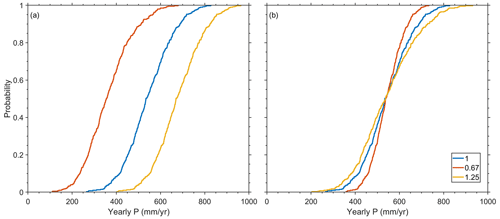
Figure 2An example for the modification of the (a) mean, μ, and (b) the SD, σ, of a P time series for a specific location where a groundwater recharge flux was reported (145.711, −36.4469; Crosbie et al., 2010). The different colors correspond to the indicated modification factors.
To modify the σ of a time series, the following transformation is applied:
where σm and σo are the modified and original yearly standard deviation of the time series, respectively. . The threshold is defined similarly to the definition above for the mean modification. Figure 2 depicts an example of the modification of the average, μ, and SD, σ, of the yearly P for a specific location (145.711, −36.4469; Crosbie et al., 2010).
2.4 Modification of extreme-event statistics
In order to increase the frequency of extreme events, the time series were modified such that the mean was conserved, and events above a specified quantile (0.98, 0.95, or 0.9) were doubled (Myhre et al., 2019; Fischer and Knutti, 2016). The doubling was done by randomly selecting events with values below the specified quantile and replacing their original value with a value from those above the quantile. We established two separate scenarios. The first doubles the frequency of the extreme events without preserving the seasonal cycle. Namely, an extreme event may be introduced into any day in the original series regardless of the season. In the second scenario, we preserve the seasonal cycle and double the extreme events for each calendar month separately. In the latter case, the added extreme events correspond to observed events in the same calendar month. For both scenarios, in order to preserve the annual mean, we used a procedure similar to the one outlined above for the annual mean modification (see Eq. 4).
For the P time series, this was done without modifying the statistics of the number of rainy days; namely, only rainy days in the original time series could be randomly selected to receive one of the doubled extreme values. For the Ep time series, there was no additional constraint.
3.1 Effects of changes in the mean
The first change we considered is a simple change in the mean (μ) of climatic variables (P and Ep). Changes to the average Ep affect the ratio in all the locations (see Fig. 3). A larger mean Ep () reduces the ratio, while a smaller mean Ep () increases the ratio. The result is expected because the larger the Ea is (i.e., the estimated amount of water evaporated, determined by the numerical model; Ep≥Ea), the smaller the ratio is (in this case, the P amount does not change). However, the change in the ratio is not the same for all locations, and, obviously, it depends on the amount of water available for the actual Ea and the amount of P. It also suggests a non-linear relation between the R and P rates. Histograms of the distributions of the change in the ratio (the subscripts 0 and m correspond to the original and the modified Ep statistics, respectively) in the different locations are depicted in Fig. 4a–d. Some changes in the ratio are expressed by an increase or decrease of up to 20 % in the fraction of rainfall that becomes R (Fig. 4a–d). Note that the largest change in ratio occurs for a reduction of 0.67 in the mean annual Ep (Fig. 4a).
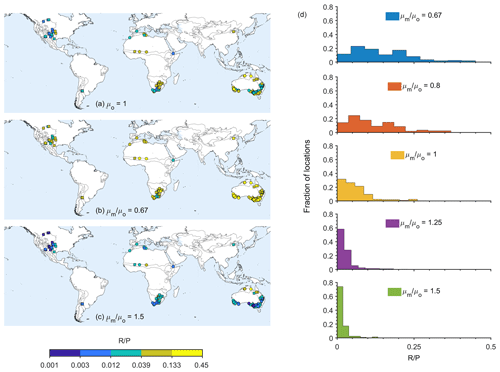
Figure 3The effect of Ep yearly mean (μ) modification on the ratio. The left panels (a–c) depict the modified ratio in different locations for the mean annual Ep that is measured (a), reduced by a factor of (b), and increased by a factor of 1.5 (c). The right panels (d) depict the histograms of the fraction of locations with different ratios under different mean Ep modifications. The ratios between the modified annual mean Ep (μm) and the original one (μ0) are denoted in the figure.
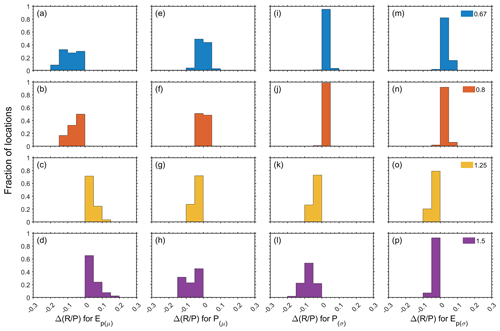
Figure 4The panels depict the histograms of the change in the ratio (; the subscripts o and m correspond to the original and the modified statistics, respectively) for changes in the (a–d) Ep yearly mean, (e–h) P yearly mean, (i–l) P yearly SD, and (m–p) Ep yearly SD. The colors indicate the modification factors, which are the ratios between the modified annual mean (μm) or the SD (σm) and the original annual mean (μo) or SD (σo).
Similarly, we considered changes in the mean P (Fig. S3). The annual distribution of the P is not modified, and only the amounts are increased or reduced by the desired multiplicative factor (see the Methods section for details; see also Fig. 2). In Fig. S3, the ratios of in relation to different changes to the mean P are shown. In general, reducing the P results in a higher fraction of locations with a smaller ratio, while increasing the mean P results in a higher fraction of locations with larger ratios. The histograms of the fraction of locations with different changes in the ratio (Fig. 4e–h) reveal a more interesting response. Lowering the mean P results in a mixed response. The ratio decreases in some locations, while it increases in others. In most locations with summer P (92 %, 73 of the considered locations), decreasing the mean annual P results in an increase in the ratio (Fig. 4e and f). The R in these locations is mostly a result of large P events, and the decrease in the mean P hardly affects the fraction of R during these events.
3.2 Effects of changes in the SD
The second change in the statistics of the climate variables that we considered is a change in the SD of the variables while keeping the mean unchanged (see Fig. 2). This is equivalent to uniformly broadening the distribution of the Ep or the P (see the Methods section for details; Fig. 2). We find that increasing the SD of the Ep (Fig. S4) or the P (Fig. S5) results in increasing the ratio in almost all the locations. This is also reflected by the change in the ratio, where most estimated ratios are larger than the original ratios, as indicated by the negative differences (Fig. 4k, l, o, and p).
Reducing the Ep (Fig. S4) or the P (Fig. S5) SD reduces the ratio in most locations. This is illustrated by the positive values of the differences (Fig. 4i, j, m, and n). Overall, the reduction in the SD of the Ep or the P has the smallest effect on the ratio.
3.3 Effects of changes in the frequency of extreme events
Under some future climate predictions, the frequency of extreme events is expected to double (Myhre et al., 2019). Therefore, modifications of the extreme statistics as outlined in Sect. 2.4 were considered. In Fig. 5, the histograms of the fraction of locations with specific ratios are depicted for the doubling of P (panels (a) and (c)) and Ep (panels (b) and (d)) extreme events above the 90 %, 95 %, and 98 % quantiles. For reference, the panels also depict the histogram based on the measured climate conditions. It is apparent in panel (a) that doubling the extreme P events results in more locations with higher ratios. Note that, with this change, the total P is not modified; therefore, the increase in the ratio implies an increase in the actual R. The results are similar in panel (c), where the extreme events of each calendar month were doubled. In Fig. S6, the differences in are presented, showing that, for all the locations considered, increasing the frequency of extreme events increases the R despite the fact that the total P is unchanged. Panel (b) shows that doubling the extreme Ep has a much smaller effect on the R. Preserving the seasonality while doubling the extreme Ep events results in a somewhat stronger effect and more locations with higher R, as shown in panel (d) and Fig. S6. In panels (b) and (d) of Fig. S6, it is shown that, in most locations, doubling the extreme Ep results in larger R, while, in a small fraction of the locations, it reduces the R. Note that these results differ from those of increasing the Ep SD, in which all locations showed an increase in the R.
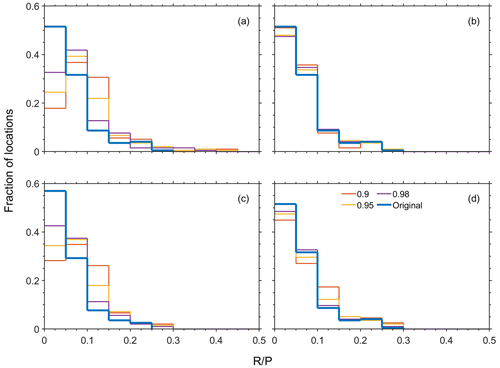
Figure 5The fraction of locations with the specified ratios due to an increase in the occurrence of annual extreme (a) daily P or (b) daily Ep. The ratios due to an increase in the occurrence of extreme P or Ep events for each calendar month separately are depicted in panels (c) and (d), respectively. See the Methods section for a detailed explanation of the changes to the extreme-event statistics. The values of 0.98, 0.95, or 0.9 represent specified quantiles, where all events above the corresponding values were doubled to establish extreme climate scenarios. The blue line (“original”) corresponds to scenarios with no changes in the extreme statistics.
Understanding the response of R to varying climate conditions involves a broad range of possible changes to the statistics of the climate variables and renders the task overly complicated. Here, we investigated the effects of various aspects of the climate statistics on groundwater recharge in semi-arid and arid locations. We used the Richards equation (with the VGM hydraulic functions) to simulate the groundwater recharge under varying climate conditions. The use of the Richard equation assumes that groundwater recharge is dominated by diffuse recharge. In regions with significant topography and rocky terrains, considerable runoff is expected (Casenave and Valentin, 1992; Mounirou et al., 2021). Furthermore, in regions where focused recharge and preferential flow paths prevail (van chaik et al., 2008), using the Richards equation might not accurately capture the dynamics of groundwater recharge (Mirus and Nimmo, 2013; Hartmann et al., 2015, 2017; Appels et al., 2015). Therefore, we limit our analysis to regions where independent estimation of R agreed with our simulated R, suggesting that our method is adequate for these locations. In addition, as expected from the agreement, we found that runoff was not dominant in our simulations.
In our analyses above, we attempted to deal with this complexity by separately considering different changes in climate statistics. Reducing the mean P resulted in mixed outcomes. Some locations illustrated a decrease in the ratio, while, in others, it increased. The increase in the ratio mostly occurred in locations with summer P. Two main explanations are suggested for this counterintuitive change. The first reason is related to the P characteristics in regions with heavy P events that promote deep drainage and R. The decrease in the mean P hardly affects the fraction of R during these events. Therefore, the ratio is increased because the R only decreases slightly, while the P substantially decreases. An additional explanation is associated with reducing the amount of water available for evaporation. The reduction in the amount of P results in longer periods over which the Ea is smaller than the Ep, thereby increasing the fraction of P going to the R (on most days, the Ea is either equal to the Ep when there is a continuum of water reaching the topsoil, and it is close to zero when there is not). Only 25 % of the locations with winter P showed the same behavior – most likely because the Ep during the rainy season is relatively low in these locations, and the effect of the second process mentioned above is weaker. When the mean annual P increases, all locations show a larger ratio (see Figs. 4e–h and S5).
We find that the ratio shows higher sensitivity to changes in the mean Ep than to changes in the mean annual P. The P is equal to the sum of the R and Ea under the assumption that, in a steady state, the change in the total soil water storage is negligible and the assumption that the runoff is negligible (this was verified for the locations considered in this study). Mathematically, we express it as follows:
and, therefore,
If one assumes that the evapotranspiration is a function of the ratio (Budyko, 1974), the changes in are expected to be the same regardless of whether the change in Ea is due to changes in Ep or changes in P. However, if Ea depends not only on but also on the actual water content of the top soil layer (Gerrits et al., 2009), one can expect different sensitivity to changes in Ep or changes in P, as we observed.
The response to changes in the P SD is easily understood considering the fact that most of the R is triggered by large P events. The increase in the ratio due to an increase in the Ep SD can be attributed to the fact that, in some years, the Ep becomes small enough to allow significant R, while during the years with higher Ep, the reduction in R is much smaller because there is not always water available for Ea; i.e., larger values of Ep do not affect the Ea because it has already reached an upper limit. Ultimately, we found that changes in the statistics of extreme rainfall events have a much greater effect on R than in extreme Ep events.
Understanding the combined effects of all the changes in climate variables on groundwater recharge is an ongoing effort and is expected to play a critical role in future studies. Many factors affect groundwater recharge, making it a complicated process to quantify. Some of these processes are hard to predict, and others are related to human activity affecting, directly (such as urbanization) and indirectly (such as deforestation), the fraction of precipitation infiltrating deep soil levels. Anthropogenic factors, such as land use changes, are expected to strongly affect groundwater recharge. Those changes are expected to occur much faster than changes in climate statistics. In our study, we examined the effects of changes in climate statistics, i.e., non-anthropogenic, on groundwater recharge in arid and semi-arid regions.
We considered locations worldwide. The selected locations are characterized by bare soil or sparse vegetation to avoid the effect of water loss due to transpiration. Furthermore, the site selection process included comparisons of simulated and reported yearly groundwater recharge fluxes to verify that only sites for which the model represents the natural conditions are considered and that locations influenced by factors such as human disturbances are excluded. Despite the simplicity of the modeling approach, we found that, in many places, worldwide, the model provides good estimates of the fraction of precipitation infiltrating deep soil.
Our simulations show that changes in climate statistics may have various effects on groundwater recharge. In most locations, increasing the mean P results in higher ratios and vice versa, while increasing the mean Ep reduces the ratio and vice versa. Increasing the SD of both P and Ep results in a higher ratio. In most locations, doubling the frequency of extreme P or Ep events results in a higher ratio. However, the effect of more frequent P events is stronger than the effect of more frequent Ep events.
Previous studies suggested different trends and changes in future groundwater recharge. The differences between the projected climate statistics used in those studies may explain those seemingly contradictory assessments of future groundwater recharge fluxes. To enhance our understanding and better explain the predicted groundwater recharge changes, results should be augmented by an analysis of the projected changes in potential evapotranspiration and rainfall statistics. As demonstrated above, considering only changes in the mean and the SD is not enough, and changes in the statistics of extreme events are essential. This is attributed to the non-linear responses of groundwater recharge to changes in climate statistics. The conclusions drawn in this analysis are valid for locations where diffuse recharge dominates the overall recharge. In areas where groundwater recharge occurs predominantly through focused processes (e.g., preferential flow and recharge of runoff at specific locations on the landscape), future analyses should include additional factors at the sub-catchment scale, such as topographic attributes and spatiotemporal variability in precipitation. Separate studies are required to investigate the effects of climate change on groundwater recharge in humid regions or in agricultural fields, where the root uptake and the transpiration are significant.
The data and code used in this research are available at the following DOI: https://doi.org/10.4211/hs.5a28b74c55c74a7e9ad2b59a0a5d9ab3 (Turkeltaub, 2024).
The supplement related to this article is available online at: https://doi.org/10.5194/hess-28-4263-2024-supplement.
TT and GB designed the research, analyzed the data, and wrote the paper. TT performed the numerical simulations.
The contact author has declared that neither of the authors has any competing interests.
Publisher's note: Copernicus Publications remains neutral with regard to jurisdictional claims made in the text, published maps, institutional affiliations, or any other geographical representation in this paper. While Copernicus Publications makes every effort to include appropriate place names, the final responsibility lies with the authors.
Golan Bel acknowledges support from AdAgriF – Advanced methods of greenhouse gases emission reduction and sequestration in agriculture and forest landscape for climate change mitigation (grant no. CZ.02.01.01/00/22_008/0004635) and the Israel Science Foundation (ISF) under grant no. 547/23. Golan Bel thanks Ester Levi for being a lifelong inspiration.
This paper was edited by Thom Bogaard and reviewed by two anonymous referees.
Al Atawneh, D., Cartwright, N., and Bertone, E.: Climate change and its impact on the projected values of groundwater recharge: A review, J. Hydrol., 601, 126602, https://doi.org/10.1016/j.jhydrol.2021.126602, 2021. a
Allan, R. P. and Soden, B. J.: Atmospheric warming and the amplification of precipitation extremes, Science, 321, 1481–1484, https://doi.org/10.1126/science.1160787, 2008. a
Allison, G. B., Cook, P. G., Barnett, S. R., Walker, G. R., Jolly, I. D., and Hughes, M. W.: Land clearance and river salinisation in the western Murray Basin, Australia, J. Hydrol., 119, 1–20, 1990. a
Andualem, T. G., Demeke, G. G., Ahmed, I., Dar, M. A., and Yibeltal, M.: Groundwater recharge estimation using empirical methods from rainfall and streamflow records, Journal of Hydrology: Regional Studies, 37, 100917, https://doi.org/10.1016/j.ejrh.2021.100917, 2021. a
Appels, W. M., Graham, C. B., Freer, J. E., and McDonnell, J. J.: Factors affecting the spatial pattern of bedrock groundwater recharge at the hillslope scale, Hydrol. Process., 29, 4594–4610, 2015. a
Barnett, T., Pierce, D., Hidalgo, H., Bonfils, C., Santer, B., Das, T., Bala, G., Wood, A., Nozawa, T., Mirin, A., Cayan, D., and Dettinger, M.: Human-induced changes in the hydrology of western United States, Science, 319, 1080–1083, https://doi.org/10.1126/science.1152538, 2008. a
Berghuijs, W. R.: An amplified groundwater recharge response to climate change, Nat. Clim. Change, 14, 1758–6798, 2024. a
Berghuijs, W. R., Collenteur, R. A., Jasechko, S., Jaramillo, F., Luijendijk, E., Moeck, C., van der Velde, Y., and Allen, S. T.: Groundwater recharge is sensitive to changing long-term aridity, Nat. Clim. Change, 14, 357–363, 2024. a
Bierkens, M. F. P. and Wada, Y.: Non-renewable groundwater use and groundwater depletion: a review, Environ. Res. Lett., 14, 063002, https://doi.org/10.1088/1748-9326/ab1a5f, 2019. a
Budyko, M. I.: Climate and Life, Academic, NY, ISBN 9780080954530, 1974. a
Cao, L., Bala, G., Caldeira, K., Nemani, R., and Ban-Weiss, G.: Importance of carbon dioxide physiological forcing to future climate change, P. Natl. Acad. Sci. USA, 107, 9513–9518, https://doi.org/10.1073/pnas.0913000107, 2010. a
Casenave, A. and Valentin, C.: A runoff capability classification system based on surface features criteria in semi-arid areas of West Africa, J. Hydrol., 130, 231–249, 1992. a
Chengcheng, G., Wenke, W., Zaiyong, Z., Hao, W., Jie, L., and Philip, B.: Comparison of field methods for estimating evaporation from bare soil using lysimeters in a semi-arid area, J. Hydrol., 590, 125334, https://doi.org/10.1016/j.jhydrol.2020.125334, 2020. a
Collenteur, R. A., Bakker, M., Klammler, G., and Birk, S.: Estimation of groundwater recharge from groundwater levels using nonlinear transfer function noise models and comparison to lysimeter data, Hydrol. Earth Syst. Sci., 25, 2931–2949, https://doi.org/10.5194/hess-25-2931-2021, 2021. a
Condon, L. E., Atchley, A. L., and Maxwell, R. M.: Evapotranspiration depletes groundwater under warming over the contiguous United States, Nat. Commun., 11, 1–8, https://doi.org/10.1038/s41467-020-14688-0, 2020. a
Crosbie, R. S., Jolly, I. D., Leaney, F. W., and Petheram, C.: Can the dataset of field based recharge estimates in Australia be used to predict recharge in data-poor areas?, Hydrol. Earth Syst. Sci., 14, 2023–2038, https://doi.org/10.5194/hess-14-2023-2010, 2010. a, b
Crosbie, R. S., Pickett, T., Mpelasoka, F. S., Hodgson, G., Charles, S. P., and Barron, O. V.: An assessment of the climate change impacts on groundwater recharge at a continental scale using a probabilistic approach with an ensemble of GCMs, Climatic Change, 117, 41–53, https://doi.org/10.1007/s10584-012-0558-6, 2013. a, b
Cuthbert, M. O., Gleeson, T., Moosdorf, N., Befus, K. M., Schneider, A., Hartmann, J., and Lehner, B.: Global patterns and dynamics of climate–groundwater interactions, Nat. Clim. Change, 9, 137–141, https://doi.org/10.1038/s41558-018-0386-4, 2019a. a
Cuthbert, M. O., Taylor, R. G., Favreau, G., Todd, M. C., Shamsudduha, M., Villholth, K. G., MacDonald, A. M., Scanlon, B. R., Valerie Kotchoni, D. O., Vouillamoz, J.-M., Lawson, F. M. A., Adjomayi, P. A., Japhet, K., Seddon, D., Sorensen, J. P. R., Ebrahim, G. Y., Owor, M., Nyenje, P. M., Nazoumou, Y., Goni, I., Ousmane, B. I., Tenant, S., Ascott, M. J., Macdonald, D. M. J., Agyekum, W., Koussoubé, Y., Wanke, H., Kim, H., Wada, Y., Lo, M.-H., Oki, T., and Kukuric, N.: Observed controls on resilience of groundwater to climate variability in sub-Saharan Africa, Nature, 572, 230–234, https://doi.org/10.1038/s41586-019-1441-7, 2019b. a, b, c
Dee, D. P., Uppala, S. M., Simmons, A. J., Berrisford, P., Poli, P., Kobayashi, S., Andrae, U., Balmaseda, M. A., Balsamo, G., Bauer, P., Bechtold, P., Beljaars, A. C. M., van de Berg, I., Biblot, J., Bormann, N., Delsol, C., Dragani, R., Fuentes, M., Greer, A. J., Haimberger, L., Healy, S. B., Hersbach, H., Holm, E. V., Isaksen, L., Kallberg, P., Kohler, M., Matricardi, M., McNally, A. P., Mong-Sanz, B. M., Morcette, J.-J., Park, B.-K., Peubey, C., de Rosnay, P., Tavolato, C., Thepaut, J. N., and Vitart, F.: The ERA-Interim reanalysis: Configuration and performance of the data assimilation system, Q. J. Roy. Meteor. Soc., 137, 553–597, https://doi.org/10.1002/qj.828, 2011. a
De Filippi, F. M. and Sappa, G.: The Simulation of Bracciano Lake (Central Italy) Levels Based on Hydrogeological Water Budget: A Tool for Lake Water Management when Climate Change and Anthropogenic Impacts Occur, Environmental Processes, 11, 1–15, 2024. a
Döll, P. and Fiedler, K.: Global-scale modeling of groundwater recharge, Hydrol. Earth Syst. Sci., 12, 863–885, https://doi.org/10.5194/hess-12-863-2008, 2008. a, b
Fan, Y., Li, H., and Miguez-Macho, G.: Global patterns of groundwater table depth, Science, 339, 940–943, https://doi.org/10.1126/science.1229881, 2013. a
Favreau, G., Cappelaere, B., Massuel, S., Leblanc, M., Boucher, M., Boulain, N., and Leduc, C.: Land clearing, climate variability, and water resources increase in semiarid southwest Niger: A review, Water Resour. Res., 45, W00A16, https://doi.org/10.1029/2007WR006785, 2009. a
Field, C. B., Barros, V., Stocker, T. F., Dahe, Q., Dokken, D. J., Ebi, K. L., Mastrandrea, M. D., Mach, K. J., Plattner, G. K., Allen, S. K., Tignor, M., and Midgley, P. M.: Managing the risks of extreme events and disasters to advance climate change adaptation,Special Report of Working Groups I and II of the Intergovernmental Panel on Climate Change (IPCC), Cambridge University Press, https://www.ipcc.ch/site/assets/uploads/2018/03/SREX_Full_Report-1.pdf (last access: 12 August 2023), 2012. a, b
Fischer, E. M. and Knutti, R.: Observed heavy precipitation increase confirms theory and early models, Nat. Clim. Change, 6, 986–991, https://doi.org/10.1038/NCLIMATE3110, 2016. a
Fu, G., Crosbie, R. S., Barron, O., Charles, S. P., Dawes, W., Shi, X., Niel, T. V., and Li, C.: Attributing variations of temporal and spatial groundwater recharge: A statistical analysis of climatic and non-climatic factors, J. Hydrol., 568, 816–834, https://doi.org/10.1016/j.jhydrol.2018.11.022, 2019. a
Gerrits, A., Savenije, H., Veling, E., and Pfister, L.: Analytical derivation of the Budyko curve based on rainfall characteristics and a simple evaporation model, Water Resour. Res., 45, W04403, https://doi.org/10.1029/2008WR007308, 2009. a
Goni, I. B., Taylor, R. G., Favreau, G., Shamsudduha, M., Nazoumou, Y., and Ngatcha, B. N.: Groundwater recharge from heavy rainfall in the southwestern Lake Chad Basin: evidence from isotopic observations, Hydrolog. Sci. J., 66, 1359–1371, https://doi.org/10.1080/02626667.2021.1937630, 2021. a
Green, T. R., Taniguchi, M., Kooi, H., Gurdak, J. J., Allen, D. M., Hiscock, K. M., Treidel, H., and Aureli, A.: Beneath the surface of global change: Impacts of climate change on groundwater, J. Hydrol., 405, 532–560, https://doi.org/10.1016/j.jhydrol.2011.05.002, 2011. a
Harris, I., Jones, P., Osborn, T., and Lister, D.: Updated high-resolution grids of monthly climatic observations – the CRU TS3.10 Dataset, Int. J. Climatol., 34.3, 623–642, https://doi.org/10.1002/joc.3711, 2014. a, b
Hartmann, A., Gleeson, T., Rosolem, R., Pianosi, F., Wada, Y., and Wagener, T.: A large-scale simulation model to assess karstic groundwater recharge over Europe and the Mediterranean, Geosci. Model Dev., 8, 1729–1746, https://doi.org/10.5194/gmd-8-1729-2015, 2015. a
Hartmann, A., Gleeson, T., Wada, Y., and Wagener, T.: Enhanced groundwater recharge rates and altered recharge sensitivity to climate variability through subsurface heterogeneity, P. Natl. Acad. Sci. USA, 114, 2842–2847, https://doi.org/10.1073/pnas.1614941114, 2017. a, b
Healy, R. W. and Scanlon, B. R.: Estimating Groundwater Recharge, Cambridge University Press, https://doi.org/10.1017/CBO9780511780745, 2010. a
Hellwig, D.: Evaporation of water from sand, 4: the influence of the depth of the water-table and the particle size distribution of the sand, J. Hydrol., 18, 317–327, https://doi.org/10.1016/0022-1694(73)90055-3, 1973. a
Hengl, T., De Jesus, J. M., MacMillan, R. A., Batjes, N. H., Heuvelink, G. B., Ribeiro, E., Samuel-Rosa, A., Kempen, B., Leenaars, J. G., Walsh, M. G., and Gonzalez, M. R.: SoilGrids1km – Global soil information based on automated mapping, PLoS ONE, 9, e105992, https://doi.org/10.1371/journal.pone.0105992, 2014. a, b
Huang, Z., Yuan, X., Sun, S., Leng, G., and Tang, Q.: Groundwater Depletion Rate Over China During 1965–2016: The Long-Term Trend and Inter-annual Variation, J. Geophys. Res.-Atmos., 128, e2022JD038109, https://doi.org/10.1029/2022JD038109, 2023. a
Langman, J. B., Martin, J., Gaddy, E., Boll, J., and Behrens, D.: Snowpack aging, water isotope evolution, and runoff isotope signals, Palouse Range, Idaho, USA, Hydrology, 9, 94, https://doi.org/10.3390/hydrology9060094, 2022. a
Lorenzi, V., Banzato, F., Barberio, M. D., Goeppert, N., Goldscheider, N., Gori, F., Lacchini, A., Manetta, M., Medici, G., Rusi, S., and Petitta, M.: Tracking flowpaths in a complex karst system through tracer test and hydrogeochemical monitoring: Implications for groundwater protection (Gran Sasso, Italy), Heliyon, 10, e24663, https://doi.org/10.1016/j.heliyon.2024.e24663, 2024. a
McKenna, O. P. and Sala, O. E.: Groundwater recharge in desert playas: current rates and future effects of climate change, Environ. Res. Lett., 13, 014025, https://doi.org/10.1088/1748-9326/aa9eb6, 2018. a
Meixner, T., Manning, A. H., Stonestrom, D. A., Allen, D. M., Ajami, H., Blasch, K. W., Brookfield, A. E., Castro, C. L., Clark, J. F., Gochis, D. J., Flint, A. L., Neff, K. L., Niraula, R., Rodell, M., Scanlon, B. R., Singha, K., and Walvoord, M. A.: Implications of projected climate change for groundwater recharge in the western United States, J. Hydrol., 534, 124–138, https://doi.org/10.1016/j.jhydrol.2015.12.027, 2016. a, b
Mirus, B. B. and Nimmo, J. R.: Balancing practicality and hydrologic realism: A parsimonious approach for simulating rapid groundwater recharge via unsaturated-zone preferential flow, Water Resour. Res., 49, 1458–1465, 2013. a
Moeck, C., Brunner, P., and Hunkeler, D.: The influence of model structure on groundwater recharge rates in climate-change impact studies, Hydrogeol. J., 24, 1171, https://doi.org/10.1007/s10040-016-1367-1, 2016. a
Moeck, C., Grech-Cumbo, N., Podgorski, J., Bretzle, A., Gurdak, J. J., Berg, M., and Schirmer, M.: A global-scale dataset of direct natural groundwater recharge rates: A review of variables, processes and relationships, Sci. Total Environ., 717, 137042, https://doi.org/10.1016/j.scitotenv.2020.137042, 2020. a
Mounirou, L. A., Yonaba, R., Koïta, M., Paturel, J.-E., Mahé, G., Yacouba, H., and Karambiri, H.: Hydrologic similarity: Dimensionless runoff indices across scales in a semi-arid catchment, J. Arid Environ., 193, 104590, https://doi.org/10.1016/j.jaridenv.2021.104590, 2021. a
Mualem, Y.: A New Model for Predicting the Hydraulic Conductivity of Unsaturated Porous Media, Water Resour. Res., 12, 513–522, https://doi.org/10.1029/WR012i003p00513, 1976. a
Myhre, G., Alterskjær, K., Stjern, C. W., Hodnebrog, Ø., Marelle, L., Samset, B. H., Sillmann, J., Schaller, N., Fischer, E., Schulz, M., and Stohl, A.: Frequency of extreme precipitation increases extensively with event rareness under global warming, Sci. Rep.-UK, 9, 16063, https://doi.org/10.1038/s41598-019-52277-4, 2019. a, b, c
Ng, G.-H. C., McLaughlin, D., Entekhabi, D., and Scanlon, B. R.: Probabilistic analysis of the effects of climate change on groundwater recharge, Water Resour. Res., 46, W07502, https://doi.org/10.1029/2009WR007904, 2010. a
Or, D., Lehmann, P., Shahraeeni, E., and Shokri, N.: Advances in soil evaporation physics – A review, Vadose Zone J., 12, 1–16, 2013. a
Pino-Vargas, E., Espinoza-Molina, J., Chávarri-Velarde, E., Quille-Mamani, J., and Ingol-Blanco, E.: Impacts of Groundwater Management Policies in the Caplina Aquifer, Atacama Desert, Water, 15, 2610, https://doi.org/10.3390/w15142610, 2023. a
Pulido-Velazquez, D., García-Aróstegui, J. L., Molina, J. L., and Pulido-Velazquez, M.: Assessment of future groundwater recharge in semi-arid regions under climate change scenarios (Serral-Salinas aquifer, SE Spain). Could increased rainfall variability increase the recharge rate?, Hydrol. Process., 29, 828–844, https://doi.org/10.1002/hyp.10191, 2015. a, b, c
Quandt, A., Larsen, A. E., Bartel, G., Okamura, K., and Sousa, D.: Sustainable groundwater management and its implications for agricultural land repurposing, Reg. Environ. Change, 23, 120, https://doi.org/10.1007/s10113-023-02114-2, 2023. a
Reinecke, R., Müller Schmied, H., Trautmann, T., Andersen, L. S., Burek, P., Flörke, M., Gosling, S. N., Grillakis, M., Hanasaki, N., Koutroulis, A., Pokhrel, Y., Thiery, W., Wada, Y., Yusuke, S., and Döll, P.: Uncertainty of simulated groundwater recharge at different global warming levels: a global-scale multi-model ensemble study, Hydrol. Earth Syst. Sci., 25, 787–810, https://doi.org/10.5194/hess-25-787-2021, 2021. a, b
Sappa, G., De Filippi, F. M., Ferranti, F., and Iacurto, S.: Environmental issues and anthropic pressures in coastal aquifers: a case study in Southern Latium Region, Acque Sotterranee – Italian Journal of Groundwater, 8, 1, https://doi.org/10.7343/as-2019-373, 2019. a
Scanlon, B. R., Keese, K. E., Flint, A. L., Flint, L. E., Gaye, C. B., Edmunds, W. M., and Simmers, I.: Global synthesis of groundwater recharge in semiarid and arid regions, Hydrol. Process., 20, 3335–3370, https://doi.org/10.1002/hyp.6335, 2006. a
Shamsudduha, M. and Taylor, R. G.: Groundwater storage dynamics in the world's large aquifer systems from GRACE: uncertainty and role of extreme precipitation, Earth Syst. Dynam., 11, 755–774, https://doi.org/10.5194/esd-11-755-2020, 2020. a
Šimŭnek, J., Van Genuchten, M. T., and Šejna, M.: The HYDRUS software package for simulating the two-and three-dimensional movement of water, heat, and multiple solutes in variably-saturated porous media, version 4.08, HYDRUS Software Series 3, Dept. Environmental Sciences, Univ. Calif., Riverside, CA, https://www.pc-progress.com/Downloads/Pgm_hydrus1D/HYDRUS1D-4.17.pdf (last access: 15 September 2024), 2009. a
Singh, A., Panda, S. N., Uzokwe, V. N., and Krause, P.: An assessment of groundwater recharge estimation techniques for sustainable resource management, Groundwater for Sustainable Development, 9, 100218, https://doi.org/10.1016/j.gsd.2019.100218, 2019. a
Smerdon, B. D.: A synopsis of climate change effects on groundwater recharge, J. Hydrol., 555, 125–128, https://doi.org/10.1016/j.jhydrol.2017.09.047, 2017. a
Taylor, R. G., Scanlon, B., Döll, P., Rodell, M., Van Beek, R., Wada, Y., Longuevergne, L., Leblanc, M., Famiglietti, J. S., Edmunds, M., Leonard, K., Timothy, R. G., Jianyao, C., Makoto, T., Marc, F. P. B., Alan, M., Fan, Y., Reed, M. M., Yossi, Y., Gurdak, J. J., Allen, D. M., Shamsudduha, M., Hiscock, K., Yeh, P. J.-F., Holman, I., and Treidelothers, H.: Ground water and climate change, Nat. Clim. Change, 3, 322–329, https://doi.org/10.1038/nclimate1744, 2013a. a, b, c, d
Taylor, R. G., Todd, M. C., Kongola, L., Maurice, L., Nahozya, E., Sanga, H., and MacDonald, A. M.: Evidence of the dependence of groundwater resources on extreme rainfall in East Africa, Nat. Clim. Change, 3, 374–378, https://doi.org/10.1038/nclimate1731, 2013b. a, b, c
Tillman, F. D., Gangopadhyay, S., and Pruitt, T.: Changes in groundwater recharge under projected climate in the upper Colorado River basin, Geophys. Res. Lett., 43, 6968–6974, 2016. a, b
Touhami, I., Chirino, E., Andreu, J. M., Sánchez, J. R., Moutahir, H., and Bellot, J.: Assessment of climate change impacts on soil water balance and aquifer recharge in a semiarid region in south east Spain, J. Hydrol., 527, 619–629, https://doi.org/10.1016/j.jhydrol.2015.05.012, 2015. a
Turkeltaub, T.: Simulated and reported groundwater recharge fluxes in 196 locations in arid and semi-arid regions, Hydroshare [code and data set], https://doi.org/10.4211/hs.5a28b74c55c74a7e9ad2b59a0a5d9ab3, 2024. a
Turkeltaub, T. and Bel, G.: The effects of rain and evapotranspiration statistics on groundwater recharge estimations for semi-arid environments, Hydrol. Earth Syst. Sci., 27, 289–302, https://doi.org/10.5194/hess-27-289-2023, 2023. a, b, c, d
Turkeltaub, T., Jia, X., Zhu, Y., Shao, M.-A., and Binley, A.: Recharge and nitrate transport through the deep vadose zone of the loess plateau: a regional-scale model investigation, Water Resour. Res., 54, 4332–4346, 2018. a
Uppala, S. M., Kållberg, P. W., Simmons, A. J., Andrae, U., Da Costa Bechtold, V., Fiorino, M., Gibson, J., Haseler, J., Hernandez, A., Kelly, G. A., Li, X., Onogi, K., Saarinen, S., Sokka, N., Allan, R. P., Anderson, E., Arpe, K., Balmaseda, M. A., Beljaars, A. C. M., Van De Berg, L., Bidlot, J., Bormann, N., Caires, S., Chevallier, F., Dethof, A., Dragosavac, M., Fisher, M., Fuentes, M., Hagemann, S., Hólm, E., Hoskins, B. J., Isaksen, L., Janssen, P. A. E. M., Jenne, R., Mcnally, A. P., Mahfouf, J.-F., Morcrette, J.-J., Rayner, N. A., Saunders, R. W., Simon, P., Sterl, A., Trenbreth, K. E., Untch, A., Vasiljevic, D., Viterbo, P., and Woollen, J.: The ERA-40 re-analysis, Q. J. Roy. Meteor. Soc., 131, 2961–3012, https://doi.org/10.1256/qj.04.176, 2005. a
van Beek, L. P. H.: Forcing PCR-GLOBWB with CRU data, Tech. Rep., https://vanbeek.geo.uu.nl/suppinfo/vanbeek2008.pdf (last access: 12 August 2023), 2008. a
Van Genuchten, M. T.: A closed-form equation for predicting the hydraulic conductivity of unsaturated soils, Soil Sci. Soc. Am. J., 44, 892–898, https://doi.org/10.2136/sssaj1980.03615995004400050002x, 1980. a
van Schaik, N. L. M. B., Schnabel, S., and Jetten, V. G.: The influence of preferential flow on hillslope hydrology in a semi-arid watershed (in the Spanish Dehesas), Hydrol. Process., 22, 3844–3855, https://doi.org/10.1002/hyp.6998, 2008. a
Viaroli, S., Mastrorillo, L., Lotti, F., Paolucci, V., and Mazza, R.: The groundwater budget: a tool for preliminary estimation of the hydraulic connection between neighboring aquifers, J. Hydrol., 556, 72–86, 2018. a
Vivek, S., Umamaheswari, R., Subashree, P., Rajakumar, S., Mukesh, P., Priya, V., Sampathkumar, V., Logesh, N., and Ganesh Prabhu, G.: Study on groundwater pollution and its human impact analysis using geospatial techniques in semi-urban of south India, Environ. Res., 240, 117532, https://doi.org/10.1016/j.envres.2023.117532, 2024. a
Wada, Y., Van Beek, L. P., Van Kempen, C. M., Reckman, J. W., Vasak, S., and Bierkens, M. F.: Global depletion of groundwater resources, Geophys. Res. Lett., 37, 1–5, https://doi.org/10.1029/2010GL044571, 2010. a
Zhang, Y. and Schaap, M.: Weighted recalibration of the Rosetta pedotransfer model with improved estimates of hydraulic parameter distributions and summary statistics (Rosetta3), J. Hydrol., 547, 39–53, https://doi.org/10.1016/j.jhydrol.2017.01.004, 2017. a





