the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Effects of passive-storage conceptualization on modeling hydrological function and isotope dynamics in the flow system of a cockpit karst landscape
Guangxuan Li
Xi Chen
Zhicai Zhang
Lichun Wang
Chris Soulsby
Conceptualizing passive storage in coupled flow–isotope models can improve the simulation of mixing and attenuation effects on tracer transport in many natural systems, such as catchments or rivers. However, the effectiveness of incorporating different conceptualizations of passive storage in models of complex karst flow systems remains poorly understood. In this study, we developed a coupled flow–isotope model that conceptualizes both “fast-flow” and “slow-flow” processes in heterogeneous aquifers as well as hydrological connections between steep hillslopes and low-lying depression units in cockpit karst landscapes. The model tested contrasting configurations of passive storage in the fast- and slow-flow systems and was optimized using a multi-objective optimization algorithm based on detailed observational data of discharge and isotope dynamics in the Chenqi Catchment in southwestern China. Results show that one to three passive-storage zones distributed in hillslope fast-/slow-flow reservoirs and/or depression slow-flow reservoirs provided optimal model structures in the study catchment. This optimization can effectively improve the simulation accuracy for outlet discharge and isotope signatures. Additionally, the optimal tracer-aided model reflects dominant flow paths and connections of the hillslope and depression units, yielding reasonable source area apportionment for dominant hydrological components (e.g., more than ∼ 80 % of fast flow in the total discharge) and solute transport in the steep hillslope unit of karst flow systems. Our coupled flow–isotope model for karst systems provides a novel, flexible tool for more realistic catchment conceptualizations that can easily be transferred to other cockpit karst catchments.
- Article
(5240 KB) - Full-text XML
- BibTeX
- EndNote
Karst areas cover extensive areas of the Earth's surface and provide important water resources. For example, the karst region in southwestern China is one of the world's largest continuous karst areas, covering ∼ 540 × 103 km2 over eight provinces and providing water resources for more than 100 million people (Chen et al., 2018). The strong dissolution of carbonate rocks in the humid tropics and subtropics of southwestern China creates unique cockpit karst landscapes, covering an area of ∼ 140× 103–160 × 103 km2. Such cockpit karst morphology also occurs in areas in Southeast Asia, Central America and the Caribbean. In polje/tower karst systems, depression areas are interconnected with isolated towers scattered throughout the terrain (Lyew et al., 2007). As hillslope runoff is regarded as a “water tower”, often supplying agriculture in the depression, the development of hydrological models representing the hillslope and depression hydrological functionality is a necessary prerequisite for water resource management in cockpit karst landscapes.
A wide range of hydrological models have been developed for karst areas, ranging from lumped models at the catchment scale to (semi-)distributed models with hydrological function parameterized for grid scales or landscape unit scales (Martínez-Santos and Andreu, 2010; Hartmann et al., 2013; Husic et al., 2019; Dubois et al., 2020; Ollivier et al., 2020; Xu et al., 2020; Jeannin et al., 2021; Wunsch et al., 2022). A key function of karst hydrological models is to capture the dual- or multi-phase flows in a complex porous medium, thereby capturing low velocities in the matrix and small fractures as well as very high velocities in large fractures and conduits (White, 2007; Worthington, 2009; Jourde et al., 2018; Ding et al., 2020). Model structures endowed with process-based conceptualization of complex distributed flow systems often lead to overparameterization and large uncertainties in the resulting simulations (Perrin et al., 2001; Beven, 2006; Adinehvand et al., 2017). More generally, in recent years, isotope-aided hydrological models have been developed to fully couple hydrological processes with stable isotope dynamics (Birkel and Soulsby, 2015). These coupled models are effective in quantifying hydrological functions, such as water storage, flux and ages (Long and Putnam, 2004; Carey and Quinton, 2004; Delavau et al., 2017; Chacha et al., 2018; Z. Zhang et al., 2020; Elghawi et al., 2021; Mayer-Anhalt et al., 2022), which are useful metrics to characterize the karst critical zone and associated flow systems.
In isotope-aided hydrological models, flow routing is driven by pressure gradients, creating a dynamic (active) water storage that is influenced by water balance considerations (Fenicia et al., 2010; Soulsby et al., 2011), while tracer mixing, attenuation and transport require additional storage volumes (passive storage), such as unsaturated storage below field capacity (Birkel et al., 2011b) or saturated storage at depths far below the stream or water table. The conceptual combination of active storage with passive storage in isotope-aided hydrological models enhances solute mixing and resultant tracer retardation. As summarized in Table 1, previous tracer-aided hydrological models incorporate at least one passive storage. Generally, the number of passive storages increases with the subdivision of storage according to landscape units. For example, simple models with one (unsaturated/saturated or total) storage unit have one passive-storage parameter (Barnes and Bonell, 1996; Fenicia et al., 2010; Ala-aho et al., 2017). For more complex models with at least two geographical units of uplands and lowlands, the number of passive storages could increase to between two and five (Birkel et al., 2011a; Capell et al., 2012; Birkel et al., 2015; Mayer-Anhalt et al., 2022). Although these studies have provided a useful proof of concept, assessment of alternative configurations of passive-storage functions has rarely been systematically tested.
For the complex flow systems in cockpit karst landscapes, a few studies have recently incorporated passive storage into coupled flow–isotope models for simulating hydrological and solute transport processes. For example, Zhang et al. (2019) developed a semi-distributed conceptual model for capturing discharge and isotope dynamics in the Chenqi Catchment. The model has a function for passive storage to affect isotope mixing only within a conceptual hillslope unit, but it does not incorporate any passive storages in fast and slow reservoirs in the depression unit. Chang et al. (2020) compared lumped model structures with different connections of epikarst and the underlying slow and fast reservoirs according to observations of spring discharge and electrical conductivity (EC) in the Yaji Catchment in southwestern China. They set a passive storage for the fast-flow reservoir but neglected passive storage in the slow-flow system. These previous model structures with only one passive storage (Zhang et al., 2019; Chang et al., 2020) may not always be sufficient to simulate the distributed functioning of chemical mixing between active and passive storages and the hillslope flow–depression flow interconnections. Moreover, previous coupled models (listed in Table 1) are mostly calibrated and validated only against daily and/or weekly streamflow and isotope signatures. In karst catchments, as discharge responses and isotope concentrations can vary extremely rapidly, the coarse-resolution field data cannot capture the hydrological and isotopic dynamics.
The overall aim of this study is to evaluate the effectiveness of alternative ways of incorporating passive storage into a generic coupled flow–isotope model for cockpit karst landscapes. The specific objectives were to (1) develop a model that characterizes the functions of fast- and slow-flow paths from hillslope to depression units for water and tracer transport in cockpit karst landscapes; (2) systematically test alternative passive-storage configurations into the generalized model structure using a multi-objective optimization algorithm based on detailed observational data of discharge and isotope dynamics in the Chenqi Catchment in southwestern China; and (3) identify the most appropriate model structures that most efficiently describe the hydrological functioning of the catchment in terms of simulating the streamflow and tracer responses.
Table 1Summary of the previous studies that account for passive storages in hydrological models using at least one isotopic tracer.
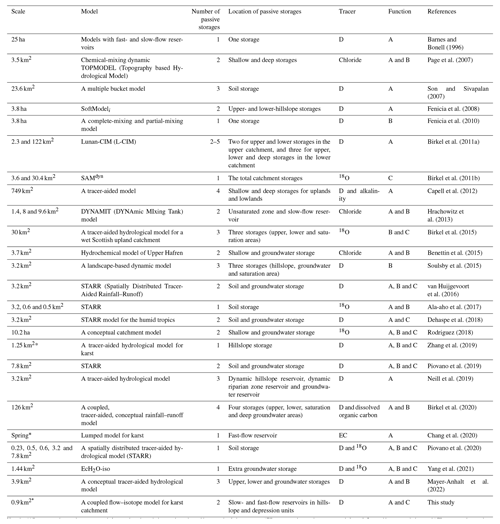
Note that “A” represents that passive storage can help reproduce the main isotope dynamics and improve simulation accuracy; “B” represents that passive storage can help track flux, resident or transit time; and “C” represents that passive storage can help estimate catchment storage. “D” is the abbreviation for deuterium. “*” refers to application in a karst catchment.
2.1 Study area
Chenqi is a small karst catchment located at the Puding Karst Ecohydrological Observation Station, Guizhou Province, southwestern China (Fig. 1). Chenqi is situated in the subtropical monsoon climate zone and experiences a mean annual temperature of 14.2 ∘C, a mean annual rainfall of 1140 mm and a mean annual humidity of 78 %. Precipitation mainly occurs in the rainy season (May–August), accounting for more than 80 % of the annual amount. The catchment is a typical karst peak cluster landform, in which a central depression is surrounded by hillslopes with elevations ranging from 1340 to 1530 m. Considering its distinct topographic features, the catchment is conveniently divided into two dominant geomorphic units: hillslopes and depressions. These two units comprise an area of 0.73 and 0.17 km2, respectively (Table 2). Due to the peak cluster depression landforms, runoff generated from hillslopes mostly flows into depression aquifers prior to contributing to streamflow at the catchment outlet (Zhang et al., 2019; R. Zhang et al., 2020).
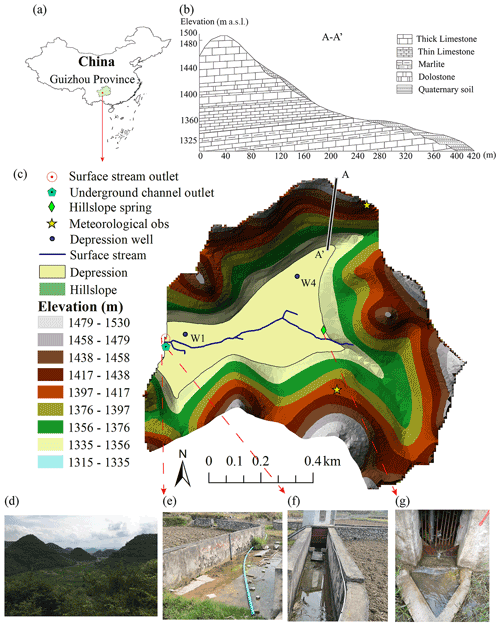
Figure 1The location of Chenqi Catchment (a); the stratigraphic profile (b) and topography of the catchment (c); a photo taken in the catchment (d); and photos of the observation sites at the surface stream outlet (e), the underground channel outlet (f) and the hillslope spring (g).
2.2 Hydrogeological properties
Geological characteristics of the catchment include Quaternary soil, thick and thin limestone, dolostone, and marlite. The limestone formations with a thickness of 150–200 m lie above an impervious marlite formation (see the A–A' profile in Fig. 1b) (Chen et al., 2018). On hillslopes, field investigations have shown a rich fracture zone (epikarst) that has a thickness of 7.5–12.6 m (Zhang et al., 2011). Quaternary soils consist of mostly sand (56 %–80 %), fine sand (20 %–40 %), and calcareous soil and silt (1 %–10 %). The soils are thin (less than 30 cm) and irregularly developed on carbonate rocks. Outcrops of carbonate rocks cover 10 %–30 % of the hillslope area. In some specific areas where a shallow impermeable layer (marlite) exists, hillslope springs appear on lower hillslopes. Deciduous broadleaved trees and shrubs mostly grow on the upper and middle parts of hillslopes, and corn is grown at the foot of the gentle hillslopes (Chen et al., 2018).
In the low-lying depressions, the accumulated soils are thicker (∼ 2 m), and they are cultivated for corn or used as rice paddies. The underlying limestone is strongly dissolved, producing underground conduits. These are sporadically distributed in the upper depression areas in connection with hillslope flows and are gradually concentrated towards the catchment outlet (Cheng et al., 2019). The bedrock comprising the impervious marlite is located at depths of 30–50 m. Meanwhile, there are depression ditches that drain flood flow when the groundwater level is higher than the ditch bottom (see surface stream in Fig. 1). Thus, the total outlet discharge is predominantly composed of underground conduit flow in the study catchment, with surface channel flow only present during larger events.
2.3 Observational dataset of hydrometry and stable isotopes
An automatic meteorological station (Fig. 1c) was installed in the Chenqi Catchment to continuously record rainfall, temperature, air pressure, wind speed, humidity and solar radiation. These data were used to calculate the potential evaporation via the Penman formula. Discharge at a hillslope spring and the catchment outlet was measured by v-notch weirs with a time interval of 15 min. All observational datasets were collected from 8 October 2016 to 12 June 2018.
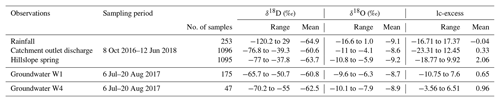
For stable isotope analysis, the hillslope spring, the catchment outlet flows and rainfall were sampled using an autosampler set. The sampling frequency was daily in the dry season (September–April) and hourly in the rainy season (May–August). In total, we collected 253 rainfall samples, 1095 hillslope spring samples and 1096 water samples at the catchment outlet of the underground channel during the study period (Table 3).
As shown in Fig. 1c, there are two observation wells (W1 and W4) near the catchment outlet and the upstream depression. W1 is located in a locally confined aquifer, consisting of extensively fractured carbonate rock surrounded by rock with low secondary porosity. W4 is located in an unconfined aquifer with the vertical permeability decreasing from a large rock fracture and high secondary porosity to low secondary porosity (Chen et al., 2018). The depression groundwater in the two wells (W1 and W4 in Fig. 1c) was manually sampled. Samples were taken at depths of 35 and 13 m for W1 and W4, respectively, with a sampling frequency of two occasions before and after the four rainfall events from 6 July to 20 August 2017.
The sampled water was sealed by using plastic bags to avoid evaporation. Water samples were taken to the laboratory every day and stored at about 4 ∘C. The water samples were tested and analyzed by a MAT 253 laser isotope analyzer (instrument precision was ±0.5 ‰ for δD and ±0.1 ‰ for δ18O) at the State Key Laboratory of Hydrology and Water Resources of Hohai University.
2.4 Characteristics of the observed hydrograph and stable isotope dynamics
The observed surface, subsurface and total outlet flow (discharge) are shown in Fig. 2. The discharge response to rainfall is rapid, characterized by a sharp rise and decline in hydrographs. During the study period, the surface flow and underground flow are 43 % and 57 % of the total discharge, respectively. Various lines of evidence have demonstrated the hillslope–depression fast-flow connection, particularly during heavy-rainfall events. In the mid-season, after extremely heavy rainfall, hillslope spring discharge is highly synchronized with outlet flow, and the relationship between hillslope spring discharge and outlet discharge approaches a monotonic function (details in R. Zhang et al., 2020). It is worth noting that, due to the impact of agricultural irrigation, there were unreasonable sudden declines in surface and subsurface flow in June.
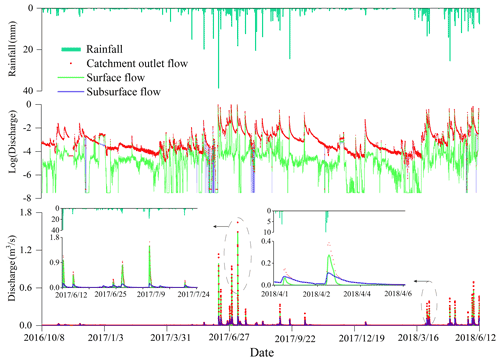
Figure 2The observed surface, subsurface and catchment total outlet flow (discharge) during the study period.
The mean values of δD and δ18O (Table 3) clearly show that the isotopic composition of water in the catchment becomes more enriched from the hillslope spring to the depression groundwater and the catchment outlet discharge. This implies increased mixing with more enriched groundwater affected by evaporative fractionation over the course of water flow paths from the hillslopes towards the outlet (Zhang et al., 2019; R. Zhang et al., 2020). This is also illustrated by the fact that the δD–δ18O regression lines for hillslope spring and outlet discharge deviate from the local meteoric water line (LMWL) (δD = 8.18δ18O + 9.52), as shown in Fig. 3. Additionally, the regression line of hillslope flow is close to that of the catchment outlet discharge, inferring that hillslope flow is a primary source of outlet discharge. The strong connection between hillslope flow and outlet discharge is attributed to the wide spread of the high-permeability zone in depressions (e.g., at W4). The more depleted isotope signals at W4 show that the groundwater there receives more new water (fast flow) from the hillslope spring and rainfall. By contrast, some older water in the less-permeable area of depressions (e.g., at W1) still contributes to the outlet discharge. The more enriched δ18O and δD values at W1 show that flow there seldom mixes with new water (rainfall) (Chen et al., 2018), which could lead to a marked departure from the LMWL (Fig. 3).
The monthly statistical summaries of δD and lc-excess (lc-excess =δD-a ⋅ δ18O − β) are shown in Fig. 4. In the wet season, from May to October, δD is gradually depleted, reflecting rainfall inputs; in contrast, in the dry season, from November to April, δD is gradually enriched. This indicates that both the hillslope spring and outlet discharge change from receiving more new rainwater in wet season to being dominated by older water in the dry season. Meanwhile, δD is more depleted and the lc-excess is more positive for the hillslope flow, compared with the outlet discharge. This means that additional flow sources in the depression join the hillslope flow. This depression flow is older but undergoes less evaporation because of the flat topography and thicker soils. Nevertheless, the additional depression flow has little influence on discharge variability at the catchment outlet, as the various patterns of δD and lc-excess at the catchment outlet closely correspond to those of the hillslope spring.
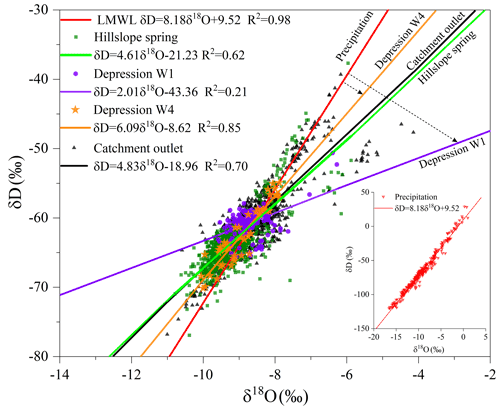
Figure 3Plot of δ18O–δD for rainwater, catchment outlet discharge, hillslope spring and depression groundwater at wells W1 and W4. The correlation between δ18O and δD at W1 is 0.21 (tested to be significant at the significance level of p < 0.001).
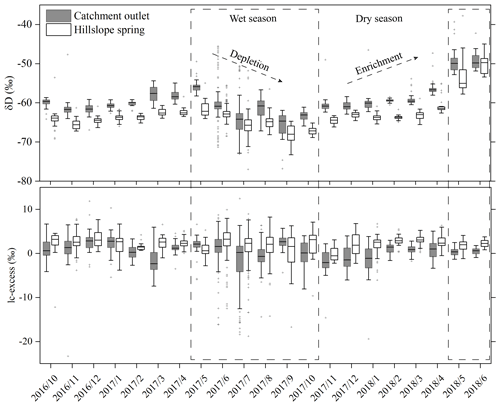
Figure 4Monthly summaries of observed δD and lc-excess of outlet discharge and the hillslope spring during the study period.
3.1 Conceptual model structure
Considering the contrasting features of the catchment landscape, the catchment area is conveniently subdivided into hillslope and depression units, and the model structure can be conceptualized by focusing on the hydrologic connectivity of the “hillslope–depression–stream” continuum (R. Zhang et al., 2020). In each of the hillslope and depression units, the vertical profile is separated into an unsaturated zone, comprising the soil and epikarst layers, and a saturated zone, representing the deep aquifer (Fig. 5). The effect of spatial heterogeneity on hydrological functions is described by a distribution curve of storage in the unsaturated zone, and a dual-flow system in the saturated zone. The distribution curve of storage, like a set of compartments in the VarKarst model (Hartmann et al., 2013), has functions to quantify various recharge mechanisms (e.g., diffusive and concentrated allogenic and autogenic recharge). The dual-flow system consists of a fast-flow reservoir and a slow-flow reservoir that are interconnected and can be used for groundwater routing (Hartmann et al., 2013; Zhang et al., 2019).
The steep hillslope flow moves to the low-lying depression with the following possible connections: hillslope fast flow to depression fast/slow flow (HF–DF/DS), and hillslope slow flow (HS) to depression fast/slow flow (Fig. 5). As hillslope fast flow is primarily concentrated into depression conduits, the connection of HF–DS is neglected in this study.
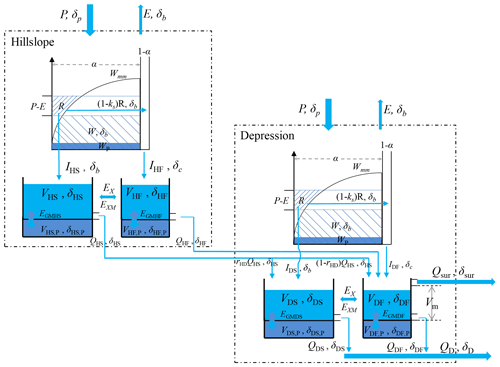
Figure 5Conceptualized structure for the coupled flow–isotope model. The light blue shades indicate active storage, and the dark blue shades indicate passive storage. Detailed descriptions of the model parameters are given in Table 5.
3.1.1 Hydrological routing
In each of the hillslope and depression units, the spatial heterogeneity of unsaturated storage volumes is described by a distribution curve of the storage capacity, such as the Xinanjiang model in Fig. 5 (Zhao, 1992), following:
where f represents the free water yield area, F represents the total of the area (α), is the areal mean tension water storage at f, Wmm is the maximum value of and b is a parameter.
Based on Eq. (1), the initial areal average storage W is an integration of within 0−A in the area ():
When A=Wmm, the storage in the entire area reaches storage capacity. Thus, the mean storage capacity Wm is equal to (Zhao, 1992).
When the net precipitation (P–E) > 0 and P–E+A < Wmm, the water yield R is
Note that P is precipitation, and E is actual evaporation estimated by , where kc is a coefficient of evapotranspiration, and EP is potential evapotranspiration.
If , the water yield R is
The water yield R recharges the deep aquifer, which is separated into diffusive recharge IS and concentrated allogenic and autogenic recharge IF. The IS recharges the slow-flow reservoir of the matrix or the small fracture area with a ratio to hillslope or depression area of α (i.e., IS=ks × R × α, where ks is the ratio of water yield into slow-flow reservoir). The IF is the remaining runoff ((1−ks) × R × α) and rainfall P falling on the swallow holes (1−α), which directly recharges the fast-flow reservoir (i.e., IF= P× (1−α) + R × (1−ks) × α).
Consequently, in the saturated zone, the water balance in the fast and slow reservoirs is
Here, VS and VF are storages of the slow- and fast-flow reservoirs, respectively; QS and QF are discharges from the slow and fast reservoirs, respectively; and EX is flux between fast-flow and slow-flow reservoirs.
EX is estimated as the difference in the saturated storages (or water heads) between the fast-flow and slow-flow reservoirs (i.e., EX =ke × (VS−VF), where ke is a coefficient of exchange flux between the slow- and fast-flow reservoirs). QS and QF are estimated according to the linear relationship between storage V and discharge (i.e., QS=ηS × VS, and QF=ηF × VF, where ηS and ηF are outflow coefficients of the slow- and fast-flow reservoirs, respectively).
3.1.2 Isotopic tracer routing
In each of the hillslope and depression units, the isotope mass balance in the unsaturated zone storage can be expressed as
where ) is the moisture storage consisting of active storage W or mobile water (Sprenger et al., 2017; Sprenger et al., 2018) and passive storage WP; ls is the coefficient of evaporation fractionation; and δp and δb are the stable isotope ratios of rainwater (P) and moisture (and water yield R), respectively. Equation (7) assumes instantaneous mixing of rainwater (P), water yield (R) and soil moisture (W), and complete mixing of the active storage (W) with passive storage (WP) in the area (α) because soils are very thin.
For the deeper aquifer, the mass balance in the slow- and fast-flow reservoirs is given by
Here, EXM is the exchange mass between the slow-flow and fast-flow reservoirs (estimated by ke × (VS−VF) × δS for EXM > 0 and by ke × (VS−VF) × δF for EXM ≤ 0); EGMS and EGMF represent the mixing of the solute between the active and passive storages for the slow- and fast-flow reservoirs, respectively; and δS and δF are the stable isotope δ of the slow flow and fast flow, respectively.
As IF comes from percolation of both unsaturated zone and direct rainfall recharge, the recharge water mass IF × δc is equal to
The mass balance of the passive storage (VP × δ) affected by EGMS and EGMF for slow- and fast-flow reservoirs is
Here, VS,P and VF,P are the passive storage of the slow-flow and fast-flow reservoirs, respectively; δS,P and δF,P are the stable isotope δ of passive storage for the slow-flow and fast-flow reservoirs, respectively; and EGMS=ϕS × VS × ( and EGMF=ϕF × VF × (, where ϕS and ϕF are the exchange coefficient between the active and passive storages for slow flow and fast flow, respectively.
The above Eqs. (8) and (11) describe partial mixing between VS and VS,P for the slow-flow reservoir, and Eqs. (9) and (12) describe partial mixing between VF and VF,P for the fast-flow reservoir. Moreover, the partial mixing could be static or dynamic depending on whether the exchange coefficients between active and passive storages (ϕS and ϕF) are constant or vary over time, respectively (Hrachowitz et al., 2013).
3.1.3 Hillslope–depression connectivity and schematic model structures incorporating passive storage
The hillslope fast flow is assumed to fully connect with fast pathways in the depression (i.e., HF–DF in Table 4), whereas the hillslope slow flow passes through both the slow matrix and fast pathways in the depression (i.e., HF–DF/DS in Table 4). Therefore, the storages of VS and VF in the depression unit receive additional recharge from the hillslope slow flow. Hence, the hillslope slow- or fast-flow contribution to the depression slow or fast flow is or , respectively, where rHD is a ratio of hillslope slow flow into depression slow flow, and AH and AD are hillslope and depression areas, respectively. Correspondingly, VS × δS and VF × δF in the depression are influenced by the isotope composition of the hillslope inputs ( and from the hillslope slow flow and fast flow, respectively).
Table 4Different model structures that incorporate passive storages into fast-flow and/or slow-flow reservoirs at hillslope and/or depression units.

Note that “P” and “–” represent the fast- and slow-flow reservoirs with and without passive storage, respectively.
There is a dual-drainage system, comprising both a surface stream and underground channel, in the depression. Here, we set a critical volume Vm in the depression. The catchment flow drains from the surface stream Qsur only when the depression groundwater storage meets VDF > Vm (i.e., ). As a consequence, the total flow discharge at the catchment outlet Q is composed of fast flow (QF) and slow flow (QS) in the subsurface, with additional contributions from the surface stream Qsur.
Passive storage may exist in any flow system (fast and slow flow) or geographical unit (hillslope and depression) in karst catchments (Fig. 5). To optimize the number and positions of passive storage in the flow system, we set 14 schemes (scenarios) that incorporate zero to four passive storages in different positions of the fast and slow reservoirs for hillslope and depression units (indicated by the subscript “P” in Table 4). The model parameters and their definitions are listed in Table 5.
Table 5The definitions of model parameters with their ranges.
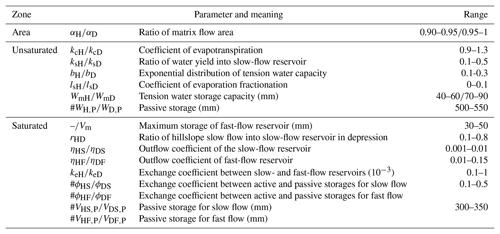
Note that the upper and lower parameters in values separated by “” represent the hillslope and depression, respectively. The parameters indicated by “#” refer to those used for isotope concentration simulation. “–” represents not available.
3.2 Model calibration and validation
The observational data were used separately for the calibration and validation periods. More specifically, the model parameters were calibrated against the observed discharge and isotope concentration (δD) from 8 October 2016 to 30 October 2017. Afterwards, the model was validated against observations from 1 November 2017 to 12 June 2018. Note that, as δD and δ18O fluctuated with virtually the same dynamic over time and both were driven by the same hydrological factors, only δD was used for calibration. The flow–isotope coupled models with different combinations of the active and passive storages (Table 4) were run at hourly time steps.
In this study, the multi-objective optimization algorithm, i.e., the non-dominated sorting genetic algorithm II (NSGA-II) proposed by Deb et al. (2002), was applied for the model parameter calibration. The NSGA-II algorithm (Kollat and Reed, 2006), based on the NSGA algorithm, can identify sets of Pareto-optimal solutions. As Pareto-optimal sets of solutions are not dominated by any one of the factors, as a result of trade-off effects, the “best” solution is achieved by satisfying the demands of the performance objective functions, including the modified Kling–Gupta efficiency (KGE) and the absolute value of the bias (Abiasq) (Fenicia et al., 2007). The KGE criterion comprehensively considers the linear correlation and standard deviation between the numerical and observed values (Kling et al., 2012):
Here, r is the linear correlation coefficient between the simulated and observed values; SD is the ratio of the standard deviation of the numerical and observed values; μ is the ratio of the average numerical value to the observed value; and represents the goodness of fit for flow discharge or isotope concentration, respectively. The closer KGE is to 1, the better the overall performance of the coupled model.
The Abiasq is
where Si is the simulated discharge, and Oi is the observed discharge. The closer Abiasq is to 0, the better the performance of the model with respect to matching flow discharge at the outlet.
For a number of iterations (e.g., 1000 in this study), 50 parameter sets were initially retained. The remaining sets with an Abiasq value less than or equal to 0.2 in the 50 parameter sets were then sorted from largest to the smallest according to the sum of corresponding KGEq and KGEc. Finally, 30 sets were selected as the Pareto-optimal solution (Nan et al., 2021). The corresponding objective function values (average of the optimal solution sets) for both the calibration and validation periods were extracted.
The range of each parameter value is initially set for model calibration according to our previous investigations (Zhang et al., 2019; R. Zhang et al., 2020; Xue et al., 2019). The volumes of passive storages (WH,P and WD,P; VS,P and VF,P) are generally 1 order of magnitude larger than those of active storage (Dunn et al., 2010; Soulsby et al., 2011; Ala-aho et al., 2017). Thus, the ranges of WH,P and WD,P in the unsaturated zone are set as 500–550 mm, and the ranges of VH,P and VD,P in saturated zone are set as 300–350 mm. Considering the rapid hydrological response of the fast-flow system or the hillslope unit to precipitation, the initial values of active storage (VHF, VDF and VHS) are set to 0 mm, whereas the initial value of VDS is 20 mm (Xue et al., 2019). Meanwhile, the isotope ratios for deuterium are all initially set to the measurement at the catchment outlet (i.e., −61.3 ‰); this initialization contributes negligible errors because isotope transport is driven by the rainfall input boundary condition.
A regional sensitivity analysis (Freer et al., 1996) was executed to identify the most important model parameters. The sensitive parameters targeting KGEq are the ratio of water yield into the slow-flow reservoir (), the maximum storage of the fast-flow reservoir Vm and the outflow coefficient of the fast-flow reservoir in the hillslope unit (ηHF). There are other sensitive parameters when targeting KGEc, including αH, kcH, ksH, bH, WmH and ηHS in the hillslope unit as well as αD, kcD and ηDS in the depression unit. Overall, the parameters in the hillslope unit are more sensitive to discharge and isotopic ratios compared with those in the depression unit.
4.1 Performance of models during calibration and validation periods
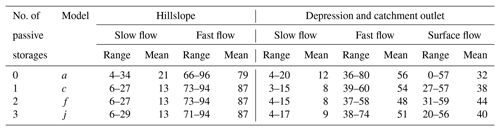
The 30 optimal solutions and their means for the objective functions of KGEq, KGEc and Abiasq are obtained from the parameter calibration of 14 models, as shown in Table 6 and Fig. 6. Most models obtain a higher KGEq but a lower KGEc, which has also been reported by other studies (Soulsby et al., 2015; Dehaspe et al., 2018; Mudarra et al., 2019; Birkel et al., 2020). For the models incorporating one to four passive storages in Table 4, the accuracy of the simulated discharge and isotopic concentration does not increase with the number of passive storages. Comparatively, models c, f and j give higher mean values for both KGEq (> 0.65) and KGEc (> 0.55) (Table 6), and models c and f also obtain a more constrained range of KGEq and KGEc from the 30 sets of optimal solutions (Fig. 6) in the calibration and validation periods. All three models showing better performance have a passive storage in the hillslope fast reservoir but do not incorporate any passive storage in the depression fast reservoir (see Table 4). This indicates that hillslope (fast) flow and isotope mixing control catchment outlet discharge and isotopic concentration are consistent with the inferences from the observational data analysis.
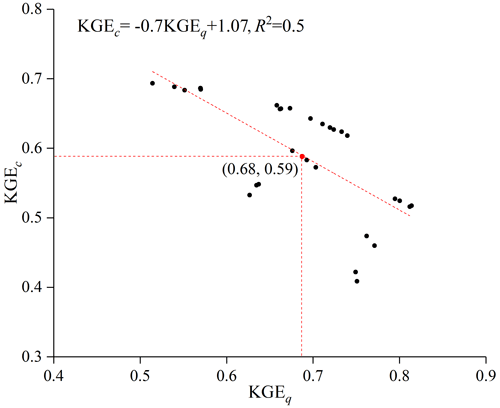
As an example, Figs. 7 and 8 show the respective outlet discharge and isotope (δD) variations simulated by model f. Model f can generally capture the flood peaks (Fig. 7) and the isotope (δD) variations (Fig. 8). The average KGEq and KGEc from model f are higher than 0.59 in the calibration and validation periods, and Abiasq is relatively small (Table 6). Figure 9 shows that KGEq is negatively correlated with KGEc according to the 30 optimal solution sets from the NSGA-II algorithm. Therefore, the multi-objective calibration gives a pair of high trade-off solution values for both KGEq and KGEc for the calibrated model f as well as for models c and j. The other models do not balance the trade-off between KGEc and KGEq as effectively. For example, model n, with four passive storages, obtains a high KGEq (> 0.6) but low KGEq (< 0.3) (Table 6).
Table 6Model performance based on the average of 30 optimal solution sets for each individual model structure.
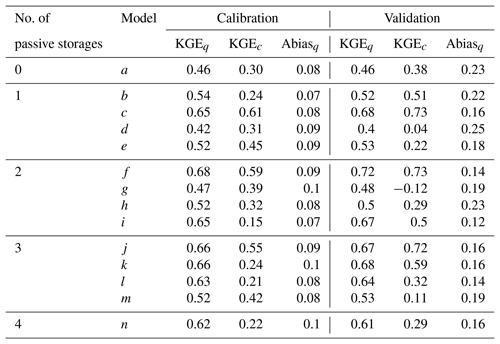
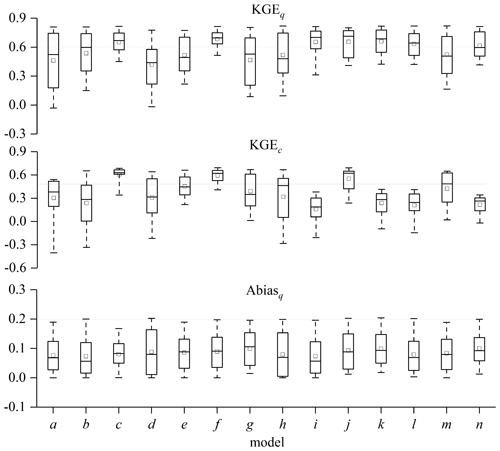
Figure 6A box plot of the 30 optimal solutions for the objective functions of KGEq, KGEc and Abiasq obtained from the parameter calibration of 14 models.
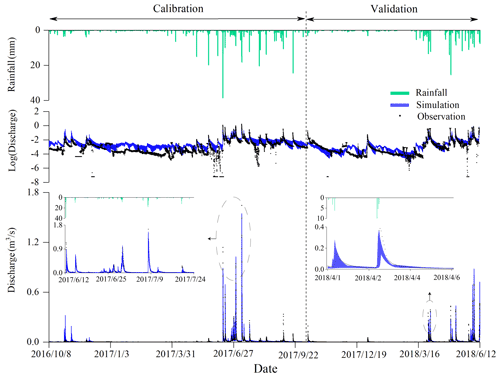
Figure 7Simulated discharge concentrations of the 30 sets of optimal solutions by model f in the calibration and validation periods. Note that the blue shades represent the simulated range of the 30 optimal solution sets, and the black dots represent the observed discharge (the total of surface and subsurface discharge) at the catchment outlet.
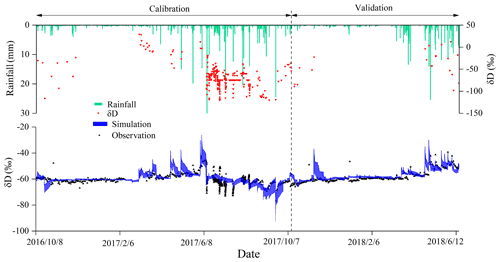
Figure 8Simulated isotope concentrations of the 30 sets of optimal solutions by model f in the calibration and validation periods. Note that the blue shades represent the simulated range of the 30 optimal solution sets, and the black dots represent the observed isotope concentrations at the catchment outlet.
4.2 Calibrated parameter values
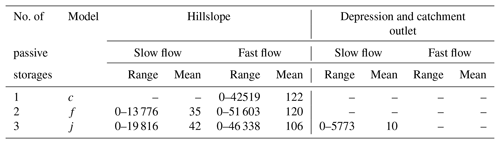
The calibrated parameter values for the models with better performance, models c, f and j, are listed in Table 7. These parameter values reasonably delineate the hydrological features of karst landforms. For example, the calibrated ks ranges from 0.13 to 0.24 in hillslope and depression units, suggesting that about 76 %–87 % of the net precipitation recharges the fast-flow reservoir through large fractures and sinkholes in terms of (1−α)(1−ks)α. This high percentage is consistent with the numerical results of Zhang et al. (2011), which were independently derived using a distributed model that considered the role of sinkholes in facilitating fast-flow recharge into the aquifer in the studied catchment. Charlier et al. (2012) found that about 60 % of recharge water entered the conduit network (fast channelized flow paths) in a small karst system in the French Jura Mountains. Worthington et al. (2000) also revealed that more than 90 % of total flow is fast-flow component in four typical karst aquifers in Kentucky, USA. Wm, representing the soil moisture retention capacity, ranges from 52 to 58 mm for thin soils over hillslope, but it is substantially smaller than 81–90 mm for thick soils over depressions according to the calibrated results of the three models with better performance. The outflow coefficient of the fast-flow reservoir ηF (0.14–0.150.01–0.02 for the hillslope/depression) is much greater than that of the slow-flow reservoir ηS (0.002–0.0040.003–0.005), especially for the hillslope unit. This suggests that fast-flow discharge is much more sensitive to active storage variability than slow-flow discharge because . In addition, the optimized ratio of the hillslope slow-flow contribution to the depression slow flow rHD is close for models c and f (0.37 and 0.39, respectively), which are smaller than the 0.55 reported for model j. The larger rHD value for model j means more hillslope slow-flow allocation to the depression slow-flow reservoir.
Table 7The mean values of model parameters for the 30 optimal solution sets from the three models with better performance.

Note that the upper and lower parameters in values separated by “**” represent the hillslope and depression, respectively. The parameters indicated by “#” refer to those used for isotope concentration simulation. “–” represents not available in the models.
4.3 The effects of passive storage on simulated flow composition and isotopic concentration
We further compared the simulated flow components and their isotopic concentrations for the three models showing better performance (models c, f and j with one to three passive storages in Table 6). The results of model a without any passive storage are also used as a benchmark for comparison. The partitioning of the simulated outlet discharge by the four models is listed in Table 8. All three of the better models with passive stores set in the hillslope unit have a high proportion of discharge from the fast-flow system, particularly in the hillslope unit. In the hillslope unit, model a obtains 79 % of the fast-flow component and 21 % of the slow-flow component, while the three better models with passive stores in the hillslope give a higher proportion of discharge from the fast-flow system (87 %). In the depression unit and at the catchment outlet, the simulated slow-flow composition is slightly different, while the simulated proportions of the underground fast flow and surface flow are largely different in the three models. As shown in Table 8, model f gives 44 % of surface streamflow and 56 % of underground channel flow (the total of fast and slow flow), which are close to observed values at the surface stream (43 %) and underground channel (57 %) outlets. By contrast, models a, c and j (particularly model a) underestimate surface streamflow and overestimate underground channel flow.
The simulated isotope values of the flow components in the hillslope–depression–outlet continuum are listed in Table 9. Compared with model a, models c, f and jwith passive storages increase isotope mixing and lead to a reduction in the δD variability (see the narrower range of δD for models c, f and j in Table 9). Meanwhile, as the number of passive storages increases in the models, the mixing of the fast flow and slow flow is enhanced, leading to the mean δD values of slow flow approaching that of fast flow. Nevertheless, for the three better models, the strengthened mixing of slow flow only has a limited effect on the mean δD of fast flow, as the mean δD of the catchment outlet flow is closer to that of fast flow. This further supports the hypothesis that hillslope fast-flow dynamics control the catchment flow and isotopic concentration at the outlet.
Table 8The proportions of flow components in the hillslope–depression–outlet continuum for the 30 optimal solution sets of the selected representative models during the study period ( %).
Note that the total flow at the catchment outlet is the sum of slow flow, fast flow and surface flow.
5.1 The importance of passive storage for tracer-aided hydrological modeling
Involving passive storage in a coupled flow–isotope model helped to improve the performance of the discharge simulations while also allowing one to capture tracer dynamics, which has been demonstrated by most previous studies (see Table 1). However, the exact configuration of how passive storage is involved in the model can be set in different positions in different models (Table 1) or even in a specific model. Using the STARR (Spatially Distributed Tracer- Aided Rainfall–Runoff) model as an example, van Huijgevoort et al. (2016), Dehaspe et al. (2018) and Piovano et al. (2019) added two passive storages for the soil and groundwater stores, whereas Ala-Aho et al.(2017) and Piovano et al. (2020) only used a passive storage in the soil store. Of all the studies listed in Table 1, only Fenicia et al. (2008) and Birkel et al. (2011b) compared the simulation effects of the model structure on discharge with and without passive storages.
Most previous studies have focused on non-karst catchments, and passive storages are usually represented in slow-flow reservoirs (Hrachowitz et al., 2013; Yang et al., 2021; see Table 1). Birkel et al. (2011a) and Hrachowitz et al. (2013) suggested that this passive storage can be interpreted as soil moisture below field capacity or groundwater below the dynamic storage. For more complex model structures, delineating flow components and connections in heterogeneous landscape units usually requires more flow routing compartments and, thus, additional passive storages. For example, Capell et al. (2012) identified that only three passive storages were necessary for a tracer-aided model with four possible passive storages in upland and lowland units in the North Esk Catchment in northeastern Scotland. They found that passive storage in the shallow zone for the upland unit was negligible, as sufficient damping was available in the dynamic (active) storage.
Required model structures are usually more complex in karst catchments due to different conceptualization of recharge and flow mechanisms. Most studies have demonstrated that the fast channelized flow paths control the sharp rise and decline in the hydrograph; thus, setting passive storage in the fast-flow reservoir can improve simulation accuracy of the catchment flow and tracer dynamics in karst catchments, particularly in cockpit karst landscapes. For example, Zhang et al. (2019) assumed that hillslope flow is rapid, and they showed that directly setting a passive storage in the hillslope flow reservoir can successfully capture the dynamics of flow discharge and stable isotopes in the same study catchment. Similarly, elsewhere, Chang et al. (2020) developed a model capturing the functioning of a dual-flow (fast-flow and slow-flow) system, showing that setting a passive storage in the fast-flow reservoir can reproduce the dynamics of flow discharge and spring EC.
Our study was novel in that we comprehensively analyzed the functioning of alternative configurations of passive storage in a complex model structure for cockpit karst catchments, based on a comparison of the performances of 14 different models. Through this comparison, we demonstrated that adding passive storage in the fast-flow reservoir in the hillslope unit is more efficient for simulating flow components and isotope dynamics, with three alternative choices to set passive storages in our developed model. The most parsimonious model is to add a passive storage in the hillslope fast-flow reservoir, as in model c. The “best” model is to add two passive storages in the fast-flow and slow-flow reservoirs of the hillslope unit, as is the case in model f. This best model can appropriately estimate flow components in addition to the total discharge and isotope concentration at the catchment outlet. Adding an additional passive storage in the depression slow-flow reservoir, such as in model j, does not further substantially increase the simulation accuracy, even though the model obtains higher KGEq and KGEc, as shown in Table 6.
5.2 The dominant transport processes: advection, dispersion or molecular diffusion?
Generally, the transport process is largely controlled by advection (with the tracer traveling with water), by molecular diffusion in the slow-velocity (or immobile) zone and by hydrodynamic dispersion in the fast-velocity (or mobile) zone (Karadimitriou et al., 2016; Schumer et al., 2003; Wang et al., 2020). In karst flow systems, larger fractures and conduit media have permeabilities that can be several orders of magnitude higher than those of matrix flow in micropores. In cockpit karst catchments, the hillslope unit has a higher flow velocity but longer flow paths to the outlet. Tracers input farthest from the stream at the hillslope unit will undergo more dispersion (Kirchner et al., 2001). In our study catchment, the hillslope unit has a higher flow velocity, as the outflow coefficient of fast flow in the modeled hillslope unit is much greater than that of the depression unit (Table 7) for the models showing the best performance (c, f and j). Meanwhile, configuring passive storage in the hillslope fast flow alone is sufficient to damp the δD variability effectively. This points to the fact that hydrodynamic dispersion dominates the chemical mixing. Indeed, the dominance of hydrodynamic dispersion has been widely reported in flow-conductive (preferential flow) zones (Roubinet et al., 2012). For example, Zhao et al. (2019, 2021) used a transient storage model (TSM) to study the tailing of breakthrough curves (BTCs) of tracers in karst conduits, with experimental results suggesting that the dispersion coefficient was positively correlated with the flow velocity.
Table 10The simulated (m3 × ‰) of flow components in the hillslope–depression–outlet continuum for the 30 optimal solution sets from the selected representative models during the study period.
“–” represents not available.
The mass exchange fluxes (EGMF and EGMS in Eqs. 11 and 12) between active and passive storages are given in Table 10. The mass exchange flux of hillslope fast flow is greater than that of slow flow, and it is over 10 times larger than that of slow flow in the depression unit. This result also supports the fact that the hillslope unit has stronger dispersion effects. Therefore, the stronger variations in discharge and isotopes can only be better captured simultaneously when the functioning of the advection and dispersion of the hillslope unit is incorporated in the models.
5.3 Uncertainties in adding passive storage in the tracer-aided hydrological modeling
Our model uses a distribution curve of unsaturated storage capacity to describe the spatial heterogeneity of storage volumes, and it employs fast-flow and slow-flow systems to conceptualize dual-karst-flow systems on a large scale (e.g., hillslope and depression units). Optimizing the number of storages balances the need to minimize model complexity and uncertainty while also improving the simulation performance of both flow and tracers. Particularly for karst catchments, this optimization needs to be based on short-time-interval observation data, such as hourly data in our study catchment, to capture the rapid hydrological response. Only such fine-resolution data can capture the dramatic variability in the hydrograph and tracer dynamic and, thus, can be used to successfully optimize the model structure. Nevertheless, the optimized passive storages and model structures are not unique, as the three better models with one to three passive storages performed similarly well in the study catchment, in terms of the catchment input–output responses.
These uncertainties imply that additional observations are needed to enhance our ability to constrain complex model structures and the ranges of model parameters in karst catchments. These additional observations should include not only the catchment input–output responses but also some key hydrological internal state components and their isotope concentrations, such as water fluxes and isotope transport in micropore, fracture and conduit media in karst catchments. Moreover, detailed observations of human activities are also important to reduce the modeling uncertainties. As shown in our study catchment, the depression is occupied by agricultural land. Groundwater pumping for agriculture use causes sudden declines in streamflow and isotopic concentrations in June, as shown in Fig. 7, which makes that the model overestimates low flow.
Our study catchment at Chenqi is broadly representative of extensive regions of headwater catchments in cockpit karst landscapes, and while the model parameters still need to be calibrated for specific catchments, the model is generic and transferable to other areas. The approach also has the potential to be used in upscaling to large catchments, although the model would then need to incorporate river and channel routing, as these play an important role in regulating streamflow variations at larger scales.
In cockpit karst landscapes dominated by poljes and surrounding tower areas, depression areas are interconnected with isolated towers scattered throughout the terrain (Lyew et al., 2007). In this study, we developed and tested a coupled flow–tracer model for simulating discharge and isotope signatures for cockpit karst landscapes, represented using a “hillslope–depression–outlet” continuum. We tested 14 simulation cases with alternative model structures by varying the number and configuration of passive storage in the fast-/slow-flow reservoirs of hillslope/depression units. The model structures and parameters were optimized using a multi-objective optimization algorithm to match the observed discharge and isotope dynamics in the Chenqi Catchment in southwestern China.
We found that, for complex models developed for cockpit karst catchments, capturing the main hydrological flow paths and organizing passive storages in relation to these flow paths can efficiently improve model performance. In the Chenqi Catchment, the main hydrological pathways are hillslope flow and its connection with the catchment outlet. The models with one to three passive storages achieve similarly optimal results that are supported by the KGEq, KGEc and Abiasq values. All three models have a passive storage in the dominant flow domain (hillslope fast flow).
The optimal model structure is supported by the simulated discharge and tracer dynamics. The hillslope fast-flow system contributes about ∼ 80 % of the outlet discharge. The passive storages in the optimal models strengthen isotope mixing and, thus, constrain the δD and discharge variability. Further comparison of the simulated results by the three optimal models with one to three passive storages showed that the “best” model structure is to incorporate two passive storages in the fast- and slow-flow reservoirs of the hillslope unit. This best model can appropriately estimate flow components in addition to the total discharge and isotope fluctuations at the catchment outlet.
Characterizing the dynamics of flow paths and connections in complex geological settings karst landscapes is central to better understanding fluid flow and solute transport processes. This study provided evidence that the protection of hillslope environments is significant for the prevention of natural hazards, such as droughts, floods and contamination, in karst landscapes.
The code that supports the findings of this study is available from the corresponding author upon reasonable request.
The discharge and isotope data that support the findings of this study can be shared following the completion of our project, as per the project executive policy. In the meantime, the data can be made available from the corresponding author upon request.
GL was responsible for writing the original draft, developing the methodology, curating the data and creating the figures. XC conceptualized the project, reviewed and edited the manuscript, conducted the formal analysis, and acquired funding. ZZ and LW developed the methodology and curated the data. CS reviewed and edited the manuscript.
The contact author has declared that none of the authors has any competing interests.
Publisher's note: Copernicus Publications remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This research was supported by the National Natural Science Foundation of China (grant nos. 42030506 and 41971028). We thank Natalie Orlowski, the two reviewers (Catherine Bertrand and the anonymous reviewer) and Thom Bogaard for their constructive comments that significantly improved the manuscript.
This research has been supported by the National Natural Science Foundation of China (grant nos. 42030506 and 41971028).
This paper was edited by Thom Bogaard and reviewed by Catherine Bertrand and one anonymous referee.
Adinehvand, R., Raeisi, E., and Hartmann, A.: A step-wise semi-distributed simulation approach to characterize a karst aquifer and to support dam construction in a datascarce environment, J. Hydrol., 554, 470–481, https://doi.org/10.1016/j.jhydrol.2017.08.056, 2017.
Ala-aho, P., Tetzlaff, D., McNamara, J. P., Laudon, H., and Soulsby, C.: Using isotopes to constrain water flux and age estimates in snow-influenced catchments using the STARR (Spatially distributed Tracer-Aided Rainfall–Runoff) model, Hydrol. Earth Syst. Sci., 21, 5089–5110, https://doi.org/10.5194/hess-21-5089-2017, 2017.
Barnes, C. J. and Bonell, M.: Application of unit hydrograph techniques to solute transport in catchments, Hydrol. Process., 10, 793–802, 1996.
Benettin, P., Kirchner, J. W., Rinaldo, A., and Botter, G.: Modeling chloride transport using travel time distributions at Plynlimon, Wales, Water Resour. Res., 51, 3259–3276, https://doi.org/10.1002/2014WR016600, 2015.
Beven, K.: A manifesto for the equifinality thesis, J. Hydrol., 320, 18–36, https://doi.org/10.1016/j.jhydrol.2005.07.007, 2006.
Birkel, C. and Soulsby, C.: Advancing tracer-aided rainfall-runoff modelling: A review of progress, problems and unrealised potential, Hydrol. Process., 29, 5227–5240, https://doi.org/10.1002/hyp.10594, 2015.
Birkel, C., Tetzlaff, D., Dunn, S. M., and Soulsby, C.: Using lumped conceptual rainfall-runoff models to simulate daily isotope variability with fractionation in a nested mesoscale catchment, Adv. Water Resour., 34, 383–394, https://doi.org/10.1016/j.advwatres.2010.12.006, 2011a.
Birkel, C., Soulsby, C., and Tetzlaff, D.: Modelling catchment-scale water storage dynamics: reconciling dynamic storage with tracer-inferred passive storage, Hydrol. Process., 25, 3924–3936, https://doi.org/10.1002/hyp.8201, 2011b.
Birkel, C., Soulsby, C., and Tetzlaff, D.: Conceptual modelling to assess how the interplay of hydrological connectivity, catchment storage and tracer dynamics controls non-stationary water age estimates, Hydrol. Process., 29, 2956–2969, https://doi.org/10.1002/hyp.10414, 2015.
Birkel, C., Duvert, C., Correa, A., Munksgaard, N. C., Maher, D. T., and Hutley, L. B.: Tracer-aided modeling in the low-relief, wet-dry tropics suggests water ages and DOC export are driven by seasonal wetlands and deep groundwater, Water Resour. Res., 55, e2019WR026175, https://doi.org/10.1029/2019WR026175, 2020.
Capell, R., Tetzlaff, D., and Soulsby, C.: Can time domain and source area tracers reduce uncertainty in rainfall-runoff models in larger heterogeneous catchments?, Water Resour. Res., 48, W09544, https://doi.org/10.1029/2011wr011543, 2012.
Carey, S. and Quinton, W.: Evaluating snowmelt runoff generation in a discontinuous permafrost catchment using stable isotope, hydrochemical and hydrometric data, Hydrol. Res., 35, 309–324, https://doi.org/10.2166/nh.2004.0023, 2004.
Chacha, N., Njau, K. N., Lugomela, G. V., and Muzuka, A. N. N.: Groundwater age dating and recharge mechanism of Arusha aquifer, northern Tanzania: application of radioisotope and stable isotope techniques, Hydrogeol. J., 26, 2693–2706, https:// doi.org/10.1007/s10040-018-1832-0, 2018.
Chang, Y., Hartmann, A., Liu, L., Jiang, G., and Wu, J.: Identifying more realistic model structures by electrical conductivity observations of the karst spring, Water Resour. Res., 57, e2020WR028587, https://doi.org/10.1029/2020WR028587, 2020.
Charlier, J.-B., Bertrand, C., and Mudry, J.: Conceptual hydrogeological model of flow and transport of dissolved organic carbon in a small Jura karst system, J. Hydrol., 460, 52–64, https://doi.org/10.1016/j.jhydrol.2012.06.043, 2012.
Chen, X., Zhang, Z., Soulsby, C., Cheng, Q., Binley, A., Jiang, R., and Tao, M.: Characterizing the heterogeneity of karst critical zone and its hydrological function: an integrated approach, Hydrol. Process., 2018, 2932–2946, https://doi.org/10.1002/hyp.13232, 2018.
Cheng, Q., Chen, X., Tao, M., and Binley, A.: Characterization of karst structures using quasi-3D electrical resistivity tomography, Environ. Earth Sci., 78, 285, https://doi.org/10.1007/s12665-019-8284-2, 2019.
Deb, K., Pratap, A., Agarwal, S., and Meyarivan, T.: A fast and elitist multi-objective genetic algorithm: NSGA-II, IEEE T. Evol. Comput., 6, 182–197, https://doi.org/10.1109/4235.996017, 2002.
Dehaspe, J., Birkel, C., Tetzlaff, D., Sánchez-Murillo, R., Durá-Quesada, A. M., and Soulsby, C.: Spatially-distributed tracer-aided modelling to explore water and isotope transport, storage and mixing in a pristine, humid tropical catchment, Hydrol. Process., 32, 3206–3224, https://doi.org/10.1002/hyp.13258, 2018.
Ding, H., Zhang, X., Chu, X., and Wu, Q.: Simulation of groundwater dynamic response to hydrological factors in karst aquifer system, J. Hydrol., 587, 124995, https://doi.org/10.1016/j.jhydrol.2020.124995, 2020.
Delavau, C. J., Stadnyk, T., and Holmes, T.: Examining the impacts of precipitation isotope input (δ18Oppt) on distributed, tracer-aided hydrological modelling, Hydrol. Earth Syst. Sci., 21, 2595–2614, https://doi.org/10.5194/hess-21-2595-2017, 2017.
Dubois, E., Doummar, J., Pistre, S., and Larocque, M.: Calibration of a lumped karst system model and application to the Qachqouch karst spring (Lebanon) under climate change conditions, Hydrol. Earth Syst. Sci., 24, 4275–4290, https://doi.org/10.5194/hess-24-4275-2020, 2020.
Dunn, S. M., Birkel, C., Soulsby, C., and Tetzlaff, D.: Transit time distributions of a conceptual model: their characteristics and sensitivities, Hydrol. Process., 24, 1719–1729, https://doi.org/10.1002/hyp.7560, 2010.
Elghawi, R., Pekhazis, K., and Doummar, J.: Multi-regression analysis between stable isotope composition and hydrochemical parameters in karst springs to provide insights into groundwater origin and subsurface processes: regional application to Lebanon, Environ. Earth Sci., 80, 1–21, https://doi.org/10.1007/s12665-021-09519-4, 2021.
Fenicia, F., Savenije, Hubert, H. G., Matgen, P., and Pfister, L.: A comparison of alternative multiobjective calibration strategies for hydrological modeling, Water Resour. Res., 43, W03434, https://doi.org/10.1029/2006wr005098, 2007.
Fenicia, F., McDonnell, J. J., and Savenije, H. H. G.: Learning from model improvement: on the contribution of complementary data to process understanding, Water Resour. Res., 44, W06419, https://doi.org/10.1029/2007WR006386, 2008.
Fenicia, F., Wrede, S., Kavetski, D., Pfister, L., Hoffmann, L., Savenije, H. H. G., and McDonnell, J. J.: Assessing the impact of mixing assumptions on the estimation of streamwater mean residence time, Hydrol. Process., 24, 1730–1741, https://doi.org/10.1002/hyp.7595, 2010.
Freer, J., Beven, K., and Ambroise, B.: Bayesian estimation of uncertainty in runoff prediction and the value of data: An application of the GLUE approach, Water Resour. Res., 32, 2161–2173, https://doi.org/10.1029/96WR03723, 1996.
Hrachowitz, M., Savenije, H., Bogaard, T. A., Tetzlaff, D., and Soulsby, C.: What can flux tracking teach us about water age distribution patterns and their temporal dynamics?, Hydrol. Earth Syst. Sci., 17, 533–564, https://doi.org/10.5194/hess-17-533-2013, 2013.
Hartmann, A., Barberá, J. A., Lange, J., Andreo, B., and Weiler, M.: Progress in the hydrologic simulation of time variant recharge areas of karst systems-Exemplified at a karst spring in Southern Spain, Adv. Water Resour., 54, 149–160, https://doi.org/10.1016/j.advwatres.2013.01.010, 2013.
Husic, A., Fox, J., Adams, E., Ford, W., Agouridis, C., Currens, J., Backus, J.: Nitrate Pathways, processes, and timing in an agricul-tural karst system: Development and application of a numerical model, Water Resour. Res., 55, 2079–2103, https://doi.org/10.1029/2018WR023703, 2019.
Jeannin, P. Y., Artigue, G., Butscher, C., Chang, Y., Charlier, J. B., Duran, L., Gill, L., Hartmann, A., Johannet, A., Jourde, H., Kavousi, A., Liesch, T., Liu, Y., Lüthi, M., Malard, A., Mazzilli, N., Pardo-Igúzquiza, E., Thiéry, D., Reimann, T., Schuler, P., Wöhling, T., and Wunsch, A.: Karst modelling challenge 1: Results of hydrological modelling, J. Hydrol., 600, 126508, https://doi.org/10.1016/j.jhydrol.2021.126508, 2021.
Jourde, H., Massei, N., Mazzilli, N., Binet, S., Batiot-Guilhe, C., Labat, D., Steinmann, M., Bailly-Comte, V., Seidel, J. L., Arfib, B., Charlier, J. B., Guinot, V., Jardani, A., Fournier, M., Aliouache, M., Babic, M., Bertrand, C., Brunet, P., Boyer, J. F., Bricquet, J. P., Camboulive, T., Carrière, S. D., Celle- Jeanton, H., Chalikakis, K., Chen, N., Cholet, C., Clauzon, V., Soglio, L. D., Danquigny, C., Défargue, C., Denimal, S., Emblanch, C., Hernandez, F., Gillon, M., Gutierrez, A., Sanchez, L. H., Hery, M., Houillon, N., Johannet, A., Jouves, J., Jozja, N., Ladouche, B., Leonardi, V., Lorette, G., Loup, C., Marchand, P., de Montety, V., Muller, R., Ollivier, C., Sivelle, V., Lastennet, R., Lecoq, N., Maréchal, J. C., Perotin, L., Perrin, J., Petre, M. A., Peyraube, N., Pistre, S., Plagnes, V., Probst, A., Probst, J. L., Simler, R., Stefani, V., Valdes-Lao, D., Viseur, S., and Wang, X.: SNO KARST: A French Network of Observatories for the Multidisciplinary Study of Critical Zone Processes in Karst Watersheds and Aquifers, Vadose Zone J., 17, 180094, https://doi.org/10.2136/vzj2018.04.0094, 2018.
Lyew-Ayee, P., Viles, H, A., and Tucker, G, E.: The use of GIS-based digital morphometric techniques in the study of cockpit karst, Earth Surf. Process. Land., 32, 165–179, https://doi.org/10.1002/esp.1399, 2007.
Mayer-Anhalt, L., Birkel, C., Sánchez-Murillo, R., and Schulz, S.: Tracer-aided modelling reveals quick runoff generation and young streamflow ages in a tropical rainforest catchment, Hydrol. Process., 36, e14508, https://doi.org/10.1002/hyp.14508, 2022.
Mudarra, M., Hartmann, A., and Andreo, B.: Combining experimental methods and modeling to quantify the complex recharge behavior of karst aquifers, Water Resour. Res., 55, 1384–1404, https://doi.org/10.1029/2017WR021819, 2019.
Neill, A. J., Tetzlaff, D., Strachan, N. J. C., and Soulsby, C.: To what extent does hydrological connectivity control dynamics of faecal indicator organisms in streams? Initial hypothesis testing using a tracer-aided model, J. Hydrol., 570, 423–435, https://doi.org/10.1016/j.jhydrol.2018.12.066, 2019.
Kirchner, J. W., Feng, X., and Neal, C.: Catchment-scale advection and dispersion as a mechanism for fractal scaling in stream tracer concentrations, J. Hydrol., 254, 82–101, https://doi.org/10.1016/s0022-1694(01)00487-5, 2001.
Kling, H., Fuchs, M., and Paulin, M.: Runoff conditions in the upper Danube basin under an ensemble of climate change scenarios, J. Hydrol., 424, 264–277, https://doi.org/10.1016/j.jhydrol.2012.01.011, 2012.
Kollat, J. B. and Reed, P. M.: Comparing state-of-the-art evolutionary multi-objective algorithms for long-term groundwater monitoring design, Adv. Water Resour., 29, 792–807, https://doi.org/10.1016/j.advwatres.2005.07.010, 2006.
Karadimitriou, N. K., Joekar-Niasar, V., Babaei, M., and Shore, C. A.: Critical Role of the Immobile Zone in Non-Fickian Two-Phase Transport: A New Paradigm, Environ. Sci. Technol., 50, 4384–4392, https://doi.org/10.1021/acs.est.5b05947, 2016.
Long, A. J. and Putnam, L. D.: Linear model describing three components of flow in karst aquifers using 18O data, J. Hydrol., 296, 254–270, https://doi.org/10.1016/j.jhydrol.2004.03.023, 2004.
Martínez-Santos, P. and Andreu, J. M.: Lumped and distributed approaches to model natural recharge in semiarid karst aquifers, J. Hydrol., 388, 389–398, https://doi.org/10.1016/j.jhydrol.2010.05.018, 2010.
Nan, Y., Tian, L., He, Z., Tian, F., and Shao, L.: The value of water isotope data on improving process understanding in a glacierized catchment on the Tibetan Plateau, Hydrol. Earth Syst. Sci., 25, 3653–3673, https://doi.org/10.5194/hess-25-3653-2021, 2021.
Ollivier, C., Mazzilli, N., Olioso, A., Chalikakis, K., Carrière, S. D., Danquigny, C., and Emblanch, C.: Karst recharge-discharge semi distributed model to assess spatial variability of flows, Sci. Total Environ., 703, 134368, https://doi.org/10.1016/j.scitotenv.2019.134368, 2020.
Page, T., Beven, K. J., Freer, J., and Neal, C.: Modelling the chloride signal at Plynlimon, Wales, using a modified dynamic TOPMODEL incorporating conservative chemical mixing (with uncertainty), Hydrol. Process., 21, 292–307, https://doi.org/10.1002/hyp.6186, 2007.
Perrin, C., Michel, C., and AndreÂassian, V.: Does a large number of parameters enhance model performance? Comparative assessment of common catchment model structures on 429 catchments, J. Hydrol., 242, 275–301, https://doi.org/10.1016/S0022-1694(00)00393-0, 2001.
Piovano, T. I., Tetzlaff, D., Carey, S. K., Shatilla, N. J., Smith, A., and Soulsby, C.: Spatially distributed tracer-aided runoff modelling and dynamics of storage and water ages in a permafrost-influenced catchment, Hydrol. Earth Syst. Sci., 23, 2507–2523, https://doi.org/10.5194/hess-23-2507-2019, 2019.
Piovano, T. I., Tetzlaff, D., Maneta, M., Buttle, J. M., Carey, S. K., Laudon, H., McNamarah, J., and Soulsby, C.: Contrasting storage-flux-age interactions revealed by catchment inter-comparison using a tracer-aided runoff model, J. Hydrol., 590, 125226, https://doi.org/10.1016/j.jhydrol.2020.125226, 2020.
Roubinet, D., Dreuzy, J., and Tartakovsky, D. M.: Semi-analytical solutions for solute transport and exchange in fractured porous media, Water Resour. Res., 48, 273–279, https://doi.org/10.1029/2011WR011168, 2012.
Rodriguez, N. B., McGuire, K. J., and Klaus, J.: Time-varying storage-Water age relationships in a catchment with a Mediterranean climate, Water Resour. Res., 54, 3988–4008, https://doi.org/10.1029/2017WR021964, 2018.
Son, K. and Sivapalan, M.: Improving model structure and reducing parameter uncertainty in conceptual water balance models through the use of auxiliary data, Water Resour. Res., 43, W01415, https://doi.org/10.1029/2006wr005032, 2007.
Soulsby, C., Piegat, K., Seibert, J., and Tetzlaff, D.: Catchment scale estimates of flow path partitioning and water storage based on transit time and runoff modelling, Hydrol. Process., 25, 3960–3976, https://doi.org/10.1002/hyp.8324, 2011.
Soulsby, C., Birkel, C., Geris, J., Dick, J., Tunaley, C., and Tetzlaff, D.: Stream water age distributions controlled by storage dynamics and nonlinear hydrologic connectivity: Modeling with high-resolution isotope data, Water Resour. Res., 51, 7759–7776, https://doi.org/10.1002/2015WR017888, 2015.
Sprenger, M., Tetzlaff, D., and Soulsby, C.: Soil water stable isotopes reveal evaporation dynamics at the soil–plant–atmosphere interface of the critical zone, Hydrol. Earth Syst. Sci., 21, 3839–3858, https://doi.org/10.5194/hess-21-3839-2017, 2017.
Sprenger, M., Tetzlaff, D., Buttle, J., Laudon, H., Leistert, H., Mitchell, C. P. J., Snelgrove, J., Weiler, M., and Soulsby, C.: Measuring and modeling stable isotopes of mobile and bulk soil water, Vadose Zone J., 17, 170149, https://doi.org/10.2136/vzj2017.08.0149, 2018.
Schumer, R., Benson, D. A., Meerschaert, M. M., Baeumer, B.: Fractal mobile/immobile solute transport, Water Resour. Res., 39, 1296, https://doi.org/10.1029/2003WR002141, 2003.
van Huijgevoort, M. H. J., Tetzlaff, D., Sutanudjaja, E. H., and Soulsby, C.: Using high resolution tracer data to constrain water storage, flux and age estimates in a spatially distributed rainfall-runoff model, Hydrol. Process., 30, 4761–4778, https://doi.org/10.1002/hyp.10902, 2016.
Wang, L., Cardenas, M. B., Zhou, J. Q., and Ketcham, R. A.: The complexity of nonlinear flow and non-Fickian transport in fractures driven by three-dimensional recirculation zones, J. Geophys. Res.-Sol. Ea., 125, e2020JB020028, https://doi.org/10.1029/2020JB020028, 2020.
White, W. B.: A brief history of karst hydrogeology: contributions of the NSS, J. Cave Karst Stud., 69, 13–26, 2007.
Worthington, S. R. H.: Diagnostic hydrogeologic characteristics of a karst aquifer (Kentucky, USA), Hydrogeol. J., 17, 1665–1678, https://doi.org/10.1007/s10040-009-0489-0, 2009.
Worthington, S. R. H., Davies, G. J., and Ford, D. C.: Matrix, fracture and channel components of storage and flow in a Paleozoic limestone aquifer, in: Groundwater flow and contaminant transport in carbonate aquifers, edited by: Sasowsky, I. D. and Wicks, C. M.,Balkema, Rotterdam, 113–128, ISBN 90-5410-498-8, 2000.
Wunsch, A., Liesch, T., Cinkus, G., Ravbar, N., Chen, Z., Mazzilli, N., Jourde, H., and Goldscheider, N.: Karst spring discharge modeling based on deep learning using spatially distributed input data, Hydrol. Earth Syst. Sci., 26, 2405–2430, https://doi.org/10.5194/hess-26-2405-2022, 2022.
Xu, C., Xu, X., Liu, M., Li, Z., Zhang, Y., Zhu, J., Wang, K., Chen, X., Zhang, Z., Peng, T.: An improved optimization scheme for representing hillslopes and depressions in karst hydrology, Water Resour. Res., 56, e2019WR026038, https://doi.org/10.1029/2019WR026038, 2020.
Xue, B., Chen, X., Zhang, Z., Cheng, Q.: A Semi-distributed Karst Hydrological Model Considering the Hydraulic Connection Between Hillslope and Depression: a case Study in Chenqi Catchment, China Rural Water And Hydropower., 437, 1–5, 2019 (in Chinese).
Yang, X., Tetzlaff, D., Soulsby, C., Smith, A., and Borchardt, D.: Catchment functioning under prolonged drought stress: tracer-aided ecohydrological modeling in an intensively managed agricultural catchment, Water Resour. Res., 57, e2020WR029094, https://doi.org/10.1029/2020WR029094, 2021.
Zhang, R., Chen, X., Zhang, Z., and Soulsby, C.: Using hysteretic behavior and hydrograph classification to identify hydrological function across the “hillslope-depression-stream” continuum in a karst catchment, Hydrol. Process., 34, 3464–3480, https://doi.org/10.1002/hyp.13793, 2020.
Zhang, Z., Chen, X., Ghadouani, A., and Peng, S.: Modelling hydrological processes influenced by soil, rock and vegetation in a small karst basin of southwest China, Hydrol. Process., 25, 2456–2470, https://doi.org/10.1002/hyp.8022, 2011.
Zhang, Z., Chen, X., Cheng, Q., and Soulsby, C.: Storage dynamics, hydrological connectivity and flux ages in a karst catchment: conceptual modelling using stable isotopes, Hydrol. Earth Syst. Sci., 23, 51–71, https://doi.org/10.5194/hess-23-51-2019, 2019.
Zhang, Z., Chen, X., Cheng, Q., and Soulsby, C.: Characterizing the variability of transit time distributions and young water fractions in karst catchments using flux tracking. Hydrol. Process., 34, 3156–3174, https://doi.org/10.1002/hyp.13829, 2020.
Zhao, R. J.: The xinanjiang model applied in china. J. Hydrol., 135, 371–381, https://doi.org/10.1016/0022-1694(92)90096-E, 1992.
Zhao, X., Chang, Y., Wu, J., and Xue, X.: Effects of flow rate variation on solute transport in a karst conduit with a pool, Environ. Earth Sci., 78, 237, https://doi.org/10.1007/s12665-019-8243-y, 2019.
Zhao, X., Chang, Y., Wu, J., Li, Q., and Cao, Z.: Investigating the relationships between parameters in the transient storage model and the pool volume in karst conduits through tracer experiments, J. Hydrol., 593, 125825, https://doi.org/10.1016/j.jhydrol.2020.125825, 2021.