Impact of cry wolf effects on social preparedness and the efficiency of flood early warning systems

To improve the efficiency of flood early warning systems (FEWS), it is important to understand the interactions between natural and social systems. The high level of trust in authorities and experts is necessary to improve the likeliness of individuals to take preparedness actions responding to warnings. Despite many efforts to develop the dynamic model of human and water in socio-hydrology, no socio-hydrological models explicitly simulate social collective trust in FEWS. Here, we develop the stylized model to simulate the interactions of flood, social collective memory, social collective trust in FEWS, and preparedness actions responding to warnings by extending the existing socio-hydrological model. We realistically simulate the cry wolf effect in which many false alarms undermine the credibility of the early warning systems and make it difficult to induce preparedness actions. We found that (1) considering the dynamics of social collective trust in FEWS is more important in the technological society with infrequent flood events than in the green society with frequent flood events; and (2) as the natural scientific skill to predict flood events is improved, the efficiency of FEWS gets more sensitive to the behavior of social collective trust, so that forecasters need to determine their warning threshold by considering the social aspects.

1 Introduction

The number of severe flood events is expected to increase in many regions due to climate change (Hirabayashi et al., 2013, 2021). Based on the advances of weather forecasting (e.g., Bauer et al., 2015; Miyoshi et al., 2016; Sawada et al., 2019) and hydrodynamic modeling (e.g., Yamazaki et al., 2011; Trigg et al., 2016), flood early warning systems (FEWS) have become a promising tool to efficiently mitigate the damage of severe floods. However, to maximize the potential of FEWS, it is crucially important to understand the interactions between flood and social systems. The likeliness of individuals to take preparedness actions responding to flood warnings strongly depends on the individual's risk perception, which is controlled by the complex interaction between natural hazards and stakeholders (Wachinger et al., 2013).

In the literature of weather forecasting, the “cry wolf effect” has been intensively investigated as an important interaction between weather prediction and social systems. In Aesop's fable, “The Boy who Cried Wolf”, a young boy repeatedly tricks neighboring villagers into believing that a wolf is attacking the sheep. When a wolf actually appears and the young boy seriously calls for help, the villagers no longer trust the warning and fail to protect their sheep. Many false alarms undermine the credibility of the early warning systems. The cry wolf effect on mitigation and protection actions against meteorological disasters has been investigated in economics, sociology, and psychology. Many previous studies have found and quantified the cry wolf effects in meteorological disasters. Simmons and Sutter (2009) performed econometric analysis of a disaster database and revealed that tornadoes that occurred in areas with higher false alarm ratio killed and injured more people. Ripberger et al. (2015) performed a web-based questionnaire survey and revealed that subjective perceptions of warning systems' accuracy are systematically related to trust in a weather agency and stated responses to warnings. Trainor et al. (2015) performed large-scale telephone interviews and revealed the significant relationship between actual false alarm ratio and behavioral responses to tornado warnings. Jauernic and van den Broeke (2017) revealed that the odds of students initialing sheltering decreases nearly 1 % for every 1 % increase in perceived false alarm ratio based on their online questionnaire survey of 640 undergraduate students. Roulston and Smith (2004) found that the warning threshold of the actual weather warning systems can be justified only if the cry wolf effects were considered. This finding implies that many forecasters believe the existence of the cry wolf effects, and the design of early warning systems is affected by how the cry wolf effects are considered. It should be noted that while these previous works supported the cry wolf effect as an important factor to be considered for the design of warning systems, some studies discussed the myth of cry wolf effects, implying that they do not exist. For example, LeClerc and Joslyn (2015) performed a psychological experiment in which participants decided whether to apply salt brine to a town's roads to prevent icing according to weather forecasting. In their experiment, the effects of false alarms are so small that they found no evidence suggesting lowering false alarm ratio significantly increases compliance with weather warnings. Lim et al. (2019) performed an online questionnaire survey and found no significant relationship between actual false alarm ratio and responses to warnings. In addition, they found that the increase of perceived false alarm ratio enhanced protective behavior, which contradicted the other works. Although Trainor et al. (2015) supported the existence of the cry wolf effects, they also found that there is a wide variation in public definition of false alarms, and actual false alarm ratio does not predict perception of false alarm ratio. Although the existence of the cry wolf effect is still debatable due mainly to the lack of field data and the ambiguity of the quantification of the public perception of false alarms, the current evidence suggests the importance of understanding the effect of false alarms on behavioral responses to warning in order to design efficient flood early warning systems.

Socio-hydrology is an emerging research field contributing to understanding the interactions between flood and social systems (Sivapalan et al., 2012, 2014; Di Baldassarre et al., 2019). The primary approach of socio-hydrology is to develop the dynamic model of water and human. Many socio-hydrological models used social preparedness as a key driver of human–water interactions (e.g., Di Baldassarre et al., 2013; Viglione et al., 2014; Ciullo et al., 2017; Yu et al., 2017; Albertini et al., 2020). The pioneering work of Girons Lopez et al. (2017) revealed the effect of social preparedness on the efficiency of FEWS. Their main finding is that social preparedness is an important factor for flood loss mitigation especially when the accuracy of the forecasting system is limited. However, to our best knowledge, the existing socio-hydrological models simulated social preparedness as a function of social collective memory or personal experience of past disasters, and they considered no effect of trust in authorities and experts. Therefore, the cry wolf effect cannot be analyzed in the existing models. The systematic review of Wachinger et al. (2013) indicated that both personal experience of past disasters and trust in authorities and experts have substantial impact on risk perception. It is crucially important to include the social collective trust in FEWS in the socio-hydrological model to improve the design of FEWS considering social system dynamics.

The aim of this study is to develop the stylized model of the responses of social systems to FEWS as a simple extension of Girons Lopez et al. (2017). By modeling the dynamics of social collective trust in FEWS as a function of the recent success and failure of the forecasting system, we realistically simulate the cry wolf effect. By analyzing our newly developed model, we provide useful implication to maximize the potential of FEWS considering social system dynamics.

2 Model

Here, we slightly modified the model proposed by Girons Lopez et al. (2017). For brevity, the detailed explanation of equations shared with Girons Lopez et al. (2017) is omitted in this paper. See Gironz Lopez et al. (2017) and references therein for the complete description, including empirical evidence which supports each equation.

A synthetic time series of river discharge is generated. Following Girons Lopez et al. (2017), a simple bivariate gamma distribution, Γ, is used:

$$\begin{array}{}\text{(1)}& Q\sim \mathrm{\Gamma }\left({\mathit{\kappa }}_{\mathrm{c}}{\mathit{\theta }}_{\mathrm{c}}\right),\end{array}$$

where Q is maximum annual flow [L³ T⁻¹]. The bivariate gamma distribution is characterized by shape κ_c and scale θ_c.

This maximum annual flow, Q, is forecasted. In our model, the ensemble flood forecasting system (e.g., Cloke and Pappenberger, 2009) is installed, and the probabilistic forecast can be issued. The forecast probability distribution, F, is calculated by the following:

$$\begin{array}{}\text{(2)}& F\sim N(Q+N\left({\mathit{\mu }}_m,{\mathit{\sigma }}_m^{\mathrm{2}}\right),N\left({\mathit{\mu }}_v,{\mathit{\sigma }}_v^{\mathrm{2}}\right)),\end{array}$$

where N(.) is the Gaussian distribution, $N\left({\mathit{\mu }}_m,{\mathit{\sigma }}_m^{\mathrm{2}}\right)$ controls the prediction accuracy, and $N\left({\mathit{\mu }}_v,{\mathit{\sigma }}_v^{\mathrm{2}}\right)$ controls the prediction precision. Negative $N\left({\mathit{\mu }}_v,{\mathit{\sigma }}_v^{\mathrm{2}}\right)$ is truncated to $\mathrm{1.0}\times {\mathrm{10}}^{-\mathrm{6}}$ to prevent from obtaining negative values of variance. While Girons Lopez et al. (2017) change μ_m in their simulation, we set μ_m=0 assuming the forecast is unbiased. While Girons Lopez et al. (2017) used the bivariate gamma distribution to model the prediction precision, we used the Gaussian distribution to make it easier to interpret results. Although this simplification of the forecasting system unrealistically assigns non-zero probability to negative values of discharge, it does not affect the process dynamics since the model evolution depends only on whether forecasted discharge is above the damage threshold, as we explain in the next paragraph.

Table 1 Summary of the outcomes of the flood early warning system. Loss by each outcome is also shown (see also Sect. 2).

There is a damage threshold [L³ T⁻¹], δ, which is the proxy of levee height. When Q>δ, flood occurs. The forecast system calculates the probability of river discharge exceeding δ, and issues a warning if this probability of exceedance, P, is larger than a predefined probability threshold, π. Table 1 summarizes four different outcomes of forecasting: true positive, false positive, false negative, and true negative. When forecasters choose lower π, they issue many warnings with low forecasted probability of flooding, which inevitably increases false alarms. When forecasters choose higher π, they can reduce the number of false alarms by issuing the smaller number of warnings, which inevitably increases missed events.

Based on these four different outcomes shown in Table 1, damages and costs are calculated. Flood damage is assumed to be negligible when river discharge is smaller than a damage threshold (i.e., Q<δ). When Q≥δ, the damage function is defined as a simple exponential function, which is often used in the socio-hydrological literature (e.g., Di Baldassarre et al., 2013):

$$\begin{array}{}\text{(3)}& D_Q=\left\{\begin{array}{lr}\mathrm{0}& (Q<\mathit{\delta })\\ \mathrm{1}-e^{-\frac{Q-\mathit{\delta }}{\mathit{\beta }}}& (Q\ge \mathit{\delta })\end{array}\right.,\end{array}$$

where D_Q is damage [.], β is a model parameter [L⁻³ T]. If a flood event is successfully forecasted and a warning is issued (i.e., P≥π), this damage is mitigated by preparedness actions such as evacuation and safekeeping of assets. Note that preparedness actions which are not triggered by FEWS were not considered in this stylized model to focus only on the impact of social preparedness on the efficiency of FEWS. How much damage can be mitigated depends on social preparedness, P_r [.]. The mitigated damage (called residual damage in Girons Lopez et al., 2017), D_r [.], is calculated by the following:

$$\begin{array}{}\text{(4)}& D_r=D_Q{e}^{-P_r\ln \left(\frac{\mathrm{1}}{{\mathit{\alpha }}_{\mathrm{0}}}\right)},\end{array}$$

where α₀ is a model parameter [.] which determines the minimum possible damage. In summary, the flood damage [.], D, can be described by Eq. (5):

$$\begin{array}{}\text{(5)}& D=\left\{\begin{array}{lr}\mathrm{0}& (Q<\mathit{\delta })\\ \mathrm{1}-e^{-\frac{Q-\mathit{\delta }}{\mathit{\beta }}}& (Q\ge \mathit{\delta }\text{ and }P<\mathit{\pi })\\ \left(\mathrm{1}-e^{-\frac{Q-\mathit{\delta }}{\mathit{\beta }}}\right)e^{-P_r\ln \left(\frac{\mathrm{1}}{{\mathit{\alpha }}_{\mathrm{0}}}\right)}& (Q\ge \mathit{\delta }\text{ and }P\ge \mathit{\pi })\end{array}\right..\end{array}$$

Whenever a warning is issued, the cost [.], C, arises from mitigation and protection actions. Whenever a warning is issued, C is included in the total loss. Following Girons Lopez et al. (2017), we assumed that the cost is calculated by

$$\begin{array}{}\text{(6)}& C=\left\{\begin{array}{lr}\mathrm{0}& P<\mathit{\pi }\\ \mathit{\eta }Q& P\ge \mathit{\pi }\end{array}\right.,\end{array}$$

where η is a parameter [L⁻³ T]. Note that this cost has been found to be negligibly small compared with avoidable damage. For instance, Schroter et al. (2008) showed that the cost C is approximately 2 % of avoidable damage. In previous works, this cost was often neglected (e.g., Pappenberger et al., 2015; Hallegatte, 2012). Although Gironz Lopez et al. (2017) assumed there are significant costs of mitigation and protection actions, we will discuss how differently their model and our newly proposed model work with no mitigation costs (i.e., η=0) and with the original settings of Gironz Lopez et al. (2017).

The dynamics of social preparedness, P_r, in this study is different from Girons Lopez et al. (2017). We assumed that the social preparedness consisted of social collective memory and social collective trust in FEWS,

$$\begin{array}{}\text{(7)}& P_r\left(t\right)=\mathit{\gamma }E\left(t\right)+\left(\mathrm{1}-\mathit{\gamma }\right)T\left(t\right),\end{array}$$

where E(t) and T(t) are social collective memory [.] and social collective trust [.] in FEWS at time t, respectively. γ is a model parameter [.] that weights E(t) and T(t). Social collective memory is shared knowledge and information about past flood disasters that occurred in a community. In many socio-hydrological models, social collective memory is driven by the recency of past flood experience. Following Girons Lopez et al. (2017), the dynamics of social collective memory is described by the following:

$$\begin{array}{}\text{(8)}& E\left(t+\mathrm{1}\right)=\left\{\begin{array}{lr}E\left(t\right)-\mathit{\lambda }E\left(t\right)& (D=\mathrm{0})\\ E\left(t\right)+\mathit{\chi }D& (D>\mathrm{0})\end{array}\right.,\end{array}$$

where λ and χ are model parameters [.]. When E becomes larger than 1, it is truncated to 1.

Social collective trust is defined as shared knowledge and perception of the reliability of information issued from authorities. We assumed that social collective trust in FEWS is affected by the recent accuracy of FEWS. Previous studies pointed out that the recent forecast accuracy and false alarm ratio affected the performance of preparedness actions (Simmons and Sutter, 2009; Trainor et al., 2015; Ripberger et al., 2015; Jauernic and van den Broeke, 2017). In the controlled experiment of LeClerc and Joslyn (2015), medium-range trust ratings are increased by decreased false alarm levels. Their experiments revealed that trust ratings are based on the pattern of forecasts and observations over the previous month. It is reasonable to assume that trust in FEWS increases (decreases) when prediction succeeds (fails). We propose the following simple equation to describe the dynamics of social collective trust in FEWS:

$$\begin{array}{}\text{(9)}& T\left(t+\mathrm{1}\right)=\left\{\begin{array}{lr}T\left(t\right)& \text{ for true negative}\\ T\left(t\right)+{\mathit{\tau }}_{\mathrm{TP}}& \text{ for true positive}\\ T\left(t\right)-{\mathit{\tau }}_{\mathrm{FN}}& \text{ for false negative}\\ T\left(t\right)-{\mathit{\tau }}_{\mathrm{FP}}& \text{ for false positive}\end{array}\right.,\end{array}$$

where τ_TP, τ_FN, and τ_FP are positive parameters [.]. When T becomes larger than 1, it is truncated to 1. When T becomes smaller than 0, it is truncated to 0. By changing the value of these parameters, we can change the sensitivity of social collective trust in FEWS to the accuracy of FEWS. We will analyze the behavior of our model associated with several different combinations of these three parameters.

In our Eqs. (7–9), we can consider both social collective memory and social collective trust to analyze behavioral responses to warnings. For instance, please assume that a severe flood occurs and substantially damages a community, and this flood event cannot be predicted. In this case, social collective memory increases due to the large damage (Eq. 8). This increase of social collective memory E(t) contributes to increasing social preparedness towards the next severe flood event (Eq. 7). However, the failure of predicting this flood event decreases social collective trust in FEWS and authorities related to warning systems (Eq. 9), which negatively impacts to the capability of a community to deal with the next flood event by decreasing social preparedness (Eq. 7).

If social preparedness is determined only by social collective memory as Girons Lopez et al. (2017) proposed, small social collective memory directly results in insufficient social preparedness actions. In our proposed model, high social collective trust in FEWS can induce social preparedness actions even if a community loses past flood experiences to some extent (Eq. 7). However, if a weather agency repeatedly issues false alarms, social collective trust in FEWS decreases (Eq. 9), which negatively impacts on social preparedness (Eq. 7). Therefore, the dynamics of social preparedness in our proposed model is greatly different from Girons Lopez et al. (2017).

The additive form of the Eq. (7) implies that preparedness actions are taken even if either social collective memory E(t) or social collective trust T(t) goes to zero. Note that E(t)≈0 does not mean that a community does not know the existence of a flood event, while it means most citizens have never experienced water levels above damage thresholds by themselves. Many disasters prevention measures such as education, evaluation drills, and FEWS are designed to let people take preparedness actions even if they have no personal experiences of flood disasters. Forecasters expect that people take preparedness actions based on information from their trusted authorities even if they have never experienced damages themselves. To evaluate the effectiveness of these measures, P_r(t)=0 with E(t)=0 is not an appropriate behavior of the model, although the effectiveness of FEWS highly depends on E(t) as Girons Lopez et al. (2017) found. Therefore, we chose the additive form of the Eq. (7) rather than the other simple alternatives such as multiplicative forms.

Table 2 Fixed model parameters.

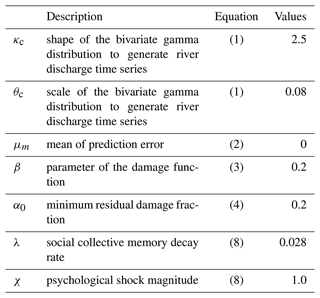
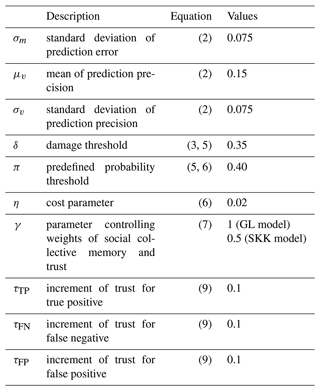
Many of the model parameters are fixed in our analysis. Table 2 summarizes the description and values of the fixed parameters. These parameters are not focused on in our analysis, and we chose their values from the previous works. The values of κ_c, θ_c, α₀, and χ are same as Girons Lopez et al. (2017). We set μ_m=0 assuming the forecast is unbiased (see also Eq. 2 and its description). Our specified β is within the range proposed by Girons Lopez et al. (2017). In addition, the results of Girons Lopez et al. (2017) indicated that this parameter is not sensitive to relative loss. We set λ assuming that social collective memory has 25-year half-life, which is within the range of previously quantified values (e.g., Fanta et al., 2019; Barendrecht et al., 2019). Some parameters are changed in our analysis to check their sensitivity to the performance of FEWS. Those parameters are explained in the next section.

3 Experiment design

3.1 Metrices

We used several metrices to evaluate the performance of FEWS. The purpose of FEWS is to reduce the total loss (D+C). We used the relative loss as Girons Lopez et al. (2017) did. The relative loss, L_r, is defined by Eq. (10):

$$\begin{array}{}\text{(10)}& L_{\mathrm{r}}={\displaystyle \frac{L_{\mathrm{FEWS}}}{L_{\mathrm{noFEWS}}}}.\end{array}$$

We performed the long-term (1000-year) numerical simulation by solving Eqs. (1–9) and calculated the total loss, L_FEWS. We also performed the simulation without FEWS in which flood damage is always calculated by Eq. (3) and D is always equal to D_Q. The total loss of this additional simulation is defined as L_noFEWS. The relative loss measures the efficiency of FEWS.

In addition to relative loss, we used hit rate, false alarm ratio, and threat score to evaluate the prediction accuracy which is not related to social system dynamics. They are defined by Eqs. (11–13):

$$\begin{array}{}\text{(11)}& {\displaystyle }\text{hit rate}={\displaystyle \frac{O_{\mathrm{TP}}}{O_{\mathrm{TP}}+O_{\mathrm{FN}}}}\text{(12)}& {\displaystyle }\text{false alarm ratio}={\displaystyle \frac{O_{\mathrm{FP}}}{O_{\mathrm{FP}}+O_{\mathrm{TP}}}}\text{(13)}& {\displaystyle }\text{threat score}={\displaystyle \frac{O_{\mathrm{TP}}}{O_{\mathrm{TP}}+O_{\mathrm{FP}}+O_{\mathrm{FN}}}},\end{array}$$

where O_TP, O_FN, and O_FP are the total number of true positive, false negative, and false positive events, respectively.

3.2 Simulation settings

We firstly compared the original model proposed by Girons Lopez et al. (2017) with our modified model. When we set γ=1 in Eq. (7), our model reduces to Girons Lopez et al. (2017) since we have no contributions of social collective trust in FEWS to social preparedness. In this paper, this original model is hereafter called the GL (Gironz Lopez) model. On the other hand, when we set γ=0.5 in Eq. (7), our model considers both social collective memory and social collective trust in FEWS with same weights to calculate social preparedness. There is no existing knowledge about the relative importance of social collective memory and social collective trust. Assuming the same weights gives us the most straightforward interpretation of the contributions of social collective trust and memory to social preparedness and the total loss by floods, since we do not need to consider asymmetric contributions of the two factors in Eq. (7). Therefore, γ=0.5 is appropriate to analyze the essential behavior of our proposed model. This new model with γ=0.5 is hereafter called the SKK (Sawada, Kanai, and Kotani) model. The behavior of the models with the different γ is also discussed in the supplement material.

Table 3 Model parameters in Experiment 1.

In Experiment 1, the time series of state variables of the two models are compared to demonstrate how differently the SKK and GL models work. The parameter variables in Experiment 1 are shown in Table 3. The initial conditions of E and T are randomly chosen and set to 0.49 and 0.77, respectively.

Table 4 Model parameters in Experiment 2.

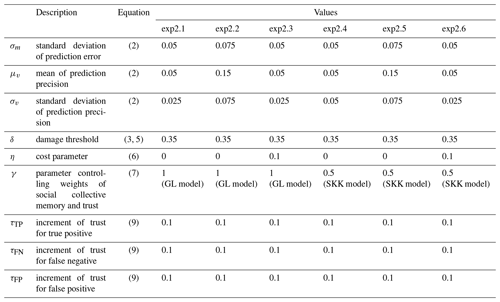
We mainly focused on the relationship between relative loss and a predefined probability threshold, π. This warning threshold is important for forecasters to determine whether they require general citizens to take preparedness actions. In Experiment 2, we used the same damage threshold, δ, as Girons Lopez et al. (2017), and compared the relationship between relative loss and predefined probability thresholds in the GL model with that in the SKK model under the different prediction skills and the cost parameter η. The settings of the parameters in Experiment 2 can be found in Table 4. The prediction skill is controlled by σ_m, μ_v, and σ_v. The greater values of these parameters provide inaccurate prediction. We prepared two sets of the parameter for relatively accurate and inaccurate prediction systems (see Table 4). Following the settings of Girons Lopez et al. (2017), we set η=0.1. In addition, we also performed the numerical simulation with η=0 (i.e., negligible costs of mitigation and protection actions), which is more consistent to the published literature than the original settings (see Sect. 2).

Table 5 Model parameters in Experiment 3.

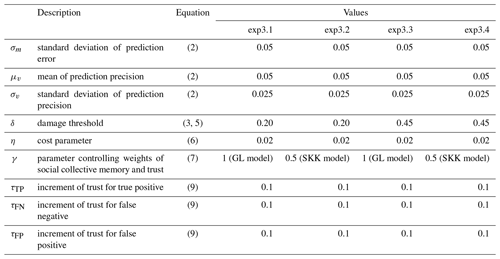
In Experiment 3, we also compared the GL and SKK models under different damage thresholds, δ. In socio-hydrology, previous works focused on the difference between “green” and “technological” society (Ciullo et al., 2017). In green society, risk is dealt with mainly by non-structural measures. In this society, the flood protection level is so low that many flood events occur, which increases social collective memory of flood events. In technological society, the flood protection level is so high that risk can be dealt with by structural measures and non-structural measures. Since flood events occur less frequently in the technological society, the high level of social collective memory cannot be maintained. By changing the damage threshold, we analyzed how differently the GL and SKK models behave in the different society. The settings of the parameters in Experiment 3 can be found in Table 5. From the original value of the damage threshold proposed by Girons Lopez et al. (2017) (i.e., δ=0.35), we decreased and increased δ to simulate the green and technological societies, respectively (see Table 5).

Table 6 Model parameters in Experiment 4.

In Experiment 4, we analyzed only the SKK model. The primary purpose of this Experiment 4 is to find the optimal predefined probability threshold, which minimizes relative loss, in not only different society and prediction accuracy but also different combinations of parameters related to the dynamics of social collective trust in FEWS (i.e., τ_TP,τ_FN, and τ_FP in Eq. 9). The settings of the parameters in Experiment 4 can be found in Table 6. We analyzed how the optimal warning threshold is changed by changing τ_FN and τ_FP (see Table 6).

In Experiments 2–4, we performed the 250-member Monte Carlo simulation by randomly perturbing a predefined probability threshold, π, and the initial conditions of social collective memory and social collective trust in FEWS. We used the same random seed to generate 250-member Monte Carlo simulation in each experiment, so that the differences between experiments do not depend on random processes. We analyzed the sensitivity of the efficiency of FEWS to predefined probability thresholds.

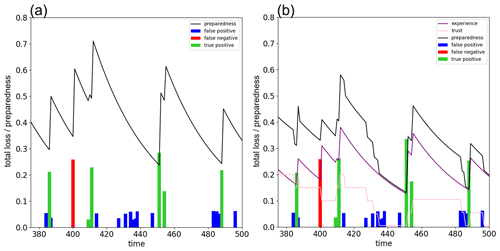
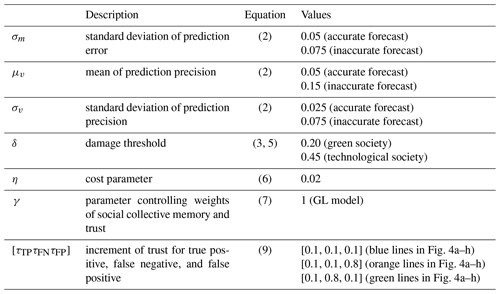
Figure 1 Time series of (a) the GL model and (b) the SKK model of Experiment 1 (see Sect. 3 and Table 2 for model parameters). Black, purple, and pink lines are social preparedness, half of social collective memory, and half of social collective trust in FEWS, respectively. Since social preparedness is identical to social collective memory and social collective trust is not considered in the GL model, there are no purple and pink lines in (a). Note that the sum of half of social collective memory and half of social collective trust in FEWS is social preparedness in (b). Blue, red, and green bars show total loss by the outcomes of false positive, false negative, and true positive, respectively (see Table 2).

4 Results

Figure 1 shows the time series of social preparedness of the GL and SKK models in Experiment 1 (see Table 3). The purpose of Fig. 1 is to demonstrate how differently the SKK and GL models work by showing the time series. While Fig. 1 shows the subset of the entire time series to clearly demonstrate the differences between two models, the entire time series can be found in Fig. S1 in the Supplement. In the GL model (Fig. 1a), social preparedness (black line) increases when flood occurs (red and green bars) and is not affected by false alarms (blue bars). In the SKK model (Fig. 1b), false alarms negatively impact social preparedness by reducing social collective trust in FEWS (pink line). From t=430 to t=440, consecutive false alarms substantially decrease social collective trust in FEWS and social preparedness, so that the damage of severe flood at t=452 in the SKK model is larger than that in the GL model despite the accurate warning being issued. It is the cry wolf effect.

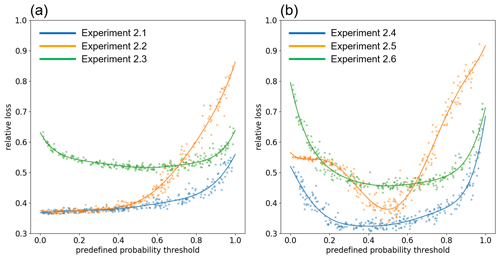
Figure 2 The relationship between relative loss and predefined probability thresholds in (a) the GL model and (b) the SKK model in Experiment 2. In (a), blue, orange, and green lines show the results of Experiments 2.1, 2.2, and 2.3, respectively. In (b), blue, orange, and green lines show the results of Experiments 2.4, 2.5, and 2.6, respectively. Each dot shows the result of the individual Monte Carlo simulation and we smoothed them by Gaussian process regression. See also Table 4 for detailed parameter settings.

Figure 2a shows the relationship between relative loss and predefined probability thresholds simulated by the GL model in Experiment 2 (see Table 4). We firstly assumed that there is no cost of the mitigation and protection action, and is the relatively accurate prediction system (Experiment 2.1; see Table 4). In this case, FEWS can minimize the relative loss with the extremely small predefined probability thresholds (blue line). When we degrade the prediction skill (Experiment 2.2; see Table 4), forecasters still maintain the same level of relative loss by setting low (or zero) predefined probability thresholds, issuing many false alarms (orange line). It is apparently unrealistic. In the framework of the GL model, this unrealistic model's behavior can be eliminated by setting the high cost of the mitigation and protection action responding to the issued warning. When we assume the high cost of preparedness actions (Experiment 2.3; see Table 4), the small predefined probability threshold induces high relative loss (green line). Forecasters need to avoid issuing false alarms when the cost which should be paid with false alarms is large. Note that the total costs of mitigation and protection actions with η=0.1 in Experiment 2.3 is comparable to the total flood damages. As discussed above, this high cost of mitigation and protection actions was not supported by previous works, although Girons Lopez et al. (2017) used this parameter.

The SKK model can give a different explanation of the avoidance of false alarms. Figure 2b shows the relationship between relative loss and predefined probability thresholds simulated by the SKK model in Experiment 2 (see Table 4). Although we assumed no cost and an accurate prediction system (Experiment 2.4; see Table 4), forecasters need to avoid issuing false alarms by the relatively high predefined probability thresholds to minimize relative loss (blue line). Due to the cry wolf effect found in Fig. 1b, forecasters need to decrease the number of false alarms to mitigate the damage of flooding even if there was no cost of false alarms. In other words, forecasters in the SKK model need to pay “implicit cost” of false alarms because false alarms induce not only the cost of mitigation and protection actions for nothing at the current time, but also the increase of damages of the future floods by reducing the social collective trust and preparedness. Considering that the previous works indicated that the cost of mitigation and protection actions is negligibly small (i.e., it is realistic to assume η=0), the SKK model reproduces the relationship between warning thresholds and total losses more realistically than the GL model. When we degrade the prediction accuracy (Experiment 2.5; see Table 4), relative loss is more sensitive to predefined probability thresholds (orange line) because the selection of the threshold is more important to accurately detect flood events and reduce the number of false alarms when the prediction is more inaccurate and uncertain. When we consider the high cost of mitigation and protection actions (Experiment 2.6; see Table 4), small predefined probability thresholds further increase relative loss (green line).

Figure S2 shows how γ in the Eq. (7) affects the relationship between relative loss and predefined probability threshold. When the contribution of social collective trust to social preparedness increases (i.e., γ gets smaller), the “implicit cost” of false alarms induced by relatively small predefined probability thresholds increases. Figure S2 also shows that moderate changes of γ from the default setting of the SKK model (i.e., 0.5) do not qualitatively change the relationship between relative loss and predefined probability threshold. In addition, the qualitative behavior of our SKK model is robust to different discharge time series (Fig. S3). Figure S3 reveals that the uncertainty induced by different discharge time series is comparable to that quantified by 250 Monte Carlo simulations with different initial conditions and forecast outcomes.

Figure 3 (a–b) The relationship between relative loss and predefined probability thresholds in (a) the green society and (b) the technological society. In (a), blue and green lines show the results of Experiments 3.1 and 3.2, respectively. In (b), blue and green lines show the results of Experiments 3.3 and 3.4, respectively. (c, d) The relationship between time-averaged social preparedness and predefined probability thresholds in (c) the green society and (d) the technological society. Black, purple, and pink lines show time-averaged social preparedness, social collective memory, and social collective trust in FEWS. Each dot shows the result of the individual Monte Carlo simulation, and we smoothed them by Gaussian process regression.

Figure 3a compares the GL and SKK models in the green society. In the previous Experiments 1 and 2, the damage threshold, δ, is set to 0.35, which is same as Girons Lopez et al. (2017). In Experiments 3.1 and 3.2 (see Table 5), the damage threshold is reduced to 0.20 so that the number of flood events increases. In this case, the GL and SKK models behave similarly. Figure 3c shows time-averaged social collective memory, social collective trust in FEWS, and social preparedness as functions of predefined probability thresholds. In the green society, frequent flood events make social collective memory high. In addition, it is easy to maintain the high social collective trust in FEWS since there are many opportunities to gain trust when flood frequently occurs. Therefore, both social collective memory and social collective trust in FEWS are large in the green society. Although the GL model neglects the social collective trust in FEWS to calculate social preparedness, the social preparedness of both GL and SKK models is high.

On the other hand, the GL and SKK models work more differently in the technological society than the green society. The damage threshold, δ, is increased to 0.45 in Experiments 3.3 and 3.4 (see Table 5), so that the number of flood events is smaller than Girons Lopez et al. (2017). Figure 3b indicates that the relationship between relative loss and predefined probability thresholds in the GL model is substantially different from that in the SKK model. The SKK model produces smaller relative loss than the GL model when the appropriate predefined probability threshold is chosen. The sensitivity of relative loss to predefined probability thresholds is larger in the technological society than the green society. Figure 3d indicates that it is difficult to maintain the high level of social collective memory in the technological society, so that considering social collective trust in FEWS can increase social preparedness. In addition, the choice of a predefined probability threshold is more important to maintain the high level of social collective trust in the technological society than the green society. These behaviors of the models can be found when damage threshold is further increased to 0.6, although the 1000-year averaged statistics are strongly affected by random processes due to the insufficient number of disaster events within the 1000-year computation period (not shown).

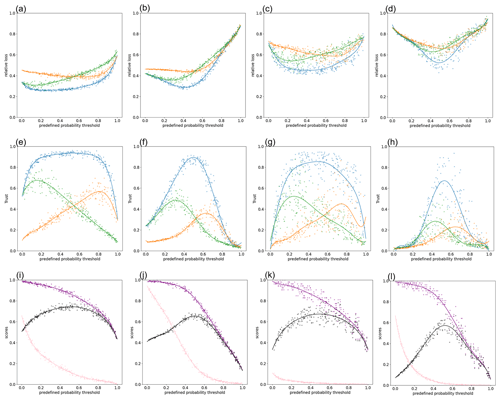
Figure 4 Results of Experiment 4. (a–d) The relationship between relative loss and predefined probability thresholds in (a) the green society with accurate forecasts, (b) the green society with inaccurate forecasts, (c) the technological society with accurate forecasts, and (d) the technological society with inaccurate forecasts. Increments of trust for true positive, false negative, and false positive are set to 0.1, 0.1, and 0.1 (blue lines), 0.1, 0.1, and 0.8 (orange lines), and 0.1, 0.8, and 0.1 (green lines). See Table 6 for detailed model parameters' settings. (e–h) Same as (a–d) but for time-averaged social collective trust in FEWS. (i–l) Same as (a–d) but for threat score (black lines), hit rate (purple lines), and false alarm ratio (pink lines). Each dot shows the result of individual Monte Carlo simulation, and we smoothed them by Gaussian process regression.

In Experiment 4, we further analyze the SKK model to discuss the optimal predefined probability threshold and to provide the useful implication for the design of FEWS in the various kind of social systems. We have three sets of parameters in Eq. (9) (see also Table 6). The first set of parameters is same as Experiments 1–3. Changes in social collective trust by false negative and false positive are the same (τ_FN=τ_FP). In the second set of parameters, we assume social collective trust substantially decreases by false positive (false alarms) (τ_FN<τ_FP): $\left[{\mathit{\tau }}_{\mathrm{TP}}{\mathit{\tau }}_{\mathrm{FN}}{\mathit{\tau }}_{\mathrm{FP}}\right]=[\mathrm{0.1},\mathrm{0.1},\mathrm{0.8}]$. In the third set of parameters, we assume social collective trust substantially decreases when forecasters miss a flood event (τ_FN>τ_FP): $\left[{\mathit{\tau }}_{\mathrm{TP}}{\mathit{\tau }}_{\mathrm{FN}}{\mathit{\tau }}_{\mathrm{FP}}\right]=[\mathrm{0.1},\mathrm{0.8},\mathrm{0.1}]$. The blue, orange, and green lines in Fig. 4a–d show that the optimal predefined probability threshold depends on how social collective trust is affected by false alarms and missed events. When social collective trust is affected by false alarms more substantially than missed events (orange lines), forecasters need to have relatively high predefined probability thresholds to maintain the high level of social collective trust (see Fig. 4e–h) and minimize relative loss. Figure 4a–d also shows that the differences of optimal predefined probability thresholds in three sets of parameters become larger as forecasts become accurate. The optimal predefined thresholds are bounded by the range in which the high threat scores can be obtained (see Fig. 4i–l). Thus, more accurate prediction systems make it more important to change the predefined probability threshold according to the dynamics of social collective trust. It implies that forecasters need to prioritize the meteorologically accurate forecasting by maximizing threat scores. Then, they have room for improvement to change their warning thresholds based on the dynamics of social collective trust in FEWS.

5 Discussion and conclusions

In this study, we included the dynamics of social collective trust in FEWS into the existing socio-hydrological model. By formulating social preparedness as a function of social collective trust and social collective memory, we realistically simulate the cry wolf effect in which many false alarms undermine the credibility of the early warning systems. Please note that the previous version of the model proposed by Girons Lopez et al. (2017) cannot do it. Although our model is simple and stylized, we can provide practically useful implications to improve the design of FEWS. First, considering the dynamics of social collective trust in FEWS is more important in the technological society with infrequent flood events than in the green society with frequent flood events. It implies that weather agencies need more efforts to be trusted by general citizens to induce their preparedness actions when a community is more heavily protected by flood protection infrastructures such as levees and dams. Second, as the natural scientific skill to predict floods is improved, the efficiency of FEWS gets more sensitive to the behavior of social collective trust, so that forecasters need to determine their warning threshold by considering the social aspects. Considering the recent advances of the skill to predict extreme hydrometeorological events, it implies that it is becoming more important for forecasters to take social dynamics responding to weather forecasts into consideration.

Although our model is the small extension of Girons Lopez et al. (2017), the implication of our study is completely different from Girons Lopez et al. (2017). Girons Lopez et al. (2017) mainly focused on the influence of the recency of flood experience on social preparedness and the efficiency of FEWS. Since their social preparedness is determined only by the flood experiences and they did not consider social collective trust in FEWS and weather agencies, the outcome of prediction did not directly influence the people's behavior in the model of Girons Lopez et al. (2017). By formulating social preparedness as a function of both social collective memory and trust, we could evaluate the effects of missed events and false alarms on preparedness actions. We contributed to connecting the modeling approaches of system dynamics in socio-hydrology to the existing literature about complex human behaviors against disaster warnings such as cry wolf effects in economics, sociology, and psychology (e.g., Simmons and Sutter, 2009; Ripberger et al., 2015; Trainor et al., 2015; LeClerc and Joslyn, 2015; Jauernic and van den Broeke, 2017; Lim et al., 2019).

Our findings of the optimal predefined probability thresholds are similar to Roulston and Smith (2004). Roulston and Smith (2004) developed the simple model to optimize predefined probability thresholds considering the damage, cost, and imperfect compliance with forecasting (i.e., the cry wolf effect). They also revealed that it is necessary to choose high warning thresholds if intolerance of false alarms of the society is high. However, there are substantial differences between our study and the previous cost–loss analysis such as Roulston and Smith (2004). First, Roulston and Smith (2004) developed the static model in which the cry wolf effect is treated exogenously, while our model is the dynamic model in which the cry wolf effect is endogenously simulated. Therefore, our model can consider the temporal change in the design and accuracy of FEWS, the flood protection level, and social systems, which may be the significant advantage to analyze the actual socio-hydrological phenomena. Second, by fully utilizing the previous achievements of Girons Lopez et al. (2017), we can also consider social collective memory of past disasters, which is not considered by Roulston and Smith (2004). This feature of our model can reveal that the social collective memory also contributes to the optimal predefined probability thresholds. Similar to Roulston and Smith (2004), our stylized model has a potential to help forecasters determine the optimal warning threshold if it can be appropriately calibrated by empirical data.

Our stylized model and findings are consistent with the previous works. In our model, the subjective perception of warning systems' accuracy controls social collective trust in a weather agency and preparedness actions, which is consistent to Ripberger et al. (2015). Our simulation results reveal that more actual false alarms hamper preparedness actions and induce more damages, which is consistent to the findings of Simmons and Sutter (2009) and Trainor et al. (2015). The behavior of the optimal warning threshold is similar to Roulston and Smith (2004). While the GL model realistically simulates the behavior of the optimal warning threshold only if unrealistically high costs of mitigation and protection actions are assumed, our stylized model needs no costs of mitigation and protection actions to realistically simulate the behavior of the optimal warning threshold. Our stylized model is more consistent with the previous works in which the costs of mitigation and protection actions responding to warnings were found to be negligibly small (e.g., Schroter et al., 2008; Hallegatte, 2012; Pappenberger et al., 2015). Our results justify the optimal warning thresholds which balance false alarms with missed events, and imply that forecasters believe the existence of cry wolf effects, although it does not necessarily mean that cry wolf effects exist.

However, the major limitation of this study is that our modeling of social collective trust is simple and is not fully supported by empirical data. We assumed that social collective trust in FEWS is affected only by the outcome of FEWS in our stylized model although there are many other factors which affect social collective trust in FEWS, such as social activities and education. Although intuition and theory suggest that many false alarms reduce the preparedness actions responding to warnings, the existence of the cry wolf effect in the weather-related disasters is still debatable (see a comprehensive review of Lim et al., 2019). Simmons and Sutter (2009) indicated that the recent false alarms negatively impacted the preparedness actions, so that we modeled the change in social collective trust by the recent forecast outcome. However, Ripberger et al. (2015) could not find the statistically significant short-term effect of false alarms, although they found the statistically significant cry wolf effect using the long-term data. It should be noted that most of the previous studies related to the cry wolf effect focused on tornado disasters, and the systematic econometric analyses have not been implemented for flood disasters, which makes it difficult to validate our proposed model. The effect of social collective memory on catastrophic disasters in the actual society is also debatable (e.g., Fanta et al., 2019). As Mostert (2018) suggested, it is crucially important to perform case study analyses, obtain empirical data, and integrate those data into the dynamic model to deepen our understanding of the hypothesis of the models (e.g., Roobavannan et al., 2017; Ciullo et al., 2017; Barendrecht et al., 2019; Sawada and Hanazaki, 2020).

As discussed above, systematic econometric analyses and field surveys on cry wolf effects have not been implemented for flood disasters, so it is important to design such kinds of analyses. Our modeling work provides useful implications for the design of future field analyses. First, our results show that the sensitivity of relative loss to predefined probability threshold is small around its optimal value in many cases. In many field surveys such as Simmons and Sutter (2009) and Trainor et al. (2015), pairs of false alarm ratio and damage in many regions of one country are collected and compared to show the increase of false alarm ratio increases damage. Assuming that nationwide criteria of issuing warnings are near-optimal, our study implies that the detectable signal of cry wolf effects in this approach is weak. Our modeling work implies that it is difficult to quantify cry wolf effects using time–mean performance of warnings and damages. It may be the reason why several field surveys contradict with each other, and the negative effect of false alarm ratio cannot be found in some surveys (Lim et al., 2019). We recommend analyzing the temporal change in behaviors responding to recent forecast outcomes, although this strategy is costly and time-consuming. Second, our Experiment 3 implies that it is better to choose technological societies as a research field because it is more difficult to distinguish the contributions of experience and trust in less protected areas.

In socio-hydrology, researchers have mainly focused on the functions of land use change and water-related infrastructures such as dams, levees, and dikes in the complex social systems. Although the interactions between social systems and weather forecasting such as the cry wolf effect are interesting, the function of FEWS and weather-related disaster forecasting has not been intensively investigated in socio-hydrology. We call for the new research regime, socio-meteorology, as the extension of socio-hydrology. In socio-meteorology, researchers may focus on how social systems interact with water-related disaster forecasting, how the efficiency of weather forecasting is affected by other hydrological factors such as land use and flood protection infrastructures, and how weather forecasting affects the design of land use and flood protection infrastructures.