Modeling the response of soil moisture to climate variability in the Mediterranean region

Future climate scenarios for the Mediterranean region indicate a possible decrease in annual precipitation associated with an intensification of extreme rainfall events in the coming years. A major challenge in this region is to evaluate the impacts of changing precipitation patterns on extreme hydrological events such as droughts and floods. For this, it is important to understand the impact of climate change on soil moisture since it is a proxy for agricultural droughts, and the antecedent soil moisture condition plays a key role on runoff generation. This study focuses on 10 sites, located in southern France, with available soil moisture, temperature, and precipitation observations for a 10-year time period. Soil moisture is simulated at each site at the hourly time step using a model of soil water content. The sensitivity of the simulated soil moisture to different changes in precipitation and temperature is evaluated by simulating the soil moisture response to temperature and precipitation scenarios generated using a delta change method for temperature and a stochastic model (the Neyman–Scott rectangular pulse model) for precipitation. Results show that soil moisture is more impacted by changes in precipitation intermittence than precipitation intensity and temperature. Overall, increased temperature and precipitation intensity associated with more intermittent precipitation leads to decreased soil moisture and an increase in the annual number of days with dry soil moisture conditions. In particular, a temperature increase of +4 ^∘C combined with a decrease of annual rainfall between 10 % and 20 %, corresponding to the current available climate scenarios for the Mediterranean, lead to a lengthening of the drought period from June to October with an average of +28 d of soil moisture drought per year.

1 Introduction

The Mediterranean region is a transitional zone between dry and wet climates, and in these semiarid areas the direct evaporation from the soil plays an important role on the surface energy balance, with evapotranspiration strongly dependent on available soil moisture (Koster et al., 2004; Seneviratne et al., 2010; Taylor, 2015). Consequently, the Mediterranean has been identified as a region with a strong coupling between the atmosphere and the land surface, with feedback effects of soil moisture on temperature and precipitation (Seneviratne et al., 2010; Knist et al., 2017; Hertig et al., 2019). Indeed, soil moisture is a key variable in the hydrological cycle for the partitioning of rainfall into infiltration and runoff and also for the mass and energy balance between land surface and the atmosphere (Seneviratne et al., 2010; Brocca et al., 2017). The water contained in the unsaturated, or vadose zone, is an important driver for floods with soils close to saturation having more probability to produce runoff when subjected to precipitation inputs (Zehe et al., 2005; Ivancic and Shaw, 2015; Woldemeskel and Sharma, 2016; Bennett et al., 2018; Wasko and Nathan, 2019). This is particularly true in the Mediterranean context where several studies have shown the strong influence of soil moisture on flood generation processes (Brocca et al., 2008; Penna et al., 2011; Tramblay et al., 2010, 2019; Uber et al., 2018). Similarly, soil moisture is an important parameter for drought analysis, since low soil moisture content is a good proxy for drought impacts on agriculture or wildfires occurrence (Vidal et al., 2010; Ruffault et al., 2013).

There is a climatic trend towards a drying of the Mediterranean region, both during the historical period but also in future climate scenarios, showing a decrease in precipitation amounts and occurrence, associated with an increasing frequency of drought episodes (Hoerling et al., 2012; Polade et al., 2014, 2017; Hertig and Tramblay, 2017; Lionello and Scarascia, 2018; Tramblay et al., 2020). For a RCP8.5 emission scenario, Giannakopoulos et al. (2009) and Polade et al. (2014) both estimate a mean decrease up to −30 % of the annual precipitation in the Mediterranean region by the end of the century and an increase of dry days ranging between +1 to +3 weeks per year. The precipitation decrease associated with higher temperatures leading to stronger evaporation rates is causing a decrease in soil moisture for large parts of the Mediterranean (Vidal et al., 2010; Vicente-Serrano et al., 2014; Hanel et al., 2018). Samaniego et al. (2018) and Grillakis (2019) provided future projections of soil moisture for Europe using different combinations of climate scenarios from general circulation models (GCMs), regional climate models (RCMs), and hydrological and land surface models, showing a clear climate signal towards a future decrease in soil moisture content and consequently an increase in agricultural droughts for Mediterranean regions.

Only a few studies have attempted to validate the soil moisture simulated by the GCM or RCM land surface schemes, probably due to the lack of sufficient networks with in situ soil moisture measurements, which show high spatial variability (Brocca et al., 2007; Crow et al., 2012; Holgate et al., 2016). Yuan and Quiring (2017) validated the ensemble of Coupled Model Intercomparison Project Phase 5 (CMIP5) GCMs over North America with in situ and satellite soil moisture observations. Knist et al. (2017) evaluated the Coordinated Regional Climate Downscaling Experiment (CORDEX) RCMs over Europe using GLEAM (Global Land Evaporation Amsterdam Model) and FLUXNET reference data. Hertig et al. (2019) tested the ability of two GCMs (CNRM-CM5 and MPI-ESM-MR) from CMIP5 to reproduce soil moisture dynamics as modeled by the Global Land Data Assimilation System (GLDAS) over Europe. If the main patterns of seasonal soil moisture were found to be adequately represented from climate models, these studies also pointed out the large multimodel variability in particular in the transitional climate zones. Indeed, many studies reported a high model dependence of soil moisture simulations (Koster et al., 2009; Berg et al., 2017). This is particularly true for the Mediterranean regions due to structural uncertainty, different process representations, soil depths, and interactions with vegetation that are not currently adequately reproduced by land surface models (Knist et al., 2017; Quintana-Seguí et al., 2020). As a consequence, the direct use of soil moisture from climate models may not be the best option to assess small-scale soil moisture variability in relation with climate conditions.

Besides the use of climate models, scenario-neutral approaches are increasingly employed to assess the vulnerability of water resources under different climate change scenarios (Prudhomme et al., 2010; Guo et al., 2017; Stephens et al., 2018; Keller et al., 2019). The approach is similar to a sensitivity analysis aiming at quantifying the changes in a given hydrological variable for a plausible range of changes in hydrometeorological conditions. Several studies have previously used stochastic approaches to investigate the sensitivity of soil moisture to precipitation patterns with various levels of complexity in the representation of precipitation properties and soil moisture dynamics (Rodriguez-Iturbe et al., 1999; Milly, 2001; Calanca, 2004; Laio et al., 2001; Teuling et al., 2007; Zhu et al., 2020). This type of approach can provide useful information to identify the hydrometeorological parameters that have the greatest impact on a given response variable. Guo et al. (2018) provided an example of such a scenario-neutral approach based on a stochastic weather generator to explore possible rates of changes in rainfall intermittence and extremes in southern Australia. Yoo et al. (2005) coupled a stochastic generator of rainfall to a soil moisture model in the Walnut Gulch experimental watershed in southeastern Arizona to estimate soil moisture changes due to rainfall variability. They found that the rainfall arrival rate was the most sensitive parameter, with decreasing soil moisture content and increasing rain intermittence, even without a decrease of the total volume of rainfall. Yet, this type of approach needs to be applied to other land regions and different sites in order to evaluate the possible spatial variability in addition to the temporal variability of rainfall. These bottom-up approaches are complementary to the modeling chains linking climate and land surface models and document the most relevant process leading to soil moisture changes that in turn can be used to improve the land surface schemes.

The objective of this study is to analyze the variability of soil moisture for a set of Mediterranean sites according to changes in precipitation and temperature. The method relies on the use of a stochastic precipitation generator coupled with the soil moisture model proposed by Brocca et al. (2008). The scientific questions addressed in the present work are: which precipitation characteristics (intermittency, intensity) influence soil moisture changes in conjunction with changes in temperature as a proxy for evapotranspiration changes, and how does the response of soil moisture to changes in climate drivers vary in space for a range of different locations with different topographical and soil properties?

Figure 1 Localization of the study sites in southern France.

The paper is structured as follows: Sect. 2 describes the study area and collected datasets; Sect. 3 provides a description of the soil moisture and stochastic rainfall models (Sect. 3.1 to 3.3) and of the experimental design for the simulation of the soil moisture scenarios (Sect. 3.4); Sect. 4 presents the validation of stochastic rainfall model (Sect. 4.1) and soil moisture model (Sect. 4.2) after calibration and the sensitivity analysis of the median (Sect. 4.3) and extreme soil moisture (Sect. 4.4) to precipitation and temperature variations; and Sect. 5 discusses the results and summarizes the main conclusions of the paper.

2 Data

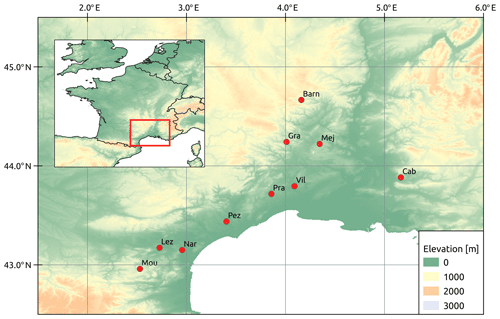
This study uses soil moisture, precipitation, and temperature in situ data from 10 stations of the SMOSMANIA network (Calvet et al., 2007; Albergel et al., 2008) located in the French Mediterranean region (Fig. 1).

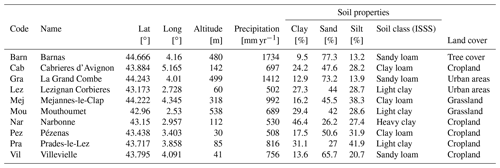
Stations all present a characteristic Mediterranean precipitation seasonal cycle with a hot and dry summer followed by heavy precipitation between September and November (Fig. 2). This precipitation cycle directly impacts soil moisture with lower soil moisture values during summer and higher values during winter. Although all stations are located in the French Mediterranean region, they differ in altitudes, ranging from 30 m a.s.l. (Pézenas) to 538 m a.s.l. (Mouthoumet), in mean annual precipitation, ranging from 500 mm (Lézignan Corbières, Pézenas) to 1734 mm (Barnas), and in soil characteristics (Table 1). The station altitude is correlated to mean annual precipitation (r=0.7), except for the station Mouthoumet with lower annual precipitation than stations with comparable altitude (if this station is removed, r=0.92 between altitude and mean annual precipitation).

Table 1 Station characteristics.

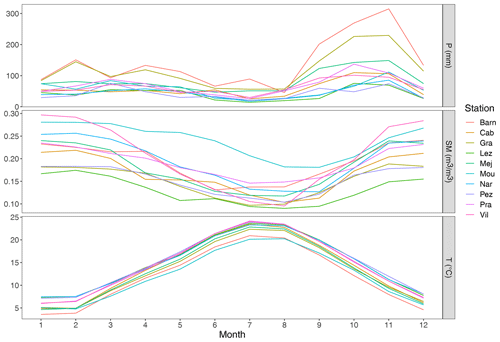
Figure 2 Observed seasonal cycle of precipitation, soil moisture, and air temperature at the stations.

In situ data are collected at hourly time steps and covers the period 1 July 2007 to 31 December 2016. Soil moisture data series used in this study are computed from measurements at four different depths (5, 10, 20, and 30 cm) as the weighted average as a function of soil layer depth. The integration of the measurements at various depths enables representation of the average soil moisture in the root zone layer.

3 Method

3.1 Soil moisture model

The soil moisture model developed by Brocca et al. (2008) is used to simulate present soil moisture and soil moisture response under different climate scenarios. The soil moisture model (SMmodel) incorporates a Green–Ampt approach for infiltration, a gravity-driven approximation for drainage, and a linear relationship between potential evapotranspiration and soil saturation to estimate actual evapotranspiration. The SMmodel simulates the hourly temporal evolution of soil moisture and actual evapotranspiration. Hourly precipitation and air temperature are used as input into the SMmodel and potential evapotranspiration is computed from air temperature through the Blaney and Criddle approach. Details on the model equations can be found in Brocca et al. (2008) and Brocca et al. (2014). The model has been applied at multiple sites in Italy and Europe (e.g., Brocca et al., 2014) with satisfactory results.

3.2 Soil moisture model calibration

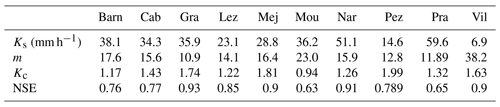
The SMmodel uses fixed and calibrated parameters. The fixed parameter values (Table 2) were estimated based on the observed soil moisture and geographic location of the stations. Four parameters were calibrated: hydraulic conductivity K_s, root zone depth Z, exponent of drainage m, and coefficient for evapotranspiration K_c (calibration ranges in Table 2). These parameters are calibrated for each station using the total period of observed data, but two additional calibrations were performed on subperiods (first half and second half of the total period) in order to analyze the stability of the calibration. For the calibration process, missing precipitation and temperature data are reconstructed by replacing missing precipitation with an intensity of 0 mm h⁻¹ and by linearly interpolating temperature data for gaps of less than 3 h or otherwise using the climate mean. Time steps with reconstructed precipitation and temperature are not taken into account in the calculation of the NSE (Nash–Sutcliffe efficiency) coefficient used as the optimization criterion for the calibration (Nash and Sutcliffe, 1970). Details on missing data at each station are presented in Table S1 in the Supplement.

Table 2 Fixed parameter values and ranges of calibrated parameters of the soil moisture model. Fixed parameter L is calculated as the monthly percentage of the total daytime hours out of the total daytime hours of the year.

3.3 Generation of temperature and rainfall scenarios

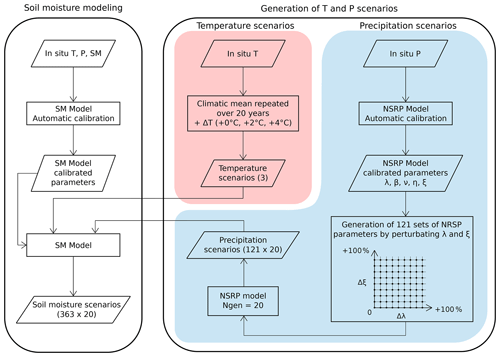
For each station, a 20-year temperature data series is generated by repeating the hourly climatic mean. Temperature scenarios are generated by applying a delta ranging between +0 and +4 ^∘C.

The stochastic weather generator, the standard version of the Neyman–Scott rectangular pulse model (NSRP) (Cowpertwait et al., 1996), is used to generate 20 series of hourly rainfall data time series. The peculiarity of the model lies in its capability to preserve the statistical properties of rainfall time series over a range of time scales. As the model has been extensively described in previous papers (e.g., Cowpertwait et al., 1996; Camici et al., 2011) only a brief discussion is given here.

The NSRP model has five parameters:

• λ: mean waiting time between adjacent storm origins [h],

• β: mean waiting time between rain cell origins after storm origins [h],

• ν: mean number of rain cell per storm,

• η: mean duration of rain cell [h],

• ξ: mean intensity of rain cell [mm h⁻¹].

A Poisson process with parameter λ controls the generation of storm origins. For each storm origin, a random ν number of rain cell origins are generated displaced from the storm origin according to a β parameter exponentially distributed process. The duration and intensity of each rain cell are expressed by two other independent random variables assumed exponentially distributed with parameter η and ξ, respectively. These parameters are estimated, for each month of the year, by minimizing an objective function evaluated as the weighted sum of the normalized residuals between the statistical properties of the observed time series and their theoretical expression derived from the model. The statistical properties of rainfall included in the objective function to calibrate the model are hourly mean, hourly variance, daily variance, lag1 autocorrelation of daily data, hourly skewness, daily skewness, and the percentage of dry days. Once the model parameters are estimated for each month, the NSRP model is run to produce continuous rainfall simulations.

As studies on future precipitation patterns in the Mediterranean region predict an increase of the dry days frequency associated with an intensification of extreme precipitation events (Paxian et al., 2015; Polade et al., 2017; Tramblay and Somot, 2018; Chan et al., 2020; Pichelli et al., 2021), we generate precipitation scenarios with increasing precipitation intermittence and increasing mean intensity by applying deltas from +0 % to +100 % on the λ and ξ parameters (see details in Sect. 3.4). It should be noted that in some studies all the parameters of the rainfall generator are recalibrated after the perturbation of rainfall statistics according to a climate change signal (Bordoy and Burlando, 2014). Other authors fixed some parameters while allowing others to change according to climate variability (Wasko et al., 2015). The latter approach is adopted herein, since preliminary experiments based on the recalibration of the NSRP generator were not satisfactory due to the parameters' instability when performing multiple model calibration procedures. For each precipitation scenario produced by the modification of the NSRP model parameters λ and ξ, 20 precipitation data series are generated with the NSRP model over a 20-year period and used as input in the soil moisture model.

Figure 3 Flowchart of the experimental design for the simulation of the soil moisture scenarios.

3.4 Sensitivity analysis of the simulated soil moisture to precipitation and temperature changes

3.4.1 Direct analysis

We first analyze the sensitivity of the simulated soil moisture for specific changes in temperature and precipitation. We consider three temperature scenarios with $\mathrm{\Delta }T=+\mathrm{0}$, +2, +4 ^∘C, and 121 precipitation scenarios with Δξ and Δλ regularly spaced between +0 % and +100 % with a 10 % increment. The soil moisture model is then run for each precipitation and temperature scenario (i.e., 363 scenarios per station) to analyze the sensitivity of the simulated soil moisture to temperature and precipitation changes. Figure 3 presents the process for the simulation of the soil moisture scenarios. The simulation with no change in temperature or precipitation intensity and intermittence is called the reference scenario and is used to represent soil moisture conditions under the present climate. The evolution of extreme soil moisture events is evaluated by estimating the mean number of days per year under either soil water excess or drought conditions. We consider episodes of soil water excess as consecutive days with a daily soil moisture above the reference scenario 95th percentile and drought episodes as days with soil moisture below the 5th percentile. Considering the modeling chain as (i) the NSRP model (depending on the calibrated values of β, ν, η, λ, and ξ and the applied perturbations Δλ and Δξ); (ii) the temperature scenario generation perturbed of ΔT, and (iii) the SM model, for a given set of parameters, a simulated ensemble of 20 stochastic replicates is generated. Quantiles and annual numbers of days under drought or soil water excess are computed for each of the 20 corresponding soil moisture results and then averaged to produce a unique scenario.

3.4.2 Global sensitivity analysis

A global sensitivity analysis (GSA) (Saltelli et al., 2008; Pianosi et al., 2016) assesses the model behavior (model output sensitivity to the input parameters) in the whole parameter space using a variance decomposition method. Consider $Y=f\left(\underset{\mathrm{¯}}{X}\right)$ with Y being the output of the model f to a set of parameters $\underset{\mathrm{¯}}{X}=(X_{\mathrm{1}}$, X₂, …, X_N). A functional ANOVA decomposition is applied to Y (e.g., Sobol, 1993; Saltelli et al., 2010):

$$\begin{array}{}\text{(1)}& V\left(Y\right)=\sum _{i=\mathrm{1}}^N{V}_i+\sum _{i=\mathrm{1}}^N\sum _{j>i}^N{V}_{i,j}+\mathrm{\dots }+V_{\mathrm{1},\mathrm{2},\mathrm{\dots },N},\end{array}$$

where N represents the number of sampled parameters. V(Y) is the total variance of the model output, V_i is the first-order variance of Y due to parameter X_i, V_ij is the second-order variance (covariance) of Y due to X_i, and X_j is the higher-order variance due to more than two parameters. A first-order Sobol index S_i corresponds to the ratio of the corresponding variance V_i to the total variance V(Y): $S_i=V_i/V\left(Y\right)$ and is thus always between 0 and 1. The sum of all the (first- and higher-order) Sobol indices is equal to unity.

Assuming that the changes in temperature and precipitation are stochastic variables, the first-order Sobol indices are computed using the state-dependent parameter modeling proposed by (Ratto et al., 2007). For the GSA, a different set of 1000 sets of temperature and precipitation changes, generated randomly in the range of values presented in Sect. 3.3, is used in order to cast continuously the range of values ($\mathrm{\Delta }T=[+\mathrm{0}$; +4 ^∘C], Δλ=[0; +100 %]λ, and Δξ=[0; +100 %]ξ). The objective of this sensitivity analysis is to estimate the relative influences of changes in temperature and precipitation characteristics on soil moisture.

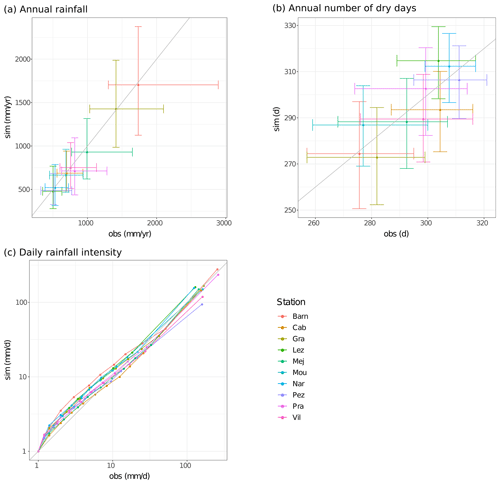
Figure 4 Characteristics of simulated rainfall with the NSRP model for the reference scenario and observed rainfall. Comparison of simulated and observed (a) annual rainfall and (b) annual number of dry days (dots represent mean values and bars represent the range from minimal to maximal simulated or observed values). (c) Q–Q plot of daily rainfall intensities (dots represent deciles values).

4 Results

4.1 NSRP model calibration and generated rainfall scenarios

Rainfall series generated with the NSRP model for the reference scenario show good agreement with the observed rainfall characteristics. Figure 4a shows that the mean annual amount of rainfall is well reproduced by the model (r²=0.99) and that the range of values of annual amount of rainfall is also comparable to the range of observed values. The mean annual number of dry days (i.e., days with precipitation below 1 mm) is similar to observations reproduced (r²=0.71) but with a bias going from −11 d (Cabrieres d'Avignon station) to +10 d (Mouthoumet station) (Fig. 4b). The NSRP model tends to slightly overestimate lower values of the daily intensities distribution (Fig. 4c), but overall, the simulated distributions are in good agreement with observed distributions (see Fig. S1 in the Supplement for the calibrated NSRP parameters).

The perturbation of the NSRP parameters ξ and λ from +0 % to +100 % enables one to produce rainfall scenarios with different patterns in annual rainfall, mean daily intensity, and annual number of dry days (Fig. 5). An equal perturbation of ξ and λ leads to an unchanged annual rainfall with an increase in rainfall intensity and increased intermittence compared to the reference scenario. A perturbation of +100 % of the ξ parameter with no perturbation on the λ parameter leads to an increase of 100 % the annual rainfall across all sites, associated with an increase of mean rainfall intensity of wet days of +9.5 mm d⁻¹ (+83 % of original rainfall intensity). Alternatively, an increase of +100 % of the lambda parameter with an unchanged value of ξ leads to a mean decrease of the annual rainfall of 50 % and an increase of +34 d yr⁻¹ of dry days (+11 %). However, some stations are more sensitive to the perturbation of parameters than others. Figure 5d shows that the change in the annual number of dry days for Δλ=100 % ranges between +8 % and +16 %.

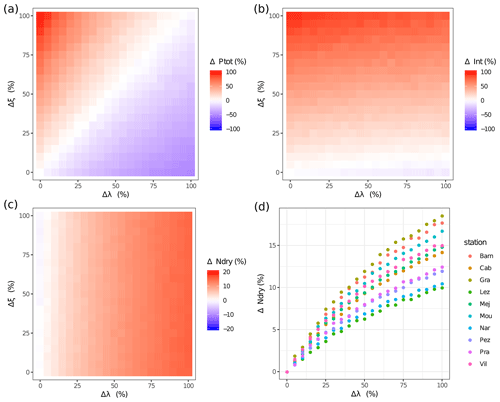
Figure 5 Impact of the perturbation of NSRP parameters λ and ξ on (a) the total annual precipitation, (b) the mean daily precipitation intensity, and (c) the annual number of dry days. Panels (a–c) show averaged results for the 10 study sites and panel (d) shows the relation between the perturbation of λ and the change in number of dry days for each station when ξ=0.

Table 3 Calibrated parameters of the SM model and NSE validation values while calibrating on the total period.

4.2 SM model calibration

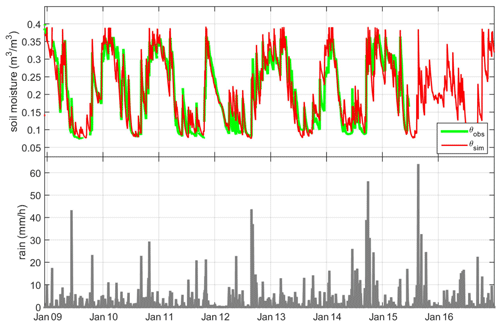
Table 3 presents the calibrated parameters of the SM model and NSE values after calibration. The NSE values for the calibration on the total period are all above 0.6, and nine stations out of 11 have an NSE value above 0.75. RMSE values range from 0.015 to 0.032 m³ m⁻³. Calibrations on the subperiods (first and second halves of each station time series) lead to similar parameters (see Table S2 in the Supplement) and NSE values on both subperiods, showing that the calibration is stable for the selected period. Lower NSE values for the calibration on subperiods are due to missing observed data unevenly distributed over the total period. These results show that the SMmodel is able to simulate soil moisture accurately in the present 2007–2016 period. Calibrated values of K_s are consistent with the range of hydraulic conductivities for natural soils (Angerer et al., 2014) (Table S3 in the Supplement). Figure 6 shows an example of soil moisture simulation after calibration at the Villevielle station.

Figure 6 Soil moisture simulation at the Villevielle station.

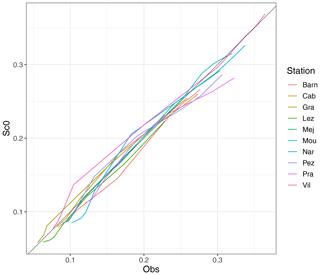
The calibrated parameters are then used to simulate soil moisture under different scenarios of temperature and precipitation. Figure 7 compares the distributions of observed daily soil moisture with simulated daily soil moisture forced with the reference scenario. Results show that in the reference scenario the soil moisture distribution is in very good agreement with the distribution of observed soil moisture. The bias between the mean soil moisture from the reference scenario and the mean observed soil moisture is low and ranges from −0.006 to 0.01 m³ m⁻³, all sites considered.

Figure 7 Q–Q plot of simulated (reference scenario) and observed daily soil moisture.

4.3 Sensitivity of soil moisture to precipitation and temperature changes

Figure 8 shows the sensitivity of the median simulated soil moisture to changes in precipitation patterns. Results show that the median soil moisture is more sensitive to changes in precipitation intermittence (Δλ) than to changes in precipitation mean intensity (Δξ). For the +0 ^∘C scenario, an increase of the precipitation intermittence of +100 % leads to a decrease between −16 % and −37 % on the median soil moisture, whereas an increase of 100 % in the precipitation mean intensity only leads to an increase of the median soil moisture ranging between +3 % and +26 %. Results also show that stations have different sensitivity to precipitation and temperature changes. Stations such as Villevielle, Narbonne, and Lézignan seem to be more sensitive to climate variability, whereas the Barnas, La Grand-Combe, Mouthoumet, and Prades-le-Lez stations show a lower impact of changing precipitation patterns and temperature on the median soil moisture. The sensitivity of soil moisture response to changes in temperature and precipitation pattern seems to be correlated to the station local temperature and also to local precipitation to a lesser extent (Fig. 9). Southern stations presenting a warmer and dryer climate seem to be more impacted by changes in precipitation and temperature than northern stations located in the Cevennes mountain range with a colder and wetter climate. No correlation was found between the soil moisture response and the NSRP model and SM model parameter values, meaning that the observed variability between stations is independent from the model calibrations.

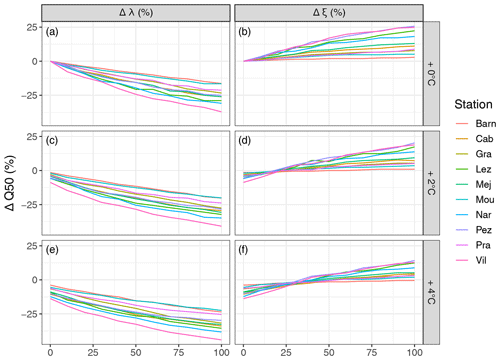
Figure 8 Sensitivity of the median of the simulated soil moisture to an increase of the precipitation intermittence (a, c, e) and to an increase of mean precipitation intensity (b, d, f) under different temperature scenarios (+0, +2, +4 ^∘C).

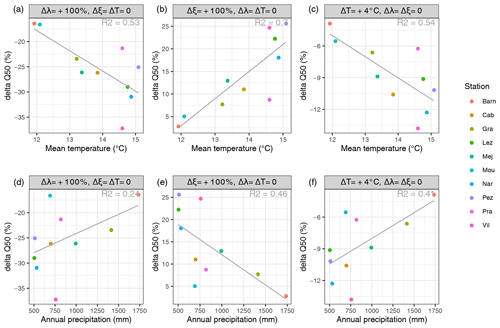
Figure 9 Sensitivity of the median of the simulated soil moisture to precipitation and temperature scenarios (ξ: precipitation intensity scenario, λ: precipitation intermittence scenario, T: temperature scenario) related to the observed mean annual (a) temperature and (b) precipitation.

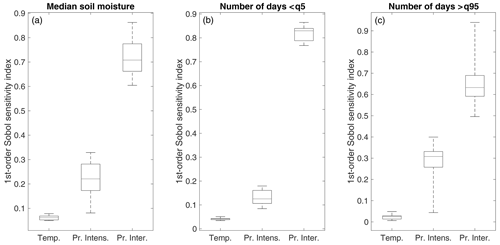
Figure 10 First-order Sobol sensitivity index of median soil moisture (a), the number of days under drought conditions (b), and the number of days with water excess (c) to temperature, precipitation intensity, and precipitation intermittence changes. Boxplots represent the distribution of the first-order Sobol indices for the 10 stations.

Figure 10 presents the distribution for the 10 stations of the first-order Sobol indices of the median soil moisture (resp. number of days under drought or excess condition) to the parameter change (temperature, precipitation intensity, and precipitation intermittence). For instance, the Sobol index of the soil moisture to a parameter is the percentage of the soil moisture variance explained by the considered parameter. Over all the stations, the sum of the first-order Sobol indices are between 0.99 and 1.003, this indicates that the GSA is based on a sufficient number of simulations. The Sobol sensitivity analysis shows that soil moisture variance is more impacted by changes in precipitation intermittence than changes in precipitation intensity and temperature, especially for the median soil moisture and the number of days with drought (i.e., low soil moisture values). Changes in precipitation intensities have a larger impact on higher soil moisture values and can be almost equivalent to the changes in precipitation intermittence as, for example, in the Pézenas station. There is a link with the mean precipitation and Sobol indices related to changes in precipitation intermittence and intensity. Indeed, the smaller the annual precipitation, the higher the Sobol index of the precipitation intermittence is for the median and 95th percentile of soil moisture (with correlations equal to, respectively, $r=-\mathrm{0.71}$, $r=-\mathrm{0.56}$). It is the opposite relationship between annual precipitation and precipitation intensity (with correlations equal to r=0.77 for median soil moisture, r=0.33 for the 5th percentile, and r=0.74 for the 95th percentile). This indicates that changes in precipitation intermittence are more strongly impacting soil moisture in locations with low annual precipitation.

4.4 Impact of changing precipitation and temperature on extreme soil moisture

In this section we analyze the response of extreme soil moisture to the precipitation and temperature scenarios. Figure 11 shows the relative change of the mean annual number of days under saturation or drought conditions with respect to the reference scenario for the Barnas and Pézenas stations (complete results are presented in the Supplement). Days under saturation (drought) conditions are defined as days with soil moisture above the 95th (below the 5th) percentile of the reference scenario.

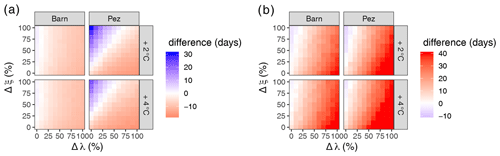
Figure 11 Sensitivity of the annual number of days (a) with saturated soil (i.e., with soil moisture above the observed 95th percentile) and (b) under drought conditions (i.e., with soil moisture below the observed 5th percentile) according to changes in precipitation intensity (y axis), precipitation intermittence (x axis), and temperature for the Barnas and Pézenas stations.

There is a large variability in the evolution of the mean annual number of days with wet conditions, with results ranging from −16 to +30 d yr⁻¹ for the +2 ^∘C scenario and from −17 to +22 d yr⁻¹ for the +4 ^∘C scenario (Fig. 11a). For the +2 ^∘C scenario, only 24 % of the scenarios result in an increase of annual days with wet conditions on average for the 10 stations. On average, an increase in dry days (i.e., days with no precipitation) above +16 d yr⁻¹ results in a decrease of the number of days with saturated soil moisture condition regardless of the increase in precipitation intensity. Regarding the +4 ^∘C scenario, only 18 % of the scenarios result in an increase of the number of days with wet soil moisture conditions, and all scenarios with an increase of dry days above +13 d yr⁻¹ result in a decrease of the period under saturated soil moisture conditions. Scenarios similar to those of Polade et al. (2017) corresponding to RCP8.5 (i.e., scenarios corresponding to a decrease of annual precipitation ranging between −10 % and −20 % and a +4 ^∘C temperature increase; red triangles on Fig. 12) lead to an average of 10 d yr⁻¹ with wet conditions, i.e., a decrease of 8 d yr⁻¹ relative to the reference scenario (blue dots on Fig. 12).

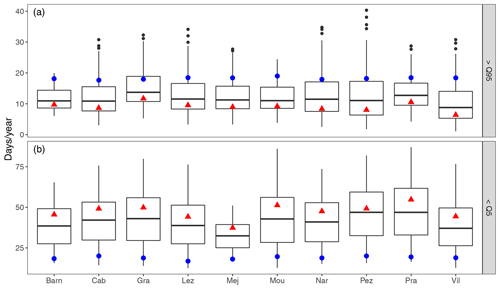
Figure 12 Variability of the annual number of days under saturated conditions (SM above the observed 95th percentile, a) and under drought conditions (SM below the observed 5th percentile, b) at each station for a +4 ^∘C temperature scenario. Boxplots represent the results for all precipitation scenarios with increasing precipitation intensity and intermittence. Blue dots represent the reference scenario, with no change in temperature or precipitation pattern. Red triangles represent the mean of the scenarios with a decrease of annual precipitation between −10 % and −20 % (corresponding to scenario RCP8.5; Polade et al., 2017).

Concerning the impact of changing precipitation and temperature on dry soil moisture conditions, Fig. 11b shows that changes in precipitation and temperature have a strong impact on droughts as almost all scenarios lead to an increase of dry soil moisture conditions. RCP8.5 scenarios show a mean number of days with dry soil moisture conditions ranging between 37 and 55 d yr⁻¹, corresponding to a mean increase of +28 d yr⁻¹ compared to the reference scenario (Fig. 12). This increase of dry days mainly impacts the summer and autumn seasons from June to October (Fig. 13). None of the stations show an increase of extreme dry days during winter. These results show that agricultural drought events in the Mediterranean region are likely to be more intense with longer episodes extending until the months of October and November.

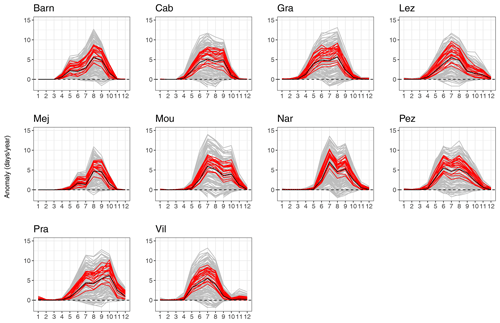
Figure 13 Monthly anomaly of days under extreme drought for a +4 ^∘C temperature scenario. Gray lines represent the results for all precipitation scenarios with increasing precipitation intensity and intermittence. Black lines represent the median of the scenarios ensemble. Red lines represent the change of drought days for the scenarios with a decrease of annual precipitation between −10 % and −20 % (corresponding to scenario RCP8.5, Polade et al., 2017).

Overall, the results show that changes in precipitation patterns and temperature have a larger impact on the lowest range of the soil moisture distribution than on the highest. This means that climate change is very likely to have a major impact on agricultural droughts with dryer soil moisture and longer drought events. Regarding the impact on flood events, it is difficult to make conclusions based on the results of this study as we do not simulate runoff generation. Our results show a decrease of the median soil moisture for most of the considered scenarios as well as a decrease of days under saturated conditions suggesting a higher infiltration capacity of the surface soil layer with a potential lower runoff generation.

5 Discussion

One of the main limitations to this study lies in the constant soil moisture model parameters under different climate scenarios. The use of constant parameters implies that processes such as the adaptation of vegetation to soil water stress or the impact of rising CO₂ on the vegetation physiology, which may have a sensitive impact on evapotranspiration and thus soil moisture (Berg and Sheffield, 2018) are not taken into account in this study. To avoid this issue, it would be required to consider land surface modeling schemes that are able to take into account the feedback effects between vegetation and land surface processes (Albergel et al., 2017). In addition, offline computation of potential evapotranspiration with standard formulas such as the Blaney and Criddle or Penman–Monteith equations can be problematic since it neglects several factors, in particular the surface conditions (Barella-Ortiz et al., 2013). The impact of different formulations of potential evapotranspiration on soil moisture changes needs also to be investigated, since simple temperature-based formulas may overestimate the temperature effects on evapotranspiration (Sheffield et al., 2012; Vicente-Serrano et al., 2020).

Another source of uncertainty is related to the selection of temperature and precipitation scenarios. Currently the majority of available climate simulations are at the daily time step. The projected changes on hourly climate characteristics remains largely unknown, and this is why we adopted a stochastic simulation approach to encompass the plausible range of future scenarios. However, convection-permitting regional climate models (CPRCMs) have been increasingly implemented over Europe in recent years to reproduce hourly changes in precipitation (Coppola et al., 2018) and these simulations should be considered in future experiments. Similarly, the approach considered in the present paper is based on distributional changes, while the impact of possible changes in the seasonal to interannual variability of precipitations on soil moisture cannot be taken into account. This issue could be also resolved by using CPRCM simulations instead of a stochastic rainfall generator to simulate the soil moisture response to various changes in precipitation including seasonal and interannual variability.

Finally, this study relies on a set of soil moisture observations from different sites located in southern France and, despite different annual precipitation and temperature patterns, the vegetation at the different locations belongs to the same biome. It would be interesting to perform this type of analysis on a larger set of sites located in various Mediterranean environments, including North Africa and the Middle East, with more arid climate conditions to investigate the possible relationships between soil moisture dynamics and soil types, vegetation cover, and climate characteristics for different degrees of aridity. Indeed, the Mediterranean region includes a great variety of types of vegetation, forming mosaic patterns created by variations in soil, topography, climate, fire history, and human activity (Geri et al., 2010). Therefore, it would be very useful to produce a typology of the sensitivity of soil moisture changes for a variety of Mediterranean landscapes.

6 Conclusions

Soil moisture is an important variable to consider in a climate change context since it strongly influences agricultural droughts and flood generation processes. Future climate scenarios for the Mediterranean indicate an increase in temperature associated with an increased frequency of dry days but also an intensification of extreme rainfall events. This study considered soil moisture monitored at 10 plots located in southern France in a modeling framework aimed at estimating its sensitivity to changes in precipitation and temperature. For that purpose, a range of precipitation and temperature variations coherent with current climate scenarios available for the Mediterranean region have been generated with a stochastic model to investigate the response of soil moisture to these climatic changes. The main result of this study shows that the sensitivity of soil moisture to changes in precipitation and temperature is similar at the different sites, with a higher sensitivity of soil moisture to intermittent precipitation and the number of dry days rather than rainfall intensity or the temperature increase. However, these changes are modulated by the climate characteristics of the different stations, with a higher sensitivity of soil moisture to precipitation intermittence in locations with dryer and warmer climate characteristics. Overall, it is observed that changes in precipitation and temperature have a greater impact on low soil moisture values than on conditions close to soil saturation. This implies that the current climate change scenarios may induce longer periods of depleted soil moisture content, corresponding to agricultural drought conditions. About the potential impacts of soil moisture changes on flood generation, more research is needed to better understand the joint influence of lower antecedent soil moisture conditions associated with higher rainfall intensity on flood magnitude and occurrence.