Bending of the concentration discharge relationship can inform about in-stream nitrate removal

Nitrate (${{\mathrm{NO}}_{\mathrm{3}}}^{-}$) excess in rivers harms aquatic ecosystems and can induce detrimental algae growths in coastal areas. Riverine ${{\mathrm{NO}}_{\mathrm{3}}}^{-}$ uptake is a crucial element of the catchment-scale nitrogen balance and can be measured at small spatiotemporal scales, while at the scale of entire river networks, uptake measurements are rarely available. Concurrent, low-frequency ${{\mathrm{NO}}_{\mathrm{3}}}^{-}$ concentration and streamflow (Q) observations at a basin outlet, however, are commonly monitored and can be analyzed in terms of concentration discharge (C–Q) relationships. Previous studies suggest that steeper positive log (C)–log (Q) slopes under low flow conditions (than under high flows) are linked to biological ${{\mathrm{NO}}_{\mathrm{3}}}^{-}$ uptake, creating a bent rather than linear log (C)–log (Q) relationship. Here we explore if network-scale ${{\mathrm{NO}}_{\mathrm{3}}}^{-}$ uptake creates bent log (C)–log (Q) relationships and when in turn uptake can be quantified from observed low-frequency C–Q data. To this end we apply a parsimonious mass-balance-based river network uptake model in 13 mesoscale German catchments (21–1450 km²) and explore the linkages between log (C)–log (Q) bending and different model parameter combinations. The modeling results show that uptake and transport in the river network can create bent log (C)–log (Q) relationships at the basin outlet from log–log linear C–Q relationships describing the ${{\mathrm{NO}}_{\mathrm{3}}}^{-}$ land-to-stream transfer. We find that within the chosen parameter range the bending is mainly shaped by geomorphological parameters that control the channel reactive surface area rather than by the biological uptake velocity itself. Further we show that in this exploratory modeling environment, bending is positively correlated to percentage of ${{\mathrm{NO}}_{\mathrm{3}}}^{-}$ load removed in the network (L_r.perc) but that network-wide flow velocities should be taken into account when interpreting log (C)–log (Q) bending. Classification trees, finally, can successfully predict classes of low (∼4 %), intermediate (∼32 %) and high (∼68 %) L_r.perc using information on water velocity and log (C)–log (Q) bending. These results can help to identify stream networks that efficiently attenuate ${{\mathrm{NO}}_{\mathrm{3}}}^{-}$ loads based on low-frequency ${{\mathrm{NO}}_{\mathrm{3}}}^{-}$ and Q observations and generally show the importance of the channel geomorphology on the emerging log (C)–log (Q) bending at network scales.

1 Introduction

Transport and transformation of nitrate (${{\mathrm{NO}}_{\mathrm{3}}}^{-}$) in river networks are major controls of downstream exports to receiving lakes, reservoirs and coastal systems (Alexander et al., 2000; Billen et al., 1991; Peterson et al., 2001; Seitzinger et al., 2002; Seybold and McGlynn, 2018). Increased ${{\mathrm{NO}}_{\mathrm{3}}}^{-}$ concentrations in surface waters can induce detrimental algae growths (Beusen et al., 2016; Canfield et al., 2010; Galloway et al., 1995), compromise river ecosystem health and jeopardize drinking water supplies. Since the beginning of the 20th century, human activities such as agricultural expansion and fossil fuel burning have mobilized additional reactive nitrogen (N), initiating and later exacerbating this problem (Seitzinger et al., 2002). In arable landscapes, which include large parts of Europe, the efficient management of aquatic ${{\mathrm{NO}}_{\mathrm{3}}}^{-}$ at network scales is complicated by the spatiotemporal variability in loading patterns and hydrologic regimes as well as the lack of understanding of nutrient pathways, connected transit times and removal processes from input to export. Nevertheless, nitrate concentration and load variability can be predicted at catchment scales when relying on detailed process understanding regarding transport and biogeochemical processing (Alexander et al., 2009; Schlesinger et al., 2006; Wollheim et al., 2008). Moving beyond small-scale variability and characterizing nitrate processing at the catchment scale however remains a challenge (McDonnell et al., 2007; Li et al., 2020).

Within river reaches and streams, reactive solutes like ${{\mathrm{NO}}_{\mathrm{3}}}^{-}$ are affected by complex interactions of physical, biological and chemical processes. Physical transport is driven by local discharge and channel geomorphology and dictates the ${{\mathrm{NO}}_{\mathrm{3}}}^{-}$ residence time in a reach, thus influencing the timescales at which biogeochemical processing can take place (Kirchner et al., 2000; Runkel and Bencala, 1995; Zarnetske et al., 2011). ${{\mathrm{NO}}_{\mathrm{3}}}^{-}$ is removed and transformed by denitrifying bacteria in the anoxic river sediment (Birgand et al., 2007; Peterson et al., 2001); ammonified; or retained through assimilation processes in the oxic or anoxic river compartments by bacteria, fungi and primary producers such as algae and macrophytes, potentially entering higher trophic levels. In the latter case, N in the form of DON (dissolved organic nitrogen) and more commonly DIN (dissolved inorganic nitrogen), together with phosphorus (P), may be released to the water column later on (Durand et al., 2011; Vanni, 2002; Vanni and McIntyre, 2016). The nutrient spiraling model (Newbold et al., 1981; Stream Solute Workshop, 1990) that formally describes these processes has been used to quantify and compare ${{\mathrm{NO}}_{\mathrm{3}}}^{-}$ transport and uptake (the net result of all removal and release processes) in river reaches (Peterson et al., 2001; Mulholland et al., 2008; Hall et al., 2009) and stream networks (Ensign et al., 2006; Doyle, 2005; Marce and Armengol, 2009). Quantifying in situ ${{\mathrm{NO}}_{\mathrm{3}}}^{-}$ uptake is labor-intensive and may involve local nutrient additions, potentially altering the ambient uptake rate (Hensley et al., 2014; Mulholland and Tank, 2002). Other methods require high-frequency measurements (Jarvie et al., 2018; Kunz et al., 2017) that are mostly limited to small spatial scales (i.e., reach scale) and can vary considerably between measuring points (Boyer et al., 2006). At the scale of entire river networks contrarily, uptake measurements are rarely available (but see Wollheim et al., 2017), and models are applied instead to predict spatiotemporal uptake patterns (Boyer et al., 2006; Yang et al., 2018). These models account for the spatial configuration of the stream network, an important aspect for stream biogeochemistry that is often ignored in small-scale experimental approaches (Fisher et al., 2004). Spatially distributed models, however, require calibration of uncertain spatiotemporal parameters and may not reflect the essential features of the system despite fitting observed data well (Klemes, 1986).

River networks link terrestrial source zones to coastal areas and integrate biogeochemical and hydrological catchment functions across scales (Bouwman et al., 2013; Helton et al., 2018). Small streams (usually headwaters) are known to influence the export signal disproportionally because of their overall (high) contribution to total stream length and effective ${{\mathrm{NO}}_{\mathrm{3}}}^{-}$ removal capacity (Alexander et al., 2000; Horton, 1945), explained by high sediment-surface-to-water-volume ratios. Generally, high removal efficiencies have been reported for river network areas with lower specific discharges (Hall et al., 2009; Hensley et al., 2014) under favorable circumstances such as high light availability and heavy in-stream vegetation (Hensley et al., 2014; Rode et al., 2016) as well as for streams with a high capacity for lateral and hyporheic exchange (Gomez-Velez et al., 2015; Kiel and Cardenas, 2014). The scaling of in-stream uptake processes beyond the river reach has been approached by combined experimental-modeling studies with defined explicit scaling relationships (e.g., Basu et al., 2011; Aguilera et al., 2013; Bertuzzo et al., 2017; Lindgren and Destouni, 2004) and theoretical frameworks explaining how the river network capacity regulates solute export (e.g., Wollheim et al., 2018). Abbott et al. (2018) shows how spatially heterogeneous patterns of water chemistry stabilize while the temporal variability in nutrient concentrations persists when moving downstream, facilitating the temporal scaling of headwater measurements. Nevertheless, insights into linking the interplay of nitrate removal processes at the network scale to downstream export patterns in space and time are largely missing.

Concentrations (C) for in-stream solutes such as carbon, major ions, particulates and nutrients are commonly monitored concurrently with discharge (Q) at the basin outlet. C–Q relationships integrate the effect of biogeochemical and hydrological processes within the catchment and have mainly been discussed in terms of land–stream transfer and source configuration in catchments as well as subsurface retention processes (Godsey et al., 2009; Musolff et al., 2017; Bieroza et al., 2018). The shape of long-term (multiple years) C–Q relationships in the log–log space is typically described by the slope of a linear regression model (Godsey et al., 2009). Here, three archetypes have been distinguished: (i) a positive log (C)–log (Q) slope, indicating enrichment, occurs when an increasing discharge additionally mobilizes solutes; (ii) a negative C–Q slope or dilution pattern is commonly linked with source limitations; and (iii) a neutral or chemostatic slope implies low variability in in-stream concentrations across a high range of discharges, a pattern observed for example for solutes derived from weathering bedrock (Ameli et al., 2017; Godsey et al., 2009). The potential information loss associated with linear and monotonic ${{\mathrm{NO}}_{\mathrm{3}}}^{-}$ log (C)–log (Q) analysis was addressed by Moatar et al. (2017) and Minaudo et al. (2019) for more than 200 French catchments and by Diamond and Cohen (2018) for 44 rivers in Florida, USA. These studies identified distinct linear low-flow and high-flow ${{\mathrm{NO}}_{\mathrm{3}}}^{-}$ log (C)–log (Q) regression slopes for a majority of the cases using low-frequency monitoring data. Moatar et al. (2017) found that stronger positive slopes under low-flow conditions correlate positively with chlorophyll a concentrations (associated with biological processes) and attributed this condition to biological ${{\mathrm{NO}}_{\mathrm{3}}}^{-}$ concentration mediation in the stream. This is consistent with the findings of Hall et al. (2009) and Hensley et al. (2014) among others that in-stream uptake is more efficient under low-flow than under high-flow conditions. Furthermore, Wollheim et al. (2017) illustrate non-linear ${{\mathrm{NO}}_{\mathrm{3}}}^{-}$ C–Q relationships conceptually for storm flow dynamics in a river network, showing high retention capacities in the headwater catchments that decrease under increasing flows, changing the slope of C–Q relationships from dilution to enrichment. Based on these studies we hypothesize that the magnitude (or efficiency) of in-stream ${{\mathrm{NO}}_{\mathrm{3}}}^{-}$ uptake is encoded within observed C–Q relationships, and their analysis therefore can improve our understanding of in-stream uptake processes by providing an alternative to elaborate fieldwork and modeling work aimed at quantifying ${{\mathrm{NO}}_{\mathrm{3}}}^{-}$ removal in stream networks. Low-frequency ${{\mathrm{NO}}_{\mathrm{3}}}^{-}$ observations are widely available (e.g., biweekly to monthly grab sampling; Ebeling et al., 2020; Minaudo et al., 2019; Moatar et al., 2017), but if and how these data can be utilized to characterize catchment-scale in-stream processing has yet to be investigated.

In this paper, it is postulated that network-scale uptake effects can be inferred from the degree of non-linearity or the amount of bending of low-frequency, multi-annual concentration (C) and discharge (Q) observations. To test this hypothesis, we apply a parsimonious river network model (similar to Bertuzzo et al., 2017; Helton et al., 2018, 2010; and Mulholland et al., 2008) in 13 German catchments to explore the catchment-scale transport and uptake processes that influence downstream log (C)–log (Q) patterns. The specific objectives are to (i) introduce the maximum curvature (Curv_max) as a robust metric to quantify bending of low-frequency C–Q time series in the log–log space, (ii) explore the sensitivity of Curv_max to hydrological and in-stream biogeochemical parameters (e.g., channel shape, water velocity and biological ${{\mathrm{NO}}_{\mathrm{3}}}^{-}$ uptake velocity), (iii) explore how C–Q bending is linked to network-scale in-stream uptake, and (iv) provide guidelines if and under what circumstances the C–Q bending can offer conclusive information on effective in-stream uptake. In this proof-of-concept exploratory study, we demonstrate how (existing) low-frequency monitoring data can be effectively utilized to quantify nitrate uptake in river networks and show how small-scale uptake processes shape emerging patterns at catchment scales.

2 Methods

2.1 Maximum curvature – Curv_max

The shape of log (C)–log (Q) relationships is often described as linear (Bieroza et al., 2018; Godsey et al., 2009; Musolff et al., 2017) or segmented linear (Meybeck and Moatar, 2012; Moatar et al., 2017; Marinos et al., 2020), implying a limit on the possible log (C)–log (Q) shapes (Tunqui Neira et al., 2020) and setting assumptions such as “fixed breaking points”. Here, we introduce the concept of maximum curvature (Curv_max) to quantify rather than describe the shape of “broken-stick” log (C)–log (Q) relationships without the assumption of a fixed form. In a strict geometrical sense the curvature (−∞; +∞) is the instantaneous rate of change in direction of a point that moves on a curve. A straight line for example has a curvature of zero, and a large circle has a lower absolute curvature than a small circle (Pressley, 2001). Here, Curv_max identifies the magnitude and direction of the log (C)–log (Q) section with the largest instantaneous change. To calculate Curv_max for an observed (noisy) log (C)–log (Q) relationship, a smoothed spline, f, is iteratively fitted with increasing degrees of freedom (df) to capture the general log (C)–log (Q) shape accurately but avoid overfitting (Fig. B1). Initially, df=3, and the log (Q) region of the largest instantaneous change is identified as Q_m±0.05, with $Q_{\mathrm{m}}=\arg {max}_{\log Q}\left|f^{\prime \prime }\right|$. Then, df is increased until, at df=i, the log (Q) corresponding to the largest instantaneous change is not within the initial Q_m region anymore. Consequently, Curv_max is calculated for a smoothed spline fit, f, with

$$\text{df}=i-\mathrm{1}\text{ as }\left\{\begin{array}{c}\underset{\log Q}{max}{f}^{\prime \prime }\text{ if }\left|\underset{\log Q}{max}{f}^{\prime \prime }\right|\ge \left|\underset{\log Q}{min}{f}^{\prime \prime }\right|\\ \underset{\log Q}{min}{f}^{\prime \prime }\text{ if }\left|\underset{\log Q}{max}{f}^{\prime \prime }\right|<\left|\underset{\log Q}{min}{f}^{\prime \prime }\right|\end{array}\right..$$

The Curv_max metric, computed for a log (C)–log (Q) relationship, could be considered to be a complementary metric to the slope of the linear regression model (Godsey et al., 2009) and could serve as an alternative for segmented linear regression fits (Meybeck and Moatar, 2012; Moatar et al., 2017; Marinos et al., 2020) (Fig. S1 in the Supplement) as it quantifies the degree of non-linearity as the amount of bending.

We assume here that a multi-annual (6 to 15 years) low-frequency (biweekly to monthly) C–Q relationship without temporal (significant) trends in a given station has one Curv_max. To verify this assumption in a realistic setting, Curv_max was computed for observed nitrate (C) and Q data (1995–2010) of French water quality stations with biweekly to monthly sampling frequencies (Dupas et al., 2019). Following the removal of C outliers (falling outside of μ±3.5σ in the log space, with μ and σ representing the sample mean and standard deviation, respectively), 444 stations were selected that satisfy the following four criteria: (i) the station should have at least 70 coupled C and Q observations (the maximum number of samples within one station was 402), (ii) a minimum of 6 years of data are represented, (iii) there is no bias in the intra-annual distribution of the data (i.e., never less than 10 % of the C–Q observations in one season, Fig. S2 in the Supplement), and (iv) the station C observations had no significant temporal trends (Mann–Kendall test, p value>0.05) (Ebeling et al., 2021). We then assessed the robustness of Curv_max to the low-frequency C–Q observations in a time series by selecting different subsamples of C–Q data from the entire available time series for a given station. More specifically, 100 random time series subsamples (each with a minimum length of 70) without replacement but with overlap were taken for each station, with the subsamples passing the four criteria above, and Curv_max was calculated for each subsampled time series. On average, the subsamples represented nearly 80 % of the complete time series for a station.

2.2 Network model

In this work an explorative grid-based (100 m×100 m) mass balance network model (comparable to Bertuzzo et al., 2017; Helton et al., 2018, 2010; and Mulholland et al., 2008; conceptually shown in Fig. B2) was used to simulate in-stream nitrate transport and biological removal on a daily basis. The model was developed in R (R Core Team, 2013).

2.2.1 Stream network and hydrological properties

Following Bertuzzo et al. (2017) and Helton et al. (2018), each river network node (i.e., grid cell) i ($\mathrm{1}\le i\le N$) has a drainage area A_i [m²] that is calculated as the sum of the total upstream drainage area ∑_jW_jiA_j [m²] and the direct drainage area a_i [m²] (e.g., laterally contributing drainage area) to grid cell i (Eq. 1):

$$\begin{array}{}\text{(1)}& A_i=\underset{\text{Upstream drainage areas}}{\underbrace{{\sum }_j{W}_{ji}{A}_j}}+\underset{\text{Direct drainage area}}{\underbrace{a_i}},\end{array}$$

where W_ji [–] is an element in the connectivity matrix W (N×N) such that W_ji=1 if j is directly neighboring and flowing into i, and W_ji=0 otherwise. A_j [m²] is the total drainage area to node j.

It is the spatially varying contribution of the total upstream and direct drainage area to each river network node that creates the spatial variability in the river network. The temporal variability in the river network is driven by the time-varying but spatially homogeneous specific discharge Q_t.sp [m³ s⁻¹], calculated as the ratio of the daily discharge at the catchment outlet and the total number of catchment grid cells. The total local discharge Q_i [m³ s⁻¹] at a given grid cell i is thus proportional to the total drainage area at that grid cell, A_i, (following Bergstrom et al., 2016, and Bertuzzo et al., 2017) (Eq. 2). It is Q_i, which in turn dictates the downstream and at-a-station hydraulic geometry relationships of river geomorphic parameters channel width, (w_i; m) and average channel depth (d_i; m) (Leopold and Maddock, 1953) (Eqs. 2a and b). The local velocity in a grid cell v_i [m s⁻¹] is calculated according to Eq. (2c), and the corresponding travel time, T_i [d], is computed in Eq. (2d):

$$\begin{array}{}\text{(2)}& {\displaystyle }& {\displaystyle }{Q}_i=Q_{\text{t.sp}}\cdot A_i\text{(2a)}& {\displaystyle }& {\displaystyle }{w}_i=K_{\mathrm{w}}\cdot Q_i^{a_{\mathrm{w}}}\text{(2b)}& {\displaystyle }& {\displaystyle }{d}_i=K_{\mathrm{d}}\cdot Q_i^{a_{\mathrm{d}}}\text{(2c)}& {\displaystyle }& {\displaystyle }{v}_i={\displaystyle \frac{Q_i}{w_i\cdot d_i}}\text{(2d)}& {\displaystyle }& {\displaystyle }{T}_i={\displaystyle \frac{l_i}{v_i}},\end{array}$$

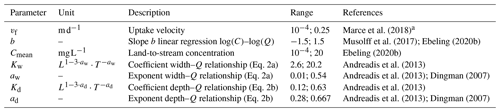
where the flow length through a grid cell i, l_i [m], equals 100 or $\mathrm{100}\sqrt{\mathrm{2}}$ m for horizontal and vertical or diagonal flow directions, respectively. Parameters a_w [–] and K_w [–] are the respective exponent and coefficient parameters in the river width–discharge relationship (Eq. 2a), while a_d [–] and K_d [–] compose the exponent and coefficient parameters of the depth–discharge relationship (Eq. 2b), respectively. The ratio of a_d to a_w corresponds to a parameter $r\text{[–]}\in {\mathrm{R}}^{+}$, which prescribes the cross-section geometry relation such that a triangular channel cross-section is represented by r=1, a parabolic channel cross-section by r=2, and channel cross-sections with progressively flatter bottoms and steeper banks by increasing values of r (Dingman, 2007). The width–discharge relation in Eq. (2a) is conceptually illustrated in Fig. B3 for two sets of a_w and K_w, where a low a_w corresponds to the width of a channel that does not change much with varying discharge, while a high a_w can result in highly varying channel widths.

2.2.2 Nitrate uptake

Similar to Eq. (1) the incoming load, L_in,i [mg s⁻¹], to a river network grid cell i is composed as the sum of upstream load contributions L_in.up,i [mg s⁻¹] and direct land-to-stream loading L_in.ls,i [mg s⁻¹], given that L=CQ (Eq. 3). The contribution of direct land-to-stream loading concentration can be expressed as a power law (Musolff et al., 2017) with the exponent b [–], the slope in the log (C)–log (Q) relationship that is an indicator of the C–Q archetype (Godsey et al., 2009) and coefficient c [–]. Here, b is assumed to be constant over the seasons, which considers that ${{\mathrm{NO}}_{\mathrm{3}}}^{-}$ loading is transport-limited rather than source-limited as explicitly shown for agricultural catchments (Basu et al., 2011; Winter et al., 2021). Following Jawitz and Mitchell (2011), the coefficient c is calculated to yield the long-term mean in-stream input concentration C_mean [mg L⁻¹] (Eq. A1). Additional ${{\mathrm{NO}}_{\mathrm{3}}}^{-}$ sources such as the load resulting from ${{\mathrm{NO}}_{\mathrm{3}}}^{-}$ release within the stream network and point sources are not considered here (similar to Bertuzzo et al., 2017, and Wollheim et al., 2006). This assumption is supported by large-scale assessments in France (Moatar et al., 2017) and Germany (Ebeling et al., 2021), where it was found that, with the exception of pure urban catchments, diffuse sources rather than point sources control the C–Q shape in typical European mixed-land-use settings. Also, we do not consider other loading processes that may create bending at the catchment outlet (e.g., shifts in transport pathways and solute sources; Marinos et al., 2020).

$$\begin{array}{ll}{\displaystyle }{L}_{\text{in},i}& {\displaystyle }=\underset{\text{Upstream loads}}{\underbrace{L_{\text{in.up},i}}}+\underset{\text{Direct land-to-stream loading}}{\underbrace{L_{\text{in.ls},i}}}\\ \text{(3)}& {\displaystyle }& {\displaystyle }=\sum _j{W}_{ji}{L}_j+c\cdot (Q_{\text{t.sp}}\cdot a_i{)}^{b+\mathrm{1}}\end{array}$$

The modeled in-stream ${{\mathrm{NO}}_{\mathrm{3}}}^{-}$ uptake follows first-order removal kinetics (Alexander et al., 2000; Boyer et al., 2006; Ensign and Doyle, 2006), such that the outgoing load from grid cell i L_i [mg s⁻¹] is a fraction of the incoming load L_in,i (Eq. 4), and the absolute removed load L_r,i [mg s⁻¹] can be described as (Eq. 5). Here, L_r,i is influenced by separate hydrological ($P_i\cdot l_i/Q_i$) and biological (v_f) components (similar to Bertuzzo et al., 2017).

$$\begin{array}{}\text{(4)}& {\displaystyle }& {\displaystyle }{L}_i=L_{\text{in},i}\cdot {\mathrm{e}}^{-\frac{v_{\mathrm{f}}\cdot P_i\cdot l_i}{Q_i}}\text{(5)}& {\displaystyle }& {\displaystyle }{L}_{\mathrm{r},i}=L_{\text{in},i}-L_i=L_{\text{in},i}\cdot (\mathrm{1}-{\mathrm{e}}^{-\frac{v_{\mathrm{f}}\cdot P_i\cdot l_i}{Q_i}}),\end{array}$$

where P_i is the wetted perimeter of the cross-section calculated from the Manning equation (using the bed slope S_i and assuming a fixed roughness coefficient = 0.03 [m m⁻¹]) in open channels (Eq. A2). The uptake velocity parameter v_f [m d⁻¹] refers to the vertical movement of ${{\mathrm{NO}}_{\mathrm{3}}}^{-}$ molecules from the water column towards the biofilm at the pelagic–benthic interfaces and the sediments, where the in-stream processing chiefly occurs with v_f=k_id_i, and k_i is the first-order removal constant (Ensign and Doyle, 2006; Wollheim et al., 2006; Marcé et al., 2018). The parameter v_f accounts for the processes altering the rate and form of downstream ${{\mathrm{NO}}_{\mathrm{3}}}^{-}$ delivery (Doyle, 2005) (therefore it is not limited to denitrification only). We assume that v_f is independent of the in-stream ${{\mathrm{NO}}_{\mathrm{3}}}^{-}$ concentration C_mean (Pennino et al., 2014; O'Brien et al., 2007) such that the areal uptake rate $U=v_{\mathrm{f}}\cdot C_{\text{mean}}$ [$\mathrm{mg}{\mathrm{m}}^{-\mathrm{2}}{\mathrm{d}}^{-\mathrm{1}}$] is tightly linked with C_mean in a first-order relationship. Others (e.g., Hensley et al., 2014; Mulholland et al., 2008; O'Brien et al., 2007) contrarily found explicit scaling relationships, where v_f decreases non-linearly for increasing C_mean (10⁻⁴–10¹ mg L⁻¹) when considering distinct catchments. However, in Germany, the ${{\mathrm{NO}}_{\mathrm{3}}}^{-}$ concentration range across a range of catchments is small (10⁻¹–10¹ mg L⁻¹ according to Ebeling et al., 2021), and rivers generally have minor longitudinal concentration variability (Hensley et al., 2014; Ensign and Doyle, 2006), which suggests independent definitions of v_f and C_mean.

The Damköhler number Da [–] is calculated as the ratio between transport (τ_T) and reaction (τ_R) (Eq. 6) timescales and is often used to characterize the relative importance of hydrological and biogeochemical processes in hydrologically connected systems (Oldham et al., 2013; Kumar et al., 2020):

$$\begin{array}{}\text{(6)}& \text{Da}={\displaystyle \frac{{\mathit{\tau }}_{\mathrm{T}}}{{\mathit{\tau }}_{\mathrm{R}}}}={\displaystyle \frac{\text{TT}}{k^{-\mathrm{1}}}},\end{array}$$

where τ_T represents the effective travel time, TT [d], or the exposure timescale under advective conditions. We estimated the catchment-wide TT as the spatiotemporal median of the sum of all downstream T_i (Eq. 2d) for a grid cell in the network $\left({\sum }_i^{\text{Out}}{T}_i\right)$ (similar to Bergstrom et al., 2016), whereas τ_R represents the reactive timescale of biological processes. It is approximated as k⁻¹ [d⁻¹], with the effective catchment-wide k estimated as the spatiotemporal median of the grid-scale first-order reaction constant $k_i=d_i/v_{\mathrm{f}}$.

Table 1 Network model parameter ranges for the Monte Carlo simulations.

^a For v_f, the selected range is an order of magnitude smaller than the one proposed by Marce et al. (2018) as we focus the analysis on the lower v_f, where most of the bending happens (Sect. 3.3).

2.3 Exploring Curv_max with Monte Carlo simulations

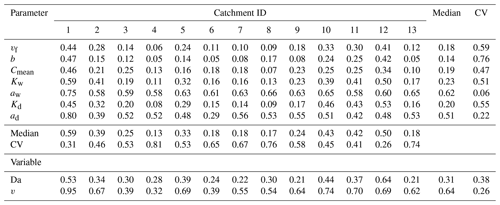
Monte Carlo simulations are performed to explore how Curv_max evolves from a range of model input parameter combinations in a variety of catchments (Sect. 2.3.1 below). These simulations utilize the same ensemble of 11 107 unique parameter combinations in each of the individual study catchments with distinct observed discharge time series to account for the differences one parameter combination may have in each of the catchments. The unique parameter combinations are generated by Latin hypercube sampling from uniform parameter ranges that are set according to literature values (Table 1). Some physical constraints were also imposed such that the channel geometry parameters a_w and a_d must obey continuity principles ($a_{\mathrm{w}}+a_{\mathrm{d}}<\mathrm{1}$ and a_w>a_d, following Leopold and Maddock, 1953). Similar to Bertuzzo et al. (2017) the chosen parameter combination is kept constant in time and uniform in space for simplicity during one model run. The simulated variables are (i) Curv_max [–], deduced from simulated log (C)–log (Q) relationships when a minimum of 80 % of the C data are above the “detection limit” of 0.002 mg L⁻¹ ${{\mathrm{NO}}_{\mathrm{3}}}^{-}$; (ii) the network-wide percentage of load removed L_r.perc [%], which is calculated as the median of the ratio between the daily absolute removed load and the daily absolute incoming load in the river network; (iii) the median network travel time, TT [d]; (iv) the Damköhler number Da [–]; (v) the slope of the linear regression fit of the log (C)–log (Q) relationship at the catchment outlet, b_out [–]; and (vi) the median concentration at the catchment outlet, C_out [mg L⁻¹], and the median water velocity, v [m s⁻¹]. While all outputs can be spatially and temporally explicit on a daily time step, Curv_max is examined at the catchment outlet, integrating both spatial and temporal aspects. The Monte Carlo results are subsequently subjected to a global sensitivity analysis with the PAWN method (Pianosi and Wagener; 2015) to elucidate influential model parameters. Furthermore a correlation analysis is conducted to explore how these influential parameters impact simulated Curv_max. Finally, a classification and regression tree algorithm (CART; Breiman et al., 1984) allowed us to visualize parameter interactions as detailed in Sect. 2.3.2 below.

2.3.1 Catchment selection

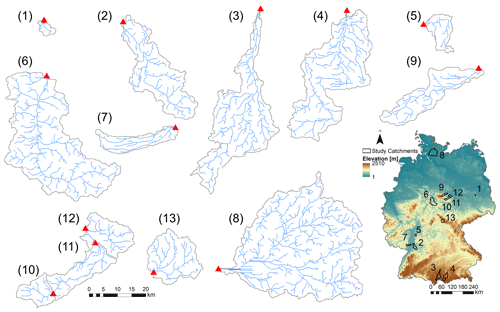
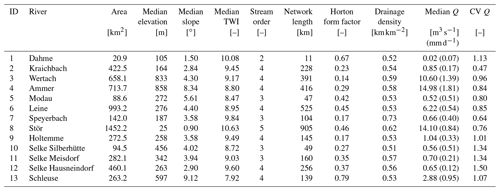
The river networks of 13 mesoscale catchments across Germany (areas between 21 and 1450 km²; Ebeling, 2020a; Table 2) are extracted together with the corresponding daily discharge data at the outlet (uninterrupted for ∼10 years between 1995 and 2010; Musolff, 2020) as inputs for the exploratory river network model. The selected catchments include three nested sub-catchments for the Selke as well as the Holtemme river system, both part of the Bode, a well-studied river system near the Harz mountains in central Germany (Fig. 1; Ehrhardt et al., 2019; Rode et al., 2016; Winter et al., 2021; Mueller et al., 2018). All catchments have distinct geophysical settings as stream order, median discharge and catchment shape (quantified with the Horton form factor; Horton, 1945; Table 2), which is needed to obtain a realistic range of simulated Curv_max using the explorative network model in the Monte Carlo mode. The selected catchments were delineated in ArcMap (ESRI, 2011) from a 100 m×100 m digital elevation model (DEM) (EEA, 2013; Ebeling et al., 2021). A flow direction, flow accumulation and valley slope grid in the same resolution were established. The channel threshold drainage area for the network delineation was set to 150 grid cells (1.5 km²), which agreed well with the observed river network, resulting in a tree-shaped river network with N grid cells or nodes.

Table 2 Catchment properties summary: catchment area, median elevation, slope and topographical wetness index (TWI), maximum Strahler stream order, Horton form factor, drainage density, median discharge at the basin mouth over time (Q) with the corresponding runoff (area specific discharge) between brackets, and the coefficient of variation in the discharge in time (CV Q). The latter variable CV Q integrates the frequency of runoff events and the differences in recession constant (so the catchment's “flashiness” in response to rainfall) (Botter et al., 2013).

Figure 1 Germany DEM with the location and outline (shape) of selected catchments, along with their drainage networks (in blue) and outlet location (red triangle). See Table 2 for catchment IDs and properties.

2.3.2 Model evaluation

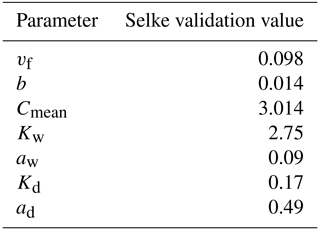
To verify the network model's ability to reproduce realistic concentration time series and Curv_max, the observed monthly nitrate concentrations and the simulated time series were compared in 1 of the 13 selected catchments, the Selke catchment (at Meisdorf gauging station, 282 km²; Table 2; Winter et al., 2021), where extensive field campaigns and modeling studies have been conducted related to in-stream processes (Rode et al., 2016; Dupas et al., 2017; Yang et al., 2019, 2018). Note that such a model validation was performed only in the Selke Meisdorf catchment as the model aim is to explore how certain input parameter combinations may result in log (C)–log (Q) bending at the catchment outlet rather than to reproduce catchment-specific concentrations by performing parameter calibration. This explorative approach is comparable to Bertuzzo et al. (2017) and Helton et al. (2018), who applied a similar model in synthetic river networks but did not validate the model structure in a realistic setting. The Meisdorf catchment is a relatively homogeneous upstream part of the Selke, consisting of forest and cropland, and is characterized by constant export regimes (Winter et al., 2021). For an input parameter combination set to reasonable values for this catchment (Table C1; Rode et al., 2016), the land-to-stream ${{\mathrm{NO}}_{\mathrm{3}}}^{-}$ inputs averaged 1.2 $\mathrm{kg}\mathrm{N}{\mathrm{d}}^{-\mathrm{1}}{\mathrm{km}}^{-\mathrm{2}}$, which is similar to the 1.9 $\mathrm{kg}\mathrm{N}{\mathrm{d}}^{-\mathrm{1}}{\mathrm{km}}^{-\mathrm{2}}$ reported by Winter et al. (2021) for the Selke river (Meisdorf), and it is well within the general 0.001 to 100 $\mathrm{kg}\mathrm{N}{\mathrm{d}}^{-\mathrm{1}}{\mathrm{km}}^{-\mathrm{2}}$ range established by Mulholland et al. (2008). The simulated flow velocity had a spatiotemporal median value of 0.47 m s⁻¹, which is also comparable with measured flow velocities (Risse-Buhl et al., 2017). Additionally, the Selke catchment was used to gain an insight into how the interplay of transport and uptake processes at every network grid cell can result in a curved C–Q pattern at the catchment outlet for one parameter combination, while in the other catchments the network model outputs were only considered at the catchment outlet for the entire range of input parameter combinations in the Monte Carlo approach. Finally, the simulated range of Curv_max, obtained from applying the network model in the 13 different catchments with >10 000 input parameters, was compared to a range of observed Curv_max computed from the C–Q relationships of 444 French catchments (Dupas et al., 2019; Sect. 2.1). Other Monte Carlo simulation outputs, such as ranges of L_r.perc and Da, were compared to literature values for validation purposes.

2.3.3 PAWN sensitivity analysis and correlation analysis

We performed a global sensitivity analysis (GSA) using the moment-independent PAWN method (Pianosi and Wagener, 2015). The method allowed for estimating the effect of the parameter inputs on the entire model output distribution and can be applied to rank the inputs and identify the uninfluential ones. The resulting PAWN sensitivity indices were estimated from generic input–output samples created with the numerical approximation strategy proposed by Pianosi and Wagener (2018). With this strategy, the range of variation in each input x_i is partitioned into a number n_i of equally probable “conditioning” intervals (I_i,k, $k=\mathrm{1},\mathrm{\dots },n_i$); i.e., each interval contains the same number of data points. Given a scalar model output y (here Curv_max), the PAWN method compares the output cumulative distribution function (CDF) (F_y(y)), computed by concurrently varying all the inputs, and the n_i conditional CDFs for that input ($F_{y\mathrm{|}{x}_i}(y\mathrm{|}{x}_i\in I_{i,k})$). Each conditional CDF is obtained by varying all inputs within their entire range except for x_i, whose values are contained within one of the n_i conditioning intervals. The Kolmogorov–Smirnov statistic (KS) is then calculated as the maximum vertical distance between the conditional and unconditional CDFs, while the PAWN sensitivity index (S_i) for input x_i aggregates the results over all conditional CDFs through a summary statistic as presented in Eq. (7):

$$\begin{array}{}\text{(7)}& S_i=\underset{k=\mathrm{1}\mathrm{\dots }{n}_i}{\text{stat}}\text{KS}\left(I_{i,k}\right),\end{array}$$

where $\text{KS}\left(I_{i,k}\right)={max}_y\left|F_y\right(y)-F_{y\mathrm{|}{x}_i}(y\mathrm{|}{x}_i\in I_{k,i}\left)\right|$.

In this study, we applied Eq. (7) using n_i=10 conditioning intervals for each input parameter and used the maximum KS value, KS_max (ranging from 0 to 1), as a summary statistic, which is appropriate for screening non-influential input parameters. For a given parameter, the highest value of KS_max of 1 would indicate a direct dependence of the model output (in this case Curv_max) on that parameter, while a value of KS_max of 0 would mean that the parameter is completely non-influential. We estimated confidence intervals of the sensitivity indices using 15 000 bootstrap resamples and checked the robustness of the results. The PAWN analysis was carried out using the Python version of the SAFE toolbox for global sensitivity analysis (Pianosi et al., 2015).

To explore the direction of change in the C–Q bending at the catchment outlet resulting from variations in the model parameters and the catchment in-stream uptake, a Spearman rank correlation analysis was performed including all the simulated catchment responses and parameter combinations. These correlations were visualized in a correlation matrix using the “corrplot” package in R (Wei and Simko, 2017).

2.3.4 Identify parameter and model output interactions with classification tree

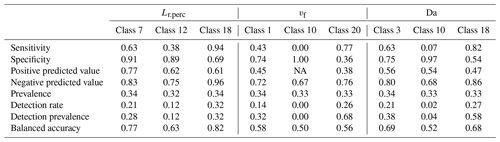
Finally, we aim to determine if, within this modeling framework, C–Q bending at the catchment outlet (specifically Curv_max) informs about the network-wide in-stream uptake. Thereto, a recursive modeling approach is proposed, using the classification and regression trees algorithm (CART; Breiman et al., 1984), which allows for the identification of non-linear synergistic interactions among model parameters and output variables. This non-parametric method segregates classes for a response variable by progressively splitting selected predictor variables in a binary way. The resulting decision tree is intuitive to interpret and can facilitate the fast characterization of river networks. The response variables include the effective catchment-wide removal efficiency L_r, the Damköhler number Da and the uptake velocity v_f, while the predictors are Curv_max, the median network velocity v and all of the model input parameters except for v_f (Table 1). For each response variable, three classes are defined representing low, intermediate and high ranges found in the literature (Table 3) that each contain 5 % of the simulation outputs (obtained by distributing the non-missing model simulations over 20 percentiles). The overall CART accuracy for each response variable is assessed by attributing 80 % of the simulation outputs in the low, intermediate and high classes to a training sample and assigning the remaining 20 % to a test sample. The training sample is then used to construct the classification tree, while the test sample is needed to assess the prediction accuracy and calculate the performance statistics for each class. The CART analysis was performed using the “caret” package in R with the Gini impurity measure as a splitting criterion (Kuhn, 2020).

Table 3 Classes containing low, medium and high values for response variables v_f (uptake velocity), L_r.perc (percentage of load removed) and Da (Damköhler number) are used for the CART training and testing samples. Similar classes are obtained for model output Curv_max. These classes stem from distributing the non-missing simulation data over 20 percentiles and selecting the percentiles corresponding to low, medium and high literature values, with the respective percentile number (1–20) indicated in brackets. This was done to ensure that for one variable, each class contains the same number of simulation data points. The training sample for constructing the CART model was then allocated 80 % of this data and the test sample 20 %.

3 Results and discussion

3.1 Empirical Curv_max

The estimated Curv_max for the French observed ${{\mathrm{NO}}_{\mathrm{3}}}^{-}$ log (C)–log (Q) data (Dupas et al., 2019) ranges between −5.25 and 3.88 (median is −0.23; Fig. B4), and 77 % of the stations are characterized by Curv_max≤0 or a linear or concave shape (similar to Moatar et al., 2017). The time series subsamples for each station generally had a small Curv_max variability (interquartile range, IQR, for a given station below 1) for 93 % of the stations, with some exceptions demonstrating a larger IQR up to 8. This indicates that Curv_max quantification for most low-frequency C–Q time series is robust. The Spearman rank correlation (ρ=0.53, $p\text{ value}<\mathrm{2.2}\times {\mathrm{10}}^{-\mathrm{16}}$) between the absolute observed Curv_max and IQR for each station is significant and positive, implying that C–Q relationships with a higher absolute Curv_max have a higher uncertainty when quantifying the C–Q bending. However, Curv_max variability (IQR) in the subsamples for each station has no significant correlation with the number of data points available for one station. This implies that Curv_max tends to be temporally robust when the C–Q data obey the four criteria in Sect. 2.1 so that the length of the low-frequency time series does not impact the estimated Curv_max. Overall, the proposed Curv_max metric is suitable to quantify bending in multi-annual, temporally stable log (C)–log (Q) relationships.

3.2 Model evaluation in the Selke river (Meisdorf)

To evaluate the network model performance in a realistic setting, we implemented the model with a fixed parameter combination (Table C1) in the Selke catchment and aimed to capture C–Q dynamics at the basin outlet. The simulated ${{\mathrm{NO}}_{\mathrm{3}}}^{-}$ concentration time series (simulated C with uptake) for the Meisdorf station in Fig. 2a shows a seasonal pattern that follows the observation concentration data reasonably well (Nash–Sutcliffe efficiency, NSE=0.50; percent bias, $\text{pbias}=-\mathrm{0.4}\mathit{\%}).$ This seasonality is also reflected in simulated daily percentage of load removed (the ratio between the daily total removed load and the daily total incoming load in the river network) and ranges from almost 0 % to 3.4 % in this case, with the median L_r.perc value equal to 0.41 %. The highest removal efficiencies are simulated in fall and summer and coincide with low simulated ${{\mathrm{NO}}_{\mathrm{3}}}^{-}$ concentrations at the catchment outlet. The conservative ${{\mathrm{NO}}_{\mathrm{3}}}^{-}$ concentration (simulated C no uptake) is stable around 3 mg L⁻¹. The observed nitrate concentrations generally show an enrichment export pattern in the log (C)–log (Q) space (b_out=0.40, R²=0.56) and a Curv_max of −0.35, which agrees well with the simulated Curv_max of −0.28 (Fig. 2b) and deviates significantly from the conservative scenario of simulated C without uptake (b=0.014; Table C1). The observed low nitrate concentrations coincide with low discharges in fall and summer, while high concentrations occur mainly in winter, when discharges are higher.

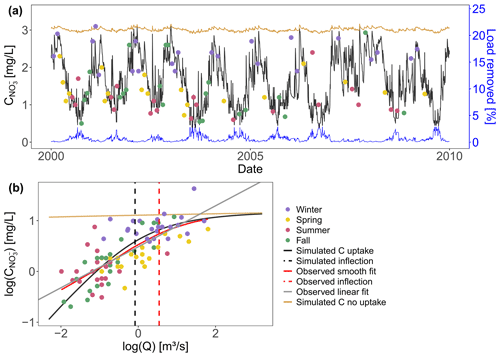
Figure 2 (a) Simulated and observed ${{\mathrm{NO}}_{\mathrm{3}}}^{-}$ concentrations at the Selke Meisdorf gauging station for a 10-year simulation period (2000–2010; NSE=0.50). One data point (C∼5 mg L⁻¹) is not shown here. The simulated median percentage of load removed in the stream network (blue line) is given during the same time period as well as the simulated C with no uptake (v_f=0). (b) The observed ${{\mathrm{NO}}_{\mathrm{3}}}^{-}$ concentrations and Q are log-transformed and plotted together with the simulated C–Q data for 2000–2010. A smoothed spline is fitted to the observed and simulated C–Q data (described as observed smooth fit and simulated C, respectively, in the legend), and Curv_max values of −0.35 and −0.28 are calculated at the respective discharges of 1.72 and 0.92 m³ s⁻¹, indicating the smoothed spline inflection points.

Within the Selke Meisdorf river network the simulated Curv_max is largely contained within −1.12 to −0.29 (10th and 90th quantiles, respectively) for the given parameter combination (Table C1, Fig. 3). Low Curv_max ($<-\mathrm{1.12}$) is found exclusively at grid cells with a low total drainage area (A_i<9 km²), and Curv_max stabilizes at higher values with increasing drainage areas (inset Fig. 3, Fig. S3 in the Supplement). The incoming (L_in.ls and L_in.up; Eq. 3), removed (L_r; Eq. 5) and outgoing absolute load (L_i; Eq. 4 with L=CQ) as a function of Q in the log–log space are shown in Fig. 3 for three selected grid cells on the main river stem with low (C), intermediate (B) and high (A) drainage areas. The corresponding log (C)–log (Q) relationship for the outgoing load (L_i) at the outlet (A) is presented in Fig. 2b for simulated and observed values. Note that Curv_max is calculated from log (C)–log (Q) relationships rather than log (L)–log (Q). The loads in grid cell A, B and C generally increase with discharge, while the load removal efficiency decreases with discharge. The highest removal efficiencies are found in the headwater grid cell C (39 % for low discharge), followed by mid-stream grid cell B (3 % for low discharge) and the outlet A (0.5 % for low discharge). The total absolute load removed (L_r, sum per year per grid cell) is largest for first-order grid cells (average 24.1 kg N yr⁻¹) that represent 55 % of the river network, followed by second- and third-order grid cells (averaging both around 20 kg N yr⁻¹) that represent 20 % and 25 % of the network (inset Fig. 3). Finally, the total yearly incoming load (L_in.ls+L_in.up, sum per year per grid cell) increases with stream order from 1329 kg N yr⁻¹ on average in a first-order grid cell to 5128 and 42 124 kg N yr⁻¹ in second-order and third-order river cells.

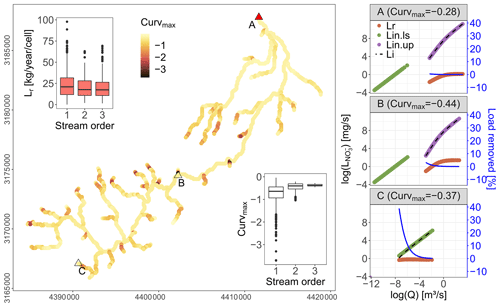
Figure 3 Spatial distribution of simulated Curv_max in the Selke river network (Meisdorf) for a selected parameter set (see Table C1). Three representative grid cells covering low (A), intermediate (B) and high (C) total drainage areas show the incoming land-to-stream load as L_in.ls (Eq. 3), the incoming load from upstream as L_in.up (Eq. 3), the absolute removed load as L_r (Eq. 5) and the outgoing load as L_i (Eq. 4) in the log (L)–log (Q) space. The load removed as a percentage of the incoming load is presented on the secondary axis. Note that the corresponding Curv_max values for these grid cells are calculated from the log (C)–log (Q) relationships rather than log (L)–log (Q). The insets show the distribution of Curv_max and L_r for each grid cell within a certain stream order. In Fig. 2a the observed and simulated concentrations are compared at point A.

With uniform, constant parameters the network model does not account for a spatiotemporal parameter variability. Nevertheless, it successfully (see NSE and pbias) reproduces the seasonality of the observed concentrations over the 2000–2010 period for the Selke Meisdorf catchment (Fig. 2a). For comparison, Yang et al. (2018) found a similar performance (NSE=0.47, $\text{pbias}=-\mathrm{3.35}$ %) when applying a fully distributed model with 16 calibrated parameters in this catchment between 1997 and 2009. The uptake velocity v_f for our simulation was set to 0.098 m d⁻¹ to closely match the observed (assimilatory) uptake range of 0.009 to 0.103 m d⁻¹ for the Selke Meisdorf river network (Rode et al., 2016); the median annual percentage of load removed equals 4.7 %, which is within a comparable range reported in prior studies (Rode et al., 2016, and Yang et al., 2018, found annual means of 4.8 % and 7.6 %, respectively). Note that the annual percentage of load removed accounts for load taken up throughout the entire river network, which may be higher in the headwaters (15 t) than in downstream locations (7 and 5 t for second- and third-order stream sections; inset Fig. 3). Yang et al. (2018) reported very high uptake efficiencies (up to 75 %) for summer seasons that were caused by low ${{\mathrm{NO}}_{\mathrm{3}}}^{-}$ concentrations (0.21 mg N L⁻¹) and load (L=CQ), which are not represented in our model simulation (the lowest simulated ${{\mathrm{NO}}_{\mathrm{3}}}^{-}$ concentration equaled 0.4 mg N L⁻¹). Additionally, due to the parsimonious structure of the proposed model, we did not account for the temporally changing effects of environmental factors like temperature and light availability that might (seasonally) influence uptake efficiencies in the river network (Kadlec and Reddy, 2001). Nevertheless, these high uptake efficiencies under low flows in summer are not a main contributor to the annual percentage of load removed that is dominated by high flows, generally recorded during winter. Thus for the Monte Carlo simulations we calculated L_r.perc as the median of the daily percentage of load removed rather than the total removal efficiency for the entire simulated time period to better represent an effective long-term network-wide removal capacity.

The interplay of incoming, removed and outgoing load at each network grid cell shapes the log (L) and log (C)–log (Q) relationships and consequently Curv_max at the catchment outlet (Fig. 3). Land-to-stream loading (L_in.ls) that varies linearly with direct incoming discharge at a given grid cell in the log space (Eq. 3 with L=CQ; Curv_max=0) can lead to a bent outgoing log (C)–log (Q) relationship where concentration or load (L_i) varies non-linearly with discharge (Curv_max≠0). The onset of a bent log (C)–log (Q) pattern (${\text{Curv}}_{\text{max}}=-\mathrm{0.37}$) is illustrated in the headwater grid cell C in Fig. 3, where L_in.ls is the only incoming load (upstream incoming load, L_in.up, equals 0 in this case). The absolute removed load in a grid cell is higher under increasing Q, while the percentage of load removed is lower, which explains observed C–Q patterns with higher log (C)–log (Q) slopes for low flows than for high flows (Moatar et al., 2017; Wollheim et al., 2008, 2017; Doyle, 2005; Basu et al., 2011). This decreased ${{\mathrm{NO}}_{\mathrm{3}}}^{-}$ load removal efficiency in the downstream direction (spatial scale) or during events (temporal scale) can arise because stream morphology characteristics such as depth and water velocity that correlate with varying discharge constitute higher surface-to-volume ratios at low flows (generally in the headwaters) than at higher flows (at the outlet) (Peterson et al., 2001; Hensley et al., 2014). The uptake and land-to-stream loading at the downstream grid cells (B and A in Fig. 3) have a decreasing local impact on the outgoing load due to the large upstream load contributions that increase in the downstream direction (see explicit scaling relationship for input flux in Bertuzzo et al., 2017). This is also explained by Wollheim et al. (2018), who suggest that the river network saturates as supply exceeds biological “demand”, causing the log (C)–log (Q) relationship to approach the slope of the loading function (presented as the simulated C without uptake in Fig. 2b). Dupas et al. (2017) on the other hand show how ${{\mathrm{NO}}_{\mathrm{3}}}^{-}$ uptake effects are decreasingly visible in C–Q observations downstream, and concentrations largely matched those estimated by a conservative mixing model. The saturation effect with the accumulation of large load is reflected in the Curv_max converging to a constant value when moving from upstream to downstream or from a lower-order to a higher-order river reach (Figs. 3 and S3). This also corroborates the recent findings of Abbott et al. (2018), who found that the temporal variability (here reflected in the C–Q relationship) in nutrients is preserved moving downstream in a river network. Overall the Selke example shows that the network model can realistically reproduce the bending of observed ${{\mathrm{NO}}_{\mathrm{3}}}^{-}$ C–Q relationships that evolve from the decreasing removal efficiency at higher discharges.

3.3 Monte Carlo simulation results

The overview of the model outputs for each of the 13 study catchments in Table 4 shows that catchments 1, 5 and 11 display the lowest 10th quantile Curv_max values of −1.61, −1.40 and −1.24 (more bending), while the catchments 4 and 6 registered higher (less bending) and less variable Curv_max (10th quantiles at −0.31 and −0.35) (Fig. B5). Catchments 3, 4 and 8 are characterized by high runoff and Q (Table 2) at the catchment outlet and demonstrate low percentages of load removed, L_r.perc (90th quantile at 29.8 %, 32.1 % and 19.3 %, respectively). The highest L_r.perc values are found in catchments 1 and 10 (98.4 % and 95.1 % for the respective 90th quantiles). The regression slope of the log (C)–log (Q) relationship at the basin outlet, b_out, is positively skewed for all the catchments (most positive slopes found in catchment 5), while the slope b of the land-to stream loading function had no positive or negative preference (Table 1, Eq. 3). The distribution of the concentrations at the catchment outlet, C_out, are generally similar across all catchments (10th and 90th percentiles within 0 to 6.2 mg L⁻¹) and are significantly less variable than the land-to-stream incoming concentration (parameter C_mean) that varied from 10⁻⁴ to 20 mg L⁻¹ across all the simulations (Table 1). The highest C_out values are found in catchment 8, the largest catchment. The median water velocity v (Eq. 2c) is between 0.01 and 0.5 m s⁻¹ for the 10th and 90th quantiles of all the study catchments, and the largest v is simulated for catchments 3 and 4, which also have the highest discharge. The median river network travel time, TT, for all simulations and catchments ranges from 0.1 to 4 d between their respective 10th and 90th quantiles and remarkably has no clear relationship with catchment properties such as the total river network length (Table 2). Finally, the Damköhler number, Da (Eq. 6), is variable around 1 with the highest values, indicating reaction-driven conditions, found for catchments 2 and 12 (respective ranges from 0.6 to 10.3 and 0.7 to 10.8 for the 10th and 90th quantiles). The lowest Da values are found for catchments 4 and 10 (90th quantile <2), implying more transport-driven conditions.

Table 4 The 10th, 50th and 90th quantiles of model outputs Curv_max, percentage of load removed, (L_r.perc) Damköhler number (Da), regression slope of the log (C)–log (Q) relationship at the basin outlet (b_out), the median concentration at the basin outlet (C_out), the median water velocity (v) and median river network travel times (TT) for each of the 13 German catchments.

The Monte Carlo output in Table 4 shows reasonable values for the different variables, taking into account that the goal of this modeling exercise was not to reproduce catchment-specific conditions but rather to explore how ${{\mathrm{NO}}_{\mathrm{3}}}^{-}$ uptake influences C–Q bending for a range of parameter combinations that represent a spectrum of possible catchment conditions. The simulated Curv_max values for all 13 German study catchments and parameter combinations (80 % of the values between −0.70 and −0.012; Table 4 and Fig. B5) are comparable with the range of Curv_max from ${{\mathrm{NO}}_{\mathrm{3}}}^{-}$ log (C)–log (Q) relationships in the French catchments (80 % of the values between −0.41 and −0.067; Fig. B4) (Dupas et al., 2019). Simulated Curv_max is always smaller than or equal to zero as explained in Sect. 2.2.2. For the model output L_r.perc, a wide range of uptake efficiencies were captured from almost 0 % to near to 100 % for some simulations and a median value of 14.4 % across simulations. This simulated range exceeds the proposed range by Birgand et al. (2007) of 10 % to 70 % of N removal for agricultural drainage networks at annual timescales. High removal percentages (median over the simulated time period of daily percentage of load removed in the network exceeding 95 %) are registered for 3.4 % of all simulations, while very limited load removal (L_r.perc<5 %) occurred for 32.1 % of all the simulations. Other simulation outputs such as the effective velocity v surprisingly rendered similar distributions across the catchments (Table 4) given that the median Q varied for almost 3 orders of magnitude at the basin outlet (Table 2). Their specific discharges (Sect. 2.2.1) however are similar, and by taking the spatiotemporal median v as an effective catchment value for each simulation the (more numerous) headwater grid cells were better represented than the grid cells close to the basin outlet. A similar effect is found for the range of the effective travel time TT. Generally these similar v and TT distributions from model simulations between catchments align with the notion of Langbein and Leopold (1964) that drainage networks evolve naturally to transport water (and sediment) most efficiently such that an equilibrium between channel form and water and sediment load is imposed (Leopold and Maddock, 1953). Also Damköhler numbers Da exhibited realistic ranges, mostly distributed around 1 (Fig. S3; Oldham et al., 2013; Ocampo et al., 2006), with 36.5 % of the simulations <0.8 % and 50.8 % > 1.2, indicating that more simulations are reaction-driven than transport driven. Finally, other variables such as the range of the modeled river widths are found to be reasonable to a large degree (Fig. S4 in the Supplement).

As for the simulations, the same >10 000 parameter input sets are applied in each catchment, differences between the catchments result from the different network structures and hydrological regimes that control transport and uptake processes for each parameter input set in each catchment. From Tables 4 and 2 it is clear that differences in model outputs (i.e., Curv_max, L_r.perc and Da) between the catchments cannot be attributed to a single catchment property such as total network length or basin area. For example Curv_max has the highest variability between simulations in the catchment 1, the smallest catchment, compared to the other catchments, which could be attributed to the variability in local loading and uptake patterns in the network (driven by Q) that are still visible at the catchment outlet. Following the simulated Selke Meisdorf example in Sect. 3.1 (Figs. 3 and S3), we show that Curv_max tends to converge to a constant value with increasing drainage areas (similar to Abbott et al., 2018, for nutrient concentrations; Dupas et al., 2017, for nutrient uptake; and Bertuzzo et al., 2017, for DOC removal). Drainage area is however not the only catchment property influencing Curv_max at the outlet. For example, catchment 6 is the second-largest catchment (Table 2) and has the least bent (and least variable) log (C)–log (Q) relationships. The network structure could possibly play a role here as the largest catchment, catchment 8, has some large tributaries near the basin outlet (Fig. 1), which could bypass removal and transport high load during events, introducing a more variable Curv_max (Mineau et al., 2015; Helton et al., 2018). The percentage of load removed, L_r.perc, is notably lower for catchments with high runoff or Q – like 3, 4 and 8 (Table 4) – which corresponds with findings in Sect. 3.1 that uptake efficiency decreases with increasing Q because of increasing loads to the system (Wollheim et al., 2018; Mulholland et al., 2008) and that increasing Q results in less efficient uptake within the reactive surface area (Peterson et al., 2001; Hensley et al., 2014). The high L_r.perc in small catchments 1 and 10 could then be attributed to their low Q; however why the small catchment 5 does not have similar uptake performance is not evident. Generally the model output variability between the catchments (as a result of different network and discharge properties) is minor compared to the output variability within the catchments (due to the effect of the chosen input parameter set).

3.4 Curv_max sensitivity analysis and model parameter correlation

The PAWN sensitivity index KS_max in Fig. 4 and Table C2 shows that across all catchments Curv_max is most sensitive to the exponents in the width–Q relation a_w (KS_max=0.62) and depth–Q relation a_d (KS_max=0.51). Here, there is little variability between the catchments (KS_max has a low coefficient of variation, CV, of 0.06 and 0.22, respectively). Overall, the slope of the linear loading function, b, is least important in shaping Curv_max (KS_max=0.14). Nevertheless, a high variability in KS_max is observed (CV=0.76) that is caused by larger sensitivities for catchments 1 and 12 (KS_max near 0.45). Curv_max is equally sensitive to v_f and C_mean (KS_max 0.18 and 0.19), but v_f exhibits higher variability in KS_max than C_mean (CV of 0.59 and 0.47). Furthermore, over all the catchments Curv_max is sensitive to the median velocity v and the Damköhler number Da (KS_max equals 0.64 and 0.31, respectively; CV of 0.26 and 0.38). When considering the catchments individually, basin 1, with the smallest discharge, has the highest median KS_max (0.59) across all input parameters, while catchment 4, which has the highest discharge, exhibits the lowest median KS_max (0.13). Additionally, Curv_max is very sensitive to the velocity v in catchment 1 (KS_max=0.95), while it is least sensitive to v in catchment 4. Nevertheless, the other catchments show no clear order in Curv_max sensitivity according to catchment properties such as Q. For example in nested catchments 10, 11 and 12 (Fig. 1), the largest catchment, catchment 12, has the highest KS_max (0.50) and lowest CV (0.26) over all the input parameters, indicating that here Curv_max is more sensitive to the input parameters than in the smaller sub-catchments 10 and 11.

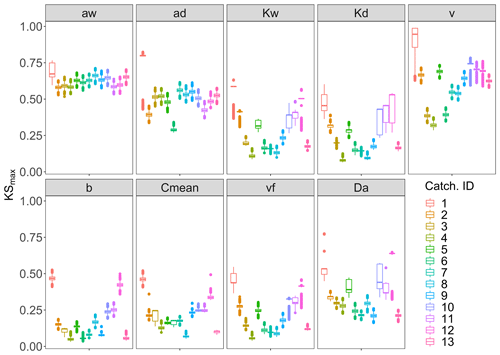
Figure 4 The KS_max sensitivity index for each of the model input parameters and each of the 13 simulated catchments. The input parameters related to the channel geometry (a_d, a_w, K_d and K_w), land-to-stream loading (b and C_mean) and biogeochemistry (v_f) are shown together with two variables derived from some of the input parameters: the median velocity v and the Damköhler number Da. Each boxplot displays 15 000 bootstrapped estimates of KS_max for each of the 13 simulated catchments.

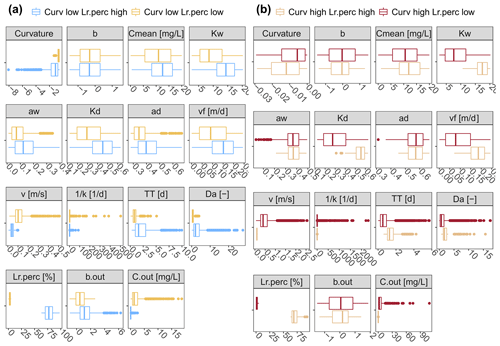
In a next step the estimated Curv_max across all simulations is correlated to the model input parameters as well as to output variables like the percentage of load removed (L_r.perc) the log (C)–log (Q) slope at the catchment outlet (b_out), the median concentration at the basin outlet (C_out) and the uptake constant (k) to identify the strength and direction of their relationship. The resulting Spearman correlation matrix (Fig. 5) reflects the PAWN sensitivity findings, with the highest Curv_max correlation found with parameters a_w (ρ=0.68) and a_d (ρ=0.56) and input variable v (ρ=0.57). Curv_max is independent of v_f ($\mathit{\rho }=-\mathrm{0.04}$) but shows a negative correlation with L_r.perc ($\mathit{\rho }=-\mathrm{0.36}$), suggesting that lower Curv_max (more bending) can be related to a higher L_r.perc. Furthermore, Curv_max is negatively correlated to the log (C)–log (Q) regression slope at the catchment outlet b_out ($\mathit{\rho }=-\mathrm{0.28}$) such that higher bending coincides with more positive b_out. The variable v is additionally strongly negatively correlated with L_r.perc ($\mathit{\rho }=-\mathrm{0.87}$), so a high percentage of load removed occurs at low velocities. Da on the other hand is positively correlated to L_r.perc (ρ=0.58), which indicates that higher Da values are occurring together with higher load removed. Da thereby seems to be controlled more tightly by variation in k⁻¹ ($\mathit{\rho }=-\mathrm{0.71}$) than by TT (ρ=0.48). Finally C_out is negatively correlated with L_r.perc ($\mathit{\rho }=-\mathrm{0.82}$) and Da ($\mathit{\rho }=-\mathrm{0.61}$).

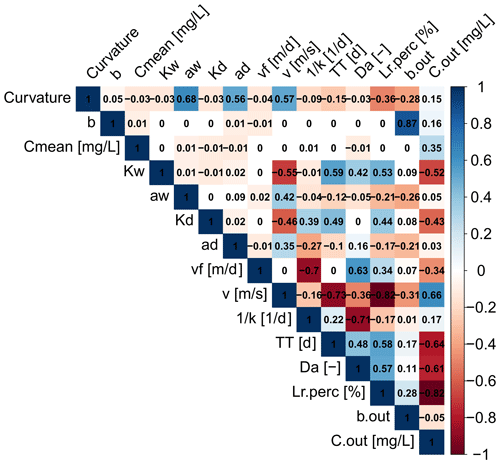
Figure 5 Correlation matrix for the model parameter inputs: channel depth and width exponents (a_d, a_w) and coefficients (K_d, K_w); slope of the land-to-stream loading (b); concentration of the land-to-stream load (C_mean); uptake velocity (v_f); and the outputs bending of the log (C)–log (Q) relationship at the catchment outlet (Curv_max), effective stream velocity (v), first-order uptake constant (k), travel time (TT), Damköhler number (Da), daily percentage of load removed (L_r.perc), and slope of the log (C)–log (Q) relationship and median concentration at the outlet (b_out and C_out). The Spearman rank correlation coefficients (ρ) are given for each combination.

The PAWN and correlation analysis results suggest that the input parameters dictating the channel morphology, a_w and a_d (Sect. 2.3), are controlling factors for the magnitude of the bending in log (C)–log (Q) relationships at the catchment outlet. More specifically parameters a_w and a_d influence the response of the wetted perimeter (P_i; Eq. A2) in a given reach in the network and drive the reactive surface area (P_i⋅l_i) with changes in discharge (Eq. 2a and b, Figs. 5 and B3). The absolute load removed L_r,i (Eq. 5) can be written with the width and depth exponents a_w and a_d explicitly (Eq. A3) so that $L_{\mathrm{r},i}\sim \mathrm{1}/\left(Q^{\mathrm{1}-a_{\mathrm{w}}-a_{\mathrm{d}}}\right)$. When the denominator is large (small a_w and a_d) the effect of low and high Q's on the local absolute removed load increases and can lead to a lower Curv_max (more bending; Sect. 3.1, Fig. B6). Network-based modeling studies often set the width exponent a_w to a value of 0.5 that was found to be representative of rivers globally (Bertuzzo et al., 2017; Rode et al., 2016; Wollheim et al., 2018). This a priori fixed a_w may, however, strongly affect the simulated C–Q dynamics at the basin outlet as is demonstrated here. Curv_max finally shows the lowest sensitivity to the loading parameters b and C_mean that influence the incoming load to a grid cell (Eq. 3) and thus impact the local absolute load removed L_r,i (Eq. 5) rather than the percentage of removed load L_r.perc. This indicates that the contribution of local incoming load in the downstream direction has a limited impact on the log (C)–log (Q) bending at the catchment outlet. For example in the Selke Meisdorf catchment, the locally contributing Q's are generally smaller (or equal for the headwaters) than the total Q in a given reach so that the influence of the loading parameters b and C_mean on the total load decreases in downstream reaches (Sect. 3.1, Fig. 3).

Although Curv_max only has an intermediate sensitivity to the uptake velocity v_f, and they do not correlate well, v_f is an important “boundary condition” for log (C)–log (Q) bending at the catchment outlet. No biological demand (low v_f) would mean that none of the incoming load would be removed from the river network. The outlet signal would in this case be solely driven by the discharge-controlled transport processes, and no bending would be observed (Curv_max=0). Although increasing v_f does correlate with decreasing concentrations ($\mathit{\rho }=-\mathrm{0.34}$) and increasing load removed (ρ=0.34), it does not always lead to more bending, as illustrated in Fig. B6 for the Selke example. Because v_f is defined as a constant within one simulation that is independent of the local nutrient concentration (Sect. 2.2.2), the percentage of load removed in the network is mainly controlled by the varying hydrological conditions here, represented by the effective network-wide velocity v (L_r.perc and v, $\mathit{\rho }=-\mathrm{0.82}$). This confirms that discharge and channel morphology are among the most important predictors of removal (Alexander et al., 2000; Seitzinger et al., 2002; Wollheim et al., 2006). The role of v was further examined in the context of restored and channelized streams (Kunz et al., 2017) and agrees with our findings that decreased v influences N cycling (Peterson et al., 2001).

The PAWN and correlation analysis results show that Curv_max is sensitive to the Damköhler number Da (KS_max=0.31; Fig. 4, Table C2), which has a high positive correlation with the percentage of load removed L_r.perc (ρ=0.58; Fig. 5). This indicates that high Da occurs concurrently with more efficient removal and is in line with others (Ocampo et al., 2006) who found sometimes almost 100 % ${{\mathrm{NO}}_{\mathrm{3}}}^{-}$ removal in the riparian zones of an agricultural catchment with Da exceeding 2. The transport timescale TT that makes up Da (ρ=0.48; Fig. 5) together with the inverse of the first-order uptake constant k⁻¹ ($\mathit{\rho }=-\mathrm{0.71}$; Eq. 6) is examined for classes of low, median and high Da (defined in Table 3) in Fig. 6a to disentangle which values of k⁻¹ and TT occur together and can constitute a certain Da range (each class contains 5 % of all simulations). It is shown here that low Da values are driven by both low TT and high, variable k⁻¹, implying a transport-driven system with limited ${{\mathrm{NO}}_{\mathrm{3}}}^{-}$ removal (median L_r.perc equals 2.4 % in Fig. 6a for low Da). High Da values, contrarily, have high TT and low k⁻¹, fostering intermediate uptake percentages (median L_r.perc=27.1 %). Although also v_f clearly differentiates for classes of low, medium and high Da in Fig. 6a, the corresponding Curv_max values are similar in their range and mean. Nevertheless, this does not mean that Da is not influencing Curv_max at the basin outlet as there could be interactions with other inputs that are not captured here (which is supported by the PAWN findings, where Da appears to be influential).

From the Curv_max perspective (Fig. 6b) we identify model output ranges of L_r.perc, Da and input variable v_f that constitute low, median and high Curv_max classes (Table 3). High Curv_max (less bending, $\sim -\mathrm{0.02}$) is thereby linked to low L_r.perc (median 4.8 %), while low Curv_max (more bending, $\sim -\mathrm{0.60}$) is connected to higher and more variable L_r.perc (median 33.6 %), generally indicating that more bent systems are more efficient in terms of removal and vice versa. To explore some cases when this latter statement might not be true, we examine the input parameter ranges where more bent simulations (${\text{Curv}}_{\text{max}}<-\mathrm{0.51}$, 13.1 % of all simulations) occur concurrently with low percentage of removal (L_r.perc<5.2 %, 0.9 % of all simulations) on the one hand and high percentage of removal (L_r.perc>63.0 %, 4.9 % of all simulations) on the other hand in Fig. B7a. Here, it is seen that high-bending, low-uptake cases mainly occur for simulations with a high effective velocity v (driven by lower values for the channel shape parameters K_w, K_d, a_w and a_d). Low a_w and a_d are correlated with more bending (low Curv_max), and Curv_max is most sensitive to these parameters. However, low a_w and a_d do not lead to a more efficient ${{\mathrm{NO}}_{\mathrm{3}}}^{-}$ uptake if the other channel shape parameters K_w and K_d cause relatively high velocities (median v>0.1 m s⁻¹) throughout the network. The latter case is shown to be true for a minor percentage of all simulations (0.9 %) and explains why low Curv_max (more bending) can be connected to a wider range of L_r.perc. Figure B7b shows that concurrent simulations of less bending (${\text{Curv}}_{\text{max}}>-\mathrm{0.03}$) and high removal (L_r.perc>63.0 %) are even rarer (0.1 % of all simulations) compared to concurrent less bending (${\text{Curv}}_{\text{max}}>-\mathrm{0.03}$) and low removal (L_r.perc>5.2 %; 7.4 % of all simulations). Deviations from the expected high Curv_max–low L_r.perc pattern are also here driven by (very low) v. In the latter case however, a_w and a_d are generally high (leading to high Curv_max), and the different v values stem from coefficients K_w and K_d, which are higher in high-removal simulations. Finally, Fig. 6d illustrates that low, medium and high uptake velocities v_f lead to distinct Da and L_r.perc but do not show up in the bent signal at the catchment outlet.

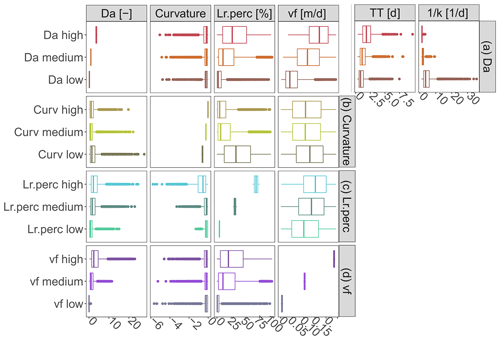
Figure 6 The corresponding simulated ranges for high, median and low values (Table 3) of the main simulation outputs: (a) Damköhler number Da, (b) Curv_max, (c) percentage of load removed L_r.perc and (d) uptake velocity v_f are shown for the same variables (in the columns). The median travel time, TT, and the inverse of the first-order uptake constant, k⁻¹, are given additionally for low, medium and high Da.

3.5 Predicting in-stream processing with Curv_max

To determine if observed C–Q bending at the catchment outlet (here Curv_max) can be utilized to quantify in-stream uptake in the upstream river network and to visualize model parameter interactions, a classification tree was established for low, medium and high values (Table 3, Fig. 6) of the response variables L_r.perc, Da and v_f (Fig. 7). The prediction accuracy metrics in Table C3 and the probability histograms in Fig. 7 show that L_r.perc can be predicted relatively well (overall accuracy of 0.66) compared to the other response variables Da (accuracy 0.51) and v_f (accuracy 0.40). The fitted CART models all perform significantly better than a random allocation of simulation results to each class for each response variable (accuracy > no information rate, $p\text{ value}<\mathrm{2.2}\times {\mathrm{10}}^{-\mathrm{16}}$). While the classes for L_r.perc and v_f are partitioned using only the network effective velocity v and Curv_max, predicting Da in our case requires information on the channel geomorphology parameters width coefficient K_w and depth exponent a_d. The histograms for each of the response variables in Fig. 7 indicate the probability of a test sample being of a certain class when following the partition rules in the respective decision tree. For example, for L_r.perc the probability that the daily percentage of load removed is small (around 8 %) exceeds 0.95 when the effective velocity v in the catchment is larger than 0.22 m s⁻¹, while the probability that L_r.perc is high (around 70 %) in this case is close to 0 (Fig. 7a). For v_f the lowermost (1) and highest (20) classes are predicted most accurately (0.58 and 0.56, respectively; Table C3) and indicate that when the velocity is not very small, and Curv_max is smaller than −0.51 (more bent), v_f is most likely high (probability 0.59). For Da, the lower and higher classes can be predicted most accurately (0.69 and 0.68, respectively); for example, Da is small with a probability of 0.58 when K_w is relatively low (<6.8). When on the other hand K_w exceeds 6.8 and a_d is larger than 0.4 or when a_d is smaller than 0.4 but Curv_max is smaller than −0.45 and v is very small (<0.04 m s⁻¹), it is most likely that Da is large.

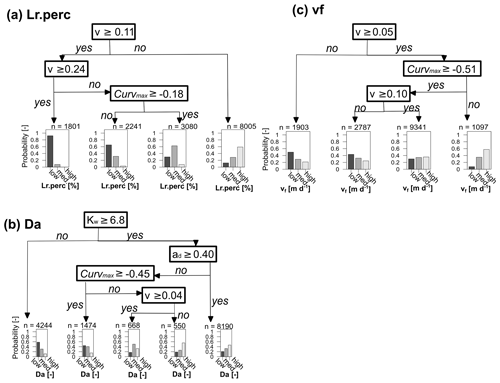
Figure 7 CART decision trees for the response variables L_r.perc (accuracy = 0.66), Da (accuracy = 0.51) and v_f (accuracy = 0.40). The trees are read from top to bottom, where the binary splits are followed to arrive at a histogram, illustrating the probability of a test sample having low, medium or high values (Table 3) for a certain response variable. The variables at the binary splits differ per response variable and consist of the median stream velocity (v; m d⁻¹) and Curv_max for response variables L_r.perc and v_f, while width coefficient K_w and depth exponent a_d are identified additionally for Da. The prediction metrics for each of these classes and response variables are stated in Table C3.

These findings demonstrate that log (C)–log (Q) bending at the catchment outlet, together with the median velocity and the response of the width and the depth of a channel to discharge (parameters K_w, K_d, a_w and a_d) can help to classify the in-stream daily percentage of load removed L_r.perc, the Damköhler number Da and to a certain extent the uptake velocity v_f. This conclusion depends of course on the initial assumptions of our model setup (e.g., linear land-to-stream loading vs. Q with a constant slope b and no dominant influence of waste water sources as well as no seasonality in uptake velocity v_f). The velocity may be computed from the channel shape, discharge (Eq. 2c) and the topography with the channel shape parameters that are sometimes available from rating curve information or detectable from high-resolution satellite pictures. The CART models could help obtain an initial probability of ${{\mathrm{NO}}_{\mathrm{3}}}^{-}$ removal efficiency in a river network, especially in a context where network-wide uptake measurements are scarce (Wollheim et al., 2017; Hensley et al., 2014), and physical, fully distributed models are not always feasible to apply (Boyer et al., 2006; Klemes, 1986). Although the CART models are developed using “only” the 13 German catchments included in the Monte Carlo analysis, in Sect. 3.3 and Table 4 we have shown that the output variability between the catchments (as a result of different catchment properties) is minor compared to the output variability within the catchments (due to the effect of the input parameter set), thus justifying the CART model use. Nevertheless, the prediction performance of these CART models might be influenced in unknown ways when applied to catchments with dissimilar catchment sizes, network structures or hydrological regimes.

4 Conclusions

In this study, we explore how low-frequency ${{\mathrm{NO}}_{\mathrm{3}}}^{-}$ log (C)–log (Q) relationships, observed at a basin outlet, can display bending as a result of network-scale in-stream uptake processes. We established a parsimonious grid-based river network model for 13 distinct German catchments and investigated the influence of in-stream loading, transport and uptake parameters on the bending of log (C)–log (Q) relationships. Based on our exploratory analysis we conclude the following.

• Noisy, multi-annual and low-frequency ${{\mathrm{NO}}_{\mathrm{3}}}^{-}$ log (C)–log (Q) relationships at a basin outlet can be described as bent, and the amount of bending can be robustly quantified with the new Curv_max metric. Curv_max is temporally stable on multi-annual timescales and can be computed alongside existing log (C)–log (Q) descriptors, such as the slope of the linear regression model.

• A bent log (C)–log (Q) relationship (Curv_max<0) at the basin outlet can arise from log–log linear land-to-stream C–Q relationships if uptake is present within the river network (v_f≠0). This supports the hypothesis that more positive slopes under low flow (bent log (C)–log (Q) curves) are linked to biological ${{\mathrm{NO}}_{\mathrm{3}}}^{-}$ concentration mediation in the stream (Moatar et al., 2017) and connects Curv_max (as a quantitative measure) to observations of increased removal efficiency under low flows (Wollheim et al., 2017). Our findings also stress the need to monitor the entire discharge range and capture low flows as well as high flows in a catchment.

• The bending at the catchment outlet is primarily shaped by the channel geomorphological parameters a_w and a_d (exponents in the respective stream width and depth to discharge relationships, with Curv_max sensitivity indices KS_max equal to 0.62 and 0.51 and Spearman correlation coefficient ρ equaling 0.68 and 0.56, respectively) and less by the uptake velocity v_f (KS_max=0.18, $\mathit{\rho }=-\mathrm{0.04}$), given that v_f differs from zero. In the latter case Curv_max would equal zero, and the log (C)–log (Q) relationship would be solely shaped by the accumulation of upstream load. Thus, the change in reactive channel bed area with discharge (mediated by a_w and a_d) has a greater influence on the bending at the outlet than the biological removal capacity (here v_f). Additionally we demonstrate that an a priori fixed a_w might strongly affect the simulated C–Q dynamics at the basin outlet. This calls for a better representation of channel geomorphological parameters at stream networks to allow for better modeling assessments.

• Curv_max at the basin outlet can be linked to the network-wide removal efficiency L_r.perc ($\mathit{\rho }=-\mathrm{0.36})$ under certain conditions, generally showing that systems with more bending in their log (C)–log (Q) relationship are more efficient in terms of removal and vice versa. It is, however, clear that also cases with high bending (${\text{Curv}}_{\text{max}}<-\mathrm{0.51}$) and low removal (L_r.perc<5.2 %, 0.9 % of all simulations) or low bending (${\text{Curv}}_{\text{max}}>-\mathrm{0.03}$) with high removal (L_r.perc>63.0 %, 0.1 % of all simulations) exist that are imposed by respective higher and lower network-wide median velocities. This shows how the velocity, v, (calculated from the channel shape parameters a_w, a_d, K_w and K_d) may mediate the connection between L_r.perc and Curv_max and indicates that v should be considered when interpreting log (C)–log (Q) bending. Consequently, anthropogenic impacts in terms of channelization of river networks might lead to lower removal efficiencies.

• Classification trees – like CART – can be useful for predicting low, median and high classes of response variables L_r.perc, the Damköhler number Da and v_f. They provide useful insights on how catchments with low-frequency concentration and discharge time series (that are generally available) can reveal information on the upstream river network uptake performance.

  To evaluate the generality of the results presented here, Curv_max should be calculated for ${{\mathrm{NO}}_{\mathrm{3}}}^{-}$ concentration observations of a larger range of catchments and linked to the respective catchment properties. Properties such as light and stream ecological state can serve as proxies for uptake performance, and for example topographic gradient can be a proxy for network transport velocity. Finally, including conservative tracers in the analysis can be used to estimate loading scenarios. Such a data-driven exploration would further elucidate the linkages between nutrient uptake efficiency and low-frequency C and Q observations.

Appendix A

Calculation of c is performed as follows (Jawitz and Mitchell, 2011):

$$\begin{array}{}\text{(A1)}& c={\mathrm{e}}^{{\mathit{\mu }}_c-b\cdot {\mathit{\mu }}_q},\end{array}$$

with

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }{\mathit{\mu }}_q=\text{mean}(\log Q_{\text{t.sp}}\cdot a_i)\\ {\displaystyle }& {\displaystyle }{\mathit{\mu }}_c=\log \text{mean}C-{\displaystyle \frac{{\mathit{\sigma }}_c^{\mathrm{2}}}{\mathrm{2}}}\\ {\displaystyle }& {\displaystyle }{\mathit{\sigma }}_c=\sqrt{b^{\mathrm{2}}\cdot {\mathit{\sigma }}_q^{\mathrm{2}}}\\ {\displaystyle }& {\displaystyle }{\mathit{\sigma }}_q=\sqrt{\text{var}(\log Q_{\text{t.sp}}\cdot a_i)}.\end{array}$$

Stream channel wetted perimeter P_i [L] (where A is the cross-sectional area [L²]; R_H [L] is the hydraulic radius; and w_i [L], d_i [L] and v_i [L T⁻¹] are the local stream width, average depth and velocity, respectively) is calculated in Eq. (A2). S_i [L L⁻¹] is the stream bed slope, and n [–] is the Manning roughness coefficient that is equal to 0.03 for all simulations.

$$\begin{array}{}\text{(A2)}& P_i={\displaystyle \frac{A}{R_{\mathrm{H}}}}={\displaystyle \frac{w_i\cdot d_i\cdot S_i^{\frac{\mathrm{3}}{\mathrm{4}}}}{{\left(v_i\cdot n\right)}^{\frac{\mathrm{3}}{\mathrm{2}}}}}\end{array}$$

The load removed in a grid cell (Eq. 5) with the width and depth exponents a_w and a_d stated explicitly is calculated as follows:

$$\begin{array}{}\text{(A3)}& L_{\mathrm{r},i}=L_{\text{in},i}\cdot (\mathrm{1}-{\mathrm{e}}^{-\frac{v_{\mathrm{f}}\cdot {\left(K_{\mathrm{w}}\cdot K_{\mathrm{d}}\right)}^{\frac{\mathrm{5}}{\mathrm{2}}}\cdot S^{\frac{\mathrm{3}}{\mathrm{4}}}\cdot n^{\frac{\mathrm{3}}{\mathrm{2}}}}{Q_i^{\mathrm{1}-a_{\mathrm{w}}-a_{\mathrm{d}}}}}).\end{array}$$

The velocity in a grid cell (Eq. 2c) with the width and depth exponents a_w and a_d stated explicitly is calculated as follows:

$$\begin{array}{}\text{(A4)}& v_i={\displaystyle \frac{Q^{\mathrm{1}-a_{\mathrm{w}}-a_{\mathrm{d}}}}{K_{\mathrm{w}}\cdot K_{\mathrm{d}}}}.\end{array}$$

Appendix B

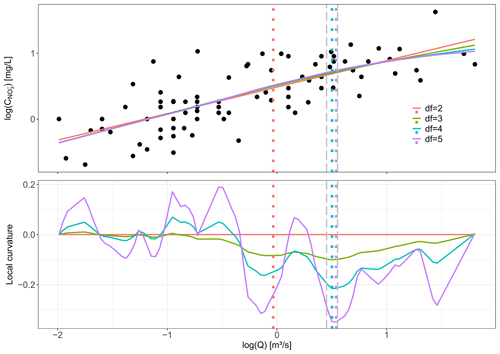
Figure B1 Conceptual figure explaining Curv_max. The upper panel shows the log (C)–log (Q) relationship for Selke Meisdorf with the smoothed spline fits to these data for different degrees of freedom (df). The corresponding colors in the lower plot show then the local curvature values for these fitted smoothed splines. Also the log (Q) is indicated, for which the largest local curvature was found for each of the smoothed splines. Curv_max is then calculated as the largest local curvature value for a degree of freedom of 5 in this specific case as it is the largest degree of freedom that has the largest local curvature within Q_m±0.05, with Q_m equal to the log (Q) of the largest local curvature for df=3. Note that when Curv_max<0, the curve is concave, while for Curv_max>0 the curve is convex.

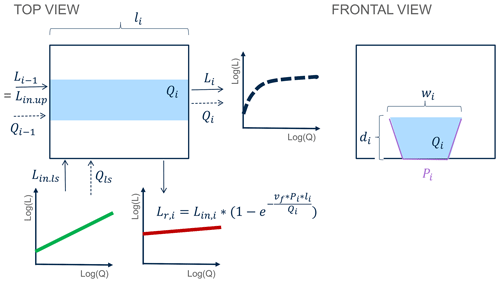
Figure B2 Network model, illustrated for one grid cell. Here, the flow length through a grid cell i is l_i [L]; w_i [L] and d_i [L] are the respective width and average depth of the reach, and P_i [L] is the corresponding stream channel wetted perimeter. The uptake velocity is denoted as v_f. The local discharge Q_i [L³ T⁻¹] consists of upstream incoming discharge Q_i−1 [L³ T⁻¹] and land-to-stream runoff Q_ls [L³ T⁻¹]. Similarly, the local load L [M T⁻¹] consists of upstream incoming load L_in.up [M T⁻¹] and the land-to-stream load L_in.ls [M T⁻¹], where $L_{\text{in.}}=L_{\text{in.up}}+L_{\text{in.ls}}$. Finally, the local load removed is denoted as L_r,i [M T⁻¹].

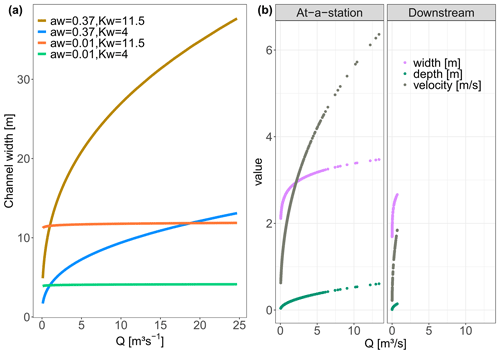
Figure B3 (a) The effect of parameters a_w and K_w on the channel width illustrated for the Q time series at the Selke Meisdorf station. (b) In the “At-a-station” panel the changes in velocity, depth and width with Q for grid cell B (Fig. 3) in the middle of the Selke network are evaluated. The “Downstream” panel, which considers all the network grid cells, shows the channel characteristics width, depth and velocity for a time t, with a Q of 0.70 m³ s⁻¹ at the outlet. The values for the parameters a_w, K_w, a_d and K_d are the same for both scenarios (Table C1).

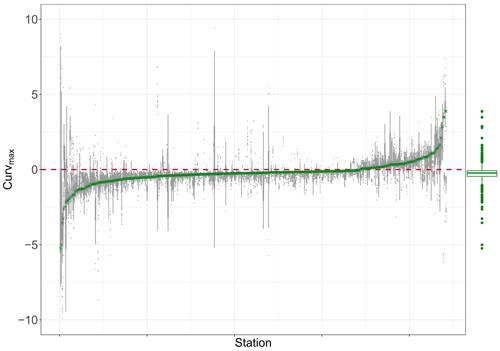
Figure B4 Curv_max of nitrate log (C)–log (Q) data for 444 French monitoring stations arranged from left to right with increasing Curv_max (green crosses). For a given station, the gray boxplot represents the temporal robustness of this metric by subsampling 100 times from the original time series. The green boxplot indicates the range and distribution of all observed station Curv_max values.

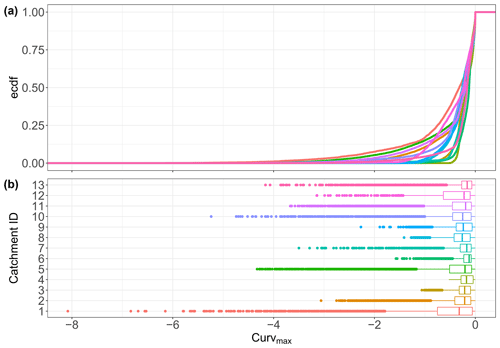
Figure B5 Curv_max distributions resulting from running the same 11 107 input parameter combinations in each of the 13 catchments. Panel (a) shows the elemental cumulative distribution and (b) boxplots. None of the catchments have a normally distributed Curv_max set according to the Kruskal–Wallis (p<0.05) test.

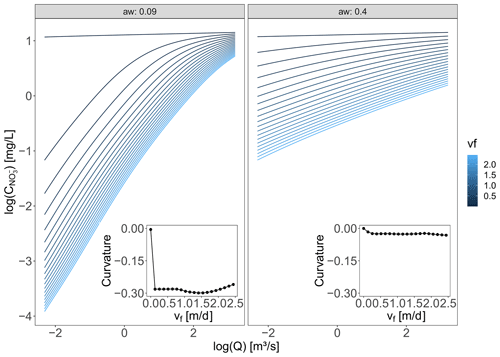
Figure B6 Log(C)–log (Q) relationships and Curv_max for increasing uptake velocities (v_f) resulting from network model simulations of the Selke Meisdorf catchment. As an example, two different a_w values are displayed, and v_f is varied from almost 0 to 2.5 m d⁻¹ with the other parameter values as stated in Table C1.

Figure B7 Two specific cases of Fig. 6: (a) when Curv_max is low (high bending) and L_r.perc is low as opposed to high and (b) when Curv_max is high (low bending) and L_r.perc is high as opposed to low.

Appendix C

Table C1 Estimated parameter values for the Selke catchment.

Table C2 PAWN sensitivity indices KS_max for all the parameters and all the catchments, together with median and coefficients of variation (CV).

Table C3 Performance statistics for each of the classes for the variables L_r.perc, Da and v_f predicted by CART.