Daily soil temperature modeling improved by integrating observed snow cover and estimated soil moisture in the USA Great Plains

Soil temperature (T_s) plays a critical role in land–surface hydrological processes and agricultural ecosystems. However, soil temperature data are limited in both temporal and spatial scales due to the configuration of early weather station networks in the USA Great Plains. Here, we examined an empirical model (EM02) for predicting daily soil temperature (T_s) at the 10 cm depth across Nebraska, Kansas, Oklahoma, and parts of Texas that comprise the USA winter wheat belt. An improved empirical model (iEM02) was developed and calibrated using available historical climate data prior to 2015 from 87 weather stations. The calibrated models were then evaluated independently, using the latest 5-year observations from 2015 to 2019. Our results suggested that the iEM02 had, on average, an improved root mean square error (RMSE) of 0.6 ^∘C for 87 stations when compared to the original EM02 model. Specifically, after incorporating the changes in soil moisture and daily snow depth, the improved model was 50 % more accurate, as demonstrated by the decrease in RMSE. We conclude that, in the USA Great Plains, the iEM02 model can better estimate soil temperature at the surface soil layer where most hydrological and biological processes occur. Both seasonal and spatial improvements made in the improved model suggest that it can provide a daily soil temperature modeling tool that overcomes the deficiencies of soil temperature data used in assessments of climatic changes, hydrological modeling, and winter wheat production in the USA Great Plains.

1 Introduction

A reliable estimate of soil temperature (T_s) is useful for understanding agricultural ecological systems, hydrological processes, and land–atmosphere interactions (Lembrechts et al., 2020; Qi et al., 2016; Zhang et al., 2018) due to the fact that T_s governs physical, chemical, and biological processes of the soil and interactions between the atmosphere and land surface (Smith, 2000; Soong et al., 2020). In particular, T_s has been widely used for a better understanding of changes in soil moisture (Lakshmi et al., 2003), the ecosystem carbon balance (Goulden et al., 1998), and the nitrogen mineralization process (Persson and Wirén, 1995), although a larger prevalence of air temperature observations are available as a soil temperature proxy. From a practical perspective, T_s is critical for agricultural system models, such as the crop environmental resource synthesis (CERES) models, to assess the impacts of extreme climate on crop production and stress tolerance, thereby allowing producers to better prepare for proactive and reactive field management (Bergjord et al., 2008; Persson et al., 2017; Williams et al., 1989). Frequent extreme climate events, such as spring freezes and summer heat stress, can impact winter wheat (Triticum aestivum L.) growth and development, reducing grain yields by more than 7 % in the USA winter wheat belt (Tack et al., 2015; Paulsen and Heyne, 1983). These effects are also modulated through land–surface interaction processes (Hillel, 1998; Araghi et al., 2017).

To improve the accuracy of crop management modeling, a bare soil temperature (T_s) at the 10 cm depth, a standard soil temperature variable, has commonly been considered as being a more direct and useful variable than air temperature (T_a) measured at 1.5 or 2 m height in crop phenology (Onwuka and Mang, 2018), plant photosynthesis and soil respiration (Meyer et al., 2018; Wu and Jansson, 2013), plant nutrient uptake (Yan et al., 2012), and estimate of crop production (Araghi et al., 2017; Hillel, 1998). There are many T_s modeling techniques, mostly based on the land–surface interaction process (Qi et al., 2019; Yener et al., 2017). Most T_s models are rooted in theories of soil heat exchange and surface energy balance (Rankinen et al., 2004; Nobel and Geller, 1987; Chalhoub et al., 2017). The theory-based simulation for surface energy balance usually includes solar radiation (incoming and outgoing), infrared radiation (absorbed and reflected), turbulent flux energy (latent heat and sensible heat), and net ground heat flux through the ground surface into soil layers thermodynamically (Mihalakakou et al., 1997; Chalhoub et al., 2017). Obviously, the energy-balance-based model usually requires more detailed near-surface and soil variables, such as turbulent flux quantities (sensible heat flux and latent heat flux), to make the model reliable and accurate; however, determining quality turbulent flux quantities is not a trivial task (Dhungel et al., 2021; Kutikoff et al., 2021). In addition, seasonal variations in soil thermal conductivity and underestimates of actual evapotranspiration usually lead to overestimated surface soil temperatures (Bittelli et al., 2008). Therefore, simpler empirical models with fewer dynamic processes for T_s prediction have been explored (Zheng et al., 1993; Plauborg, 2002; Liang et al., 2014; Badache et al., 2016; Kang et al., 2000). However, these empirical models might result in relatively large estimated errors of over 2 ^∘C due to the lack of details about physical processes, such as uncertainties of the soil volumetric heat capacity and thermal conductivity (Badía et al., 2017). For example, the volumetric heat capacity was higher for a clay soil (1.48–3.54 MJ m^−3 ∘C⁻¹) than for a sand soil (1.09–3.04 MJ m^−3 ∘C⁻¹) when the soil moisture content was between 0 to 0.25 kg kg⁻¹ (Abu-Hamdeh, 2003). Currently, the USA Department of Agriculture (USDA) provides a high-resolution Gridded Soil Survey Geographic (gSSURGO) database product (https://gdg.sc.egov.usda.gov/, last access: 23 July 2021) that includes static soil physical property data at 10 km resolution. The gSSURGO data facilitate T_s modeling, especially for better performance in large-scale T_s modeling due to its spatial variations in soil properties and soil moisture. These data sets have been widely used in the estimation of root zone soil water content (Miller et al., 2018) and subsurface hydrologic properties (Dirmeyer and Norton, 2018). The empirical model proposed by Plauborg (2002) performed better than energy-balance-based models when applied in the USA Great Plains for the last 5 years. Due to the lack of information about static soil properties on a large scale 1 or 2 decades ago, either over- or underestimates of T_s occurred, which, in turn, leads to large deviations in the assessment of crop stress and crop production (Gupta et al., 1990; Stone et al., 1999).

Recent studies have shown that estimated soil temperature usually deviates from observed soil temperature in the winter due to snow cover, frozen soil, and wide spatial and temporal heterogeneity in frozen soil properties (Nagare et al., 2012; Zhang et al., 2008; Rankinen et al., 2004). The impact of snow cover on soil temperature has been investigated (Rankinen et al., 2004) and is partially accounted for by incorporating correcting factors in land surface modeling and ecosystem models (Zhang et al., 2008) and soil and water assessment tools (SWAT; Qi et al., 2019). For both empirically and physically based soil temperature modules embedded in SWAT, the predictions of soil temperature in regions with thick snow cover seldom agree with field measurements in winter (Qi et al., 2019).

In the USA Great Plains, there has been increasing interest in improving hydrological process modeling of surface water and groundwater due to the Ogallala Aquifer's depletion in recent decades (Haacker et al., 2019). However, the automated weather station networks that observed soil temperature were not commissioned in this region until the late 1980s and early 1990s (Brock and Crawford, 1995). Not only were there few continuous observations for T_s earlier than the 1990s, these automated weather station networks also had limited stations in each state of the USA Great Plains. Such a lack of reliable soil temperature data both spatially and temporally makes the long-term assessment of water resources, crop phenology, and crop production modeling difficult.

The objectives of this study include the following: (1) to develop a robust T_s model using limited surface climate variables by integrating soil moisture and snow depth observations, (2) to demonstrate the error contributions in soil temperature modeling, and (3) to evaluate the performance of an improved model to predict T_s compared to current models. The data sets and methods are described in Sect. 2. Section 3 provides modeling results, and conclusions are presented in Sect. 4.

Figure 1 Specific soil textures (a) and soil bulk density (b) at 87 weather stations in the USA winter wheat belt, including the states of Nebraska (NE), Kansas (KS), Oklahoma (OK), and part of Texas (TX) in the USA Great Plains.

2 Data sets and methods

2.1 Weather stations and data sets

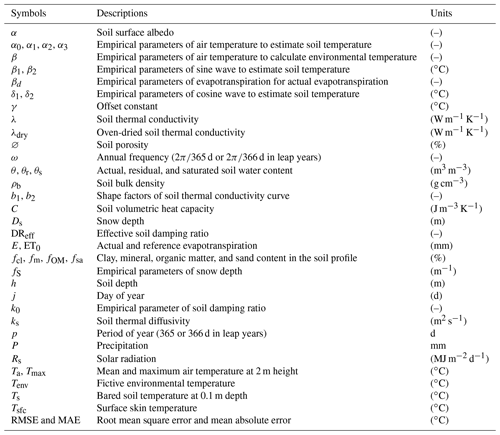
The spatial domain of this study covers the winter wheat belt in the USA Great Plains, comprising the states of Nebraska (NE), Kansas (KS), Oklahoma (OK), and part of Texas (TX), where soil texture and bulk density vary (Fig. 1). In this study, three surface climate data sets were obtained from (1) the Automated Weather Data Network (AWDN) (https://hprcc.unl.edu/awdn/, last access: 23 July 2021), commissioned in the 1980s for Nebraska and Kansas; (2) the Oklahoma Mesonet (OK Mesonet), a daily climate data source for Oklahoma, which started in the 1990s (http://www.mesonet.org/, last access: 23 July 2021); and (3) the Soil and Climate Analysis Network (SCAN), which gives daily climate observations (https://www.wcc.nrcs.usda.gov/scan/, last access: 23 July 2021) that we selected for Texas due to limited quality data available in its automated weather station network. The number of selected stations was 26 in NE, 8 in KS, 44 in OK, and 9 in TX. The selection of these 87 stations was based on the completeness of climate data and data length (at least longer than periods of continuous 15 years). In addition to the weather station data sets, soil data sets providing soil attributes and characteristics were obtained from the standard USDA-NRCS Soil Survey Geographic (gSSURGO) database product (https://gdg.sc.egov.usda.gov/, last access: 23 July 2021) from which soil bulk density (ρ_b; grams per cubic centimeter), soil organic matter (f_OM; percent), sand (f_sa; percent), clay (f_cl; percent), silt (f_sl; percent) contents, soil porosity (Ø; percent), and soil surface albedo (α; –) were used for all weather stations. Note that all symbols and corresponding descriptions for variables used in this study are listed in the Table A1 (see the Appendix). The snow depth data were taken from the daily Global Historical Climatology Network (GHCN; Menne et al., 2009; Lin et al., 2017). Detailed data set sources and data variables used in each data set are shown in Table A2.

2.2 Soil temperature models

2.2.1 Empirical model

There are two common soil temperature models, i.e., empirical and process based. After examining both types of models for our study region, the current empirical model was selected because it was more accurate than the process-based model in this area. Plauborg (2002) developed a statistical soil temperature (T_s; degrees Celsius) model based on the current and previous 2 d air temperatures (T_a; degrees Celsius), annual and semi-annual cycles in the soil temperature fluctuations, and a daily soil temperature offset at a specific site, as shown in Eq. (1) (called EM02, thereafter) as follows:

$$\begin{array}{}\text{(1)}& \begin{array}{rl}{T}_{\mathrm{s},j}& =\mathit{\gamma }+{\mathit{\alpha }}_{\mathrm{0}}{T}_{\mathrm{a},j}+{\mathit{\alpha }}_{\mathrm{1}}{T}_{\mathrm{a},j-\mathrm{1}}+{\mathit{\alpha }}_{\mathrm{2}}{T}_{\mathrm{a},j-\mathrm{2}}+{\mathit{\beta }}_{\mathrm{1}}\sin \left(\mathit{\omega }j\right)\\ & +{\mathit{\delta }}_{\mathrm{1}}\cos \left(\mathit{\omega }j\right)+{\mathit{\beta }}_{\mathrm{2}}\sin \left(\mathrm{2}\mathit{\omega }j\right)+{\mathit{\delta }}_{\mathrm{2}}\cos \left(\mathrm{2}\mathit{\omega }j\right),\end{array}\end{array}$$

where γ is an offset constant (degrees Celsius), and coefficients α₀, α₁, and α₂ are dimensionless. The units of the coefficients β₁, β₂, δ₁, and δ₂ are in degrees Celsius. The j and ω denote day of the year and annual frequency ($\mathrm{2}\mathit{\pi }/\mathrm{365}$ d or $\mathrm{2}\mathit{\pi }/\mathrm{366}$ d in leap years) in an annual soil temperature signal.

Figure 2 Effects of soil moisture on (a) thermal conductivity (λ) and (b) soil thermal diffusivity (k), as obtained by Eqs. (7)–(11).

2.2.2 Improved empirical model

The improved model, based on the EM02, was developed through the following three steps: (1) prolonging the time window of T_a to include 1 extra prior day T_a; (2) constructing a new fictive environmental temperature (T_env; degrees Celsius), defined as a function of air temperature and surface skin temperature (T_sfc; degrees Celsius; Williams et al., 1984) by utilizing T_env to replace the original T_a; and, most importantly (3), incorporating site-specific daily soil thermal diffusivity and snow depth. This improved empirical model (iEM02) can be described by Eqs. (2)–(6) as follows:

$$\begin{array}{}\text{(2)}& \begin{array}{rl}{T}_{\mathrm{s},j}& =\left(\mathit{\gamma }+{\mathit{\alpha }}_{\mathrm{0}}{T}_{\mathrm{env},j}+{\mathit{\alpha }}_{\mathrm{1}}{T}_{\mathrm{env},j-\mathrm{1}}+{\mathit{\alpha }}_{\mathrm{2}}{T}_{\mathrm{env},j-\mathrm{2}}\right.\\ & +{\mathit{\alpha }}_{\mathrm{3}}{T}_{\mathrm{env},j-\mathrm{3}}+{\mathit{\beta }}_{\mathrm{1}}\sin \left(\mathit{\omega }j\right)+{\mathit{\delta }}_{\mathrm{1}}\cos \left(\mathit{\omega }j\right)\\ & \left.+{\mathit{\beta }}_{\mathrm{2}}\sin \left(\mathrm{2}\mathit{\omega }j\right)+{\mathit{\delta }}_{\mathrm{2}}\cos \left(\mathrm{2}\mathit{\omega }j\right)\right)\times f\left(D_{\mathrm{S},j}\right)\times {\mathrm{DR}}_{\mathrm{eff},j}\end{array}\end{array}$$

$$\begin{array}{}\text{(3)}& {\displaystyle }{T}_{\mathrm{env},j}=\mathit{\beta }{T}_{\mathrm{a},j}+(\mathrm{1}-\mathit{\beta })T_{\mathrm{sfc},j}\text{(4)}& {\displaystyle }\begin{array}{rl}{T}_{\mathrm{sfc},j}& =(\mathrm{1}-\mathit{\alpha })\left({\stackrel{\mathrm{‾}}{T}}_{\mathrm{a},j}+\left({\stackrel{\mathrm{‾}}{T}}_{\max ,j}-{\stackrel{\mathrm{‾}}{T}}_{\mathrm{a},j}\right)\sqrt{{\displaystyle \frac{R_{\mathrm{s},j}}{\mathrm{33.5}}}}\right)\\ & +\mathit{\alpha }{T}_{\mathrm{sfc},j-\mathrm{1}}\end{array}\text{(5)}& {\displaystyle }f\left(D_{\mathrm{S},j}\right)=\exp \left(-f_{\mathrm{S}}{D}_{\mathrm{S},j}\right)\text{(6)}& {\displaystyle }{\mathrm{DR}}_{\mathrm{eff},j}=\exp \left(k_{\mathrm{0}}\sqrt{-h{\displaystyle \frac{\mathit{\pi }}{k_{\mathrm{s},j}p}}}\right),\end{array}$$

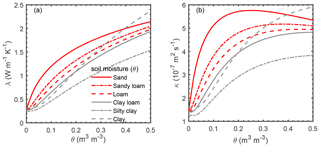
where a fictive environmental temperature (T_env) is assumed to be the weighted mean of air temperature (T_a) at 2 m and surface temperature (T_sfc). The β refers to the weighting coefficient, which defines the relative weight of the air temperature. This weighted fictive temperature will help weigh surface cooling and heating due to radiative and convective process (Dolschak et al., 2015). The T_sfc in Eq. (2) was estimated iteratively from the 3 d running average of daily air temperature (${\stackrel{\mathrm{‾}}{T}}_{\mathrm{a}}$), daily maximum temperature (${\stackrel{\mathrm{‾}}{T}}_{\max }$; degrees Celsius), and daily solar radiation (R_s; megajoule per square meter per day, hereafter MJ m⁻² d⁻¹). The α denotes soil surface albedo (–) and initial $T_{\mathrm{sfc},j-\mathrm{1}}$ was set as annual mean T_a in Eq. (3). The constant of 33.5 is an empirical constant (MJ m⁻² d⁻¹; Williams et al., 1984). The function of snow cover on the jth day is given as f(D_S,j) and was introduced based on the work of Rankinen et al. (2004). The f_S and D_S are empirical soil heat damping parameters (meters) and snow depth (meters). The damping ratio of soil at the soil depth of h (h=0.1 m in this study) is DR_eff,j (Rosenberg et al., 1983). The weighting coefficient for the damping ratio (–) is k₀. The p represents the period (365 or 366 d in leap years) in an annual cycle. The thermal diffusivity k_s,j (square meters per second) is equivalent to thermal conductivity (λ; watts per meter per kelvin) divided by volumetric heat capacity (C; joule per cubic meter per kelvin) and reflects both the ability of soil to transfer heat and to change temperature when the heat is supplied or dissipated (Fig. 2). The estimate of thermal conductivity (λ) and volumetric heat capacity (C) can be described by Eqs. (7)–(11) (Lu et al., 2014) as follows:

$$\begin{array}{}\text{(7)}& {\displaystyle }& {\displaystyle }{\mathit{\lambda }}_j={\mathit{\lambda }}_{\mathrm{dry}}+\exp \left(b_{\mathrm{1}}-{\mathit{\theta }}_j^{-b_{\mathrm{2}}}\right)\text{(8)}& {\displaystyle }& {\displaystyle }{\mathit{\lambda }}_{\mathrm{dry}}=-\mathrm{0.56}\mathrm{\varnothing }+\mathrm{0.51}\text{(9)}& {\displaystyle }& {\displaystyle }{b}_{\mathrm{1}}=\mathrm{1.97}{f}_{\mathrm{sa}}+\mathrm{1.87}{\mathit{\rho }}_{\mathrm{b}}-\mathrm{1.36}{f}_{\mathrm{sa}}{\mathit{\rho }}_{\mathrm{b}}-\mathrm{0.95}\text{(10)}& {\displaystyle }& {\displaystyle }{b}_{\mathrm{2}}=\mathrm{0.67}{f}_{\mathrm{cl}}+\mathrm{0.24}\text{(11)}& {\displaystyle }& {\displaystyle }{C}_j=\mathrm{1.92}\times {\mathrm{10}}^{\mathrm{6}}{f}_{\mathrm{m}}+\mathrm{2.51}\times {\mathrm{10}}^{\mathrm{6}}{f}_{\mathrm{OM}}+\mathrm{4.18}\times {\mathrm{10}}^{\mathrm{6}}{\mathit{\theta }}_j,\end{array}$$

where λ_dry is oven-dried soil thermal conductivity derived from a linear function of soil porosity (Ø; percent). Both b₁ and b₂ are the shape factors of the λ curve that are estimated by soil texture components. Soil water content is defined as θ_j on the jth day (cubic centimeters per cubic centimeter) and was calculated by the soil water balance model (Chalhoub et al., 2017). Briefly, the iEM02 operates on a daily time step as daily soil moisture is a function of soil moisture storage capacity (θ^*; millimeters), 24 h precipitation (P; millimeters), and Penman–Monteith reference evapotranspiration (ET₀; millimeters) and is estimated by Eqs. (12)–(15) as follows:

$$\begin{array}{}\text{(12)}& {\displaystyle }& {\displaystyle }{\mathit{\theta }}_{\mathrm{r}}=\mathrm{0.026}+\mathrm{0.005}{f}_{\mathrm{cl}}+\mathrm{0.0158}{f}_{\mathrm{OM}}\text{(13)}& {\displaystyle }& {\displaystyle }{\mathit{\beta }}_{\mathrm{d},j}=\mathrm{1}-\exp \left(-{\displaystyle \frac{\mathrm{6.68}{\mathit{\theta }}_{j}h}{\left({\mathit{\theta }}_{\mathrm{s}}-{\mathit{\theta }}_{\mathrm{r}}\right)h}}\right)\text{(14)}& {\displaystyle }& {\displaystyle }{E}_j=\left\{\begin{array}{ll}{P}_j+{\mathit{\beta }}_{\mathrm{d},j}\left({\mathrm{ET}}_{\mathrm{0},j}-P_j\right)& P_j<{\mathrm{ET}}_{\mathrm{0},j}\\ {\mathrm{ET}}_{\mathrm{0},j}& P_j\ge {\mathrm{ET}}_{\mathrm{0},j}\end{array}\right.\text{(15)}& {\displaystyle }& {\displaystyle }{\mathit{\theta }}_{j}h=\left\{\begin{array}{ll}{\mathit{\theta }}_{\mathrm{r}}h& {\mathit{\theta }}_{j}h\le {\mathit{\theta }}_{\mathrm{r}}h\\ {\mathit{\theta }}_{j-\mathrm{1}}h+\left(P_{j-\mathrm{1}}-E_{j-\mathrm{1}}\right)& {\mathit{\theta }}_{\mathrm{r}}h<{\mathit{\theta }}_{j}h<{\mathit{\theta }}^{*}h\\ {\mathit{\theta }}_{\mathrm{s}}h& {\mathit{\theta }}_{j}h\ge {\mathit{\theta }}^{*}h\end{array}\right.,\end{array}$$

where θ_r and θ_s define residual and saturated volumetric soil water contents (cubic centimeters per cubic centimeter). θ_s is assumed to be equal to soil porosity while β_d,j is a weighting coefficient for the difference between ET₀ (Allen et al., 1998) and P on the jth day (–). The initial soil water content (θ_j−1) is assumed to be equal half of soil porosity.

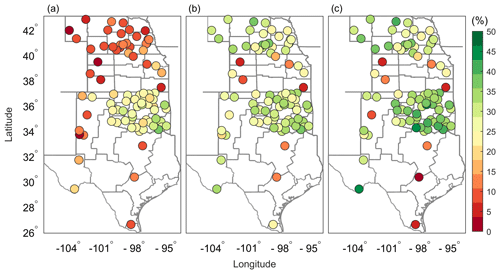
Figure 3 Percentage increments of soil temperature modeling improvement in iEM02, as determined by RMSE changes $\left[-\frac{\mathrm{100}\left({\mathrm{RMSE}}_{\mathrm{improved}}-{\mathrm{RMSE}}_{\mathrm{original}}\right)}{{\mathrm{RMSE}}_{\mathrm{original}}}\right]$ (a) after introducing an air temperature of $T_{\mathrm{a},j-\mathrm{3}}$, (b) after substituting the air temperature T_a with a fictive environmental temperature (T_env), and (c) after integrating the impacts of soil thermal diffusivity and snow cover. The color bar was coded by the improved percentage of iEM02 against the EM02 model.

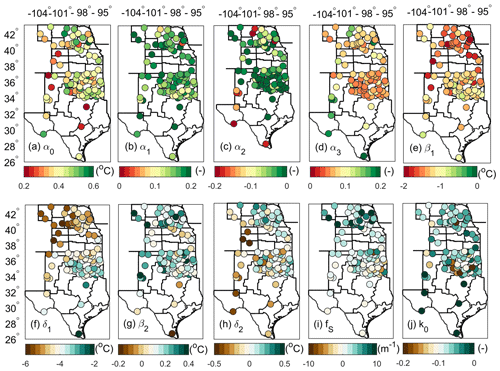
Figure 4 Spatial variations in the improved empirical model (iEM) coefficients are as follows: (a–d) for α₀, α₁, α₂, and α₃; and (e–h) for β₁, δ₁, β₂, and δ₂. Panel (i) shows the snow damping ratio (f_s) and (j) the soil damping ratio coefficients (k₀). The color bar defines the values of the model's coefficients.

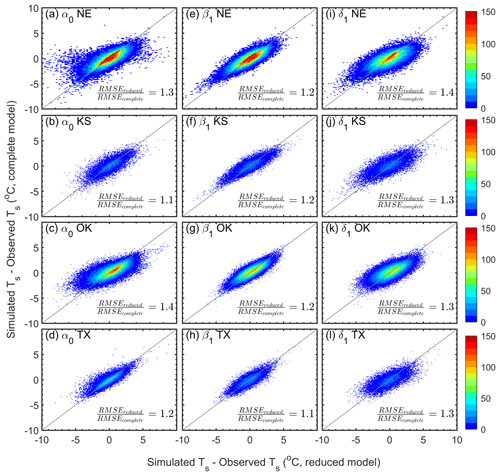
Figure 5 The 1:1 plots of absolute mean errors between the complete model and reduced model, where one independent variable term was removed in the improved empirical model (iEM02). Panels (a–d) compare results with vs. without α₀ in Nebraska (NE), Kansas (KS), Oklahoma (OK), and Texas (TX), respectively; panels (e–h) compare results with vs. without β₁ in NE, KS, OK, and TX, respectively; and panels (i–l) compare results with vs. without δ₁ in NE, KS, OK, and TX, respectively. The ratio of the root mean square error (RMSE) shown includes both RMSE values calculated from complete and reduced models, respectively. The color bar indicates the number of observed data points.

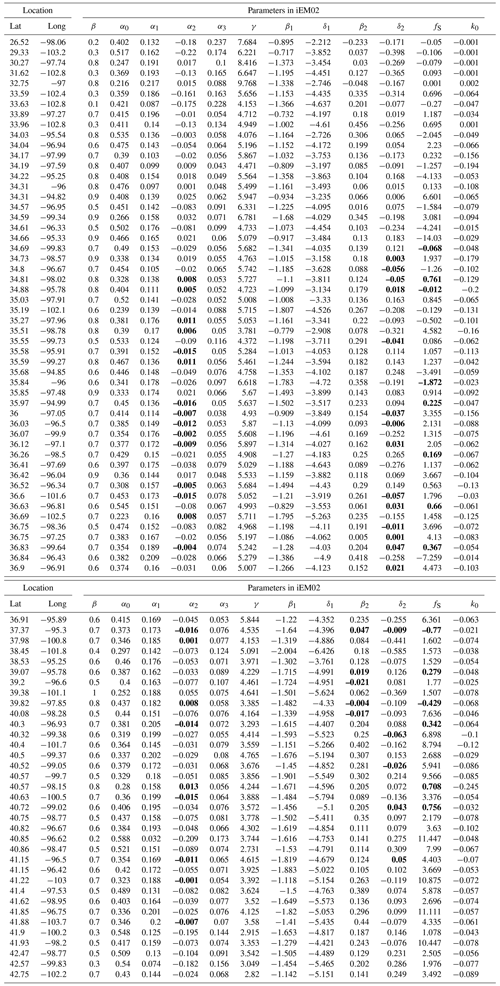
Climate observation data prior to the year 2015 were selected to calibrate the iEM02 for each station. For NE, KS, and OK, daily soil temperature observations at each station had at least 10 years of daily time series for calibrations. Data sets from TX had at least 4 years available for calibrations. Climate variables used for calibration included air temperature, precipitation, snow depth, solar radiation daily observations, and the site's static soil property. The optimal parameter values for each weather station were estimated when a minimum root mean square error (RMSE) between estimated and observed soil temperature was achieved. These parameters, for all 87 stations, are listed in Table A3.

2.3 iEM02 evaluation

In the data sets selected, all 87 station observations were longer than 15 years, except for the stations located in Texas. The last 5-year observations (2015 to 2019) were used to independently conduct model validation for all 87 stations. The metrics used to evaluate model performance were RMSE and mean absolute error (MAE). Soil temperature modeling improvement was evaluated by relative RMSE changes $\left[-\frac{\mathrm{100}\left({\mathrm{RMSE}}_{\mathrm{improved}}-{\mathrm{RMSE}}_{\mathrm{original}}\right)}{{\mathrm{RMSE}}_{\mathrm{original}}}\right]$ and by intercomparison between the fully complete model and the reduced model.

Figure 6 Spatial distribution of the mean absolute error (MAE) (a, c) and RMSE (b, d) for an empirical model (EM02; a, b) and improved modelEM02 (iEM02; c, d). The color bar defines values of MAE (in degrees Celsius) and RMSE (in degrees Celsius).

3 Results and discussion

3.1 Improved empirical model (iEM02)

The iEM02 was evaluated from 2015 to 2019 for 87 weather stations. Soil temperature modeling, using different soil textures, was improved in different ways in the iEM02 model (Fig. 3). The improvement in soil temperature modeling was indicated by relative RMSE changes that were different across sites. The weather stations located in NE and KS, as well as TX, showed less improvement after introducing the air temperature of $T_{\mathrm{a},j-\mathrm{3}}$ compared to OK (Fig. 3a). The soil types in OK are more clay and silt compared to NE and KS (Fig. 1). However, the improvement, when using the fictive environmental temperature, was significant in northern areas of NE and KS (sandy soil) but not in the southern area of OK and part of TX (clay and silt soil; Fig. 3b). Overall, latitude-dominated air temperature should play a role in improving estimated soil temperature. Most of the 87 stations achieved a 15 % to 40 % improvement in simulated soil temperature by introducing air temperature $T_{\mathrm{a},j-\mathrm{3}}$ and replacing T_a with T_env. This improvement was in agreement with a previous study (Dolschak et al., 2015). By incorporating changes in soil moisture and daily snow depth, additional improvements in soil temperature simulation of up to 50 % could be achieved (Fig. 3c) compared to the original model (EM02). It should be noted that there were fewer stations available in KS and TX compared to NE and OK. Overall, integrating snow cover and soil moisture data in iEM02 improved the simulated soil temperature (Fig. 3). The daily soil temperature modeling could be further improved if high-resolution (e.g., 30 m and daily), satellite-based soil moisture and/or snow cover products become available, for example, products based on the Soil Moisture Active Passive (SMAP) or Sentinel satellites (Das et al., 2019).

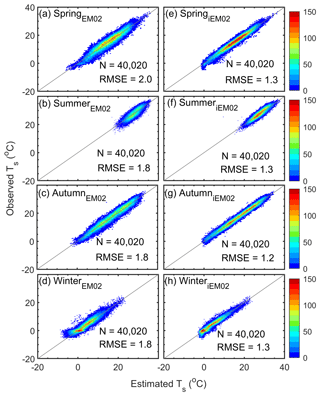
Figure 7 Seasonal comparison between the estimated and observed soil temperatures. (a–d) The empirical model (EM). (e–h) The improved empirical model (iEM02). RMSE was calculated as the root mean square error between estimated and observed soil temperature. N refers to the sample size, and the gray line represents the 1:1 line. The color bar describes the number of data points.

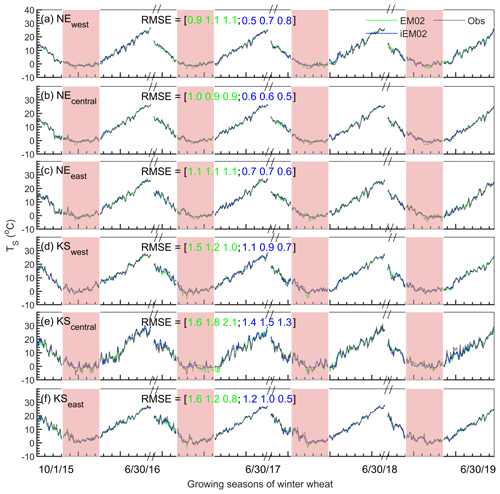
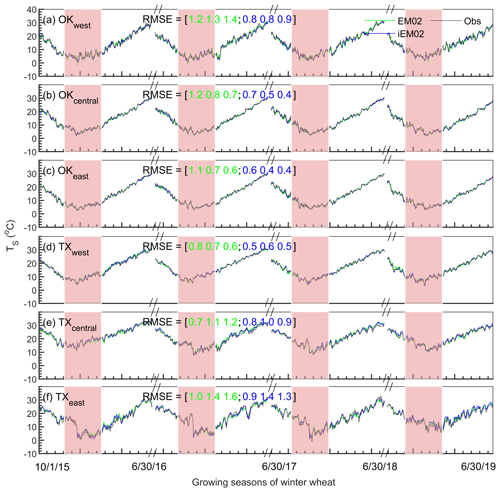
Figure 8 Daily soil temperature comparison between the observed (gray line), original model (EM02; green line), and improved model (iEM02; blue line) in western (>100^∘ W), central (between 97 and 100^∘ W), and eastern (<97^∘ W) Nebraska (a–c) and Kansas (d–f) during the winter wheat growing seasons from 2015 to 2019. RMSE is the root mean square error (degrees Celsius). The values in brackets refer to both the RMSE values of the original model (green numbers) and the improved model (blue numbers) during the periods of October–November, December–February, and March–June, respectively. Shaded areas highlight the winter season (December–February).

3.2 iEM02's parameters

The parameters described in iEM02 for each weather station are indicative of soil temperature sensitivities for each independent variable in Eq. (1), although, strictly speaking, they are not mathematical sensitivities (Fig. 4 and Table A2). For T_env, the current day T_env was the most weighted, as expected (Fig. 4a). The parameters of T_env for the prior day 1 to day 3 were relatively weak in terms of absolute magnitudes due to autoregression properties in the soil temperature (Fig. 4b–d). Interestingly, in the iEM02 model, the prior day 2 was negatively associated with soil temperature (Fig. 4c), which cannot be interpreted by soil physical processes but rather in a more autoregressive sense in which the soil temperature signals are superimposed. The periodic property embedded in iEM02 was two low-frequency components (i.e., semi-annual and annual signals). Obviously, the annual signal strength indicated by β₁ and δ₁ was 1 order of magnitude stronger than the semi-annual signal strengths in soil temperature (Fig. 4e–h). The result also suggested that the strong β₁ and δ₁ spatial contexts of the northern region (e.g., in Nebraska and Kansas) were differently weighted from those in the southern region (e.g., in Oklahoma and Texas). For the snow damping factor, the snow cover had a larger impact on soil temperature in the northern region when compared to the southern region (Fig. 4i). However, the soil damping ratio factor was relatively evenly distributed (Fig. 4j).

Figure 9 The same as Fig. 8 but for western, central, and eastern Oklahoma (a–c) and Texas (d–f).

RMSE performance is shown in Fig. 5, when the iEM02 was a complete model vs. the reduced iEM02 model, where one independent variable term from the complete model was removed. When removing any one independent variable, the modeled soil temperature RMSE increased from 110 % to 130 % (Fig. 5), indicating a 20 % rise in RMSE. Specifically, the iEM02 model performance decreased (i.e., RMSE increased from 0.1 to 0.4 ^∘C) when the α₀ term was removed (Fig. 5a–d). Unlike α₀, removing the β₁ term was not as sensitive and gave an increase of 0.1–0.2 ^∘C RMSE, on average, for all states in the region (Fig. 5e–h). However, it is clear that the iEM02 model was the most sensitive to δ₁. With the removal of δ₁ from the complete iEM02 model, the RMSE increased 0.3–0.4 ^∘C for all four states (Fig. 5i–l). Due to the location dependency of the above coefficients, further spatial interpolation of the iEM02 model would be beneficial to predict soil temperature for irrigated agricultural areas without weather stations in the USA Great Plains and to improve water and crop management modeling.

3.3 Spatial and temporal modeling performance

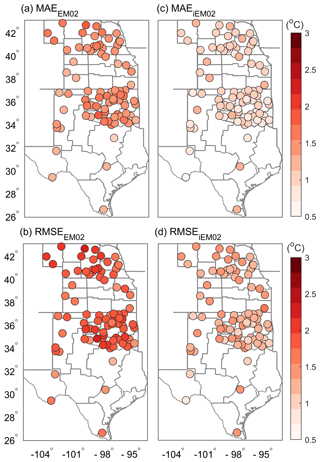
A graphical summary of how closely the modeled soil temperature agreed with the observed soil temperature for each weather station is shown in Fig. 6. Daily T_s estimated in the iEM02 model outperformed that in the original EM02 model for all 87 weather stations. For example, both MAE and RMSE were decreased, on average, by 0.6 ^∘C when the iEM02 model was used to estimate T_s. Individually, the improved model showed a less than 1.6 ^∘C RMSE for any individual station, but 16 % of the stations had a larger than 2 ^∘C RMSE in the original EM02. In addition, we compared the performance of iEM02 against a recent energy balance model (Chalhoub et al., 2017). Our prediction of T_s was improved by 1.2 ^∘C RMSE compared to the energy balance model (not shown).

Spatial distributions of RMSE showed that the majority of weather stations had better performance in Oklahoma, with a mean RMSE of 1.9 and 1.1 ^∘C for EM02 and iEM02, respectively, whereas Nebraska had a RMSE of 2.1 and 1.3 ^∘C for EM02 and iEM02, respectively. The different modeling performance was associated with the soil heat transport process and how frequent snowfall could be observed in Nebraska and Oklahoma. Similar results were presented in a recent study by Huang et al. (2017). On the other hand, the high quality of weather data from the Oklahoma Mesonet is considered to be the gold standard for the statewide weather network (Lin et al., 2016), thus ensuring the quality of both model calibrations and observed soil temperature in Oklahoma.

Seasonal T_s indicated that iEM02 modeling was mostly improved in the spring season, from 2 to 1.3 ^∘C RMSE (Fig. 7a), but the original model (EM02) showed that the uncertainty was in good agreement with the performance achieved in Plauborg (2002). All other seasons were improved in similar ways, from 1.8 to 1.2 or 1.3 ^∘C RMSE. The improvement for all seasons could be attributed to introducing soil diffusivity, which changed with daily soil moisture and snow cover, and this affected the soil thermal conductivity (Rankinen et al., 2004; Zhang, 2005). Moreover, although modeling wintertime soil temperature improved from 1.8 to 1.3 ^∘C RMSE, which was the same as in the summer (Fig. 7), the soil temperature located in more frequent snow-covered states (e.g., Nebraska and Kansas), was better improved when T_env and snow depth were introduced into the model. Our findings confirmed those reported by Rankinen et al. (2004) and Dutta et al. (2018).

Since precipitation gradients exist in the USA Great Plains from western to eastern regions (Evett et al., 2020), three subregions were classified for each state as western (100^∘ W; towards the west), central (between 97 and 100^∘ W), and eastern (97^∘ W; towards the east). Figure 8 displays the time series of EM02 modeled, iEM02 modeled, and observed soil temperatures only covering winter wheat growing seasons (1 October to 30 June) for four growing seasons from 2015 to 2019 (validation periods) in Nebraska and Kansas. All subregions in Nebraska and Kansas showed improvement when using the iEM02 model (Fig. 8). Similarly, the iEM02 improved the RMSE during four growing seasons in Oklahoma and Texas (Fig. 9). The EM02 model had the best performance in Oklahoma, with a mean RMSE of 1.0 ^∘C, while the mean RMSE in Kansas was 1.4 ^∘C in EM02. Soil temperatures estimated by iEM02 had approximately a 0.3 to 1.4 ^∘C RMSE (Figs. 8 and 9). In addition, larger improvements by iEM02 were observed in most subregions during wintertime, which would be beneficial for modeling winter wheat yields and potential yields (Persson et al., 2017).

4 Conclusion

The primary intention of this work was to develop an improved soil temperature model for the USA Great Plains that can predict soil temperature by using common weather station variables as inputs. The improved empirical model (iEM02) integrated soil thermal diffusivity and snow cover factors, and these significantly improved the estimate of soil temperature for the 87 weather stations in the USA Great Plains that were studied. Specifically, after incorporating changes in soil moisture and daily snow depth, the improved model showed a near 50 % gain in performance in terms of RMSE decrease when compared to the original model. The value of RMSE across 87 stations was 0.6 ^∘C lower, on average, than the original model from 2015 to 2019. We concluded that the iEM02 model can better estimate soil temperature at the surface soil layer where most hydrological and biological processes occur. Both seasonal and spatial improvements made in the improved model demonstrated the robustness of the iEM02 model, suggesting that this improved model can provide a reliable simulation of soil temperature to use in modeling hydrological processes and crop production in the USA Great Plains.

Appendix A

Table A1 Table of symbols and corresponding descriptions used in this paper.

Table A2 List of data sets used in this study, including the data source (Networks), state names (Coverage states), and specific data variables (Variables). Data sources include the Gridded Soil Survey Geographic (gSSURGO), the Automated Weather Data Network (AWDN) – High Plains Regional Climate Center (HPRCC), the Oklahoma Mesonet (OK Mesonet), the Soil Climate Analysis Network (SCAN), and the daily Global History Climatology Network (dGHCN). Weather stations from four states were located in the USA Great Plains, including Nebraska (NE), Kansas (KS), Oklahoma (OK), and Texas (TX). Climate data report the daily maximum (T_max; degrees Celsius) and minimum air temperature (T_min; degrees Celsius) at 2 m height, relative humidity (RH; percent), rainfall (prcp; millimeters), solar radiation (R_s; MJ m⁻² d⁻¹), wind speed at 2 m (WS; meters per second), and snow depth (D_s; millimeters). Soil data consist of the daily bare soil temperature at 10 cm depth (T_s; degrees Celsius), albedo of soil surface (α; –), organic matter content (f_OM; percent), bulk density (ρ_b; grams per cubic meter), porosity (Ø; percent), sand (f_sa), silt (f_sl), and clay (f_cl) content (percent).

Table A3 List of model parameters for each weather station in the USA Great Plains. The location consists of latitude (Lat) and longitude (Long). There are 12 parameters in the improved EM model, including parameters of air temperature (β; –); parameters for current day to the previous 3 d of T_env, including α₀ (–), α₁ (–), α₂ (–), α₃ (–), and constant offset γ (degrees Celsius); annual and semi-annual waves of sine and cosine functions parameters are β₁, β₂, δ₁, and δ₂ (degrees Celsius); and parameters for the snow depth damping factor (f_S; meters) and the soil damping factor (k₀; –). The bold font indicates that estimated coefficients are not statistically significant at 95 % confidence intervals.