Identifying robust bias adjustment methods for European extreme precipitation in a multi-model pseudo-reality setting

Severe precipitation events occur rarely and are often localised in space and of short duration, but they are important for societal managing of infrastructure. Therefore, there is a demand for estimating future changes in the statistics of the occurrence of these rare events. These are often projected using data from regional climate model (RCM) simulations combined with extreme value analysis to obtain selected return levels of precipitation intensity. However, due to imperfections in the formulation of the physical parameterisations in the RCMs, the simulated present-day climate usually has biases relative to observations; these biases can be in the mean and/or in the higher moments. Therefore, the RCM results are adjusted to account for these deficiencies. However, this does not guarantee that the adjusted projected results will match the future reality better, since the bias may not be stationary in a changing climate. In the present work, we evaluate different adjustment techniques in a changing climate. This is done in an inter-model cross-validation set-up in which each model simulation, in turn, performs pseudo-observations against which the remaining model simulations are adjusted and validated. The study uses hourly data from historical and RCP8.5 scenario runs from 19 model simulations from the EURO-CORDEX ensemble at a 0.11^∘ resolution. Fields of return levels for selected return periods are calculated for hourly and daily timescales based on 25-year-long time slices representing the present-day (1981–2005) and end-21st-century (2075–2099). The adjustment techniques applied to the return levels are based on extreme value analysis and include climate factor and quantile-mapping approaches. Generally, we find that future return levels can be improved by adjustment, compared to obtaining them from raw scenario model data. The performance of the different methods depends on the timescale considered. On hourly timescales, the climate factor approach performs better than the quantile-mapping approaches. On daily timescales, the superior approach is to simply deduce future return levels from pseudo-observations, and the second-best choice is using the quantile-mapping approaches. These results are found in all European subregions considered. Applying the inter-model cross-validation against model ensemble medians instead of individual models does not change the overall conclusions much.

1 Introduction

Severe precipitation events typically occur either as stratiform precipitation of moderate intensity or as intense localised cloudbursts lasting up to a few hours only. Such extreme events may cause flooding, with the risk of loss of life and damage to infrastructure. It is expected that future changes in the radiative forcing from greenhouse gases and other forcing agents will influence large-scale atmospheric conditions, such as air mass humidity, vertical stability, the formation of convective systems and typical low pressure tracks. Therefore, the statistics of the occurrence of severe precipitation events will also most likely change.

Global climate models (GCMs) are the main tools for estimating future climate conditions. A GCM is a global representation of the atmosphere, the ocean and the land surface and the interaction between these components. The GCM is then forced with observed greenhouse gas concentrations, atmospheric compositions, land use, etc., to represent the past and present climate and with stipulated scenarios of future concentrations of radiative forcing agents to represent the future climate.

Present state-of-the art GCMs from the Coupled Model Intercomparison Project Phase 5 (CMIP5; Taylor et al., 2012) and the recent Coupled Model Intercomparison Project Phase 6 (CMIP6; Eyring et al., 2016) typically have a grid spacing of around 100 km or even more. This resolution is too coarse to describe the effect of regional and local features, such as mountains, coastlines and lakes, and to adequately describe convective precipitation systems (Eggert et al., 2015). To model the processes on smaller spatial scales, dynamical downscaling is applied. Here, the atmospheric and surface fields from a GCM simulation are used as boundary conditions for a regional climate model (RCM) over a smaller region, with a much finer grid spacing, which is typically around 10 km or even less at present.

An alternative to dynamical downscaling is statistical downscaling. Here, large-scale circulation patterns (e.g. the North Atlantic Oscillation) are related to small-scale variables, such as precipitation mean at a station. One assumes that the large-scale circulation pattern is modelled well by the GCM, and therefore, the approach is called perfect prognosis. Using the relationship with the small-scale variables calibrated on observations, one can obtain modelled local-scale variables (present-day and future) from the modelled large-scale patterns. A recent overview of these methods and validation of them can be found in Gutiérrez et al. (2019).

The ability of present-day RCMs to reproduce observed extreme precipitation statistics on daily and sub-daily timescales is essential and has been of concern. Earlier studies analysing this topic have mostly focused on a particular country, probably due to the lack of sub-daily observational data covering larger regions, such as, for example, Europe. Thus, Hanel and Buishand (2010), Kendon et al. (2014), Olsson et al. (2015) and Sunyer et al. (2017) studied daily and hourly extreme precipitation in different European countries and reached similar conclusions. First, that the bias of extreme statistics decreases with a smaller grid spacing of the model, and second, that extreme statistics for a 24 h duration are satisfactorily simulated with a grid spacing of 10 km, while 1 h extreme statistics exhibit substantial biases even at this resolution. Recently, Berg et al. (2019) evaluated high-resolution RCMs from the EURO-CORDEX ensemble (Jacob et al., 2014) also used here and reached similar conclusions for several countries across Europe. They found that RCMs underestimate hourly extremes and give an erroneous spatial distribution.

Extreme convective precipitation of a short duration is thus one of the more challenging phenomena to physically represent accurately in RCMs. The reason is that convective events take place on a spatial scale comparable to the RCM grid spacing of, presently, around 10 km. Therefore, the convective plumes cannot be directly modelled. Instead, the effects of convection are parameterised, i.e. modelled as processes on larger spatial scales (Arakawa, 2004). Thus, the inability to reproduce these short-duration extremes can be explained by the imperfect parameterisation of a sub-grid-scale convection (Prein et al., 2015), which generally leads to a too early onset of convective rainfall in the diurnal cycle and the subsequent dampening of the build-up of convective available potential energy (Trenberth et al., 2003).

Thus, even RCMs with their small grid spacing may exhibit systematic biases for variables related to convective precipitation. If there is a substantial bias, we should consider adjusting for this in a statistical sense before conducting any further data analysis. Such adjustment techniques are thoroughly discussed, including requirements and limitations, in Maraun (2016) and Maraun et al. (2017). There are basically two main adjustment approaches. In the delta change approach, a transformation is established from the present to the future climate in the model run. This transformation is then applied to the observations to obtain the projected future climate. In the bias correction approach, a transformation is established from present model climate data to the observed climate, and this transformation is then applied to the future model climate to obtain the projected future climate.

Both adjustment approaches come in several varieties. In the simplest one, the transformation consists of an adjustment of the mean, in the case of precipitation, by multiplying the mean by a factor. In the more elaborate flavour, the transformation is defined by quantile mapping, which also preserves the higher moments. Quantile mapping can use either empirical quantiles or analytical distribution functions. The ability of quantile mapping to reduce bias has been demonstrated for daily precipitation in the present-day climate by using observations which are split into calibration and validation samples (Piani et al., 2010; Themeßl et al., 2011).

Bias adjustment techniques originate in the field of weather and ocean forecast modelling, where they are known as model output statistics (MOSs). Here, output from a forecast model is adjusted for model deficiencies and local features not explicitly resolved by the model. Applying similar adjustment techniques to climate model simulations, however, has a complication not present in forecast applications. Climate models are set up and tuned to present-day conditions and verified against observations but are then applied to future, changed conditions without any possibility of directly verifying the model's performance under these conditions. Therefore, showing that bias adjustment works for the present-day climate is a necessary but insufficient condition for the adjustment to work in the changed climate.

A central concept of adjustment methods is the assumption of the stationarity of the bias. For bias correction, this means that the transformation from model to observations is unchanged from the present-day climate to the future climate, while, for delta change, the transformation from the present-day climate to future climate is unchanged from model to observation. In the ideal case of stationarity being fulfilled, the adjustment methods will work perfectly and produce perfect future projections. If stationarity is not fulfilled, adjustments may improve projections or, in the worst cases, may degrade projections, compared to using raw model output. We also note that the adjustment methods themselves may influence the climate change signal of the model, depending on the bias and the method used (Berg et al., 2012; Haerter et al., 2011; Themeßl et al., 2012).

Stationarity has been debated in recent years in the literature (e.g. Boberg and Christensen, 2012; Buser et al., 2010). Kerkhoff et al. (2014) review and discuss the following two hypotheses: (1) constant bias, which is unchanged between the present-day and future (i.e. stationarity), and (2) constant relation, where the bias varies linearly with the signal. Van Schaeybroeck and Vannitsem (2016) used a pseudo-reality setting with a simplified model and found large changes in the bias between the present-day and future for many variables and a violation of both constant bias and constant relation hypothesis. Chen et al. (2015) concluded that precipitation bias is clearly non-stationary over North America in that variations in bias are comparable to the climate change signal. Velázquez et al. (2015) used a pseudo-reality setting involving two models and concluded that the constancy of bias was violated for both precipitation and temperature on monthly timescales. Hui et al. (2019) used a pseudo-reality setting with GCMs and found a significant non-stationarity of bias for annual and seasonal temperatures. Besides, they point to a large effect on non-stationarity from internal variability.

To thoroughly validate adjustment methods, both a calibration data set and an independent data set for validation are needed. There are two different approaches to obtain this. In split-sample testing, the observations are divided into calibration and validation parts, often in the form of a cross-validation (e.g. Gudmundsson et al., 2012; Li et al., 2017a, b; Refsgaard et al., 2014; Themeßl et al., 2011). One variant is differential split-sample testing (Klemeš, 1986), where the split in calibration and validation parts is based on climatological factors, such as wet and dry years, encompassing climate changes and variations into the validation.

An alternative approach, which we use here, is inter-model cross-validation as pursued by Maraun (2012), Räisänen and Räty (2013) and Räty et al. (2014), among others. The rationale here is that the members of a multi-model ensemble of simulations represent different descriptions of the physics of the climate system, with each of them being not too far from the real climate system. Thus, one member of the ensemble alternatively plays the role of the pseudo-observation against which the remaining adjusted models are validated. Thus, the trick is that we know both present and future pseudo-observations.

The advantage of inter-model cross-validation is that the adjustment methods are calibrated under present-day conditions and validated under future climatic conditions. Therefore, it embraces modelled physical changes between present and future climate as, for instance, a shift in the ratio between stratiform and convective precipitation. In this respect, it is a more realistic setting than validation based on split-sample test. Also, model and pseudo-observations have the same spatial scale, thus avoiding comparing pointwise observations with area-averaged model data as is done in the split-sample testing. On the other hand, the method assumes that the modelled present-day is not too different from observations. If this is violated, the method will give error estimates that are too optimistic compared to what can be expected in the real World. Please also see the discussion in Sect. 5.2.

Inter-model cross-validation has been applied on daily precipitation to evaluate different adjustment methods (Räty et al., 2014). Here, we apply a similar methodology, Europe-wide, to extreme precipitation on hourly and daily timescales. This has been made possible with the advent of the EURO-CORDEX, a large ensemble of high-resolution RCM simulations with precipitation at an hourly time resolution. Being more specific, we apply the standard extreme value analysis to the ensemble of model data for present-day and end-21st-century conditions to estimate return levels for daily and hourly duration. Then, we will apply inter-model cross-validation on these return levels in order to address the following questions:

1. Do adjusted return levels perform better, according to the inter-model cross-validation, than using raw model data from scenario simulations?

2. Is there any difference in performance between different adjustment methods?

3. Are there systematic differences between point 1 and 2, depending on the daily and hourly duration?

4. Are there regional differences across Europe in the performance of the different adjustment methods?

Giving qualified answers to these questions can serve as important guidelines for analysis procedures for obtaining future extreme precipitation characteristics.

The rest of the paper contains a description of the EURO-CORDEX data (Sect. 2) and a description of the methods used (Sect. 3). Then follow the results (Sect. 4), a discussion of these (Sect. 5) and, finally, the conclusions (Sect. 6).

Table 1 Overview of the 19 EURO-CORDEX GCM–RCM combinations used. The rows show the GCMs while the columns show the RCMs. The full names of the RCMs are SMHI-RCA4, CLMcom-CCLM4-8-17, KNMI-RACMO22E, DMI-HIRHAM5, MPI-CSC-REMO2009 and CLMcom-ETH-COSMO-crCLIM-v1-1. Each GCM–RCM combination used is represented by a number (1, 3 or 12) indicating which realisation of the GCM is used for the particular simulation.

2 EURO-CORDEX data

The model simulations used here have been performed within the framework of EURO-CORDEX (Jacob et al., 2014; http://euro-cordex.net, last access: January 2021), which is an international effort aimed at providing RCM climate simulations for a specific European region (see Fig. 1) in two standard resolutions with a grid spacing of 0.44^∘ (EUR-44; ∼50 km) and 0.11^∘ (EUR-11; ∼12.5 km), respectively. All GCM simulations driving the RCMs follow the CMIP5 protocol (Taylor et al., 2012) and are forced with historical forcing for the years 1850–2005, followed by the representative concentration pathway (RCP) 8.5 scenario for the years 2006–2100 (until 2099 only for HadGEM-ES).

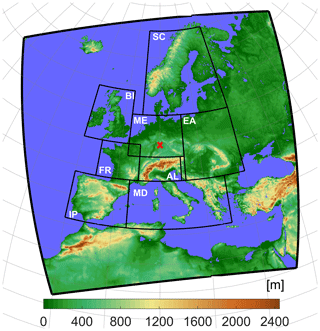
Figure 1 Map showing the EURO-CORDEX region (outer frame) with elevation in colours. PRUDENCE subregions (Christensen and Christensen, 2007) used in the analysis are also shown. Note: BI – British Isles; IP – Iberian Peninsula; FR – France, ME – mid-Europe; SC – Scandinavia; AL – Alps; MD – Mediterranean; EA – Eastern Europe. Red cross marks the point used in Fig. 4.

We analyse precipitation data in hourly time resolutions from 19 different GCM–RCM combinations from the EUR-11 simulations shown in Table 1, and we analyse two 25-year-long time slices from each of these simulations, namely a present-day (years 1981–2005) and end-21st-century (years 2075–2099) time slice.

All GCM–RCM combinations we use are represented by one realisation only, and therefore, the data material used represents 19 different possible realisations of climate model physics, though we acknowledge that some GCMs/RCMs might originate from the same or similar model codes and, therefore, may not be fully independent. The EURO-CORDEX ensemble includes a few simulations which do not use the standard EUR-11 grid. These were not included in the analysis since they should have been re-gridded to the EUR-11 grid, which would dampen extreme events, thus introducing an unnecessary error source.

Generally, GCM results are quite comparable to reality, and many validation studies of GCMs exist that also keep an eye on Europe (e.g. McSweeney et al., 2015). We are aware of the use in some papers of procedures for selecting how to choose subsets of available GCMs (e.g. McSweeney et al., 2015; Rowell, 2019). There is, however, no simple quality index that can be generally applied. Any discrimination of GCMs depends on area, season and the meteorological field and property being investigated (Gleckler et al., 2008; e.g. their Fig. 9). Furthermore, these tests and selection procedures are based on subjective criteria and come with major caveats that impact the uncertainty range largely (Madsen et al., 2017). We therefore choose, in accordance with most other similar studies, to use an ensemble of opportunity for the present study.

3 Methods

3.1 Duration

Extreme precipitation statistics are often described as a function of the timescale involved as intensity–duration–frequency or depth–duration–frequency curves (e.g. Overeem et al., 2008). We consider two timescales or durations. One is a duration of 1 h, which is simply the time series of hourly precipitation sums available in each RCM grid point. The other is a duration of 24 h, where a 24 h sum is calculated in a sliding window with a 1 h time step. We will refer to these as hourly and daily duration, respectively. Our daily duration corresponds to the traditional climatological practice of reporting daily sums but allows heavy precipitation events to occur over 2 consecutive days. We also emphasise that the duration, as defined here, is not the actual length of the precipitation events in the model data but merely a concept for defining timescales.

3.2 Extreme value analysis

Extreme value analysis (EVA) provides methodologies to estimate high quantiles of a statistical distribution from observations. The theory relies on the fundamental convergence properties of the time series of extreme events; for details, we refer to Coles (2001).

There are two main methodologies in EVA for obtaining estimates of the high percentiles and the corresponding return levels. In the classical or block maxima method, a generalised extreme value distribution is fitted to the series of maxima over a time block, which is usually 1 year. Alternatively, in the peak-over-threshold (POT) or partial-duration series method, which is used here, all peaks with maximum above a (high) threshold, x₀, are considered. The peaks are assumed to occur independently at an average rate per year of λ₀. To ensure independence between peaks, a minimum time separation between peaks is specified. Theory tells us that, when the threshold goes to infinity, the distribution of the exceedances above the threshold, x−x₀, converges to a generalised Pareto distribution for which the cumulative distribution function is as follows:

$${\displaystyle }G\left(x-x_{\mathrm{0}}\right)=\mathrm{1}-{\left(\mathrm{1}+\mathit{\xi }{\displaystyle \frac{x-x_{\mathrm{0}}}{\mathit{\sigma }}}\right)}^{-\frac{\mathrm{1}}{\mathit{\xi }}},x>x_{\mathrm{0}}.$$

The parameter σ is the scale and a measure of the width of the distribution. The parameter ξ is the shape and describes the character of the upper tail of the generalised Pareto distribution (GPD); ξ>0 implies a heavy tail, which usually is the case for extreme precipitation events, while ξ<0 implies a thin tail. Note that, quite confusingly, an alternative sign convention of ξ occurs in the literature (e.g. Hosking and Wallis, 1987).

If we now consider an arbitrary level x with x>x₀, the average number of exceedances per year of x will be the following:

$$\begin{array}{}\text{(1)}& {\mathit{\lambda }}_x={\mathit{\lambda }}_{\mathrm{0}}\left[\mathrm{1}-G(x-x_{\mathrm{0}})\right].\end{array}$$

The T year return level, x_T, is defined as the precipitation intensity, which is exceeded on average once every T years, as follows:

$${\displaystyle }{\mathit{\lambda }}_{x_T}T=\mathrm{1},$$

and by combining with Eq. (1) we obtain an expression for the return level, x_T, as follows:

$${\displaystyle }{\mathit{\lambda }}_{\mathrm{0}}\left[\mathrm{1}-G(x_T-x_{\mathrm{0}})\right]T=\mathrm{1},$$

from which we calculate the following:

$$\begin{array}{}\text{(2)}& x_T=G^{-\mathrm{1}}\left(\mathrm{1}-{\displaystyle \frac{\mathrm{1}}{{\mathit{\lambda }}_{\mathrm{0}}T}}\right)+x_{\mathrm{0}}.\end{array}$$

Data points to be included in the POT analysis can be selected in two different ways. Either the threshold x₀ is specified and λ₀ is then a parameter to be determined or, alternatively, λ₀ is specified and x₀ is determined as a parameter. We choose the latter approach, since it is most convenient when working with data from many different model simulations.

Choosing λ₀ is a point to consider. Too high a value would include too few data points in the estimation, and too low a value implies the risk that the exceedances x_T−x₀ cannot be considered as being distributed according to GPD. We choose λ₀=3 in accordance with Berg et al. (2019), which gives 75 data points for an estimation of the 25-year-long time slices. Hosking and Wallis (1987) investigated the estimation of parameters of the GPD and, based on this, warn against using the often-applied maximum likelihood estimation for a sample size below 500. Instead, they recommend probability-weighted moments, and we have followed this advice here.

We required a minimum of a 3 and 24 h separation between peaks for a 1 and 24 h duration, respectively. This is in accordance with Berg et al. (2019), and furthermore, synoptic experience tells us that this will ensure that neighbouring peaks are from independent weather systems. We found only a weak influence of these choices on the results of our analysis.

In practical applications of EVA, the parameters are estimated with large uncertainties due to the limited length of the time series. The threshold has the smallest relative uncertainty, the scale has a larger relative uncertainty and the shape has the largest relative uncertainty. Therefore, the relative uncertainty of the return levels also increase with increasing T, as can be seen from Eq. (2).

3.3 Bias adjustments and extreme value analysis

The delta change and bias correction approaches were introduced in general terms in Sect. 1. Now we will formulate EVA-based analytical quantile mapping based versions of the two approaches. In what follows, O_T is the T year return level estimated from present-day pseudo-observations, while C_T (control) and S_T (scenario) denote the corresponding return levels, estimated from present-day and end-21st-century model data, respectively. Finally, P_T (projection) denotes the end-21st-century return level after a bias adjustment has been applied.

3.3.1 Climate factor on the return levels (FAC)

The simplest adjustment approach is to assume a climate factor on the return level (FAC) as follows:

$${\displaystyle }{P}_T=\underset{\begin{array}{c}\text{Delta change}\\ \text{climate factor}\end{array}}{\underbrace{S_T/C_T}}\cdot O_T=\underset{\begin{array}{c}\text{Bias correction}\\ \text{climate factor}\end{array}}{\underbrace{O_T/C_T}}\cdot S_T.$$

We note that the delta change and bias correction approach are identical for the FAC method.

3.3.2 Analytical quantile mapping based on EVA

In the EVA-based quantile mapping, two POT-based extreme value distributions with different parameters are matched. Being more specific, we want to construct a transformation from x→y defined by the requirement that exceedance rates above x and y, respectively, are equal for any x as follows:

$${\displaystyle }{\mathit{\lambda }}_x={\mathit{\lambda }}_y.$$

This implies, according to Eq. (1), that in the following:

$${\displaystyle }{\mathit{\lambda }}_{\mathrm{0}x}\left[\mathrm{1}-G_x\left(x-x_{\mathrm{0}}\right)\right]={\mathit{\lambda }}_{\mathrm{0}y}\left[\mathrm{1}-G_y\left(y-y_{\mathrm{0}}\right)\right],$$

where G_x is the GPD distribution of the exceedances, x−x₀ and λ_0x are the associated exceedance rate, and G_y and λ_0y are the similar entities for y.

To simplify, we let λ_0x=λ_0y (see Sect. 3.2) and, therefore, obtain the following:

$${\displaystyle }{G}_x\left(x-x_{\mathrm{0}}\right)=G_y\left(y-y_{\mathrm{0}}\right),$$

from which we obtain the following transformation:

$$\begin{array}{}\text{(3)}& y=y_{\mathrm{0}}+G_y^{-\mathrm{1}}\left(G_x\left(x-x_{\mathrm{0}}\right)\right).\end{array}$$

For the delta change (DC) approach, the modelled GPD distribution functions for present-day and end-21st-century conditions are quantile mapped, and the transformation obtained this way is then applied to return levels determined from present-day pseudo-observations O_T. Thus, the corresponding projected T year return level is the following, according to Eq. (3):

$${\displaystyle }{P}_T=S_{\mathrm{0}}+G_{\mathrm{S}}^{-\mathrm{1}}\left(G_{\mathrm{C}}\left(O_T-C_{\mathrm{0}}\right)\right),$$

where G_C and G_S are the GPD cumulative distribution functions for the data modelled on the present-day (control) and end-21st-century (scenario), respectively, and C₀ and S₀ are the corresponding threshold values.

For the bias correction (BC) approach, the present-day (control) and pseudo-observed GPD cumulative distribution functions are quantile mapped to obtain the model bias, which is then applied, using Eq. (3), to the modelled return levels for end-21st-century (scenario).

$${\displaystyle }{P}_T=O_{\mathrm{0}}+G_{\mathrm{O}}^{-\mathrm{1}}\left(G_{\mathrm{C}}\left(S_T-C_{\mathrm{0}}\right)\right),$$

where G_O is the GPD cumulative distribution function for the observations and O₀ the corresponding threshold.

3.3.3 Reference adjustment methods

The performance of the bias adjustment methods described above will be compared with the performance of two reference adjustment methods, which are defined below. This is similar to what is practised when verifying predictions, where the performance of the prediction should be superior to the performance of reference predictions such as persistence or climatology.

We choose two reference methods. One reference is to simply use, for a given model, the return level calculated from (pseudo-) observations as the projected return level (OBS) as follows:

$${\displaystyle }{P}_T=O_T.$$

Another reference is to use the raw scenario model output data without any adjustment (SCE) as follows:

$${\displaystyle }{P}_T=S_T.$$

For an overview of the methods, see Table 2.

Table 2 Overview of methods used in the inter-comparison.

3.4 The inter-model cross-validation procedure in detail

The inter-model cross-validation goes in detail as follows. Each of the N models are successively regarded as being pseudo-observations. The individual adjustment methods are calibrated on the present-day parts of the pseudo-observations and model return levels (present-day and end-21st-century) as appropriate, depending on whether it is a bias correction or delta change method. The calibration is done as described above. The adjustment methods are then applied to present-day observations and model data, again as appropriate, to obtain the adjusted return levels for end-21st-century. These are then validated against the return levels for end-21st-century derived from pseudo-observations.

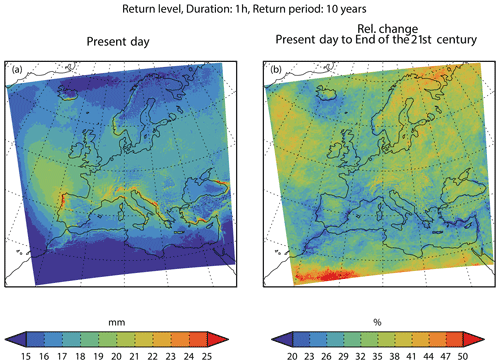
Figure 2 Geographical distribution of the 10-year return level of precipitation intensity for 1 h duration for the present-day (a) and relative change from the present-day to end-21st-century (b). In each grid point, values are the median return level over all 19 model simulations.

The basic validation metric will be the relative error of the return levels for end-21st-century for a given duration and return period T, as follows:

$${\displaystyle }RE=\left|P_T-V_T\right|/V_T.$$

Thus, this determines the absolute difference between the projected return level P_T obtained from using an adjustment and the validation return level V_T estimated from pseudo-observations for end-21st-century divided by the validation return level. This metric is calculated for every grid point and for every combination of model or pseudo-observations. Since we have N=19 model simulations in the ensemble, we have $N\times \left(N-\mathrm{1}\right)=\mathrm{342}$ different combinations for validating each adjustment method and can make statistics of the relative error. This quantifies the average performance of the different methods.

End-user scenarios are often constructed as the median or mean from ensembles. We also tested this in the inter-model cross-validation set-up. The calibration is performed, as before, on each of the remaining models and adjusted return levels for end-21st-century are calculated. But then the median of these adjusted future return levels is calculated, and this is validated against the future pseudo-observations. Note that this gives only N=19 different combinations and, therefore, less robust statistics compared to the above.

4 Results

4.1 Modelled return levels for conditions in the present-day and end-21st-century

Figure 2 displays the geographical distribution of the 10-year return level for precipitation intensity of a 1 h duration, calculated as the median return level over all 19 model simulations. The smallest return levels are mainly found in the arid North African region and, to some extent, in the Norwegian Sea, while the largest return levels are found in southern Europe and in the Atlantic northwest of the Iberian Peninsula. Mountainous regions, such as the Alps and western Norway, stand out as having higher return levels than their surroundings. This supports the idea that the models are not totally unrealistic in modelling extreme precipitation.

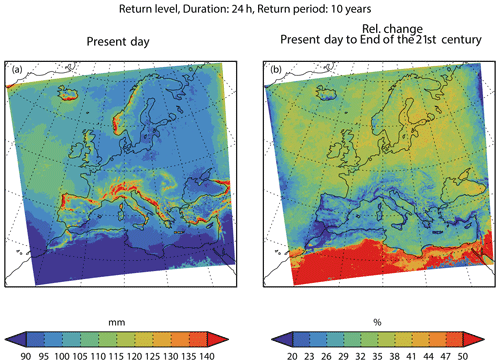
There is a general increase in the range of 20 %–40 % in climatic conditions from the present-day to end-21st-century. The relative changes are geographically quite uniform across the area. For instance, no evident difference between the land and sea appears. Moreover, the mountainous regions do not stand out from their surroundings.

We also show, in Fig. 3, the median 10-year return level for a 24 h duration. Again, the largest return levels are found in southern Europe and northwest of the Iberian Peninsula. Also, the mountainous regions stand out with higher return levels that are even more pronounced than for a 1 h duration. The return levels generally increase conditions from the present-day to end-21st-century by around the same percentage as for a 1 h duration, and they are also geographically homogeneous.

Figure 3 As in Fig. 2 but for a 24 h duration.

Figure 4 Modelled return levels at 50^∘ N, 10^∘ E (northern Germany; marked with a red cross in Fig. 1) for the present and future for a 10-year return period and 1 and 24 h durations. Different colours represent the 19 different GCM–RCM simulations listed in Table 1.

To obtain a more detailed impression of the data, Fig. 4 shows the return levels and their changes from the present-day to end-21st-century for a grid point in northern Germany for all 19 model simulations. For a 1 h duration (Fig. 4a), return values increase from the present-day to end-21st-century in all cases. For a 24 h duration (Fig. 4b), the return levels typically increase from the present-day to end-21st-century but with some exceptions. This behaviour is common to all regions. For both durations, we also note the large spread in return levels within the ensemble. The spread is much higher than the change between the present and future for most models; in other words, there is a poor signal-to-noise ratio. This is probably a combined effect of different climate signals in different models and natural variability (Aalbers et al., 2018).

4.2 Inter-model cross-validation

In the following, we will present results using two different types of displays. First, we will use spatial maps of the median relative error, calculated from all combinations of model/pseudo-observations. Second, we will, for each adjustment method and for each combination of model/pseudo-observations, calculate the median relative error over each of the eight PRUDENCE subregions defined in Christensen and Christensen (2007) and shown in Fig. 1. For each region, we will illustrate the distribution of the relative error across all combinations of model/pseudo-observations by showing the median and the 5th and 95th percentiles of this distribution.

4.2.1 Results for a 1 h duration

Figure 5 shows the median, across all model/pseudo-observation combinations, the relative error for all five methods for 1 h duration and the 10-year return period.

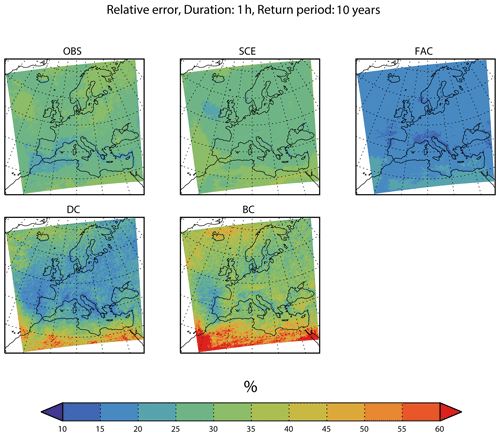
Figure 5 Geographical distribution of the relative error of the end-21st-century 10-year return level for a 1 h duration precipitation intensity from the inter-model cross-validation. Colours show the median of the relative error calculated over all model/pseudo-observation combinations. Panels show the different adjustment methods.

First, we look at the reference methods. Relative errors from the OBS method are in the range of 20 %–40 %. The lowest values are found in the Mediterranean, western France and the Atlantic west of the Mediterranean; the highest values are in the Atlantic west of Ireland and in Scandinavia. The SCE method has errors in the interval of 25 %–45 %, with the lowest values in the Atlantic west of Ireland; the largest values are over parts of the Atlantic and northern Africa. The two reference methods give rather similar results, but the OBS method slightly outperforms SCE in the south, while the opposite is true in the north.

The relative error of FAC is below 20 % in most places. Everywhere it is smaller than the relative error of the reference methods OBS and SCE. The DC method has a relative error comparable to (e.g. western France, western Iberia and eastern Atlantic) or larger than (in particular, northern Africa) that of FAC. That said, the concept of relative error should be used with care in an arid region, such as northern Africa. But, from this result, it is not justifiable to use the more complicated DC in favour of the simpler FAC. Finally, the relative error of BC is above both DC and FAC everywhere, indicating the poorest performance of all methods considered.

The statistical distribution of the relative error is shown in Fig. 6 for the eight PRUDENCE subregions (see Fig. 1). We first note that the distribution of relative error is shifted towards higher values for larger return periods, as expected. Next, we note that the two reference methods, OBS and SCE, behave differently. SCE generally has a slightly larger median relative error, but the 95th percentile is much larger for SCE than for OBS, in particular for large return periods. Thus, OBS performs better overall than SCE, meaning that using present-day pseudo-observations to estimate the projected return levels for end-21st-century yields a better relative error than using raw modelled scenario data.

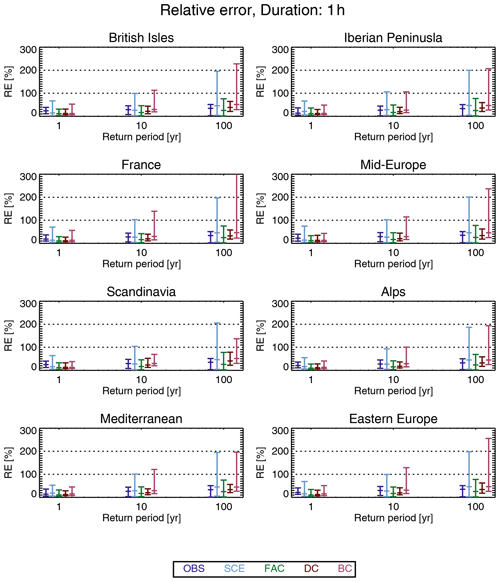
Figure 6 Statistical distribution (median and 5th and 95th percentile) of the relative error of the inter-model cross-validation for a 1 h duration for 1, 10 and 100-year return periods. Panels represent the PRUDENCE subregions shown in Fig. 1. Each colour represents an adjustment method (see Table 2).

The FAC method generally has the best overall performance, both in terms of the median and the 95th percentile of the relative error. The DC method has a slightly poorer performance than FAC, both in terms of the median and the 95th percentile of the relative error. Finally, BC has a poorer performance than DC, when comparing the median of the relative error and, in particular, the 95th percentile.

In summary, for a 1 h duration, the method with the best performance is using a climate factor on the return levels (FAC). This method outperforms both reference methods and the more sophisticated methods based on quantile mapping, i.e. DC and BC, with the latter having the poorest overall performance of them all. Note that DC is comparing GPDs from the same model, whereas BC is comparing GPDs from different models. If the difference, in terms of GPD parameters, between two models in the present-day climate is typically larger than the difference between the same model for the climate in the present-day and end-21st-century, it can explain the different results.

4.2.2 Results for a 24 h duration

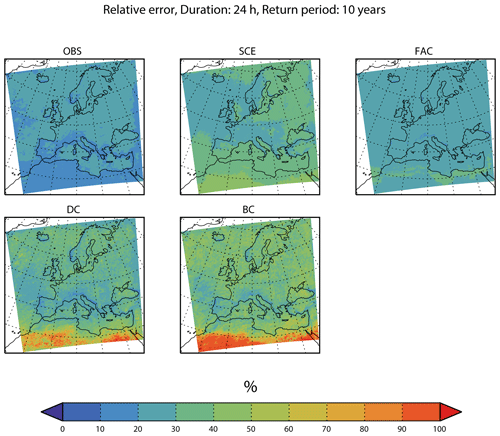
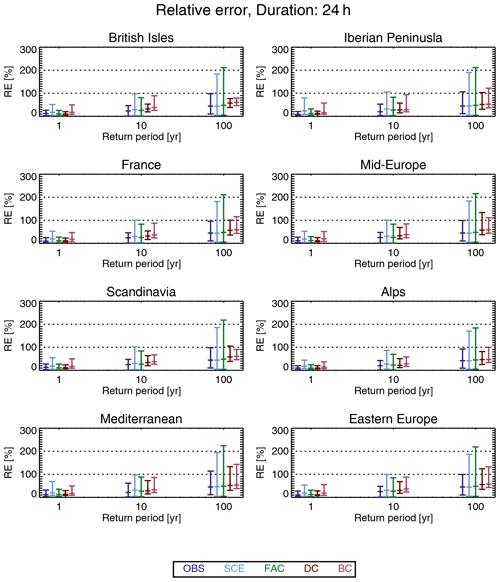
For a 24 h duration (see Fig. 7), OBS has the lowest median relative error (less than 30 %) in most regions of all the adjustment methods, while SCE has higher relative error in the interval of approximately 30 %–60 %, with the highest values in North Africa. FAC has relative errors in between those of OBS and SCE. Of the quantile-mapping methods, DC has relative errors in the interval of approximately 20 %–80 %, which is larger than FAC in most places, and finally, BC has, as for a 1 h duration, the largest median relative errors of all the methods.

Figure 7 As in Fig. 5 but for a 24 h duration.

As for the 1 h duration, we also compare the entire statistical distribution of the relative error of the different adjustment methods for all three return periods (Fig. 8), and again, both the median and 95th percentile of the relative error increases for larger return periods, as expected. Furthermore, OBS seems, surprisingly, to have a small median relative error and the smallest 95th percentile of all methods considered for all subregions. SCE has a median not too different from that of OBS, but the 95th percentile is much larger. Similar characteristics hold for FAC. The quantile-mapping methods DC and BC have slightly larger median values, but the 95th percentile is smaller than for FAC. All these characteristics hold for all subregions.

Figure 8 As in Fig. 6 but for a 24 h duration.

4.2.3 Ensemble median

Inter-model cross-validation of pseudo-observations against the model ensemble median, as described in Sect. 3.4, was also carried out. For a 1 h duration, the distribution of the relative error is shown in Fig. 9. By comparing this with Fig. 6, the distribution of the relative error does not change much overall. However, for many of the subregions considered, and for the longer return periods, FAC and BC have a smaller 95th percentile for cross-validation against model ensemble means than against individual models.

Figure 9 As in Fig. 6 but for the inter-model cross-validation against ensemble medians.

In addition, the distribution of the relative errors does not change much for a 24 h duration when shifting to a validation against the ensemble median (not shown).

4.3 Further analysis on conditions for skill

To obtain further insight into the difference in performance between hourly and daily precipitation, we consider, for a given return period, the relationship between the bias factor for present-day $B_{P,T}=\frac{C_T}{O_T}$ and $B_{F,T}=\frac{S_T}{V_T}$ end-21st-century for all model/pseudo-observation combinations (see Fig. 10).

Figure 10 Relationship between bias factors in the present-day and end-21st-century in 10-year return levels for the mid-Europe subregion for all model/pseudo-observation combinations. (a) The 1 h duration and (b) 24 h duration, respectively. Numbers in upper left corners are the R indices. See text for details.

In this figure, the relationship between bias factors in the present-day and end-21st-century appears more pronounced for 1 h duration than for 24 h duration. That said, it must be borne in mind that if the point (x,y) is in the plot, then so is the point $\left(\mathrm{1}/y,\mathrm{1}/x\right)$, and this implies an inherent tendency towards a fan-like spread of points from (0,0), as seen on both plots.

To quantify the strength of the above relationship, we define an index as follows:

$${\displaystyle }R=〈{\displaystyle \frac{\left|B_F-B_P\right|}{\left(B_F+B_P\right)/\mathrm{2}}}〉,$$

where 〈⋅〉 means averaging over combinations of model/pseudo-observations. This index is an extension of the index introduced by Maurer et al. (2013). It is the ensemble average of the relative absolute difference between the present-day and future bias. A value of R=0 means that these biases are equal, i.e. perfect stationarity, and the smaller the value of R, the closer to stationarity (in an ensemble sense).

Values of R are given in the upper left corner of each panel of Fig. 10, and they also support the partial relationships described above and a stronger one for hourly duration. These relations are important since they could explain the generally good performance of the FAC method seen in the previous section. Suppose that $B_{P,T}=B_{F,T}$, then, in the following:

$${\displaystyle }{P}_T={\displaystyle \frac{S_T}{C_T}}{O}_T=S_T{\displaystyle \frac{O_T}{C_T}}=S_T{B}_P=S_T{B}_F=S_T{\displaystyle \frac{V_T}{S_T}}=V_T,$$

and the FAC method will therefore adjust perfectly.

We also note that daily data, due to the summation, would have less erratic behaviour than hourly data, and therefore, we would expect any relationship to be less masked by noise for daily data than for hourly data from purely statistical grounds. Therefore, any explanation as to why it is opposite should probably be found in physics or the details of modelling. We will discuss this further in Sect. 5.3.

5 Discussion

5.1 Relation with other studies

The study by Räty et al. (2014) touches upon issues related to ours. However, our study includes smaller temporal scales (hourly and daily) and higher return periods (up to 100 years vs. the 99.9th percentile of daily precipitation corresponding to a return period of around 3 years). Nevertheless, the two studies agree in their main conclusion, namely that applying a bias adjustment seems to offer an additional level of realism to the processed data series, including in the climate projections, as compared to using unadjusted model results. The two studies both support the somewhat surprising conclusion that using present-day (pseudo-) observations as the scenario gives a skill comparable to that of the bias adjustment methods.

Kallache et al. (2011) proposed a correction method for extremes, i.e. cumulative distribution function transfer (CDF-t), and obtained good validation result with the calibration/validation split of historical data from southern France. The CDF-t method was applied by Laflamme et al. (2016) on daily New England data, who concluded that “downscaled results are highly dependent on RCM and GCM model choice”.

5.2 Convection in RCMs

The grid spacing of present state-of-the-art RCMs available in large ensembles, such as CORDEX, is around 10 km, and at this resolution, it is necessary to describe convection through parameterisations. This is obviously an important deficit for our purpose, since this could represent a systematic bias in all our simulations and, therefore, violate our underlying assumptions that the individual model simulations and the real-world observations behave similarly in a physical sense. Thus, we do not promote naively applying the presented adjustment methods to hourly data from these models. Instead, the present work should be seen as a statistical exercise, and the methods can, in the future, be applied to convection-permitting model simulations that better represent the convective process. The results from the present work would apply equally to that case.

With the advent of convective-permitting models, a more realistic modelling of convective precipitation events is within reach, and a change in the characteristics of such events is seen (Kendon et al., 2017; Lenderink et al., 2019; Prein et al., 2015). This next generation of convection-permitting RCMs with a grid spacing of a few kilometres allows a much better representation of the diurnal cycle and convective systems as a whole (Prein et al., 2015). With that in mind, we foresee redoing the analysis when a suitable ensemble of convective-permitting RCM simulations becomes available.

5.3 Stationarity of bias

The success of applying bias adjustment to climate model simulations is linked to the biases being stationary, i.e. present and future biases being more or less identical. In Sect. 4.3, we showed (in Fig. 10) that this was the case for a 1 h duration and less so for a 24 h duration in our pseudo-reality setting. Such a relationship is an example of an emergent constraint (Collins et al., 2012). This is a model-based concept, originally introduced to explain that models which have too warm (cold) a present-day climate tend to have a relatively warmer (colder) future climate. The reason for this is that it is the same underlying physics which generates the present-day and future temperatures (Christensen and Boberg, 2012).

We suggest that our observed emergent constraints could be explained in a similar manner, namely as a result of the Clausius–Clapeyron relation linking atmospheric temperature changes to changes in its humidity content and, thereby, precipitation changes. The change prescribed by the Clausius–Clapeyron equation is usually termed the thermodynamic contribution. In addition to this, there is a dynamic contribution, and this may explain the differences between the hourly and daily relation seen in Fig. 10. The rationale is that hourly extremes are entirely due to convective precipitation events with almost no dynamic contribution (Lenderink et al., 2019), while daily extremes are a mixture of convective events and large-scale strong precipitation, of which the latter has a more significant dynamic contribution (Pfahl et al., 2017), causing the less marked emergent constraint for the daily timescale. This interpretation is also supported in Fig. 4, in which daily precipitation sees some crossovers (future return level smaller than the present), whereas hourly precipitation does not have any crossovers.

5.4 The spatial scale

In the definition of model bias, it is tacitly assumed that the observational data set has the same spatial resolution as the model data. In practice, however, it is rarely possible to separate the bias from a spatial-scale mismatch. For instance, if we compare modelled precipitation, which represents averages over a grid box, with rain gauge data, which represent a point, there can be a quite substantial mismatch for extreme events (Eggert et al., 2015; Haylock et al., 2008). Therefore, if the bias is adjusted towards such point values, it may lead to further complications (Maraun, 2013).

Sometimes, though, it is desirable to include the scale mismatch in the bias adjustment. Many impact models, e.g. hydrological models, are tuned to perform well with local observational data as input. This presents an additional challenge if this impact model is to be driven by climate model data for climate change studies, since the climate model will have biases in its climate characteristics (mean, variability, etc.) compared to those of the observed data. Applying the adjustment step, the hydrological model can rely on its calibration to observed conditions (Haerter et al., 2015; Refsgaard et al., 2014).

5.5 Adjustment methods not included in the study

Only the basic adjustment methods have been included in our study. The simple climate factor approach has been applied in numerous hydrological applications (DeGaetano and Castellano, 2017; Sunyer et al., 2015 and other sources). We also wanted to test quantile-mapping approaches, which in extreme value theory takes the form of a parametric transfer function. This we have applied in two flavours in the spirit of Räty et al. (2014). Finally, we wanted to benchmark against the canonical benchmark methods, namely observations and raw model output.

There is a myriad of more specialised methods which are each tailored to account for a particular deficit of the simpler methods. First, there is the issue of whether it is, for precipitation, more reasonable to map relative quantile changes rather than absolute ones (Cannon et al., 2015). It has also been argued that a bias correction method should preserve long-term trends, i.e. the climate signal, and only adjust the shorter timescales, as extensively discussed in Cannon et al. (2015). Then multivariate methods have been argued for and applied in order to preserve relationships between variables (Cannon, 2018) and nested methods to account for different biases for different timescales (Mehrotra et al., 2018). Also, methods to correct for systematic displacement of variable features in complex terrain have been suggested and applied (Maraun and Widmann, 2015). Finally, Li et al. (2018) adjust stratiform and convective precipitation separately instead of adjusting the total precipitation. In this way, any future change in the ratio between the two types of precipitation is accounted for.

It could be interesting to examine the above methods in future studies, though we acknowledge it would be a quite extensive work. We can, at present, only guess at the outcome of such work, but the more refined methods may not perform too well in the inter-model cross-validation setting. The reason for this suspicion is that these methods, while being more elaborate, in most cases also have more parameters to be estimated, implying a higher risk of overfitting. An argument in favour of this is that the present study shows that the more elaborate quantile-mapping methods of DC or BC do not outperform the simpler FAC method.

6 Conclusions

Based on hourly precipitation data from a 19-member ensemble of climate simulations, we have investigated the benefit of bias adjusting extreme precipitation return levels on hourly and daily timescales and evaluated the different methods. This is done in a pseudo-reality setting, where one model simulation in turn from the ensemble plays the role of observations extending into the future. The return levels obtained from each of the remaining model simulations are then adjusted in the present-day period, using different adjustment methods. Then the same adjustment methods are applied to the model data for end-21st-century to obtain projected return levels, which are then compared with the corresponding pseudo-realistic future return levels.

The main result of this inter-comparison is that, compared to using the unadjusted model runs, applying bias adjustment methods improves projected extreme precipitation return levels. Can an overall superior adjustment methodology be appointed? For an hourly duration, the method to recommend (with the smallest relative error) is the simple climate factor approach, FAC, which is better in terms of the relative error than the more complicated analytical quantile-mapping methods based on EVA, DC and, in particular, BC. For a daily duration, the OBS method performs surprisingly well, with the smallest 95th percentile of the relative error. Furthermore, the quantile-mapping methods perform better than FAC, with DC having the smallest relative error. These conclusions hold regardless of the subregion considered. We also cross-validated against model ensemble means; this gave, in general, similar results without significant changes in the distribution of the relative error.

Finally, we registered emergent constraints between biases in the present-day and end-21st-century. This was more pronounced for hourly than for daily timescales. This could be caused by hourly precipitation being more directly linked to the Clausius–Clapeyron response, but this requires more clarification in future work.