the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Learning about precipitation lapse rates from snow course data improves water balance modeling
Francesco Avanzi
Giulia Ercolani
Simone Gabellani
Edoardo Cremonese
Paolo Pogliotti
Gianluca Filippa
Umberto Morra di Cella
Sara Ratto
Hervè Stevenin
Marco Cauduro
Stefano Juglair
Precipitation orographic enhancement is the result of both synoptic circulation and topography. Since high-elevation headwaters are often sparsely instrumented, the magnitude and distribution of this enhancement, as well as how they affect precipitation lapse rates, remain poorly understood. Filling this knowledge gap would allow a significant step ahead for hydrologic forecasting procedures and water management in general. Here, we hypothesized that spatially distributed, manual measurements of snow depth (courses) could provide new insights into this process. We leveraged over 11 000 snow course data upstream of two reservoirs in the western European Alps (Aosta Valley, Italy) to estimate precipitation orographic enhancement in the form of lapse rates and, consequently, improve predictions of a snow hydrologic modeling chain (Flood-PROOFS). We found that snow water equivalent (SWE) above 3000 m a.s.l. (above sea level) was between 2 and 8.5 times higher than recorded cumulative seasonal precipitation below 1000 m a.s.l., with gradients up to 1000 mm w.e. km−1. Enhancement factors, estimated by blending precipitation gauge and snow course data, were consistent between the two hydropower headwaters (median values above 3000 m a.s.l. between 4.1 and 4.8). Including blended gauge course lapse rates in an iterative precipitation spatialization procedure allowed Flood-PROOFS to remedy underestimations both of SWE above 3000 m a.s.l. (up to 50 %) and – importantly – of precipitation vs. observed streamflow. Annual runoff coefficients based on blended lapse rates were also more consistent from year to year than those based on precipitation gauges alone (standard deviation of 0.06 and 0.19, respectively). Thus, snow courses bear a characteristic signature of orographic precipitation, which opens a window of opportunity for leveraging these data sets to improve our understanding of the mountain water budget. This is all the more important due to the essential role of high-elevation headwaters in supporting water security and ecosystem services worldwide.
- Article
(5158 KB) - Full-text XML
-
Supplement
(11572 KB) - BibTeX
- EndNote
Orographic precipitation is a critical driver of the Earth's water budget (Jiang, 2003), particularly as it affects amount and distribution of snowpack at high elevations and, thus, freshwater supply and water security during the warm season (Serreze et al., 1999; Bales et al., 2006; Viviroli et al., 2007b; Blanchet et al., 2009; Mott et al., 2014; Sarmadi et al., 2019). On shorter timescales, orographic precipitation may concur in generating floods (Buzzi et al., 1998; Galewsky and Sobel, 2005; Panziera et al., 2015) and in triggering landslides and avalanches (Roe, 2005). A feature of both stratiform and convective systems (Roe, 2005), orographic precipitation introduces sharp transitions between wet, windward, and dry leeward slopes that are ubiquitous across continents (rain shadows, see Houston and Hartley, 2003; Anders et al., 2006; Galewsky, 2009; Viale and Nuñez, 2011). Because these mechanisms shape local climates and ecosystem services (see Michalet et al., 2003; Roe, 2005; Poschlod, 2015, and references therein), gaining a better understanding of how precipitation interacts with elevation has important implications within and beyond geosciences.
Orographic precipitation has already been subject of extensive research (Bonacina, 1945; Sarker, 1966; Alpert, 1986; Barros and Kuligowski, 1997; Smith and Barstad, 2004; Roe, 2005; Smith, 2006; Rotunno and Houze, 2007; Allamano et al., 2009; Avanzi et al., 2015; Napoli et al., 2019; Ruelland, 2020). The emerging consensus is that the distribution, intensity, and duration of orographic precipitation depend on the following three main modulating factors (Rotunno and Houze, 2007): the synoptic circulation patterns, intensity of mesoscale lifting along slopes, and timing of water condensation through convection and turbulence. Interactions across these three primary factors are notoriously elusive, with cloud microphysics, local terrain heterogeneity, and boundary layer thermodynamics challenging the somewhat naive notion that precipitation increases with elevation (see Roe, 2005, for a review). For example, Napoli et al. (2019) have shown a saturation-like effect in orographic enhancement above ∼ 1000 m a.s.l. (above sea level) in the Alps, associated with a monotonous increase in annual precipitation variability with elevation. This saturation effect was also highlighted by Blanchet et al. (2009) for mean and maximum snowfall across Switzerland. Avanzi et al. (2015) observed increased variability in extreme precipitation quantiles with elevation and a reverse orographic effect for annual maximum precipitation of a short duration, which is even enhanced for subhourly durations (Marra et al., 2021).
The complex nature of precipitation orographic enhancement means that some of its fundamental aspects are still poorly understood, especially across headwaters with complex terrain. This includes the magnitude and seasonality of precipitation gradients, how they vary across the landscape during specific events, and how they interact with temperature and relative humidity to determine precipitation phase (Harpold et al., 2017; Avanzi et al., 2020a). Such knowledge gaps are exacerbated by precipitation measurements in snow-dominated headwaters being prone to large errors, such as wind-driven undercatch and snow plugging (Rasmussen et al., 2012; Avanzi et al., 2014), issues that have progressively discouraged the deployment of measurement stations in snow-dominated regions unless frequent maintenance and ground truthing is performed – which is very rare due to its high costs and logistical constraints. Meanwhile, radar- or satellite-based measurements in mountain terrain are challenged by complex topography, radar beam shielding, and ground echoing (Germann et al., 2006). Despite substantial efforts in recent years to achieve more reliable precipitation measurements (such as the WMO SPICE initiative, see Nitu et al., 2018), the world's water towers (Viviroli et al., 2007b) remain largely ungauged.
Better understanding of precipitation distribution across mountain landscapes is not only an open question for fundamental research but also for operational forecasting (Frei and Isotta, 2019). Precipitation spatialization in mountain hydrology models is generally performed through assigning a priori precipitation lapse rates (e.g., see Bergström., 1992; Viviroli et al., 2007a; Markstrom et al., 2015) or interpolating precipitation gauge data with various degrees of geostatistical complexity (Frei and Schär, 1998; Daly et al., 2008; Isotta et al., 2014; Foehn et al., 2018; Frei and Isotta, 2019). While cross-validation accuracy of these spatialization methods is high at measurement sites (e.g., mean absolute errors for monthly precipitation below ∼ 12 mm in Daly et al., 2008), gauge-based spatialization approaches cannot fully overcome the lack of signal at high elevations. For instance, the seminal work by Frei and Schär (1998) considered an advanced distance-weighting scheme to spatialize daily precipitation across the European Alps, but the vast majority of measurement sites was located below ∼ 2500 m a.s.l. In the US, the Parameter-elevation Relationships on Independent Slopes Model (PRISM; see Daly et al., 2008) adopts a weighted climate–elevation relationship based on physiographic similarity, but Zhang et al. (2017) showed that this approach underestimates both precipitation totals above ∼ 2400 m a.s.l. and the seasonal precipitation lapse rate in the central Sierra Nevada, California. It follows that predicting precipitation above this “precipitation gauge line” at ∼ 2500 m a.s.l. will always imply some degrees of extrapolation.
A largely unexplored solution for grasping precipitation gradients above the precipitation gauge line is provided by snow courses, a snow survey protocol based on collecting measurements of snow depth (HS), and, optionally, snow density (ρS) at regular intervals over transects of various extent (generally 1+ km) to inform water supply forecasting or other applications (see, e.g., Hart and Gehrke, 1990; Rice and Bales, 2010). This approach captures snow depth distribution in a way that is more representative of snow water resources across the landscape than stand-alone stations like ultrasonic depth sensors, which, instead, tend to overestimate both peak snow water equivalent (SWE) and snow duration (Malek et al., 2017). Snow course data are collected, for example, in the western US (Pagano et al., 2004), Norway (Skaugen et al., 2012), and Finland (Lundberg and Koivusalo, 2003) and have frequently been used to develop and evaluate snow hydrologic models (Jost et al., 2009), snow mapping algorithms (Margulis et al., 2016), or satellite retrieval methods (Metsämäki et al., 2005).
Snow course measurements are the result of a broad spectrum of processes acting at multiple scales, including wind drift (Winstral et al., 2013), aspect-driven melt patterns (Da Ronco et al., 2020), preferential deposition of snowfall (Gerber et al., 2017, 2019), and snow canopy interactions (Lundquist et al., 2013). In the present study, we hypothesized that snow courses bear an additional, characteristic signature of seasonal orographic enhancement, which can be leveraged to fill the gap in precipitation measurements above the precipitation gauge line and improve hydrologic model predictive skills as a result. In order to verify this hypothesis, we focused on two high-elevation hydropower catchments in the western European Alps (Aosta Valley, Italy) where more than 10 000 snow course data points have been collected for water supply forecasting since 2008. We combined these data with ground-based precipitation to first investigate the relationship between seasonal precipitation totals below the precipitation gauge line and peak accumulation snow course water equivalent above 3000 m a.s.l., and, thus, derive a climatology of lapse rates obtained by merging these two data sets (blended lapse rates). Second, we leveraged these blended lapse rates to develop an iterative, two-step spatialization procedure of precipitation that accounts for seasonal orographic effects in addition to daily precipitation variability below the precipitation gauge line. Third, we evaluated this spatialization procedure using streamflow measurements and operational snow hydrologic modeling (S3M and Continuum; see Silvestro et al., 2013; Laiolo et al., 2014).
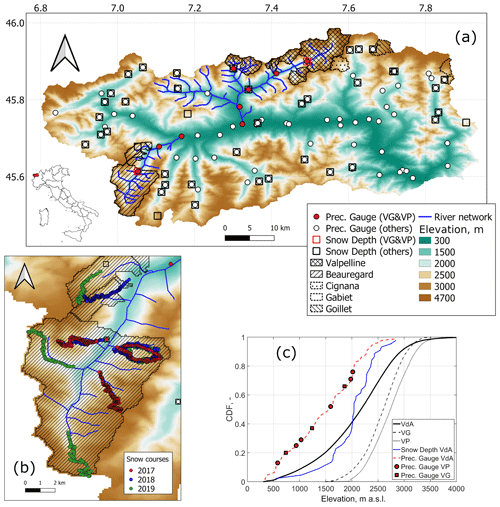
Figure 1(a) Topography of Aosta Valley (VdA; our focus region), along with hydrography and hydropower catchment delineation of the two valleys for which we reconstructed blended precipitation lapse rates (VG is Beauregard, and VP is Valpelline). This panel also reports the location of all precipitation gauges and snow depth sensors available to the present study, as well as catchment delineation of three other hydropower systems in Aosta Valley where snow courses were collected (see Table 1). (b) Examples of snow course locations for 3 water years at Beauregard. (c) Report on the elevation distribution of the Aosta Valley, Beauregard, and Valpelline and of the precipitation gauge and snow depth sensor networks.
2.1 Study area
Aosta Valley (one of the 20 Italian administrative regions) is located at the northwestern edge of the Italian peninsula (Fig. 1a). Embraced by some of the highest peaks in the Alps (Mont Blanc – 4808 m a.s.l.; Monte Rosa – 4634 m a.s.l.; and Gran Paradiso – 4061 m a.s.l.), Aosta Valley is a typical inner-Alpine valley with marked rain shadows (Isotta et al., 2014). Annual precipitation totals can be as high as ∼ 1600–1800 mm across the southeastern windward slopes or the Mont Blanc area in the northwestern corner of the region and lower than 600 mm in the central valley. Such comparatively low precipitation totals, coupled with pronounced temperature gradients, make this region prone to droughts and the associated vegetation stress (Cremonese et al., 2017). Precipitation is year round, with somewhat bimodal seasonality and prevalent peaks in spring and fall (Crespi et al., 2018). Its topographic imbalance in the precipitation distribution and the associated marked orographic gradients make Aosta Valley an ideal region for the present study. An area of about 134 km2 out of 3261 km2 of the Aosta Valley is covered by glaciers (4 %), meaning that this is the most glacierized region in Italy (Smiraglia et al., 2015; Patro et al., 2018). While specific measurements to quantify the contribution of glaciers to total runoff are missing, qualitative inspection of the observed hydrographs suggest that glacier melt contributes particularly to late summer streamflow when input from snowmelt declines. This is in line with other catchments across the Alps.
We focus on two hydropower catchments to test our research hypothesis, namely Valpelline (VP) and Beauregard in Valgrisenche (VG; see Fig. 1a and c). The total drainage area of Beauregard is ∼ 110 km2, 14 % of which is covered by glaciers (11.4 km2); elevation ranges from ∼ 1800 m a.s.l. at the outlet to ∼ 3500 m a.s.l. Moreover, Valpelline spans both a larger extent and a higher elevation range than Beauregard, and the total drainage area is ∼ 130 km2, while minimum and maximum elevation are 1539 and 3934 m a.s.l., respectively. About 12.4 km2 of the drainage area of Valpelline is glacierized (9.5 %). Beauregard and Valpelline are located on two opposite sides of the Aosta Valley and, thus, have different prevalent aspects (northwards and westwards, respectively). Both systems are composed of a reservoir and a number of auxiliary intakes, which we lumped together as a single catchment. Both catchments are ungauged with regard to precipitation or snow depth automatic weather stations (Fig. 1a and c).
2.2 Data
We employed (1) weather and snow data from the network of monitoring stations of the regional authority (https://cf.regione.vda.it/portale_dati.php, last access: 6 June 2020), (2) reconstructed streamflow data for the two hydropower catchments of Beauregard and Valpelline, and (3) high-elevation, manual peak snow depth snow courses. The study period covered water years 2008 through 2019, based on data availability, with a specific focus on water years 2017 through 2019 when most of the snow course data were collected. We define a “water year” as the period between September 1 and the following 31 August, using the calendar year in which it ends (e.g., water year 2019 went from 1 September 2018 to 31 August 2019). We used September to August rather than October to September (which is frequent elsewhere) because snow accumulation in this region may start as early as September.
Weather data comprise hourly air temperature, relative humidity, incoming shortwave solar radiation, wind, and total precipitation data at up to ∼ 100 (temperature), ∼ 50 (relative humidity), ∼ 30 (incoming shortwave solar radiation), ∼ 60 (wind), and ∼ 80 (total precipitation) measurement points. The actual number of available measurement points changed from day to day because of potential malfunctioning or communication issues. Data were collected, processed, quality checked, and stored by the civil protection regional authority (data access and geometry of the monitoring network: http://presidi2.regione.vda.it/str_dataview, last access: 12 June 2020). Quality checks were based on a mixture of automatic filtering and visual screening, including out-of-range or negative values (where applicable; e.g., snow depth).
Figure 1a reports the location of precipitation measurement points used in the present study, while Fig. 1c highlights that these precipitation gauges cover only low to medium elevations, with the highest one at ∼ 2700 m a.s.l. Considered precipitation gauges comprise both heated and unheated sensors, but the hourly precipitation spatialization technique used in the following automatically excludes unheated sensors when they are above the rain–snow transition line (Sect. 3.2). Regarding undercatch, previous work by the author team compared precipitation totals at snow depth sensor locations with concurrent snow depth increases (see next the paragraph with regard to snow depth data). Precipitation totals were estimated using various parameterizations and that of Allerup et al. (1997) was found to yield the lowest error (unpublished work). Applying this correction corresponds to gaining 5 % to 15 % of total precipitation, compared to using non-corrected precipitation data. Given that the comparison was performed between precipitation and snow depth increases, this accuracy is more representative of solid than liquid precipitation.
The data set of the regional authority also comprises hourly snow depth data at ∼ 50 locations (see Fig. 1a). The measurement technique is based on ultrasonic ranging, with precision of a few centimeters (Ryan et al., 2008; Avanzi et al., 2014). While the average elevation of these snow depth stations is higher than that of the precipitation gauges, locations above ∼ 2700 m a.s.l. remain largely ungauged (Fig. 1c). Snow cover is also routinely monitored by a cooperative consortium collecting manual samples of snow depth and density across the whole region, with weekly to monthly revisit times for the same measurement plot. These manual, periodical data were not directly employed in the present study given their discontinuous nature, but we did use interpolated SWE maps based on combining these manual, periodical data and the ∼ 50 automatic snow depth stations (see details in Sect. 3). These maps were produced by the local Environmental Protection Agency (ARPA VdA) and were used as an assimilation source for our snow hydrologic forecasting chain (Sect. 3.2). Figure S1 in the Supplement shows an example of all input samples used by ARPA VdA for the period 1–8 March 2020. Note that these manual, periodical measurements are not classifiable as snow courses because they consist of stand-alone measurements at open sites.
Reconstructed streamflow data for the closure sections of Valpelline and Beauregard were provided by Compagnia Valdostana delle Acque (CVA), the company managing both hydropower systems. These estimates were based on measurements of inflow to the plants and changes in reservoir storage, with a proprietary reconstruction method. The uncertainty of this data set has never been fully quantified, but such a reconstruction approach corresponds to the standard method used for unimpaired flow estimation in other regions in the world (Avanzi et al., 2020b). Annual runoff totals for the closure sections of Valpelline and Beauregard, according to these reconstructed data (∼ 1000–1500 mm), are consistent with other gauged sections in the region. Data were daily and ranged from water year 2008 to 2019, consistent with weather and snow course data.
Table 1Inventory of available snow course surveys, including survey date (day/month), number of samples per survey (N), and mean survey elevation (ZMEAN). Only a subset of the five areas was surveyed every year, due to budgetary and logistical constraints. The spatial distribution of these samples is shown in Figs. S2–S12 in the Supplement. Note that 2641 out of 5349 measurements collected at Goillet in 2017 were performed on 10 April. Snow courses for this area and water year were part of a large intercomparison workshop, and hence, this explains the much larger sample size than other years and areas. Note: m – meters.
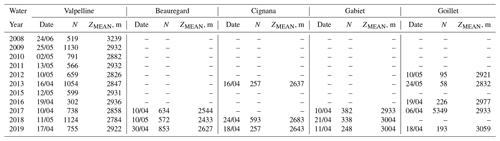
Snow course data were available for five areas of interest, including the two hydropower catchments of Valpelline and Beauregard and three much smaller hydropower catchments (i.e., Cignaga, Gabiet, and Goillet; see Fig. 1a). Because of logistical constraints, only a subset of these five areas of interest was sampled every year, with a markedly larger data set starting from the water year 2017 (see Table 1 for an inventory). Data were collected around peak-accumulation day, which changed from year to year and from catchment to catchment, as assessed by ARPA VdA based on weather forecasts and snow accumulation patterns (see Table 1 for survey dates). Snow depth measurements were taken every 50 to 100 m along transects of several kilometers, which spanned the whole elevation gradient from the local snow line to the catchment drainage divide (see Fig. 1b for an example of these transects for Beauregard and Figs. S2 to S12 for details of all transects).
Mean elevation of these snow courses was much higher than the elevation captured by the precipitation gauge and snow depth sensor networks (often above 3000 m a.s.l.). The location of the transects across each catchment was chosen to explore the whole elevation gradient from the local snow line up to the drainage divide and to capture a variety of physiographic characteristics. The sampling protocol avoided known deposition or erosion areas, as far as possible. The number of transects for each catchment year depended on available resources. Snow depth was measured using manual probes, and the location of each measurement was recorded using a portable GPS with a precision of the order of meters. Snow course data for each area of interest were accompanied by a few measurements of bulk snow density at representative locations, which were averaged to provide a reference estimate for each survey and, hence, derive SWE.
3.1 Estimating blended gauge course lapse rates
We derived blended precipitation gauge snow course lapse rates for Beauregard (water years 2017 through 2019) and Valpelline (water years 2008 through 2013 and 2015 through 2019) by first detecting the onset of the snow season for each catchment and each water year as the first hour with at least 20 cm of snow on the ground for a mid-elevation nearby the snow depth sensor (red squares in Fig. 1; elevation was ∼ 1860 and 1970 m a.s.l. for the snow depth sensors of Beauregard and Valpelline, respectively). We then accumulated hourly precipitation between this onset date and the snow course date for every precipitation gauge in the same valley of each hydropower catchment – this was done separately for each water year. We, finally, derived orographic-precipitation enhancement factors for each valley and water year by dividing seasonally cumulative precipitation at gauges and average SWE above 3000 m a.s.l. by seasonally cumulative precipitation at the lowest-elevation precipitation gauge in the same valley; these adimensional enhancement factors measure the magnitude of orographic precipitation elevation gradients, regardless of seasonal precipitation totals.
Blended precipitation gauge snow course lapse rates were computed as a least square error regression fit between elevation and these enhancement factors. Although snow course data were also available for the other three study areas (Fig. 1 and Table 1), these were too small, compared to the respective valleys, for deriving robust precipitation lapse rates. We, therefore, calibrated blended precipitation gauge snow course lapse rates only using data from Beauregard and Valpelline (separately; see Sect. 3.3 for details on the use of the additional courses in this paper).
The general assumption behind blended precipitation gauge snow course lapse rates is that snow course measurements above 3000 m a.s.l. are representative of total precipitation fallen at those elevations from the onset of the snow season through the snow course date. In other words, such blended lapse rates assume that the snowpack above 3000 m a.s.l. behaves as a natural precipitation gauge, with no significant mass loss throughout the accumulation season due to snowpack runoff, evaporation, or sublimation. In this framework, we accumulated precipitation since the first hour with at least 20 cm of snow on the ground that aimed to capture precipitation totals for the bulk of the accumulation season, while excluding early season snowfall events that might result in complete or partial depletion of the snowpack. Note that the occurrence of ephemeral snowpacks (as defined in Sturm et al., 1995) would challenge this orographic gradient estimation method; such instances are very rare at the investigated elevations above 3000 m a.s.l.
While no continuous time measurement of SWE was available to validate the 3000 m elevation threshold above which to compute average snow course SWE, and while prescribing a constant threshold for all water years necessarily neglects interannual variability in weather, Hantel et al. (2012) have found snow line elevations across the Alps of the order of ∼ 800 m a.s.l. in winter and ∼ 3000 m a.s.l. in summer (period 1961–2010). Thus, our chosen threshold can be used to assume absence of significant snowmelt before at least May.
Because we computed blended lapse rates using seasonally cumulative precipitation and peak-SWE data, these lapse rates are representative of winter precipitation gradients. Correctly capturing these seasonal gradients is vital for estimating peak snow cover distribution and amount and, thus, forecasting summer water supply (e.g., see Pagano et al., 2004; Harrison and Bales, 2016), although precipitation gradients for specific storms may significantly diverge from the observed seasonal lapse rates. Similarly, these lapse rates may be not representative of summer storm elevation gradients; in this region, and across the Alps in general, summer storms are mostly convection driven (Giorgi et al., 2016), a process that is rare during winter and, therefore, cannot be fully captured by peak-season SWE measurements. Note that liquid precipitation during winter above 3000 m a.s.l. is negligible in this region, so these blended lapse rates are mostly representative of solid precipitation.
3.2 Spatialization of precipitation based on blended lapse rates
Blended precipitation gauge snow course lapse rates developed in Sect. 3.1 were used to design an iterative, two-step precipitation spatialization procedure accounting for orographic effects above the precipitation gauge line. The ultimate goal of designing such a spatialization procedure was twofold. On the one hand, we aimed to confirm whether annual precipitation totals obtained by blended precipitation gauge snow course lapse rates agreed with annual reconstructed runoff, especially in terms of annual runoff coefficients. On the other hand, we aimed to assess whether blended precipitation lapse rates could improve hydrologic predictions (Sect. 3.3).
To this end, we employed the operational snow hydrologic forecasting chain Flood-PROOFS, as validated in this region by Laiolo et al. (2014). Flood-PROOFS consists of automatic spatialization downscaling procedures for weather input data, a distributed, pixel-based snow model (S3M), a distributed, pixel-based hydrologic model (Continuum), and snow depth mapping algorithms used for snow data assimilation (Rebora et al., 2006; Boni et al., 2010; Laiolo et al., 2014; Silvestro et al., 2013). In this paper, we forced Flood-PROOFS with historical data, and this corresponds to a standard hydrologic simulation in reanalysis mode. The implementation of Flood-PROOFS considered in this paper runs with a spatial resolution of 120 m; the computational domain covers the entire Aosta Valley region. More details about Flood-PROOFS's parameterizations and spatialization techniques can be found in Sect. S1.
Similar to other snow hydrologic models, precipitation spatialization in Flood-PROOFS relies on in situ precipitation measurements. In the current spatialization procedure, these precipitation measurements are interpolated using a modified kriging approach called GRISO (Random Generator of Spatial Interpolation from uncertain Observations; see Pignone et al., 2010; Puca et al., 2014). The most significant asset of GRISO is that interpolated precipitation for pixels including a precipitation gauge will maintain the same value as that measured by that precipitation gauge (in other words, measurements at precipitation gauge locations are preserved during interpolation). The covariance structure for each precipitation gauge is dynamic, while precipitation field values far from all precipitation gauges tend either towards the mean of the precipitation field observed by gauges, or towards zero. In this paper, we chose the second option, but also set an influence radius for each precipitation gauge equal to 20 km following previous validations of GRISO in Aosta Valley. No pixel of the study area was thus “far enough” from all gauges for this choice to be relevant.
This one-step precipitation spatialization procedure assumes that measurements taken by the precipitation gauge network are representative of the overall range of variability in precipitation across the study domain. As we outlined in the Introduction, and will further show in Sect. 4, this assumption does not necessarily hold true in the mountainous regions that straddle the precipitation gauge line because interpolated precipitation fields will likely underestimate precipitation totals due to orographic effects missed by the ground-based measurement network. We overcame this issue by developing a modified, two-step GRISO approach as follows. For each time step of interest (in our case, each hour), GRISO was first run using precipitation gauges alone (GRISO1). Second, interpolated precipitation values at select pixels above 2700 m a.s.l. (the precipitation gauge line in this region) were enhanced according to their elevation and the seasonal winter enhancement factor profile calibrated in Sect. 3.1. Third, GRISO was re-run using the measurements from the physical precipitation gauges and estimates at these select pixels (GRISO2) as input. In this two-step procedure, these orographically enhanced precipitation estimates act as virtual precipitation gauges at high elevations (see locations in Fig. S13), with orographic enhancement being informed by snow course measurements at peak accumulation.
High-elevation pixels were selected by first defining a regular grid with spacing equal to 5 % of the longitudinal and latitudinal range of the study area and then taking as candidate locations for these virtual gauges the nodes of this grid. Second, we filtered out any candidate virtual gauge with elevation below 2700 m a.s.l. and those falling outside the study area. Figure S13 shows that the final location of these virtual precipitation gauges is coherent with the orography of our study region and complements the spatial coverage of the physical precipitation gauge network (Fig. 1).
3.3 Evaluating blended precipitation gauge snow course lapse rates from a water balance perspective
We evaluated precipitation estimates informed by blended precipitation gauge snow course lapse rates by comparing predictions of Flood-PROOFS using GRISO1 vs. those using GRISO2 (see Sect. 3.2). The evaluation period was water years 2017 to 2019, since these 3 water years saw a peak in evaluation data availability (particularly snow course data). Although water years 2017 to 2019 were also used to calibrate the blended precipitation gauge snow course lapse rates, and therefore, this was not a fully independent evaluation, doing so was necessary given the lack of snow course data before 2017 for one of the hydropower catchments (Beauregard) and the need for considering as many years as possible for lapse rate calibration to capture interannual variability.
Input data maps were first used to force the snow model of Flood-PROOFS (S3M) and generate hourly equivalent precipitation fields that were then used as an input for the hydrologic model Continuum; equivalent precipitation is the pixel-wise sum of rainfall, snowpack runoff, and glacier runoff, if any (see Sect. S1 for details on these models). S3M can be run in two different modes, that is, only relying on weather inputs (open loop or OL run), or assimilating SWE information from independent sources (full assimilation or Full-Assim run). SWE is assimilated as both weekly maps produced by ARPA VdA through interpolation of manual measurements according to physiographic features (see Sect. 2.2) and daily maps produced within Flood-PROOFS by training a multilinear regression across concurrent ultrasonic snow depth sensor measurements (predictand) and physiographic features like elevation, slope, and aspect (predictors). In the present study, evaluation of peak-SWE predictions by S3M against snow courses was carried out, with reference to both OL and Full-Assim simulations, to disentangle the impact of precipitation spatialization from that of data assimilation. Simulations of the complete Flood-PROOFS chain (S3M and Continuum) were only performed in Full-Assim mode because of computational time constraints.
As we show in Sect. 4, assimilated snow maps – and in particular those derived from snow depth sensors – suffer from a similar bias to that of precipitation at elevations above the snow depth sensor line (see Fig. 1). This bias is likely due to the snow depth sensor network being skewed toward representing the mid-elevation snowpack. Assimilating these biased snow maps would largely nullify the potentially positive effect of enhancing the orographic effects in GRISO2, so we developed a correction factor by first recalibrating the snow depth multilinear regression model with snow course data in addition to snow depth sensor data. This recalibration was performed for each week where snow course data were available between the water years 2017 and 2019 and considering all five areas of interest. The mean value of the ratio between recalibrated snow depth maps and the original ones was then used as a multiplicative factor for the original maps to remedy for high-elevation biases. This correction was only estimated for snow-depth-sensor-based maps because preliminary assessments showed that they are the major source of bias compared to weekly SWE maps and because they are assimilated daily and, as such, play a much more important role than weekly SWE maps in driving the accuracy of Flood-PROOFS.
We focused on three evaluation exercises. First, we compared basin-wide estimated precipitation according to GRISO1 and GRISO2 with measured reconstructed streamflow, hence deriving runoff coefficients; second, we ground-truthed the peak-SWE predictions by Flood-PROOFS's snow model (S3M) which were forced using GRISO1 vs. GRISO2 against snow course data; third, we compared cumulative daily streamflow predicted by Flood-PROOFS's hydrologic model (Continuum) forced using GRISO1 vs. GRISO2 against reconstructed streamflow. The first and third evaluation exercises had a traditional water balance perspective; they determined whether estimated precipitation with and without orographic enhancement can explain annual total runoff and its seasonal patterns (both important targets for water supply forecasting). The second exercise assessed the impact of orographic precipitation enhancement on the simulation of snow storage, an intermediate prediction target between precipitation and runoff with significant implications beyond hydrology (e.g., avalanche forecasting and glacier mass balance).
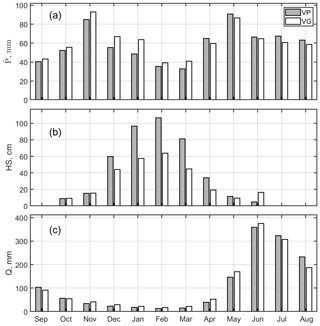
Figure 2Average monthly cumulative precipitation (a), snow depth (b), and cumulative reconstructed streamflow (c) for Beauregard and Valpelline. Precipitation was calculated across all gauges in the valleys of Beauregard and Valpelline (variable ; see gauge locations in Fig. 1). Snow depth was from two representative, mid-elevation sensors (elevation was ∼ 1860 and 1970 m a.s.l. for the snow depth sensor of Beauregard and Valpelline, respectively). Reconstructed streamflow refers to the hydropower catchments delineated in Fig. 1. The reference period used for these statistics varied from variable to variable due to data gaps (see Sect. 4.1 for details). VG and VP are Beauregard and Valpelline, respectively.
4.1 Water balance climatology
Average monthly precipitation across gauges in the valleys of Beauregard and Valpelline (variable ; in millimeters) was bimodal, with peaks in November and May (Fig. 2a; the reference period was water years 2009 through 2019 due to earlier gaps in for Beauregard, Fig. S14a). Monthly precipitation was similar between the two valleys (mean difference −2.5 ± 7.1 mm). Nonetheless, precipitation in Beauregard was up to 15 mm higher than in Valpelline during fall and winter (September to March) and up to ∼ 6 mm lower during summer (April to August), which highlighted that Beauregard may be more exposed to winter storms coming from the Mediterranean Sea, with Valpelline being more affected by summer storms from the Atlantic Ocean. This tallies with the bimodal and the summer-dominated precipitation regimes of the southern and northern sides of the Alps, respectively (Frei and Schär, 1998; Isotta et al., 2014). However, we stress that only accounts for precipitation gauges, meaning precipitation totals above the precipitation gauge line remained unaccounted for. Annual in both valleys was consistent from year to year, i.e., and mm in Valpelline and Beauregard, respectively (Figs. 3a and S14a).
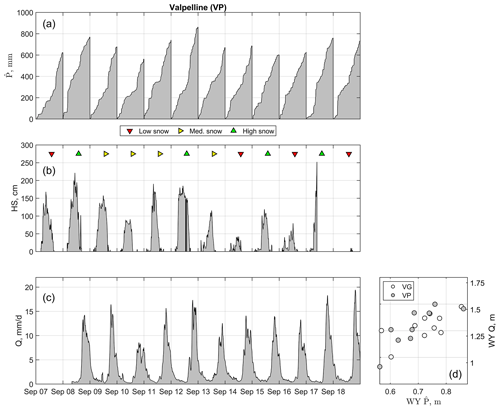
Figure 3Summary of daily precipitation (a), snow depth (b), and reconstructed streamflow (c) for Valpelline. Precipitation was calculated across all gauges in the valleys of Valpelline (variable ; see gauge locations in Fig. 1). Snow depth was from a representative, mid-elevation sensor (elevation was ∼ 1970 m a.s.l.). Reconstructed streamflow refers to the hydropower catchment delineated in Fig. 1. Low, medium, and high snow seasons were estimated based on percentiles of mean seasonal snow depth at Beauregard, which had a complete record between water years 2008 and 2019 (Fig. S14). Any water year with mean seasonal snow depth below the 33∘ percentile was classified as a low snow water year, while medium snow water years had a mean seasonal snow depth between the 66∘ and the 33∘ percentiles, and high snow water years had a mean seasonal snow depth above the 66∘ percentile. This classification is only functional with respect to the scope of this paper and has no long-term climatological implications. Note that ephemeral snow water years at these mid-elevation snow stations were not attributed to any of these classes a priori, although it is likely that ephemeral snow water years also have a low mean seasonal snow depth. (d) The estimated precipitation–runoff relationship for both hydropower catchments, where WY and WY Q are water year cumulative precipitation and reconstructed streamflow, respectively ( is systematically smaller than Q because high-elevation headwaters are ungauged).
According to the reference snow depth sensors used in Sect. 3.1 to accumulate winter precipitation, the average snow season started in October in both Beauregard and Valpelline (Fig. 2b; reference period is water years 2008 through 2017 due to later gaps in snow depth data for Valpelline; see Fig. 3b). The end-of-season date generally occurred in May, with both catchments being exposed to late snowfall events even in June. In contrast to precipitation, peak snow depth showed a remarkable interannual variability (standard deviation of maximum annual snow depth was 31 and 77 cm at Beauregard and Valpelline, respectively), with 3 of the 4 water years with shallow snowpacks occurring between 2014 and 2019 (Figs. 3b and S14b). During some of these shallow snowpack water years, the snow cover was ephemeral at these snow depth sensor sites (e.g., water year 2017 at Beauregard; Fig. S15b). Monthly snow depth at the reference sensor of Valpelline was significantly higher during winter compared to that of Beauregard (Fig. 2b), which we explain because the former is at a higher elevation than the latter (∼ 100 m).
Reconstructed streamflow in both catchments was highly seasonal, with minimum flow during winter and maximum flow in June, when precipitation, snowmelt, and ice melt overlap (Fig. 2c; reference period is water years 2008 through 2019). Monthly streamflow was similar between the two catchments (mean difference was −0.11 ± 18 mm), with the only exception being that streamflow in Beauregard was higher (up to ∼ 20 mm) between November and June and lower (up to ∼ 45 mm) between July and October than in Valpelline. This is likely connected to the average monthly precipitation in Beauregard being higher and lower during winter and summer than in Valpelline, respectively (see Fig. 2a). A second argument in favor of Beauregard and Valpelline being hydrologically similar catchments is the similarity in the precipitation–runoff relationship (Fig. 3d), that is, the fundamental rule relating annual precipitation to annual runoff (Saft et al., 2016; Avanzi et al., 2020b). Compared to precipitation climatology, reconstructed streamflow in both catchments showed comparatively large interannual variability (Figs. 3c and S14c) owing to both precipitation and climate variability.
In summary, ground-based precipitation, streamflow, and snow depth sensor data showed that water supply generation in both hydropower catchments is fundamentally cryosphere dominated. They also showed that ground-based sensor data located across low- and mid-elevations are largely insufficient for grasping the full water balance of these cryosphere-dominated headwaters, as also demonstrated by (1) annual being systematically smaller than the corresponding annual streamflow totals (Fig. 3d) and (2) peak monthly snow depth occurring in February in both catchments. While no continuous time measurement of snow depth and SWE was available above ∼ 2700 m a.s.l. (Fig. 1), general consensus in the Alps and in our experience is that SWE peaks around 1 April or later in high-elevation Alpine catchments (Marty et al., 2017).
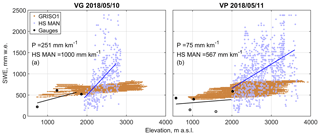
Figure 4Winter orographic gradients estimated by precipitation gauges (black dots and line) vs. those estimated by snow courses (blue dots and line; HS MAN – snow courses manual measurements) in 2018. The grayscale for precipitation gauge data points measures the amount of gaps in the time series, with black meaning a complete time series and white a time series with nearly 100 % missing data points. The brown cloud is the winter orographic gradient estimated by GRISO1, which only relied on precipitation gauges. VG and VP are Beauregard and Valpelline, respectively. Similar plots for other water years are reported in Figs. S15 to S25.
4.2 Precipitation vs. SWE orographic gradients
We report, in Fig. 4a, b, examples of precipitation gauge vs. snow course orographic gradients obtained in 2018 for Beauregard and Valpelline, respectively. At Beauregard, precipitation gauges recorded a positive, but mild, precipitation lapse rate of the order of ∼ 250 mm km−1. At Valpelline, the lapse rate recorded by precipitation gauges was even smaller at ∼ 75 mm km−1. The orographic trend recorded by gauges agreed with GRISO1 (see again Fig. 4a, b), which was expected given that GRISO1 used precipitation gauges as a starting point for the distribution of precipitation across the landscape. Snow course data, however, drew a substantially different picture from precipitation gauges, with SWE sharply increasing with elevation (Fig. 4a, b), i.e, ∼ 1000 and 567 mm w.e. km−1 in Beauregard and Valpelline, respectively. Thus, peak SWE close to (or above) 3000 m a.s.l. in 2018 was 2–3 times the total winter precipitation measured by precipitation gauges below the precipitation gauge line.
Examining all water years for which snow course surveys were available confirmed that these surveys yield much larger orographic gradients than precipitation gauges in both hydropower catchments (Figs. 5a, b, and S15 through S25, where missing panels imply that some of the information needed to perform this comparison was missing for that water year). In particular, precipitation gradients based on gauges hardly exceeded 200 mm w.e. km−1, whereas snow course gradients were often higher than 400 mm w.e. km−1 and reached values as high as 1000 mm w.e. km−1; snow-course-based gradients were particularly high at Beauregard compared to Valpelline. This sharp increase in snow accumulation with elevation was consistent across water years and was generally underestimated by both snow maps assimilated by Flood-PROOFS in proximity of the snow course surveys (Figs. 5a, b and S15 to S25); note that these independent maps do take physiography into account. This is another piece of evidence that ground-based sensor data located across low- and mid-elevations do not capture the complete range of variability in snow distribution at high elevations.
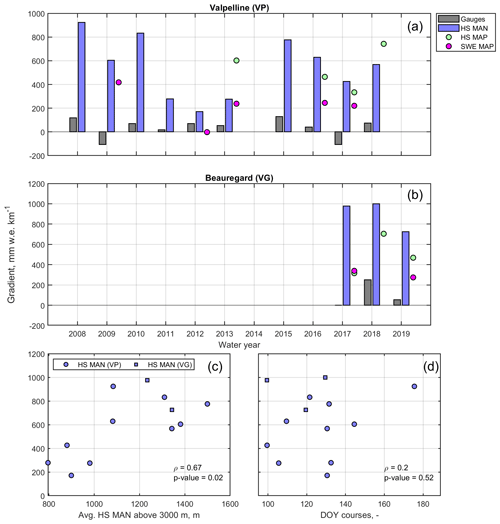
Figure 5Annual winter orographic gradients estimated by precipitation gauges, snow courses (HS MAN), and the two snow maps assimilated by Flood-PROOFS at Valpelline (a) and Beauregard (b). The HS map and SWE map are the snow depth sensor map and the SWE map, respectively. Details on Flood-PROOFS and these assimilated maps are reported in Sect. 3.3. Panels (c) and (d) show estimated orographic gradients by snow courses as a function of mean course snow depth above 3000 m a.s.l. (average HS MAN) and survey day of the year (DOY), respectively. ρ is the Pearson correlation coefficient.
Snow-course-based orographic gradients increased with average snow depth above 3000 m a.s.l. (correlation coefficient ρ=0.67; see Fig. 5c), whereas the correlation between these gradients and snow course survey date was much weaker (ρ=0.2; see Fig. 5d). Moreover, the correlation of snow course orographic gradients with average snow depth above 3000 m a.s.l. was statistically significant, while that with snow course survey date was not (p values of 0.02 and 0.52, respectively). Thus, the choice of survey date had a limited impact on the quantification of snow course orographic gradients, which suggests that these gradients may preserve themselves through time.
4.3 Orographic enhancement factors
Snow course measurements of peak SWE above 3000 m a.s.l. were between ∼ 2 and ∼ 8.5 times and between ∼ 4 and ∼ 5.5 times the winter cumulative precipitation at the lowest precipitation gauge of Valpelline and Beauregard valleys, respectively (Fig. 6). Interannual variability was significant and partially driven by the snowpack amount, with the four highest enhancement factors being associated with water years with low or medium snowpack (see again Fig. 6). However, this was not systematic, since the five lowest enhancement factors were recorded during years with mixed characteristics (two with low snowpack, one with medium snowpack, and two with high snowpack). This tallies with Fig. 5c, where only some dependency between snowpack amount and orographic gradients was found.
Contrary to snow courses, precipitation-gauge-based enhancement factors at low- and mid-elevations showed little to no orographic trends and less interannual variability. Also, they never exceeded 2, meaning that precipitation at precipitation gauge locations was (at best) twice that at the lowest measurement point in the same valley (Fig. 6). At Valpelline, a substantial number of these precipitation-gauge-based enhancement factors were even lower than 1, meaning that seasonal cumulative precipitation at intermediate elevations was often lower than that at the lowest elevation gauge in the valley. This outcome is coherent with the negative elevation trend occasionally reported in Figs. S15 to S25.
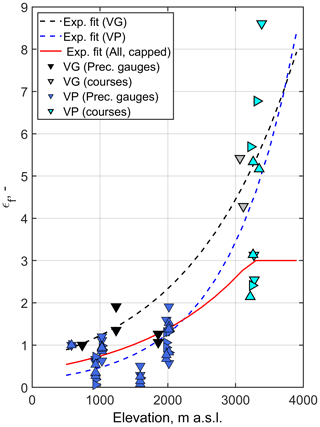
Figure 6Orographic enhancement factors ϵf for Beauregard (VG) and Valpelline (VP) across all water years as estimated using precipitation gauges (blue and black) and snow courses (gray and light blue). The dashed lines are exponential fits between orographic enhancement factors and elevation, while the red line is a capped exponential fit that was chosen to be implemented in Flood-PROOFS (Eq. 1). Details on this choice are reported in Sect. 4.3, while details on Flood-PROOFS are reported in Sect. 3. Enhancement factors are the ratio between winter cumulative precipitation measured by gauges or estimated through snow courses above 3000 m a.s.l. and precipitation measured by the lowest elevation gauge in the same valley. The orientation of the triangles relates to the classification of each water year in terms of mean snow depth (see Fig. 3).
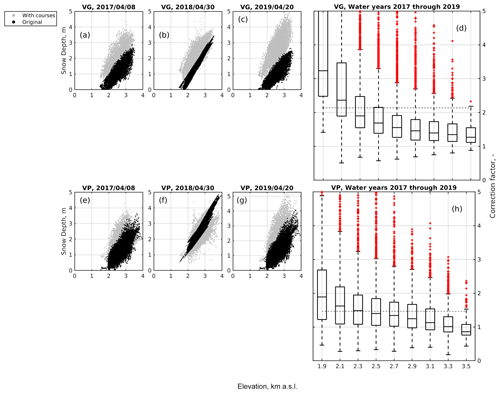
Figure 7Orographic gradients of snow depth maps derived by only using snow depth sensors vs. those derived by including high-elevation snow courses in the calibration pool (a to c for Beauregard and e to g for Valpelline). Panels (d) and (h) show the orographic trend of the ratio between maps derived by including snow courses in the calibration pool and those derived by only using snow depth sensors. VG and VP are Beauregard and Valpelline, respectively.
Deriving a single blended lapse rate from Fig. 6 was challenging owing to the remarkable interannual variability in enhancement factors, especially above 3000 m a.s.l. Several options were considered, and a first assumption was made to exclude a indefinitely exponential growth such as that depicted by the dashed lines in Fig. 6. We also assumed that enhancement factors larger than 6 were suspicious, and so we restricted the fitting pool to factors lower than 6. We finally postulated a maximum value of 3 for the fitted curve, supported by an evident cluster of snow-course-based enhancement factors from 2 to 3. While no consensus on this matter has been reached in the literature, these choices were based on scattered, but consistent, pieces of evidence showing that precipitation gradients tend to saturate at very high elevation once the bulk of orographic precipitation has been exhausted (e.g., see Alpert, 1986; Napoli et al., 2019). The resulting curve is depicted in red in Fig. 6 and follows this equation:
where ϵf is the predicted enhancement factor, z is elevation in kilometers, and ϵf is capped to 3 where Eq. (1) exceeds 3. The 95 % confidence bounds for the two parameters read (0.2857, 0.5041) and (0.5223, 0.7328), respectively, with the coefficient of determination (r2=0.44) and root mean square error (RMSE is 0.76).
Equation (1) was implemented in GRISO1 and used to correct predicted precipitation at virtual gauges above the precipitation gauge line; this spatialization procedure was then re-run to take into account orographic gradients (GRISO2; see Sect. 3.2). We stress that Eq. (1) only serves the scopes of this paper and is no definitive answer to the problem of capturing orographic gradients. More work should be dedicated to fully comprehend the large scatter in enhancement factors at high elevations and, thus, derive a more robust parameterization. Some starting points for future investigations are discussed in Sect. 5.
Snow depth maps produced by including snow course data in the calibration pool allocated, on average, more snowpack than those produced using only snow depth sensors for all elevations and all water years at Beauregard (Fig. 7a to c). At Valpelline, the map obtained by including snow courses predicted, on average, more snow in 2017 and 2019 and less snow in 2018 than the snow-depth-sensor-based map (Fig. 7e to g). On average, across all elevations and these three water years, the ratio between maps including snow courses and those using only snow depth sensors was ∼ 1.5 at Beauregard and ∼ 2.1 at Valpelline, confirming a general underestimation obtained by using snow depth sensors only. Snow-depth-sensor-based maps were multiplied by these ratios to remedy for this bias, as explained in Sect. 3.3.
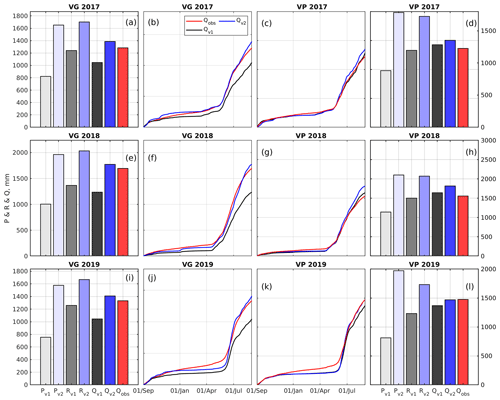
Figure 8Water balance evaluation of Flood-PROOFS simulations driven by GRISO1 vs. those driven by GRISO2.(a, e, i) A comparison at Beauregard (VG) between annual precipitation (P), equivalent precipitation (R), and streamflow (Q), according to GRISO1 and GRISO2 (v1 and v2, respectively). (d, h, l) A similar comparison at Valpelline (VP). Panels (b–c), (f–g), and (j) and (k) compare observed daily cumulative reconstructed streamflow with simulated streamflow using GRISO1 or GRISO2. Equivalent precipitation is the sum of rainfall, snowpack runoff, and glacier runoff. Simulations were carried out in full-Assim mode (see Sect. 3.3).
Note that the bias of snow depth maps was not caused by an underestimation of snow depth lapse rates, as it could be expected based on results for precipitation (e.g., Fig. 5). Instead, maps calibrated by including snow course data predicted steeper gradients than snow depth sensors only in one case out of six (water year 2019 at Beauregard). This means that the relative underestimation of snowpack storage was often larger at the lowest elevations of the considered hydropower catchments (that is, ∼ 2000 m a.s.l.) and progressively smaller at higher elevations.
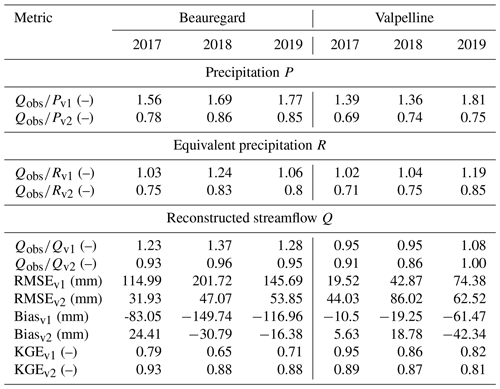
Table 2Evaluation metrics of Flood-PROOFS simulations driven by GRISO1 vs. those driven by GRISO2. The first distributed precipitation used only precipitation gauges, whereas the second included an orographic correction developed in the present study based on snow courses. Q, P, and R are annual streamflow, precipitation, and equivalent precipitation, respectively (with equivalent precipitation being the sum of rainfall, snowpack runoff, and glacier runoff). The terms obs, v1, and v2 refer to observed data and simulated data, according to GRISO1 and GRISO2, respectively. RMSE is the root mean square error, bias is simulated minus observed, and KGE is the Kling–Gupta efficiency, according to Kling et al. (2012).
4.4 Evaluation of water balance predictive accuracy
Water year cumulative precipitation obtained using only precipitation gauges (GRISO1; variable Pv1) was consistently smaller than observed water year cumulative streamflow (variable Qobs) for all water years and both hydropower catchments (Fig. 8). In particular, the ratio between Qobs and Pv1 (runoff coefficient) was between 1.56 and 1.77 at Beauregard and between 1.36 and 1.81 at Valpelline (Table 2). On the contrary, runoff coefficients, using GRISO2 as informed by blended precipitation gauge snow course lapse rates, were between 0.78 and 0.85 at Beauregard and between 0.69 and 0.75 at Valpelline (Table 2). This means that, in contrast to GRISO1, GRISO2 predicted more annual precipitation (variable Pv2) than streamflow in both catchments, which is generally expected in mountain catchments where changes in subsurface storage play a minor role in the annual water balance (see Sect. 5). Runoff coefficients using GRISO2 were also more consistent from year to year than those based on GRISO1 (Beauregard – standard deviation of 0.1 and 0.04 for GRISO1 and GRISO2, respectively; Valpelline – standard deviation of 0.25 and 0.03 for GRISO1 and GRISO2, respectively). This is a further piece of evidence that GRISO2 better captured precipitation patterns across the mountain landscape than GRISO1.
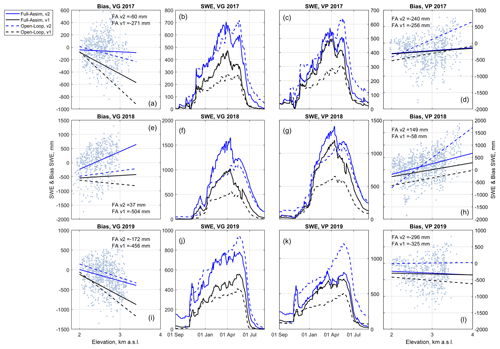
Figure 9Evaluation of Flood-PROOFS simulations of snow water equivalent (SWE) driven by GRISO1 vs. those driven by GRISO2 (v1 and v2, respectively). (a, e, i) Orographic trends of model bias with respect to snow-course-measured SWE at Beauregard (VG). (d, h, l) A similar comparison at Valpelline (VP). Panels (b–c), (f–g), and (j–k) compare simulated SWE using both GRISO1 or GRISO2. Simulations were carried out both in OL and in Full-Assim mode (see Sect. 3.3).
The underestimation of annual precipitation using GRISO1 was confirmed when looking at Full-Assim annual equivalent precipitation (Fig. 8; variable Rv1 and Rv2 for GRISO1 and GRISO2, respectively); equivalent precipitation is the sum of rainfall, snowpack runoff, and glacier runoff (see Sect. 3.3). Values of Rv1 were closer to Qobs than Pv1, with ratios of Qobs and Rv1 between 1.03 and 1.24 at Beauregard and between 1.02 and 1.19 at Valpelline (Table 2). This confirms that assimilating snow maps in Flood-PROOFS successfully compensated for S3M's conceptual uncertainty in snow distribution across the landscape (Boni et al., 2010), although some underestimation remained. Ratios between Qobs and Rv2 were, instead, consistently lower than 1 for all water years and both catchments (Table 2). Assimilating snow maps also reduced interannual variability in compared to (standard deviation of 0.11 and 0.09 at Beauregard and Valpelline, respectively), but was still much more consistent from water year to water year than (standard deviation of 0.04 and 0.07 at Beauregard and Valpelline, respectively).
Consistent with this general underestimation of incoming precipitation, simulated annual streamflow, according to GRISO1 (Qv1), was smaller than Qobs in 4 out of 6 catchment water years ( between 1.23 and 1.37 in Beauregard and between 0.95 and 1.08 in Valpelline; see Table 2). Based on visual screening of observed vs. simulated cumulative hydrographs, the unexpected overestimation of Qobs by Qv1 for 2 water years at Valpelline could be explained by an overestimation of late summer runoff, likely because of underestimated evapotranspiration or overestimated convective rainfall (Fig. 8c and g). In all other catchment water years, underestimation started from the beginning of the water year and, thus, regarded both winter baseflow and summer peaks (Fig. 8b, f, j, k). Despite those 2 water years at Valpelline with more simulated than observed streamflow, biases of Qv1 were negative for all water years and catchments and ranged from −150 to −10 mm (Table 2). This, together with the comparatively high root mean square errors (RMSEs; from ∼ 20 to ∼ 200 mm in Table 2), confirmed that Flood-PROOFS simulations forced by GRISO1 generally underestimated water supply in these catchments. Yet, Kling–Gupta efficiencies (KGEs; see Gupta et al., 2009; Kling et al., 2012) for Qv1 were consistently higher than 0.65 and, thus, well above the benchmark represented by mean flow (−0.41; see Knoben et al., 2019), which has been often regarded as an arguable threshold between “bad” and “good” model performance (Schaefli and Gupta, 2007; Knoben et al., 2019). Contrary to RMSE and biases, KGE is the composition of bias, variability, shape, and timing error terms (Santos et al., 2018), meaning that the issue with GRISO1-based simulations was really with total volume rather than with seasonal patterns.
Simulations using GRISO2 improved compared to for 4 out of 6 catchment water years (Table 2 and Fig. 8). Predictions of Qv2 also yielded smaller biases and RMSEs (as absolute values) for all water years and catchments (Table 2). The improvement of Qv2 over Qv1 was particularly evident during the late melt period (that is, from May onward), when the highest elevations in these catchments start contributing runoff (Fig. 8). Improvements during the accumulation period were much more modest, likely because streamflow generation during that period of the year is governed by processes that we did not focus on here (e.g., groundwater flow and year-round glacier runoff due to basal melt). KGE coefficients also improved in 5 out of 6 catchment water years, reaching values as high as 0.93.
Focusing on SWE, simulations of S3M using GRISO1 underestimated snow course measurements, regardless of whether an OL or a Full-Assim mode was used (Fig. 9). This underestimation was particularly significant for OL simulations, which agreed with results for precipitation vs. equivalent precipitation above (Table 2), whereas it showed no consistent trend with elevation, which is instead consistent with results in Sect. 4.3 and Fig. 7 with regard to snowpack elevation gradients being particularly elusive to capture. Biases using GRISO2 were smaller than those using GRISO1 in 5 out of 6 catchment water years (Full-Assim mode), but again, elevation trends were inconsistent (Fig. 9). Using OL simulations with GRISO2 would actually overestimate at the highest elevations in two out of six cases (2017 and 2018; Valpelline; Fig. 9d, h).
We derived two main results from this final focus on SWE. The first is an expected net improvement in predicting high-elevation SWE when snow course measurements are used in model development (especially at Beauregard). The second is that precipitation orographic gradients are highly seasonal and spatially variable and remain challenging to fully capture with a one-fits-all approach like the one we used here (e.g., Eq. 1 and Fig. 7d, h).
5.1 Main findings
Snow courses have been a frequent option for conducting snow surveys since the seminal 1910 campaign by Church (1914, 1933) at Mount Rose, Nevada (USA). Compared to stand-alone devices like snow pillows (Cox et al., 1978), courses allow operators to capture spatial variability in snow cover and derive a more representative estimate of SWE across the landscape (Malek et al., 2017). This is why courses are now a cornerstone of water supply forecasting in the western USA (Pagano et al., 2004; Harrison and Bales, 2016) and elsewhere (Metsämäki et al., 2005). In addition to their century-old role as an indicator of snow water resources, in this paper we hypothesized that snow courses could be rethought as natural precipitation gauges in the hope that they could provide new information about precipitation totals and their orographic trends at elevations that are usually ungauged. This hypothesis follows intuitions by other authors, such as Lundquist et al. (2015) or Zhang et al. (2017), who used pillow SWE and snow depth as a surrogate of precipitation, respectively. Others, such as Immerzeel et al. (2015), addressed this problem by inferring precipitation from glacier mass balances and runoff. Our novelty was to mine new information from snow courses, which provide spatial snapshots in lieu of point values.
The main findings of this paper, in this regard, are two. First, peak-season snow course SWE above 3000 m a.s.l. can be 2 to 8.5 times higher than measured winter cumulative precipitation at elevations below 2000 m a.s.l. (Fig. 6), with orographic trends that are up to 5 times those captured by the precipitation gauge network (Fig. 2). While orographic precipitation has been a target of extensive research so far (see the Introduction), extrapolating precipitation gauge signal above the precipitation gauge line still lacks solid guidelines (Ruelland, 2020). In this paper, we contributed highly needed, multiyear estimates of orographic trends across sharp altitudinal gradients.
Second, leveraging snow courses to refine the precipitation and snow depth spatialization algorithms of an operational flood forecasting chain (Flood-PROOFS) allowed for improvements in modeling accuracy, not only for SWE (Fig. 9) but, more importantly, for the whole water balance (Fig. 8). This result is encouraging given that no model recalibration was performed, and as such, we did not mix the effect of precipitation correction with other confounding factors that may lead to equifinality issues (Beven and Freer, 2001; Lundquist et al., 2015). Although the bulk of mountain river basins in the European Alps lies below 2000 m a.s.l. (Elsen et al., 2020), areas above the precipitation gauge line are a fundamental hydropower resource and represent a significant portion of higher-elevation mountain ranges, such as the Himalayas. This paper outlined opportunities to obtain more robust hydrologic predictions without necessarily investing in long recalibration efforts.
Despite these promising findings, the question of whether our blending approach (Sect. 3.1) reconstructed the true precipitation lapse rate or whether it captured other drivers of snowpack distribution at high elevations, such as wind drift or preferential deposition of snowfall, remains (Gerber et al., 2017, 2019). While both scenarios would be an argument in favor of using snow courses for informing hydrologic predictions, only the first would imply that we achieved the right answer for the right reason (Kirchner, 2006). In essence, this question points to determining whether snow course data are primarily a reflection of orographic precipitation, with other processes like wind drift or solar radiation playing a second-order role at the mountain ridge scale we investigated here.
Several hints point to our reconstruction method capturing actual orographic trends in precipitation, rather than other snow distribution processes. First, previous studies in the Alps already showed that annual mean precipitation at 1000–2000 m a.s.l. is generally up to 2 times the precipitation below 1000 m a.s.l. (Frei and Schär, 1998; Napoli et al., 2019), a mechanism that the precipitation network at Beauregard and Valpelline did not fully capture but that is consistent with our estimates of blended orographic enhancement factors (Fig. 6 and Eq. 1). Second, several previous attempts to improve estimates of hydrologic models in mountain regions through snow data assimilation alone reported inconclusive results (Tang and Lettenmaier, 2010), whereas the clear improvements in this study suggest that we did capture at last some components of orographic precipitation in addition to snow patterns. Third, we computed orographic enhancement factors by averaging snow course measurements above 3000 m a.s.l., rather than considering each of them individually, in an effort to reduce the effects of small-scale spatial variability. Fourth, values of snow course SWE at elevations close to the local precipitation gauge line (∼ 2000 m a.s.l.) are comparable to cumulative precipitation estimated by the nearest gauge (Fig. 4), which suggests that the connection between precipitation-gauge-based and snow-course-based lapse rates was smooth and realistic. Thus, we conclude that snow courses do bear a characteristic signature of precipitation orographic enhancement.
5.2 Implications
The fact that snow courses reflect orographic gradients has three main implications. First, it shows that the lack of measurements above the precipitation gauge line plays an important role in the misrepresentation of orographic gradients. Many previous papers have already reported that precipitation gauge networks tend to underestimate precipitation at high elevations, including Zhang et al. (2017) in the Sierra Nevada of California, USA, or Ruelland (2020) in the French Alps, among others. However, this misrepresentation has often been explained in combination with undercatch (Valery et al., 2009; Zhang et al., 2017; Collados-Lara et al., 2018) rather than as a peculiar effect of precipitation undersampling at high elevations (Lundquist et al., 2015; Ruelland, 2020). In fact, the magnitude of orographic enhancement inferred through snow courses (Fig. 6) was certainly larger than what could be estimated based on standard correction approaches for undercatch (see Rasmussen et al., 2012; Kochendorfer et al., 2017, and Sect. 2.2). Also, both GRISO1 and snow-depth-sensor-based maps underestimated these orographic gradients; we conclude that the main cause of this misrepresentation was the lack of data above the precipitation gauge line. Even though measuring precipitation across cryosphere-dominated headwaters is no easy task (Rasmussen et al., 2012), this paper shows that this is still an urgent priority for future research.
Second, snow courses emerge as a valuable source of information, not only to estimate snow water resources but, more generally, precipitation distribution. This role of snow courses has been at the foundation of their use as predictors of annual runoff in water supply forecasting (Hart and Gehrke, 1990; Pagano et al., 2004), but in that context, snow courses are used in a lumped way, and their orographic signature is never fully leveraged. More generally, the value of snow courses has often been overlooked in favor of temporally more dense, but also much less spatially diverse, automatic devices like snow pillows or snow depth sensors. The result is that snow courses, or other labor-intensive survey methods, are a rare feature of operational snow surveys, when they have not been discontinued already (see “The Historical Snow Survey of Great Britain” in Spencer et al., 2014). The significant variability in enhancement factors between Beauregard and Valpelline, along with the fact that snow-course-based enhancement factors were significantly larger than those based on precipitation gauges, demonstrates that collecting spatially distributed snow data is still worth the effort. Moreover, the longest snow course time series will soon approach 1 century (Huning and AghaKouchak, 2020), meaning that these courses could be used to explore orographic enhancement from a climatological standpoint. Recent advances in survey techniques, such as the Airborne Snow Observatory (Painter et al., 2016), ground-penetrating radar (Griessinger et al., 2018), unoccupied aerial vehicles (De Michele et al., 2016), or the Sentinel-1-based snow depth retrieval algorithm by Lievens et al. (2019), could also be considered as less time-consuming alternatives, with only a minor drop in accuracy – if any.
Third, correctly capturing orographic gradients matters, despite this component often being simplified in many hydrologic models (see Ruelland, 2020, and the Introduction). More specifically, our results quantified that only relying on low- to mid-elevation precipitation gauges may lead to underestimating both headwater snowpack (Fig. 9) and annual runoff (Table 2) by up to 50 % or more. This agrees with Lundquist et al. (2015), who also found errors of 50 % or more with respect to high-elevation snow pillows for specific storms, as represented by gridded precipitation data sets that only used low-elevation precipitation data. Also, our results suggest that snow (and consequently runoff) predictions benefit from a multisource framework, where both precipitation spatialization and snow assimilation protocols are involved (see again Fig. 9).
5.3 Sources of uncertainty and outlook
We made a number of assumptions that may have represented sources of potential uncertainty and, thus, opportunities for future work. First, we primarily focused on elevation gradients, since these are the most important factors driving the mountain water budget (Bales et al., 2006). Doing so was at the expense of exploring other spatial patterns, such as those driven by aspect and slope. The variability in enhancement factors between the predominantly north-facing Beauregard and the south-to-west-facing Valpelline suggests that these additional factors are important. Our results also showed significant interannual variability in enhancement factors, which somehow disagrees with the recurring finding that snow patterns are consistent from year to year (Zheng et al., 2018). Future work could focus on deriving a multivariate alternative to Eq. 1 that fully embraced physiographic features besides elevation and, in particular, aspect, slope, and canopy cover (Malek et al., 2017). For example, Vögeli et al. (2016) showed significant improvements for a spatially distributed snow model when scaling its predictions with remote sensing data. Winter climatology may also be considered as an additional predictor of orographic enhancement, e.g., in the form of predominant synoptic conditions, as done by Garavaglia et al. (2010).
Second, we neglected other drivers of snow distribution besides orographic precipitation, i.e., wind drift and its interactions with convex–concave topographic features (Winstral et al., 2013). From this standpoint, Grünewald et al. (2014), Kirchner et al. (2014), and Collados-Lara et al. (2018) showed that the elevation dependence of snow depth is nonlinear, with a peak at medium-high elevations, followed by a decline at the highest elevations because of the exhaustion of orographic precipitation effects (Napoli et al., 2019), enhanced sublimation of blowing snow, and avalanching. Our choice of spatially averaging snow course data above 3000 m a.s.l., rather than considering each data point, aimed at minimizing the impact of such local effects on our estimates of precipitation gradients. While one may consider spatially averaging snow course data across smaller elevation bands to capture such multilinear patterns, estimating such small-scale gradients based on snow courses may confound wind-driven and precipitation-driven effects, thus undermining the overarching idea of our precipitation lapse rate reconstruction method. Because our predictions of the water balance significantly improved, even by using only spatially averaged snow course data above 3000 m a.s.l., we conclude that multilinearity in lapse rates for very high elevations is likely a second-order effect in mountain hydrology when compared to orographic enhancement, at least across elevation gradients of various kilometers.
Third, we applied GRISO2 across the whole water year (September to August), although we estimated our orographic enhancement factors only with winter data. This was done both for consistency reasons, and because we expect orographic enhancement to be at play during summer too. Nonetheless, mechanisms behind summer precipitation are significantly different from those behind winter precipitation (convective vs. stratiform; see, e.g., Avanzi et al., 2015). While one may compare simulations with or without summer orographic enhancement to draw some preliminary conclusions on this matter, doing so would raise further issues. For example, would the difference between simulations be due to orographic precipitation or would it be related to how Flood-PROOFS parameterizes evapotranspiration? Would the parametrization of snowmelt infiltration and, thus, groundwater recharge also play a role? No specific data set can replace our snow courses during summer, but at the same time, the efficiency of precipitation gauges is much higher for rainfall than snowfall (Peck, 1972). Thus, measuring precipitation at elevations above 3000 m a.s.l. is much more feasible during summer than winter, which could be leveraged in the future to explore specific parameterizations of Eq. (1) for summer. Accordingly, we are considering limiting this orographic enhancement spatialization approach to winter only in the operational version of this algorithm.
Fourth, we converted snow course snow depth to SWE using one average density value for each catchment water year, with density being measured to a significantly smaller number of locations than snow depth due to logistical constraints. We expect this assumption to play a minor role in our assessment, given that snow density spatial variability is much smaller than that of snow depth (López Moreno et al., 2013). Yet, Raleigh and Small (2017) showed that snow density modeling becomes the major source of uncertainty when mapping basin‐wide SWE with lidar. This means that targeted campaigns measuring snow density variability across the landscape would still be beneficial for improving this work.
Fifth, a peak-SWE date was assessed based on expert knowledge and changed from year to year. This protocol was different from other snow course surveys, which are generally performed on recurring dates every year (Hart and Gehrke, 1990). Based on the results in Fig. 5, we expect this assumption to have little to no impact on our estimates of orographic gradients. On the other hand, changing the survey date based on when peak SWE is supposed to occur favored our work because it allowed us to assume that snow course SWE represented total winter precipitation falling at that location, and doing so with monthly courses performed on predefined dates would have been challenging.
Sixth, our assessment in Fig. 8 assumed that changes in subsurface storage were a secondary source of annual streamflow compared to precipitation, so that rather than was the desired outcome. We lack the necessary data to fully resolve the water budget of these catchments, as done in California by Avanzi et al. (2020b). Still, the interannual consistency in , based on GRISO2 together with the quasi-linearity in the precipitation–runoff relationship (Fig. 3), does suggest a clear correspondence between annual precipitation and annual runoff and, thus, that by GRISO1 was suspicious.
Seventh, we did not use any additional precipitation data set in addition to precipitation gauges (e.g., radars). Besides known issues with radars in mountain regions (see the Introduction), this was also because the present study leveraged the precipitation spatialization algorithm that is currently being maintained by the author team in Aosta Valley (Laiolo et al., 2014). Future efforts by this team include an operational deployment of GRISO2 for flood forecasting, potentially in combination with a newly developed, in-house precipitation product based on conditional merging between precipitation gauges and radar.
We addressed the recurring challenge of estimating precipitation across ungauged, high-elevation headwaters above the precipitation gauge line. We did so by hypothesizing that snow courses could be rethought as natural precipitation gauges and, thus, be leveraged to reconstruct blended precipitation gauge snow course lapse rates. We found that winter precipitation estimated through peak-SWE snow course data was 2 to 8.5 times higher than what was recorded by nearby precipitation gauges, giving evidence that orographic precipitation in this inner-Alpine valley develops with unexpectedly large orographic gradients that would be missed by using low-to-mid-elevation precipitation gauges. These gradients were also miscaptured by snow depth sensors, both because their elevation range is only slightly larger than that of precipitation gauges, and because they are installed in open and flat areas. Elevation trends of snow course data were highly seasonal, with only some correlation with mean seasonal snow depth; this revealed a feedback mechanism between orographic enhancement and winter precipitation climatology that partially challenged the generalization of our results. Blending precipitation gauge and snow course data into a unique lapse rate and using this information in an operational hydrologic modeling chain (Flood-PROOFS) allowed us to improve predictions, not just for SWE but, more importantly, also for the water budget (specifically, the interannual consistency of runoff coefficients). Snow courses bear a signature of orographic enhancement, which we successfully mined to gain insight into the process of orographic precipitation and improve real-world hydrologic models.
Sources of data used in this paper are reported in Sect. 2.2 and are derived from the Aosta Valley Regional Authority (https://cf.regione.vda.it/portale_dati.php, last access: 30 July 2020), Compagnia Valdostana delle Acque (https://www.cvaspa.it/_welcome_/, last access: 30 July 2020), and the Aosta Valley Environmental Protection Agency (http://www.arpa.vda.it/it/, last access: 30 July 2020). Flood-PROOFS is described in Laiolo et al. (2014) and is partially available at https://github.com/c-hydro (last access: 30 July 2020).
The supplement related to this article is available online at: https://doi.org/10.5194/hess-25-2109-2021-supplement.
FA, GE, and SG conceived the investigation, with contributions from all coauthors. FA and GE carried out the analyses and performed the model simulations. EC, PP, GF, and UMdC collected snow course data and prepared the SWE maps and shared general knowledge about cryospheric processes in the study catchments. SR and HS provided the weather and snow data collected by the Aosta Valley Regional Authority and shared general knowledge about hydrologic processes in the study catchments. MC and SJ provided reconstructed streamflow data and shared general knowledge about hydropower processes in the study catchments. FA, GE, SG, and EC led the interpretation of the results, with input from all coauthors. FA prepared the paper, with input from all coauthors.
The authors declare that they have no conflict of interest.
This research has been supported by the Aosta Valley Regional Administration and CVA S.p.A.
This paper was edited by Bettina Schaefli and reviewed by two anonymous referees.
Allamano, P., Claps, P., Laio, F., and Thea, C.: A data-based assesment of the dependence of short-duration precipitation on elevation, Phys. Chem. Earth, 34, 635–641, https://doi.org/10.1016/j.pce.2009.01.001, 2009. a
Allerup, P., Madsen, H., and Vejen, F.: A Comprehensive Model for Correcting Point Precipitation, Hydrol. Res., 28, 1–20, https://doi.org/10.2166/nh.1997.0001, 1997. a
Alpert, P.: Mesoscale indexing of the distribution of orographic precipitation over high mountains, J. Clim. Appl. Meteorol., 25, 532–545, https://doi.org/10.1175/1520-0450(1986)025<0532:MIOTDO>2.0.CO;2, 1986. a, b
Anders, A. M., Roe, G. H., Hallet, B., Montgomery, D. R., Finnegan, N. J., and Putkonen, J.: Spatial patterns of precipitation and topography in the Himalaya, in: Tectonics, Climate, and Landscape Evolution, Geol. Soc. Am., 398, https://doi.org/10.1130/2006.2398(03), 2006. a
Avanzi, F., De Michele, C., Ghezzi, A., Jommi, C., and Pepe, M.: A processing-modeling routine to use SNOTEL hourly data in snowpack dynamic models, Adv. Water Res., 73, 16–29, https://doi.org/10.1016/j.advwatres.2014.06.011, 2014. a, b
Avanzi, F., De Michele, C., Gabriele, S., Ghezzi, A., and Rosso, R.: Orographic Signature on Extreme Precipitation of Short Durations, J. Hydrometeorol., 16, 278–294, https://doi.org/10.1175/JHM-D-14-0063.1, 2015. a, b, c
Avanzi, F., Maurer, T., Glaser, S. D., Bales, R. C., and Conklin, M. H.: Information content of spatially distributed ground-based measurements for hydrologic-parameter calibration in mixed rain-snow mountain headwaters, J. Hydrol., 582, 124478, https://doi.org/10.1016/j.jhydrol.2019.124478, 2020a. a
Avanzi, F., Rungee, J., Maurer, T., Bales, R., Ma, Q., Glaser, S., and Conklin, M.: Climate elasticity of evapotranspiration shifts the water balance of Mediterranean climates during multi-year droughts, Hydrol. Earth Syst. Sci., 24, 4317–4337, https://doi.org/10.5194/hess-24-4317-2020, 2020b. a, b, c
Bales, R., Molotch, N. P., Painter, T. H., Dettinger, M. D., Rice, R., and Dozier, J.: Mountain hydrology of the western United States, Water Resour. Res., 42, W08432, https://doi.org/10.1029/2005WR004387, 2006. a, b
Barros, A. P. and Kuligowski, R. J.: Orographic effects during a severe wintertime rainstorm in the Appalachian mountains, Mon. Weather Rev., 126, 2648–2672, https://doi.org/10.1175/1520-0493(1998)126<2648:OEDASW>2.0.CO;2, 1997. a
Bergström, S.: The HBV model – its structure and applications., Tech. Rep., SMHI Reports Hydrology, 1992. a
Beven, K. and Freer, J.: Equifinality, data assimilation, and uncertainty estimation in mechanistic modelling of complex environmental systems using the GLUE methodology, J. Hydrol., 249, 11–29, https://doi.org/10.1016/S0022-1694(01)00421-8, 2001. a
Blanchet, J., Marty, C., and Lehning, M.: Extreme value statistics of snowfall in the Swiss Alpine region, Water Resour. Res., 45, W05424, https://doi.org/10.1029/2009WR007916, 2009. a, b
Bonacina, L. C. W.: Orographic rainfall and its place in the hydrology of the globe, Q. J. Roy. Meteor. Soc., 71, 41–55, https://doi.org/10.1002/qj.49707130705, 1945. a
Boni, G., Castelli, F., Gabellani, S., Machiavello, G., and Rudari, R.: Assimilation of MODIS snow cover and real time snow depth point data in a snow dynamic model, in: 2010 IEEE International Geoscience and Remote Sensing Symposium, 1788–1791, 2010. a, b
Buzzi, A., Tartaglione, N., and Malguzzi, P.: Numerical Simulations of the 1994 Piedmont Flood: Role of Orography and Moist Processes, Mon. Weather Rev., 126, 2369–2383, https://doi.org/10.1175/1520-0493(1998)126<2369:NSOTPF>2.0.CO;2, 1998. a
Church, J. E.: Recent studies of snow in the United States, Q. J. Roy. Meteor. Soc., 40, 43–52, https://doi.org/10.1002/qj.49704016905, 1914. a
Church, J. E.: Snow Surveying: Its Principles and Possibilities, Geogr. Rev., 23, 529–563, 1933. a
Collados-Lara, A.-J., Pardo-Igúzquiza, E., Pulido-Velazquez, D., and Jiménez-Sánchez, J.: Precipitation fields in an alpine Mediterranean catchment: Inversion of precipitation gradient with elevation or undercatch of snowfall?, Int. J. Clim., 38, 3565–3578, https://doi.org/10.1002/joc.5517, 2018. a, b
Cox, L., Bartee, L., Crook, A., Farnes, P., and Smith, J.: The care and feeding of snow pillows, in: Proceedings of the 46th Annual Western Snow Conference, 40–47, Otter Rock, Oregon, 1978. a
Cremonese, E., Filippa, G., Galvagno, M., Siniscalco, C., Oddi, L., Morra di Cella, U., and Migliavacca, M.: Heat wave hinders green wave: The impact of climate extreme on the phenology of a mountain grassland, Agr. Forest Meteorol., 247, 320–330, https://doi.org/10.1016/j.agrformet.2017.08.016, 2017. a
Crespi, A., Brunetti, M., Lentini, G., and Maugeri, M.: 1961–1990 high-resolution monthly precipitation climatologies for Italy, Int. J. Clim., 38, 878–895, https://doi.org/10.1002/joc.5217, 2018. a
Da Ronco, P., Avanzi, F., De Michele, C., Notarnicola, C., and Schaefli, B.: Comparing MODIS snow products Collection 5 with Collection 6 over Italian Central Apennines, Int. J. Remote Sens., 41, 4174–4205, https://doi.org/10.1080/01431161.2020.1714778, 2020. a
Daly, C., Halbleib, M., Smith, J. I., Gibson, W. P., Doggett, M. K., Taylor, G. H., Curtis, J., and Pasteris, P. P.: Physiographically sensitive mapping of climatological temperature and precipitation across the conterminous United States, Int. J. Clim., 28, 2031–2064, https://doi.org/10.1002/joc.1688, 2008. a, b, c
De Michele, C., Avanzi, F., Passoni, D., Barzaghi, R., Pinto, L., Dosso, P., Ghezzi, A., Gianatti, R., and Della Vedova, G.: Using a fixed-wing UAS to map snow depth distribution: an evaluation at peak accumulation, The Cryosphere, 10, 511–522, https://doi.org/10.5194/tc-10-511-2016, 2016. a
Elsen, P. R., Monahan, W. B., and Merenlender, A. M.: Topography and human pressure in mountain ranges alter expected species responses to climate change, Nat. Commun., 11, 1–10, 2020. a
Foehn, A., Hernández, J. G., Schaefli, B., and Cesare, G. D.: Spatial interpolation of precipitation from multiple rain gauge networks and weather radar data for operational applications in Alpine catchments, J. Hydrol., 563, 1092–1110, https://doi.org/10.1016/j.jhydrol.2018.05.027, 2018. a
Frei, C. and Isotta, F. A.: Ensemble Spatial Precipitation Analysis From Rain Gauge Data: Methodology and Application in the European Alps, J. Geophys. Res.-Atmos., 124, 5757–5778, https://doi.org/10.1029/2018JD030004, 2019. a, b
Frei, C. and Schär, C.: A precipitation climatology of the Alps from high-resolution rain-gauge observations, Int. J. Clim., 18, 873–900, https://doi.org/10.1002/(SICI)1097-0088(19980630)18:8<873::AID-JOC255>3.0.CO;2-9, 1998. a, b, c, d
Galewsky, J.: Rain shadow development during the growth of mountain ranges: An atmospheric dynamics perspective, J. Geophys. Res.-Earth, 114, https://doi.org/10.1029/2008JF001085, 2009. a
Galewsky, J. and Sobel, A.: Moist Dynamics and Orographic Precipitation in Northern and Central California during the New Year’s Flood of 1997, Mon. Weather Rev., 133, 1594–1612, https://doi.org/10.1175/MWR2943.1, 2005. a
Garavaglia, F., Gailhard, J., Paquet, E., Lang, M., Garçon, R., and Bernardara, P.: Introducing a rainfall compound distribution model based on weather patterns sub-sampling, Hydrol. Earth Syst. Sci., 14, 951–964, https://doi.org/10.5194/hess-14-951-2010, 2010. a
Gerber, F., Lehning, M., Hoch, S. W., and Mott, R.: A close-ridge small-scale atmospheric flow field and its influence on snow accumulation, J. Geophys. Res.-Atmos., 122, 7737–7754, https://doi.org/10.1002/2016JD026258, 2017. a, b
Gerber, F., Mott, R., and Lehning, M.: The Importance of Near-Surface Winter Precipitation Processes in Complex Alpine Terrain, J. Hydrometeorol., 20, 177–196, https://doi.org/10.1175/JHM-D-18-0055.1, 2019. a, b
Germann, U., Galli, G., Boscacci, M., and Bolliger, M.: Radar precipitation measurement in a mountainous region, Q. J. Roy. Meteor. Soc., 132, 1669–1692, https://doi.org/10.1256/qj.05.190, 2006. a
Giorgi, F., Torma, C., Coppola, E., Ban, N., Schär, C., and Somot, S.: Enhanced summer convective rainfall at Alpine high elevations in response to climate warming, Nat. Geosci., 9, 584–589, 2016. a
Griessinger, N., Mohr, F., and Jonas, T.: Measuring snow ablation rates in alpine terrain with a mobile multioffset ground-penetrating radar system, Hydrol. Proc., 32, 3272–3282, https://doi.org/10.1002/hyp.13259, 2018. a
Grünewald, T., Bühler, Y., and Lehning, M.: Elevation dependency of mountain snow depth, The Cryosphere, 8, 2381–2394, https://doi.org/10.5194/tc-8-2381-2014, 2014. a
Gupta, H. V., Kling, H., Yilmaz, K. K., and Martinez, G. F.: Decomposition of the mean squared error and NSE performance criteria: Implications for improving hydrological modelling, J. Hydrol., 377, 80–91, https://doi.org/10.1016/j.jhydrol.2009.08.003, 2009. a
Hantel, M., Maurer, C., and Mayer, D.: The snowline climate of the Alps 1961–2010, Theoretical and Applied Climatology, 110, 517–537, 2012. a
Harpold, A. A., Kaplan, M. L., Klos, P. Z., Link, T., McNamara, J. P., Rajagopal, S., Schumer, R., and Steele, C. M.: Rain or snow: hydrologic processes, observations, prediction, and research needs, Hydrol. Earth Syst. Sci., 21, 1–22, https://doi.org/10.5194/hess-21-1-2017, 2017. a
Harrison, B. and Bales, R.: Skill Assessment of Water Supply Forecasts for Western Sierra Nevada Watersheds, J. Hydrol. Eng., 21, 04016002, https://doi.org/10.1061/(ASCE)HE.1943-5584.0001327, 2016. a, b
Hart, D. and Gehrke, F.: Status of the California cooperative snow survey program, in: Proceedings of the 58th Annual Western Snow Conference, Sacramento, California, 9–14, 1990. a, b, c
Houston, J. and Hartley, A. J.: The central Andean west-slope rainshadow and its potential contribution to the origin of hyper-aridity in the Atacama Desert, Int. J. Clim., 23, 1453–1464, https://doi.org/10.1002/joc.938, 2003. a
Huning, L. S. and AghaKouchak, A.: Approaching 80 years of snow water equivalent information by merging different data streams, Sci. Data, 7, 1–11, 2020. a
Immerzeel, W. W., Wanders, N., Lutz, A. F., Shea, J. M., and Bierkens, M. F. P.: Reconciling high-altitude precipitation in the upper Indus basin with glacier mass balances and runoff, Hydrol. Earth Syst. Sci., 19, 4673–4687, https://doi.org/10.5194/hess-19-4673-2015, 2015. a
Isotta, F. A., Frei, C., Weilguni, V., Perčec Tadić, M., Lassègues, P., Rudolf, B., Pavan, V., Cacciamani, C., Antolini, G., Ratto, S. M., Munari, M., Micheletti, S., Bonati, V., Lussana, C., Ronchi, C., Panettieri, E., Marigo, G., and Vertačnik, G.: The climate of daily precipitation in the Alps: development and analysis of a high-resolution grid dataset from pan-Alpine rain-gauge data, Int. J. Clim., 34, 1657–1675, https://doi.org/10.1002/joc.3794, 2014. a, b, c
Jiang, Q.: Moist dynamics and orographic precipitation, Tellus A, 55, 301–316, https://doi.org/10.1034/j.1600-0870.2003.00025.x, 2003. a
Jost, G., Dan Moore, R., Weiler, M., Gluns, D. R., and Alila, Y.: Use of distributed snow measurements to test and improve a snowmelt model for predicting the effect of forest clear-cutting, J. Hydrol., 376, 94–106, https://doi.org/10.1016/j.jhydrol.2009.07.017, 2009. a
Kirchner, J. W.: Getting the right answers for the right reasons: Linking measurements, analyses, and models to advance the science of hydrology, Water Resour. Res., 42, https://doi.org/10.1029/2005WR004362, 2006. a
Kirchner, P. B., Bales, R. C., Molotch, N. P., Flanagan, J., and Guo, Q.: LiDAR measurement of seasonal snow accumulation along an elevation gradient in the southern Sierra Nevada, California, Hydrol. Earth Syst. Sci., 18, 4261–4275, https://doi.org/10.5194/hess-18-4261-2014, 2014. a
Kling, H., Fuchs, M., and Paulin, M.: Runoff conditions in the upper Danube basin under an ensemble of climate change scenarios, J. Hydrol., 424, 264–277, https://doi.org/10.1016/j.jhydrol.2012.01.011, 2012. a, b
Knoben, W. J. M., Freer, J. E., and Woods, R. A.: Technical note: Inherent benchmark or not? Comparing Nash–Sutcliffe and Kling–Gupta efficiency scores, Hydrol. Earth Syst. Sci., 23, 4323–4331, https://doi.org/10.5194/hess-23-4323-2019, 2019. a, b
Kochendorfer, J., Rasmussen, R., Wolff, M., Baker, B., Hall, M. E., Meyers, T., Landolt, S., Jachcik, A., Isaksen, K., Brækkan, R., and Leeper, R.: The quantification and correction of wind-induced precipitation measurement errors, Hydrol. Earth Syst. Sci., 21, 1973–1989, https://doi.org/10.5194/hess-21-1973-2017, 2017. a
Laiolo, P., Gabellani, S., Rebora, N., Rudari, R., Ferraris, L., Ratto, S., Stevenin, H., and Cauduro, M.: Validation of the Flood-PROOFS probabilistic forecasting system, Hydrol. Proc., 28, 3466–3481, https://doi.org/10.1002/hyp.9888, 2014. a, b, c, d, e
Lievens, H., Demuzere, M., Marshall, H.-P., Reichle, R. H., Brucker, L., Brangers, I., de Rosnay, P., Dumont, M., Girotto, M., Immerzeel, W. W., et al.: Snow depth variability in the Northern Hemisphere mountains observed from space, Nat. Commun,, 10, 1–12, 2019. a
López Moreno, J. I., Fassnacht, S. R., Heath, J. T., Musselman, K. N., Revuelto, J., Latron, J., Móran-Tejeda, E., and Jonas, T.: Small scale spatial variability of snow density and depth over complex alpine terrain: Implications for estimating snow water equivalent, Adv. Water Res., 55, 40–52, 2013. a
Lundberg, A. and Koivusalo, H.: Estimating winter evaporation in boreal forests with operational snow course data, Hydrol. Proc., 17, 1479–1493, https://doi.org/10.1002/hyp.1179, 2003. a
Lundquist, J. D., Dickerson-Lange, S. E., Lutz, J. A., and Cristea, N. C.: Lower forest density enhances snow retention in regions with warmer winters: A global framework developed from plot-scale observations and modeling, Water Resour. Res., 49, 6356–6370, https://doi.org/10.1002/wrcr.20504, 2013. a
Lundquist, J. D., Hughes, M., Henn, B., Gutmann, E. D., Livneh, B., Dozier, J., and Neiman, P.: High-Elevation Precipitation Patterns: Using Snow Measurements to Assess Daily Gridded Datasets across the Sierra Nevada, California*, J. Hydrometeorol., 16, 1773–1792, https://doi.org/10.1175/JHM-D-15-0019.1, 2015. a, b, c, d
Malek, S. A., Avanzi, F., Brun-Laguna, K., Maurer, T., Oroza, C. A., Hartsough, P. C., Watteyne, T., and Glaser, S. D.: Real-Time Alpine Measurement System Using Wireless Sensor Networks, Sensors, 17, https://doi.org/10.3390/s17112583, 2017. a, b, c
Margulis, S. A., Cortés, G., Girotto, M., and Durand, M.: A Landsat-Era Sierra Nevada Snow Reanalysis (1985-2015), J. Hydrometeorol., 17, 1203–1221, https://doi.org/10.1175/JHM-D-15-0177.1, 2016. a
Markstrom, S. L., Regan, R. S., Hay, L. E., Viger, R. J., Webb, R. M., Payn, R. A., and LaFontaine, J. H.: PRMS-IV, the Precipitation-Runoff Modeling System, Version 4, Tech. Rep., U.S. Geological Survey Techniques and Methods, https://doi.org/10.3133/tm6B7, 2015. a
Marra, F., Armon, M., Borga, M., and Morin, E.: Orographic effect on extreme precipitation statistics peaks at hourly time scales, Geophys. Res. Lett., 48, e2020GL091498, https://doi.org/10.1029/2020GL091498, 2021. a
Marty, C., Tilg, A.-M., and Jonas, T.: Recent Evidence of Large-Scale Receding Snow Water Equivalents in the European Alps, J. Hydrometeorol., 18, 1021–1031, https://doi.org/10.1175/JHM-D-16-0188.1, 2017. a
Metsämäki, S. J., Anttila, S. T., Markus, H. J., and Vepsäläinen, J. M.: A feasible method for fractional snow cover mapping in boreal zone based on a reflectance model, Remote Sens. Environ., 95, 77–95, https://doi.org/10.1016/j.rse.2004.11.013, 2005. a, b
Michalet, R., Rolland, C., Joud, D., Gafta, D., and Callaway, R.: Associations between canopy and understory species increase along a rainshadow gradient in the Alps: habitat heterogeneity or facilitation?, Plant Ecol., 165, 145–160, 2003. a
Mott, R., Scipión, D., Schneebeli, M., Dawes, N., and Lehning, M.: Orographic effects on snow deposition patterns in mountainous terrain, J. Geophys. Res., 119, 1419–1439, https://doi.org/10.1002/2013JD019880, 2014. a
Napoli, A., Crespi, A., Ragone, F., Maugeri, M., and Pasquero, C.: Variability of orographic enhancement of precipitation in the Alpine region, Sci. Rep., 9, 1–8, https://doi.org/10.1038/s41598-019-49974-5, 2019. a, b, c, d, e
Nitu, R., Roulet, Y.-A., Wolff, M., Earle, M., Reverdin, A., Smith, C., Kochendorfer, J., Morin, S., Rasmussen, R., Wong, K., Alastrué, J., Arnold, L., Baker, B., Buisán, S., Collado, J., Colli, M., Collins, B., Gaydos, A., Hannula, H.-R., Hoover, J., Joe, P., Kontu, A., Laine, T., Lanza, L., Lanzinger, E., Lee, G., Lejeune, Y., Leppänen, L., Mekis, E., Panel, J.-M., Poikonen, A., Ryu, S., Sabatini, F., Theriault, J., Yang, D., Genthon, C., van den Heuvel, F., Hirasawa, N., Konishi, H., Motoyoshi, H., Nakai, S., Nishimura, K., Senese, A., and Yamashita, K.: WMO Solid Precipitation Intercomparison Experiment (SPICE), Tech. Rep., World Meteorological Organization, 2018. a
Pagano, T., Garen, D., and Sorooshian, S.: Evaluation of Official Western U.S. Seasonal Water Supply Outlooks, 1922-2002, J. Hydrometeorol., 5, 896–909, https://doi.org/10.1175/1525-7541(2004)005<0896:EOOWUS>2.0.CO;2, 2004. a, b, c, d
Painter, T. H., Berisford, D. F., Boardman, J. W., Bormann, K. J., Deems, J. S., Gehrke, F., Hedrick, A., Joyce, M., Laidlaw, R., Marks, D., Mattmann, C., McGurk, B., Ramirez, P., Richardson, M., Skiles, S. M., Seidel, F. C., and Winstral, A.: The Airborne Snow Observatory: Fusion of scanning lidar, imaging spectrometer, and physically-based modeling for mapping snow water equivalent and snow albedo, Remote Sens. Environ., 184, 139–152, https://doi.org/10.1016/j.rse.2016.06.018, 2016. a
Panziera, L., James, C. N., and Germann, U.: Mesoscale organization and structure of orographic precipitation producing flash floods in the Lago Maggiore region, Q. J. Roy. Meteor. Soc., 141, 224–248, https://doi.org/10.1002/qj.2351, 2015. a
Patro, E. R., De Michele, C., and Avanzi, F.: Future perspectives of run-of-the-river hydropower and the impact of glaciers’ shrinkage: The case of Italian Alps, Appl. Energ., 231, 699–713, https://doi.org/10.1016/j.apenergy.2018.09.063, 2018. a
Peck, E. L.: Snow measurement predicament, Water Resour. Res., 8, 244–248, 1972. a
Pignone, F., Rebora, N., Silvestro, F., , and Castelli, F.: GRISO (Generatore Random di Interpolazioni Spaziali da Osservazioni incerte) – Piogge, Tech. Rep., 2010. a
Poschlod, P.: The origin and development of the central European man-made landscape, habitat and species diversity as affected by climate and its changes – a review, Interdisciplinaria Archaeologica, Natural Sciences in Archaeology, 6, 197–221, 2015. a
Puca, S., Porcu, F., Rinollo, A., Vulpiani, G., Baguis, P., Balabanova, S., Campione, E., Ertürk, A., Gabellani, S., Iwanski, R., Jurašek, M., Kaňák, J., Kerényi, J., Koshinchanov, G., Kozinarova, G., Krahe, P., Lapeta, B., Lábó, E., Milani, L., Okon, L'., Öztopal, A., Pagliara, P., Pignone, F., Rachimow, C., Rebora, N., Roulin, E., Sönmez, I., Toniazzo, A., Biron, D., Casella, D., Cattani, E., Dietrich, S., Di Paola, F., Laviola, S., Levizzani, V., Melfi, D., Mugnai, A., Panegrossi, G., Petracca, M., Sanò, P., Zauli, F., Rosci, P., De Leonibus, L., Agosta, E., and Gattari, F.: The validation service of the hydrological SAF geostationary and polar satellite precipitation products, Nat. Hazards Earth Syst. Sci., 14, 871–889, https://doi.org/10.5194/nhess-14-871-2014, 2014. a
Raleigh, M. S. and Small, E. E.: Snowpack density modeling is the primary source of uncertainty when mapping basin-wide SWE with lidar, Geophys. Res. Lett., 44, 3700–3709, https://doi.org/10.1002/2016GL071999, 2017. a
Rasmussen, R., Baker, B., Kochendorfer, J., Meyers, T., Landolt, S., Fischer, A. P., Black, J., Thériault, J. M., Kucera, P., Gochis, D., Smith, C., Nitu, R., Hall, M., Ikeda, K., and Gutmann, E.: How Well Are We Measuring Snow: The NOAA/FAA/NCAR Winter Precipitation Test Bed, B. Am. Meteorol. Soc., 93, 811–829, https://doi.org/10.1175/BAMS-D-11-00052.1, 2012. a, b, c
Rebora, N., Ferraris, L., von Hardenberg, J., and Provenzale, A.: RainFARM: Rainfall Downscaling by a Filtered Autoregressive Model, J. Hydrometeorol., 7, 724–738, https://doi.org/10.1175/JHM517.1, 2006. a
Rice, R. and Bales, R. C.: Embedded-sensor network design for snow cover measurements around snow pillow and snow course sites in the Sierra Nevada of California, Water Resour. Res., 46, W03537, https://doi.org/10.1029/2008WR007318, 2010. a
Roe, G. H.: Orographic Precipitation, Annu. Rev. Earth Planet. Sci., 33, 645–671, https://doi.org/10.1146/annurev.earth.33.092203.122541, 2005. a, b, c, d, e
Rotunno, R. and Houze, R. A.: Lessons on orographic precipitation from the Mesoscale Alpine Programme, Q. J. Roy. Meteor. Soc., 133, 811–830, https://doi.org/10.1002/qj.67, 2007. a, b
Ruelland, D.: Should altitudinal gradients of temperature and precipitation inputs be inferred from key parameters in snow-hydrological models?, Hydrol. Earth Syst. Sci., 24, 2609–2632, https://doi.org/10.5194/hess-24-2609-2020, 2020. a, b, c, d, e
Ryan, W. A., Doesken, N. J., and Fassnacht, S. R.: Evaluation of Ultrasonic Snow Depth Sensors for U.S. Snow Measurements, J. Atmos. Ocean. Tech., 25, 667–684, https://doi.org/10.1175/2007JTECHA947.1, 2008. a
Saft, M., Peel, M. C., Western, A. W., and Zhang, L.: Predicting shifts in rainfall-runoff partitioning during multiyear drought: Roles of dry period and catchment characteristics, Water Resour. Res., 52, 9290–9305, https://doi.org/10.1002/2016WR019525, 2016. a
Santos, L., Thirel, G., and Perrin, C.: Technical note: Pitfalls in using log-transformed flows within the KGE criterion, Hydrol. Earth Syst. Sci., 22, 4583–4591, https://doi.org/10.5194/hess-22-4583-2018, 2018. a
Sarker, R. P.: A dynamical model of orographic rainfall, Mon. Weather Rev., 94, 555–572, https://doi.org/10.1175/1520-0493(1966)094<0555:ADMOOR>2.3.CO;2, 1966. a
Sarmadi, F., Huang, Y., Thompson, G., Siems, S. T., and Manton, M. J.: Simulations of orographic precipitation in the Snowy Mountains of Southeastern Australia, Atmos. Res., 219, 183–199, https://doi.org/10.1016/j.atmosres.2019.01.002, 2019. a
Schaefli, B. and Gupta, H.: Do Nash values have value?, Hydrol. Proc., 21, 2075–2080, https://doi.org/10.1002/hyp.6825, 2007. a
Serreze, M. C., Clark, M. P., Armstrong, R. L., McGinnis, D. A., and Pulwarty, R. S.: Characteristics of the western United States snowpack from snowpack telemetry (SNOTEL) data, Water Resour. Res., 35, 2145–2160, https://doi.org/10.1029/1999WR900090, 1999. a
Silvestro, F., Gabellani, S., Delogu, F., Rudari, R., and Boni, G.: Exploiting remote sensing land surface temperature in distributed hydrological modelling: the example of the Continuum model, Hydrol. Earth Syst. Sci., 17, 39–62, https://doi.org/10.5194/hess-17-39-2013, 2013. a, b
Skaugen, T., Stranden, H. B., and Saloranta, T.: Trends in snow water equivalent in Norway (1931–2009), Hydrol. Res., 43, 489–499, https://doi.org/10.2166/nh.2012.109, 2012. a
Smiraglia, C., AzzONI, R. S., D’Agata, C., Maragno, D., Fugazza, D., Diolaiuti, G. A., et al.: The evolution of the Italian glaciers from the previous data base to the New Italian Inventory. Preliminary considerations and results, Geografia Fisica e Dinamica Quaternaria, 38, 79–87, 2015. a
Smith, R. B.: Progress on the theory of orographic precipitation, Tech. Rep. 398, Geological Society of America, https://doi.org/10.1130/2006.2398(01), 2006. a
Smith, R. B. and Barstad, I.: A linear theory of orographic precipitation, J. Atmos. Sci., 61, 1377–1391, https://doi.org/10.1175/1520-0469(2004)061<1377:ALTOOP>2.0.CO;2, 2004. a
Spencer, M., Essery, R., Chambers, L., and Hogg, S.: The historical snow survey of Great Britain: digitised data for Scotland, Scottish Geographical Journal, 130, 252–265, 2014. a
Sturm, M., Holmgren, J., and Liston, G. E.: A seasonal snow cover classification system for local to global applications, J. Climate, 8, 1261–1283, 1995. a
Tang, Q. and Lettenmaier, D. P.: Use of satellite snow-cover data for streamflow prediction in the Feather River Basin, California, International J. Remote Sens., 31, 3745–3762, https://doi.org/10.1080/01431161.2010.483493, 2010. a
Valery, A., Andréassian, V., Perrin, C., et al.: Inverting the hydrological cycle: when streamflow measurements help assess altitudinal precipitation gradients in mountain areas, Iahs Publ, 333, 281–286, 2009. a
Viale, M. and Nuñez, M. N.: Climatology of Winter Orographic Precipitation over the Subtropical Central Andes and Associated Synoptic and Regional Characteristics, J. Hydrometeorol., 12, 481–507, https://doi.org/10.1175/2010JHM1284.1, 2011. a
Viviroli, D., Gurtz, J., and Zappa, M.: The Hydrological Modelling System PREVAH, Tech. rep., Geographica Bernensia P40, Berne: Institute of Geography, University of Berne, 2007a. a
Viviroli, D., Messerli, H. H. D. B., Meybeck, M., and Weingartner, R.: Mountains of the world, water towers for humanity: Typology, mapping, and global significance, Water Resour. Res., 43, W07447, https://doi.org/10.1029/2006WR005653 2007b. a, b
Vögeli, C., Lehning, M., Wever, N., and Bavay, M.: Scaling Precipitation Input to Spatially Distributed Hydrological Models by Measured Snow Distribution, Front. Earth Sci., 4, 108, https://doi.org/10.3389/feart.2016.00108, 2016. a
Winstral, A., Marks, D., and Gurney, R.: Simulating wind-affected snow accumulations at catchment to basin scales, Adv. Water Res., 55, 64–79, https://doi.org/10.1016/j.advwatres.2012.08.011, 2013. a, b
Zhang, Z., Glaser, S., Bales, R., Conklin, M., Rice, R., and Marks, D.: Insights into mountain precipitation and snowpack from a basin-scale wireless‐sensor network, Water Resour. Res., 53, 6626–6641, https://doi.org/10.1002/2016WR018825, 2017. a, b, c, d
Zheng, Z., Molotch, N. P., Oroza, C. A., Conklin, M. H., and Bales, R. C.: Spatial snow water equivalent estimation for mountainous areas using wireless-sensor networks and remote-sensing products, Remote Sens. Environ., 215, 44–56, https://doi.org/10.1016/j.rse.2018.05.029, 2018. a





