the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
A universal multifractal approach to assessment of spatiotemporal extreme precipitation over the Loess Plateau of China
Jianjun Zhang
Guangyao Gao
Bojie Fu
Cong Wang
Hoshin V. Gupta
Xiaoping Zhang
Rui Li
Extreme precipitation (EP) is a major external agent driving various natural hazards in the Loess Plateau (LP), China. However, the characteristics of the spatiotemporal EP responsible for such hazardous situations remain poorly understood. We integrate universal multifractals with a segmentation algorithm to characterize a physically meaningful threshold for EP (EPT). Using daily data from 1961 to 2015, we investigate the spatiotemporal variation of EP over the LP. Our results indicate that (with precipitation increasing) EPTs range from 17.3 to 50.3 mm d−1, while the mean annual EP increases from 35 to 138 mm from the northwestern to the southeastern LP. Further, historically, the EP frequency (EPF) has spatially varied from 54 to 116 d, with the highest EPF occurring in the mid-southern and southeastern LP where precipitation is much more abundant. However, EP intensities tend to be strongest in the central LP, where precipitation also tends to be scarce, and get progressively weaker as we move towards the margins (similarly to EP severity). An examination of atmospheric circulation patterns indicates that the central LP is the inland boundary with respect to the reach and impact of tropical cyclones in China, resulting in the highest EP intensities and EP severities being observed in this area. Under the control of the East Asian monsoon, precipitation from June to September accounts for 72 % of the total amount, and 91 % of the total EP events are concentrated between June and August. Further, EP events occur, on average, 11 d earlier than the wettest part of the season. These phenomena are responsible for the most serious natural hazards in the LP, especially in the central LP region. Spatiotemporally, 91.4 % of the LP has experienced a downward trend in precipitation, whereas 62.1 % of the area has experienced upward trends in the EP indices, indicating the potential risk of more serious hazardous situations. The universal multifractal approach considers the physical processes and probability distribution of precipitation, thereby providing a formal framework for spatiotemporal EP assessment at the regional scale.
- Article
(12761 KB) - Full-text XML
- BibTeX
- EndNote
Extreme precipitation (EP) is the dominant external agent driving processes such as floods, erosion, and debris flow, which have adverse impacts on human life, the social economy, the natural environment, and ecosystems (Min et al., 2011; Pecl et al., 2017; Walther et al., 2002). These impacts are especially severe in arid and semiarid areas because of the sparsity of vegetation and the fragility of the eco-environment (Bao et al., 2017; Huang et al., 2016). In recent decades, worldwide climate change has given rise to spatially heterogeneous changes in the EP regime (Donat et al., 2016; Manola et al., 2018; Zheng et al., 2015). Such uneven changes in EP have the potential to aggravate adverse impacts on human life and the eco-environment; consequently, EP has recently received increased attention (Eekhout et al., 2018; Li et al., 2017; Wang et al., 2017). In this regard, there is a fundamental need to evaluate the regional spatiotemporal variation of EP, thereby providing important information that is crucial for natural resource management and sustainable social development.
The Loess Plateau (LP), which is located in the middle reaches of the Yellow River, is a typical arid and semiarid region, characterized by serious EP-induced natural hazards, including soil erosion and consequent hyperconcentrated flooding and occasional landslides (Cai, 2001). In the LP area, EP-induced soil erosion generates some of the highest sediment yields observed on Earth, ranging from 3×104 to 4×104 t km−2 yr−1. For example, sediment delivered to the Yellow River in recent decades has been estimated to be 16×108 t yr−1 (Ran et al., 2000; Tang, 2004), and sediment deposition has resulted in the river bed of the lower Yellow River aggrading by 8–10 m above the surrounding floodplain (Shi and Shao, 2000). As the river flows on the aggraded thalweg, the extreme-precipitation-driven hyperconcentrated floodwaters cause the lower Yellow River to burst its channel. Over the past 2500 years, this has caused 1593 floods and 26 changes to the course of the river channel, leading to unimaginable death and devastation (Ren, 2006; Tang, 2004). To control such EP-induced natural hazards, ecological restoration projects have been implemented over the LP. For example, the “Grain for Green” project (the largest investment project in China) was implemented to control natural hazards, such as soil erosion and flooding, and has cost more than USD 75 billion over the past 20 years.
Accordingly, a better understanding of spatiotemporal EP changes in this area is of considerable interest for various fields, such as risk estimation, land management, flood control, and infrastructure planning (Feng et al., 2016; Wang et al., 2015). Considerable past work has been devoted to investigating the spatiotemporal variation of total precipitation and precipitation extremes in this region, with a consensus obtained with respect to precipitation “amount” (Li et al., 2010a, b; Miao et al., 2016; Wan et al., 2014; Xin et al., 2009). However, the spatial distribution of EP in the LP is still poorly understood, with considerable disagreement regarding EP and the inability to account for the spatial distribution of EP-induced hazards such as soil erosion (Li et al., 2010a, b; Miao et al., 2016; Wan et al., 2014; Xin et al., 2009). Thus, it is important to account for the spatiotemporal role of EP in natural hazards in order to facilitate better catchment management with respect to issues such as freshwater shortage (Feng et al., 2012).
To understand spatiotemporal variations in EP, scientists are often required to collect more detailed data, including maximum depth, duration, and area observations (Dulière et al., 2011; Herold et al., 2017; Miao et al., 2016). Despite sophisticated methodologies, such efforts rely on data from various sources, which are typically absent in the long-term historical observational records, especially over large areas. Therefore, any investigation of spatiotemporal variation in EP must make use of the information in the available historical data that were observed at fixed time intervals (e.g., daily). In EP assessment using historical daily data, it is a crucial step to identify EP events by extreme precipitation threshold (EPT) determination. However, EP events tend to be relatively rare, unpredictable, and often short-lived (Liu et al., 2013); this uncertainty, combined with varying geographical and meteorological conditions, increases the complexity of EP assessment.
In general, existing methods for EPT determination can be grouped into two categories: nonparametric and parametric. Nonparametric methods use fixed critical values or percentiles to define the thresholds for extreme events. Because the corresponding classification of EPTs varies from region to region (e.g., a 50 mm daily precipitation event is considered normal in South China but would be an EP event in the LP), the application of nonparametric methods can require considerable subjectivity (Liu et al., 2013) and significantly affect the results of the analysis. For instance, using an absolute value of 50 mm d−1, Xin et al. (2009) reported a spatiotemporal decreasing zone of EP in the central eastern LP, whereas, using the 95 % percentile to determine EP, Li et al. (2010a, b) found an increasing trend in the EP frequency in the southeastern LP. However, these reports did not explain the rational for the spatial variation in EP and its impacts on the most serious soil erosion in the central LP.
Parametric statistical methods based on empirical distributions have recently become popular. A variety of special distribution functions and parameter estimation techniques have been proposed to characterize observed EP (Anagnostopoulou and Tolika, 2012; Beguería et al., 2009; Deidda and Puliga, 2006; Dong et al., 2011; Li et al., 2005; Pfahl et al., 2017). A recent focus that has emerged is to obtain a better physical understanding of EPTs and, thereby, to assess regional variations in EP. For example, Liu et al. (2013) adopted a multifractal detrended fluctuation analysis (MFDFA) to determine EPTs, and Du et al. (2013) applied MFDFA to investigate EPTs and consequent EP variation in northeastern China. To date, however, no international standards for the selection of such methods exist.
Recent investigations of precipitation using the universal multifractal technique have demonstrated its multifractal nature. Universal multifractals were conceived to study the multiplying cascades governing the dynamics of various geophysical fields (Lovejoy and Schertzer, 2013; Schertzer and Lovejoy, 1987). For precipitation, a scaling break separating the meteorological and climatological regimes varies from several days to 1 month, with an average of about 2 weeks (Tessier et al., 1993, 1994, 1996). The meteorological scaling interval indicates that (from the multifractal perspective) data collected at time intervals of 1 d and those at intervals finer than minutes can equivalently characterize the physical processes associated with precipitation (Pandey et al., 1998; Tessier et al., 1996), indicating that EP events can, in principle, be characterized by the study of daily data observed at gauging stations. Of course, it is vitally important that the universal multifractal characterizes how extremes occur in a natural manner (Lovejoy and Schertzer, 2007; Tessier et al., 1996).
In this study, we use the universal multifractal technique to obtain a physically meaningful characterization of EPT. Our objectives are to (1) apply the universal multifractal approach to determine a unique set of EPTs for the LP area, (2) investigate how spatial variations in EP are responsible for the severe nature of soil erosion, and (3) assess the spatiotemporal variation of EP over the LP during the period from 1961 to 2015.
2.1 The relationship between precipitation extremes and multifractals
The approach outlined below was used to identify EP events at the observation timescale. In the method of universal multifractals, two equivalent routes can be followed to investigate time series scaling: the probability distribution and the statistical moments. A fundamental property of multifractal fields related to the probability distribution is given by the following equation (Lovejoy and Schertzer, 2013; Schertzer and Lovejoy, 1987):
where λ represents the resolution of the measure (i.e., the ratio of the external scale L to the measurement scale l; ), φλ is the intensity of the field (in this case accumulated precipitation) measured at resolution λ, γ is the order of singularity (maximum precipitation) corresponding to φλ, and the codimension function c(γ) characterizes the sparseness of the γ-order singularities (this function is a basic multifractal probability relation for cascades). Accordingly, the statistical moments are given by
where K(q) is the multiple scaling exponent function for moments; q is the order of the statistical moment, and 〈 〉 denotes the average of the field (averaged precipitation) at scale ratio λ. The two equivalent routes are related via a Legendre transform (Parisi and Frisch, 1985). The universal K(q) functions and the codimension function c(γ) are expressed as
where α is the multifractal index, which describes how rapidly the fractal dimensions vary as we leave the mean. For time series in this paper, , and α′ is the auxiliary variable defined by (Lovejoy and Schertzer, 2013). The term C1, the codimension of the mean of the process, varies as (D is space dimension; D=1 for time series) and quantifies the sparseness of the mean. In this paper, the parameters α and C1 of the multifractal model were estimated using the double trace moment (DTM) technique (Lavallée et al., 1993).
As noted by Gagnon et al. (2006) and Lovejoy and Schertzer (2007), the parameters C1 and α characterize the mean of the field, whereas the extremes are expressed by the singularity, γ, and the codimension function c(γ) (Hubert et al., 1993). For and considering a time series of infinite length, a finite maximum order of singularity, γ0, can be determined as follows:
However, in general, any time series of finite length will almost surely miss the presence of rare extremes in the field. In this case, the observed singularities will be bounded by an effective maximum singularity, γs:
where D is the embedding space dimension (D=1 for the time series). The total dimension of this problem is actually (D+Ds), where is the sampling dimension, and Ns is the number of independent time series at each location. The parameter γs links the physical processes that generate precipitation events to the conceptual model of multiplicative cascades, and it allows the extremes to be cast in a probabilistic framework, γs>0. Thus, it was used to infer the extreme events of precipitation fields over well-defined scales.
For parameter estimation, the parameters α and C1 of the multifractal model are estimated by the DTM technique (Lavallée et al., 1993). The q, η DTM at resolution λ and Λ is defined as
where the sum is obtained over all the disjoint D dimensional balls Bλ,i (with intervals of length ) that are required to cover the time series. K(q, η) is the double trace scaling exponent, and is the scaling exponent. This relation can be expressed as
where the notation indicates that the multifractal φ at a (finest) resolution Λ is first raised to the power η then degraded to resolution λ, and the qth power of the result is averaged over the available data. The scaling exponent K(q, η) is related to and is given by
In the case of universal multifractals, by plugging Eq. (3) into Eq. (9), K(q, η) has a particularly simple dependence on η:
where α can be estimated from a simple plot of K(q, η) versus log (η) for fixed q. Thus, based on the DTM technique, all parameters can be estimated.
2.2 Determination of the extreme precipitation threshold
The approach outlined below was used to estimate the EPTs and EP events for each station, using the singularity parameter (γs). Given that the multifractal parameters α and γs naturally characterize extremes, both of these parameters will change if we gradually remove extreme values from the data set. The singularity of the precipitation data series will be completely changed, and the two parameters will significantly change if all of the extreme values are deleted. To obtain a physically meaningful value for the EPT, we attempted to estimate the multifractal parameter series by applying the universal multifractal approach to our precipitation series and successively eliminating maximum values of precipitation. However, as shown by Fig. 1a and c, the degree of convergence of the original value is not unique, with the values fluctuating slightly around the original α and γs. Accordingly, the variance series of index series αj and γs,j were computed to eliminate the fluctuation while identifying the point of convergence. The procedure is as follows:
-
eliminate the data point xj, {xj, from the precipitation time series {xi, i=1, 2, …, n}, where xmax is the maximum, xave is the average, and d is the interval space (we set d to 1 mm in this case);
-
compute the selected parameters;
-
repeat (1) and (2) for j varying from 1 to int(().
Using the obtained parameter series, we applied the segmentation algorithm proposed by Bernaola Galván et al. (2001) to determine the point of abrupt change, which we define as the EPT. The segmentation algorithm is based on the calculation of the statistic t of each data point in a series or subseries:
where is the pooled variance. The μL∕μR, sL∕sR, and NL∕NR are the mean, standard deviation, and number of points from the data to the left/right of the series, respectively. The significance level P(τ) of the largest value tmax obtained from Eq. (11) is defined as the probability of obtaining a value equal to or less than τ within a random sequence (Swendsen and Wang, 1987):
If the significance exceeds a selected threshold P0 (usually taken to be 95 %), an abrupt point is selected and the series is cut into two subsets at this point.
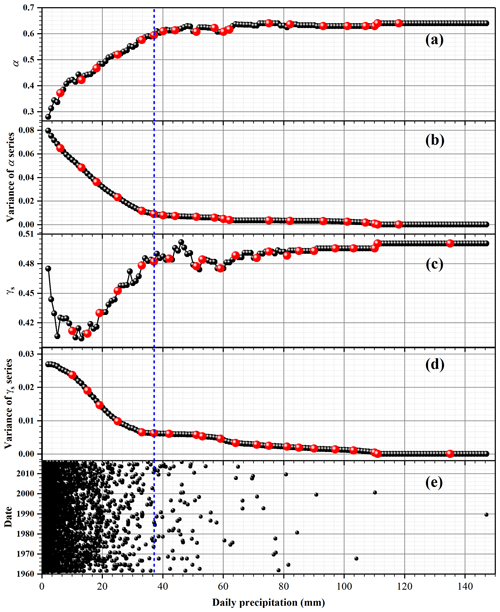
Figure 1Procedure for the EPT determination of the Xingxian station. (a) The multifractal index α (black dots) and the alternative abrupt points (red dots). (b) Pooled variances (black dots) as calculated from the α series with the significant abrupt points (red dots) of the variances. (c) As in panel (a) but for the singularity γS. (d) As in panel (b) but for the variance calculated from the γS series. (e) The time variation of daily precipitation ranging from 1961 to 2015. The blue dotted line represents the determined EPT.
The pooled variances and the abrupt points of the α and γs series are shown in Fig. 1b–d. The abrupt point, where sD differs from its left-side points but is approximately equal to its right-side points, is selected to be the EPT. As shown for the determined EPT in Fig. 1, there is a steep slope of the pooled variance on the left and a gentle slope on the right of 37.1 mm daily precipitation. Thus, the EPT for Xingxian station is estimated to be 37.1 mm d−1, and 90 EP events have occurred over the past 55 years (Fig. 1c).
2.3 EP indices
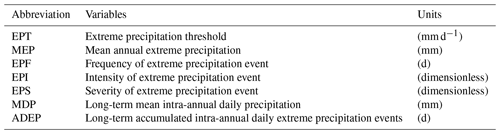
All of the variables characterizing spatiotemporal EP over the LP are shown in Table 1. For individual stations, the annual precipitation at each station was accumulated using daily data. Annual EP is accumulated using daily EP determined by the EPT, and EP frequency (EPF) is the number of daily EP events. Mean annual EP (MEP) is averaged from annual EP interpolated using ArcGIS 10.1. For a year with n EP events, the EP intensity (EPI) is calculated by the following equation:
where EPi represents the magnitude of EP event i, respectively.
As noted by IPCC (2007), neither the cases of high frequency with low intensity nor the cases of low frequency with high intensity can reflect the severity of EP events given a long-term time series for an area, whereas the severity of EP (EPS) events relies on both intensity and frequency. Consequently, we examine the extreme precipitation intensity (EPI), extreme precipitation frequency (EPF, defined below), and EPS to characterize the spatiotemporal nature of EP over the LP. To obtain the concordant EPS, each annual EPF/EPI series is standardized to the range from 0 to 1 using Eq. (10):
where Xmin and Xmax represent the lowest and highest annual EP frequency/intensity, respectively. The annual EPS for each station (0 ≤ EPS ≤ 1) is calculated from the standardized EPI and EPF by
where k1 and k2 are the weight coefficients of frequency and intensity influencing EP severity, respectively, and . In this paper, k1 and k2 are set to 0.5 according to IPCC (2007).
In addition, we compute the long-term mean daily precipitation (MDP) and the long-term accumulated daily EP events (ADEP) to help characterize the intra-annual precipitation and EP. As shown in Table 1, MDP is averaged from all 87 stations, and ADEP is accumulated from 87 stations over the past 55 years.
2.4 Spatiotemporal EP presentation
The spatial distributions of the EP indices were derived by interpolation via kriging (Oliver and Webster, 1990), using data observed at the gauging stations. All spatial analyses were carried out using the ArcGIS 10.1 software. Spatiotemporal trends for annual EP indices were computed for each pixel using the least squares method. Following Stow et al. (2003), the trend is defined as the slope of the least squares line that fits the inter-annual variability of individual EP indices during the study period and is given by
where m is the total of years, and Pi is value of the pixel in the j-th year.
3.1 Study area
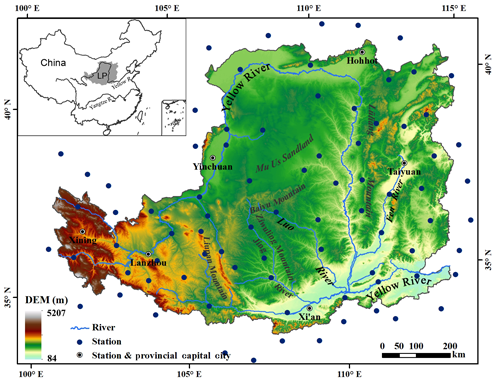
The LP (640 000 km2) is a typical arid and semiarid area located in the middle reaches of the Yellow River (750 000 km2) and is characterized by a continental monsoon climate. Elevations range from 84 to 5207 m (Fig. 2). The desert steppe, typical steppe, and forest steppe (deciduous broadleaf forest) zones are distributed from northwest to southeast and correspond to mean annual isohyets of 250, 450, and 550 mm in the arid, semiarid, and semi-humid areas, respectively. The continuous loess covering ranges from 100 to 300 m in thickness on the mountains, hills, basins, and alluvial plains of different heights. The northwestern part of the region is dominated by flat sandy areas. The middle and southeastern parts are characterized by EP-induced water-erosion landforms (Zhang et al., 1997), with a rugged undulating ground surface that is broken, barren, and dissected by gullies and ravines (Cai, 2001). EP-induced flooding episodes occur occasionally in the summer, with sediment concentrations generally exceeding 300 kg m−3, although they have been observed to be as large as 1240 kg m−3. The hyperconcentrated flooding has historically resulted in numerous disasters, with severe consequences for people and livestock (Zhang et al., 2017). The amount of soil erosion has been estimated to be larger than 2×109 to 3×109 t yr−1 (Tang, 1990). Soil erosion has resulted in the density of gullies and ravines in the LP being larger than 3–4 km km−2, with the maximum exceeding 10 km km−2.
3.2 Database
To conduct the EP assessment, we used daily data that were available for 87 national meteorological stations in and around the LP (Fig. 2), consisting of continuous time series from 1961 to 2015. All of the precipitation data were obtained from the China Meteorological Data Sharing Service System (http://data.cma.cn/, last access: 19 February 2020). Missing data accounted for less than 0.1 % of the total sample, and they were replaced by a value of zero in this paper; this replacement of a few missing values does not influence the analysis. Data regarding the severity of soil erosion were provided by the LP Science Data Center of the data sharing infrastructure of the National Earth System Science Data Center of China (http://loess.geodata.cn, last access: 19 February 2020). These data were compiled during the Soil Erosion Census of the China Census for Water (Ministry of Water Resources and National Bureau of Statistics, 2013). Mean annual vegetation coverage at an 8 km spatial resolution and a 15 d temporal resolution were computed using data for the period from 1982 to 2006, which were produced by the Global Inventory Modeling and Mapping Studies (GIMMS) group from measurements of the Advanced Very-High-Resolution Radiometer (AVHRR) onboard the NOAA 7, NOAA 9, NOAA 11, and NOAA 14 satellites. Data from the National Center for Environmental Prediction/National Center for Atmospheric Research (NCEP/NCAR) Reanalysis Project (Kalnay et al., 1996) were also used in this study. The variables selected for analysis were the monthly mean geopotential height, monthly mean wind, daily mean sea level pressure, and daily mean wind from 1961 to 2013 on a 2.5∘ × 2.5∘ spatial grid (http://www.esrl.noaa.gov/psd/, last access: 19 February 2020).
4.1 Spatial characteristics of extreme precipitation
Figure 3a shows that the mean annual precipitation (for the period from 1961 to 2015) varied from 115 mm in the northwestern LP to the 845 mm in the southeastern LP. The associated EPTs ranged from 17 mm d−1 in the northwest to 50 mm d−1 in the southeast (Fig. 3b); these EPT isohyets are generally consistent with those of mean annual precipitation. Figure 3b indicates that the area around the Dongsheng station is a regional EP center: the EPTs around the station are higher than those of the surrounding areas, whereas the isohyets of mean annual precipitation are smooth. The spatial distribution of MEP is also similar to that of mean annual precipitation, increasing from northwest to southeast and ranging from 35 to 138 mm yr−1 (as shown in Fig. 3c). MEP maximums occur in the southern and southeastern LP.
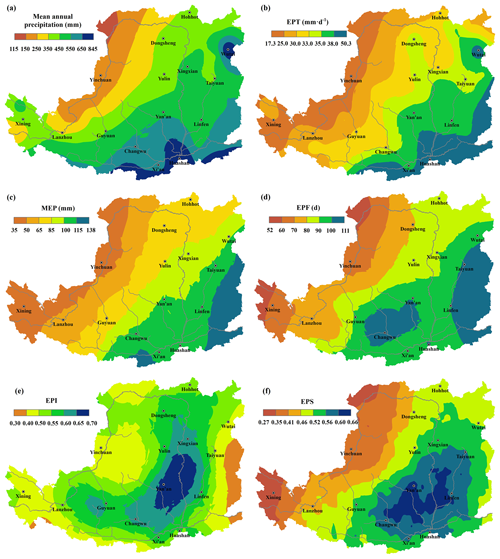
Figure 3Spatial distributions of (a) mean annual precipitation, (b) EPTs, (c) MEP, (d) total EPF, (e) mean EPI, and (f) mean annual EPS in the LP from 1961 to 2015.
Figure 3d indicates that EPFs have ranged from 54 to 115 d (i.e., mean annual EPF ranged from 1.0 to 2.1 d) over the region during the past 5 decades. Notable occurrences of high EPF can be seen in and around the Ziwuling Mountains in the mid-southern LP, whereas the highest frequency occurred to the east of the Fenhe Valley in the southeastern LP. Meanwhile, the lowest frequency occurred in the northwestern LP, the western Mu Us sandy land, and the western Liupan Mountains.
Figure 3e indicates that the averaged EPIs mainly ranged between 0.3 and 0.7. The spatial variations in EPI and EPF contrast with each other, with the highest EPIs centered in the mid-eastern LP, where EPFs were comparatively lower, and the lowest EPIs centered in the southeastern LP, which had the maximum mean annual precipitation and EPF. The highest values of EPI dominated the central LP area. The northern boundary of the area was positioned southeast of the Mu Us Desert (Dongsheng and Xingxian); the western boundary was positioned west of the Liupan Mountains (Guyuan County); the eastern boundary was positioned northeast of the Lüliang Mountains and the Fenhe Valley (Taiyuan and Linfen); the southern boundary was positioned to the north of the central Shaanxi Plain (Huashan, Xi'an and Changwu). The EPI presents the event EP power causing natural hazards. This high value of EPI partially explains why this area is characterized by very serious soil erosion that releases more than 2×109 t of sediment into channels of the Yellow River annually.
Figure 3f indicates that the spatial distribution of EPS in the LP increased from the northwest to the southeast, ranging from 0.27 to 0.66, but the highest EPSs were centered in the southeast central LP. The areas with the highest EPSs covered the basins of the Jing, Luo, and Fen rivers. Although EP events always occurred over a small range, the spatial maps of EPI, EPF, and EPS indicate that the areas with serious EP events are regularly distributed.
4.2 Spatiotemporal variation of EP
Our results (Fig. 4a) indicate that 91.4 % of the LP was characterized by a negative annual precipitation trend over the study period, whereas only 8.6 % of the total area presented a positive trend. A total of 9 out of 87 stations showed a significant negative trend, whereas 2 stations showed positive trends (p<0.1). At the same time, the spatiotemporal trends in the annual EP ranged from −0.78 to +0.48 mm yr−1 (Fig. 4b), with 23.8 % of the total area showing a positive trend and increased annual EP distributed mainly in the southwestern LP (west of Lanzhou) and the central southern LP (Beiluo and Jing river basins and an area around the Xingxian station). Meanwhile, the annual EPF has changed by −0.6 to +0.5 d over the past 55 years, with a change rate ranging from to d yr−1 (as shown in Fig. 4c). Of the 87 stations, 4 stations showed a significant negative trend in EPF, whereas 3 stations showed positive trends (p<0.1). The areas with a negatively trending EPF covered 86.4 % of the total area, whereas the areas with positively trending EPF covered 13.6 %; the latter regions mainly occurred in the southwestern LP (around the Xining station) and in the areas around the Xi'an and Xingxian stations. The areas with notably decreasing trends mainly occurred in the central western and southeastern regions of the LP.
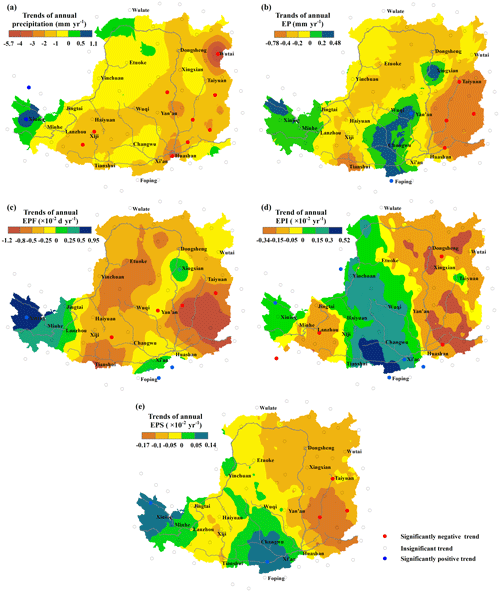
Figure 4The spatial distribution of the trends and the stations with significant trends (p<0.1) for (a) annual precipitation, (b) annual EP, (c) annual EPF, (d) annual EPI, and (e) annual EPS in the LP from 1961 to 2015.
Figure 4d indicates that the changes in annual EPI ranged from −0.18 to +0.27, with a changing rate ranging from to yr−1. We found that 34 of the 87 stations showed upward slopes (5 stations with a significance level of p<0.1), and 53 stations showed negative slopes (4 stations with a significance level of p<0.1). As shown in Fig. 4d, areas with positive trends in EPI accounted for 42.2 % of the total area, with the areas delineated by the Wulate, Yan'an, and Huashan stations and the Jingtai, Xiji, and Tianshui stations as well as the area west of the Minhe station. The areas with a negative slope covered 57.8 % of the total area.
Figure 4e indicates that the annual EPSs changed by −0.09 to +0.07 during the study period, with rates varying from to yr−1. Of the 87 stations, 39 stations showed a positive slope (3 stations with a significance level of p<0.05), while 54 stations exhibited a negative slope (2 station with a significance level of p<0.05). The areas with increased EPSs covered 25.4 % of the total area and were mainly found in an area delineated by the Wuqi, Tianshui, and Huashan stations and an area west of the Xiji station. The areas with negative trends accounted for 74.6 % of the total area.

Figure 5Intra-annual distribution of daily precipitation (MDP) and the number of daily EP events (ADEP) for the 87 stations from 1961 to 2015 and their fitting curves with respect to a Weibull function.
The trend estimates computed for annual EP, EPF, and EPI are associated with strong uncertainty. For instance, the upward trend in annual EP in and around the Xingxian station relied heavily on the upward trend in the EPF and not the downward trend in the EPI. The EPF around the Changwu station decreased, but both the annual EP and EPS increased with the upward trend in the EPI. However, nearly all of the areas with positive trends for annual EP, EPI, EPF, and EPS had a negative trend in annual precipitation (Fig. 4). It should be noted that 62.1 % of the LP area with a negative trend in annual precipitation has more than one EP indices with positive trends, potentially indicating the risk of more serious hazardous situations.
4.3 Intra-annual EP characteristics and their relationship with large-scale atmospheric circulation
4.3.1 The intra-annual distribution of EP events
Figure 5 displays the intra-annual distributions of the MDP and the ADEP for the 87 stations from 1961 to 2015. Precipitation from June to September accounts for 72 % of the total amount, while 91 % of the total EP events occur from June to August. According to the fitted curve (Fig. 5), the highest MDP occurred on 26 July, which is 11 d earlier than the maximum ADEP on 6 August. Based on fitting the four-parameter Weibull curve (p<0.0001), the MDP for the 224 d from 26 March to 4 November accounted for 95 % of the mean annual precipitation. Meanwhile, the ADEP from 21 May to 18 September accounted for 95 % of the total EPF.
Therefore, the high concentration of the amount of daily precipitation into a limited period results in a significant alternation of wet and dry seasons in the LP. In addition, low precipitation, the annual alteration of dry and wet seasons, and highly concentrated intra-annual EP events with an occurrence 11 d earlier than the wettest days contribute to a fragile eco-environment subject to severe natural hazards. Specifically, lower precipitation coupled with the occurrence of the highest EPI and EPS are responsible for the most severe hazard situations in the central LP, such as soil erosion.
4.3.2 Atmospheric circulation factors for the spatial variation of extreme precipitation
Atmospheric circulation is the leading factor causing the abovementioned phenomena. The LP is located in the East Asian monsoon region. According to the average sea level pressure and winds in winter from 1961 to 2015 (see Fig. 6a), the dry winter in the region is influenced by the interactions between two high-pressure areas in southwestern China (the Tibet Plateau high-pressure system) and North China (the Mongolian high-pressure system). The prevailing East Asian winter monsoon (which has a north-northwest direction) circulates in East China and brings cold and dry airstreams. In contrast, the summer climate of the LP is affected by interactions between two high-pressure systems, the Pacific high-pressure system and the Tibet Plateau high-pressure system. Figure 6b shows that the prevailing East Asian summer monsoon (which has a south-southeast wind direction) brings warm and humid maritime airstreams that spread from the West Pacific to central China. However, the Tibet Plateau high-pressure system has a notable effect on the climate of the northwestern LP, and the airstream humidity decreases gradually as the distance from the Pacific increases. The resulting effect and decreased humidity form a vast arid region in northwestern China, including the northwestern LP, with a prevailing west-southwest wind direction. This explains why precipitation decreases from the southeast to the northwest, and precipitation is scarce in the northwestern LP.
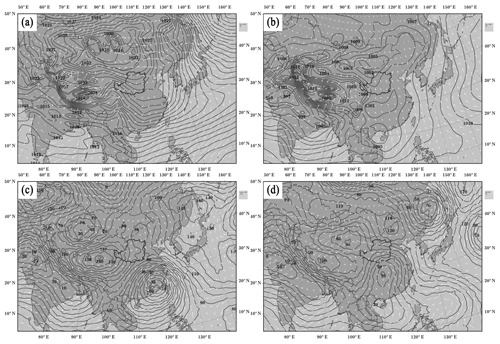
Figure 6Average sea level pressure and winds: (a) the mean for all winters (from December to February) and (b) the mean for all summers (from June to August) from 1961 to 2015. Characteristics of the average 1000 hPa geopotential height and winds on (c) 1 August 1996 and (d) 3 August 1996. The data were derived from global NCEP/NCAR reanalysis average monthly and daily data.
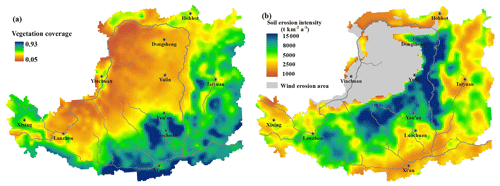
Figure 7(a) Spatial distribution of mean vegetation coverage in summer (from June to August) on the Loess Plateau from 1982 to 2006 at a spatial resolution of 8 km. (b) Spatial distribution of the soil erosion intensity, which was resampled to a spatial resolution of 8 km.
Nevertheless, tropical cyclones occasionally enter the central LP, accompanied by EP events. For instance, in August 1996 a western Pacific cyclone landed in the southeastern coastal area of China and weakened gradually as it moved northwest, as shown by the 1000 hPa geopotential height and winds in Fig. 6c. Plenty of rainstorms or intense rainfall events that accompanied the cyclone occurred in its transit area. On 3 August 1996, the weakened cyclone reached the southeastern LP (as shown in Fig. 6d). However, due to the control of the Tibet Plateau high-pressure system, the central LP is generally the northwestern inland boundary with respect to the reach and impact of tropical cyclones. Thus, as shown in Fig. 6d, the cyclone was blocked from entering the northwestern LP, moved towards the northeast, and gradually dissipated. These phenomena illustrate why this region has limited precipitation but severe EP events.
5.1 Rationality of spatial EP characteristics
Natural hazards related to EP can be divided into two categories: (1) hazards accompanied by EP and (2) hazards that follow the occurrence of EP. For the former, one focus is the dependence between EP and storm surges in the coastal zone. Using such dependence structures, EP and storm surges can be quantified to provide information for successful hazard management (Svensson and Jones, 2004; Zheng et al., 2013). For the latter, the LP is such that the area suffers from EP-induced natural hazards that exceed the general tolerance of the natural environment, existing ecosystems, human life, and the social economy. In this case, the rational characteristics of EP responsible for spatial hazards can be studied.
Here, we use the widely distributed soil erosion to verify the rationality of our results. According to the universal soil loss equation (Wischmeier, 1976), the rational characteristics of EP should correlate well with soil erosion and vegetation coverage (Fig. 7). To examine this, partial correlation analyses were performed between soil erosion intensity and EPI/EPS as well as with the vegetation coverage. Our results indicate that water-based erosion intensity correlates significantly with vegetation coverage (negatively, Fig. 7a) and EPS (positively, Fig. 3f); the related coefficients are −0.61 (p<0.001) and 0.53 (p<0.001), respectively. For the correlations between water-erosion intensity and vegetation coverage as well as with EPI (Fig. 3e), the coefficients are −0.58 (p<0.001) and 0.76 (p<0.001), respectively. This finding demonstrates the rationality of our results. Note that, the higher correlation between EPI and soil erosion agrees with the results of plot experiments by Tang (1993), who noted that high-intensity precipitation is the primary driving force of erosion.
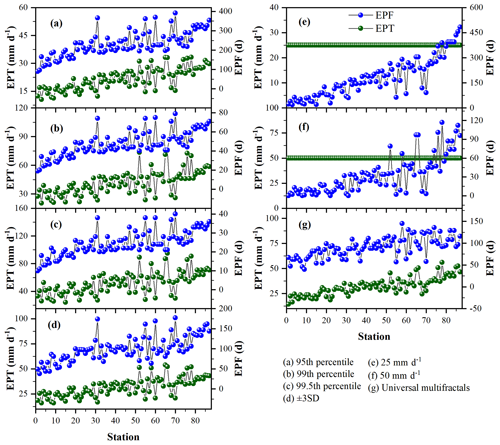
Figure 8EPTs determined by different methods and the corresponding EP frequencies for 87 stations over the Loess Plateau. The abscissa represents the stations with an increase in the mean annual precipitation from 104 to 918 mm.
Zhou and Wang (1992) divided the LP into three zones of raindrop kinetic energy (<1000, 1000–1500, and 1500–2000 J m−2 yr−1, respectively), based on observations of the raindrop kinetic energies of rainstorms during 1980s. We found that the 30 and 35 mm d−1 EPT contours closely overlap with the raindrop kinetic energy contours of 1000 and 1500 J m−2 yr−1. Further, soil erosion in the LP in recent decades has been found to be approximately 5000–10 000 t km−2 yr−1 (Ludwig and Probst, 1998; Shi and Shao, 2000). Such high rates of sediment erosion are generally induced by several rainstorm events during the year, with the top five daily sediment yields accounting for 70 %–90 % of the annual total soil loss (Rustomji et al., 2008; Zhang et al., 2017). For instance, a 200-year precipitation event in Wuqi on 30 August 1994 induced a flooding event with a daily sediment concentration of 1060 kg m−3. The streamflow was 2.41 times the mean annual streamflow from 2002 to 2011, and the sediment load was equivalent to 9.6 % of the total sediment yields from 1963 to 2011 (Zhang et al., 2016). Therefore, the EPF obtained in this study, about twice every year on average, is rational to explain such serious sediment erosion. In the LP, spring drought is the limiting factor with respect to vegetation (especially herbaceous vegetation) recovery from winter every year, and grass generally germinates on an extensive scale after the first effective rainfall event (>5 mm) in spring (Cai, 2001; Tang, 1993, 2004). However, as shown in Fig. 5, the highest EPF occurred 11 d earlier than the day of maximum daily precipitation in the LP. This means that the days on which the LP experiences most serious EP events tend to be days when precipitation is low. In other words, every year, the vegetation has not sufficiently recovered when frequent EP events occur in the LP. Such an intra-annual distribution of precipitation is one of the climatic reasons why there is serious soil erosion in the semiarid LP. Further, the sparse spatial nature of precipitation is insufficient for the growth of high-coverage vegetation, especially in the northwestern LP (Fig. 7a). However, the highest EPI provides the strongest erosion force, which contributes to the severe rates of erosion (Fig. 7b) in the central LP. Thus, these results regarding the EP responsible for hazardous situations (both spatially and temporally) are important for sustainable catchment management, ecosystem restoration, and water resource planning and management within the LP. Given that 62.1 % of the total LP with a negative trend in annual precipitation has one or more positive EP indices, the underlying upward trends in water erosion and sediment yield should be taken into account in catchment management efforts.
5.2 Uncertainty in EP identification
The uncertainties in the identification and assessment of EP events stem from two aspects: (1) the stochasticity in climate (Miao et al., 2019) and (2) the methodology (Papalexiou et al., 2013). For the former, significant spatiotemporal variations occur in EP events as a result of varying geographical and meteorological conditions (Pinya et al., 2015). Extreme precipitation events are relatively rare, poorly predictable, and often short-lived, resulting in uncertainty in EP event identification. The uncertainties regarding EPT determination from parametric and nonparametric methods has been discussed in Sect. 2.
Figure 8 shows the results of the EPF obtained using nonparametric methods for all 87 stations over the LP during the period from 1961 to 2015. Large variances among the results, calculated at different percentile levels, are shown in Fig. 8a–c. Trivially, the EPTs are smaller but with larger EPFs for lower percentiles. The “±3 SD (standard deviation)” method (Fig. 8d) provided results with a similar variance among stations in comparison with the universal multifractal method (Fig. 8g). The EPTs determined by individual methods generally increase as annual precipitation increases. As shown in Figs. 8e–f and 3a, no precipitation event exceeded 50 mm d−1, as the mean annual precipitation is <200 mm in the northwestern LP. A 50 mm d−1 threshold is probably suitable for the southeast LP, which has higher mean annual precipitation, whereas a 25 mm d−1 threshold may be more suitable for some stations in the northwestern LP. Therefore, regardless of the varying geographical and meteorological conditions, the selection of these thresholds can be quite subjective and empirical. Note that, although a similar variance of EPTs among stations can be obtained using individual methods, the spatial causes for hazards situations cannot be theoretically explained by these methods in Fig. 8a–f.

Figure 9The passing rates of the goodness-of-fit test for individual distribution functions, with EP data series selected by different preset thresholds. (a1) The K–S test, (a2) the A–D test, and (a3) the C–S test for different distribution functions using preset percentile thresholds. (b1) The K–S test, (b2) the A–D test, and (b3) the C–S test for different distribution functions using thresholds of fixed values. The significance level is 0.05. The symbol lines of the passing rate of Gumbell functions in (a1)–(a3) were arbitrarily offset upward by −5 units, respectively, in order to separate them.
Parametric methods require a predetermined threshold value, above which the data can be chosen as the EP series if the data series passed the goodness-of-fit test. As shown in Fig. 9, both fixed values and percentiles were adopted to preset EPT. The selected rainfall data series were fitted to the gamma, GPA (generalized Pareto distribution), Gumbel, Pearson type III, GEV (generalized extreme value distribution), and the GNO (generalized normal) distributions, whose parameters were estimated utilizing the L-moments method (Haddad et al., 2011) at a 0.05 significance level, using goodness-of-fit tests including the K–S (Kolmogorov–Smirnov test), A–D (Anderson–Darling K-Sample test) and C–S (Pearson's Chi-squared test) tests. As shown in Fig. 9a1–a3 and b1–b3, the results of the three tests are similar, although they differ with respect to the details for the preset fixed value and percentile thresholds.
Further, these results for different distribution functions are quite different from each other. As shown in Fig. 9a1 and a2 (by the K–S and A–D tests), the passing rates from the GEV, Gumbell, GNO, and Pearson type III distribution functions are high, whereas there are very low passing rates from the GPA and Gamma functions. In addition, the passing rates are different between the preset methods of percentiles and fixed values. As shown in Fig. 9, the GEV and Gumbell distribution function have high passing rates for EP series obtained by preset percentiles when the percentile is less than or equal to 99 % (Fig. 9a1, a2), whereas the passing rates for the series obtained using fixed values decrease with increasing values (Fig. 9b1, b2). We also found that these distribution functions are not sensitive to the percentile or fixed value changes. These findings indicates that the fitting accuracy can be greatly affected by the selection of the extreme value distribution functions, the goodness-of-fit tests, and the methods used for the EPT preset. Liu et al. (2013) noted that the fitting accuracy is also affected by the size of rainfall series. Thus, unavoidably, applications of parametric methods also depend on personal subjectivity and empiricism. We have attempted to explore EP using fixed values of spatiotemporal variation in precipitation analysis in the LP; however, we found that the results did not explain the rainfall-induced natural hazards well nor did they agree (spatially) with plot experiments by Wan et al. (2014) or results obtained using fixed values (Xin et al., 2009) and percentiles (Li et al., 2010a, b). These uncertainties may be the reason why prior EP studies over the LP tend to disagree with each other.
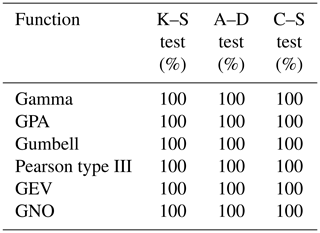
As noted by Pandey et al. (1998) and Douglas and Barros (2003), these methodological uncertainties arise due to the wide gap between mathematical modeling and the physical understanding of precipitation processes. As previously mentioned, the multifractal technique can be used to describe the statistical probability and physical processes associated with observed data (Lovejoy and Schertzer, 2013; Tessier et al., 1996), while the scale invariance of multifractals enables the multifractal technique to also overcome the influence of the sample size (Pandey et al., 1998; Tessier et al., 1996). Further, the segmentation algorithm helps to overcome the problem of uncertainty. In the present study, the general correspondence and the specific divergences between the EPT and precipitation isohyets (Fig. 3) further exhibits the varying meteorological and geographical influences. As shown in Table 2, by fitting EP series derived using universal multifractals to the six distribution functions, the 100 % passing rate of the goodness-fit test strongly supports that the universal multifractal approach is advanced in identifying EP events. Overall, the universal multifractal method provides a much superior approach to addressing uncertainties and providing a unique set of EPTs.
Using data from 87 meteorological stations from 1961 to 2015, we have proposed an approach that integrates universal multifractals with a segmentation algorithm to enable the identification of EP events and, thereby, to assess the spatiotemporal EP characteristics in the LP. We find that the spatial distribution of the EPTs increased from 17.3 mm d−1 in the northwestern LP to 50.3 mm d−1 in the southeastern LP. Similarly, the MEP increased from 35 mm to 138 mm yr−1, with the maximum MEP occurring in the southern and southeastern LP. The EPF over the LP has been within a range of 54–116 d over the last 55 years. Notable occurrences of EPFs have mainly been observed in the central southern and southeastern LP. An examination of atmospheric circulation patterns demonstrates that the central LP is the inland boundary with respect to the reach and impact of tropical cyclones in China; therefore, the highest EP intensity and EP severity are found in this area. Correlation analysis significantly supported the reasonability of the spatial estimates of the EP characteristics that are responsible for hazardous situations over the LP. The climate factors for the most serious hazardous situations in the LP, especially in the central LP, stem from the low precipitation, the highest EPI, and the high ADEPs that are concentrated 11 d earlier than the wet season.
Spatiotemporally, annual EP increased in the southwestern and central southern LP. Areas with a positive EPF trend were found in the southwestern LP as well as the regions around the Xi'an and Xingxian stations, whereas areas with a positive trend in EPI occurred among the Wulate, Yulin, Yan'an, and Huashan stations and the Jingtai, Xiji, and Tianshui stations, as well as the region west of the Minhe station. The annual EPSs (with increased slope) covered an area delineated by the Wuqi, Tianshui, and Huashan stations and an area west of the Xiji station. Overall, the areas with upward trends in the annual EP, EPF, EPI, and EPS accounted for 23.8 %, 13.6 %, 42.2 %, and 25.4 % of the LP area, respectively. It should be noted that 62.1 % of the LP area with negative annual precipitation experienced upward trends in one or more of the EP variables. It can be concluded that EP over the LP intensified, potentially imposing a risk of more serious hazardous situation. Sustainable countermeasures should be considered in the catchment management to address the underlying hazards.
In conclusion, the universal multifractal approach considers both the physical processes and their probability distribution and, thereby, provides an approach to overcome uncertainties and identify EP events without the need for empirical adjustments. Thus, this approach is useful for application to spatiotemporal EP assessment at the regional scale.
All of the data used in this study are available upon request.
JZ, XZ, and RL prepared the research project. JZ, HVG, GG, BF, and CW conceptualized the methodology. JZ developed the code and performed the analysis. JZ prepared the paper with contributions from all the co-authors.
The authors declare that they have no conflict of interest.
We thank the China Meteorological Data Sharing Service System, the Yellow River Conservancy Commission, the LP Science Data Center of the data sharing infrastructure of the National Earth System Science Data Center of China, and the NCEP/NCAR for providing data used in this paper. All data sources are publicly accessible, and these websites are listed in Sect. 3.2.
This research was funded by the National Natural Science Foundation of China (grant nos. 41701207 and 41822103), the State Key Project of Research and Development Plan of China (grant no. 2016YFC0501603), the Open Foundation of the State Key Laboratory of Urban and Regional Ecology of China (grant no. SKLURE2019-2-5), and the Fundamental Research Funds for the Central Universities of China (grant no. 2652018034). The corresponding author acknowledges partial support from the Australian Centre of Excellence for Climate System Science (grant no. CE110001028).
This paper was edited by Nadia Ursino and reviewed by three anonymous referees.
Anagnostopoulou, C. and Tolika, K.: Extreme precipitation in Europe: statistical threshold selection based on climatological criteria, Theor. Appl. Climatol., 107, 479-489, 2012.
Bao, J., Sherwood, S. C., Alexander, L. V., and Evans, J. P.: Future increases in extreme precipitation exceed observed scaling rates, Nat. Clim. Change, 7, 128–132, 2017.
Beguería, S., Vicente-Serrano, S. M., López-Moreno, J. I., and García-Ruiz, J. M.: Annual and seasonal mapping of peak intensity, magnitude and duration of extreme precipitation events across a climatic gradient, northeast Spain, Int. J. Climatol., 29, 1759–1779, 2009.
Bernaola Galván, P., Ivanov, P. C., Amaral, L. A. N., and Stanley, H. E.: Scale invariance in the nonstationarity of human heart rate, Phys. Rev. Lett., 87, 168–105, 2001.
Cai, Q.: Soil erosion and management on the Loess Plateau, J. Geogr. Sci., 11, 53–70, 2001.
Deidda, R. and Puliga, M.: Sensitivity of goodness-of-fit statistics to rainfall data rounding off, Phys. Chem. Earth, 31, 1240–1251, 2006.
Donat, M. G., Lowry, A. L., Alexander, L. V., O'Gorman, P. A., and Maher, N.: More extreme precipitation in the world's dry and wet regions, Nat. Clim. Change, 6, 508–513, https://doi.org/10.1038/NCLIMATE2941, 2016.
Dong, Q., Chen, X., and Chen, T.: Characteristics and Changes of Extreme Precipitation in the Yellow–Huaihe and Yangtze–Huaihe Rivers Basins, China, J. Climate, 24, 3781–3795, 2011.
Douglas, E. M. and Barros, A. P.: Probable maximum precipitation estimation using multifractals: application in the Eastern United States, J. Hydrometeorol., 4, 1012–1024, 2003.
Du, H., Wu, Z., Zong, S., Meng, X., and Wang, L.: Assessing the characteristics of extreme precipitation over Northeast China using the multifractal detrended fluctuation analysis, J. Geophys. Res.-Atmos., 118, 52013, https://doi.org/10.1002/jgrd.50487, 2013.
Dulière, V., Zhang, Y., and Salathé Jr, E. P.: Extreme precipitation and temperature over the US Pacific Northwest: A comparison between observations, reanalysis data, and regional models, J. Climate, 24, 1950–1964, 2011.
Eekhout, J. P. C., Hunink, J. E., Terink, W., and de Vente, J.: Why increased extreme precipitation under climate change negatively affects water security, Hydrol. Earth Syst. Sci., 22, 5935–5946, https://doi.org/10.5194/hess-22-5935-2018, 2018.
Feng, X. M., Sun, G., Fu, B. J., Su, C. H., Liu, Y., and Lamparski, H.: Regional effects of vegetation restoration on water yield across the Loess Plateau, China, Hydrol. Earth Syst. Sci., 16, 2617–2628, https://doi.org/10.5194/hess-16-2617-2012, 2012.
Feng, X., Fu, B., Piao, S., Wang, S., Ciais, P., Zeng, Z., Lü, Y., Zeng, Y., Li, Y., and Jiang, X.: Revegetation in China's Loess Plateau is approaching sustainable water resource limits, Nat. Clim. Change, 6, 1019–1022, 2016.
Gagnon, J.-S., Lovejoy, S., and Schertzer, D.: Multifractal earth topography, Nonlin. Processes Geophys., 13, 541–570, https://doi.org/10.5194/npg-13-541-2006, 2006.
Haddad, K., Rahman, A., and Green, J.: Design rainfall estimation in Australia: a case study using L moments and generalized least squares regression, Stoch. Environ. Res. Risk A., 25, 815–825, 2011.
Herold, N., Behrangi, A., and Alexander, L. V.: Large uncertainties in observed daily precipitation extremes over land, J. Geophys. Res.-Atmos., 122, 668–681, 2017.
Huang, J., Yu, H., Guan, X., Wang, G., and Guo, R.: Accelerated dryland expansion under climate change, Nat. Clim. Change, 6, 166–171, 2016.
Hubert, P., Tessier, Y., Lovejoy, S., Schertzer, D., Schmitt, F., Ladoy, P., Carbonnel, J., Violette, S., and Desurosne, I.: Multifractals and extreme rainfall events, Geophys. Res. Lett., 20, 931–934, 1993.
IPCC – Intergovernmental Panel on Climate Change: Climate Change 2007: Synthesis Report. Contribution of Working Groups I, II and III to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change, edited by: Core Writing Team, Pachauri, R. K. and Reisinger, A., Geneva, Switzerland, 104 pp., 2007.
Kalnay, E., Kanamitsu, M., Kistler, R., Collins, W., Deaven, D., Gandin, L., Iredell, M., Saha, S., White, G., and Woollen, J.: The NCEP/NCAR 40-year reanalysis project, B. Am. Meteorol. Soc., 77, 437–471, 1996.
Lavallée, D., Lovejoy, S., Schertzer, D., and Ladoy, P.: Nonlinear variability and landscape topography: analysis and simulation, in: Fractals in geography, edited by: Lam, N. S.-N. and Cola, L. D., PTR Prentice-Hall, London, 1993.
Li, Y., Cai, W., and Campbell, E.: Statistical modeling of extreme rainfall in southwest Western Australia, J. Climate, 18, 852–863, 2005.
Li, Z., Zheng, F.-L., Liu, W.-Z., and Flanagan, D. C.: Spatial distribution and temporal trends of extreme temperature and precipitation events on the Loess Plateau of China during 1961–2007, Quatern. Int., 226, 92–100, 2010a.
Li, Z., Zheng, F., and Liu, W.: Analyzing the spatial temporal changes of extreme precipitation events in the loess plateau from 1961 to 2007, J. Nat. Res., 25, 291–299, 2010b.
Li, Z., Xu, X., Xu, C., Liu, M., Wang, K., and Yu, B.: Annual Runoff is Highly Linked to Precipitation Extremes in Karst Catchments of Southwest China, J. Hydrometeorol., 18, 2745–2759, 2017.
Liu, B., Chen, J., Chen, X., Lian, Y., and Wu, L.: Uncertainty in determining extreme precipitation thresholds, J. Hydrol., 503, 233–245, 2013.
Lovejoy, S. and Schertzer, D.: Scaling and multifractal fields in the solid earth and topography, Nonlin. Processes Geophys., 14, 465–502, https://doi.org/10.5194/npg-14-465-2007, 2007.
Lovejoy, S. and Schertzer, D.: The weather and Climate: emergent laws and multifractal cascades, Cambridge University Press, Cambridge, 2013.
Ludwig, W. and Probst, J. L.: River sediment discharge to the oceans; present-day controls and global budgets, Am. J. Sci., 298, 265-295, 1998.
Manola, I., van den Hurk, B., De Moel, H., and Aerts, J. C. J. H.: Future extreme precipitation intensities based on a historic event, Hydrol. Earth Syst. Sci., 22, 3777–3788, https://doi.org/10.5194/hess-22-3777-2018, 2018.
Miao, C., Sun, Q., Duan, Q., and Wang, Y.: Joint analysis of changes in temperature and precipitation on the Loess Plateau during the period 1961–2011, Clim. Dynam., 47, 3221–3234, 2016.
Miao, C., Duan, Q., Sun, Q., Lei, X., and Li, H.: Non-uniform changes in different categories of precipitation intensity across China and the associated large-scale circulations, Environ. Res. Lett., 14, 025004, https://doi.org/10.1088/1748-9326/aaf306, 2019.
Min, S., Zhang, X., Zwiers, F. W., and Hegerl, G. C.: Human contribution to more-intense precipitation extremes, Nature, 470, 378–381, 2011.
Ministry of Water Resources and National Bureau of Statistics: Bulletin of First National Census for Water, China Water & Power Press, Beijing, 2013.
Oliver, M. A. and Webster, R.: Kriging: a method of interpolation for geographical information systems, Int. J. Geogr. Inf. Syst., 4, 313–332, 1990.
Pandey, G., Lovejoy, S., and Schertzer, D.: Multifractal analysis of daily river flows including extremes for basins of five to two million square kilometres, one day to 75 years, J. Hydrol., 208, 62–81, 1998.
Papalexiou, S. M., Koutsoyiannis, D., and Makropoulos, C.: How extreme is extreme? An assessment of daily rainfall distribution tails, Hydrol. Earth Syst. Sci., 17, 851–862, https://doi.org/10.5194/hess-17-851-2013, 2013.
Parisi, G. and Frisch, U.: A multifractal model of intermittency, in: Turbulence and predictability in geophysical fluid dynamics and climate dynamics, edited by: Ghil, M., Benzi, R., and Parisi, G., Elsevier North Holland, New-York, 1985.
Pecl, G. T., Araújo, M. B., Bell, J. D., Blanchard, J., Bonebrake, T. C., Chen, I.-C., Clark, T. D., Colwell, R. K., Danielsen, F., and Evengård, B.: Biodiversity redistribution under climate change: Impacts on ecosystems and human well-being, Science, 355, eaai9214, https://doi.org/10.1126/science.aai9214, 2017.
Pfahl, S., O'Gorman, P. A., and Fischer, E. M.: Understanding the regional pattern of projected future changes in extreme precipitation, Nat. Clim. Change, 7, 423–427, https://doi.org/10.1038/NCLIMATE3287, 2017.
Ran, D., Liu, L., Zhao, L., Bai, Z., Liu, B., and Wang, H.: The soil conservation practices and streamflow and sediment load changes in the Hekou-Longmen region of middle reaches of Yellow River, Yellow River Water Conservancy Press, Zhengzhou, 2000.
Ren, M.-E.: Sediment discharge of the Yellow River, China: past, present and future – a synthesis, Adv. Earth Sci., 21, 551–563, 2006.
Rustomji, P., Zhang, X., Hairsine, P., Zhang, L., and Zhao, J.: River sediment load and concentration responses to changes in hydrology and catchment management in the Loess Plateau region of China, Water Resour. Res., 44, W00A04, https://doi.org/10.1029/2007WR006656, 2008.
Schertzer, D. and Lovejoy, S.: Physical modeling and analysis of rain and clouds by anisotropic scaling multiplicative processes, J. Geophys. Res.-Atmos., 92, 9693–9714, 1987.
Shi, H. and Shao, M.: Soil and water loss from the Loess Plateau in China, J. Arid Environ., 45, 9–20, 2000.
Stow, D., Daeschner, S., Hope, A., Douglas, D., Petersen, A., Myneni, R., Zhou, L., and Oechel, W.: Variability of the seasonally integrated normalized difference vegetation index across the north slope of Alaska in the 1990s, Int. J. Remote Sens., 24, 1111–1117, 2003.
Sunyer, M. A., Hundecha, Y., Lawrence, D., Madsen, H., Willems, P., Martinkova, M., Vormoor, K., Bürger, G., Hanel, M., Kriauǐūnienė, J., Loukas, A., Osuch, M., and Yücel, I.: Inter-comparison of statistical downscaling methods for projection of extreme precipitation in Europe, Hydrol. Earth Syst. Sci., 19, 1827–1847, https://doi.org/10.5194/hess-19-1827-2015, 2015.
Svensson, C. and Jones, D. A.: Dependence between sea surge, river flow and precipitation in south and west Britain, Hydrol. Earth Syst. Sci., 8, 973–992, https://doi.org/10.5194/hess-8-973-2004, 2004.
Swendsen, R. H. and Wang, J.-S.: Nonuniversal critical dynamics in Monte Carlo simulations, Phys. Rev. Lett., 58, 86–88, 1987.
Tang, K.: The soil conservation practices and streamflow and sediment load changes in the Hekou-Longmen region of middle reaches of Yellow River, Yellow River Water Conservancy Press, Zhengzhou, 1990.
Tang, K.: The changes of erosion, runoff and sediment in the Yellow River, Science China Press, Beijing, 1993.
Tang, K.: Soil and water conservation in China, Science China Press, Beijing, 2004.
Tessier, Y., Lovejoy, S., and Schertzer, D.: Universal multifractals: theory and observations for rain and clouds, J. Appl. Meteorol., 32, 223–250, 1993.
Tessier, Y., Lovejoy, S., and Schertzer, D.: Multifractal analysis and simulation of the global meteorological network, J. Appl. Meteorol., 33, 1572–1586, 1994.
Tessier, Y., Lovejoy, S., Hubert, P., Schertzer, D., and Pecknold, S.: Multifractal analysis and modeling of rainfall and river flows and scaling, causal transfer functions, J. Geophys. Res., 101, 26427–26440, 1996.
Walther, G.-R., Post, E., Convey, P., Menzel, A., Parmesan, C., Beebee, T. J., Fromentin, J.-M., Hoegh-Guldberg, O., and Bairlein, F.: Ecological responses to recent climate change, Nature, 416, 389–395, 2002.
Wan, L., Zhang, X., Ma, Q., Zhang, J., Ma, T., and Sun, Y.: Spatiotemporal characteristics of precipitation and extreme events on the Loess Plateau of China between 1957 and 2009, Hydrol. Process., 28, 4971–4983, 2014.
Wang, G., Wang, D., Trenberth, K. E., Erfanian, A., Yu, M., Bosilovich, M. G., and Parr, D. T.: The peak structure and future changes of the relationships between extreme precipitation and temperature, Nat. Clim. Change, 7, 268–274, 2017.
Wang, S., Fu, B., Piao, S., Lü, Y., Ciais, P., Feng, X., and Wang, Y.: Reduced sediment transport in the Yellow River due to anthropogenic changes, Nat. Geosci., 9, 38–41, 2015.
Wischmeier, W. H.: Use and misuse of the universal soil loss equation, J. Soil Water Conserv., 31, 5–9, 1976.
Xin, Z., Xu, J., and Ma, Y.: Spatio-temporal Variation of Erosive Precipitation in Loess Plateau during Past 50 Years, Sci. Geogr. Sin., 29, 98–104, 2009.
Zhang, J., Zhang, T., Lei, Y., Zhang, X., and Li, R.: Streamflow regime variations following ecological management on the Loess Plateau, China, Forests, 7, 1–18, https://doi.org/10.3390/f7010006, 2016.
Zhang, J., Zhang, X., Li, R., Chen, L., and Lin, P.: Did streamflow or suspended sediment concentration changes reduce sediment load in the middle reaches of the Yellow River?, J. Hydrol., 546, 357–369, 2017.
Zhang, X., Walling, D. E., Quine, T. A., and Wen, A.: Use of reservoir deposits and caesium-137 measurements to investigate the erosional response of a small drainage basin in the rolling loess plateau region of China, Land Degrad. Dev., 8, 1–16, 1997.
Zheng, F., Westra, S., and Sisson, S. A.: Quantifying the dependence between extreme rainfall and storm surge in the coastal zone, J. Hydrol., 505, 172–187, 2013.
Zheng, F., Westra, S., and Leonard, M.: Opposing local precipitation extremes, Nat. Clim. Change, 5, 389–390, 2015.
Zhou, P. and Wang, Z.: A Study on Rainstorm Causing Soil Erosion in the Loess Plateau, J. Soil Water Conserv., 6, 1–5, 1992.