Flowing wells: terminology, history and role in the evolution of groundwater science

The gushing of water from flowing wells attracted public attention and scientific curiosity as early as the 17th century, but little attention has been paid to the influence of flowing wells on the evolution of groundwater science. This study asserts that questions posed by flowing wells since the early 19th century led to the birth of many fundamental concepts and principles of physical hydrogeology. Due to the widespread occurrence of flowing wells in basins with regional aquitards, there is a long-lasting misconception that flowing wells could only occur in regionally confined aquifers. However, the recognition of possible occurrence of flowing wells in unconfined aquifers was anticipated at the turn of the 20th century based on observed increases in hydraulic head with depth in topographic lows of basins without apparent aquitards. This was later verified in the 1960s by field and modeling studies that gave birth to quantitative analysis of topographically driven groundwater flow systems, which was a paradigm shift in hydrogeology. Following this paradigm, several preconditions for flowing wells established in the 19th century were found unnecessary. Intermingled in the evolution of flow system concepts are inconsistencies and confusion concerning the use of the term “artesian”, so we propose avoidance of this term. This historical perspective of the causes of flowing well conditions and the influence of flowing wells on groundwater science could lead to a deeper understanding of the evolution of groundwater science and guide future studies on hydraulics of flowing wells.

1 Introduction

The primary motivation for the study of groundwater is its importance as a resource (Back and Herman, 1997; Freeze and Cherry, 1979). Groundwater from springs was utilized in the Middle East some 10 000 years ago (Beaumont, 1973) and produced from shallow flowing wells in the Western Desert of Egypt in the first millennium BCE as dug wells reached greater depths (Commander, 2005). However, hydrogeology did not emerge as a distinct science until the 19th century (Fetter, 2004), which corresponds to a period when deeper-drilled flowing wells became a substantial source of water supply in Europe (Howden and Mather, 2013). It was acknowledged that the recognition of the great value of flowing wells in Europe in the 18th century stimulated the advancement of water well drilling technology (Davis and De Wiest, 1966), and the maturation of geological and hydrological sciences in the 19th century led to the birth of hydrogeology in the 19th century (Meyer et al., 1988). However, little attention has been paid to the importance of the scientific questions prompted by flowing wells in the early evolution of groundwater science in the 19th century.

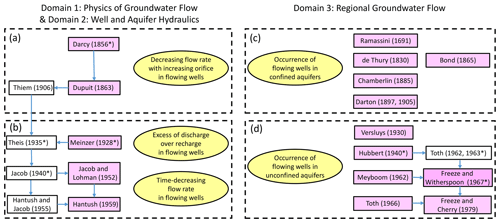
Figure 1 Four threads of evolution of physical hydrogeology stemmed from flowing wells. The yellow ellipses are field phenomena of flowing wells, the purple boxes are papers directly related to flowing wells, and the white boxes are papers less or not directly related to flowing wells but have connections to previous or follow-up studies on flowing wells. The publications labeled with a “^*” are the seven classical studies identified by both Freeze and Back (1983) and Anderson (2008).

This review aims to demonstrate that flowing wells contributed to not only the birth but also the evolution of several aspects of hydrogeology. Freeze and Back (1983) divided physical hydrogeology into three domains, i.e., physics of groundwater flow, well hydraulics and regional groundwater flow. Following these domains, studies directly or indirectly related to flowing wells are divided into four threads (Fig. 1), covering all of the three domains. The first three threads shown in Fig. 1 stem from flowing wells in confined aquifers, while the fourth is from flowing wells in unconfined aquifers. Following Freeze and Cherry (1979), a confined aquifer is a saturated permeable geologic unit that is confined between two aquitards, while an unconfined aquifer is the saturated part of a permeable geologic unit in which the water table forms the upper boundary. The seven classical studies that were selected by both Freeze and Back (1983) and Anderson (2008) as benchmark papers of physical hydrogeology (groundwater hydrology) have been included in the four threads. Moreover, four out of the seven papers are directly related to flowing wells, implying that flowing wells can be considered, at least, one of the roots of physical hydrogeology.

The paper is organized as follows. We first introduce the terms used to represent flowing wells, with conceptual examples of the root difference between confined and unconfined sources for these wells (Sect. 2). Section 3 summarizes the history of drilling flowing wells in selected regions that have inspired hydrogeologists. Sections 4 through 7 then historically sequence the principal hydrogeological publications through which flowing wells played a major role in the evolution of the science as we know it today. Finally, concluding remarks are given in Sect. 8.

2 Terms related to flowing wells and confusion of “artesian”

2.1 Terms representing flowing wells

In the groundwater hydrology, hydrogeology or hydrology textbooks available to the authors, we found that the phenomenon of a well that overflows at the surface is defined or at least mentioned in 34 textbooks. The widely used terms include “flowing well”, “artesian well” and “flowing artesian well”, which appear in 17, 15 and 13 textbooks, respectively (sometimes more than one term is used in one book). Other less frequently used terms include “artesian flowing well”, “overflowing well” and “free flowing well”. For convenience of discussion, we divide these six terms into two categories: those using the term “artesian”, and those not using “artesian”.

The terms “flowing well”, “overflowing well” and “free flowing well” stem purely from the phenomenon of water overflow at the well outlet, presumably at grade level. The term “overflowing well” has been used in Britain since at least as early as the 1820s (Anonymous, 1822) and currently is still widely used in Britain, as found in several textbooks (Hiscock and Bense, 2014; Price, 1996; Rushton, 2003). To the best of the authors' knowledge, the term “flowing well” was first used in the USGS (United States Geological Survey) hydrogeologic report The Requisite and Qualifying Conditions of Artesian Wells (Chamberlin, 1885) and is currently the one most widely used. The term “free flowing well” can be found in three textbooks available to us (Fitts, 2013; Kruseman and de Ridder, 1990; Nonner, 2003). By including the adjectives “flowing”, “overflowing” or “free flowing”, these terms have clear meaning to represent wells that groundwater could flow out of without the aid of pumping.

The number of textbooks that use one or two of the terms “artesian well”, “flowing artesian well” or “artesian flowing well” is as high as 28, indicating the popularity of the adjective “artesian”. The term “artesian well” originates from “well of Artois” (“Artesia” is the historical Latin name of Artois, an ancient province in northern France). It is unquestionable that it was the phenomenon of water overflow at the surface which attracted people's attention to wells of Artois drilled in 1126 (Fuller, 1906; Norton, 1897). The term “artesian fountain” was applied in French scientific literature to represent flowing wells in 1805 (Lionnais, 1805), and the term “artesian well” was widely used in France, Britain and the United States in the 1820s and 1830s (Arago, 1835; Buckland, 1836; de Thury, 1830; Garnier, 1822; Storrow, 1835). Currently, an artesian well is synonymous with a flowing well in the majority of European textbooks we have inspected (Hendriks, 2010; Kruseman and de Ridder, 1990; Price, 1996; Rushton, 2003; Brassington, 2017; Davie, 2008; de Marsily, 1986; Hölting and Coldewey, 2019) and in at least eight textbooks in North America (Deming, 2002; Domenico and Schwartz, 1998; Driscoll, 1986; Pinder and Celia, 2006; Yeh et al., 2015; Hornberger et al., 2014; Fitts, 2013; Alley and Alley, 2017) . Since the late 19th century, the term artesian well was not restricted to flowing wells but was divided into flowing artesian wells and non-flowing artesian wells (Carpenter, 1891; Norton, 1897; Slichter, 1899). In the 10 textbooks in North America that we inspected (Fetter, 2001; Freeze and Cherry, 1979; Batu, 1998; Kasenow, 2010; LaMoreaux et al., 2009; Mays, 2012; McWhorter and Sunada, 1977; Heath, 1983; Schwartz and Zhang, 2003; Todd and Mays, 2004), the term flowing artesian well is used to represent a flowing well, and an artesian well is equivalent to a well penetrating a confined aquifer but not necessarily flowing at the surface.

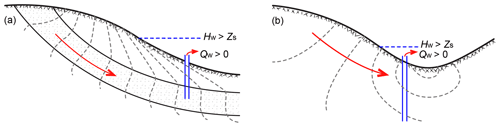
Due to the widespread occurrence of aquitards, it was initially believed that only a confined aquifer bounded by aquitards has the possibility for the static water level to have hydraulic head higher than the ground surface elevation, i.e., flowing wells could occur only in confined aquifers. Later studies found that flowing wells could also occur in an unconfined aquifer, i.e., a homogeneous aquifer without aquitards (Hubbert, 1940; Tóth, 1966; Versluys, 1930). Because the adjective “artesian” indicates the type of aquifer in Artois, i.e., a confined aquifer, according to the definitions given by the USGS, the term “flowing artesian well” was restricted to flowing wells in confined aquifers (Lohman, 1972b), and it was explicitly pointed out that “a flowing well does not necessarily indicate artesian conditions” (Heath, 1983). To differentiate flowing wells in confined and unconfined aquifers, Tóth (1966) defined confined-flow flowing wells and unconfined-flow flowing wells as two end-members of flowing wells, while Freeze and Cherry (1979) defined geologically controlled flowing wells and topographically controlled flowing wells. As shown in Fig. 2, geologically controlled flowing wells are equivalent to Tóth's confined-flow flowing wells, while topographically controlled flowing wells correspond to Tóth's unconfined-flow flowing wells. Note that in geologically controlled flowing wells, topography is still the driving force of groundwater flow from the topographic highs to topographic lows. Therefore, we avoid the terms of geologically controlled and topographically controlled flowing wells, and we use the terminology by Tóth (1966) in the following discussion.

Figure 2 (a) Geologically controlled or confined-flow flowing wells; (b) topographically controlled or unconfined-flow flowing wells (modified from Freeze and Cherry, 1979). It is assumed that the screened intake for the respective well is at its bottom.

2.2 Confusing uses of “artesian” in the literature

The adjective “artesian”, which was initially used in terms “artesian fountain” and “artesian well”, has been applied to such terms as “artesian water”, “artesian aquifer” and “artesian pressure”. Following the definitions given by the USGS (Lohman, 1972a), and as used in many USGS publications, the term “artesian aquifer” is equivalent to “confined aquifer”, “artesian water” refers to groundwater from or within a confined aquifer, and “artesian pressure” is the water pressure in a confined aquifer. An artesian basin was defined by Meinzer (1923b) to be a basin in which water is confined under artesian pressure, implying that the hydraulic head being greater than the elevation of ground surface is not a necessary condition. The Great Artesian Basin in Australia is one of the largest artesian basins in the world and is well known for its numerous flowing wells in confined aquifers. In the United States, there are many artesian basins, like the artesian basin of the Dakotas (Darton, 1905; Swenson, 1968), the great Paleozoic artesian basin of the Mississippi Valley region (Meinzer, 1923a), the Roswell artesian basin in New Mexico (Fiedler and Nye, 1933), and the Grand Junction artesian basin in Colorado (Jacob and Lohman, 1952), all of which had many flowing wells in the initial stage of groundwater development, but many of which currently have static water levels significantly below grade.

The different meanings of “artesian” caused confusion not only to beginners of hydrogeology but also to professional hydrogeologists, which has been realized by some textbook authors. Deming (2002) and Younger (2007) both chose photos of a flowing well for their cover image, but they have quite opposite viewpoints on “artesian”. Deming (2002) held the opinion that “artesian” implies that the hydraulic head is greater than the elevation of ground surface; defining “artesian aquifer” to be identical to confined aquifer would make the definition not only conceptually useless but also etymologically incorrect, because wells drilled in Artois could flow spontaneously. On the contrary, Younger (2007) believed that “artesian” is a synonym of “confined” and pointed out that “artesian” is also widely misused to refer to any well from which water flows without pumping, a phenomenon which is not restricted to confined aquifers. Younger also discouraged further use of “artesian”, because it lacks intuitive meaning in modern English.

To sum up, hydrogeologists are keenly interested in flowing wells, but the literature is confusing concerning the qualifier of “artesian”. This confusion has likely led to the groundwater community underestimating the role that flowing wells have played in the evolution of its science. Given that the meaning of the adjective “artesian” has a few meanings in the literature, the meaning can be unclear unless it is defined in each publication of use. There is no necessity to preserve this term in groundwater science; therefore, we propose that its use be avoided.

3 The history of drilling flowing wells in selected regions

Here, we briefly review the history of both shallow and deep flowing wells in regions that most directly contributed to the development of modern groundwater science.

3.1 France

As early as 1126, a shallow flowing well tapping the confined fringe of the chalk aquifer was identified in Artois in northern France (Margat et al., 2013). In the early 19th century, the technique of cable-tool drilling (also called percussion drilling) resulted in drilling of deeper flowing wells in France. Garnier (1822) published the first technical guidebook on drilling “artesian” wells. It was stated that with the exception of some provinces, there are few parts of France where artesian wells are not to be expected. Garnier obtained a prize from the Society for the Encouragement of Industry due to the publication of this book, which reflects the interest of the French government in flowing wells.

According to Arago (1835), most flowing wells up to that time ranged in depth from 36 to 177 m. Between 1833 and 1841, a flowing well with a depth of 548 m was drilled in Grenelle within the Paris Basin. The water level in this flowing well could rise to a height of 33 m above ground surface in a pipe supported by a wooden scaffolding accessible by steps. In 1855, an article titled The Artesian Well at Grenelle, in France was reproduced in California Farmer and Journal of Useful Sciences in the United States (Anonymous, 1855). It was commented that “This splendid achievement at that date may be looked upon as the pioneer effort, and at the present time, and within a very few years, the most astonishing results may be expected.”. In 1861, another flowing well with a depth of 586 m was completed in Passy near Paris, which is the last flowing well in Paris still in use today. Darcy (1856) and Dupuit (1863) were both inspired by flow rate measurements at different orifices in these deep flowing wells. The details are given in Sect. 5.

3.2 Italy

According to Norton (1897), nearly equal in antiquity with the flowing wells of Artois are those of Modena in northern Italy, which might have disputed with Artois on the right to provide their name to flowing wells. It was noteworthy that two well-borer's augers were used in the municipal coat of arms, indicating the influence of wells on the town. Giovanni Cassini (1625–1712) referred to flowing wells in Modena and Bologna and developed one himself at the castle of Urbin (Merdinger, 1955). A shallow flowing well can be obtained by digging to a depth of ∼20 m and boring a hole for the next ∼1.5 m by using an auger (Biswas, 1970).

Based on the famous flowing wells of Modena, Bernardino Ramazzini (1633–1714) and Antonio Vallisnieri (1661–1730) connected flowing wells to the water cycle and pioneered the theory of artesian water pressure in the late 1600s and early 1700s (Duffy, 2017). The details are introduced in Sect. 4.1.

3.3 Great Britain

By the end of the 1700s, some shallow flowing wells had been dug in Great Britain. In 1785, a flowing well (artificial spring) with a depth of ∼3.7 m was dug ∼91 m away from the Derwent River in Derby (“Darwent”; Darwin, 1785). One of the first flowing wells near London was completed in 1794 (Buckland, 1836). The successful experiences of water supply from flowing wells led to sinking of more flowing wells. According to Macintosh (1827), James Ryan obtained a patent on boring for minerals and water in 1805, while John Goode obtained a patent on boring for the purpose of obtaining and raising water in 1823, indicating that drilling was active in Great Britain in the early 19th century. According to an article in Monthly Magazine and British Register (Anonymous, 1822), two flowing wells with depths of 32 and 37 m were drilled in the town of Tottenham in 1821, and many flowing wells had existed for a period of time in various parts of the country by 1822.

The publication of Garnier (1822) in France aroused further interest in flowing wells in Great Britain (Farey, 1823). Although many flowing wells had been drilled in the London Basin, many boreholes failed to become flowing wells. Therefore, Buckland (1836) called for a theory of flowing wells. The experience gained from the costly failures improved understanding of conditions necessary for the success of a flowing well; the details of which are discussed in Sect. 4.1.

3.4 The United States

Accompanying the increase in population due to immigration and western expansion in the US, there was a higher demand of water resources for drinking and for agriculture. As a result of the increased drilling technology since the 19th century, deep groundwater was utilized by drilling numerous wells, many of which were flowing wells, at least in the initial stage of development. Here, we list some regions where flowing wells were drilled, resulting in significant advances in groundwater science.

Development of the Cambrian–Ordovician aquifer system in the northern US Midwest can be traced to 1864 when a flowing well with a depth of 217 m was drilled in Chicago (Konikow, 2013). By the end of the 19th century, flowing wells were common in topographically low areas in the Mississippi, Missouri and Illinois river valleys; near Lake Michigan; and around Lake Winnebago in northeastern Wisconsin (Young, 1992). At the beginning of the 21st century, there were still many flowing wells newly drilled in Michigan (Gaber, 2005). Chamberlin's (1885) classic report based on the hydrogeologic conditions in Wisconsin is considered one of the roots of groundwater science in Wisconsin (Anderson, 2005). In 1876, a flowing well with a depth of 293 m and an initial flow rate of 3270 m³ d⁻¹ drilled in Prairie du Chien, Wisconsin, was named “The Greatest Artesian Fountain in America” (Meiter, 2019). A photo of this flowing well served as the frontispiece of Chamberlin (1885) and Freeze and Back (1983) and the cover image of Deming (2002), and it was also cited in Anderson (2005).

In the US Great Plains, interest in groundwater emerged due to the irrigation demands beginning in the 1880s, due to the widespread drought. In early 20th century, flowing wells were common in topographic lows near rivers, e.g., in the Arkansas River valley of southeastern Colorado, much of South Dakota, and parts of southeastern North Dakota and northeastern Nebraska in the Missouri River valley (Darton, 1905). In South Dakota and North Dakota within the Great Plains, some 400 deep wells were drilled into the Dakota sandstone by 1896, of which over 350 were flowing wells (Darton, 1897). Due to the introduction of the jetting method of drilling in around 1900, thousands of small-diameter wells were drilled to the Dakota sandstone during the following 2 decades. There were about 10 000 deep wells in South Dakota in 1915 and between 6000 and 8000 deep wells in North Dakota in 1923 (Meinzer and Hard, 1925). Due to the increased withdrawal of deep groundwater, many flowing wells became non-flowing wells, accompanied by decreasing flow rates in the flowing wells that still flowed. The condition of flowing wells led to improved understanding of the pattern of groundwater circulation in confined aquifers (Darton, 1905), while the changing production rates led to the birth of the concept of compressibility and the role of compressibility on production in confined aquifers (Meinzer and Hard, 1925; Meinzer, 1928). The details are discussed in Sect. 6.1.

In flowing wells of the Dakota aquifer, it was noted that “the pressure increases for several hours or even days after the flow is shut off, and when opened the flow decreases in the same way until the normal flow is reached” (Meinzer, 1928). Several decades later, based on field observations of decreasing flow rate with time in flowing wells in the Grand Junction artesian basin and in the Roswell artesian basin in New Mexico, constant-drawdown aquifer tests were proposed to obtain hydraulic parameters (Jacob and Lohman, 1952; Hantush, 1959). More details are discussed in Sect. 6.2.

3.5 Australia

The Great Artesian Basin, which covers one-fifth of the total area of Australia, is one of the largest and best-known groundwater basins in the world (Ordens et al., 2020). The first shallow flowing well was dug to a depth of 43 m by using an auger near a spring in New South Wales in 1878, while the first deep machine-drilled flowing well was completed in 1887 at a depth of 393 m near Cunnamulla, Queensland (Williamson, 2013). By the end of the 19th century, there were already around 1000 flowing wells on the continent (van der Gun, 2019). The exploitation of flowing wells and artesian water contributed to the emergence of hydrogeology as a discipline in Australia (Williamson, 2013), and the development of such sources has played a vital role in the pastoral industry in the arid and semiarid regions of Australia (Habermehl, 2020).

Due to the occurrence of intervening aquifers and aquitards, the Great Artesian Basin is a multilayered confined aquifer system. Although head drawdowns of up to 100 m have been recorded in highly developed areas, hydraulic heads in the Jurassic and Lower Cretaceous aquifers are still above ground surface throughout most of the basin (Habermehl, 2020). A comprehensive review of the history and recent research status of the basin can be found in Ordens et al. (2020).

3.6 Canada

The hydrogeology of the Canadian Prairies has been studied since the beginning of the 20th century. Groundwater in this region is largely obtained from surficial Pleistocene glacial drift and the underlying bedrock of Tertiary or Cretaceous age. Due to the occurrence of a large number of flowing wells, either in the glacial drift or in the bedrock, great attention was paid to the relation between topography, geology and areas with flowing wells during basin-scale groundwater surveys (Meyboom, 1966). A similarity between the potentiometric surface and the local topography was widely observed in many parts of the Canadian Prairies (Jones, 1962; Meyboom, 1962; Tóth, 1962; Farvolden, 1961).

The Trochu area in central Alberta, which covers an area of 67 km², is representative of the hydrogeology of the Canadian Prairies. There were 10 shallow flowing wells ranging in depth from 9 to 27 m in topographic lows (Tóth, 1966). Because the glacial deposits have low contents of clay, they are efficient for infiltration of rainfall and evaporation of soil water. Combined with previous theoretical findings on topographically driven flow systems (Hubbert, 1940; Tóth, 1962, 1963), these flowing wells were considered to be controlled by topography and typical manifestations of groundwater discharge (Tóth, 1966). The details are discussed in Sect. 7.

3.7 China

As early as in the 11th century, deep drilling using bamboo pipes was employed in Sichuan Province, China, to reach brines from 100 m deep boreholes (Vogel, 1993). In the 16th century, a flowing well in Beijing became a site of tourism known as “Manjing” (literally meaning a well full of water). In the 17th century, due to the success of developing flowing wells for brines, “Ziliujing” (meaning flowing well) became the name of a town in Sichuan Province. In 1835, the 1001 m deep flowing well at Shenhai (frequently mistaken to be Xinhai in the English literature) was constructed for producing brines and gases (Vogel, 1993). However, these early drilling techniques and experiences of drilling deep flowing wells did not substantially produce follow-on activity in the development of groundwater science in China. In the early 1950s, the large demand of groundwater in (semi)arid regions led to exploration of groundwater and resulted in the establishment of hydrogeology as a distinct discipline in several universities. In the late 1950s, the success of drilling some flowing wells led to a campaign for finding more flowing wells for agriculture in many basins of the country. Unfortunately, due to overexploitation, flowing wells have disappeared in many regions, including the North China Plain.

One of the most intensively studied groundwater basins is the Ordos Plateau in northwestern China, composed mainly of a thick sandstone aquifer of Cretaceous age, up to around 1000 m thick. Because the overlying thin Quaternary deposits have much higher permeability and there is no continuous aquitard within the Cretaceous sandstone, the Ordos Plateau can be conceptualized as a thick unconfined aquifer (Hou et al., 2008; Jiang et al., 2018). As early as the 1950s, several flowing wells were established in deep boreholes in the Cretaceous sandstone in topographic lows; subsequently, numerous flowing wells were drilled for agricultural water. For example, in the Wudu lake catchment, on this plateau with an area of approximately 200 km², there were 15 flowing wells in 2015 (J. Z. Wang et al., 2015). In recent years, additional flowing wells have been drilled. The majority of flowing wells in this catchment range in depth from 70 to 300 m, with one well reaching the bottom of the Cretaceous sandstone at a depth of 800 m.

To reduce costs, the flowing wells drilled into the Cretaceous sandstone are cased only in the very shallow part that corresponds to the Quaternary deposits. These wells provide a prime example to study the hydraulics of flowing wells in a macroscopically homogeneous basin. The steady-state hydraulics of flowing wells in homogeneous basins is introduced in Sect. 7.3.

4 Confined-flow flowing wells and confined flow bounded by aquitards (1690s–current)

4.1 Conditions of confined-flow flowing wells

Based on his observations of flowing wells in Modena, Italy, in 1691, Ramassini plotted a geological section showing the occurrence of flowing wells penetrating a confined aquifer, receiving its water from an underground reservoir at a higher level in the surrounding mountain (Biswas, 1970). Therefore, for the occurrence of flowing wells, Ramassini already suspected the role of topography or the hydraulic gradient between the well and the underground reservoir in the surrounding mountain (de Vries, 2007). Unfortunately, he thought the source of water in the underground reservoir in the surrounding mountain was more likely to be from the sea. Later, Valniseri argued in 1726 that the source of water in the flowing wells of Modena must be rainfall and snowmelt in the adjacent Apennine Mountains (Duffy, 2017), which was the start of thinking about the simultaneous control of topography and precipitation on flowing wells.

In the evolution of thinking about groundwater, it was universally accepted by the early 19th century that the water from flowing wells came from rainfall, which found its way through the pores or fractures of a permeable stratum sandwiched between two water-tight strata at depth (Garnier, 1822). De Thury (1830) summarized three conditions of flowing wells. In his words, the first is to reach a flow of deep water coming from higher basins and passing along the bosom of the Earth between compact and impermeable rocks; the second is to afford this deep water the possibility of rising to the surface by using an artificially bored well; and the third is to prevent the spreading of the ascending water into the surrounding sand or rock by inserting tubes into the bored well.

Following the successful drilling of flowing wells in France, the theory of the mechanism of flowing wells became well understood in Britain. For example, Buckland (1836) illustrates the cause of two flowing wells in the confined aquifer of the London Basin. The successful experiences coupled with the costly failures of drilling in Britain led to the recognition of three necessary conditions for the success of a flowing well (Bond, 1865):

(1) The existence of a porous stratum having a sufficient outcrop on the surface to collect an adequate amount of rainfall and passing down between two impermeable strata; (2) the level of the outcropping portion of the porous stratum must be above that of the orifice of the well, so as to give a sufficient rise to the water; and (3) there must be no outlet in the porous stratum by which its drainage can leak out, either in the shape of a dislocation, by which it can pass into lower strata, or a natural vent, by which it can rise to the surface at a lower level than the well.

Based on his North American experience with the Wisconsin portion of the Cambrian–Ordovician aquifer system, Chamberlain (1885) published The Requisite and Qualifying Conditions of Artesian Wells and listed seven conditions of flowing wells, which include the following:

(1) A pervious stratum to permit the entrance and the passage of the water; (2) a water-tight bed below to prevent the escape of the water downward; (3) a like impervious bed above to prevent escape upward, for the water, being under pressure from the fountain-head, would otherwise find relief in that direction; (4) an inclination of these beds, so that the edge at which the waters enter will be higher than the surface at the well; (5) a suitable exposure of the edge of the porous stratum, so that it may take in a sufficient supply of water; (6) an adequate rainfall to furnish this supply; and (7) an absence of any escape for the water at a lower level than the surface at the well.

In fact, the seven prerequisites given by Chamberlain (1885) are inclusive of the three conditions given by de Thury (1830) and Bond (1865) several decades earlier. However, Bond (1865) did not cite de Thury (1830), and Chamberlin (1885) did not cite either Bond (1865) or de Thury (1830); therefore, we assume their findings were obtained independently.

4.2 Confined flow bounded by aquitards

In the late 1890s, Darton (1897) with the USGS investigated the occurrence of flowing wells in the Dakotas and plotted the cross section of the Dakota aquifer (Fig. 3). By constructing contours of hydraulic head of the Dakota confined aquifer across South Dakota, which shows the head loss through the confined aquifer, Darton (1905) concluded that groundwater discharged by the flowing wells in the east had flowed hundreds of kilometers horizontally through the aquifer from outcrops in the west. This study popularized the pattern of groundwater flow in a confined aquifer that outcrops in topographic highs as shown in Fig. 2a. There was also a long-lasting conceptual model for the Great Artesian Basin of Australia that each aquifer can be considered to be laterally continuous across the extent of the basin (Habermehl, 2020).

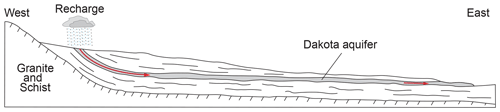
Figure 3 The profile of the Dakota confined aquifer and the confined flow bounded by aquitards (modified from Darton, 1897).

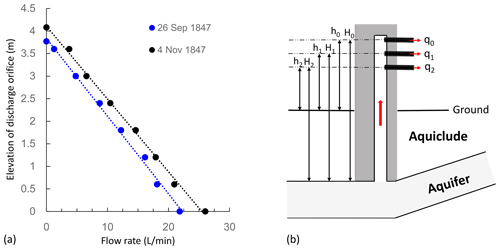
Figure 4 (a) The changes in flow rate with elevation of discharge orifice of a flowing well (data from Darcy, 1856); (b) the device for measuring flow rate (only one discharge orifice is open during measurement). The higher flow rate in November shown in (a) can be a result of higher hydraulic head surrounding the flowing well, probably due to the contribution of groundwater recharge.

As shown in Fig. 3, groundwater flow in a confined aquifer, which is bounded by the adjacent aquitards, is similar to flow through a pipe. Such a flow pattern is commonly utilized to interpret groundwater age in confined aquifers, which is known as piston flow age (Bethke and Johnson, 2008; Hinkle et al., 2010). Because many hydrogeochemical processes are dependent on travel time through the aquifer, hydrochemical facies (Back, 1960, 1966) usually evolve along the flow path bounded by aquitards. Therefore, such a flow pattern, which stemmed from analyzing confined-flow flowing wells, is the cornerstone of sampling and analyzing groundwater geochemistry and isotopes in confined aquifers.

5 Darcy's law and steady-state well hydraulics inspired by flowing wells (1850s–1910s)

5.1 The birth of Darcy's law evoked by flowing wells

It is widely known that Darcy's law, which represents the beginning of groundwater hydrology as a quantitative science in 1856 (Freeze and Back, 1983), was established based on sand column experiments. In fact, the sand column experiments were designed to confirm a linear correlation between flow rate and head loss in sands which was first recognized in flowing wells (Brown, 2002; Ritzi and Bobeck, 2008). Flowing wells were important sources of water supply in the Paris Basin since the early 19th century, and this led to flow rates being measured at different elevations of discharge orifices in several flowing wells in the 1840s (Fig. 4). In fact, such experiments can be regarded as constant-head (drawdown) tests at multiple discharge orifices in single wells. As shown in Fig. 4a, in either September or November, the flow rates increased linearly as the elevation of discharge orifice decreased. Henry Darcy's (1803–1858) interest in this linear correlation instigated his famous lab experiments with sand column (Brown, 2002; Ritzi and Bobeck, 2008).

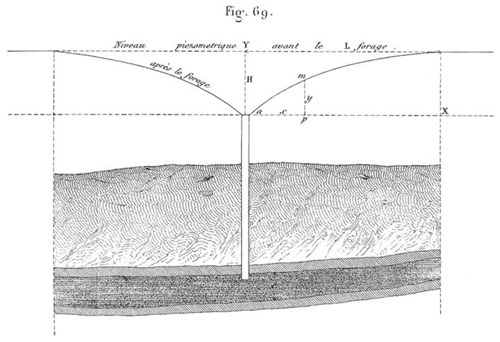
Figure 5 Plot from Dupuit (1863) showing the radial flow toward a flowing well penetrating a confined aquifer, which caused head loss with a cone of depression in the potentiometric level (“niveau piezometrique”). It is clear that the potentiometric level of the cone of depression is still above the land surface.

Theoretically, the head loss from the recharge area to the discharge orifice can be divided into head loss in the aquifer and head loss along the well pipe. According to the Chezy equation describing head loss at high flow velocities in pipes, head loss in the well pipe should be proportional to the square of flow rate. Based on the linear trend between head loss and flow rate shown in Fig. 4a, it was inferred that the head loss in the short-distance well pipe with high velocities is limited compared with the well loss in the long-distance aquifer with low velocities. To identify the control of flow velocity on head loss, Darcy conducted pipe flow experiments during 1849 and 1851 and proposed equations on the dependence of head loss on flow rate. At low velocity, the head loss was found to be linear to discharge rate, which can be written as

$$\begin{array}{}\text{(1)}& h_{\mathrm{L}}={\displaystyle \frac{La}{\mathit{\pi }{r}^{\mathrm{4}}}}q,\end{array}$$

and at high water velocity, the head loss was found to be linear to the square of discharge rate, which can be written as

$$\begin{array}{}\text{(2)}& h_{\mathrm{L}}={\displaystyle \frac{Lb}{\mathit{\pi }{r}^{\mathrm{5}}}}{q}^{\mathrm{2}},\end{array}$$

where L is length, r is pipe radius, q is the volume discharge rate, and a and b are empirical coefficients of proportionality. Equation (1) verified the Poiseuille (1841) equation by experiments under completely different circumstances, and Eq. (2) can be considered another form of the Chezy equation. Note that Eq. (2) led to the co-naming of the Darcy–Weisbach pipe friction formula. About 30 years later, Reynolds (1883) fully quantified the occurrence and differences between laminar and turbulent flow by introducing the Reynolds number.

By assuming that head loss from a position in the aquifer with constant head away from the flowing well to the discharge orifice occurs in both the aquifer and the well pipe, equations similar to the following forms were obtained:

$$\begin{array}{}\text{(3a)}& {\displaystyle }& {\displaystyle }{h}_{\mathrm{1}}+{\displaystyle \frac{a{L}^{\prime }}{\mathit{\pi }{r^{\prime }}^{\mathrm{4}}}}{q}_{\mathrm{1}}+{\displaystyle \frac{b{H}_{\mathrm{1}}}{\mathit{\pi }{r}^{\mathrm{5}}}}{q}_{\mathrm{1}}^{\mathrm{2}}\cong h_{\mathrm{2}}+{\displaystyle \frac{a{L}^{\prime }}{\mathit{\pi }{r^{\prime }}^{\mathrm{4}}}}{q}_{\mathrm{2}}+{\displaystyle \frac{b{H}_{\mathrm{2}}}{\mathit{\pi }{r}^{\mathrm{5}}}}{q}_{\mathrm{2}}^{\mathrm{2}},\text{(3b)}& {\displaystyle }& {\displaystyle }\left(h_{\mathrm{1}}-h_{\mathrm{2}}\right)+{\displaystyle \frac{b}{\mathit{\pi }{r}^{\mathrm{5}}}}\left(H_{\mathrm{1}}{q}_{\mathrm{1}}^{\mathrm{2}}-H_{\mathrm{2}}{q}_{\mathrm{2}}^{\mathrm{2}}\right)\cong -C\left(q_{\mathrm{1}}-q_{\mathrm{2}}\right),\end{array}$$

where L^′ is flow distance in the aquifer from the position with constant head to the flowing well, r^′ is radius representative of pores in the aquifer, h₁ and h₂ are the elevations of the discharge orifices measured from the ground and can be considered aquifer potentiometric heads, H₁ and H₂ are the lengths of well pipes from the bottom to the discharge orifice, and C is an unnamed constant. From the angle of a constant-head well test, the first part of the left-hand side of Eq. (3b) is the difference in aquifer head loss at the well created by changing the elevation of the discharge orifice, and the second part is the difference in the well loss from riser pipes with different flow distances. The linear relationship between h₁–h₂ and q₁–q₂ shown in Fig. 4a indicates that the second part on the left-hand side of Eq. (3b) is negligible. Therefore, Eq. (3b) changes into

$$\begin{array}{}\text{(4)}& h_{\mathrm{1}}-h_{\mathrm{2}}\cong -C\left(q_{\mathrm{1}}-q_{\mathrm{2}}\right),\end{array}$$

where C can be interpreted as the slope shown in Fig. 4a.

To confirm Eq. (4), in 1855, Darcy conducted the sand column experiments by assuming that water flow through sands is similar to water flow through the aquifer and obtained the well-known empirical equation of Darcy's law. Note that the coefficient today known as hydraulic conductivity was not named by Darcy. Hubbert (1940) rigorously interpreted hydraulic conductivity and examined Darcy's law in the light of the microscopic Navier–Stokes flow theory, which raised the sophistication of understanding of Darcy's law.

5.2 Steady-state well hydraulics in confined aquifers: Dupuit equation

In 1850, Jules Dupuit (1804–1866) succeeded Henry Darcy as Chief Director for Water and Pavements and started his research on groundwater hydraulics. The field data shown in Fig. 4a triggered Dupuit to quantify the constant C in Eq. (4). Dupuit realized that groundwater flow would radially converge to the flowing well, and head loss in the confined aquifer away from the flowing well would form a cone of depression (Fig. 5).

In radial flow, Darcy's law can be written as

$$\begin{array}{}\text{(5)}& q=k\left(\mathrm{2}\mathit{\pi }xB\right){\displaystyle \frac{\mathrm{d}y}{\mathrm{d}x}},\end{array}$$

where B is the thickness of the confined aquifer, x is the radius within the cone of depression and y is the corresponding head with reference to the elevation of the discharge orifice. Dupuit (1863) obtained the following equation by integrating Eq. (5) from the radius of the well, r_w, to the radius of influence, R:

$$\begin{array}{}\text{(6)}& h_{\mathrm{0}}-h_{\mathrm{w}}={\displaystyle \frac{q}{\mathrm{2}\mathit{\pi }kB}}\ln \left({\displaystyle \frac{R}{r_{\mathrm{w}}}}\right),\end{array}$$

where h_w is the elevation of the discharge orifice, and h₀ is the hydraulic head at the radius of influence, which equals the initial hydraulic head of the flowing well when the well has been closed for a duration of time. By comparing Eqs. (4) and (6), it can be interpreted that $C=\frac{\mathrm{1}}{\mathrm{2}\mathit{\pi }kB}\ln \left(\frac{R}{r_{\mathrm{w}}}\right)$. Dupuit (1863) explicitly stated that Eq. (6) is supported by the measurements of flow rate versus elevation of discharge orifice of flowing wells reported in Darcy (1856).

Although Eq. (6) was derived based on the hydrogeologic condition of a flowing well in a confined aquifer, it is applicable to non-flowing wells in a confined aquifer. A limitation of the equation is the difficulty of determining the radius of influence in the field. Thiem (1906) improved Eq. (6) by integrating Eq. (5) between two wells within the cone of depression and obtained an equation to determine hydraulic conductivity, which is known as the Thiem equilibrium method. Although the Thiem equation (Thiem, 1906) was introduced in almost all textbooks, Dupuit's pioneering study on steady-state radial flow to a flowing well in confined aquifers (Dupuit, 1863), which is applicable to a non-flowing well in confined aquifers, was seldom mentioned in textbooks.

Dupuit (1863) also derived similar equations for a well in unconfined aquifers by neglecting the vertical hydraulic gradient, which is currently known as the Dupuit–Forchheimer approximation. Although the vertical hydraulic gradient is neglected, the Dupuit–Forchheimer approximation is still useful in interpreting regional-scale groundwater flow problems (Haitjema and Mitchell-Bruker, 2005).

6 Compressibility of confined aquifers and transient well hydraulics inspired by flowing wells (1920s–current)

6.1 Compressibility of confined aquifers: concepts instigated by flowing wells

In the 1920s, groundwater resources were undergoing development in the United States, therefore, much of the effort of the USGS turned toward developing an inventory of wells and their production (Domenico and Schwartz, 1998). The inventory of groundwater resources in the Dakota aquifer indicated that the number of flowing wells that were still flowing was decreasing., The imbalance between groundwater discharge through flowing wells and groundwater recharge led to significant insight into the role of aquifer compressibility (Meinzer, 1928; Meinzer and Hard, 1925).

Groundwater development in the Dakota aquifer started with flowing wells in the 1880s. After active drilling in the 1900s, investigations in the 1910s showed that many flowing wells had stopped flowing. To determine the groundwater budget, a study area of 18 townships near Ellendale, North Dakota (ranges 48 to 65 west along township 129 north), with a total of 320 flowing wells supplied by the Dakota sandstone, was selected. The rate of discharge through flowing wells was estimated to be close to 0.189 m³ s⁻¹ (3000 gallons per minute) during the 38-year period from 1886 to 1923, but the rate of lateral recharge through eastward percolation was inferred to be less than 0.063 m³ s⁻¹ (1000 gallons per minute) (Meinzer and Hard, 1925). Although these estimates could be very inaccurate, they were sufficient to demonstrate the excess of discharge through flowing wells over recharge. Meinzer and Hard (1925) concluded that most of the water discharged through the flowing wells was taken out of storage in the sandstone aquifer, indicating that the sandstone aquifer was compressible. It was also observed that the artesian head would increase gradually for some time after a flowing well was shut off, which is a manifestation of elasticity of the aquifer medium (Meinzer and Hard, 1925).

By summarizing these observations of flowing wells – as well as the evidence of compressibility and elasticity of compacted sand, land subsidence in an oil field, water level fluctuations produced by ocean tides, and water level fluctuations produced by railroad trains – Meinzer (1928) concluded that confined aquifers are compressible and elastic. Although geochemical and numerical studies several decades later showed that leakage also contributed to well discharge in the Dakota aquifer (Bredehoeft et al., 1983; Leonard et al., 1983; Swenson, 1968), this did not undermine the role of flowing wells that had intrigued the interest of hydrogeologists.

Several years later, by assuming that discharge of groundwater from storage as head falls is similar to release of heat as temperature decreases, Theis (1935) recognized that confined aquifers possess a property analogous to heat capacity and derived the equation characterizing the transient behavior of hydraulic head due to discharge of a well. Theis's solution was not understood by the groundwater hydrology community until Jacob (1940) defined the coefficient of storage as a combination of vertical compressibility of the porous medium and compressibility of water. Thereafter, numerous efforts were devoted to determining the aquifer parameters using transient well hydraulics and identifying the behavior of drawdown or flow rate in other aquifers (leaky aquifers, unconfined aquifers).

6.2 Transient well hydraulics in flowing and non-flowing wells in confined aquifers

In the early 1930s, the high demand for groundwater led to evaluation of groundwater in different parts of the United States, and pumping tests using the Thiem equilibrium method were conducted to obtain hydraulic conductivity in several regions (Lohman, 1936; Theis, 1932; Wenzel, 1936). Unfortunately, it was found to be difficult to consistently obtain aquifer parameters because of the increasing drawdown with time (Wenzel, 1936).

To interpret the time-varying drawdown, Charles Vernon Theis (1900–1987) assumed that groundwater flow disturbed by a sink withdrawing water was analogous to heat conduction disturbed by a sink withdrawing heat and resorted to Clarence Isador Lubin (1900–1989), a mathematician at the University of Cincinnati, for the solution of temperature distribution of a uniform plate under two different conditions (White and Clebsch, 1993). The first condition is the introduction of a sink kept at a temperature which corresponds to the constant-drawdown aquifer test problem and is applicable to flowing wells, and the second condition is the introduction of a sink with a uniform heat flow rate, which corresponds to the constant-rate pumping test problem. It was fortunate that the solution of the second problem was readily available in the field of heat conduction (Carslaw, 1921). In this way, Theis (1935) obtained the analytical solution of time-dependent drawdown induced by pumping and opened the door to determining aquifer parameters using transient well hydraulics.

When a flowing well has been shut off for a duration of time, upon reopening the discharge rate decreases with time, which can be considered a constant-drawdown aquifer test. Based on Smith (1937) solution to the analogous problem in heat conduction (the first problem raised by Theis), Jacob and Lohman (1952) derived a solution to the constant-drawdown well test problem in a confined aquifer and verified the results based on flowing wells in the Grand Junction artesian basin, Colorado. Several years later, after the classical work on constant-rate pumping problem in leaky aquifers (Hantush and Jacob, 1955), Hantush (1959) derived a solution to the constant-drawdown well hydraulics to a flowing well in leaky aquifers. In fact, constant-drawdown tests can also be carried out in non-flowing wells either by using a specially designed pump or by connecting the well to a pressurized water container at the surface (Mishra and Guyonnet, 1992). Such constant-drawdown tests have been found to be particularly useful in low-permeability aquifers (Jones, 1993; Tavenas et al., 1990; Wilkinson, 1968).

In summary, although the door of transient well hydraulics was directly opened by Theis (1935) based on constant-rate pumping tests, constant-drawdown well tests triggered by flowing wells belong to an indispensable component of transient well hydraulics and are still receiving active attention in the current century (Chang and Chen, 2002; Wen et al., 2011; Tsai and Yeh, 2012; Feng and Zhan, 2019). It is worth noting that current models on transient well hydraulics did not fully account for the relationship between groundwater recharge from precipitation and groundwater discharge in wells, e.g., the higher flow rate in November than that in September shown in Fig. 4a can not be explained by current theories.

7 Unconfined-flow flowing wells and topographically driven flow systems (1890s–current)

7.1 Qualitative understanding of topographically driven groundwater flow and unconfined-flow flowing wells

At the turn of the 20th century, there was initial field evidence of topographically driven groundwater flow, namely, upward groundwater flow below surface waterbodies (King, 1899) and increase in hydraulic head with depth in the discharge area (Pennink, 1905) in homogeneous aquifers. Versluys (1930) explicitly pointed out that the occurrence of artesian pressure exceeding the land surface corresponds to an increase in hydraulic head with depth and would necessarily lead to upward groundwater flow. By calculating head distribution based on the analogy between temperature and hydraulic head, Versluys concluded that aquitards are not necessary conditions of flowing wells. Due to the poor understanding of the potential of subsurface water, Versluys wrongly assumed that pressure head difference is the driving force of groundwater flow.

Based on the principle of conservation of mass and the laws of thermodynamics, Hubbert (1940) defined the potential of subsurface water and obtained graphical solutions to regional groundwater flow in a homogeneous and isotropic aquifer with a symmetrical topography between two streams (Fig. 6). Hubbert (1940) found that flowing wells could occur in topographic lows without an overlying confining bed and pointed out that a confined aquifer outcrops in the highlands and is overlain by impermeable strata in the lowlands as shown in Fig. 2a is by no means a necessary condition for flowing wells.

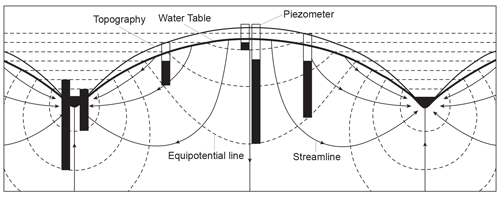
Figure 6 The flow net of groundwater flow between two rivers obtained by Hubbert (1940) and the head in selected piezometers (modified from Fetter, 1994).

Because there was no aquitard in the studies of Versluys (1930) or Hubbert (1940), the pattern of groundwater flow is mainly controlled by topography. Such flowing wells in homogeneous unconfined aquifers driven by topography belong to unconfined-flow flowing wells (Tóth, 1966).

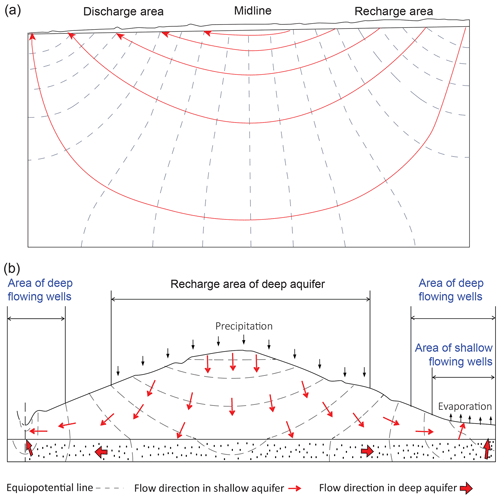
Figure 7 Topographically driven flow systems: (a) homogeneous basin (modified from Tóth, 1962) and (b) heterogeneous basin with a higher permeability layer in the bottom (modified from Meyboom, 1962).

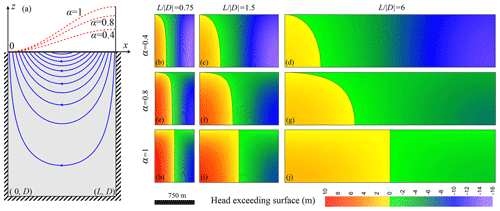
Figure 8 (a) The geometry of a unit basin with a length of L, depth of $\left|D\right|$ and three scenarios of water table undulations (corresponding to different α); (b–j) the distribution of head exceeding surface in the unit basin under three different water table undulations and basin length-to-width ratios ($L/\left|D\right|$) (modified from Wang et al., 2015).

7.2 Quantitative analysis of topographically driven groundwater flow systems

In the 1950s and 1960s, the high demand for water on the Canadian Prairies led to institutional programs of groundwater exploration and research. The phenomena described by King (1899) and Hubbert (1940), such as the mean water table closely follows the topography and flowing wells occur in topographic lows, were quite common in the Canadian Prairies (Meyboom, 1962, 1966; Tóth, 1962, 1966). Based on the field observations, two similar but slightly different conceptual models of topographically induced groundwater flow (Fig. 7) were developed by Tóth (1962) and Meyboom (1962). Because the mean water table which closely follows the topography can be considered a priori known, Tóth (1962) solved the Laplace equation for a homogeneous unit basin with a known water table that changes linearly from the divide to the valley (Fig. 7a). Based on intuitive thinking founded on field observations, Meyboom (1962) considered the permeability difference between the shallow and deep aquifers and qualitatively obtained the flow pattern (Fig. 7b). They agreed that the combination of the two models “gives a good description of the unconfined region of groundwater flow in the western Canadian Prairies” (Tóth, 2005).

According to Tóth (1962), groundwater discharge could cover the entire lower half of the unit basin, and the whole discharge area has higher hydraulic head than the corresponding elevation of water table, which fulfills the definition of “artesian water” by Meinzer (1923b). To quantify the occurrence of flowing wells in topographic lows of homogeneous unconfined aquifers, J. Z. Wang et al. (2015) examined the zone with flowing wells under different water table undulations and basin width-to-depth ratios. By fixing the basin depth, increases in water table undulation and decreases in basin length both led to increased hydraulic gradient between recharge and discharge areas. Based on the distribution of head exceeding surface (termed artesian head in their paper), it was found that the zone with flowing wells is always within the discharge area and the ratio of its size to the whole basin is proportional to the hydraulic gradient (Fig. 8). Therefore, in homogeneous basins, the hydraulic gradient is the main control factor for flowing wells.

When the undulation of the topography is more complex, Tóth (1963) analytically obtained a flow net showing the simultaneous occurrence of several local flow systems, one intermediate flow system and one regional flow system in a homogeneous basin. Note that the Canadian Prairies is semiarid and the impetus for advancing flow systems thinking came from the need to understand terrain patterns of soil salinity, vegetation and groundwater chemistry for which the spatial variations are flow system based. Several years later, R. Allan Freeze, who was a protégé of Meyboom, combined the ideas of Meyboom and Tóth together in his PhD thesis by numerically simulating steady-state regional groundwater flow in heterogeneous basins with any desired water table configuration (Freeze, 2012). As reported in Freeze and Witherspoon (1967), heterogeneity would perturb the distribution of flow systems but does not affect the basic flow pattern induced by topography (Fig. 9). It was also found that confined aquifers need not outcrop to produce flowing well conditions (Fig. 9b and c). In some recent studies, it was found that depth-decaying hydraulic conductivity would lead to weakening of regional flow systems and thus deepening of local flow systems (Jiang et al., 2009, 2011; Wang et al., 2011; Zlotnik et al., 2011).

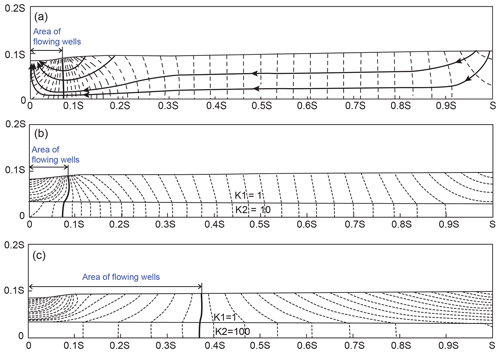
Figure 9 The distribution of equipotential lines and area of flowing wells in homogeneous (a) and heterogeneous basins (b, c) (modified from Freeze and Witherspoon, 1967). Also shown in (a) is the streamlines showing the pattern of groundwater flow from the recharge to the discharge area.

As illustrated above, although horizontal flow dominates when the basin width-to-depth ratio is high and/or hydraulic conductivity in the deep layer is much higher, vertical components of groundwater flow are widespread in either thick unconfined aquifers or aquitards overlying confined aquifers, which is quite different from the flow pattern shown in Figs. 2a and 3. The spatial distribution of groundwater age in thick unconfined aquifers is also more complicated than that in a confined aquifer (Jiang et al., 2010, 2012). Therefore, quantitative analysis of the topographically driven groundwater flow systems became a paradigm shift in hydrogeology. This paradigm shift has been expressed by others in similar words. Anderson (2008) comments that “The Tóth model is an important early exploration of the analysis of regional flow systems.”. Bredehoeft (2018) points out that “Tóth's conceptual model of groundwater flow” represents the beginning of a new era in hydrogeology and termed the paradigm shift to be “the Tóth revolution”.

In his book about flow systems, Tóth (2009) states that since the 1960s, hydrogeology's basic paradigm has shifted from confined flow in aquifers (aquitard-bound flow) to cross-formational flow in drainage basins, i.e., flow paths change from through a confined aquifer to across aquitards and different depths of aquifers in heterogeneous basins. Although cross-formational flow (inter-aquifer leakage) had already been anticipated by Chamberlin (1885), it was identified in the Dakota artesian basin through aquitards in the 1960s (Swenson, 1968), and it was recently identified in the Great Artesian Basin through faults (Pandey et al., 2020; Smerdon and Turnadge, 2015). Moreover, although the concept of flowing wells in the context of aquitard bounding is introduced in almost every groundwater textbook, the concept of unconfined-flow flowing wells in homogeneous basins has been included in few textbooks (Domenico and Schwartz, 1998; Freeze and Cherry, 1979; Heath, 1983; Kasenow, 2010; Lohman, 1972b). Therefore, the acceptance of the new paradigm is a slow process.

7.3 Hydraulics of unconfined-flow flowing wells

The steady-state hydraulics of confined-flow flowing wells had been examined by Glee in the 1930s, but the study of unconfined-flow flowing wells is most recent. Z. Y. Zhang et al. (2018) simulated the water exchange between the unconfined aquifer and a flowing well in a three-dimensional homogeneous unit basin. As a result of the increasing hydraulic head with depth in the discharge area of the aquifer, hydraulic head in the shallow part is smaller than hydraulic head of the flowing well, and in the deep part it is larger than hydraulic head of the flowing well. Therefore, there is groundwater inflow from the aquifer to the flowing well (Q_in) in the deep part and groundwater outflow from the flowing well to the aquifer (Q_out) in the shallow part. Because Q_in is larger than Q_out, cumulative flow rate at the well outlet is above 0 (Fig. 10a), which results in water overflow at the surface. In some extreme cases, e.g., if the water table coincides with the ground surface or the shallow part is cased, Q_out equals 0 and cumulative flow rate at the well outlet is determined by Q_in (Fig. 10b). Z. Y. Zhang et al. (2018) found that the simultaneous occurrence of inflow and outflow could also occur in a thick confined aquifer. Therefore, the third condition proposed by both de Thury (1830) and Bond (1865), as well as the seventh condition given by Chamberlin (1885), is not a necessary condition for flowing wells. Moreover, as shown in Fig. 10a, groundwater in the shallow part of the aquifer could not enter the flowing well, indicating that the well outlet is a “window” to the deep groundwater, i.e., groundwater sampled at the well outlet could represent deep groundwater (Zhang et al., 2019). This has been verified in the flowing wells in the Ordos Plateau, China, by using hydrochemistry and stable isotopes such as ²H, ¹⁸O, ⁸⁷Sr∕⁸⁶Sr and ²⁶Mg (H. Wang et al., 2015; H. Zhang et al., 2018).

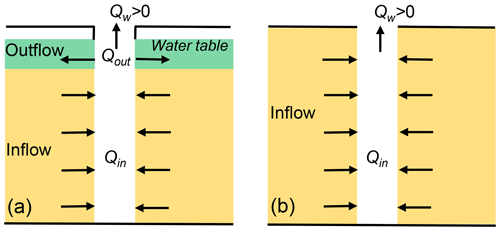
Figure 10 Conceptual cross-sectional views of flow around flowing wells. (a) A flowing well with Q_in>Q_out; (b) a flowing well with $Q_{\mathrm{in}}>Q_{\mathrm{out}}=\mathrm{0}$ (modified from Z. Y. Zhang et al., 2018). Q_w means the flow rate at the well outlet.

Based on the plots shown in Figs. 6 to 10, several qualifying conditions of flowing wells proposed in the 19th century have been found to be unnecessary since the turn of the 20th century. Although the transient behavior of groundwater flow to flowing wells in confined aquifers has been studied in the 1950s (Hantush, 1959; Jacob and Lohman, 1952), there has been no research on transient groundwater flow to flowing wells in unconfined aquifers. Moreover, research coupling groundwater recharge from precipitation and groundwater discharge through flowing wells, which is critical to interpret the increased flow rate with time as shown in Fig. 4a and the sustainability of flowing wells, is also missing.

8 Conclusions and suggestions

The evolution of nearly all domains of physical hydrogeology can be connected to flowing wells. The advent of modern cable-tool drilling equipment in Europe in the early 19th century made flowing wells common in the 19th century. Because flowing wells are spectacular visual evidence of groundwater occurrence, they became the impetus for both qualitative and quantitative groundwater science. The pursuit of answers to fundamental questions generated by flowing wells in confined aquifers bounded by aquitards moved the science forward for more than a century until pumping became the main form of groundwater development. Moreover, since the turn of the 20th century, flowing wells in unconfined aquifers were an impetus for the paradigm shift from aquitard-bound flow to cross-formational flow driven by topography.

Given the spectacular flowing wells in Paris and London in the early 19th century, it was not a coincidence that Darcy (1856) did his monumental laboratory experiments soon after he did pipe flow experiments prompted by flowing wells. He was followed by his colleague Dupuit (1863) to develop the hydraulics of steady flow to wells. The term “flowing well” was introduced by Chamberlain (1885) in his classic USGS report, which provided a comprehensive explanation of flowing wells using hydrogeological principles. Based on field investigations of the Cambrian–Ordovician aquifer system in Wisconsin, he recognized the role of confining beds in creating flowing well conditions and also that these confining beds are leaky. This was followed soon after by the classic work by Darton (1897, 1905), who studied the Dakota aquifer. Meinzer and Hard (1925) and Meinzer (1928) deduced from declining discharge of flowing wells and excess of discharge over recharge that confined aquifers are elastic and have storage capability related to compressibility. This prompted Theis (1935) of the USGS to initiate transient well hydraulics for non-leaky aquifers, although leakage recognized decades earlier set the stage for Hantush to pioneer the hydraulics of pumping wells and flowing wells in aquifers with leaky confining beds in the 1950s (Hantush and Jacob, 1955; Hantush, 1959).

The wide occurrence of regional-scale confined aquifers showing ubiquitous flowing wells in sedimentary rocks in France, Britain, the United States and Australia resulted in confined flow in aquifers being a broadly useful conceptualization. However, this resulted in the common misconception that flowing wells must occur in confined aquifers bounded by aquitards, and the confusion of the term “artesian”. Versluys (1930) and Hubbert (1940) realized flowing wells can occur in entirely unconfined and homogeneous conditions controlled only by topography, which was supported by Tóth's (1962, 1963) and Freeze and Witherspoon's (1967) quantitative studies of topographically driven groundwater flow systems. An introduction to confined-flow and unconfined-flow flowing wells has been given by Tóth (1966) in a journal paper and included in the textbook by Freeze and Cherry (1979), while quantitative analysis of topographically driven groundwater flow systems has been considered to be a paradigm shift in modern hydrogeology (Bredehoeft, 2018; Madl-Szonyi, 2008; Tóth, 2005). Generally in Earth sciences, it takes decades for a paradigm shift to achieve completeness when completeness is judged by the paradigm being the primary basis for teaching as manifested in what is included in textbooks. For example, the paradigm shift from steady-state to non-steady-state well hydraulics in confined aquifers that began in the 1930s was completed by the late 1950s, and transient well hydraulics has been included in almost all groundwater textbooks since then.

Although there have been great advances in how we think about groundwater flow systems and the current paradigm is well advanced, it is not yet comprehensive. The misconception that flowing wells must occur in confined aquifers is still impeding the acceptance of the new paradigm, which is reflected by the limited number of textbooks introducing flowing wells in unconfined aquifers. Based on the summary of the role of flowing wells in the evolution of many concepts and principles of groundwater hydrology, acknowledgement of the role of flowing wells as the main root of groundwater hydrology would lead to a deeper understanding of the science of groundwater. Avoidance of the term “artesian” is needed to eradicate confusion in terminology that crept into groundwater science long after the classic work by Darcy, Dupuit and others established the foundation. A complete description of confined-flow and purely unconfined-flow flowing wells and their connections to evolution of hydrogeology and quantitative methods for topographically driven groundwater flow systems are expected in all future groundwater textbooks. However, because purely confined flow and purely unconfined flow are two end-members of groundwater flow, clearer concepts for the simultaneous control of aquitards and topography on the occurrence of flowing wells are needed.