the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Numerical investigation on the power of parametric and nonparametric tests for trend detection in annual maximum series
Vincenzo Totaro
Andrea Gioia
Vito Iacobellis
The need to fit time series characterized by the presence of a trend or change points has generated increased interest in the investigation of nonstationary probability distributions in recent years. Considering that the available hydrological time series can be recognized as the observable part of a stochastic process with a definite probability distribution, two main topics can be tackled in this context: the first is related to the definition of an objective criterion for choosing whether the stationary hypothesis can be adopted, whereas the second regards the effects of nonstationarity on the estimation of distribution parameters and quantiles for an assigned return period and flood risk evaluation. Although the time series trend or change points are usually detected using nonparametric tests available in the literature (e.g., Mann–Kendall or CUSUM test), the correct selection of the stationary or nonstationary probability distribution is still required for design purposes. In this light, the focus is shifted toward model selection criteria; this implies the use of parametric methods, including all of the issues related to parameter estimation. The aim of this study is to compare the performance of parametric and nonparametric methods for trend detection, analyzing their power and focusing on the use of traditional model selection tools (e.g., the Akaike information criterion and the likelihood ratio test) within this context. The power and efficiency of parameter estimation, including the trend coefficient, were investigated via Monte Carlo simulations using the generalized extreme value distribution as the parent with selected parameter sets.
- Article
(2641 KB) - Full-text XML
- BibTeX
- EndNote
The long- and medium-term prediction of extreme hydrological events under nonstationary conditions is one of the major challenges of our times. Streamflow, as well as temporal rainfall and many other hydrological phenomena, can be considered as stochastic processes (Chow, 1964), i.e., families of random variables with an assigned probability distribution, and time series are the observable part of this process. One of the main goals of extreme event frequency analysis is the estimation of distribution quantiles related to a certain non-exceedance probability. They are usually obtained after fitting a probabilistic model to observed data. As Koutsoyiannis and Montanari (2015) depicted in their historical review of the “concept of stationarity”, Kolmogorov, in 1931, “used the term stationary to describe a probability density function that is unchanged in time”, whereas Khintchine (1934) provided a formal definition of stationarity of a stochastic process.
In this context, detecting the existence of time-dependence in a stochastic process should be considered a necessary task in the statistical analysis of recorded time series. Thus, several considerations should be made with respect to updating some important hydrological concepts while assuming that the non-exceedance probability varies with time or other covariates. For example, the return period may be reformulated in two different ways, the “expected waiting time” (EWT; Olsen et al., 1998) or the “expected number of events” (ENE; Parey et al., 2007, 2010), which lead to a different evaluation of quantiles within a nonstationary approach. As proved by Cooley (2013), the EWT and ENE are affected differently by nonstationarity, possibly producing ambiguity in engineering design practice (Du et al., 2015; Read and Vogel, 2015). Salas and Obeysekera (2014) provided a detailed report regarding relationships between stationary and nonstationary EWT values within a parametric approach for the assessment of nonstationary conditions. In such a framework, a strong relevance is given to statistical tools for detecting changes in non-normally distributed time series (Kundewicz and Robson, 2004).
To date, the vast majority of research regarding climate change and the detection of nonstationary conditions has been developed using nonparametric approaches. One of the most commonly used nonparametric measures of trend is Sen's slope (Gocic and Trajkovic, 2013); however, a wide array of nonparametric tests for detecting nonstationarity is available (e.g., Kundewicz and Robson, 2004). Statistical tests include the Mann–Kendall (MK; Mann, 1945; Kendall, 1975) and Spearman (Lehmann, 1975) tests for detecting trends, and the Pettitt (Pettitt, 1979) and CUSUM (Smadi and Zghoul, 2006) tests for change point detection. All of these tests are based on a specific null hypothesis and have to be performed for an assigned significance level. Nonparametric tests are usually preferred over parametric tests as they are distribution-free and do not require knowledge of the parent distribution. They are traditionally considered more suitable for the frequency analysis of extreme events with respect to parametric tests because they are less sensitive to the presence of outliers (Wang et al., 2005).
In contrast, the use of null hypothesis significance tests for trend detection has raised concerns and severe criticisms in a wide range of scientific fields for many years (e.g., Cohen, 1994), as outlined by Vogel et al. (2013). Serinaldi et al. (2018) provided an extensive critical review focusing on logical flaws and misinterpretations often related to their misuse.
In general, the use of statistical tests involves different errors, such as type I error (rejecting the null hypothesis when it is true) and type II error (accepting the null hypothesis when it is false). The latter is related to the test power, i.e., the probability of rejecting the null hypothesis when it is false; however, as recognized by a few authors (e.g., Milly et al., 2015; Beven, 2016), the importance of the power has been largely overlooked in Earth system science fields. Strong attention has always been paid to the level of significance (i.e., type I error), although, as pointed out by Vogel et al. (2013), “a type II error in the context of an infrastructure decision implies under-preparedness, which is often an error much more costly to society than the type I error (over-preparedness)”.
Moreover, as already proven by Yue et al. (2002a), the power of the Mann–Kendall test, despite its nonparametric structure, actually shows a strong dependence on the type and parametrization of the parent distribution.
Using a parametric approach, the estimation of quantiles of an extreme event distribution requires the search for the underlying distribution and for time-dependant hydrological variables. If variables are time-dependent, they are “i/nid” (independent/non-identically distributed) and the model is considered nonstationary; otherwise, the variables are “iid” (independent, identically distributed) and the model is a stationary one (Montanari and Koutsoyiannis, 2014; Serinaldi and Kilsby, 2015).
From this perspective, the detection of nonstationarity may exploit (besides traditional statistical tests) well-known properties of model selection tools. Even in this case, several measures and criteria are available for selecting a best-fit model, such as the Akaike information criterion (AIC; Akaike, 1974), the Bayesian information criterion (BIC; Schwarz, 1978), and the likelihood ratio test (LR; Coles, 2001); the latter is suitable when dealing with nested models.
The purpose of this paper is to provide further insights into the use of parametric and nonparametric approaches in the framework of extreme event frequency analysis under nonstationary conditions. The comparison between those different approaches is not straightforward. Nonparametric tests do not require knowledge of the parent distribution, and their properties strongly rely on the choice of the null hypothesis. Parametric methods for model selection, in comparison, require the selection of the parent distribution and the estimation of its parameters, but are not necessarily associated with a specific null hypothesis. Nevertheless, in both cases, the evaluation of the rejection threshold is usually based on a statistical measure of trend that, under the null hypothesis of stationarity, follows a specific distribution (e.g., the Gaussianity of the Kendall statistic for the MK nonparametric test, and the χ2 distribution of deviance statistic for the LR parametric test).
Considering the pros and cons of the different approaches, we believe that specific remarks should be made about the use of parametric and nonparametric methods for the analysis of extreme event series. For this purpose, we set up a numerical experiment to compare the performance of (1) the MK as a nonparametric test for trend detection, (2) the LR parametric test for model selection, and (3) the AICR parametric test, as defined in Sect. 2.3. In particular, the AICR is a measure for model selection, based on the AIC, whose distribution was numerically evaluated, under the null hypothesis of a stationary process, for comparison purposes with other tests.
We aim to provide (i) a comparison of test power between the MK, LR, and AICR; (ii) a sensitivity analysis of test power to parameters of a known parent distribution used to generate sample data; and (iii) an analysis of the influence of the sample size on the test power and the significance level.
We conducted the analysis using Monte Carlo techniques; this entailed generating samples from parent populations assuming one of the most popular extreme event distributions, the generalized extreme value (GEV; Jenkinson, 1955), with a linear (and without any) trend in the position parameter. From the samples generated, we numerically evaluated the power and significance level of tests for trend detection, using the MK, LR, and AICR tests. For the latter, we also checked the option of using the modified version of AIC, referred to as AICc, suggested by Sugiura (1978) for smaller samples.
Considering that parametric methods involve the estimation of the parent distribution parameters, we also analyzed the efficiency of the maximum likelihood (ML) estimator by comparing the sample variability of the ML estimate of trend with the nonparametric Sen’s slope. Furthermore, we scoped the sample variability of the GEV parameters in the stationary and nonstationary cases.
This section is divided into five parts. Sect. 2.1, 2.2, and 2.3 report the main characteristics of the MK, LR, and AICR tests, respectively. In Sect. 2.4, the probabilistic model used for sample data generation, based on the use of the GEV distribution, is described in the stationary and nonstationary cases. Finally, Sect. 2.5 outlines the procedure for the numerical evaluation of the tests' power and significance level.
2.1 The Mann–Kendall test
Hydrological time series are often composed by non-normally independent realizations of phenomena, and this characteristic makes the use of nonparametric trend tests very attractive (Kundzewicz and Robson, 2004). The Mann–Kendall test is a widely used rank-based tool for detecting monotonic, and not necessarily linear, trends. Given a random variable z, and assigned a sample of L independent data z=(z1, …, zL), the Kendall S statistic (Kendall, 1975) can be defined as follows:
where “sgn” is the sign function.
The null hypothesis of this test is the absence of any statistically significant trend in the sample, whereas the presence of a trend represents an alternative hypothesis. Yilmaz and Perera (2014) reported that serial dependence can lead to a more frequent rejection of the null hypothesis. For L≥8, Mann (1945) reported that Eq. (1) is approximatively a normal variable with a zero mean and variance which, in the presence of tm ties of length m, can be expressed as
In practice, the Mann–Kendall test is performed using the Z statistic
which follows a standard normal distribution. Using this approach, it is simple to evaluate the p value and compare it with an assigned level of significance or, equivalently, to calculate the Zα threshold value and compare it with Z, where Zα is the (1−α) quantile of a standard normal distribution.
Yue et al. (2002b) observed that autocorrelation in time series can influence the ability of the MK test to detect trends. To avoid this problem, a correct approach with respect to trend analysis should contemplate a preliminary check for autocorrelation and, if necessary, the application of pre-whitening procedures.
A nonparametric tool for a reliable estimation of a trend in a time series with N pairs of data is the Sen's slope estimator (Sen, 1968), which is defined as the median of the set of slopes δj:
where i>k.
2.2 Likelihood ratio test
The likelihood ratio statistical test allows for the comparison of two candidate models. As its name suggests, it is based on the evaluation of the likelihood function of different models.
The LR test has been used multiple times (Tramblay et al., 2013; Cheng et al., 2014; Yilmaz et al., 2014) to select between stationary and nonstationary models in the context of nested models. Given a stationary model characterized by a parameter set θst and a nonstationary model, with parameter set θns, if and are their respective maximized log likelihoods, the likelihood ratio test can be defined using the deviance statistic
D is (for large L) approximately distributed, with degrees of freedom. The null hypothesis of stationarity is rejected if D>Cα, where Cα is the (1−α) quantile of the distribution (Coles, 2001).
Besides the analysis of power, we also checked (in Sect. 3.3) the approximation as a function of the sample size L for the evaluation of the level of significance.
2.3 Akaike information criterion ratio test
Information criteria are useful tools for model selection. It is reasonable to retain that the Akaike information criterion (AIC; Akaike, 1974) is the most famous among these tools. Based on the Kullback–Leibler discrepancy measure, if θ is the parameter set of a k-dimensional model (k=dim(θ)), AIC is defined as
The model that best fits the data has the lowest value of the AIC between candidates. It is useful to observe that the term proportional to the number of model parameters allows one to account for the increase of the estimator variance as the number of model parameters increases.

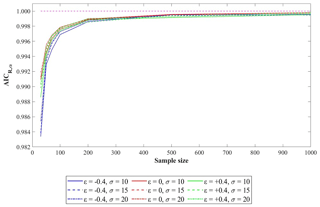
Figure 1An empirical distribution of AICR and the rejection threshold AICR,α of the null hypothesis (stationary GEV parent).
Sugiura (1978) observed that the AIC can lead to misleading results for small samples; thus, he proposed a new measure for the AIC:
where a second-order bias correction is introduced. Burnham and Anderson (2004) suggested only using this version when , with kmax being the maximum number of parameters between the models compared. However, for larger L, AICc converges to AIC. For a quantitative comparison between the AIC and AICc in the extreme value stationary model selection framework, the reader is referred to Laio et al. (2009).
In order to select between stationary and nonstationary candidate models, we use the ratio
where the subscripts indicate the AIC value obtained for a stationary (st) and a nonstationary (ns) model, both fitted with maximum likelihood to the same data series.
Considering that the better fitting model has a lower AIC, if the time series arises from a nonstationary process, the AICR should be less than 1; the opposite is true if the process is stationary.
In order to provide a rigorous comparison between the use of the MK, LR, and AICR, we evaluated the AICR,α threshold value corresponding to the significance level α using numerical experiments.
More in detail, we adopted the following procedure:
-
N=10 000 samples are generated from a stationary GEV parent distribution, with known parameters;
-
for each of these samples the AICR is evaluated by fitting the stationary and nonstationary GEV models described in Sect. 2.4, thus providing its empirical distribution (see probability density function, pdf, in Fig. 1);
-
exploiting the empirical distribution of AICR, the threshold associated with a significance level of α=0.05 is numerically evaluated. This value, AICR,α, represents the threshold for rejecting the null hypothesis of stationarity (which in these generations is true) in 5 % of the synthetic samples.
This procedure was applied both for the AIC and AICc. The experiment was repeated for a few selected sets of the GEV parameters, including different trend values, and different sample lengths, as detailed in Sect. 3.
2.4 The GEV parent distribution
The cumulative distribution function of the generalized extreme value (GEV) distribution (Jenkinson, 1955) can be expressed as follows:
where ζ, σ, and ε are known as the position, scale, and shape parameters, respectively; θst=[ζ, σ, ε] is a general and comprehensive way to express the parameter set in the stationary case. The flexibility of the GEV, which accounts for the Gumbel, Fréchet, and Weibull distributions as special cases (for ε=0, ε>0 and ε<0 respectively) makes it eligible for a more general discussion about the implications of nonstationarity.
Traditional extreme value distributions can be used in a nonstationary framework, modeling their parameters as function of time or other covariates (Coles, 2001), producing , σt, εt].
In this study, only a deterministic linear dependence on the time t of the position parameter ζ has been introduced, leading Eq. (7) to be expressed as follows:
with
and θns=[ζ0, ζ1, σ, ε].
It is important to note that Eq. (8) is a more general way of defining the GEV and has the property of degenerating into Eq. (7) for ζ1=0; in other words, Eq. (7) represents a nested model of Eq. (8) which would confirm the suitability of the likelihood ratio test for model selection.
According to Muraleedharan et al. (2010), the first three moments of the GEV distribution are as follows:
Here, , with and Γ(⋅), is the gamma function. It is worth noting that, following Eqs. (10)–(12), the trend in the position parameter only affects the mean, while the variance and skewness remain constant.
In this work, we used the maximum likelihood method (ML) to estimate the GEV parameters from sample data. The ML allows one to treat ζ1 as an independent parameter, as well as ζ0, σ and ε. For this purpose, we exploited the “extRemes” R package (Gilleland and Katz, 2016).
2.5 Numerical evaluation of test power and significance level
The power of a test is related to the type II error and is the probability of correctly rejecting the null hypothesis when it is false. In particular, defining α (level of significance), the probability of a type I error, and β, the probability of a type II error, we have a power value of 1−β. The maximum value of power is 1, which correspond to β=0, i.e., no probability of a type II error. In most applications, the conventional values are α=0.05 and β=0.2, meaning that a 1-to-4 trade-off between α and β is accepted. Thus, in our experiment we always assumed a significance level of 0.05, and, for the following description of results and discussion, we considered a power level of less than 0.8 to be too low and, hence, unacceptable. In Sect. 4, we report further considerations regarding this choice. For each of the tests described in Sect. 2.1, 2.2, and 2.3, the power was numerically evaluated according to the following procedure:
-
N=2000 Monte Carlo synthetic series, each of length L, are generated using the nonstationary GEV in Eqs. (8) and (9) as a parent distribution with a fixed parameter set θns=[ζ0, ζ1, σ, ε] with ζ1≠0.
-
The threshold AICR,α associated with a significance level of α=0.05 is numerically evaluated, as described in Sect. 2.3, using the corresponding parameter set θst=[ζ0, σ, ε] of the GEV parent distribution.
-
From these synthetic series, the power of the test is estimated as
where Nrej is the number of series for which the null hypothesis is rejected, as in Yue et al. (2002a).
The same procedure, with N=10 000, was used in order to check the actual significance level of the test, which is the probability of type I error, i.e., the probability of rejecting the null hypothesis of stationarity when it is true. The task was performed by following the abovementioned steps 1 to 3 while replacing θns with θst in step 1); in such a case, the rejection rate Nrej∕N represents the actual level of significance α.
We used a reduced number of generations (N=2000) for the evaluation of power as a good compromise between the quality of the results and computational time. N=2000 was also used by Yue et al. (2002a).
A comparative evaluation of the tests' performance was carried out for different GEV parameter sets θns, considering three values of ε (−0.4, 0, and 0.4) and three values of σ (10, 15, and 20). The position parameter was always kept constant and equal to ζ0=40. Then, for any possible pair of σ and ε values, we considered ζ1 ranging from −1 to 1 with a step size of 0.1. Such a range of parameters represents a wide domain in the hydrologically feasible parameter space of annual maximum daily rainfall. Upper-bounded (), EV1 (ε=0), and heavy-tailed () cases are included. Moreover, for each of these parameter sets θns, N samples of different sizes (30, 50, and 70) were generated.
For a clear exposition of the results, this section is divided into four subsections. In Sect. 3.1, we focus on the opportunity to use the AIC or AICc for the evaluation of AICR; in Sect. 3.2, the comparison of test power and its sensitivity analysis to the parent distribution parameters and the sample size is shown; in Sect. 3.3, the evaluation of the level of significance for all tests and, in particular, the validity of the χ2 approximation for the D statistic is discussed; and finally in Sect. 3.4, the numerical investigation of the sample variability of the parameters is reported.
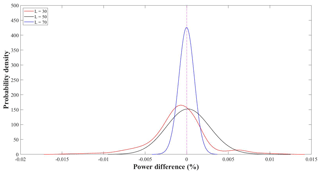
Figure 2Distributions of the differences between the power of AICR evaluated with the AIC and AICc for ε=0.4.
3.1 Evaluation of AICR, with the AIC and AICc
Considering the nonstationary GEV four-parameter model, in order to satisfy the relation suggested by Burnham and Anderson (2004), a time series with a record length no less than 160 should be available. Following this simple reasoning, the AIC should be considered not to be applicable to any annual maximum series showing a changing point between the 1970s and 1980s (e.g., Kiely, 1999). In our numerical experiment, the second-order bias correction of Sugiura (1978) should always be used, as we have for the nonstationary GEV for a maximum sample length of L=70. Nevertheless, we checked if using the AIC or AICc may affect results. For this purpose, we evaluated the percentage differences between the power of the AICR obtained by means of the AIC and AICc from synthetic series. In Fig. 2, the empirical probability density functions of such percentage differences, grouped according to sample length, are plotted for generations with ε=0.4 and different values of σ. It is interesting to note that the error distribution only shows a regular and unbiased bell-shaped distribution for L=70. We then observe a small negative bias (about −0.02 %) for L=50, while a bias of −0.08 with a multi-peak and negatively skewed pdf is noted for L=30. The latter pdf also has a higher variance than the others. The purpose of this figure is to show that the difference between the power obtained with the AIC and the power obtained with the AICc is negligible. Different peaks in one curve (L=30) can be explained by the merging of sample errors obtained for different values of σ. Similar results were obtained for all values of ε, which always provided very low differences and allow for the conclusion to be reached that the use of the AIC or AICc does not significantly affect the power of AICR for the cases examined. This follows the combined effect of the sample size (whose minimum value considered here is 30) and the limited difference in the number of parameters in the selected models. In the following, we will refer to and show only the plots obtained for the AICR in Eq. (6) with the AIC evaluated as in Eq. (4).
3.2 Dependence of the power on the parent distribution parameters and sample size
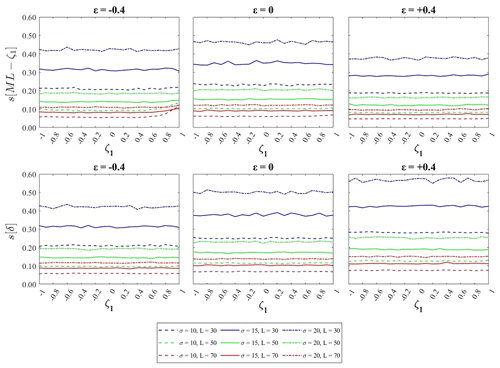
The effect of the parent distribution parameters and the sample size on the numerical evaluation of the power and significance level of the MK, LR, and AICR tests for different values of ε, σ, and ζ1 is shown in Fig. 3. The curves represent both the significance level, which is shown for ζ1=0 (true parent is the stationary GEV), and the power, which is shown for all other values ζ1≠0 (true parent is the nonstationary GEV). Each panel in Fig. 3 shows the dependence of the power and significance level of MK, LR and AICR on the trend coefficient for one set of parameter values and different sample sizes. In all panels, the test power strongly depends on the trend coefficient and sample size. This dependence is also affected by the parent parameter values. In all cases, the power reaches 1 for a strong trend and approaches 0.05 (the chosen level of significance) for a weak trend (ζ1 close to 0). In all combinations of the shape and scale parameters (and especially for short samples) for a wide range of trend values, the power exhibits values well below the conventional value of 0.8. The curves' slope between 0.05 and 1 is sharp for long samples and gentle for short samples. It also depends on the parameter set, with slopes generally being gentler for higher values of the scale (σ) and shape (ε) parameters of the parent distribution. A significant difference in the power between the MK, LR, and AICR tests is observable when the sample size is smaller and even more so when the parent distribution is heavy-tailed ().
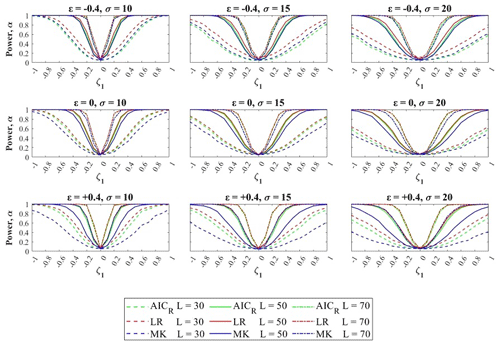
Figure 3Dependence of test power on the trend coefficient, sample size, scale, and shape of the parent parameters.
In particular, for ε=0, −0.4 and L=50, 70, it is possible to report a slightly larger power of LR with respect to the AICR and MK, but values are very close to each other. However, the reciprocal position of MK and AICR power curves is interesting; in fact, the AICR power is always larger than that of the MK, except when , for all values of the scale parameter.
A higher difference is found for a heavy-tailed parent distribution (). While LR still has the largest power value, the difference with respect to AICR remains small and the MK power value almost always collapses to values smaller than 0.5.
The practical consequences of such patterns are very important and are discussed in Sect. 4.
3.3 Sensitivity and evaluation of the actual significance level
We evaluated the threshold values (corresponding to a significance level of 0.05) for accepting/rejecting the null hypothesis of stationarity according to the methodologies recalled in Sect. 2.1 and 2.2 for the MK and LR tests and introduced in Sect. 2.3 for AICR. Based on these thresholds, we exploited the generation of series from a stationary model (ζ1=0) in order to numerically evaluate the rate of rejection of the null hypothesis, i.e., the actual significance level of the tests considered in the numerical experiment, following the procedure described in Sect. 2.5.
Table 1 shows the numerical values of the actual level of significance, obtained numerically, to be compared with the theoretical value of 0.05 for all of the sets of parameters and sample sizes considered. Among the three measures for trend detection, the LR shows the worst performance. The results in Table 1 show that the rejection rate of the (true) null hypothesis is systematically higher than it should be, and it is also dependent on parent parameter values. This effect is exalted when the parent distribution has an upper boundary () and for shorter series (L=30). In practice, this implies that when using the LR test, as described in Sect. 2.2, there is a higher probability of rejecting the null hypothesis of stationarity (if it is true) than expected or designed.
Table 1The actual level of significance of the tests for different sample sizes, scales, and shapes of the parent parameters.
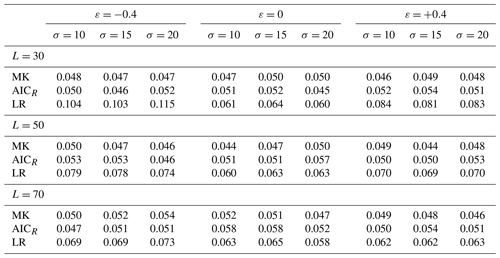
Conversely, the performance of MK with respect to the designed level of significance is less biased and is independent of the parameter set. Similar good performance is trivially obtained for the AICR, whose rejection threshold is numerically evaluated.
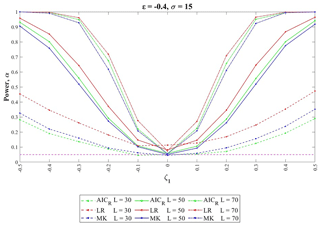
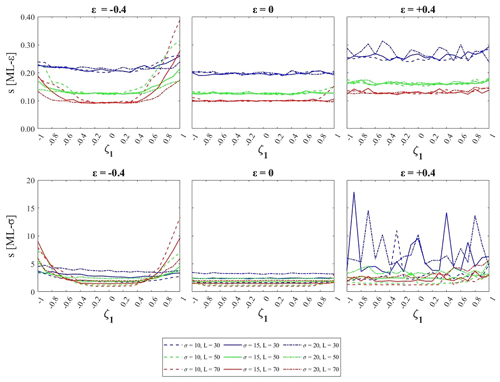
Figure 4Enlargement of the power test curves in the case (σ=15, ), with focus on the actual level of significance (ζ1=0).
The plot in Fig. 4 is displayed in order to focus on the actual value of the level of significance and, in particular, on the LR approximation as a function of the sample length L. The difference between the theoretical and numerical values of the significance level is represented by the distance between the bottom value of the curve (obtained for ζ1=0, i.e., the stationary GEV model) and the chosen level of significance 0.05, represented by the horizontal dotted line. In particular, in Fig. 4, results for the parameter set (σ=15, ) show that the actual rate of rejection is always higher than the theoretical one and changes significantly with the sample size; this means that the approximation leads to a significant underestimation of the rejection threshold of the D statistic. Moreover, it seems that the LR power curves (in red) are shifted toward higher values as a consequence of the significance level overestimation, meaning that the LR test power is also overestimated due to the approximation . These results suggest the use of a numerical procedure for the LR test (such as that introduced for AICR in Sect. 2.3) for evaluating the D distribution and the rejection threshold.
Other considerations can be made regarding the use of AICR. As explained in Sect. 2.3, we empirically evaluated the AICR,α threshold value using numerical generations with a significance level 0.05 for each of the parameter sets and sample sizes considered. Similar results were obtained using the AICc, which are not shown for brevity. We found a significant dependence of AICR,α on the sample size. Figure 5 shows the AICR,α curves obtained for each of the parameter sets vs. sample size. It is also worth noting that all curves asymptotically trend to 1 as L increases. This property is due to the structure of the AIC and the peculiarity of the nested models used in this paper: while using a sample generated with weak nonstationarity (i.e., when ζ1→0 in Eq. 9), the maximum likelihood of the model shown in Eq. 7, , tends toward of the model shown in Eq. 8, leaving only the bias correction (2k in equation 4) to discriminate between competing AIC values in model selection applications. As a consequence, the AICR,α should always be lower than 1; however, when increasing the sample size, both the likelihood terms and in Eq. (4) will also increase, pushing AICR toward the limit 1. Conversely, Fig. 5 shows that the threshold value AICR,α is significantly smaller than 1 up to L values well beyond the length usually available in this kind of analysis. Hence, the numerical evaluation of the threshold has to be considered as a required task in order to provide an assigned significance level to model selection. In contrast, the simple adoption of the selection criteria AICR<1 (i.e., AIC) would correspond to an unknown significance level that is dependent on the parent distribution and sample size. In order to highlight this point, we evaluated the significance level α corresponding to AIC, following the procedure described in Sect. 2.5, by generating N=10 000 synthetic series (from a stationary model) for any parameter set and sample length. The results, provided in Table 2, show that α ranges between 0.16 and 0.26 in the explored GEV parameter domain and mainly depends on the sample length and the shape parameter of the parent distribution.
3.4 Sample variability of parent distribution parameters
In our opinion, the results shown above, with respect to the performance of parametric and nonparametric tests, are quite surprising and important. It is proved that the preference widely accorded to nonparametric tests, due to the fact that their statistics are allegedly independent from the parent distribution, is not well founded. Conversely, the use of parametric procedures raises the problem of correctly estimating the parent distribution and, for the purpose of this paper, its parameters. Moreover, as the trend coefficient ζ1 is a parameter of the parent distribution under nonstationary conditions, the proposed parametric approach provides a maximum likelihood-based estimation of the same trend coefficient, which is hereafter referred to as ML-ζ1. For a comparison with nonparametric approaches, we also evaluated the sample variability of the Sen's slope measure (δ) of the imposed linear trend. Furthermore, in order to provide insights into these issues, we analyzed the sample variability of the maximum likelihood estimates ML-ε and ML-σ (from the same sets of generations exploited above) for different parameter sets and sample lengths.
We evaluated sample variability s[⋅], as the standard deviation of the ML estimates of parameter values obtained from synthetic series. In the upper panels of Fig. 6, we show s[ML-ζ1], and in the lower panels, we show the Sen's slope median s[δ]. In both cases, the sample variability of the linear trend is strongly dependent on sample size and independent from the true ζ1 value in the range examined [−1, 1]. It reaches high values for short samples and, in such cases, its dependence on the scale and shape parent parameters is also relevant. The ML estimation of the trend coefficient is always more efficient than Sen's slope, and this is observed for heavy-tailed distributions in particular.
In Fig. 7, we show the empirical distributions of the Sen's slope δ and ML-ζ1 estimates obtained from samples of size L=30 with a parent distribution characterized by σ=15 and , 0, 0.4], providing visual information about the range of trend values that may result from a local evaluation. Similar results, characterized by smaller sample variability, as shown in Fig. 6, are obtained for L=50 and L=70 and are not shown for brevity.
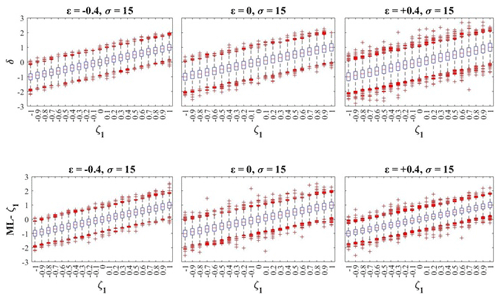
Figure 7Empirical distributions of δ and ML-ζ1 evaluated from samples with L=30 and σ=15 vs. the trend coefficient ζ1.
Figure 8 shows the sample variability of ML-ε and ML-σ, which is still independent of the true ζ1 for values of ε=0 and 0.4, whereas for the upper-bounded GEV distributions () it shows a significant increase for higher values of σ and high trend coefficients (). The randomness of results for L=30 and σ=[15, 20] is probably due to the reduced efficiency of the algorithm that maximizes the log-likelihood function for heavy-tailed distributions.

Figure 9Empirical distributions of ML-ε evaluated for σ=15 from samples with L=30 and L=70 vs. the trend coefficient ζ1.
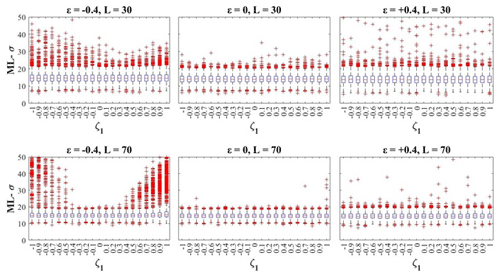
Figure 10Empirical distributions of ML-σ evaluated for σ=15 from samples with L=30 and L=70 vs. the trend coefficient ζ1.
In order to better analyze such patterns, for the scale and shape parent parameters we also report the distribution of their empirical ML estimates for different parameter sets vs. the true ζ1 value used in generation. The sample distribution of ML-ε for σ=15 is shown in Fig. 9 for L=30 and L=70. The sample distribution of ML-σ for σ=15 is shown in Fig. 10 for L=30 and L=70. The panels show that the presence of a strong trend coefficient may produce significant loss in the estimator efficiency, which is probably due to deviation from the normal distribution of the sample estimates for long samples. This suggests the need for more robust estimation procedures that provide higher efficiency for estimates of ε and σ in the case of a strong observed trend. It should be highlighted that efficiency in the parameter estimation increases with sample size for ε=[0, 0.4], whereas it decreases for both ε and σ in the case of where the trend of the location parameter implies a shift in time of the distribution upper bound.
The results shown have important practical implications. The dependence of test power on the parent distribution parameters may significantly affect results of both parametric and nonparametric tests, including the widely used Mann–Kendall test.
Considering the feasibility of the numerical evaluation of power, allowed by the parametric approach, we observe that, while awareness of the crucial role of type II error has been growing in recent years in the hydrological literature, a common debate would deserve more development about which power values should be considered acceptable. Such an issue is much more enhanced in other scientific fields where the experimental design is traditionally required to estimate the appropriate sample size to adequately support results and conclusions. In psychological research, Cohen (1992) proposed 0.8 to be a conventional value of power to be used with level of significance of 0.05, thus leading to a 4 : 1 ratio between the risk of type II and type I error. The conventional value proposed by Cohen (1992) has been taken as a reference by thousands of papers in social and behavioral sciences. In pharmacological and medical research, depending on the real implications and the nature of the type II error, conventional values of power may be as high as 0.999. This was the value suggested by Lieber (1990) for testing a treatment for patients' blood pressure. The author stated, while “guarding against cookbook application of statistical methods”, “it should also be noted that, at times, type II error may be more important to an investigator then type I error”.
We believe that, when selecting between stationary and nonstationary models for extreme hydrological event prediction, a fair comparison between the null and the alternative hypotheses of should be utilized, which provides a power value of 0.95. In our discussion, we considered 0.8 to be a minimum threshold for acceptable power values.
For all of the generation sets and tests conducted, under the null hypothesis of stationarity, the power has values ranging between the chosen significance level (0.05) and 1 for large (and larger) ranges of the trend coefficient. The test power always collapses to very low values for weak (but climatically important) trend values (e.g., in the case of annual maximum daily rainfall, ζ1 was equal to 0.2 or 0.3 mm yr−1). In the presence of a trend, the power is also affected by the scale and shape parameters of the GEV parent distribution. This observation can be made with reference to samples of all of the lengths considered in this paper (from 30 to 70 years of observations), but the use of smaller samples significantly reduces the test power and dramatically extends the range of ζ1 values for which the power is below the conventional value of 0.8. The use of this sample size is not rare considering that significant trends due to anthropic effects are typically investigated in periods following a changing point often observed in the 1980s.
These results also imply that in spatial fields where the alternative hypothesis of nonstationarity is true but the parent's parameters (including the trend coefficient) and the sample length are variable in space, the rate of rejection of the false null hypothesis may be highly variable from site to site and the power, if left without control, de facto assumes random values in space. In other words, the probability of recognizing the alternative hypothesis of nonstationarity as true from a single observed sample may unknowingly change (between 0.05 and 1) from place to place. For small samples (e.g., L=30 in our analysis) and heavy-tailed distributions, the power is always very low for the entire investigated range of the trend coefficient.
Therefore, considering the high spatial variability of the parent distribution parameters and the relatively short period of reliable and continuous historical observations usually available, a regional assessment of trend nonstationarity may suffer from the different probability of the rejection of the null hypothesis of stationarity (when it is false).
These problems affect both parametric and nonparametric tests (to slightly different degrees). While these considerations are generally applicable to all of the tests considered, differences also emerge between them. For heavy-tailed parent distributions and smaller samples, the MK test power decreases more rapidly than for the other tests considered. Low values of power are already observable for L=50. The LR test slightly outperforms the AICR for small sample sizes and higher absolute values of the shape parameter. Nevertheless, the higher value of the LR power seems to be overestimated as a consequence of the approximation for the D statistic distribution (see Sect. 3.3).
Results also suggest that the theoretical distribution of the LR test-statistic based on the null hypothesis of stationarity may lead to a significant increase in the rejection rate compared with the chosen level of significance, i.e., an abnormal rate of rejection of the null hypothesis when it is true. In this case, the use of numerical techniques, based on the implementation of synthetic generations performed by exploiting a known parent distribution, should be preferred.
In light of these results, we conclude that the assessment of the parent distribution and the choice of the null hypothesis should be considered as fundamental preliminary tasks in trend detection on annual maximum series. Therefore, it is advisable to make use of parametric tests by numerically evaluating both the rejection threshold for the assigned significance level and the power corresponding to alternative hypotheses. This also requires the development of robust techniques for selecting the parent distribution and estimating its parameters. To this end, the use of a parametric measure such as the AICR, may take different choices for the parent distribution into account and, even more importantly, allow one to set the null hypothesis differently from the stationary case, based on a priori information.
The need for robust procedures to assess the parent distribution and its parameters is also proven by the numerical simulations that we conducted. Sample variability of parameters (including the trend coefficient) may increase rapidly for series with L values as low as 30 years of the annual maxima. Moreover, we observed that, in the case of high trends, numerical instability and non-convergence of algorithms may affect the estimation procedure for upper-bounded and heavy-tailed distributions. Nevertheless, the sample variability of the ML trend estimator was always found to be smaller than the Sen's slope sample variability. Finally, it is worth noting that the nonparametric Sen's slope method, applied to synthetic series, also showed dependence on the parent distribution parameters, with sample variability being higher for heavy-tailed distributions.
This analysis shed light on important eventual flaws in the at-site analysis of climate change provided by nonparametric approaches. Both test power and trend evaluation are affected by the parent distribution as is also the case for parametric methods. It is not by chance, in our opinion, that many technical studies that have recently been conducted around the world provide inhomogeneous maps of positive/negative trends and large areas of stationarity characterized by weak trends that are not considered statistically significant.
As already stated, an advantage of using parametric tests and numerical evaluation of the test statistic distribution is given by the possibility of assuming a null hypothesis based on a preliminary assessment of the parent distribution, including trend detection via the evaluation of nonstationary parameters. This could lead to a regionally homogeneous and controlled assessment of both the significance level and the power in a fair mutual relationship. With respect to the estimation of the parameters of the parent distribution, results suggest that at-site analysis may provide highly biased results. More robust procedures are necessary, such as hierarchic estimation procedures (Fiorentino et al., 1987), and procedures that provide estimates of ε and σ from detrended series (Strupczewski et al., 2016; Kochanek et al., 2013).
As a final remark, concerning real data analysis, in our numerical experiment we showed that a weak linear trend in the mean suffices to reduce power to unacceptable values in some cases. However, we explored the simplest nonstationary working hypothesis by introducing a deterministic linear dependence of the location parameter of the parent distribution on time. Obviously, when making inference from real observed data, other sources of uncertainty may affect statistical inference (trend, heteroscedasticity, persistence, nonlinearity, and so on); moreover, if considering a nonstationary process with underlying deterministic dynamics, the process becomes non-ergodic, implying that statistical inference from sampled series is not representative of the process's ensemble properties (Koutsoyiannis and Montanari, 2015).
As a consequence, when considering a nonstationary stochastic process as being produced by a combination of a deterministic function and a stationary stochastic process, other sources of information and deductive arguments should be exploited in order to identify the physical mechanism underlying such relationships. Also, in this case observed time series have a crucial role in the calibration and validation of deterministic modeling; in other words, they are important for confirming or disproving the model hypotheses.
In the field of frequency analysis of extreme hydrological events, considering the high spatial variability of the sample length, the trend coefficient, the scale, and the shape parameters, among others, physically based probability distributions could be further developed and exploited for the selection and assessment of the parent distribution in the context of nonstationarity and change detection. The physically based probability distributions we refer to are (i) those arising from stochastic compound processes introduced by Todorovic and Zelenhasic (1970), which also include the GEV (see Madsen et al., 1997) and the TCEV (Rossi et al., 1984), and (ii) the theoretically derived distributions following Eagleson (1972) whose parameters are provided by clear physical meaning and are usually estimated with the support of exogenous information in regional methods (e.g., Gioia et al., 2008; Iacobellis et al., 2011; see Rosbjerg et al., 2013 for a more extensive overview).
Hence, we believe that “learning from data” (Sivapalan, 2003), will remain a key task for hydrologists in future years, as they face the challenge of consistently identifying both deterministic and stochastic components of change (Montanari et al., 2013). This involves crucial and interdisciplinary research to develop suitable methodological frameworks for enhancing physical knowledge and data exploitation, in order to reduce the overall uncertainty of prediction in a changing environment.
No data sets were used in this article.
All authors contributed in equal measure to all stages of the development and production of this paper.
The authors declare that they have no conflict of interest.
The authors thank the three anonymous reviewers and the editor Giuliano Di Baldassarre, who all helped to extend and the improve the paper.
The present investigation was partially carried out with support from the Puglia Region (POR Puglia FESR-FSE 2014–2020) through the “T.E.S.A.” – Tecnologie innovative per l'affinamento Economico e Sostenibile delle Acque reflue depurate rivenienti dagli impianti di depurazione di Taranto Bellavista e Gennarini – project.
This paper was edited by Giuliano Di Baldassarre and reviewed by three anonymous referees.
Akaike, H.: A new look at the statistical model identification, IEEE T. Automat. Control, 19, 716–723, https://doi.org/10.1109/TAC.1974.1100705, 1974.
Beven, K.: Facets of uncertainty: Epistemic uncertainty, non-stationarity, likelihood, hypothesis testing, and communication, Hydrolog. Sci. J., 61, 1652–1665, https://doi.org/10.1080/02626667.2015.1031761, 2016.
Burnham, K. P. and Anderson, D. R.: Model selection and multimodel inference, Springer, New York, 2004.
Cheng, L., AghaKouchak, A., Gilleland, E., and Katz, R. W.: Non-stationary extreme value analysis in a changing climate, Climatic Change, 127, 353–369, https://doi.org/10.1007/s10584-014-1254-5, 2014.
Chow, V. T. (Ed.): Statistical and probability analysis of hydrologic data, in: Handbook of applied hydrology, McGraw-Hill, New York, 8.1–8.97, 1964.
Cohen, J.: A power primer, Psycholog. Bull., 112, 155–159, 1992.
Cohen, J.: The Earth Is Round (p<.05), Am. Psychol., 49, 997–1003, 1994.
Coles, S.: An Introduction to Statistical Modeling of Extreme Values, Springer, London, 2001.
Cooley, D.: Return Periods and Return Levels Under Climate Change, in: Extremes in a Changing Climate, edited by: AghaKouchak, A., Easterling, D., Hsu, K., Schubert, S., and Sorooshian, S., Springer, Dordrecht, 97–113, https://doi.org/10.1007/978-94-007-4479-0_4, 2013.
Du, T., Xiong, L., Xu, C. Y., Gippel, C. J., Guo, S., and Liu, P.: Return period and risk analysis of nonstationary low-flow series under climate change, J. Hydrol., 527, 234–250, https://doi.org/10.1016/j.jhydrol.2015.04.041, 2015.
Eagleson, P. S.: Dynamics of flood frequency, Water Resour. Res., 8, 878–898, https://doi.org/10.1029/WR008i004p00878, 1972.
Fiorentino, M., Gabriele, S., Rossi, F., and Versace, P.: Hierarchical approach for regional flood frequency analysis, in: Regional Flood Frequency Analysis, edited by: Singh, V. P., D. Reidel, Norwell, Massachusetts, 35-49, 1987.
Gilleland, E. and Katz, R. W.: extRemes 2.0: An Extreme Value Analysis Package in R, J. Stat. Soft., 72, 1–39, 2016.
Gioia, A., Iacobellis, V., Manfreda, S., and Fiorentino, M.: Runoff thresholds in derived flood frequency distributions, Hydrol. Earth Syst. Sci., 12, 1295–1307, https://doi.org/10.5194/hess-12-1295-2008, 2008.
Gocic, M. and Trajkovic, S.: Analysis of changes in meteorological variables using Mann-Kendall and Sen's slope estimator statistical tests in Serbia, Global Planet. Change, 100, 172–182, https://doi.org/10.1016/j.gloplacha.2012.10.014, 2013.
Iacobellis, V., Gioia, A., Manfreda, S., and Fiorentino, M.: Flood quantiles estimation based on theoretically derived distributions: regional analysis in Southern Italy, Nat. Hazards Earth Syst. Sci., 11, 673–695, https://doi.org/10.5194/nhess-11-673-2011, 2011.
Jenkinson, A. F.: The frequency distribution of the annual maximum (or minimum) values of meteorological elements, Q. J. Roy. Meteorol. Soc., 81, 158–171, 1955.
Kendall, M. G.: Rank Correlation Methods, 4th Edn., Charles Griffin, London, UK, 1975.
Khintchine, A.: Korrelationstheorie der stationären stochastischen Prozesse, Math. Ann., 109, 604–615, https://doi.org/10.1007/BF01449156, 1934.
Kiely, G.: Climate change in Ireland from precipitation and streamflow observations, Adv. Water Resour., 23, 141–151, https://doi.org/10.1016/S0309-1708(99)00018-4, 1999.
Kochanek, K., Strupczewski, W. G., Bogdanowicz, E., Feluch, W., and Markiewicz, I.: Application of a hybrid approach in nonstationary flood frequency analysis – a Polish perspective, Nat. Hazards Earth Syst. Sci. Discuss., 1, 6001–6024, https://doi.org/10.5194/nhessd-1-6001-2013, 2013.
Kolmogorov, A. N.: Über die analytischen Methoden in der Wahrscheinlichkeitsrechnung. Mathematische Annalen, 104, 415–458 (English translation: On analytical methods in probability theory, in: Kolmogorov, A. N., 1992. Selected Works of A. N. Kolmogorov – Volume 2, Probability Theory and Mathematical Statistics, edited by: Shiryayev, A. N., Kluwer, Dordrecht, the Netherlands, 62–108, https://doi.org/10.1007/BF01457949, 1931.
Koutsoyiannis, D. and Montanari A.: Negligent killing of scientific concepts: the stationarity case, Hydrolog. Sci. J., 60, 1174–1183, https://doi.org/10.1080/02626667.2014.959959, 2015.
Kundzewicz, Z. W. and Robson, A. J.: Change detection in hydrological records – a review of the methodology, Hydrolog. Sci. J., 49, 7–19, https://doi.org/10.1623/hysj.49.1.7.53993, 2004.
Laio, F., Baldassarre, G. D., and Montanari, A.: Model selection techniques for the frequency analysis of hydrological extremes, Water Resour. Res., 45, W07416, https://doi.org/10.1029/2007wr006666, 2009.
Lehmann, E. L.: Nonparametrics, Statistical Methods Based on Ranks, Holden-Day, Oxford, England, 1975
Lieber, R. L.: Statistical significance and statistical power in hypothesis testing, J. Orthop. Res., 8, 304–309, https://doi.org/10.1002/jor.1100080221, 1990.
Madsen, H., Rasmussen, P., and Rosbjerg, D.: Comparison of annual maximum series and partial duration series for modelling exteme hydrological events: 1. At-site modeling, Water Resour. Res., 33, 747–757, https://doi.org/10.1029/96WR03848, 1997.
Mann, H. B.: Nonparametric tests against trend, Econometrica, 13, 245–259, https://doi.org/10.2307/1907187, 1945.
Milly, P. C. D., Betancourt, J., Falkenmark, M., Hirsch, R. M., Kundzewicz, Z. W., Lettenmaier, D. P., Stouffer, R. J., Dettinger, M. D., and Krysanova, V.: On Critiques of “stationarity is Dead: Whither Water Management?”, Water Resour. Res., 51, 7785–7789, https://doi.org/10.1002/2015WR017408, 2015.
Montanari, A. and Koutsoyiannis, D.: Modeling and mitigating natural hazards: Stationarity is immortal!, Water Resour. Res., 50, 9748–9756, https://doi.org/10.1002/2014wr016092, 2014.
Montanari, A., Young, G., Savenije, H. H. G., Hughes, D., Wagener, T., Ren, L. L., Koutsoyiannis, D., Cudennec, C., Toth, E., Grimaldi, S., Blöschl, G., Sivapalan, M., Beven, K., Gupta, H., Hipsey, M., Schaefli, B., Arheimer, B., Boegh, E., Schymanski, S. J., Di Baldassarre, G., Yu, B., Hubert, P., Huang, Y., Schumann, A., Post, D., Srinivasan, V., Harman, C., Thompson, S., Rogger, M., Viglione, A., McMillan, H., Characklis, G., Pang, Z., and Belyaev, V.: “Panta Rhei—Everything Flows”: Change in hydrology and society – The IAHS Scientific Decade 2013–2022, Hydrolog. Sci. J., 58, 1256–1275, 2013.
Muraleedharan, G., Guedes Soares, C., and Lucas, C.: Characteristic and moment generating functions of generalised extreme value distribution (GEV), in: Sea Level Rise, Coastal Engineering, Shorelines and Tides, Nova Science, New York, 2010.
Olsen, J. R., Lambert, J. H., and Haimes, Y. Y.: Risk of extreme events under nonstationary conditions, Risk Anal., 18, 497–510, https://doi.org/10.1111/j.1539-6924.1998.tb00364.x, 1998.
Parey, S., Malek, F., Laurent, C., and Dacunha-Castelle, D.: Trends and climate evolution: statistical approach for very high temperatures in France, Climatic Change, 81, 331–352, https://doi.org/10.1007/s10584-006-9116-4, 2007.
Parey, S., Hoang, T. T. H., and Dacunha-Castelle, D.: Different ways to compute temperature return levels in the climate change context, Environmetrics, 21, 698–718, https://doi.org/10.1002/env.1060, 2010.
Pettitt, A. N.: A non-parametric approach to the change-point problem, Appl. Stat., 28, 126–135, https://doi.org/10.2307/2346729, 1979.
Read, L. K. and Vogel, R. M.: Reliability, return periods, and risk under nonstationarity, Water Resour. Res., 51, 6381–6398, https://doi.org/10.1002/2015WR017089, 2015.
Rosbjerg, D., Blöschl, G., Burn, D., Castellarin, A., Croke, B., Di Baldassarre, G., Iacobellis, V., Kjeldsen, T. R., Kuczera, G., Merz, R., Montanari, A., Morris, D., Ouarda, T. B. M. J., Ren, L., Rogger, M., Salinas, J. L., Toth, E., and Viglione, A.: Prediction of floods in ungauged basins, in: Runoff Prediction in Ungauged Basins: Synthesis across Processes, Places and Scales, edited by: Blöschl, G., Sivapalan, M., Wagener, T., Viglione, A., and Savenije, H., Cambridge University Press, Cambridge, 189–226, https://doi.org/10.1017/CBO9781139235761.012, 2013.
Rossi, F., Fiorentino, M., and Versace, P.: Two-Component Extreme Value Distribution for Flood Frequency Analysis, Water Resour. Res., 20, 847–856, https://doi.org/10.1029/WR020i007p00847, 1984.
Salas, J. D. and Obeysekera, J.: Revisiting the concepts of return period and risk for nonstationary hydrologic extreme events, J. Hydrol. Eng., 19, 554–568, https://doi.org/10.1061/(ASCE)HE.1943-5584.0000820, 2014.
Schwarz, G.: Estimating the dimension of a model, Ann. Stat., 6, 461–464, 1978.
Sen, P. K.: Estimates of the regression coefficient based on Kendall's tau, J. Am. Stat. Assoc., 63, 1379–1389, https://doi.org/10.2307/2285891, 1968.
Serinaldi, F. and Kilsby, C. G.: Stationarity is undead: Uncertainty dominates the distribution of extremes, Adv. Water Resour., 77, 17–36, https://doi.org/10.1016/j.advwatres.2014.12.013, 2015.
Serinaldi, F., Kilsby, C. G., and Lombardo, F.: Untenable nonstationarity: An assessment of the fitness for purpose of trend tests in hydrology, Adv. Water Resour., 111, 132–155, https://doi.org/10.1016/J.ADVWATRES.2017.10.015, 2018.
Sivapalan, M., Prediction in Ungauged Basins: A Grand Challenge for Theoretical Hydrology, Hydrol. Process., 17, 3163–3170, 2003.
Smadi, M. M. and Zghoul A.: A sudden change in rainfall characteristics in Amman, Jordan during the mid 1950s, Am. J. Environ. Sci., 2, 84–91, https://doi.org/10.3844/ajessp.2006.84.91, 2006.
Strupczewski, W. G., Kochanek, K., Bogdanowicz, E., Markiewicz, I., and Feluch, W.: Comparison of two nonstationary flood frequency analysis methods within the context of the variable regime in the representative polish rivers, Acta Geophys., 64, 206–236, https://doi.org/10.1515/acgeo-2015-0070, 2016.
Sugiura, N.: Further analysis of the data by Akaike's information criterion and the finite corrections, Commun. Stat. Theor. Meth., A7, 13–26, https://doi.org/10.1080/03610927808827599, 1978.
Todorovic, P. and Zelenhasic, E.: A Stochastic Model for Flood Analysis, Water Resour. Res., 6, 1641–1648, https://doi.org/10.1029/WR006i006p01641, 1970.
Tramblay, Y., Neppel, L., Carreau, J., and Najib, K.: Non-stationary frequency analysis of heavy rainfall events in southern France, Hydrolog. Sci. J., 58, 280–194, https://doi.org/10.1080/02626667.2012.754988, 2013.
Vogel, R. M., Rosner, A., and Kirshen, P. H.: Brief Communication: Likelihood of societal preparedness for global change: trend detection, Nat. Hazards Earth Syst. Sci., 13, 1773–1778, https://doi.org/10.5194/nhess-13-1773-2013, 2013.
Wang, W., Van Gelder, P. H., and Vrijling, J. K.: Trend and stationarity analysis for streamflow processes of rivers in Western Europe in the 20th Century, in: IWA International Conference on Water Economics, Statistics, and Finance, 8–10 July 2005, Rethymno, Greece, 2005.
Yilmaz, A. G. and Perera, B. J. C.: Extreme rainfall nonstationarity investigation and intensity–frequency–duration relationship, J. Hydrol. Eng., 19, 1160–1172, https://doi.org/10.1061/(ASCE)HE.1943-5584.0000878, 2014.
Yilmaz, A. G., Hossain, I., and Perera, B. J. C.: Effect of climate change and variability on extreme rainfall intensity–frequency–duration relationships: a case study of Melbourne, Hydrol. Earth Syst. Sci., 18, 4065–4076, https://doi.org/10.5194/hess-18-4065-2014, 2014.
Yue, S., Pilon, P., and Cavadias, G.: Power of the Mann–Kendall and Spearman's rho tests for detecting monotonic trends in hydrological series, J. Hydrol., 259, 254–271, https://doi.org/10.1016/S0022-1694(01)00594-7, 2002a.
Yue, S., Pilon, P., Phinney, B., and Cavadias, G.: The influence of autocorrelation on the ability to detect trend in hydrological series, Hydrol. Process., 16, 1807–1829, https://doi.org/10.1002/hyp.1095, 2002b.