Novel Keeling-plot-based methods to estimate the isotopic composition of ambient water vapor

The Keeling plot approach, a general method to identify the isotopic composition of source atmospheric CO₂ and water vapor (i.e., evapotranspiration), has been widely used in terrestrial ecosystems. The isotopic composition of ambient water vapor (δ_a), an important source of atmospheric water vapor, is not able to be estimated to date using the Keeling plot approach. Here we proposed two new methods to estimate δ_a using the Keeling plots: one using an intersection point method and another relying on the intermediate value theorem. As the actual δ_a value was difficult to measure directly, we used two indirect approaches to validate our new methods. First, we performed external vapor tracking using the Hybrid Single Particle Lagrangian Integrated Trajectory (HYSPLIT) model to facilitate explaining the variations of δ_a. The trajectory vapor origin results were consistent with the expectations of the δ_a values estimated by these two methods. Second, regression analysis was used to evaluate the relationship between δ_a values estimated from these two independent methods, and they are in strong agreement. This study provides an analytical framework to estimate δ_a using existing facilities and provides important insights into the traditional Keeling plot approach by showing (a) a possibility to calculate the proportion of evapotranspiration fluxes to total atmospheric vapor using the same instrumental setup for the traditional Keeling plot investigations and (b) perspectives on the estimation of isotope composition of ambient CO₂ (δ_a¹³C).

1 Introduction

Stable isotopes of hydrogen and oxygen (¹H²HO and ${\mathrm{H}}_{\mathrm{2}}^{\mathrm{18}}\mathrm{O}$) have been widely used in root water uptake source identification (Corneo et al., 2018; Mahindawansha et al., 2018; Lanning et al., 2020) and evapotranspiration (ET) partitioning (Brunel et al., 1997; Wang et al., 2010; Cui et al., 2020) in terrestrial ecosystems based on the Craig–Gordon model (Craig and Gordon, 1965), isotope mass balance and mechanisms of isotopic fractionation (Majoube, 1971; Merlivat and Jouzel, 1979). With the advent of laser isotope spectrometry capable of high-frequency (1 Hz) measurements of the isotopic composition of atmospheric water vapor (δ_v) and atmospheric water vapor content (C_v) (Kerstel and Gianfrani, 2008; Wang et al., 2009), the number of studies based on high-frequency ground-level isotope measurements was continuously increasing. These studies generate new insights into the processes that affect δ_v, including meteorological factors (Galewsky et al., 2011; Steen-Larsen et al., 2013), biotic factors (Wang et al., 2010) and multiple factors (Parkes et al., 2016). Such an increase in δ_v measurements allows isotope-enabled global circulation models (Iso-GCMs) to estimate the variation of water vapor isotope parameters at a global scale (Werner et al., 2011). Concomitantly, more than δ_v, several new methods using high-frequency ground-level isotope measurements were devised to directly estimate the isotopic composition of leaf water (Song et al., 2015) and leaf-transpired vapor (Wang et al., 2012).

Evapotranspiration is a crucial component of the water budget across scales such as the field (Wagle et al., 2020), watershed (Zhang et al., 2001), regional (Hobbins et al., 2001) and global (Jung et al., 2010, Wang et al., 2014) scales. The water isotopic composition of ET (δ_ET) was generally estimated by the Keeling plot approach (Keeling, 1958). It was first used to explain carbon isotope ratios of atmospheric CO₂ and to identify the sources that contribute to increases in atmospheric CO₂ concentration, and it has been further used to estimate δ_ET in the past 2 decades (Yakir and Sternberg, 2000). The Keeling plot analyses can be applied using δ_v and C_v output by a laser-based analyzer either from different heights (Yepez et al., 2003; Zhang et al., 2011; Good et al., 2012) or at one height with continuous observations (Wei et al., 2015; Keppler et al., 2016). Although the intercept of the linear-regression line was commonly used as estimated δ_ET, the slope of the Keeling plot was also used to estimate δ_ET by re-arranging the Keeling plot equations (Miller and Tans, 2003; Fiorella et al., 2018). The Keeling plot approach was based on isotope mass balance and a two-source assumption using two equations with three unknowns. As a result, the isotopic composition of other potential sources (e.g., water vapor not from ET), as well as the isotopic composition of ambient water vapor (δ_a), were not able to be estimated directly using the Keeling plot approach. That is one of the reasons why field scale moisture recycling has been difficult to estimate to date.

In this study, we proposed two new methods to estimate δ_a, one based on the intersection of two Keeling plots of two continuous observation moments and the other based on the intermediate value theorem. Proposition and proof were provided, and the new methods were tested using field observations. As direct observations of δ_a rarely exist (Griffis et al., 2016), we tested our methods by (a) performing an investigation of external water vapor tracking according to the Hybrid Single Particle Lagrangian Integrated Trajectory (HYSPLIT) model to explain the variations of estimated δ_a and (b) making a regression analysis on a daily scale and point-to-point scale using δ_a estimated by these two independent methods.

2 Materials and methods

2.1 Theory

The atmospheric vapor concentration in an ecosystem reflects the combination of ambient vapor that already exists in the atmosphere and the vapor that is added through evaporation (E) and transpiration (T) (Yakir and Sternberg, 2000). The Keeling plot approach is based on the combination of a bulk water mass balance equation and an isotope mass balance equation:

$$\begin{array}{}\text{(1)}& {\displaystyle }{C}_{\mathrm{v}}=C_{\mathrm{a}}+C_{\text{ET}},\text{(2)}& {\displaystyle }{C}_{\mathrm{v}}{\mathit{\delta }}_{\mathrm{v}}=C_{\mathrm{a}}{\mathit{\delta }}_{\mathrm{a}}+C_{\text{ET}}{\mathit{\delta }}_{\text{ET}},\end{array}$$

where δ_a, δ_ET and δ_v are the isotope composition of ambient water vapor, ET and atmospheric water vapor, respectively, and C_a, C_ET and C_v are the corresponding concentrations of water vapor. Note that all quantities here are time dependent, and δ_v and C_v also depend on heights.

Combining Eqs. (1) and (2), we have the following traditional linear Keeling plot relationship between δ_v and 1∕C_v with intercept δ_ET and slope C_a(δ_a−δ_ET),

$$\begin{array}{}\text{(3)}& {\mathit{\delta }}_{\mathrm{v}}=C_{\mathrm{a}}({\mathit{\delta }}_{\mathrm{a}}-{\mathit{\delta }}_{\text{ET}})/C_{\mathrm{v}}+{\mathit{\delta }}_{\text{ET}}.\end{array}$$

For a given time, with various measurements of δ_v and C_v collected at different heights, we are able to estimate the intercept δ_ET and slope $k=C_{\mathrm{a}}({\mathit{\delta }}_{\mathrm{a}}-{\mathit{\delta }}_{\text{ET}})$ for this moment from regression analysis (Zhang et al., 2011; Wang et al., 2013). Here we focus on the estimation of δ_a using two new methods proposed below.

Intersection point (IP) method. Note that for two nearby time points t₁ and t₂, we could use local-constant approximation to estimate δ_a within this time interval, since it remains relatively constant over a short period of time. By assuming a local constant for C_a and δ_a within this time interval, we have

$$\begin{array}{}\text{(4)}& {\displaystyle }{k}_{\mathrm{1}}& {\displaystyle }=C_{\mathrm{a}}({\mathit{\delta }}_{\mathrm{a}}-{\mathit{\delta }}_{{\text{ET}}_{\mathrm{1}}}),\text{(5)}& {\displaystyle }{k}_{\mathrm{2}}& {\displaystyle }=C_{\mathrm{a}}({\mathit{\delta }}_{\mathrm{a}}-{\mathit{\delta }}_{{\text{ET}}_{\mathrm{2}}}),\end{array}$$

where k_i and ${\mathit{\delta }}_{{\text{ET}}_i}$ represent the value at t_i for $i=\mathrm{1},\mathrm{2}$. From Eqs. (4) and (5), we can solve δ_a as

$$\begin{array}{}\text{(6)}& {\mathit{\delta }}_{\mathrm{a}}={\displaystyle \frac{k_{\mathrm{1}}{\mathit{\delta }}_{{\text{ET}}_{\mathrm{2}}}-k_{\mathrm{2}}{\mathit{\delta }}_{{\text{ET}}_{\mathrm{1}}}}{k_{\mathrm{1}}-k_{\mathrm{2}}}}.\end{array}$$

Algebraically, δ_a and C_a are solutions in Eqs. (4) and (5). Geometrically, point (δ_a, 1∕C_a) is the intersection of two Keeling plots at t₁ and t₂. That is the reason the method was named the IP method. The local-constant approximation idea was first described in Yamanaka and Shimizu (2007) as an assumption to quantify the contribution of local ET to total atmospheric vapor.

Intermediate value theorem (IVT) method. Denote the slope as $k=C_{\mathrm{a}}({\mathit{\delta }}_{\mathrm{a}}-{\mathit{\delta }}_{\text{ET}})$. As $C_{\mathrm{a}}<C_{\mathrm{v}}=C_{\mathrm{a}}+C_{\text{ET}}$, we have $C_{\mathrm{a}}=\frac{k}{({\mathit{\delta }}_{\mathrm{a}}-{\mathit{\delta }}_{\text{ET}})}<C_{\mathrm{v}}$. We can rearrange $\frac{k}{({\mathit{\delta }}_{\mathrm{a}}-{\mathit{\delta }}_{\text{ET}})}<C_{\mathrm{v}}$ to attain δ_a: ${\mathit{\delta }}_{\mathrm{a}}<\frac{k}{C_{\mathrm{v}}}+{\mathit{\delta }}_{\text{ET}}={\mathit{\delta }}_{\mathrm{v}}$ when k<0 and ${\mathit{\delta }}_{\mathrm{a}}>\frac{k}{C_{\mathrm{v}}}+{\mathit{\delta }}_{\text{ET}}={\mathit{\delta }}_{\mathrm{v}}$ when k>0.

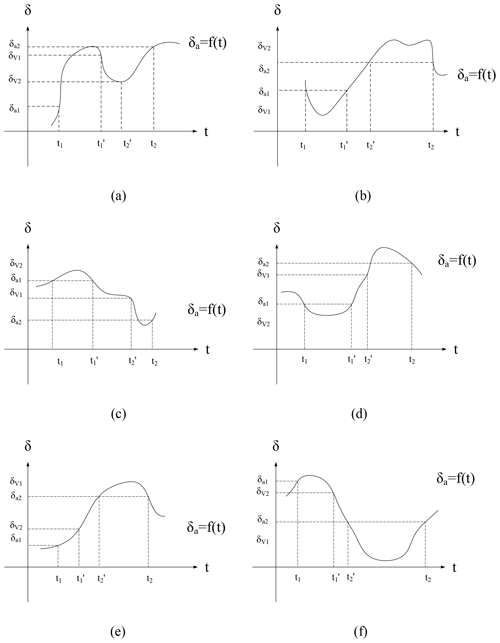
Figure 1 Theoretical diagrams of all possible combinations of the relationships between isotope composition of ambient vapor (δ_a) and the observed isotope composition of atmospheric vapor (δ_v) of two continuous moments t₁ and t₂, (t₁<t₂). δ_a1 and δ_a2 represent the δ_a value in t₁ and t₂, respectively. δ_v1 and δ_v2 represent the δ_v value in t₁ and t₂, respectively. $t_{\mathrm{1}}^{\prime }$ and $t_{\mathrm{2}}^{\prime }$ represent the time of two specific moments between t₁ and t₂ with $t_{\mathrm{1}}<t_{\mathrm{1}}^{\prime }<t_{\mathrm{2}}^{\prime }<t_{\mathrm{2}}$. For all of the six situations, there are some subintervals $[t_{\mathrm{1}}^{\prime },t_{\mathrm{2}}^{\prime }]\subset \left[t_{\mathrm{1}}{t}_{\mathrm{2}}\right]$ such that the whole range of ${\mathit{\delta }}_{\mathrm{a}}\left(t\right):t\in \left[t_{\mathrm{1}}^{\prime },t_{\mathrm{2}}^{\prime }\right]$ is within $[min({\mathit{\delta }}_{{\mathrm{v}}_{\mathrm{1}}}{\mathit{\delta }}_{{\mathrm{v}}_{\mathrm{2}}}),max({\mathit{\delta }}_{{\mathrm{v}}_{\mathrm{1}}}{\mathit{\delta }}_{{\mathrm{v}}_{\mathrm{2}}}\left)\right]$.

For the smooth function δ_a(t) defined on the interval [t₁, t₂] with the two time points satisfying k(t₁) k(t₂)<0, depending on the sign of the slopes k(t₁) and k(t₂) and the order of ${\mathit{\delta }}_{{\mathrm{v}}_{\mathrm{1}}}={\mathit{\delta }}_{\mathrm{v}}\left(t_{\mathrm{1}}\right)$ and ${\mathit{\delta }}_{{\mathrm{v}}_{\mathrm{2}}}={\mathit{\delta }}_{\mathrm{v}}\left(t_{\mathrm{2}}\right)$ at the two time points t₁ and t₂, it will correspond to one of the situations in Fig. 1. For all of the situations, following the intermediate value theorem, there exists a subinterval $[t_{\mathrm{1}}^{\prime },t_{\mathrm{2}}^{\prime }]\subset \left[t_{\mathrm{1}}{t}_{\mathrm{2}}\right]$ such that the whole range of $\left\{{\mathit{\delta }}_{\mathrm{a}}\left(t\right):t\in \left[t_{\mathrm{1}}^{\prime },t_{\mathrm{2}}^{\prime }\right]\right\}$ is within $[min({\mathit{\delta }}_{{\mathrm{v}}_{\mathrm{1}}}{\mathit{\delta }}_{{\mathrm{v}}_{\mathrm{2}}}),max({\mathit{\delta }}_{{\mathrm{v}}_{\mathrm{1}}}{\mathit{\delta }}_{{\mathrm{v}}_{\mathrm{2}}}\left)\right]$. Proof details of this proposition are shown in the Supplement. Thus for the two nearby time points t₁ and t₂ with k₁ and k₂ having different signs, δ_a will be between ${\mathit{\delta }}_{{\mathrm{v}}_{\mathrm{1}}}$ and ${\mathit{\delta }}_{{\mathrm{v}}_{\mathrm{2}}}$. This provides a prerequisite for estimating the parameter of interest δ_a based on the intermediate value theorem, which leads to an approximation of δ_a within the time interval between t₁ and t₂ using ${\mathit{\delta }}_{{\mathrm{v}}_{\mathrm{1}}}$ and ${\mathit{\delta }}_{{\mathrm{v}}_{\mathrm{2}}}$:

$$\begin{array}{}\text{(7)}& {\mathit{\delta }}_{\mathrm{a}}\approx {\displaystyle \frac{{\mathit{\delta }}_{{\mathrm{v}}_{\mathrm{1}}}+{\mathit{\delta }}_{{\mathrm{v}}_{\mathrm{2}}}}{\mathrm{2}}}.\end{array}$$

Using this method, we are able to compute δ_a using data points when the slopes of Keeling plots change signs between two adjacent time points.

2.2 Field observations

2.2.1 Study site

A field measurement was conducted over a maize field (39 ha) from 1 May 2017 to 30 September 2017 at the Shiyanghe Experimental Station of China Agricultural University, located in Wuwei of Gansu province, northwestern China (37^∘ 85^′ N, 102^∘ 88^′ E; altitude 1581 m). The region belongs to a temperate continental climate and is in the oasis within the Shiyang River basin. The annual mean temperature of the study area is about 8.8^∘ with pan evaporation of 2000 mm, annual precipitation of 164.4 mm, mean sunshine duration of 3000 h and frost-free period of more than 150 d. The local crops are irrigated using groundwater with electrical conductivity of 0.62 dS m⁻¹. The groundwater table is 30–40 m below the surface. Maize was sowed in April and harvested in September 2017, with a row spacing of 40 cm and plant spacing of 23 cm. The maize growing stage was divided into the seedling stage (21 April–20 May), jointing stage (21 May–10 July), heading period (11–31 July), pustulation period (1–31 August) and mature period (1–20 September).

2.2.2 Instrumental setup and measurement design

A 24 m flux tower, located in the middle of the maize field, was used to measure the ET flux and isotopic composition of water vapor at different heights. The field is approximately 600 m long and 240 m wide, with a 1 % slope decreasing from southwest to northeast. Five gas traps were installed on the flux tower at heights of 4, 8, 12, 16 and 20 m, respectively. An iron pillar was placed 20 m away from the flux tower. Three gas traps were installed on the iron pillar; one was close to the canopy, and the other two were 2 and 3 m above the ground. The gas trap by the canopy was adjusted weekly according to the height of maize.

In situ δ_v and C_v collected by the eight gas traps were monitored by a water vapor isotope analyzer (L2130-i, Picarro Inc., Sunnyvale, CA, USA), which was a wavelength-scanned cavity ring-down spectroscope (WS-CRDS) instrument. Vapor specifications include a measurement range from 1000 to 50 000 ppm; the precision is 0.04 ‰ to 0.25 ‰ for δ¹⁸O (Zhao et al., 2019). Interfacing with the gas trap and the isotope analyzer, a teflon tube was wrapped by thermal insulation cotton to avoid vapor condensation during transmission. The measurement of δ_v and C_v was conducted from May to September, which should have 153 d of data; 49 d among them were complete with 24 h continuous datasets. There were missing data for either a whole day or several hours of a day for other days due to the calibration and maintenance of the analyzer. These 49 d were chosen in our study for data analysis.

2.2.3 Calibration of δ_v and C_v

Our calibration procedure mainly followed the study by Steen-Larsen et al. (2013) with some modifications to fit our specific experimental setup. The water vapor from eight inlets was sampled continuously over a 24 h period. Since only one analyzer was used to measure δ_v and C_v, the values of eight sampling inlets were recorded in turn every 225 s in a 30 min cycle. The switch procedure was automatic. As the analyzer makes a measurement every 0.9–1 s, approximately 259–264 values for each inlet was recorded within the cycle. For each 225 s measurement period, data points 195 to 253 were used to avoid a memory issue and the influence of transient pressure variation. The absolute value of the coefficient of variation (|CV|) of δ_v and C_v was no more than 0.016 and 0.002, respectively, which was far below the critical value of 15 % (Lovie, 2005). The mean value of the selected data points was regarded as the measured δ_v and C_v in a specific inlet. Measured C_v was used directly as actual C_v, while measured δ_v was calibrated to minimize the influence of isotopic-concentration dependence. The C_v in our measurement ranged from 5386 to 30 255 ppm. Thus, C_v gradients of 10 000, 20 000 and 30 000 ppm were selected as calibration concentrations to improve the precision of δ_v. As we need continuous data, the observation should last uninterrupted as long as possible. As a result, the calibration was made every 5–10 d, which is consistent with the frequency of calibration by other researchers such as Steen-Larsen et al. (2013). According to our calibration data on standards, the average drift (absolute value) was about 0.16 ‰ between two adjacent calibrations.

Table 1 The number of the estimated isotope composition of ambient vapor meeting the criteria using the intersection point method (δ_a(IP)) and the intermediate value theorem method (δ_a(IVT)) among all 49 d.

2.3 Data quality control for δ_a estimation

With a 30 min interval for 49 d, we should in theory produce 2352 δ_a values for both the IP method and IVT method. However, because of the precondition of k₁k₂<0 required for the IVT method, 166 δ_a values were able to be calculated using the IVT method (δ_a(IVT)). δ_a values using the IP method (δ_a(IP)) were not restricted by this precondition. Furthermore, a filter (${\mathit{\delta }}_{\text{ET}}<{\mathit{\delta }}_{\mathrm{v}}<{\mathit{\delta }}_{\mathrm{a}}$ or ${\mathit{\delta }}_{\text{ET}}>{\mathit{\delta }}_{\mathrm{v}}>{\mathit{\delta }}_{\mathrm{a}}$) was used for both methods because δ_v was a mixture of δ_ET and δ_a. Therefore, δ_a values that meet both precondition k₁k₂<0 and the condition of ${\mathit{\delta }}_{\text{ET}}<{\mathit{\delta }}_{\mathrm{v}}<{\mathit{\delta }}_{\mathrm{a}}$ or ${\mathit{\delta }}_{\text{ET}}>{\mathit{\delta }}_{\mathrm{v}}>{\mathit{\delta }}_{\mathrm{a}}$ were considered to satisfy the criteria for the IVT method; δ_a values that meet the condition of ${\mathit{\delta }}_{\text{ET}}<{\mathit{\delta }}_{\mathrm{v}}<{\mathit{\delta }}_{\mathrm{a}}$ or ${\mathit{\delta }}_{\text{ET}}>{\mathit{\delta }}_{\mathrm{v}}>{\mathit{\delta }}_{\mathrm{a}}$ were considered to satisfy the criteria for the IP method. In the end, we obtained 1264 and 103 δ_a values using IP and IVT methods, respectively (Table 1). A total of 88 time points were overlapped between the IP- and IVT-based δ_a results. These 88 time points were selected to test the reliability of two methods at a point-to-point scale. During the 49 d, there were 21 d when more than one δ_a(IVT) was attained for each day. These 21 d was also used to investigate the time series of daily-scale δ_a variations and other isotopic variations. Further analysis in Sect. 2.4 of the following was made on these 21 d.

2.4 Explanations of δ_a using backward trajectories

To explain the variations of estimated δ_a, air mass backward trajectories were calculated using the Hybrid Single Particle Lagrangian Integrated Trajectory (HYSPLIT) model (Draxler and Hess, 1997; Draxler, 2003; Stein et al., 2015; Kaseke et al., 2018) and meteorological data from the Global Data Assimilation System 0.5 ^∘ (GDAS0p5) dataset with 0.5^∘ × 0.5^∘ spatial resolution and 3 h time resolution for the 21 d mentioned in Sect. 2.3. A height of 500 m was selected in the modeling. Each backward trajectory was initialized from the station (37^∘ 85^′ N, 102^∘ 88^′ E) at 12:00 (LT) and calculated backward for 72 h; 18 trajectories were computed, excluding 21 June, 18 August and 29 September, when vertical velocity data were missing. Finally, we used these 18 trajectories representing the vapor origin in the corresponding 18 d.

3 Results

3.1 Time series variations of δ_ET, δ_v, δ_a and k

Time series of isotopic variations were shown in Fig. 2. The δ_v here is the average value of eight heights. The average δ_ET, δ_v, δ_a(IP) and δ_a(IVT) were −11.04 ‰, −13.00 ‰, −13.60 ‰ and −13.29 ‰, respectively, in those 21 d when more than one δ_a(IVT) was attained for each day. Daytime-average (07:00–19:00) δ_ET, δ_v, δ_a(IP) and δ_a(IVT) were −10.73 ‰, −13.33 ‰, −14.08 ‰ and −13.63 ‰, respectively. While at nighttime (19:00 to 07:00 the next day), average δ_ET was lower than that at daytime, which was contrary to δ_v, δ_a(IP) and δ_a(IVT). The trend of δ_a(IP) and δ_a(IVT) was similar to δ_v. In the majority of circumstances, δ_ET is the largest of those four isotopic parameters, except on 19 May, 4 June and 9 June. About 76 % of k values were negative, and most positive k values occurred at nighttime (60 %). The percentage of positive k values were 33 %, 34 %, 24 %, 34 % and 10 % in May, June, July, August and September, respectively. The standard deviation (SD) was used here to evaluate the constancy among isotopic parameters at a daily scale. The SD of δ_ET, δ_v, δ_a(IP) and δ_a(IVT) was 6.08 ‰, 0.91 ‰, 1.38 ‰ and 0.59 ‰, respectively. Therefore, the constancy of δ_a was similar to the constancy of δ_v at a daily scale.

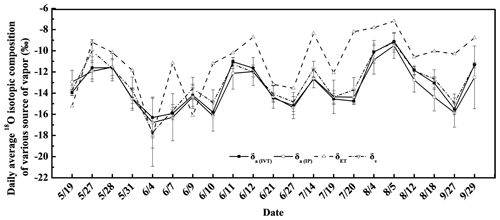
Figure 2 The daily average values of the isotope composition of evapotranspiration vapor (δ_ET), the isotope composition of atmospheric vapor (δ_v), the estimated isotope composition of ambient vapor using the intersection point method (δ_a(IP)) and the intermediate value theorem method (δ_a(IVT)) in the 21 d time frame (see the method in Sect. 2.3). Please note that the date format in this figure is month/day.

3.2 Daily variations of HYSPLIT backward trajectories and δ_a using two methods

The 500 m height water vapor backward trajectories revealed that water vapor was from outside the study regions for 10 d (Fig. 3a), and water vapor was from local ET for 8 d (Fig. 3b).

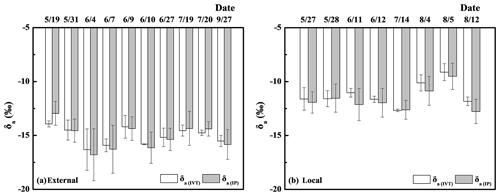
Figure 3 The daily average values of the estimated isotope composition of ambient vapor using the intersection point method (δ_a(IP)) and the intermediate value theorem method (δ_a(IVT)) after filtering. The Hybrid Single Particle Lagrangian Integrated Trajectory (HYSPLIT) backward trajectory showed both external (a) and local origins (b), respectively. Please note that the date format in this figure is month/day.

As for the IP method, 53.7 % of δ_a(IP) values met the criteria, and 49.4 % of δ_a(IP) values meeting the criteria were during the daytime (07:00–19:00). The range of δ_a(IP) values meeting the criteria were between −16.79 ‰ and −12.95 ‰ for the 10 d with external origins (Fig. 3a). The range of δ_a(IP) values meeting the criteria were between −12.77 ‰ and −9.51 ‰ for the 8 d with local origins (Fig. 3b).

As for the IVT method, only 4.4 % of δ_a values met the criteria, and 35.9 % of δ_a values meeting the criteria were during the daytime (07:00–19:00). The range of δ_a(IVT) values meeting the criteria were between −16.31 ‰ and −13.93 ‰ for the 10 d with external origins (Fig. 3a). The range of δ_a(IVT) values meeting the criteria were between −12.67 ‰ and −9.12 ‰ for the 8 d with local origins (Fig. 3b).

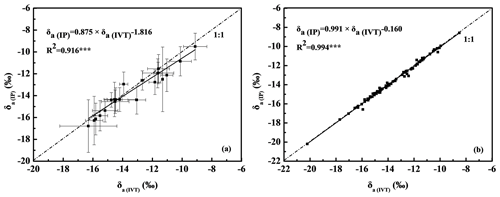
3.3 Linear regression between δ_a(IP) and δ_a(IVT)

A method comparison was performed at both a daily scale (Fig. 4a) and point-to-point scale (Fig. 4b). The 21 d time frame (see the method in Sect. 2.3) in Fig. 3a and b was selected to figure out the daily-scale relationship between δ_a(IP) and δ_a(IVT). Point-to-point scale data were based on the 88 points of overlapped δ_a(IP) and δ_a(IVT) (see the method in Sect. 2.3) among all 49 d, which accounted for 7.0 % of δ_a values using the IP method and 85.4 % of δ_a values using the IVT method. A linear regression between δ_a(IP) and δ_a(IVT) was significant at both a daily scale and point-to-point scale. The degree of agreement was less for the daily timescale than a point-to-point scale, and the RMSE between these two methods at a daily scale and point-to-point scale was 0.618 ‰ and 0.167 ‰, respectively.

Figure 4 Linear regression between the estimated isotope composition of ambient vapor using the intersection point method (δ_a(IP)) and the intermediate value theorem method (δ_a(IVT)) on a daily scale (a) and point-to-point scale (b), respectively.

4 Discussion

4.1 The reliability of δ_a estimating methods

The IP method was based on the assumption that the ambient sources were the same between two continuous observation moments. This is a reasonable assumption for short time intervals. For the IVT method, δ_a was derived from δ_v in two continuous moments when their Keeling plot slopes were opposite. The opposite slopes of the Keeling plots were the only requirement. As δ_v was almost constant in two continuously moments, δ_a(IVT) was able to be constrained into a small range. The derivation was supported by the intermediate value theorem. Therefore, both methods of estimating δ_a were theoretically sound.

The δ_a results were also examined by HYSPLIT backward trajectories to identify the different sources of water vapor, which assesses the reliability of both methods indirectly. Based on the trajectory analysis, water vapor in the study area came from westerlies, the northern polar region and local recirculation. Water vapor from southwestern monsoons and the northwestern Pacific were not detected in this study. Based on the isotope variation of meteoric water (Fricke et al., 1999), water vapor from westerlies and the northern polar region was more ¹⁸O depleted than local recycled moisture through ET. It was also reported that the water vapor from outside the study regions will lower δ_v values (Ma et al., 2014; Chen et al., 2015). The calculated δ_a values of the 10 d with external sources (Fig. 3a) based on the IP method and IVT approach were lower than those of 8 d with local origins (Fig. 3b), which was consistent with our expectation. The results indicate that quantifying δ_a using both the IP method and IVT approach was reliable. The reliability of two methods at a point-to-point scale was also supported by the close relationship of δ_a using these two independent methods. A daily-timescale result is less reliable than a point-to-point scale.

4.2 The application of δ_a for moisture recycling

When δ_a was estimated, moisture recycling (e.g., f_ET, the contribution of ET fluxes to the total water vapor) can be estimated using the following equations with known δ_a, δ_ET, δ_v, C_ET and C_v:

$$\begin{array}{}\text{(8)}& {\displaystyle }{C}_{\text{ET}}& {\displaystyle }=C_{\mathrm{v}}{\displaystyle \frac{{\mathit{\delta }}_{\mathrm{a}}-{\mathit{\delta }}_{\mathrm{v}}}{{\mathit{\delta }}_{\mathrm{a}}-{\mathit{\delta }}_{\text{ET}}}},\text{(9)}& {\displaystyle }{f}_{\text{ET}}& {\displaystyle }={\displaystyle \frac{C_{\text{ET}}}{C_{\mathrm{v}}}}.\end{array}$$

According to Eqs. (8) and (9), f_ET was only related to δ_a, δ_v and δ_ET. These three parameters were obtained for relatively small temporal and spatial scales in this study, making it possible to estimate f_ET at a tower scale. The f_ET estimate will provide a baseline value for rainfall recycling ratio calculations. Previous studies quantified the contribution of recycled vapor to annual or monthly precipitation in river basins using a two-element mixture model (Kong et al., 2013) and three-element mixture (Peng et al., 2011). At the watershed scale, the recycled vapor rate refers to the contributions of moisture from terrestrial ET to annual or monthly precipitation (Trenberth, 1999). It is a key part of local water cycle and the atmospheric water vapor balance (Seneviratne et al., 2006; Aemisegger et al., 2014). In our study, the role of f_ET to regional vapor is similar to the role of recycled vapor rate to annual or monthly precipitation, but f_ET was calculated with fine temporal (e.g., hourly) and spatial (i.e., field scale) scales. At the watershed scale, an assumption was made that there was no isotopic fractionation between transpiration and the source water (Flanagan et al., 1991); advected vapor was assumed to be the precipitation vapor of the upwind station (Peng et al., 2011). However, the isotope composition of plant-transpired vapor is variable within a day, especially under non-steady-state conditions (Farquhar and Cernusak, 2005; Lai et al., 2008; Song et al., 2011). In addition, sometimes it is difficult to select an upwind station without precipitation events. In this study, a field site was selected to calculate the proportion of ET fluxes to total atmospheric vapor, and f_ET was only related to δ_a, δ_v and δ_ET according to Eqs. (8) and (9). This indicates that f_ET calculations are possible for fine temporal and spatial scales after estimating δ_a using the methods we proposed.

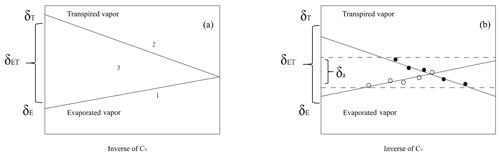
Figure 5 Hypothetical graph of the idealized Keeling plots of the isotope composition of evaporation vapor (δ_E) (line 1), the isotope composition of transpiration vapor (δ_T) (line 2) and the isotope composition of evapotranspiration vapor (δ_ET) (area 3) (a). Hypothetical graph of idealized δ_E and δ_T lines and the interval of the possible isotope composition of ambient vapor (δ_a) in the Keeling plots (b).

We assumed that the parameter δ_v in Eq. (8) is the average δ_v value measured from all the eight heights. f_ET in this study was 23.3 % and 12.7 % from May to September 2017 based on daily δ_a(IP) and daily δ_a(IVT), respectively. It was reported that the recycled vapor rate in all of the Shiyang River basin, oasis region, mountain region and desert region were 23 %, 28 %, 17 % and 15 %, respectively (Li, et al., 2016; Zhu, et al., 2019). The f_ET based on daily δ_a(IP) in our study was close to these earlier studies. The deviation of f_ET based on daily δ_a(IVT) from previous studies may be because 64.1 % of point-to-point δ_a(IVT) was observed at nighttime. Normally, nighttime ET is lower than that of the daytime. f_ET may be underestimated using daily δ_a(IVT). It could also be inferred that f_ET estimation using Eq. (9) may be more reliable using daily δ_a(IP) than daily δ_a(IVT).

4.3 Implications of δ_a

The concept of δ_E and δ_T and their relationships with δ_ET were first introduced by a hypothetical graph shown in Fig. 5a (Moreira et al., 1997). Line 1 and line 2 were idealized Keeling plots with pure T and pure E. The area 3 between line 1 and line 2 represents all the possible Keeling plots with mixed T and E. The IVT method in this study provided a general explanation of this figure. As T is a major component of ET in the daytime in a non-arid region (Wang et al., 2014), the slope is generally negative. When E dominates ET in an ecosystem, such as in the nighttime in a non-arid region or in an arid region, the slope should be positive. Mathematically, a negative slope is due to δ_ET>δ_a, and a positive slope is due to δ_ET<δ_a. It also reflected that the IVT method could only be used in non-arid ecosystems to ensure the occurrence of a sign switch (e.g., from negative to positive) in Keeling plot slopes. On the contrary, the IP method may not be restricted by the type of ecosystems. Yamanaka and Shimizu (2007) used the assumption that δ_a of an area of 219.9 km² was represented by the intersection point of two Keeling plot lines in different sites with synchronous measurements, and they used the intersection value as an approximate value of δ_a. This study was conducted in a maize field using 30 min interval measurements. The results verified Yamanaka and Shimizu's (2007) assumption in such a fine spatial and temporal scale and indicate that accurate δ_a(IP) could be estimated from the intersection of two Keeling plots regardless of whether the slope is positive or negative, while the δ_a(IVT) should be restricted in the area between two dotted lines as shown in Fig. 5b (i.e., between the minimum value of δ_v in a positive slope and the maximum value of δ_v in a negative slope). Although the IVT method relies on a more stringent precondition for data filtering, this method requires a very simple expression, which only needs two parameters to be measured according to Eq. (7).

While this study is about water vapor ¹⁸O, the “Keeling plot” was first used by Keeling (1958, 1961) to interpret carbon isotope ratios of mixed CO₂ and to identify the sources that contribute to increases in atmospheric CO₂ concentrations on a regional basis. Compared with ET in water vapor, which consists of E and T, net ecosystem CO₂ exchange is comprised of soil respiration (R) and gross primary productivity (GPP). As a ¹³CO₂ isotopic Keeling plot reveals a positive slope during both daytime and nighttime (Yakir and Wang, 1996; Unger et al., 2010), the IVT method may not be able to estimate ambient ¹³CO₂ isotopic composition (δ_a¹³C), since there are no opposite slopes in a day. In such a case, the IP method may be implemented in two continuous moments to estimate δ_a¹³C and may consequently further calculate the contribution of net ecosystem exchange (NEE) to atmospheric CO₂.

5 Conclusions

In this study, we established two methods to quantify δ_a using the intersection point method and the intermediate value theorem method. The IVT method was used under the condition of opposite slopes of Keeling plots in two continuous moments. The results of estimated δ_a(IP) and δ_a(IVT) were consistent with the expectation regardless of whether it was of a local or external origin using an investigation of external vapor tracking by the HYSPLIT model. The linear regression between δ_a(IP) and δ_a(IVT) was highly significant at both a daily timescale and point-to-point scale.

This study provided insights into the underexplored traditional Keeling plots and provided two methods to estimate δ_a using the same instrumental setup for the traditional Keeling plot investigations. The estimated δ_a will make it possible to calculate the ET contribution to regional vapor at a 30 min interval at a field scale. The results also indicate that using similar framework, δ_a¹³C may also be solvable by the IP method.