Climate-dependent propagation of precipitation uncertainty into the water cycle

Precipitation is a crucial variable for hydro-meteorological applications. Unfortunately, rain gauge measurements are sparse and unevenly distributed, which substantially hampers the use of in situ precipitation data in many regions of the world. The increasing availability of high-resolution gridded precipitation products presents a valuable alternative, especially over poorly gauged regions. This study examines the usefulness of current state-of-the-art precipitation data sets in hydrological modeling. For this purpose, we force a conceptual hydrological model with multiple precipitation data sets in >200 European catchments to obtain runoff and evapotranspiration. We consider a wide range of precipitation products, which are generated via (1) the interpolation of gauge measurements (E-OBS and Global Precipitation Climatology Centre (GPCC) V.2018), (2)  data assimilation into reanalysis models (ERA-Interim, ERA5, and Climate Forecast System Reanalysis – CFSR), and (3) a combination of multiple sources (Multi-Source Weighted-Ensemble Precipitation; MSWEP V2). Evaluation is done at the daily and monthly timescales during the period of 1984–2007. We find that simulated runoff values are highly dependent on the accuracy of precipitation inputs; in contrast, simulated evapotranspiration is generally much less influenced in our comparatively wet study region. We also find that the impact of precipitation uncertainty on simulated runoff increases towards wetter regions, while the opposite is observed in the case of evapotranspiration. Finally, we perform an indirect performance evaluation of the precipitation data sets by comparing the runoff simulations with streamflow observations. Thereby, E-OBS yields the particularly strong agreement, while ERA5, GPCC V.2018, and MSWEP V2 show good performances. We further reveal climate-dependent performance variations of the considered data sets, which can be used to guide their future development. The overall best agreement is achieved when using an ensemble mean generated from all the individual products. In summary, our findings highlight a climate-dependent propagation of precipitation uncertainty through the water cycle; while runoff is strongly impacted in comparatively wet regions, such as central Europe, there are increasing implications for evapotranspiration in drier regions.

1 Introduction

Precipitation is a key quantity in the water cycle since it controls water availability, including both blue and green water resources (Falkenmark and Rockström, 2006; Orth and Destouni, 2018). In this way, changes in precipitation translate into changes in water resources, which could have severe impacts on ecosystems and consequently the economy and society (Oki and Kanae, 2006; Kirtman et al., 2013; Abbott et al., 2019). Changes in precipitation can be induced or intensified by climate change and consequently lead to amplified impacts (Blöschl et al., 2017, 2019). Thus, accurate precipitation information is essential for monitoring water resources and managing related impacts.

Despite the necessity of accurate precipitation data sets, in most regions, reliable gauge measurements are not widely available. Furthermore, these measurements need to be corrected for potential errors such as wind-induced inaccuracies or precipitation undercatch, especially in higher altitudes (Sevruk et al., 2009; Mekonnen et al., 2015; Zandler et al., 2019; Duethmann et al., 2020). Next to gauge measurements, precipitation information can be inferred from satellite observations and/or model simulations. Based on these sources, a variety of global gridded precipitation data sets have emerged. While some of these data sets make direct use of gauge measurements to interpolate them in time and space, others make indirect use of the gauge information to calibrate satellite retrieval algorithms or models, enabling them to estimate gridded large-scale precipitation.

Across these data sets there are ample discrepancies in space and time, highlighting the need for comparative assessments (e.g., Koutsouris et al., 2016; Alijanian et al., 2017, 2019; Balsamo et al., 2018; Sun et al., 2018; Massari et al., 2020; Brocca et al., 2019; Sharifi et al., 2019; Caroletti et al., 2019; Levizzani and Cattani, 2019; Roca et al., 2019; Fallah et al., 2020; Satgé et al., 2020; Contractor et al., 2020; Xu et al., 2020; Zhou et al., 2020). In particular, indirect evaluation of the data sets through application in hydrological modeling is a valuable alternative in this context as precipitation is translated into variables with more reliable observations, such as runoff, as long as runoff is measured in catchments with near-natural dynamics (Thiemig et al., 2013; Nerini et al., 2015; Beck et al., 2017a, b, 2019a, b; Fereidoon et al., 2019; Ehsan Bhuiyan et al., 2019; Mazzoleni et al., 2019; Arheimer et al., 2020; Dembélé et al., 2020). However, while this approach relies on the propagation of precipitation uncertainty into runoff, it is largely underexplored with respect to when and where this propagation pathway is active. Conversely, it is unclear in which regions or conditions the gridded data sets of runoff (Gudmundsson and Seneviratne, 2016) or evapotranspiration (e.g., Martens et al., 2017; Jung et al., 2019) are impacted by the existing precipitation uncertainties.

In this study, we investigate the uncertainty across six widely used gridded precipitation data sets, including their propagation into the hydrological cycle, i.e., runoff and evapotranspiration (ET). Thereby, we consider gauge-interpolated (E-OBS v17.0 and GPCC V.2018), reanalysis (ERA-Interim, ERA5, and CFSR), and multisource (MSWEP V2) data sets. With each of them, and with an ensemble mean computed from all of them, we force a conceptual land surface model and compare the respectively simulated runoff and ET. This is done separately for different hydro-climatological regimes. In addition, by validating the runoff simulations against respective observations we can indirectly infer the performance of the precipitation data sets. This further allows us to obtain guidelines with respect to the usefulness of the different types of precipitation products in the considered regimes.

Section 2 introduces the reference, forcing data sets, and model calibration used in the study, and Sect. 3 illustrates the results and discussion. Finally, in Sect. 4 the conclusions of this study are presented.

2 Data and methodology

2.1 Forcing data

Runoff and ET are modeled with a conceptual hydrological model, the simple water balance model (SWBM). The underlying framework was initially presented by Koster and Mahanama (2012), where runoff (normalized by precipitation) and ET (normalized by net radiation) are assumed to be polynomial functions of soil moisture (Whan et al., 2015). We use the model version introduced by Orth and Seneviratne (2015) in which the original model is adapted to the daily timescale by the addition of an implicit form of the water balance equation and a streamflow recession parameter, which enables streamflow that is delayed with respect to the respective precipitation event. Please refer to Orth and Seneviratne (2015) for the relevant model equations and validation results. Note that the basic concept and the governing equations of runoff and ET formation used here are well established and employed in many similar conceptual models, such as Hydrologiska Byråns Vattenbalansavdelning (HBV; Bergström, 1995; Orth and Seneviratne, 2015). As inputs, the model uses temperature, net radiation, and precipitation. For each catchment, temperature and net radiation are used from the respective grid cells from the E-OBS (Cornes et al., 2018) and ERA-Interim (Dee et al., 2011) data sets, respectively. Corresponding grid-cell-based precipitation data are used from various data sets derived from different sources, namely gauge-based (E-OBS and GPCC V.2018), reanalysis (ERA-Interim, ERA5, and CFSR), and multisource data sets (MSWEP V2). A summary of all precipitation data sets and their respective characteristics is shown in Table 1.

Table 1 Summary of the precipitation data sets evaluated in this study.

Before using the precipitation data sets to force the SWBM, they are regridded to a common 0.5^∘ spatial resolution, if necessary. This was done through conservative remapping, which preserves the water mass (Jones, 1999), using climate data operators (Schulzweida, 2019). The SWBM simulations are performed with a daily time step, and the analysis thereof is done at daily and monthly timescales.

2.2 Reference data

Modeled runoff is evaluated against streamflow observations obtained from 416 catchments distributed across Europe (Stahl et al., 2010). The streamflow data were collected from the European water archive, national ministries and meteorological agencies and from the Water and Global Change (WATCH) project. These daily data are available for the period 1984–2007. There is no or little human influence on the streamflow in these catchments, which are mostly between 10 and 100 km² in size. More details on the data and catchments can be found in Stahl et al. (2010).

2.3 Model calibration

The simple water balance model employed in this study includes six adjustable parameters, namely water-holding capacity, inverse streamflow recession timescale, runoff ratio exponent, ET ratio exponent, maximum evaporative fraction, and a snowmelt parameter (as in Orth and Seneviratne, 2015; see also Table S1). For model calibration, 500 parameter sets are tested, which are randomly sampled from the entire parameter space using Latin hypercube sampling (LHS; McKay et al., 1979). The ranges for each parameter within this parameter space are obtained from O et al., 2020 (see also Table S1). In this way, we performed 500 corresponding simulations for each catchment over the entire considered time period (1984–2007). For each simulation, we computed the resulting Nash–Sutcliffe efficiency (NSE; Nash and Sutcliffe, 1970) between the observed and simulated runoff to determine the best-performing parameter set. The results are shown in Fig. S1 in the Supplement. In addition, any catchments with NSE <0.36 in the case of the best parameter set were disregarded from the further analyses. This NSE threshold for the catchment selection is adopted from Motovilov et al. (1999) and Moriasi (2007). The model was deemed not applicable there due to, e.g., human influence on the local runoff dynamics or model shortcomings. In this way, out of the original >400 catchments, 264 are retained for the actual analyses, which are well distributed across the European continent and its climate regimes.

Note that we perform only the calibration of the model and no validation. This is because we focus on the influence of the precipitation forcing on the modeled runoff performance and not on the simulation capacity of the model outside training conditions. A satisfactory predictive performance of the model has been shown in previous studies (Orth et al., 2015; Orth and Seneviratne, 2014, 2015; Schellekens et al., 2017; O et al., 2020).

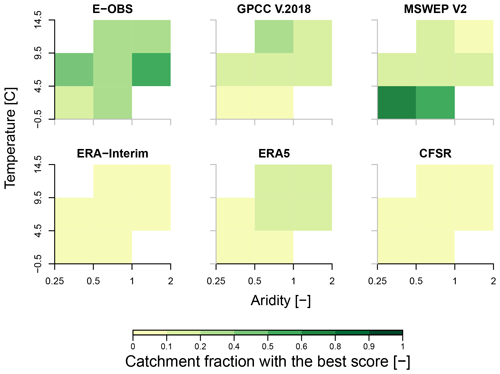
As shown in Fig. 1, the hydro-climatological regime is characterized through long-term average temperature and aridity (Budyko, 1974). Thereby, for each catchment the temperature is taken from the E-OBS data set, and aridity is computed as the ratio of the mean annual net radiation to mean annual precipitation calculated from ERA-Interim and E-OBS, respectively.

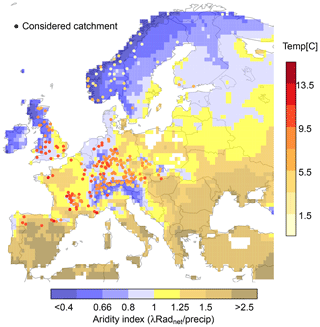
Figure 1 Map of the study area. Points mark the position of the 264 study catchments, with colors indicating their annual average temperature. Map colors show the aridity index of regions, as determined by a ratio of long-term average net radiation and precipitation (1984–2007).

In each of the 264 catchments, the SWBM is forced with temperature, net radiation, and the different precipitation data sets, respectively, as illustrated in Fig. 2. In this way, six simulations with the six different precipitation data sets are performed for each catchment, leaving the temperature and net radiation data unchanged. The model parameters are thereby obtained from the abovementioned calibration using E-OBS precipitation. As this can potentially introduce biases into our results, we additionally calibrated the model using GPCC V.2018 precipitation data to derive alternative parameters with which we recomputed the main analyses.

Figure 2 Overview of the modeling approach. The simple water balance model (SWBM) is forced with consistent net radiation and temperature data and six different precipitation data sets. The obtained runoff and evapotranspiration are assessed in terms of the variability between the simulations. The performance of the runoff simulations is determined against streamflow observations.

All analyses are performed during the warm season (May–September) to minimize the impact of snow and ice, even though snowmelt can locally affect streamflow even in the warm season (Jenicek et al., 2016).

3 Results and discussion

3.1 Impact of precipitation uncertainty on runoff and ET

Figure 3 illustrates the propagation of precipitation uncertainty into simulated runoff and ET at the monthly scale. Each point denotes the standard deviation across the six simulations obtained with the different precipitation data sets and represents a particular month (May–September) in a specific catchment. Runoff simulations are impacted by precipitation uncertainty, while the ET simulations are much less influenced by precipitation uncertainty, as indicated by the regression slope. The clear relationship between runoff and precipitation is in line with previous studies (e.g., Beck et al., 2017a, b; Sun et al., 2018; Blöschl et al., 2019). It is related to the fact that most of the considered catchments are located in relatively wet climates (aridity <1), such that soils are often saturated, triggering a rather direct runoff response to precipitation (Ghajarnia et al., 2020). Also, in these climate regimes ET is typically energy controlled rather than water controlled (Koster et al., 2004; Zheng et al., 2019; Pan et al., 2020; Denissen et al., 2020), leading to the observed low sensitivity of ET to precipitation (uncertainty).

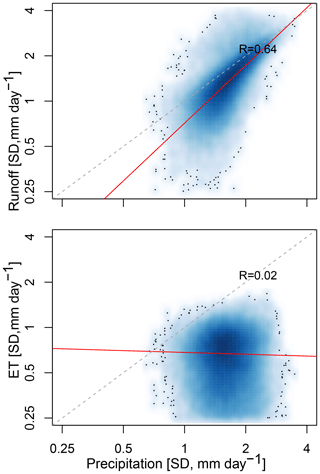
Figure 3 Propagation of precipitation uncertainty into the runoff and ET simulations. Standard deviations (SDs) are computed across the precipitation estimates and the resulting runoff and evapotranspiration values. This is done at every grid cell and for every month between May and September. Red lines indicate linear regression lines. Note that a log–log scale is used.

3.2 Climate-dependent propagation of precipitation uncertainty

In addition to examining the role of precipitation uncertainty for runoff and ET across all considered catchments, we analyze this uncertainty propagation within individual hydro-climatological regimes (Fig. 4). For this purpose, we compute the median of the standard deviations from catchments within each regime, considering all respective warm season months. Figure S2 shows the number of catchments located within each regime. Only regimes with >5 catchments are considered in the analysis. The uneven distribution of catchments across the regimes induces higher uncertainties in the results obtained for the wettest and driest regimes. As shown in Fig. 4a, the precipitation variability across the considered products is higher in comparatively cold and wet regions. This could be related to especially sparse gauge networks and more intense rainfall in these regions which are known to increase precipitation uncertainty (Dinku et al., 2008; Hu et al., 2016; Beck et al., 2017b; O and Kristetter, 2018).

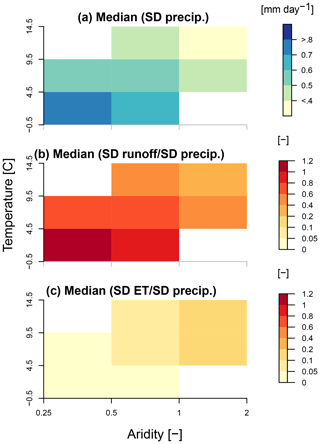
Figure 4 Climate-dependent propagation of precipitation uncertainty into runoff and ET. Panel (a) shows the standard deviation across precipitation products, while panels (b) and (c) show the relative standard deviation of resulting runoff and ET simulations with respect to precipitation, respectively.

Similarly, Fig. 4b and c illustrate the fraction of precipitation uncertainty propagating into runoff and ET, respectively. Interestingly, we find systematic variations in this uncertainty propagation with respect to climate. In wet and cold regions, precipitation uncertainty almost exclusively affects runoff, whereas ET remains unchanged. Towards drier and warmer climates the uncertainty propagation shifts, affecting runoff less and increasingly influencing ET.

In addition to the previous analyses using monthly averaged data, we recompute Fig. 4 using daily data. The results are shown in Fig. S3. The similarity between Figs. 4 and S3 suggests that our findings on the climate-dependent propagation of precipitation uncertainty are valid across daily and monthly timescales. Furthermore, we repeat the uncertainty propagation analysis (i) using model parameters obtained from calibration with GPCC V.2018 precipitation forcing instead of E-OBS precipitation (Fig. S4); (ii) using all months instead of focusing on the warm season (Fig. S5); and (iii) using an NSE limit of 0.5 instead of 0.36 to select catchments where the SWBM is applicable (Fig. S6). We find that Figs. S4–S6 show similar patterns to Fig. 4, which confirms that our findings are robust with respect to the methodological approach, particularly in terms of the precipitation data set employed for model calibration, the considered season, and the applied NSE threshold to determine the applicability of the model (see also Sect. 2.3).

3.3 Indirect validation of precipitation data set qualities

Given the preferential propagation of precipitation uncertainty to runoff in the considered European catchments, we focus in the following on runoff only. In this context, we use streamflow measurements from the catchments to validate the modeled runoff, which also allows us to draw conclusions on the usefulness of the employed precipitation forcing data sets and of a mean ensemble thereof. This is, however, not possible in the case of ET due to the lacking relationship between ET and the precipitation forcing in our study region (Fig. 3). For the runoff validation, we consider the correlation of monthly anomalies in each catchment and the absolute bias. To obtain anomalies, we remove the mean seasonal cycle from the observed and modeled runoff time series of each catchment. The six runoff simulations derived with the individual precipitation products alongside the runoff simulation obtained with the mean ensemble are then ranked in each catchment with respect to (i) correlation and (ii) bias. The sum of these two ranks is used to obtain an overall ranking of runoff simulations and corresponding precipitation forcing data sets in each catchment.

Figure 5 shows the number of catchments in which each precipitation product yields the best-ranked runoff simulation. Our findings show that overall the performance of modeled runoff is clearly dependent on the employed precipitation product. This is expected given the considerable disagreement between precipitation products and the preferential propagation of this uncertainty to runoff (Fig. 4). Generally, among the individual products, the runoff computed with E-OBS precipitation agrees best with observations. Also, ERA5, MSWEP V2, and GPCC V.2018 yield comparatively good runoff estimates. In contrast, runoff simulations obtained with ERA-Interim and CFSR agree less well with observations. The precipitation ensemble outperforms all individual products, highlighting the usefulness of multisource and multiproduct approaches in the derivation of suitable precipitation data sets for hydrological modeling. Furthermore, we compute runoff performance assessments separately for anomaly correlation and absolute bias (Fig. S10). This reveals that the performance of the precipitation data sets is rather similar in terms of resulting runoff biases. Only ERA5 seems to lead to reduced biases when compared with the other products; this is probably because it does not suffer from a gauge-based precipitation undercatch. In contrast, there are considerable differences in terms of the runoff anomaly correlation performance across the products. This indicates that the differences across products shown in Fig. 5 are mostly resulting from contrasting performance with respect to runoff anomaly correlation.

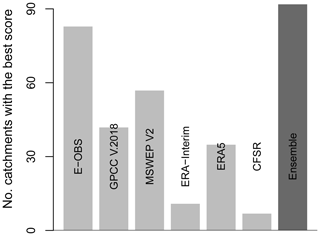
Figure 5 Number of catchments where each precipitation product yields the best agreement with runoff observations (May–September). Multiple data products can be best performing at a catchment since they are ranked based on a merged score by combining anomaly correlation and absolute error.

When repeating the evaluation from Fig. 5 with the daily data (Fig. S7) we find similar results. This suggests that the relative quality of the considered precipitation is comparable across daily and monthly timescales. In addition, we recompute Fig. 5, using all months of the year (Fig. S8), and GPCC-derived SWBM parameters (Fig. S9), which both largely confirm the described results. Note that, not surprisingly, model calibration with a particular precipitation product, e.g., E-OBS or GPCC V.2018, leads to the better performance of that respective product.

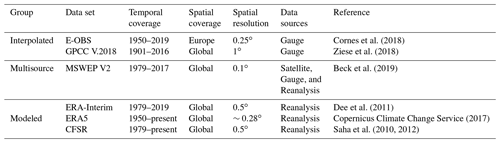
Figure 6 shows the runoff performance resulting from the various precipitation products for the previously considered hydro-climatological regimes. Interestingly, we find remarkable performance differences across the regimes, suggesting differential usefulness of precipitation products for hydrological modeling across different climate zones. Also, we can identify regimes in which the precipitation products perform particularly well or not. For example, MSWEP V2 leads to strong agreement between modeled and observed runoff, mostly in comparatively cold and wet climate and less so in warmer and drier regimes. This might be related to problems of the products incorporated in MSWEP V2 in capturing convective rainfall in warm and dry regions while this is less problematic in colder regions (Ebert et al., 2007; Beck et al., 2017a, b; Massari et al., 2017; Fallah et al., 2020). The opposite performance pattern is observed for GPCC V.2018. The weaker performance in the cold climate, which is also present in the case of E-OBS, might be related to smaller gauge network density and more complex topography in colder areas (Beck et al., 2017b; Ziese et al., 2018). For the other products, such as CFSR and ERA-Interim, the performance is less dependent on the hydro-climatological regime.

Figure 6 Runoff-based performance of precipitation products across climate regimes. Colors refer to the percentage of catchments within each box recognized as the best performance based on anomaly correlation and absolute bias during May–September.

4 Conclusions

In this study, we investigate how the remarkable discrepancy across state-of-the-art gridded precipitation data sets propagates through the water cycle. This is essential for hydrological modeling and the applicability of resulting simulations of water balance components such as runoff or ET. Our findings reveal that the uncertainty across precipitation data sets propagates mainly into runoff rather than ET simulations in Europe. In addition, the partitioning of precipitation uncertainty between runoff and ET is climate dependent. In comparatively cold and wet regions, such as Europe, runoff is more impacted, whereas in drier and warmer regions the uncertainty partitioning shifts towards ET. This applies across daily and monthly timescales.

The results in this study are obtained with a single model and are potentially dependent on the choice of that model. Even though this model has been validated thoroughly and applied in previous studies (Orth et al., 2015; Orth and Seneviratne, 2014, 2015; Schellekens et al., 2017; O et al., 2020), future research needs to explore precipitation error propagation with other models (as in Ehsan Bhuiyan et al., 2019). This should particularly include distributed models, adding to our use of a lumped scheme. However, we do obtain similar results with different calibrations of this model, while previous research indicated that differences across model calibrations can be similar to those across models (Tebaldi and Knutti, 2007).

The strong link between precipitation and runoff in Europe allowed us to perform an indirect validation of precipitation products through the performance of the respectively modeled runoff. Overall, the E-OBS precipitation data set yields the most reliable streamflow simulations in Europe across the considered precipitation products. Weaker but still comparatively good agreement between modeled and observed streamflow is obtained with ERA5, GPCC V.2018, and MSWEP V2. Thus, the products differ mostly with respect to the temporal dynamics rather than the overall amount of precipitation (Sun et al., 2018; Fallah et al., 2020). The interpolated products overall outperform the satellite-derived products in Europe. This is probably due to the high density of gauge observations, as previous research found contrasting conclusions in regions with low gauge density (e.g., Thiemig et al., 2013, for Africa). We further find that the ensemble mean of the considered precipitation data sets outperforms the individual data sets, suggesting that such approaches are promising to obtain more reliable precipitation forcing for hydrological modeling as shortcomings in individual data sets seem to cancel out to some extent when used within an ensemble. Further, we study the performance of the considered precipitation products with respect to climate. We find systematic variations for data sets like MSWEP V2 and GPCC V.2018, whereas ERA5, ERA-Interim, and CFSR perform more similarly across climate regimes. Revealing climate-dependent accuracies in some precipitation data sets supports focused development of these products. In this way, innovative hydrological validation of precipitation data, in addition to direct validation against ground truth, can contribute to addressing the still considerable uncertainty across state-of-the-art gridded products in future efforts.

Furthermore, these findings allow a more targeted combination of products to compensate for individual weaknesses and preserve respective strengths. The climate-dependent (propagation of) precipitation uncertainties illustrates that there is no best overall product but instead a careful regional, climate-based selection can support hydrological applications. Overall, these findings highlight the usefulness of streamflow measurements capturing truly large-scale hydrological dynamics, which can then be used to make inferences on the accuracy of precipitation data sets (Behrangi et al., 2011; Thiemig et al., 2013; Beck et al., 2017a, 2019a; Ehsan Bhuiyan et al., 2019; Mazzoleni et al., 2019; Alnahit et al., 2020; Arheimer et al., 2020).

Another important outcome of our analyses is that ET simulations are mostly insensitive to precipitation uncertainty in the European climate, confirming previous studies (Ehsan Bhuiyan et al., 2019; Zheng et al., 2019). However, in warmer and drier regions, such as the Middle East, central North America, or Australia, the link between ET and precipitation should be stronger. Wherever available in these regions, ET measurements can and should be used for the indirect evaluation of large-scale precipitation products to complement the results in this study where we focused more on comparatively wet regions.

Moreover, our findings suggest that, across Europe and regions with similar climate, gridded runoff data sets (e.g., Gudmundsson and Seneviratne, 2016) inevitably suffer from the existing uncertainty in state-of-the-art precipitation data sets, although this depends on the extent to which they rely on precipitation data. In contrast, gridded ET products (e.g., Martens et al., 2017; Jung et al., 2019) are not impacted by precipitation uncertainty in these regions. In warmer and drier regions, however, the gridded ET products are more challenged than the runoff products.

Overall, our findings highlight the important role of precipitation accuracy and the understanding of the propagation of existing inaccuracies through the water cycle. By revealing the climate dependency of this propagation, this study contributes to improved modeling and monitoring of water resources, which is of particular relevance in the case of extreme events, such as floods and droughts (e.g., Golian et al., 2019; Alexander et al., 2020), that might increase in a changing climate.