Comparison of generalized non-data-driven lake and reservoir routing models for global-scale hydrologic forecasting of reservoir outflow at diurnal time steps

Large-scale hydrologic forecasts should account for attenuation through lakes and reservoirs when flow regulation is present. Globally generalized methods for approximating outflow are required but must contend with operational complexity and a dearth of information on dam characteristics at global spatial scales. There is currently no consensus on the best approach for approximating reservoir release rates in large spatial scale hydrologic forecasting, particularly at diurnal time steps. This research compares two parsimonious reservoir routing methods at daily steps: Döll et al. (2003) and Hanasaki et al. (2006). These reservoir routing methods have been previously implemented in large-scale hydrologic modeling applications and have been typically evaluated seasonally. These routing methods are compared across 60 reservoirs operated by the U.S. Army Corps of Engineers. The authors vary empirical coefficients for both reservoir routing methods as part of a sensitivity analysis. The method proposed by Döll et al. (2003) outperformed that presented by Hanasaki et al. (2006) at a daily time step and improved model skill over most run-of-the-river conditions. The temporal resolution of the model influences model performances. The optimal model coefficients varied across the reservoirs in this study and model performance fluctuates between wet years and dry years, and for different configurations such as dams in series. Overall, the method proposed by Döll et al. (2003) could enhance large-scale hydrologic forecasting, but can be subject to instability under certain conditions.

1 Introduction

1.1 Importance of dams in hydrologic simulations

Improvements in numerical weather prediction, the increasing abundance of computational power, and greater precision of remotely sensed observations make global hydrologic forecasting and flood warning systems increasingly feasible (Alfieri et al., 2013; Wu et al., 2014; Emerton et al., 2016; Salas et al., 2017). Lack of information concerning anthropogenic influences on runoff is a major deficiency of large-scale flood forecasting systems (Emerton et al., 2016). Reservoir operations tend to distort natural flow patterns, effectively redistributing surface water spatially and temporally (Zhao et al., 2016). Impoundments significantly influence the downstream flow regime at small and large spatial scales (Batalla et al., 2004; Magilligan and Nislow, 2005). Over half of the world's large river systems are now substantially altered by dams (Nilsson et al., 2005) resulting in a seven-fold increase in water storage within the global river system (Vörösmarty et al., 1997). Furthermore, the cumulative alterations from global reservoir impoundments are so significant that it has been suggested that they could buffer global sea-level rise (Chao et al., 2008).

Dams primarily impact the hydrologic cycle by changing the magnitude and timing of the discharges downstream (Haddeland et al., 2006; Döll et al., 2009; Biemans et al., 2011; Wu et al., 2014; Zajac et al., 2017), often with the specific intent to mitigate hydrologic extremes (i.e., floods and droughts) (Zajac et al., 2017). Dams reduce peak discharges by roughly a third on average while dampening the daily variation by a similar amount (Graf, 2006). In hydrologic forecasting, accuracy of the timing and magnitude of hydrologic extremes is fundamentally important to the usefulness of the forecasts. Therefore, the significant impacts from dams make inclusion of reservoir operations, or reservoir routing, critical in large-scale hydrologic flood forecasting.

Integrating dam operations within large-scale river routing and flood forecasting improves model performance downstream of reservoir locations (Snow et al., 2016; Tavakoly et al., 2017; Salas et al., 2017; Zajac et al., 2017). This is often not feasible at large scales since there may be multiple entities responsible for regulating flow, particularly with respect to transboundary waters. Among other things, operational knowledge, site-specific rule curves, reservoir uses, and local decision-making practices at each individual project dictate dam releases. Thus, dam operations are typically non-linear, complex processes, driven by anthropogenic and environmental influences. This makes generalizing reservoir operations difficult, particularly in the context of predicting dam-induced hydrologic responses at diurnal or sub-diurnal time steps. Heuristically accounting for dams within existing routing schemes should improve flood forecast results when scheduled releases are not readily known.

Reservoir routing methodologies are generally divided into two basic categories: data-driven and non-data-driven. Machine-learning, artificial intelligence (Coerver et al., 2018; Macian-Sorribes and Pulido-Velazquez, 2017; Ehsani et al., 2016; Mohan and Ramsundram, 2016; Ticlavilca and McKee, 2011; Chaves and Chang, 2008; Khalil et al., 2005), and remote sensing (Bonnema et al., 2016; Yoon and Beighley, 2015) are examples of data-driven approaches. Such data-driven methodologies can be effectively applied to dynamic non-linear systems, particularly when the governing influence on the system does not follow any particular deterministic model. These types of approaches require training data or specific knowledge of a particular reservoir to effectively parameterize and apply them. This is often an insurmountable limitation for data-driven approaches. For that reason, the focus of this paper is on non-data-driven reservoir routing methodologies as an incremental improvement over schemes that effectively neglect dams when information is scarce.

1.2 Non-data-driven reservoir storage and outflow simulation

Non-data-driven approaches to reservoir routing rely on conceptualizing reservoir responses without explicitly observing the actual reservoir operations. The optimal method for a given application depends on a balance between complexity and available information (De Vos, 2015). Therefore, this paper focuses on selecting for parsimony.

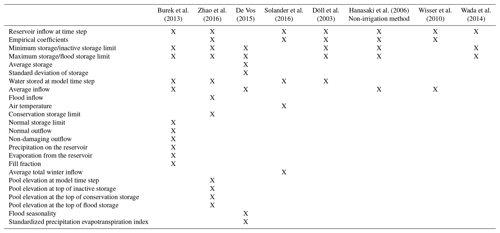
Existing non-data-driven reservoir models range from simple approaches to sophisticated methods. Solander et al. (2016) showed that a temperature-based schema best fits the modeling of discharge, Q_out, t. The Solander et al. (2016) rule is driven by temperature shifts at each model time step above and below the mean temperature. The Solander et al. (2016) method indicates that temperature is the main proxy governing reservoir release, due to the assumption that seasonality drives agricultural production and reservoir operation. However, the Solander et al. (2016) study focuses on long-term climatic forecasting. Diurnal temperature variations are not likely to describe day-to-day reservoir operations. Zhao et al. (2016) developed a reservoir routing scheme based on reservoir stage and storage rules. However, real-time insights related to current reservoir stages throughout a region can involve considerable remotely sensed information. The stage information must then be related somehow to storage volume making this a much more data-driven process. Burek et al. (2013) also developed a non-data-driven approach to reservoir routing which was implemented by Zajac et al. (2017). This approach is built into the LISFLOOD model. The Burek et al. (2013) model requires a number of assumptions about storage capacity limits and naturalized streamflow thresholds. For example, the minimum, normal, and maximum storage values are assumed to be 0.1, 0.3, and 0.97, respectively. To maintain the objective of investigating parsimonious models, the approach by Burek et al. (2013) was not included in this evaluation.

Döll et al. (2003), Wada et al. (2014), and Wisser et al. (2010) presented non-data-driven methods to simulate reservoir operation that can be considered as simple approaches. The Wisser et al. (2010) method follows a simple, rule-based approach to define the reservoir outflow at each time step (Q_out,t). The rule that Wisser et al. (2010) enacts is that when the inflow at each model time step moves above or below the long-term average inflow, the behavior of the reservoir release changes. De Vos (2015) suggested that this model is too simple to effectively model reservoir outflow. In a similar vein, Wada et al. (2014) introduced a daily estimate of reservoir outflow that is simply the product of the proportion of available reservoir storage and daily inflow, which can be too simplistic to estimate reservoir outflow since no coefficient is introduced into the simulation to account for reservoir heterogeneity.

Döll et al. (2003) derived a reservoir routing scheme that can be applied to man-made reservoirs and natural water bodies. The Döll et al. (2003) methodology found genesis in the reservoir outflow model proposed by Meigh et al. (1999). Meigh et al. (1999) proposed a simple reservoir release methodology, which intended to mimic outflow at reservoirs from a theoretical rectangular weir. A more substantive version of the Meigh et al. (1999) method is formulated by Döll et al. (2003). Despite its simplicity, the Döll et al. (2003) method demonstrated good performance compared to several other routing methods (De Vos, 2015). The form of the Döll et al. (2003) equation is similar to that proposed by Wada et al. (2014). However, the Döll et al. (2003) methodology incorporates a coefficient that can incorporate a portion of reservoir heterogeneity.

Compared to the aforementioned methods, Hanasaki et al. (2006) derived a demand-driven approach to reservoir routing, which can be considered a complicated non-data-driven reservoir routing model. They distinguished between irrigation and non-irrigation reservoirs and offered two distinct algorithms for each. Water demands for irrigation, domestic, and industrial uses are considered in the irrigation reservoirs, whereas the releases from non-irrigation reservoirs are simply a proportion of inflow.

De Vos (2015) also proposed a within-year/over-year reservoir routing method comprised of two systems of equations, which was considered a non-data-driven approach. Within-year reservoir operations are driven by yearly fill and release cycles and typically have a small storage capacity relative to their total annual demand. Thus, water accumulates during wet periods and decreases during dry periods. Over-year reservoir operation, on the other hand, is based on long-term, multi-year drawdowns. Over-year reservoirs have storage which is sufficiently large, relative to inflow, so that yearly cycles of water storage and release are not necessary (Adeloye and Montaseri, 2000; Vogel et al., 1999). De Vos (2015) compared his methodology to those of Hanasaki et al. (2006), Döll et al. (2003), and Neitsch et al. (2011). The De Vos (2015) over-year simulation assumes knowledge of the mean and standard deviation of reservoir storage and is still too data-driven for the purposes of this study. Table 1 summarizes each of the inputs required by each non-data-driven approach described above.

Table 1 Input requirements for the various reservoir routing methods.

The Döll et al. (2003) and Hanasaki et al. (2006) require minimal input data to implement: reservoir inflow, average inflow, and storage volume characteristics. Each of these variables are available in existing datasets, such as the Global Reservoir and Dam (GRanD) database (Lehner et al., 2011) or can be generated using climate reanalysis data (Snow et al., 2016). Other non-data-driven methods require data inputs that are not globally available or produced within the hydrologic simulation (De Vos, 2015; Zhao et al., 2016; Burek et al., 2013; Zajac et al., 2017). For example, the Global Flood Awareness System (GloFAS) is the only existing operational flood forecasting system that accounts for reservoirs at continental to global spatial extents. However, the reservoir routing component of GloFAS requires operational assumptions be made because of a lack of global reservoir operational records (Zajac et al., 2017). Döll et al. (2003) (hereafter referred to as D03) and Hanasaki et al. (2006) (hereafter referred to as H06) do not require that these assumptions be made because of the minimal inputs which they require. Thus, D03 and H06 meet the requirements of being parsimonious with respect to available reservoir information.

The Döll et al. (2003) and Hanasaki et al. (2006) methods also provide enough complexity to account for a portion of the model complexity inherent in reservoir operations. De Vos (2015) does not employ the reservoir routing approach of Wisser et al. (2010) and neither does this research, as it does not account for the status of the reservoir storage at each simulation time step. The approach taken by Wada et al. (2014) is similar to D03 but represents reservoirs with similar inflow and storage characteristics homogeneously.

Furthermore, D03 and H06 methods have been implemented in large-scale hydrologic models. D03 was used in the WaterGAP model and the application of H06 was implemented in the TRIP model by the same authors. The main difference in this evaluation and previous evaluations (i.e., Hanasaki et al., 2006; Masaki et al., 2017) of these reservoir routing schemes is that this research evaluates model performance at a diurnal time step.

The aim of this study is to assess non-data-driven reservoir routing methods that are parsimonious and align with available information for use in hydrologic forecasting schemes applicable across the global domain at diurnal time steps. Considering these research aims, the non-data-driven reservoir routing methods developed by Döll et al. (2003) and Hanasaki et al. (2006) were considered.

The following research questions are addressed with respect to the D03 and H06 approaches: (1) How well do the selected reservoir routing models improve outflow estimates relative to simulation of naturalized flow (i.e., neglecting dams altogether)? (2) How do reservoir routing coefficients affect model performance? (3) How does the time step affect model performance and stability? This is a critical point for the current regional- to continental-scale forecasting schemes that operate at daily or sub-daily time steps. (4) How sensitive are the reservoir routing schemes to various real-world dam operations and climate variability?

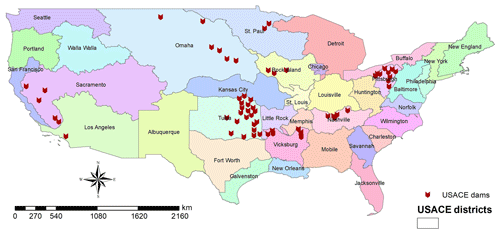
To achieve the research objectives of the study, reservoir data including daily inflow and outflow from 2006–2012 for 60 U.S. Army Corps of Engineers (USACE) reservoirs were used to evaluate the reservoir routing schemes. The data were obtained from nine USACE districts: Pittsburg, Nashville, St. Paul, Rock Island, Omaha, Tulsa, Sacramento, Los Angeles, and Vicksburg. The selected dams are representative of a wide range of reservoir sizes, flow regimes, and climatologic settings but are predominately managed for flood control. The results of this analysis will benefit readers in determining if the reservoir routing models implemented within existing, large-scale hydrologic forecasts adequately represent reservoir effects.

2 Methodology

2.1 Simulation specifications

The storage ratio (Vogel et al., 1999) or impoundment ratio is an important metric in previous works examining generalizing reservoir operation (De Vos, 2015; Hanasaki et al., 2006). The impoundment ratio is described as follows:

$$\begin{array}{}\text{(1)}& \mathrm{IR}={\displaystyle \frac{\left(S_{\max }-S_{\min }\right)}{Q_{\mathrm{in}}\times \mathrm{86}\mathrm{400}\times \mathrm{365}}},\end{array}$$

where S_max and S_min are the maximum and minimum volumes of the reservoir's active storage (m³), and Q_in is the mean annual inflow to the reservoir (m³ s⁻¹).

A higher impoundment ratio indicates that the capacity of the reservoir is large relative to mean inflows, while the opposite is true of low IR values. De Vos (2015) considered IR values greater than unity “large” reservoirs, as they are capable of storing the average yearly volume of water flowing into them. To utilize H06, the release coefficient (k_r) needs to be determined.

$$\begin{array}{}\text{(2)}& k_{\mathrm{r}}={\displaystyle \frac{S_{\mathrm{begin}}}{\mathit{\alpha }{S}_{\max }}},\end{array}$$

where S_begin is the storage (m³) at the beginning of each year and α is a dimensionless coefficient, which was set to 0.85 in the Hanasaki et al. (2006) study. In the current study, the α parameter was varied from 0.45 to 0.95 by increments of 0.10 and solve k_r for each α value.

Outflow is the quantity of most interest for hydrologic flood forecasting because these forecasts generally occur over a relatively short 0–10 d lead time. H06 relates outflow based on the incoming flow. In this study, only the non-irrigation methodology from H06 was used to simulate reservoir outflow at each time step (Q_out,t) since one cannot assume seasonal irrigation demands will be known globally. Further, the primary purpose of reservoirs selected in this study is not irrigation. The H06 method estimates outflow as follows:

$$\begin{array}{}\text{(3)}& Q_{\mathrm{out},t}=\left\{\begin{array}{l}{k}_{\mathrm{r}}{Q}_{\mathrm{in},t}(\mathrm{IR}=\mathrm{0.5}),\\ {\left(\frac{\mathrm{IR}}{\mathrm{0.5}}\right)}^{\mathrm{2}}{Q}_{\mathrm{in},t}+Q_{\mathrm{in},t}\left\{\mathrm{1}-{\left(\frac{\mathrm{IR}}{\mathrm{0.5}}\right)}^{\mathrm{2}}\right\}\left(\mathrm{0}<\mathrm{IR}<\mathrm{0.5}\right),\end{array}\right.\end{array}$$

where Q_in,t is the inflow (m³ s⁻¹) at time t and k_r is the release coefficient which is calculated based on Eq. (2). The 0.5 threshold value for IR is an empirical condition derived by Hanasaki et al. (2006).

Unlike H06, D03 relates outflow (Q_out,t) to current available storage capacity of the reservoir:

$$\begin{array}{}\text{(4)}& Q_{\mathrm{out},t}={\displaystyle \frac{k_{\mathrm{rd}}}{\mathrm{\Delta }t}}\left(S_t-S_{\min }\right){{\displaystyle \frac{\left(S_t-S_{\min }\right)}{\left(S_{\max }-S_{\min }\right)}}}^{\mathrm{1.5}},\end{array}$$

where Döll empirically derives the release coefficient, k_rd=0.01, Δt is the simulation time step (s), and S_t is the current volume of storage (m³ s⁻¹) at time t. For this study the D03, k_rd was varied using values of 0.01, 0.02, 0.04, 0.06, 0.08, 0.10, 0.20, 0.40, 0.50, 0.60, 0.70, 0.80, and 0.90.

The sensitivity analysis of k_r and k_rd can provide useful information on how coefficients may vary based on geographical and reservoir characteristics such as the impoundment ratio. The two methods were evaluated and results compared to actual outflow records provided by the USACE districts. Two approaches were used to evaluate model performance: hydrograph assessment of daily and monthly reservoir outflow and statistical evaluation. The statistical evaluation was performed for daily and monthly averaged simulated results vs. observations using the Kling–Gupta efficiency (KGE, Gupta et al., 2009), coefficient of determination (R²), and root mean square error (RMSE). The KGE value ranges from negative infinity to one. Four levels of performance were defined for KGE in this study (Tavakoly et al., 2017): poor performance (KGE <0), acceptable (0< KGE <0.4), good (0.4< KGE <0.7), and very good (0.7< KGE). Goodness-of-fit values were evaluated to compare simulated discharge to the actual outflow records provided by the USACE districts. These are indicators of how well the models perform. The same goodness-of-fit values are calculated to compare actual discharge with inflow to assess baseline performance. The baseline condition represents the treatment of reservoir outflow as naturalized, altogether neglecting reservoir operations. Thus, the baseline condition is that inflow into the reservoir equals outflow from the reservoir. To be viable, the reservoir routing scheme should improve results over the baseline condition in virtually all cases.

A true directly measured daily inflow is not available for most reservoirs, including those maintained by the USACE. There are two ways that one can acquire a daily reservoir inflow: estimated using a streamflow model (as in Masaki et al., 2017; Zajac et al., 2017) or estimated using a back-calculated inflow based on the known discharge and observed changes in reservoir storage (as in De Vos, 2015). The authors have chosen to utilize a back-calculated inflow because this methodology inherently accounts for all other withdrawals from the reservoir, such as irrigation, evapotranspiration, seepage, etc. This allows the study to focus exclusively on the reservoir routing methodology. In fact, that would double count withdrawals from the reservoir.

2.2 Study area

The model evaluations were conducted on 60 reservoirs in the United States maintained by the USACE. Figure 1 illustrates reservoirs used in this study. The primary purpose of 43 of the reservoirs is flood control, 6 are hydroelectric, 4 are recreational, 3 are for water supply, 2 are classified as other, 1 is for irrigation, and 1 is a fish and wildlife pond. Despite most reservoirs in the sample being primarily purposed as flood control reservoirs, only three of these reservoirs are exclusively purposed for flood control. Table 1 describes pertinent characteristics of each reservoir in this analysis.

Figure 1 USACE districts and location of reservoirs in this study.

Table 2 Select statistical characteristics of reservoirs analyzed in this study.

3 Results and discussion

This section describes the overall results of the study. There is significant improvement in skill over the baseline (the use of inflow as an estimate of outflow) when the optimal D03 coefficient is chosen. D03 tends to outperform the baseline. H06 generally mirrors the results of the baseline. For this reason the discussion largely focuses on D03. The authors examine the distribution of the best-fitting k_rd values. We discuss how dam systems, annual variability, and simulation time step can influence the ability of D03 to estimate reservoir outflow. The authors also discuss the potential for numeric instability in D03 simulations and offer an initial solution to this instability. We also provide an overview of the limitations of this study and suggested future work.

3.1 Overall model performances

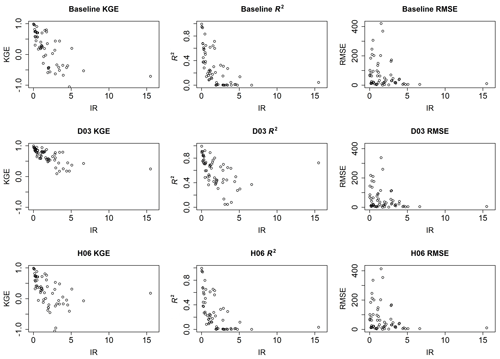
The goodness-of-fit metrics were calculated for each reservoir in the study. Observed inflow is compared with observed outflow to establish a benchmark used to show whether implementing the two non-data-driven reservoir routing schemes improves estimates for reservoir outflow over the use of unregulated flow as the reservoir outflow estimate. Figure 2 illustrates the comparison of skill metrics between the baseline and the use of D03 and H06 to simulate outflow. The KGE, R², and RMSE for D03 and H06 in Fig. 2 represent the best-fit results from the sensitivity study. Data points in Fig. 2 that fall below the dashed line represent instances where KGE, R², and RMSE are lower for the reservoir routing method compared to the baseline. Data points falling above the dashed line indicate instances where the KGE, R², and RMSE obtained were higher than the baseline for this study. H06 tends to show minimal utility over the baseline scenario. In general, H06 does not appear to make outflow estimates worse. Estimates that have acceptable KGE values in the baseline scenario tend to produce acceptable results using H06. On the other hand, Fig. 2 illustrates that D03 generally tends to increase KGE and R² and, with this increase in goodness-of-fit, decrease RMSE. Thus, the general conclusion is that selecting the optimum D03 release coefficient will ultimately produce an improved estimate of reservoir outflow compared to the baseline. Generally, H06 will produce an estimated reservoir outflow that performs similarly to the baseline scenario.

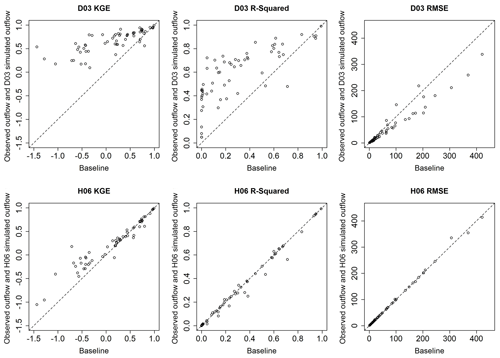
Figure 2 Scatter plots of skill metrics between the use of daily observed inflow as outflow (baseline) and simulated outflow from the best-performing D03 and H06 simulations. The dashed line indicates the plane separating increased and decreased skill that results from using either reservoir routing method.

Figure 3 is a geographic representation of the KGE values from the baseline scenario as well as the best-performing implementation of the two routing models for each reservoir. In general, D03 outperforms the baseline and H06, particularly in the Tulsa and Pittsburg Districts. H06 tends to provide, at best, minimal improvement in accuracy over the baseline.

D03 tends to improve KGE values at nearly all reservoirs and tends to preserve high KGE values at locations where the baseline is already a good or very good estimator of outflow. Only one of the 60 reservoirs in this study demonstrates a significant reduction in accuracy when D03 is applied. This reservoir, Martis Creek Dam in the Sacramento District, appears to be an outlier in the reservoir sample. Reservoirs with a similar IR and average inflow to Martis Creek Dam and in the same USACE district tended to experience improvement in model skill with D03. Overall, when the appropriate k_rd value is applied, D03 improves simulation results over the baseline.

Figure 3a illustrates the wide range of reservoir operating conditions present in the study. The reservoir dataset contains reservoirs in which the outflow correlates poorly with the inflow regime as others that correlates well. Figure 3a also portrays significant geographic clustering where reservoirs in certain regions tend to be less correlated with inflow and other clusters where observed inflow and observed outflow correlate strongly. This could indicate that operations at these reservoirs may have a particularly regional context and may bias towards a particular reservoir routing scheme. However, correlation between observed inflow and observed outflow and geographic proximity of the reservoirs does not influence the implementation of either D03 or H06. Thus, the results of this research indicate no significant geographic constraints in the context of this study.

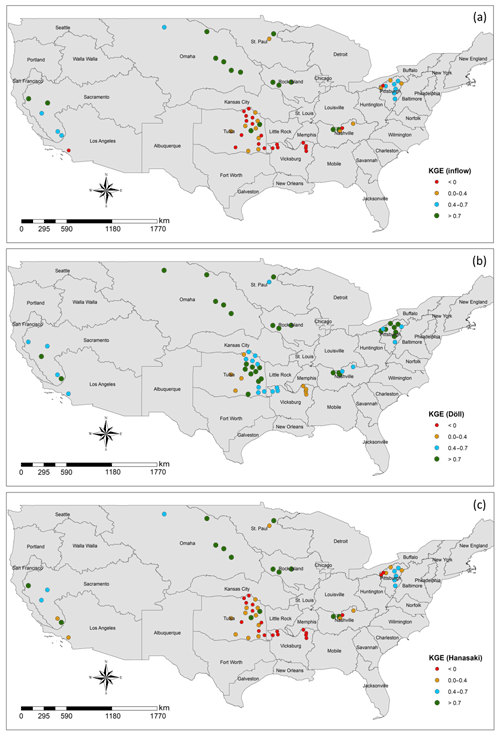
Figure 3 Spatial distribution of KGE comparing observed daily outflow to each best estimate of outflow: (a) observed inflow, (b) Döll method simulated outflow, (c) Hanasaki method simulated outflow for all reservoirs in this study. KGE values for the Döll method and the Hanasaki method are the maximum KGE values from all coefficient treatments.

Figure 4 presents a proportional bar chart comparing baseline KGE and the highest KGE value for the range D03 and H06 coefficients. This plot categorizes KGE performance using the same bins as Fig. 3. Figure 4 indicates that the best-performing H06 simulation provides only marginal improvement over the baseline condition. However, the best-performing instance of D03 eliminates all poorly performing baseline conditions. Nearly 87 % of all best-performing D03 simulations are considered to be good or very good at accurately capturing reservoir outflows, a 45 %increase above the baseline simulation.

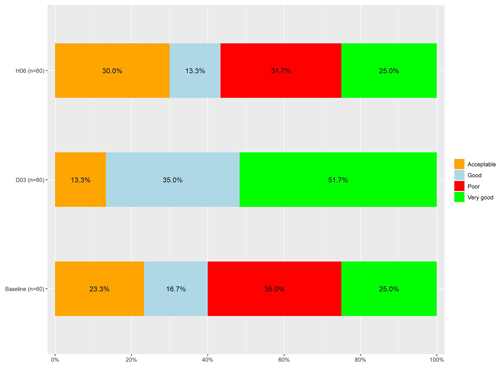
Figure 4 Proportional bar chart comparing the baseline outflow estimation and the best KGE results for D03 and H06.

From multivariate comparison, a negative relationship between two of the best-fit results (KGE and R²) and reservoir IR was found. Figure 5 illustrates this comparison between IR and each goodness-of-fit metric for the baseline, D03, and H06. KGE in particular appears to be non-linearly correlated to IR. A similar, yet less significant, negative relationship was found between IR and R². Little statistical correlation appears to occur between IR and RMSE. However, KGE and R² values in Fig. 5 indicate that the ability to predict outflow using the reservoir routing techniques applied in this study decreases with reservoir with high IR values.

Figure 5 Comparison of IR and best KGE, R², and RMSE from goodness-of-fit metrics for the baseline, D03, and H06.

3.2 Sensitivity analysis of models

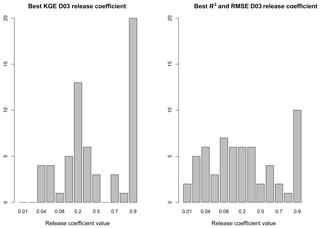
Because D03 consistently outperforms H06 at daily time steps, D03 was selected for the sensitivity analysis at daily time steps. The value of k_rd coefficient was introduced as 0.01 in the Döll et al. (2003) study. In this study, k_rd values were varied to obtain maximum KGE and R² and minimum RMSE. Figure 6 demonstrates the dispersion of k_rd values which maximize the model skill for all reservoirs in this study. For all model skill metrics, k_rd=0.90 tends to be the most prevalent k_rd value that maximizes model skill. In only 2 of the 60 reservoirs (Sardis Dam and Enid Dam) k_rd=0.01 maximizes R² and minimizes RMSE for the range of k_rd coefficients. This research suggests that the k_rd=0.01 is not necessarily the optimum coefficient to maximize model performance using a daily simulation time step.

Figure 6 Bar charts of k_rd values that maximize KGE and correlation and minimize RMSE.

Investigating the linkage between dam characteristics and the best-performing k_rd yields no clear relationship. Evaluation of the correlation between IR, coefficient of variation of inflow, ratio of average inflow to average outflow, and geographic location shows low correlation between each variable and the best-performing k_rd value. However, the range of best-performing k_rd within this analysis and as demonstrated in Fig. 6 suggests that the value is not constant across all reservoirs. Thus, as one implements D03 within their hydrologic forecasting framework, k_rd may be adjusted to optimize streamflow estimates to gage observations, like those curated by the Global Runoff Data Centre (GRDC, 2018), when available.

3.3 Dam systems and reservoir routing

Reservoirs in the Vicksburg and Omaha districts were selected to evaluate performance of D03 in environments where reservoirs operate in a coordinated fashion. We broadly refer to these as dam systems. The case of the Vicksburg and Omaha district reservoirs highlights two distinct types of dam systems: one where the dams do not contribute inflow into one another but still coordinate their releases (in parallel) and another where upstream releases flow into downstream reservoirs (in series).

A subset of the reservoirs in the Vicksburg District comprises the Yazoo Basin Headwaters Project. Although the reservoirs in the Yazoo Basin Headwaters Project are not directly connected, the reservoir operators coordinate operations in order to minimize flooding in Mississippi's delta region (Arkabutla Lake History, 2017; USACE, 1987). The operation of these reservoirs presents an interesting case in which the non-data-driven models in this study do not characterize the nature of the dam releases well. The modeled results at four Vicksburg District dams yield only minimal improvement over unregulated (i.e., naturalized) flow at these reservoirs. The decrease in reservoir routing performance can be attributed to the large impoundment ratios at these dams indicating the reservoir storage is large relative to the annual volume of inflow.

The reservoirs of interest in the Vicksburg District include Arkabutla, Sardis, Enid, and Grenada. These dams function in parallel on tributaries of the lower Mississippi River, namely the Coldwater River, Little Tallahatchie River, Yocona River, and Yalobusha River, respectively. Together, these dams control flooding in northern Mississippi as part of the Yazoo Basin Headwaters Project (Arkabutla Lake History, 2017; USACE, 1987). The Yazoo Basin reservoirs discharge directly into the heavily regulated Mississippi River (Meade and Moody, 2010). The reservoirs operate to ensure high releases are not concurrent with large flows upstream on the Mississippi to avoid devastating flooding to the low-lying Louisiana delta regions. This requires a high level of coordination throughout the Yazoo Basin Headwater Project and with regulation upstream on the Mississippi. Additionally, each of the Yazoo Basin reservoirs have a substantial impoundment ratio, ranging from 2.96 to 3.95. In other words, the reservoirs are capable of containing large volumes of water to mitigate downstream impacts. Thus, current pool levels and forecasted inflow at these four reservoirs do not substantially influence release decisions. The reservoirs also have the capacity to absorb large flood events. As a result, they do not seem to follow the same functional form as the majority of dams in this study.

Figure 7 from Sardis Dam in the Yazoo Basin Headwaters Project demonstrates the hydrograph comparing observed inflow and outflow and the modeled outflow that provides the highest KGE (D03, k_rd=0.90) for the year 2008. Figure 7 demonstrates that peak outflows tend not to correspond to the time at which peak inflow occurs. In fact, release rates at Sardis Dam are at a minimum during the peak inflow time period. This pattern repeats at each of the reservoirs in the Yazoo Basin Headwaters Project indicating that inflow and consumed storage are not substantial predictors of outflow timing at these reservoirs. This exemplifies the lack of correlation between observed inflow and observed outflow at reservoirs within the Yazoo Basin Headwaters Project.

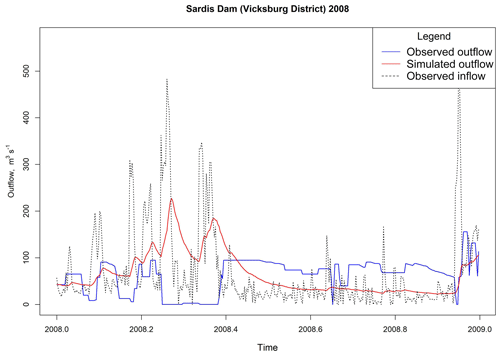
Figure 7 Hydrographs of observed inflow and outflow versus simulated outflow with the highest KGE value at Sardis Dam (Döll method k_rd=0.90). KGE comparing observed inflow and outflow = −0.34; KGE comparing simulated and observed outflows = 0.095.

Dams operating in series represent a specific case where compounding model error is a particular concern. USACE operates several large dams in series on the Missouri River. These include Fort Peck, Garrison, Oahe, Big Bend, Fort Randall, and Gavins Point within in the Omaha District (Lund and Ferreira, 1996). For this cascading system on the Missouri River, inflow appears to be a progressively stronger predictor of outflow from upstream to downstream. At the upstream end the baseline yielded a KGE = 0.43 at Fork Peck with a KGE = 0.99 downstream at Gavins Point Dam. Figure 8 provides a comparison of observed inflow and outflow along with simulated outflow for Gavins Point Dam. D03 tends to provide a slightly better estimate of outflow compared with inflow, except in the instance of Big Bend Dam. At Big Bend Dam, H06 produces an estimate of outflow more consistent with observed outflow than either D03 or inflow alone. However, the differences are almost trivial considering how well inflow alone performed in this case. D03 is particularly accurate during peak inflow conditions, for example the large hydrologic event in mid-2011 at Gavins Point Dam in Fig. 8. The performance of non-data-driven approaches in this instance is promising since compounding errors are a large concern in this type of system. Other instances involving dams in series should be evaluated to determine whether these findings hold more generally.

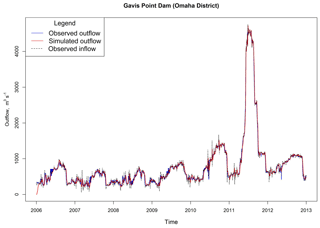
Figure 8 Hydrographs of observed inflow and outflow versus simulated outflow with the highest KGE value at Gavins Point Dam (Döll method k_rd=0.04). KGE comparing observed inflow and outflow = 0.99; KGE comparing simulated and observed outflows = 0.99.

Reservoir management is unique in both the Yazoo Basin Headwaters Project and the Missouri River. The operators of dams within the Yazoo Basin Headwaters Project tend to regulate outflow in a manner that is more in line with downstream conditions. The attention to downstream conditions is due mainly to the impact that downstream floods will have on the low-lying communities within the Louisiana Delta. The dams in the Yazoo Basin Headwaters Project have among the highest impoundment ratios, which inherently reduces the influence of upstream conditions in discharge decisions. The non-data-driven approaches evaluated here do not account for downstream conditions and thus do not perform well in this instance, particularly where large impoundment ratios allow operators considerable leeway.

On the other hand, the non-data-driven approaches tend to perform well when inflow conditions dictate discharge decisions as we see on the Missouri River system. Reservoirs with smaller impoundment ratios are naturally more responsive to inflow requiring greater consideration for upstream conditions. D03 showed a relatively small improvement of outflow estimates compared to inflow as a predictor of outflow in the Yazoo Basin Reservoirs, while the method provided reasonable estimates in dam systems like the Missouri River system. Therefore, it can be inferred that D03 is more applicable for dam systems where reservoir management focuses on upstream hydrologic conditions, while large impoundment ratios may be indicative of reservoirs where downstream conditions are more likely to prevail. This would likely apply for H06 as well since that method links outflow to inflow more directly.

3.4 Wet- and dry-year comparison

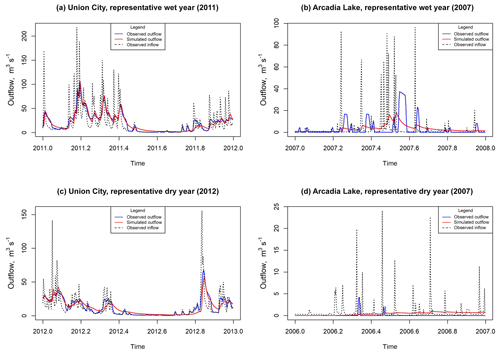
Figure 8 shows results for wet and dry years at two reservoirs considered to be representative of this study. D03 provides a relatively good estimate of outflow at Union City Dam (Pittsburg District) in Fig. 9a and c. D03 performs relatively poorly at Arcadia Lake (Tulsa District) in Fig. 9b and d. In the case of Union City Dam, D03 tends to produce a noticeable improvement in model skill during both a relatively wet year and a relatively dry year. The performance (Fig. 9a and c) seems to be independent of wet or dry conditions, at least on an annual basis. This does not hold for Arcadia Lake. The model shows modest skill at Arcadia Lake during the wet year (Fig. 9b), but almost none during the dry year.

There appears to be a difference between the timing discharges at the two locations in Fig. 9. D03 appears to estimate the right amount of volume released during the wet year at Arcadia Lake (Fig. 9b). However, the timing of the observed release is delayed until a relatively dry period begins. The lag could indicate that water is being retained, possibly for use in irrigation or domestic supply. In this instance, Arcadia Lake supplies water to the city of Edmond, Oklahoma, which may influence release decisions (Arcadia Lake, 2020).

D03 performs much more poorly during the 2006 dry year at Arcadia Lake (Fig. 9d). The model does not predict the sporadic releases throughout the year. The inflow events in that year are not substantial enough to affect storage meaningfully; thus we see almost no response in the modeled output. Observed outflows demonstrate that beyond two relatively high-volume reservoir releases during 2006, the reservoir releases are restricted to practically no outflow the rest of the year. D03 does not anticipate the two large releases, as the reservoir storage does not dramatically shift in either instance. D03 estimates a near-constant discharge over the entire year with almost no storage change.

Results for wet years and dry years appear to be fairly mixed. Indications are that the performance of D03 could be somewhat site-specific. However, reservoirs that tend to be less responsive to storage fluctuations are not represented well in D03 since storage fluctuations drive the model. Arcadia Lake has an IR of about 4.75, which is relatively high. Union City Dam has an IR of about 0.24, which is relatively low. IR is a good indicator of reservoir responsiveness to storage fluctuations. A lack of reservoir responsiveness to storage fluctuations could result in two different types of error when D03 is implemented within a large-spatial-scale hydrologic model. First, forecasted outflow could easily mistime a hydrologic event, particularly during wet years, as Fig. 9b demonstrates. Second, the authors anticipate that if the storage does not dramatically fluctuate during a dry year the estimated reservoir release will not anticipate sporadic releases for irrigation and other purposeful discharges. Unaccounted for, these large but short-duration releases may lead to a consistent overestimation of reservoir outflow for the entire dry-year period.

Figure 9 Two reservoirs where D03 tends to perform very well and poorly. Outflow: (a) wet year, 2011, Union City Dam; (b) wet year, 2007, Arcadia Lake; (c) dry year, 2012, Union City Dam; and (d) dry year, 2006, Arcadia Lake.

3.5 Effects of time step on model performance

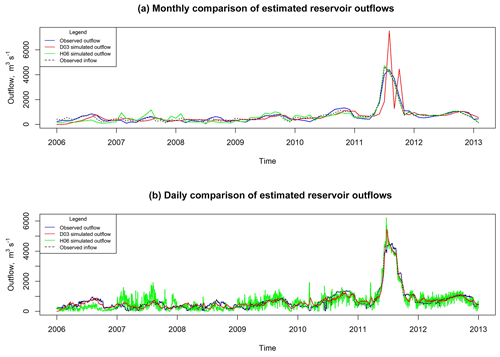
Model comparisons are conducted for daily and monthly time steps. Table 2 illustrates the results at Fort Peck, Garrison Dam, Oahe Dam, and Fort Randall Dam, each of which appears in the Hanasaki et al. (2006) study and this research. Table 2 also contains Sardis Dam, Mosquito Creek Dam, and Prado Dam, which are not included in Hanasaki et al. (2006). Results illustrate that the timescale at which comparisons are conducted can influence simulation results. The monthly comparison amongst Fort Peck, Garrison, Oahe, and Fort Randall is in agreement with the conclusions of Hanasaki et al. (2006). However, when the simulation time step changes to a daily time step, the skills of H06 and D03 reverse and D03 tends to outperform H06. In additional reservoirs (Sardis and Prado), the results indicate that D03 outperformed H06 at both daily and monthly time steps, based upon KGE. However, the results at Mosquito Creek reservoir tend to follow the original Hanasaki et al. (2006) results.

The timescale effect upon model performance may relate to how well observed inflow correlates with observed outflow. Examining Table 2, H06 outperforms D03 when observed inflow and observed outflow are relatively well correlated. The effect is nullified when the inverse is true. H06 estimates outflow as a ratio of inflow, which may be a better estimate of outflow at the monthly timescale, particularly when discharge tracks closely with inflow. However, H06 will fluctuate at the smaller time steps due to inherent variations in inflow. D03 tends to vary less at a daily time step and may be a better estimate of outflow at sub-monthly time steps.

The hydrographs from Fort Randall Dam further illustrate the relationships between time step and model skill, particularly during high-flow events. Daily and monthly comparisons between observation and simulations for Fort Randall Dam are shown in Fig. 10. Figure 10 compares the daily and monthly simulations with observations. Figure 10a shows that the H06 simulations perform better than D03 for monthly time steps, particularly during the high-inflow periods in 2011. D03 tends to overestimate reservoir outflow, while H06 correlates well with inflow and better matches the peak flow of 2011. At a diurnal time step (Fig. 10b), H06 tends to be hypersensitive to inflow variations and overestimates outflow, whereas D03 provides a better approximation of outflow during the 2011 high-flow event at a daily time step.

Table 3 Comparison of daily and monthly KGE values at selected reservoirs. The α and k_rd values represent the highest KGE values for Hanasaki and Döll methods respectively.

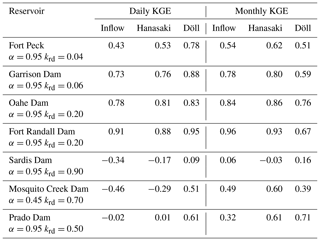
It is possible that the conclusions of Hanasaki et al. (2006) suggesting better performance of H06 at the monthly scale depend on how closely discharge from the dam tracks inflow. D03 may be a better candidate for integration into daily flow forecasting models.

Figure 10 Comparison of simulated outflow for the Fort Randall Dam with Hanasaki and Döll methods for (a) monthly and (b) daily time steps.

3.6 Model stability

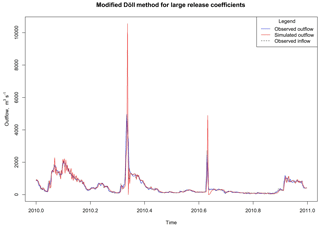
Although D03 outperformed H06 when using a daily time step, D03 demonstrated some instability for high k_rd values. This instability occurs at three reservoirs in this study. The cause of the instability is a combination of a reservoir having a low IR and a sharp change in the inflow to a reservoir. For instance, inflow into Old Hickory Dam in the Nashville District (IR =0.04) increased by roughly 2 orders of magnitude in a matter of a few days in May 2010. During this event, the available storage filled up, necessitating a substantial increase in release flow to prevent overtopping. This occurred within a single time step in the model (D03) and the outflow responded in kind in the next subsequent time step which then drained the reservoir below the specified minimum storage resulting in a non-computable imaginary number as the next solution.

Several solutions are posited to address D03 instability. One solution could be to varying k_rd values dynamically to mimic reservoir behavior. During large hydrologic events the value of k_rd could reduce the peak of the outflow hydrograph, and then increase during normal events. Another solution is the inclusion of rules and an expanded system of equations that govern the solution. Because the intention of D03 is to approximate flow at a free-flowing weir, coupling operational rules with the simulation may better approximate reality. The rules may be as simple as switching behavior or the algorithm when storage approaches either minimum or maximum reservoir storage. A simple condition was tested for when storage drops below the minimum storage during the daily time step:

$$\begin{array}{}\text{(5)}& \mathrm{if}{S}_t\le S_{\min }\Rightarrow \left\{\begin{array}{l}{S}_t=S_{\min },\\ Q_{\mathrm{out}}=Q_{\mathrm{in}}+\frac{S_t-S_{\min }}{\mathrm{\Delta }t}.\end{array}\right.\end{array}$$

This condition prevents the reservoir from falling below the minimum storage. Outflow from Old Hickory Dam was re-simulated with k_rd=0.9 and the new minimum storage condition (Eq. 5). The proposed modification resulted in simulated outflow shown in Fig. 11. Outflow is substantially overestimated for one time step and drops to zero at the next time step. While an oversimplification of actual operations, this condition is similar to an emergency spillway discharge to prevent overtopping. The dam releases tremendous flow for a brief period when the maximum storage is nearly exceeded and then inhibits the discharge when the storage is at the minimum capacity. The benefit of this modification is that additional reservoir information is not required. However, further testing and evaluation should be performed to validate this refinement.

Figure 11 Outflow simulation for the Old Hickory Dam using the proposed modification of the Döll method for k_rd=0.4.

3.7 Limitations

The available sample of dams for this study has some inherent limitations. The vast majority of reservoirs in the sample are primarily purposed as flood control reservoirs with various secondary purposes. They are all commonly operated by USACE. And the dams function within a predominately temperate climate across the United States. These limitations preclude assertions regarding the effects of the operating objective, dam ownership, or country of operation on reservoir routing performance.

The abbreviated length of the historical records presents another limitation. The evaluation period is limited to a 6-year window which may not account for the total range of operational environments for each dam. Thus, this evaluation likely does not capture and evaluate D03 and H06 under absolute extreme circumstances.

All inflow utilized in this study is back-calculated from observed changes in storage and known discharges. This indirect method can lead to negative inflow values when losses due to seepage, evapotranspiration, or other types of withdrawals are underestimated. De Vos (2015) also noted that they used back-calculated inflow in their study. It is unclear whether Hanasaki et al. (2006) made use of direct observations, but it is worth noting that direct observations of total reservoir inflow are not readily available in most cases.

This study is limited to models that only require inputs related to reservoir inflow and storage, primarily to provide insight into the reliability of these measures as indicators of reservoir outflow. Because this study utilizes a back-calculated reservoir inflow, inclusion of reservoir withdrawal would also lead to an overestimation of water withdrawals from the reservoir. Both D03 and H06 can account for withdrawals but because of the focus of this study and the data utilized, the authors do not pursue an estimation of reservoir withdrawal in this study. Thus, we have not included more sophisticated approaches, such as Burek et al. (2013) or Zhao et al. (2016), within this study. Beyond this study of sensitivity analysis, no formal calibration procedure was undertaken. A formal calibration of k_rd in both D03 and H06 would be better suited for the insertion of the reservoir routing scheme within a hydrologic routing scheme. This study is investigating the feasibility of these methods in 0–10 d lead time with diurnal forecasting and is a precursor to implementation in hydrologic routing schemes. There is limited benefit to standalone calibration of the k_rd coefficients, given that reservoir outflow information is rarely available at global scales. Operational calibration of k_rd would be challenging without reservoir release records. Zajac et al. (2017) discuss the need for an open-access database of daily reservoir records, but no such database is known to be available at this time. Thus, this study does not undertake any standalone, formal calibration of k_rd.

3.8 Future work

D03 consistently improved simulated, daily streamflow estimates over naturalized flow conditions in the selected reservoirs of this study, suggesting that D03 can potentially improve global streamflow forecasting that do not already account for lakes and reservoirs. D03 performed particularly well at daily time steps commensurate with many large-scale stream routing models. The incorporation of D03 and H06 can be considered as modules in large-scale river routing models such as Routing Application for Parallel computatIon of Discharge (RAPID, David et al., 2011). The RAPID model is a river routing model that can simultaneously compute streamflow in river networks with thousands of river reaches. This will enable widespread testing and evaluation over large hydrologically diverse areas.

The research presented in this article should guide a number of follow-up evaluations that will broaden the scope of this evaluation.

• We determined that k_rd can be varied to improve performance but have no guidance on how to relate k_rd to a given reservoir. Future studies should determine how to assign release coefficients to reservoirs.

• We have chosen parsimonious approaches that minimize assumptions. We have not compared D03 or H06 to more complex models such as Burek et al. (2013) or Zhao et al. (2016) which require these assumptions. Future work will examine tradeoffs between model complexity and performance.

• Insertion of D03 into large-scale river routing models can facilitate studies of how their results influence overall hydrologic performance, particularly at locations downstream of reservoirs.

• The main purpose of three-quarters of the sampled dams is flood control. Efforts to fill the existing dataset with reservoirs that are primarily irrigation, water supply, hydroelectric, recreation, and fish and wildlife habitat and analyze the impacts of use on model performance should be undertaken.

• The non-data-driven methods considered are conceptualizations of reservoir operations that can be adapted to utilize remotely sensed information, much like the data-driven methods previously mentioned. Non-data-driven methods can be linked to statistical fitting techniques, but they are capable of being employed independent of such pairings. However, the non-data-driven reservoir routing schemes could be enhanced by assimilating remotely sensed data, e.g., near-real-time changes in storage resolved from satellite altimetry, and eventually the planned NASA Surface Water and Ocean Topography (SWOT) Mission. This information could constrain reservoir simulations to improve global streamflow forecasts (Yoon and Beighley, 2015).

• Because D03 skill tends to decline with increases in IR, an over-year simulation capability similar to that proposed by De Vos (2015) may allow for a better means of simulating diurnal reservoirs from reservoirs with large IR. Over-year reservoirs have high IRs and yearly cycles of water storage and release are not necessary (Adeloye and Montaseri, 2000; Vogel et al., 1999).

4 Conclusions

This research compares two parsimonious reservoir routing methods (D03 and H06) with the intent to determine if these methods can be effective at estimating diurnal reservoir outflow in diurnal, medium-range streamflow forecasting. These methods were compared across 60 USACE operated reservoirs at a daily time step. Results show that D03 tends to outperform H06 at a daily time step. An in-depth examination of these results yields the following conclusions.

• The complexity and data requirements of both D03 and H06 are low and thus computationally inexpensive. Both can be feasibly implemented at large spatial scales at a daily or sub-daily time step.

• When the best-performing k_rd is implemented within D03 we find a substantial improvement in the model skill over the baseline for nearly all reservoirs at a daily time step. H06 offers only a minimal improvement over the baseline when the best k_rd is implemented for a daily time step. For the categories of KGE specified (Tavakoly et al., 2017), the best-performing D03 eliminates all baseline conditions with poor performance and increases the proportion of sites with good or very good performance by 45 %.

• There is a statistical relationship between reservoir IR and two of the skill metrics applied (KGE and R²). Given that reservoirs with high IR typically are less responsive to short-term fluctuations in inflow and storage, the correlation between these variables is plausible. Further investigation of dam characteristics, such as whether the dams operate in series or in parallel and wet- and dry-year considerations are further evidence of the correlation between the IR and D03 and H06 skill.

• Simulation time step appears to be an important component in reservoir routing skill. The comparison of the two methods by Hanasaki et al. (2006) are based on monthly reservoir outflows and conclusions may not hold within diurnal forecasting schemes. At overlapping locations, this study replicates the results reported by Hanasaki et al. for monthly time steps. However, the Hanasaki et al. findings do not hold for a daily time step evaluation.

• The best value for the empirical Döll coefficient, k_rd, can vary. Optimal values were typically greater than the k_rd=0.01 value which Döll et al. (2003) derived. This suggests that k_rd could be a potential calibration parameter within a large-scale hydrologic modeling framework much like a weir coefficient which is specific to a particular type of weir.

• The Yazoo Basin Headwaters Project (Arkabutla Lake History, 2017; USACE, 1987) is an interesting case study in how reservoir system complexity can be difficult to model. The Yazoo Basin Headwaters Project considers downstream flow conditions as the dominant criteria in dam operation. Thus, the inflow and available storage volume are poor predictors for determining reservoir discharge in this type of management scheme. D03 appeared to scale flow correctly at these reservoirs and improve reservoir overall skill, but timing of the releases is not well represented and thus skill improvement is only minimal.

• Dam discharges in the Missouri River Reservoir System (Lund and Ferreira, 1996) are more correlated with storage volume and inflow conditions, which lends itself to the two non-data-driven approaches evaluated here. D03 is particularly capable of accurately modeling daily reservoir outflows in reservoir systems that correlate well with storage and inflow fluctuations. Concerns related to model error being compounded through a series of dams may be mitigated somewhat by the fact that inflow appears to be a progressively stronger predictor of outflow further downstream in these types of systems.

• The numerical stability of D03 is a concern, particularly with higher k_rd values. These stability concerns originate at reservoirs with small active storage capacity during high-inflow events. Additional model refinement can overcome these stability concerns.

• D03 showed minimal bias during relatively wet and dry years. Timing of releases can be influenced by wet years and the magnitude appears to be affected during dry years. D03 appears to be most applicable for dam systems where reservoir management focuses on upstream hydrologic conditions. Large IRs could indicate reservoirs where downstream conditions are more likely to influence release decisions at the reservoir.