A line-integral-based method to partition climate and catchment effects on runoff

It is a common task to partition the synergistic impacts of drivers in the environmental sciences. However, there is no mathematically precise solution to this partition task. Here I present a line-integral-based method, which addresses the sensitivity to the drivers throughout the drivers' evolutionary paths so as to ensure a precise partition. The method reveals that the partition depends on both the change magnitude and pathway (timing of the change) but not on the magnitude alone unless used for a linear system. To illustrate this method, I applied the Budyko framework to partition the effects of climatic and catchment conditions on the temporal change in the runoff for 19 catchments from Australia and China. The proposed method reduces to the decomposition method when assuming a path in which climate change occurs first, followed by an abrupt change in catchment properties. The proposed method re-defines the widely used sensitivity at a point as the path-averaged sensitivity. The total-differential and the complementary methods simply concern the sensitivity at the initial and/or the terminal state, so they cannot give precise results. Although the path-averaged sensitivities varied greatly among the catchments, they can be readily predicted within the Budyko framework. As a mathematically accurate solution, the proposed method provides a generic tool for conducting quantitative attribution analyses.

1 Introduction

The impacts of certain drivers on observed changes of interest often require quantification in environmental sciences. In the hydrology community, both climate and human activities have posed global-scale impact on hydrologic cycle and water resources (Barnett et al., 2008; Xu et al., 2014; Wang and Hejazi, 2011). Diagnosing their relative contributions to runoff is of considerable relevance to the researchers and managers. Unfortunately, performing a quantitative attribution analysis of runoff changes remains a challenge (Wang and Hejazi, 2011; Berghuijs and Woods, 2016; Zhang et al., 2016); this is to a considerable degree due to a lack of a mathematically precise method of decoupling synergistic and often confounding impacts of climate change and human activities.

Numerous studies have detected the long-term variability in runoff and attempted to partition the effects of climate change and human activities through various methods (Dey and Mishra, 2017); these include the paired-catchments method and the hydrological modeling method. The paired-catchment method can filter the effect of climatic variability and thus isolate the runoff change induced by vegetation changes (Brown et al., 2005). However, this method is capital intensive; moreover, it generally involves small catchments and experiences difficulties when extrapolating to large catchments (Zhang et al., 2011). Physically based hydrological models often have limitations such as a high data requirement, labor-intensive calibration and validation processes, and inherent uncertainty and interdependence in parameter estimations (Binley et al., 1991; Wang et al., 2013; Liang et al., 2015). Conceptual models such as Budyko-type equations (see Sect. 2.1) have consequently gained interest in recent years.

Within the Budyko framework, studies (Roderick and Farquhar, 2011; Zhang et al., 2016) have used the total differential of runoff as a proxy for the runoff change and the partial derivatives as the sensitivities (hereafter called the total-differential method). The total differential, however, is simply a first-order approximation of the observed change (Fig. 1a). This approximation has caused an error in the calculation of climate impact on runoff, with the deviation ranging from 0 to $\mathrm{20}\times {\mathrm{10}}^{-\mathrm{3}}$ m (or −118 to 174 %) in China (Yang et al., 2014). The elasticity method proposed by Schaake (1990) is also based on the total-differential expression (Sankarasubramanian et al., 2001; Zheng et al., 2009). The method uses the “elasticity” concept to assess the climate sensitivity of runoff. The elasticity coefficients, however, have been estimated in an empirical way and are not physically sound (Roderick and Farquhar, 2011; Liang et al., 2015).

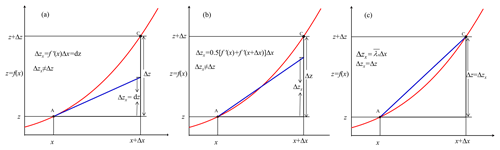
Figure 1 For a nonlinear function z=f(x), the total-differential method (a) and the complementary method (b) do not accurately estimate the effect (Δz_x) of x on z when x changes by Δx, but the LI method (c) does. For a univariate function, the z change is exclusively driven by x, so that Δz_x should be equal to Δz. Δz_x=Δz in (c) but not in (a) and (b). $\stackrel{\mathrm{‾}}{{\mathit{\lambda }}_x}$ in (c) represents the average sensitivity along the curve AC and $\stackrel{\mathrm{‾}}{{\mathit{\lambda }}_x}=\mathrm{\Delta }z/\mathrm{\Delta }x$; see Appendix E for details.

The so-called decomposition method developed by Wang and Hejazi (2011) has also been widely used. The method assumes that climate changes cause a shift along a Budyko curve and then human interferences cause a vertical shift from one Budyko curve to another (Fig. 2). Under this assumption, the method extrapolates the Budyko models that are calibrated using observations of the reference period, in which human impacts remain minimal, to determine the human-induced runoff changes that occur during the evaluation period.

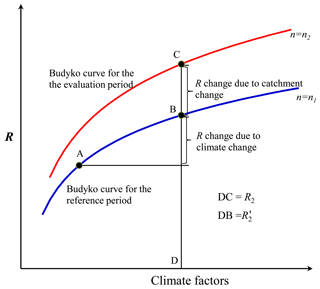
Figure 2 A schematic plot illustrating the decomposition method. Point A denotes the initial state (the reference period), and point C denotes the terminal state (the evaluation period). The decomposition method assumes that the catchment state first evolves from Point A to B along the Budyko curve for the reference period, then jumps to Point C. R₂ represents the mean annual runoff of the evaluation period, and R₂^′ the mean annual runoff given the climate conditions of the evaluation period and the catchment conditions of the reference period. See Sect. 2.4 for details.

Recently, Zhou et al. (2016) established a Budyko complementary relationship for runoff and further applied it to partitioning the climate and catchment effects. Superior to the total-differential method, the complementary method culminates by yielding a no-residual partition. Nevertheless, this method depends on a given weighted factor that is determined in an empirical but not a precise way. Furthermore, Zhou et al. (2016) argued that the partition is not unique in the Budyko framework because the path of the climate and catchment changes cannot be uniquely identified.

Obtaining a precise partition remains difficult, even when giving a precise mathematical model. This difficulty can be illustrated by using a precise hydrology model R=f (x, y), where R represents runoff, and x and y represent the climate factors and catchment characteristics, respectively. We assumed that R changes by ΔR when x changes by Δx and y changes by Δy; i.e., $\mathrm{\Delta }R=f(x+\mathrm{\Delta }x,y+\mathrm{\Delta }y)-f(x,y)$. To determine the effect of x on ΔR – i.e., ΔR_x – a common practice is to assume that y remains constant when x changes by Δx. We thus obtain $\mathrm{\Delta }{R}_x=f(x+\mathrm{\Delta }x,y)-f(x,y)$. Similarly, we can obtain $\mathrm{\Delta }{R}_y=f(x,y+\mathrm{\Delta }y)-f(x,y)$. Although this derivation seems quite reasonable, it is problematic as $\mathrm{\Delta }{R}_x+\mathrm{\Delta }{R}_y\ne \mathrm{\Delta }R$. A further examination shows that a variable's effect on R seems to differ depending on the changing path (timing of the change). For example, $\mathrm{\Delta }{R}_x=f(x+\mathrm{\Delta }x,y)-f(x,y)$ and $\mathrm{\Delta }{R}_y=f(x+\mathrm{\Delta }x,y+\mathrm{\Delta }y)-f(x+\mathrm{\Delta }x,y)$ if x changes first and y subsequently changes (note that the partition is precise with $\mathrm{\Delta }{R}_x+\mathrm{\Delta }{R}_y=\mathrm{\Delta }R$ at this moment). If y changes first and x subsequently changes, the partition then becomes $\mathrm{\Delta }{R}_x=f(x+\mathrm{\Delta }x,y+\mathrm{\Delta }y)-f(x,y+\mathrm{\Delta }y)$ and $\mathrm{\Delta }{R}_y=f(x,y+\mathrm{\Delta }y)-f(x,y)$. In the case of x and y changing simultaneously, unfortunately, the current literature seems not to provide a mathematically precise solution.

The aim of this study is to propose a mathematically precise method to conduct a quantitative attribution to drivers. The method is based on the line integer (called the LI method hereafter) and takes into account the sensitivity throughout the evolutionary path of the drivers rather than at a point as the total-differential method does. To present and evaluate the proposed method, I decomposed the relative influences of climate and catchment conditions on runoff within the Budyko framework using data from 19 catchments from Australia and China.

2 Methodology

2.1 Budyko framework and the MCY equation

Budyko (1974) argued that mean annual evapotranspiration (E) is largely determined by the water and energy balance of a catchment. Using precipitation (P) and potential evapotranspiration (E₀) as proxies for water and energy availabilities, respectively, the Budyko framework relates evapotranspiration losses to the aridity index defined as the ratio of E₀ over P. The Budyko framework has gained wide acceptance in the hydrology community (Berghuijs and Woods, 2016; Sposito, 2017). In recent decades, several equations have been developed to describe the Budyko framework. Among them, the Mezentsev–Choudhury–Yang equation (Mezentsev, 1955; Choudhury, 1999; Yang et al., 2008) (called the MCY equation hereafter) has been widely accepted and was used in this study:

$$\begin{array}{}\text{(1)}& {\displaystyle \frac{E}{P}}={\displaystyle \frac{E_{\mathrm{0}}/P}{{\left(\mathrm{1}+{\left(E_{\mathrm{0}}/P\right)}^n\right)}^{\mathrm{1}/n}}},\end{array}$$

where $n\in (\mathrm{0},\mathrm{\infty })$ is an integration constant that is dimensionless and represents catchment properties. Equation (1) requires a relatively long timescale whereby the water storage of a catchment is negligible and the water balance equation reduces to be $R=P-E$. Here I adopted a “tuned” n value that can obtain an exact accordance between the E calculated by Eq. (1) and that actually encountered (P−R).

The partial differentials of R with respect to P, E₀, and n are given as

$$\begin{array}{}\text{(2a)}& {\displaystyle \frac{\partial R}{\partial P}}=R_P(P,E_{\mathrm{0}},n)=\mathrm{1}-{\displaystyle \frac{E_{\mathrm{0}}^{n+\mathrm{1}}}{{\left(P^n+E_{\mathrm{0}}^n\right)}^{\mathrm{1}/n}}},\text{(2b)}& {\displaystyle \frac{\partial R}{\partial E_{\mathrm{0}}}}=R_{E_{\mathrm{0}}}(P,E_{\mathrm{0}},n)=-{\displaystyle \frac{P^{n+\mathrm{1}}}{{\left(P^n+E_{\mathrm{0}}^n\right)}^{\mathrm{1}/n}}},\text{(2c)}& {\displaystyle }\begin{array}{rl}{\displaystyle \frac{\partial R}{\partial n}}=& R_n(P,E_{\mathrm{0}},n)={\displaystyle \frac{-E_{\mathrm{0}}P{n}^{-\mathrm{1}}}{{\left(P^n+E_{\mathrm{0}}^n\right)}^{\mathrm{1}/n}}}\\ & \left[{\displaystyle \frac{\ln \left(P^n+E_{\mathrm{0}}^n\right)}{n}}-{\displaystyle \frac{P^n\ln P+E_{\mathrm{0}}^n\ln E_{\mathrm{0}}}{P^n+E_{\mathrm{0}}^n}}\right].\end{array}\end{array}$$

2.2 Theory of the line-integral-based method

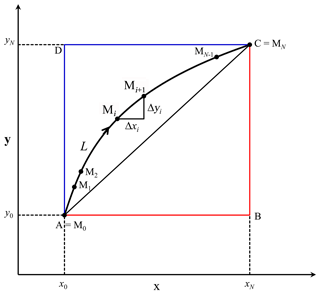
We start by considering an example of a two-variable function $z=f(x,y)$ and assuming that x and y are independent. The function has continuous partial derivatives $\partial z/\partial x=f_x(x,y)$ and $\partial z/\partial y=f_y(x,y)$. Suppose that x and y vary along a smooth curve L (e.g., in Fig. 3) from the initial state (x₀, y₀) to the terminal state (x_N, y_N), and z co-varies from z₀ to z_N. Let $\mathrm{\Delta }z=z_N-z_{\mathrm{0}}$, $\mathrm{\Delta }x=x_N-x_{\mathrm{0}}$, and $\mathrm{\Delta }y=y_N-y_{\mathrm{0}}$. Our goal is to determine a mathematical solution that quantifies the effects of Δx and Δy on Δz, i.e., Δz_x and Δz_y. Δz_x and Δz_y should be subject to the constraint $\mathrm{\Delta }{z}_x+\mathrm{\Delta }{z}_y=\mathrm{\Delta }z$.

Figure 3 A schematic plot illustrating the LI method.

As shown in Fig. 3, points M₁(x₁,y₁), …, $M_{N-\mathrm{1}}(x_{N-\mathrm{1}},y_{N-\mathrm{1}})$ partition L into N distinct segments. Let $\mathrm{\Delta }{x}_i=x_{i+\mathrm{1}}-x_i$, $\mathrm{\Delta }{y}_i=y_{i+\mathrm{1}}-y_i$, and $\mathrm{\Delta }{z}_i=z_{i+\mathrm{1}}-z_i$. For each segment, Δz_i can be approximated as dz_i: $\mathrm{\Delta }{z}_i\approx \mathrm{d}{z}_i=f_x(x_i,y_i)\mathrm{\Delta }{x}_i+f_y(x_i,y_i)\mathrm{\Delta }{y}_i$. We then have $\mathrm{\Delta }z=\sum _{i=\mathrm{1}}^N\mathrm{\Delta }{z}_i\approx \sum _{i=\mathrm{1}}^N{f}_x(x_i,y_i)\mathrm{\Delta }{x}_i+\sum _{i=\mathrm{1}}^N{f}_y(x_i,y_i)\mathrm{\Delta }{y}_i$. We thus obtain the following respective approximation of Δz_x and Δz_y: $\mathrm{\Delta }{z}_x\approx \sum _{i=\mathrm{1}}^N{f}_x(x_i,y_i)\mathrm{\Delta }{x}_i$ and $\mathrm{\Delta }{z}_y\approx \sum _{i=\mathrm{1}}^N{f}_y(x_i,y_i)\mathrm{\Delta }{y}_i$. Next, define τ as the maximum length of the N segments. The smaller the value of τ, the closer the value of dz_i is to Δz_i and thus the more accurate the approximations are. The approximations become exact in the limit τ→0. Taking the limit τ→0 then converts the sum into integrals and gives a precise expression (this is an informal derivation; please see Appendix A for a formal one): $\mathrm{\Delta }z=\underset{\mathit{\tau }\to \mathrm{0}}{lim}\sum _{i=\mathrm{1}}^N{f}_x(x_i,y_i)\mathrm{\Delta }{x}_i+\underset{\mathit{\tau }\to \mathrm{0}}{lim}\sum _{i=\mathrm{1}}^N{f}_y(x_i,y_i)\mathrm{\Delta }{y}_i={\int }_L{f}_x(x,y)\mathrm{d}x+{\int }_L{f}_y(x,y)\mathrm{d}y$, where ${\int }_L{f}_x(x,y)\mathrm{d}x=\underset{\mathit{\tau }\to \mathrm{0}}{lim}\sum _{i=\mathrm{1}}^N{f}_x(x_i,y_i)\mathrm{\Delta }{x}_i$ and ${\int }_L{f}_y(x,y)\mathrm{d}y=\underset{\mathit{\tau }\to \mathrm{0}}{lim}\sum _{i=\mathrm{1}}^N{f}_y(x_i,y_i)\mathrm{\Delta }{y}_i$ denote the line integral of f_x and f_y along L (termed integral path) with respect to x and y, respectively. ${\int }_L{f}_x(x,y)\mathrm{d}x$ and ${\int }_L{f}_y(x,y)\mathrm{d}y$ exist provided that f_x and f_y are continuous along L. We thus obtain a precise evaluation of Δz_x and Δz_y:

$$\begin{array}{}\text{(3a)}& {\displaystyle }\mathrm{\Delta }{z}_x={\int }_L{f}_x(x,y)\mathrm{d}x,\text{(3b)}& {\displaystyle }\mathrm{\Delta }{z}_y={\int }_L{f}_y(x,y)\mathrm{d}y.\end{array}$$

Unlike the total-differential method, the sum of Δz_x and Δz_y persistently equals Δz (Appendix B). If f(x,y) is linear, then f_x and f_y are constant. Let f_x(x,y) and f_y(x,y) remain constant at C_x and C_y, respectively; then Δz_x=C_xΔx and Δz_y=C_yΔy. Δz_x and Δz_y are thus independent of L. If f(x,y) is nonlinear, however, both Δz_x and Δz_y vary with L, as is exemplified in Appendix C. Hence, the initial and the terminal states, together with the path connecting them, determine the resultant partition unless f(x,y) is linear.

The mathematical derivation above applies to a three-variable function as well. By doing the line integrals for the MCY equation, we obtain the desired results:

$$\begin{array}{}\text{(4a)}& {\displaystyle }\mathrm{\Delta }{R}_P={\int }_L{\displaystyle \frac{\partial R}{\partial P}}\mathrm{d}P,\text{(4b)}& {\displaystyle }\mathrm{\Delta }{R}_{E_{\mathrm{0}}}={\int }_L{\displaystyle \frac{\partial R}{\partial E_{\mathrm{0}}}}\mathrm{d}{E}_{\mathrm{0}},\text{(4c)}& {\displaystyle }\mathrm{\Delta }{R}_n={\int }_L{\displaystyle \frac{\partial R}{\partial n}}\mathrm{d}n.\end{array}$$

where ΔR_p, $\mathrm{\Delta }{R}_{E_{\mathrm{0}}}$, and ΔR_n denote the effects on runoff change of P, E₀, and n, respectively. The sum of ΔR_p and $\mathrm{\Delta }{R}_{E_{\mathrm{0}}}$ represents the effect of climate change, and ΔR_n is often related to human activities although it probably includes the effects of other factors, such as climate seasonality (Roderick and Farquhar, 2011; Berghuijs and Woods, 2016). L denotes a three-dimensional curve along which climate and catchment changes have occurred. I approximated L by a series of line segments. ΔR_p, $\mathrm{\Delta }{R}_{E_{\mathrm{0}}}$, and ΔR_n were finally determined by summing up the integrals along each of the line segments (see Sect. 2.3).

2.3 Using the LI method to determine ΔR_p, $\mathrm{\Delta }{R}_{E_{\mathrm{0}}}$, and ΔR_n within the Budyko framework

1. Determining ΔR_p, $\mathrm{\Delta }{R}_{E_{\mathrm{0}}}$, and ΔR_n assuming a linear integral path:

   A curve can always be approximated as a series of line segments. Hence, we can first handle the case of a linear integral path. Given two consecutive periods and assuming that the catchment state has evolved from (P₁, E₀₁, n₁) to (P₂, E₀₂, n₂) along a straight line L, let $\mathrm{\Delta }P=P_{\mathrm{2}}-P_{\mathrm{1}}$, $\mathrm{\Delta }{E}_{\mathrm{0}}=E_{\mathrm{02}}-E_{\mathrm{01}}$, and $\mathrm{\Delta }n=n_{\mathrm{2}}-n_{\mathrm{1}}$; then the line L is given by parametric equations: $P=\mathrm{\Delta }Pt+P_{\mathrm{1}}$, $E_{\mathrm{0}}=\mathrm{\Delta }{E}_{\mathrm{0}}t+E_{\mathrm{01}}$, $n=\mathrm{\Delta }nt+n_{\mathrm{1}}$, and $t\in [\mathrm{0},\mathrm{1}]$. Given these equations, Eq. (2) becomes a univariate function of t, i.e., $\partial R/\partial P=R_p\left(t\right)$, $\partial R/\partial E_{\mathrm{0}}=R_{E_{\mathrm{0}}}\left(t\right)$, and $\partial R/\partial n=R_n\left(t\right)$. Then, ΔR_P, $\mathrm{\Delta }{R}_{E_{\mathrm{0}}}$, and ΔR_n can be evaluated as

   $$\begin{array}{}\text{(5a)}& {\displaystyle }\begin{array}{rl}\mathrm{\Delta }{R}_P& ={\int }_L{\displaystyle \frac{\partial R}{\partial P}}\mathrm{d}P={\int }_{\mathrm{0}}^{\mathrm{1}}{R}_P\left(t\right)\mathrm{d}(\mathrm{\Delta }Pt+P_{\mathrm{1}})\\ & =\mathrm{\Delta }P{\int }_{\mathrm{0}}^{\mathrm{1}}{R}_P\left(t\right)\mathrm{d}t,\end{array}\text{(5b)}& {\displaystyle }\begin{array}{rl}\mathrm{\Delta }{R}_{E_{\mathrm{0}}}=& {\int }_L{\displaystyle \frac{\partial R}{\partial E_{\mathrm{0}}}}\mathrm{d}{E}_{\mathrm{0}}={\int }_{\mathrm{0}}^{\mathrm{1}}{R}_{E_{\mathrm{0}}}\left(t\right)\mathrm{d}(\mathrm{\Delta }{E}_{\mathrm{0}}t+E_{\mathrm{01}})\\ & =\mathrm{\Delta }{E}_{\mathrm{0}}{\int }_{\mathrm{0}}^{\mathrm{1}}{R}_{E_{\mathrm{0}}}\left(t\right)\mathrm{d}t,\end{array}\text{(5c)}& {\displaystyle }\begin{array}{rl}\mathrm{\Delta }{R}_n& ={\int }_L{\displaystyle \frac{\partial R}{\partial n}}\mathrm{d}n={\int }_{\mathrm{0}}^{\mathrm{1}}{R}_n\left(t\right)\mathrm{d}(\mathrm{\Delta }nt+n_{\mathrm{1}})\\ & =\mathrm{\Delta }n{\int }_{\mathrm{0}}^{\mathrm{1}}{R}_n\left(t\right)\mathrm{d}t.\end{array}\end{array}$$

   Unfortunately, I could not determine the antiderivatives of R_P(t)dt, $R_{E_{\mathrm{0}}}\left(t\right)\mathrm{d}t$, and R_n(t)dt and had to make approximate calculations. As the discrete equivalent of integration is a summation, we can approximate the integration as a summation. I divided the $t\in [\mathrm{0},\mathrm{1}]$ interval into 1000 subintervals of the same width, i.e., setting dt identically equal to 0.001, and then calculated R_P(t)dt, $R_{E_{\mathrm{0}}}\left(t\right)\mathrm{d}t$, and R_n(t)dt for each subinterval. Let t_i=0.001i; $i\in [\mathrm{0},\mathrm{999}]$ and is integer-valued. ΔR_p, $\mathrm{\Delta }{R}_{E_{\mathrm{0}}}$, and ΔR_n are approximated as

   $$\begin{array}{}\text{(6a)}& {\displaystyle }\mathrm{\Delta }{R}_P\approx \mathrm{0.001}\mathrm{\Delta }P\sum _{i=\mathrm{0}}^{\mathrm{999}}{R}_P\left(t_i\right),\text{(6b)}& {\displaystyle }\mathrm{\Delta }{R}_{E_{\mathrm{0}}}\approx \mathrm{0.001}\mathrm{\Delta }{E}_{\mathrm{0}}\sum _{i=\mathrm{0}}^{\mathrm{999}}{R}_{E_{\mathrm{0}}}\left(t_i\right),\text{(6c)}& {\displaystyle }\mathrm{\Delta }{R}_n\approx \mathrm{0.001}\mathrm{\Delta }n\sum _{i=\mathrm{0}}^{\mathrm{999}}{R}_n\left(t_i\right).\end{array}$$

2. Dividing the evaluation period into a number of subperiods:

   I first determined a change point and divided the whole observation period into the reference and evaluation periods. To determine the integral path, the evaluation period was further divided into a number of subperiods. The Budyko framework assumes a steady-state condition of a catchment and therefore requires no change in soil water storage. Over a time period of 5–10 years, it is reasonable to assume that changes in soil water storage will be sufficiently small (Zhang et al., 2001). Here, I divided the evaluation period into a number of 7-year subperiods with the exception for the final subperiod, which varied from 7 to 13 years in length depending on the length of the evaluation period.

3. Determining ΔR_p, $\mathrm{\Delta }{R}_{E_{\mathrm{0}}}$, and ΔR_n by approximating the integral path as a series of line segments:

   For a short period, the integral path L can be considered as linear, which implies a temporally invariant change rate. For a long period in which the change rate varies over time, L can be fitted using a number of line segments. Given a reference period and an evaluation period comprising N subperiods, the catchment state was assumed to evolve from (P₀, E₀₀, n₀), …, (P_i, E_0i, n_i), …, to (P_N, E_0N, n_N), where the subscript “0” denotes the reference period, and “i” and “N” denote the ith and the final subperiods of the evaluation period, respectively. I used a series of line segments L₁, L₂, …, L_N to approximate the integral path L, where L_i connects points (P_i−1, $E_{\mathrm{0},i-\mathrm{1}}$, n_i−1) with (P_i, E_0i, n_i). Then ΔR_p, $\mathrm{\Delta }{R}_{E_{\mathrm{0}}}$, and ΔR_n were evaluated as the sum of the integrals along each of the line segments, which were calculated using Eq. (6).

Table 1 Summary of the long-term hydrometeorological characteristics of the selected catchments^a.

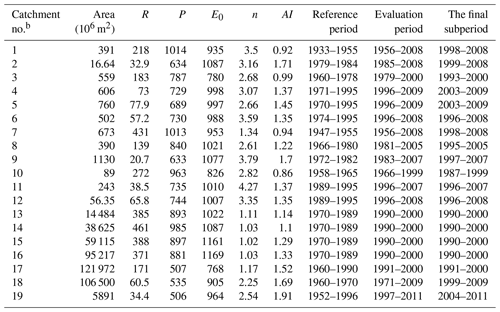
^a R, P, and E₀ represent the mean annual runoff, precipitation, and potential evaporation, all in 10⁻³m yr⁻¹. n (dimensionless) is the parameter representing catchment properties in the MCY equation. AI is the dimensionless aridity index ($\mathit{\text{AI}}=E_{\mathrm{0}}/P$). Data of catchments 1–12 were derived from Zhang et al. (2010). Data of catchments 13–16 were from Sun et al. (2014). Data of catchments 17, 18, and 19 were from Zheng et al. (2009), Jiang et al. (2015), and Gao et al. (2016), respectively. I used the change points given in the literatures to divide the observation period into the reference and elevation periods. The LI method further divides the evaluation period into a number of subperiods. The column “The final subperiod” denotes the final subperiod, which was used as the evaluation period for the total-differential method, the decomposition method, and the complementary method. ^b Catchments 1–12 are in Australia, and the others are in China. (1) Adjungbilly Creek; (2) Batalling Creek; (3) Bombala River; (4) Crawford River; (5) Darlot Creek; (6) Eumeralla River; (7) Goobarragandra Creek; (8) Jingellic Creek; (9) Mosquito Creek; (10) Traralgon Creek; (11) upper Denmark River; (12) Yate Flat Creek; (13) Yangxian station, Han River; (14) Ankang station, Han River; (15) Baihe station, Han River; (16) Danjiangkou station, Han River; (17) headwaters of the Yellow River basin; (18) Wei River; (19) Yan River.

2.4 Total-differential, decomposition, and complementary methods

To evaluate the LI method, I compared it with the existing methods, including the decomposition method, the total-differential method, and the complementary method. The total-differential method approximated ΔR as dR:

$$\begin{array}{}\text{(7)}& \begin{array}{rl}\mathrm{\Delta }R\approx \mathrm{d}R& ={\displaystyle \frac{\partial R}{\partial P}}\mathrm{\Delta }P+{\displaystyle \frac{\partial R}{\partial E_{\mathrm{0}}}}\mathrm{\Delta }{E}_{\mathrm{0}}+{\displaystyle \frac{\partial R}{\partial n}}\mathrm{\Delta }n\\ & ={\mathit{\lambda }}_P\mathrm{\Delta }P+{\mathit{\lambda }}_{E_{\mathrm{0}}}\mathrm{\Delta }{E}_{\mathrm{0}}+{\mathit{\lambda }}_n\mathrm{\Delta }n,\end{array}\end{array}$$

where ${\mathit{\lambda }}_P=\partial R/\partial P$, ${\mathit{\lambda }}_{E_{\mathrm{0}}}=\partial R/\partial E_{\mathrm{0}}$, and ${\mathit{\lambda }}_n=\partial R/\partial n$, representing the sensitivity coefficient of R with respect to P, E₀, and n, respectively. Within the total-differential method,ΔR_P=λ_PΔP, $\mathrm{\Delta }{R}_{E_{\mathrm{0}}}={\mathit{\lambda }}_{E_{\mathrm{0}}}\mathrm{\Delta }{E}_{\mathrm{0}}$, and ΔR_n=λ_nΔn. I used the forward approximation, i.e., substituting the observed mean annual values of the reference period into Eq. (2), to estimate λ_P, ${\mathit{\lambda }}_{E_{\mathrm{0}}}$, and λ_n, as is standard in most studies (Roderick and Farquhar, 2011; Yang and Yang, 2011; Sun et al., 2014).

The decomposition method (Wang and Hejazi, 2011) calculated ΔR_n as follows:

$$\begin{array}{}\text{(8)}& \begin{array}{rl}\mathrm{\Delta }{R}_n=R_{\mathrm{2}}-R_{\mathrm{2}}{}^{\prime }& =(P_{\mathrm{2}}-E_{\mathrm{2}})-(P_{\mathrm{2}}-E_{\mathrm{2}}{}^{\prime })\\ & =E_{\mathrm{2}}{}^{\prime }-E_{\mathrm{2}},\end{array}\end{array}$$

where R₂, P₂, and E₂ represent the mean annual runoff, precipitation, and evapotranspiration of the evaluation period, respectively; R₂^′ and E₂^′ represent the mean annual runoff and evapotranspiration, respectively, given the climate conditions of the evaluation period and the catchment conditions of the reference period (Fig. 2). Both E₂ and E₂^′ were calculated by Eq. (1) but using n values of the evaluation period and the reference period, respectively.

The complementary method (Zhou et al., 2016) uses a linear combination of the complementary relationship for runoff to determine ΔR_p, $\mathrm{\Delta }{R}_{E_{\mathrm{0}}}$, and ΔR_n:

$$\begin{array}{}\text{(9)}& \begin{array}{rl}\mathrm{\Delta }R& =a\left[{\left({\displaystyle \frac{\partial R}{\partial P}}\right)}_{\mathrm{1}}\mathrm{\Delta }P+{\left({\displaystyle \frac{\partial R}{\partial E_{\mathrm{0}}}}\right)}_{\mathrm{1}}\mathrm{\Delta }{E}_{\mathrm{0}}\right.\\ & \left.+P_{\mathrm{2}}\mathrm{\Delta }\left({\displaystyle \frac{\partial R}{\partial P}}\right)+E_{\mathrm{0},\mathrm{2}}\mathrm{\Delta }\left({\displaystyle \frac{\partial R}{\partial E_{\mathrm{0}}}}\right)\right]\\ & +(\mathrm{1}-a)\left[{\left({\displaystyle \frac{\partial R}{\partial P}}\right)}_{\mathrm{2}}\mathrm{\Delta }P+{\left({\displaystyle \frac{\partial R}{\partial E_{\mathrm{0}}}}\right)}_{\mathrm{2}}\mathrm{\Delta }{E}_{\mathrm{0}}\right.\\ & \left.+P_{\mathrm{1}}\mathrm{\Delta }\left({\displaystyle \frac{\partial R}{\partial P}}\right)+E_{\mathrm{0},\mathrm{1}}\mathrm{\Delta }\left({\displaystyle \frac{\partial R}{\partial E_{\mathrm{0}}}}\right)\right],\end{array}\end{array}$$

where the subscripts “1” and “2” denotes the reference and the evaluation periods, respectively. a is a weighting factor and varies from 0 to 1. As suggested by Zhou et al. (2016), I set a=0.5. Equation (9) thus gave an estimation of ΔR_p, $\mathrm{\Delta }{R}_{E_{\mathrm{0}}}$, and ΔR_n as follows:

$$\begin{array}{}\text{(10a)}& {\displaystyle }\mathrm{\Delta }{R}_P=\mathrm{0.5}\mathrm{\Delta }P\left[{\left({\displaystyle \frac{\partial R}{\partial P}}\right)}_{\mathrm{1}}+{\left({\displaystyle \frac{\partial R}{\partial P}}\right)}_{\mathrm{2}}\right],\text{(10b)}& {\displaystyle }\mathrm{\Delta }{R}_{E_{\mathrm{0}}}=\mathrm{0.5}\mathrm{\Delta }{E}_{\mathrm{0}}\left[{\left({\displaystyle \frac{\partial R}{\partial E_{\mathrm{0}}}}\right)}_{\mathrm{1}}+{\left({\displaystyle \frac{\partial R}{\partial E_{\mathrm{0}}}}\right)}_{\mathrm{2}}\right],\text{(10c)}& {\displaystyle }\begin{array}{rl}\mathrm{\Delta }{R}_n& =\mathrm{0.5}\mathrm{\Delta }\left({\displaystyle \frac{\partial R}{\partial P}}\right)(P_{\mathrm{1}}+P_{\mathrm{2}})\\ & +\mathrm{0.5}\mathrm{\Delta }\left({\displaystyle \frac{\partial R}{\partial E_{\mathrm{0}}}}\right)(E_{\mathrm{0},\mathrm{1}}+E_{\mathrm{0},\mathrm{2}}).\end{array}\end{array}$$

2.5 Data

I collected runoff and climate data from 19 selected catchments evaluated in previous studies (Table 1). The change-point years given in these studies were directly used to determine the reference and evaluation periods for the LI method. As mentioned above, the LI method further divides the evaluation period into a number of subperiods. For the sake of comparison, the final subperiod of the evaluation period was used as the evaluation period for the decomposition, the total-differential, and the complementary methods (it can be equally considered that all of the four methods used the final subperiod as the evaluation period, but the LI method cares about the intermediate period between the reference and the evaluation periods, and the other methods do not). Eight of the 19 catchments had a reference period comprising only one subperiod (Table 1), and the others had two to seven subperiods.

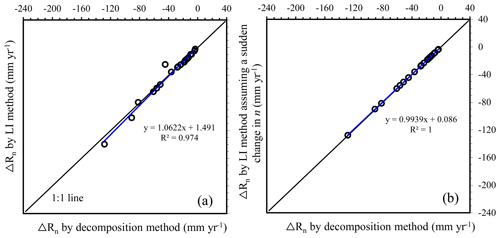
Figure 4 Comparisons between the LI method and the decomposition method. (a) Comparison of the estimated contributions to the runoff changes from the catchment changes (ΔR_n). (b) The decomposition method is equivalent to the LI method that assumes a sudden change in catchment properties following climate change. In this case, the integral path of the LI method can be considered as the path ABC in Fig. 3 (x represents climate factors, and y catchment properties, i.e., n) and $\mathrm{\Delta }{R}_n={\int }_{\mathrm{AB}+\mathrm{BC}}\frac{\partial R}{\partial n}\mathrm{d}n={\int }_{\mathrm{AB}}\frac{\partial R}{\partial n}\mathrm{d}n+{\int }_{\mathrm{BC}}\frac{\partial R}{\partial n}\mathrm{d}n=\mathrm{0}+{\int }_{\mathrm{BC}}\frac{\partial R}{\partial n}\mathrm{d}n={\int }_{n_{\mathrm{1}}}^{n_{\mathrm{2}}}{f}_n(P_{\mathrm{2}},E_{\mathrm{02}},n)\mathrm{d}n$, where the subscript “1” denotes the reference period and “2” denotes the final subperiod of the evaluation period.

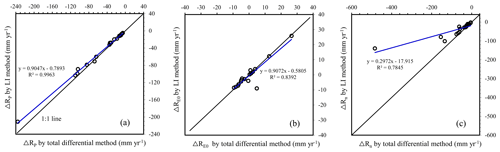
Figure 5 Comparisons of the estimated contribution to runoff from the changes in (a) precipitation (ΔR_P), (b) potential evapotranspiration ($\mathrm{\Delta }{R}_{E_{\mathrm{0}}})$, and (c) catchment properties (ΔR_n) between the LI method and the total-differential method.

The 19 selected catchments have diverse climates and landscapes, with 12 from Australia and seven from China (Table 1). The catchments span from tropical to subtropical and temperate areas and from humid to semi-humid and semiarid regions, with the mean annual rainfall varying from 506 to $\mathrm{1014}\times {\mathrm{10}}^{-\mathrm{3}}$ m and potential evaporation from 768 to $\mathrm{1169}\times {\mathrm{10}}^{-\mathrm{3}}$ m. The dryness index ranges between 0.86 and 1.91. The catchment areas vary by 5 orders of magnitude from 1.95 to 121 972 with a median 606×10⁶ m². The key data include annual runoff, precipitation, and potential evaporation. The record length varied between 19 and 76 with a median of 39 years. All the catchments experienced changes in climate and catchment properties over the observation periods. The precipitation changes from the reference to the evaluation period ranged between −153 and $\mathrm{79}\times {\mathrm{10}}^{-\mathrm{3}}$ m yr⁻¹, and between −35 and $\mathrm{41}\times {\mathrm{10}}^{-\mathrm{3}}$ m yr⁻¹ for potential evaporation (Table 2). The coeval change in the parameter n of the MCY equation ranged between −0.2 and 1.4. The mean annual streamflow reduced for all catchments, ranging from 0.4 to 169 with a median $\mathrm{38}\times {\mathrm{10}}^{-\mathrm{3}}$ m yr⁻¹. The change in catchment properties mainly refers to the vegetation cover or land use change. More details on the data and the catchments can be found in Zhang et al. (2010, 2011), Sun et al. (2014), Zheng et al. (2009), Jiang et al. (2015), and Gao et al. (2016).

Table 2 Comparisons of R (mm yr⁻¹), P (mm yr⁻¹), E₀ (mm yr⁻¹), and n (dimensionless) between the reference and the evaluation periods^*.

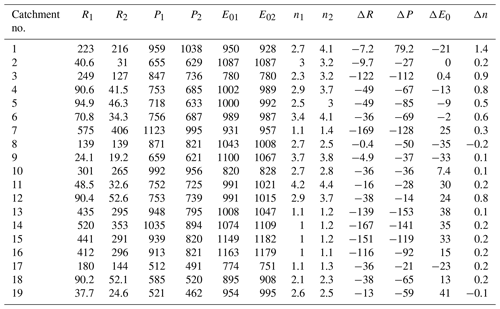
^* The subscript “1” denotes the reference period, and ”2” denotes the evaluation period. $\mathrm{\Delta }X=X\mathrm{2}-X\mathrm{1}$ (X as a substitute for R, P, E₀, and n).

Table 3 Effects of precipitation (ΔR_P, 10⁻³ m yr⁻¹), potential evapotranspiration ($\mathrm{\Delta }{R}_{E_{\mathrm{0}}}$, 10⁻³ m yr⁻¹), and catchment changes (ΔR_n, 10⁻³ m yr⁻¹) on the mean annual runoff determined from the four evaluated methods.

3 Results

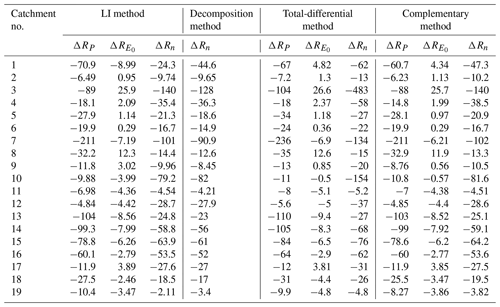
Table 3 lists the resultant values of ΔR_p, $\mathrm{\Delta }{R}_{E_{\mathrm{0}}}$, and ΔR_n from the LI method and the three other methods. Please see the Supplement for detailed calculation steps.

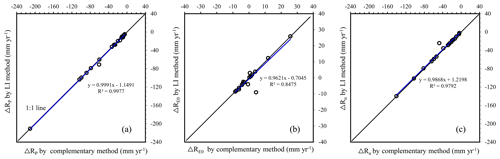
Figure 6 Comparisons of (a) ΔR_P, (b) $\mathrm{\Delta }{R}_{E_{\mathrm{0}}}$, and (c) ΔR_n between the LI method and the complementary method (a=0.5).

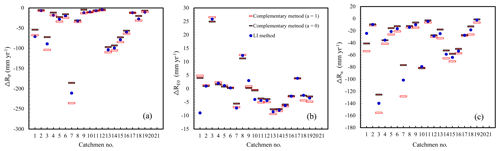
Figure 7 Comparisons of (a) ΔR_P, (b) $\mathrm{\Delta }{R}_{E_{\mathrm{0}}}$, and (c) ΔR_n by the LI method with the upper and lower bounds given by the complementary method. According to Zhou et al. (2016), ΔR_P, $\mathrm{\Delta }{R}_{E_{\mathrm{0}}}$, and ΔR_n reach their bounds when a is 0 or 1.

Figure 4a compares the resultant ΔR_n of the LI method and the decomposition method. Although they are quite similar, the discrepancies can be $\mathit{>}\mathrm{20}\times {\mathrm{10}}^{-\mathrm{3}}$ m yr⁻¹. The decomposition method assumes that climate change occurs first and then human interferences cause a sudden change in catchment properties (Fig. 2). Such a fictitious path is identical to the path ABC in Fig. 3, provided that x represents climate factors and y catchment properties. When ABC was adopted as the integral path, the LI method yielded the same results as the decomposition method did (Fig. 4b). Hence, the decomposition method can be considered as a case of the LI method that uses a special integral path.

The total-differential method is predicated on an approximate equation, i.e., Eq. (7). The LI method reveals that the precise form of the equation is $\mathrm{\Delta }R=\stackrel{\mathrm{‾}}{{\mathit{\lambda }}_P}\mathrm{\Delta }P+\stackrel{\mathrm{‾}}{{\mathit{\lambda }}_{E_{\mathrm{0}}}}\mathrm{\Delta }{E}_{\mathrm{0}}+\stackrel{\mathrm{‾}}{{\mathit{\lambda }}_n}\mathrm{\Delta }n$ (Appendix D), where $\stackrel{\mathrm{‾}}{{\mathit{\lambda }}_P}$, $\stackrel{\mathrm{‾}}{{\mathit{\lambda }}_{E_{\mathrm{0}}}}$, and $\stackrel{\mathrm{‾}}{{\mathit{\lambda }}_n}$ denote the path-averaged sensitivity of R to P, E₀, and n, respectively. All points along the path have the same weight in determining $\stackrel{\mathrm{‾}}{{\mathit{\lambda }}_P}$, $\stackrel{\mathrm{‾}}{{\mathit{\lambda }}_{E_{\mathrm{0}}}}$, and $\stackrel{\mathrm{‾}}{{\mathit{\lambda }}_n}$. To determine them, the total-differential and the complementary methods utilize only the initial and/or the terminal states. Neglecting the intermediate states results in an imprecise partition, as was illustrated in Figs. 5 and 6 as well as in Fig. 1 using a univariate function, and even a reverse trend estimation (see $\mathrm{\Delta }{R}_{E_{\mathrm{0}}}$ for catchment no. 1 in Table 3).

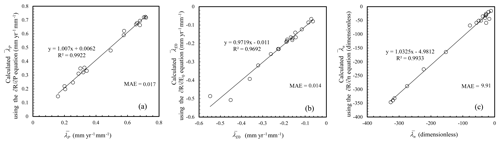
Figure 8 Performances of Eq. (2) to be used to predict $\stackrel{\mathrm{‾}}{{\mathit{\lambda }}_P}$, $\stackrel{\mathrm{‾}}{{\mathit{\lambda }}_{E_{\mathrm{0}}}}$, and $\stackrel{\mathrm{‾}}{{\mathit{\lambda }}_n}$ with the long-term mean values of P, E₀, and n as inputs. $MAE=N^{-\mathrm{1}}\sum _{i=\mathrm{1}}^N\left|O_i-P_i\right|$ is the mean absolute error, where O and P are values that were actually encountered (given in Table S4) and predicted using Eq. (2), respectively, and N is the number of selected catchments.

As with the LI method, the complementary method produced ΔR_P, $\mathrm{\Delta }{R}_{E_{\mathrm{0}}}$, and ΔR_n that exactly summed up to ΔR. Although its resultant ΔR_p, $\mathrm{\Delta }{R}_{E_{\mathrm{0}}}$, and ΔR_n values were all in accordance with the LI method (Fig. 6), the LI method often yielded values beyond the bounds given by the complementary method (Fig. 7); this is because the maximum or minimum sensitivities do not necessarily occur at the initial or terminal states.

$\stackrel{\mathrm{‾}}{{\mathit{\lambda }}_P},\stackrel{\mathrm{‾}}{{\mathit{\lambda }}_{E_{\mathrm{0}}}}$, and $\stackrel{\mathrm{‾}}{{\mathit{\lambda }}_n}$ imply the average runoff change induced by a unit change in P, E₀, and n, respectively (Appendix D). $\stackrel{\mathrm{‾}}{{\mathit{\lambda }}_P}$, $\stackrel{\mathrm{‾}}{{\mathit{\lambda }}_{E_{\mathrm{0}}}}$, and $\stackrel{\mathrm{‾}}{{\mathit{\lambda }}_n}$ all varied by up to several times or even 10-fold between the studied catchments (Table S4). Figure 8 shows that Eq. (2) reproduced $\stackrel{\mathrm{‾}}{{\mathit{\lambda }}_P}$, $\stackrel{\mathrm{‾}}{{\mathit{\lambda }}_{E_{\mathrm{0}}}}$, and $\stackrel{\mathrm{‾}}{{\mathit{\lambda }}_n}$ very well when taking the long-term means of P, E₀, and n as inputs, a reflection of the fact that the dependent variable approached its average when the independent variables were set to be their averages. This finding is of relevance to the spatial prediction of $\stackrel{\mathrm{‾}}{{\mathit{\lambda }}_P}$, $\stackrel{\mathrm{‾}}{{\mathit{\lambda }}_{E_{\mathrm{0}}}}$, and $\stackrel{\mathrm{‾}}{{\mathit{\lambda }}_n}$.

4 Discussion

The LI method highlights the role of the evolutionary path in determining the resultant partition. Yet it seems that no studies have accounted for the path issue while evaluating the relative influences of drivers. The limit of the LI method is high data requirements for obtaining the evolutionary path. When the path data are unavailable, the complementary method can be considered as an alternative. The complementary method is free of residuals; moreover, it employs data from both the reference and the evaluation periods, thereby generally yielding sensitivities closer to the path-averaged results than the total-differential method.

While using the Budyko models, a reasonable timescale is relevant to meet the assumption that changes in catchment water storage are small relative to the magnitude of fluxes of P, R, and E (Donohue et al., 2007; Roderick and Farquhar, 2011). A 7-year timescale was used in the present study, as most studies have suggested that a time period of 5–10 years (Zhang et al., 2001, 2016; Wu et al., 2017a, b; Li et al., 2017) or even 1 year (Roderick and Farquhar, 2011; Sivapalan et al., 2011; Carmona et al., 2014; Ning et al., 2017) is reasonable. Nevertheless, some studies have argued that the time period should be longer than 10 years (Li et al., 2016; Dey and Mishra, 2017). Using the Gravity Recovery and Climate Experiment (GRACE) satellite gravimetry, Zhao et al. (2011) detected the water storage variations for the three largest river basins of China, namely, the Yellow, Yangtze, and Zhujiang. The Yellow River mostly drains an arid and semiarid region (P, $\mathrm{450}\times {\mathrm{10}}^{-\mathrm{3}}$ m; R, $\mathrm{70}\times {\mathrm{10}}^{-\mathrm{3}}$ m; E, $\mathrm{380}\times {\mathrm{10}}^{-\mathrm{3}}$ m), and the Yangtze (P, $\mathrm{110}\times {\mathrm{10}}^{-\mathrm{3}}$ m; R, $\mathrm{550}\times {\mathrm{10}}^{-\mathrm{3}}$ m; E, $\mathrm{550}\times {\mathrm{10}}^{-\mathrm{3}}$ m) and the Zhujiang River basins (P, $\mathrm{1400}\times {\mathrm{10}}^{-\mathrm{3}}$ m; R, $\mathrm{780}\times {\mathrm{10}}^{-\mathrm{3}}$ m; E, $\mathrm{620}\times {\mathrm{10}}^{-\mathrm{3}}$ m) are humid. The amplitude of the water storage variations between years was 7, 37.2, and $\mathrm{65}\times {\mathrm{10}}^{-\mathrm{3}}$ m for the three rivers, respectively, at 1 order of magnitude smaller than the fluxes of P, R and E. Although the observations cannot be directly extrapolated to other regions, the possibility seems remote that the use of a 7-year aggregated time period strongly violates the assumption of the steady-state condition.

The mutual independence of the drivers is crucial for a valid partition. In the present study, although annual P and E₀ exhibited significant correlation for most catchments (p<0.05), the aggregated P, E₀, and n over a 7-year period showed minimal correlation (mostly p>0.1). The interdependence between the drivers can considerably confound the resultant partitions of the LI method and other existing methods.

The LI method revises the concept of sensitivity at a point as the path-averaged sensitivity. Mathematically, the LI method is unrelated to a functional form and hence applies to communities other than just hydrology. For example, identifying the carbon emission budgets (an allowable amount of anthropogenic CO₂ emission consistent with a limiting warming target) is crucial for global efforts to mitigate climate change. The LI method suggested that the emission budgets depends on both the emission magnitude and pathway (timing of emissions), which is in line with a recent study by Gasser et al. (2018). An optimal pathway would facilitate an elevated carbon budget unless the carbon–climate system behaves in a linear fashion.

This study presented the LI method using time-series data, but it applies equally to the case of spatial series of data. Given a model that relates fluvial or eolian sediment load to the influencing factors (e.g., rainfall and topography), for example, the LI method can be used to separate their contributions to the sediment-load change along a river or in the along-wind direction.

5 Conclusions

Based on the line integral, I created a mathematically precise method to partition the synergistic effects of several factors that cumulatively drive a system to change from one state to the other. The method is relevant for quantitative assessments of the relative roles of the factors behind the change in the system state. I applied the LI method to partition the effects of climatic and catchment conditions on runoff within the Budyko framework. The method reveals that, in addition to the change magnitude, the change pathways of climatic and catchment conditions also play a role. Instead of using the runoff sensitivity at a point, the LI method uses the path-averaged sensitivity, thereby ensuring a mathematically precise partition. As a mathematically accurate scheme, the LI method has the potential to be a generic attribution approach in the environmental sciences.

Appendix A: Mathematical proof of $\mathrm{\Delta }z={\int }_L{f}_x(x,y)\mathrm{d}x+{\int }_L{f}_y(x,y)\mathrm{d}y$

Proof. In order to prove the equation above, we define the curve L in Fig. 3 as being given by a parametric equation: x=x(t), y=y(t), $t\in [t_{\mathrm{0}},t_N]$, and therefore $\mathrm{\Delta }z=z_N-z_{\mathrm{0}}=f\left[x\right(t_N),y(t_N\left)\right]-f\left[x\right(t_{\mathrm{0}}),y(t_{\mathrm{0}}\left)\right]$. Substituting the parametric equations, the right-hand side of the equation can be rewritten as
${\int }_L{f}_x(x,y)\mathrm{d}x+{\int }_L{f}_y(x,y)\mathrm{d}y$

$$\begin{array}{}\text{(A1)}& \begin{array}{rl}& ={\int }_{t_{\mathrm{0}}}^{t_N}{f}_x\left[x\right(t),y(t\left)\right]\mathrm{d}x\left(t\right)\\ & +{\int }_{t_{\mathrm{0}}}^{t_N}{f}_y\left[x\right(t),y(t\left)\right]\mathrm{d}y\left(t\right)\\ & ={\int }_{t_{\mathrm{0}}}^{t_N}\left\{f_x\left[x\right(t),y(t\left)\right]\right.x^{\prime }\left(t\right)\\ & +\left.f_y\left[x\right(t),y(t\left)\right]y^{\prime }\left(t\right)\right\}\mathrm{d}t.\end{array}\end{array}$$

Let $g\left(t\right)=f\left[x\right(t),y(t\left)\right]$, and after using the chain rule to differentiate g with respect to t we obtain

$$\begin{array}{}\text{(A2)}& \begin{array}{rl}{g}^{\prime }\left(t\right)& ={\displaystyle \frac{\partial g}{\partial x}}{\displaystyle \frac{\mathrm{d}x}{\mathrm{d}t}}+{\displaystyle \frac{\partial g}{\partial y}}{\displaystyle \frac{\mathrm{d}y}{\mathrm{d}t}}\\ & =f_x\left[x\right(t),y(t\left)\right]x^{\prime }\left(t\right)+f_y\left[x\right(t),y(t\left)\right]y^{\prime }\left(t\right).\end{array}\end{array}$$

Thus, g^′(t) is just the integrand in Eq. (A1), and the right-hand side of the equation can be further rewritten as follows.

The right-hand side of the equation $={\int }_{t_{\mathrm{0}}}^{t_N}{g}^{\prime }\left(t\right)\mathrm{d}t={\left[g\left(t\right)\right]}_{t_{\mathrm{0}}}^{t_N}=g\left(t_N\right)-g\left(t_{\mathrm{0}}\right)=f\left[x\right(t_N),y(t_N\left)\right]-f\left[x\right(t_{\mathrm{0}}),y(t_{\mathrm{0}}\left)\right]=$ the left-hand side of the equation. Q.E.D.

Appendix B: Mathematical proof that the sum of ${\int }_L{f}_x(x,y)\mathrm{d}x$ and ${\int }_L{f}_y(x,y)\mathrm{d}y$ is path independent

Preliminary theorem: Given an open, simply connected region G (i.e., no holes in G) and two functions P(x,y) and Q(x,y) that have continuous first-order derivatives, if and only if $\partial P/\partial y=\partial Q/\partial x$ throughout G, then ${\int }_{L}P(x,y)\mathrm{d}x+{\int }_{L}Q(x,y)\mathrm{d}y$ is path independent; i.e., it depends solely on the starting and ending points of L.

Proof. We have $\partial f_x/\partial y={\partial }^{\mathrm{2}}z/\partial x\partial y$ and $\partial f_y/\partial x={\partial }^{\mathrm{2}}z/\partial y\partial x$. As ${\partial }^{\mathrm{2}}z/\partial x\partial y={\partial }^{\mathrm{2}}z/\partial y\partial x$, we can state that $\partial f_x/\partial y=\partial f_y/\partial x$, meeting the above condition and proving that ${\int }_L{f}_x(x,y)\mathrm{d}x+{\int }_L{f}_y(x,y)\mathrm{d}y$ is path independent. The statement was further exemplified using a fictitious example in Appendix C. Q.E.D.

Appendix C: A fictitious example to show how the LI method works

Runoff (R, 10⁻³ m yr⁻¹) at a site is assumed to increase from 120 to $\mathrm{195}\times {\mathrm{10}}^{-\mathrm{3}}$ m yr⁻¹ with $\mathrm{\Delta }R=\mathrm{75}\times {\mathrm{10}}^{-\mathrm{3}}$ m yr⁻¹; meanwhile, precipitation (P, 10⁻³ m yr⁻¹) varies from 600 to $\mathrm{650}\times {\mathrm{10}}^{-\mathrm{3}}$ m yr⁻¹ ($\mathrm{\Delta }P=\mathrm{75}\times {\mathrm{10}}^{-\mathrm{3}}$ m yr⁻¹) and the runoff coefficient (C_R, dimensionless) varies from 0.2 to 0.3 (ΔC_R=0.1). The goal is to partition ΔR into the effects of the precipitation (ΔR_P) and runoff coefficient ($\mathrm{\Delta }{R}_{C_{\mathrm{R}}}$), provided that P and C_R are independent. We have a function R=PC_R and its partial derivatives $\partial R/\partial P=C_{\mathrm{R}}$ and $\partial R/\partial C_{\mathrm{R}}=P$. Given a path L along which P and C_R change and using Eq. (3), the LI method evaluates ΔR_P and $\mathrm{\Delta }{R}_{C_{\mathrm{R}}}$ as

$$\begin{array}{}\text{(C1)}& \begin{array}{rl}\mathrm{\Delta }{R}_{C_{\mathrm{R}}}& ={\int }_L\partial R/\partial C_{\mathrm{R}}\mathrm{d}{C}_{\mathrm{R}}={\int }_{L}P\mathrm{d}{C}_{\mathrm{R}},\\ \mathrm{\Delta }{R}_P& ={\int }_L\partial R/\partial P\mathrm{d}P={\int }_L{C}_{\mathrm{R}}\mathrm{d}P.\end{array}\end{array}$$

The result differs depending on L, but the sum of ΔR_P and $\mathrm{\Delta }{R}_{C_{\mathrm{R}}}$ uniformly equals ΔR. This dynamic is demonstrated using Fig. 3, in which we considered that the x axis represents C_R, and the y axis P. Point A denotes the initial state (C_R=0.2, P=600), and point C the terminal state (C_R=0.3, P=650). I calculated ΔR_P and $\mathrm{\Delta }{R}_{C_{\mathrm{R}}}$ along three fictitious paths as follows:

1. L= AC. Line segment AC has equation $P=\mathrm{500}{C}_{\mathrm{R}}+\mathrm{500}$, $\mathrm{0.2}\le C_{\mathrm{R}}\le \mathrm{0.3}$. Let us take C_R as the parameter and write the equation in the parametric form as $P=\mathrm{500}{C}_{\mathrm{R}}+\mathrm{500}$, C_R=C_R, $\mathrm{0.2}\le C_{\mathrm{R}}\le \mathrm{0.3}$. By substituting the equation into Eq. (C1), we have

   $$\begin{array}{rl}\mathrm{\Delta }{R}_{C_{\mathrm{R}}}& ={\int }_{\mathrm{AC}}P\mathrm{d}{C}_{\mathrm{R}}={\int }_{\mathrm{0.2}}^{\mathrm{0.3}}(\mathrm{500}{C}_{\mathrm{R}}+\mathrm{500})\mathrm{d}{C}_{\mathrm{R}}=\mathrm{62.5},\\ \mathrm{\Delta }{R}_P& ={\int }_{\mathrm{AC}}{C}_{\mathrm{R}}\mathrm{d}P={\int }_{\mathrm{AC}}{C}_{\mathrm{R}}\mathrm{d}(\mathrm{500}{C}_{\mathrm{R}}+\mathrm{500})\\ & =\mathrm{500}{\int }_{\mathrm{0.2}}^{\mathrm{0.3}}{C}_{\mathrm{R}}\mathrm{d}{C}_{\mathrm{R}}=\mathrm{12.5}.\end{array}$$

2. L= AB + BC. To evaluate on the broken line, we can evaluate separately on AB and BC and then sum them up. The equation for AB is P=600, $\mathrm{0.2}\le C_{\mathrm{R}}\le \mathrm{0.3}$, while for BC it is C_R=0.3, $\mathrm{600}\le P\le \mathrm{650}$. Note that a constant C_R or P implies that dC_R=0 or dP=0. Eq. (C1) then becomes

   $$\begin{array}{rl}\mathrm{\Delta }{R}_{C_{\mathrm{R}}}& ={\int }_{\mathrm{AB}+\mathrm{BC}}P\mathrm{d}{C}_{\mathrm{R}}={\int }_{\mathrm{AB}}P\mathrm{d}{C}_{\mathrm{R}}+{\int }_{\mathrm{BC}}P\mathrm{d}{C}_{\mathrm{R}}\\ & ={\int }_{\mathrm{0.2}}^{\mathrm{0.3}}\mathrm{600}\mathrm{d}{C}_{\mathrm{R}}+\mathrm{0}=\mathrm{60},\\ \mathrm{\Delta }{R}_P& ={\int }_{\mathrm{AB}+\mathrm{BC}}{C}_{\mathrm{R}}\mathrm{d}P={\int }_{\mathrm{AB}}{C}_{\mathrm{R}}\mathrm{d}P+{\int }_{\mathrm{BC}}{C}_{\mathrm{R}}\mathrm{d}P\\ & =\mathrm{0}+{\int }_{\mathrm{600}}^{\mathrm{650}}\mathrm{0.3}\mathrm{d}P=\mathrm{15}.\end{array}$$

3. $L=\mathrm{AD}+\mathrm{DC}$. The equation for AD is C_R=0.2, $\mathrm{600}\le P\le \mathrm{650}$, and for DC it is P=650, $\mathrm{0.2}\le C_{\mathrm{R}}\le \mathrm{0.3}$. ΔR_P and $\mathrm{\Delta }{R}_{C_{\mathrm{R}}}$ are evaluated as

   $$\begin{array}{rl}\mathrm{\Delta }{R}_{C_{\mathrm{R}}}& ={\int }_{\mathrm{AD}+\mathrm{DC}}P\mathrm{d}{C}_{\mathrm{R}}={\int }_{\mathrm{AD}}P\mathrm{d}{C}_{\mathrm{R}}+{\int }_{\mathrm{DC}}P\mathrm{d}{C}_{\mathrm{R}}\\ & =\mathrm{0}+{\int }_{\mathrm{0.2}}^{\mathrm{0.3}}\mathrm{650}\mathrm{d}{C}_{\mathrm{R}}=\mathrm{65},\\ \mathrm{\Delta }{R}_P& ={\int }_{\mathrm{AD}+\mathrm{DC}}{C}_{\mathrm{R}}\mathrm{d}P={\int }_{\mathrm{AD}}{C}_{\mathrm{R}}\mathrm{d}P+{\int }_{\mathrm{DC}}{C}_{\mathrm{R}}\mathrm{d}P\\ & ={\int }_{\mathrm{600}}^{\mathrm{650}}\mathrm{0.2}\mathrm{d}P+\mathrm{0}=\mathrm{10}.\end{array}$$

   As expected, the sum of ΔR_P and $\mathrm{\Delta }{R}_{C_{\mathrm{R}}}$ persistently equals ΔR although ΔR_P and $\mathrm{\Delta }{R}_{C_{\mathrm{R}}}$ varies with L.

Appendix D: Mathematical proof of the path-averaged sensitivity

If the interval [x₀, x_N] in Fig. 3 is partitioned into N distinct bins of the same width $\mathrm{\Delta }{x}_i=\mathrm{\Delta }x/N$, Eq (3a) can then be rewritten as

$$\begin{array}{rl}\mathrm{\Delta }{Z}_x& ={\int }_L{f}_x(x,y)\mathrm{d}x=\underset{\mathit{\tau }\to \mathrm{0}}{lim}\sum _{i=\mathrm{0}}^{N-\mathrm{1}}{f}_x(x_i,y_i)\mathrm{\Delta }{x}_i\\ & =\underset{\mathit{\tau }\to \mathrm{0}}{lim}N\mathrm{\Delta }{x}_i{\displaystyle \frac{\sum _{i=\mathrm{0}}^{N-\mathrm{1}}{f}_x(x_i,y_i)}{N}}\\ & =\mathrm{\Delta }x\underset{\mathit{\tau }\to \mathrm{0}}{lim}{\displaystyle \frac{\sum _{i=\mathrm{0}}^{N-\mathrm{1}}{f}_x(x_i,y_i)}{N}}=\stackrel{\mathrm{‾}}{{\mathit{\lambda }}_x}\mathrm{\Delta }x,\end{array}$$

where $\stackrel{\mathrm{‾}}{{\mathit{\lambda }}_x}=\underset{\mathit{\tau }\to \mathrm{0}}{lim}\frac{\sum _{i=\mathrm{1}}^N{f}_x(x_i,y_i)}{N}$, denoting the average of f_x(x, y) along the curve L. Likewise, we have $\mathrm{\Delta }{Z}_y=\stackrel{\mathrm{‾}}{{\mathit{\lambda }}_y}\mathrm{\Delta }y$, where $\stackrel{\mathrm{‾}}{{\mathit{\lambda }}_y}$ denotes the average of f_y(x,y) along the curve L. As a result

$$\begin{array}{}\text{(D1)}& \mathrm{\Delta }Z=\stackrel{\mathrm{‾}}{{\mathit{\lambda }}_x}\mathrm{\Delta }x+\stackrel{\mathrm{‾}}{{\mathit{\lambda }}_y}\mathrm{\Delta }y.\end{array}$$

The result can readily be extended to a function of three variables. Applying the mathematic derivation determined above to the MCY equation results in a precise form of Eq. (7):

$$\begin{array}{}\text{(D2)}& \begin{array}{rl}\mathrm{\Delta }R& =\mathrm{\Delta }{R}_P+\mathrm{\Delta }{R}_{E_{\mathrm{0}}}+\mathrm{\Delta }{R}_n\\ & =\stackrel{\mathrm{‾}}{{\mathit{\lambda }}_P}\mathrm{\Delta }P+\stackrel{\mathrm{‾}}{{\mathit{\lambda }}_{E_{\mathrm{0}}}}\mathrm{\Delta }{E}_{\mathrm{0}}+\stackrel{\mathrm{‾}}{{\mathit{\lambda }}_n}\mathrm{\Delta }n,\end{array}\end{array}$$

where $\mathrm{\Delta }{R}_P=\stackrel{\mathrm{‾}}{{\mathit{\lambda }}_P}\mathrm{\Delta }P$; $\mathrm{\Delta }{R}_{E_{\mathrm{0}}}=\stackrel{\mathrm{‾}}{{\mathit{\lambda }}_{E_{\mathrm{0}}}}\mathrm{\Delta }{E}_{\mathrm{0}}$; $\mathrm{\Delta }{R}_n=\stackrel{\mathrm{‾}}{{\mathit{\lambda }}_n}\mathrm{\Delta }n$; and $\stackrel{\mathrm{‾}}{{\mathit{\lambda }}_P}$, $\stackrel{\mathrm{‾}}{{\mathit{\lambda }}_{E_{\mathrm{0}}}}$, and $\stackrel{\mathrm{‾}}{{\mathit{\lambda }}_n}$ denote the arithmetic mean of $\partial R/\partial P$, $\partial R/\partial E_{\mathrm{0}}$, and $\partial R/\partial n$ along a path of climate and catchment changes, respectively. Because $\stackrel{\mathrm{‾}}{{\mathit{\lambda }}_P}=\mathrm{\Delta }{R}_P/\mathrm{\Delta }P$, $\stackrel{\mathrm{‾}}{{\mathit{\lambda }}_{E_{\mathrm{0}}}}=\mathrm{\Delta }{R}_{E_{\mathrm{0}}}/\mathrm{\Delta }{E}_{\mathrm{0}}$, and $\stackrel{\mathrm{‾}}{{\mathit{\lambda }}_n}=\mathrm{\Delta }{R}_n/\mathrm{\Delta }n$, $\stackrel{\mathrm{‾}}{{\mathit{\lambda }}_P}$, $\stackrel{\mathrm{‾}}{{\mathit{\lambda }}_{E_{\mathrm{0}}}}$, and $\stackrel{\mathrm{‾}}{{\mathit{\lambda }}_n}$ also imply the runoff change due to a unit change in P, E₀, and n, respectively.

Appendix E: Path-averaged sensitivity in one-dimensional cases

Given a one-dimensional function z=f(x) and its derivative f^′(x), we assumed that f^′(x) averages $\stackrel{\mathrm{‾}}{{\mathit{\lambda }}_x}$ over the range $(x,x+\mathrm{\Delta }x)$, i.e., $\stackrel{\mathrm{‾}}{{\mathit{\lambda }}_x}=\underset{\mathit{\tau }\to \mathrm{0}}{lim}\frac{\sum _{i=\mathrm{1}}^N{f}^{\prime }\left(x_i\right)}{N}$. According to the mean value theorem for integrals, $\stackrel{\mathrm{‾}}{{\mathit{\lambda }}_x}={\int }_x^{x+\mathrm{\Delta }x}{f}^{\prime }\left(x\right)\mathrm{d}x/\mathrm{\Delta }x$. In terms of the Newton–Leibniz formula, ${\int }_x^{x+\mathrm{\Delta }x}{f}^{\prime }\left(x\right)\mathrm{d}x=f(x+\mathrm{\Delta }x)-f\left(x\right)=\mathrm{\Delta }z$. Thus, we obtain $\stackrel{\mathrm{‾}}{{\mathit{\lambda }}_x}=\mathrm{\Delta }z/\mathrm{\Delta }x$.