Basin-scale multi-objective simulation-optimization modeling for conjunctive use of surface water and groundwater in northwest China

In the arid inland basins of China, the long-term unregulated agricultural irrigation from surface water diversion and groundwater abstraction has caused the unsustainability of water resources and the degradation of ecosystems. This requires the integrated management of surface water (SW) and groundwater (GW) at basin scale to achieve scientific decisions which support sustainable water resource allocation in China. This study developed a novel multi-objective simulation-optimization (S-O) modeling framework. The optimization framework integrated a new epsilon multi-objective memetic algorithm (ε-MOMA) with a MODFLOW-NWT model to implement real-world decision-making for water resource management while pondering the complicated groundwater–lake–river interaction in an arid inland basin. Then the optimization technique was validated through the SW–GW management in Yanqi Basin (YB), a typical arid region with intensive agricultural irrigation in northwest China. The management model, involving the maximization of total water supply rate, groundwater storage, surface runoff inflow to the terminal lake, and the minimization of water delivery cost, was proposed to explore the trade-offs between socioeconomic and environmental factors. It is shown that the trade-off surface can be achieved in the four-dimensional objective space by optimizing spatial groundwater abstraction in the irrigation districts and surface water diversion in the river. The Pareto-optimal solutions avoid the prevalence of decision bias caused by the low-dimensional optimization formulation. Decision-makers are then able to identify their desired water management schemes with preferred objectives and achieve maximal socioeconomic and ecological benefits simultaneously. Moreover, three representative runoff scenarios in relation to climate change were specified to quantify the effect of decreasing river runoff on the water management in YB. Results show that runoff depletion would have a great negative impact on the management objectives. Therefore, the integrated SW and GW management is of critical importance for the fragile ecosystem in YB under changing climatic conditions.

1 Introduction

In arid and semi-arid inland basins, intensive irrigation for agricultural development caused the deterioration of natural ecosystems sustained by scarce water resources (Wichelns and Oster, 2006; Wu et al., 2016). In such cases, water managers are faced with choosing the optimal water supply scheme for local economic development and eco-environmental conservation. In general, the pattern of water allocation in such regions incorporates groundwater (GW) abstraction from aquifer systems and surface water (SW) diversion from surface rivers (Liu et al., 2010; Wu et al., 2014). Hence, it is essential for the conjunctive management of GW and SW to deal with the contradiction between the supply and demand of water resources in the arid regions with water shortages (Khare et al., 2006; Safavi and Esmikhani, 2013; Singh, 2014; Hassanzadeh et al., 2014; Wu et al., 2016).

In water resource planning and management, simulation-optimization (S-O) methods can provide optimal schemes to guide and inform stakeholders (Maier et al., 2014). In the S-O framework, the simulation model explains the physical behaviors of water resource systems, and the management model explains the evaluation criteria of the water supply options (Singh, 2014). The management model includes objective functions as the performance metrics of candidate schemes and constraint conditions defining the feasible decision space. However, real-world water management problems are often complex and associated with nonlinear and multimodal objectives and constraints. This complexity probably leads to the unavailability of the classical optimization algorithms such as mathematical programming and dynamic programming (Woodruff et al., 2013). For this reason, evolutionary algorithms have extensively proved to be effective and reliable in solving complex SW and GW management problems (McPhee and Yeh, 2004; Yang et al., 2009; Safavi and Esmikhani, 2013; Singh and Panda, 2013; Rothman and Mays, 2014; Wu et al., 2014, 2016; Parsapour-Moghaddam et al., 2015). Yang et al. (2009) considered conflicting bi-objectives with the conjunctive use of GW and SW to achieve optimal pumping and recharge schemes. Rothman and Mays (2014) developed an optimization model including cost control, aquifer protection, and growth objectives using a multi-objective genetic algorithm. Wu et al. (2016) performed the temporal optimization of the monthly volume of surface water diverted from the Heihe River by linking physical-based integrated modeling with a simple single-objective management model. However, these studies rarely consider multi-objective optimization in basin-scale water management with the conjunctive use of SW and GW. The management model, including the typical single objective or bi-objective formulation, probably results in decision bias (i.e., cognitive myopia or short-sightedness) due to the suboptimal solution of only considering a few preference criteria (Kasprzyk et al., 2012, 2016; Woodruff et al., 2013; Matteo et al., 2019). Therefore, water resource management with strong and complex interactions between SW and GW calls for decision-makers to consider many-objective optimization, which refers to a system design with four or more objectives (Fleming et al., 2005).

Multi-objective evolutionary algorithms (MOEAs) can obtain the trade-off solutions that cater to multiple competing objectives and reflect comprehensive decision information for practitioners in real-world applications (Reed et al., 2013; Beh et al., 2017; Eker and Kwakkel, 2018; Maier et al., 2019). However, many-objective optimization often suffers from the domination resistance phenomenon (Purshouse and Fleming, 2007; Hadka and Reed, 2013), which shows that the diminishing Pareto-sorting capacity triggers many non-dominated solutions in the population and then results in the stagnation of the evolutionary search. In order to alleviate the difficulty, the Borg MOEA (Hadka and Reed, 2013) employed auto-adaptive recombination operators to enhance the evolutionary search ability, an ε-box technique to ensure the diversity, and an adaptive population sizing scheme to avoid search stagnation. The hybrid MOEA framework, namely a multi-objective memetic algorithm composed of the biological process of natural selection and cultural evolution capable of local refinement, was applied to overcome some shortcomings of the traditional MOEA (e.g., slow convergence, inefficient termination criterion) (Sindhya et al., 2011, 2013). These state-of-the-art MOEAs have been extensively validated and evaluated in addressing multi-objective optimization problems. However, due to the diversity and complexity of real-word decision-making problems, the algorithms may be inefficient in maintaining the diversity and convergence of the Pareto front simultaneously. For example, Zheng et al. (2016) implemented the comparison of NSGAII, SAMODE, and Borg in designing water distribution systems. The result indicated that Borg can converge quickly to the Pareto-optimal front, while decreasing the diversity of Pareto-optimal solutions. Hence, further efforts should be focused on advancing the MOEAs. This study aims at developing a new MOEA, named epsilon multi-objective memetic algorithm (ε-MOMA), which integrates the ε-dominance archive process, the auto-adaptive recombination operator, and a local search operator into the basic framework of NSGAII (Deb et al., 2002b). Then, the proposed multi-objective optimization framework is applied to solve the integrated management of SW and GW in Yanqi Basin (YB).

YB is a typical oasis in an arid inland basin located to the south of the Tianshan mountains in Xinjiang Province, northwest China. The surface water resources in YB are composed of the Kaidu River and Bosten Lake, the largest freshwater inland lake in China (Wang et al., 2014; Zhou et al., 2015). The Kaidu River, as the largest river in the basin, supplies the vast majority of surface water for agricultural irrigation and recharge for Bosten Lake (Gao and Yao, 2005; Liu et al., 2013; Yao et al., 2018). Therefore, surface water diversion in the river dominates the water balance in Bosten Lake, which is the main water source for the lower reaches of the Tarim River where a serious water crisis has taken place. With the intensive agricultural development in the past decades, surface water diverted from the Kaidu River can no longer meet crop water requirements. Hence, groundwater became the alternative water source for crop production, and the excessive groundwater abstraction has caused the deterioration of local ecosystems associated with the decline of groundwater level and has altered the hydraulic interaction between GW and SW (Hu et al., 2007; Zhang et al., 2014; Tian et al., 2015; Yao et al., 2015). Current water resource regulations in YB have shown the low performance in maintaining regional water balance, e.g., the decline of lake level in Bosten Lake. Therefore, the spatial pattern of water utilization (i.e., decision variables) should be regulated to satisfy the preferred management objectives. The pattern is composed of groundwater abstraction in irrigation districts and surface water diversion through the aqueduct system connected to the river. The management objectives comprise minimizing the capital and operation costs of water delivery and maximizing water-use demands for agricultural development (i.e., total volume of surface water and groundwater use) and the environmental flow for hydro–ecosystem conservation (i.e., the regional groundwater storage and surface runoff inflow to the terminal lake). This study implements the integrated management of SW and GW by investigating the performance of trade-offs, including environmental, economic, and social factors, in designing optimal water allocation schemes with the new optimization framework. To our knowledge, there has been very little research on many-objective optimization for the conjunctive management of SW and GW involving complex groundwater–river–lake interactions in arid inland basins within an S-O framework.

In the changing world, the optimized schemes probably exhibit low performance and are even unfeasible under future conditions (Maier et al., 2016). In YB, the Kaidu River mainly gains water from seasonal precipitation that runs off the mountainous landscape and from snow and glaciers that melt in the upper Tianshan mountain region, known as a main water source in Central Asia. Therefore, the runoff variation in the Kaidu River, which is highly sensitive to the changes in precipitation and glacier mass loss dominated by climate change, greatly affects the water resources and water cycle in the basin. Three representative runoff scenarios in relation to climate change are specified to explore the effects of runoff reduction in the Kaidu River on the integrated SW and GW management practices.

This study firstly constructed the multi-objective SW–GW management model to consider water demands and environmental benefits including regional groundwater storage and surface runoff inflow to the terminal lake. Then the spatial conjunctive optimization of surface water diversion and groundwater abstraction was implemented based on the proposed optimization framework. The optimization results demonstrate that decision-makers can achieve the Pareto-optimal schemes when constrained by satisfying the water demands and sustaining the fragile ecosystem in the arid inland basin with strong and complex SW–GW interactions. The implication from the multi-objective optimization under the runoff reduction scenarios shows that the conservative water management options may be desirable in the face of deep uncertainty associated with climate change. The study results can also provide valuable insights for water allocation in other arid inland basins.

2 Methodology

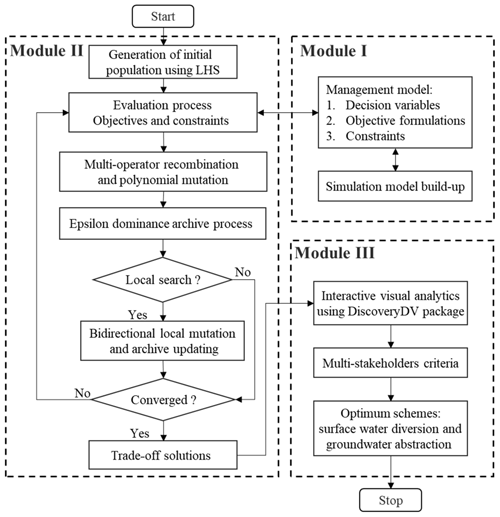
As shown in Fig. 1, this study aims to develop a multi-objective decision-making framework to optimize the irrigation schemes of surface water diversion and groundwater abstraction for integrated SW and GW management. The optimal schemes can assist water managers to achieve water demands and ensure the water balance of ecosystems in an arid inland basin. The optimization framework includes three main modules, and their details are stated in the following sections.

Figure 1 Framework of multi-objective optimization for integrated SW–GW management.

2.1 Problem formulation

Module I in the optimization framework (Fig. 1) is to formulate an integrated SW and GW management model to implement water resource management in the basin. The water utilization patterns for agricultural irrigation are composed of diverting surface water from the inland reach of the river basin and pumping groundwater from the regional aquifer. Therefore, the decision variables comprise the volume of surface water diversion in the aqueduct system and groundwater abstraction in the irrigation districts. In general, the optimal water supply strategies are maximizing the total volume of water supply and minimizing the capital and operation costs of water delivery. However, in the arid inland basin with water scarcity, the intensive agricultural development requires enough irrigation water to ensure local economic development, while the sustainability of ecosystems also needs to follow specific requirements for maintaining environmental flows. For example, the excessive surface water diversion can significantly reduce the runoff inflow to the terminal lake, which causes an obvious decline in lake level and results in the degradation of local ecosystems associated with the lake. Meanwhile, immoderate exploitation of groundwater stored in the aquifer to offset the surface water shortage triggers a series of environment problems (e.g., dramatic decrease in groundwater storage). Therefore, the conflict between agricultural development and environmental conservation constrained by water scarcity stimulates the local water resource authority to implement scientific water management practices. The water managers should consider the total water supply rate and the cost of water delivery from multiple sources as socioeconomic metrics and describe the runoff inflow to the lake and groundwater storage as environmental metrics. Water managers can then assess water-use practices by weighing these preference criteria. The performances of all schemes are evaluated based on the well-calibrated numerical model. The detailed formulation of the management model can be seen in Sect. 3.3. Finally, the optimization model formulates water-use practices as decision variables, socioeconomic and environmental metrics as management objectives, and practical limitations of water exploitation and water demands for ecosystems as constrained conditions for the basin-scale SW and GW management.

2.2 Optimization approach

2.2.1 Main algorithmic structure

Module II in the optimization framework (Fig. 1) illustrates the algorithmic process of the ε-MOMA. The main steps can be recapitulated as follows:

• Step 1: generation of initial population. N_pop individuals are first sampled over the decision space using Latin hypercube sampling (LHS), which is an effective sample scheme to ensure the uniform distribution of initial population.

• Step 2: evaluation process of objectives and constraints. The simulation model is run with the calibrated parameters. Then objectives and constraints are calculated from the model output variables (i.e., state variables).

• Step 3: evolutionary operators for the creation of offspring population. The auto-adaptive multi-operator recombination proposed by Hadka and Reed (2013) is a promising technique to select the optimal operator for real-world optimization problems. The crossover probability of each operator is updated periodically based on the proportion of the solutions generated by each operator in the ε-dominance archive. The recombination strategy is essential for intricate multi-objective optimization in real-world problems due to the inability to know a priori the optimal recombination operator. This study integrated the six real-valued recombination operators (i.e., simulated binary crossover – SBX; Deb and Agrawal, 1994; differential evolution – DE; Storn and Price, 1997; simplex crossover – SPX; Tsutsui et al., 1999; parent-centric crossover – PCX; Deb et al., 2002a; Laplace crossover – LX; Deep and Thakur, 2007; uniform mutation – UM) into the ε-MOMA to enhance the potential of the evolutionary search in higher-order objective spaces. Additionally, the polynomial mutation is applied to the recombination population.

• Step 4: the ε-domination archive process. The ε-box technique proposed by Laumanns et al. (2002) attempts to ensure the convergence and diversity of the approximate Pareto-optimal solutions. Moreover, decision-makers can define the minimum resolution of the objective vector with the epsilon vector to satisfy their acceptable precision target and restrict the archive size. This study implemented the ε-dominance archive process after the fast non-dominated sorting of offspring individuals and alleviated the difficulties derived from the domination resistance in the many-objective optimization.

• Step 5: bidirectional local mutation. The archived solutions are operated based on Gaussian perturbations in the neighborhood of decision variables. Given an archived individual v=(v₁, v₂, v₃, …, v_n), the mutated individuals can be stated as follows:

  $$\begin{array}{}\text{(1)}& {\displaystyle }& {\displaystyle }{\mathit{v}}^{+}=\left(v_{\mathrm{1}},v_{\mathrm{2}},\mathrm{\dots },v_i+p\times \left(m_i-w_i\right),\mathrm{\dots },v_n\right),\text{(2)}& {\displaystyle }& {\displaystyle }{\mathit{v}}^{-}=\left(v_{\mathrm{1}},v_{\mathrm{2}},\mathrm{\dots },v_i-p\times \left(m_i-w_i\right),\mathrm{\dots },v_n\right),\end{array}$$

  where v=(v₁, v₂, …, v_n) is an n-dimensional decision variable vector; m=(m₁, m₂, …, m_n) and w=(w₁, w₂, …, w_n) are two individuals randomly selected from the archive; and p follows standard Gaussian distribution. The process is effective with the probability of 1∕n (Chen et al., 2015). The algorithm revives the local search operator every several generations and then updates the archive again.

• Step 6: evaluation of termination criterion. If the termination criterion is not satisfied, return to Step 2; otherwise, output the trade-off solutions. This study specified the number of evaluation functions completed by the algorithm as the termination condition.

In the many-objective optimization, the ε-MOMA utilizes the ε-dominance concept to archive elite individuals for the maintenance of diversity and the auto-adaptive recombination operator with local search for the enhancement of convergence on the basis of the framework of NSGAII. Hence, the algorithm possesses the ability of a highly effective global search with an auto-adaptive recombination operator and ε-dominance archive to find higher-quality and diverse solutions with local search operators.

2.2.2 Benchmark test

To investigate the performance of the ε-MOMA in the many-objective optimization, we implement a benchmark test with the three-to-six-objective DTLZ1 and DTLZ3 problems (Deb et al., 2002c). The test instances are deceptive and probably converge at the suboptimal Pareto front, which provides a severe challenge for the algorithm to get close to the global Pareto-optimal front. The hypervolume metric (HV) is applied to evaluate the convergence and diversity of the approximate Pareto front (Zitzler et al., 2003). The global Pareto-optimal front for DTLZ problems is known and can be considered as the reference set. The HV metric indicates the dominated region of the non-dominated solutions relative to the reference point, which is the extent of the reference set. The HV of the reference set (HV_rs) and the approximate set (HV_as) can be calculated using the fast search algorithm proposed by Bader and Zitzler (2011) in the high-dimensional objective space. This study uses the normalized HV (i.e., ${\mathrm{HV}}_n={\mathrm{HV}}_{\mathrm{as}}/{\mathrm{HV}}_{\mathrm{rs}}$) to evaluate the performance of the ε-MOMA for these test problems. The approximate Pareto front completely converges at the reference set when HV_n is equal to one. The test results show that the ε-MOMA is capable of achieving a larger value of HV_n metric (over 95 %), indicating that the approximate Pareto front is very close to the global optimal Pareto front (Table S1 in the Supplement). In higher-dimensional objective space, the performance of the ε-MOMA can be maintained by augmenting the number of function evaluations. Therefore, the proposed ε-MOMA is effective at addressing many-objective optimization from the benchmark test.

2.3 Visual analytics of Pareto front

In many-objective optimization, it is difficult for water managers to distinguish the performance of a single solution and discover desirable schemes without interactive visual analytics. Module III (Fig. 1) used a visual analytics package, DiscoveryDV (Hadka et al., 2015; Kollat and Reed, 2007), to explore and analyze water management practices in the high-order objective spaces. The package employed a multi-dimensional coordinate plot and a parallel coordinate plot (Inselberg, 2009) to visualize Pareto solutions. Visualizing performance objectives can assist stakeholders in comparing the scheme before optimization and select key trade-off schemes with a clearer perspective (Matteo et al., 2019; Maier et al., 2014). Moreover, decision-makers can eliminate redundant schemes with the preferred objectives or concerns and filter the optimal subsets of those probably adopted by the experienced practitioners.

Figure 2 The location of Yanqi Basin and the model domain of interest for this study. Source: DigitalGlobal, Inc. (imagery).

3 Case study

3.1 Study area

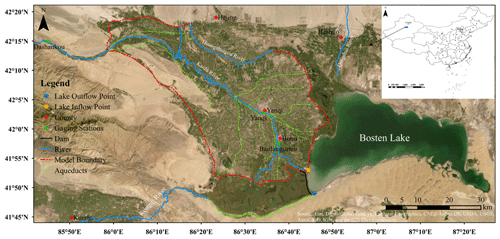
The Yanqi Basin is a typical oasis in an arid inland desert basin in the southern Tianshan mountains, Xinjiang Province, northwest China, and includes Yanqi County, Hejing County, Bohu County, and Heshuo County with a total area of about 7600 km² (Fig. 2). In the model domain, the northwest is mountainous, the south is a low-lying desert, and the terrain slopes from the northwest to the lower southeast. YB is located in the temperate zone of continental desert climate with an annual mean temperature of 14.6 ^∘C, an annual precipitation of 50.7–79.9 mm, and a potential evaporation of 2000.5–2449.7 mm (Mamat et al., 2014). The basin is mainly composed of the Kaidu River, the Huangshuigou River, and the Qingshui River. The Kaidu River originates from the Hargat valley and the Jacsta valley in the middle part of the Tianshan mountains with a maximum altitude of 5000 m and ends in Bosten Lake (Xu et al., 2016). The Kaidu River is the largest river in YB, which provides annual mean runoff of 3.41×10⁹ m³ (Wang et al., 2013), and it plays an utmost role in protecting the lake and its surrounding ecology and environment. The Dashankou station is the point that divides the main stream of the river into the middle and lower reaches. In YB, the runoff in the Kaidu River is mainly diverted for agricultural irrigation and finally flows into Bosten Lake, which contributes to about 95 % of the water recharge for the lake (Yao et al., 2018). Bosten Lake is the largest freshwater inland lake in China, covering an area of about 1005 km² with a length of 55 km and a width of 25 km. The lake water volume is approximately 8.80×10⁹ m³ with an average depth of 7 m and a maximum depth of 17 m (Xiao et al., 2010). Evaporation and an artificial discharge by a pumping station built in 1983 control the outflow of the lake. As shown in Fig. 2, the pumping channel starting from the outflow point is used to divert the lake water to recharge the Kongqi River and supply water to the lower Tarim River. The dam was built to sustain higher lake levels for the water diversion. Therefore, Bosten Lake is a main water source to the lower reaches of the Tarim River, which has suffered from the severe degradation of the ecological environment resulting from unregulated water exploitation in the past decades. In order to regenerate the “green corridor” in the lower reaches of the Tarim River, the Chinese government has been implementing the ecological water conveyance project since 2000 to increase the recharge of the groundwater system, which is crucial for the growth of natural vegetation (Xu et al., 2007; Hao and Li, 2014). As illustrated in Fig. S1 in the Supplement, the project firstly transfers water through the Kongqi River from Bosten Lake to the Daxihaizi reservoir, then to the lower reaches of the Tarim River, and finally to the terminal lake (Chen et al., 2010). However, YB is an intensive agricultural area which is mostly made up of farmland growing crops of tomatoes and peppers. The irrigation water demands accounted for 90 % of the total water consumption in the basin due to the rapid increase in farmland area in recent years (Yao et al., 2018). Consequently, the scientific water management strategies should aim to balance the demands of existing irrigation with eco-environmental water use to sustain enough water inflowing from the Kaidu River to the lake and the regional aquifer.

This study selects the core part of YB, which comprises the majority of irrigation districts and the Kaidu River. The river plays a vital role in regulating and maintaining regional water balance in the basin. The model domain (Fig. 2) is bounded by the mountains to the northwest, Huangshuigou River to the northeast, and swamp areas and Bosten Lake to the south. As shown in Fig. 2, an aqueduct system conveys and redistributes the surface runoff from the main stream of the Kaidu River and the wells are used to pump groundwater in the aquifer system.

3.2 Numerical model

The numerical model in this study is modified from the previous work of Wu et al. (2018) using MODFLOW-NWT. The program applies the Newton-Raphson formulation and unstructured, asymmetric matrix solvers to solve drying and rewetting nonlinearities of the complex unconfined groundwater flow problem (Niswonger et al., 2011), which supports most modular packages in MODFLOW-2005 (Harbaugh, 2005). Then we perform a multi-objective optimization with the corrected model. The specified boundary conditions in the model are illustrated in Fig. 3. The northwest border was defined as the flow boundary to simulate recharge of groundwater runoff in the interface between mountains and plain. The Huangshuigou River and southwest border were considered the specified head boundary based on observed groundwater level. The swamps and Bosten Lake were modeled using the general head boundary (GHB) package and lake package (LAK3) (Michael and Leonard, 2000), respectively. The LAK3 package models the lake and aquifer interactions by calculating the exchange rate, which is determined by the difference between lake level and groundwater, the hydraulic conductivity of the adjacent aquifer, and the material of the lake bed. The lake level responses to the hydraulic stresses include lake atmospheric recharge and evaporation, overland runoff, and any direct withdrawal or recharge of the lake volume. The bathymetric contours of Bosten Lake were used to confirm the lake bottom topography. The Kaidu River and aqueducts were simulated using the streamflow-routing (SFR2) package (Richard and David, 2010). The SFR2 package, as a modular package in MODFLOW-NWT, can be used to model the interactions between streams and underlying aquifers while considering the unsaturated flow beneath streams for the disconnected river. The streamflow is routed based on the continuity equation assuming steady and uniform flow. The Manning equation and Darcy's law are used to represent the relation between river stage and discharge and calculate the infiltration/exfiltration rate between streams and aquifers, respectively. The simulation period in the transient model was defined from November 2003 to October 2013. In total, 20 stress periods were discretized – two periods for each year, including non-irrigation periods (from November to March) and irrigation periods (from April to October of each year) – over the entire simulation period. The key parameters for both SW and GW were adjusted to reproduce the fluctuation of groundwater levels at the observation wells and streamflow in the gaging stations (i.e., Yanqi and Baolangsumu stations). The observed lake levels in the simulation period were employed to calibrate the numerical model. More data details can be found in Table S2.

Figure 3 The boundary conditions of the model domain, monitoring locations of groundwater level and surface runoff, aqueduct system, and bathymetric contours in meters for Bosten Lake.

The model calibration was manually implemented by the trial-and-error method. The Nash–Sutcliffe efficiency (NSE) was applied to evaluate the simulated precision of runoff and lake level. The predicted precision of groundwater head was assessed based on root mean square error (RMSE) and correlation coefficient (R). The performance criteria can be stated as follows:

$$\begin{array}{}\text{(3)}& {\displaystyle }& {\displaystyle }\mathrm{NSE}=\mathrm{1}-{\displaystyle \frac{\sum _{t=\mathrm{1}}^T{\left(y_{\mathrm{m},t}-y_{\mathrm{o},t}\right)}^{\mathrm{2}}}{\sum _{t=\mathrm{1}}^T{\left(y_{\mathrm{o},t}-{\stackrel{\mathrm{‾}}{y}}_{\mathrm{o}}\right)}^{\mathrm{2}}}},\text{(4)}& {\displaystyle }& {\displaystyle }\mathrm{RMSE}=\sqrt{\sum _{i=\mathrm{1}}^N{\left(y_{\mathrm{m},i}-y_{\mathrm{o},i}\right)}^{\mathrm{2}}/N},\text{(5)}& {\displaystyle }& {\displaystyle }R={\displaystyle \frac{\sum _{i=\mathrm{1}}^N\left(y_{\mathrm{m},i}-{\stackrel{\mathrm{‾}}{y}}_{\mathrm{m}}\right)\left(y_{\mathrm{o},i}-{\stackrel{\mathrm{‾}}{y}}_{\mathrm{o}}\right)}{\sqrt{\sum _{i=\mathrm{1}}^N{\left(y_{\mathrm{m},i}-{\stackrel{\mathrm{‾}}{y}}_{\mathrm{m}}\right)}^{\mathrm{2}}\times \sum _{i=\mathrm{1}}^N{\left(y_{\mathrm{o},i}-{\stackrel{\mathrm{‾}}{y}}_{\mathrm{o}}\right)}^{\mathrm{2}}}}},\end{array}$$

where y_m,t and y_o,t are the simulated and observed runoff or lake level for tth stress period; T is the number of stress periods; y_m,i and y_o,i are the simulated and observed groundwater head at the ith observation well; N is the number of observation wells; and ${\stackrel{\mathrm{‾}}{y}}_{\mathrm{m}}$ and ${\stackrel{\mathrm{‾}}{y}}_{\mathrm{o}}$ are the average values of simulated and observed data. Figures S2a and b compare the simulated and observed runoff at the Yanqi and Baolangsumu stations over the stress periods between 2004 and 2012 (lack of observed runoff in 2013) and suggest that the long-term fluctuation of runoff in the Kaidu River can be well reproduced with NSEs of 0.89 and 0.90. Figure S2d shows that the simulated groundwater heads have a good fit with observed heads at all observation wells with an RMSE of 1.80 m and R of 0.98. Figure S2e compares the observed and calibrated groundwater levels over time in the three observation wells, and the groundwater variation trend in the irrigation and non-irrigation periods can be achieved.

Figure 4 The water balance terms of Bosten Lake and resulting lake volume in the simulation period.

The interaction between Bosten Lake and the aquifer is dominated by the hydraulic conductivity of the lake bed, whose value is very small owing to the existence of the thick, low-permeable sediment in the region. The main inflow term of the lake is the surface runoff from the Kaidu River, which has been calibrated with the runoff data at the gaging stations. The recharge for the lake from precipitation is not significant in the arid inland basin. The outflow terms are mainly composed of evaporation and the artificial pumping to divert water from the lake to the Kongqi River. The local water resource authority in YB provided the data of artificial pumping in the simulation period. However, the average evaporation in Bosten Lake, calculated using potential evaporation data or the Penman equation, is not accurate because the temperature and relative humidity exhibit significant differences over the approximately 945.0 km² evaporation surface. Therefore, the observed lake stages were applied to calibrate the evaporation rate in the lake. Figure S2c illustrates the calibration results of the lake level (NSE=0.97) and indicates that the declining trend of the lake level can be adequately captured. Then, the water balance of Bosten Lake can be achieved as shown in Fig. 4. In the simulation period from 2004 to 2013, surface runoff inflow in the Kaidu River represents 97.4 % of the total annual inflow to Bosten Lake. The total annual outflow of the lake consists of 54.9 % lake evaporation and 44.2 % artificial pumping. Therefore, the surface runoff in the Kaidu River is a crucial factor to maintain the water balance of Bosten Lake. The surface runoff inflow can be considered as a significant performance metric to evaluate the water-use practices in the basin. Finally, the well-calibrated model can be employed to integrate SW and GW management.

3.3 Management model

The integrated SW and GW management focuses not only on water resource exploitation, which is subject to social and economic benefits, but also the effect of water exploitation on environment benefits. The study formulated an integrated SW and GW optimization problem including four management objectives: (1) to maximize total water supply rate (f_TWS); (2) to minimize total cost of water delivery from water intake points to water-use destinations (f_TCOST); (3) to maximize the groundwater storage change of the saturated zone between the beginning and end of the management period (f_GSC), which is negative when the storage decreases and vice versa; and (4) to maximize surface runoff inflow from the Kaidu River to Bosten Lake (f_SRI). f_TWS and f_TCOST are defined as the metrics to satisfy the local irrigation water demands while maintaining the lower costs of water use. f_GSC is formulated as the metric indicating the extent of groundwater abstraction, and the greater value shows the preferred situation. f_SRI is defined as evaluating the influence of surface runoff from the Kaidu River on the water balance in Bosten Lake, which contributes about 97.4 % of the total inflow (Fig. 4). As shown in Fig. 5, the decision variables are the total volume of surface water diverted in the main stream of the Kaidu River at the diversion points (DP1–DP7) and groundwater abstraction in the irrigation districts (ID1–ID11).

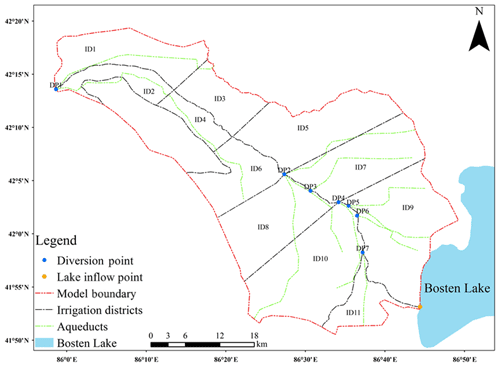
Figure 5 The locations of surface water diversion points and subdomains of irrigation districts for groundwater abstraction.

The formulations of the management model are given as follows:

$$\begin{array}{}\text{(6)}& {\displaystyle }\mathrm{Max}{f}_{\mathrm{TWS}}=\sum _{i=\mathrm{1}}^{N_{\mathrm{p}}}{Q}_{\mathrm{g},i}+\sum _{i=\mathrm{1}}^{N_{\mathrm{d}}}{Q}_{\mathrm{s},i}\text{(7)}& {\displaystyle }\begin{array}{rl}\mathrm{Min}{f}_{\mathrm{TCOST}}& =\sum _{k=\mathrm{1}}^{N_{\mathrm{t}}}\sum _{i=\mathrm{1}}^{N_{\mathrm{w}}}{q}_{\mathrm{g},i,k}{C}_{\mathrm{g}}\left(H_i-h_{i,k}\right)T_k\\ & +\sum _{k=\mathrm{1}}^{N_{\mathrm{t}}}\sum _{i=\mathrm{1}}^{N_{\mathrm{d}}}{q}_{\mathrm{s},i,k}{C}_{\mathrm{s}}{T}_k\end{array}\text{(8)}& {\displaystyle }\mathrm{Max}{f}_{\mathrm{GSC}}=\sum _{j=\mathrm{1}}^{N_{\mathrm{g}}}\left(h_{\mathrm{end},j}-h_{\mathrm{ini},j}\right){\mathrm{Sy}}_j{A}_j\text{(9)}& {\displaystyle }\mathrm{Max}{f}_{\mathrm{SRI}}=f_{\mathrm{gaging}}\left(\mathit{X}\right)\text{(10)}& {\displaystyle }\mathit{X}=\left(Q_{\mathrm{g},\mathrm{1}},Q_{\mathrm{g},\mathrm{2}},\mathrm{\dots },Q_{\mathrm{g},N_{\mathrm{p}}};Q_{\mathrm{s},\mathrm{1}},Q_{\mathrm{s},\mathrm{2}},\mathrm{\dots },Q_{\mathrm{s},N_{\mathrm{d}}}\right)\end{array}$$

where Q_g,i is the total groundwater abstraction rate at the ith irrigation district (m³ yr⁻¹); Q_s,i is total volume of surface water diverted from the ith diversion point (m³ yr⁻¹); N_p is the number of irrigation districts; N_d is the number of diversion points based on the locations of aqueducts; N_t is the number of stress period, including irrigation and non-irrigation periods; N_w is the total number of pumping wells; $q_{\mathrm{g},i,k}$ is the pumping rate at the ith well in the kth stress periods (m³ d⁻¹); C_g is the cost per unit pumping rate per length of hydraulic lift in the case of wells (CNY 0.015 m⁻³ m⁻¹; CNY stands for Chinese yuan); H_i is the surface elevation at the ith pumping well (m); h_i,k is the groundwater level at the ith well in the kth stress period (m); T_k is the length of the kth stress period (d); $q_{\mathrm{s},i,k}$ is the surface water diversion rate at the ith diversion point in the kth stress period (m³ d⁻¹); C_s is the cost per unit diversion volume (CNY 0.055 m⁻³); N_g is the total number of active cells in the model domain; h_end,j, h_ini,j is the groundwater level at the end and beginning of the management period (m); Sy_j is the specific yield at jth active cell; A_j is the area of the jth grid cell (m²); f_gaging outputs the surface runoff in the Kaidu River at the inflow point of Bosten Lake (m³ d⁻¹); and X is a water-use scheme.

The management model consists of a set of constraints given as follows:

$$\begin{array}{}\text{(11)}& {\displaystyle }& {\displaystyle }{Q}_{\mathrm{g},\min }\le Q_{\mathrm{g},i}\le Q_{\mathrm{g},\max }{Q}_{\mathrm{s},\min }\le Q_{\mathrm{s},i}\le Q_{\mathrm{s},\max },\text{(12)}& {\displaystyle }& {\displaystyle }{d}_{\max }\le d_{\mathrm{c}}{h}_{\mathrm{lake}}\ge h_{\mathrm{c}},\text{(13)}& {\displaystyle }& {\displaystyle }\sum _{i=\mathrm{1}}^{N_{\mathrm{p}}}{Q}_{\mathrm{g},i}\ge {\mathrm{TP}}_{\min }\sum _{i=\mathrm{1}}^{N_{\mathrm{d}}}{Q}_{\mathrm{s},i}\ge {\mathrm{TD}}_{\min },\text{(14)}& {\displaystyle }& {\displaystyle }{Q}_{\mathrm{out},i}>\mathrm{0.0},\end{array}$$

where Q_g,min and Q_g,max are the capacity of total groundwater abstraction in specified irrigation districts (Q_g,min is uniformly assumed to be 1.0×10⁶ m³ yr⁻¹ (Mm³ yr⁻¹) and Q_g,max is assumed to be 100.0 Mm³ yr⁻¹); Q_s,min and Q_s,max are the constraints of surface water diversion at diversion points (Q_s,min is 10.0 Mm³ yr⁻¹ at DP1–DP2 and 5.0 Mm³ yr⁻¹ at DP3–DP7; Q_s,max is 400.0 Mm³ yr⁻¹ at DP1, 200.0 Mm³ yr⁻¹ at DP2, and 100.0 Mm³ yr⁻¹ at DP3–DP7); d_max is the maximum drawdown and must be less than the permission value d_c, which is set to 5 m based on the existing management schemes; h_lake is lake level and must be greater than the minimum level h_c (1045 m in this study) to divert lake water to recharge the Kongqi River; TP_min and TD_min are the prescribed minimum water demands of total groundwater abstraction and total surface water diversion to satisfy agricultural development, and they are set to 300.0 and 550.0 Mm³ yr⁻¹ based on the reports from the local water resource authority; Q_out,i represents the outflow of the end reach of the ith stream segment, and it must greater than zero, which means the potential diversion at each diversion point does not exceed the available streamflow in the current segment to avoid significant error of water budgets in the optimization (Wu et al., 2015). This study aims at optimizing the spatial distribution of groundwater abstraction in different irrigation districts and surface water diversion at each diversion point. The management period was set to 1 year with duplicated model inputs and parameters from November 2012 to October 2013 including the non-irrigation and irrigation periods. Then the conjunctive management of SW and GW was implemented based on the multi-objective optimization framework carried out with MATLAB software (http://www.mathworks.com/products/matlab, last access: 1 June 2019).

4 Results and discussion

4.1 Pareto-optimal solutions

This study applied the ε-MOMA to solve the integrated SW and GW management model with four objectives (f_TWS, f_TCOST, f_GSC, and f_SRI) to search for optimal water-use schemes. The algorithm parameters and objective epsilon values are summarized in Table 1. Figure 6 shows a global view of the trade-off surface in the four-dimensional coordinate plot. The management model consists of maximizing the f_TWS, f_GSC, and f_SRI objectives and minimizing the f_TCOST objective. The f_TWS, f_SRI, and f_GSC are plotted on the x, y, and z axes, and f_TCOST is represented with color in Fig. 6. The green arrow indicates the direction of optimality in each objective. It can be observed that the trade-off relationship exists between f_TWS and the other objectives (f_TCOST, f_GSC, and f_SRI). Augmenting the total amount of water supply increases the cost of transporting water with the solutions marked in red and reduces surface runoff inflow to the lake and groundwater storage at the end of the management period. Therefore, regional water resource exploitation conflicts with the socioeconomic and environmental benefits in YB. The scheme before optimization is marked with the square red box in Fig. 6. We can see that the scheme is located above the trade-off surface and exhibits a larger cost value. Thus, the current management scheme is suboptimal and can be regulated to obtain optimal performance.

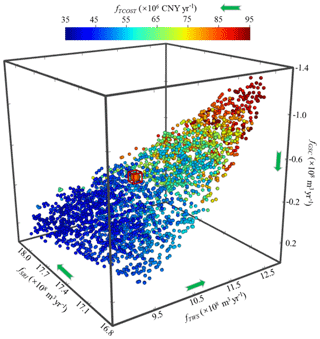
Figure 6 The trade-off surface to the integrated SW–GW management in YB. Each spherical symbol represents a water-use scheme corresponding to specific objective values of the total water supply rate (f_TWS), total cost of water delivery (f_TCOST), surface runoff inflow to the lake (f_SRI), and groundwater storage change (f_GSC). f_TCOST is represented in color to identify the objective value against the others. The green arrow is the direction of better performance for each objective. The scheme before optimization is marked in a square red box.

Table 1 The control parameters of the ε-MOMA and epsilon value of objectives.

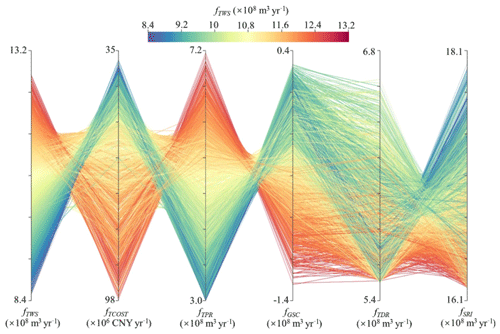
To explain the discrepancy of the Pareto-optimal solutions, the parallel coordinates (PCs) are used to explore the trade-off surface. PC is composed of N equal-spaced parallel axes representing the N-dimensional objective vector. Each polyline intersecting its axis in terms of objective value represents the decision scheme in the Pareto-optimal solutions. Meanwhile, the total pumping rate (f_TPR) and total surface water diversion rate (f_TDR) are added to elucidate the effect of the conjunctive use of SW and GW. In Fig. 7, the segments with higher f_TWS exist for higher f_TCOST and lower f_GSC and f_SRI, showing that increasing water demands requires more financial investment and depletes more surface runoff inflow to the lake and groundwater storage. The findings are consistent with the previous inferences in Fig. 6. Moreover, many slope segments exist between f_TPR and f_GSC, and between f_TDR and f_SRI, which indicates that enlarging groundwater abstraction and surface water diversion are the dominant factors for the depletion of groundwater storage and surface runoff recharge for the lake, respectively. It is noteworthy that the variation trend of f_TPR is very close to the change in f_TWS, while there are obvious differences in the change in f_TDR. The increment of f_TPR can reach 416.0 Mm³ yr⁻¹, whereas the growth of f_TDR is only 114.0 Mm³ yr⁻¹ across all the Pareto solutions. Therefore, groundwater abstraction can be adjusted to satisfy management objectives based on the decision-maker's preference, whereas surface water diversion should be restricted. The reasons behind this bias are that surface water diversion is highly sensitive to the lake level, and the intensive groundwater abstraction augments the river leakage that indirectly causes the decrease in available runoff.

Figure 7 The objective values (y axis) are plotted over management objectives f_TWS, f_TCOST, f_GSC, f_SRI, total pumping rate f_TPR, and total surface water diversion rate f_TDR (x axis). f_TWS is represented in color. The preferred direction for each index is upward.

4.2 Optimized management schedule

The superiority in many-objective optimization is the full exploration of optimal solutions to avoid the decision bias derived from the lower-dimensional objective formulation. The decision-makers can firstly analyze the performance of Pareto solutions in the subproblem (e.g., single or two-objective optimization) and then explore the trade-off solutions using the previous analysis in the higher-order objective space to satisfy the multi-stakeholder benefits. Figure 8a–c illustrate the projections of four-objective Pareto solutions onto two-objective space with the non-dominated front of the subproblem constructed by the f_TWS and other objectives (f_TCOST, f_GSC, and f_SRI). As shown in Fig. 8a–c, solutions 1–3 are the compromise solutions in the Pareto front in the two-objective subproblem, which may be selected by decision-makers with no preference for certain objectives. However, these high-performance solutions in the two-objective optimization exhibit worse performance in the other objective spaces. As illustrated in the plots (Fig. 8), solutions 2 and 3 have higher f_TCOST than Solution 1 in Fig. 8a, solutions 1 and 3 have lower f_GSC than Solution 2 in Fig. 8b, and solutions 1 and 2 show lower f_SRI than Solution 3 in Fig. 8c. Therefore, the decision-makers need to identify the true compromise solution that performs well in the four objectives simultaneously. In this study, Solution 4 is closest to the corresponding objective values of the compromise solutions (solutions 1–3) simultaneously and can be the true compromise solution in the four-dimensional trade-off surface. Additionally, Solution 5 has the largest objective value of total water supply rate in the approximate Pareto front satisfying the constraints of maximum groundwater drawdown and minimum lake level. Solution 6 corresponds to the compromise solution in the non-dominated front of f_GSC and f_SRI, which indicates the perfect performance in the protection of regional groundwater storage and the water balance of the lake.

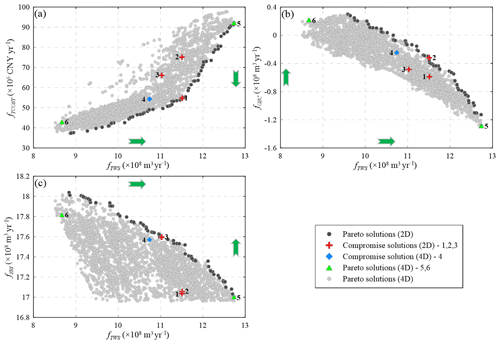
Figure 8 Identification of six interesting solutions (solutions 1–6) from the four-dimensional approximate Pareto set, and the green arrow is the preferred direction for each objective.

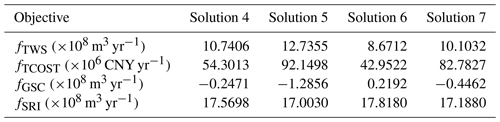
In this study, solutions 4–6 are selected to elucidate the variation of groundwater abstraction and surface water diversion compared to the scheme before optimization (Solution 7). The objective values of selected solutions are listed in Table 2. It can be observed that Solution 4 can achieve a similar total water supply rate while the cost of water delivery can be reduced by 34.4 % compared to Solution 7. The result shows that Solution 7 is suboptimal from the aspect of the expenditure of the water supply. Moreover, the surface runoff inflow to the lake in Solution 4 achieves an increment of 38.2 Mm³ yr⁻¹, and the depletion in groundwater storage obtains a reduction of 19.9 Mm³ yr⁻¹. However, f_GSC of Solution 4 is still less than zero, which demonstrates the loss of groundwater storage compared to the initial state. Therefore, Solution 6 is a preferred water-use scheme from the aspect of the maximization of groundwater storage and the surface runoff inflow to the lake simultaneously. The objectives of Solution 6 in Table 2 show that reducing 143.2 Mm³ yr⁻¹ of f_TWS in the scheme before optimization can achieve an increment of groundwater storage of 21.9 Mm³ yr⁻¹ and augment 63.0 Mm³ yr⁻¹ of surface runoff inflow to the lake. Solution 5 represents the potential water resource exploitation in YB and can augment 26 % of the total water supply rate compared to Solution 7. Interestingly, it can be found that, in solutions 5 and 7, groundwater storage depletion (83.9 Mm³ yr⁻¹) is more rapid than the reduction of surface runoff inflow to the lake (18.5 Mm³ yr⁻¹). Hence, groundwater abstraction is probably the preferred option to provide the resiliency of the water supply in the face of the increased water demands.

Table 2 The objective values corresponding to several solutions.

Figure 9 illustrates the spatial distribution of the pumping rates of the selected solutions in 11 irrigation districts. As shown in Fig. 9a and b, Solution 4 shows that groundwater abstraction in ID3, ID5, and ID7–ID11 can be increased in comparison to Solution 7. It can be noted that the pumping rates in ID7 and ID9 can be greatly elevated due to less exploitation in the past and shallow groundwater depth. The groundwater abstraction in ID1, ID2, ID4, and ID6 should be reduced especially for the pumping rate in ID6 which exhibits an abrupt decline. As shown in Fig. 9c, Solution 5 with the maximization of f_TWS demonstrates that a large amount of groundwater can be abstracted in ID5–ID9 (greater than 80.0 Mm³ yr⁻¹), which implies water managers can implement groundwater abstraction in those districts to satisfy the augmentation of the water supply. In Fig. 9d, Solution 6 is a desirable scheme with the maximization of environmental benefits in groundwater storage and runoff recharge to the lake. The spatial differentiation of groundwater abstraction in Solution 6 is similar to those in the four-dimensional compromise solution (Solution 4). However, in Solution 6, the pumping rates in ID5 and ID8 show obvious decline, which implies that water managers can lower the groundwater abstraction in these regions to achieve more environmental benefits in groundwater storage.

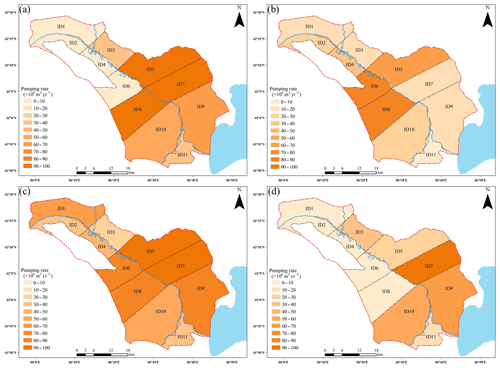
Figure 9 The spatial distribution of the pumping rates in the 11 irrigation districts for the four selected schemes: (a) Solution 4; (b) Solution 7; (c) Solution 5; and (d) Solution 6.

Figure 10 illustrates the spatial patterns of surface water diversion along the main stream of the Kaidu River. As shown in Fig. 10a, seven diversion points (DP1–DP7) with the reduction of runoff are clearly identified. The runoff at 35 km from DP1 exhibits an obvious rise due to the inflow in the tributary. The river runoff at the lake inflow point is the surface runoff inflow to the lake that is the f_SRI objective. It can be observed that the surface runoff in the scheme before optimization (Solution 7) in DP1 shows the abrupt decline more than the Pareto-optimal solutions (solutions 4–6), which respond to the distribution of surface diversion in Fig. 10b. Moreover, Solution 7 has the lowest runoff between DP1 and DP4 even though there exists a slight increase in the lake inflow point. Therefore, a significant increase in surface water diversion in DP1 controls the available runoff in the downstream segments. The water managers should reduce the surface water diversion in DP1 to ensure sufficient runoff in the lower reaches of the Kaidu River for the adjustment of multi-stakeholder benefits. Solution 4 is a compromise scheme that exhibits lower runoff compared to Solution 6 from DP4 to the end of the river due to the larger water diversion in DP4, which triggers the reduction of surface runoff inflow to the lake. Solution 5 is a potential point of regional water resource exploitation in YB and has smaller available runoff than solutions 4 and 6, approximating to more water diversion in the Kaidu River. Figure 10c further demonstrates the interaction of surface water and groundwater along the main stream of the river. The upper segment (Segment I) is a losing segment, which indicates surface water exchange from stream to aquifer, and the middle segment (Segment II) is a gaining segment, which indicates groundwater exchange from aquifer to stream. Then the lower segment (Segment III) turns into a losing segment. It can be noted that Segment I and Segment II have a strong interaction between SW and GW, whereas Segment III exhibits an exchange with a lower leakage rate. As illustrated in Fig. 10d, the distribution of total river leakage shows that Solution 5 with the potential water supply corresponds to the maximum river leakage caused by the maximum groundwater abstraction. The river leakage in solutions 6 and 7 corresponds to lower groundwater abstraction. Consequently, groundwater abstraction is a dominant factor for the interaction of SW and GW in the basin. The river leakage in Solution 4 is clearly larger than Solution 7, which is seemingly undesirable for water managers. However, augmenting groundwater abstraction (131.0 Mm³ yr⁻¹) at the cost of river leakage (30.0 Mm³ yr⁻¹) can lower surface water diversion (67.0 Mm³ yr⁻¹), which is highly sensitive to the runoff inflow to Bosten Lake. Therefore, groundwater abstraction is probably a desirable water-use pattern in YB.

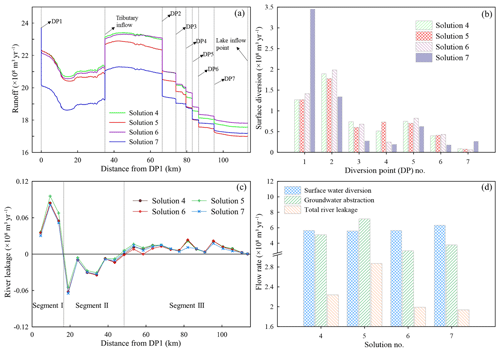
Figure 10 Variation of surface runoff and river leakage along the stem stream of the Kaidu River: (a) the profile of river runoff; (b) the distribution of surface water diversion at the different diversion points; (c) the profile of river leakage; (d) the components of total river leakage, groundwater abstraction, and surface water diversion for several typical solutions 4–7.

4.3 Impacts of runoff change

The Kaidu River plays a crucial role in sustaining the regional water balance in YB, and it flows through Dashankou station (Fig. 2) into the basin. The river supplies the majority of surface water diversion by an aqueduct system for agricultural irrigation and constitutes about 97 % of total annual inflow to Bosten Lake. The runoff in the Kaidu River mainly originates from mountainous precipitation and melting glacier water in the Tianshan mountain region. However, the remarkable climate changes have caused a significant increase in both temperature and precipitation over the past 50 years in Xinjiang (Li et al., 2013). The changing climate probably increased the glacier melt and snowmelt in the upper part of the Kaidu River and then caused the growth of the river runoff between 1999 and 2002, with the highest runoff in 2002 of 5.7×10⁹ m³ yr⁻¹ (Zhou et al., 2015). However, long-term climate change may reduce runoff in the Kaidu River, contributing to the depletion of small or midsize glaciers and the snow line receding in the middle Tianshan mountain region. Li et al. (2012) observed that the surface area of snow in the Kaidu River basin reduced largely between 2000 and 2010. Therefore, it is essential to explore the impact of runoff reduction in the Kaidu River on the regional water resource management for local socioeconomic and environmental development.

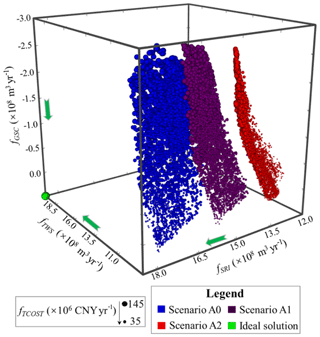
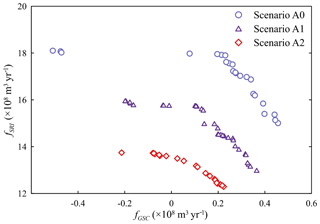
Figure 11 The trade-off solutions under scenarios A0 (maintain current runoff), A1 (reduce the runoff by 10 %), and A2 (reduce the runoff by 20 %). The sphere size indicates the value of f_TCOST. The green arrow is the direction of better performance for each objective.

The last part of our study implemented multi-objective optimization by resetting the runoff inflow at the first diversion point (DP1) in the Kaidu River with the duplicated model parameters and the inputs of source and sink terms. Ba et al. (2018) employed the SWAT model with three RCMs (regional climate models) to analyze the influences of climate change on the streamflow at Dashankou station. The study results show that the annual streamflow will decrease between 2020 and 2049 and reach the largest reduction percentage of 20.1 % and 22.3 % between 2040 and 2049 under RCP4.5 and RCP8.5 scenarios, respectively. We defined three runoff scenarios in relation to climate change in terms of the work of Ba et al. (2018), which are to maintain the current runoff (Scenario A0), reduce 10 % of the runoff (Scenario A1), and reduce 20 % of the runoff (Scenario A2). In the management model, the constraint of lake level is altered to the smaller value (1044.5 m), and maximum groundwater drawdown is reset to 10 m to avoid much more unfeasible solutions in the population, which probably inhibits the convergence of the optimization. Figure 11 shows all Pareto-optimal solutions in the four-dimensional objective space under the runoff scenarios. It is clearly observed that the trade-off surface with current runoff (Scenario A0) is closest to the ideal solution, and those with runoff reduction are farther from the solution. Solutions based on Scenario A2 exhibit the worst performance owing to the greatest extent of runoff reduction. Moreover, we rescaled the objective range to the interval [0, 1] and set the reference point to the objective vector [1, 1, 1, 1] to calculate the HV metric of approximate Pareto solutions under the runoff scenarios. Figure 12 shows the evolution of HV and the number of the generation. Judged from the performance evolution, trade-off solutions under Scenario A0 achieve the largest HV, and those in Scenario A2 have the lowest HV, which shows the solutions are far from the ideal Pareto solution. Therefore, the exploitation extent of surface diversion and groundwater abstraction should be diminished in the face of runoff reduction in relation to climate change. In Fig. 11, the absence of approximate Pareto-optimal fronts when f_SRI is greater than 1801.33 Mm³ yr⁻¹ in Scenario A0, 1596.33 Mm³ yr⁻¹ in Scenario A1, and 1374.58 Mm³ yr⁻¹ in Scenario A2 shows the loss of diversity in the Pareto solutions. The reason is that augmenting f_TWS causes more decline of f_SRI and the lake level compared to no reduction in runoff in Scenario A0, which probably generates a large number of unfeasible solutions violating the constraint of minimum lake level. The finding also shows that runoff in the Kaidu River through YB is a dominant factor controlling the variation in lake level. To investigate the effect of runoff reduction on the environmental benefits, Fig. 13 shows the non-dominated fronts in the f_GSC and f_SRI objective spaces across scenarios A0–A2. The solutions in Scenario A2 are completely dominated by the solutions in scenarios A0 and A1. The solutions in Scenario A0 show the best Pareto optimality. Therefore, runoff reduction results in an obvious loss of environmental benefits. It is noteworthy that f_SRI with scenarios A1 and A2 will be reduced under the similar f_GSC. In the optimization, in order to maximize irrigation water supply, sustaining similar groundwater storage in scenarios A1 and A2 has to come at the cost of river runoff decline to increase surface water diversion. Hence, it is essential for water managers to realize the conflict of the conjunctive use of SW and GW for water resource management in arid inland basins.

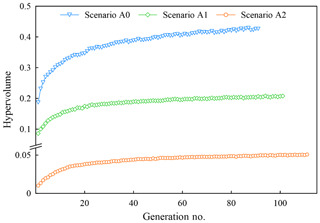
Figure 12 Evolution of the hypervolume metric over the generation number for scenarios A0, A1, and A2.

Figure 13 Non-dominated fronts of scenarios A0, A1, and A2 between the objectives  f_GSC vs. f_SRI.

5 Conclusions

The study proposed a multi-objective optimization framework for the integrated surface water and groundwater management and demonstrated its effectiveness through a spatial optimization of water-use practices for agricultural irrigation in YB, a typical arid inland basin in northwest China. The well-calibrated simulation model with MODFLOW-NWT was developed to model the interaction of surface water (i.e., the Kaidu River and Bosten Lake) and groundwater. Then this study presented a new MOEA, the epsilon multi-objective memetic algorithm (ε-MOMA), and linked it with the numerical model to solve the multi-objective management model. The optimization model is composed of the four conflicting objectives: maximizing total water supply rate; minimizing total cost of transporting water from water intake points to water-use destinations; maximizing the groundwater storage in the aquifer; and maximizing the surface runoff inflow from the Kaidu River to Bosten Lake. An interactive visualization tool was applied to explore the four-dimensional trade-off surface in a global view. Results showed that augmenting water supply caused a larger cost of water delivery, reduced the runoff inflow to the lake, and aggravated the loss of groundwater storage. The two-dimensional compromise schemes selected from the non-dominated fronts between f_TWS and other objectives exhibited significant decision bias in the higher-order objective spaces. Therefore, it is crucial for water managers to explore water management schemes in the multi-objective trade-off surface.

The four-dimensional compromise solution is obtained to investigate the performance of the existing scheme. The result shows that the water-use practices before optimization have to be regulated to avoid unnecessary capital expenditure of transporting water. However, the compromised solution indicates groundwater storage is still decreasing. Thus, water managers may be inclined to adopt the Pareto-optimal scheme satisfying minimum water demands to prevent the loss of groundwater storage and runoff inflow to the lake. In the practical application, water managers should identify specific irrigation water demands and environmental constraints to discover preferred water-use schemes. Moreover, the regulation of groundwater abstraction is more flexible than surface water diversion in the Pareto-optimal solutions, which is an important implication for the resiliency of water resource management. The water-use schemes are subject to the spatial complexity of strong SW–GW interactions. That is to say, it is highly desirable that the integrated management of SW–GW reflects the complex interactions of water resource systems in optimization. The scenarios of runoff change were then generated to investigate the effect of runoff depletion in the Kaidu River on regional water resource management. The findings showed that reducing runoff inflow to the basin could lead to the degradation of Pareto solutions compared with those based on the current runoff scenario. In this light, it is crucial to implement stricter water resource management and explore potential water-saving strategies under future conditions.

The findings are applicable to regional water resource management in other typical arid inland basins with complex groundwater–river–lake interactions and intensive agricultural development. Due to the scarcity of data in the basin-scale full-coupled modeling and the limitations of the simulation model, the predictive uncertainty is inevitable. However, the simulation model can reflect the responses of water resource system to the conjunctive use of SW and GW for agricultural irrigation. The parameter uncertainty can be addressed with the construction of adequate monitoring systems for modeling in the future work. Meanwhile, future research should focus on exploiting fully coupled simulation models to accurately model basin-scale water resource systems and avoid decision bias derived from the limitations of models. Moreover, the deep uncertainty showing the lack of consensus on their underlying probability distribution and consequences (e.g., land-use change, climate change) is a key factor affecting the robustness and reliability of the optimal solutions in the changing world. In the simulation-optimization framework, integrating these factors into the management model to explore optimal schemes is a future research focus.