Historical and future changes in global flood magnitude – evidence from a model–observation investigation

To improve the understanding of trends in extreme flows related to flood events at the global scale, historical and future changes of annual maxima of 7 d streamflow are investigated, using a comprehensive streamflow archive and six global hydrological models. The models' capacity to characterise trends in annual maxima of 7 d streamflow at the continental and global scale is evaluated across 3666 river gauge locations over the period from 1971 to 2005, focusing on four aspects of trends: (i) mean, (ii) standard deviation, (iii) percentage of locations showing significant trends and (iv) spatial pattern. Compared to observed trends, simulated trends driven by observed climate forcing generally have a higher mean, lower spread and a similar percentage of locations showing significant trends. Models show a low to moderate capacity to simulate spatial patterns of historical trends, with approximately only from 12 % to 25 % of the spatial variance of observed trends across all gauge stations accounted for by the simulations. Interestingly, there are statistically significant differences between trends simulated by global hydrological models (GHMs) forced with observational climate and by those forced by bias-corrected climate model output during the historical period, suggesting the important role of the stochastic natural (decadal, inter-annual) climate variability. Significant differences were found in simulated flood trends when averaged only at gauged locations compared to those averaged across all simulated grid cells, highlighting the potential for bias toward well-observed regions in our understanding of changes in floods. Future climate projections (simulated under the RCP2.6 and RCP6.0 greenhouse gas concentration scenarios) suggest a potentially high level of change in individual regions, with up to 35 % of cells showing a statistically significant trend (increase or decrease; at 10 % significance level) and greater changes indicated for the higher concentration pathway. Importantly, the observed streamflow database under-samples the percentage of locations consistently projected with increased flood hazards under the RCP6.0 greenhouse gas concentration scenario by more than an order of magnitude (0.9 % compared to 11.7 %). This finding indicates a highly uncertain future for both flood-prone communities and decision makers in the context of climate change.

1 Introduction

Global hydrological models (GHMs) are critical tools for diagnosing factors of rising trends in flood risk (Munich Re, 2015; Swiss Re, 2015; Miao, 2018; Smith, 2003; Guha-Sapir et al., 2015; CRED, 2015) and can help identify the contribution of changing flood hazard characteristics relative to the changing exposure of human assets to floods. GHMs are also used to project future changes in flood hazard, owing to their ability to simulate streamflow under projected atmospheric forcing. Using GHM simulations, several studies have found more regions showing increasing trends than decreasing trends in flood hazards at the global scale and have attributed these changes to anthropogenic climate change (Dankers et al., 2014; Arnell and Gosling, 2016; Alfieri et al., 2015; Kettner et al., 2018; Willner et al., 2018; Asadieh and Krakauer, 2017). The pattern of increasing trends obtained from GHM simulations is consistent with observations of increases in precipitation extremes (Westra et al., 2013, 2014; Donat et al., 2013; Guerreiro et al., 2018) that have been used by a number of studies as a proxy to suggest that flood hazard may increase as a result of climate change (Alfieri et al., 2017; Pall et al., 2011; IPCC, 2012; Forzieri et al., 2016).

The inference of changes in flood hazard following the same direction as extreme precipitation may be appropriate over regions where rainfall plays the dominant role in flood occurrence (Hoegh-Guldberg et al., 2018; Mallakpour and Villarini, 2015; Mangini et al., 2018), but recent evidence based on instrumental trends in flood hazard suggests it is not necessarily globally applicable (Ivancic and Shaw, 2015; Blöschl et al., 2019). This is due to a “dichotomous relationship” between trends exhibited in extreme precipitation and extreme streamflow (Sharma et al., 2018), highlighted in recent observation-based studies of trends in streamflow magnitudes (Wasko and Sharma, 2017; Do et al., 2017; Hodgkins et al., 2017; Gudmundsson et al., 2019). The hypothesised reason for this potentially inconsistent relationship is the complexity of the drivers of flood risk (Johnson et al., 2016; Blöschl et al., 2017; Do et al., 2019; Berghuijs et al., 2016), with the implication that historical and future changes to flood hazard at the global scale are unlikely to be reflected by changes to a single proxy variable alone, such as annual maximum rainfall. For example, even though trends in extreme flows are highly correlated to changes in extreme rainfall when rainfall plays the dominant role (Mallakpour and Villarini, 2015; Blöschl et al., 2017), snowmelt-related flood magnitude has been found to decrease in a warmer climate, potentially due to a shift in snowmelt timing (Burn and Whitfield, 2016; Cunderlik and Ouarda, 2009). The sign of change is also unclear for locations where antecedence soil moisture plays an important role (Woldemeskel and Sharma, 2016; Sharma et al., 2018), owing to the combined influences of seasonal and annual precipitation, potential evaporation, and extreme precipitation (Bennett et al., 2018; Ivancic and Shaw, 2015; Leonard et al., 2008; Wasko and Nathan, 2019). The sensitivity of changes in streamflow to anthropogenic influences such as urbanisation, dams and reservoir operations, or river morphology (FitzHugh and Vogel, 2011; Slater et al., 2015) further suggests that it is not possible to use trends in extreme precipitation alone to infer changes in flood hazards.

To better understand historical and future trends in streamflow, the emphasis has therefore moved to analysing trends directly in streamflow measurements. Investigations using streamflow observations at global, continental and regional scales (see Do et al., 2017, and references therein) have generally detected a mixed pattern of trends, with some global-scale studies finding more stations having decreasing trends than increasing trends (Do et al., 2017; Hodgkins et al., 2017; Kundzewicz et al., 2004). These conclusions appear prima facie to be inconsistent with model-based evidence, which generally suggests the opposite (more locations showing increasing trends). However, varying sampling strategies, statistical techniques and reference periods make it difficult to derive a common perspective of trends in global flood hazards from a composite of observational and modelling studies. In addition, data coverage limitations (Hannah et al., 2011; Gupta et al., 2014; Do et al., 2018a) remain a barrier to reliably benchmarking trends over some areas such as the flood-prone regions of South and East Asia.

GHMs, with the advantage of better spatial coverage, remain an important line of evidence about historical and future trends. GHMs also enable the possibility to explore the individual roles of atmospheric forcing, land use change and other drivers of change on streamflow trends by including or excluding a specific factor from simulation setting. However, no study has evaluated the performance of GHMs in terms of reproducing trends of streamflow indices, including flood indicators. To date, GHMs have been assessed extensively on their capacity to represent physical features of the hydrological regime, such as streamflow percentiles, the seasonal cycle or the timing of peak discharge (Gudmundsson et al., 2012a; Zaherpour et al., 2018; Beck et al., 2017; Zhao et al., 2017; Veldkamp et al., 2018; Pokhrel et al., 2012; Biemans et al., 2011; Giuntoli et al., 2018). Nevertheless, streamflow variability can be subject not only to long-term changes in atmospheric forcing, but also to climate variability (e.g. inter-annual, inter-decadal) as well as human activities across the drainage basin (Zhang et al., 2015; Zhan et al., 2012). Thus, the GHMs' capacity to represent physical features of a hydrological regime is not necessarily sufficient to determine their performance in simulating characteristics of trends. The absence of a holistic understanding of GHMs' capacity to simulate trends implies that model-based inferences on changes in flood hazards are highly uncertain (Dankers et al., 2014), limiting the usefulness of GHMs in developing flood adaptation policy in a warming climate.

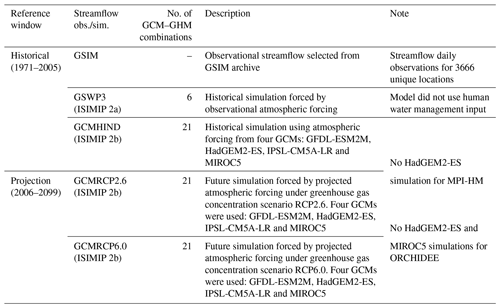
To address this limitation and further improve GHMs' applicability, this study provides the first comprehensive evaluation of GHMs' capacity in simulating historical trends of a flood hazard indicator. This study also explores the uncertainty in developing projected changes in flood hazards using an ensemble with GHMs and general circulation models (GCMs). Specifically, we used the Global Streamflow Indices and Metadata (GSIM) archive (Do et al., 2018b; Gudmundsson et al., 2018a), to date the largest possible global streamflow database, to identify observed changes in annual maxima of 7 d streamflow (MAX7 index) over the 1971–2005 period. Streamflow simulations, available through the Inter-Sectoral Impact Model Intercomparison Project ISIMIP phase 2a and 2b (Warszawski et al., 2014), were used to derive historical (1971–2005) and projected (2006–2099) changes in the MAX7 index simulated by GHMs. Observed and simulated trends were then analysed to achieve three research objectives.

• Objective 1: to evaluate the capacity of GHMs to reproduce observed trends of an indicator of flood hazard (MAX7). Of particular interest is the reconciling model- and observation-based inferences of historical changes in flood hazard at the global and continental scale.

• Objective 2: to determine the representativeness of observation locations (streamflow gauges) in GHM simulations. This objective is motivated by the sparse coverage of streamflow observations over several regions (e.g. South and East Asia), which could lead to biased inferences of observation-based studies over large spatial domains wherever gauges are not a representative sample.

• Objective 3: to assess the implication of model uncertainty for projections of flood hazard, focusing on the uncertainty of the mean or the spread of trends together with the spatial pattern of trends in annual maximum streamflow. We are also curious about whether the regions consistently projected with an increase in flooding have been adequately observed by the global observation networks.

2 Data and methods

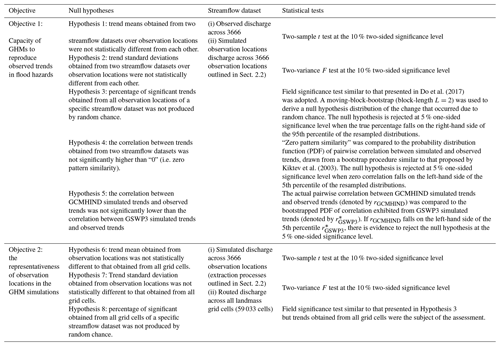
This section summarises the workflow to achieve three objectives of this study (Fig. 1). Observed and simulated streamflow (Sect. 2.1) were used to estimate the magnitude and significance of changes in an indicator of flood hazards (Sect. 2.3). To enable an observation–model comparison, a procedure was developed to extract streamflow for a subset of observed catchments that meet data quality criteria (Sect. 2.2). A range of statistical techniques were then applied to trends of an indicator of flood magnitude (Sect. 2.4) to assess (i) the capacity of GHMs to reproduce characteristics of observed trends, (ii) the representativeness of observation locations in GHM simulations and (iii) the implication of simulation uncertainty on projected trends (results are discussed in Sect. 3.1–3.3).

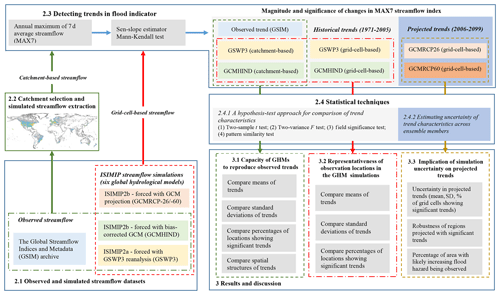
Figure 1 Flowchart of the datasets and methodologies used to achieve three research objectives of this study.

2.1 Observed and simulated streamflow datasets

The GSIM archive is used as daily observational discharge for this analysis. Daily streamflow simulations available through the ISIMIP are used, with historical simulations (forced with observational climate in ISIMIP2a and bias-corrected climate model outputs in ISIMIP2b) spanning from 1971 to 2005 (Gosling et al., 2019) and future simulations (ISIMIP2b) covering the 2006–2099 period (Frieler et al., 2017). Six GHMs are considered: H08 (Hanasaki et al., 2008a, b), LPJmL (Schaphoff et al., 2013), MPI-HM (Stacke and Hagemann, 2012), ORCHIDEE (Guimberteau et al., 2014, 2018), PCR-GLOBWB (Wada et al., 2014; Sutanudjaja et al., 2018) and WaterGAP2 (Müller Schmied et al., 2014, 2016). These models were selected as they have provided discharge data within phases 2a and 2b of ISIMIP at the time this study began (June 2018). A summary of the similarities and differences across participating GHMs is provided in Sect. 1.2 in the Supplement.

To assess the model structural uncertainty across GHMs, trends in streamflow extremes simulated under observational atmospheric forcing, available through the Global Soil Wetness Project Phase 3 (GSWP3) reanalysis (Kim, 2017), were compared to observed trends. The influence of the high uncertainty in climate models (Kumar et al., 2013; Kiktev et al., 2003) on streamflow simulations was assessed by comparing observed trends and trends simulated when using atmospheric forcing from four GCMs for the historical period (“hindcast” simulations; hereafter referred to GCMHIND atmospheric forcing). These GCMs were bias-corrected but their simulations have different sub-monthly, inter-annual and decadal variability, and thus the hindcast simulations reflect both GHM and GCM uncertainty. To quantify the implication of model uncertainty for future projections of flood hazard, trends simulated under projected climate change by the end of this century (using the same four GCMs) were also assessed for two greenhouse gas concentration scenarios, RCP2.6 (hereafter referred to GCMRCP2.6 atmospheric forcing) and RCP6.0 (hereafter referred to GCMRCP6.0 atmospheric forcing). As a result, four simulation settings were used in this study, denoted by the atmospheric forcing; an overview is given in Table 1. These settings comprise two historical runs (GSWP3 and GCMHIND runs) and two future runs (GCMRCP2.6 and GCMRCP6.0), collectively amounting to a total of 69 simulations (see Table S3 with full list of simulations).

Table 1 Summary of streamflow observation and simulation datasets used in this study. GSIM was used as the observed streamflow database. Streamflow simulations were obtained from six GHMs (H08, LJPmL, MPI-HM, ORCHIDEE, PCR-GLOBWB and WaterGAP2). One observational atmospheric forcing dataset (GSWP3) and outputs of four GCMs were used as input for streamflow simulations.

For GSWP3 simulations, a preliminary analysis (see Sect. 4 in the Supplement) shows that both “naturalised runs” (i.e. human water management not taken into account) and “human impact runs” (i.e. human water management inputs were used) exhibit similar characteristic of trends in MAX7 index. Some potential reasons for negligible impacts of human water management are the spatial distribution of stream gauges (may be biased toward regions with insignificant changes in water management during the 1971–2005 period), or the inclusion of small catchments (more that 3000 catchments with reported area less than 9000 km²); thus, floods are more sensitive to changes in climate forcing relative to the accumulated basin-wide influence of human impacts. Naturalised runs were therefore chosen, since this setting is available for more GHMs (six) when compared to the human impact setting (four). Although significant efforts were made by ISIMIP to keep the setting across simulations as consistent as possible, there were some differences in model versions and input data (e.g. WaterGAP2.2 (ISIMIP2a) was used in ISIMIP2a while WaterGAP2.2c was used in ISIMIP2b; ORCHIDEE (Guimberteau et al., 2014) was used in ISIMIP2a while ORCHIDEE-MICT (Guimberteau et al., 2018), with improvements on high latitude processes, was used in ISIMIP2b). Although the influence of versioning is minor for WaterGAP2, the potential effects of technical discrepancies cannot be checked in the context of this study, as not all required simulations are readily available (see our discussion in Sect. 3.3 in the Supplement). In addition, owing to technical requirements across GHMs, different models do not have the same set of coastal cells, which may lead to some minor effect to the statistics when averaged across all simulation grid cells.

2.2 Catchment selection and simulated streamflow extraction for observation–model comparison

To enable an observation–model comparison, simulated discharge needs to be extracted from gridded model output. Large-scale hydrological models, however, generally do not simulate discharge accurately over small-to-medium size catchments due to the coarse resolution of river network datasets in their routing schemes (Hunger and Döll, 2008). To address this limitation, previous GHM evaluations usually selected large catchments (a threshold of 9000 km² was adopted, approximating the size of a 1^∘ longitude–latitude grid cell), and routed discharge (unit: m³ s⁻¹) at the outlet of the catchment was used as simulated streamflow for a specific catchment (Zhao et al., 2017; Veldkamp et al., 2018; Zaherpour et al., 2018, 2019; Liu et al., 2017). For evaluation studies that used relatively small catchments (e.g. area less than 9000 km²), the un-routed runoff simulation (unit: mm d⁻¹) was extracted while observed discharge was converted to runoff using catchment area prior to comparison (Gudmundsson et al., 2012b; Beck et al., 2017). To increase the sample size for the model–observation comparison (the first objective), the present study used both (i) daily un-routed runoff for small catchments and (ii) daily routed discharge simulations for large ones, and thus two extraction procedures were adopted. A summary of these extraction procedures is provided below while detailed technical descriptions are provided in Sect. 2 in the Supplement.

• For catchments with an area from 0 to 9000 km²: un-routed runoff (mm d⁻¹) was extracted and then converted into discharge (m³ s⁻¹) by multiplying averaged runoff with catchment area reported in the station metadata. Specifically, catchment boundaries were superimposed on the GHM grid to obtain the weighted-area tables, which were then used to derive averaged runoff from the un-routed runoff simulation. To avoid double-counting runoff from the same grid points, runoff for catchments that share similar weighted-area tables (i.e. similar simulated streamflow would be extracted – see Sect. 2 in the Supplement for a detailed description) was averaged (using catchment areas as weights) and a single “averaged time series” was used in place of the runoff from the component catchments.

• For catchments with an area greater than 9000 km²: the “discharge output” approach (Zhao et al., 2017) was adopted to extract routed discharge (m³ s⁻¹) from the GHM cell corresponding to the outlet of each catchment.

To ensure sufficient data are available for historical trend analysis, only GSIM stations with at least 30 years of data available during the 1971–2005 period were considered (each year having at least 335 d of available records, implying that annual maximum of a specific year is identified only when more than 90 % of the daily record is available). These relatively strict selection criteria also enable a comparison between this study and preceding observation-based investigations (Gudmundsson et al., 2019; Hodgkins et al., 2017). As catchment boundary shapefiles (Do et al., 2018a) were used to extract simulated streamflow for small catchments, stations were further filtered using two criteria: (i) availability of reported catchment area and (ii) catchment boundary being accompanied by a “high” or “medium” quality flag (i.e. the discrepancy between reported and estimated catchment area is less than 10 %).

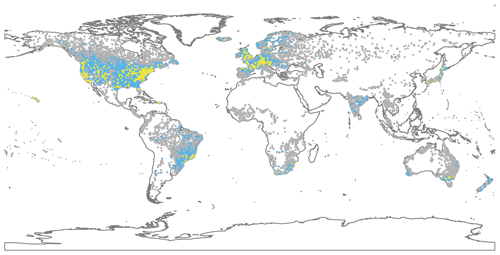
Figure 2 Locations of 3666 streamflow observations (blue dots: 3024 non-averaged time series; yellow dots: 624 averaged time series, where geographical coordinates were averaged from all component gauging coordinates) selected from GSIM archive for the model–observation comparison. Grey dots indicate GSIM time series that were removed due to insufficient data availability or quality.

A total of 4595 stations satisfied the quality selection criteria, of which large catchments (i.e. area greater than 9000 km²) where no suitable grid cell could be identified were further removed (11 catchments). For cases of two or more small catchments (i.e. area less than or equal to 9000 km²) with similar weighted-area tables, the “averaged time series” (using catchment areas as weights) was calculated. A total number of 1542 time series fell in this category and were aggregated into 624 “averaged time series”. Figure 2 shows the spatial distribution of the final dataset for model–observation comparison, containing data for 3666 locations (3042 non-averaged time series and 624 averaged time series). The majority of available catchments are located in North America and Europe, with some regions over Asia, Oceania and South America also covered.

2.3 Detecting trends in annual maximum streamflow

For each streamflow dataset, daily discharge was smoothed to 7 d averages to reduce variability in simulated streamflow, which can arise from the coarse routing parameters of GHMs (Dankers et al., 2014). The annual maximum time series of 7 d averaged discharge (labelled as the MAX7 index in the GSIM archive) was then derived to represent peak flow events. For gridded datasets, the “centre averaged approach” (e.g. averaged streamflow of 7 January is the mean value of 4–10 January) was used (the common setting of the CDO software, freely available at https://code.mpimet.mpg.de/projects/cdo, last access: 1 March 2020), and the MAX7 time series was therefore derived for each GSIM station using this same approach. As a result, the derived value of the MAX7 index is slightly different to the value available in the online version of GSIM (Gudmundsson et al., 2018b), which applied a “backward-moving average” technique (e.g. averaged streamflow of 7 January is the mean value of 1–7 January). Our preliminary analysis (not shown), however, indicated that this difference did not lead to substantial changes in the key findings (i.e. similar spatial composition between increasing and decreasing trends).

The magnitude of trends in the MAX7 index at a specific catchment or grid cell was quantified using the normalised Theil–Sen slope (Gudmundsson et al., 2019; Stahl et al., 2010), and the results are expressed in percentage change per decade. The significance of the local trend was assessed using a Mann–Kendall test at the 10 % two-sided significance level (Wilks, 2011). The null hypothesis (no trend) is rejected if the two-sided p value of the test statistic (Kendall's τ) is lower than 0.1, while the direction of the trend (i.e. increasing or decreasing) was determined using the sign of τ.

2.4 Statistical techniques

To explore GHMs' capacity to simulate observed trends and the implication of model uncertainty for projected trends, trends in streamflow extremes obtained from GSIM (observed trends) and ISIMIP simulations (simulated trends) are analysed. The observed trends were available for 3666 observation locations. Simulated trends were available for all 59 033 GHM grid cells (estimated from routed discharge of each grid cell; Antarctica and Greenland were removed). To enable a model–observation comparison, we also extract a subset of simulated trends over the 3666 observation locations (described in Sect. 2.2).

2.4.1 A hypothesis-test approach for comparison of trend characteristics

A range of hypothesis tests (summarised in Table 2; GSWP3 simulations were used to assess GHM uncertainty while GCMHIND simulations were used to assess the combined GCM–GHM uncertainty) was applied to address the first two objectives, which require comparing trend characteristics exhibited from different streamflow datasets. Four characteristics of trends were assessed.

• Trend mean: the mean (percentage change per decade) of trends in streamflow extremes across all gauge- or cell-based time series over a spatial domain. A hypothesis test was adopted to assess whether the trend means exhibited from two specific streamflow datasets (e.g. model vs. observed) are significantly different from each other.

• Trend standard deviation: the standard deviation (percentage change per decade) of trends in streamflow extremes across all gauge- or cell-based time series over a spatial domain. A hypothesis test was adopted to assess whether the trend standard deviations exhibited from two specific streamflow datasets are significantly different from each other.

• Percentage of significant trends (%): the percentage of trends in a domain that are statistically significant, with gauge- or cell-based significance calculated using the Mann–Kendall test at the 10 % significance level. To assess whether the percentage of significant (increasing or decreasing) trends exhibited from a specific streamflow dataset is produced by random chance, a field significance test (Do et al., 2017) was adopted (described in Table 2).

• Trend spatial pattern: the spatial distribution of trends in streamflow extremes over a spatial domain. Pearson's correlation (r statistic) (Galton, 1886; Kiktev et al., 2003) between trends of MAX7 index obtained from two datasets was used as a measure of similarity in the trend spatial structure. The hypothesis test (pattern similarity test) was adopted to assess whether (i) the correlation between simulated trends introduced by GHMs and observed trends is significantly higher than zero, and (ii) the correlation between trends simulated under hindcast atmospheric forcing and observed trends is significantly lower than that between trends simulated under observational atmospheric forcing and observed trends.

Table 2 Hypothesis tests conducted to address the first two objectives.

2.4.2 Estimating uncertainty of trend characteristics across ensemble members

The third and final objective, which focused on the implications of GCM–GHM uncertainty on projected changes in flood hazard, was addressed by quantifying the spread of trend characteristics (i.e. trend mean, trend standard deviation and percentage of significant trends) exhibited from routed discharge projections under two representative concentration pathways.

The spatial uncertainty of projected trends (GCMRCP2.6 and GCMRCP6.0) was also quantified by calculating intra- and inter-model correlation of the trend patterns across all ensemble members available under the two projections. Intra-model correlation represents spatial uncertainty introduced by the GCM and was calculated from simulated trends introduced by the same GHM (using different simulated atmospheric forcing). Inter-model correlation represents the combined GCM–GHM spatial uncertainty and was calculated for each pair of simulated trends that were (i) introduced by the different GHMs and (ii) forced with different projected atmospheric forcing.

To assess the robustness of GHMs in projecting changes in flood hazard, each grid cell available in the discharge simulation grid was then categorised into one of the five “flood-risk” (here “flood-risk” level is defined as the number of ensemble members projecting significant increasing trends) groups based on the number of GCMRCP2.6 and GCMRCP6.0 simulation members projecting a significant increasing trend (Group 1: no members, Group 2: from 1 to 5 members, Group 3: from 6 to 10 members, Group 4: from 11 to 15 members and Group 5: from 16 to 18 members).

Finally, to assess whether locations projected with an increasing trend by the majority simulations are adequately monitored, each GSIM gauge was sorted into one of these five groups based on the gauge's geographical coordinates. The allocation of gauges to these groups was then analysed to determine whether the most comprehensive global database of daily streamflow records to-date was evenly distributed across the five “flood risk regions”. An inadequate coverage of stream-gauge networks over high-risk regions indicates potentially high vulnerability to future changes in flood hazards, as insufficient data are available to inform decision makers.

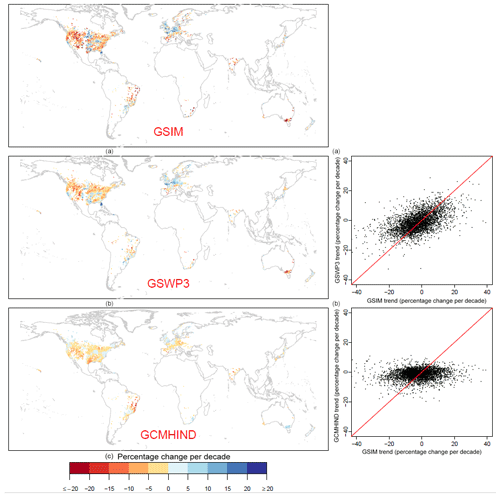
Figure 3 Normalised Theil–Sen slope for historical trends in flood magnitude (MAX7 index) exhibited over 3666 locations across three streamflow datasets (a: GSIM; b: GSWP3; c: GCMHIND). Multi-model average is shown for simulated trends. Trend is expressed in percentage change per decade. Scatter plots between trends obtained from GSIM and GSWP3/GCMHIND simulated streamflow are provided in (d) and (e).

3 Results and discussion

3.1 Capacity of GHMs to reproduce observed trends in flood hazards

Visual inspection of the normalised Theil–Sen slope across the GSIM time series (Fig. 3a; regional maps provided in Fig. S4) shows a spatial pattern that is consistent with recent findings on trends in observed flood magnitude (Mangini et al., 2018; Do et al., 2017; Mallakpour and Villarini, 2015; Gudmundsson et al., 2019; Burn and Whitfield, 2018; Ishak et al., 2013). Specifically, decreasing trends tend to dominate Asia (most stations located in Japan and India), Australia, the Mediterranean, the western and north-eastern US, and northern Brazil, while increasing trends appear mostly over central North America, southern Brazil and the northern part of western Europe (including the UK). Note that the observation locations are not evenly distributed (86 % in North America and Europe), and thus the confidence of this assessment varies substantially across continents.

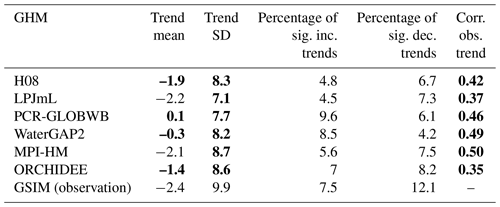
Table 3 Characteristics of trends in the MAX7 index over the 1971–2005 period across 3666 locations for GSIM observed trends and GSWP3 simulated trends (six GHMs available). Trend mean and trend standard deviation are expressed in percentage change per decade. Correlation was obtained from GSIM observed trends and GSWP3 simulated trends for each GHM. Boldface texts represent values that reject the null hypotheses outlined in Table 2 (hypothesis 1 to 4).

The multi-model average of GSWP3 simulated trends (trends simulated under observational atmospheric forcing; Fig. 3b and d) has generally good capacity to reproduce spatial patterns of observed trends. The multi-model average of GCMHIND simulated trends (trends simulated under hindcast atmospheric forcing; Fig. 3c and e), however, could not reproduce some spatial agglomerations of trends in streamflow maxima (e.g. the decreasing trends in south-eastern Australia, increasing trends over north-eastern Europe). This feature indicates the inconsistent climate variability between GCMs and the real world, suggesting GCM climate forcing cannot account for observed trends at sub-continental scale. In addition, GCMs uncertainty can potentially contribute to this inconsistency. Interestingly, the multi-model average of both GSWP3 and GCMHIND simulations generally exhibits a lower magnitude of changes (i.e. closer to “zero change”) compared to the observed trends. This feature is more prominent in GCMHIND (21 simulations available) compared to GSWP3 (six simulations available) and can be explained by two possibilities. The first possible explanation is the nature of averaging, which tends to smooth out variability in trend magnitude across ensemble members, leading to a relatively “close to zero” change across the globe (given that each GCM has stochastic decadal climate variability, so that averaging results forced by GCMs tends to cancel trends). An alternative explanation is that individual simulations also exhibit a lower magnitude of change relative to observation. As Fig. 3 is not sufficient to evaluate the latter possibility, a more detailed comparative analysis between observed trends and individual simulated trends using both historical climate forcings (via GSWP3) and GCM hindcasts was conducted. Specifically, four characteristics of trends in extreme flows (i.e. trend mean, trend standard deviation, percentage of significant trends and trend spatial structure) were assessed for individual simulations and the results are reported in following sections. At the global scale, GSIM observed trends exhibit a mean and standard deviation of −2.4 % and 9.9 % change per decade over the 1971–2005 historical period. Furthermore, there are 7.5 % (12.1 %) stations showing significant increasing (decreasing) trends (detected by the Mann–Kendall test at the 10 % significance level). These numbers, however, are not statistically significant at the global scale.

Table 3 shows the results of the global model–observation comparison using GSWP3 simulated trends across the six GHMs. Compared to observed trends, most simulated trends have a significantly higher global trend mean at the observed locations and lower trend standard deviation. The percentage of locations showing significant trends varies substantially across simulations, but the values were not statistically significant. All GHMs demonstrate low-to-moderate capacity in simulating the spatial pattern of trends (spatial correlation coefficients range from 0.35 to 0.50, indicating that GSWP3 simulated trends account for between 12 % and 25 % of the cross-location variability in the observed trend signal). There is, however, a notable difference in terms of the overall sign of trends simulated by each GHM. This feature indicates that using different GHMs can lead to different interpretations about the overall change in flood hazard at the global scale, despite having a common boundary forcing. Therefore, the “closer to zero” trends of ensemble averages (illustrated in Fig. 3) likely reflect the implication of averaging rather than a systematic bias of GHMs toward a low magnitude of change. As an implication, ensemble averages, though useful, should not be used as the sole reason to infer changes in floods, as it may undermine the actual magnitude of simulated trends. As a result, the following analyses will report the full range (and mean) of each trend characteristic estimated across all ensemble members to communicate the uncertainty underlying the results.

Table 4 Characteristics of trends in the MAX7 index over the 1971–2005 period across 3666 locations for GCMHIND simulated trends. Trend mean and trend standard deviation are expressed in percentage change per decade. Intra-model averages of trend characteristics are shown for each GHM. Values in the parentheses show the number of simulations rejecting the null hypothesis (from 1 to 4) outlined in Table 2 (out of four GCMs). Multi-model minimum, maximum, and average values together with those exhibited from GSIM are also provided.

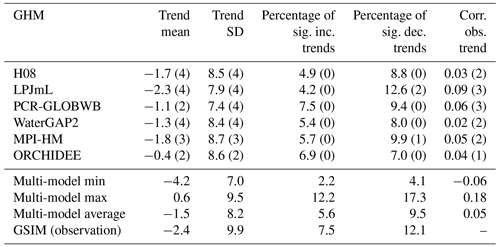
Table 4 provides the results of the model–observation comparison using GCMHIND simulated trends (intra-model averages are shown while results of individual simulations are reported in Sect. 4 in the Supplement). Similar to GSWP3 trends, intra-model averages (i.e. calculated from simulations of one GHM) of GCMHIND trends tend to have a higher global mean and lower trend standard deviation than observed. The composition between the percentages of locations showing significant trends varies substantially across simulations and statistical significance was found only for decreasing trends in 3 out of 21 simulations (2 LPJmL simulations and 1 MPI-HM simulation). The multi-model ranges encapsulate the observed trend mean and percentage of significant trends, while the observed trend standard deviation is clearly above the range exhibited from all GCMHIND simulations. The significantly lower simulated trend standard deviation can be partially attributable to the coarse resolution of GHMs' atmospheric and land surface inputs, which may not sufficiently reflect the variation of hydrological processes across small-to-medium catchments.

Among 21 GCMHIND simulations, the “zero similarity” hypothesis (hypothesis 5) was rejected over 13 simulations, indicating that GCM–GHM ensemble members possess some capacity to simulate the spatial structure of observed trends in streamflow extremes. The correlation between GCMHIND simulated trends and GSIM observed trends, however, is significantly lower than that exhibited from GSWP3 simulated trends across all GHMs (reported at Table 3). The results of the similarity assessment are illustrated for a single GHM (H08, as the results were similar for other GHMs) in Fig. 4, where the correlation between observed trends and GSWP3 simulated trends is significantly different from zero. In contrast, the correlation between observed trends and each of the simulated trends under hindcast atmospheric forcing (GCMHIND simulations) is much lower, with two of the four not being statistically higher than zero. These results confirm the substantial influence of atmospheric forcing on the simulated trend pattern relative to the GHM's structure.

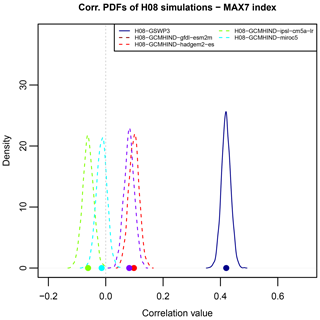
Figure 4 Model–observation correlation between observed trends and simulated trends across all simulations (GSWP3 and four GCMHIND simulations) of a single model (H08; similar results for other GHMs). Coloured dots indicate actual correlation between a specific simulated trend pattern and observed trend pattern across 3666 locations. Colour lines represent the PDFs of correlation between simulated trend pattern and observed trend pattern obtained through a bootstrap resampling procedure (B=2000).

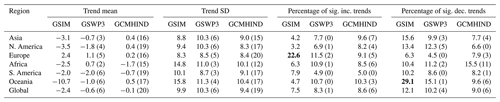
Table 5 Characteristics of trends exhibited from the GSIM/GSWP3/GCMHIND streamflow dataset at the continental scale (each observation location of 3666 sites was sorted into one of the six continents). For simulated trends, only the multi-model average is shown for each region. Trend mean and trend standard deviation are expressed in percentage change per decade. Values in the parentheses show the number of simulations rejecting the null hypothesis described in Table 2 (up to 6 for GSWP3 simulations and 21 for GCMHIND simulations). For GSIM, field significance of increasing and decreasing trends was highlighted by boldface texts. For GSIM, field significance of increasing and decreasing trends was highlighted by boldface text.

To further quantify changes at the regional scale, a model–observation comparison (identical to that at the global scale) was conducted over six continents, and the results are summarised in Table 5 (multi-model averages are shown). The trend mean exhibited from GSIM ranges from −10.7 % (Oceania) to 2.4 % change per decade (Europe), while trend standard deviation ranges from 8.3 % (Europe) to 15.8 % change per decade (Oceania). The percentage of significant increasing (decreasing) trends exhibited from GSIM ranges from 3.2 % to 22.6 % (from 6.3 % to 29.1 %), and the composition of significant trends across the six continents is consistent with a previous investigation (Do et al., 2017). The observed percentage of significant trends is found to be above random chance for Europe (increasing flood magnitude) and Australia (decreasing flood magnitude), and this feature is captured quite well by GSWP3 simulated trends, with at least half of the simulations confirming field significance detected from GSIM. Trend characteristics simulated by GHMs at continental scale confirm some important findings from global-scale assessments, suggesting substantial uncertainty of trends in streamflow extremes introduced by GHMs at the continental scale:

• both GSWP3 and GCMHIND simulations generally exhibit a higher trend mean and lower trend standard deviation compared to the observed trend at the continental scale (see also Sect. 3.1 in the Supplement);

• GCMHIND simulations generally exhibit lower capacity to reproduce trend characteristics relative to GSWP3 simulations due to the combined GCM–GHM uncertainty.

For GSWP3 simulations, the spatial correlation is weakest in Asia, as no simulation rejects the null hypothesis of “zero similarity”, while the spatial correlation is strongest in Oceania (mainly southern Australia; correlation of 0.63). Oceania, however, exhibits the highest model–observation discrepancy in trend mean and trend standard deviation, indicating the capacity of a given GHM in terms of the trend spatial structure is not necessarily consistent with its performance in terms of the mean and spread of trends.

GCMHIND trends also suggest the opposite composition between percentages of significant trends compared to GSIM trends (e.g. simulated trends suggest more locations showing significant increasing trends while observed trends suggest the opposite). Among six continents, GCMHIND trends exhibited the lowest correlation (−0.14) in Oceania, whereas GSWP3 suggested the strongest correlation in this continent. This assessment further indicates the substantial impact of atmospheric forcing relative to GHM model structure on the simulated trends in high flow events. It is informative to note that this result is expected, as GCMs (despite having been bias-corrected) generally have low capacity in reproducing the timing of wet or dry periods or the spatial distribution of climate extremes (Kiktev et al., 2007), and GHMs are likely to inherit these limitations when using GCMs' outputs as climate forcing data.

3.2 Determining the representativeness of observation locations in the GHM simulations

To assess the representativeness of observation locations in GHM grid cells, trend characteristics obtained from all simulated grid cells were compared to those estimated from the observation locations (3666 sites globally). For GSWP3 simulations, the results suggest a significant difference between trend characteristics from all model grid cells compared to those obtained from the observation locations (Table 6; multi-model averages shown). This feature is consistent at both global and continental scales, including North America and Europe – the continents with the best stream-gauge density. Specifically, the trend mean tends to get closer to zero, while the trend standard deviation obtained from all grid cells tends to be higher than that over observation locations. The difference between the percentages of significant increasing and decreasing trends across all grid cells also gets smaller. For instance, the percentage of observation locations showing significant increasing (decreasing) trends over Oceania is 3.7 % (22.1 %) for GSWP3 multi-model averages (reported in Table 5), while the corresponding values are 10.7 % (15.1 %) when all grid cells are considered (reported in Table 6). Additionally, field significance for increasing (decreasing) trends is detected in two (four) out of six simulations over Oceania, while the same feature could not be detected over the observation locations. These findings confirm that trends exhibited from observation locations are not a representative sample of trends obtained from all simulation grid cells, which has also been suggested through Fig. 2. As a result, a common model–observation picture of changes in global flood hazard remains elusive. To enable a holistic perspective of changes in extreme flows, it is therefore crucial to improve not only models' capacity, but also data accessibility and expand streamflow observational networks to ensure unbiased samples are available for large-scale investigations.

Table 6 Characteristics of simulated trends across all grid cells at both continental and global scales (multi-model averages are shown). For each simulation, cell-based trend mean and trend standard deviation were compared to those of gauge-based trends (reported in Table 4). Values in parentheses represent the number of simulations that reject the null hypothesis described in Table 2 (up to 6 simulations for GSWP3 and 21 simulations for GCMHIND). GSIM results are also provided for reference. For GSIM, field significance of increasing and decreasing trends was highlighted by boldface text.

The findings using GCMHIND simulations are similar in terms of the trend mean (closer to zero) and trend standard deviation (higher) across all grid cells relative to the observation locations. Across all land areas, the composition of the percentages of land mass showing significant trends exhibited by GCMHIND simulations contradicts that obtained from the GSWP3 simulations for many continents. For example, GSWP3 simulations suggest more land areas showing significant decreasing trends than increasing trends over Asia and Oceania while GCMHIND simulations indicate an overall increasing change in extreme flows over the same continents. This feature further confirms the importance of uncertainty in atmospheric forcing in driving the spatial structure of the simulated trends, which will be explored further in the next section.

3.3 The implication of simulation uncertainty on the projection of trends in flood hazard

This section focuses on the uncertainty in simulated trends under projected climate forcing at the global scale. For MPI-HM (no simulation for HadGEM2-ES forcing), streamflow was only simulated across the main stream network (approximately 45 % of the global land grid cells), and thus three simulations of this GHM were removed from the analysis. As a result, only 18 ensemble members were used to explore the uncertainty in projected trends (GCMRCP2.6 and GCMRCP6.0 – trends estimated for the 2006–2099 period and all cells were considered).

Table 7 The uncertainty in the characteristics of projected trends (GCMRCP2.6 and GCMRCP6.0) across 18 members at the global scale (five GHMs). Trend mean and trend standard deviation have unit of %-change per decade. At-site significance of trend was identified using Mann–Kendall test at 10 % level and the percentage of grid cells showing significant increasing and decreasing trends was reported (no field significance test was conducted). Intra-model average value of each metric across is shown for each GHM (numbers of simulations are provided in the first column).

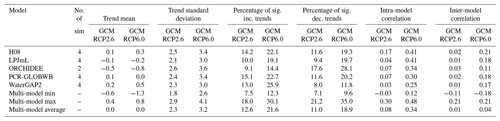
Table 7 shows a relatively low spread of the global trend mean (ranging from −1.3 % to 0.8 % change per decade; multi-model average of 0.0 % change per decade for both GCMRCP2.6 and GCMRCP6.0) and trend standard deviation (ranging from 1.8 % to 4.1 % change per decade) across ensemble members. LPJmL and ORCHIDEE generally suggest a decreasing trend at the global scale, evident through the negative global mean and more grid cells showing significant decreasing trends. The standard deviation of trends in future simulations is substantially lower than the historical run (reported in Table 6). This feature is potentially due to the capacity of longer time series in capturing the inter-decadal variability of the streamflow regimes, with both dry and wet periods being considered (Hall et al., 2014). Projected trends under the RCP2.6 scenario generally have lower mean and lower standard deviation closer to zero compared to those introduced by the RCP6.0 scenario, reflecting the nature of an ambitious “low-end warming” scenario, when anthropogenic climate change reaches its peak in the middle of the 21st century followed by a generally stable condition.

Interestingly, although most models suggest relatively moderate changes in the global trend mean, the composition between percentages of grid cells showing significant trends varies substantially, ranging from 7.5 % (7.1 %) to 30.1 % (35.0 %) for significant increasing (decreasing) trends at the 10 % level, with RCP6.0 generally exhibiting higher values. This finding indicates that inferences of changes focusing on global averages may mask significant regional trends, as there was a substantially high percentage of locations exhibiting significant increasing and decreasing trends exhibited in individual models.

Uncertainty in the spatial structure of trends in streamflow extremes is further investigated using both intra-model (to reflect GCM uncertainty) and inter-model correlations (to reflect the combined GCM–GHM uncertainty). A more robust spatial pattern of projected trends under RCP6.0 was found, indicated through generally higher intra- and inter-model correlation compared to those exhibited from trends simulated under RCP2.6 across all GHMs. This feature potentially reflects the less contrasted regional climate change of RCP2.6 relative to RCP6.0. The inter-model correlation is consistently lower than intra-model correlation due to the combined uncertainty of both GHMs and GCMs.

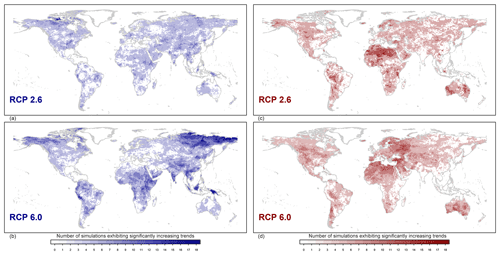
Figure 5 Number of simulations showing statistically significant trends at the 10 % level at each grid cell. Panels (a) and (b) show results for the assessment of increasing trends, while (c) and (d) show results for significant decreasing trends. (a, c) Results of GCMRCP2.6 simulations; (b, d) results of GCMRCP6.0 simulations.

To quantify the robustness in terms of regions with significant trends in streamflow extremes, the number of simulations showing significant increasing and decreasing trends was counted for each grid cell (values ranging from 0 to 18). As shown in Fig. 5a and c, the projections under RCP2.6 do not suggest many regions with an increasing trend for most ensemble members, but consistently suggest decreasing trends over the majority of Africa, Australia and western North America. Although both scenarios suggested a similar spatial pattern, projections under the RCP6.0 scenario (Fig. 5b and d) show a substantially higher robustness in terms of regions with significant changes over time in streamflow extremes. For instance, significant increasing trends are projected consistently over southern and south-eastern Asia, eastern Africa, and Siberia, while high agreement of decreasing trends is found over southern Australia, north-eastern Europe, the Mediterranean and north-western North America. These findings share some similarity with a previous investigation that used the ISIMIP Fast Track simulations (published before the ISIMIP2a and 2b simulations used here) to identify regions projected with an increasing magnitude of 30-year return level of river flow (Dankers et al., 2014). Specifically, both studies suggest overall (1) an increasing trend over Siberia and South-East Asia and (2) a decreasing trend over north-eastern Europe and north-western North America. The present study, however, additionally highlights a dominant decreasing trend over Australia, which was not shown previously. The different numbers of ensemble members (45 in Dankers et al., 2014, and 18 in the present study) and greenhouse gas concentration scenario (RCP8.5 in Dankers et al., 2014, and RCP2.6 and RCP6.0 in the present study) between two studies indicate that the choice of GCM–GHM ensemble and greenhouse gas concentration scenarios could lead to substantially different projections of changes in flood hazard at the regional scale.

These results suggest the key role of GCM uncertainty in projections of changes in flood hazards, emphasising the importance of a flexible adaptation strategy at the regional scale that can take this uncertainty into account (Dankers et al., 2014) such as increasing flexibility in reservoir operations, focusing on improved infrastructure resilience and preparing for uncertain changes in flood hazards. Such a strategy is achievable only through a reliable and robust understanding of the change in flood hazards. The assessment of the representativeness of streamflow observations (Sect. 3.2), however, demonstrated that the observation locations selected for this assessment are not a representative sample of the entire land mass. As a result, inference of changes in flood hazard may be biased toward well-observed regions. To further highlight the potential impact of limitations in observed streamflow datasets, the proportion of available stream gauges located in regions with different levels of projected “flood risk” was assessed. We first categorised each simulation grid cell into one of the five “flood-risk” groups. Note that in this analysis, “risk” is defined as the number of simulations projecting a significant increasing trend, rather than the prominent definition of risk as the combination of hazard, exposure and vulnerability (Kron, 2005). In this analysis, the RCP6.0 scenario was chosen as it yielded a higher global “risk” of flood hazard relative to the RCP2.6 scenario.

Figure 6 presents the percentage of all simulated grid cells (a) categorised in each of the five groups, and of GSIM stations located in each group (b). As can be seen, 11.7 % of grid cells fell into the “high-risk” groups (8.9 % from Group 4 with 11–15 ensemble members, and 1.8 % in Group 5 with 16–18 ensemble members), while 68.9 % of grid cells fell into the “low-risk” groups (22.0 % for Group 1 with no ensemble members, and 46.9 % for Group 2 with 1–5 ensemble members). Of all GSIM stations, only 0.9 % are located in high-risk grid cells (no station located in Group 5 grid cells) compared to 89.5 % of stations located in low-risk grid cells (35.4 % for Group 1 and 54.1 % for Group 2). The uneven distribution of stream gauges indicates potential difficulties in using observational records to provide an assessment of global or regional changes in flood hazard, which in part arises from data caveats associated with the spatio-temporal coverage and quality of observed gauge records across the globe. This finding further suggests the urgent demand for ongoing efforts to make streamflow observation more accessible. In addition, new innovations in remote sensing (Gouweleeuw et al., 2018) or development of runoff reanalysis (Ghiggi et al., 2019) should also be supported to complement the understanding of changes in floods for locations that were not observed by stream gauges.

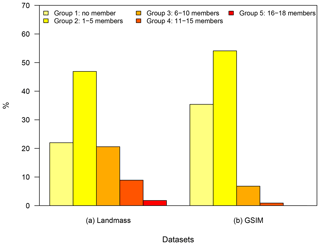
Figure 6 Percentage of grid cells (“Landmass”) grouped by the number of simulations projecting a significant increasing trend under the RCP6.0 scenario, and the percentage of streamflow stations (“GSIM”) assigned into each group. The range of possible simulations is from 0 to 18 and binned into five groups (Group 1: no members, Group 2: from 1 to 5 members, Group 3: from 6 to 10 members, Group 4: from 11 to 15 members and Group 5: from 16 to 18 members). To identify which group a specific station belongs to, the geographical coordinates of that station was superimposed on top of the global “flood-risk” map.

4 Summary and conclusions

To explore the appropriateness of GHMs in simulating changes in flood hazards, this study evaluated the capacity of six GHMs to reproduce the characteristics of historical trends in 7 d annual maximum streamflow over the 1971–2005 period. The study also explored the implications of simulation uncertainty to projected changes in flood hazards over the 2006–2099 period. The findings of these investigations are summarised as follows.

1. Using observations from the Global Streamflow Indices and Metadata (GSIM) archive, this study confirms previous findings about changes in flood hazard over data-covered regions (Do et al., 2017), in which significant decreasing trends were found mostly in Australia, the Mediterranean region, the western US, eastern Brazil and Asia (Japan and southern India), while significant increasing trends were more common over the central US, southern Brazil and the northern part of western Europe.

2. Trends simulated by GHMs, when using an observational climate forcing, show moderate capacity to reproduce the characteristics of observed trends (i.e. the mean and standard deviation of trends, the percentage of stations showing significant increasing and decreasing trends, and the spatial structure of trends).

3. Climate variability and climate model uncertainty (i.e. the effect of using different GCMs to simulate the historical climate) significantly reduced the extent to which the GHMs' captured the observed spatial structure of trends. This was evident through significantly lower correlation between observed trends and simulated trends, when GCMs were used for the climate forcing, than when climate observations were used.

4. The simulated trends over observed areas inadequately represented spatially averaged trends simulated for wider spatial areas from all GHM grid cells at the continental and global scales. This was evident in most simulations for trend mean and trend standard deviation, indicating a potential bias toward well-observed regions of observation-based inferences about changes in flood hazard.

5. Under the RCP2.6 and RCP6.0 greenhouse gas concentration scenarios, simulated trends in 7 d maximum streamflow across ensemble members have relatively low uncertainty in terms of the global trend mean (ranging from −1.3 % to 0.8 % change per decade) and trend standard deviation (ranging from 1.8 % to 4.1 % change per decade).

6. Projected trends have wide spread of the percentage of land mass showing significant changes, ranging from 7.5 % (7.1 %) to 30.1 % (35.0 %) for significant increasing (decreasing) trends. This result indicates that limited changes to the global mean flood hazard could potentially mask out significant regional changes.

7. Projected trends in flood hazards show low inter-model spatial correlations (ranging from −0.18 to 0.21), indicating high uncertainty in future changes in flood hazards at the global scale. Under the RCP6.0 scenario, some regions, e.g. south-eastern Asia, eastern Africa and Siberia, were consistently projected with significant increasing trends, which has some similarity to previous findings that used ISIMIP Fast Track simulations (Dankers et al., 2014).

8. High-risk regions (consistently projected with a significant increase in floods) of future changes in floods are sparsely sampled, covered by less than 1 % of all available stream gauges listed in the catalogue of GSIM. Data coverage, as a result, remains the key limitation of this study, which could potentially lead to an erroneous conclusion of our understanding of historical trends in flood hazard globally. Specifically, substantial changes, although having occurred, might not be captured by available streamflow records.

Our findings also show that individual models may provide a contradictory signal of changes in flood hazards for a specific region, indicating high uncertainty in model-based inferences of changes in flood hazards. As a result, alternatives for the conventional approach in estimating changes in streamflow extremes at the global and regional scale (i.e. unweighted mean across all grid points) should be investigated. For instance, the spatial weighted averages (e.g. using inverse distance relative to observed locations as weights) could be used to compute global means of changes. Regional analysis using homogenised regions as the basis of reporting spatial domains (Zaherpour et al., 2018; Gudmundsson et al., 2019) could be a potential alternative for continental-scale assessment.

The substantial discrepancy of trends simulated by different GHMs, despite having a common forcing boundary, represents another challenge in using the GHM ensemble, as there are a wide range of factors that could contribute to these discrepancies. This study provides a (non-exhaustive) list of key differences across participating GHMs (Sect. 1 in the Supplement) that could individually or collectively lead to different model outputs. Diagnosing the influence of these factors on models' capacity in simulating trends is still under-represented in the literature and is an important research agenda for future investigations. For instance, the impact of different methods to simulate snow dynamic could be assessed by investigating model performances across catchments where snowmelt plays an (in)significant role in flood generations.

Improved performance of GHMs in terms of simulating changes in flood hazard, considering the many factors influencing model capacity, is achievable only through the combined efforts of many communities. The spread of trends in streamflow extremes (trend standard deviation) could be simulated more accurately by finer spatio-temporal resolution GHMs. Such an improvement in GHMs, however, is highly dependent on the quality of input datasets (e.g. dam operations, historical irrigation databases, land use and land cover, in addition to atmospheric forcing), which are driven by advances in other geophysical disciplines (Bierkens et al., 2015; Wood et al., 2011). The moderate capacity of GHMs in terms of simulating the spatial structure of trends in streamflow extremes indicates the need for improved representation of runoff generation at the global scale (e.g. to better reflect rainfall-runoff relationship and the contribution of snow dynamics), which is also a focus of large-sample hydrology (Gupta et al., 2014; Addor et al., 2017). Uncertainty in GCMs, a long-standing challenge for the climate community, should also be addressed to enable robust projections of flood hazard in a warmer climate. One possibility is through constraining model performance using historical observations (to prevent climate models projecting an unrealistic state of the future climate system such as atmosphere energy balance or cloud feedbacks), which could potentially reduce the uncertainties of atmospheric forcing projections (Greve et al., 2018; Lorenz et al., 2018; He and Soden, 2016; Padrón et al., 2019). In addition, future development of GHMs should also pay attention to model's capacity to simulate flood timing, an important metric to represent flood generation processes (Blöschl et al., 2017; Hall and Blöschl, 2018; Do et al., 2019). Integrating more sophisticated and effective routing schemes into future generations of GHM should also be emphasised to ensure runoff is accurately converted into river discharge (Zhao et al., 2017).

This study presents a comprehensive investigation of historical and future changes in flood hazard using a hybrid model–observation approach. The results highlighted a substantial difference between trend characteristics simulated by GHMs and those obtained from the GSIM archive. Our findings, therefore, suggest more attention should be paid to investigating GHMs performance in the context of historical and future flood hazard, which is important not only for the scientific community but also for stakeholders when using the results of GHM simulations (Krysanova et al., 2018). This is particularly important to determine the appropriateness of GHMs in specific investigations, as model performance may vary substantially across different variables (e.g. moderate capacity in simulating the spatial structure of trends may be accompanied by a low performance in terms of simulating the trend mean).

Large-sample evaluations, however, are highly dependent on data availability, which is one of the key barriers to a holistic perspective of changes in floods. In this study, the unevenly distributed GSIM stations, partially due to the constraint in data accessibility, do not provide representative samples at both global and continental scale. Sustained and collective efforts from the broad hydrology community (Addor et al., 2019), therefore, are required to make streamflow data become more FAIR (findable, accessible, interoperable and reusable; see Wilkinson et al., 2016) and ultimately complement our limited understanding of flood hazards. Data providers, considering their tremendous investments in maintaining and making streamflow observations publicly available, remain key agencies to enhance the evidence base of the global terrestrial water cycle and changes in flood hazard. The important contribution of these agencies should be acknowledged appropriately when streamflow data are being used. Centralised organisations such as GRDC or WMO should also push forward the movement of making streamflow data accessible to the research community. More initiatives based on citizen science (Paul et al., 2018) should be adopted, as this is a potential option to crowdsource water data and offset the limitation of a traditional observation system. Finally, attention should also be paid to stream-gauge maintenance, data housekeeping and data sharing to ensure ongoing flood monitoring is available to the present and future generations.