Ability of a soil–vegetation–atmosphere transfer model and a two-source energy balance model to predict evapotranspiration for several crops and climate conditions

The heterogeneity of Agroecosystems, in terms of hydric conditions, crop types and states, and meteorological forcing, is difficult to characterize precisely at the field scale over an agricultural landscape. This study aims to perform a sensitivity study with respect to the uncertain model inputs of two classical approaches used to map the evapotranspiration of agroecosystems: (1) a surface energy balance (SEB) model, the Two-Source Energy Balance (TSEB) model, forced with thermal infrared (TIR) data as a proxy for the crop hydric conditions, and (2) a soil–vegetation–atmosphere transfer (SVAT) model, the SEtHyS model, where hydric conditions are computed from a soil water budget. To this end, the models' skill was compared using a large and unique in situ database covering different crops and climate conditions, which was acquired over three experimental sites in southern France and Morocco. On average, the models provide 30 min estimations of latent heat flux (LE) with a RMSE of around 55 W m⁻² for TSEB and 47 W m⁻² for SEtHyS, and estimations of sensible heat flux (H) with a RMSE of around 29 W m⁻² for TSEB and 38 W m⁻² for SEtHyS. A sensitivity analysis based on realistic errors aimed to estimate the potential decrease in performance induced by the spatialization process. For the SVAT model, the multi-objective calibration iterative procedure (MCIP) is used to determine and test different sets of parameters. TSEB is run with only one set of parameters and provides acceptable performance for all crop stages apart from the early growing season (LAI < 0.2 m² m⁻²) and when hydric stress occurs. An in-depth study on the Priestley–Taylor key parameter highlights its marked diurnal cycle and the need to adjust its value to improve flux partitioning between the sensible and latent heat fluxes (1.5 and 1.25 for France and Morocco, respectively). Optimal values of 1.8–2 were highlighted under cloudy conditions, which is of particular interest due to the emergence of low-altitude drone acquisition. Under developed vegetation (LAI > 0.8 m² m⁻²) and unstressed conditions, using sets of parameters that only differentiate crop types is a valuable trade-off for SEtHyS. This study provides some scientific elements regarding the joint use of both approaches and TIR imagery, via the development of new data assimilation and calibration strategies.

1 Introduction

Exchange of water at the soil–vegetation–atmosphere interface is of prime importance for weather forecasting and for climate studies (Shukla and Mintz, 1982); it is also a key component for hydrology, and therefore catchment water balance (Milly, 1994), as well as for agronomy in order to improve irrigation scheduling (Allen et al., 1998). Despite the abundant literature on the subject, there is no consensual approach regarding its spatialized estimation, and the contribution of evapotranspiration (ET) to the global hydrologic cycle remains uncertain (Jasechko et al., 2013). There are several in situ techniques available to measure ET (Allen et al., 2011) but most suffer from a lack of spatial representativeness. This prevents their use as a sustainable solution for regional applications, especially for agricultural landscapes where spatial heterogeneity – in terms of farming and technical itineraries, including the resulting pattern of moisture conditions – is high. By contrast, remote sensing offers an attractive alternative due to the synoptic and repeated data acquisition it provides. Indeed, even if ET is not directly observable from space, remote sensing data in different parts of the electromagnetic spectrum are related to the characteristics of the land surface governing the evapotranspiration process.

Within this context, several approaches combining remote sensing data and land surface models of various complexity have been proposed for the regional monitoring of ET (Courault et al., 2005), from the most conceptual approaches that modulate the evaporative demand by an empirical coefficient (the so called “crop coefficient”, Allen et al., 1998), to the complex and mechanistically based soil–vegetation–atmosphere transfer (SVAT) models that require a large number of inputs. In-between, the surface energy balance (SEB) models, constrained by thermal infrared radiative temperature observations, have been gaining influence over the last decade (Choi et al., 2009; Diarra et al., 2017). Several authors have intercompared the different SEB-based approaches for mapping ET with noticeable discrepancies (see Zhan et al., 1996; French et al., 2005; Timmermans et al., 2007, 2011; Chirouze et al., 2014). Among the different SEB models, the Two-Source Energy Balance (TSEB Norman et al., 1995) emerged as a robust and accurate model for evapotranspiration mapping over semiarid crops (Anderson et al., 2007; Chirouze et al., 2014; Diarra et al., 2017). This model is now extensively used in the scientific community and has been the subject of numerous refinements since the original Norman et al. (1995) version (Kustas and Norman, 1999, 2000; Anderson et al., 2008; Colaizzi et al., 2012, 2014, etc.). Nevertheless, both approaches have rarely been compared, although the joint use (via data assimilation technics) of snapshot evapotranspiration maps from SEB approaches and dynamic SVAT predictions appears promising (Crow et al., 2005, 2008). This is certainly attributed to the different underlying diagnostic or prognostic equations of the models with respect to the distinct purposes of the approaches in terms of temporal and/or spatial resolutions of evapotranspiration estimates.

Based on either SVAT or SEB models, the estimation of surface evapotranspiration implies dealing with the method–model complexity issue (Carlson, 2007; Kalma et al., 2008), as well as with incomplete knowledge available to document or to constrain them. For instance, with regards to remotely sensed TIR data, McCabe and Wood (2006) showed how the spatial resolution of TIR data used as input in the SEB method impacted the spatial variation of flux estimates. At a higher resolution, another source of uncertainty is the surface temperature fluctuations in relation to atmospheric turbulence (Lagouarde et al., 2013). The lack of knowledge on scaling effects when fluxes are intercompared at the same scales using aggregation or disaggregation methods has also been pointed out by several authors as a scientific issue for evapotranspiration mapping (Kustas et al., 2003, 2004; Norman et al., 2003). Although limited in time and focused on semiarid and sparse grasses and crops, several studies have also been dedicated to analyzing the sensitivity of the TSEB model to uncertain inputs, including radiative temperature, meteorological forcings or vegetation descriptors (Zhan et al., 1996; Anderson et al., 1997; Kustas and Norman, 1997; Li et al., 2005; Timmermans et al., 2007; Kustas et al., 2012). Likewise, others have focused on the sensitivity of SVATs to these inputs (Franks et al., 1997; Calvet et al., 1998; Wood et al., 1998; Pitman et al., 1999; Olioso et al., 1999; Robock et al., 2003; Petropoulos et al., 2009). Within this context, the comparative study of Crow et al. (2008) that focused on a SVAT model and the TSEB approach is the basis of our work. Indeed, as a preliminary step toward the joint use of both approaches via data assimilation, the purpose of this study is the comparison of the TSEB model (Norman et al., 1995) and the SEtHyS SVAT model (described in Coudert et al., 2006), in terms of overall performance, errors and domains of validity where model inputs and parameters are uncertain. This is carried out here using a large and unique in situ database covering several crops and seasons under relatively well-watered conditions and in a limited advection environment.

This paper is organized as follows. After briefly introducing the datasets and both models (Sect. 2), the analysis of the models' performance is presented (Sect. 3.1). Then, we focus on the sensitivity analysis results (Sect. 3.2) and on discussions related to parameters and inputs (Sect. 4). Finally, conclusions and perspectives are drawn in Sect. 5.

2 Data and methods

2.1 Model descriptions

The two-source energy balance budget, which is similar for both models, is first described. Then, differences in the solving methods and associated assumptions, as well as differences in flux parameterization, are briefly discussed.

2.1.1 The two-source energy budget

In the two-source energy balance, total sensible (H) and total latent heat (LE) fluxes arise from the soil and vegetation heat and vapor sources. Applying energy conservation and continuity principles, the energy budget can be described using the following set of equations:

$$\begin{array}{}\text{(1)}& {\displaystyle }& {\displaystyle }H=H_{\left[\mathrm{soil}\right]}+H_{\left[\mathrm{veg}\right]},\text{(2)}& {\displaystyle }& {\displaystyle }\mathrm{LE}={\mathrm{LE}}_{\left[\mathrm{soil}\right]}+{\mathrm{LE}}_{\left[\mathrm{veg}\right]},\text{(3)}& {\displaystyle }& {\displaystyle }{R}_{\mathrm{n}}=R_{\mathrm{n}\left[\mathrm{soil}\right]}+R_{\mathrm{n}\left[\mathrm{veg}\right]},\text{(4)}& {\displaystyle }& {\displaystyle }{R}_{\mathrm{n}\left[\mathrm{soil}\right]}=H_{\left[\mathrm{soil}\right]}+{\mathrm{LE}}_{\left[\mathrm{soil}\right]}+G,\text{and}\text{(5)}& {\displaystyle }& {\displaystyle }{R}_{\mathrm{n}}=H+\mathrm{LE}+G,\end{array}$$

where G is the ground heat flux and R_n is the net radiation. All fluxes are expressed in Watts per meter squared (W m⁻²). The H and LE flux expressions are given in Shuttleworth and Wallace (1985, Eqs. 6 and 7, p. 843) for a resistive scheme (following analogy with Ohm’s law) of a one-dimensional description of energy partition for sparse crops assuming horizontal uniformity. The respective H and LE expressions for the complete canopy between the level of mean canopy flow and the reference height can then be written as follows:

$$\begin{array}{}\text{(6)}& {\displaystyle }& {\displaystyle }H=-{\displaystyle \frac{\mathit{\rho }{c}_{\mathrm{p}}}{r_{\mathrm{a}}^{\mathrm{a}}}}\left(T_x-T_{\mathrm{0}}\right)\text{and}\text{(7)}& {\displaystyle }& {\displaystyle }\mathrm{LE}=-{\displaystyle \frac{\mathit{\rho }{c}_{\mathrm{p}}}{r_{\mathrm{a}}^{\mathrm{a}}\mathit{\gamma }}}\left(e_x-e_{\mathrm{0}}\right)\end{array}$$

where γ is the psychrometric constant (mb K⁻¹); $r_{\mathrm{a}}^{\mathrm{a}}$ is the aerodynamic resistance between canopy source height and reference level (s m⁻¹); e_x and e₀ are vapor pressure (mb) at canopy source height and reference height, respectively; and T_x and T₀ are temperature (^∘C) at canopy source height and at reference height, respectively. The components' elements from soil and vegetation (LE_[soil], LE_[veg], H_[soil] and H_[veg]) are expressed in the same way, according to the associated resistances. Afterwards, the vapor pressure deficit at the canopy source height is introduced. The system now becomes a set of five equations with six unknowns, namely vegetation temperature T_[veg], soil temperature T_[soil], canopy-space temperature T_[canopy], and the corresponding water vapor pressures e_[veg], e_[soil] and e_[canopy]. The next steps of the classical solving of a two-source energy balance system are to express T_[canopy] as a function of T_[veg] and T_[soil] using the continuity equation in H, and T_[veg] as a function of T_[soil] using the energy budget of vegetation. In addition, the heat conduction flux in soil (G) is either estimated from the net radiation (TSEB model) or the residual of the energy budget (SEtHyS model) as detailed in the Appendix. The solving method consists in the linearization of the equations of the previous system. The basic differences between the approaches is that for SVATs models, soil temperatures at different depths are prognostic variables tightly linked to water mass balance, whereas radiative temperature is a forcing input for the SEB models used to infer T_[veg] and T_[soil] as detailed below.

2.1.2 TSEB

The TSEB model was first described in Norman et al. (1995) and has been the subject of several refinements. The solving principle is briefly described below, and the version of TSEB used is described in Sect. 2.4. TSEB is forced by a radiometric surface temperature T_rad so that soil and vegetation temperatures contribute to T_rad in proportion to the fraction of the radiometer field of view (f_θ) that is occupied by each component, thus adding a sixth equation to the system above:

$$\begin{array}{}\text{(8)}& T_{\mathrm{rad}}\left(\mathit{\theta }\right)={\left[f_{\mathit{\theta }}\times T_{\left[\mathrm{veg}\right]}^n+\left(\mathrm{1}-f_{\mathit{\theta }}\right)\times T_{\left[\mathrm{soil}\right]}^n\right]}^{\mathrm{1}/n},\end{array}$$

where the factor n is usually fixed to 4 (Becker and Li, 1990). The available energy at the soil surface is computed considering an exponential extinction of net radiation (i.e., Beer’s law):

$$\begin{array}{}\text{(9)}& R_{\mathrm{n}\left[\mathrm{soil}\right]}=R_{\mathrm{n}}\times \exp {\displaystyle \frac{-\mathit{\kappa }\times \mathrm{LAI}}{\sqrt{\mathrm{2}\cos \mathit{\theta }}}},\end{array}$$

where the factor κ is set to 0.45 for the spherical distribution of leaves following Roos (1991), and R_n is estimated from measured shortwave and longwave components. The conduction flux in the soil is expressed as a fraction of the available energy at the soil surface:

$$\begin{array}{}\text{(10)}& G=\mathrm{\Gamma }\times R_{\mathrm{n}\left[\mathrm{soil}\right]},\end{array}$$

where Γ is an empirical coefficient that is usually equal to 0.35 (Choudhury et al., 1987). Finally, the resolution of this set of equations relies on the (strong) assumption that vegetation generally transpires at a potential rate. The Priestley–Taylor equation gives a first estimation of canopy transpiration (Norman et al., 1995, Eq. 12):

$$\begin{array}{}\text{(11)}& {\mathrm{LE}}_{\left[\mathrm{veg}\right]}={\mathit{\alpha }}_{\mathrm{PT}}\times f_{\mathrm{g}}\times {\displaystyle \frac{\mathrm{\Delta }}{\mathrm{\Delta }+\mathit{\gamma }}}\times R_{\mathrm{n}\left[\mathrm{veg}\right]},\end{array}$$

where α_PT is the Priestley–Taylor parameter, f_g is the green vegetation fraction cover, Δ is the slope of the saturation vapor pressure vs. temperature curve and γ is the psychrometric constant. α_PT values ranges between 0.5 and 2.0 (Hssaine et al., 2018) according to meteorological conditions including advections, the green fraction of vegetation and the soil water availability with an average value of around 1.3.

In the “series” resistance network used in this study (see justification below) and described in Norman et al. (1995, Fig. 11), the sensitive heat fluxes are expressed as follows:

$$\begin{array}{}\text{(12)}& H_{\left[\mathrm{soil}\right]}=\mathit{\rho }{c}_{\mathrm{p}}{\displaystyle \frac{T_{\left[\mathrm{soil}\right]}-T_{\left[\mathrm{canopy}\right]}}{r_{\mathrm{s}}}}\end{array}$$

between the soil surface and the canopy air space,

$$\begin{array}{}\text{(13)}& H_{\left[\mathrm{veg}\right]}=\mathit{\rho }{c}_{\mathrm{p}}{\displaystyle \frac{T_{\left[\mathrm{veg}\right]}-T_{\left[\mathrm{canopy}\right]}}{r_x}}\end{array}$$

between vegetation and canopy air space, and

$$\begin{array}{}\text{(14)}& H=\mathit{\rho }{c}_{\mathrm{p}}{\displaystyle \frac{T_{\left[\mathrm{canopy}\right]}-T_{\mathrm{a}}}{r_{\mathrm{a}}}}\end{array}$$

between canopy air space and the reference height for atmospheric measurements. Here r_s, r_x and r_a are the associated respective resistances given in Eqs. B1, A8 and 6 in Norman et al. (1995). H_[veg] is then computed as the residual of the vegetation energy balance (Eq. 1). T_[veg] is derived from H_[veg]; T_[soil] is derived from Eq. (8); H_[soil] is computed from T_[soil] and LE_[soil] as a residual of the soil energy balance (Eq. 1). Should LE_[soil] be found to be negative, meaning that there is condensation on the soil surface, which is very unlikely during the day, then the initial value of the Priestley–Taylor coefficient α_PT is iteratively reduced until LE_[soil]=0 following Anderson et al. (2005) and Li et al. (2005).

In agreement with Li et al. (2005), the “series” layout of resistance (Norman et al., 1995) was found to provide more accurate results overall (not shown) and also less sensitivity to vegetation cover estimate. Furthermore, for model comparison, it was also relevant that both resistance networks were similar in TSEB and SEtHyS models.

2.1.3 SEtHyS

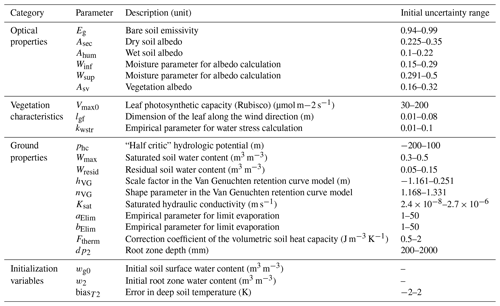
The SEtHyS – French acronym for “Suivi de l'Etat Hydrique des Sols” or monitoring of the hydric condition of the soils – SVAT model physics and the main parameterizations are described in Coudert et al. (2006). The main equations of SEtHyS are summarized in Appendix A. The model belongs to the “two sources, two layers” SVAT model category. Specifically, the coupled water and energy budget is solved for the vegetation and soil sources, and the soil description for water and heat transfers is based on the force–restore Deardorff formalism (Deardorff, 1978). The model requires atmospheric and radiative forcing as well as surface biophysical parameters as inputs. It calculates the energy and water fluxes between surface and atmosphere and simulates the evolution of soil and canopy temperatures, air temperature and specific humidity within the canopy, as well as the surface and the root zone soil water content. The heat and water transfer calculation within the soil–vegetation–atmosphere continuum is based on a resistance concept. The resistance network is made of four nodes: the reference height for the low atmospheric weather forcing, inside the vegetation at the displacement height plus the roughness length, just above ground at the soil roughness length and at ground level. The aerodynamic resistances – above and inside the vegetation canopy – are determined with the wind speed profile description inside the canopy from Shuttleworth and Wallace (1985) and Lafleur and Rouse (1990). The evapotranspiration calculation takes partitioning between free water in the canopy and the rest of the leaves into account (Monteith, 1965; Deardorff, 1978) and is based on the stomatal resistance for the “big leaf” model from Collatz et al. (1991). The vegetation photosynthesis and stomatal resistance parameterizations are the same as those used by the SiB model (Sellers et al., 1996). The soil hydrodynamic properties to calculate water transfer processes within the soil porous network are given by Genuchten (1980). The ground heat flux conduction is obtained as the residual of the soil energy budget. Finally, the radiative transfer model included in the model for the TIR domain (François, 2002) allows for the simulation of brightness temperature and radiative temperature, and thus presents the possibility to constrain the model with TIR data (Coudert and Ottlé, 2007; Coudert et al., 2008). The SEtHyS model requires a set of about 22 parameters, which are presented in Table 2.

Figure 1 Locations of the experimental sites in France (a) and Morocco (b).

Table 1 TSEB input parameters (nine parameters in total) with reference values and optimal values obtained from the sensitivity analyses.

Table 2 SEtHyS input parameters (22 parameters in total) with initial uncertainty ranges used for MCIP calibration.

2.2 Sites description and data

The experimental dataset was gathered in the southwest of France (Béziat et al., 2009) and the southeast of Morocco (Chehbouni et al., 2008; Jarlan et al., 2015) as shown in Fig. 1. As presented in Table 3, all necessary data to run, calibrate and evaluate models were collected over three agricultural sites, spanning a total of seven culture cycles from seeding to harvest: four wheat (Triticum aestivum L.) crops, one sunflower (Helianthus annuus L.) crop and two corn (Zea mays L.) crops. Experimental sites differ by management practice (culture rotation and irrigation), soil properties, topography and climate (six temperate crop cycles and one semiarid crop cycle). The Auradé (43.55^∘ N, 1.11^∘ E) and Lamasquère (43.50^∘ N, 1.24^∘ E) experimental sites are located near Toulouse in southwestern France and are part of the “Sud-Ouest” project (Dedieu et al., 2001; Béziat et al., 2009). Both experimental sites experience a temperate climate. A rotation of wheat and sunflower is cultivated in Auradé, whereas a rotation of wheat and irrigated corn is cultivated in Lamasquère. A complete description of the site features and datasets are presented in Béziat et al. (2009). The Sidi Rahal (31.67^∘ N, 7.60^∘ W) experimental site is located on the Haouz Plain in central Morocco and is part of the “SUDMED” project (Chehbouni et al., 2008; Jarlan et al., 2015). It is part of an irrigated agricultural area that experiences a semiarid climate, where wheat is the most widely grown crop. More information about the site and dataset is given in Duchemin et al. (2006).

Table 3 Site characteristics and overview of available cultures and crop cycles.

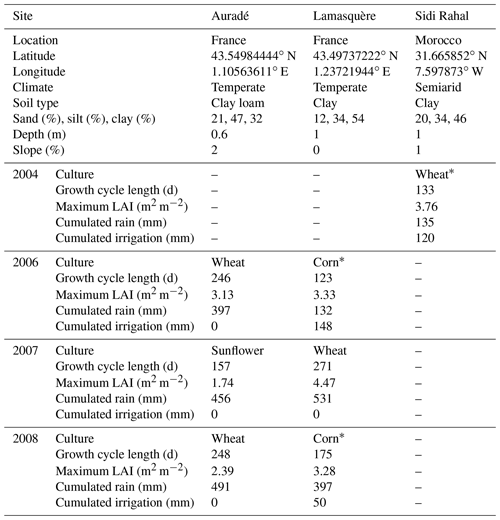
^* Irrigated cultures.

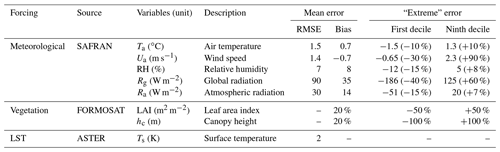
Each experimental station collected standard meteorological data at 30 min time step intervals: global incoming shortwave and longwave radiation (R_g and R_a, respectively), wind speed (U_a), air temperature (T_a), atmospheric pressure (P_a), relative humidity (RH) and rainfall. The four components of the net radiation (R_n) were measured using a CNR1 radiometer (Kipp and Zonen, Delft, NL). Land surface temperature (LST) was computed from measured upward and downward longwave components of the net radiation, using the Stefan–Boltzmann law and an estimation of surface emissivity (Becker and Li, 1995). Sensible (H) and latent (LE) heat fluxes were measured continuously using eddy covariance (EC) systems (Moncrieff et al., 1997; Aubinet et al., 2000). Fluxes were processed with classical EC filters and corrections (Béziat et al., 2009). The accuracy of flux estimates is expected to range between 5 % and 30 % (Eugster et al., 1997; Wilson et al., 2002). Soil heat flux (G) was sampled using heat flux plates located at depths ranging from 5 cm to 100 cm. Automatic measurements were then complemented by vegetation samples. Vegetation height (h_c) and the green leaf area index (LAI) were collected periodically along crop cycles and interpolated using the piecewise cubic Hermite algorithm. Green LAI was determined from destructive measurements with a LiCor planimeter (LI-3100, LiCor, Lincoln, NE, USA). In order to obtain an estimation of the fraction of green (f_g), total LAI (LAI_green+LAI_yellow) was extrapolated from green LAI data by applying a linear decrease starting at the LAI maximum and ending at harvest with a value of ${\mathrm{LAI}}_{\mathrm{total}}=\mathrm{0.8}\times {\mathrm{LAI}}_{\max }$. In order to assess the potential loss of accuracy of meteorological inputs at the landscape scale and the impact on model simulations, SAFRAN reanalysis data (Quintana-Seguí et al., 2008) were used within this study. SAFRAN is based on an optimal interpolation between a background estimate obtained from Météo-France's numerical weather prediction model (ALADIN) and weather station observations, except for precipitation, which relied on the ground station network only, and the incoming radiation fluxes (downwelling surface shortwave and longwave), which were computed from the radiation scheme of Ritter and Geleyn (1992) from the outputs of a numerical weather forecast model and the solar constant at the top of the atmosphere (for shortwave incoming radiation). Data were kindly provided by Météo-France.

2.3 Assessing the model skills

Keeping in mind that we plan to spatialize a SVAT model, whose parameters are highly dependent on growth stage of vegetation, we must be able to determine sets of parameters representing specific phenological stages and hydric conditions (stressed/non-stressed). For this reason, evaluation was not performed continuously over the entire crop cycles, but specific periods of interests were identified to assess the model skill. These periods were chosen to be 10 d long in order to catch synoptic-scale variability of the weather, as shown by Eugster et al. (1997) with the help of spectral analysis. This duration is also short enough to remain representative of a specific phenological stage, and long enough to gather a sufficient amount of data. For each crop cycle, four specific study periods were chosen, each corresponding to the following phenological stages: rising/emergence stage (0.1 < LAI < 0.3), growth stage (rapid increase of LAI and LAI ≈ 1), maximum development stage (around LAI maximum value) and senescence stage (LAI decreases). Starting days of periods were adjusted to optimize the quality of available data, as the datasets are subject to sporadic measurement issues and energy closure inconsistencies (filtered to a minimum of 80 %).

In order to better assess the differences of model skills during stress periods, water stress is quantified along the whole crop cycles using two indicators:

• the evaporation stress (SE, Boulet et al., 2007) related to the ratio between real and potential evapotranspiration events:

  $$\begin{array}{}\text{(15)}& \mathrm{SE}=\mathrm{1}-{\displaystyle \frac{\mathrm{LE}}{{\mathrm{LE}}_{\mathrm{pot}}}},\end{array}$$

  where LE_pot is computed using the Penman–Monteith equation (canopy resistance is estimated following Jarvis, 1976 formulation with a minimum value of 90 s m⁻¹);

• the soil wetness index (SWI, Douville, 1998, among others) of the root zone ranging from zero at wilting point to one at field capacity:

  $$\begin{array}{}\text{(16)}& \mathrm{SWI}={\displaystyle \frac{W_{\mathrm{2}}-W_{\mathrm{wilt}}}{W_{\mathrm{fc}}-W_{\mathrm{wilt}}}},\end{array}$$

  where W₂ is the root zone water content, W_fc is the water content at field capacity, and W_wilt is the water content at wilting point.

As cultures from our dataset are irrigated or in temperate areas, most stress periods are found during senescence phases, when water resources are low or irrigation is stopped. The model skills are assessed using classical statistical metrics including the root-mean-square error (RMSE), the mean absolute percentage deviation (MAPD), bias and the determination coefficient (r²).

2.4 Implementation of the models

Considering our objective was to compare a complex SVAT model with the TSEB tool (which was taken as an example of a simple and robust approach), a different strategy was applied for the implementation of the two models. The 22 parameters of the SEtHyS model were finely tuned for each crop and each phenological stage. The objective of this calibration was not to fit the data best, but rather to evaluate the sensitivity of model outputs to potentially poorly calibrated parameters when the model is to be applied to an heterogeneous agricultural landscape at the field or intra-field scale. To this end, four different cases corresponding to four different sets of parameters were considered to quantify the potential loss of performance due to incorrect parameter values. The four cases are listed below from the “best” conditions (when the parameters are calibrated for each site, each crop and each phenological stage) to the worst conditions (when generic values are used):

1. site and period specific parameter sets (hereafter referred to as “optimal”) for each site, crop class (i.e., type of culture) and phenological stage. Note that the analysis of the model skill (Sect. 3.1) is performed using this parameters set;

2. more generic parameter sets depending on crop class and phenological stages only (hereafter referred to as “pheno + cult”);

3. if no information is available for characterizing phenology, a calibrated set of parameters for the entire cultural crop cycle is computed (hereafter referred to as “culture only”);

4. the last case corresponds to the “optimal” parameter set but is applied to another crop class in order to take potential errors that are likely to occur when working with a land use map into account (referred to as “unadapted”).

What we consider the “best” case is very unlikely for a spatialized application of the tool, as even the largest available database will never cover all of the conditions encountered at the scale of an heterogeneous agricultural landscape where each plot has its specific soil, technical itinerary, hydric status, an so on. Thus, our objective is to get different parameter sets with values close to what is expected for each type of condition (crops, climate, site, phenological stage, etc.) but without assigning too much importance to the values themselves. To help perform the calibration, a stochastic multi-objective calibration method (multi-objective calibration iterative procedure, or MCIP; Demarty et al., 2004, 2005) is implemented in order to minimize the RMSE values between simulations and measurements at 30 min time intervals. Five objective functions are identified: the RMSE of H and LE fluxes, surface brightness temperature (T_b), net global radiation (R_n) and root zone soil water content (SWC). An ensemble of simulations based on a Monte Carlo sampling of the parameter space is carried out, and the objective functions are optimized jointly following a Pareto ranking. The basic principle is that a simulation is classified as “better” than the others if all of the objective functions have lower values. For more details on the MCIP methodology, see Demarty et al. (2004, 2005).

For TSEB, the most robust configuration of the model is sought. To this end, as a first step, the most sensitive parameters for convection fluxes prediction are calibrated on the whole database at once (Diarra et al., 2017). These parameters are the Priestley–Taylor coefficient (α_PT), the coefficient of net radiation extinction (κ) and the empirical coefficient (Γ) relating R_n[soil] to G. The objective functions are the RMSEs of H and LE. These calibrated values are reported in Table 1. They are almost the same as those proposed by Norman et al. (1995) and will be kept for the TSEB runs in the next section of the paper. A more optimal calibration by crop, site and phenological stage was also carried out (not shown). Main finding can be summarized as follows:

1. The RMSE difference between values from Norman et al. (1995) and the optimal value calibrated for each crop and stage did not exceed 10 W m⁻² for LE. In addition, most of the optimal κ values ranged between 0.38 and 0.58; the only notable exceptions were fully covering wheat with lower interception (κ value around 0.3), which may have been attributed to the erectophile distribution of wheat leaves, and fully covering maize and sunflower characterized by a higher interception (κ values reaching 0.7).

2. Likewise, the RMSE difference between initial values from Norman et al. (1995) and the optimal values for the α_PT parameter remained below 6 W m⁻² except during the senescence stages where they could reach more than 35 W m⁻². Thus, errors due to taking the literature value of 1.3 were very limited. Finally, the range of optimal values was relatively narrow (1.05 to 1.6).

3. For the Γ parameter, differences of RMSE between the optimal values and 0.35 proposed by Norman et al. (1995) were below 8 W m⁻² apart from the rising stage where we observed errors up to 79 W m⁻² on the sunflower site. Values ranged between 0.05 and 0.7.

Still with the goal of identifying the most robust configuration of the TSEB model, several refinements proposed by different authors to improve models' prediction for specific crop and climate conditions were also tested with our database. The Priestley–Taylor formulation, although relatively simple, provides accurate potential transpiration in a wide range of conditions but neglects the aerodynamic resistance. Colaizzi et al. (2014) proposed replacing the Priestley–Taylor expression with the Penman–Monteith equation (Monteith, 1965), in particular for advective conditions; thus, the increase in the value of the α_PT parameters (as proposed by Kustas and Norman (2000) for such conditions) could be avoided. Unfortunately, the Penman–Monteith version worsened the results by about 6.3 % on average over the whole database and was not retained in this study. Several parameterizations aiming to represent the diurnal course of Γ have also been proposed. Those of Santanello et al. (2003) and Chávez et al. (2005) have been tested. The overall performance of the model with respect to predicting convective fluxes was slightly worsened on average except under some very specific conditions. Interestingly enough, a multiplicative factor for κ lower than 1 was proposed by Campbell and Norman (1998) in the divergence equation (Eq. 9) to take the clumping of some crops into account; this clumping may intercept a lower portion of the incoming radiation compared with leaves that are randomly distributed (Kustas and Norman, 1999). The calibrated values of κ for sunflower and maize are above the 0.45 proposed by Norman et al. (1995) (cf. point 1 above). This tends to show that a higher fraction is intercepted and is most likely due to a dominantly planophile leaf orientation for both crops rather than a clumping effect. Finally, the simple radiative transfer model of Kustas and Norman (1999) has been tested as an alternative to the Beer law proposed by Norman et al. (1995). Although close on average (RMSE differences on R_n<17 W m⁻²), significantly worse RMSE values were obtained during the rising stage for wheat and sunflower.

3 Results

3.1 Models skills by crops and phenological stages

Model simulations of heat fluxes are compared to tower flux measurements at 30 min and daily time steps, with a focus on performance by crops and by growth stage. RMSEs for LE, H and R_n are displayed in Table 4, and MAPDs for H and LE are displayed in Fig. 2. Biases (not shown) are very limited and ranged between −23 and +10 W m⁻² for both models, except during the rising phase where they reached −47 and +43 W m⁻² for SEtHyS and TSEB, respectively (see Sect. 4). Available energy is well simulated for both models with daily averaged RMSEs of 43 and 19 W m⁻² for TSEB and SEtHyS, respectively.

Table 4 Intercomparison of the performance (RMSE) of TSEB and SEtHyS, with the influence of time resolution, phenological stage, culture and climate.

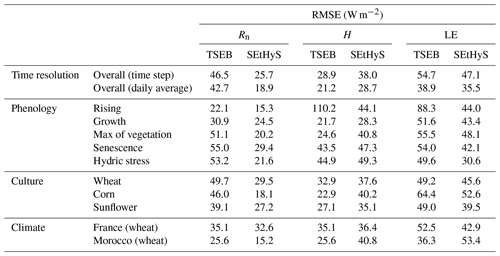
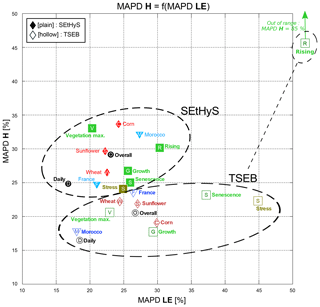
Figure 2 Comparison of TSEB (hollow markers) and SEtHyS (plain markers) estimations of H and LE for various time resolutions (circles), phenological stages (squares), cultures (diamonds) and climates (triangles). SEtHyS results are computed using the “optimal” parameter sets (see Sect. 2.4). MAPD stands for mean absolute percentage deviation.

Regarding heat fluxes, Table 4 shows good performance for the TSEB model on daily averaged values despite the relative simplicity of the approach compared with SEtHyS, which relies on a systematic parameter calibration. Both models exhibit similar statistics regarding LE estimations (RMSEs of 35.5 vs. 38.9 W m⁻² for SEtHyS and TSEB, respectively), whereas TSEB behaves slightly better with respect to H estimations (21.2 vs. 28.7 W m⁻²). These values are close to the errors found in the literature for TSEB (Norman et al., 1995; Zhan et al., 1996; Anderson et al., 1997; Kustas and Norman, 1999; French et al., 2005; Kalma et al., 2008; Diarra et al., 2013, 2017) and also within the range of expected errors from EC tower measurements (Eugster et al., 1997; Wilson et al., 2002). The 30 min values lead to similar conclusions, except that the drop in retrieved LE's performance associated with this change of reference time interval is stronger for TSEB than for SEtHyS. Interestingly enough, this first analysis highlights important disparities in terms of LE prediction skill between the various growth stages. Indeed, Fig. 2 emphasizes some regularity in the SEtHyS model's skill regardless of the growth stage and crop, as evidenced by the narrow group formed by the SEtHyS points. By contrast, the range of MAPD values for TSEB is much wider. In particular, limitations of the model are clearly highlighted during the rising and senescence stages. During the senescence phase, these discrepancies may both be attributed to stress (see Sect. 4) but could also be related to poor partitioning of available energy between the soil and vegetation. Indeed, the change in the radiative features of the canopy, including albedo, which occurs on senescent plants, is not taken into account by the model. However, regarding irrigation practices, it should be noted that assessing accurate ET during senescence is not as important as during the growth season.

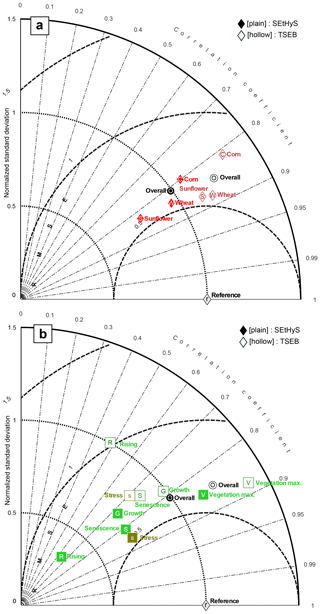
Figure 3 Taylor diagram for the LE performance of TSEB (hollow markers) and SEtHyS (plain markers). Diagram (a) compares various cultures; diagram (b) focuses on phenological stages. Concentric lines centered on zero indicate the normalized standard deviation with observations, radial lines indicate the correlation coefficient between simulations and observations, and normalized RMSE isolines are the concentric circles centered on “r” (reference for the overall time series of observations: the RSME is 0, the correlation coefficient is 1 and the normalized standard deviation is 1).

The poor performance during the rising stage is due to excessive limitation of the soil sensible heat flux, induced by the parameterization of the roughness length for momentum ($Z_{\mathrm{0}\mathrm{m}}=h_{\mathrm{c}}/\mathrm{8}$) in the denominator of the expression of the aerodynamic resistance r_a, leading to very high resistance when the canopy height is very low. As the vegetation net radiation is very limited during that stage, vegetation sensible heat is also close to zero. The soil resistance r_s also plays an important role on bare and sparsely vegetated surfaces, and recent studies (Li et al., 2019; Kustas et al., 2016) have shown that adapted formulation or modeling improved TSEB performance in arid or semiarid conditions. Thus, the observed high MAPD of LE during the rising phase shall be attributed to significant bias of TSEB estimates. To a lesser extent, SEtHyS skill is also mitigated during the rising phase. Generally, when evaporation is predominant over transpiration, more weight is given to soil transfer processes that are harder to characterize due to the high heterogeneity of soil characteristics and the limited soil measurements available for calibration. The poor performance is more conspicuous with TSEB, leading to the estimation of H with a MAPD of 85 %. By contrast, both models tend to show better performance when vegetation is fully developed (MAPD less than 23 % for LE). The model performance by crop and growth stage is detailed in Fig. 3a and b, respectively, as normalized Taylor diagrams (Taylor, 2001). This diagram is a concise way to display the ratio between the variances of the model outputs and the observed data, the correlation coefficient (r), and the RMSE between model estimates and observations normalized by the variance of the observed dataset. The further from the point marked “observed reference” on the abscissa axis, the higher the normalized RMSE; likewise, dots on the right (left) side of the circle cutting the ordinate axis at “observed reference” overestimate (underestimate) the observation variance. Figure 3a and b show higher normalized standard deviations for TSEB LE estimations. These noisier outputs are likely due to the instantaneous (“snapshot”) computing architecture of the TSEB model, whereas SEtHyS is better constrained by its continuous evolution of the soil water content which leads to smoother predictions of the daily cycle. This explains the drastic drops in the TSEB RMSE values on LE when going from daily to 30 min observations, as already underlined above. Finally, no significant skill differences are observed between crops, which seems to indicate that (1) the set of parameters used in TSEB describes vegetation characteristics well and that (2) the SEtHyS formalism can be adapted to various crops, provided that parameters are properly calibrated. More focused discussion on the selected sets of parameters is given in Sect. 4. Models performs well in both climates: SEtHyS showed slightly better performances for flux estimates in France (MAPD for LE of 23 % in France and 30,% in Morocco), whereas TSEB showed slightly better performances for flux estimates in Morocco (MAPD for LE of 26 % in France and 18 % in Morocco). However, differences in crop management between France and Morocco and the availability of only one crop cycle in Morocco do not allow for final conclusions about climate impact on model skill to be drawn. TSEB shows worse performance during senescence periods (including hydric stress) with respect to LE estimation (MAPD of 45 %). This is partly due to the Priestley–Taylor approximation, which is suitable for unstressed vegetation in potential conditions (Priestley and Taylor, 1972), and to the fact that it does not have a water budget description. Increased LST resulting from water stress does not limit LE significantly enough in the TSEB scheme (see Sect. 3.2.7). Several authors have already pointed out that TSEB do not faithfully reproduce periods of senescence and water stress (Kustas et al., 2003; Crow et al., 2008; Boulet et al., 2015). SEtHyS includes descriptions of soil water transfers and leaf processes – in particular stomatal resistance – and can better reproduce the hydric stress impact on LE flux (MAPD of 28 %).

3.2 Sensitivity analyses to inputs

3.2.1 Overview

Given the overall purpose of our research, which was dedicated to the spatialized estimation of evapotranspiration at various scales, quantifying the decrease of model performance due to the deterioration of input data quality combined with change of spatial scale from the field to a heterogeneous agricultural landscape is a prerequisite. Applying the models at the landscape scale is not performed the same way for both approaches: TSEB is designed to be driven by remote sensing data with ET computed directly at the resolution of the TIR pixel, whereas SEtHyS is spatially distributed by separately computing fluxes at the crop scale for each homogeneous entity. As a consequence, both models' performance is expected to exhibit sensitivity to the quality of auxiliary spatialized meteorological and vegetation forcing variables, TSEB's performance is expected to depend on the quality of the TIR data, and SEtHyS's performance is expected to depend on the quality of the description of the state of each homogeneous entity (i.e., soil water content initialization, and sets of parameters describing soil properties and vegetation behavior).

The specific purpose of this section is twofold: (1) to identify the most sensitive inputs and (2) to quantify the expected model performances when realistic input errors are introduced. Expected uncertainties on input variables have been evaluated by comparing available in situ data to the spatialized datasets (SAFRAN meteorological reanalysis and ASTER, LANDSAT and FORMOSAT-2 satellite imagery and products). Results are presented in Table 5 and details are given in the following sections.

Table 5 Comparison of in situ data and spatial data (SAFRAN, ASTER and inversed NDVI).

3.2.2 Intercomparison of SAFRAN and in situ meteorological data

Comparison results between the two available meteorological stations in the southwest of France and the closest SAFRAN 8 km grid points (inverse interpolated distance) are reported in Table 5 in terms of RMSE and bias values (2006–2008 period). On average, SAFRAN provides consistent results for air temperature and relative humidity, with reasonable RMSE values and biases close to zero. To a lesser extent, wind speed is also well reproduced, although slightly biased. The SAFRAN ability to predict incoming radiation is less convincing: bias is low but the RMSE reaches 90 W m⁻² (about 20 % on average). This comparison corroborates the conclusions of Quintana-Seguí et al. (2008), who also highlight a strong weakness of SAFRAN in terms of incoming radiation predictions. Er-Raki et al. (2010) used a forecast model (ALADIN from Météo-France) over the Tensift Basin in Morocco. The results showed that the ALADIN forecasts are in good agreement with the station measurements in terms of solar radiation (R_g) and air temperature (T_a). However, the comparison of the station and the forecasted values of relative humidity (RH) and wind speed (U_a) are much more scattered. Besides the RMSE values and biases representing time-averaged statistical characteristics of the difference between SAFRAN and the two ground stations, it is also interesting to consider more extreme error values. To do so, the first and ninth deciles of the difference distribution are shown in Table 5 in absolute values and as a percentage. The probability of the occurrence of such errors is far from insignificant, as 20 % of the data are involved. These “extreme” errors are considered for the sensitivity study regarding (1) the instantaneous estimates provided by the TSEB model depending on satellite overpass time, leading to potential instantaneous errors much higher than the average; and (2) the poorest quality of reanalysis data in the semiarid areas because the meteorological station network may be scarcer.

Figure 4 Sensitivity analysis (realistic white noise) of both models to meteorological inputs and the impact on the estimation of H and LE.

3.2.3 Sensitivity analysis to meteorological inputs

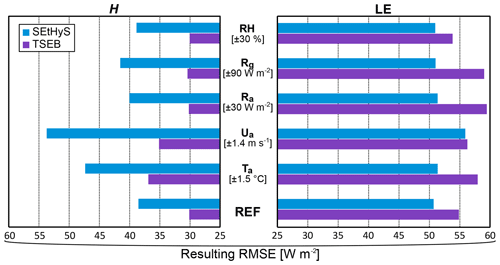
Impact of realistic and more extreme errors on convection flux simulations are shown in Figs. 4 and 5, respectively. Focusing on noise (Fig. 4) is of interest as biases are often limited on reanalysis systems thanks to bias reduction procedures. On average, SEtHyS simulations are less sensitive to noisy inputs for LE than for H, whereas the opposite conclusion can be drawn for TSEB. Adding white noise to meteorological inputs with the objective of scaling up to agricultural landscape with realistic error has almost no impact on the RMSE for SEtHyS when compared to the reference simulation for latent heat predictions. Nevertheless, wind speed has a greater impact on LE, with an increase of 10 % on the LE RMSE. Conversely, a realistic level of white noise added to incoming radiation and, to a lesser extent, air temperature, deteriorates TSEB predictions with the RMSE of LE simulations increasing from the reference value of 55 W m⁻² to nearly 60 W m⁻². Indeed, while the partition between latent and sensible fluxes is moderated by the slowly varying soil moisture content in SEtHyS, TSEB partitioning relies on measured available energy and surface temperature inputs only. By contrast, noisier wind speed, air temperature and, to a lesser extent, solar radiation, significantly deteriorate sensible heat estimations for SEtHyS. TSEB appears, on average, less sensitive to noisy meteorological inputs for H. When considering extreme errors (Fig. 5) on meteorological forcing, the same variables are identified as the most sensitive ones: R_a, R_g and T_a for TSEB, and R_a, R_g and RH for SEtHyS. However, whilst SEtHyS's performance remains acceptable despite these high errors on forcing, TSEB's performance for both LE and H collapses in response to incoming radiation errors in particular. Interestingly enough, incoming solar radiation can also be retrieved from satellite measurements such as Meteosat Second Generation (MSG). In particular, Carrer et al. (2012) points out a significant improvement of MSG derived shortwave and longwave downwelling surface radiation with regards to the SAFRAN analysis system, which could represent a valuable alternative for regional assessment of evapotranspiration. To limit the sensitivity to T_a and absolute surface–air temperature differences, time differencing modeling schemes have been developed (Anderson et al., 1997; Norman et al., 2000) with particular interest regarding large-scale applications, provided early morning atmospheric soundings and/or at least two near acquisitions of T_rad are available.

Figure 5 Sensitivity analysis of both models to positive and negative realistic biases applied to meteorological and vegetation inputs.

3.2.4 Sensitivity analysis to vegetation forcing inputs

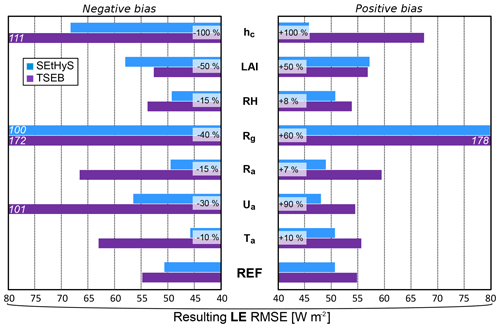
The focus here is on evaluating the bias effect on SEtHyS and TSEB flux predictions. Indeed, on the one hand, errors on vegetation characteristics are much more difficult to evaluate as in situ measurements are time-consuming and therefore not always available at a small time interval. On the other hand, biases on satellite estimates are more likely to occur than white noise errors due to the detection limit of visible sensors in the case of sparse vegetation and a possible saturation effect when the leaf area index is above 3 m² m⁻². On average, Claverie (2011); Claverie et al. (2012) highlight a potential bias of 20 % for the LAI estimated from FORMOSAT data. Canopy height (h_c) is not directly available from remote sensing data but can be estimated from the LAI. Canopy height (h_c) was deduced from LAI = f(h_c) relations, applying linear regression to each culture and phenological stage available in our in situ data. This methodology provides estimations of h_c with a MAPD of 30 %, and “extreme” bias up to 100 % (Bigeard, 2014). The results shown in Fig. 5 demonstrate that TSEB and SEtHyS sensitivity to bias on the LAI remains limited. By contrast, TSEB and, to a lesser extent, SEtHyS exhibit a much higher sensitivity to bias on canopy height (h_c) due to erratic transfer resistances when h_c is too close to the height of the micrometeorological measurements, or when soil is considered bare (h_c=0). As LE is computed from the residual of the energy budget in TSEB, a problem is observed with respect to both H and LE fluxes, whereas LE is less affected in SEtHyS (not shown).

3.2.5 Sensitivity analysis to radiative temperature for TSEB

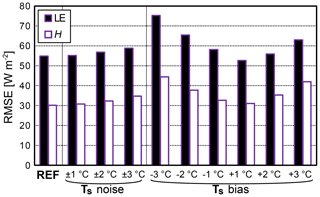
The comparison between in situ LST measurements and retrieval from the LANDSAT7 and ASTER images yielded a maximum absolute difference of 2.2 K (four points), which is in agreement with values reported in the literature ranging from 1 to 3 ^∘C (Hall et al., 1992; Gillespie et al., 1998; Schmetz et al., 2002; Peres and DaCamara, 2004; Li, 2004; Liu et al., 2006; Wan, 2008, among others). As the LST is expected to be a determining input of TSEB, an in-depth analysis of sensitivity to this variable was carried out considering white noise and biases of 1, 2 and 3 ^∘C. Indeed, the spatial scale mismatch between the spatial sensor operating, at best, at a 90 m resolution and the SVAT model operating at the scale of an “agricultural unit” (potentially lower than a parcel) is likely to be important. Regarding the strong heterogeneity of the agricultural landscape (in terms of crops, development stage, irrigation, hydric stress, etc.), bias is also likely to be important and quite impossible to correct. The results of adding errors to measured radiative temperature on TSEB flux predictions are shown in Fig. 6. For limited white noise up to 2 K, the drop in TSEB skill is small on both H and LE. By contrast, biases are much more influential. In particular, a negative bias of 3 K could worsen the LE RMSE from 58 to 78 W m⁻². Interestingly enough, a negative bias, which is likely to occur when the observed pixel is partly irrigated (i.e., cold), while the agricultural unit studied is under stress (i.e., hot) for instance, has a stronger effect than a positive bias. This is likely to occur in many practical situations: a mixed pixel including forest and stressed field, irrigation heterogeneity within a pixel (for instance irrigation that is in progress within a field including a gravity or center pivot system or the use of a localized sprinkler).

Figure 6 Sensitivity analysis to radiative temperature input for TSEB.

3.2.6 Sensitivity analysis to water inputs and soil water content for SEtHyS

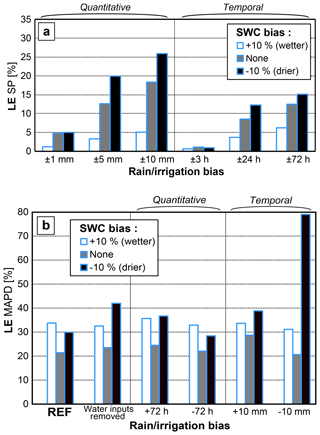
Water inputs, i.e., rainfall and irrigation, are difficult to assess accurately over an agricultural landscape when the spatial scale considered exceeds 1 km². Even in this case, a good knowledge of irrigation input at the field level requires costly field surveys, as farmers' associations or regional offices responsible for irrigation water often work at a larger scale made of several plots. In addition to this potential uncertainty, the initial condition of the soil water content (SWC) should also be considered uncertain as a result – for instance, from errors piling up from previous inputs. Figure 7 shows the results of a sensitivity analysis of the models to these three factors: uncertainty with respect to irrigation amount and timing and with respect to the SWC initial condition. Unsurprisingly, all factors had a significant impact on the LE predictions. Even if input timing was correct, a bias of 1 mm with correct initial SWC worsened the SEtHyS skill by 5 %. If the input bias reaches 10 mm and the initial SWC is negatively biased by the same amount, the loss of model performance is above 25 %. Considering that the total amount of an irrigation round can reach 100 mm, a 10 mm uncertainty is very likely to occur in practice. In addition, a negative bias on SWC impacts significantly more LE predictions than a positive bias. Indeed, going towards drier conditions may lead to stress and, as a consequence, to a drastic drop in the predicted LE compared with the reference, whereas increasing the SWC when the surface is already close to potential conditions will not have any effect on LE. Within this context, data assimilation of surface soil moisture retrieved from spatial sensors could provide an interesting solution to improve the accuracy of SWC initial conditions (Prevot et al., 1984; Demarty et al., 2005; Li et al., 2006). By contrast, the timing, although important, has a secondary influence on model skill. Even when water input is applied 3 d before or after the actual date, the decrease in LE prediction skill remains limited at around 15 %. Indeed, considering that agricultural landscape is often well-watered in order to maximize production, vegetation is able, through transpiration processes, to maintain high levels of LE over long periods. The resulting dynamics of LE is relatively smooth compared with bare soil that is dominated by evaporation processes. Finally, the main conclusion is that emphasis should be laid on a water amount prescription, whereas timing appears of secondary importance.

Figure 7 SEtHyS sensitivity analysis to rain and irrigation inputs, with influence of bias on soil water content (SWC). SP in (a) is defined as SP = $\frac{|{\mathrm{LE}}_{\left[\mathrm{positive}\mathrm{bias}\right]}-{\mathrm{LE}}_{\left[\mathrm{negative}\mathrm{bias}\right]}|}{{\mathrm{LE}}_{\left[\mathrm{reference}\right]}}$.

3.2.7 Cross sensitivity analyses of models through linkage of radiative temperature and SWC

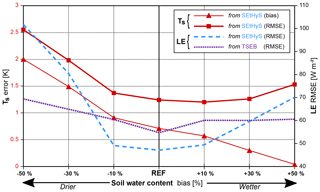
Sensitivity of the TSEB and SEtHyS models to surface water status has to be detailed in order to compare how the models respond to a change in water conditions. The difficulty lies in the conceptual difference between both models: surface water status is an explicit variable state for SEtHyS, whereas, surface radiative temperature is an indirect proxy of the surface hydric conditions in the TSEB model. For the set of simulation periods considered in this study, initial soil water contents (for surface and root zone) were biased in SEtHyS inputs by ±10 %, ±30 % or ±50 %. As a consequence, the simulated radiative surface temperature by SEtHyS diverges from the reference, and the differences between both temperature simulation time-series are added to the TSEB model input radiative temperature as an equivalent water bias converted into temperature. It is assumed that the SEtHyS model, used with a calibrated set of parameters, is able to simulate a realistic temperature equivalent to the water status biases (Coudert et al., 2006; Coudert and Ottlé, 2007).

Figure 8 shows the average variation of the temperature bias as a function of the SWC bias. As expected, temperature increases with water content deficit. Beyond the [−10 %–+10 %] interval, temperature and water contents biases evolve quasi-linearly with a greater increment for dry conditions. On the contrary, one can expect a more rapid limitation in temperature decrease with wet conditions, when soil reaches field capacity or saturation. The consequence with respect to the evapotranspiration deviation from reference clearly shows that beyond the [−10 %–+10 %] interval for water content biases, the error also increases linearly with a greater increment for dry conditions. Under −20 % bias, the impact on LE flux exceeds 50 W m⁻². This result is important for our purpose to spatialize models for evapotranspiration estimates, as accurate root zone and surface water content retrievals from thermal and microwave remote sensing are a real challenge over heterogeneous landscapes (Barrett and Renzullo, 2009; Hain et al., 2011). The shift in temperature simulated by SEtHyS from −50 % to +50 % water content biases does not exceed 2 K and therefore lies within the typical remotely sensed surface temperature uncertainty range. For such a temperature bias, the TSEB model evapotranspiration divergence is lower than 40 W m⁻². As a consequence, TSEB is less “reactive” to soil water content variation compared with the SEtHyS model. This result is critical for dry or stress conditions as previously mentioned. Actually, water status is only taken into account in the TSEB model via the surface temperature, which is not sufficient, and no additional limitation of surface evapotranspiration is carried out by modulating, for instance, the Priestley–Taylor parameter.

Figure 8 Error of T_s simulated by SEtHyS for increased and decreased SWC, and impact on models LE estimates. TSEB is forced with T_s estimates from SEtHyS.

4 Discussion

4.1 Influence of the parameters sets for model spatialization

The four calibration cases for the SEtHyS model going from site and period specific to more generic parameters from the literature are considered in order to evaluate the potential loss of model performance when specific calibration is not possible due to lack of data. Figure 9 shows the impact of the parameters set used on the SEtHyS performance to predict LE fluxes. Global results (for all crop classes and the whole cultural cycles) corresponding to the label “overview” in Fig. 9 give a MAPD of 30 % for the generic “culture only” set of parameters. This result does not differ much from the performance obtained with more specific sets of parameters “pheno + cult ” or “optimal” showing a 25 % and 23 % MAPD, respectively. However, when a set of parameters from another crop class is used, the MAPD reaches 58 %. The finest analysis by phenological stage indicates an overall stability of the results with the pheno + cult parameter set with regards to culture only. There are actually two exceptions: one for the vegetation senescence periods which require specific parameter sets – a mean set of parameters for the crop class increases MAPD from 30 % to 40 %; and a second that relates to crop rising periods – a generic one based only on the crop class (culture only) increases MAPD up to 50 % compared with 45 % for pheno + cult when taking the phenology into account. As a conclusion, a mean parameter set associated with a specific crop without considering phenology implies only a slight decrease in the performance for growth or maximum vegetation development. By contrast, the relevance of the parameter sets becomes noticeable when specific information is not available for rising and senescence periods (including potential water stress phases). With the same purpose, a specific analysis is dedicated to the Priestley–Taylor α_PT key parameter of the TSEB model in the next section.

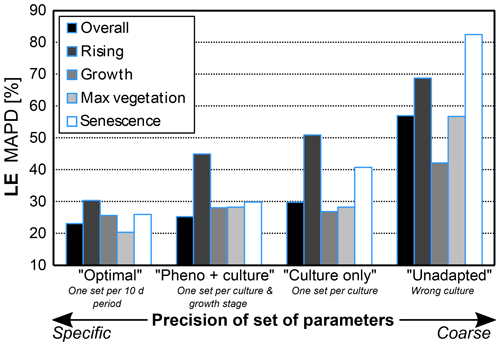
Figure 9 Impact of the precision of sets of parameters on simulated fluxes;: “optimal” is the most accurate per 10 d period; “pheno + culture” refers to the fact that the per culture and phase of growth is used for spatialization; “culture only” refers to per culture (when only soil occupancy is known); and “unadapted” is incoherent (wrong culture).

4.2 A deeper look at the α_PT parameter for spatialization

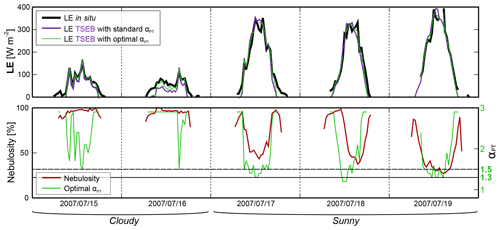
A first estimation of the LE_vegetation canopy transpiration flux is obtained from the Priestley–Taylor approximation and depends on the fraction of green f_g and on the α_PT parameter. Most studies (Norman et al., 1995; Kustas and Norman, 1999; French et al., 2003; Anderson et al., 1997, 2008; Li et al., 2006, 2008, among others) have generally used a α_PT value of about 1.3 for semiarid or subhumid agricultural areas. However, this value may vary with vegetation type (as mentioned in Norman et al., 1995), low values of LAI, atmospheric demand (Anderson et al., 2008; Agam et al., 2010; Colaizzi et al., 2014) or dry air advection conditions (Kustas and Norman, 1999). As a first step, the calibration is performed for the midday time interval series over various surface and atmospheric conditions in order to be compared with previous studies using TSEB instantaneously for water flux mapping purpose when thermal imagery is available.

Figure 10 shows the influence of α_PT values on H and LE fluxes for wheat, corn and sunflower crops over the sites in both the southwest of France and Morocco. Optimal values for irrigated wheat in Morocco (semiarid climate) and sunflower in the southwest of France (temperate climate) are close to the original value of 1.3 from the literature. For wheat and irrigated corn in the southwest of France, mean optimal values are higher and reach 1.6 for wheat. A mean optimal value of 1.5 is obtained for temperate climate, whereas a lower value of 1.25 is obtained for a semiarid climate. In a second step, the 30 min data are used for the calibration in order to study the diurnal cycle of the α_PT parameter. The α_PT parameter shows a U-shaped diurnal cycle evolution, as displayed in Fig. 11, with smaller values around midday and higher values in both the morning and evening when stability conditions are changing, enhancing the LE_vegetation transpiration canopy flux. This is particularly emphasized under clear-sky conditions, when TIR data from space are most likely to be collected. The original α_PT parameter is defined for a system at equilibrium with constant temperature, a condition which is specifically not met in the morning and in the evening when temperature temporal gradients are highest. As a consequence, such variations integrated over the diurnal cycle lead to slightly higher α_PT fixed optimal values for daily 30 min time interval simulations. Moreover, results indicate a decrease of the RMSE of about 10 % for both the H and LE fluxes when optimal values at the original time interval are used instead of a fixed daily average. Nevertheless, as more error on flux estimations is likely to occur around midday, when turbulent fluxes are maximal, the optimal daily value of α_PT tends towards its value around midday and is not much affected by increased morning and evening values. Despite the fact that thermal imagery from space is not available with the presence of clouds, the emergence of drone acquisition (Hoffmann et al., 2016) makes the characterization of α_PT under these conditions of special interest. On cloudy days, Fig. 11 highlights that fixed daily optimal values of 1.8–2 (higher instantaneously) are required to optimize H and LE fluxes, again enhancing the LE_vegetation transpiration flux for such reduced atmospheric demand. Hence, for simulation under cloudy conditions, α_PT value can be raised by +0.4 in a view to interpolating time series between satellite overpasses or running the TSEB model with in situ or low-altitude aircraft remotely sensed surface temperature. An improvement of about 10 % on the LE flux simulation is likely to be expected when taking the abovementioned impact of vegetation and cloudy condition considerations on the α_PT parameter retrieval into account. However, Colaizzi et al. (2014) noted that larger α_PT values did not mitigate the discrepancies on the evaporation (E) and transpiration (T) components of the total latent heat flux (ET). These authors proposed a revised version of TSEB, replacing the Priestley–Taylor formulation with the Penman–Monteith equation in order to better account for large variations of water vapor pressure deficits and correct the evaporation, transpiration and total LE simulations. Thus, Boulet et al. (2015) built the SPARSE model based on Penman–Monteith; this model showed satisfying performance with respect to the Morocco wheat site dataset, which was better than that of TSEB with default parameter values.

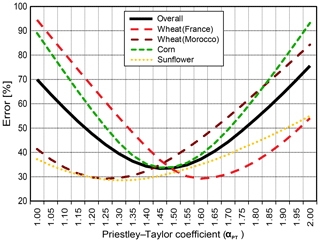
Figure 10 Sensitivity analyses of the α_PT TSEB parameter during vegetation periods. Error was computed as a cost function (Euclidian distance) taking the MAPD of LE and H into account simultaneously: error = $\sqrt{{\mathrm{MAPD}}_{\left[\mathrm{LE}\right]}^{\mathrm{2}}+{\mathrm{MAPD}}_{\left[H\right]}^{\mathrm{2}}}$.

Figure 11 Influence of using optimal α_PT or averaged α_PT on LE estimates by TSEB, and the influence of nebulosity on optimal α_PT estimates. Nebulosity was computed using photosynthetically active radiation (PAR) measurements as follows: nebulosity = $\frac{{\mathrm{PAR}}_{\left[\mathrm{diffuse}\right]}}{{\mathrm{PAR}}_{\left[\mathrm{total}\right]}}$. Sample from Auradé 2007 sunflower plot.

5 Summary and conclusions

Monitoring evapotranspiration at the field scale over a large agricultural landscape is a challenge as it requires detailed information about the surface state and meteorological forcing, which is prone to uncertainties and unavailability. This study aimed at evaluating the ability of a SVAT model (SEtHyS, described in Coudert et al., 2006) and an instantaneous energy balance model (TSEB, described in Norman et al., 1995) for mapping evapotranspiration over agricultural landscapes as a preliminary step to the joint use of both approaches via data assimilation, as first proposed by Crow et al. (2005, 2008). Within this context, our specific objectives were (1) to assess the skills and domains of validity of both modeling approaches at the field scale for various crop conditions, and (2) to characterize model errors resulting from realistic uncertainties on inputs that can be expected from application at the landscape scale. To this end, this study takes advantage of a large and unique in situ database spanning two climates and seven different crop cycles. The main results drawn from this study can be summarized as follows:

• On average, over the entire database, both models provide close statistical metrics with respect to daily average values of LE (RMSEs of 36 W m⁻² for SEtHyS vs. 39 W m⁻² for TSEB), whereas TSEB is slightly better regarding H predictions (21 vs. 29 W m⁻²). This emphasizes the remarkable performance of the TSEB model compared with the relative simplicity of the approach, all the more given that SEtHyS parameters are calibrated for each crop, each phenological stage and each site.

• SEtHyS skill appears more stable regardless of the growth stage or crop, whereas limitations of the TSEB model are clearly emphasized during rising and senescence stages.

• SEtHyS simulations of LE are less sensitive to noisy meteorological inputs than TSEB, for which performances are significantly worse – particularly when incoming radiation inputs are uncertain. Indeed, the partitioning between latent and sensible fluxes is moderated by the slowly varying soil moisture content in SEtHyS, whereas the TSEB partitioning relies on the instantaneous measurement of available energy and surface temperature input only.

• The sensitivity analysis of surface temperature, which is one of the more important inputs for TSEB, shows that the drop in TSEB skill is small on both H and LE for limited white noise up to 2 K. By contrast, biases are much more influential as a negative bias of 3 K could deteriorate the LE RMSE from 58 to 78 W m⁻².

• Similarly, the sensitivity of SEtHyS skills to uncertain water inputs and initial soil water content was also analyzed and showed that emphasis should be put on water amount retrieval, whereas timing of water supply appears of secondary importance; in particular a 10 mm negative bias on input coupled with a negatively biased initial SWC of 10 % with the same level lead to a loss of model performance above 25 %.

• A cross sensitivity analysis of the TSEB and SEtHyS models to surface water status was carried out by simulating several surface temperature time series with SEtHyS and biased soil water contents (±10 %, ±30 % or ±50 %). The difference in surface temperature compared with a reference simulation is added as input to the TSEB model as an equivalent water bias converted into temperature. The shift in temperature simulated by SEtHyS for −50 % to 50 % water contents biases does not exceed 2 K and is therefore within the typical remotely sensed surface temperature uncertainty range. For such a temperature bias, the TSEB model evapotranspiration divergence is lower than 20 W m⁻², whereas it reaches 50 W m⁻² for SEtHyS, which indicates that TSEB is less “reactive” to soil water contents variations than the SEtHyS model.

• Still with the intention to anticipate uncertainties induced by spatial distribution, SEtHyS was run with various sets of parameters with decreasing accuracies regarding the phenological stage and type of culture. This showed that when no precise information is known about surface condition, a valuable trade-off is to consider a set of parameters only representative of the type of crop, provided vegetation is sufficiently developed. By contrast, the relevance of the parameter sets becomes noticeable when specific information is not available for rising and senescence periods (including potential water stress periods).

• For TSEB, an in-depth study of the Priestley–Taylor parameter α_PT highlighted optimal values of 1.8–2 under cloudy conditions, which is of particular interest due to the emergence of low-altitude drone acquisition, while most studies focus on clear-sky conditions when TIR acquisition from space is possible.

In addition to the characterization of the model and background errors, this study provided some insights to guide the implementation of a data assimilation algorithm at the scale of an agricultural landscape for the joint use of both approaches by highlighting deficiencies in specific conditions. Nevertheless, our current database suffers from a lack of hydric stress conditions and does not allow for the precise characterization of this crucial aspect. A new experiment in Morocco (seasons 2017–2018 and 2018–2019) focusing on water stress on a wheat field is currently being carried out. Our perspectives will focus on the exploitation of TIR data by using TSEB as a proxy to be assimilated in SEtHyS following Crow et al. (2008), but also by taking advantage of the MCIP methodology to tune parameters to better fit surface temperature measurements following Coudert et al. (2008). Special consideration will be given to diurnal dynamics and to the exploitation of relative differences inside plots and inter-plots.

Appendix A: SEtHyS main equations

This section presents the governing equations for the SEtHyS SVAT model variables.

A1 Basic set of equations for the SEtHyS model

The mass and energy budget is solved jointly for both soil and vegetation sources using the following system:

$$\begin{array}{}\text{(A1)}& \left\{\begin{array}{l}{R}_{\mathrm{n}\left[\mathrm{soil}\right]}=H_{\left[\mathrm{soil}\right]}+{\mathrm{LE}}_{\left[\mathrm{soil}\right]}+G\\ R_{\mathrm{n}\left[\mathrm{veg}\right]}=H_{\left[\mathrm{veg}\right]}+{\mathrm{LE}}_{\left[\mathrm{veg}\right]}\\ H=H_{\left[\mathrm{veg}\right]}+H_{\left[\mathrm{soil}\right]}\\ E=E_{\left[\mathrm{veg}\right]}+E_{\left[\mathrm{soil}\right]}\end{array}\right.,\end{array}$$

where R_n[soil] and R_n[veg] are the respective net radiations at the soil and vegetation levels and G is the soil heat flux. Parameterization of the soil behavior is based on Deardorff's formalism (Deardorff, 1978). The soil surface temperature T_[soil], the vegetation temperature T_[veg], the air temperature inside the canopy T_[canopy] and the air humidity inside the canopy q_[canopy] are determined by a first-order linearization of the previous equation system.

The soil surface temperature prediction method utilized is the force–restore method (Bhumralkar, 1975; Blackadar, 1976) and requires deep soil temperature T₂. T₂ can be estimated from the mean air temperature over the preceding 24 h for short-range studies (Blackadar, 1976). The heat capacity is prescribed by the model from de Vries (1963) and hydrodynamic properties result from pedotransfer functions (retention curve, hydraulic conductivity) based on the approach from Genuchten (1980) under the Mualem (1976) hypothesis.

The prognostic equation for ground surface temperature is written as follows:

$$\begin{array}{}\text{(A2)}& {\displaystyle \frac{\partial T_{\left[\mathrm{soil}\right]}}{\partial t}}={\displaystyle \frac{\mathrm{2}\sqrt{\mathit{\pi }}}{C_{\mathrm{e}}}}\left(R_{\mathrm{n}}-H-\mathrm{LE}\right)-{\displaystyle \frac{\mathrm{2}\mathit{\pi }}{\mathit{\tau }}}\left(T_{\left[\mathrm{soil}\right]}-T_{\mathrm{2}}\right).\end{array}$$

The factor C_e is an equivalent heat capacity related to the diurnal thermal wave damping layer. In SEtHyS, the parameterization of the equivalent heat capacity has been weighted by introducing an empirical factor (F_therm: see the parameter list in Table 2) compared with Deardorff (1978).

Deardorff (1978) proposed a similar approach for ground soil moisture, leading to the following equations:

$$\begin{array}{}\text{(A3)}& {\displaystyle }& {\displaystyle \frac{\partial w_{\mathrm{g}}}{\partial t}}=-{\displaystyle \frac{E_{\mathrm{g}}+\mathrm{0.2}{E}_{\mathrm{v}}\left(\frac{w_{\mathrm{g}}}{w_{\max }}\right)-P}{{\mathrm{dp}}_{\mathrm{1}}}}-C\left(w_{\mathrm{g}},w_{\mathrm{2}}\right)\left(w_{\mathrm{g}}-w_{\mathrm{2}}\right)\text{(A4)}& {\displaystyle }& {\displaystyle \frac{\partial w_{\mathrm{2}}}{\partial t}}=-{\displaystyle \frac{E_{\mathrm{g}}+E_{\mathrm{v}}-P}{{\mathrm{dp}}_{\mathrm{2}}}},\end{array}$$

where w_max is the soil moisture at soil saturation; w_g and w₂ are surface and root zone water contents, respectively; P is the precipitation rate; and dp₁ and dp₂ are the surface and root zone layers depths, respectively.

A2 Radiative budget

Incoming radiation partitioning for the optical (VIS) and infrared (IR) wavelengths is performed using a shielding factor σ_f that is tightly linked to vegetation density. Its expression, which considers a spherical distribution of leaves (François, 2002) with the hypothesis of diffuse radiation for the longwave domain and direct vertical radiation in the shortwave domain, is as follows:

$$\begin{array}{}\text{(A5)}& \left\{\begin{array}{ll}{\mathit{\sigma }}_{\mathrm{f}}=\mathrm{1}-e^{-\mathrm{0.825}\mathrm{LAI}}& \mathrm{for}\mathrm{the}\mathrm{longwave}\mathrm{domain}\\ {\mathit{\sigma }}_{\mathrm{f}}=\mathrm{1}-e^{-\mathrm{0.5}\mathrm{LAI}}& \mathrm{for}\mathrm{the}\mathrm{shortwave}\mathrm{domain}\end{array}\right..\end{array}$$

The radiative budget is then solved jointly at the soil and at the vegetation level for short and long wavelengths. Concerning short wavelengths, soil albedo (α_soil) is linearly linked to surface soil moisture. Vegetation albedo (α_veg) is a model parameter. The net radiation for the soil (R_n[soil],SW) and for the vegetation (R_n[veg],SW) are as follows (“Mod3” parameterization as proposed in François, 2002):

$$\begin{array}{}\text{(A6)}& R_{\mathrm{n}\left[\mathrm{soil}\right],\mathrm{SW}}=S^{\downarrow }{\displaystyle \frac{\left(\mathrm{1}-{\mathit{\sigma }}_{\mathrm{f}}\right)\left(\mathrm{1}-{\mathit{\alpha }}_{\mathrm{soil}}\right)}{\mathrm{1}-{\mathit{\sigma }}_{\mathrm{f}}{\mathit{\alpha }}_{\mathrm{veg}}{\mathit{\alpha }}_{\mathrm{soil}}}}.\end{array}$$

At canopy level this becomes

$$\begin{array}{}\text{(A7)}& R_{\mathrm{n}\left[\mathrm{veg}\right],\mathrm{SW}}=S^{\downarrow }\left(\mathrm{1}-{\mathit{\alpha }}_{\mathrm{veg}}\right){\mathit{\sigma }}_{\mathrm{f}}\left[\mathrm{1}+{\mathit{\alpha }}_{\mathrm{soil}}{\displaystyle \frac{\left(\mathrm{1}-{\mathit{\sigma }}_{\mathrm{f}}\right)}{\mathrm{1}-{\mathit{\sigma }}_{\mathrm{f}}{\mathit{\alpha }}_{\mathrm{soil}}{\mathit{\alpha }}_{\mathrm{veg}}}}\right],\end{array}$$

where S^↓ is the incoming shortwave radiation.

Concerning long wavelengths, the net radiation for soil (R_n[soil],LW) and vegetation (R_n[veg],LW) are given by

$$\begin{array}{}\text{(A8)}& {\displaystyle }\begin{array}{rl}{R}_{\mathrm{n}\left[\mathrm{soil}\right],\mathrm{LW}}& =\left(\mathrm{1}-{\mathit{\sigma }}_{\mathrm{f}}\right){\displaystyle \frac{{\mathit{\epsilon }}_{\mathrm{g}}\left(R_{\mathrm{a}}^{\downarrow }-\mathit{\sigma }{T}_{\left[\mathrm{soil}\right]}^{\mathrm{4}}\right)}{\mathrm{1}-{\mathit{\sigma }}_{\mathrm{f}}\left(\mathrm{1}-{\mathit{\epsilon }}_{\mathrm{f}}\right)\left(\mathrm{1}-{\mathit{\epsilon }}_{\mathrm{g}}\right)}}\\ & -{\displaystyle \frac{{\mathit{\epsilon }}_{\mathrm{g}}{\mathit{\epsilon }}_{\mathrm{f}}{\mathit{\sigma }}_{\mathrm{f}}\mathit{\sigma }\left(T_{\left[\mathrm{soil}\right]}^{\mathrm{4}}-T_{\left[\mathrm{veg}\right]}^{\mathrm{4}}\right)}{\mathrm{1}-{\mathit{\sigma }}_{\mathrm{f}}\left(\mathrm{1}-{\mathit{\epsilon }}_{\mathrm{f}}\right)\left(\mathrm{1}-{\mathit{\epsilon }}_{\mathrm{g}}\right)}}\end{array}\text{(A9)}& {\displaystyle }\begin{array}{rl}{R}_{\mathrm{n}\left[\mathrm{veg}\right],\mathrm{LW}}& ={\mathit{\sigma }}_{\mathrm{f}}\left[{\mathit{\epsilon }}_{\mathrm{f}}\left(R_{\mathrm{a}}^{\downarrow }-\mathit{\sigma }{T}_{\mathrm{f}}^{\mathrm{4}}\right)+{\displaystyle \frac{{\mathit{\epsilon }}_{\mathrm{g}}{\mathit{\epsilon }}_{\mathrm{f}}\mathit{\sigma }\left(T_{\left[\mathrm{soil}\right]}^{\mathrm{4}}-T_{\left[\mathrm{veg}\right]}^{\mathrm{4}}\right)}{\mathrm{1}-{\mathit{\sigma }}_{\mathrm{f}}\left(\mathrm{1}-{\mathit{\epsilon }}_{\mathrm{f}}\right)\left(\mathrm{1}-{\mathit{\epsilon }}_{\mathrm{g}}\right)}}\right]\\ & +{\mathit{\sigma }}_{\mathrm{f}}{\displaystyle \frac{\left(\mathrm{1}-{\mathit{\epsilon }}_{\mathrm{f}}\right)\left(\mathrm{1}-{\mathit{\epsilon }}_{\mathrm{g}}\right){\mathit{\epsilon }}_{\mathrm{f}}\left(R_{\mathrm{a}}^{\downarrow }-\mathit{\sigma }{T}_{\left[\mathrm{veg}\right]}^{\mathrm{4}}\right)}{\mathrm{1}-{\mathit{\sigma }}_{\mathrm{f}}\left(\mathrm{1}-{\mathit{\epsilon }}_{\mathrm{f}}\right)\left(\mathrm{1}-{\mathit{\epsilon }}_{\mathrm{g}}\right)}}.\end{array}\end{array}$$

Direct solar shortwave radiation (S^↓) and atmospheric longwave radiation (R^↓) are input model data.

The thermal infrared surface temperature T_B (observed above the canopy) results from the partitioning of the surface and the radiative interaction between soil (whose temperature is T_[soil]) and the vegetation above (whose temperature is T_[veg]).

A3 Heat flux expressions

The mass and energy transfers in equilibrium with net surface radiation are momentum, and sensible and latent heat fluxes. A conductance formalism allows for their expression by considering the canopy as a single vegetation layer (at some height Z_af) above ground (Thom, 1972). Thus, following the electrical (Ohm's law) analogy, soil surface, leaves surface, air canopy space and atmosphere above canopy are the levels between which differences of potential (temperature and humidity gradients) and transfer coefficients, i.e., aerodynamic conductances, can be calculated.

Heat fluxes H and LE (sensible and latent heat fluxes, respectively) are then determined at three levels: at the atmospheric reference level,

$$\begin{array}{}\text{(A10)}& {\displaystyle }& {\displaystyle }H=\mathit{\rho }{c}_{\mathrm{p}}{C}_{\mathrm{h}}\left(T_{\left[\mathrm{canopy}\right]}-T_{\mathrm{a}}\right)\text{(A11)}& {\displaystyle }& {\displaystyle }\mathrm{LE}={\displaystyle \frac{\mathit{\rho }{c}_{\mathrm{p}}}{\mathit{\gamma }}}{C}_{\mathrm{h}}\left(q_{\left[\mathrm{canopy}\right]}-q_{\mathrm{a}}\right)\end{array}$$

at the vegetation level,

$$\begin{array}{}\text{(A12)}& {\displaystyle }& {\displaystyle }{H}_{\left[\mathrm{veg}\right]}=\mathit{\rho }{c}_{\mathrm{p}}{C}_{\mathrm{h}\left[\mathrm{veg}\right]}\left(T_{\left[\mathrm{veg}\right]}-T_{\left[\mathrm{canopy}\right]}\right)\text{(A13)}& {\displaystyle }& {\displaystyle }{\mathrm{LE}}_{\left[\mathrm{veg}\right]}={\displaystyle \frac{\mathit{\rho }{c}_{\mathrm{p}}}{\mathit{\gamma }}}{C}_{\mathrm{h}\left[\mathrm{veg}\right]}{R}^{\prime }\left(q_{\mathrm{sat}}\left(T_{\left[\mathrm{veg}\right]}\right)-q_{\left[\mathrm{canopy}\right]}\right)\end{array}$$

and at the ground level,

$$\begin{array}{}\text{(A14)}& {\displaystyle }& {\displaystyle }{H}_{\left[\mathrm{soil}\right]}=\mathit{\rho }{c}_{\mathrm{p}}{C}_{\mathrm{h}\left[\mathrm{soil}\right]}\left(T_{\left[\mathrm{soil}\right]}-T_{\left[\mathrm{canopy}\right]}\right)\text{(A15)}& {\displaystyle }& {\displaystyle }{\mathrm{LE}}_{\left[\mathrm{soil}\right]}={\displaystyle \frac{\mathit{\rho }{c}_{\mathrm{p}}}{\mathit{\gamma }}}{C}_{\mathrm{h}\left[\mathrm{soil}\right]}{C}_{\mathrm{s}}\left(q_{\mathrm{sat}}\left(T_{\left[\mathrm{soil}\right]}\right)-q_{\left[\mathrm{canopy}\right]}\right).\end{array}$$

Here

$$\begin{array}{}\text{(A16)}& {\displaystyle }& {\displaystyle }\mathrm{LE}={\mathrm{LE}}_{\left[\mathrm{soil}\right]}+{\mathrm{LE}}_{\left[\mathrm{veg}\right]}\text{(A17)}& {\displaystyle }& {\displaystyle }H=H_{\left[\mathrm{soil}\right]}+H_{\left[\mathrm{veg}\right]}\end{array}$$

and the G conduction heat flux in soil is the residual of the energy budget:

$$\begin{array}{}\text{(A18)}& G=R_{\mathrm{n}\left[\mathrm{soil}\right],\mathrm{LW}}+R_{\mathrm{n}\left[\mathrm{soil}\right],\mathrm{SW}}-H_{\left[\mathrm{soil}\right]}-{\mathrm{LE}}_{\left[\mathrm{soil}\right]},\end{array}$$

where C_p is the specific heat at constant pressure; γ is the psychrometric constant; T and q are temperature and water vapor pressure, respectively; and a, g and “canopy” are indices relative to air, ground, and canopy air space, respectively.

C_h, C_h[veg] and C_h[soil] are the respective aerodynamic conductances between the canopy air space and the overlaying atmosphere, leaf surfaces and canopy air space, and ground and canopy air space; the R^′ factor is defined below. These variables are derived from the eddy flux theory between two atmospheric levels. In SEtHyS model, the formulation follows the parameterization proposed by Shuttleworth and Wallace (1985) with a constant extinction coefficient in the exponential wind speed profile.

C_s is the ground evaporation conductance; it depends on soil moisture conditions and potential evaporation E_pot[soil] (Bernard et al., 1986; Wetzel and Chang, 1988; Soares et al., 1988):

$$\begin{array}{}\text{(A19)}& C_{\mathrm{s}}=\min \left(\mathrm{1},{\displaystyle \frac{E_{\lim }}{E_{\mathrm{po}\left[\mathrm{soil}\right]}}}\right),\end{array}$$

where E_lim depends on soil properties (composition and moisture). Soares et al. (1988) gives the expression:

$$\begin{array}{}\text{(A20)}& E_{\lim }=a_{\mathrm{Elim}}\left(\exp \left(b_{\mathrm{Elim}}{\left(w_{\mathrm{g}}-w_{\mathrm{resid}}\right)}^{\mathrm{2}}\right)-\mathrm{1}\right).\end{array}$$

a_Elim and b_Elim are model parameters related to soil evaporation response.

The R^′ factor in Eq. (A13) accounts for stomatal resistance and for the fact that only the fraction of the canopy area which is not covered by water will contribute to evapotranspiration. Thus, Deardorff (1978) proposed the following expression:

$$\begin{array}{}\text{(A21)}& {\displaystyle }& {\displaystyle }{R}^{\prime }={\left({\displaystyle \frac{\mathrm{dew}}{d_{\max }}}\right)}^{\mathrm{2}/\mathrm{3}}+\left[\mathrm{1}-{\left({\displaystyle \frac{\mathrm{dew}}{d_{\max }}}\right)}^{\mathrm{2}/\mathrm{3}}\right]{\displaystyle \frac{\mathrm{1}}{\left(\mathit{\beta }+C_{\mathrm{fh}}\mathrm{RST}\right)}},\text{(A22)}& {\displaystyle }& {\displaystyle }{R}^{\prime }=\mathrm{1}\mathrm{for}\mathrm{condensation},\end{array}$$

where “dew” (“d_max”) is the fraction (the maximal fraction) of free water on the foliage. RST is the stomatal resistance, and this factor governs the canopy participation to the energy budget and is responsible for partitioning between the sensible and latent heat fluxes.

In the model, calculation of RST is based on Collatz et al. (1991, 1992) and is the same as in the SiB models (Sellers et al., 1992, 1996). Biophysical and environmental variables manage photosynthesis processes giving the CO₂ assimilation rate and then stomatal conductance of the foliage.

Ball (1988) gives the following leaf stomatal conductance expression:

$$\begin{array}{}\text{(A23)}& g_{\mathrm{s}}=m{\displaystyle \frac{A_{\mathrm{n}}}{c_{\mathrm{s}}}}{h}_{\mathrm{s}}p+b,\end{array}$$

where A_n is net assimilation rate calculated by the model of Farquhar et al. (1980); c_s and h_s are the CO₂ partial pressure and relative humidity at leaf surface, respectively; p is atmospheric pressure; and m and b are empirical factors from observations depending on vegetation type (C₃ or C₄).

The assimilation rate is determined by means of three factors: a photosynthetic enzyme (Rubisco) limiting rate, a light limiting rate and a limiting rate owing to the leaves' capacity to export or utilize the photosynthesis products (Collatz et al., 1991). In the model, the iterative solution method for the photosynthesis stomatal conductance calculation proposed by Collatz et al. (1991) was implemented. Indeed, canopy is considered to be a “big leaf”, assuming bulk or integral values over canopy depth used in the integrated form of Eq. (A23) (see Sellers et al., 1992). Stomatal conductance and net assimilation rate are then determined for the canopy.