Modeling boreal forest evapotranspiration and water balance at stand and catchment scales: a spatial approach

Vegetation is known to have strong influence on evapotranspiration (ET), a major component of terrestrial water balance. Yet hydrological models often describe ET by methods unable to include the variability of vegetation characteristics in their predictions. To take advantage of the increasing availability of high-resolution open GIS data on land use, vegetation and soil characteristics in the boreal zone, a modular, spatially distributed model for predicting ET and other hydrological processes from grid cell to catchment level is presented and validated. An improved approach to upscale stomatal conductance to canopy scale using information on plant type (conifer/deciduous) and stand leaf-area index (LAI) is proposed by coupling a common leaf-scale stomatal conductance model with a simple canopy radiation transfer scheme. Further, a generic parametrization for vegetation-related hydrological processes for Nordic boreal forests is derived based on literature and data from a boreal FluxNet site. With the generic parametrization, the model was shown to reproduce daily ET measured using an eddy-covariance technique well at 10 conifer-dominated Nordic forests whose LAI ranged from 0.2 to 6.8 m² m⁻². Topography, soil and vegetation properties at 21 small boreal headwater catchments in Finland were derived from open GIS data at 16 m × 16 m grid size to upscale water balance from stand to catchment level. The predictions of annual ET and specific discharge were successful in all catchments, located from 60 to 68^∘ N, and daily discharge was also reasonably well predicted by calibrating only one parameter against discharge measurements. The role of vegetation heterogeneity in soil moisture and partitioning of ET was demonstrated. The proposed framework can support, for example, forest trafficability forecasting and predicting impacts of climate change and forest management on stand and catchment water balance. With appropriate parametrization it can be generalized outside the boreal coniferous forests.

1 Introduction

The boreal region, encompassing ca. 12 % of world's land area, is characterized by a mosaic of peatlands, lakes and forests of different ages and structures. Landscape heterogeneity has a major influence on the hydrological cycle, carbon balance and land–atmosphere interactions in the region (McDonnell et al., 2007; Govind et al., 2011; Stoy et al., 2013; Chapin et al., 2000; McGuire et al., 2002; Karlsen et al., 2016). Understanding spatial and temporal patterns of hydrological fluxes and state variables is becoming increasingly important in the context of intensifying the use of boreal forests under the pressures of climate change (Bonan, 2008; Gauthier et al., 2015; Price et al., 2013; Spittlehouse, 2005; Laudon et al., 2016). Thus, model approaches that can effectively utilize available environmental data, open high-resolution GIS data and remote-sensing products for hydrological predictions are necessary for climate-smart and environmentally sustainable use of boreal ecosystems (Mendoza et al., 2002).

Diverse modeling approaches are used to predict point-scale, catchment and regional hydrological balance, which reflects the broad spectrum of practical needs and research questions addressed, as well as historical development of hydrological models. The approaches range from lumped rainfall–runoff schemes (Beven and Kirkby, 1979; Bergström, 1992) to semi-distributed and fully distributed physically based models (Vivoni et al., 2011; Panday and Huyakorn, 2004; Ivanov et al., 2004; Ma et al., 2016; Clark et al., 2015a, b; Best et al., 2011; Niu et al., 2011; Ala-aho et al., 2017). Lumped models are often based on the conceptual representation of hydrological processes and calibrated against a few integrative measures, such as stream discharge. They are computationally inexpensive but cannot adequately address the spatial variability of hydrological fluxes and state variables within a catchment. Distributed mechanistic models, on the other hand, use first principles to predict water flow and state variables through the landscape and can incorporate topography, soil texture and vegetation heterogeneity in their predictions (Samaniego et al., 2010). However, high computational costs and challenges in estimating spatially variable parameters hamper their use and performance (Freeze and Harlan, 1969; Montanari and Koutsoyiannis, 2012; Grayson et al., 1992; Reed et al., 2004). It has been questioned whether fully distributed models are suitable for operative hydrological forecasts over large areas (Khakbaz et al., 2012), and semi-distributed models that combine physical and conceptual elements are often suggested as practical solutions (Khakbaz et al., 2012; Gao et al., 2014a; Savenije, 2010).

The common scientific questions in hydrological modeling are, as proposed by Clark et al. (2015a), related to describing and parametrizing water and energy fluxes and representing landscape variability and hydrological connectivity at the spatial and temporal scales of the model discretization. The availability of high-quality high-resolution open data on land use, topography, vegetation and soil characteristics has increased significantly during the recent decade. In Finland, for instance, high-accuracy digital elevation models (DEMs) are openly available at 2 and 10 m resolution (NSLF, 2017), reasonably good soil maps cover the country at scale of 1:20 000 or 1:200 000 (GSF, 2015), and the multi-source National Forest Inventory (mNFI; Mäkisara et al., 2016; Kangas et al., 2018) provides information on various forest and site type attributes at 16 m resolution throughout the country. To take full advantage of open GIS data and fine-resolution (i.e. tens to hundreds of meters) remote-sensing products of hydrological fluxes and state variables (Ryu et al., 2011; Herman et al., 2018), computationally efficient models capable of accounting for landscape variability are necessary. Further, these models should be sufficiently generic in their parametrization and use standard meteorological data to allow their use on large, often data-sparse areas. As the appropriate level of detail is strongly driven by the research question or practical application at hand (Clark et al., 2011; Savenije, 2010), effective development of hydrological models requires moving from a specific model towards modular frameworks (Clark et al., 2011, 2015a; Wagener et al., 2001).

Increasing the availability of high-resolution data on vegetation and its functioning paves the way to improving descriptions of spatial and temporal variability of evapotranspiration (ET), a major component of the terrestrial water balance. Within a specific biome and climatic region, vegetation characteristics such as species composition and leaf-area index (LAI) have major influence on the variability of ET (Williams et al., 2012; Zeng et al., 2018; Launiainen et al., 2016). In modern land surface models, ET components are computed either using a big-leaf framework or by describing the microclimatic gradients and exchange rates explicitly throughout a multi-layer canopy–soil system and upscaling these directly to ecosystem scale (Katul et al., 2012; Bonan et al., 2014). In both cases upscaling of stomatal conductance g_s and transpiration rate from leaf to canopy scale is based on physical arguments and constrained by plant carbon economy (Cowan and Farquhar, 1977; Katul et al., 2012; Medlyn et al., 2012) and hydraulic architecture (Sperry, 2000; Tyree and Zimmermann, 2002). The nonlinear dependency of ET components on vegetation characteristics and microclimate, however, remain mostly unresolved or are highly parameterized in most hydrological models, where the bulk ET is commonly computed by using Penman–Monteith equation or as a crop- or vegetation-type-dependent fraction of potential evaporation (Zhao et al., 2013; Fisher et al., 2005; Allen et al., 1998). Thus, improving ET description by a more physiologically phased approach could be proposed as one potential area to reduce uncertainties in predictions of the hydrological budget and resulting streamflow and soil moisture patterns.

Motivated both by scientific needs and potential practical applications, this study addresses two independent but interrelated objectives: first, we develop a generic model for daily ET in boreal forest and peatland ecosystems and explore how daily and annual ET can be predicted based on plant functional traits, canopy LAI, and open data on landscape structure and meteorological forcing. We distinguish between evaporative fluxes and transpiration, and predict canopy conductance G_c and the canopy transpiration rate by coupling the unified stomatal model (Medlyn et al., 2012) with a simplified canopy radiative transfer theory (Saugier and Katerji, 1991; Kelliher et al., 1995; Leuning et al., 2008). We perform parameter sensitivity analysis and validate the model predictions against eddy-covariance (EC) measurements of stand-scale ET at 10 boreal forest and peatland sites in Finland and Sweden (Launiainen et al., 2016).

Second, we extend the analysis to catchment scale and propose the modular, semi-distributed Spatial Forest Hydrology (SpaFHy) model for predicting spatial and temporal patterns of hydrologic fluxes and state variables across the boreal catchments. The SpaFHy aims to provide a reasonably simple, practically applicable and extensible framework that can effectively use open GIS data and basic meteorological data. We apply SpaFHy to 21 headwater catchments located throughout Finland to validate its predictions against daily stream discharge and annual ET derived from the catchment water balance. The spatial variability of ET, snow water equivalent (SWE) and soil moisture, and temporal variability of stream discharge are demonstrated, and potential applications are discussed. Although developed for boreal ecosystems, the proposed methods can be extended to other biomes with appropriate parametrizations.

2 Model description

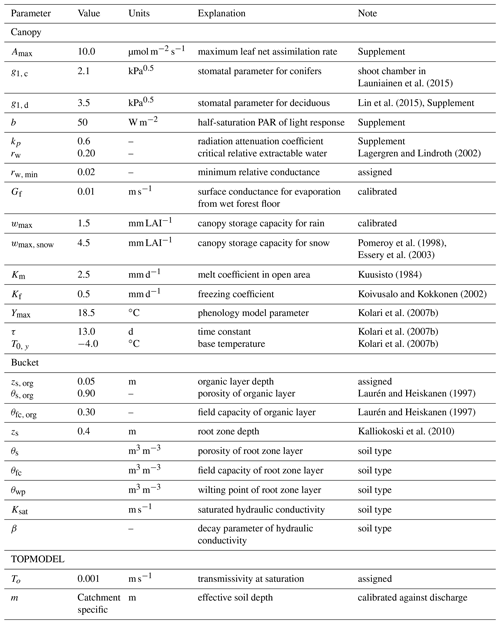
SpaFHy framework consists of three submodels (Fig. 1). Hydrological processes in vegetation and two-layer topsoil are explicitly modeled for each grid cell, while the TOPMODEL concept (Beven and Kirkby, 1979) is used to link grid-cell and catchment water budgets, and to describe baseflow and return flow generation mechanisms. The SpaFHy submodels and equations are presented in the next sections, and complemented in the Supplement. Throughout, we use notation where angle parenthesis 〈y〉 indicate spatial and $\stackrel{\mathrm{‾}}{y}$ temporal averages of quantity y, and units of millimeter (mm) correspond to kilograms of H₂O per square meter (kg H₂O m⁻²) of surface.

Figure 1 Structure of SpaFHy. At each grid cell, aboveground and topsoil hydrology is solved by Canopy and Bucket submodels whereas the lumped TOPMODEL is used to model saturated zone. The arrows correspond to interfacial fluxes: P precipitation; T_f throughfall to virtual snowpack; I_p potential infiltration to organic layer; I_f infiltration to root zone; D_r drainage to saturated zone; E evaporation or sublimation of canopy storage; E_f evaporation from ground; T_r transpiration; Q_r return flow; Q_s surface runoff; 〈Q_b〉 baseflow.

2.1 Canopy submodel: above-ground water budget and fluxes at a grid cell

Hydrological processes in the vegetation canopy, forest floor, snowpack, and organic moss–humus layer and underlying root zone are solved for each grid cell using information on stand structure and soil type (Fig. 1; Canopy and Bucket submodels).

2.1.1 P-M equation and ET

Total evapotranspiration is defined as the sum of physiologically controlled transpiration (T_r) and physically regulated evaporation from the wet canopy (E) and forest floor (E_f). To account for different controls of these processes, a three-source model is applied to describe ET at a grid-cell scale (Fig. 1). The Penman–Monteith (hereafter referred as P-M) equation gives each component of ET (mm d⁻¹) as follows (Monteith and Unsworth, 2008):

$$\begin{array}{}\text{(1)}& E_i={\displaystyle \frac{\mathrm{1}}{{\mathit{\rho }}_{\mathrm{w}}{L}_{\mathrm{v}}}}{\displaystyle \frac{\mathrm{\Delta }{A}_{\mathrm{e}}+{\mathit{\rho }}_{\mathrm{a}}{c}_{\mathrm{p}}{G}_{\mathrm{a}}D}{\mathrm{\Delta }+\mathit{\gamma }(\mathrm{1}+G_{\mathrm{a}}/G_i)}}\mathrm{\Delta }t,\end{array}$$

where L_v is latent heat of vaporization (J kg⁻¹), Δ and γ (Pa K⁻¹) are the slope of the saturation vapor pressure curve and psychrometric constant, respectively, ρ_w and ρ_a are densities of liquid water and air (kg m⁻³), c_p is the heat capacity of dry air at constant pressure (J kg⁻¹ K⁻¹), D is the vapor pressure deficit at air temperature (Pa), A_e is the available energy (W m⁻²), and Δt is the daily time step (86 400 s). Depending on the specific ET component E_i, the surface conductance G_i (m s⁻¹) and the aerodynamic conductance G_a have different forms. For canopy layer, which contributes to T_r and E, the G_a represents the efficiency of within-canopy turbulent transport and transport through laminar boundary layers on leaf surfaces, and it is computed as a function of wind speed U, canopy height h_c and LAI (Magnani et al., 1998; Leuning et al., 2008) (Sect. S2 in the Supplement).

2.1.2 Transpiration and canopy conductance

To calculate T_r and resulting water uptake from the root zone, an estimate of the canopy conductance G_c is needed. Analyzing a large corpus of leaf gas-exchange data through stomatal optimization arguments, Medlyn et al. (2012) proposed that leaf-scale stomatal conductance (g_s, mol m⁻² s⁻¹) is related to leaf net photosynthetic rate (A, µmol m⁻²s⁻¹) as

$$\begin{array}{}\text{(2)}& g_{\mathrm{s}}=g_o+\mathrm{1.6}\left(\mathrm{1}+{\displaystyle \frac{g_{\mathrm{1}}}{\sqrt{D}}}\right){\displaystyle \frac{A}{C_{\mathrm{a}}}},\end{array}$$

where C_a is the atmospheric CO₂ mixing ratio (ppm), D (kPa) is the vapor pressure deficit, g_o is the residual (or cuticular) conductance and g₁ is a species-specific parameter that depends on plant water use strategy. Noting that g_o≪g_s (Medlyn et al., 2012) and representing photosynthetic light response by saturating hyperbola (Saugier and Katerji, 1991), Eq. (2) can be approximated as follows:

$$\begin{array}{}\text{(3)}& g_{\mathrm{s}}=\mathrm{1.6}\left(\mathrm{1}+{\displaystyle \frac{g_{\mathrm{1}}}{\sqrt{D}}}\right){\displaystyle \frac{A_{\max }}{C_{\mathrm{a}}}}{\displaystyle \frac{\mathrm{PAR}}{\mathrm{PAR}+b}}{C}_{\mathrm{air}},\end{array}$$

where A_max (µmol m⁻² s⁻¹) is the light-saturated photosynthesis rate, b (W m⁻²) is the half-saturation value of photosynthetically active radiation (PAR) and the molar density of air C_air (mol m⁻³) converts units of g_s to meters per second (m s⁻¹).

Assuming PAR decays exponentially within the canopy, $\mathrm{PAR}\left(L\right)={\mathrm{PAR}}_o\exp (-k_{p}L)$ (where L is the cumulative leaf area from canopy top, k_p is the attenuation coefficient and PAR_o is the incoming PAR above canopy) and, neglecting vertical variations in D, Eq. (3) can be integrated analytically over L, yielding canopy conductance (m s⁻¹) as follows:

$$\begin{array}{}\text{(4)}& \begin{array}{rl}{G}_{\mathrm{c}}& =\left[\mathrm{1.6}\left(\mathrm{1}+{\displaystyle \frac{g_{\mathrm{1}}}{\sqrt{D}}}\right){\displaystyle \frac{A_{\max }}{C_{\mathrm{a},\mathrm{ref}}}}\right]\\ & \left({\displaystyle \frac{\mathrm{1}}{k_p}}{\displaystyle \frac{{\mathrm{PAR}}_o+b}{{\mathrm{PAR}}_o\times \exp }}(-k_p\mathrm{LAI})+b/k_p\right)C_{\mathrm{air}}\\ & \times f\left({\mathit{\theta }}_{\mathrm{rew}}\right)\times f_Y,\end{array}\end{array}$$

where the first term of Eq. (4) is the canopy-scale light and D response, and f(θ_rew) and f_Y (–) are dimensionless scaling factors introduced to represent the effect of soil moisture availability (Eq. 6) and phenology (Eq. 8). Equation (4) shows that at a given LAI, G_c is constrained by leaf water use traits (via g₁), photosynthetic capacity and light response (via A_max and b). Such traits are readily measurable by leaf gas exchange and widely available in the literature and in plant trait databases such as TRY (Kattge et al., 2011). Derivation of parameters is presented and predictions of Eq. (4) compared against a common gas-exchange model in Sect. S3.

Water use strategies and to a lesser extent photosynthetic capacity of common coniferous and deciduous species in boreal forests differ (see for example Lin et al., 2015). Thus, LAI-weighted effective values of g₁ and A_max are calculated for a grid cell as follows:

$$\begin{array}{}\text{(5)}& p=(\mathrm{1}-f_{\mathrm{d}})p_{\mathrm{c}}+f_{\mathrm{d}}{p}_{\mathrm{d}},\end{array}$$

where p is the parameter, the subscript c and d refer to conifer and deciduous trees, respectively, and $f_{\mathrm{d}}={\mathrm{LAI}}_{\mathrm{d}}/({\mathrm{LAI}}_{\mathrm{c}}+{\mathrm{LAI}}_{\mathrm{d}})$ the contribution of deciduous trees on total LAI. A seasonal cycle of LAI_d is described using a scheme based on accumulated degree days (Launiainen et al., 2015) calibrated using leaf phenology observations in southern and northern Finland.

The effect of soil moisture availability on G_c is based on a sap-flow study on Scots pine and Norway Spruce in central Sweden (Lagergren and Lindroth, 2002):

$$\begin{array}{}\text{(6)}& f\left({\mathit{\theta }}_{\mathrm{rew}}\right)=\left\{\begin{array}{ll}{\displaystyle \frac{{\mathit{\theta }}_{\mathrm{rew}}}{x_{\mathrm{r}}}},& {\mathit{\theta }}_{\mathrm{rew}}<x_{\mathrm{r}}\\ \mathrm{1},& {\mathit{\theta }}_{\mathrm{rew}}\ge x_{\mathrm{r}},\end{array}\right.\end{array}$$

where θ_rew (m³ m⁻³) is relative plant-available water θ_rew, and x_r (m³ m⁻³) is the threshold below which reduction in G_c occurs. θ_rew relates volumetric water content θ (–) in the root zone to soil-type-dependent field capacity (θ_fc) and wilting point (θ_wp) as follows:

$$\begin{array}{}\text{(7)}& {\mathit{\theta }}_{\mathrm{rew}}={\displaystyle \frac{\mathit{\theta }-{\mathit{\theta }}_{\mathrm{wp}}}{{\mathit{\theta }}_{\mathrm{fc}}-{\mathit{\theta }}_{\mathrm{wp}}}}.\end{array}$$

The phenology factor f_Y (–) describes seasonal acclimation of photosynthetic capacity as a function of the delayed temperature sum (Kolari et al., 2007a):

$$\begin{array}{}\text{(8)}& f_Y\left(t\right)=\max \left[\mathrm{0.1},\min \left(\mathrm{1},{\displaystyle \frac{Y\left(t\right)-T_{\mathrm{0},y}}{Y_{\max }-T_{\mathrm{0},y}}}\right)\right],\end{array}$$

where t is time, Y(t) (^∘C) describes the stage of development (Kolari et al., 2007b), T_0, y a threshold temperature and Y_max the value at which full recovery of photosynthetic capacity occurs. The Y is accumulated from the beginning of the year and its rate of change is

$$\begin{array}{}\text{(9)}& {\displaystyle \frac{\mathrm{d}Y}{\mathrm{d}t}}={\displaystyle \frac{T_{\mathrm{a}}-T_{\mathrm{0},y}}{\mathit{\tau }}},\end{array}$$

where τ is time constant of the recovery (Table 1).

Launiainen et al. (2015)Lin et al. (2015)Lagergren and Lindroth (2002)Pomeroy et al. (1998)Essery et al. (2003)Kuusisto (1984)Koivusalo and Kokkonen (2002)Kolari et al. (2007b)Kolari et al. (2007b)Kolari et al. (2007b)Laurén and Heiskanen (1997)Laurén and Heiskanen (1997)Kalliokoski et al. (2010)

Table 1 Generic parameter set used in stand- and catchment-scale simulations.

2.1.3 Evaporation from the forest floor

Forest floor evaporation E_f is extracted from the organic moss–humus layer on the top of the root zone (Fig. 1). We compute E_f (mm d⁻¹) as follows:

$$\begin{array}{}\text{(10)}& E_{\mathrm{f}}=f\times E_{\mathrm{f},\mathrm{0}},\end{array}$$

where E_f, 0 is the evaporation rate when moisture supply in the organic layer does not limit E_f and is calculated by Eq. (1), where $R_{\mathrm{n}}=R_{\mathrm{n},o}{\exp }^{-k_p\mathrm{LAI}}$ (R_n, o is net radiation above canopy); G_a depends on surface roughness length and modeled U 0.5 m above the forest floor; and G_i now represents the conductance of saturated ground surface (G_f) and is calibrated against EC data from a boreal fen as described later. The factor f accounts for the decay of E_f in drying organic matter as follows:

$$\begin{array}{}\text{(11)}& f=\left\{\begin{array}{ll}{\displaystyle \frac{{\mathit{\theta }}_{\mathrm{org}}}{x_{\mathrm{r},o}}},& {\mathit{\theta }}_{\mathrm{org}}<x_{\mathrm{r},o},\\ \mathrm{1},& {\mathit{\theta }}_{\mathrm{org}}\ge x_{\mathrm{r},o},\end{array}\right.\end{array}$$

where θ_org (m² m⁻²) is the organic layer water content, and $x_{\mathrm{r},o}=\mathrm{0.8}{\mathit{\theta }}_{\mathrm{fc},\mathrm{org}}$ based on a linear decrease in moss evaporation below the threshold moisture content (Williams and Flanagan, 1996).

2.1.4 Interception, throughfall and evaporation from canopy storage

Canopy water storage is described as a single pool filled by the interception I_c of precipitation and snowfall (P) and drained by evaporation or sublimation E and snow unloading U_s (all in mm d⁻¹). The change in canopy water storage W (mm) is

$$\begin{array}{}\text{(12)}& {\displaystyle \frac{\mathrm{\Delta }W}{\mathrm{\Delta }t}}=I_{\mathrm{c}}-E-U_{\mathrm{s}}.\end{array}$$

The interception submodel assumes that full storage is approached asymptotically (Aston, 1979; Hedstrom and Pomeroy, 1998):

$$\begin{array}{}\text{(13)}& I_{\mathrm{c}}=\left(W_{\max }-W_{\mathrm{0}}\right)\left(\mathrm{1}-e^{-\frac{c_f}{W_{\max }}P\mathrm{\Delta }t}\right),\end{array}$$

where c_f (–) is the canopy closure, W₀ is the initial water storage, and the canopy storage capacity W_max=w_max LAI (mm) is linearly proportional to LAI. The empirical storage parameter w_max (mm LAI⁻¹) is known to be greater for rain and snow (Koivusalo and Kokkonen, 2002); if W exceeds W_max of liquid water and daily mean temperature is above zero, the excess snow storage is removed as snow unloading and added into throughfall input to the snow model. In snow-free conditions, all throughfall is routed to forest floor surface and provides input to the Bucket submodel.

Evaporation and sublimation from canopy storage is calculated by the P-M equation (Eq. 1), where the G_a is defined as for T_r, while the canopy surface conductance G_i is set to be infinite for evaporation from the wet canopy and computed for snow sublimation as in Essery et al. (2003) and Pomeroy et al. (1998) (Sect. S4).

2.1.5 Snow accumulation and melt

Snowpack on the ground is modeled in terms of snow water equivalent (SWE, mm), a lumped storage receiving throughfall and unloading from the canopy and releasing water by snowmelt. The melt rate M (mm d⁻¹) is based on a temperature-index approach:

$$\begin{array}{}\text{(14)}& M=\min [\mathrm{SWE},K_{\mathrm{m}}(T_{\mathrm{a}}-T_o\left)\right],\end{array}$$

where T_o=0.0 ^∘C is the threshold temperature and T_a is the daily mean air temperature. The melting coefficient K_m (mm d^−1 ∘C⁻¹) decreases with increasing canopy closure as follows (Kuusisto, 1984):

$$\begin{array}{}\text{(15)}& K_{\mathrm{m}}=K_{\mathrm{m},\mathrm{o}}-\mathrm{1.64}{c}_f,\end{array}$$

where K_m, o is the melting coefficient in an open area. The snowpack can retain only a certain fraction of liquid water (Table 1 and Sect. S4), and the excess is routed to the soil module.

2.2 Bucket model: topsoil water balance

The topsoil water balance at each grid cell is described as a two-layer bucket model (Bucket, Fig. 1). An organic layer of depth z_org (mm), representing living mosses and poorly decomposed humus, overlies the root zone and acts as an interception storage for throughfall and snowmelt. Its volumetric water content θ_org (m³ m⁻³) is bounded between field capacity θ_fc, org and residual water content θ_r, org and varies according to

$$\begin{array}{}\text{(16)}& {\displaystyle \frac{\mathrm{\Delta }{\mathit{\theta }}_{\mathrm{org}}}{\mathrm{\Delta }t}}={\displaystyle \frac{I_{\mathrm{org}}-E_{\mathrm{f}}+Q_{\mathrm{r},\mathrm{ex}}}{z_{\mathrm{org}}}},\end{array}$$

where I_org is the interception rate, restricted either by throughfall or available storage space, and Q_r, ex is return flow from the hillslope through the root zone described below. All E_f is extracted from the organic layer.

The water content θ in the root zone of depth z_z (mm) changes according to

$$\begin{array}{}\text{(17)}& {\displaystyle \frac{\mathrm{\Delta }\mathit{\theta }}{\mathrm{\Delta }t}}={\displaystyle \frac{I_f-T_{\mathrm{r}}-D_{\mathrm{r}}+Q_{\mathrm{r}}}{z_{\mathrm{s}}}},\end{array}$$

where infiltration I_f (mm d⁻¹) and return flow from the catchment subsurface storage (Sect. 2.3) Q_r provide input and transpiration T_r, and drainage D_r outflows from the root zone. The maximum water storage is determined by root zone depth z_s and porosity θ_s, and I_f is restricted either by potential infiltration or available storage space. In the case of infiltration or return flow excess, the organic layer storage is first updated, and the remaining flow is routed to the stream outlet without delay as surface runoff (Q_s).

Drainage D_r (mm d⁻¹) from the root zone occurs whenever θ is above field capacity θ_fc as follows (Campbell, 1985):

$$\begin{array}{}\text{(18)}& D_{\mathrm{r}}\left(\mathit{\theta }\right)=\left\{\begin{array}{l}{K}_{\mathrm{sat}}{\left({\displaystyle \frac{\mathit{\theta }}{{\mathit{\theta }}_{\mathrm{s}}}}\right)}^{\mathrm{2}\mathit{\beta }+\mathrm{3}},\mathit{\theta }>{\mathit{\theta }}_{\mathrm{fc}},\\ \mathrm{0},\mathit{\theta }\le {\mathit{\theta }}_{\mathrm{fc}},\end{array}\right.\end{array}$$

where the saturated hydraulic conductivity K_sat (mm d⁻¹) and its decay parameter β depend on soil type.

2.3 TOPMODEL: integration from point to catchment level

To achieve computational efficiency and applicability at large scales, lateral flow in the saturated zone is not explicitly solved, but grid-cell and catchment water balances are conceptually linked by the TOPMODEL approach (Beven and Kirkby, 1979). In TOPMODEL, the catchment subsurface storage is described as a single bucket (Fig. 1). The change in the average saturation deficit 〈S〉 (mm), i.e. the average amount of water per unit area required to bring the catchment subsurface storage (below the root zone) to saturation, is

$$\begin{array}{}\text{(19)}& {\displaystyle \frac{\mathrm{\Delta }〈S〉}{\mathrm{\Delta }t}}=-〈D_{\mathrm{r}}〉+〈Q_{\mathrm{b}}〉+〈Q_{\mathrm{r}}〉,\end{array}$$

where 〈D_r〉 (mm d⁻¹) is catchment-average root zone drainage, 〈Q_b〉 (mm d⁻¹) is the catchment baseflow and 〈Q_r〉 (mm d⁻¹) is the average return flow from the subsurface storage. Assuming soil transmissivity is spatially uniform and decays exponentially with depth, the 〈Q_b〉 becomes (Beven, 1997)

$$\begin{array}{}\text{(20)}& 〈Q_{\mathrm{b}}〉=Q_o{\exp }^{-〈S〉/m}=T_o{\exp }^{-〈\mathrm{TWI}〉}{\exp }^{-〈S〉/m},\end{array}$$

where m (mm) is a scaling parameter reflecting the effective water-conducting soil depth, T_o the soil transmissivity at saturation, and Q_o (mm d⁻¹) baseflow rate when 〈S〉 is zero. 〈TWI〉 represents the catchment average of local topographic wetness index TWI defined by the natural logarithm of the area draining through a grid cell a from upslope and a tangent of the local surface slope α (Beven and Kirkby, 1979):

$$\begin{array}{}\text{(21)}& \mathrm{TWI}=\ln \left({\displaystyle \frac{a}{\tan \mathit{\alpha }}}\right).\end{array}$$

The saturation deficit S (mm) of a grid cell is uniquely related to 〈S〉 by

$$\begin{array}{}\text{(22)}& S=〈S〉+m\left(〈\mathrm{TWI}〉-\mathrm{TWI}\right),\end{array}$$

which implies that grid cells with high TWI have a higher probability to become saturated, and the catchment saturated area fraction is related both to the TWI distribution and to the amount of water in the catchment subsurface storage. Furthermore, Eq. (21) shows a high value of TWI can result either from large contributing area or flat local topography.

At grid cells where saturation excess (S<0) occurs, return flow $Q_{\mathrm{r}}=-S/\mathrm{\Delta }t$ from the subsurface storage is routed through the root zone and organic layer and their water storages are sequentially updated at next Δt. This creates an approximate feedback from local S, controlled by catchment water storage and topography, to topsoil water budget (Sect. 2.2) and delays drying of the root zone and organic layer at lowland grid cells receiving Q_r from the hillslope.

Specific discharge Q_f (mm d⁻¹) at the catchment outlet is finally computed as

$$\begin{array}{}\text{(23)}& 〈Q_f〉=〈Q_{\mathrm{b}}〉+〈Q_{\mathrm{s}}〉,\end{array}$$

where 〈Q_s〉 is the catchment average surface runoff (Sect. 2.2).

2.4 Model inputs

SpaFHy requires daily mean air temperature T_a (^∘C), global radiation R_g (Wm⁻²), relative humidity RH (%), wind speed (m s⁻¹) and daily accumulated precipitation P (mm d⁻¹) as forcing. The forcing can be either spatially uniform or vary for each grid cell in the spatial simulations. Available energy is computed from R_g, accounting for the effect of LAI on R_n (Fig. 2a in Launiainen et al., 2016), and PAR${}_o=\mathrm{0.5}\times R_{\mathrm{g}}$.

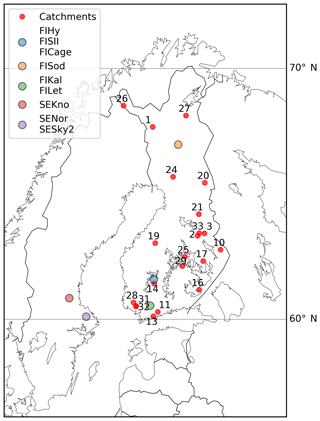
Figure 2 Location of the forest and peatland eddy-covariance sites and the 21 boreal headwater catchments used in the study.

The model requires following variables to be provided at a user-defined grid:

1. Canopy and Bucket submodels

   • Conifer and deciduous tree one-sided leaf-area index (LAI_c and LAI_d, respectively)

   • canopy height h_c (m)

   • Organic layer depth, root zone depth and hydraulic properties (Table S1)

2. TOPMODEL submodel

   • topographic wetness index TWI

   • masks of catchment area and permanent water bodies

All the above variables are derived from open GIS data available throughout Finland. The SpaFHy structure is modular and the three submodels are linked via water fluxes and feedbacks based on state variables such as θ_rew (Fig. 1). Each submodel can thus be used alone when appropriate forcing data are provided. The model is written in pure Python 2.7/3.6 and uses element-wise operations of Numpy arrays for all computations. The GIS data for model initialization are given as raster arrays, while the NetCDF format is used for storing the model outputs that include daily grids of all state variables and fluxes.

2.5 Model parametrization and sensitivity analysis at stand scale

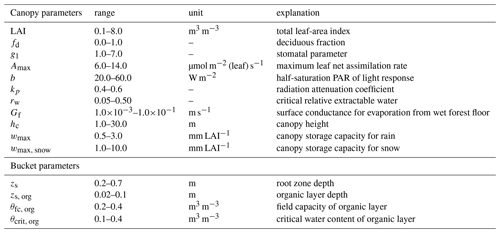
Parameters required by each submodel are given in Table 1 with their generic values. We applied a sequential approach to determine the generic parameter set to describe above-ground hydrology of coniferous-dominated landscape. First, we derived likely ranges of Canopy submodel parameters from the literature and predictions of a common leaf gas-exchange model (Sect. S3). The rainfall interception capacity was calibrated against spatially averaged throughfall measurements (2001–2010) made at the Hyytiälä research station in Juupajoki, southern Finland (FIHy; Table 2, Fig. 2). An overview of the site is given by Hari and Kulmala (2005) while Ilvesniemi et al. (2010) describe the hydrological measurements. The parameter f in surface conductance for evaporation from wet soil surface (G_f, Eq. 10) was calibrated against eddy-covariance based ET from a boreal fen site (FISii, Alekseychik et al., 2017) located next to FIHy (Table 2). Monte Carlo simulations (n=100), where parameter candidates were sampled from the uniform distribution and the objective function was set to minimize bias between modeled and measured values, were performed.

Hari and Kulmala (2005)Launiainen et al. (2015)Rannik et al. (2002)Kolari et al. (2004)Kolari et al. (2004)Aurela (2005)Thum et al. (2007)Lohila et al. (2011)Koskinen et al. (2014)Lundin et al. (1999)Lindroth et al. (2008)Berggren et al. (2004)Lindroth et al. (2008)Gioli et al. (2004)Alekseychik et al. (2017)

Table 2 Eddy-covariance sites used in stand-scale validation.

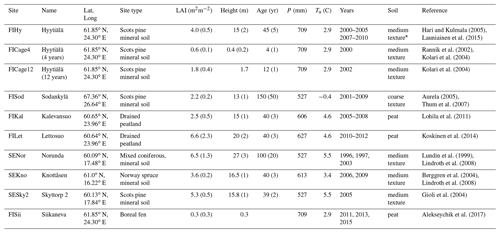
LAI is ecosystem one-sided leaf-area index (deciduous LAI in parenthesis); P is mean annual precipitation; T_a mean annual air temperature and soil type refers to Table 2 in the main document. ^* For runs at FIHy, site-specific field capacity θ_fc=0.3 and wilting point θ_wp=0.1 corresponding to main root zone (Launiainen et al., 2015) were used.

After parameter ranges were determined, global sensitivity analysis was performed to identify the key parameters controlling annual ET and its components, and annual maximum SWE. For this analysis, the Canopy and Bucket modules were coupled and the resulting stand-scale model run with various parameter combinations using daily forcing data from FIHy site (2000–2010) as input. We used the Morris method, a global extension of an elementary effect test used to determine which model parameters are negligible, linear and additive, or nonlinear or involved in interactions with other parameters (Morris, 1991; Campolongo et al., 2007). In the Morris method, three sensitivity measures are calculated from the distribution of scaled elementary effects. The mean of distribution (μ) is the overall effect of a parameter on the output, and the standard deviation (σ) is the effect of a parameter due to nonlinearity or due to interactions with other parameters. The third measure is the mean of the distribution of the absolute values of the elementary effects (μ^*) that provides ranking of parameters which is not biased by possible non-monotonic behavior of the model. The sensitivity measures are interpreted graphically together with rank parameters according to their overall influence; the intuitive interpretation is that the greater the absolute value of the measure the more important the parameter is for the studied model output. To ease graphical interpretation, the standard error of the mean as $\mathrm{SEM}=\mathit{\sigma }/\sqrt{r}$, where r is the number of trajectories, was estimated and used as suggested by Morris (1991). Analysis was conducted by using a Python package SALib (v. 1.1.2; Herman and Usher, 2017).

The ranges of the 14 parameters considered in the sensitivity analysis are listed in Table 3. In the analysis, leaf area indices for conifers and deciduous were calculated from the total one-sided LAI and deciduous fraction. Each parameter was allowed to vary over eight levels, and 60 optimal trajectories were generated from 600 initial trajectories by the sampling scheme introduced by Ruano et al. (2012). In total, 900 samples were generated and the number of optimal trajectories was determined following Ruano et al. (2011).

Table 3 Parameters and their ranges used in the global sensitivity analysis (Morris method) at stand scale.

After sensitivity analysis, most of the parameters could be fixed (those deemed less influential), and only the “generic” values for A_max and g₁ in Eq. (4) were confirmed by calibrating them against eddy-covariance (EC) – measured ET (years 2005–2007) at FIHy site. The possible ranges of these parameters were constrained by physiological arguments. Monte Carlo simulations (N=100), where parameters were sampled from the uniform distribution and the objective function was set to minimize bias between modeled and measured daily ET, were performed. We considered only dry-canopy conditions, i.e. no rain during the current or previous day.

2.6 Model validation at stand scale

To validate how daily ET can be predicted across LAI, site type and latitudinal gradient using a single parameter set (Table 1), the stand-level model was run using daily meteorological data from nine additional EC-flux sites in Finland and Sweden (Table 2, Fig. 2). The sites range from dense mixed coniferous forests (SENor) to a recently harvested stand (FICage4) and pristine fen peatland site (FISii), and the measurements, flux calculation and data post-processing have been described elsewhere (Launiainen et al., 2016; Minunno et al., 2016). For each site, LAI_c, LAI_d, h_c and soil properties were set according to measured or inferred values, and predicted daily growing-season (May–October) ET in dry-canopy conditions ($ET\simeq T_{\mathrm{r}}+E_{\mathrm{f}}$) was compared to measured ET. At FIHy, the soil moisture in the root zone was measured continuously, and SWE was recorded bi-weekly during five winters and used to compare respective model predictions.

2.7 Model validation at catchment scale

To address how well SpaFHy can predict daily specific discharge and annual partitioning of P into ET and Q_f at catchment scale, we applied the model to 21 small boreal headwater catchments located throughout Finland (Fig. 2, Table S2) using same generic parameter set as in the stand-level validation (Table 1). All the catchments belong to the Finnish network for monitoring water quality impacts of forestry (Finér et al., 2017), and their characteristics can be found in Table S2. Water levels at V-notch weirs were measured continuously at the catchment outlets by limnigraphs or pressure-sensors, and manual reference measurements were taken ca. 20 times per year adjacent to water quality sampling and used to calibrate the weir water-level data whenever necessary. Weir equations and catchment area were used to convert water level to specific discharge Q_f. In the absence of in situ weather data, daily 10 km × 10 km grid data provided by the Finnish Meteorological Institute were used as model forcing, taking values from a grid point nearest to the catchment outlets. Since wind speed was not available, it was set to a constant value of 2 m s⁻¹, corresponding to annual mean 2 m wind speed in Finland.

2.7.1 Processing of GIS data

Examples of GIS data used to set up the model for catchment C3 Porkkavaara in eastern Finland are shown in Fig. 3. The catchment boundaries and TWI were derived from DEM provided by National Survey of Finland (NSLF, 2017). The DEM original resolution was 2 or 10 m depending on catchment location. The resolution was aggregated with the mean elevation value into 16 m resolution, which corresponds to the resolution of the multi-source National Forest Inventory of Finland (mNFI) data. The mNFI data provide essential data layers for the model (e.g. stand volume, basal area, mean height, age, site fertility class and estimates of root, stem, branch and needle/leaf biomasses for pine, spruce and aggregated deciduous trees) at 16 m resolution throughout Finland (Mäkisara et al., 2016).

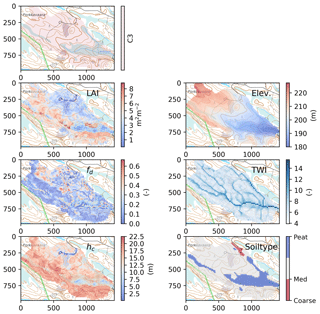
Figure 3 Spatial data at 16 m resolution used to set up the model for the catchment C3 Porkkavaara in eastern Finland (see Table S2). LAI: total one-sided leaf-area index; f_d: deciduous fraction; h_c: canopy height; Elev: elevation; TWI: topographic wetness index; soiltype refers to Table S2. Rasters overlay topographic basemap provided by National Survey of Finland and the scale of x and y axis is meters.

The DEM pre-processing, definition of the catchment boundaries and calculation of TWI based on the aggregated DEM were conducted in the WhiteBox GIS program (Lindsay, 2014). Pre-processing included consideration of the road and stream intersections derived from the Topographical Database (NSLF, 2017), which were burned into the DEM to account for culverts and ensure a continuous stream network. Further, all water elements were burned into the DEM with a 1 m upper threshold and a decay factor accounting for possible misaligned stream data. The filling of artificial pits in DEM was conducted using the “Fast Breach Depressions” tool (Lindsay, 2016) and the flow direction and flow accumulation (a) rasters were calculated with the D-infinity method (Tarboton, 1997). The TWI was finally calculated by Eq. (21), and small lakes within the catchments, derived from the Topographic Database (NSLF, 2017), were reset as “nodata” and omitted from further computations. The needle and leaf mass rasters were converted into LAI_c and maximum deciduous tree LAI LAI_d, max using specific one-sided leaf areas for pine, spruce and birch (6.8, 4.7 and 12.0 m² kg⁻¹, respectively; Härkönen et al., 2015). The canopy closure and h_c were obtained directly from the mNFI data.

Topsoil classification was derived from soil maps and peatland boundaries. Soil information is provided for parts of Finland at 1:20 000 scale while all of Finland is covered with a coarser 1:200 000 scale soil map (GSF, 2015). Peatland classification is available as detailed polygon elements from the Topographical Database. The soil information was transferred to the 16 m grid based on the majority principle, and then re-classified into four classes: coarse, medium and fine-textured mineral soils and organic peat soils whose hydrologic properties are given in Table S1. Fine-textured soils correspond to clayey and silt soils, whereas coarse-textured soils are fine sand and coarser. The majority of the mineral soils in the study catchments belong to the medium-textured class (Table S2).

2.7.2 Calibration of TOPMODEL against specific discharge

Catchment-specific calibration was performed to determine the effective soil depth m of TOPMODEL, a parameter that defines the shape of the Q_f recession and catchment average storage deficit 〈S〉 (Eq. 22). The parameter T_o was fixed to 0.001 m s⁻¹ since it was found to not markedly affect the model performance, as also observed elsewhere (Beven, 1997). The m was calibrated against measured daily specific discharge using Monte Carlo sampling from uniform distribution (N=100). We used a modified Willmott's index of agreement (Krause et al., 2005) as an objective function to quantify the goodness of fit:

$$\begin{array}{}\text{(24)}& d_j=\mathrm{1}-{\displaystyle \frac{{\sum }_{i=\mathrm{1}}^n\left|〈Q_{\mathrm{m},i}〉-〈Q_{f,i}〉\right|}{{\sum }_{i=\mathrm{1}}^n\left|〈Q_{\mathrm{m},i}〉-〈\stackrel{\mathrm{‾}}{Q_{\mathrm{m}}}〉\right|}},\end{array}$$

where d is in a range of 0 to 1 (the higher the value, the better the match), 〈Q_f, i〉 and 〈Q_m, i〉 are modeled and measured specific discharges at day i, and $\stackrel{\mathrm{‾}}{〈Q_{\mathrm{m}}〉}$ represents temporal average of the measurements. These model goodness statistics provided visually determined better fits of streamflow recession than other commonly used statistical criteria; e.g. Nash–Sutcliffe model efficiency was overly sensitive to high-flow peaks and affected by potential biases in P. The initial state of the model was set through a 1-year spin-up period. The value of m significantly affected the dynamics of specific discharge 〈Q_f(t)〉 and 〈S(t)〉 but had a negligible impact on catchment $〈\stackrel{\mathrm{‾}}{\mathrm{ET}}〉$ or $〈\stackrel{\mathrm{‾}}{Q_{\mathrm{m}}}〉$ at annual scale.

3 Results

3.1 Sensitivity analysis at stand scale

The sensitivity measures μ and σ for maximum SWE and annual ET and its components are shown in Table 4, and the ranking of parameters (via μ_*) in Fig. S1.

Table 4 Sensitivity of Canopy submodel predictions to parameter variability. Mean (μ) and standard deviation (σ) of the distribution of elementary effects for evapotranspiration (ET), transpiration (T_r), evaporation from canopy interception (E), ground evaporation (E_f), and annual maximum snow water equivalent (SWE). A negative sign of μ indicate output variable decreases when parameter value increases. Units are in millimeters per year (mm a⁻¹) except for SWE (mm).

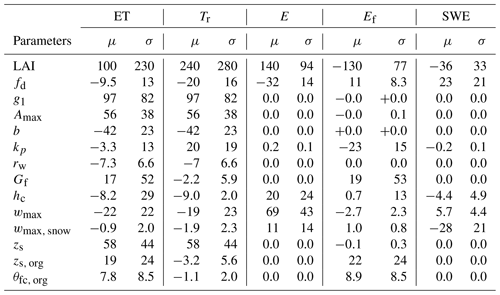
Total LAI was ranked the most influential parameter for all studied Canopy submodel outputs. In addition to LAI, the parameters that affect leaf level water use (g₁, z_s, A_max, and b) were among the most influential parameters for total ET and transpiration. The most influential parameters for ground evaporation E_f were LAI and k_p, which jointly define radiation availability at the ground. LAI also affects wind speed and thus aerodynamic conductance at the ground layer. In addition, surface conductance for wet forest floor G_f and z_s, org and θ_fc, org that define water storage capacity of the organic layer were significant for E_f. The most influential parameters for interception evaporation E were LAI, w_max, f_d, h_c and w_max, snow, which define interception capacity and the subsequent evaporation or sublimation of rain and snow. The most influential parameters affecting annual maximum snow water equivalent were LAI, w_max, snow, f_d, w_max and h_c.

LAI had also the largest σ, meaning either interactions with other parameters or strong nonlinearity. In the case of ET and T_r, the coefficient of variation ($\mathit{\sigma }/{\mathit{\mu }}^{*}$ ratio) was over 1.0 and for E, E_f, and SWE it was smaller but over 0.5. The most influential parameters of all studied outputs had the coefficient of variation over 0.5. Non-monotonic behavior (i.e. $\mathit{\mu }/{\mathit{\mu }}_{*}$ ratio is significantly different from unity) of the model was only observed in the case of ET for LAI.

3.2 Validation at stand scale

Predicted daily dry-canopy ET and root zone moisture content are compared against 10 years of measurements at the pine-dominated FIHy site in Fig. 4. The results indicate the model reproduces the observed seasonal patterns of ET and θ well during both the calibration (2005–2007) and validation period. The regression plots indicate ET predictions have negligible bias and represent the variability well, while the soil moisture changes are not fully captured. The SWE was also well reproduced by a snow model parametrized by literature values (Pomeroy et al., 1998; Essery et al., 2003).

ET predictions for the nine additional EC sites are shown in Fig. 5. The growing season (doy 120–273) dry-canopy ET is reasonably well predicted compared to independent observations across broad LAI range (from 0.7 to 6.8 m² m⁻²) and over latitudinal and site-type gradient (Table 2, Fig. 2). At the youngest, recently clear-cut site FICage4 the model underestimates ET, while slight overestimation is observed in particular at the northernmost, old-growth Scots pine site on coarse textured soil (FISod). In terms of explained variability, the model performance is the weakest at SESky2 (spruce), FIKal and FILet (drained peatland forests), potentially because poorly represented moisture limitations of transpiration and/or that of E_f. The nonlinear behavior at SENor and less clearly at SESky2 and FILet is primarily caused by slower than observed spring recovery at these sites, which have a high abundance of Norway spruce. As the Norway spruce has been observed to recover more rapidly from winter dormancy than pine (Linkosalo et al., 2014; Minunno et al., 2016), this can be partly related to a biased phenology model that is based on Scots pine (Kolari et al., 2007a).

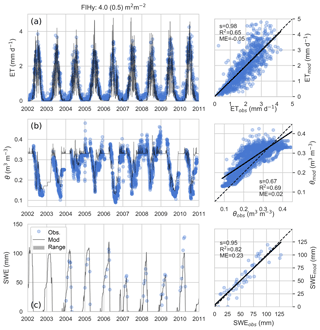
Figure 4 Modeled vs. measured dry-canopy ET at FIHy (a), root zone water content θ (b) and snow water equivalent SWE (c). As soil freezing is not modeled, comparison of θ is restricted to conditions when measured soil temperature was ≥0 ^∘C.

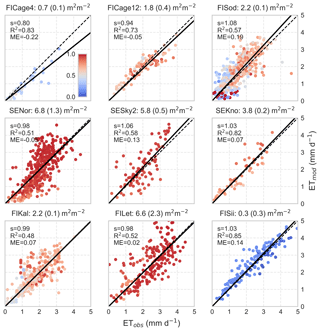
Figure 5 Scatter plots between modeled and observed daily stand-level ET during the growing season at the eddy-covariance flux sites in Finland and Sweden (Table 2). The title of each panel shows LAI (maximum deciduous LAI in parenthesis). The slope s and R² of linear regression forced through the origin and mean error ME are given and dashed line is the 1:1 line. Only dry canopy conditions, i.e. no rain during the day or previous day is included. At the pristine fen peatland site FISii, E_f was assumed to be non-limited by organic layer moisture. Color coding is according to transpiration to the ET ratio $T_{\mathrm{r}}/(T_{\mathrm{r}}+E_{\mathrm{f}})$.

ET at the pristine fen peatland site FISii, where E_f≫T_r, was also accurately predicted when the moisture limitation of E_f was neglected (f=1 in Eq. 10). Such cases can be expected due to a strong capillary connection between peat moss (Sphagnum sp.) and shallow water table maintained by lateral inflows from the surrounding landscape and weak drainage (Rouse, 1998; Ferone and Devito, 2004). When the organic layer moisture content feedback to E_f was activated, ET at FISii was frequently underestimated during summer dry spells (not shown); in point-scale simulations this represents the case where the organic layer water storage is recharged only by P.

Overall, the model performance at stand scale was satisfactory and dry-canopy ET was well predicted over a range of forest sites and climatic gradient in Finland. This suggests that the proposed three-source ET formulation and its generic parametrization for T_r, E_f and snow interception should be scalable over the landscape-scale variability of LAI, site types and latitude-driven weather forcing. Since EC measurements are known to be problematic during rainfall events (van Dijk et al., 2015; Kang et al., 2018), the comparison of stand-level ET was restricted to dry-canopy conditions.

3.3 Catchment water balance and specific discharge

On annual scales, changes in catchment water storage are negligible compared to annual 〈ET〉 and 〈Q_f〉, and a water balance approach provides an independent check for the upscaled ET predictions at catchment level. Figure 6 shows the comparison of the modeled and water-balance-based annual evapotranspiration fraction $〈\stackrel{\mathrm{‾}}{\mathrm{ET}}/\stackrel{\mathrm{‾}}{P}〉$ for the 21 headwater catchments across Finland (Fig. 2, Table S2). Results show a close agreement between measured and modeled P partitioning across the catchment space, especially considering the uncertainties in both axes. The uncertainty range of modeled $〈\stackrel{\mathrm{‾}}{\mathrm{ET}}/\stackrel{\mathrm{‾}}{P}〉$ implies the impact of model parameter uncertainty. The uncertainty range in Fig. 6 was derived by varying the most influential parameters for total ET and its partitioning (LAI, g₁, w_max, w_max, snow) by ±20 % and grouping the combinations into “high” and “low” ET scenarios, respectively. While the model is mass-conserving, the uncertainty of $〈\stackrel{\mathrm{‾}}{\mathrm{ET}}/\stackrel{\mathrm{‾}}{P}〉$ derived from catchment water balance is linearly proportional to uncertainty of Q_f derived from streamflow measurements and catchment area. Systematic and random errors in the annual P also cause respective uncertainties in $〈\stackrel{\mathrm{‾}}{\mathrm{ET}}/\stackrel{\mathrm{‾}}{P}〉$. In Fig. 6 the horizontal error bars correspond to a modest 10 % uncertainty assumed for P and catchment area.

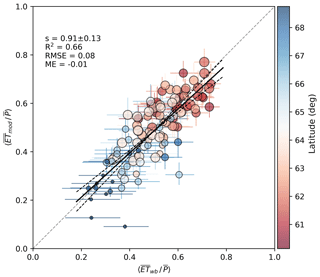
Figure 6 Modeled annual catchment evaporation fraction $〈{\stackrel{\mathrm{‾}}{\mathrm{ET}}}_{\mathrm{mod}}/\stackrel{\mathrm{‾}}{P}〉$ compared to that inferred from catchment water balance $〈{\stackrel{\mathrm{‾}}{\mathrm{ET}}}_{\mathrm{wb}}/\stackrel{\mathrm{‾}}{P}〉$. The vertical and horizontal error bars show the effect of parameter uncertainty and that of catchment area and P, respectively (see text). The colors refer to latitude and symbol size to catchment mean LAI (from 0.2 to 4.6 m² m⁻²). Using median year for each catchment (N=21), the respective statistics are slope $s=\mathrm{0.99}\pm \mathrm{0.30}$, R²=0.67, RMSE=0.06, ME−0.003.

Overall, the model predictions are reasonably good across the catchment space. Stepwise linear regression was tested to explain the annual residuals by catchment characteristics in Table S2 but no significant relationships were found. Interannual variability of $〈\stackrel{\mathrm{‾}}{\mathrm{ET}}/\stackrel{\mathrm{‾}}{P}〉$ was also well captured for majority of the catchments (not shown).

Figure 7 shows specific discharge and modeled soil moisture at catchment C3 Porkkavaara in eastern Finland (Table S2) over 2 years, characterized by wet (2012, P=452 mm in June–September) and dry (2013, P=246 mm) growing seasons. In 2012, the high snow accumulation resulted in a stronger streamflow peak, and frequent rainfall events kept the catchment average root zone moisture 〈θ〉≥0.3 m² m⁻² throughout the year. Q_f also remained significantly higher throughout the summer compared to 2013 and responded rapidly to rainfall. During the drier 2013, transpiration depleted the root zone moisture well below field capacity and 〈θ〉 dropped frequently to ∼0.15 m² m⁻² in June–August. The model was well able to predict spring Q_f peaks and recession curve, and also rainfall-induced peaks during the wet summer. During drier conditions, however, the small-magnitude peaks in summer Q_f were not well captured by the model. This suggests overly high Bucket storage capacity and thus an underestimated fraction of saturated area that contributes to overland flow during and after precipitation events. This is, however, not general behavior for the model as a better comparison between measured and modeled specific discharge was observed at several other catchments (Fig. S2).

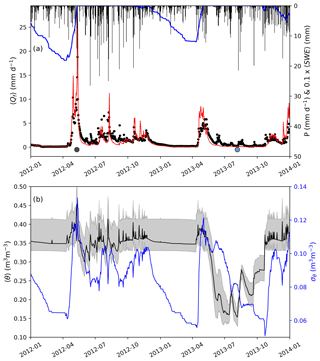
Figure 7 (a) Measured (black) and modeled (red) specific discharge Q_f, daily precipitation P (black bars) and mean snow water equivalent SWE (blue); (b) mean volumetric soil moisture 〈θ〉 and its spatial standard deviation σ_θ (blue) over two hydrologically contrasting years at C3 Porkkavaara, eastern Finland. In (b) the grey range shows the interquartile range. The points correspond to dates in Fig. 9. The Willmot's index of agreement (Eq. 23) for specific discharge over 2012–2013 period is 0.77.

3.4 Within-catchment variability

3.4.1 Soil moisture

To illustrate how vegetation, soil and topography create within-catchment variability to local water fluxes and state variables, the relationship between 〈θ〉 and its spatial standard deviation σ_θ at C3 Porkkavaara is shown in Fig. 8 for the two hydrologically contrasting years. Snapshots of the spatial variability of θ and local saturation deficit of TOPMODEL (Eq. 22) are further shown for dry and wet conditions in Fig. 9.

During winter, root zone moisture content decreases and its spatial variability is dampened by slow drainage. The onset of snowmelt is followed by an infiltration peak and saturated soils nearly throughout the catchment (Figs. 7–9). This leads to a rapid increase in σ_θ, mainly because of spatial variation in soil porosity. In 2012, a wet year, drainage rapidly decreased σ_θ after snowmelt, while the spatial variability was preserved until early July in the drier 2013. The latter result is because of a spatially heterogeneous transpiration rate that created spatial variance of soil moisture and compensated for the dampening effect of drainage until ca. doy 180. After that σ_θ started to decrease because transpiration at grid cells characterized by coarse and medium-textured soil and high LAI (Fig. 3) become soil-moisture limited (Eq. 7). In the summer of 2013, when 〈θ〉 was most of the time well below field capacity, rainfall events tended to dampen spatial variability of soil moisture (Fig. 7). In wetter conditions (most of 2012, autumn 2013), however, the effect of infiltration is opposite and resembles that of spring snowmelt.

As a result, there is clear hysteresis of σ_θ with respect to antecedent 〈θ〉 in the dry year, while such patterns are less visible in moist conditions. This indicates soil and vegetation variability in the model can either create or destroy spatial variability of soil moisture, as has been proposed both by theoretical arguments (Albertson and Montaldo, 2003) and analysis of soil moisture observations (Teuling and Troch, 2005). To conclude, the role of landscape heterogeneity as a driver of modeled soil moisture variability depends on antecedent soil moisture conditions and season; during drier spells variability is primarily driven by heterogeneous vegetation and plant water use, while soil type and topography become the primary controls in wet conditions and outside the growing season (Seyfried and Wilcox, 1995; Teuling and Troch, 2005; Robinson et al., 2008).

3.4.2 ET and snow

The predicted spatial variability of evaporation fraction $\stackrel{\mathrm{‾}}{\mathrm{ET}/P}$ and its components are illustrated in Fig. 10. The model results, averaged over the 2006–2016 period, reveal the strong sensitivity of component ET fluxes to stand leaf-area index, and secondary impacts of soil type and topography. The model predicts $\stackrel{\mathrm{‾}}{\mathrm{ET}/P}$ increases nonlinearly with LAI and varies from >0.25 at grid cells where LAI <1 m² m⁻² to ∼0.65 at locations where the standing tree volume and LAI (Fig. 3) are largest. The shape of the LAI response results from the nonlinear scaling of component fluxes with LAI, which also explains the inflection point at LAI ∼3 m² m⁻².

The interception of rainfall and snow contributes from less than 5 % to 30 % of long-term P, which is in line with measurements from boreal forests (Barbier et al., 2009; Toba and Ohta, 2005). The linear scaling of interception capacity with LAI and the asymptotic approach of full storage (Eq. 13), as well as the temporal distribution of precipitation, lead to the near-linear increase in $\stackrel{\mathrm{‾}}{E/P}$ with increasing LAI (Fig. 10). At grid cells with a high fraction of deciduous trees, low wintertime LAI leads to weaker snow interception and smaller annual $\stackrel{\mathrm{‾}}{\mathrm{ET}/P}$ compared to coniferous-dominated stands.

The model predictions suggest transpiration contributes from <10 % to more than 35 % of annual P, being the largest ET component in stands whose LAI >1.5 m² m⁻² (Fig. 10). The shape of T_r to LAI response is mostly caused by saturation of G_c because of light limitations in dense stands (Eq. 4). The more liberal water use strategy of deciduous species ($g_{\mathrm{1},\mathrm{d}}>g_{\mathrm{1},\mathrm{c}}$, Table 1) is reflected as a higher transpiration rate at grid cells where deciduous trees form a significant part of total LAI. Moreover, the lower envelope of points occurs at grid cells corresponding to coarse-textured soils (Fig. 3), where drought limitations become most frequent. This is also visible in $\stackrel{\mathrm{‾}}{\mathrm{ET}/P}$ at LAI >2 m² m⁻².

Evaporation from forest floor $\stackrel{\mathrm{‾}}{\mathrm{ET}/P}$ decreases asymptotically with LAI, showing a complementary relationship to T_r, as expected by the decreased available energy in denser stands. The upper envelope curve corresponds to grid cells with high TWI and a large tendency to be permanently saturated due to return flow from the hillslope. In these grid cells E_f is mainly determined by available energy; however, rapid drying of the forest floor in sparse stands between rainfall events decreases $\stackrel{\mathrm{‾}}{E_{\mathrm{f}}/P}$ and explains its less steep decrease with LAI at grid cells receiving less frequent or no return flow (lower TWI).

The spatial pattern of maximum SWE (Fig. 11) indicates snow accumulation in the densest stands (LAI >7 m² m⁻²) was ∼75 % of that on open areas; the exact fraction was found to be sensitive to winter weather conditions, being lowest during mild winters in the southern catchments, and in years with smaller annual snowfall. The predicted impact of forest canopy on snow accumulation is in good agreement with observational studies from similar climatic conditions in Finland and Sweden (Koivusalo and Kokkonen, 2002; Lundberg and Koivusalo, 2003), although higher snow interception losses have also been reported (see Kozii et al., 2017 for summary). The near-linear increase in snow interception and resulting decrease in SWE with LAI is supported by Hedstrom and Pomeroy (1998) and Pomeroy et al. (2002).

4 Discussion

4.1 Modeling ET at stand and catchment scales

At stand scale, SpaFHy was shown to reproduce daily ET measured using the eddy-covariance technique well at several forest and peatland sites in Finland and Sweden (Figs. 4 and 5). The good performance using the generic parametrization, derived mainly from literature sources and process-specific data, suggests the model is capable of accounting for the key drivers of temporal and site-to-site variability of ET. The sensitivity analysis reveals that for given meteorological forcing, total LAI is the primary parameter affecting ET and its partitioning into component fluxes. In the case of transpiration, the dominant role of LAI and parameters defining leaf water use efficiency (g₁ and A_max) and insensitivity to parameters related to aerodynamic conductance of the P-M equation (Eq. 1) indicate variations in T_r are mainly governed by that of canopy conductance (Eq. 4). The root zone depth, soil hydraulic properties and size of interception storage in the organic layer (z_org and θ_fc, org) are important for the probability of drought occurrence and a consequent reduction of transpiration (Table 4, Fig. 10). As rooting depths vary across species, site types and ecosystems (Gao et al., 2014b) and soil heterogeneity is not fully represented by existing soil maps, uncertainties in these properties are large in general. It was, however, recently shown that the root zone storage capacity can be estimated from satellite-based evaporation (Wang-Erlandsson et al., 2016), which may in future provide data to constrain these model parameters.

The multiplicative formulation for canopy conductance (Eq. 4) was developed by coupling the commonly used unified stomatal model (Medlyn et al., 2012) and leaf-scale light response with a simplified canopy radiative transfer scheme (see Sect. S3). The approach accounts for the nonlinear scaling between G_c and g_s similarly to the methods of Saugier and Katerji (1991) and Kelliher et al. (1995). To derive bulk surface conductance for remote-sensing applications, Leuning et al. (2008) combined their G_c scheme with a ground evaporation model based on equilibrium evaporation (Priestley and Taylor, 1972). They showed that after site-specific optimization, the dry-canopy ET was accurately predicted by the P-M equation across different vegetation types. That particular model, however, still requires an arbitrary and non-measurable maximum g_s and a few other parameters to be specified or calibrated. In our work g_s and its response to D were derived from stomatal optimization arguments and are tightly constrained by plant water use traits and photosynthetic capacity. These traits start to be widely available in databases such as TRY (Kattge et al., 2011) and can also be readily measured using leaf gas-exchange techniques. Due to these constraints on g_s, we consider Eq. (4) as a major advancement of the Leuning et al. (2008) approach. The good comparison between modeled and measured dry-canopy ET for sites with strongly different T_r∕ET and E_f∕ET ratios (Figs. 4 and 5) is indeed supportive of the proposed G_c formulation. However the comparison was done within a single vegetation type and further evaluation across ecosystem types are necessary to extend the approach outside boreal forests.

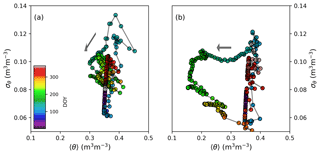
Figure 8 The relationship between catchment daily mean soil moisture 〈θ〉 and its spatial standard deviation σ_θ over the course a wet (2012) and dry (2013) year at C3 Porkkavaara. The color scale shows day of year (doy).

The sensitivity analysis (Table 4 and Fig. S1) proposes that the P-M equation could be replaced with simpler approaches. Making the assumption that the canopy is well-coupled to the atmosphere, a reasonable assumption for aerodynamically rough boreal forests, leads to $T_{\mathrm{r}}=G_{\mathrm{c}}\frac{D}{p_{\mathrm{a}}}$, where p_a (Pa) is the ambient pressure. Evaporation from the ground and canopy storage was also found to be relatively insensitive to aerodynamic terms, which suggests these water fluxes could be computed proportionally to equilibrium evaporation $E_i=\frac{{\mathit{\alpha }}_i}{L_{\mathrm{v}}}\frac{\mathrm{\Delta }{R}_{\mathrm{n},i}}{\mathrm{\Delta }+\mathit{\gamma }}$, where α_i (–) is a proportionality factor calibrated against measurements, and R_n, i is available energy. Moving to such approaches would relax input data requirements by eliminating the canopy height and wind speed from model forcing.

Open GIS data on LAI, species composition, soil type and topography were used to apply SpaFHy at 16 m × 16 m grid size to 21 headwater catchments in Finland. Results indicate the model reproduces the variability of annual evaporation fraction well across catchments (Fig. 6), as well as interannual variability at most of the studied catchments (not shown). It should be noted that the variability of annual $〈\stackrel{\mathrm{‾}}{\mathrm{ET}/P}〉$ across the catchment space is dominated by the latitudinal climate gradient, and further testing across different catchments on similar climatic conditions is needed.

The validation of spatial predictions of θ, ET or SWE (Figs. 9–11) was not attempted in this work. This would require either extensive spatially distributed and continuous in situ measurements, or high-resolution (i.e. order of tens of meters) remote sensing data that can be already obtained by near-ground microwave radiometry or low-frequency radars using unmanned aerial vehicles as a platform (Robinson et al., 2008). Ongoing advances in satellite-based soil moisture (Chen et al., 2014) and ET products (Hu et al., 2015) could also be used to evaluate the modeled spatial patterns and temporal evolution of these hydrological components.

The results of site- and catchment-scale validation suggest that ET and water budget partitioning in a boreal-forest-dominated landscape can be reasonably well predicted by the model based on generic parametrization, which is advantageous for scalability and applicability for areas and locations where data for model calibration is scarce or lacking. Moreover, the model–data comparison at catchment scale proposes ET components, and water budgets can be upscaled from stand to catchment scale using a relatively simple mechanistic approach that derives the characteristics of the modeling domain from open GIS data.

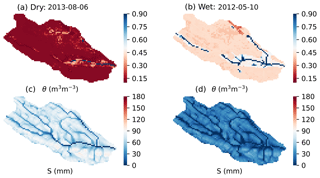
Figure 9 Snapshots of soil moisture patterns during wet and dry conditions (Fig. 7) at C3 Porkkavaara. Water content θ in the root zone (a) and local saturation deficit S of TOPMODEL (b).

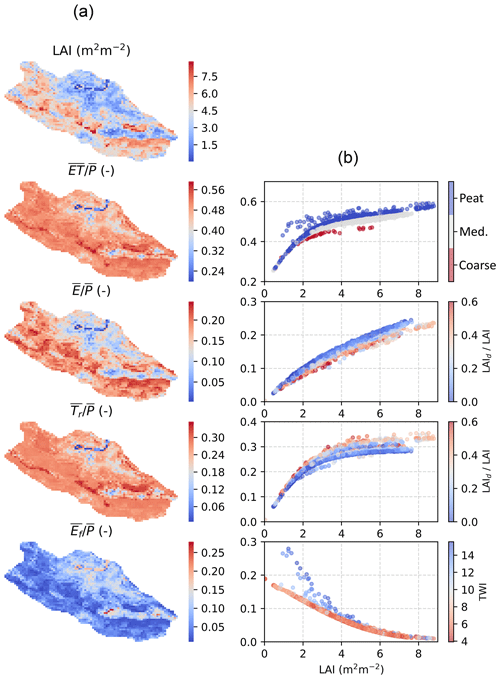
Figure 10 Spatial variability of evaporation fraction $\stackrel{\mathrm{‾}}{\mathrm{ET}/P}$ and its components at C3 catchment in Eastern Finland from a long-term (2006–2016) run (a). The relationship of component fluxes interception evaporation E, transpiration T_r and forest floor evaporation E_f on LAI (b) is modified with spatial variability of soil type, proportion of deciduous trees (LAI_d∕LAI) and topographical wetness index (TWI).

4.2 Capabilities and limitations of the model framework

This study presented a semi-distributed model for boreal forest hydrology at stand and catchment scales (Fig. 1). The model consists of three independent components: a Canopy model for above-ground hydrology, a Bucket model for topsoil water balance and a TOPMODEL for point to catchment integration. The modularity of SpaFHy provides clear advantages since all model components are independently parametrized, which allows their stand-alone development and use, as well as inclusion in other distributed or lumped hydrological models. Moreover, parameters of each submodel were obtained separately and calibrated based on good-quality data that clearly enhance the predictive power of SpaFHy by reasonably constraining the degree of freedom in model parametrization (Jakeman et al., 2006; Jackson-Blake et al., 2015).

In SpaFHy, the above-ground hydrology and root zone water balance (Eqs. 16 and 17) are solved distributively (Fig. 1), which propagates the spatial variability of vegetation (LAI, c_f, species composition) and soil type into the local hydrological fluxes, SWE, and organic layer and root zone water contents. Applied alone, such an approach would assume grid-cell water balances are independent from each other and omits the role of lateral flows and topographic position of a grid cell on a hillslope. The role of TOPMODEL (Sect. 2.3) can be considered as a nonlinear streamflow generation routine, which delays the average root zone drainage signal $\stackrel{\mathrm{‾}}{D_{\mathrm{r}}}$, leading to a realistic response of streamflow to P as controlled by TWI distribution. The other catchment properties are lumped into the parameter m, the effective subsurface water-conducting depth. It is this parameter that primarily controls both the shape of rainfall–runoff response and streamflow recession. The SpaFHy can thus be used as a simple catchment model to predict the signals of vegetation changes, forest management or varying climatic drivers on streamflow at daily or longer timescales. Indeed, the daily time series of streamflow (Figs. 7 and S2) were well reproduced for majority of the 21 studied catchments although m was the only parameter specifically calibrated for each catchment (Table S2).

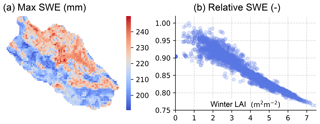
Figure 11 Spatial variability of maximum snow water equivalent (SWE) at C3 (a). The SWE relative to open area scales near-linearly with wintertime leaf-area index LAI (b).

On the other hand, SpaFHy can assist in mapping how soil saturation may vary spatially and temporally as a response to weather forcing (Fig. 9). The TWI-based scaling in TOPMODEL is used to predict the magnitude and location of return flow formation based on the state of the catchment subsurface storage. The spatial Q_r field is then used to update Bucket submodel water storages and θ at respective grid cells. In this way, SpaFHy can be used to predict local soil saturation that depends on both local (via vegetation and soil characteristics) and approximative landscape (via topography) controls (Fig. 9). In essence, the effect of return flow formation is to delay drying of grid cells that receive water from the surrounding landscape. Depending on the TWI distribution and value of m, this conceptualization implies that some grid cells never receive water from the surrounding landscape (those with low TWI) while some receive Q_r in high-flow conditions but not in baseflow conditions. At the other extreme, there are permanently inundated areas (high TWI) that contribute constantly to overland flow.

We emphasize that linking grid-cell water balances through TOPMODEL is a conceptual rather than physically correct approach (Beven, 1997; Seibert et al., 1997; Kirkby, 1997) and driven by the goal to develop a simple and practically applicable representation of topographic controls of soil moisture. Future work should explore whether m can be related to catchment characteristics to derive a more generic parametrization for TOPMODEL, as well as analyze the impact of parameter uncertainty on streamflow and saturated area predictions. For applications requiring more rigorous treatment of subsurface flows, the TOPMODEL can be replaced with 2-D ground water flow schemes.

Figures 9 and 10 show that landscape position (accounted via TWI) can markedly affect grid-cell soil moisture and ET. In this work, other topographic controls were omitted for simplicity. While likely to have small impact on annual catchment water balance, including topographic effects on radiation (Dubayah and Rich, 1995), this is presumed to alter the spatial patterns of ET and θ. In addition, the shade provided by vegetation at the neighboring grid cells should be considered to derive a more comprehensive understanding of the landscape-level hydrological variability. Adding submodels to simulate spatial and temporal patterns of soil temperature and frost depth, vegetation productivity and carbon balance would also be relatively straightforward future developments.

As shown in this work, the mNFI data (Mäkisara et al., 2016) can provide estimates of LAI, canopy height, site type and conifer/deciduous composition at 16 m × 16 m resolution throughout Finland. Härkönen et al. (2015) compared mNFI-based LAI estimates against ground-based estimates and MODIS AI and found good agreement between the methods. Consequently, the mNFI data can provide an easy way to obtain vegetation characteristics for hydrological and biogeochemical models at spatial scale currently unresolved by, for example, MODIS and other satellite products. Similar high-resolution data on forest resources are openly available also from the other Nordic countries (Kangas et al., 2018).

4.3 Potential applications

The proposed modular framework can provide support to a variety of questions benefiting from spatial and temporal hydrological predictions. These include, but are not limited to the following: (1) predicting soil moisture necessary for forecasting forest soil trafficability (Vega-Nieva et al., 2009; Jones and Arp, 2017), precision forestry and confronting climate-induced risks (Muukkonen et al., 2015); (2) identifying how saturated areas, considered as biogeochemical and biodiversity hotspots particularly sensitive to negative environmental impacts of human activities, evolve over time (Laudon et al., 2016; Ågren et al., 2015); (3) addressing impacts of forest structure, management and climate change on ET partitioning, streamflow dynamics and soil moisture (Zhang et al., 2017; Karlsen et al., 2016); (4) supporting water-quality modeling in headwater catchments (Guan et al., 2018); and (5) providing a starting point for developing a spatially distributed forest productivity and sustainability framework that combines open data streams, statistical approaches and mechanistic models. Moreover, we propose the Canopy submodel, in particular the leaf-to-canopy upscaling of canopy conductance, to be tested more widely in other ecosystems.

5 Conclusions

A distributed hydrological model framework for predicting ET and other hydrological processes from a grid cell to catchment level using open GIS data and daily meteorological data was presented and validated for boreal coniferous-dominated forests and peatlands. SpaFHy consists of coupled, stand-alone modules for aboveground, topsoil and subsurface domains. An improved approach to upscale stomatal conductance to canopy scale was proposed, and a generic parametrization of vegetation and snow-related hydrological processes for Nordic boreal forest and peatland ecosystems was derived. With the generic parametrization, daily ET was well reproduced across conifer-dominated forest stands whose LAI ranged from 0.2 to 6.8 m² m⁻². Predictions of annual ET were successful for the considered 21 boreal headwater catchments in Finland located from 60 to 68^∘ N, and daily specific discharge could be reasonably well predicted for the majority of the catchments by calibrating only one parameter against streamflow data. In subsequent studies, the model will be used to support forest trafficability forecasting and predict the impacts of climate change and forest management on stand and catchment water balance.