A general analytical model for head response to oscillatory pumping in unconfined aquifers: effects of delayed gravity drainage and initial condition

Oscillatory pumping tests (OPTs) provide an alternative to constant-head and constant-rate pumping tests for determining aquifer hydraulic parameters when OPT data are analyzed based on an associated analytical model coupled with an optimization approach. There are a large number of analytical models presented for the analysis of the OPT. The combined effects of delayed gravity drainage (DGD) and the initial condition regarding the hydraulic head are commonly neglected in the existing models. This study aims to develop a new model for describing the hydraulic head fluctuation induced by the OPT in an unconfined aquifer. The model contains a groundwater flow equation with the initial condition of a static water table, Neumann boundary condition specified at the rim of a partially screened well, and a free surface equation describing water table motion with the DGD effect. The solution is derived using the Laplace, finite-integral, and Weber transforms. Sensitivity analysis is carried out for exploring head response to the change in each hydraulic parameter. Results suggest that the DGD reduces to instantaneous gravity drainage in predicting transient head fluctuation when the dimensionless parameter $a_{\mathrm{1}}=\mathit{ϵ}{S}_{\mathrm{y}}b/K_z$ exceeds 500 with empirical constant ϵ, specific yield S_y, aquifer thickness b, and vertical hydraulic conductivity K_z. The water table can be regarded as a no-flow boundary when $a_{\mathrm{1}}<{\mathrm{10}}^{-\mathrm{2}}$ and P<10⁴ s, with P being the period of the oscillatory pumping rate. A pseudo-steady-state model without the initial condition causes a time-shift from the actual transient model in predicting simple harmonic motion of head fluctuation during a late pumping period. In addition, the present solution agrees well with head fluctuation data observed at the Savannah River site.

Highlights. An analytical model of the hydraulic head due to oscillatory pumping in unconfined aquifers is presented. Head fluctuations affected by instantaneous and delayed gravity drainages are discussed. The effect of the initial condition on the phase of head fluctuation is analyzed. The present solution agrees well with head fluctuation data taken from field oscillatory pumping.

1 Introduction

Numerous attempts have been made by researchers to the study of the oscillatory pumping test (OPT) that is an alternative to constant-rate and constant-head pumping tests for determining aquifer hydraulic parameters (e.g., Le Vine et al., 2016; Christensen et al., 2017; Watlet et al., 2018). The concept of the OPT was first proposed by Kuo (1972) in petroleum literature. The process of the OPT contains extraction stages and injection stages. The pumping rate, in other words, varies periodically as a sinusoidal function of time. Compared with traditional constant-rate pumping, the OPT in contaminated aquifers has the following advantages: (1) it is low cost because it does not dispose contaminated water from the well, (2) it has a reduced risk of treating contaminated fluid, (3) it has smaller contaminant movement, and (4) it has a stable signal that is easily distinguished from background disturbance such as the tide effect and varying river stage (e.g., Spane and Mackley, 2011). However, the disadvantages of the OPT include the need of an advanced apparatus producing periodic rate. Oscillatory hydraulic tomography adopts several oscillatory pumping wells with different frequencies (e.g., Yeh and Liu, 2000; Cardiff et al., 2013; Zhou et al., 2016; Muthuwatta et al., 2017). Aquifer heterogeneity can be mapped by analyzing multiple data collected from observation wells. Cardiff and Barrash (2011) reviewed articles associated with hydraulic tomography and classified them according to nine categories in a table.

Various groups of researchers have worked with analytical and numerical models for the OPT; each group has its own model and investigation. For example, Black and Kipp (1981) assumed the response of confined flow to the OPT to be simple harmonic motion (SHM) in the absence of the initial condition. Cardiff and Barrash (2014) built an optimization formulation strategy using the Black and Kipp analytical solution. Dagan and Rabinovich (2014) also assumed hydraulic head fluctuation to be SHM for the OPT at a partially screened well in unconfined aquifers. Cardiff et al. (2013) characterized aquifer heterogeneity using the finite element-based COMSOL software that adopts SHM hydraulic head variation for the OPT. In contrast, Rasmussen et al. (2003) found that hydraulic head response tends toward SHM at a late period of pumping time when considering the initial condition prior to the OPT. Bakhos et al. (2014) used the Rasmussen et al. (2003) analytical solution to quantify the time after which hydraulic head fluctuation can be regarded as SHM since the OPT began. As mentioned above, most of the models for the OPT assume hydraulic head fluctuation to be SHM without the initial condition, and all of them treat the pumping well as a line source with infinitesimal radius.

Field applications of the OPT for determining aquifer parameters have been conducted in recent years. Rasmussen et al. (2003) estimated aquifer hydraulic parameters based on 1 or 2 h period of the OPT at the Savannah River site. Maineult et al. (2008) observed spontaneous potential temporal variation in aquifer diffusivity at a study site in Bochum, Germany. Fokker et al. (2012, 2013) presented spatial distributions of aquifer transmission and the storage coefficient derived from curve fitting based on a numerical model and field data from experiments at the southern city limits of Bochum, Germany. Rabinovich et al. (2015) estimated aquifer parameters of equivalent hydraulic conductivity, specific storage, and specific yield at the Boise Hydrogeophysical Research Site by curve fitting based on observation data and the Dagan and Rabinovich (2014) analytical solution. They conclude that the equivalent hydraulic parameters can represent the actual aquifer heterogeneity of the study site.

Although a large number of studies have been made in developing analytical models for the OPT, little is known about the combined effects of delayed gravity drainage (DGD), a finite-radius pumping well, and the initial condition prior to the OPT. An analytical solution to such a question will not only have important physical implications but will also shed light on OPT model development. This study builds an improved model describing hydraulic head fluctuation induced by the OPT in an unconfined aquifer. The model is composed of a typical flow equation with the initial condition of a static water table, an inner boundary condition specified at the rim of the partially screened well for incorporating the finite-radius effect, and a free surface equation describing the motion of the water table with the DGD effect. The analytical solution of the model is derived by the methods of the Laplace transform, finite-integral transform, and Weber transform. Based on the present solution, sensitivity analysis is performed to explore the hydraulic head in response to the change in each hydraulic parameter. The effects of DGD and instantaneous gravity drainage (IGD) on the head fluctuations are compared. The quantitative criterion for treating the well radius as infinitesimal is discussed. The effect of the initial condition on the phase of head fluctuation is investigated. In addition, curve fitting of the present solution to head fluctuation data recorded at the Savannah River site is presented.

2 Methodology

2.1 Mathematical model

Consider an OPT in an unconfined aquifer, illustrated in Fig. 1. The aquifer is of unbound lateral extent with a finite thickness b. The radial distance from the centerline of the well is r; an elevation from the impermeable bottom of the aquifer is z. The well with an outer radius r_w is screened from elevation z_u to z_l.

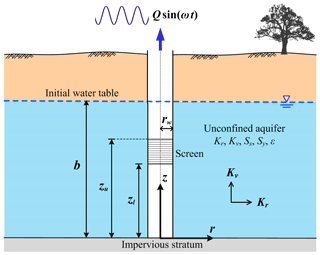
Figure 1 Schematic diagram for oscillatory pumping test at a partially screened well of finite radius in an unconfined aquifer.

The flow equation describing spatiotemporal head distribution in aquifers can be written as

$$\begin{array}{ll}{\displaystyle }{D}_{\mathrm{r}}& {\displaystyle }\left({\displaystyle \frac{{\partial }^{\mathrm{2}}h}{\partial r^{\mathrm{2}}}}+{\displaystyle \frac{\mathrm{1}}{r}}{\displaystyle \frac{\partial h}{\partial r}}+\mathit{\alpha }{\displaystyle \frac{{\partial }^{\mathrm{2}}h}{\partial z^{\mathrm{2}}}}\right)={\displaystyle \frac{\partial h}{\partial t}}\mathrm{for}{r}_{\mathrm{w}}\le r<\mathrm{\infty },\\ \text{(1)}& {\displaystyle }& {\displaystyle }\mathrm{0}\le z\le b\mathrm{and}t\ge \mathrm{0},\end{array}$$

where $D_{\mathrm{r}}=K_{\mathrm{r}}/S_{\mathrm{s}}$ and $\mathit{\alpha }=K_z/K_{\mathrm{r}}$, h(r, z, t) is the hydraulic head at location (r, z) and time t, K_r, and K_z are respectively the radial and vertical hydraulic conductivities, and S_s is the specific storage. Considering that the water table is a reference datum where the elevation head is set to zero, the initial condition is expressed as

$$\begin{array}{}\text{(2)}& {\displaystyle }h=\mathrm{0}\mathrm{at}t=\mathrm{0}.\end{array}$$

The rim of the well bore is regarded as an inner boundary under the Neumann condition, expressed as

$$\begin{array}{}\text{(3)}& {\displaystyle }{\displaystyle }\mathrm{2}\mathit{\pi }{r}_{\mathrm{w}}{K}_{\mathrm{r}}l{\displaystyle \frac{\partial h}{\partial r}}=\left\{\begin{array}{l}Q\sin \left(\mathit{\omega }t\right)\mathrm{for}{z}_{\mathrm{l}}\le z\le z_{\mathrm{u}}\\ \mathrm{0}\mathrm{outside}\mathrm{screen}\mathrm{interval}\end{array}\right.\mathrm{at}r=r_{\mathrm{w}},\end{array}$$

where $l=z_{\mathrm{u}}-z_{\mathrm{l}}$ is screen length, and Q and $\mathit{\omega }=\mathrm{2}\mathit{\pi }/P$ are respectively the amplitude and frequency of the oscillatory pumping rate (i.e., Qsin (ωt)) with a period P. Water table motion can be defined by Eq. (4a) for IGD (Neuman, 1972) and Eq. (4b) for DGD (Moench, 1995):

$$\begin{array}{}\text{(4a)}& {\displaystyle }& {\displaystyle \frac{\partial h}{\partial z}}=-{\displaystyle \frac{\mathrm{1}}{C_{\mathrm{y}}}}{\displaystyle \frac{\partial h}{\partial t}}\mathrm{at}z=b\mathrm{for}\mathrm{IGD},\text{(4b)}& {\displaystyle }& {\displaystyle \frac{\partial h}{\partial z}}={\displaystyle \frac{\mathrm{1}}{\mathit{\kappa }{C}_{\mathrm{y}}}}\underset{\mathrm{0}}{\overset{t}{\int }}{\displaystyle \frac{\partial h}{\partial \mathit{\tau }}}\exp (-(t-\mathit{\tau })/\mathit{\kappa })\mathrm{d}\mathit{\tau }\mathrm{at}z=b\mathrm{for}\mathrm{DGD},\end{array}$$

where $C_{\mathrm{y}}=K_z/S_{\mathrm{y}}$ and $\mathit{\kappa }=\mathrm{1}/\mathit{ϵ}$, with ϵ being an empirical constant and S_y being the specific yield. Note that Eq. (4b) reduces to Eq. (4a) when κ→∞ or ϵ=0. The impervious aquifer bottom is under the no-flow condition:

$$\begin{array}{}\text{(5)}& {\displaystyle }{\displaystyle \frac{\partial h}{\partial z}}=\mathrm{0}\mathrm{at}z=\mathrm{0}.\end{array}$$

The hydraulic head far away from the pumping well remains constant, written as

$$\begin{array}{}\text{(6)}& {\displaystyle }{\displaystyle }\underset{r\to \mathrm{\infty }}{lim}h(r,z,t)=\mathrm{0}.\end{array}$$

Define dimensionless variables and parameters as follows:

$$\begin{array}{ll}{\displaystyle }\stackrel{\mathrm{‾}}{h}& {\displaystyle }={\displaystyle \frac{\mathrm{2}\mathit{\pi }l{K}_{\mathrm{r}}}{Q}}h,\stackrel{\mathrm{‾}}{r}={\displaystyle \frac{r}{r_{\mathrm{w}}}},\stackrel{\mathrm{‾}}{z}={\displaystyle \frac{z}{b}},{\stackrel{\mathrm{‾}}{z}}_{\mathrm{l}}={\displaystyle \frac{z_{\mathrm{l}}}{b}},{\stackrel{\mathrm{‾}}{z}}_{\mathrm{u}}={\displaystyle \frac{z_{\mathrm{u}}}{b}},\stackrel{\mathrm{‾}}{t}\\ \text{(7)}& {\displaystyle }& {\displaystyle }={\displaystyle \frac{D_{\mathrm{r}}}{r_{\mathrm{w}}^{\mathrm{2}}}}t,\stackrel{\mathrm{‾}}{\mathit{\tau }}={\displaystyle \frac{D_{\mathrm{r}}}{r_{\mathrm{w}}^{\mathrm{2}}}}\mathit{\tau },\stackrel{\mathrm{‾}}{P}={\displaystyle \frac{D_{\mathrm{r}}}{r_{\mathrm{w}}^{\mathrm{2}}}}P,\end{array}$$

$${\displaystyle }{\displaystyle }\mathit{\gamma }={\displaystyle \frac{\mathit{\omega }{r}_{\mathrm{w}}^{\mathrm{2}}}{D_{\mathrm{r}}}},\mathit{\mu }={\displaystyle \frac{\mathit{\alpha }{r}_{\mathrm{w}}^{\mathrm{2}}}{b^{\mathrm{2}}}},a={\displaystyle \frac{b{D}_{\mathrm{r}}}{C_{\mathrm{y}}{r}_{\mathrm{w}}^{\mathrm{2}}}},a_{\mathrm{1}}={\displaystyle \frac{b}{\mathit{\kappa }{C}_{\mathrm{y}}}},a_{\mathrm{2}}={\displaystyle \frac{r_{\mathrm{w}}^{\mathrm{2}}}{\mathit{\kappa }{D}_{\mathrm{r}}}},$$

where the over bar stands for a dimensionless symbol. Note that the magnitude of a₁ is related to the DGD effect (Moench, 1995) and γ is a dimensionless frequency parameter. With Eq. (7), the dimensionless forms of Eqs. (1)–(6) become, respectively,

$$\begin{array}{ll}{\displaystyle \frac{{\partial }^{\mathrm{2}}\stackrel{\mathrm{‾}}{h}}{\partial {\stackrel{\mathrm{‾}}{r}}^{\mathrm{2}}}}& {\displaystyle }+{\displaystyle \frac{\mathrm{1}}{\stackrel{\mathrm{‾}}{r}}}{\displaystyle \frac{\partial \stackrel{\mathrm{‾}}{h}}{\partial \stackrel{\mathrm{‾}}{r}}}+\mathit{\mu }{\displaystyle \frac{{\partial }^{\mathrm{2}}\stackrel{\mathrm{‾}}{h}}{\partial {\stackrel{\mathrm{‾}}{z}}^{\mathrm{2}}}}={\displaystyle \frac{\partial \stackrel{\mathrm{‾}}{h}}{\partial \stackrel{\mathrm{‾}}{t}}}\mathrm{for}\mathrm{1}\le \stackrel{\mathrm{‾}}{r}<\mathrm{\infty },\mathrm{0}\le \stackrel{\mathrm{‾}}{z}<\mathrm{1}\\ \text{(8)}& {\displaystyle }& {\displaystyle }\mathrm{and}\stackrel{\mathrm{‾}}{t}\ge \mathrm{0},\end{array}$$

$$\begin{array}{}\text{(9)}& {\displaystyle }& {\displaystyle }\stackrel{\mathrm{‾}}{h}=\mathrm{0}\mathrm{at}\stackrel{\mathrm{‾}}{t}=\mathrm{0},\text{(10)}& {\displaystyle }& {\displaystyle \frac{\partial \stackrel{\mathrm{‾}}{h}}{\partial \stackrel{\mathrm{‾}}{r}}}=\left\{\begin{array}{l}\sin \left(\mathit{\gamma }\stackrel{\mathrm{‾}}{t}\right)\mathrm{for}{\stackrel{\mathrm{‾}}{z}}_{\mathrm{l}}\le \stackrel{\mathrm{‾}}{z}\le {\stackrel{\mathrm{‾}}{z}}_{\mathrm{u}},\\ \mathrm{0}\mathrm{outside}\mathrm{screen}\mathrm{interval}\end{array}\right.\mathrm{at}\stackrel{\mathrm{‾}}{r}=\mathrm{1},\end{array}$$

$$\begin{array}{}\text{(11a)}& {\displaystyle }& {\displaystyle \frac{\partial \stackrel{\mathrm{‾}}{h}}{\partial \stackrel{\mathrm{‾}}{z}}}=-a{\displaystyle \frac{\partial \stackrel{\mathrm{‾}}{h}}{\partial \stackrel{\mathrm{‾}}{t}}}\mathrm{at}\stackrel{\mathrm{‾}}{z}=\mathrm{1}\mathrm{for}\mathrm{IGD},\text{(11b)}& {\displaystyle }& {\displaystyle \frac{\partial \stackrel{\mathrm{‾}}{h}}{\partial \stackrel{\mathrm{‾}}{z}}}=-a_{\mathrm{1}}\underset{\mathrm{0}}{\overset{\stackrel{\mathrm{‾}}{t}}{\int }}{\displaystyle \frac{\partial \stackrel{\mathrm{‾}}{h}}{\partial \stackrel{\mathrm{‾}}{\mathit{\tau }}}}\exp \left(-a_{\mathrm{2}}(\stackrel{\mathrm{‾}}{t}-\stackrel{\mathrm{‾}}{\mathit{\tau }})\right)\mathrm{d}\stackrel{\mathrm{‾}}{\mathit{\tau }}\mathrm{at}\stackrel{\mathrm{‾}}{z}=\mathrm{1}\mathrm{for}\mathrm{DGD},\end{array}$$

$$\begin{array}{}\text{(12)}& {\displaystyle }& {\displaystyle \frac{\partial \stackrel{\mathrm{‾}}{h}}{\partial \stackrel{\mathrm{‾}}{z}}}=\mathrm{0}\mathrm{at}\stackrel{\mathrm{‾}}{z}=\mathrm{0},\text{(13)}& {\displaystyle }& {\displaystyle }\underset{\stackrel{\mathrm{‾}}{r}\to \mathrm{\infty }}{lim}\stackrel{\mathrm{‾}}{h}(\stackrel{\mathrm{‾}}{r},\stackrel{\mathrm{‾}}{z},\stackrel{\mathrm{‾}}{t})=\mathrm{0}.\end{array}$$

Equations (8)–(13) represent the transient DGD model when excluding Eq. (11a) and represent the transient IGD model when excluding Eq. (11b).

2.2 Transient solution for unconfined aquifer

The Laplace transform and finite-integral transform are applied to solve Eqs. (8)–(13) (Latinopoulos, 1985; Liang et al., 2017, 2018). The transient solution can then be expressed as

$$\begin{array}{}\text{(14a)}& {\displaystyle }{\displaystyle }\stackrel{\mathrm{‾}}{h}(\stackrel{\mathrm{‾}}{r},\stackrel{\mathrm{‾}}{z},\stackrel{\mathrm{‾}}{t})={\stackrel{\mathrm{‾}}{h}}_{\exp }(\stackrel{\mathrm{‾}}{r},\stackrel{\mathrm{‾}}{z},\stackrel{\mathrm{‾}}{t})+{\stackrel{\mathrm{‾}}{h}}_{\mathrm{SHM}}(\stackrel{\mathrm{‾}}{r},\stackrel{\mathrm{‾}}{z},\stackrel{\mathrm{‾}}{t}),\end{array}$$

with

$$\begin{array}{ll}\text{(14b)}& {\displaystyle }& {\displaystyle }{\stackrel{\mathrm{‾}}{h}}_{\exp }(\stackrel{\mathrm{‾}}{r},\stackrel{\mathrm{‾}}{z},\stackrel{\mathrm{‾}}{t})={\displaystyle \frac{-\mathrm{2}\mathit{\gamma }}{\mathit{\pi }}}\sum _{n=\mathrm{1}}^{\mathrm{\infty }}\underset{\mathrm{0}}{\overset{\mathrm{\infty }}{\int }}\cos \left({\mathit{\beta }}_n\stackrel{\mathrm{‾}}{z}\right)\exp \left(p_{\mathrm{0}}\stackrel{\mathrm{‾}}{t}\right)\mathrm{Im}\left({\mathit{\epsilon }}_{\mathrm{1}}{\mathit{\epsilon }}_{\mathrm{2}}\right)\mathrm{d}\mathit{\zeta },\text{(14c)}& {\displaystyle }& {\displaystyle }{\stackrel{\mathrm{‾}}{h}}_{\mathrm{SHM}}(\stackrel{\mathrm{‾}}{r},\stackrel{\mathrm{‾}}{z},\stackrel{\mathrm{‾}}{t})={\stackrel{\mathrm{‾}}{A}}_{\mathrm{t}}(\stackrel{\mathrm{‾}}{r},\stackrel{\mathrm{‾}}{z})\cos \left(\mathit{\gamma }\stackrel{\mathrm{‾}}{t}-{\mathit{\varphi }}_{\mathrm{t}}(\stackrel{\mathrm{‾}}{r},\stackrel{\mathrm{‾}}{z})\right),\text{(14d)}& {\displaystyle }& {\displaystyle }{\stackrel{\mathrm{‾}}{A}}_{\mathrm{t}}(\stackrel{\mathrm{‾}}{r},\stackrel{\mathrm{‾}}{z})=\sqrt{a_{\mathrm{t}}(\stackrel{\mathrm{‾}}{r},\stackrel{\mathrm{‾}}{z}{)}^{\mathrm{2}}+b_{\mathrm{t}}(\stackrel{\mathrm{‾}}{r},\stackrel{\mathrm{‾}}{z}{)}^{\mathrm{2}}},\text{(14e)}& {\displaystyle }& {\displaystyle }{a}_{\mathrm{t}}(\stackrel{\mathrm{‾}}{r},\stackrel{\mathrm{‾}}{z})={\displaystyle \frac{\mathrm{2}}{\mathit{\pi }}}\sum _{n=\mathrm{1}}^{\mathrm{\infty }}\underset{\mathrm{0}}{\overset{\mathrm{\infty }}{\int }}{p}_{\mathrm{0}}\cos \left({\mathit{\beta }}_n\stackrel{\mathrm{‾}}{z}\right)\mathrm{Im}\left({\mathit{\epsilon }}_{\mathrm{1}}{\mathit{\epsilon }}_{\mathrm{2}}\right)\mathrm{d}\mathit{\zeta },\text{(14f)}& {\displaystyle }& {\displaystyle }{b}_{\mathrm{t}}(\stackrel{\mathrm{‾}}{r},\stackrel{\mathrm{‾}}{z})={\displaystyle \frac{\mathrm{2}\mathit{\gamma }}{\mathit{\pi }}}\sum _{n=\mathrm{1}}^{\mathrm{\infty }}\underset{\mathrm{0}}{\overset{\mathrm{\infty }}{\int }}\cos \left({\mathit{\beta }}_n\stackrel{\mathrm{‾}}{z}\right)\mathrm{Im}\left({\mathit{\epsilon }}_{\mathrm{1}}{\mathit{\epsilon }}_{\mathrm{2}}\right)\mathrm{d}\mathit{\zeta },\text{(14g)}& {\displaystyle }& {\displaystyle }{\mathit{\varphi }}_{\mathrm{t}}(\stackrel{\mathrm{‾}}{r},\stackrel{\mathrm{‾}}{z})={\cos }^{-\mathrm{1}}\left(b_{\mathrm{t}}(\stackrel{\mathrm{‾}}{r},\stackrel{\mathrm{‾}}{z})/{\stackrel{\mathrm{‾}}{A}}_{\mathrm{t}}(r,\stackrel{\mathrm{‾}}{z})\right),{\displaystyle }{\mathit{\epsilon }}_{\mathrm{1}}=& {\displaystyle }{K}_{\mathrm{0}}\left({\mathit{\lambda }}_{\mathrm{0}}\stackrel{\mathrm{‾}}{r}\right)\left(\sin \left({\stackrel{\mathrm{‾}}{z}}_{\mathrm{u}}{\mathit{\beta }}_n\right)-\sin \left({\stackrel{\mathrm{‾}}{z}}_{\mathrm{l}}{\mathit{\beta }}_n\right)\right)/\left({\mathit{\beta }}_n{\mathit{\lambda }}_{\mathrm{0}}{K}_{\mathrm{1}}\left({\mathit{\lambda }}_{\mathrm{0}}\right)\right.\\ \text{(14h)}& {\displaystyle }& {\displaystyle }\left.\left(p_{\mathrm{0}}^{\mathrm{2}}+{\mathit{\gamma }}^{\mathrm{2}}\right)\right),\end{array}$$

$$\begin{array}{}\text{(14i)}& {\displaystyle }& {\displaystyle }{\mathit{\epsilon }}_{\mathrm{2}}=\left({\mathit{\beta }}_n^{\mathrm{2}}+c_{\mathrm{0}}^{\mathrm{2}}\right)/\left({\mathit{\beta }}_n^{\mathrm{2}}+c_{\mathrm{0}}^{\mathrm{2}}+c_{\mathrm{0}}\right),\text{(14j)}& {\displaystyle }& {\displaystyle }{p}_{\mathrm{0}}=-\mathit{\zeta }-\mathit{\mu }{\mathit{\beta }}_n^{\mathrm{2}},\text{(14k)}& {\displaystyle }& {\displaystyle }{\mathit{\lambda }}_{\mathrm{0}}=\sqrt{\mathit{\zeta }}i.\end{array}$$

where c₀=ap₀ for IGD and is $a_{\mathrm{1}}{p}_{\mathrm{0}}/(p_{\mathrm{0}}+a_{\mathrm{2}})$ for DGD, i is the imaginary unit, Im (–) is the imaginary part of a complex number, K₀ (–) and K₁ (–) are the modified Bessel functions of the second kind of zero order and one, respectively, and β_n is the positive roots of the following equation:

$$\begin{array}{}\text{(15)}& {\displaystyle }{\displaystyle }\tan {\mathit{\beta }}_n=c_{\mathrm{0}}/{\mathit{\beta }}_n.\end{array}$$

The method for finding the roots of β_n is discussed in Sect. 2.3. The detailed derivation of Eqs. (14a)–(14k) is presented in the Supplement. The first term on the right-hand side (RHS) of Eq. (14a) exhibits exponential decay due to the initial condition since pumping began; the second term defines SHM with amplitude ${\stackrel{\mathrm{‾}}{A}}_{\mathrm{t}}(\stackrel{\mathrm{‾}}{r}$, $\stackrel{\mathrm{‾}}{z})$ and phase shift ${\mathit{\varphi }}_{\mathrm{t}}(\stackrel{\mathrm{‾}}{r}$, $\stackrel{\mathrm{‾}}{z})$ at a given point ($\stackrel{\mathrm{‾}}{r}$, $\stackrel{\mathrm{‾}}{z}$). The numerical results of the integrals in Eqs. (14b), (14e), and (14f) are obtained by the Mathematica NIntegrate function.

2.3 Calculation of β_n

The eigenvalues β₁, …, β_n and the roots of Eq. (15) can be determined by applying the Mathematica function FindRoot based on Newton's method with reasonable initial guesses. The roots are located at the intersection of the curves plotted by the RHS and left-hand side (LHS) functions of β_n in Eq. (15). The roots are very close to the vertical asymptotes of the periodical tangent function tan β_n. When c₀=ap₀, the initial guess for each β_n can be considered to be ${\mathit{\beta }}_{\mathrm{0},n}+\mathit{\delta }$, where ${\mathit{\beta }}_{\mathrm{0},n}=(\mathrm{2}n-\mathrm{1})\mathit{\pi }/\mathrm{2}$, n∈(1, 2, …  ∞), and δ is a small positive value set to 10⁻¹⁰. When $c_{\mathrm{0}}=a_{\mathrm{1}}{p}_{\mathrm{0}}/(p_{\mathrm{0}}+a_{\mathrm{2}})$, the initial guess is set to ${\mathit{\beta }}_{\mathrm{0},n}-\mathit{\delta }$ for $a_{\mathrm{2}}-\mathit{\zeta }\le \mathrm{0}$. There is an additional vertical asymptote at ${\mathit{\beta }}_n=\sqrt{(a_{\mathrm{2}}-\mathit{\zeta })/\mathit{\mu }}$ derived from the RHS function of Eq. (15) (i.e., $p_{\mathrm{0}}+a_{\mathrm{2}}=\mathrm{0}$) if $a_{\mathrm{2}}-\mathit{\zeta }>\mathrm{0}$. The initial guess is therefore set to ${\mathit{\beta }}_{\mathrm{0},n}+\mathit{\delta }$ for β_0,n on the LHS of the asymptote and is set to ${\mathit{\beta }}_{\mathrm{0},n}-\mathit{\delta }$ for β_0,n on the RHS.

2.4 Transient solution for confined aquifer

When S_y=0 (i.e., a=0 or a₁=0), Eqs. (11a) or (11b) reduces to $\partial \stackrel{\mathrm{‾}}{h}/\partial \stackrel{\mathrm{‾}}{z}=\mathrm{0}$ for the no-flow condition at the top of the aquifer, indicating that the unconfined aquifer becomes a confined one. Under this condition, Eq. (15) becomes tan β_n=0 with roots β_n=0, π, 2π, …, nπ, …, ∞; Eq. (14i) reduces to ε₂=1; and factor 2 in Eqs. (14b), (14e), and (14e) is replaced by unity for β_n=0 and remains for the others. The analytical solution of the transient head for the confined aquifer can be expressed as Eqs. (14a)–(14k), with

$$\begin{array}{ll}{\displaystyle }{\stackrel{\mathrm{‾}}{h}}_{\exp }(\stackrel{\mathrm{‾}}{r},\stackrel{\mathrm{‾}}{z},\stackrel{\mathrm{‾}}{t})=& {\displaystyle \frac{-\mathit{\gamma }}{\mathit{\pi }}}\underset{\mathrm{0}}{\overset{\mathrm{\infty }}{\int }}\mathrm{Im}\left({\mathit{\epsilon }}_{\mathrm{0}}\right)\exp (-\mathit{\zeta }\stackrel{\mathrm{‾}}{t})\mathrm{d}\mathit{\zeta }-{\displaystyle \frac{\mathrm{2}\mathit{\gamma }}{\mathit{\pi }}}\sum _{n=\mathrm{1}}^{\mathrm{\infty }}\\ \text{(16a)}& {\displaystyle }& {\displaystyle }\underset{\mathrm{0}}{\overset{\mathrm{\infty }}{\int }}\cos \left(n\mathit{\pi }\stackrel{\mathrm{‾}}{z}\right)\mathrm{Im}\left({\mathit{\epsilon }}_{\mathrm{1}}\right)\exp \left(p_{\mathrm{0}}\stackrel{\mathrm{‾}}{t}\right)\mathrm{d}\mathit{\zeta },\end{array}$$

$$\begin{array}{ll}{\displaystyle }{a}_{\mathrm{t}}(\stackrel{\mathrm{‾}}{r},\stackrel{\mathrm{‾}}{z})=& {\displaystyle }-{\displaystyle \frac{\mathrm{1}}{\mathit{\pi }}}\underset{\mathrm{0}}{\overset{\mathrm{\infty }}{\int }}\mathit{\zeta }\mathrm{Im}\left({\mathit{\epsilon }}_{\mathrm{0}}\right)\mathrm{d}\mathit{\zeta }+{\displaystyle \frac{\mathrm{2}}{\mathit{\pi }}}\sum _{n=\mathrm{1}}^{\mathrm{\infty }}\underset{\mathrm{0}}{\overset{\mathrm{\infty }}{\int }}{p}_{\mathrm{0}}\cos \left(n\mathit{\pi }\stackrel{\mathrm{‾}}{z}\right)\\ \text{(16b)}& {\displaystyle }& {\displaystyle }\mathrm{Im}\left({\mathit{\epsilon }}_{\mathrm{1}}\right)\mathrm{d}\mathit{\zeta },\end{array}$$

$$\begin{array}{ll}{\displaystyle }{b}_{\mathrm{t}}(\stackrel{\mathrm{‾}}{r},\stackrel{\mathrm{‾}}{z})=& {\displaystyle \frac{\mathit{\gamma }}{\mathit{\pi }}}\underset{\mathrm{0}}{\overset{\mathrm{\infty }}{\int }}\mathrm{Im}\left({\mathit{\epsilon }}_{\mathrm{0}}\right)\mathrm{d}\mathit{\zeta }+{\displaystyle \frac{\mathrm{2}\mathit{\gamma }}{\mathit{\pi }}}\sum _{n=\mathrm{1}}^{\mathrm{\infty }}\underset{\mathrm{0}}{\overset{\mathrm{\infty }}{\int }}\cos \left(n\mathit{\pi }\stackrel{\mathrm{‾}}{z}\right)\\ \text{(16c)}& {\displaystyle }& {\displaystyle }\mathrm{Im}\left({\mathit{\epsilon }}_{\mathrm{1}}\right)\mathrm{d}\mathit{\zeta },\end{array}$$

$$\begin{array}{}\text{(16d)}& {\displaystyle }{\displaystyle }{\mathit{\epsilon }}_{\mathrm{0}}=\left({\stackrel{\mathrm{‾}}{z}}_{\mathrm{u}}-{\stackrel{\mathrm{‾}}{z}}_{\mathrm{l}}\right)K_{\mathrm{0}}\left({\mathit{\lambda }}_{\mathrm{0}}\stackrel{\mathrm{‾}}{r}\right)/\left({\mathit{\lambda }}_{\mathrm{0}}{K}_{\mathrm{1}}\left({\mathit{\lambda }}_{\mathrm{0}}\right)\left({\mathit{\zeta }}^{\mathrm{2}}+{\mathit{\gamma }}^{\mathrm{2}}\right)\right).\end{array}$$

Note that Eq. (14h) reduces to Eq. (16d) based on β_n=0 and l'Hospital's rule. When ${\stackrel{\mathrm{‾}}{z}}_{\mathrm{u}}=\mathrm{1}$ and ${\stackrel{\mathrm{‾}}{z}}_{\mathrm{l}}=\mathrm{0}$ for the case of the full screen, Eq. (14h) gives ε₁=0 for β_n>0, and the second RHS terms of Eqs. (16a)–(16c) can therefore be eliminated. This causes the solution for confined aquifers to be independent of dimensionless elevation $\stackrel{\mathrm{‾}}{z}$, indicating only horizontal flow in the aquifer.

2.5 Pseudo-steady-state solution for unconfined aquifer

A pseudo-steady-state (PSS) solution ${\stackrel{\mathrm{‾}}{h}}_{\mathrm{s}}$ accounts for SHM of head fluctuation at a late period of pumping time and satisfies the following form (Dagan and Rabinovich, 2014):

$$\begin{array}{}\text{(17)}& {\displaystyle }{\displaystyle }{\stackrel{\mathrm{‾}}{h}}_{\mathrm{s}}(\stackrel{\mathrm{‾}}{r},\stackrel{\mathrm{‾}}{z},\stackrel{\mathrm{‾}}{t})=\mathrm{Im}\left(\stackrel{\mathrm{‾}}{H}(\stackrel{\mathrm{‾}}{r},\stackrel{\mathrm{‾}}{z})e^{i\mathit{\gamma }\stackrel{\mathrm{‾}}{t}}\right),\end{array}$$

where $\stackrel{\mathrm{‾}}{H}(\stackrel{\mathrm{‾}}{r}$, $\stackrel{\mathrm{‾}}{z})$ is a space function of $\stackrel{\mathrm{‾}}{r}$ and $\stackrel{\mathrm{‾}}{z}$. This defines a PSS IGD model as Eqs. (8)–(13), excludes Eqs. (9) and (11b), and replaces $\sin \left(\mathit{\gamma }\stackrel{\mathrm{‾}}{t}\right)$ in Eq. (10) by $e^{i\mathit{\gamma }\stackrel{\mathrm{‾}}{t}}$. Substituting Eq. (17) and $\partial {\stackrel{\mathrm{‾}}{h}}_{\mathrm{s}}/\partial \stackrel{\mathrm{‾}}{t}=\mathrm{Im}\left(i\mathit{\gamma }\stackrel{\mathrm{‾}}{H}\right(\stackrel{\mathrm{‾}}{r}$, $\stackrel{\mathrm{‾}}{z}\left)e^{i\mathit{\gamma }\stackrel{\mathrm{‾}}{t}}\right)$ into the model results in

$$\begin{array}{}\text{(18)}& {\displaystyle }& {\displaystyle \frac{{\partial }^{\mathrm{2}}\stackrel{\mathrm{‾}}{H}}{\partial {\stackrel{\mathrm{‾}}{r}}^{\mathrm{2}}}}+{\displaystyle \frac{\mathrm{1}}{\stackrel{\mathrm{‾}}{r}}}{\displaystyle \frac{\partial \stackrel{\mathrm{‾}}{H}}{\partial \stackrel{\mathrm{‾}}{r}}}+\mathit{\mu }{\displaystyle \frac{{\partial }^{\mathrm{2}}\stackrel{\mathrm{‾}}{H}}{\partial {\stackrel{\mathrm{‾}}{z}}^{\mathrm{2}}}}=i\mathit{\gamma }\stackrel{\mathrm{‾}}{H},\text{(19)}& {\displaystyle }& {\displaystyle \frac{\partial \stackrel{\mathrm{‾}}{H}}{\partial \stackrel{\mathrm{‾}}{r}}}=\left\{\begin{array}{l}\mathrm{1}\mathrm{for}{\stackrel{\mathrm{‾}}{z}}_{\mathrm{l}}\le \stackrel{\mathrm{‾}}{z}\le {\stackrel{\mathrm{‾}}{z}}_{\mathrm{u}}\\ \mathrm{0}\mathrm{outside}\mathrm{screen}\mathrm{interval}\end{array}\right.\mathrm{at}\stackrel{\mathrm{‾}}{r}=\mathrm{1},\text{(20)}& {\displaystyle }& {\displaystyle \frac{\partial \stackrel{\mathrm{‾}}{H}}{\partial \stackrel{\mathrm{‾}}{z}}}=-ia\mathit{\gamma }\stackrel{\mathrm{‾}}{H}\mathrm{at}\stackrel{\mathrm{‾}}{z}=\mathrm{1}\mathrm{for}\mathrm{IGD},\text{(21)}& {\displaystyle }& {\displaystyle \frac{\partial \stackrel{\mathrm{‾}}{H}}{\partial \stackrel{\mathrm{‾}}{z}}}=\mathrm{0}\mathrm{at}\stackrel{\mathrm{‾}}{z}=\mathrm{0},\text{(22)}& {\displaystyle }& {\displaystyle }\underset{\stackrel{\mathrm{‾}}{r}\to \mathrm{\infty }}{lim}\stackrel{\mathrm{‾}}{H}=\mathrm{0}.\end{array}$$

The resultant model is independent of $\stackrel{\mathrm{‾}}{t}$, indicating that the analytical solution of $\stackrel{\mathrm{‾}}{H}(\stackrel{\mathrm{‾}}{r}$, $\stackrel{\mathrm{‾}}{z})$ is tractable. This similarly considers a PSS DGD model that is the same as the PSS IGD model but replaces Eqs. (11a) by (11b). Substituting Eq. (17) into the result yields a model that depends on $\stackrel{\mathrm{‾}}{t}$, indicating that the solution ${\stackrel{\mathrm{‾}}{h}}_{\mathrm{s}}$ to the PSS DGD model is not tractable.

The Weber transform, defined in Eq. (B1) of the supporting material, may be considered to be a Hankel transform with a more general kernel function. It can be applied to diffusion-type problems with a radial-symmetric region from a finite distance to infinity. For groundwater flow problems, it can be used to develop the analytical solution for the flow equation with a Neumann boundary condition specified at the rim of a finite-radius well (e.g., Lin and Yeh, 2017; Povstenko, 2015). Taking the transform and the formula of $e^{i\mathit{\gamma }\stackrel{\mathrm{‾}}{t}}=\cos \left(\mathit{\gamma }\stackrel{\mathrm{‾}}{t}\right)+i\sin \left(\mathit{\gamma }\stackrel{\mathrm{‾}}{t}\right)$ to solve Eqs. (18)–(22) yields the solution of ${\stackrel{\mathrm{‾}}{h}}_{\mathrm{s}}$, expressed as

$$\begin{array}{}\text{(23a)}& {\displaystyle }& {\displaystyle }{\stackrel{\mathrm{‾}}{h}}_{\mathrm{s}}(\stackrel{\mathrm{‾}}{r},\stackrel{\mathrm{‾}}{z},\stackrel{\mathrm{‾}}{t})={\stackrel{\mathrm{‾}}{A}}_{\mathrm{s}}(\stackrel{\mathrm{‾}}{r},\stackrel{\mathrm{‾}}{z})\cos \left(\mathit{\gamma }t-{\mathit{\varphi }}_{\mathrm{s}}(\stackrel{\mathrm{‾}}{r},\stackrel{\mathrm{‾}}{z})\right),\text{(23b)}& {\displaystyle }& {\displaystyle }{\stackrel{\mathrm{‾}}{A}}_{\mathrm{s}}(\stackrel{\mathrm{‾}}{r},\stackrel{\mathrm{‾}}{z})=\sqrt{a_{\mathrm{s}}(\stackrel{\mathrm{‾}}{r},\stackrel{\mathrm{‾}}{z}{)}^{\mathrm{2}}+b_{\mathrm{s}}(\stackrel{\mathrm{‾}}{r},\stackrel{\mathrm{‾}}{z}{)}^{\mathrm{2}}},\text{(23c)}& {\displaystyle }& {\displaystyle }{a}_{\mathrm{s}}(\stackrel{\mathrm{‾}}{r},\stackrel{\mathrm{‾}}{z})=\mathrm{Re}\left(\stackrel{\mathrm{‾}}{H}\right(\stackrel{\mathrm{‾}}{r},\stackrel{\mathrm{‾}}{z}\left)\right),\text{(23d)}& {\displaystyle }& {\displaystyle }{b}_{\mathrm{s}}(\stackrel{\mathrm{‾}}{r},\stackrel{\mathrm{‾}}{z})=\mathrm{Im}\left(\stackrel{\mathrm{‾}}{H}\right(\stackrel{\mathrm{‾}}{r},\stackrel{\mathrm{‾}}{z}\left)\right),\text{(23e)}& {\displaystyle }& {\displaystyle }{\mathit{\varphi }}_{\mathrm{s}}(\stackrel{\mathrm{‾}}{r},\stackrel{\mathrm{‾}}{z})={\cos }^{-\mathrm{1}}\left(b_{\mathrm{s}}(\stackrel{\mathrm{‾}}{r},\stackrel{\mathrm{‾}}{z})/A_{\mathrm{s}}(\stackrel{\mathrm{‾}}{r},\stackrel{\mathrm{‾}}{z})\right),\text{(23f)}& {\displaystyle }& {\displaystyle }\stackrel{\mathrm{‾}}{H}(\stackrel{\mathrm{‾}}{r},\stackrel{\mathrm{‾}}{z})=\left\{\begin{array}{l}\underset{\mathrm{0}}{\overset{\mathrm{\infty }}{\int }}{\stackrel{\mathrm{̃}}{H}}_{\mathrm{u}}\mathit{\xi }\mathrm{\Omega }\mathrm{d}\mathit{\xi }\mathrm{for}{\stackrel{\mathrm{‾}}{z}}_{\mathrm{u}}<\stackrel{\mathrm{‾}}{z}\le \mathrm{1}\\ \underset{\mathrm{0}}{\overset{\mathrm{\infty }}{\int }}{\stackrel{\mathrm{̃}}{H}}_{\mathrm{m}}\mathit{\xi }\mathrm{\Omega }\mathrm{d}\mathit{\xi }\mathrm{for}{\stackrel{\mathrm{‾}}{z}}_{\mathrm{l}}\le \stackrel{\mathrm{‾}}{z}\le {\stackrel{\mathrm{‾}}{z}}_{\mathrm{u}}\\ \underset{\mathrm{0}}{\overset{\mathrm{\infty }}{\int }}{\stackrel{\mathrm{̃}}{H}}_{\mathrm{l}}\mathit{\xi }\mathrm{\Omega }\mathrm{d}\mathit{\xi }\mathrm{for}\mathrm{0}\le \stackrel{\mathrm{‾}}{z}<{\stackrel{\mathrm{‾}}{z}}_{\mathrm{l}}\end{array}\right.,\text{(23g)}& {\displaystyle }& {\displaystyle }\mathrm{\Omega }=\left(J_{\mathrm{0}}\left(\mathit{\xi }\stackrel{\mathrm{‾}}{r}\right)Y_{\mathrm{1}}\left(\mathit{\xi }\right)-Y_{\mathrm{0}}\left(\mathit{\xi }\stackrel{\mathrm{‾}}{r}\right)J_{\mathrm{1}}\left(\mathit{\xi }\right)\right)/\left(J_{\mathrm{1}}^{\mathrm{2}}\left(\mathit{\xi }\right)+Y_{\mathrm{1}}^{\mathrm{2}}\left(\mathit{\xi }\right)\right),\end{array}$$

with the Bessel functions of the first kind of zero order, J₀ (–) and one J₁ (–), as well as the second kind of zero order, Y₀ (–) and one Y₁ (–):

$$\begin{array}{}\text{(23h)}& {\displaystyle }& {\displaystyle }\left\{\begin{array}{l}{\stackrel{\mathrm{̃}}{H}}_{\mathrm{u}}={\stackrel{\mathrm{̃}}{H}}_{\mathrm{p}}\left(c_{\mathrm{1}}\exp \left({\mathit{\lambda }}_{\mathrm{w}}\stackrel{\mathrm{‾}}{z}\right)+c_{\mathrm{2}}\exp \left(-{\mathit{\lambda }}_{\mathrm{w}}\stackrel{\mathrm{‾}}{z}\right)\right)\mathrm{for}{\stackrel{\mathrm{‾}}{z}}_{\mathrm{u}}<\stackrel{\mathrm{‾}}{z}\le \mathrm{1}\\ {\stackrel{\mathrm{̃}}{H}}_{\mathrm{m}}={\stackrel{\mathrm{̃}}{H}}_{\mathrm{p}}\left(c_{\mathrm{3}}\exp \left({\mathit{\lambda }}_{\mathrm{w}}\stackrel{\mathrm{‾}}{z}\right)+c_{\mathrm{4}}\exp \left(-{\mathit{\lambda }}_{\mathrm{w}}\stackrel{\mathrm{‾}}{z}\right)-\mathrm{1}\right)\mathrm{for}{\stackrel{\mathrm{‾}}{z}}_{\mathrm{l}}\le \stackrel{\mathrm{‾}}{z}\le {\stackrel{\mathrm{‾}}{z}}_{\mathrm{u}}\\ {\stackrel{\mathrm{̃}}{H}}_{\mathrm{l}}={\stackrel{\mathrm{̃}}{H}}_{\mathrm{p}}{c}_{\mathrm{5}}\left(\exp \left({\mathit{\lambda }}_{\mathrm{w}}\stackrel{\mathrm{‾}}{z}\right)+\exp \left(-{\mathit{\lambda }}_{\mathrm{w}}\stackrel{\mathrm{‾}}{z}\right)\right)\mathrm{for}\mathrm{0}\le \stackrel{\mathrm{‾}}{z}<{\stackrel{\mathrm{‾}}{z}}_{\mathrm{l}}\end{array}\right.,\text{(23i)}& {\displaystyle }& {\displaystyle }{c}_{\mathrm{1}}=-e^{-{\mathit{\lambda }}_{\mathrm{w}}}\left({\mathit{\lambda }}_{\mathrm{w}}-\mathit{\sigma }\right)\left(\sinh \left({\stackrel{\mathrm{‾}}{z}}_{\mathrm{l}}{\mathit{\lambda }}_{\mathrm{w}}\right)-\sinh \left({\stackrel{\mathrm{‾}}{z}}_{\mathrm{u}}{\mathit{\lambda }}_{\mathrm{w}}\right)\right)/D,\text{(23j)}& {\displaystyle }& {\displaystyle }{c}_{\mathrm{2}}=-e^{{\mathit{\lambda }}_{\mathrm{w}}}\left({\mathit{\lambda }}_{\mathrm{w}}+\mathit{\sigma }\right)\left(\sinh \left({\stackrel{\mathrm{‾}}{z}}_{\mathrm{l}}{\mathit{\lambda }}_{\mathrm{w}}\right)-\sinh \left({\stackrel{\mathrm{‾}}{z}}_{\mathrm{u}}{\mathit{\lambda }}_{\mathrm{w}}\right)\right)/D,\end{array}$$

$$\begin{array}{ll}{\displaystyle }{c}_{\mathrm{3}}& {\displaystyle }={\displaystyle \frac{e^{-\left(\mathrm{1}+{\stackrel{\mathrm{‾}}{z}}_{\mathrm{l}}+{\stackrel{\mathrm{‾}}{z}}_{\mathrm{u}}\right){\mathit{\lambda }}_{\mathrm{w}}}}{\mathrm{2}D}}\left(\mathit{\sigma }\left(e^{\left(\mathrm{2}+{\stackrel{\mathrm{‾}}{z}}_{\mathrm{l}}\right){\mathit{\lambda }}_{\mathrm{w}}}+e^{{\stackrel{\mathrm{‾}}{z}}_{\mathrm{u}}{\mathit{\lambda }}_{\mathrm{w}}}-e^{\left(\mathrm{2}{\stackrel{\mathrm{‾}}{z}}_{\mathrm{l}}+{\stackrel{\mathrm{‾}}{z}}_{\mathrm{u}}\right){\mathit{\lambda }}_{\mathrm{w}}}\right)\right.\\ {\displaystyle }& {\displaystyle }+\left(\mathit{\sigma }-{\mathit{\lambda }}_{\mathrm{w}}\right)e^{\left({\stackrel{\mathrm{‾}}{z}}_{\mathrm{l}}+\mathrm{2}{\stackrel{\mathrm{‾}}{z}}_{\mathrm{u}}\right){\mathit{\lambda }}_{\mathrm{w}}}+{\mathit{\lambda }}_{\mathrm{w}}\left(e^{\left(\mathrm{2}+{\stackrel{\mathrm{‾}}{z}}_{\mathrm{l}}\right){\mathit{\lambda }}_{\mathrm{w}}}-e^{{\stackrel{\mathrm{‾}}{z}}_{\mathrm{u}}{\mathit{\lambda }}_{\mathrm{w}}}\right.\\ \text{(23k)}& {\displaystyle }& {\displaystyle }\left.\left.+e^{\left(\mathrm{2}{\stackrel{\mathrm{‾}}{z}}_{\mathrm{l}}+{\stackrel{\mathrm{‾}}{z}}_{\mathrm{u}}\right){\mathit{\lambda }}_{\mathrm{w}}}\right)\right),\end{array}$$

$$\begin{array}{ll}{\displaystyle }{c}_{\mathrm{4}}=& {\displaystyle \frac{e^{-\left(\mathrm{1}+{\stackrel{\mathrm{‾}}{z}}_{\mathrm{l}}+{\stackrel{\mathrm{‾}}{z}}_{\mathrm{u}}\right){\mathit{\lambda }}_{\mathrm{w}}}}{\mathrm{2}D}}\left(\left(\mathit{\sigma }-{\mathit{\lambda }}_{\mathrm{w}}\right)e^{\left({\stackrel{\mathrm{‾}}{z}}_{\mathrm{l}}+\mathrm{2}{\stackrel{\mathrm{‾}}{z}}_{\mathrm{u}}\right){\mathit{\lambda }}_{\mathrm{w}}}+\left(\mathit{\sigma }+{\mathit{\lambda }}_{\mathrm{w}}\right)\right.\\ \text{(23l)}& {\displaystyle }& {\displaystyle }\left.\left(e^{\left(\mathrm{2}+{\stackrel{\mathrm{‾}}{z}}_{\mathrm{l}}\right){\mathit{\lambda }}_{\mathrm{w}}}-e^{\left(\mathrm{2}+{\stackrel{\mathrm{‾}}{z}}_{\mathrm{u}}\right){\mathit{\lambda }}_{\mathrm{w}}}+e^{\left(\mathrm{2}+\mathrm{2}{\stackrel{\mathrm{‾}}{z}}_{\mathrm{l}}+{\stackrel{\mathrm{‾}}{z}}_{\mathrm{u}}\right){\mathit{\lambda }}_{\mathrm{w}}}\right)\right),\end{array}$$

$$\begin{array}{ll}{\displaystyle }{c}_{\mathrm{5}}=& {\displaystyle \frac{\mathrm{1}}{\mathrm{2}D}}{e}^{-\left(\mathrm{1}+{\stackrel{\mathrm{‾}}{z}}_{\mathrm{l}}+{\stackrel{\mathrm{‾}}{z}}_{\mathrm{u}}\right){\mathit{\lambda }}_{\mathrm{w}}}\left(e^{{\stackrel{\mathrm{‾}}{z}}_{\mathrm{l}}{\mathit{\lambda }}_{\mathrm{w}}}-e^{{\stackrel{\mathrm{‾}}{z}}_{\mathrm{u}}{\mathit{\lambda }}_{\mathrm{w}}}\right)\\ \text{(23m)}& {\displaystyle }& {\displaystyle }\left(\left({\mathit{\lambda }}_{\mathrm{w}}-\mathit{\sigma }\right)e^{\left({\stackrel{\mathrm{‾}}{z}}_{\mathrm{l}}+{\stackrel{\mathrm{‾}}{z}}_{\mathrm{u}}\right){\mathit{\lambda }}_{\mathrm{w}}}+\left({\mathit{\lambda }}_{\mathrm{w}}+\mathit{\sigma }\right)e^{\mathrm{2}{\mathit{\lambda }}_{\mathrm{w}}}\right),\end{array}$$

where ${\mathit{\lambda }}_{\mathrm{w}}^{\mathrm{2}}=({\mathit{\xi }}^{\mathrm{2}}+i\mathit{\gamma })/\mathit{\mu }$, σ=iγa, ${\stackrel{\mathrm{̃}}{H}}_{\mathrm{p}}=\mathrm{2}/\left(\mathit{\pi }\mathit{\mu }\mathit{\xi }{\mathit{\lambda }}_{\mathrm{w}}^{\mathrm{2}}\right)$ and $D=\mathrm{2}(\mathit{\sigma }\cosh {\mathit{\lambda }}_{\mathrm{w}}+{\mathit{\lambda }}_{\mathrm{w}}\sinh {\mathit{\lambda }}_{\mathrm{w}})$, and Re (–) is the real part of a complex number. Again, one can refer to the supporting material for the derivation of the solution. Equation (23a) indicates SHM for the response of the hydraulic head at any point to oscillatory pumping. Note that Eq. (23f) reduces to $\stackrel{\mathrm{‾}}{H}(\stackrel{\mathrm{‾}}{r}$, $\stackrel{\mathrm{‾}}{z})=\underset{\mathrm{0}}{\overset{\mathrm{\infty }}{\int }}{\stackrel{\mathrm{̃}}{H}}_{\mathrm{m}}\mathit{\xi }\mathrm{\Omega }\mathrm{d}\mathit{\xi }$ for a fully screened well when ${\stackrel{\mathrm{‾}}{z}}_{\mathrm{l}}=\mathrm{0}$ and ${\stackrel{\mathrm{‾}}{z}}_{\mathrm{u}}=\mathrm{1}$.

2.6 Pseudo-steady-state solution for confined aquifers

Applying the finite Fourier cosine transform to the model, Eqs. (18)–(22) with S_y=0 (i.e., a=0) for the confined condition, leads to an ordinary differential equation with two boundary conditions. In solving the boundary-value problem, the solution of ${\stackrel{\mathrm{‾}}{h}}_{\mathrm{s}}$ for confined aquifers can be expressed as Eqs. (23a)–(23e) with $\stackrel{\mathrm{‾}}{H}(\stackrel{\mathrm{‾}}{r}$, $\stackrel{\mathrm{‾}}{z})$, defined as

$$\begin{array}{ll}{\displaystyle }\stackrel{\mathrm{‾}}{H}(\stackrel{\mathrm{‾}}{r},\stackrel{\mathrm{‾}}{z})& {\displaystyle }=-\mathrm{2}\sum _{m=\mathrm{0}}^{\mathrm{\infty }}{\displaystyle \frac{K_{\mathrm{0}}\left(\stackrel{\mathrm{‾}}{r}{\mathit{\lambda }}_{\mathrm{m}}\right)}{{\mathit{\lambda }}_{\mathrm{m}}{K}_{\mathrm{1}}\left({\mathit{\lambda }}_{\mathrm{m}}\right)}}\\ \text{(24)}& {\displaystyle }& {\displaystyle }\times \left\{\begin{array}{l}\mathrm{0.5}\left({\stackrel{\mathrm{‾}}{z}}_{\mathrm{u}}-{\stackrel{\mathrm{‾}}{z}}_{\mathrm{l}}\right)\mathrm{for}m=\mathrm{0}\\ {\displaystyle \frac{\cos \left(m\mathit{\pi }\stackrel{\mathrm{‾}}{z}\right)}{m\mathit{\pi }}}\left(\sin \left({\stackrel{\mathrm{‾}}{z}}_{\mathrm{u}}m\mathit{\pi }\right)-\sin \left({\stackrel{\mathrm{‾}}{z}}_{\mathrm{l}}m\mathit{\pi }\right)\right)\mathrm{for}m>\mathrm{0}\end{array}\right.,\end{array}$$

where ${\mathit{\lambda }}_{\mathrm{m}}^{\mathrm{2}}=\mathit{\gamma }i+\mathit{\mu }(m\mathit{\pi }{)}^{\mathrm{2}}$. The derivation of Eq. (24) is also listed in the supporting material. For a fully screened well (i.e., ${\stackrel{\mathrm{‾}}{z}}_{\mathrm{u}}=\mathrm{1}$, ${\stackrel{\mathrm{‾}}{z}}_{\mathrm{l}}=\mathrm{0}$), the first term of the series (i.e., m=0) remains and the others equal zero because of $\sin \left({\stackrel{\mathrm{‾}}{z}}_{\mathrm{u}}m\mathit{\pi }\right)-\sin \left({\stackrel{\mathrm{‾}}{z}}_{\mathrm{l}}m\mathit{\pi }\right)=\mathrm{0}$. The result is independent of dimensionless elevation $\stackrel{\mathrm{‾}}{z}$, indicating that the confined flow is only horizontal.

2.7 Special cases of the present solution

Table 1 classifies the present solution (i.e., Solution 1) and its special cases (i.e., Solutions 2 to 6) according to transient or PSS flow, unconfined or confined aquifer, and IGD or DGD. Each of the solutions (Solutions 1 to 6) reduce to a special case for a fully screened well. Existing analytical solutions can be regarded as special cases of the present solution, as discussed in Sect. 3.4 (e.g., Black and Kipp, 1981; Rasmussen et al., 2003; Dagan and Rabinovich, 2014).

Table 1 The present solution and its special cases.

Solution 1 consists of Eqs. (14a)–(14k) with the roots of Eq. (15) and $c_{\mathrm{0}}=a_{\mathrm{1}}{p}_{\mathrm{0}}/(p_{\mathrm{0}}+a_{\mathrm{2}})$ for DGD. Solution 2 is the same as Solution 1 but has c₀=ap₀ for IGD. Solution 3 equals Solution 1 with Eqs. (16a)–(16d) and β_n=0, π, 2π, …, nπ. Solution 4 is the component ${\stackrel{\mathrm{‾}}{h}}_{\mathrm{SHM}}$ of Solution 1 for DGD. Solution 5 consists of Eqs. (23a)–(23m) for IGD. Solution 6 consists of Eqs. (23a)–(23e), with $\stackrel{\mathrm{‾}}{H}(\stackrel{\mathrm{‾}}{r}$, $\stackrel{\mathrm{‾}}{z})$ defined by Eq. (24). ^a ${\stackrel{\mathrm{‾}}{z}}_{\mathrm{u}}=\mathrm{1}$ and ${\stackrel{\mathrm{‾}}{z}}_{\mathrm{l}}=\mathrm{0}$ for fully screened well. ^b The solution is independent of elevation.

2.8 Sensitivity analysis

Sensitivity analysis evaluates hydraulic head variation in response to the change in each of K_r, K_z, S_s, S_y, ω, and ε. The normalized sensitivity coefficient can be defined as (Liou and Yeh, 1997)

$$\begin{array}{}\text{(25)}& {\displaystyle }{\displaystyle }{S}_i=P_i{\displaystyle \frac{\partial X}{\partial P_i}},\end{array}$$

where S_i is the sensitivity coefficient of ith parameter, P_i is the magnitude of the ith input parameter, and X represents the present solution in dimensional form. Equation (25) can be approximated as

$$\begin{array}{}\text{(26)}& {\displaystyle }{\displaystyle }{S}_i=P_i{\displaystyle \frac{X\left(P_i+\mathrm{\Delta }{P}_i\right)-X\left(P_i\right)}{\mathrm{\Delta }{P}_i}},\end{array}$$

where ΔP_i, a small increment, is chosen as 10⁻³P_i.

3 Results and discussion

The following sections demonstrate the response of the hydraulic head to oscillatory pumping using the present solution. The default values in calculation are r=0.05 m, z=5 m, b=10 m, $Q={\mathrm{10}}^{-\mathrm{3}}$ m³ s⁻¹, r_w=0.05 m, z_u=5.5 m, z_l=4.5 m, $K_{\mathrm{r}}={\mathrm{10}}^{-\mathrm{4}}$ m s⁻¹, $K_z={\mathrm{10}}^{-\mathrm{5}}$ m s⁻¹, $S_{\mathrm{s}}={\mathrm{10}}^{-\mathrm{5}}$ m⁻¹, $S_{\mathrm{y}}={\mathrm{10}}^{-\mathrm{4}}$, $\mathit{\omega }=\mathrm{2}\mathit{\pi }/\mathrm{30}$ s⁻¹, and κ=100 s. The corresponding dimensionless parameters and variables are $\stackrel{\mathrm{‾}}{r}=\mathrm{1}$, $\stackrel{\mathrm{‾}}{z}=\mathrm{0.5}$, ${\stackrel{\mathrm{‾}}{z}}_{\mathrm{u}}=\mathrm{0.55}$, ${\stackrel{\mathrm{‾}}{z}}_{\mathrm{l}}=\mathrm{0.45}$, $\mathit{\gamma }=\mathrm{5.24}\times {\mathrm{10}}^{-\mathrm{5}}$, $\mathit{\mu }=\mathrm{2.5}\times {\mathrm{10}}^{-\mathrm{6}}$, $a=\mathrm{4}\times {\mathrm{10}}^{\mathrm{5}}$, and a₁=1 and $a_{\mathrm{2}}=\mathrm{2.5}\times {\mathrm{10}}^{-\mathrm{6}}$.

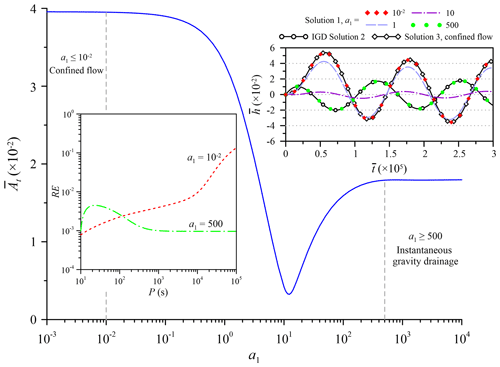
Figure 2 Influence of delayed gravity drainage on the dimensionless amplitude ${\stackrel{\mathrm{‾}}{A}}_{\mathrm{t}}$ and transient head $\stackrel{\mathrm{‾}}{h}$ at $\stackrel{\mathrm{‾}}{r}=\mathrm{1}$, $\stackrel{\mathrm{‾}}{z}=\mathrm{1}$, predicted by Solution 1 for different magnitudes of a₁ related to the influence.

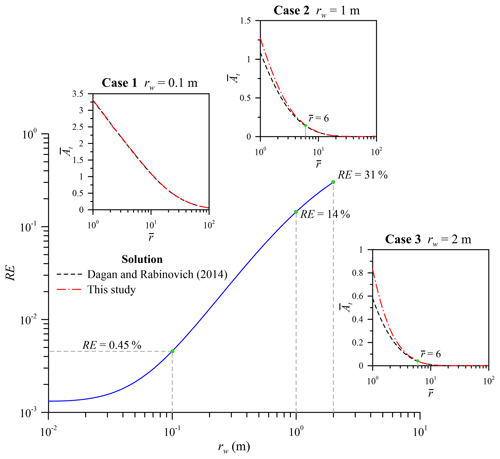
Figure 3 Relative error (RE) of the dimensionless amplitudes ${\stackrel{\mathrm{‾}}{A}}_{\mathrm{t}}$ at the rim of the pumping well (i.e., r=r_w), predicted by IGD Solution 2 and the Dagan and Rabinovich (2014) solution. The well radius is assumed to be infinitesimal in the Dagan and Rabinovich (2014) solution and finite in our solution.

3.1 Delayed gravity drainage

Previous analytical models for the OPT consider either confined flow (e.g., Rasmussen et al., 2003) or unconfined flow with IGD effect (e.g., Dagan and Rabinovich, 2014). Little attention has been paid to the consideration of the DGD effect. This section addresses the difference among these three models. Figure 2 shows the curve of the dimensionless amplitude ${\stackrel{\mathrm{‾}}{A}}_{\mathrm{t}}$ at ($\stackrel{\mathrm{‾}}{r}$, $\stackrel{\mathrm{‾}}{z})=(\mathrm{1}$, 1) of Solution 1 versus the dimensionless parameter a₁ related to the DGD effect. The transient head fluctuations are plotted based on Solution 1, with $a_{\mathrm{1}}={\mathrm{10}}^{-\mathrm{2}}$, 1, 10, 500; Solution 2 is for IGD, and Solution 3 is for confined flow. Define the relative error (RE) as

$$\begin{array}{}\text{(27)}& {\displaystyle }{\displaystyle }\mathrm{RE}=\left|{\stackrel{\mathrm{‾}}{A}}_{\mathrm{t}}^{\prime }-{\stackrel{\mathrm{‾}}{A}}_{\mathrm{t}}\right|/{\stackrel{\mathrm{‾}}{A}}_{\mathrm{t}},\end{array}$$

where ${\stackrel{\mathrm{‾}}{A}}_{\mathrm{t}}^{\prime }$ is the dimensionless amplitude predicted by Solution 2 for the case of a₁=500 or by Solution 3 for the case of $a_{\mathrm{1}}={\mathrm{10}}^{-\mathrm{2}}$. The curves of the RE versus the period of the oscillatory pumping rate (i.e., P) for these two cases are displayed. The range of P≤10⁵ s (1.16 days) contains most practical applications of the OPT. When 10${}^{-\mathrm{2}}\le a_{\mathrm{1}}\le \mathrm{500}$, the ${\stackrel{\mathrm{‾}}{A}}_{\mathrm{t}}$ gradually decreases with a₁ to the trough and then increases to the ultimate value of ${\stackrel{\mathrm{‾}}{A}}_{\mathrm{t}}=\mathrm{1.79}\times {\mathrm{10}}^{-\mathrm{2}}$. The DGD, in other words, causes an effect. When $a_{\mathrm{1}}<{\mathrm{10}}^{-\mathrm{2}}$, Solutions 1 and 3 agree on the predicted heads; the RE is below 1 % for P<10⁴ s (2.78 h), indicating that the unconfined aquifer with the DGD effect behaves like confined aquifer and that the water table can be regarded as a no-flow boundary when $a_{\mathrm{1}}<{\mathrm{10}}^{-\mathrm{2}}$ and P<10⁴ s. When a₁>500, the head fluctuations predicted by both Solutions 1 and 2 are identical; the largest RE is about 0.45 %, indicating that the DGD effect is ignorable and that Eq. (4b) reduces to Eq. (4a) for the IGD condition. This conclusion is applicable for any magnitude of P in spite of P>10⁵ s.

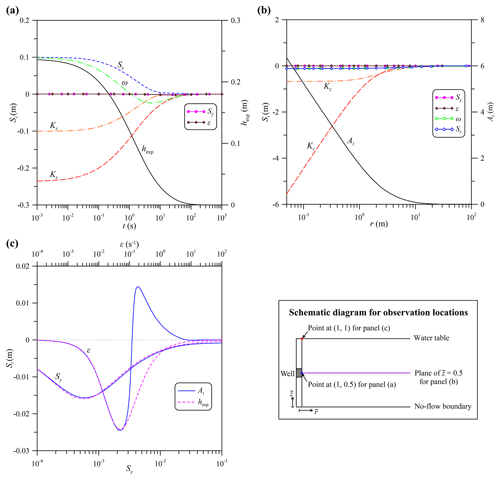
Figure 4 The normalized sensitivity coefficient S_i associated with (a) the exponential component h_exp of Solution 1 and (b) the SHM amplitude A_t for parameters K_r, K_z, S_s, S_y, ω, and ε. The observation locations for (a) and (b) are under water table (i.e., $\stackrel{\mathrm{‾}}{z}=\mathrm{0.5}$); (c) displays the curves of S_i of h_exp and A_t at water table (i.e., $\stackrel{\mathrm{‾}}{z}=\mathrm{1}$) versus S_y and ε.

3.2 Effect of finite radius of pumping well

Existing analytical models for the OPT mostly treated the pumping well as a line source with an infinitesimal radius (e.g., Rasmussen et al., 2003; Dagan and Rabinovich, 2014). The finite difference scheme for the model also treats the well as a nodal point by neglecting the radius. This will lead to significant error when a well has a radius ranging from 0.5 to 2 m (Yeh and Chang, 2013). This section discusses the relative error in predicted amplitude, defined as

$$\begin{array}{}\text{(28)}& {\displaystyle }{\displaystyle }\mathrm{RE}=\left|{\stackrel{\mathrm{‾}}{A}}_{\mathrm{D}\mathrm{\&}\mathrm{R}}-{\stackrel{\mathrm{‾}}{A}}_{\mathrm{t}}\right|/{\stackrel{\mathrm{‾}}{A}}_{\mathrm{t}},\end{array}$$

where ${\stackrel{\mathrm{‾}}{A}}_{\mathrm{t}}$ and ${\stackrel{\mathrm{‾}}{A}}_{\mathrm{D}\mathrm{\&}\mathrm{R}}$ are the dimensionless amplitudes at $\stackrel{\mathrm{‾}}{r}=\mathrm{1}$ (i.e., r=r_w) predicted by IGD Solution 2 and the Dagan and Rabinovich (2014) solution, respectively. Note that their solution assumes an infinitesimal radius of a pumping well and has a typo in that the term $e^{-D_{\mathrm{w}}+\mathrm{1}}-e^{-D_{\mathrm{w}}}$ should read $e^{\mathit{\beta }(-D_{\mathrm{w}}+\mathrm{1})}-e^{-\mathit{\beta }{D}_{\mathrm{w}}}$ (see their Eq. 25). Figure 3 demonstrates the RE for different values of radius r_w. The RE increases with r_w as expected. For case 1 of r_w=0.1 m, both solutions agree well in the entire domain of $\mathrm{1}\le \stackrel{\mathrm{‾}}{r}\le \mathrm{\infty }$, indicating that a pumping well with r_w≤0.1 m can be regarded as a line source. For the extreme case 2 of r_w=1 m or case 3 of r_w=2 m, the Dagan and Rabinovich solution underestimates the dimensionless amplitude for $\mathrm{1}\le \stackrel{\mathrm{‾}}{r}\le \mathrm{6}$ and agrees to the present solution for $\stackrel{\mathrm{‾}}{r}>\mathrm{6}$. The REs for these two cases exceed 10 %. The effect of finite radius should therefore be considered in OPT models, especially when observed hydraulic head data are taken close to the well bore of a large-diameter well.

Figure 5 Head fluctuations at $\stackrel{\mathrm{‾}}{r}=\mathrm{6}$, predicted by (a) DGD Solution 1 and (b) IGD Solution 2. Solutions 1 and 2 are expressed as $\stackrel{\mathrm{‾}}{h}={\stackrel{\mathrm{‾}}{h}}_{\exp }+{\stackrel{\mathrm{‾}}{h}}_{\mathrm{SHM}}$ for transient flow. IGD Solution 5, expressed as ${\stackrel{\mathrm{‾}}{h}}_{\mathrm{s}}={\stackrel{\mathrm{‾}}{A}}_{\mathrm{s}}\cos (\mathit{\gamma }t-{\mathit{\varphi }}_{\mathrm{s}})$, accounts for PSS flow.

3.3 Sensitivity analysis

The temporal distributions of the normalized sensitivity coefficient S_i, defined as Eq. (26), with X=h_exp as in Solution 1, are displayed in Fig. 4a for the response of exponential decay to the change in each of the six parameters, K_r, K_z, S_s, S_y, ω, and ε. The exponential decay is very sensitive to variation in each of the parameters K_r, K_z, S_s, and ω because of $\left|S_i\right|>\mathrm{0}$. Precisely, a positive perturbation in S_s produces an increase in the magnitude of h_exp, while that in K_r or K_z causes a decrease. In addition, a positive perturbation in ω yields an increase in h_exp before t=1 s and a decrease after that time. It is worth noting that the S_i for S_y or ε is very close to zero over the entire period of time, indicating that h_exp is insensitive to the change in S_y or ε and that the subtle change of gravity drainage has no influence on the exponential decay. In contrast, the spatial distributions of S_i associated with the amplitude A_t are shown in Fig. 4b in response to the changes in those six parameters. The A_t is again sensitive to the change in each of K_r, K_z, S_s, and ω but is insensitive to the change in S_y or ε. The same result as $\left|S_i\right|\cong \mathrm{0}$ for S_y or ε applies to any observation point under the water table (i.e., $\stackrel{\mathrm{‾}}{z}<\mathrm{1}$), but $\left|S_i\right|>\mathrm{0}$ at the water table (i.e., $\stackrel{\mathrm{‾}}{z}=\mathrm{1}$), shown in Fig. 4c. From those discussed above, we may conclude that the changes in the four key parameters K_r, K_z, S_s, and ω significantly affect head prediction in the entire aquifer domain. The change in S_y or ε leads to insignificant variation in the predicted head below the water table and slight variation at the water table.

Figure 6 Head fluctuations at $\stackrel{\mathrm{‾}}{r}=\mathrm{6}$ predicted by Solutions 3 and 6 for (a) partially screened pumping well and (b) fully screened pumping well. Solution 3 is expressed as $\stackrel{\mathrm{‾}}{h}={\stackrel{\mathrm{‾}}{h}}_{\exp }+{\stackrel{\mathrm{‾}}{h}}_{\mathrm{SHM}}$ for transient flow. Solution 6, expressed as ${\stackrel{\mathrm{‾}}{h}}_{\mathrm{s}}={\stackrel{\mathrm{‾}}{A}}_{\mathrm{s}}\cos (\mathit{\gamma }t-{\mathit{\varphi }}_{\mathrm{s}})$, accounts for PSS flow.

3.4 Transient head fluctuation affected by the initial condition

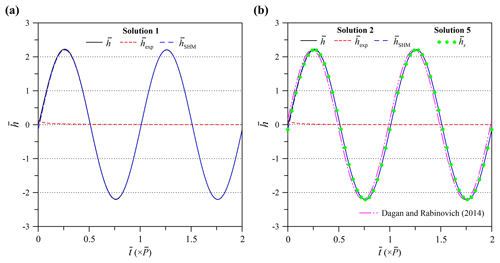
Figure 5 demonstrates head fluctuations predicted by DGD Solution 1 and IGD Solution 2, expressed as $\stackrel{\mathrm{‾}}{h}={\stackrel{\mathrm{‾}}{h}}_{\exp }+{\stackrel{\mathrm{‾}}{h}}_{\mathrm{SHM}}$ for transient flow and expressed by the IGD solution as ${\stackrel{\mathrm{‾}}{h}}_{\mathrm{s}}={\stackrel{\mathrm{‾}}{A}}_{\mathrm{s}}\cos (\mathit{\gamma }t-{\mathit{\varphi }}_{\mathrm{s}})$ for PSS flow. The transient head fluctuation starts from $\stackrel{\mathrm{‾}}{h}=\mathrm{0}$ at $\stackrel{\mathrm{‾}}{t}=\mathrm{0}$ and approaches the SHM predicted by ${\stackrel{\mathrm{‾}}{h}}_{\mathrm{SHM}}$ when ${\stackrel{\mathrm{‾}}{h}}_{\exp }\cong$ m after $\stackrel{\mathrm{‾}}{t}=\mathrm{0.5}\stackrel{\mathrm{‾}}{P}$ (i.e., 6×10⁴). Solutions 1 and 2 agree with the $\stackrel{\mathrm{‾}}{h}$ predictions because the head at $\stackrel{\mathrm{‾}}{z}=\mathrm{0.5}$ under the water table is insensitive to the change in S_y or ε, as discussed in Sect. 3.3. It is worth noting that the solution of Dagan and Rabinovich (2014) for PSS flow has a time-shift from the ${\stackrel{\mathrm{‾}}{h}}_{\mathrm{SHM}}$ of Solution 2. This indicates the phase of their solution (i.e., 1.50 rad – 1 rad approximates 57.30^∘) should be replaced by the phase of Solution 2 (i.e., ϕ_t=1.64 rad) so that their solution fits the ${\stackrel{\mathrm{‾}}{h}}_{\mathrm{SHM}}$ of Solution 2 exactly.

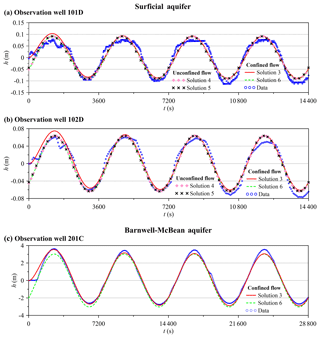
Figure 7 Comparison of field observation data with head fluctuations predicted by the present solution. Solutions 3 and 6 represent transient and PSS confined flows, respectively. PSS Solutions 4 and 5 stand for DGD and IGD conditions, respectively.

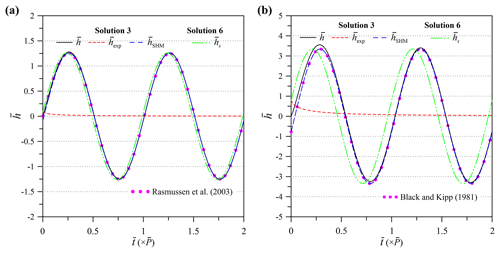
Figure 6 displays head fluctuations predicted by transient Solution 3 expressed as $\stackrel{\mathrm{‾}}{h}={\stackrel{\mathrm{‾}}{h}}_{\exp }+{\stackrel{\mathrm{‾}}{h}}_{\mathrm{SHM}}$, and PSS Solution 6 as ${\stackrel{\mathrm{‾}}{h}}_{\mathrm{s}}={\stackrel{\mathrm{‾}}{A}}_{\mathrm{s}}\cos (\mathit{\gamma }t-{\mathit{\varphi }}_{\mathrm{s}})$ for the partially screened pumping well in Fig. 6a and the full screen in Fig. 6b. The Rasmussen et al. (2003) solution for transient flow predicts the same $\stackrel{\mathrm{‾}}{h}$ as Solution 3. The Black and Kipp (1981) results for PPS flow also predict a ${\stackrel{\mathrm{‾}}{h}}_{\mathrm{SHM}}$ close to the prediction of Solution 3. The phase of Solution 6 (i.e., ϕ_s=1.50 rad for Fig. 6a and 1.33 rad for Fig. 6b) can be replaced by the phase of Solution 3 (i.e., ϕ_t=1.64 rad for Fig. 6a and 1.81 rad Fig. 6b) so that the ${\stackrel{\mathrm{‾}}{h}}_{\mathrm{SHM}}$ prediction of Solution 3 is identical to the ${\stackrel{\mathrm{‾}}{h}}_{\mathrm{s}}$ prediction of Solution 6. As concluded, excluding the initial condition with Eq. (17) for a PSS model leads to a time-shift from the SHM of the head fluctuation predicted by the associated transient model, while the transient and PSS models give the same SHM amplitude.

3.5 Application of the present solution to field experiment

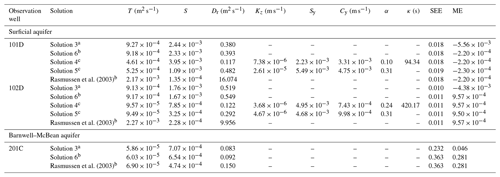
Rasmussen et al. (2003) conducted field OPTs in a three-layered aquifer system containing one surficial aquifer, the Barnwell–McBean aquifer in the middle, and the deepest Gordon aquifer at the Savannah River site. Two clay layers dividing these three aquifers may be regarded as impervious strata. For the OPT at the surficial aquifer, the formation has an average thickness of 6.25 m near the test site. The fully screened pumping well has a 7.6 cm outer radius. The pumping rate can be approximated as Qsin (ωt), with $Q=\mathrm{4.16}\times {\mathrm{10}}^{-\mathrm{4}}$ m³ s⁻¹ and ω=2π h⁻¹. The distance from the pumping well to the observation well 101D is 6 m and 11.5 m to well 102D. The screen lengths from the aquifer bottom for well 101D and from the water table for well 102D are 3 m. For the OPT at the Barnwell–McBean aquifer, the formation mainly consists of sand and fine-grained material. The pumping well has an outer radius of 7.6 cm and pumping rate of Qsin (ωt), with $Q=\mathrm{1.19}\times {\mathrm{10}}^{-\mathrm{3}}$ m³ s⁻¹ and ω=π h⁻¹. The observation well 201C is 6 m from the pumping well. The data of time-varying hydraulic heads at the observation wells (i.e., 101D, 102D, and 201C) are plotted in Fig. 7. One can refer to Rasmussen et al. (2003) for a detailed description of the Savannah River site.

The aquifer hydraulic parameters are determined based on Solutions 3 to 6 coupled with the Levenberg–Marquardt algorithm provided in the Mathematica function FindFit (Wolfram, 1991). Note that a robust Gauss–Newton algorithm (Qin et al., 2018a, b) or an automatic optimization method “SCE-UA” (Duan et al., 1992; Wang et al., 2017) provides an alternative to the parameter estimation. Solutions 4 and 5 are used to predict depth-averaged head, expressed as $(z_{\mathrm{u}}^{\prime }-z_{\mathrm{l}}^{\prime }{)}^{-\mathrm{1}}\underset{z_{\mathrm{l}}^{\prime }}{\overset{z_{\mathrm{u}}^{\prime }}{\int }}{h}_{\mathrm{s}}\mathrm{d}z$, with the upper elevation $z_{\mathrm{u}}^{\prime }$ and lower elevation $z_{\mathrm{l}}^{\prime }$ of the finite screen of the observation well 101D or 102D at the surficial aquifer. Note that Solutions 3 and 6 are independent of elevation because of the fully screened pumping well. The standard error of estimate (SEE) is defined as SEE = $\sqrt{\frac{\mathrm{1}}{M}\sum _{j=\mathrm{1}}^M{e}_j^{\mathrm{2}}}$ and the mean error (ME) as ME = $\frac{\mathrm{1}}{M}\sum _{j=\mathrm{1}}^M{e}_j$, where e_j is the difference between predicted and observed hydraulic heads and M is the number of observation data (Yeh, 1987). The estimated parameters and associated SEE and ME are displayed in Table 2. The estimates of T, S, and D_r given in Rasmussen et al. (2003) are also presented. The result shows that the estimated S_y is very small, and the estimated T and S of Solution 3, Solution 6, or the Rasmussen et al. (2003) solution for confined flow are close to those of Solution 4 or 5 for unconfined flow, indicating that the unconfined flow induced by the OPT in the surficial aquifer is negligibly small. Little gravity drainage due to the DGD effect appears with a₁=20 for wells 101D and 102D, as discussed in Sect. 3.1. Rasmussen et al. (2003) also revealed the confined behavior of the OPT-induced flow in the surficial aquifer. The estimated S_y is 1 order of magnitude less than the lower limit of the typical range of 0.01–0.3 (Freeze and Cherry, 1979), which accords with the findings of Rasmussen et al. (2003) and Rabinovich et al. (2015). Such a fact might be attributed to the problem of the moisture exchange limited by capillary fringe between the zones below and above the water table. Several laboratory research outcomes have confirmed that an estimate of S_y at a short period of the OPT is much smaller than that determined by constant-rate pumping test (e.g., Cartwright et al., 2003, 2005). In addition, the difference in T, S, or D_r estimated by Solution 6 and that estimated by the Rasmussen et al. (2003) solution may be attributed to the fact that their solution assumes isotropic hydraulic conductivity (i.e., K_r=K_z). In contrast, the transient Solution 3 gives smaller SEEs than the PSS Solution 6 or the Rasmussen et al. (2003) solution for the Barnwell–McBean aquifer and better fits the observed data at the early pumping periods as shown in Fig. 7. From those discussed above, we may conclude that the present solution is applicable to the real-world OPT.

Table 2 Hydraulic parameters estimated by the present solution and the Rasmussen et al. (2003) solution for OPT data from the Savannah River site.

^a Transient confined flow. ^b PSS confined flow. ^c PSS unconfined flow.

4 Concluding remarks

A variety of analytical models for the OPT have been proposed so far, but little attention is paid to the joint effects of DGD, the initial condition, and the finite radius of a pumping well. This study develops a new model for describing hydraulic head fluctuation due to the OPT in unconfined aquifers. A static hydraulic head prior to the OPT is regarded as an initial condition. A Neumann boundary condition is specified at the rim of a finite-radius pumping well. A free surface equation accounting for the DGD effect is considered to be the top boundary condition. The solution of the model is derived from the Laplace transform, finite-integral transform, and Weber transform. The sensitivity analysis of the head response to the change in each of hydraulic parameters is performed. The observation data obtained from the OPT at the Savannah River site are analyzed by the present solution when coupling the Levenberg–Marquardt algorithm to estimate aquifer hydraulic parameters. Our findings are summarized as follows:

1. When ${\mathrm{10}}^{-\mathrm{2}}\le a_{\mathrm{1}}\le \mathrm{500}$, the effect of DGD on head fluctuations should be considered. The amplitude of head fluctuation predicted by DGD Solution 1 decreases with increasing a₁ to a trough and then increases to the amplitude predicted by IGD Solution 2. When a₁>500, the DGD becomes IGD. Both Solutions 1 and 2 predict the same head fluctuation. When $a_{\mathrm{1}}<{\mathrm{10}}^{-\mathrm{2}}$ and P<10⁴ s, the DGD results in the water table under the no-flow condition. Solution 1 for unconfined flow gives an identical head prediction to Solution 3 for confined flow.

2. Assuming a large-diameter well as a line source with an infinitesimal radius underestimates the amplitude of head fluctuation in the domain of $\mathrm{1}\le \stackrel{\mathrm{‾}}{r}\le \mathrm{6}$ when the radius exceeds 80 cm, leading to a relative error RE > 10 %, as shown in Fig. 3. In contrast, the assumption is valid in predicting the amplitude in the domain of $\stackrel{\mathrm{‾}}{r}>\mathrm{6}$ in spite of adopting a large-diameter well. When r_w≤10 cm (i.e., RE < 0.45 %), the well radius can be regarded as infinitesimal. The result is applicable to existing analytical solutions assuming infinitesimal radius and finite difference solutions treating the pumping well as a nodal point.

3. The sensitivity analysis suggests that the changes in four parameters, K_r, K_z, S_s, and ω, significantly affect head prediction in the entire aquifer domain. The change in S_y or ε causes insignificant variation in the head under the water table but slight variation in the head at the water table.

4. Analytical solutions for the OPT are generally expressed as the sum of the exponential and the harmonic functions of time (i.e., $\stackrel{\mathrm{‾}}{h}={\stackrel{\mathrm{‾}}{h}}_{\exp }+{\stackrel{\mathrm{‾}}{A}}_{\mathrm{t}}\cos (\mathit{\gamma }t-{\mathit{\varphi }}_{\mathrm{t}}$)) for transient solutions (e.g., Solution 3) and the harmonic function (i.e., ${\stackrel{\mathrm{‾}}{h}}_{\mathrm{s}}={\stackrel{\mathrm{‾}}{A}}_{\mathrm{s}}\cos (\mathit{\gamma }t-{\mathit{\varphi }}_{\mathrm{s}})$) for PSS solutions (e.g., Solution 6), the latter assuming that without the initial condition, Eq. (17) produces a time-shift from the SHM predicted by the ${\stackrel{\mathrm{‾}}{h}}_{\mathrm{SHM}}$. The phase ϕ_s should be replaced by ϕ_t so that ${\stackrel{\mathrm{‾}}{h}}_{\mathrm{s}}$ and ${\stackrel{\mathrm{‾}}{h}}_{\mathrm{SHM}}$ are exactly the same.

Appendix A: Notation and abbreviation

a	$b{D}_{\mathrm{r}}/\left(C_{\mathrm{y}}{r}_{\mathrm{w}}^{\mathrm{2}}\right)$
a1, a2	b∕(κCy), $r_{\mathrm{w}}^{\mathrm{2}}/\left(\mathit{\kappa }{D}_{\mathrm{r}}\right)$
b	Aquifer thickness
Cy	Kz∕Sy
Dr	Kr∕Ss
DGD	Delayed gravity drainage
h	Hydraulic head
$\stackrel{\mathrm{‾}}{h}$	Dimensionless hydraulic head, i.e., $\stackrel{\mathrm{‾}}{h}=\mathrm{2}\mathit{\pi }l{K}_{\mathrm{r}}h/Q$
IGD	Instantaneous gravity drainage
Kr, Kz	Aquifer horizontal and vertical hydraulic conductivities, respectively
LHS	Left-hand side
l	Screen length, i.e., zu−zl
OPT	Oscillatory pumping test
P	Period of oscillatory pumping rate
PSS	Pseudo-steady state
$\stackrel{\mathrm{‾}}{P}$	Dimensionless period, i.e., $\stackrel{\mathrm{‾}}{P}=D_{\mathrm{r}}P/r_{\mathrm{w}}^{\mathrm{2}}$
p	Laplace parameter
Q	Amplitude of oscillatory pumping rate
RHS	Right-hand side
r	Radial distance from the center of pumping well
$\stackrel{\mathrm{‾}}{r}$	Dimensionless radial distance, i.e., $\stackrel{\mathrm{‾}}{r}=r/r_{\mathrm{w}}$
rw	Radius of pumping well
SHM	Simple harmonic motion
Ss, Sy	Specific storage and specific yield, respectively
t	Time since pumping
$\stackrel{\mathrm{‾}}{t}$	Dimensionless pumping time, i.e., $\stackrel{\mathrm{‾}}{t}=D_{\mathrm{r}}t/r_{\mathrm{w}}^{\mathrm{2}}$
z	Elevation from aquifer bottom
zl, zu	Lower and upper elevations of well screen, respectively
$\stackrel{\mathrm{‾}}{z}$	Dimensionless elevation, i.e., $\stackrel{\mathrm{‾}}{z}=z/b$
${\stackrel{\mathrm{‾}}{z}}_{\mathrm{l}}$, ${\stackrel{\mathrm{‾}}{z}}_{\mathrm{u}}$	zl∕b, zu∕b
α	Kz∕Kr
βn	Roots of Eq. (15)
κ	1∕ϵ
γ	Dimensionless frequency of oscillatory pumping rate, i.e., $\mathit{\omega }{r}_{\mathrm{w}}^{\mathrm{2}}/D_{\mathrm{r}}$
ϵ	Empirical constant associated with delayed gravity drainage
μ	$\mathit{\alpha }{r}_{\mathrm{w}}^{\mathrm{2}}/b^{\mathrm{2}}$
ω	Frequency of oscillatory pumping rate, i.e., $\mathit{\omega }=\mathrm{2}\mathit{\pi }/P$