A new probability density function for spatial distribution of soil water storage capacity leads to the SCS curve number method

Following the Budyko framework, the soil wetting ratio (the ratio between soil wetting and precipitation) as a function of the soil storage index (the ratio between soil wetting capacity and precipitation) is derived from the Soil Conservation Service Curve Number (SCS-CN) method and the variable infiltration capacity (VIC) type of model. For the SCS-CN method, the soil wetting ratio approaches 1 when the soil storage index approaches ∞, due to the limitation of the SCS-CN method in which the initial soil moisture condition is not explicitly represented. However, for the VIC type of model, the soil wetting ratio equals the soil storage index when the soil storage index is lower than a certain value, due to the finite upper bound of the generalized Pareto distribution function of storage capacity. In this paper, a new distribution function, supported on a semi-infinite interval $x\in [\mathrm{0},\mathrm{\infty })$, is proposed for describing the spatial distribution of storage capacity. From this new distribution function, an equation is derived for the relationship between the soil wetting ratio and the storage index. In the derived equation, the soil wetting ratio approaches 0 as the storage index approaches 0; when the storage index tends to infinity, the soil wetting ratio approaches a certain value (≤1) depending on the initial storage. Moreover, the derived equation leads to the exact SCS-CN method when initial water storage is 0. Therefore, the new distribution function for soil water storage capacity explains the SCS-CN method as a saturation excess runoff model and unifies the surface runoff modeling of the SCS-CN method and the VIC type of model.

1 Introduction

The Soil Conservation Service Curve Number (SCS-CN) method (Mockus, 1972) has been popularly used for direct runoff estimation in engineering communities. Even though the SCS-CN method was obtained empirically (Ponce, 1996; Beven, 2012), it is often interpreted as an infiltration excess runoff model (Bras, 1990; Mishra and Singh, 1999). Yu (1998) showed that partial area infiltration excess runoff generation on a statistical distribution of soil infiltration characteristics provided a similar runoff generation equation to the SCS-CN method. Recently, Hooshyar and Wang (2016) derived an analytical solution for Richards' equation for ponded infiltration into a soil column bounded by a water table, and they showed that the SCS-CN method, as an infiltration excess model, is a special case of the derived general solution. The SCS-CN method has also been interpreted as a saturation excess runoff model (Steenhuis et al., 1995; Lyon et al., 2004; Easton et al., 2008). During an interview, Mockus, who developed the proportionality relationship of the SCS-CN method, stated that “saturation overland flow was the most likely runoff mechanism to be simulated by the method” (Ponce, 1996). Recently, Bartlett et al. (2016a) developed a probabilistic framework, which provides a statistical justification of the SCS-CN method and extends the saturation excess interpretation of the event-based runoff of the method.

Since the 1970s, various saturation excess runoff models have been developed based on the concept of probability distribution of soil storage capacity (Moore, 1985). TOPMODEL is a well-known saturation excess runoff model based on spatially distributed topography (Beven and Kirkby, 1979; Sivapalan et al., 1987). To quantify the dynamic change of saturation area during rainfall events, the spatial variability of soil moisture storage capacity is described by a cumulative probability distribution function in the Xinanjiang model (Zhao, 1977; Zhao et al., 1992) and the variable infiltration capacity (VIC) model (Wood et al., 1992; Liang et al., 1994). The spatial distribution of storage capacity in these models is described by the generalized Pareto distribution, which has been used for catchment-scale runoff prediction and large-scale land surface hydrologic simulations. Bartlett et al. (2016b) proposed an event-based probabilistic storage framework for unifying TOPMODEL, the VIC type of model, and the SCS-CN method, and the framework includes a spatial description of the runoff concept of “prethreshold” and “threshold-excess” runoff (Bartlett et al., 2016a).

Even though the SCS-CN method has been interpreted as a saturation excess runoff model in the literature, there is a knowledge gap for the direct linkage between the SCS-CN method and the Xinanjiang and VIC type of model based on a probability distribution function for the spatial variability of soil water storage capacity. If the SCS-CN method is a saturation excess runoff model, is there a distribution function for soil water storage capacity which leads to the SCS-CN method? If yes, what is the probability density function (PDF)? This is an unsolved research question. The objective of this paper is to fill this knowledge gap, i.e., discovering the distribution function for soil water storage capacity which leads to the SCS-CN method. This is a procedure of inverse modeling, i.e., identifying the distribution function of the saturation excess runoff model for a known functional form of runoff generation.

Meanwhile, the identification of the new distribution function is intrigued by the linkage between the SCS-CN method and the Budyko equation (Budyko, 1974). By applying the generalized proportionality hypothesis from the SCS-CN method to mean annual water balance, Wang and Tang (2014) derived a one-parameter Budyko equation for the mean annual evaporation ratio (i.e., the ratio of evaporation to precipitation) as a function of the climate aridity index (i.e., the ratio of potential evaporation to precipitation). As an analogy to the Budyko framework, the SCS-CN method and the VIC type of model at the event scale can be represented by the relationship between the soil wetting ratio, defined as the ratio between soil wetting and precipitation, and the soil storage index, which is defined as the ratio between soil wetting capacity and precipitation. The representation of runoff generation in the Budyko type of framework facilitates the identification of the new distribution function for soil water storage capacity leading to the SCS-CN method.

The identified new distribution function for soil water storage capacity will unify the SCS-CN method and the VIC type of model. In Sect. 2, the SCS-CN method is presented in the form of the Budyko-type framework with two parameterization schemes. In Sect. 3, the VIC type of model is presented in the form of the Budyko-type framework. In Sect. 4, the SCS-CN method is then compared with the VIC type of model from the perspectives of the number of parameters and boundary conditions (i.e., the lower and upper bounds of the soil storage index). In Sect. 5, the proposed new distribution function is introduced and compared with the generalized Pareto distribution of the VIC type of model, and a modified SCS-CN method considering initial storage explicitly is derived from the new distribution function. Conclusions are drawn in Sect. 6.

2 SCS curve number method

In this section, the SCS-CN method is described in the form of surface runoff modeling and then is presented for infiltration modeling in the Budyko-type framework. The initial storage at the beginning of a time interval (e.g., rainfall event) is denoted by S₀ (mm), and the maximum value of average storage capacity over the catchment is denoted by S_b (mm). The storage capacity for soil wetting for the time interval, S_p (mm), is computed by

$$\begin{array}{}\text{(1)}& S_p=S_b-S_{\mathrm{0}}.\end{array}$$

The total rainfall during the time interval is denoted by P (mm). Before surface runoff is generated, a portion of rainfall is intercepted by vegetation and infiltrates into the soil. This portion of rainfall is called initial abstraction or initial soil wetting denoted by W_i (mm). The remaining rainfall (P−W_i) is partitioned into runoff and continuing soil wetting. This competition is captured by the proportionality relationship in the SCS-CN method:

$$\begin{array}{}\text{(2)}& {\displaystyle \frac{W-W_{\mathrm{i}}}{S_p-W_{\mathrm{i}}}}={\displaystyle \frac{Q}{P-W_{\mathrm{i}}}},\end{array}$$

where W (mm) is the total soil wetting, W−W_i is continuing wetting and S_p−W_i is its potential value, Q (mm) is surface runoff, and P−W_i is the available water and interpreted as the potential value of Q. Since rainfall is partitioned into total soil wetting and surface runoff, i.e., $P=W+Q$, surface runoff is computed by substituting $W=P-Q$ into Eq. (2):

$$\begin{array}{}\text{(3)}& Q={\displaystyle \frac{{\left(P-W_{\mathrm{i}}\right)}^{\mathrm{2}}}{P+S_p-\mathrm{2}{W}_{\mathrm{i}}}}.\end{array}$$

This equation is used for computing direct runoff in the SCS-CN method.

The SCS-CN method can also be represented in terms of the soil wetting ratio $\left(\frac{W}{P}\right)$. Substituting Eq. (3) into $W=P-Q$ and dividing P on both sides, the soil wetting ratio equation is obtained:

$$\begin{array}{}\text{(4)}& {\displaystyle \frac{W}{P}}={\displaystyle \frac{\frac{S_p}{P}-\frac{W_{\mathrm{i}}^{\mathrm{2}}}{P^{\mathrm{2}}}}{\mathrm{1}+\frac{S_p}{P}-\mathrm{2}\frac{W_{\mathrm{i}}}{P}}}.\end{array}$$

The climate aridity index is defined as the ratio between potential evaporation and precipitation. In the climate aridity index, both available water supply and water demand are determined by climate.

$$\begin{array}{}\text{(5)}& {\mathrm{\Phi }}_{\mathrm{sc}}={\displaystyle \frac{S_p}{P}}\end{array}$$

A similar dimensionless parameter for the ratio between the maximum soil storage capacity and mean rainfall depth of rainfall events was defined in Porporato et al. (2004). In the soil storage index, water demand is determined by soil and available water supply is determined by climate. Substituting Eq. (5) into Eq. (4), the soil wetting equation for the SCS-CN method is obtained:

$$\begin{array}{}\text{(6)}& {\displaystyle \frac{W}{P}}={\displaystyle \frac{{\mathrm{\Phi }}_{\mathrm{sc}}-\frac{W_{\mathrm{i}}^{\mathrm{2}}}{P^{\mathrm{2}}}}{\mathrm{1}+{\mathrm{\Phi }}_{\mathrm{sc}}-\mathrm{2}\frac{W_{\mathrm{i}}}{P}}}.\end{array}$$

There are two potential schemes for parameterizing the initial wetting in Eq. (6). As the first scheme, the initial wetting is usually parameterized as the ratio between initial wetting and storage capacity in the SCS-CN method. The detail of this scheme is described in Appendix A and plotted in Fig. 1. As we can see, the range of Φ_sc is dependent on the parameter $\mathit{\lambda }=\frac{W_{\mathrm{i}}}{S_p-W_{\mathrm{i}}}$.

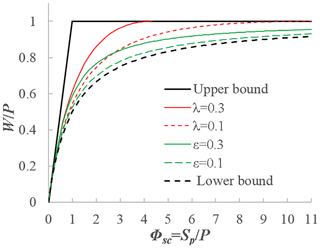
Figure 1 The wetting ratio $\left(\frac{W}{P}\right)$ versus the soil storage index $\left(\frac{S_p}{P}\right)$ from the SCS-CN method based on two parameterization schemes: $\mathit{\lambda }=\frac{W_{\mathrm{i}}}{S_p-W_{\mathrm{i}}}$ (scheme 1) and $\mathit{\epsilon }=\frac{W_{\mathrm{i}}}{W}$ (scheme 2).

In order to avoid the situation where the range of Φ_sc is dependent on the parameter λ, we can use the following parameterization scheme (Chen et al., 2013; Tang and Wang, 2017):

$$\begin{array}{}\text{(7)}& \mathit{\epsilon }={\displaystyle \frac{W_{\mathrm{i}}}{W}}.\end{array}$$

Substituting Eq. (7) into Eq. (6), we can obtain the following equation:

$$\begin{array}{}\text{(8)}& {\displaystyle \frac{W}{P}}={\displaystyle \frac{\mathrm{1}+{\mathrm{\Phi }}_{\mathrm{sc}}-\sqrt{{\left(\mathrm{1}+{\mathrm{\Phi }}_{\mathrm{sc}}\right)}^{\mathrm{2}}-\mathrm{4}\mathit{\epsilon }\left(\mathrm{2}-\mathit{\epsilon }\right){\mathrm{\Phi }}_{\mathrm{sc}}}}{\mathrm{2}\mathit{\epsilon }\left(\mathrm{2}-\mathit{\epsilon }\right)}}.\end{array}$$

Equation (8) has the same functional form as the derived Budyko equation for the long-term evaporation ratio (Wang and Tang, 2014; Wang et al., 2015). Equation (8) satisfies the following boundary conditions: $\frac{W}{P}\to \mathrm{0}$ as Φ_sc→0 and $\frac{W}{P}\to \mathrm{1}$ as Φ_sc→∞. Based on Eq. (7), the range of ε is [0, 1], and ε=1 corresponds to the upper bound (Fig. 1). Equation (8) becomes Eq. (A3) as ε→0, and it is the lower bound. Figure 1 plots Eq. (8) for ε=0.1 and 0.3. Due to the dependence of the range of Φ_sc on the parameter λ in the first parameterization scheme, the second parameterization scheme is focused on in the following sections.

In the SCS-CN method, the soil wetting ratio is a function of the soil storage index with a parameter for describing initial wetting. The average wetting capacity at the catchment scale is used for computing the soil storage index, but the spatial variability of wetting capacity is not represented in the SCS-CN method.

3 Saturation excess runoff model

The spatial variability of soil water storage capacity is explicitly represented in the saturation excess runoff models such as VIC and Xinanjiang. In these models, the spatial variation of the point-scale storage capacity (C) is represented by a generalized Pareto distribution:

$$\begin{array}{}\text{(9)}& F\left(C\right)=\mathrm{1}-{\left(\mathrm{1}-{\displaystyle \frac{C}{C_{\mathrm{m}}}}\right)}^{\mathit{\beta }},\end{array}$$

where F(C) is the cumulative probability, i.e., the fraction of the catchment area for which the storage capacity is less than C (mm), and C_m (mm) is the maximum value of the point-scale storage capacity over the catchment. The water storage capacity includes vegetation interception, surface retention, and soil moisture capacity; β is the shape parameter of the storage capacity distribution and is usually assumed to be a positive number. β ranges from 0.01 to 5.0 as suggested by Wood et al. (1992). The storage capacity distribution curve is concave down for $\mathrm{0}<\mathit{\beta }<\mathrm{1}$ and concave up for β>1. The average value of storage capacity over the catchment is equivalent to S_b in the SCS-CN method, and it is obtained by integrating the exceedance probability of storage capacity $S_b={\int }_{\mathrm{0}}^{C_{\mathrm{m}}}\left(\mathrm{1}-F\left(x\right)\right)\mathrm{d}x$:

$$\begin{array}{}\text{(10)}& S_b={\displaystyle \frac{C_{\mathrm{m}}}{\mathit{\beta }+\mathrm{1}}}.\end{array}$$

Similarly, for a given C, the catchment-scale storage S (mm) can be computed as follows (Moore, 1985):

$$\begin{array}{}\text{(11)}& S=S_b\left[\mathrm{1}-{\left(\mathrm{1}-{\displaystyle \frac{C}{C_{\mathrm{m}}}}\right)}^{\mathit{\beta }+\mathrm{1}}\right].\end{array}$$

To derive the wetting ratio as a function of the soil storage index, the initial storage at the catchment scale is parameterized by the degree of saturation:

$$\begin{array}{}\text{(12)}& \mathit{\psi }={\displaystyle \frac{S_{\mathrm{0}}}{S_b}}.\end{array}$$

Recalling Eq. (1) and the definition of the soil storage index (i.e., Eq. 5), we obtain

$$\begin{array}{}\text{(13)}& {\displaystyle \frac{S_b}{P}}={\displaystyle \frac{{\mathrm{\Phi }}_{\mathrm{sc}}}{\mathrm{1}-\mathit{\psi }}}.\end{array}$$

The value of C corresponding to the initial storage S₀ is denoted as C₀, and $S_{\mathrm{0}}=S_b\left[\mathrm{1}-{\left(\mathrm{1}-\frac{C_{\mathrm{0}}}{C_{\mathrm{m}}}\right)}^{\mathit{\beta }+\mathrm{1}}\right]$ is obtained by substituting S₀ and C₀ into Eq. (11). When $P+C_{\mathrm{0}}\ge C_{\mathrm{m}}$, each point within the catchment is saturated and soil wetting reaches its maximum value; i.e., W=S_p. Substituting $C_{\mathrm{0}}=C_{\mathrm{m}}-C_{\mathrm{m}}{\left(\mathrm{1}-\frac{S_{\mathrm{0}}}{S_b}\right)}^{\frac{\mathrm{1}}{\mathit{\beta }+\mathrm{1}}}$ into $P+C_{\mathrm{0}}\ge C_{\mathrm{m}}$, we obtain

$$\begin{array}{}\text{(14)}& {\mathrm{\Phi }}_{\mathrm{sc}}\le b,\text{where}b={\left(\mathit{\beta }+\mathrm{1}\right)}^{-\mathrm{1}}{\left(\mathrm{1}-\mathit{\psi }\right)}^{\frac{\mathit{\beta }}{\mathit{\beta }+\mathrm{1}}}.\end{array}$$

Therefore, this condition is equivalent to

$$\begin{array}{}\text{(15)}& {\displaystyle \frac{W}{P}}={\mathrm{\Phi }}_{\mathrm{sc}}\text{when}{\mathrm{\Phi }}_{\mathrm{sc}}\le b.\end{array}$$

Next, we will derive $\frac{W}{P}$ for the condition of Φ_sc>b. The storage at the end of the modeling period (e.g., rainfall–runoff event) is denoted as S₁, which is computed by

$$\begin{array}{}\text{(16)}& S_{\mathrm{1}}=S_b\left[\mathrm{1}-{\left(\mathrm{1}-{\displaystyle \frac{P+C_{\mathrm{0}}}{C_{\mathrm{m}}}}\right)}^{\mathit{\beta }+\mathrm{1}}\right].\end{array}$$

From Eq. (16) one obtains (see Appendix B for details)

$$\begin{array}{}\text{(17)}& {\displaystyle \frac{W}{P}}={\mathrm{\Phi }}_{\mathrm{sc}}\left[\mathrm{1}-{\left(\mathrm{1}-b{\mathrm{\Phi }}_{\mathrm{sc}}^{-\mathrm{1}}\right)}^{\mathit{\beta }+\mathrm{1}}\right]\text{when}{\mathrm{\Phi }}_{\mathrm{sc}}>b.\end{array}$$

The limit of Eq. (17) for Φ_sc→∞ can be obtained as follows (see Appendix C for details):

$$\begin{array}{}\text{(18)}& \underset{{\mathrm{\Phi }}_{\mathrm{sc}}\to \mathrm{\infty }}{lim}{\displaystyle \frac{W}{P}}={\left(\mathrm{1}-\mathit{\psi }\right)}^{\frac{\mathit{\beta }}{\mathit{\beta }+\mathrm{1}}}.\end{array}$$

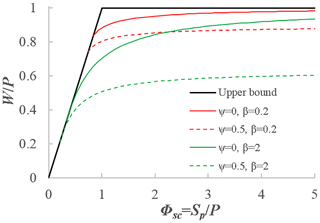
Equations (15) and (17) provide $\frac{W}{P}$ as a function of Φ_sc with two parameters (ψ and β). Figure 2 plots Eqs. (15) and (17) for ψ=0 and 0.5 when β=0.2 and 2. As we can see, $\frac{W}{P}$ decreases as β increases for given values of ψ and Φ_sc, and $\frac{W}{P}$ decreases as ψ increases for given values of β and Φ_sc, implicating that the soil wetting ratio decreases with the degree of initial saturation under a given the soil storage index.

Figure 2 The impact of β and the degree of initial storage $\left(\mathit{\psi }=S_{\mathrm{0}}/S_b\right)$ on the soil wetting ratio (W∕P).

Table 1 The boundary conditions of the functions for relating the wetting ratio $\left(\frac{W}{P}\right)$ to the soil storage index (Φ_sc): (1) the SCS-CN method, (2) the VIC type of model, and (3) the modified SCS-CN method based on the proposed new distribution for the VIC type of model.

4 Comparison between the SCS-CN model and the VIC type of model

The SCS-CN model with the parameterization of the ratio between initial wetting and total wetting is compared with the VIC type of saturation excess runoff model. In Sects. 2 and 3, we derived $\frac{W}{P}$ as a function of Φ_sc based on the SCS-CN method and the VIC type of model, which uses a generalized Pareto distribution to describe the spatial distribution of storage capacity. The SCS-CN method is a function of storage capacity S_p, but the VIC type of model is a function of storage capacity S_p and the degree of initial saturation $\frac{S_{\mathrm{0}}}{S_b}$. As a result, the function of $\frac{W}{P}\sim \frac{S_p}{P}$ for the SCS-CN method has only one parameter (ε), but it has two parameters (β and ψ) for the VIC type of model.

Table 1 shows the boundary conditions for the relationships between $\frac{W}{P}$ and Φ_sc from the SCS-CN method and the VIC type of model. The lower boundary of the SCS-CN method with parameter ε is $\frac{W}{P}\to \mathrm{0}$ as Φ_sc→0. However, for the VIC type of model, $\frac{W}{P}={\mathrm{\Phi }}_{\mathrm{sc}}$ when Φ_sc≤b. For the SCS-CN method, W reaches its maximum (S_p) when rainfall reaches infinity, while for the VIC type of model, W reaches its maximum value (S_p) when rainfall reaches a finite number (C_m−C₀). In other words, for the SCS-CN method, the entire catchment becomes saturated when rainfall reaches infinity, while for the VIC-type model, the entire catchment becomes saturated when rainfall reaches a finite number.

As shown in Table 1, the upper boundary of the SCS-CN method (with parameter ε) is 1. However, for the VIC type of model, the upper boundary is ${\left(\mathrm{1}-\mathit{\psi }\right)}^{\frac{\mathit{\beta }}{\mathit{\beta }+\mathrm{1}}}$ instead of 1. This is due to the effect of initial storage in the VIC type of model. When initial storage is 0 (i.e., ψ=0), the wetting ratio $\frac{W}{P}$ for the VIC type of model has the same upper boundary condition as the SCS-CN method.

5 Unification of the SCS-CN method and the VIC type of model

Based on the comparison between the SCS-CN method and the VIC type of model, a new distribution function is proposed in this section for describing the spatial distribution of soil water storage capacity, which unifies the SCS-CN method and the VIC type of model. As discussed in Sect. 4, the upper boundary condition of the SCS-CN model (i.e., $\frac{W}{P}\to \mathrm{1}$ as Φ_sc→∞) does not depend on the initial storage. This upper boundary condition needs to be modified by including the effect of initial storage so that the limit of $\frac{W}{P}$ as Φ_sc→∞ is dependent on the degree of initial saturation like the VIC type of model. However, the lower boundary condition of the VIC model needs to be modified so that the lower boundary condition follows that of $\frac{W}{P}\to \mathrm{0}$ as Φ_sc→0 like the SCS-CN method. Through these modifications, the SCS-CN method and the VIC type of saturation excess runoff model can be unified from the functional perspective of the soil wetting ratio.

Based on the comparison one may have the following questions. (1) Can the SCS-CN method be derived from the VIC type of model by setting initial storage to 0? (2) If yes, what is the distribution function for soil water storage capacity? Once we answer these questions, a modified SCS-CN method considering initial storage explicitly can be derived as a saturation excess runoff model based on a distribution function of water storage capacity, and it unifies the SCS-CN method and the VIC type of model. In this section, a new distribution function is proposed for describing the spatial variability of soil water storage capacity, from which the SCS-CN method is derived as a VIC type of model.

5.1 A new distribution function

The probability density function (PDF) of the new distribution for describing the spatial distribution of water storage capacity is represented by

$$\begin{array}{}\text{(19)}& f\left(C\right)={\displaystyle \frac{\left(\mathrm{2}-a\right){\mathit{\mu }}^{\mathrm{2}}}{{\left[{\left(C+\mathit{\mu }\right)}^{\mathrm{2}}-\mathrm{2}a\mathit{\mu }C\right]}^{\mathrm{3}/\mathrm{2}}}},\end{array}$$

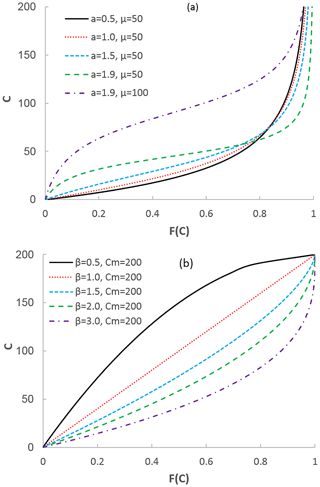
where C is the point-scale water storage capacity and supported on a positive semi-infinite interval (C≥0), a is the shape parameter and its range is $\mathrm{0}<a<\mathrm{2}$, and μ is the mean of the distribution (i.e., the scale parameter). Figure 3a plots the PDFs for five sets of shape and scale parameters. When a≤1, the PDF monotonically decreases with the increase of C; i.e., the peak of the PDF occurs at C=0, while when a>1 the peak of the PDF occurs at C>0 and the location of the peak depends on the values of a and μ. For comparison, Fig. 3b plots the PDF for the VIC model. As shown by the solid black curve in Fig. 3b, when $\mathrm{0}<\mathit{\beta }<\mathrm{1}$, f(C) approaches infinity as C→C_m. It is a uniform distribution when β=1. The peak of the PDF occurs at C=0 when β>1. Therefore, the peak of the PDF for the VIC model occurs at C=0 or C_m.

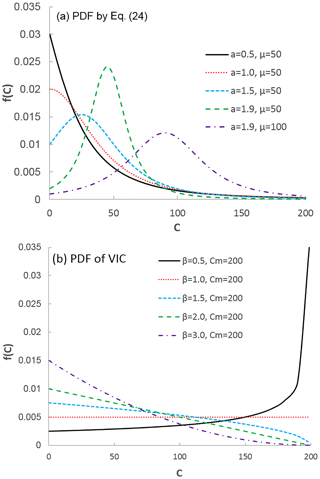
Figure 3 The probability density functions (PDFs) with different parameter values: (a) the proposed PDF represented by Eq. (24) and (b) the generalized Pareto distribution of the VIC model, i.e., Eq. (25).

The cumulative distribution function (CDF) corresponding to the proposed PDF is obtained by integrating Eq. (19):

$$\begin{array}{}\text{(20)}& F\left(C\right)=\mathrm{1}-{\displaystyle \frac{\mathrm{1}}{a}}+{\displaystyle \frac{C+\left(\mathrm{1}-a\right)\mathit{\mu }}{a\sqrt{{\left(C+\mathit{\mu }\right)}^{\mathrm{2}}-\mathrm{2}a\mathit{\mu }C}}}.\end{array}$$

Figure 4a plots the CDFs corresponding to the PDFs in Fig. 3a. For comparison, Fig. 4b plots the CDFs corresponding to the PDFs in Fig. 3b. The storage capacity distribution curve for the proposed distribution is concave up for a≤1 and S shaped for a>1 (Fig. 4a), while the storage capacity distribution curve for the VIC model is concave up for β>1 and concave down for $\mathrm{0}<\mathit{\beta }<\mathrm{1}$ (Fig. 4b). The S shape of the CDF (Fig. 4a) is more significant with a higher value of a (e.g., a=1.9). For a smaller value of a, the difference between the new PDF and the VIC type of model becomes smaller. The proposed distribution can fit the S shape of the cumulative distribution for storage capacity which is observed from soil data (Huang et al., 2003), but the generalized Pareto distribution of the VIC type of model is not able to fit the S shape of the CDF.

Figure 4 The cumulative distribution functions (CDFs) with different parameter values: (a) the proposed distribution function represented by Eq. (26) and (b) the generalized Pareto distribution of the VIC model represented by Eq. (13).

5.2 Deriving the SCS-CN method from the proposed distribution function

The soil wetting and surface runoff can be computed when Eq. (20) is used to describe the spatial distribution of soil water storage capacity in a catchment. The average value of storage capacity over the catchment is the mean of the distribution:

$$\begin{array}{}\text{(21)}& \mathit{\mu }=S_b.\end{array}$$

For a given C, the catchment-scale storage S can be computed by $S={\int }_{\mathrm{0}}^C\left[\mathrm{1}-F\left(x\right)\right]\mathrm{d}x$ (Moore, 1985). From Eq. (20), we obtain

$$\begin{array}{}\text{(22)}& S={\displaystyle \frac{C+S_b-\sqrt{{\left(C+S_b\right)}^{\mathrm{2}}-\mathrm{2}a{S}_{b}C}}{a}}.\end{array}$$

For a rainfall–runoff event, the average initial storage at the catchment scale is denoted as S₀ and the corresponding value of C is denoted as C₀. Substituting S₀ and C₀ into Eq. (22), we obtain

$$\begin{array}{}\text{(23)}& m={\displaystyle \frac{\mathit{\psi }\left(\mathrm{2}-a\mathit{\psi }\right)}{\mathrm{2}\left(\mathrm{1}-\mathit{\psi }\right)}},\end{array}$$

where $\mathit{\psi }=\frac{S_{\mathrm{0}}}{S_b}$ is defined in Eq. (12) and $m=\frac{C_{\mathrm{0}}}{S_b}$.

The rainfall in the catchment is assumed to be spatially uniform and the rainfall depth is denoted as P. If the spatial distribution of rainfall is not uniform, the method is applied to sub-catchments where the effect of spatial variability of rainfall is negligible. The average storage at the catchment scale after infiltration is computed by substituting $C=C_{\mathrm{0}}+P$ into Eq. (22):

$$\begin{array}{}\text{(24)}& S_{\mathrm{1}}={\displaystyle \frac{C_{\mathrm{0}}+P+S_b-\sqrt{{\left(C_{\mathrm{0}}+P+S_b\right)}^{\mathrm{2}}-\mathrm{2}a{S}_b\left(C_{\mathrm{0}}+P\right)}}{a}}.\end{array}$$

The soil wetting is computed as the difference between S₁ and S₀:

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }W=\\ \text{(25)}& {\displaystyle }& {\displaystyle }{\displaystyle \frac{P+\sqrt{{\left(C_{\mathrm{0}}+S_b\right)}^{\mathrm{2}}-\mathrm{2}a{S}_b{C}_{\mathrm{0}}}-\sqrt{{\left(C_{\mathrm{0}}+P+S_b\right)}^{\mathrm{2}}-\mathrm{2}a{S}_b\left(C_{\mathrm{0}}+P\right)}}{a}}.\end{array}$$

Dividing P on both sides of Eq. (25) and substituting $m=\frac{C_{\mathrm{0}}}{S_b}$, we obtain

$$\begin{array}{ll}{\displaystyle }& {\displaystyle \frac{W}{P}}=\\ \text{(26)}& {\displaystyle }& {\displaystyle }{\displaystyle \frac{\mathrm{1}+\frac{S_b}{P}\sqrt{{\left(m+\mathrm{1}\right)}^{\mathrm{2}}-\mathrm{2}\mathrm{am}}-\sqrt{{\left(\mathrm{1}+(m+\mathrm{1})\frac{S_b}{P}\right)}^{\mathrm{2}}-\mathrm{2}\mathrm{am}{\left(\frac{S_b}{P}\right)}^{\mathrm{2}}-\mathrm{2}a\frac{S_b}{P}}}{a}}.\end{array}$$

Substituting Eq. (13) into Eq. (26), we obtain

$$\begin{array}{ll}{\displaystyle }& {\displaystyle \frac{W}{P}}=\\ \text{(27)}& {\displaystyle }& {\displaystyle }{\displaystyle \frac{\mathrm{1}+\frac{\sqrt{{\left(m+\mathrm{1}\right)}^{\mathrm{2}}-\mathrm{2}\mathrm{am}}}{\mathrm{1}-\mathit{\psi }}{\mathrm{\Phi }}_{\mathrm{sc}}-\sqrt{{\left(\mathrm{1}+\frac{m+\mathrm{1}}{\mathrm{1}-\mathit{\psi }}{\mathrm{\Phi }}_{\mathrm{sc}}\right)}^{\mathrm{2}}-\mathrm{2}\mathrm{am}{\left(\frac{{\mathrm{\Phi }}_{\mathrm{sc}}}{\mathrm{1}-\mathit{\psi }}\right)}^{\mathrm{2}}-\frac{\mathrm{2}a}{\mathrm{1}-\mathit{\psi }}{\mathrm{\Phi }}_{\mathrm{sc}}}}{a}}.\end{array}$$

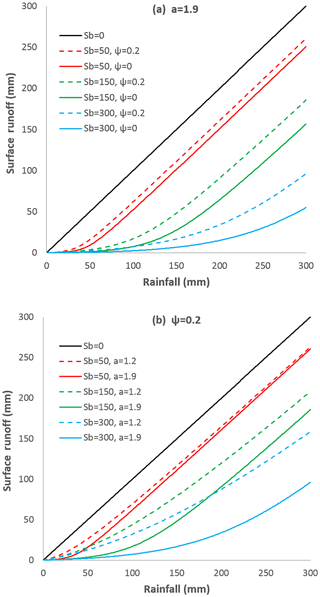
Figure 5 plots Eq. (27) for ψ=0, 0.4, and 0.6 when a=0.6 and 1.8. As we can see, $\frac{W}{P}$ increases with a for given values of ψ and Φ_sc, and $\frac{W}{P}$ decreases with ψ for given values of a and Φ_sc, which is consistent with the VIC model and implicates that the soil wetting ratio decreases with the degree of initial saturation under a storage index. As shown in Fig. 5, Eq. (27) satisfies the lower boundary of the SCS-CN method and the upper boundary of the VIC model. Specifically, Eq. (27) satisfies the following boundary conditions (see Appendix D for details) shown in Table 1:

$$\begin{array}{}\text{(28a)}& {\displaystyle }& {\displaystyle }\underset{{\mathrm{\Phi }}_{\mathrm{sc}}\to \mathrm{0}}{lim}{\displaystyle \frac{W}{P}}=\mathrm{0},\text{(28b)}& {\displaystyle }& {\displaystyle }\underset{{\mathrm{\Phi }}_{\mathrm{sc}}\to \mathrm{\infty }}{lim}{\displaystyle \frac{W}{P}}={\displaystyle \frac{\sqrt{{\left(m+\mathrm{1}\right)}^{\mathrm{2}}-\mathrm{2}\mathrm{am}}+a-m-\mathrm{1}}{a\sqrt{{\left(m+\mathrm{1}\right)}^{\mathrm{2}}-\mathrm{2}\mathrm{am}}}}.\end{array}$$

When the effect of initial storage is negligible (i.e., ψ=0), $\frac{S_b}{P}={\mathrm{\Phi }}_{\mathrm{sc}}$ from Eq. (13) and m=0 from Eq. (23). Then, Eq. (27) becomes

$$\begin{array}{}\text{(29)}& {\displaystyle \frac{W}{P}}={\displaystyle \frac{\mathrm{1}+\frac{S_b}{P}-\sqrt{{\left(\mathrm{1}+\frac{S_b}{P}\right)}^{\mathrm{2}}-\mathrm{2}a\frac{S_b}{P}}}{a}}.\end{array}$$

Equation (29) is same as Eq. (8) with $a=\mathrm{2}\mathit{\epsilon }\left(\mathrm{2}-\mathit{\epsilon }\right)$. We can obtain the following equation from Eq. (29) (see Appendix E for a detailed derivation):

$$\begin{array}{}\text{(30)}& {\displaystyle \frac{Q}{P-\mathit{\epsilon }W}}={\displaystyle \frac{W-\mathit{\epsilon }W}{S_b-\mathit{\epsilon }W}},\end{array}$$

where εW is defined as initial abstraction (W_i) in the SCS-CN method. Since S_b=S_p when ψ=0, Eq. (30) is same as Eq. (2), i.e., the proportionality relationship of the SCS-CN method.

Figure 5 The effects of the degree of initial storage (ψ=0, 0.4, and 0.6) and shape parameter (a=0.6 and 1.8) on soil wetting in the modified SCS-CN method derived from the proposed distribution function for soil water storage capacity.

Equation (27) is derived from the VIC-type model by using Eq. (20) to describe the spatial distribution of soil water storage capacity. From this perspective, Eq. (27) is a saturation excess runoff model. Since Eq. (27) becomes the SCS-CN method when initial storage is negligible, Eq. (27) is the modified SCS-CN method which considers the effect of initial storage on runoff generation explicitly. Therefore, the new distribution function represented by Eq. (20) unifies the SCS-CN method and the VIC type of model.

Bartlett et al. (2016a) developed an event-based probabilistic storage framework including a spatial description of prethreshold and threshold-excess runoff, and the framework has been utilized for unifying TOPMODEL, VIC, and SCS-CN (Bartlett et al., 2016b). The extended SCS-CN method (SCS-CNx) from the probabilistic storage framework is derived given the following assumptions: (1) the spatial distribution of rainfall is exponential, (2) the spatial distribution of the soil moisture deficit is uniform, and (3) the spatial distribution of storage capacity is exponential. When prethreshold runoff is 0 (i.e., there is only threshold-excess or saturation excess runoff), the SCS-CNx method leads to the SCS-CN method without the initial abstraction term (i.e., there is no εW term in Eq. 30). In this paper, the new probability distribution function is used for storage capacity in the VIC model in which the spatial distribution of precipitation is assumed to be uniform. The obtained equation for saturation excess runoff leads to the exact SCS-CN method as shown in Eq. (30).

This research started with the following research question: if the SCS-CN method is a saturation excess runoff generation model, what is the distribution function of soil water storage capacity? Wang and Tang (2014) showed that Eq. (29) is derived from the proportionality relationship of the SCS-CN method, i.e., Eq. (30). From the comparison of boundary conditions between the SCS-CN method and the VIC type of model discussed in Sect. 4, it is observed that Eq. (29) does not include initial soil water storage, and the derived one from the distribution function will include initial soil water storage (e.g., Eq. 26). However, Eq. (29) can be viewed as the result of S₀=0, and W for Eq. (29) can be written as

$$\begin{array}{}\text{(31)}& W=\underset{\mathrm{0}}{\overset{P}{\int }}\left[\mathrm{1}-F\left(x\right)\right]\mathrm{d}x.\end{array}$$

From Eq. (29), one obtains

$$\begin{array}{}\text{(32)}& W={\displaystyle \frac{P+S_b-\sqrt{{\left(S_b+P\right)}^{\mathrm{2}}-\mathrm{2}aP{S}_b}}{a}}.\end{array}$$

Substituting Eq. (32) into Eq. (31), one obtains

$$\begin{array}{}\text{(33)}& {\displaystyle \frac{P+S_b-\sqrt{{\left(S_b+P\right)}^{\mathrm{2}}-\mathrm{2}aP{S}_b}}{a}}=\underset{\mathrm{0}}{\overset{P}{\int }}\left[\mathrm{1}-F\left(C\right)\right]\mathrm{d}C.\end{array}$$

Equation (20) is obtained from Eq. (33).

Figure 6 (a) The effects of average storage capacity and initial storage on the rainfall–runoff relation and (b) the effects of average storage capacity and shape parameter on the rainfall–runoff relation.

5.3 Surface runoff of the unified SCS-CN and VIC model

From the unified SCS-CN and VIC model (i.e., Eq. 26), surface runoff (Q) can be computed as

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }Q=\\ \text{(34)}& {\displaystyle }& {\displaystyle }{\displaystyle \frac{\left(a-\mathrm{1}\right)P-S_b\sqrt{{\left(m+\mathrm{1}\right)}^{\mathrm{2}}-\mathrm{2}\mathrm{am}}+\sqrt{{\left[P+(m+\mathrm{1})S_b\right]}^{\mathrm{2}}-\mathrm{2}\mathrm{am}{S}_b^{\mathrm{2}}-\mathrm{2}a{S}_{b}P}}{a}}.\end{array}$$

The parameter m is computed by Eq. (23) as a function of ψ and a. Equation (34) represents surface runoff as a function of precipitation (P), average soil water storage capacity (S_b), the shape parameter of the storage capacity distribution (a), and initial soil moisture (ψ). Fig. 6 plots Eq. (34) under different values of P, S_b, a, and ψ. Figure 6a shows the effects of S_b and ψ on the rainfall–runoff relationship with a given shape parameter of a=1.9. The solid lines show the rainfall–runoff relations with zero initial storage (ψ=0) and the dashed lines show the rainfall–runoff relations with ψ=0.2. Given the same amount of precipitation and storage capacity, wetter soil (ψ=0.2) generates more surface runoff than drier soil (ψ=0), and the difference of runoff is higher for watersheds with larger average storage capacity. Figure 6b shows the effects of S_b and a on the rainfall–runoff relationship with a given initial soil moisture (ψ=0.2). The solid lines show the rainfall–runoff relations for a=1.9 and the dashed lines show the rainfall–runoff relations for a=1.2. As we can see, the shape parameter affects the runoff generation significantly for watersheds with larger average storage capacity.

In the SCS-CN method, surface runoff is computed as $Q=\frac{{\left(P-\mathrm{0.2}{S}_b\right)}^{\mathrm{2}}}{P+\mathrm{0.8}{S}_b}$. The effect of initial soil moisture on runoff is considered implicitly by varying the curve number for normal, dry, and wet conditions depending on the antecedent moisture condition. In the unified SCS-CN model shown in Eq. (34), the effect of initial soil moisture is explicitly included through ψ, which is the ratio between average initial water storage and average storage capacity. In the SCS-CN method, the value of initial abstraction W_i is parameterized as a function of average storage capacity; i.e., W_i=0.2S_b. In the unified SCS-CN model shown in Eq. (34), W_i is dependent on the shape parameter a. Therefore, the unified SCS-CN model extends the original SCS-CN method for including the effect of initial soil moisture explicitly and estimating the parameter for initial abstraction.

6 Conclusions

In this paper, the SCS-CN method and the saturation excess runoff models based on distribution functions (e.g., VIC model) are presented in terms of soil wetting (i.e., infiltration). Like the Budyko framework, the relationship between the soil wetting ratio and the soil storage index is obtained for the SCS-CN method and the VIC type of model. It is found that the boundary conditions for the obtained functions do not fully match. For the SCS-CN method, the soil wetting ratio approaches 1 when the soil storage index approaches infinity, and this is due to the limitation of the SCS-CN method; i.e., the initial soil moisture condition is not explicitly represented in the proportionality relationship. However, for the VIC type of model, the soil wetting ratio equals the soil storage index when the soil storage index is lower than a certain value, and this is due to the finite bound of the distribution function of storage capacity.

In this paper, a new distribution function, which is supported by $x\in [\mathrm{0},\mathrm{\infty })$ instead of a finite upper bound, is proposed for describing the spatial distribution of soil water storage capacity. From this new distribution function, an equation is derived for the relationship between the soil wetting ratio and the storage index, and this equation satisfies the following boundary conditions: when the storage index approaches 0, the soil wetting ratio approaches 0; when the storage index approaches infinity, the soil wetting ratio approaches a certain value (≤1) depending on the initial storage (e.g., at the beginning of a rainfall event, runoff is generated at the initially saturated areas, Yu et al., 2001; Gao et al., 2018). Meanwhile, the model becomes the exact SCS-CN method when initial storage is negligible. Therefore, the new distribution function for soil water storage capacity explains the SCS-CN method as a saturation excess runoff model and unifies the SCS-CN method and the VIC type of model for surface runoff modeling.

Future potential work could test the performance of the proposed new distribution function for quantifying the spatial distribution of storage capacity by analyzing the spatially distributed soil data. On the one hand, the distribution functions of the probability distributed model (Moore, 1985), VIC model, and Xinanjiang model could be replaced by the new distribution function and the model performance would be further evaluated. On the other hand, the extended SCS-CN method (i.e., Eq. 27), which includes initial storage explicitly, could be used for surface runoff modeling in the SWAT (Soil and Water Assessment Tool) model, and the model performance would be evaluated.

Appendix A

The potential for continuing wetting is called potential maximum retention and is denoted by $S_{\mathrm{m}}=S_p-W_{\mathrm{i}}$. S_m is computed as a function of curve number which is dependent on land use–land cover and soil permeability. The ratio between W_i and S_m in the SCS curve number method is denoted by $\mathit{\lambda }=\frac{W_{\mathrm{i}}}{S_p-W_{\mathrm{i}}}$, and then the ratio between initial soil wetting and storage capacity is computed by

$$\begin{array}{}\text{(A1)}& {\displaystyle \frac{W_{\mathrm{i}}}{S_p}}={\displaystyle \frac{\mathit{\lambda }}{\mathrm{1}+\mathit{\lambda }}}.\end{array}$$

The value of λ varies in the range of $\mathrm{0}\le \mathit{\lambda }\le \mathrm{0.3}$, and a value of 0.2 is usually used (Ponce and Hawkins, 1996). Substituting Eq. (A1) into Eq. (6) leads to

$$\begin{array}{}\text{(A2)}& {\displaystyle \frac{W}{P}}={\displaystyle \frac{\mathrm{1}-{\left(\frac{\mathit{\lambda }}{\mathrm{1}+\mathit{\lambda }}\right)}^{\mathrm{2}}{\mathrm{\Phi }}_{\mathrm{sc}}}{\mathrm{1}-\frac{\mathrm{2}\mathit{\lambda }}{\mathrm{1}+\mathit{\lambda }}+{\mathrm{\Phi }}_{\mathrm{sc}}^{-\mathrm{1}}}}.\end{array}$$

Equation (A2) is plotted in Fig. 1 for λ=0.1 and 0.3. As we can see, the range of Φ_sc is dependent on the parameter λ. Since W_i≤P, Φ_sc is in the range of $\left[\mathrm{0},\mathrm{1}+\frac{\mathrm{1}}{\mathit{\lambda }}\right]$. Equation (A2) satisfies the following boundary conditions: $\frac{W}{P}\to \mathrm{0}$ as Φ_sc→0 and $\frac{W}{P}\to \mathrm{1}$ as ${\mathrm{\Phi }}_{\mathrm{sc}}\to \frac{\mathit{\lambda }+\mathrm{1}}{\mathit{\lambda }}$. When λ→0, Eq. (A2) becomes

$$\begin{array}{}\text{(A3)}& {\displaystyle \frac{W}{P}}={\displaystyle \frac{\mathrm{1}}{\mathrm{1}+{\mathrm{\Phi }}_{\mathrm{sc}}^{-\mathrm{1}}}}.\end{array}$$

Equation (A3) is the lower bound for $\frac{W}{P}$ based on this parameterization scheme.

Appendix B

Substituting $W=S_{\mathrm{1}}-S_{\mathrm{0}}$ into Eq. (16), wetting is computed by

$$\begin{array}{}\text{(B1)}& W=S_b\left[\mathrm{1}-{\left(\mathrm{1}-{\displaystyle \frac{P+C_{\mathrm{0}}}{C_{\mathrm{m}}}}\right)}^{\mathit{\beta }+\mathrm{1}}\right]-S_{\mathrm{0}}.\end{array}$$

The following equation is obtained by dividing P on both sides of Eq. (B1):

$$\begin{array}{}\text{(B2)}& {\displaystyle \frac{W}{P}}={\displaystyle \frac{S_b-S_{\mathrm{0}}}{P}}-{\displaystyle \frac{S_b}{P}}{\left(\mathrm{1}-{\displaystyle \frac{P+C_{\mathrm{0}}}{C_{\mathrm{m}}}}\right)}^{\mathit{\beta }+\mathrm{1}}.\end{array}$$

Substituting $\frac{C_{\mathrm{0}}}{C_{\mathrm{m}}}=\mathrm{1}-{\left(\mathrm{1}-\frac{S_{\mathrm{0}}}{S_b}\right)}^{\frac{\mathrm{1}}{\mathit{\beta }+\mathrm{1}}}$ into Eq. (B2), we obtain

$$\begin{array}{}\text{(B3)}& {\displaystyle \frac{W}{P}}={\displaystyle \frac{S_b-S_{\mathrm{0}}}{P}}-{\displaystyle \frac{S_b}{P}}{\left(\mathrm{1}-{\displaystyle \frac{P}{C_{\mathrm{m}}}}-\left[\mathrm{1}-{\left(\mathrm{1}-{\displaystyle \frac{S_{\mathrm{0}}}{S_b}}\right)}^{\frac{\mathrm{1}}{\mathit{\beta }+\mathrm{1}}}\right]\right)}^{\mathit{\beta }+\mathrm{1}}.\end{array}$$

Substituting Eq. (10) into Eq. (B3), we obtain

$$\begin{array}{}\text{(B4)}& {\displaystyle \frac{W}{P}}={\displaystyle \frac{S_b-S_{\mathrm{0}}}{P}}-{\left({\left({\displaystyle \frac{S_b-S_{\mathrm{0}}}{P}}\right)}^{\frac{\mathrm{1}}{\mathit{\beta }+\mathrm{1}}}-{\displaystyle \frac{{\left(\frac{S_b}{P}\right)}^{-\frac{\mathit{\beta }}{\mathit{\beta }+\mathrm{1}}}}{\mathit{\beta }+\mathrm{1}}}\right)}^{\mathit{\beta }+\mathrm{1}}.\end{array}$$

Substituting Eqs. (5) and (13) into Eq. (B4), we obtain

$$\begin{array}{}\text{(B5)}& {\displaystyle \frac{W}{P}}={\mathrm{\Phi }}_{\mathrm{sc}}-{\left({\mathrm{\Phi }}_{\mathrm{sc}}^{\frac{\mathrm{1}}{\mathit{\beta }+\mathrm{1}}}-{\displaystyle \frac{{\left(\frac{{\mathrm{\Phi }}_{\mathrm{sc}}}{\mathrm{1}-\mathit{\psi }}\right)}^{-\frac{\mathit{\beta }}{\mathit{\beta }+\mathrm{1}}}}{\mathit{\beta }+\mathrm{1}}}\right)}^{\mathit{\beta }+\mathrm{1}},\end{array}$$

which leads to

$$\begin{array}{}\text{(B6)}& {\displaystyle \frac{W}{P}}={\mathrm{\Phi }}_{\mathrm{sc}}\left[\mathrm{1}-{\left(\mathrm{1}-b{\mathrm{\Phi }}_{\mathrm{sc}}^{-\mathrm{1}}\right)}^{\mathit{\beta }+\mathrm{1}}\right],\end{array}$$

where b is defined in Eq. (14).

Appendix C

$$\begin{array}{}\text{(C1)}& \underset{{\mathrm{\Phi }}_{\mathrm{sc}}\to \mathrm{\infty }}{lim}{\displaystyle \frac{W}{P}}=\underset{{\mathrm{\Phi }}_{\mathrm{sc}}\to \mathrm{\infty }}{lim}{\mathrm{\Phi }}_{\mathrm{sc}}\left[\mathrm{1}-{\left(\mathrm{1}-b{\mathrm{\Phi }}_{\mathrm{sc}}^{-\mathrm{1}}\right)}^{\mathit{\beta }+\mathrm{1}}\right]\end{array}$$

The right-hand side of Eq. (C1) is rewritten as

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }\underset{{\mathrm{\Phi }}_{\mathrm{sc}}\to \mathrm{\infty }}{lim}{\mathrm{\Phi }}_{\mathrm{sc}}\left[\mathrm{1}-{\left(\mathrm{1}-b{\mathrm{\Phi }}_{\mathrm{sc}}^{-\mathrm{1}}\right)}^{\mathit{\beta }+\mathrm{1}}\right]=\\ \text{(C2)}& {\displaystyle }& {\displaystyle }\underset{{\mathrm{\Phi }}_{\mathrm{sc}}\to \mathrm{\infty }}{lim}{\displaystyle \frac{\mathrm{1}-{\left(\mathrm{1}-b{\mathrm{\Phi }}_{\mathrm{sc}}^{-\mathrm{1}}\right)}^{\mathit{\beta }+\mathrm{1}}}{{\mathrm{\Phi }}_{\mathrm{sc}}^{-\mathrm{1}}}}.\end{array}$$

Since ${lim}_{{\mathrm{\Phi }}_{\mathrm{sc}}\to \mathrm{\infty }}\mathrm{1}-{\left(\mathrm{1}-\mathrm{b}{\mathrm{\Phi }}_{\mathrm{sc}}^{-\mathrm{1}}\right)}^{\mathit{\beta }+\mathrm{1}}=\mathrm{0}$ and ${lim}_{{\mathrm{\Phi }}_{\mathrm{sc}}\to \mathrm{\infty }}{\mathrm{\Phi }}_{\mathrm{sc}}^{-\mathrm{1}}=\mathrm{0}$, we apply the L'Hospital's rule,

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }\underset{{\mathrm{\Phi }}_{\mathrm{sc}}\to \mathrm{\infty }}{lim}{\displaystyle \frac{\left[\mathrm{1}-{\left(\mathrm{1}-\mathrm{b}{\mathrm{\Phi }}_{\mathrm{sc}}^{-\mathrm{1}}\right)}^{\mathit{\beta }+\mathrm{1}}\right]{}^{\prime }}{\left({\mathrm{\Phi }}_{\mathrm{sc}}^{-\mathrm{1}}\right){}^{\prime }}}=\\ \text{(C3)}& {\displaystyle }& {\displaystyle }\underset{{\mathrm{\Phi }}_{\mathrm{sc}}\to \mathrm{\infty }}{lim}\mathrm{b}\left(\mathit{\beta }+\mathrm{1}\right){\left(\mathrm{1}-\mathrm{b}{\mathrm{\Phi }}_{\mathrm{sc}}^{-\mathrm{1}}\right)}^{\mathit{\beta }}.\end{array}$$

Since ${lim}_{{\mathrm{\Phi }}_{\mathrm{sc}}\to \mathrm{\infty }}{\left(\mathrm{1}-\mathrm{b}{\mathrm{\Phi }}_{\mathrm{sc}}^{-\mathrm{1}}\right)}^{\mathit{\beta }}=\mathrm{1}$, the limit for $\frac{W}{P}$ is obtained as follows:

$$\begin{array}{}\text{(C4)}& \underset{{\mathrm{\Phi }}_{\mathrm{sc}}\to \mathrm{\infty }}{lim}{\displaystyle \frac{W}{P}}=b\left(\mathit{\beta }+\mathrm{1}\right).\end{array}$$

Substituting Eq. (14) into Eq. (C4), we obtain

$$\begin{array}{}\text{(C5)}& \underset{{\mathrm{\Phi }}_{\mathrm{sc}}\to \mathrm{\infty }}{lim}{\displaystyle \frac{W}{P}}={\left(\mathrm{1}-\mathit{\psi }\right)}^{\frac{\mathit{\beta }}{\mathit{\beta }+\mathrm{1}}}.\end{array}$$

Appendix D

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }\underset{{\mathrm{\Phi }}_{\mathrm{sc}}\to \mathrm{\infty }}{lim}{\displaystyle \frac{W}{P}}=\underset{{\mathrm{\Phi }}_{\mathrm{sc}}\to \mathrm{\infty }}{lim}\\ \text{(D1)}& {\displaystyle }& {\displaystyle }{\displaystyle \frac{\mathrm{1}+\frac{\sqrt{{\left(m+\mathrm{1}\right)}^{\mathrm{2}}-\mathrm{2}\mathrm{am}}}{\mathrm{1}-\mathit{\psi }}{\mathrm{\Phi }}_{\mathrm{sc}}-\sqrt{{\left(\mathrm{1}+\frac{m+\mathrm{1}}{\mathrm{1}-\mathit{\psi }}{\mathrm{\Phi }}_{\mathrm{sc}}\right)}^{\mathrm{2}}-\mathrm{2}\mathrm{am}{\left(\frac{{\mathrm{\Phi }}_{\mathrm{sc}}}{\mathrm{1}-\mathit{\psi }}\right)}^{\mathrm{2}}-\frac{\mathrm{2}a}{\mathrm{1}-\mathit{\psi }}{\mathrm{\Phi }}_{\mathrm{sc}}}}{a}}\end{array}$$

Multiplying

$$\begin{array}{ll}{\displaystyle }\mathrm{1}& {\displaystyle }+{\displaystyle \frac{\sqrt{{\left(m+\mathrm{1}\right)}^{\mathrm{2}}-\mathrm{2}\mathrm{am}}}{\mathrm{1}-\mathit{\psi }}}{\mathrm{\Phi }}_{\mathrm{sc}}\\ \text{(D2)}& {\displaystyle }& {\displaystyle }+\sqrt{{\left(\mathrm{1}+{\displaystyle \frac{m+\mathrm{1}}{\mathrm{1}-\mathit{\psi }}}{\mathrm{\Phi }}_{\mathrm{sc}}\right)}^{\mathrm{2}}-\mathrm{2}\mathrm{am}{\left({\displaystyle \frac{{\mathrm{\Phi }}_{\mathrm{sc}}}{\mathrm{1}-\mathit{\psi }}}\right)}^{\mathrm{2}}-{\displaystyle \frac{\mathrm{2}a}{\mathrm{1}-\mathit{\psi }}}{\mathrm{\Phi }}_{\mathrm{sc}}}\end{array}$$

with the denominator and numerator of the right-hand side Eq. (D1) leads to

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }\underset{{\mathrm{\Phi }}_{\mathrm{sc}}\to \mathrm{\infty }}{lim}{\displaystyle \frac{W}{P}}={\displaystyle \frac{\mathrm{1}}{a}}\underset{{\mathrm{\Phi }}_{\mathrm{sc}}\to \mathrm{\infty }}{lim}\\ \text{(D3)}& {\displaystyle }& {\displaystyle }{\displaystyle \frac{\frac{\mathrm{2}\sqrt{{\left(m+\mathrm{1}\right)}^{\mathrm{2}}-\mathrm{2}\mathrm{am}}}{\mathrm{1}-\mathit{\psi }}{\mathrm{\Phi }}_{\mathrm{sc}}-\frac{\mathrm{2}\left(m+\mathrm{1}\right)}{\mathrm{1}-\mathit{\psi }}{\mathrm{\Phi }}_{\mathrm{sc}}+\frac{\mathrm{2}a}{\mathrm{1}-\mathit{\psi }}{\mathrm{\Phi }}_{\mathrm{sc}}}{\mathrm{1}+\frac{\sqrt{{\left(m+\mathrm{1}\right)}^{\mathrm{2}}-\mathrm{2}\mathrm{am}}}{\mathrm{1}-\mathit{\psi }}{\mathrm{\Phi }}_{\mathrm{sc}}+\sqrt{{\left(\mathrm{1}+\frac{m+\mathrm{1}}{\mathrm{1}-\mathit{\psi }}{\mathrm{\Phi }}_{\mathrm{sc}}\right)}^{\mathrm{2}}-\mathrm{2}\mathrm{am}{\left(\frac{{\mathrm{\Phi }}_{\mathrm{sc}}}{\mathrm{1}-\mathit{\psi }}\right)}^{\mathrm{2}}-\frac{\mathrm{2}a}{\mathrm{1}-\mathit{\psi }}{\mathrm{\Phi }}_{\mathrm{sc}}}}}.\end{array}$$

Dividing Φ_sc in the denominator and numerator, we obtain

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }\underset{{\mathrm{\Phi }}_{\mathrm{sc}}\to \mathrm{\infty }}{lim}{\displaystyle \frac{W}{P}}={\displaystyle \frac{\mathrm{1}}{a\left(\mathrm{1}-\mathit{\psi }\right)}}\underset{{\mathrm{\Phi }}_{\mathrm{sc}}\to \mathrm{\infty }}{lim}\\ \text{(D4)}& {\displaystyle }& {\displaystyle }{\displaystyle \frac{\mathrm{2}\sqrt{{\left(m+\mathrm{1}\right)}^{\mathrm{2}}-\mathrm{2}\mathrm{am}}-\mathrm{2}\left(m+\mathrm{1}\right)+\mathrm{2}a}{\frac{\mathrm{1}}{{\mathrm{\Phi }}_{\mathrm{sc}}}+\frac{\sqrt{{\left(m+\mathrm{1}\right)}^{\mathrm{2}}-\mathrm{2}\mathrm{am}}}{\mathrm{1}-\mathit{\psi }}+\sqrt{{\left(\frac{\mathrm{1}}{{\mathrm{\Phi }}_{\mathrm{sc}}}+\frac{m+\mathrm{1}}{\mathrm{1}-\mathit{\psi }}\right)}^{\mathrm{2}}-\mathrm{2}\mathrm{am}{\left(\frac{\mathrm{1}}{\mathrm{1}-\mathit{\psi }}\right)}^{\mathrm{2}}-\frac{\mathrm{2}a}{\left(\mathrm{1}-\mathit{\psi }\right){\mathrm{\Phi }}_{\mathrm{sc}}}}}}.\end{array}$$

Therefore, the limit of $\frac{W}{P}$ as Φ_sc→∞ is

$$\begin{array}{}\text{(D5)}& \underset{{\mathrm{\Phi }}_{\mathrm{sc}}\to \mathrm{\infty }}{lim}{\displaystyle \frac{W}{P}}={\displaystyle \frac{\sqrt{{\left(m+\mathrm{1}\right)}^{\mathrm{2}}-\mathrm{2}\mathrm{am}}+a-m-\mathrm{1}}{a\sqrt{{\left(m+\mathrm{1}\right)}^{\mathrm{2}}-\mathrm{2}\mathrm{am}}}}.\end{array}$$

Appendix E

Substituting $a=\mathrm{2}\mathit{\epsilon }\left(\mathrm{2}-\mathit{\epsilon }\right)$ into Eq. (29), one can obtain

$$\begin{array}{}\text{(E1)}& {\displaystyle \frac{W}{P}}={\displaystyle \frac{\mathrm{1}+\frac{S_b}{P}-\sqrt{{\left(\mathrm{1}+\frac{S_b}{P}\right)}^{\mathrm{2}}-\mathrm{4}\mathit{\epsilon }\left(\mathrm{2}-\mathit{\epsilon }\right)\frac{S_b}{P}}}{\mathrm{2}\mathit{\epsilon }\left(\mathrm{2}-\mathit{\epsilon }\right)}}.\end{array}$$

Equation (E1) is the solution of the following quadratic function:

$$\begin{array}{}\text{(E2)}& \mathit{\epsilon }\left(\mathrm{2}-\mathit{\epsilon }\right){\left({\displaystyle \frac{W}{P}}\right)}^{\mathrm{2}}-\left(\mathrm{1}+{\displaystyle \frac{S_b}{P}}\right){\displaystyle \frac{W}{P}}+{\displaystyle \frac{S_b}{P}}=\mathrm{0}.\end{array}$$

Multiplying P² on both sides of Eq. (E2), Eq. (E2) becomes

$$\begin{array}{}\text{(E3)}& \mathit{\epsilon }\left(\mathrm{2}-\mathit{\epsilon }\right)W^{\mathrm{2}}-\left(P+S_b\right)W+S_{b}P=\mathrm{0}.\end{array}$$

Equation (E3) can be written as the following one:

$$\begin{array}{}\text{(E4)}& {\displaystyle \frac{P-W}{P-\mathit{\epsilon }W}}={\displaystyle \frac{W-\mathit{\epsilon }W}{S_b-\mathit{\epsilon }W}}.\end{array}$$

Substituting $Q=P-W$ into Eq. (E4), we obtain the proportionality relationship of the SCS-CN method:

$$\begin{array}{}\text{(E5)}& {\displaystyle \frac{Q}{P-\mathit{\epsilon }W}}={\displaystyle \frac{W-\mathit{\epsilon }W}{S_b-\mathit{\epsilon }W}}.\end{array}$$