the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Evaluating post-processing approaches for monthly and seasonal streamflow forecasts
Fitsum Woldemeskel
David McInerney
Julien Lerat
Mark Thyer
Dmitri Kavetski
Daehyok Shin
Narendra Tuteja
George Kuczera
Streamflow forecasting is prone to substantial uncertainty due to
errors in meteorological forecasts, hydrological model structure, and
parameterization, as well as in the observed rainfall and streamflow data
used to calibrate the models. Statistical streamflow post-processing is an
important technique available to improve the probabilistic properties of the
forecasts. This study evaluates post-processing approaches based on three
transformations – logarithmic (Log), log-sinh (Log-Sinh), and Box–Cox with
λ=0.2 (BC0.2) – and identifies the best-performing scheme for
post-processing monthly and seasonal (3-months-ahead) streamflow forecasts,
such as those produced by the Australian Bureau of Meteorology. Using the
Bureau's operational dynamic streamflow forecasting system, we carry out
comprehensive analysis of the three post-processing schemes across 300
Australian catchments with a wide range of hydro-climatic conditions.
Forecast verification is assessed using reliability and sharpness metrics, as
well as the Continuous Ranked Probability Skill Score (CRPSS). Results show
that the uncorrected forecasts (i.e. without post-processing) are unreliable
at half of the catchments. Post-processing of forecasts substantially
improves reliability, with more than 90 % of forecasts classified as
reliable. In terms of sharpness, the BC0.2 scheme substantially outperforms
the Log and Log-Sinh schemes. Overall, the BC0.2 scheme achieves reliable and
sharper-than-climatology forecasts at a larger number of catchments than the
Log and Log-Sinh schemes. The improvements in forecast reliability and
sharpness achieved using the BC0.2 post-processing scheme will help water
managers and users of the forecasting service make better-informed decisions
in planning and management of water resources.
Highlights. Uncorrected and
post-processed streamflow forecasts (using three transformations, namely Log,
Log-Sinh, and BC0.2) are evaluated over 300 diverse Australian catchments.
Post-processing enhances streamflow forecast reliability, increasing the
percentage of catchments with reliable predictions from 50 % to over
90 %. The BC0.2 transformation achieves substantially better forecast
sharpness than the Log-Sinh and Log transformations, particularly in dry
catchments.
- Article
(5188 KB) - Full-text XML
- BibTeX
- EndNote
Hydrological forecasts provide crucial supporting information on a range of water resource management decisions, including (depending on the forecast lead time) flood emergency response, water allocation for various uses, and drought risk management (Li et al., 2016; Turner et al., 2017). The forecasts, however, should be thoroughly verified and proved to be of sufficient quality to support decision-making and to meaningfully benefit the economy, environment, and society.
Sub-seasonal and seasonal streamflow forecasting systems can be broadly classified as dynamic or statistical (Crochemore et al., 2016). In dynamic modelling systems, a hydrological model is usually developed at a daily time step and calibrated against observed streamflow using historical rainfall and potential evaporation data. Rainfall forecasts from a numerical climate model are then used as an input to produce daily streamflow forecasts, which are then aggregated to the timescale of interest and post-processed using statistical models (e.g. Bennett et al., 2017; Schick et al., 2018). In statistical modelling systems, a statistical model based on relevant predictors, such as antecedent rainfall and streamflow, is developed and applied directly at the timescale of interest (Robertson and Wang, 2009, 2011; Lü et al., 2016; Zhao et al., 2016). Hybrid systems that combine aspects of dynamic and statistical approaches have also been investigated (Humphrey et al., 2016; Robertson et al., 2013a).
Examples of operational services based on the dynamic approach include the Australian Bureau of Meteorology's dynamic modelling system (Laugesen et al., 2011; Tuteja et al., 2011; Lerat et al., 2015); the Hydrological Ensemble Forecast Service (HEFS) of the US National Weather Service (NWS) (Brown et al., 2014; Demargne et al., 2014); the Hydrological Outlook UK (HOUK) (Prudhomme et al., 2017); and the short-term forecasting European Flood Alert System (EFAS) (Cloke et al., 2013). Examples of operational services based on a statistical approach include the Bureau of Meteorology's Bayesian Joint Probability (BJP) forecasting system (Senlin et al., 2017).
Dynamic and statistical approaches have distinct advantages and limitations. Dynamic systems can potentially provide more realistic responses in unfamiliar climate situations, as it is possible to impose physical constraints in such situations (Wood and Schaake, 2008). In comparison, statistical models have the flexibility to include features that may lead to more reliable predictions. For example, the BJP model uses climate indices (e.g. NINO3.4), which are typically not used in dynamic approaches. That said, the suitability of statistical models for the analysis of non-stationary catchment and climate conditions is questionable (Wood and Schaake, 2008).
Streamflow forecasts obtained using hydrological models are affected by uncertainties in rainfall forecasts, observed rainfall and streamflow data, as well as by uncertainties in the model structure and parameters. Progress has been made towards reducing biases and characterizing the sources of uncertainty in streamflow forecasts. These advances include improving rainfall forecasts through post-processing (Robertson et al., 2013b; Crochemore et al., 2016), accounting for input, parametric, and/or structural uncertainty (Kavetski et al., 2006; Kuczera et al., 2006; Renard et al., 2011; Tyralla and Schumann, 2016), and using data assimilation techniques (Dechant and Moradkhani, 2011). Although these steps may improve some aspects of the forecasting system, a predictive bias may nonetheless remain. Such bias can only be reduced via post-processing, which, if successful, will improve forecast accuracy and reliability (Madadgar et al., 2014; Lerat et al., 2015).
This study focuses on improving streamflow forecasting at monthly and seasonal timescales using dynamic approaches, more specifically, by evaluating several forecast post-processing approaches. Post-processing of streamflow forecasts is intended to remove systemic biases in the mean, variability, and persistence of uncorrected forecasts, which arise due to inaccuracies in the downscaled rainfall forecasts (e.g. errors in downscaling forecast rainfall from a grid with ≈250 km resolution to the catchment scale) and in the hydrological model (e.g. due to the effects of data errors in the model calibration and due to structural errors in the model itself).
A number of post-processing approaches have been investigated in the literature, including quantile mapping (Hashino et al., 2007) and Bayesian frameworks (Pokhrel et al., 2013; Robertson et al., 2013a), as well as methods based on state-space models and wavelet transformations (Bogner and Kalas, 2008). Wood and Schaake (2008) used the correlation between forecast ensemble means and observations to generate a conditional forecast. Compared with the traditional approach of correcting individual forecast ensembles, the correlation approach improved forecast skill and reliability. In another study, Pokhrel et al. (2013) implemented a BJP method to correct biases, update predictions, and quantify uncertainty in monthly hydrological model predictions in 18 Australian catchments. The study found that the accuracy and reliability of forecasts improved. More recently, Mendoza et al. (2017) evaluated a number of seasonal streamflow forecasting approaches, including purely statistical, purely dynamical, and hybrid approaches. Based on analysis of catchments contributing to five reservoirs, the study concluded that incorporating catchment and climate information into post-processing improves forecast skill. While the above review mainly focused on post-processing of sub-seasonal and seasonal forecasts (as it is the main focus of the current study), post-processing is also commonly applied to short-range forecasts (e.g. Li et al., 2016) and to long-range forecasts up to 12 months ahead (Bennett et al., 2016).
In most streamflow post-processing approaches, a residual error model is applied to quantify forecast uncertainty. Most residual error models are based on least squares techniques with weights and/or data transformations (e.g. Carpenter and Georgakakos, 2001; Li et al., 2016). In order to produce post-processed streamflow forecasts, a daily scale residual error model is used in the calibration of hydrological model parameters, and a monthly/seasonal-scale residual error model is used as part of streamflow post-processing to quantify the forecast uncertainty. In a recent study, McInerney et al. (2017) concluded that residual error models based on Box–Cox transformations with fixed parameter values are particularly effective for daily scale streamflow predictions using observed rainfall, yielding substantial improvements in dry catchments. This study investigates whether these findings generalize to monthly and seasonal forecasts using forecast rainfall.
An important aspect of this work is its focus on general findings applicable over diverse hydro-climatological conditions. Most of the studies in the published literature use a limited number of catchments and case studies to test prospective methods. Dry catchments, characterized by intermittent flows and frequent low flows, pose the greatest challenge to hydrological models (Ye et al., 1997; Knoche et al., 2014). Yet the provision of good-quality forecasts across a large number of catchments is an essential attribute of national-scale operational forecasting services, especially in large countries with diverse climatic and catchment conditions, such as Australia.
This paper develops streamflow post-processing approaches suitable for use in an operational streamflow forecasting service. We pose the following aims.
-
Aim 1: evaluate the value of streamflow forecast post-processing by comparing forecasts with no post-processing (hereafter called “uncorrected” forecasts) against post-processed forecasts.
-
Aim 2: evaluate three post-processing schemes based on residual error models with data transformations recommended in recent publications, namely the Log, Box–Cox (McInerney et al., 2017), and Log-Sinh (Wang et al., 2012) schemes, for monthly and seasonal streamflow post-processing.
-
Aim 3: evaluate the generality of results over a diverse range of hydro-climatic conditions, in order to ensure the recommendations are robust in the context of an operational streamflow forecasting service.
To achieve these aims, we use the operational monthly and seasonal (3-months-ahead) dynamic streamflow forecasting system of the Australian Bureau of Meteorology (Lerat et al., 2015). We evaluate the post-processing approaches for 300 catchments across Australia, with detailed analysis of dry and wet catchments. Forecast verification is carried out using the Continuous Ranked Probability Skill Score (CRPSS) as well as metrics measuring reliability and sharpness, which are important aspects of a probabilistic forecast (Wilks, 2011). These metrics are used by the Bureau of Meteorology to describe the streamflow forecast performance of the operational service.
The rest of the paper is organized as follows. The forecasting methodology is described in Sect. 2 and application studies are described in Sect. 3. Results are presented in Sect. 4, followed by discussions and conclusions in Sects. 5 and 6 respectively.
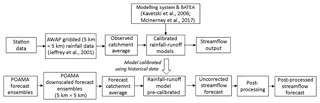
2.1 Overview
The streamflow forecasting system adopted in this study is based on the Bureau of Meteorology's dynamic modelling system (Fig. 1). Daily rainfall forecasts are input into a daily rainfall–runoff model to produce “uncorrected” daily streamflow forecasts. These streamflow forecasts are then aggregated in time and post-processed to produce monthly and seasonal streamflow forecasts, which are issued each month. Two steps are involved: calibration and forecasting, discussed below.
2.2 Uncorrected streamflow forecast procedure
2.2.1 Rainfall–runoff model
The GR4J rainfall–runoff model (Perrin et al., 2003) is used as it has been proven to provide (on average) good performance across a large number of catchments ranging from semi-arid to temperate and tropical humid (Perrin et al., 2003; Tuteja et al., 2011). GR4J is a lumped conceptual model with four calibration parameters: maximum capacity of the production store x1 (mm); ground water exchange coefficient x2 (mm); 1-day-ahead maximum capacity of the routing store x3 (mm); and time base of unit hydrograph x4 (days).
2.2.2 Rainfall–runoff model calibration
In the calibration step, the daily rainfall–runoff model is calibrated to observed daily streamflow using observed rainfall (Jeffrey et al., 2001) as forcing. The calibration of the parameters is based on the weighted least squares likelihood function, similar to that outlined in Evin et al. (2014). Markov chain Monte Carlo (MCMC) analysis is used to estimate posterior parametric uncertainty (Tuteja et al., 2011). Following MCMC analysis, 40 random sets of GR4J parameters are retained and used in the forecast step. A cross-validation procedure is implemented to verify the forecasts, as described in Sect. 3.4. The calibration and cross-validation are computationally intensive; therefore, we use the High Performance Computing (HPC) facility at the National Computing Infrastructure (NCI) in Australia.
2.2.3 Producing uncorrected streamflow forecasts
Prior to the forecast period, observed rainfall is used to force the rainfall–runoff model. During the forecast period, 166 replicates of daily downscaled rainfall forecasts from the Bureau of Meteorology's global climate model, namely the Predictive Ocean Atmosphere Model for Australia, POAMA-2, are used (see Sect. 3.2 for details on POAMA-2). These rainfall forecasts are inputted into GR4J and propagated using the 40 GR4J parameter sets to obtain 6640 (166 × 40) daily streamflow forecasts. The daily streamflow forecasts generated using GR4J are then aggregated to monthly and seasonal timescales to produce ensembles of 6640 uncorrected monthly and seasonal forecasts. The computational time required to generate 6640 streamflow forecast ensembles through this process is small compared with the time required to calibrate and cross-validate the hydrological model, and is easily achieved in an operational setting using HPC. Note that in this study the forecasting system does not use a data assimilation technique to update the GR4J state variables. This choice is based on the limited effect of initial conditions after a number of days, which generally reduces the benefit of state updating in the context of seasonal streamflow forecasting.
2.3 Streamflow post-processing procedure
2.3.1 Post-processing model
The streamflow post-processing method used in this work consists of fitting a statistical model to the streamflow forecast residual errors, defined by the differences between the observed and forecast streamflow time series over a calibration period. Typically these errors are heteroscedastic, skewed, and persistent. Heteroscedasticity and skew are handled using data transformations (e.g. the Box–Cox transformation), whereas persistence is represented using autoregressive models (e.g. the lag-one autoregressive model, AR(1); Wang et al., 2012; McInerney et al., 2017). We begin by describing the two major steps of the streamflow post-processing procedure (Sect. 2.3.2 and 2.3.3), and then describe the transformations under consideration (Sect. 2.4).
2.3.2 Post-processing model calibration
The parameters of the streamflow post-processing model are calibrated as follows.
-
Step 1: compute the transformed forecast residuals for month or season t of the calibration period:
where ηt is the normalized residual, is the observed streamflow, is the median of the uncorrected streamflow forecast ensemble, and Z is a transformation function. The transformation functions considered in this work are detailed in Sect. 2.4.
-
Step 2: compute the standardized residuals:
where and are the monthly mean and standard deviation of the residuals in the calibration period for the month m(t).
The standardization process in Eq. (2) aims to account for seasonal variations in the distribution of residuals. The quantities and are calculated independently as the sample mean and standard deviation of residuals for each monthly period (for a monthly forecast) or 3-monthly period (for seasonal forecasts). Based on Eq. (2), the standardized residuals vt are assumed to have a zero mean and unit standard deviation.
-
Step 3: assume the standardized residuals are described by a first-order autoregressive (AR(1)) model with Gaussian innovations:
where ρ is the AR(1) coefficient and is the innovation.
The parameters ρ and σy are estimated using the method of moments (Hazelton, 2011): ρ is estimated as the sample auto-correlation of the standardized residuals ν, and σy is estimated as the sample standard deviation of the observed innovations y, which in turn are calculated from the standardized residuals ν by re-arranging Eq. (3).
2.3.3 Producing post-processed streamflow forecasts
Once the streamflow post-processing scheme is calibrated, the post-processed streamflow forecasts for a given period are computed. For a given ensemble member j, the following steps are applied.
-
Step 1: sample the innovation .
-
Step 2: generate the standardized residuals using Eq. (3). Here νt,j is computed using Eq. (2) and ηt,j is computed using Eq. (1), using the streamflow forecasts and observations from the previous time step t.
-
Step 3: compute the normalized residuals by “de-standardizing” :
-
Step 4: back-transform each normalized residual to obtain the post-processed streamflow forecast:
Steps 1–4 are repeated for all ensemble members (6640 in our case).
Note that the above algorithm may occasionally generate negative streamflow predictions, which we reset to zero. In addition, the algorithm can generate predictions that exceed historical maxima; such predictions could in principle also be “adjusted” a posteriori, though we do not attempt such an adjustment in this study. These aspects are discussed further in Sect. 5.6.
2.4 Transformations used in the post-processing model
The observed streamflow and median streamflow forecasts are transformed in Step 1 of streamflow post-processing (Sect. 2.3.2), to account for the heteroscedasticity and skewness of the forecast residuals. We consider three transformations, namely the logarithmic, Log-Sinh, and Box–Cox transformations.
2.4.1 Logarithmic (Log) transformation
The logarithmic (Log) transformation is
The offset c ensures the transformed flows are defined when Q=0. Here we set , where is the average observed streamflow over the calibration period. The use of a small fixed value for c is common in the literature for coping with zero flow events (Wang et al., 2012).
2.4.2 Log-Sinh transformation
The Log-Sinh transformation (Wang et al., 2012) is
The parameters a and b are calibrated for each month by maximizing the p-value of the Shapiro–Wilk test (Shapiro and Wilk, 1965) for normality of the residuals, v. This pragmatic approach is part of the existing Bureau's operational dynamic streamflow forecasting system (Lerat et al., 2015).
2.4.3 Box–Cox transformation
The Box–Cox (BC) transformation (Box and Cox, 1964) is
where λ is a power parameter and . Following the recommendations of McInerney et al. (2017), the parameter λ is fixed to 0.2.
2.4.4 Rationale for selecting transformational approaches
The Log transformation is a simple and widely used transformation; McInerney et al. (2017) reported that in daily scale modelling it produced the best reliability in perennial catchments (from a set of eight residual error schemes, including standard least squares, weighted least squares, BC, Log-Sinh, and reciprocal transformations). However, the Log transformation performed poorly in ephemeral catchments, where its precision was far worse than in perennial ones.
The Log-Sinh transformation is an alternative to the Log and BC transformations, and was proposed by Wang et al. (2012) to improve precision at higher flows. The Log-Sinh approach has been extensively applied to water forecasting problems (see for example, Del Giudice et al., 2013; Robertson et al., 2013b, Bennett et al., 2016). However, in daily scale streamflow modelling of perennial catchments using observed rainfall, the Log-Sinh scheme did not improve on the Log transformation: its parameters tend to calibrate to values for which the Log-Sinh transformation effectively reduces to the Log transformation (McInerney et al., 2017).
Finally, the BC transformation with fixed λ=0.2 is recommended by McInerney et al. (2017) as one of only two schemes (from the set of eight schemes listed earlier in this section) that achieve Pareto-optimal performance in terms of reliability, precision and bias, across both perennial and ephemeral catchments. McInerney et al. (2017) also found that calibrating λ did not generally improve predictive performance, due to the inferred value being dominated by the fit to the low flows at the expense of the high flows.
2.5 Summary of key terms
In the remainder of the paper, the term “uncorrected forecasts” refers to streamflow forecasts obtained using the steps in Sect. 2.2.3, and the term “post-processed forecasts” refers to forecasts based on a streamflow post-processing model, which includes the standardization and AR(1) model from Sect. 2.3 as well as a transformation (Log, Log-Sinh, or BC0.2) from Sect. 2.4. As the post-processing schemes considered in this work differ solely in the transformation used, they will be referred to as the Log, Log-Sinh, and BC0.2 schemes.
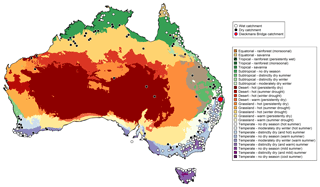
Figure 2Locations of the 300 catchments used in this study. The catchments are classified as dry or wet based on the aridity index. The Köppen climate classifications for Australia are shown. The Dieckmans Bridge catchment (site id: 145010A), used as a representative catchment in Fig. 8, is indicated by the red circle.
3.1 Study catchments
The empirical case study is carried out over a comprehensive set of 300 catchments with locations shown in Fig. 2. The figure also shows the Köppen climate zones. These catchments are selected as representative of the diverse hydro-climatic conditions across Australia. The catchment areas range from as small as 6 km2 to as large as 230 000 km2, with 90 % of the catchments having areas below 6000 km2. The seasonal streamflow forecasting service of the Bureau of Meteorology is currently evaluating these 300 catchments as part of an expansion of their dynamic modelling system.
3.2 Catchment data
In each catchment, data from 1980 to 2008 are used. Observed daily rainfall data were obtained from the Australian Water Availability Project (AWAP) (Jeffrey et al., 2001). Potential evaporation and observed streamflow data were obtained from the Bureau of Meteorology.
Catchment-scale rainfall forecasts are estimated from daily downscaled rainfall forecasts produced by the Bureau of Meteorology's global climate model, namely the Predictive Ocean Atmosphere Model for Australia (POAMA-2) (Hudson et al., 2013). The atmospheric component of POAMA-2 uses a spatial scale of approximately 250 × 250 km (Charles et al., 2013). To estimate catchment-scale rainfall, a statistical downscaling model based on an analogue approach (which could also be considered as rainfall forecast post-processing) was applied (Timbal and McAvaney, 2001). In the analogue approach, local climate information is obtained by matching analogous previous situations to the predicted climate. To this end, an ensemble of 166 rainfall forecast time series (33 POAMA ensembles ×5 replicates from downscaling +1 ensemble mean) were generated. In operation, POAMA-2 forecasts are generated every week by running 33 member ensembles out to 270 days. In this study we use rainfall forecasts up to 3 months ahead and produce 166 rainfall forecast ensembles through the analogue downscaling procedure described above.
3.3 Catchment classification
The performance of the post-processing schemes is evaluated separately in dry versus wet catchments. In this work, the classification of catchments into dry and wet is based on the aridity index (AI) according to the following equation:
where P is the total rainfall volume and PET is the total potential evapotranspiration volume. The aridity index has been used extensively to identify and classify drought and wetness conditions of hydrological regimes (Zhang et al., 2009; Carrillo et al., 2011; Sawicz et al., 2014).
Catchments with AI <0.5 are categorized as “dry”, which corresponds to hyper-arid, arid, and semi-arid classifications suggested by the United Nations Environment Programme (Middleton et al., 1997). Conversely, catchments with AI ≥ 0.5 are classified as “wet”. Overall, about 28 % of catchments used in this work are classified as dry.
3.4 Cross-validation procedure
The forecast verification is carried out using a moving-window cross-validation framework, as shown in Fig. 3. We use 5 years of data (1975–1979) to warm up the model and apply data from 1980 to 2008 for calibration in a cross-validation framework based on a 5-year moving window. Suppose we are validating the streamflow forecasts in year j (e.g. j=1990 in Fig. 3). In this case the calibration is carried out using all years except years j, j+1, j+2, j+3, and j+4. The 4-year period after year j is excluded to prevent the memory of the hydrological model from affecting model performance in the validation window period. The process is then repeated for each year during 1980–2008. Once the validation has been carried out for each year, the results are concatenated to produce a single “validation” time series, for which the performance metrics are calculated.
3.5 Forecast performance (verification) metrics
The performance of uncorrected and post-processed streamflow forecasts is evaluated using reliability and sharpness metrics, as well as the CRPSS (see Sect. 3.5.3). Note that the Bureau of Meteorology uses Root Mean Squared Error (RMSE) and Root Mean Squared Error in Probability (RMSEP) scores in the operational service in addition to CRPSS; however, these metrics have not been considered in this study.
Forecast performance (verification) metrics are computed separately for each forecast month. To facilitate the comparison and evaluation of streamflow forecast performance in different streamflow regimes, the high- and low-flow months are defined using long-term average streamflow data calculated for each month. The 6 months with the highest average streamflow are classified as “high-flow” months, and the remaining 6 months are classified as “low-flow” months. The performance metrics listed below are computed for each month separately; the indices denoting the month are excluded from Eqs. (10), (11), and (12) below to avoid cluttering the notation.
3.5.1 Reliability
The reliability of forecasts is evaluated using the probability integral transform (PIT) (Dawid, 1984; Laio and Tamea, 2007). To evaluate and compare reliability across 300 catchments, the p-value of the Kolmogorov–Smirnov (KS) test applied to the PIT is used. In this study, forecasts with PIT plots where the KS test yields a p-value ≥5 % are classified as “reliable”.
3.5.2 Sharpness
The sharpness of forecasts is evaluated using the ratio of inter-quantile ranges (IQRs) of streamflow forecasts and a historical reference (Tuteja et al., 2016). The following definition is used:
where IQRq is the IQR value corresponding to percentile q, and Fi(q) and Ci(q) are respectively the qth percentiles of forecast and the historical reference for year i.
An IQRq of 100 % indicates a forecast with the same sharpness as the reference, an IQRq below 100 % indicates forecasts that are sharper (tighter predictive limits) than the reference, and an IQRq above 100 % indicates forecasts that are less sharp (wider predictive limits) than the reference. We report IQR99, i.e. the IQR at the 99th percentile, in order to detect forecasts with unreasonably long tails in their predictive distributions.
3.5.3 CRPS skill score (CRPSS)
The CRPS metric quantifies the difference between a forecast distribution and observations, as follows (Hersbach, 2000):
where Fi is the cumulative distribution function (cdf) of the forecast for year i, y is the forecast variable (here streamflow) and yo is the corresponding observed value. Hi{y≥yo} is the Heaviside step function, which equals 1 when the forecast values are greater than the observed value and equals 0 otherwise.
The CRPS summarizes the reliability, sharpness, and bias attributes of the forecast (Hersbach, 2000). A “perfect” forecast – namely a point prediction that matches the actual value of the predicted quantity – has CRPSP=0. In this work, we use the CRPS skill score, CRPSS, defined by
where CRPSF, CRPSC and CRPSP represent the CRPS value for model forecast, climatology and “perfect” forecast respectively. A higher CRPSS indicates better performance, with a value of 0 representing the same performance as climatology.
3.5.4 Historical reference
The IQR and CRPSS metrics are defined as skill scores relative to a reference forecast. In this work, we use the climatology as the reference forecast, as it represents the long-term climate condition. To construct these “climatological forecasts”, we used the same historical reference as the operational seasonal streamflow forecasting service of the Bureau of Meteorology. This reference is resampled from a Gaussian probability distribution fitted to the observed streamflow transformed using the Log-Sinh transformation (Eq. 7). This approach leads to more stable and continuous historical reference estimates than sampling directly from the empirical distribution of historical streamflow, and can be computed at any percentile (which facilitates comparison with forecast percentiles). Although the choice of a particular reference affects the computation of skill scores, it does not affect the ranking of post-processing models when the same reference is used, which is the main aim of this paper.
3.5.5 Summary skill: summarizing forecast performance using multiple metrics
When evaluating forecast performance, a focus on any single individual metric can lead to misleading interpretations. For example, two forecasts might have a similar sharpness, yet if one of these forecasts is unreliable it can lead to an over- or under- estimation of the risk of an event of interest, which in turn can lead to a sub-optimal decision by forecast users (e.g. a water resources manager).
Given inevitable trade-offs between individual metrics (McInerney et al., 2017), it is important to consider multiple metrics jointly rather than individually. Following the approach suggested by Gneiting et al. (2007), we consider a forecast to have “high skill” when it is reliable and sharper than climatology. To determine the “summary skill” of the forecasts in each catchment, we evaluate the total number of months (out of 12) in which forecasts are reliable (i.e. with a p-value greater than 5 %) and sharper than the climatology (i.e. IQR99 <100 %). A catchment is classified as having high summary skill if “high-skill” forecasts are obtained 10–12 months per year (on average), and is classified as having low summary skill otherwise. Note that the CRPSS is not included in the summary skill, because it does not represent an independent measure of a forecast attribute (see Sect. 3.5.3 for more details).
A table providing the percentage of catchments with high and low summary skills is used to summarize the forecast performance of a given post-processing scheme. To identify any geographic trends in the forecast performance, the summary skills are plotted on a map. The summary skills together with individual skill score values are used to evaluate the overall forecast performance, and are presented separately for wet and dry catchments, as well as separately for high- and low-flow months.
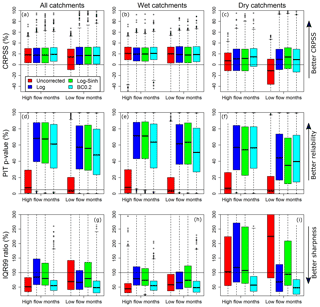
Figure 4Performance of monthly forecasts in terms of CRPSS, reliability (PIT p-value), and sharpness (IQR99 ratio).
Results for monthly and seasonal streamflow forecasts are now presented. Section 4.1 compares the uncorrected and post-processed streamflow forecast performance. Section 4.2 evaluates the performance of post-processed streamflow forecasts obtained using the Log, Log-Sinh, and BC0.2 schemes. The CRPSS, reliability, and sharpness metrics are presented in Figs. 4 and 5 for monthly and seasonal forecasts respectively.
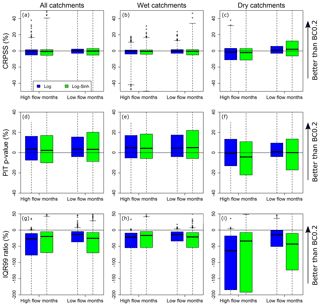
Figure 6Distributions of differences in the monthly forecast performance metrics of the Log and Log-Sinh schemes compared to the BC0.2 scheme.
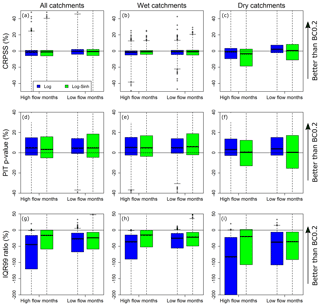
Figure 7Distributions of differences in the seasonal forecast performance metrics of the Log and Log-Sinh schemes compared to the BC0.2 scheme.
Initial inspection of results found considerable overlap in the performance metrics achieved by the error models. To determine whether the differences in metrics are consistent over multiple catchments, the Log and Log-Sinh schemes are compared to the BC0.2 scheme. This comparison is presented in Figs. 6 and 7 for monthly and seasonal forecasts respectively. The BC0.2 scheme is taken as the baseline because inspection of Figs. 4 and 5 suggests that the BC0.2 scheme has better median sharpness than the Log and Log-Sinh schemes, over all the catchments and for both high- and low-flow months individually.
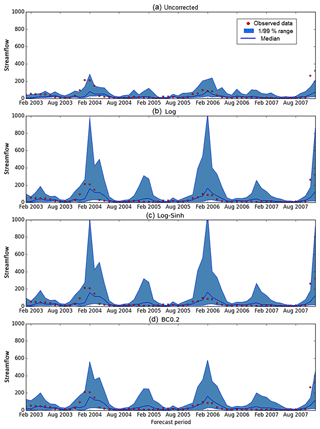
Figure 8Seasonal streamflow forecast time series (blue line) and observations (red dots) at Dieckmans Bridge catchment (site id: 145010A). The shaded area shows the 99 % prediction limits.
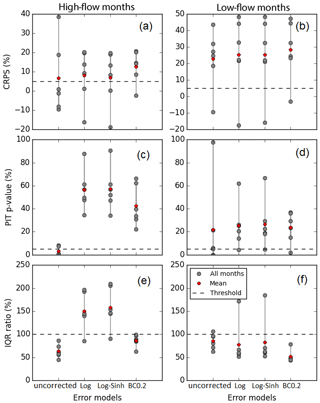
Figure 9Seasonal streamflow forecast skill scores at Dieckmans Bridge catchment, computed from the time series shown in Fig. 8 for 6 high-flow months and 6 low-flow months.
The streamflow forecast time series and corresponding skill for a single representative catchment, Dieckmans Bridge, are presented in Figs. 8 and 9 respectively.
The summary skills of the monthly and seasonal forecasts are presented in Figs. 10 and 11. The figures include a histogram of summary skills across all catchments to enable comparison between the uncorrected and post-processing approaches.

Figure 10Summary skill of monthly forecasts obtained using the Log, Log-Sinh, and BC0.2 schemes across 300 Australian catchments. The performance of uncorrected forecasts is also shown. The summary skill is defined as the number of months where high-skill forecasts (i.e. forecasts that are reliable and sharper than climatology) are obtained. The inset histogram shows the percentage of catchments in each performance category and also serves as the colour legend.
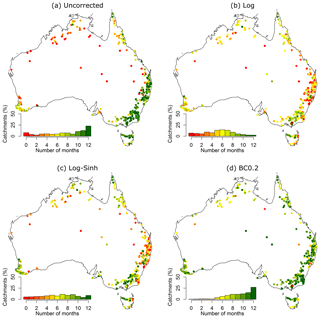
Figure 11Summary skill of seasonal forecasts obtained using the Log, Log-Sinh, and BC0.2 schemes across 300 Australian catchments. See Fig. 10's caption for details.
4.1 Comparison of uncorrected and post-processed streamflow forecasts: individual metrics
In terms of CRPSS, the largest improvement as a result of post-processing (using any of the transformations considered here) occurs in dry catchments. This finding holds for both monthly (Fig. 4c) and seasonal forecasts (Fig. 5c). For example, when post-processing is implemented, the median CRPSS of monthly forecasts in dry catchments increases from approximately 7 % (high-flow months) and −15 % (low-flow months) to more than 10 % (Fig. 4c) for both high and low flows. Visible improvement is also observed in dry catchments for seasonal forecasts; however, the improvement is not as pronounced as for monthly forecasts (Fig. 5c).
In terms of reliability, the performance of uncorrected streamflow forecasts is poor, with about 50 % of the catchments being characterized by unreliable forecasts at both the monthly and seasonal timescales (Figs. 4 and 5, middle row). In comparison, post-processing using the three transformation approaches produces much better reliability, achieving reliable forecasts in more than 90 % of the catchments.
In terms of sharpness, the uncorrected forecasts and the BC0.2 post-processed forecasts are generally sharper than forecasts generated using the other transformations (Figs. 4g and 5g). The use of post-processing achieves much better sharpness than uncorrected forecasts for low-flow months, particularly in dry catchments. For example, for low-flow months in dry catchments (Fig. 4i), the median IQR99 is greater than 200 %, while similar values range between 40 % and 100 % for post-processed forecasts. Similarly, for seasonal forecasts, post-processing approaches improve the median sharpness from 150 % (uncorrected forecasts) to 50 %–110 % (Fig. 5i).
4.2 Comparison of post-processing schemes: individual metrics
In terms of CRPSS, Figs. 4a–c and 5a–c show considerable overlap in the boxplots corresponding to all three post-processing schemes, in both wet and dry catchments. This finding suggests little difference in the performance of the post-processing schemes, and is further confirmed by Figs. 6a–c and 7a–c, which show boxplots of the differences between the CRPSS of the Log and Log-Sinh schemes versus the CRPSS of the BC0.2 scheme. Across all catchments, the distribution of these differences is approximately symmetric with a mean close to 0. In dry catchments, the BC0.2 slightly outperforms the Log scheme for high-flow months and the Log-Sinh scheme slightly outperforms the Log scheme for low-flow months. Overall, these results suggest that none of the Log, Log-Sinh, or BC0.2 schemes is consistently better in terms of CRPSS values.
In terms of reliability, post-processing using any of the three post-processing schemes produces reliable forecasts at both monthly and seasonal scales, and in the majority of the catchments (Figs. 4 and 5, middle row). The median p-value is approximately 60 % for monthly forecasts compared with 45 % for seasonal forecasts. This indicates that better forecast reliability is achieved at shorter lead times. Median reliability is somewhat reduced when using the BC0.2 scheme compared to the Log and Log-Sinh schemes in wet catchments (Fig. 6e), but not so much in dry catchments (Fig. 6f). Nevertheless, the monthly and seasonal forecasts are reliable in 96 % and 91 % of the catchments respectively. The corresponding percentages for the Log scheme are 97 % and 94 %, and for Log-Sinh they are 95 % and 90 %.
In terms of sharpness, the BC0.2 scheme outperforms the Log and Log-Sinh schemes. This finding holds in all cases (i.e. high-/low-flow months and wet/dry catchments), both for monthly and seasonal forecasts (Figs. 4 and 5, bottom row). The plot of differences in the sharpness metric (Figs. 6 and 7, bottom row) highlights this improvement. In half of the catchments, during both high- and low-flow months, the BC0.2 scheme improves the IQR99 by 30 % (or more) compared to the Log and Log-Sinh schemes. In dry catchments, the improvements are larger than in wet catchments. For example, in dry catchments during high-flow months, the BC0.2 scheme improves on the IQR99 of Log and Log-Sinh by 40 %–60 % in over a half of the catchments, and by as much as 170 %–190 % in a quarter of the catchments.
To illustrate these results, a streamflow forecast time series at Dieckmans Bridge catchment (site id: 145010A) is shown in Fig. 8 and performance metrics calculated over 6 high-flow months and 6 low-flow months are shown in Fig. 9. This catchment is selected as it is broadly representative of typical results obtained across the wide range of case study catchments. The period in Fig. 8 (2003–2007) is chosen because it highlights the difference in forecast interval between the uncorrected and post-processing approaches. The figure indicates that in terms of reliability, the uncorrected forecast has a number of observed data points outside the 99 % predictive range (Fig. 8a). This is an indication that the forecast is unreliable. This finding can be confirmed from the corresponding p-value in Fig. 9, which shows that the forecast is below the reliability threshold during most of the high-flow months and during some low-flow months. In terms of sharpness, the Log and Log-Sinh schemes produce a wider 99 % predictive range than the BC0.2 scheme (Figs. 8 and 9).
Table 1Performance of post-processing schemes, expressed as the percentage of catchments with high and low summary skill. Results shown for monthly and seasonal forecasts. A catchment with “high summary skill” is defined as a catchment where “high-skill” forecasts are achieved in 10–12 months out of the year; “high-skill” forecasts are defined as forecasts that are reliable and sharper than climatology.
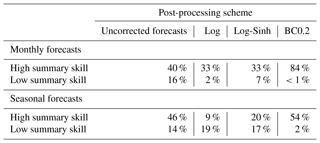
4.3 Comparison of summary skill between uncorrected and post-processing approaches
Figures 10 and 11 show the geographic distribution of the summary skill of the uncorrected and post-processing approaches for monthly and seasonal forecasts respectively. Recall that the summary skill represents the number of months with streamflow forecasts that are both reliable and sharper than climatology. Table 1 provides a summary of the percentage of catchments with high and low summary skill for the uncorrected and post-processing approaches for monthly and seasonal forecasts (see Sect. 3.5.5).
The findings for forecasts at the monthly scale are as follows (Fig. 10 and Table 1).
-
Uncorrected forecasts perform worse than post-processing techniques in the sense that they have low summary skill in the largest percentage of catchments (16 %). The percentage of catchments where high summary skill is achieved by uncorrected forecasts is 40 %.
-
Post-processing forecasts with the Log and Log-Sinh schemes reduce the percentage of catchments with low summary skills from 16 % to 2 % and 7 % respectively. However, the percentage of catchments with high summary skill also decreases (in comparison to uncorrected forecasts), from 40 % to 33 % for both the Log and Log-Sinh schemes.
Post-processing with the BC0.2 scheme provides the best performance, with the smallest percentage of catchments with low summary skills (<1 %) and the largest percentage of catchments with high summary skills (84 %), as seen in Fig. 10.
-
Figure 10: the improvement achieved by the BC0.2 scheme (compared to the Log/Log-Sinh schemes) is most pronounced in New South Wales (NSW) and in the tropical catchments in Queensland (QLD) and the Northern Territory (NT). The few catchments where the BC0.2 scheme does not achieve a high summary skill are located in the north and north-west of Australia.
The findings for forecasts at the seasonal scale are as follows (Fig. 11 and Table 1).
-
Log scheme has the largest percentage (19 %) of catchments with low summary skill and a relatively small percentage (9 %) of catchments with high summary skill.
Post-processing forecasts with the Log and Log-Sinh schemes reduce the percentage of catchments with low summary skill from 19 % to 18 % and 17 % respectively. The percentage of catchments with high summary skill increases from 9 % to 12 % and 22 % respectively.
-
Post-processing with the BC0.2 scheme once again provides the best performance: it produces forecasts with low summary skill in only 2 % of the catchments, and achieves high summary skill in 54 % of the catchments. As seen in Fig. 11, similar to the case of monthly forecasts, the biggest improvements for seasonal forecasts occur in the NSW and Queensland regions of Australia.
-
Overall, Table 1 shows that, across all schemes, BC0.2 results in a larger percentage of catchments with low summary skill and a larger percentage of catchments with high summary skill. It can also be seen that the summary skills of post-processing approaches are lower for seasonal forecasts than for monthly forecasts.
4.4 Summary of empirical findings
Section 4.1–4.3 show that post-processing achieves major improvements in reliability, as well as in CRPSS and sharpness, particularly in dry catchments. Although all three post-processing schemes under consideration provide improvements in some of the performance metrics, the BC0.2 scheme consistently produces better sharpness than the Log and Log-Sinh schemes, while maintaining similar reliability and CRPSS. This finding holds for both monthly and, to a lower degree, seasonal forecasts. Of the three post-processing schemes, the BC0.2 scheme improves by the largest margin the percentage of catchments and the number of months where the post-processed forecasts are reliable and sharper than climatology.
5.1 Benefits of forecast post-processing
A comparison of uncorrected and post-processed streamflow forecasts was provided in Sect. 4.1. Uncorrected forecasts have reasonable sharpness (except in dry catchments), but suffer from low reliability: uncorrected forecasts are unreliable at approximately 50 % of the catchments. In wet catchments, poor reliability is due to overconfident forecasts, which appears a common concern in dynamic forecasting approaches (Wood and Schaake, 2008). In dry catchments, uncorrected forecasts are both unreliable and exhibit poor sharpness. Post-processing is thus particularly important to correct for these shortcomings and improve forecast skill. In this study, all post-processing models provide a clear improvement in reliability and sharpness, especially in dry catchments. The value of post-processing is more pronounced in dry catchments than in wet catchments (Figs. 4 and 5). This finding can be attributed to the challenge of capturing key physical processes in dry and ephemeral catchments (Ye et al., 1997), as well as the challenge of achieving accurate rainfall forecasts in arid areas. In addition, the simplifications inherent in any hydrological model, including the conceptual model GR4J used in this work, might also be responsible for the forecast skill being relatively lower in dry catchments than in wet catchments. Whilst using a single conceptual model is attractive for practical operational system, there may be gains in exploring alternative structures for ephemeral catchments (e.g. Clark et al., 2008; Fenicia et al., 2011). We intend to explore such alternative model structures for difficult ephemeral catchments. In such dry catchments, the hydrological model forecasts are particularly poor and leave a lot of room for improvement: post-processing can hence make a big difference on the quality of results.
5.2 Interpretation of differences between post-processing schemes
We now discuss the large differences in sharpness between the BC0.2 scheme versus the Log and Log-Sinh schemes. The Log-Sinh transformation was designed by Wang et al. (2012) to improve the reliability and sharpness of predictions, particularly for high flows, and has worked well as part of the statistical modelling system for operational streamflow forecasts by the Bureau of Meteorology. The Log-Sinh transformation has a variance stabilizing function that (for certain parameter values) tapers off for high flows. In theory, this feature can prevent the explosive growth of predictions for high flows that can occur with the Log and Box–Cox transformations (especially when λ<0).
McInerney et al. (2017) found that, when modelling perennial catchments at the daily scale, the Log-Sinh scheme did not achieve better sharpness than the Log scheme. Instead, the parameters for the Log scheme tended to converge to values for which the tapering off of the Log-Sinh transformation function occurs well outside the range of simulated flows, effectively reducing the Log-Sinh scheme to the Log scheme. In contrast, the Box–Cox transformation function with a fixed λ>0 gradually flattens as streamflow increases, and exhibits the “desired” tapering-off behaviour within the range of simulated flows. This behaviour leads to the Box–Cox scheme achieving, on average, more favourable variance-stabilizing characteristics than the Log-Sinh scheme.
Our findings in this study confirm the insights of McInerney et al. (2017) – namely that the Log-Sinh scheme produces comparable sharpness to the Log scheme – across a wider range of catchments. This finding indicates that insights from modelling residual errors at the daily scale apply at least to some extent to streamflow forecast post-processing at the monthly and seasonal scales. Note the minor difference in the treatment of the offset parameter c in Eq. (6): in the Log scheme used in McInerney et al. (2017) this parameter is inferred, whereas in this study it is fixed a priori. This minor difference does not impact on the qualitative behaviour of the error models described earlier in this section. Overall, when used for post-processing seasonal and monthly forecasts in a dynamic modelling system, the BC0.2 scheme provides an opportunity to improve forecast performance further than is possible using the Log and Log-Sinh schemes.
5.3 Importance of using multiple metrics to assess forecast performance
The goal of the forecasting exercise is to maximize sharpness without sacrificing reliability (Gneiting et al., 2005; Wilks, 2011; Bourdin et al., 2014). The study results show that relying on a single metric for evaluating forecast performance can lead to sub-optimal conclusions. For example, if one considers the CRPSS metric alone, all post-processing schemes yield comparable performance and there is no basis for favouring any single one of them. However, once sharpness is taken into consideration explicitly, the BC0.2 scheme can be recommended due to substantially better sharpness than the Log and Log-Sinh schemes.
Similarly, comparisons based solely on CRPSS might suggest reasonable performance of the uncorrected forecasts: 55 %–80 % of months have CRPSS > 0 (with some variability across high-/low-flow months and monthly/seasonal forecasts). Yet once reliability is considered explicitly, it is found that uncorrected forecasts are unreliable at approximately 50 % of the catchments. Note that performance metrics based on the CRPSS reflect an implicitly weighted combination of reliability, sharpness, and bias characteristics of the forecasts (Hersbach, 2000). In contrast, the reliability and sharpness metrics are specifically designed to quantify reliability and sharpness attributes individually. These findings highlight the value of multiple independent performance metrics and diagnostics that evaluate specific (targeted) attributes of the forecasts, and highlight important limitations of aggregate measures of performance (Clark et al., 2011).
A number of challenges and questions remain in regards to selecting the performance verification metrics for specific forecasting systems and applications. An important question is how to include user needs into a forecast verification protocol. This could be accomplished by tailoring the evaluation metrics to the requirements of users. Another key question is to what extent do measures of forecast skill correlate to the economic and/or social value of the forecast? This challenging question was investigated by Murphy and Ehrendorfer (1987) and Wandishin and Brooks (2002), who found the relationship between quality and value of a forecast to be essentially nonlinear: an increase in forecast quality may not necessarily lead to a proportional increase in its value. This question requires further multi-disciplinary research, including human psychology, economic theory, communication and social studies (e.g. Matte et al., 2017; Morss et al., 2010).
5.4 Importance of performance evaluation over large numbers of catchments
When designing an operational forecast service for locations with streamflow regimes as diverse and variable as in Australia (Taschetto and England, 2009), it is essential to thoroughly evaluate multiple modelling methods over multiple locations to ensure the findings are sufficiently robust and general. This was the major reason for considering the large set of 300 catchments in our study. This set-up also yields valuable insights into spatial patterns in forecast performance. For example, the Log and Log-Sinh schemes perform relatively well in catchments in south-eastern Australia, and relatively worse in catchments in northern and north-eastern Australia (Figs. 10 and 11). In contrast, the BC0.2 scheme performs well across the majority of the catchments in all regions included in the evaluation. The evaluation over a large number of catchments in different hydro-climatic regions is clearly beneficial to establish the robustness of post-processing methods. Restricting the analysis to a smaller number of catchments would have led to less conclusive findings.
5.4.1 Implication of results for water resource management
The empirical results clearly show that the BC0.2 post-processing scheme improves forecast sharpness (precision) while maintaining forecast accuracy and reliability. As discussed below, this improvement in forecast quality offers an opportunity to improve operational planning and management of water resources.
The management of water resources, for example, deciding which water source to use for a particular purpose or allocating environmental flows, requires an understanding of the current and future availability of water. For water resources systems with long hydrological records, water managers have devised techniques to evaluate current water availability, water demand, and losses. However, one of the main unknowns is the volume of future system inflows. Streamflow forecasts provide crucial information to water managers and users regarding the future availability of water, thus helping reduce uncertainty in decision making. This information is particularly valuable for supporting decisions during drought events. In this study, forecast performance is evaluated separately for high- and low-flow months – providing a clearer indication of predictive ability for flows that are above and below average respectively. A detailed evaluation of forecasts for more extreme drought events is challenging as these events are correspondingly rarer. Limited sample size makes it difficult to make conclusive statements: e.g. if we focus on the lowest 5 % of historical data with a 30-year record, we may only have roughly 1.5 samples for each month/season. The uncertainty arising from limited sample size requires further development of forecast verification techniques, potentially adapting some of the approaches used by Hodgkins et al. (2017).
5.5 Opportunities for further improvement in forecast performance
There are several opportunities to further improve the seasonal streamflow forecasting system. This section describes avenues related to specialized treatment of zero flows and high-flow forecasts, uncertainty analysis of post-processing model parameters, and the use of data assimilation (state updating).
The post-processing approaches used in this work do not make special provision for zero flows in the observed data. Robust handling of zero flows in statistical models, especially in arid and semi-arid catchments, is an active research area (Wang and Robertson, 2011; Smith et al., 2015), and advances in this area are certainly relevant to seasonal streamflow forecasting.
A similar challenge is associated with the forecasting of high flows, as the post-processing approaches used in this work can produce streamflow predictions that exceed historical maxima. The IQR ratio used to assess forecast sharpness will detect unreasonably long tails (i.e. extremes) in the predictive distributions and hence can indirectly identify instances of unreasonably high-flow forecasts. Further research is needed to develop techniques to evaluate the realism of forecasts that exceed historical maxima.
Another area for further investigation is the identifiability of parameters and of the monthly post-processing model. These parameters are estimated using monthly data (see Sect. 2.3.2), and hence could be subject to substantial uncertainty and/or overfitting to the calibration period. In this study, 29 years of data were employed in the calibration, making these problems unlikely. Importantly, the use of a cross-validation procedure (Sect. 3.4) is expected to detect potential overfitting. That said, as many sites of potential application may lack the data length available in this work, the sensitivity of forecast performance to the length of calibration period warrants further investigation.
Finally, the forecasting system used in this study does not employ data assimilation to update the states of the GR4J hydrological model. Gibbs et al. (2018) showed that monthly streamflow forecasting benefits from state updating in catchments that exhibit non-stationarity in their rainfall–runoff dynamics. Note that data assimilation of ocean observations has been implemented in the climate model (POAMA2) used for the rainfall forecast (Yin et al., 2011) (see Sect. 3.2 for additional details).
This study focused on developing robust streamflow forecast post-processing schemes for an operational forecasting service at the monthly and seasonal timescales. For such forecasts to be useful to water managers and decision-makers, they should be reliable and exhibit sharpness that is better than climatology.
We investigated streamflow forecast post-processing schemes based on residual error models employing three data transformations, namely the logarithmic (Log), log-sinh (Log-Sinh), and Box–Cox with λ=0.2 (BC0.2). The Australian Bureau of Meteorology's dynamic modelling system was used as the platform for the empirical analysis, which was carried out over 300 Australian catchments with diverse hydro-climatic conditions.
The following empirical findings are obtained.
-
Uncorrected forecasts (no post-processing) perform poorly in terms of reliability, resulting in a mischaracterization of forecast uncertainties.
-
All three post-processing schemes substantially improve the reliability of streamflow forecasts, both in terms of the dedicated reliability metric and in terms of the summary skill given by the CRPSS.
-
From the post-processing schemes considered in this work, the BC0.2 scheme is found to be best suited for operational application. The BC0.2 scheme provides the sharpest forecasts without sacrificing reliability, as measured by the reliability and CRPSS metrics. In particular, the BC0.2 scheme produces forecasts that are both reliable and sharper than climatology at substantially more catchments than the alternative Log and Log-Sinh schemes.
A major practical outcome of this study is the development of a robust streamflow forecast post-processing scheme that achieves forecasts that are consistently reliable and sharper than climatology. This scheme is well suited for operational application, and offers the opportunity to improve decision support, especially in catchments where climatology is presently used to guide operational decisions.
The data underlying this research can be accessed from the following links: observed rainfall data (http://www.bom.gov.au/climate, last access: 7 November 2018), POAMA rainfall forecast generated by the Australian Bureau of Meteorology (http://poama.bom.gov.au, Charles et al., 2013), and observed streamflow data (http://www.bom.gov.au/waterdata, last access: 7 November 2018).
The authors declare that they have no conflict of interest.
Data for this study are provided by the Australian Bureau of Meteorology.
This work was supported by Australian Research Council grant LP140100978 with
the Australian Bureau of Meteorology and South East Queensland Water. We
thank the anonymous reviewers for constructive comments and feedback that
helped us substantially improve the paper.
Edited by: Albrecht Weerts
Reviewed by: two anonymous referees
Bennett, J. C., Wang, Q. J., Li, M., Robertson, D. E., and Schepen, A.: Reliable long-range ensemble streamflow forecasts: Combining calibrated climate forecasts with a conceptual runoff model and a staged error model, Water Resour. Res., 52, 8238–8259, https://doi.org/10.1002/2016WR019193, 2016.
Bennett, J. C., Wang, Q. J., Robertson, D. E., Schepen, A., Li, M., and Michael, K.: Assessment of an ensemble seasonal streamflow forecasting system for Australia, Hydrol. Earth Syst. Sci., 21, 6007–6030, https://doi.org/10.5194/hess-21-6007-2017, 2017.
Bogner, K. and Kalas, M.: Error-correction methods and evaluation of an ensemble based hydrological forecasting system for the Upper Danube catchment, Atmos. Sci. Lett., 9, 95–102, https://doi.org/10.1002/asl.180, 2008.
Bourdin, D. R., Nipen, T. N., and Stull, R. B.: Reliable probabilistic forecasts from an ensemble reservoir inflow forecasting system, Water Resour. Res., 50, 3108–3130, https://doi.org/10.1002/2014WR015462, 2014.
Box, G. E. P. and Cox, D. R.: An analysis of transformations, J. R. Stat. Soc. Ser. B, 211–252, https://doi.org/10.2307/2287791, 1964.
Brown, J. D., Wu, L., He, M., Regonda, S., Lee, H., and Seo, D. J.: Verification of temperature, precipitation, and streamflow forecasts from the NOAA/NWS Hydrologic Ensemble Forecast Service (HEFS): 1. Experimental design and forcing verification, J. Hydrol., 519, 2869–2889, https://doi.org/10.1016/j.jhydrol.2014.05.028, 2014.
Carpenter, T. M. and Georgakakos, K. P.: Assessment of Folsom lake response to historical and potential future climate scenarios: 1. Forecasting, J. Hydrol., 249, 148–175, https://doi.org/10.1016/S0022-1694(01)00417-6, 2001.
Carrillo, G., Troch, P. A., Sivapalan, M., Wagener, T., Harman, C., and Sawicz, K.: Catchment classification: hydrological analysis of catchment behavior through process-based modeling along a climate gradient, Hydrol. Earth Syst. Sci., 15, 3411–3430, https://doi.org/10.5194/hess-15-3411-2011, 2011.
Charles, A., Miles, E., Griesser, A., de Wit, R., Shelton, K., Cottrill, A., Spillman, C., Hendon, H., McIntosh, P., Nakaegawa, T., Atalifo, T., Prakash, B., Seuseu, S., Nihmei, S., Church, J., Jones, D., and Kuleshov, Y.: Dynamical Seasonal Prediction of Climate Extremes in the Pacific, in 20th International Congress on Modelling and Simulation (Modsim2013), 2841–2847, 2013.
Clark, M. P., Slater, A. G., Rupp, D. E., Woods, R. A., Vrugt, J. A., Gupta, H. V., Wagener, T., and Hay, L. E.: Framework for Understanding Structural Errors (FUSE): A modular framework to diagnose differences between hydrological models, Water Resour. Res., 44, W00B02, https://doi.org/10.1029/2007WR006735, 2008.
Clark, M. P., Kavetski, D., and Fenicia, F.: Pursuing the method of multiple working hypotheses for hydrological modeling, Water Resour. Res., 47, W09301, https://doi.org/10.1029/2010WR009827, 2011.
Cloke, H., Pappenberger, F., Thielen, J., and Thiemig, V.: Operational European Flood Forecasting, in Environmental Modelling, John Wiley & Sons, Ltd., 415–434, 2013.
Crochemore, L., Ramos, M.-H., and Pappenberger, F.: Bias correcting precipitation forecasts to improve the skill of seasonal streamflow forecasts, Hydrol. Earth Syst. Sci., 20, 3601–3618, https://doi.org/10.5194/hess-20-3601-2016, 2016.
Dawid, A. P.: Present Position and Potential Developments: Some Personal Views: Statistical theory: the prequential approach (with discussion), J. R. Stat. Soc. Ser. A, 147, 278–292, https://doi.org/10.2307/2981683, 1984.
DeChant, C. M. and Moradkhani, H.: Improving the characterization of initial condition for ensemble streamflow prediction using data assimilation, Hydrol. Earth Syst. Sci., 15, 3399–3410, https://doi.org/10.5194/hess-15-3399-2011, 2011.
Demargne, J., Wu, L., Regonda, S. K., Brown, J. D., Lee, H., He, M., Seo, D. J., Hartman, R., Herr, H. D., Fresch, M., Schaake, J., and Zhu, Y.: The science of NOAA's operational hydrologic ensemble forecast service, B. Am. Meteorol. Soc., 95, 79–98, https://doi.org/10.1175/BAMS-D-12-00081.1, 2014.
Evin, G., Thyer, M., Kavetski, D., McInerney, D., and Kuczera, G.: Comparison of joint versus postprocessor approaches for hydrological uncertainty estimation accounting for error autocorrelation and heteroscedasticity, Water Resour. Res., 50, 2350–2375, https://doi.org/10.1002/2013WR014185, 2014.
Fenicia, F., Kavetski, D., and Savenije, H. H. G.: Elements of a flexible approach for conceptual hydrological modeling: 1. Motivation and theoretical development, Water Resour. Res., 47, 1–13, https://doi.org/10.1029/2010WR010174, 2011.
Gibbs, M. S., McInerney, D., Humphrey, G., Thyer, M. A., Maier, H. R., Dandy, G. C., and Kavetski, D.: State updating and calibration period selection to improve dynamic monthly streamflow forecasts for an environmental flow management application, Hydrol. Earth Syst. Sci., 22, 871–887, https://doi.org/10.5194/hess-22-871-2018, 2018.
Del Giudice, D., Honti, M., Scheidegger, A., Albert, C., Reichert, P., and Rieckermann, J.: Improving uncertainty estimation in urban hydrological modeling by statistically describing bias, Hydrol. Earth Syst. Sci., 17, 4209–4225, https://doi.org/10.5194/hess-17-4209-2013, 2013.
Gneiting, T., Raftery, A. E., Westveld, A. H., and Goldman, T.: Calibrated Probabilistic Forecasting Using Ensemble Model Output Statistics and Minimum CRPS Estimation, Mon. Weather Rev., 133, 1098–1118, https://doi.org/10.1175/MWR2904.1, 2005.
Gneiting, T., Balabdaoui, F., and Raftery, A. E.: Probabilistic forecasts, calibration and sharpness, J. R. Stat. Soc. Ser. B, 69, 243–268, https://doi.org/10.1111/j.1467-9868.2007.00587.x, 2007.
Hashino, T., Bradley, A. A., and Schwartz, S. S.: Evaluation of bias-correction methods for ensemble streamflow volume forecasts, Hydrol. Earth Syst. Sci., 11, 939–950, https://doi.org/10.5194/hess-11-939-2007, 2007.
Hazelton, M. L.: Methods of Moments Estimation BT – International Encyclopedia of Statistical Science, edited by: Lovric, M., Springer Berlin Heidelberg, Berlin, Heidelberg, 816–817, 2011.
Hersbach, H.: Decomposition of the Continuous Ranked Probability Score for Ensemble Prediction Systems, Weather Forecast., 15, 559–570, https://doi.org/10.1175/1520-0434(2000)015<0559:DOTCRP>2.0.CO;2, 2000.
Hudson, D., Marshall, A. G., Yin, Y., Alves, O., and Hendon, H. H.: Improving Intraseasonal Prediction with a New Ensemble Generation Strategy, Mon. Weather Rev., 141, 4429–4449, https://doi.org/10.1175/MWR-D-13-00059.1, 2013.
Humphrey, G. B., Gibbs, M. S., Dandy, G. C., and Maier, H. R.: A hybrid approach to monthly streamflow forecasting: Integrating hydrological model outputs into a Bayesian artificial neural network, J. Hydrol., 540, 623–640, https://doi.org/10.1016/j.jhydrol.2016.06.026, 2016.
Jeffrey, S. J., Carter, J. O., Moodie, K. B., and Beswick, A. R.: Using spatial interpolation to construct a comprehensive archive of Australian climate data, Environ. Model. Softw., 16, 309–330, https://doi.org/10.1016/S1364-8152(01)00008-1, 2001.
Kavetski, D., Kuczera, G., and Franks, S. W.: Bayesian analysis of input uncertainty in hydrological modeling: 1. Theory, Water Resour. Res., 42, W03407, https://doi.org/10.1029/2005WR004368, 2006.
Knoche, M., Fischer, C., Pohl, E., Krause, P., and Merz, R.: Combined uncertainty of hydrological model complexity and satellite-based forcing data evaluated in two data-scarce semi-arid catchments in Ethiopia, J. Hydrol., 519, 2049–2066, https://doi.org/10.1016/j.jhydrol.2014.10.003, 2014.
Kuczera, G., Kavetski, D., Franks, S., and Thyer, M.: Towards a Bayesian total error analysis of conceptual rainfall-runoff models: Characterising model error using storm-dependent parameters, J. Hydrol., 331, 161–177, https://doi.org/10.1016/j.jhydrol.2006.05.010, 2006.
Laio, F. and Tamea, S.: Verification tools for probabilistic forecasts of continuous hydrological variables, Hydrol. Earth Syst. Sci., 11, 1267–1277, https://doi.org/10.5194/hess-11-1267-2007, 2007.
Laugesen, R., Tuteja, N. K., Shin, D., Chia, T., and Khan, U.: Seasonal Streamflow Forecasting with a workflow-based dynamic hydrologic modelling approach, in: MODSIM 2011 – 19th International Congress on Modelling and Simulation – Sustaining Our Future: Understanding and Living with Uncertainty, 2352–2358, available at: http://www.scopus.com/inward/record.url?eid=2-s2.0-84858823270&partnerID=tZOtx3y1 (last access: 7 November 2018), 2011.
Lerat, J., Pickett-Heaps, C., Shin, D., Zhou, S., Feikema, P., Khan, U., Laugesen, R., Tuteja, N., Kuczera, G., Thyer, M., and Kavetski, D.: Dynamic streamflow forecasts within an uncertainty framework for 100 catchments in Australia, in In: 36th Hydrology and Water Resources Symposium: The art and science of water, 1396–1403, Barton, ACT: Engineers Australia, 2015.
Li, M., Wang, Q. J., Bennett, J. C., and Robertson, D. E.: Error reduction and representation in stages (ERRIS) in hydrological modelling for ensemble streamflow forecasting, Hydrol. Earth Syst. Sci., 20, 3561–3579, https://doi.org/10.5194/hess-20-3561-2016, 2016.
Lü, H., Crow, W. T., Zhu, Y., Ouyang, F., and Su, J.: Improving streamflow prediction using remotely-sensed soil moisture and snow depth, Remote Sens., 8, 503, https://doi.org/10.3390/rs8060503, 2016.
Madadgar, S., Moradkhani, H., and Garen, D.: Towards improved post-processing of hydrologic forecast ensembles, Hydrol. Proc., 28, 104–122, https://doi.org/10.1002/hyp.9562, 2014.
Matte, S., Boucher, M.-A., Boucher, V., and Fortier Filion, T.-C.: Moving beyond the cost-loss ratio: economic assessment of streamflow forecasts for a risk-averse decision maker, Hydrol. Earth Syst. Sci., 21, 2967–2986, https://doi.org/10.5194/hess-21-2967-2017, 2017.
McInerney, D., Thyer, M., Kavetski, D., Lerat, J., and Kuczera, G.: Improving probabilistic prediction of daily streamflow by identifying Pareto optimal approaches for modeling heteroscedastic residual errors, Water Resour. Res., 53, 2199–2239, https://doi.org/10.1002/2016WR019168, 2017.
Mendoza, P. A., Wood, A. W., Clark, E., Rothwell, E., Clark, M. P., Nijssen, B., Brekke, L. D., and Arnold, J. R.: An intercomparison of approaches for improving operational seasonal streamflow forecasts, Hydrol. Earth Syst. Sci., 21, 3915–3935, https://doi.org/10.5194/hess-21-3915-2017, 2017.
Middleton, N., Programme, U. N. E., and Thomas, D. S. G.: World Atlas of Desertification, Arnold, 1997.
Morss, R. E., Lazo, J. K., and Demuth, J. L.: Examining the use of weather forecasts in decision scenarios: Results from a us survey with implications for uncertainty communication, Meteorol. Appl., 17, 149–162, https://doi.org/10.1002/met.196, 2010.
Murphy, A. H. and Ehrendorfer, M.: On the relationship between the accuracy and value of forecasts in the cost–loss ratio situation, Weather Forecast., 2, 243–251, https://doi.org/10.1175/1520-0434(1987)002<0243:OTRBTA>2.0.CO;2, 1987.
Perrin, C., Michel, C., and Andréassian, V.: Improvement of a parsimonious model for streamflow simulation, J. Hydrol., 279, 275–289, https://doi.org/10.1016/S0022-1694(03)00225-7, 2003.
Pokhrel, P., Robertson, D. E., and Wang, Q. J.: A Bayesian joint probability post-processor for reducing errors and quantifying uncertainty in monthly streamflow predictions, Hydrol. Earth Syst. Sci., 17, 795–804, https://doi.org/10.5194/hess-17-795-2013, 2013.
Prudhomme, C., Hannaford, J., Harrigan, S., Boorman, D., Knight, J., Bell, V., Jackson, C., Svensson, C., Parry, S., Bachiller-Jareno, N., Davies, H., Davis, R., Mackay, J., McKenzie, A., Rudd, A., Smith, K., Bloomfield, J., Ward, R., and Jenkins, A.: Hydrological Outlook UK: an operational streamflow and groundwater level forecasting system at monthly to seasonal time scales, Hydrol. Sci. J., 62, 2753–2768, https://doi.org/10.1080/02626667.2017.1395032, 2017.
Renard, B., Kavetski, D., Leblois, E., Thyer, M., Kuczera, G., and Franks, S. W.: Toward a reliable decomposition of predictive uncertainty in hydrological modeling: Characterizing rainfall errors using conditional simulation, Water Resour. Res., 47, W11516, https://doi.org/10.1029/2011WR010643, 2011.
Robertson, D. E. and Wang, Q. J.: Selecting predictors for seasonal streamflow predictions using a Bayesian joint probability (BJP) modelling approach, 18th World IMACS/MODSIM Congr. Cairns, Aust. 13–17 July 2009, 376–382, 2009.
Robertson, D. E. and Wang, Q. J.: A Bayesian Approach to Predictor Selection for Seasonal Streamflow Forecasting, J. Hydrometeorol., 13, 155–171, https://doi.org/10.1175/JHM-D-10-05009.1, 2011.
Robertson, D. E., Pokhrel, P., and Wang, Q. J.: Improving statistical forecasts of seasonal streamflows using hydrological model output, Hydrol. Earth Syst. Sci., 17, 579–593, https://doi.org/10.5194/hess-17-579-2013, 2013a.
Robertson, D. E., Shrestha, D. L., and Wang, Q. J.: Post-processing rainfall forecasts from numerical weather prediction models for short-term streamflow forecasting, Hydrol. Earth Syst. Sci., 17, 3587–3603, https://doi.org/10.5194/hess-17-3587-2013, 2013b.
Sawicz, K. A., Kelleher, C., Wagener, T., Troch, P., Sivapalan, M., and Carrillo, G.: Characterizing hydrologic change through catchment classification, Hydrol. Earth Syst. Sci., 18, 273–285, https://doi.org/10.5194/hess-18-273-2014, 2014.
Schick, S., Rössler, O., and Weingartner, R.: Monthly streamflow forecasting at varying spatial scales in the Rhine basin, Hydrol. Earth Syst. Sci., 22, 929–942, https://doi.org/10.5194/hess-22-929-2018, 2018.
Senlin, Z., Feikema, P., Shin, D., Tuteja, N. K., MacDonald, A., Sunter, P., Kent, D., Le, B., Pipunic, R., Wilson, T., Pickett-Heaps, C., and Lerat, J.: Operational efficiency measures of the national seasonal streamflow forecast service in Australia, edited by: Syme, G., MacDonald, D. H., Fulton, B., and Piantadosi, J., The Modelling and Simulation Society of Australia and New Zealand Inc, Hobart, Australia., 2017.
Seo, D.-J., Herr, H. D., and Schaake, J. C.: A statistical post-processor for accounting of hydrologic uncertainty in short-range ensemble streamflow prediction, Hydrol. Earth Syst. Sci. Discuss., 3, 1987–2035, https://doi.org/10.5194/hessd-3-1987-2006, 2006.
Shapiro, S. S. and Wilk, M. B.: An Analysis of Variance Test for Normailty (Complete Samples), Biometrika, 52, 591–611, https://doi.org/10.2307/1267427, 1965.
Smith, T., Marshall, L., and Sharma, A.: Modeling residual hydrologic errors with Bayesian inference, J. Hydrol., 528, 29–37, https://doi.org/10.1016/j.jhydrol.2015.05.051, 2015.
Tang, Q. and Lettenmaier, D. P.: Use of satellite snow-cover data for streamflow prediction in the Feather River Basin, California, Int. J. Remote Sens., 31, 3745–3762, https://doi.org/10.1080/01431161.2010.483493, 2010.
Taschetto, A. S. and England, M. H.: An analysis of late twentieth century trends in Australian rainfall, Int. J. Climatol., 29, 791–807, https://doi.org/10.1002/joc.1736, 2009.
Timbal, B. and McAvaney, B. J.: An Analogue based method to downscale surface air temperature: Application for Australia, Clim. Dynam, 17, 947–963, https://doi.org/10.1007/s003820100156, 2001.
Turner, S. W. D., Bennett, J. C., Robertson, D. E., and Galelli, S.: Complex relationship between seasonal streamflow forecast skill and value in reservoir operations, Hydrol. Earth Syst. Sci., 21, 4841–4859, https://doi.org/10.5194/hess-21-4841-2017, 2017.
Tuteja, N. K., Shin, D., Laugesen, R., Khan, U., Shao, Q., Wang, E., Li, M., Zheng, H., Kuczera, G., Kavetski, D., Evin, G., Thyer, M., MacDonald, A., Chia, T., and Le, B.: Experimental evaluation of the dynamic seasonal streamflow forecasting approach, Melbourne, 2011.
Tuteja, N. K., Zhou, S., Lerat, J., Wang, Q. J., Shin, D., and Robertson, D. E.: Overview of Communication Strategies for Uncertainty in Hydrological Forecasting in Australia, in: Handbook of Hydrometeorological Ensemble Forecasting, edited by: Duan, Q., Pappenberger, F., Thielen, J., Wood, A., Cloke, H. L., and Schaake, J. C., Springer Berlin Heidelberg, Berlin, Heidelberg, 1–19, 2016.
Tyralla, C. and Schumann, A. H.: Incorporating structural uncertainty of hydrological models in likelihood functions via an ensemble range approach, Hydrol. Sci. J., 61, 1679–1690, https://doi.org/10.1080/02626667.2016.1164314, 2016.
Wandishin, M. S. and Brooks, H. E.: On the relationship between Clayton's skill score and expected value for forecasts of binary events, Meteorol. Appl., 9, 455–459, https://doi.org/10.1017/S1350482702004085, 2002.
Wang, Q. J. and Robertson, D. E.: Multisite probabilistic forecasting of seasonal flows for streams with zero value occurrences, Water Resour. Res., 47, https://doi.org/10.1029/2010WR009333, 2011.
Wang, Q. J., Robertson, D. E., and Chiew, F. H. S.: A Bayesian joint probability modeling approach for seasonal forecasting of streamflows at multiple sites, Water Resour. Res., 45, W05407, https://doi.org/10.1029/2008WR007355, 2009.
Wang, Q. J., Shrestha, D. L., Robertson, D. E., and Pokhrel, P.: A log-sinh transformation for data normalization and variance stabilization, Water Resour. Res., 48, W05514, https://doi.org/10.1029/2011WR010973, 2012.
Wilks, D. S.: Statistical methods in the atmospheric sciences, Amsterdam, Academic Press, 2011.
Wood, A. W. and Schaake, J. C.: Correcting Errors in Streamflow Forecast Ensemble Mean and Spread, J. Hydrometeorol., 9, 132–148, https://doi.org/10.1175/2007JHM862.1, 2008.
Ye, W., Bates, B. C., Viney, N. R., Sivapalan, M., and Jakeman, A. J.: Performance of conceptual rainfall-runoff models in low-yielding ephemeral catchments, Water Resour. Res., 33, 153–166, https://doi.org/10.1029/96WR02840, 1997.
Yin, Y., Alves, O., Oke, P. R., Yin, Y., Alves, O., and Oke, P. R.: An ensemble ocean data assimilation system for seasonal prediction, Mon. Weather Rev., 139, 786–808, https://doi.org/10.1175/2010MWR3419.1, 2011.
Zhang, Q., Xu, C.-Y., and Zhang, Z.: Observed changes of drought/wetness episodes in the Pearl River basin, China, using the standardized precipitation index and aridity index, Theor. Appl. Climatol., 98, 89–99, https://doi.org/10.1007/s00704-008-0095-4, 2009.
Zhao, T., Schepen, A., and Wang, Q. J.: Ensemble forecasting of sub-seasonal to seasonal streamflow by a Bayesian joint probability modelling approach, J. Hydrol., 541, 839–849, https://doi.org/10.1016/j.jhydrol.2016.07.040, 2016.