the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Spatio-temporal assessment of annual water balance models for upper Ganga Basin
Anoop Kumar Shukla
Lalit Pal
Chandra Shekhar Prasad Ojha
Ana Mijic
Rahul Dev Garg
The upper Ganga Basin in Uttarakhand, India, has high hydropower potential and plays an important role in the development of the state economy. Thus, an accurate knowledge of annual water yield is of paramount importance to this region. This paper deals with use of contemporary water yield estimation models such as the distributed Integrated Valuation of Ecosystem Services and Tradeoffs (InVEST) model and the Lumped Zhang model and their validation to identify the most suited one for water yield estimation in the upper Ganga Basin. In previous studies utilizing these models, water yield was estimated by considering a single value of some important model parameters for the entire basin, which in fact show distributed variation at a finer (pixel) scale. Therefore, in this study, pixel-level computations are performed to assess and ascertain the need for incorporating the spatial variation of such parameters in model applications. To validate the findings, the observed sub-basin discharge data are analyzed with the computed water yield for 4 decades, i.e., 1980, 1990, 2001 and 2015. The results obtained are in good agreement with the water yield obtained at the pixel scale.
- Article
(3381 KB) - Full-text XML
- BibTeX
- EndNote
An accurate assessment of key ecosystem services (ES) such as water yield has gained focus in recent years in ES modeling, as fresh-water availability in a region is essential for agriculture, industry, human consumption, hydropower, etc. (Redhead et al., 2016). Hydrological ecosystem services generally include drinking water supply, power production, industrial use, irrigation and many more. The accurate estimation of water yield further facilitates in the identification of hotspots for storm-water harvesting in order to fulfill fresh-water demand in the region (Pathak et al., 2017). The hydrological ES are dependent on different factors, such as watershed characteristics (e.g., topography, land use and land cover – LULC, soil type and climatic condition. To incorporate these parameters into assessment and decision-making, there has been a proliferation of ecosystem-modeling tools and methods. Models for ES evaluation often focus on using globally available data, accepting large number of spatially explicit inputs producing spatially explicit output, and limiting the model structure to key biophysical processes involved in land use change (Guswa et al., 2014). The precise estimation of ES using these models is a complicated task owing to spatial variability and dependence of ES on various topographical and climatic factors. Further, the validation and uncertainty assessments in model outputs have proven to be key obstacles to the application of ES models. In the literature, studies focusing on comparison of different ES models have projected some light over the model output validation issues; however, a lack of studies highlighting the validation of these models for Indian river basins still exists. The benefits that can be derived from ES should be analyzed and quantified in a spatially explicit manner (Sánchez-Canales et al., 2012). The uncertainties involved in the determination of spatial and temporal distribution of the climatic variables, especially precipitation, constitute a major obstacle to the understanding of hydrological behavior at the catchment scales (Milly and Dunne, 2002).
The Integrated Valuation of ES and Tradeoffs (InVEST) model, developed by Natural Capital Project (Tallis et al., 2010), is a tool that provides a framework for planners and decision makers to assess trade-offs among ES and enables their comparison in various climate and land use change scenarios. The model includes a biophysical component, which facilitates the provision of fresh water or water yield from different parts of the landscape, and a valuation component, representing the benefits of water provisioning to people. The model works on simplified Budyko theory, which has a long history and still continues to receive attention in the hydrological literature (Budyko and Ronov, 1979; Zhang et al., 2001; Zhang et al., 2004; Ojha et al., 2008; Zhou et al., 2012; Donohue et al., 2012; Xu et al., 2013; Wang and Tang, 2014). The InVEST model applies a one-parameter formulation of the Budyko theory in a semi-distributed manner (Zhang et al., 2004). The model is capable of quantifying the water yield of a catchment under the influence of change in different drivers, viz. climate variables and catchment characteristics (e.g., land use change). Various studies have been carried out in the past demonstrating the application of the InVEST model to different river basins around the world. Sánchez-Canales et al. (2012) carried out a sensitivity analysis of three parameters, i.e., z (seasonal precipitation coefficient), precipitation (annual) and ET0 (annual reference evapotranspiration), and using the InVEST model for a Mediterranean basin, they found precipitation to be the most sensitive parameter for the study region. Later, Terrado et al. (2014) applied the InVEST model for the heavily inhabited defined as Llobregat river basin. The model is applied for both extreme wet and dry conditions, and the role of climatic parameters is emphasized. Hoyer and Chang (2014) applied this model in the Tualatin and Yamhill basins of northwestern Oregon under a series of urbanization and climate-change scenarios. The results show that the climatic parameters have more sensitivity than other inputs for a water yield model. Hamel and Guswa (2015) applied the same water yield model for the Cape Fear catchment, North Carolina, and concluded that the precipitation is the most influencing parameter. Goyal and Khan (2017) employed the InVEST water yield model for the hilly catchment by considering two catchments, i.e., the Sutlej River catchment and Tungabhadra River catchment. The climate parameters, i.e., precipitation and ET0, are observed to be the most influencing parameters for water yield in both the river basins. With the aforementioned studies, certain factors exist that limit the application of InVEST model such as the absence or inadequate comparison with observed data, the calibration of the model without prior identification of sensitive parameters and a lack of validation of the predictive capabilities in the context of land use and land cover change (Bai et al., 2012; Nelson et al., 2010; Su and Fu, 2013; Terrado et al., 2014).
The InVEST model operates on the principle of the Budyko theory (Budyko, 1958, 1974). Based on works of Schreiber (1904) and Ol'Dekop (1911), Budyko proposed formulations explaining the relationship between precipitation and potential evapotranspiration (PET) in order to couple water and energy balances, defined as the Budyko hypothesis. Several attempts have later been made to obtain an analytical solution of the Budyko hypothesis (Schreiber, 1904; Ol'Dekop, 1911; Turc, 1954; Mezentsev, 1955; Pike, 1964; Fu, 1981; Choudhury, 1999; Zhang et al., 2001, 2004; Porporato et al., 2004; Yang et al., 2008; Donohue et al., 2012; Wang and Tang, 2014; G. Zhou et al., 2015; S. Zhou et al., 2015). Among these studies, solutions provided by Fu (1981) called Fu's equation, gained significant attention as the work represented the effect of catchment properties on water balance components by incorporating an addition parameter “w”. Fu's equation can provide a full picture of the evaporation mechanism at the annual timescale. Therefore, Fu's equation can be used through a top-down analysis for providing insight into the dynamic interactions among climate, soils, vegetation, and their controls on the annual water balance at the regional scale (Yang et al., 2007).
Considering the lack of studies on analysis and validation of ES on the Indian subcontinent, especially for Himalayan catchments, and to assess the applicability of various water-balance models to Himalayan catchments, the present work attempts to compute and analyze water yield in the upper Ganga Basin using a semi-distributed InVEST model and a Lumped Zhang model. The work primarily considers, in detail, the spatial variation of InVEST model parameters and uses different strategies to compute water yield. Accordingly, water yield is estimated for 4 years, i.e., 1980, 1990, 2001 and 2015 and the most appropriate strategy is identified. The parameters that are adopted as lumped at the basin scale in previous studies are estimated at the pixel scale in order to avoid the dependence of the model parameters on size of the catchment. In addition, pixel-level estimations of water yield are expected to be more accurate than output obtained using the conventional approach with basin-lumped output. The term “finer scale” in the paper represents the incorporation of spatial variations through the pixel-level estimation of parameters involved in InVEST model, which are otherwise taken as lumped. The work also compares the outcomes of spatially distributed water yield models and the conventionally used Lumped Zhang model.
2.1 Water yield models
In this section, two water yield models, i.e., the InVEST water yield model, which is a distributed model, and the Lumped Zhang model, are described.
2.1.1 InVEST model
The InVEST water yield model (Tallis et al., 2010) is designed to provide information regarding the changes in the ecosystem that are likely to alter the flow. It is based on the Budyko theory, which is an empirical function that yields the ratio of actual to potential evapotranspiration (PET) (Budyko, 1979). To describe the degree to which long-term catchment water balance deviates from the theoretical limits, a number of scholars have proposed one-parameter functions that can replicate the Budyko curve (Fu, 1981; Choudhury, 1999; Zhang et al., 2004; Wang and Tang, 2014). To observe and represent pixel-level changes to the landscape, InVEST model incorporates, explicitly, the spatial variability in precipitation, PET, soil depth and vegetation. The model operates at the grid scale and acquires the inputs in the raster format into a GIS environment such as ArcGIS.
The InVEST water yield model is based on an empirical function known as the Budyko curve (Budyko, 1974). Annual water yield, Y(x), is determined at each pixel of a landscape as follows;
where AET(x) is the actual annual evapotranspiration per pixel x and P(x) is the annual precipitation per pixel x. Actual evapotranspiration (AET) is essentially determined by climatic factors (precipitation, temperature, etc.) and is mediated by catchment characteristics (vegetation cover, soil characteristics, topography, etc.). On the other hand, potential evapotranspiration (PET) represents the evaporating potential of the climate system at a specific location and time of year without the consideration of catchment characteristics and soil properties (Allen et al., 1998). Several attempts have been made in the past to establish a relationship between AET and PET, among which the solution provided by Fu (1981) has been adopted worldwide. Fu (1981) provided an analytical solution to the Budyko hypothesis and related AET with PET by incorporating a dimensionless parameter “w”, which denotes the effect of catchment characteristics.
The InVEST model uses the expression of the Budyko curve proposed by Fu (1981) and Zhang et al. (2004). The ratio of mean annual PET to annual precipitation, known as index of dryness, is expressed as
where PET(x) is the annual potential evapotranspiration per pixel x (mm), and w(x) is a non-physical parameter that influences the natural soil properties. The PET(x) is calculated using the following expression;
where ET0(x) is the annual reference evapotranspiration per pixel x, which is computed based on evapotranspiration from alfalfa grass grown at that location using Eq. (6). Kc(x) is the vegetation evapotranspiration coefficient that is influenced by the change in characteristics of land use and land cover at every pixel (Allen et al., 1998). The values of ET0(x) are adjusted by Kc(x) for each pixel over the map of land use and land cover. w(x) is an empirical parameter, and the expression given by Donohue et al. (2012) for the InVEST model has been applied to define w(x), which is expressed as follows:
Thus, the minimum value of the parameter w(x) is 1.25, corresponding to bare soil where the root depth is zero (Donohue et al., 2012). The Donohue model was originally developed for Australia, however, the online documentation on InVEST model states its application globally. The parameter z is known as the seasonality factor whose value varies from 1 to 30. It represents the nature of local precipitation and other hydrogeological parameters. The parameter AWC(x) depicts volumetric plant available water content expressed in depth (mm), which can be expressed by following formula for each pixel x:
The root-restricting layer depth is defined as the depth of the soil up to which the soil can allow the penetration of the roots, and root depth is defined as the depth where 95 % of the root biomass occurs. Plant available water content (PAWC) is generally taken as the difference between the field capacity and the wilting point. It depends upon the soil properties and can be computed by the Soil-Plant-Air-Water (SPAW) software. In the study, PAWC is calculated using the method described by McKenzie et al. (2003). The modified Hargreaves method and Hargreaves method were employed for computing reference evapotranspiration for the study area at pixel scale.
The modified Hargreaves method is expressed as
where ET0 is reference evapotranspiration, Tavg is the average daily temperature (∘C) defined as the average of mean daily maximum and mean daily minimum temperature, TD (∘C) is the temperature range computed as the difference between mean daily maximum and mean daily minimum temperature, and RA is extraterrestrial radiation (MJ m−2 day−1).
According to the Hargreaves method,
where terms involved in the equation means same as those in the modified Hargreaves method.
For computing the extraterrestrial radiation (RA), the following equation is used;
where RA is extraterrestrial radiation (MJ m−2 day−1), dr is the inverse Earth–Sun relative distance, Gsc is the solar constant equal to 0.0820 MJ m−2 min−1, ws is sunset hour angle (rad), δ is the solar declination (rad) and φ is latitude (rad).
Determination of the parameter “w”
The dimensionless parameter w depends upon the local climatic variables such as the hydrological characteristics of the area, its rainfall intensity and topography. In the InVEST water yield model (Tallis et al., 2010), parameter w can be computed in three different ways. The first method is suggested by Donohue et al. (2012), in which parameter w is computed using Eq. (4) and where sensitivity parameter z is adopted as one fifth of the number of rain events per year. The second method is suggested by Xu et al. (2013), which compares w with latitude, the NDVI (normalized difference vegetation index), area, etc. The third method experiments with various selections of w (one value of w for the entire study region) until there is a good match between observed and computed water yield. Unfortunately, this method is not suited for a pixel-based analysis, as the number of pixels will be extremely large, making the method computationally intensive.
2.1.2 Lumped Zhang model
In this model, the mean value of different parameters is used as an input to compute the average value of the water yield for the whole watershed. The average actual evapotranspiration, potential evapotranspiration, w, precipitation, etc., are described by Zhang et al. (2004).
3.1 Study area
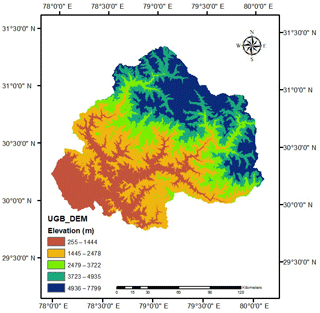
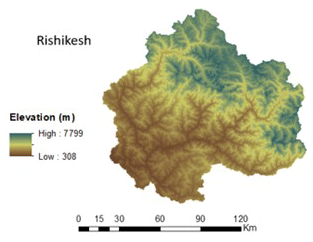
The Ganga river in India is ranked amongst the world's top 20 rivers in regards to the water discharge. The Ganga river is segregated into three zones, viz. the upper Ganga Basin, middle Ganga Basin and lower Ganga Basin. The area chosen for the present study, i.e., the upper Ganga Basin, is situated in the northern part of India within the geographical coordinates 29∘48′–31∘24′ N and 77∘49′–80∘22′ E, covering an area of 22 292.1 km2 and reaching up to Haridwar. The altitude of the study area varies from 275 m in the plains to 7512 m in the Himalayan terrains. A region of approximately 433 km2 of the basin is located under glacier landscape, and 288 km2 of the region is located under a fluvial landscape. About 60 % of the basin is utilized for agricultural practices, and 20 % of the basin is in the forest area, especially in the upper mountainous region. Nearly 2 % of the basin is permanently covered with snow in the mountain peaks. The most predominant soil groups found in the region are sand, clay, loam and their compositions. In the upper Ganga Basin, the average annual rainfall varies from 550 to 2500 mm (Bharati et al., 2011), where a major fraction of total annual rainfall is received during monsoon months (June–September). The geographical location and other information of the upper Ganga Basin are represented in Fig. 1.
3.2 Data
3.2.1 Precipitation and temperature
The daily time series of precipitation and temperature for the study area are acquired from India Meteorological Department (IMD) at a grid size of 0.25∘ and 1∘, respectively. The upper Ganga Basin comes within the dataset latitude, which ranges from 29.5∘ N to 31.5∘ N, and its longitude, ranging from 77.75 to 80.25∘ E . The daily time series of precipitation was aggregated to obtain the annual time series at each grid point. Various analyses in the study are carried out for 4 years, i.e., 1980, 1990, 2001 and 2015.
3.2.2 Soil map
Spatial maps of soil were collected from the National Bureau of Soil Survey and Land Use Planning (NBSSLUP) at 1:250 000. Digital maps of soil available at a resolution of 1200 m × 1200 m were resampled to the resolution of land use data, i.e., 30 m × 30 m, using “resample” tool in ArcGIS in order to maintain the scale homogeneity. The attribute table of the raster layer contains fields like soil depth, soil texture, carbon content percentage, drainage, slope, erosion, soil temperature and mineralogy. The relevant features, i.e., soil depth and soil texture are converted into the raster image for the upper Ganga Basin.
3.2.3 Map of land use and land cover
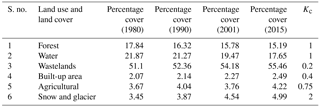
Satellite images were acquired from different sensors of Landsat, viz. Landsat 3/4 Multispectral Scanner and Thematic Mapper (MSS/TM), Landsat 4 Thematic Mapper (TM), Landsat 7 Enhanced Thematic Mapper (ETM) and Landsat 8 Operational Land Imager (OLI) sensors for the years 1980, 1990, 2001 and 2015, respectively. The images are available at different resolutions and in several wavelength bands, from which green (G), red (R) and near-infrared (NIR) band images are combined to create a false color composite (FCC) for the study area in ERDAS Imagine. FCCs are then classified using supervised classification in ERDAS in six different classes, i.e., forest, water, agricultural, wasteland, snow and glacier, and built-up land. The classification of the area is based on their similar response under different bands. Each class is then recognized with the help of ground-truth and high-resolution satellite images.
In the present work, five different strategies are employed to compute water yield. For the ease of presentation, these strategies are referred to as A–E. In strategy A, an average value of precipitation, temperature, extraterrestrial radiation and parameter w is used for the entire basin. This strategy is essentially based on Lumped Zhang model. Strategies B–E are designated, corresponding to a particular variation of the InVEST model where water yield is computed using different approach for estimating parameter w. For computing parameter w, relationships for large basins and for the global model from Xu et al. (2013) are given by Eqs. (9) and (10), respectively.
For large basins,
For the global model,
where, “slp” is the slope gradient, “lat” is the absolute latitude of basin center, “CTI” is the compound topographic index, “NDVI” is the normalized difference vegetation index, “lat” is latitude, “long” is longitude and “elev” is elevation.
In strategy B, the entire basin is considered for computing the parameter w for large basins, using Eq. (9), which is given by Xu et al. (2013). In strategy C, the parameter w is computed for entire basin using Eq. (10), which is given by Xu et al. (2013). In strategy D, parameter w is computed at each pixel in order to incorporate the spatial distribution of the hydrologic variables involved in the computations. In Strategy E, parameter z is computed according to the number of rain events in a year; subsequently, Eq. (4) is used to compute the parameter w.
For all the strategies, the extraterrestrial radiation (RA) parameter is computed for each month using Eq. (8), and a raster layer is generated. Precipitation data are obtained from Indian Meteorological Department (IMD) at a grid size of 0.25∘ for the study area. It has been interpreted and converted to the raster format by using the inverse distance weighted (IDW) interpolation technique in the ArcGIS environment for obtaining the values for all pixels at a resolution equal to the resolution of the Landsat satellite images. The temperature dataset is obtained from the IMD at a grid size of 1∘ × 1∘ for the study area and has also been converted to a raster format by using the IDW interpolation technique for obtaining the values for all pixels. Subsequently, the mean monthly value of average temperature (Tavg) and the difference between the mean daily maximum and mean daily minimum (TD) are obtained. The climate datasets used in the present study are of the finest resolution available so far for the study region. Gridded datasets of temperature and precipitation used in the present study have been developed using quality-controlled stations and well-proven interpolation techniques. Further details about the datasets of precipitation and temperature are given in Srivastava et al. (2009) and Pai et al. (2014), respectively.
The modified Hargreaves method is applied for obtaining the value of reference evapotranspiration at each pixel for each month (Droogers et al., 2002). To compute potential evapotranspiration, the yearly values obtained for the reference evapotranspiration are multiplied by the vegetation evapotranspiration coefficient (Kc), which depends on the LULC characteristics, as expressed in Eq. (3). The value of Kc is taken from Allen et al. (1998), as shown in Table 1. In this study, Kc is taken in the same was for all 4 years, as shown in Table 1, and is used to obtain potential evapotranspiration, which is subsequently used to obtain annual water yield at each pixel of the study area.
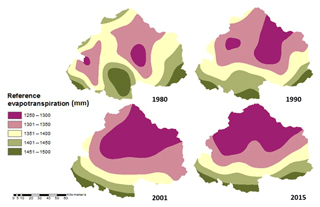
5.1 Reference evapotranspiration, ET0(x)
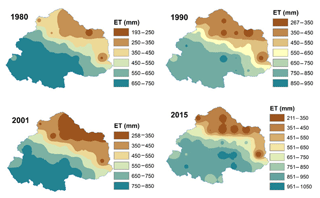
Reference Evapotranspiration (ET0) is computed for the upper Ganga Basin using a high-resolution monthly climate dataset. The modified Hargreaves method is applied for obtaining the values of reference evapotranspiration at each pixel for each month (Droogers and Allen, 2002). ET0 is a function of RA, precipitation, Tavg and TD, which are computed pixel-wise for each month of the years 1980, 1990, 2001 and 2015. Some of the months, i.e., July, July and August 1990; June, July and August 2001; and June, July and August 2015, showed negative values of reference evapotranspiration from applying the modified Hargreaves method. For these months, Hargreaves method is applied for obtaining the positive values. Subsequently, all mean monthly values are added up to get the mean annual values of evapotranspiration for the years 1980, 1990, 2001 and 2015, as represented in Fig. 2.
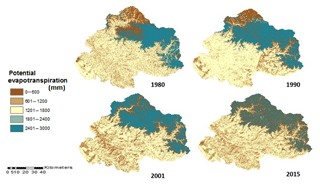
5.2 Potential evapotranspiration, PET(x)
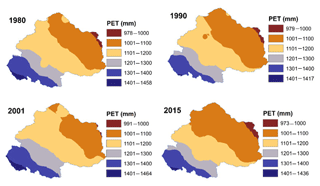
The annual values obtained for the ET0 are multiplied by the vegetation evapotranspiration coefficient (Kc), which varies with the characteristics of land use and land cover, as expressed in Eq. (3). The value of the Kc is taken from Allen et al. (1998). The values of the vegetation evapotranspiration coefficient are taken from Table 1. Thus, the potential evapotranspiration is computed for upper Ganga Basin for the years 1980, 1990, 2001 and 2015, as represented in Fig. 3.
5.3 Water yield, Y(x)
As described in the methodology, five different strategies, viz. A–E, are used to estimate water yield for the upper Ganga Basin.
Strategy A: water yield computed using the Lumped Zhang model
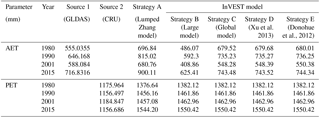
Here, the basin average values of all the input parameters are considered, and water yield is computed for the upper Ganga Basin for the years 1980, 1990, 2001 and 2015, which are obtained as 658.52, 925.68, 603.71 and 1194.25 mm, respectively.
Strategy B: water yield obtained by taking the single weighted mean value of parameter “w” from Xu et al. (2013) for large basins
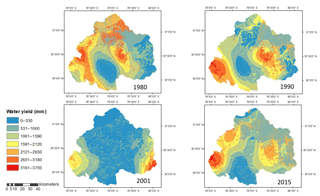
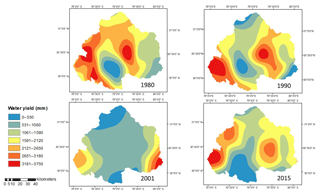
In this strategy, water yield is computed by considering a single value of the parameter w for the whole basin using Eq. (9). The weighted mean value for parameter w for the years 1980, 1990, 2001 and 2015 are obtained as 1.507, 1.541, 1.403 and 1.507, respectively. The spatial distribution of the water yield for the upper Ganga Basin computed using strategy B is represented in Fig. 4. The mean values of water yield as obtained using this method for the years 1980, 1990, 2001 and 2015 are 755.65, 959.48, 742.39 and 1131.42 mm, respectively.
Strategy C: water yield obtained by taking a single weighted mean value of parameter “w” from Xu et al. (2013) for the global model
In this strategy, water yield is computed by considering a single value of parameter w for the entire upper Ganga Basin using Eq. (10). The weighted mean value of parameter w for the years 1980, 1990, 2001 and 2015 are obtained as −0.967, −0.955, −1.010 and −0.968, respectively. The spatial distribution of the water yield for the upper Ganga Basin as computed using strategy C is shown in Fig. 5. The mean values of water yield for the years 1980, 1990, 2001 and 2015 are 1239.92, 1549.46, 1149.93 and 1754.59 mm, respectively.
Strategy D: water yield obtained using the pixel-level estimation of parameter “w” from Xu et al. (2013)
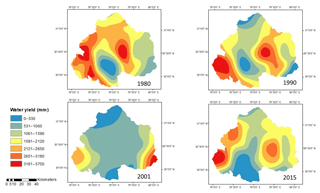
In this strategy, the values of parameter w are estimated at the pixel level. The water yield computed for the years 1980, 1990, 2001 and 2015 for upper Ganga Basin is shown in Fig. 6. The mean values of water yield as computed using strategy D for the years 1980, 1990, 2001 and 2015 are 1240.02, 1549.44, 1149.89 and 1754.62 mm, respectively.
Strategy E: water yield obtained using the pixel-level estimation of parameter “w” from Donohue et al. (2012)
Equation (4) represents the parameter w as a function of parameter “z”, AWC and precipitation. The parameter w in the equation used in strategy E has been proposed by Donohue et al. (2012), which is also cited in online documentation of InVEST model; however, the final equation used for estimating water yield is obtained from the InVEST model. Considering this fact, Donohue et al. (2012) has been cited in strategy E. The water yield as computed using strategy E for the upper Ganga Basin for different years is shown in Fig. 7. The mean values of water yield for the years 1980, 1990, 2001 and 2015 are 1241.09, 1552.38, 1153.95 and 1753.53 mm, respectively.
5.4 Validation of ET and water yield estimates
For validation of model outputs, the basin's average annual values of PET and AET estimated using various strategies are compared with the corresponding basin average values obtained from available global datasets (Table 2). Model-simulated AET values are obtained from the Global Land Data Assimilation System (GLDAS) ET dataset from Noah model outputs. Basin average values of PET are obtained from the Climate Research Unit's (CRU's) PET datasets (CRU TS v. 4.01) available at resolution of 0.5∘. From the comparison, both AET (GLDAS) and PET (CRU TS) values are found to be in fair agreement with the globally estimated values (Table 2). Spatial maps of global datasets of AET and PET are shown in Figs. 8 and 9, respectively.
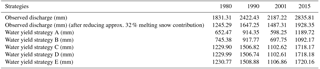
The validation of water yield obtained from various strategies is performed at the Rishikesh gauging site of the upper Ganga Basin (Fig. 10). The discharge data of the basin are obtained from Irrigation Department of the state of Uttarakhand. The discharge observed in the basin is generated from precipitation as well as snowfall in the region, where 32 % of the discharge has been removed, because it is contributed to by glacier ice melt, as explained by Maurya et al. (2011) for our study area. The aforementioned fraction of discharge had been quantified using an isotope study that separates the contribution of glacier melt in quantifying discharge (Maurya et al., 2011). A comparison of the water yield computed and observed for the study region for different years by various proposed strategies is shown in Table 3.
As can be seen in Table 3, values of water yield estimated using strategies A to E are systematically increasing but are not steady in nature, as water yield estimated using strategy A and B lies in the range 650–750 mm, whereas water yield from strategies C–E lie in range of 1229–1231 mm for the years 1980 (see Table 3). Similar results are also evident for other years, too. Also, water yield estimated using strategies C–E are more or less the same for a given year, because these strategies involve pixel-based estimations of water yield considering spatial variation in the Budyko parameters. The parameters involved in the Budyko model, such as w, are dependent on various factors, such as catchment characteristics, vegetation cover, etc., as well as climate seasonality (Li et al., 2013). Ahn and Merwade (2017) have analyzed the relationship between basin characteristics and parameter w for 175 stations spread across the USA. Considering their study, no precise conclusion can be drawn regarding relationship between basin characteristics and the value of parameter w, especially in the case of basin-area characteristics. Moreover, no definite relationship has been yet identified between basin characteristics and model parameters, and this is a subject matter for further study.
The study aimed to apply the InVEST water yield model to compute the water yield for upper Ganga Basin having highly variable topography consisting of hilly, plain and snow-covered areas. The InVEST model is based on the Budyko theory, which requires low amounts of data and low levels of expertise, thus making it acceptable worldwide. The mean monthly precipitation, temperature, monthly value of difference of the mean daily maximum and mean daily minimum, and extraterrestrial radiation parameters for the upper Ganga Basin of all 4 years, i.e., 1980, 1990, 2001 and 2015, are converted into the raster format for various analyses. The monthly reference evapotranspiration is thus computed using input parameters in GIS environment by applying the modified Hargreaves equation for all the months, except for a few months in which the modified Hargreaves equation gives negative results for the reference evapotranspiration. For those months, the Hargreaves method is applied to obtain the positive value of reference evapotranspiration, as also suggested by Goyal and Khan (2017). Reference evapotranspiration when multiplied with Kc gives the potential evapotranspiration. All monthly values are added up to obtain the annual value of reference evapotranspiration. Kc is a function of land use and land cover; thus, supervised classification is done to prepare the raster map of land use and land cover for the upper Ganga Basin. Subsequently, the annual value of potential evapotranspiration is obtained for the study area for the years 1980, 1990, 2001 and 2015.
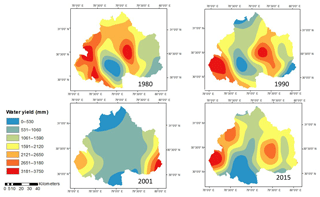
Figure 7Water yield obtained by computing pixel-wise value of parameter “w” from Donohue et al. (2012).
The paper employs various methodologies for water yield estimation, as discussed in the methodology section for the upper Ganga Basin. Thus, water yield is computed both from the InVEST model as well as the Lumped Zhang model. The value of the parameter w is computed using four different approaches, i.e., the mean single value obtained from Xu et al. (2013) for large basins, mean single value obtained from Xu et al. (2013) for the global model, pixel-level estimated value of parameter w from Xu et al. (2013) and pixel-wise value of parameter w from Donohue et al. (2012). Although the upper Ganga Basin lies in large basin category as per the definition from Xu et al. (2013), the yield computed using global model is in good agreement with the observed data for the region. In the study, the pixel-level estimation of parameter w is made in order to incorporate the spatial variability of the parameter involved in water yield estimation. Thus, two pixel-wise values of parameter w are computed for the upper Ganga Basin for years 1980, 1990, 2001 and 2015 by considering two approaches given by Xu et al. (2013) and the approach given by Donohue et al. (2012). Also, the basin-lumped water yield is computed using Lumped Zhang model, which considers the single mean values for entire basin of all the parameters involved in the computation of water yield. The water yield is computed in five different ways for the upper Ganga Basin for the years 1980, 1990, 2001 and 2015.
At the Rishikesh gauging site, surface runoff data are obtained by extracting the snowmelt from the discharge data, as the melting snow contributes about 32 % of total runoff in the Himalayan basins (Maurya et al., 2011). For validating the water yield obtained from different strategies, the observed yield is compared with the computed water yield based on different proposed strategies for the years 1980, 1990, 2001 and 2015, as represented in Table 3. The results obtained from Donohue et al. (2012) and Xu et al. (2013) are computed at pixel level (Strategy C–E); thus, they exhibit better performance than other approaches and are in good agreement with the observed data. These results exhibit the superiority of pixel-level computation to hydrological analyses for a watershed. The parameters involved in the Budyko model are dependent on various factors, such as basin characteristics (size, topography, stream length, slope, etc.), climate seasonality, etc. (Li et al., 2013). Again, the factors affecting model parameters vary both spatially and temporally. Moreover, the relationship between these factors and model parameters are not yet well defined (Ahn and Merwade, 2017). In such scenarios, adopting a hypothesis by assuming either of these controlling factors (such as “w”) to be spatially or temporally constant is inappropriate. Considering these facts, the present study attempts to incorporate the spatial variability of model parameter for estimation of water yield at the pixel level. As the computations are made at pixel level (on a grid of size 30 m × 30 m), the assumption of dependence of model parameters on the size of the catchment may also be disregarded. The computations made in the present work are based on empirical equations; however, the application of these equations has been well documented worldwide for estimations of various water balance components at various basin scales (Zhang et al., 2008; Ma et al., 2008; Ning et al., 2017; Rouholahnejad Freund and Kirchner, 2017; Wang and Zhou, 2016). Hence, it is recommended that for such a large basin, it is required to compute all the parameters involved in the computations of water yield at the pixel scale rather than adopting mean values for entire watershed.
The present study aimed to apply the InVEST annual water yield model, a tool that is gaining interest in the ecosystem services community, in the upper Ganga Basin. While such simple models have low requirements for data and level of expertise, practical applications of such a model with single representative values of the model parameter for the entire basin do not provide accurate estimates of water yield. Performing pixel scale computation of water yield in the study indicates a better performance, and the results obtained show better agreement with the observed water yield. As far as parameter w is concerned, the global model works better than other representations of parameter w available in literature, especially in the upper Ganga Basin. In the study, the water yield is computed using five different strategies, and results are validated with the observed data at the outlet of the upper Ganga Basin. The present study attempts to quantify annual water yield at the pixel level, making the computations independent of the size of catchment. Therefore, the proposed methodology is expected to perform well for a catchment of any given size. Changes in catchment water storage over time are required to be quantified in order to validate the applicability of Budyko's model to long-term data for the studied catchment. Earlier, some of the important parameters defining water yield used to be computed at a basin-level scale, which caused errors in the results.
The study attempts to incorporate the spatial variability of parameters involved in the model through the pixel-level estimation of parameters that are otherwise taken as lumped in the previous studies. Study results show that the estimated water yield, considering spatial variability in model parameters, is in better agreement with the observed water yield compared to the water yield estimated when considering the parameters to be lumped over the study region. Further, the computations of various parameters are made at the pixel level; therefore, the estimates of water balance components using this approach are expected to be independent of the assumption of dependence of parameters on catchment size. As the relationship between Budyko's model parameters and their controlling factors has not been well defined (Ahn and Merwade, 2017), the study emphasizes water yield estimation using pixel-based computations. The study outcomes can be summarized as follows: (i) between two approaches used in the study, i.e., considering the entire basin and pixel-level approach, the pixel-level approach is found to provide better results; and (ii) in pixel-based computations, results are further improved with the use of a parameter w based on a global model rather than regional models of parameter w, especially for large basins in the Himalayan region.
The meteorological data products are provided by the Indian Meteorological Department on the basis of payment. It can be purchased from the following URL: http://www.imdpune.gov.in/ndc_new/Request.html (India Meteorological Department, 2018). The hydrological data in upper Ganga basin is provided by the Uttarakhand Irrigation Department, which is available for research purposes only. Satellite datasets are acquired from the USGS web portal (https://earthexplorer.usgs.gov/, Earth Explorer – USGS, 2018). The soil maps are provided by the National Bureau of Soil Survey and Land Use Planning, India on the basis of payment from the following URL: https://www.nbsslup.in/publications.html (ICAR, 2018).
AKP assisted with data collection, data processing and data analysis; SP with data analysis and writing, the analysis of results, and the review, revision and proofreading of the paper; LP with data analysis and writing, the analysis of results, and the review, revision and proofreading the paper; CSPO with the analysis of results and the review, revision, and supervision of the whole work and proofread the paper; AM supervised the whole work; and RDG assisted with the review, revision and supervision of the whole work.
The authors declare that they have no conflict of interest.
This article is part of the special issue “The changing water cycle of the Indo–Gangetic Plain”. It does not belong to a conference.
Authors are thankful to the executive engineer of the Irrigation Department of Uttarakhand
for providing the discharge data for the Rishikesh sub-basin of upper Ganga Basin.
Edited by: Pradeep P. Mujumdar
Reviewed by: two anonymous referees
Ahn, K. H. and Merwade, V.: The Integrated Impact of Basin Characteristics on Changes in Hydrological Variables, in: chap. 12 in “Sustainable Water Resources Management”, American Society of Civil Engineers (ASCE), Virginia, USA, 317–336, 2017.
Allen, R. G., Pereira, L. S., Raes, D., and Smith, M.: Crop evapotranspiration – Guidelines for computing crop water requirements, FAO Irrigation and drainage paper 56, FAO, Rome, 300, D05109, 1998.
Bai, Y., Ouyang, Y., and Pang, J. S.: Biofuel supply chain design under competitive agricultural land use and feedstock market equilibrium, Energy Econ., 34, 1623–1633, 2012.
Bharati, L., Lacombe, G., Gurung, P., Jayakody, P., Hoanh, C. T., and Smakhtin, V.: The impacts of water infrastructure and climate change on the hydrology of the Upper Ganges River Basin, in: Vol. 142, IWMI, Colombo, Sri Lanka, 2011.
Budyko, M. I.: The Heat Balance of the Earth, Leningrad, 1956, Translation by N. A. Stepanova, US Weather Bureau, Washington, 1–254, 1958.
Budyko, M. I.: Climate and Life, Academic Press, New York, USA, 1–507, 1974.
Budyko, M. I. and Ronov, A. B.: Evolution of chemical composition of the atmosphere during the Phanerozoic, Geokhimiya, 5, 643–653, 1979.
Choudhury, B.: Evaluation of an empirical equation for annual evaporation using field observations and results from a biophysical model, J. Hydrol., 216, 99–110, 1999.
Donohue, R. J., Roderick, M. L., and McVicar, T. R.: Roots, storms and soil pores: Incorporating key ecohydrological processes into Budyko's hydrological model, J. Hydrol., 436, 35–50, 2012.
Droogers, P. and Allen, R. G.: Estimating reference evapotranspiration under inaccurate data conditions, Irrig. Drain. Syst., 16, 33–45, 2002.
Earth Explorer – USGS: available at: https://earthexplorer.usgs.gov/, last access: 15 September 2018.
Fu, B. P.: On the calculation of the evaporation from land surface, Sci. Atmos. Sin., 5, 23–31, 1981.
Goyal, M. K. and Khan, M.: Assessment of spatially explicit annual water-balance model for Sutlej River Basin in eastern Himalayas and Tungabhadra River Basin in peninsular India, Hydrol. Res., 48, 542–558, 2017.
Guswa, A. J., Brauman, K. A., Brown, C., Hamel, P., Keeler, B. L., and Sayre, S. S.: Ecosystem services: Challenges and opportunities for hydrologic modeling to support decision making, Water Resour. Res., 50, 4535–4544, 2014.
Hamel, P. and Guswa, A. J.: Uncertainty analysis of a spatially explicit annual water-balance model: case study of the Cape Fear basin, North Carolina, Hydrol. Earth Syst. Sci., 19, 839–853, https://doi.org/10.5194/hess-19-839-2015, 2015.
Hoyer, R. and Chang, H.: Assessment of freshwater ecosystem services in the Tualatin and Yamhill basins under climate change and urbanization, Appl. Geogr., 53, 402–416, 2014.
India Meteorological Department: available at: http://www.imdpune.gov.in/ndc_new/Request.html, last access: 10 October 2018.
ICAR: ICAR-NBSS&LUP Publications 2012–17, available at: https://www.nbsslup.in/publications.html, last access: October 2018.
Khatami, S. and Khazaei, B.: Benefits of GIS Application in Hydrological Modeling: A Brief summary, VATTEN – J. Water Manage. Res., 70, 41–49, 2014.
Li, D., Pan, M., Cong, Z., Zhang, L., and Wood, E.: Vegetation control on water and energy balance within the Budyko framework, Water Resour. Res., 49, 969–976, 2013.
Ma, Z. M., Kang, S. Z., Zhang, L., Tong, L., and Su, X. L.: Analysis of impacts of climate variability and human activity on streamflow for a river basin in arid region of northwest China, J. Hydrol., 352, 239–249, 2008.
Maurya, A. S., Shah, M., Deshpande, R. D., Bhardwaj, R. M., Prasad, A., and Gupta, S. K.: Hydrograph separation and precipitation source identification using stable water isotopes and conductivity: River Ganga at Himalayan foothills, Hydrol. Process., 25, 1521–1530, 2011.
McKenzie, N. J., Gallant, J., and Gregory, L.: Estimating water storage capacities in soil at catchment scales, CRC for Catchment Hydrology, CRC Publications, Monash University, Monash, Australia, 2003.
Mezentsev, V.: More on the computation of total evaporation (Yechio raz o rastchetie srednevo summarnovo ispareniia), Meteorog. i Gridrolog., 5, 24–26, 1955.
Milly, P. C. D. and Dunne, K. A.: Macroscale water fluxes 2. Water and energy supply control of their interannual variability, Water Resour. Res., 38, 241–249, 2002.
Nelson, E., Sander, H., Hawthorne, P., Conte, M., Ennaanay, D., Wolny, S., Manson, S., and Polasky, S.: Projecting global land-use change and its effect on ecosystem service provision and biodiversity with simple models, PloS One, 5, E14327, https://doi.org/10.1371/journal.pone.0014327, 2010.
Ning, T., Li, Z., and Liu, W.: Vegetation dynamics and climate seasonality jointly control the interannual catchment water balance in the Loess Plateau under the Budyko framework, Hydrol. Earth Syst. Sci., 21, 1515–1526, https://doi.org/10.5194/hess-21-1515-2017, 2017.
Ojha, C. S. P., Bhunya, P., and Berndtsson, R.: Engineering Hydrology, 1st Edn., Oxford University Press, Oxford, UK, 1–459, 2008.
Ol'Dekop, E. M.: On Evaporation from the Surface of River Basins, Univ. of Tartu, Tartu, Estonia, 1–208, 1911.
Pai, D. S., Sridhar, L., Rajeevan, M., Sreejith, O. P., Satbhai, N. S., and Mukhopadhyay, B.: Development of a new high spatial resolution (0.25×0.25) long period (1901–2010) daily gridded rainfall data set over India and its comparison with existing data sets over the region, Mausam, 65, 1–18, 2014.
Pathak, S., Ojha, C. S. P., Zevenbergen, C., and Garg, R. D.: Ranking of Storm Water Harvesting Sites Using Heuristic and Non-Heuristic Weighing Approaches, Water, 9, 710, 2017.
Pike, J. G.: The estimation of annual run-off from meteorological data in a tropical climate, J. Hydrol., 2, 116–123, 1964.
Porporato, A., Daly, E., and Rodriguez-Iturbe, I.: Soil water balance and ecosystem response to climate change, Am. Nat., 164, 625–632, 2004.
Redhead, J. W., Stratford, C., Sharps, K., Jones, L., Ziv, G., Clarke, D., Oliver, T. H., and Bullock, J. M.: Empirical validation of the InVEST water yield ecosystem service model at a national scale, Sci. Total Environ., 569, 1418–1426, 2016.
Rouholahnejad Freund, E. and Kirchner, J. W.: A Budyko framework for estimating how spatial heterogeneity and lateral moisture redistribution affect average evapotranspiration rates as seen from the atmosphere, Hydrol. Earth Syst. Sci., 21, 217–233, https://doi.org/10.5194/hess-21-217-2017, 2017.
Sánchez-Canales, M., Benito, A. L., Passuello, A., Terrado, M., Ziv, G., Acuña, V., Schuhmacher, M., and Elorza, F. J.: Sensitivity analysis of ecosystem service valuation in a Mediterranean watershed, Sci. Total Environ., 440, 140–153, 2012.
Schreiber, P.: Über die Beziehungen zwischen dem Niederschlag und der Wasserführung der Flüsse in Mitteleuropa, Z. Meteorol., 21, 441–452, 1904.
Srivastava, A. K., Rajeevan, M., and Kshirsagar, S. R.: Development of a high resolution daily gridded temperature data set (1969–2005) for the Indian region, Atmos. Sci. Lett., 10, 249–254, 2009.
Su, C. and Fu, B.: Evolution of ecosystem services in the Chinese Loess Plateau under climatic and land use changes, Global Planet. Change, 101, 119–128, 2013.
Tallis, H. T., Ricketts, T., Nelson, E., Ennaanay, D., Wolny, S., Olwero, N., Vigerstol, K., Pennington, D., Mendoza, G., Aukema, J., and Foster, J.: InVEST 1.004 beta User's Guide, The Natural Capital Project, Stanford University, USA, available at: https://naturalcapitalproject.stanford.edu/invest/ (last access: October 2018), 2010.
Terrado, M., Acuña, V., Ennaanay, D., Tallis, H., and Sabater, S.: Impact of climate extremes on hydrological ecosystem services in a heavily humanized Mediterranean basin, Ecol. Indic., 37, 199–209, 2014.
Turc, L.: Le bilan d'eau des sols: relations entre les précipitations, l'évaporation et l'écoulement, Annales Agronomiques A, 20, 491–595, 1954.
Wang, D. and Tang, Y.: A one-parameter Budyko model for water balance captures emergent behavior in darwinian hydrologic models, Geophys. Res. Lett., 41, 4569–4577, 2014.
Wang, X.-S. and Zhou, Y.: Shift of annual water balance in the Budyko space for catchments with groundwater-dependent evapotranspiration, Hydrol. Earth Syst. Sci., 20, 3673–3690, https://doi.org/10.5194/hess-20-3673-2016, 2016.
Xu, X., Liu, W., Scanlon, B. R., Zhang, L., and Pan, M.: Local and global factors controlling water-energy balances within the Budyko framework, Geophys. Res. Lett., 40, 6123–6129, 2013.
Yang, D., Sun, F., Liu, Z., Cong, Z., Ni, G., and Lei, Z.: Analyzing spatial and temporal variability of annual water-energy balance in nonhumid regions of China using the Budyko hypothesis, Water Resour. Res., 43, W04426, https://doi.org/10.1029/2006WR005224, 2007.
Yang, H., Yang, D., Lei, Z., and Sun, F.: New analytical derivation of the mean annual water-energy balance equation, Water Resour. Res., 44, W03410, https://doi.org/10.1029/2007WR006135, 2008.
Zhang, L., Dawes, W. R., and Walker, G. R.: Response of mean annual evapotranspiration to vegetation changes at catchment scale, Water Resour. Res., 37, 701–708, 2001.
Zhang, L., Hickel, K., Dawes, W. R., Chiew, F. H., Western, A. W., and Briggs, P. R.: A rational function approach for estimating mean annual evapotranspiration, Water Resour. Res., 40, W02502, https://doi.org/10.1029/2003WR002710, 2004.
Zhang, L., Potter, N., Hickel, K., Zhang, Y. Q., and Shao, Q. X.: Water balance modeling over variable time scales based on the Budyko framework – Model development and testing, J. Hydrol., 360, 117–131, 2008.
Zhou, G., Wei, X., Chen, X., Zhou, P., Liu, X., Xiao, Y., Sun, G., Scott, D. F., Zhou, S., Han, L., and Su, Y.: Global pattern for the effect of climate and land cover on water yield, Nat. Commun., 6, 5918, https://doi.org/10.1038/ncomms6918, 2015.
Zhou, S., Yu, B., Huang, Y., and Wang, G.: The complementary relationship and generation of the Budyko functions, Geophys. Res. Lett., 42, 1781–1790, 2015.
Zhou, X., Zhang, Y., Wang, Y., Zhang, H., Vaze, J., Zhang, L., Yang, Y., and Zhou, Y.: Benchmarking global land surface models against the observed mean annual runoff from 150 large basins, J. Hydrol., 470, 269–279, 2012.