Ecohydrological particle model based on representative domains

Non-uniform infiltration and subsurface flow in structured soils is observed in most natural settings. It arises from imperfect lateral mixing of fast advective flow in structures and diffusive flow in the soil matrix and remains one of the most challenging topics with respect to match observation and modelling of water and solutes at the plot scale.

This study extends the fundamental introduction of a space domain random walk of water particles as an alternative approach to the Richards equation for diffusive flow (Zehe and Jackisch, 2016) to a stochastic–physical model framework simulating soil water flow in a representative, structured soil domain. The central objective of the proposed model is the simulation of non-uniform flow fingerprints in different ecohydrological settings and antecedent states by making maximum use of field observables for parameterisation. Avoiding non-observable parameters for macropore–matrix exchange, an energy-balance approach to govern film flow in representative flow paths is employed. We present the echoRD model (ecohydrological particle model based on representative domains) and a series of application test cases.

The model proves to be a powerful alternative to existing dual-domain models, driven by experimental data and with self-controlled, dynamic macropore–matrix exchange from the topologically semi-explicitly defined structures.

1 Introduction

Non-uniform subsurface flow is omnipresent in hydrology (Uhlenbrook, 2006) and is accepted today as being the rule rather than the exception (Flury et al., 1994; Nimmo, 2011). Originally, preferential flow described water transport in non-capillary soil structures which is much faster than would be expected from classical theory of flow and transport in porous media (Bear, 1975). A considerable number of studies and model approaches have since been proposed to address the issue – as explained in several reviews (Beven and Germann, 1982, 2013; Jarvis, 2007; Köhne et al., 2009b; Weiler and McDonnell, 2007; Šimůnek et al., 2003).

Macropore settings may be very specific with respect to their topology, their temporal dynamics and their interface characteristics in their ecohydrological context: earthworm burrow configurations (Blouin et al., 2013), their spatio-temporal dynamics (Palm et al., 2012; van Schaik et al., 2014) and burrow coatings (Jarvis, 2007; Rogasik et al., 2014) affect infiltration and water redistribution. Other structure-creating animals like rodents and moles can also have an impact (Botschek et al., 2002). Plant roots affect water redistribution and soil water withdrawal dynamically (Nadezhdina et al., 2010). Connected flow paths (Wienhöfer, 2014) and periglacial cover beds (Heller, 2012) may change the hydrological regime completely.

All of these influences are rather complex and specific in detail. In addition, they challenge the model concepts since the advective processes take place in explicit structures with respective connectivity and spatial covariance and under conditions that are far from well-mixed. They extend across several scales in space and time.

Non-uniform flow arises from imperfect lateral mixing between a fast advective fraction of water and solutes (travelling mainly driven by gravity in large pores and soil structures) and a slow diffusive fraction (governed by capillary forces in the soil matrix) (Blöschl, 2005; Neuweiler and Vogel, 2007). Advective flow in structures is governed by initial supply (Weiler, 2005) and interaction with the soil matrix (Germann and Karlen, 2016; Nimmo, 2016). Thus, interaction comprises the exchange of mass and dissipation of flow kinetic energy. The proposed approaches to deal with this deviation from local equilibrium state range from (a) the early concept of stochastic convection, i.e. no mixing at all (Jury and Roth, 1990) or (b) with mixing as multiple interacting pathways (Davies et al., 2013), (c) the “scaleway” idea to convey structural fingerprints in flow and transport across scales (Vogel and Roth, 2003), (d) dual-porosity/dual-permeability approaches, relying on overlapping and exchanging continua (Gerke, 2006), to (e) spatially explicit or representative definition of macropores as vertically and laterally connected flow paths based on elevated conductivity (Klaus and Zehe, 2011; Sander and Gerke, 2009; Vogel et al., 2006). In particular the last approach corroborates the crucial importance of reliable field data or estimates characterising the distribution of the macropores at the surface and over depth for successful predictions (Loritz et al., 2017). In addition, their potential connection to lateral preferential flow paths and the catchment drainage network is of fundamental interest (Jackisch et al., 2017).

Kleidon et al. (2013) and Zehe et al. (2013) have focused on the role of preferential flow from an energy or momentum perspective. While preferential flow hinders lateral mixing, it facilitates vertical mass transfer against differences in geopotential or large gradients in matrix potential, which are established during dry spells in cohesive soils and lead to a faster depletion of the gradients (Westhoff et al., 2014). This implies a faster reduction (dissipation and export) of free energy of soil water during rainfall-driven conditions due to enhanced mixing into the main direction of the flow path (Zehe et al., 2013). Exchange between both flow domains is also associated with dissipation of kinetic energy and thus momentum (Kutilek and Germann, 2009).

Despite the fact that there has been considerable progress in the understanding of preferential flow and non-uniform infiltration, the topic remains one of the most challenging in particular with respect to scale and sub-scale representation of rapid subsurface flow and transport in hydrological models (Beven and Germann, 2013) and with respect to feedbacks between soil ecology and soil hydrology (van Schaik et al., 2014).

We thus propose a stochastic–physical model framework to jointly predict rapid advective water flows in soil structures and diffusive water flows when capillarity controls soil water dynamics, and the interaction between the two. The approach is developed for a representative plot domain with topologically explicit macropores. An overall goal of the model framework is to provide opportunities for virtual experiments on infiltration patterns and abiotic controls on specific niches for macro- and microbiota in structured subsurface domains.

The proposed model is a Lagrangian approach, treating water itself as particles moving diffusively by means of a space domain random walk and advectively as film flow in representative structures. Lagrangian approaches to solute transport with unsaturated flow in heterogeneous media are well-established tools in hydrological modelling (Delay and Bodin, 2001; Neuweiler et al., 2012). Most of these particle-tracking applications calculate the water flow as external drift based on a hydrological solver like for the Richards equation (de Rooij et al., 2013) or establish some assumption about the fate of a random walker in the time domain (Dentz et al., 2012). Lagrangian approaches to plot- and hillslope-scale water dynamics itself were, to the best of our knowledge, only followed by Ewen (1996) (subsystems and moving packets model) and Davies et al. (2011) (multiple interacting pathways model). Similar to an exchange term in dual-permeability models, both approaches solve the key problem of advective momentum dissipation by macropore–matrix interaction by means of explicit parameterisation. While Ewen (1996) introduces different types of water movement with a structural property parameter λ to govern the probability of a water particle to move, Davies et al. (2011) define an exchange or mixing parameter of the particles' “momentums”. Both approaches have proven very suitable for their application. However, both parameters have yet to be estimated by calibration. This implies strong limitations for predictions in dynamic systems and systems under change.

We have shown in a previous study (Zehe and Jackisch, 2016) that the space domain random walk (1-D) allows for a physically consistent representation of capillarity-driven, unsaturated soil water flow in accordance with the Richards equation. In this Lagrangian conceptualisation the diffusion of the water particles (and thus their potential displacement) depends on the local density of particles. The higher the local particle density (wetter), the higher the diffusion based on the soil water retention properties. In the study at hand, we extend the approach to a 2-D matrix domain which hosts a number of representative preferential flow structures like earthworm burrows or cracks as vertical 1-D elements. The scope of this echoRD model (ecohydrological particle model based on representative domains) covers the simulation of plot- and event-scale flow and transport through a topologically explicit treatment of macropores. Pore-scale processes (Moebius and Or, 2012; Schlüter et al., 2016; Shahraeeni and Or, 2012; Snehota et al., 2015) are not resolved here.

The main objectives of this study are to (a) present the model theory, to (b) test the capability of the echoRD model to simulate the fingerprints' non-uniform infiltration and to (c) reveal whether advective and diffusive flow and the interactions between them may be represented in one consistent formulation. As the model shall allow for virtual experiments we base its parameterisation as much as possible on field observables or explicitly testable hypotheses. More specifically, we derive and test an energy-balance-based approach to control the exchange between the macropore domain and the surrounding matrix in a self-limiting manner.

The software developed and data used in this study are available under the GNU General Public License (GPLv3) and the Creative Commons License (CC BY-NC-SA 4.0), respectively, through a GitHub repository (Jackisch, 2018): https://github.com/cojacoo/echoRDmodel (last access: 3 July 2018). In particular, the echoRD model, including a preprocessor, application tests and basic documentation, can be accessed there.

2 Specific motivation

2.1 General particle concept and 1-D implementation

Particle tracking is usually employed for simulating the advective dispersive transport of solutes, but not for the water phase itself (Berkowitz et al., 2006; Delay and Bodin, 2001; Koutsoyiannis, 2010; Metzler and Klafter, 2004). In such applications, particles representing a certain amount of solute are advectively displaced by the movement of the solution and diffusively within it. Most random walk applications rely on a continuous time domain representation as it performs well at minimum computational cost (Delay et al., 2008; Dentz et al., 2012). This approach is, however, not feasible when the diffusivity itself depends on the particle density as is the case for water particles. We thus employ a non-linear random walk of water particles in the space domain.

In Zehe and Jackisch (2016) we described this procedure as a 1-D model with water particles of constant mass travelling according to the Itô form of the Fokker–Planck equation. The model concept builds on established soil physics by estimating the drift velocity (gravity-induced displacement) and the diffusion term (capillarity-driven displacement) based on the soil water retention characteristics. Reduced mobility of water with decreasing size of the populated pore is accounted for using a suitable binning of the water diffusivity curve to scale the random work of different particles. Furthermore, we proposed a straightforward implementation of rapid non-equilibrium infiltration there. This binning enabled the distribution of flow velocity in the pore space to be simulated; i.e. we discussed the assumption of instant and uniform determination of bulk water velocity based on the soil water retention curve in most Eulerian models. In the Lagrangian approach infiltrating event water can travel initially in the largest pore fraction at maximum velocity and it experiences a slow diffusive mixing with the pre-event water particles within a characteristic mixing time.

2.2 Limitations of the 1-D representation

Despite the successful application of the introduced particle model approach, a 1-D version essentially lacks information about the lateral component of the non-uniform distribution and resulting macropore–matrix exchange characteristics in natural soils. One could be tempted to subsume an essence of the recent model approaches for subsurface flow in discrete structures (Gerke, 2006; Jury and Roth, 1990; Nimmo, 2011; Sander and Gerke, 2009; Vogel and Roth, 2003; Vogel et al., 2006) as a third type of particles to our previous 1-D representation. However, this would imply three problems.

The first is that macropore flow is much faster than saturated hydraulic conductivity. At the same time it is limited to a very small fraction of the soil column. This motivated the conceptualisation of multiple flow domains. However, the state of a specific flow path is substantially different from the averaged state of a elementary volume. Secondly, the topology of flow paths plays a role in this regard: macropores enable a quick vertical redistribution of event water. If the network of macropores is rather dense and lateral diffusion is not too slow, the resulting soil water dynamics can be uniformly described by some elevated, effective hydraulic conductivity. If the structures are sparse and lateral diffusion into the matrix is slower, lateral gradients in soil water potential and non-uniform flow fields are established.

As such the flow field depends on macropore topology, antecedent soil matrix state, macropore capacity and infiltration supply. In a 1-D approach such lateral gradients and their depletion cannot be described other than by some additional conceptual parameter or function and averaged matric potential states. The result would remain bound to a priori defined macropore–matrix exchange assumptions. Without proper control of the macropore–matrix interaction and thus control of the advective flow field, a fast fraction of particles would simply remain quick and drain from the domain, which contradicts the experimental findings.

The third challenge refers to the matrix pore space and exchange/mixing of rapid event water particles with the pre-event water to establish a local thermodynamic equilibrium (LTE) – the well-organised distribution of water particles in the respective smallest fractions of the available pore space, as we further explained earlier (Zehe and Jackisch, 2016).

These issues led to the preliminary finding that a lumped 1-D version of the particle model could not succeed in reproducing the observed tracer distributions without thorough calibration to one specific antecedent state and one specific realisation of the advective flow field. The requirement of non-observable and non-static mixing parameters between the domains makes an application to predict behaviour under change challenging. Thus it is not very convincing if we desire to develop the model as a virtual laboratory.

3 The echoRD model

3.1 The representative macropore–matrix domain

In order to overcome the 1-D limitations without requirement for a pore-scale determination of the macropore system or non-observable parameters, we define a representative macropore–matrix domain with explicit topology (Fig. 1). Similar to dual-permeability techniques, we determine a soil matrix and macropores as domains for diffusive and advective flow, respectively. The soil matrix is projected as a 2-D domain with a periodic lateral boundary. Macropores are represented as vertical 1-D elements linked to the matrix. As there is usually no information about the spatial clustering of macropores, they are placed at resampled distances according to an observed density distribution. Given the periodic lateral boundary of the matrix domain, it is not the macropore positions but their relative distances that matter. The lateral extent of the domain is determined by the minimum density of macropores in a given depth, such that the overall connectivity is represented. One may also choose to take a multiple of the least representative in the set-up, for instance to describe interactions with less densely occurring structures such as subsurface pipes.

The 2-D soil matrix possesses a grid for the determination of soil properties and for particle density (and thus soil moisture) calculation. The 1-D macropore domains have an internal grid for film flow calculations, the lag distance is calculated as the projection of one water particle to the mean macropore diameter. In addition, the 1-D macropore domains have an interface area with the 2-D soil matrix domain. In this area particles are considered for exchange between the domains.

Figure 1 Representative macropore–matrix domain. A 2-D soil matrix with a periodic lateral boundary hosts several 1-D macropores with their respective capacities, interfaces and lateral distributions.

3.2 Diffusion in the soil matrix based on a 2-D random walk

Similar to the use of particle tracking for simulating solute transport we conceptualise soil water as particles. Each particle represents a constant mass of water, defined by the set-up of the soil matrix calculation grid and the resolution of the porewater volume bins.

Diffusive soil water flow is simulated as a non-linear, space domain random walk in the soil matrix, as presented in our previous study (Zehe and Jackisch, 2016). We describe the trajectory of a single particle of water in a time step Δt as the Itô form of the Fokker–Planck equation based on the formal equivalence of the Richards equation and the advection dispersion equation, consisting of a vertically directed drift term $u\left({\mathit{\theta }}_{z,x,t}\right)$ = $\frac{k\left({\mathit{\theta }}_{z,x,t}\right)}{{\mathit{\theta }}_{z,x,t}}$ characterising downward water fluxes driven by gravity and a diffusive term representing water movements driven by the matric head gradient and controlled by the diffusivity $D\left({\mathit{\theta }}_{z,x,t}\right)$ of soil water or particles respectively. With this we can establish the Itô solution for the trajectory of one particle:

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }{z}_{t+\mathrm{\Delta }t}=z_t+\left[u\left({\mathit{\theta }}_{z,x,t}\right)+{\displaystyle \frac{\partial D\left({\mathit{\theta }}_{z,x,t}\right)}{\partial z_t}}\right]\mathrm{\Delta }t+{\mathit{\xi }}_z\sqrt{\mathrm{6}D\left({\mathit{\theta }}_{z,x,t}\right)\mathrm{\Delta }t}\\ \text{(1)}& {\displaystyle }& {\displaystyle }{x}_{t+\mathrm{\Delta }t}=x_t+{\displaystyle \frac{\partial D\left({\mathit{\theta }}_{z,x,t}\right)}{\partial x_t}}\mathrm{\Delta }t+{\mathit{\xi }}_x\sqrt{\mathrm{6}D\left({\mathit{\theta }}_{z,x,t}\right)\mathrm{\Delta }t},\end{array}$$

with z vertical position (m), x lateral position (m) and ξ a uniform random number [−1, 1]. Notice, that unlike the diffusion/advection of a solute this does not require referencing to the wetted pore space since our reference system is the total pore volume.

In this form diffusivity $D\left({\mathit{\theta }}_{z,x,t}\right)$ is dependent on the soil moisture θ at the location (z, x) of a particle for a certain time step (t). Although we need to assume point-like particles to apply the Itô solution in Eq. (1), each particle is referenced to a mass and theoretical spatial extent to derive θ from the density of particles. However, any kind of direct particle interaction is neglected at this stage. θ is calculated by the number particles (and thus volumetric fraction of water) in each calculation grid cell of the 2-D soil matrix. In Appendix D an evaluation of the lateral diffusion is included alongside macropore exfiltration.

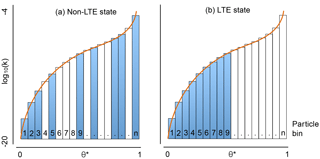
Figure 2 Example of delineation of the pore space into bins of equal volumes or particles in our study. If the bins are organised in ascending order, this refers to the LTE (local thermodynamic equilibrium) state of the pore space (b). However, at the same overall soil moisture the particle configuration could also divert from LTE (a).

Alternatively to the θ-based form which assumes LTE at any time (like most Eulerian models do), we can assign each particle to a discrete bin as surrogate of its position in the pore space (Fig. 2). With this, a particle obtains its reference to the water retention curve as explained in Zehe and Jackisch (2016). Then u and D in Eq. (1) are dependent on the particle's bin. Different from the work of Hassanizadeh and Gray (1990), who developed a theory for multiphase flow at the meniscus scale in porous media, combining averaging of microscale descriptions and macroscopic approaches by employing balance laws and the second law of thermodynamics, we conceptualise LTE relaxation associated with momentum dissipation of infiltrating water in coarser pores. As such, we assume a diffusion towards LTE without resolving individual pore-scale processes. By doing so, the reassignment of bins to the moving particles becomes crucial: in the advanced model version the bins of all particles in each calculation grid cell are frequently updated by determining the deviation from the LTE state (all bins are sorted from 0 to n, with n being the number of particles at the current relative saturation state). The relaxation time t_mix to LTE is hypothesised as diffusion time:

$$\begin{array}{}\text{(2)}& {\displaystyle }{\displaystyle }{t}_{\mathrm{mix}}={\displaystyle \frac{L_{x,z}^{\mathrm{2}}}{D_{\mathrm{mix}}}},\end{array}$$

with L_x,z as maximal diffusion length given by L_x,z = k_s(x, z) ⋅ Δt and D_mix as D at the 0.7 percentile of the free bins (the percentile is a hypothesised estimate of the effective diffusivity and can be controlled by a model parameter). With this, t_mix is the time after which LTE is assumed to be recovered from an initial population of the largest pores. The bins of all particles in a grid cell are updated to a lower deviation from LTE after each calculation step by

$$\begin{array}{}\text{(3)}& {\displaystyle }{\displaystyle }{\mathrm{bin}}_{t+\mathrm{\Delta }t}={\mathrm{bin}}_t-\max \left[\mathrm{0},\left({\mathrm{bin}}_t-{\mathrm{bin}}_{\mathrm{LTE}}\right)\right]{\displaystyle \frac{\mathrm{\Delta }t}{t_{\mathrm{mix}}}}.\end{array}$$

In addition, a counteracting stochastic process is introduced to handle the effect of high diffusivity but the low number of open slots in the pore space near saturation:

$$\begin{array}{}\text{(4)}& {\displaystyle }{\displaystyle }{p}_{\mathrm{counteract}}={\displaystyle \frac{n_{\mathrm{empty}\mathrm{bins}}}{n_{\mathrm{air}\mathrm{capacity}\mathrm{bins}}}}.\end{array}$$

Here n is the number of respective bins in the pore space. If the probability p_counteract is below 1, it is multiplied by ξ in the random walk (Eq. 1) scaling the diffusive step by the ratio of open slots tending towards zero at saturation.

Numerically, the actual step of a particle is calculated in a predictor–corrector approach, projecting the step of one particle, anticipating an updated state/binning to update D and u and calculating the geometric mean of the projected and updated D and u according to Stratonovich. In order to balance computational expenses and numerical stability, a stratified subsample (governed by a model parameter) of all particles is handled at once. The used variables are calculated based on van Genuchten parameterisation of the soil matrix properties.

3.3 Advection in the 1-D macropores as film flow

In addition to the matrix domain the set-up contains several 1-D elements as macropores (Fig. 1). They are distributed along the lateral axis of the matrix and connect to certain cells over a defined contact interface.

3.3.1 Projected drainage capacity and maximum velocity

The preferential flow network exhibits a large drainage capacity. Zehe (1999) estimated that a single burrow of a Lumbricus terrestris (r = 4.5 mm) may drain the equivalent of 1 m² saturated loess soil matrix. Based on the domain set-up, advection is structurally limited by the drainage depth of a macropore and its size.

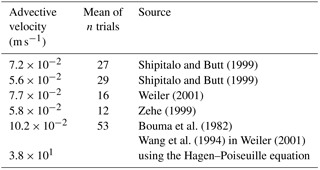
The second limit is given through the definition of initial maximum flow velocity in the structures. Literature values in Table 1 range closely around 7.5 × 10⁻² m s⁻¹. Being much larger than the saturated hydraulic conductivity of most soils, these values range several orders of magnitude below the theoretical value for pipe flow in such a pore calculated according to Hagen–Poiseuille with a unit gradient. Here we use this difference to estimate frictional losses of the advective momentum as dynamic limitation through interaction with the matrix as further explained in the following sections.

3.3.2 Dynamic film flow

Macropore flow is represented as 1-D film flow of particles along the pore wall (Fig. 3). We assume that a particle has a given kinetic energy (E_kin) which is dissipated by friction at the macropore wall and infiltration into the matrix (Fig. 3a). The maximum advection step s_proj of a particle is projected based on its current velocity v₀, which is decelerated by the a_friction and a_exchange it experiences along its path. This results in a reduced step length s_real (Fig. 3b). On its passage along s_real, a particle may possibly infiltrate into the matrix, calculated by an accumulation of an infiltration length (Fig. 3c). We account for variable film thickness depending on the number of particles in each internal grid element of the macropore. If particles overlap their vertical positions, and thus there is more than one per position slot, they form a second film layer. Particles at a higher level in a film do not experience drag or friction and travel without retardation until they reach the lowest wetted position within a continuous film stretch (Fig. 3d).

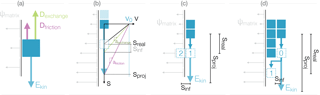
Figure 3 Macropore flow concept. (a) Concept of a water particle at the pore wall possessing a kinetic energy E_kin which is dissipated by friction in the macropore network and exchange with the matrix due to the matric potential ψ_matrix. (b) Projected advection of a particle where the potential advective velocity v₀ is decelerated by the a_friction and a_exchange it experiences along the projected path s_proj, resulting in a reduced step length s_real. (c) Reduced advection with macropore–matrix exchange (1), and possible infiltration s_inf (2). (d) Fast advection of a particle as film flow to the end of the film (0) and further decelerated advection (1).

3.3.3 Macropore–matrix interaction

Direct experimental evidence of water dynamics at the macropore–matrix interface hardly exists. Some orientation is given by findings of Hincapié and Germann (2010) and Moebius and Or (2012). Promising techniques like time-lapse X-ray or µCT tomography have recently emerged (Koestel and Larsbo, 2014; Schlüter et al., 2016). Yet, there is consensus that macropore–matrix interaction depends on the matric head and the wetting of the macropore wall (Klaus et al., 2013) and is optionally affected by organic coatings which may act hydrophobically (Jarvis, 2007; Rogasik et al., 2014). Moreover, it is dependent on the flow velocities. Current dual-permeability approaches treat this key process as either based on a leakage/exchange coefficient and the potential difference between the domains (Gerke, 2006) or based on using the geometric mean of the saturated hydraulic and actual hydraulic conductivity and the potential gradient between both domains. The latter depends on an exchange length (Beven and Germann, 1981). The drawback of these approaches is that neither the exchange length nor the leakage parameter is observable, and they depend on model grid size, state dynamics and event characteristics (Köhne et al., 2009a).

Here we propose a thermodynamic approach for describing this key process on a physical basis without introducing additional parameters based on the Bernoulli equation:

$$\begin{array}{}\text{(5)}& {\displaystyle }{\displaystyle }\underset{E_{\mathrm{kin}}}{\underbrace{\mathrm{0.5}\mathit{\varrho }\stackrel{\mathrm{const}.}{\overbrace{v_{\mathrm{adv}}^{\mathrm{2}}}}}}+\underset{E_{\mathrm{pot}}}{\underbrace{\mathit{\varrho }gz}}+\stackrel{=\mathrm{0}}{\overbrace{p}}+{\mathit{\epsilon }}_{\mathrm{friction}}=\mathrm{const}.\end{array}$$

Measured advective flow velocity values in earthworm pores range closely around 7.5 × 10⁻² m s⁻¹, as given in Table 1.

These measurements compare with a theoretical laminar flow velocity through a pipe of the same cross section and with a unit pressure gradient by a factor of about 500. A theoretical laminar flow velocity u_mx through a pipe can be calculated using the Hagen–Poiseuille equation (assuming unit pressure gradient):

$$\begin{array}{}\text{(6)}& {\displaystyle }{\displaystyle }{u}_{mx}=\mathrm{2}\cdot {\displaystyle \frac{\mathit{\rho }g{R}^{\mathrm{2}}}{\mathrm{8}\cdot \mathit{\eta }}},\end{array}$$

with ρ and η as the density and dynamic viscosity of water, g the gravitational acceleration and R the radius of the pore. The direct measurements compare with the theoretical velocity through a pipe of the same cross section by a factor of about 500. This deviation is conceptualised as friction in the macropore set-up.

Given its velocity, each particle in motion possesses an E_kin:

$$\begin{array}{}\text{(7)}& {\displaystyle }{\displaystyle }{E}_{\mathrm{kin}}=\mathrm{0.5}{m}_{\mathrm{particle}}{u}_{mx}^{\mathrm{2}}.\end{array}$$

With this and the current velocity of a particle u_real, we may estimate the dissipation by friction in the macropore ε_friction as an impulse I_friction counteracting the hypothetical E_kin by

$$\begin{array}{}\text{(8)}& {\displaystyle }{\displaystyle }{I}_{\mathrm{friction}}=E_{\mathrm{kin}}/u_{\mathrm{real}}.\end{array}$$

Shipitalo and Butt (1999)Shipitalo and Butt (1999)Weiler (2001)Zehe (1999)Bouma et al. (1982)Wang et al. (1994)Weiler (2001)

Table 1 Measured mean maximum advective velocity in burrows of the earthworm Lumbricus terrestris at a mean radius of 4.5 mm and theoretical value calculated using the Hagen–Poiseuille equation.

Following Kleidon and Schymanski (2008) and Zehe et al. (2013) soil water experiences a certain capacitative (or capillary binding) energy density dE_cap = ΨdV_θ, as the matric potential is a negative energy density. Wetting and drying due to macropore–matrix exchange affects its capillary binding energy approximately as

$$\begin{array}{}\text{(9)}& {\displaystyle }{\displaystyle }{\mathit{\epsilon }}_{\mathrm{exchange}}=\mathrm{d}{E}_{\mathrm{cap}}=\mathit{\varrho }g{\displaystyle \frac{\partial {\mathrm{\Psi }}_z}{\partial {\mathit{\theta }}_z}}\cdot \mathit{\theta }\mathrm{d}\mathit{\theta },\end{array}$$

with Ψ_z as the matric pressure head at a certain depth z and θ_z as the volumetric soil water content. With this we can estimate dissipation ε_exchange during the infiltration of one particle as an impulse by using the particle volume V_particle and a projected infiltration flux q_exchange:

$$\begin{array}{}\text{(10)}& {\displaystyle }{\displaystyle }{I}_{\mathrm{exchange}}=\mathit{\varrho }g{\displaystyle \frac{\partial {\mathrm{\Psi }}_z}{\partial {\mathit{\theta }}_z}}{\displaystyle \frac{V_{\mathrm{particle}}}{q_{\mathrm{exchange}}}}.\end{array}$$

The projected infiltration rate q_exchange is calculated as the Darcy flux: q_exchange = k_u(ψ) ⋅ $-\mathit{\psi }/\mathrm{2}{r}_{\mathrm{particle}}$. Notice that this is only the necessary assumption for the change of θ in Eq. (10) directly at the interface. All state-dependent variables are formulated as the geometric mean of the references at an initial depth z_i and a projected depth z_proj in a predictor–corrector scheme.

Now, the reduced advective velocity of a particle is estimated using friction and exchange drag acting against E_kin of the particle in a steady state:

$$\begin{array}{}\text{(11)}& {\displaystyle }{\displaystyle }{u}_x=-{\displaystyle \frac{E_{\mathrm{kin}}}{I_{\mathrm{exchange}}+I_{\mathrm{friction}}}}.\end{array}$$

If the projected infiltration exceeds the particle radius q_exchange ⋅ Δt > r_particle the particle will be transferred to the adjoining matrix. With the given equations, the dynamic film flow and infiltration into the matrix is governed by the state-dependent retention properties of the soil (van Genuchten parameters) and the supply of new particles. In Appendix D synthetic references are presented.

3.4 Infiltration into macropores and the matrix domain at the upper boundary

With the extension of the model to two dimensions, the partitioning of infiltration into macropores and the soil matrix became an important aspect of the model. As pointed out by Weiler (2005) and Nimmo (2011) and others, initialisation of the macropores is critical and non-trivial. We employ a generalisation of the concept of macropore drainage areas (Weiler, 2005; Weiler and Naef, 2003) and the concept of preferential flow initiation and partitioning according to Nimmo (2011): when precipitation is converted into particles, they are randomly distributed over the top boundary. All particles which happen to fall on soil first form a film layer similar to the macropore walls described earlier. Excess precipitation or particles directly falling on macropores are redistributed to the macropores according to proximity and capacity. If one macropore's capacity is reached, it is excluded from the redistribution process. Particles in the film layer are included in the diffusive calculation step of the top matrix cells. Particles in the macropore domain are treated as film flow advection and possible infiltration from the macropores into the matrix as described above. Thus, infiltration is only limited by the transport capacity of matrix and macropores. The higher the soil matrix infiltration capacity, the lower the share of particles entering the macropores.

3.5 Data requirements, technical implementation and numerical issues

The parameterisation of the echoRD model based on observables is a key objective of this study. As pointed out previously, the required parameters for the model are retention characteristics (van Genuchten parameters) and a lateral and vertical density distribution of macropores. The retention properties of the soil matrix can be measured in standard pedo-physical analyses.

To derive macropore density distributions, horizontal panes of dye tracer stains (e.g. Brilliant Blue experiments) can be analysed with the model preprocessor. With this we make use of experimental data directly as explained in Appendix B. Moreover initial soil water content and a precipitation time series need to be defined.

We rely on sequential calculation of the process domains:

1. infiltration at the top boundary into matrix and macropores;

2. diffusive matrix flux as a spatially explicit 2-D random walk;

3. film flow in the macropore;

4. macropore–matrix interaction (infiltration and exfiltration).

Checks for saturation and percolation below the lower boundary are performed after step 2 and 3. The time step is controlled through Courant and Neumann criteria based on the maximum possible diffusive and advective step at the current max(θ_t) or occupied bin respectively:

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }\mathrm{\Delta }{t}_D=\mathrm{\Delta }{z}^{\mathrm{2}}/\mathrm{6}\max \left(D_{\max \left({\mathit{\theta }}_t\right)}\right)\mathrm{and}\\ \text{(12)}& {\displaystyle }& {\displaystyle }\mathrm{\Delta }{t}_u=\mathrm{\Delta }z/\max \left(k_{\max \left({\mathit{\theta }}_t\right)}\right).\end{array}$$

With regard to the representative domain, the interrelation of particle size and the numerical grid is noteworthy. The desired resolution and stochastic stability of the model is controlled by the grid size and the number of particles which represent saturation. Both are required model parameters. Obviously, this quickly leads to a large number of particles if we seek to resolve processes which locally change soil moisture by a few percent only. The following tests are realised with a relatively fine grid and a relatively large number of particles to avoid instabilities and artefacts.

4 Model application tests and experimental references

In this section, we outline our application tests of the echoRD model and a reference to real-world conditions in order to examine the capability of the chosen simplifications. In order to focus on the proposed concept and hypothesised process descriptions, the following tests are realised with an underlying grid resolution for particle density calculation of 5 mm. The water particles are set to a size of 0.002 times a grid cell (equivalent to 0.33 mg).

With the extension to two dimensions and the introduction of representative macropores, the test applications shall especially address the following aspects:

• a.

  2-D diffusive, non-uniform soil water redistribution;

• b.

  interaction of 1-D advective paths with the 2-D soil matrix;

• c.

  sensitivity to state variables and model parameters;

• d.

  robustness of the representative macropore setting;

• e.

  reproduction of a real-world irrigation experiment.

4.1 Generic application test cases

The central benchmark of the model is a series of generic test applications with different soil types, precipitation intensities and antecedent soil moisture. The aim is to examine the consistency and capability of the model and the self-controlled non-uniform flow with regard to points a–c. The test matrix is spanned by

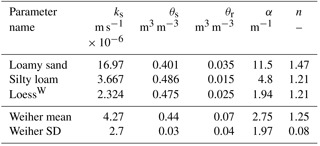
• soil water retention parameters for a sandy soil, a loamy soil and a loess soil (Table 2),

• two different antecedent moisture states at 0.15 and 0.31 m³ m⁻³ and

• precipitation intensities at 10, 40 and 60 mm h⁻¹ lasting for 30 min.

The resulting model runs are compared visually based on the infiltration patterns and numerically based on the distribution of newly added particles as breakthrough curves (BTCs). In our Lagrangian approach neither particle interaction nor solute transfer from one particle to another is considered. Hence we neglect diffusive mixing, and the breakthrough is simply the depth distribution of new particles. Additionally, we compare these resulting travel depth distributions based on means of the first three central moments. In these scenarios, the macropore network is the same. It is defined based on earthworm macropore assessments in an agricultural loess landscape using the preprocessor (Appendix B). To gain insight into the model robustness, alternative definitions of macropores based on the same input statistics are compared separately (aspect d). Moreover we test the influence of different particle resolutions with 100, 200 and 500 particles per grid cell at θ_s for some examples.

4.2 A plot-scale irrigation experiment as a real-world test case

We conducted a series of plot-scale irrigation experiments in different soil landscapes (Jackisch, 2015). Our model development is founded on these findings, based on the hypothesis that irrigation experiments can reveal the distribution of advective flow paths and the resulting non-uniform soil water redistribution characteristics (Jackisch et al., 2017). By using a sprinkler with a very fine drop spectrum and a drip irrigation pad in the presented case on undisturbed surface conditions, we neglect drop splash impact (Iserloh et al., 2013) and macropore drainage area connectivity (Weiler and Naef, 2003). Diffusive soil water transport parameters are determined based on laboratory analyses of undisturbed soil cores for their retention properties.

Table 2 Soil matrix retention parameters used in the application tests. Loamy sand and silty loam according to Carsel and Parrish (1988). Loess^W refers to measured values from soils at the location of the experiment described in Sect. 4.2. Weiher comprises seven ensemble soil matrix references of the Weiherbach basin as mean and standard deviation (SD).

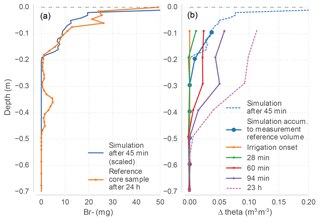
Because the model is intended as an exploration tool extending real-world experiments, a further test of the model aims at reproducing one experiment in the Weiherbach basin in south-west Germany with loess soils on a fallow plot (49.13517^∘ N, 8.74415^∘ E; 20 October 2015). The irrigation was realised with 40 mm water in 2 h on a 1 m² plot with a drip irrigation pad. The water was enriched with 5 g L⁻¹ potassium bromide (KBr) salt tracer and 4 g L⁻¹ Brilliant Blue dye tracer. The plot remained covered during the whole experiment until excavation. The state was monitored with a TDR soil moisture tube probe (Trime IPH, IMKO GmbH) and time-lapse 3-D ground-penetrating radar (Allroggen et al., 2017). The plot was excavated 20 h after irrigation onset for dye stain recovery (Fig. 4). In addition two core samples (80 mm diameter) were drawn 20 and 30 h after irrigation onset, respectively. The cores were sliced every 15 mm and were analysed for Bromide concentration as in Jackisch (2015).

Figure 4 Weiherbach irrigation experiment as model reference. Brilliant Blue dye stains in excavation horizons.

The echoRD model set-up is based on a stochastic matrix definition of seven equally valid ensembles of measurement and literature references (Plate and Zehe, 2008; Zehe, 1999; Zehe et al., 2001; see Table 2 for the case of Weiher). The macropore domain has been parameterised based on observed dye stain patterns in four depth layers using the preprocessor (Appendix B). The vertical extent of the signal guides of the TDR tube probe is 18 cm. It was manually lowered in the tube in 10 cm increments. In order to compare the observed and modelled soil water state dynamics, the mid-point of the probe is taken as reference, and the total soil moisture of the depth increment referring to the respective probe depth is averaged.

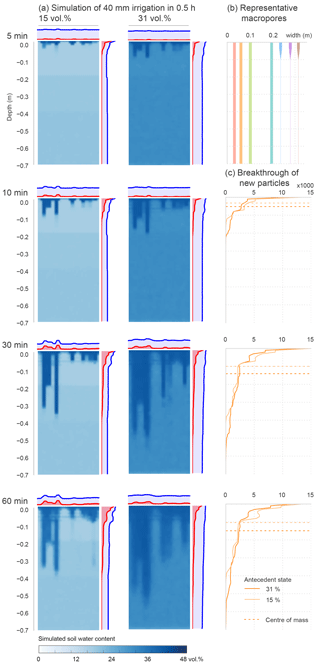
Figure 5 Simulated soil moisture dynamics in generic application tests of loess soil. The marginal plots give the distribution of all particles (blue) and newly infiltrated particles (red). (b) The definition of the representative macropore domain. (c) The breakthrough curves of new particles at the different time steps for the two antecedent states.

5 Results

5.1 Generic application tests

The generic application tests show the capability of the model to calculate self-controlled, non-uniform infiltration patterns (Figs. 5 and 6).

The simulations of 40 mm irrigation in 0.5 h on loess silt with different antecedent soil water content show the development of a non-uniform flow field conditioned by the representative macropores (Fig. 5). The overall soil water dynamics (a) exhibit a quickly expanding advection in the larger macropores. The respective BTCs (c, and marginal plots in a) allow this behaviour to be quantified. After 10 min new particles already reach a depth up to 0.2 m, while the centre of mass is around 0.05 m. The results also show that the fast advective displacement requires continuous supply. After the end of irrigation soil water is mostly redistributed diffusively, which can be seen as blur in the soil water content. This is also depicted by relatively steady BTCs. Thus the model proves to be capable of simulating advective film flow, macropore–matrix exchange and 2-D diffusive redistribution dissipating the lateral gradients. This proves aspects a and b.

Figure 6 Table of simulated soil moisture dynamics in generic application tests for loess. Marginal plots give the distribution of all particles (blue) and newly infiltrated particles (red).

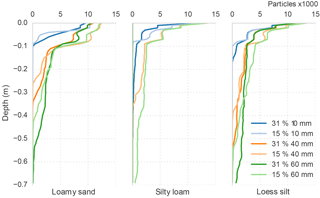
Comparing the different soil types of loamy sand, silty loam and loess silt, the two respective antecedent moisture states and three irrigation intensities, more insight into the simulated soil water dynamics is given (Fig. 6). Generally, with increased supply intensity, the non-uniform flow field becomes more prominent. However, moderate intensity can also develop such patterns, depending on the diffusive momentum. It becomes apparent that the more conductive the matrix was, the less pronounced the advective fraction became. The diffusive redistribution of particles is especially obvious for the highly conductive loamy sand. With low supply intensities and high antecedent soil water content, this leads to almost uniform infiltration. The diffusive redistribution is especially visible when comparing the results of different antecedent states. Under dry conditions the film flow is experiencing more drag with less exfiltration into the matrix. Wet conditions and more conductive soils lead to less friction but also more lateral displacement. In the long simulation runs (bottom row) the lateral gradients are increasingly dissipated as one would expect.

Moreover, the larger the supply sustaining the advective fraction, the greater the depth or breakthrough reached. When analysing the simulated dynamics this also led to different apparent velocities in the respective macropores (see video in the Supplement). This behaviour is consistent with field observations and our expectations. As such, the model proves to fulfil the required objectives a–c.

A more quantitative reference is obtained when comparing the depth distribution of new particles of the application tests directly (Fig. 7). The temporal dynamics of the infiltration patterns in loamy sand start with a largely intensity-controlled situation (low deviation between antecedent conditions). The picture changes to antecedent-state-controlled top soil retention for the higher intensities with very similar profiles. Total irrigation amount controls deeper percolation in the later course of the simulation. There, the deeper tailing is reduced by the top soil retention, leading to different reached depths of all simulations with high irrigation intensity. Low intensities resulted in similar overall breakthrough. In Appendix Fig. E1 the breakthrough curves after 1 h simulation of all generic application tests show the same dependency on soil type and antecedent state.

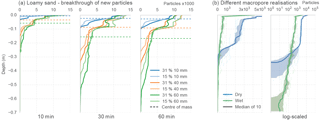
Figure 7 Simulated depth distribution of new particles in generic application tests. (a) Loamy sand at different times after irrigation start. (b) Simulations with different macropore realisations based on the same input data.

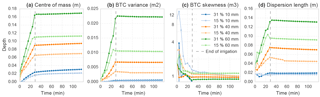
Figure 8 Dynamics of the moments of the breakthrough curves (BTCs) of loamy sand simulations. (a) First moment as centre of mass, (b) second moment as variance of depth distribution, (c) third moment as skewness of depth distribution and (d) dispersion length defined by $<A>/<B>$.

It is noteworthy to regard the development of the corresponding moments of the depth distribution of infiltrating particles (Fig. 8). The average travel depth increases with time in a clearly non-linear way during rainfall-driven conditions, and remains nearly constant during non-driven conditions afterwards. The variance exhibits a similar temporal pattern. The skewness of the travel depth distributions generally peaks shortly after the irrigation onset and decreases after that. This rising limb and the early peak marks the initial development of “flow fingers” in a single or a few macropores. The activation of additional macropores does however reduce the skewness as the median of travel depth starts to “chase” the mean. This finding shows clearly that a flow pattern that is strongly dominated by preferential flow is not necessarily skewed (Dreuzy et al., 2012). As the third moment tends to minimise for the cases with high antecedent soil moisture and thus lateral diffusion, the qualitative observations of relatively smooth infiltration patterns in Fig. 6 are reflected very well. The temporal evolution of the dispersivity in Fig. 6d reveals clearly that the transport is not well mixed during the entire duration of the rainfall forcing. It operates in the near field, as the variance grows quadratically with time. Later, diffusion dominates the soil water redistribution.

In addition, we performed model parameter-related tests drawing different realisations of the macropore setting from the same ensemble (Fig. 7, right panels). The breakthrough curves of eight alternative realisations of the representative macropores under two different antecedent conditions are given with the 0.25 and 0.75 percentiles as variability bands. In order to evaluate the effect on potential contaminant breakthrough, a log-transformed plot is given. The results are within realistic bands and well below the uncertainty of tracer recovery of such experiments. Thus, test aspect d is achieved. Variance can be narrowed by defining a larger domain width. This may become important for highly skewed macropore distributions, for which the requirement for the minimal domain width may be higher than assumed.

Tests with different particle resolutions showed that definitions that are too coarse can result in local averaging, which underestimates the actual depth distribution of the infiltrating water. A similar effect was observed with very coarse internal calculation grid definitions, which could no longer represent local state changes due to infiltration from the macropores into the surrounding matrix.

5.2 Reproduction of irrigation experiment

The last benchmark is the reproduction of observed tracer profiles based on measured parameters (test aspect e).

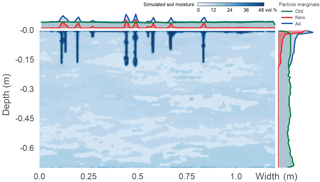
Figure 9 Simulated particle distribution in mimicry of the Weiherbach, 40 min after irrigation onset. A video of the simulated dynamics is given in the Supplement.

The simulation depicts the observed stain patterns and concentration profiles very well (Fig. 9; see video in the Supplement). Despite a lack of precise observation of the actual non-uniform flow dynamics, the simulated behaviour also matches the time-lapse GPR records. In combination with the GPR data, the simulation snapshot taken at about one-third of the irrigation period refers well to the profiles of tracer and soil water content recorded in the field (Fig. 10). For comparability, the simulated distribution of new water particles is converted to a tracer mass by assuming a domain thickness of one particle diameter, referring the simulated mass to the sampled volume and applying the Br⁻ concentration in the irrigation solution. Moreover, the snapshot is scaled to the total irrigation to be conclusively comparable to the recovered profile. Despite overall good fit with the first hump, the profile still deviates at shallow accumulation around 0.05 m and at deeper percolation to 0.3 to 0.4 m. Although the GPR records also suggest that the second concentration hump is resulting from deeper percolation just after the reference time of 45 min, the model runs had to be seized after this time due to computation time constraints. However, the generally reasonable recovery of the BTC is very much in line with the findings in the generic application tests presented earlier. The overall shape of the distribution of new particles was established relatively soon after irrigation onset, while the fast and slow fractions are fixated after the end of irrigation.

Changes in soil water content are accumulated to the integration volume of the TDR sensor for better comparison (Fig. 10b). The simulation fits between the reference records at 28 and 60 min after irrigation onset. While the overall shape of the profile is plausible, the high water content near the surface is not reflected in the early soil moisture measurements. It is noteworthy that because of the large integration volume of the sensor, many of the characteristics of the profile are strongly smoothed out.

A closer look at the outcrops in Fig. 4 exhibits a deviation of the wetting front and the stain pattern, which hints at chromatographic effects due to a shift in flow velocities switching from high velocities during well-supplied states near saturation to a purely diffusive transport. This process is represented in the model too: the flow in the macropores takes place at different velocities until very shortly after the end of irrigation. Then diffusive redistribution alone governs the lateral water transport. Similar results have been found in Brilliant Blue tracer experiments and simulations with the same model by Reck et al. (2018).

Moreover, it can be noted that the modelled depth distribution of new particles coincides with the observed tracer breakthrough. This is especially interesting because the macropores are defined as reaching through the full domain as earthworm burrows are reported to reach depths below 2 m. Hence the self-controlled limitation of advective flow in the macropores appears to be capable of reproducing the true process.

Figure 10 Simulated and observed tracer (a) and soil moisture profiles (b) in the irrigation experiment. Tracer mass scaled to core sample volume and total irrigation after 2 h.

6 Discussion

6.1 Model adequacy

The general adequacy of the echoRD model to represent non-uniform irrigation water redistribution is outlined by the generic application tests. The water particles move realistically in the conjugated domains under the tested conditions. The mimicry of an irrigation experiment based on directly measurable parameters also corroborates the proposed model framework with regard to structural adequacy (Gupta and Nearing, 2014; Gupta et al., 2012) and the intended objectives. However, further testing is required and should explore the capabilities of the model under various macropore settings in heterogeneous soils. In particular, the universality of the proposed macropore–matrix exchange concept and the derivation of site- and event-specific breakthrough references deserves further assessment for upscaling.

During the development we followed Clark et al. (2011) by testing multiple alternative working process hypotheses for (a) the initial irrigation water redistribution, (b) the initial advective velocity reference, (c) the macropore–matrix exchange and (d) the macropore film flow as further detailed in Jackisch (2015). During preliminary testings the set presented here performed most realistically. However, we encourage further testing and development of more hypotheses within the framework. Especially since the Lagrangian method using water itself as particles required the abandonment of most of the well-established theories of soil water movement in a Eulerian domain, there is ample room for further adaptations, extensions and even falsification of the proposed ideas. The provided repository of the model shall invite and prepare the community to do so.

Despite the achievements, the echoRD model also has a number of limitations: because the particles do not interact, any solute transport is governed by the fluid movement alone. For the event scale this might be an acceptable assumption. With a molecular diffusion coefficient of bromide in free water (D_mol = 2.5 × 10⁻⁹ m s⁻¹) and an event duration of a few hours (1 × 10⁴ s) the diffusion length will range in the order of 5 × 10⁻³ m, but for longer simulations this needs explicit consideration.

6.2 Representative structured domain and particle concept

Building on the idea of self-similarity in flow networks going back to the works of Rodriguez-Iturbe and Rinaldo (1997) and Rinaldo et al. (2014) we propose a topologically explicitly structured domain set-up for the plot scale. The presence and importance of interfaces in soils (Hassanizadeh and Gray, 1990; Lehmann et al., 2012) led to the proposition of the combination of a 2-D matrix, which accounts for non-equilibrium lateral and vertical diffusion, and multiple 1-D vertically oriented advective structures, which account for fast vertical redistribution. With this, we also seek to combine some of the existing modelling approaches with multi-phase soil water dynamics (Gerke, 2006; Jury and Roth, 1990; Sander and Gerke, 2009; Vogel and Roth, 2003; Vogel et al., 2006).

We explicitly avoid a direct and tortuous representation of a macropore network as commonly observed (Capowiez et al., 2003, 2011). All effects connected to friction in the macropore (which includes the inclination of the macropore gallery and pore roughness) are implicitly summed up in Eq. (8). When more information is given, this can be further differentiated in a future adaptation. The effect of coatings in earthworm burrows (Jarvis, 2007) has so far been neglected due to a lack of experimental references. As also found to be important in a study on dynamic macropore settings using the echoRD model (Reck et al., 2018), a dynamic coating factor is however foreseen to scale the macropore–matrix interface. Although most of the specific references have been drawn with relation to earthworm burrows, the current concept is intended to apply to any kind of macropore.

Representativity of the model domain for the plot scale is achieved when the integral of the dynamics is invariant to a larger domain extent under a given desired process resolution. For the mimicry of the irrigation experiment, we evaluated different domain size definitions for their respective BTC dynamics.

The combination of the particle approach with the connected domains avoids a number of implicit assumptions for the exchange between the domains. Our energy-balance approach to film flow in the macropores enables analyses of different infiltration patterns with self-controlled advection and diffusion. In addition to this process hypothesis, many alternative approaches to model the interfacial processes and the behaviour within the respective domains can be imagined. For this, the echoRD model allows for direct process hypothesis testing with the same objects.

We have shown that different infiltration patterns emerge based on different antecedent conditions and forcing of the representative structured domain (Sect. 5.1). The influence of different realisations of the representative macropore domain from the same ensemble has been small. This does corroborate the validity of the selection of the representative domain.

The non-stationary and non-linear dispersivity underpins the limitations when the processes during driven conditions are subsumed by explicit and universal parameterisation. However, diffusive transport dominates quickly after the supply ceases. This motivates a potential use of the full echoRD model to derive state- and forcing-dependent distribution references for the advective flow field, which can successively be used in more simple versions of the particle model like our 1-D approach (Zehe and Jackisch, 2016) or the MIPs model (Davies et al., 2011). Moreover, the concept can also be downscaled to analyse porewater fractionation in the vadose zone, extending our initial binning approach in the pore spectrum. Both aspects are present within the same framework. With this, an alternative scaling in the sense of the scaleway (Vogel et al., 2006), but without the need to interface different conceptualisations, is possible.

6.3 Capability and limits of the model

Although the echoRD model possesses many degrees of freedom to adjust its behaviour, it is not intended for parameter fitting. Instead, the model is proposed as an exploration tool capable of extending real-world experiments. As such, the model requires very few parameters, which can all be derived from suitable experiments: soil matrix parameters are used for the determination of the diffusive and storage properties of the soil and consist of soil water retention parameters. If desired, the van Genuchten model can be replaced by any other soil water retention model. Each calculation grid node of the matrix domain can be assigned to a different soil matrix definition. Macropores host the advective flow and are determined by the spatial distributions (relative lateral distances and connected pore depth) and a reference to maximum flow capacity. In addition some coating factor may be defined for earthworm burrow coatings (Jarvis, 2007) which scales the contact interface to the matrix.

There has been much debate about the derivation of effective parameters in hydrological models (Bashford et al., 2002; Neuweiler and Vogel, 2007). With the physical description of the two domains and their exchange, the parameters become much more specific and scale-aware. Soil water retention properties are determined for the matrix in standard lab procedures, while macropore settings can be quickly assessed with dye staining experiments in the field (Reck et al., 2018). With this, we also aim to contribute to model falsifiability (Harte, 2002). As it is making direct use of the laboriously gathered and valuable data from experiments, surveys and monitoring, it also improves the matching of model concepts and hydrological observables (Beven, 1993, 2006). However, the echoRD model is still relying on numerous conceptual assumptions and process approximations which are not scale-independent. As such the model is not suitable for blind upscaling by multiplication of the individual representative domains. Instead, the model delivers a physically based foundation for infiltration statistics which can then inform Markov processes of higher orders.

We envisage further use with dynamic macropore settings as the domain may update once it is empty and as a foundation to derive state- and forcing-dependent stochastic site properties which can be used in more lumped versions of the approach. Since the particle domain can always be converted into a Eulerian field of matric potential or soil water content and vice versa, the model can also be linked to a Richards model for periods when the diffusive flow assumption is valid.

In the application tests it was seen that the model is quite sensitive to antecedent conditions. Under hardly determinable state data this may lead to susceptibility of the model to uncertainty about the macropore–matrix exchange, which can be amplified through the non-linear retention properties. Moreover, the model has shown sensitivity to dead-ended macropores. Hence special care has to be given to provide valid data on the macropore distribution and vertical connectivity.

6.4 Numerical concerns

The simulation of soil water dynamics based on water itself as particles is generally very different from the common particle tracking for solutes. On the one hand there is no external drift and the activity of each particle depends on its neighbours. On the other hand a very large number of particles is needed to enable robust calculation of the low event signal against a rather high background or pre-event concentration. The reason for this is that the resolution of the process dynamics scales with the number of particles per volume reference (grid cell in our case). At the same time we require relatively small volume references to avoid integration over scales that are too large. All of these points demand a large number of particles which require frequent state updates about their relative concentration distributions and binning in the porewater space. Moreover, the calculation of film flow with many particles is similarly self-dependent.

The Courant and Neumann criterion for the time step control calculates a global specification. Hence local wetting causes very small time steps for the whole model. In combination with the previous concerns, this makes the model computationally very expensive. Due to the self-dependent state, we could not find any option to make use of the more efficient continuous time random walk methodology (Delay and Bodin, 2001; Dentz et al., 2012; Metzler and Klafter, 2000).

In the current state of experimental code, the model runs at about 10 to 200 times more slowly than the real time of the simulated case. Despite its potential, we abandoned trials using grid-free methods to calculate the particle density, e.g. by Voronoi polygon area calculation (Rycroft, 2009), as they multiplied the calculation effort even further. A next step will be to optimise the model for performance in the frequent state updates.

6.5 Model-based extension of real-world experiments

One of the intended uses of the model is to overcome the limitations of destructive irrigation experiments. So far it is impossible to repeat tracer-based plot irrigation experiments as the site needs excavation for sampling. Moreover the spatial and temporal scales of such experiments are very difficult to observe (Jackisch et al., 2017). Since the model is promising with regard to simulating infiltration, advective flow, macropore–matrix exchange and diffusive redistribution without explicit exchange parameterisation, it provides opportunities for virtual experiments on the controls of non-uniform subsurface flow.

Figure 7 hints at the interplay of supply rates and duration for advective flow breakthrough. Jackisch (2015) presented an initial model analysis of the effectiveness of fast drainage under different antecedent conditions and forcing. The simulations reveal that preferential flow occurs under all conditions, corroborating the findings of Nimmo (2011). Under wet antecedent conditions moderate rainfall events can also result in substantial breakthrough. The same was shown by Reck et al. (2018) in tracer experiments and subsequent modelling in different seasons.

Besides the initial development of flow fingers and the evolution of the skewness of the depth distribution of the event water (Sect. 5.1), another aspect is that a large number of macropores does not necessarily result in deeper percolation since the irrigation supply is distributed to all effective macropores. This can lead to situations whereby the supply rates in the macropores drop below the macropore–matrix exchange rates. As the model is capable of reproducing this behaviour, we hope that it can contribute to a unification of the debate about the importance of non-uniform flow and preferential flow paths.

7 Conclusions

In a recent paper (Zehe and Jackisch, 2016) we provided the foundation for an alternative representation of soil water diffusion based on a random walk of water particles in the space domain. We showed that this is a true alternative to solvers of the Richards equation. In this study, we extended the approach to a multi-domain model of infiltration, advection and diffusion in a representative structured domain, with a 2-D matrix hosting topologically explicit 1-D macropores as a physical and least adequate representation of the processes – the echoRD model (ecohydrological particle model based on representative domains).

In a series of application tests we showed the model's capability to represent (a) 2-D diffusive, non-uniform soil water redistribution, (b) self-controlled interaction of the 1-D advective paths with the 2-D soil matrix, (c) sensitivity to state variables and observable model parameters and (d) robustness of the representative macropore setting based on macropore depth distributions. Moreover, the model was successfully used to mimic a real-world irrigation experiment based on measured parameters.

This implies the structural adequacy of the model simulating advective flow as dynamic film flow in topologically explicit macropores and accounting for macropore–matrix exchange based on an energy-balance approach. The multi-domain interplay of advective and diffusive soil water redistribution exhibited a non-linear temporal evolution of the dispersivity. While the process description appears to be rather sophisticated, its parameterisation is very simple as the model relies on soil water retention properties for the soil matrix and data on the depth distribution of effective macropores.

As the model is intended to be a learning tool to extend real-world experiments, we have shown its potential for virtual experiments under different antecedent states, macropore settings and precipitation forcing. The model is also envisaged to deliver a physically based foundation for infiltration statistics, which can then inform Markov processes of higher orders in simpler 1-D versions of the model (Zehe and Jackisch, 2016) scaling the approach to the hillslope by means of definition of representative soil domains connected to an explicit lateral structure (Zehe et al., 2014).

Appendix A: Variables used

Symbol	Description	Unit
D(θ)	Diffusivity	m2 s−1
Ekin	Kinetic energy	kg m2 s−2
ε	Dissipation	kg m2 s−2
η	Dynamic viscosity of water	kg m−1 s−2
g	Gravitational acceleration	m s−1
I	Impulse counteracting Ekin	kg m s−1
k(θ)	Unsaturated hydraulic conductivity	m s−1
m	Mass	kg
n	Count	–
Ψ	Matric head	Pa
ψ	Matric head as column water	m
q	Flux	m s−1
R	Macropore radius	m
rparticle	Particle radius	m
ρ	Density of water	kg m−3
t	Time	s
θ	Volumetric soil water content	m3 m−3
u	Advective velocity in matrix	m s−1
v	Advective velocity in structures	m s−1
V	Volume	m3
x	Lateral distance	m
ξ	Uniform random number −1 … 1	–
z	Depth	m

Appendix B: echoRD model set-up and preprocessor

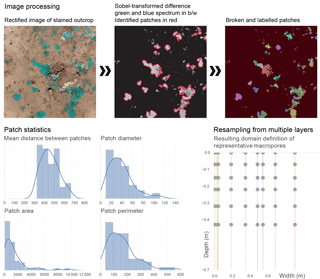
The echoRD model can be set up based on soil water retention data (as a table of van Genuchten parameters) for different soil layers and any sort of information about the macropore distribution. The easiest way is to provide images of horizontal outcrops of dye stain patterns to the preprocessor.

The rectified and cropped images with a defined resolution are read and analysed for stained patches using scikit-image (van der Walt et al., 2014) and scipy.ndimage packages. To do so, the patches are identified by using the watershed image processing in scikit-image (Beucher and Lantuejoul, 2006) based on a Sobel-transformed difference of the green and blue spectrum of the RGB image. Small patches below a given threshold are discarded. Large patches are assumed to consist of multiple macropores and are broken down by means of watershed segmentation. After removal of clutter the patches are labelled and their geometry is assessed.

In a next step these identified patches are analysed for distribution of topological parameters like total number, distance, size and diameter. Based on the least density among all horizons, the representative domain is scaled so that at least one effective macropore exists in the sparsest case. Thus, the fewer macropores, the larger the domain.

Subsequently, topological parameters are then resampled on the representative domain by allocating all representative macropores to a certain position on the 2-D matrix domain based on the observed lateral distance distribution. Moreover, contact areas are defined, depending on the circumference distribution of the patches.

An example is given in Fig. B1. The code is included in the repository and initiated by run_echoRD.preproc_echoRD.

Figure B1 Example of preprocessing of stain images, patch identification and statistics and resulting macropore positions in the representative domain.

Appendix C: The echoRD repository

This paper is accompanied by a repository at GitHub, in which the echoRD model and the presented test cases are made publicly available: https://github.com/cojacoo/echoRDmodel. The model is developed and tested based on Python 3.5.2. The examples are given as Jupyter Notebooks and as standalone scripts. The packages NumPy, SciPy, Pandas and Matplotlib are required. The preprocessor requests more specific packages as outlined there.

All software and data are given under the GNU General Public License (GPLv3) and the Creative Commons License (CC BY-NC-SA 4.0) respectively. This is scientific, experimental code without any warranty or liability in any case. The code is not fully optimised yet and calculations are computationally demanding. However, you are invited to use, test and expand the model at your own risk. If you do so, please contact the first author and repository owner to keep them informed about bugs and modifications.

The repository holds the folder echoRD with the model engine and the folder testcase with routines controlling the model and several set-ups and exemplary results. For a quick view, the Jupyter Notebooks can be accessed online from the repository home. If you want to run the model yourself, please clone and fork the repository.

Figure C1 Exfiltration time of a particle from the macropore wall into the adjoined soil matrix for different soils and soil moisture states.

Appendix D: Synthetic references for exfiltration from macropores into the surrounding matrix

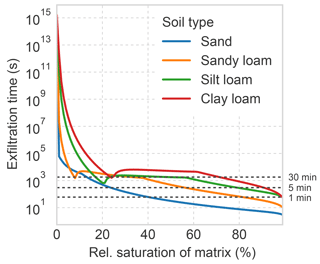
In Sect. 3.3.3 we present the dynamic calculation of macropore–matrix interaction. On this basis one can calculate a mean exfiltration time of a particle at the pore wall for different properties and states of the surrounding soil matrix. Figure C1 presents results for different soils defined according to Carsel and Parrish (1988). Counteracting saturation of the matrix in case of limited drainage is neglected.

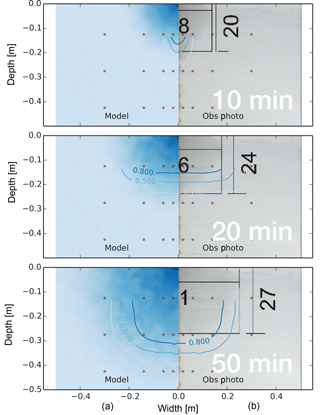
Figure D1 Diffusive exfiltration from an irrigated artificial macropore. Experiment by Germer and Braun (2015). The irrigation rate was 3.78 L h⁻¹. (a): model simulation of relative saturation (the half cylindrical column is assumed as planar column). (b): observed photograph of proceeding wetting front (vertical and lateral extent marked by black annotation). Contour lines: relative saturation calculated and interpolated from tensiometer (red dots) measurements.

To evaluate the capability of the model to simulate lateral diffusion and macropore matrix exchange, we compared the macropore–matrix simulations and diffusive redistribution of water particles to an experiment by Germer and Braun (2015). They irrigated an artificial macropore (filled with coarse sand for stability) in a packed fine sand cylinder. The exfiltration and diffusive redistribution was observed by means of time-lapse photographs and tensiometer monitoring. Similar to the simulations of Gerke and van Genuchten (1996), we set up the echoRD model according to the geometries and measured retention properties of the experiment. The model represented the observed, predominantly lateral water redistribution and the respective breakthrough very well (Fig. D1).

Appendix E: Further model figures

Figure E1 presents breakthrough curves of the different soils used in the generic application tests.

The videos of the modelled evolution of soil water content are given in the Supplement.

Figure E1 Simulated depth distribution of new particles in generic application tests. Different soil types after 1 h.