Evaluation of the ability of the Weather Research and Forecasting model to reproduce a sub-daily extreme rainfall event in Beijing, China using different domain configurations and spin-up times

The rainfall outputs from the latest convection-scale Weather Research and Forecasting (WRF) model are shown to provide an effective means of extending prediction lead times in flood forecasting. In this study, the performance of the WRF model in simulating a regional sub-daily extreme rainfall event centred over Beijing, China is evaluated at high temporal (sub-daily) and spatial (convective-resolving) scales using different domain configurations and spin-up times. Seven objective verification metrics that are calculated against the gridded ground observations and the ERA-Interim reanalysis are analysed jointly using subjective verification methods to identify the likely best WRF configurations. The rainfall simulations are found to be highly sensitive to the choice of domain size and spin-up time at the convective scale. A model run covering northern China with a 1 : 5 : 5 horizontal downscaling ratio (1.62 km), 57 vertical layers (less than 0.5 km), and a 60 h spin-up time exhibits the best performance in terms of the accuracy of rainfall intensity and the spatial correlation coefficient (R^′). A comparison of the optimal run and the initial run performed using the most common settings reveals clear improvements in the verification metrics. Specifically, R^′ increases from 0.226 to 0.67, the relative error of the maximum precipitation at a point rises from −56 to −11.7 %, and the root mean squared error decreases by 33.65 %. In summary, re-evaluation of the domain configuration options and spin-up times used in WRF is crucial for improving the accuracy and reliability of rainfall outputs used in applications related to regional sub-daily heavy rainfall (SDHR).

1 Introduction

The possibility that sub-daily heavy rainfall (SDHR) will increase with climate change is of significant societal concern. SDHR-driven flash floods (FFs) are among the most destructive natural hazards that threaten many urban areas in northern and central China and many other parts of the world. In these regions, SDHR is mainly triggered by regional mesoscale circulation systems (MCSs) and occurs with increased intensity and frequency in warm seasons (Yu et al., 2007; Chen et al., 2012). Records from the Emergency Events Database (EM-DAT) indicate that the damages and losses caused by FF events in China have increased significantly over the past several decades. The risks are expected to continue to grow, given the increase in the magnitude of SDHR predicted by most general circulation models (Chen et al., 2012; Willems et al., 2012; Westra et al., 2014). The accelerating pace of urbanization also contributes to the increase in risk; urbanization has already changed the hydrologic characteristics of the land surface considerably, resulting in higher peak flows and shorter flow concentration times (Xu and Zhao, 2016; Gao et al., 2017). In such cases, very short-term (< 6 h) rainfall predictions are not sufficient to provide adequate warning and mobilize emergency response activities. Recently developed statistically based rainfall generation methods and remote sensing data have been shown to enable the extension of the lead time to 24 h (Yu et al., 2016). However, this lead time is still insufficient to provide effective flood mitigation for medium or large urban areas with very short hydrologic response times (Shih et al., 2014; Li et al., 2017). Therefore, numerical weather prediction (NWP), which represents a means of forecasting heavy rainfall with lead times exceeding 24 h, has come into wide use in flood-related studies and applications (Cuo et al., 2011).

Precipitation uncertainty accounts for a large proportion of the uncertainty in flood forecasts. Hence, given the large uncertainties in NWP, its use in flood forecasting has long been questioned (Castelli, 1995; Bartholmes and Todini, 2005). Its usefulness was not realized until the end of the 20th century; substantial improvements in the predictive skill of NWP were made that resulted from the increases in computational power and storage capacity, which enable parallel processing of high-resolution forcing data and the resolution of convective-scale physical processes (Done et al., 2004; Clark et al., 2016). The NWP models developed during and after this period can perform regional and convective-scale modelling and display good performance in simulating heavy rainfall. Experimental studies have shown that NWP models of this kind, such as the WRF model (Skamarock et al., 2008), tend to capture greater numbers of small-scale processes and the triggers of convective storms (Klemp, 2006; Prein et al., 2015). Increasing numbers of meteorological operational centres and research groups are adopting these new NWP models to carry out simulations of heavy rainfall events or real-time forecasting. The resolutions of the rainfall products have improved from tens of kilometres to less than a kilometre, and the lead times have increased from less than a day to more than a week (WMO, 2013). Meanwhile, case studies have been carried out using regional convective-resolving models to evaluate the local rainfall predictions generated by sophisticated regional nesting techniques or the global smooth grid transition approach on unstructured grids (Swinbank and James Purser, 2006; Hong and Lee, 2009; Soares et al., 2012; Sikder and Hossain, 2016; Heinzeller et al., 2016). The results of these studies demonstrate that, over relatively short periods of time, regional modelling is often superior to large-scale modelling because it better resolves surface heterogeneities, topography, and small-scale features in air flow such as growing instabilities (Miguez-Macho et al., 2004; Yu et al., 2010; Prein et al., 2015; Brömmel et al., 2018).

Despite the great potential of NWP models to predict heavy rainfall, a number of uncertainties remain that must be considered. The errors induced by the initial and boundary conditions represent one source of these uncertainties; others stem from cognitive errors and the scale effect in the solution of physical models, both of which may be exacerbated by the chaotic nature of NWP. In regional simulations, these uncertainties are expected to be further magnified by downscaling or the use of mesh transition procedures, so re-evaluation and calibration of the related model configurations are commonly required (Warner, 2011; Vrac et al., 2012; Liu et al., 2012). As an example, running the WRF model at convective scales means that convective processes are more likely to be resolved by explicit physical schemes than when sub-grid parameterizations are used, which may incorporate new structural uncertainties related to the model physics (Done et al., 2004; Ruiz et al., 2010; Crétat et al., 2012). In addition to model physics, several other aspects of model configuration, such as the domain size, the spatial resolution, and the spin-up time, may also have a substantial impact on the uncertainty in rainfall forecasts through their effects on the initial and boundary conditions (Aligo et al., 2009; Fierro et al., 2009; Cuo et al., 2011). However, these aspects of model configuration have received less attention in regional case studies because of their insignificant effects on rainfall forecasts in coarse-resolution and long-term model simulations when compared to the physics of the WRF model. Generally, these model configuration aspects are left at the common settings recommended by the official website of the WRF model and by some experimental regional heavy rainfall studies.

Precipitation is one of the most sensitive variables to NWP model uncertainties. In this study, a re-evaluation of WRF is performed to explore whether the recommended configuration of WRF represents the best choice in reproducing a regional SDHR event that happened in Beijing. The WRF model is assessed here because of its superior scalability and computational efficiency; these traits are valued in interdisciplinary studies (Klemp, 2006; Foley et al., 2012; Coen et al., 2013; Yucel et al., 2015). As the latest NWP community model, WRF incorporates up-to-date developments in physics, numerical methods, and data assimilation and is thus widely used in theoretical studies and practical applications (Powers et al., 2017). The selected regional SDHR event occurred on 21 July 2012 and was centred over Beijing, China. Beijing is among the most vulnerable cities to SDHR-induced floods in central China (Yu et al., 2007). The precipitation in this area is caused mainly by monsoon weather systems and enhanced by local orographic effects, and 60–80 % of the total annual precipitation occurs during just a few SDHR events (Xu and Chu, 2015). The SDHR event that occurred on 21 July 2012 caused the most disastrous urban flood in Beijing since 1950. The national operational NWP system failed to predict this event, which resulted in 79 deaths and more than USD 1.6 billion in damage (Brömmel et al., 2018; Wang et al., 2013; Zhou et al., 2014). Thus, several convective-scale studies have been carried out to re-evaluate the optimal combination of the physics options used in the WRF model, such as Di et al. (2015) and Wang et al. (2015). These studies represent the background information that stimulates this research.

The second question we attempt to explore is to what extent rainfall simulations could be improved through the use of the likely best set of settings if the recommended model configurations are not the best choices. The aspects of the model configuration that are evaluated in this study are the domain size, vertical resolution, horizontal resolution, and spin-up time. These options have been found to have substantial impacts on daily-scale extreme rainfall outputs (Leduc and Laprise, 2009; Aligo et al., 2009; Goswami et al., 2012). A comparative test with four scenarios is designed. Each scenario evaluates one model configuration option to ensure that the simulated disparities can be attributed solely to a single factor each time. In addition, the test is conceived as a progressive process: the optimal setting identified in each scenario will be adopted as the primary choice for the next scenario to help quantify the overall improvement in the accuracy of rainfall outputs. The “ground truth” datasets are gridded observations obtained from Beijing Normal University and the China Meteorological Administration. A coarser-resolution reanalysis called ERA-Interim (Dee et al., 2011) is also employed in identifying departures of the WRF simulations from the driving weather fields as the model setup is varied. Seven objective verification metrics that reflect different features of the model performance are adopted and considered jointly as part of a subjective verification process because no single verification approach has been shown to provide comprehensive information about the quality of rainfall simulations (Sikder and Hossain, 2016). Most of the metrics adopted here are those used to assess the performance of WRF over daily or longer time periods (Liu et al., 2012; Tian et al., 2017). In this research, these metrics are calculated on an hourly basis and averaged over different sub-daily time spans to evaluate the performance of the WRF model using different configurations from a sub-daily and convective-scale perspective.

2 Numerical model used to forecast heavy rainfall

The advanced WRF (ARW-WRF) model, version 3.7.1, is used as the dynamical downscaling tool. ARW-WRF is a compressible non-hydrostatic and convection-permitting regional NWP model that employs the conservative form of the dynamic Euler equations. As the latest regional NWP community system, WRF is composed of two dynamic cores, a data assimilation system and a platform that facilitates parallel computation and function portability. Observations, model output or assimilated reanalysis output can be used to initialize WRF. In terms of discretization, WRF uses a third-order Runge–Kutta method for temporal separation and an Arakawa C-grid staggering scheme for spatial discretization. The model is capable of conducting either one-way or two-way nested runs for regional downscaling. A detailed introduction to the physics and numerical properties of ARW-WRF can be found in Skamarock et al. (2008). Given its emphasis on efficiency, portability, and updates to reflect the state of the art, WRF has been employed in settings ranging from research to applications and has been incorporated into various operational systems, such as the Hurricane-WRF system for hurricane forecasting and the WRF-Hydro system for hydrologic prediction.

In WRF, the domain size implicitly determines the large-scale dynamics and terrain effects, whereas the vertical and horizontal grid spacings determine the smallest resolvable scale (Goswami et al., 2012). Together, these domain configuration options affect the spectrum of the resolved scales and the nature of scale interactions in the model dynamics (Leduc and Laprise, 2009). Thus, they are responsible for the generation and distribution of precipitation. In regional simulations, small domain sizes are commonly preferred for computational efficiency. Seth and Rojas (2003) demonstrated that simulations with small domain sizes are more likely to benefit from the lateral boundary conditions (LBCs) by dampening the feedback from local perturbations on the large-scale general circulation. However, insufficiently large domains have been shown to prevent the full development of small-scale features over areas of interest. To solve this issue, the official website of WRF provides general guidance (Warner, 2011). This guidance recommends that the ranges of domains should include the major features of the leading MCSs and local surface perturbations, and more than five grid points should exist between adjacent nested domains to allow for sufficient relaxation.

As for grid spacing, it appears plausible that WRF model runs performed with relatively small grid spacings would provide more accurate outputs because such runs would resolve more small-scale phenomena of interest that are not present in the LBCs. This statement is generally accepted as true when a relatively coarse-resolution run (> 10 km horizontally or > 1 km vertically) is compared with a relatively finely resolved run at the convective scale (1–5 km horizontally or < 1 km vertically) in representing a convective storm. However, this conclusion is controversial when the comparison is conducted among convective-scale model runs. Taking the horizontal resolution as an example, although there is evidence to show that WRF runs performed at relatively high resolution capture more convective-scale features, the accuracy of rainfall outputs either shows considerable or no statistical improvement (Roberts and Lean, 2008; Kain et al., 2008; Schwartz et al., 2009). In one study, Fierro et al. (2009) suggested that some features detected in convective-scale runs with too small horizontal grid spacings tend to weaken the kinetic structures that favour torrential rainfall. A similar conclusion was drawn by Aligo et al. (2009) in evaluating the impact of the vertical grid spacing on simulations of summer rainfall performed using WRF. Thus, horizontal and vertical grid spacings of approximately 4 and 1 km, respectively, have been employed as a reasonable compromise between accuracy and computational efficiency in several regional studies.

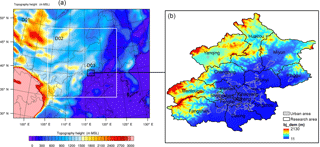
Figure 1 Relative location of the study area. (a) Shows the three nested domains adopted in most of the experiments, of which domain three (D03) covers the entire Beijing area; (b) depicts the geographic features of the Beijing area.

In regional modelling, a spin-up period is often required to balance the inconsistencies between the results simulated by the model physics and the initial and boundary conditions provided by the forcing data (Luna et al., 2013). The proper spin-up time depends on the time needed for initialization, which can be affected by the size of the domain and the local boundary perturbations (Warner et al., 1997; Kleczek et al., 2014). Moreover, the presence of chaotic behaviour, which causes reductions in the predictive skill of models over time, imposes an upper bound on the spin-up time. Therefore, in cases where short forecast lead times are expected, e.g. real-time rainfall forecasting, the spin-up time is mainly determined by the domain size and the regional initial and boundary conditions. However, in cases where long forecast lead times are needed, e.g. warnings of extreme rainfall, the effects of chaotic behaviour should be relatively evident. In practice, this issue is commonly addressed by regularly updating the lateral boundary information derived from the latest forecasts or analyses to maintain consistency between the regional model solutions and the atmospheric forcing conditions. In such cases, the best-fit performance may occur for model runs with long spin-up times. Based on most previous studies, a spin-up time of 12 h is recommended to obtain an initial state; however, this spin-up time is often regarded as the suitable choice in many regional case studies without further verification.

3 Studied event and experimental design

As mentioned above, one aim of this study is to re-evaluate whether the recommended WRF domain configuration options and spin-up time represent the optimal model configuration for reproducing a regional SDHR event when evaluated at a sub-daily timescale. Here, the SDHR event that occurred on 21 July 2012 and was centred on Beijing, China is selected as a case study. The reasons why this event is selected, the synoptic and physical features that drove this event, and the model physics adopted in this study are presented before the entire procedure of the experimental design is introduced.

3.1 Study event selection and WRF physical schemes

Beijing is selected as the study area because it is one of the most vulnerable cities to SDHR-induced FF hazards in China. Beijing is located in central China. It has an area of 16 411 km², and its weather is mainly affected by the semi-humid warm continental monsoon climate. The flows of air that favour local precipitation are cold, dry flows of air from high-latitude areas to the north and hot, wet flows of air from the ocean to the south. The interactions between these two flows of air lead to clear divergence in the temporal distribution of rainfall amount; 60–80 % of the annual precipitation occurs during just a few heavy rainfall events during the warm season. Of all of the heavy rainfall events, the intensity and frequency of SDHR events have been shown to display the greatest increasing tendencies over the past several decades. Meanwhile, Beijing, as the capital of China, has experienced a significant expansion of its urban area and rapid increases in its population and economic development. The negative effects of this expansion, such as losses of natural water bodies, increases in land cover with low permeability, and increases in urban drainage pipe networks, have led to continuous decreases in the hydrologic response time. In addition, most of the population lives in the southwestern plain area. This region is downstream of mountainous areas with steep terrain that varies in elevation from 60 to 2300 m (Fig. 1). All of these factors contribute to the continuing increase in the exposure of this city to the high risks of flooding and waterlogging caused by SDHR events (Xu and Chu, 2015).

The case study examines the largest heavy rainfall event that has occurred in Beijing in the past 65 years. The rainfall event lasted for 16 h (from 02:00 to 18:00 UTC) on 21 July 2012, and the highest hourly rainfall intensity (100 mm h⁻¹) was experienced in the southwestern part of the plain area. The associated FF hazard led to 79 deaths and damages totalling USD 1.6 billion, and more than 1.6 million people were affected. In addition to Beijing, the adjacent provinces, including Hubei and Liaoning, were all significantly affected by this event and experienced severe FF hazards. The synoptic features that triggered the rainfall were an eastward-moving vortex in the middle to high troposphere, a northward-moving zone of subtropical high pressure, and sharp vertical wind shear (Sun et al., 2013). The rainfall event as a whole can be divided into two phases. From 02:00 to 14:00 UTC, the convective rain was dominated and enhanced by the orographic effect. The frontal rain was then followed by the arrival of a cold front moving from the northwest until 18:00 UTC (Guo et al., 2015). The rainfall intensity in the second phase was relatively low compared to that in the first phase, due to the lack of strong kinetic forcing to maintain the occurrence of precipitation.

The ERA-Interim reanalysis and 30-second static geographical data are employed to initialize the surface and meteorological fields of the WRF. ERA-Interim is produced by an integrated forecasting system (IFS) used by the European Centre for Medium-Range Weather Forecasts (ECMWF). The IFS is an Earth system model that incorporates a data assimilation system and an atmospheric model that is fully coupled with land-surface and oceanic processes. The atmospheric model provides output every 30 min at a spectral resolution of T255 (approximately 81 km over Beijing). This output is then employed as prior information and combined with available observations twice a day to produce the reanalysis output using the four-dimensional variation (4D-Var) assimilation system. The final reanalysis product, ERA-Interim, is a global gridded dataset that is available at a spectral resolution of T255 and at both the 60 levels used in the model and 38 interpolated pressure levels for all dates beginning on 1 January 1979 (Berrisford et al., 2009; Dee et al., 2011). Here, the ERA-Interim pressure-level data are selected as the initial forcing. One reason is that, as is necessary, the vertical grid spacing between the adjacent pressure layers is less than 1 km in the free troposphere, where the convective processes mainly occurred during the Beijing SDHR event. In addition, the NWP models used by the China Meteorological Administration mainly employ 31 vertical levels in regional forecasting (WMO, 2013).

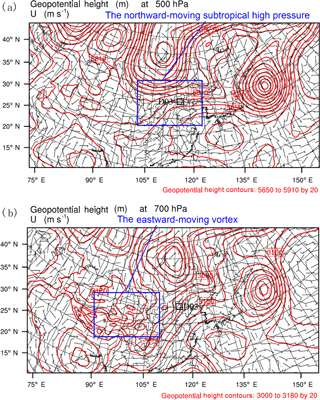
Figure 2 Initial wind field and geopotential height field at 00:00 UTC on 20 July 2012 over the Northern Hemisphere obtained from the ERA-Interim reanalysis. (a) The fields at 500 hPa; (b) the fields at 700 hPa.

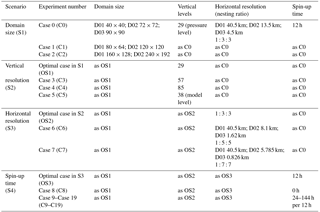
Table 1 Categories of experiments with different domain sizes, vertical resolutions, horizontal resolutions and spin-up times.

As shown in Fig. 2, ERA-Interim captures the vortex and the subtropical high pressure well that occurred at the beginning of the rainfall event. In addition, the patterns of the leading MCSs and the primary synoptic features shown in this figure also correspond well to those described in previous studies (Zhou et al., 2014). The setup of the model physics is based mainly on the results of sensitive, high-resolution studies on the physics of the WRF model in simulating the same event (Wang et al., 2015; Di et al., 2015). The “resolved rain” is driven by the single-moment 6-class microphysics scheme (Hong and Lim, 2006), whereas the “convective rain” is resolved using the Grell–Dévényi cumulus parameterization scheme (Grell and Dévényi, 2002). The Noah land-surface model (Chen and Dudhia, 2001) is used and coupled with the Monin–Obukhov surface layer model (Ek et al., 2003). The radiation processes are represented by the RRTMG shortwave radiation and the RRTMG longwave radiation schemes (Iacono et al., 2008). For the planetary boundary layer scheme, the Yonsei University method (Hong et al., 2006) is adopted.

3.2 Experimental design: domain configuration options and spin-up time

The comparative test is designed as a progressive process to help quantify the overall improvement in the performance of WRF after re-evaluating the WRF experiments performed using different domain configuration options and spin-up times. The test is classified into four successive scenarios. The first three scenarios investigate the domain configuration options, including the domain size, vertical resolution, and horizontal resolution; the fourth scenario concerns the spin-up time. During the entire procedure, the optimum configuration identified in each scenario is then adopted as the primary choice for the corresponding configuration in the following scenario. The initial datasets and the model physics are the same for all of the domains throughout the entire comparative procedure. Because the area of interest is located in the middle latitudes, the Lambert conformal projection is employed in all of the experiments, which is centred on the same latitude (42.25^∘ N) and longitude (114.0^∘ E). Moreover, sigma vertical coordinates with a top level of 50 hPa are used in all of the experiments.

Initially, the WRF domain configuration options and the spin-up time are set to the recommended values described in Sect. 2. Three levels of two-way nested domains are adopted so that the horizontal resolution in the smallest domain is sufficiently high to explicitly resolve convective-scale processes (Fig. 1). An odd downscaling ratio (1 : 3 : 3) is selected to reduce the initial error introduced by interpolating the initial fields to the assigned Arakawa grid. For the same reason, the boundaries of each domain are set along specific grid lines of the ERA-Interim dataset. Of the three nested domains, the outermost domain (D01) has the largest horizontal grid spacing of 40.5 km over north-central China, where the main perturbed synoptic features occur. The innermost domain (D03) has the smallest horizontal grid spacing of nearly 4.5 km over the area of interest, Beijing. The second domain (D02) is the child of D01 and the parent of D03 and has a horizontal grid spacing of 13.5 km. The distance between D01 and D02 is similar to that between D02 and D03, both of which exceed five grid points. The grid numbers of D01, D02, and D03 are 40 × 40, 72 × 72, and 90 × 90, respectively. The eta values utilized in the initial run are set based on the pressure values at the 29 vertical layers of the ERA-Interim pressure-level data. A spin-up time of 12 hours (12 h) is selected; the outputs are saved every 3 h in D03 and every hour in D02. The LBCs are updated every 6 h using ERA-Interim.

As shown in Table 1, the first experiment (C0) adopts the model configuration options mentioned above. To determine whether the domain configuration options and the spin-up time used in C0 are the likely best set, four scenarios are designed. The first scenario (S1) focuses on evaluating the effect of the WRF domain size. For computational efficiency, the MCS systems that drive the local synoptic features are not completely contained within the outermost domain of C0, the information of which is compensated by the updated LBCs from ERA-Interim. Two comparative experiments, C1 and C2, are devised to verify that the domain size assigned to C0 is large enough to enable the full development of small-scale features. Of the three experiments, C2 has the largest outermost domain size, which incorporates the leading MCS systems over the entire Northern Hemisphere. The intermediate domain, which is centred between the outermost and innermost domains, is then adopted as the outermost domain of C1. The purpose of scenario two (S2) is to evaluate whether the use of a higher vertical resolution in a WRF model run results in better performance. In this scenario, the starting experiment is the optimal experiment identified in S1 (OS1), forced by the ERA-Interim pressure-level data with 29 vertical levels. This starting experiment is then followed by two experiments, C3 and C4, which incorporate 1 and 2 times more vertical levels than OS1 (57 and 85 vertical levels), respectively. In the Beijing SDHR event, the pressure-level data meet the requirement of a grid spacing of less than 1 km in the troposphere; however, this condition is not necessarily satisfied in other regions. Thus, an experiment forced by the ERA-Interim model-level data with 38 vertical levels (C5) is also designed for comparison. The three experiments (OS2, C6, and C7) in scenario three (S3) differ in terms of their horizontal resolutions and nesting ratios, with increased nesting ratio of 1 : 3 : 3 (4.5 km grid spacing in D03), 1 : 5 : 5 (1.62 km in D03), and 1 : 7 : 7 (0.826 km in D03). The last scenario (S4) is designed to identify a reasonable optimal model run with the maximum spin-up time after minimizing the uncertainties introduced by inappropriate domain configuration options. It contains 1 starting experiment (OS3) and 12 comparative experiments (C8–C19). Except for C8, which includes no spin-up time, the remaining experiments (C9–C19) include spin-up times that increase from 24 to 144 h by every 12 h.

4 Verification schemes

Both objective and subjective verification methods are applied to the innermost domain (D03) at a sub-daily scale. D03 is selected because it covers the area of interest, Beijing, and the convective processes in this domain can be explicitly resolved in all of the experiments. The rainfall data used for comparison in D03 are 3-hourly 0.05^∘ data that were produced by fusing rain gauge observations and the CMORPH data (Huang et al., 2013). The ERA-Interim reanalysis is utilized as well to monitor the possible departures of the model simulations from the driving fields. Because the sub-daily rainfall is not available from the reanalysis, the atmospheric precipitable water vapour (PW), which determines the possible maximum precipitation, is instead compared with the model outputs every 6 h. In addition, the model outputs that cover a larger domain (D02) are compared with an hourly 0.1^∘ gridded dataset obtained from the China Meteorological Administration (http://data.cma.cn/data/cdcdetail/dataCode/SEVP_CLI_CHN_MERGE_CMP_PRE_HOUR_GRID_0.10.html, last access: 17 June 2018). The comparison over domain two is used only as an auxiliary method for subjective verification, based on the assumption that an experiment with good performance in the inner domain should also capture the large-scale features in the outer domain, as the appropriate representation of these large-scale features will result in more accurate boundary conditions.

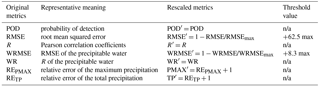
Table 2 Correlations between the original and rescaled objective verification metrics.

n/a = not applicable.

Seven error metrics that describe different features of precipitation are selected for use as objective verification metrics. Five are rainfall-related and compared by bilinear interpolation of the output of the simulations to the grid of the ground truth data. The accumulated areal rainfall is assessed using the relative error of the total precipitation (RE_TP). The percentage of correct rainfall hits is measured using the probability of detection (POD) with a threshold of 0.1 mm. The root mean squared error (RMSE) represents the amount of continuous error in the predicted precipitation. Detailed illustrations of these three metrics can be found in Liu et al. (2012) and Tian et al. (2017). The other two rainfall-related metrics are the relative error of the maximum grid precipitation (RE_PMAX) and the Pearson correlation coefficient (R), which describe the spatial association between the simulations and the ground truth data (Eqs. 1 and 2). The two metrics selected for the verification of PW (PW-related metrics) are the root mean squared error (WRMSE) and the Pearson correlation coefficient (WR). For comparison, the PW fields of the reanalysis are remapped to the grids of the model outputs using the WRF Preprocessing System (WPS). In this study, all of the metrics are calculated between the simulations and the reference data on the same grid at each time step (3 h in D03). The values of these metrics are then averaged over four different time periods (6, 12, 18, and 24 h) counted from 00:00 UTC on 21 July 2012. Different time periods are selected with the purpose of determining whether the performance of WRF differs when the evaluation is conducted using different durations.

$$\begin{array}{}\text{(1)}& {\displaystyle }& {\displaystyle }\mathrm{RE}={\displaystyle \frac{\mathrm{1}}{N}}\sum _{i=\mathrm{1}}^N\left[{\displaystyle \frac{f-r}{r}}\times \mathrm{100}\mathit{\%}\right],\text{(2)}& {\displaystyle }& {\displaystyle }R={\displaystyle \frac{\mathrm{1}}{N}}\sum _{i=\mathrm{1}}^N\left({\displaystyle \frac{\sum _{j=\mathrm{1}}^M\left(f_j-\stackrel{\mathrm{‾}}{f}\right)\left(r_j-\stackrel{\mathrm{‾}}{r}\right)}{\sqrt{\sum _{j=\mathrm{1}}^M{\left(f_j-\stackrel{\mathrm{‾}}{f}\right)}^{\mathrm{2}}\sum _{j=\mathrm{1}}^M{\left(r_j-\stackrel{\mathrm{‾}}{r}\right)}^{\mathrm{2}}}}}\right).\end{array}$$

Here, R is the empirical spatial correlation coefficient; M is the total number of grid points within the evaluated domain of the starting experiment; f_j is the value of the jth grid point in the tested field at time step i; r_j is the value of the reference field; N is the total number of time steps, depending on the time period considered; and RE is the relative error. For the maximum precipitation, f is the tested value of the maximum gridded precipitation over the area of interest, and r is the reference value of the maximum gridded precipitation over the same area.

To facilitate evaluation, the metrics are further adjusted to ensure that the ideal value of all of the metrics is 1. In this study, RMSE and WRMSE are first divided by a rescaling factor to fall into the range of 0–1 and then subtracted from 1 to provide an indication of good performance. The rescaled metrics, RMSE^′ and WRMSE^′, have the value 1 representing the lowest accumulated error (highest accuracy). The factor used for rescaling is determined by the largest values of each error metric in all of the experiments and is kept at the same value for all of the evaluated time periods (Sikder and Hossain, 2016). RE_PMAX and RE_TP are added by 1 to have the ideal value of 1. The rescaled metrics are PMAX^′ and TP^′, respectively. The other metrics are not rescaled because they already have ideal values of 1, but they are assigned a new set of symbols to distinguish them from the original metrics used before rescaling. For example, POD is replaced with POD^′, and R is replaced with R^′. Table 2 shows the correlations between the original metrics and the rescaled metrics. Given that the metrics describe different features of the rainfall simulations, the values of these metrics are checked and considered together in subjective verification to determine the likely best set of domain configuration options and to search for the longest reasonable spin-up time.

5 Results and analyses

In each scenario, the metrics are compared among the experiments that consider different durations and cover the same domain (D03). The results are presented in four sub-graphs; each sub-graph shows the values of the metrics calculated for individual evaluated time periods. The spatial distribution of rainfall is also presented over domain two (D02) when evident discrepancies are noted in the results obtained for the inner domain (D03) and the outer domain (D02). Table 1 shows the categories of the scenarios and the model configurations adopted in each experiment. In the following section, the domain size scenario (S1) is evaluated first, followed by the vertical resolution scenario (S2) and the horizontal resolution scenario (S3).

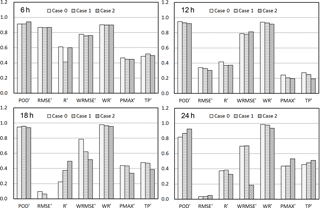
Figure 3 Spatial values of the verification metrics for the WRF domain size experiments, calculated over different temporal durations and over domain three. Case 0 (C0) incorporates the smallest domain, which covers north-central China; Case 1 (C1) incorporates a domain of intermediate size that covers northern China and part of Mongolia; and Case 2 (C2) incorporates the largest domain, which covers the Northern Hemisphere. The metrics are calculated over time periods of 6, 12, 18, and 24 h that begin at 12:00 UTC on 21 July 2012.

5.1 Results of the domain size scenario

Figure 3 shows the spatial values of the verification metrics for the WRF domain size experiments. The performance of the experiments clearly worsens as the evaluated temporal duration increases from 6 to 24 h. The most evident deteriorations are detected in the point-to-point accuracy of the rainfall; the reversed root mean squared error (RMSE^′) decreases by 0.8, which represents a 6-fold increase in the cumulative spatial error. The spatial association between the simulations and the gridded observations also declines; the Pearson correlation coefficient (R^′) decreases by 0.3 on average. Although a slight increase is observed in the percentage of correct hits (POD^′) during the first 18 h, this increase is followed by a rapid decrease of nearly 14 % during the last stage of the rainfall event. The relative bias in the accumulated areal rainfall (TP^′) indicates that the total rainfall amount is underestimated throughout the entire evaluated temporal period. The maximum gridded precipitation (PMAX^′) is also underestimated; the largest negative bias occurs during the heavy convective rainfall stage. For PW, a slight decrease is found in the reversed accumulated error (WRMSE^′), whereas an increase of 5–9 % is detected in the spatial correlation coefficient (WR^′). Such variations may be attributable to the role of the updated boundary conditions in adjusting the local model solutions to approach the large-scale atmospheric circulation conditions.

Comparison of the four sub-graphs shows that the values of the metrics do not point to a single perfect experiment in a given period, and their ranked predictive skills determined using a given metric differ when evaluated over different time periods. During the early stage of the rainfall event (6 h), C0 yields better performance than C1 and C2 in terms of RMSE^′, R^′, and PMAX^′; it simultaneously displays the lowest value of POD^′ and the largest bias in estimating the total precipitation. Although the superiority of C0 is more evident in the second period, a sharp deterioration is then observed in capturing the point-to-point accuracy of precipitation for the 18 h duration, where the lowest R^′ is obtained. Meanwhile, C1, which employs a domain of moderate size, displays greater skill than C0 in capturing the correct hits and the spatial pattern of the simulated rainfall. C2 employs the largest domain. Although it shows the best fit to the rainfall observations on the daily scale (24 h), it displays the worst performance over the three shorter time periods. For the PW fields, the highest similarity with the ERA-Interim reanalysis is found for C0, whereas the lowest similarity is found for C2. These results demonstrate indirectly that small domains are more likely to be influenced by updated boundary conditions.

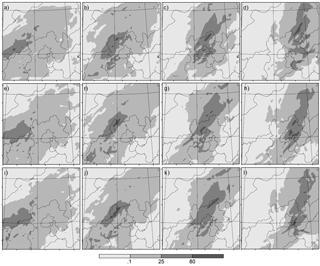
Figure 4 Spatial distribution of 6-h accumulated precipitation for the domain size experiments over the domain two area of C0 during the Beijing heavy rainfall event beginning at 12:00 UTC on 21 July 2012. (a) Accumulated precipitation (AP) in C0 during the first 6 h period (00:00–06:00 UTC); (b) AP in C0 during the second 6 h period (06:00–12:00 UTC); (c) AP in C0 during the third 6 h period (12:00–18:00 UTC); (d) AP in C0 during the fourth 6 h period (18:00–00:00 UTC); (e) AP in C1 during the first 6 h period; (f) AP in C1 during the second 6 h period; (g) AP in C1 during the third 6 h period; (h) AP in C1 during the fourth 6 h period; (i) AP in C2 during the first 6 h period; (j) AP in C2 during the second 6 h period; (k) AP in C2 during the third 6 h period; and (l) AP in C2 during the fourth 6 h period.

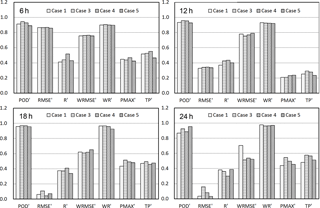
Figure 5 As in Fig. 3, but for the experiments in scenario two with different vertical resolutions. Case 1 is forced by the ERA-Interim pressure-level data with 29 vertical levels; cases 3 and 4 are forced by the same data but include double and triple the number of vertical levels, respectively; Case 5 is forced by the ERA-Interim model-level data with 38 vertical levels.

In this scenario, if the experiments are merely evaluated in D03, the conclusion that C0 displays the best performance during most of the evaluated time periods may be reached. However, when evaluated in D02, clear differences between C0 and the ground truth in both the spatial characteristics of the rainfall and the magnitude of the maximum precipitation are detected. Figure 4 shows the spatial distribution of the accumulated 6 h precipitation over the domain two area of C0. Note that the speed of movement of the belt of heavy rain simulated in C0 is a few kilometres per hour faster than those in C1 and C2, leading to an early end of the heavy rainfall event. This difference may explain why the modelling skill of C0 declines significantly as the end of the rainfall event approaches. The belt of heavy rain in C0 displays an orientation that is shifted nearly 10 degrees northward from those simulated in C1 and C2 during the first 6 h, and the storm centre in C0 displays the smallest range; it is nearly half of the area in C2. The results indicate that the domain size of C0 is not broad enough to allow the model physics to fully develop the small-scale features that favour heavy rainfall. The spatial characteristics of precipitation are relatively similar in the other two experiments, but C1 outperforms C2 in both the rainfall-related and the PW-related features over domain two. It may be that C2 does not yield better performance than C1 because of its inefficient use of boundary conditions to adjust the false perturbations generated by the local model run. Therefore, C1 is verified as reasonable from both statistical and physical perspectives and is chosen as the optimal experiment in the domain size scenario (OS1).

5.2 Results of the vertical resolution scenario

Based on the analysed results, C1 is selected as the starting experiment in the vertical resolution scenario. As mentioned above, C1 is forced with the ERA-Interim pressure-level data with 29 vertical levels. C3 and C4 are forced with the same pressure-level data with 57 and 85 vertical levels, respectively, whereas C5 is forced with the model-level data with 38 vertical levels. As shown in Fig. 5, a decline in model performance is also obtained for all of the vertical resolution experiments as the evaluated time period increases in length. Moreover, the largest deterioration in RMSE^′ is also observed; it decreases by 0.82 on average. The values of TP^′ and PMAX^′ derived from the simulations are slightly higher than those predicted in S1 but are still less than those calculated for the actual precipitation over the entire rainfall event. POD^′ displays an evident decrease during the end stage of the rainfall event, and its magnitude decreases 50 % less relative to that shown in C1. The most obvious difference from the domain size scenario is that the values of R^′ calculated between the simulations and the ground truth vary slightly and remain almost the same between the different time periods. In addition, the performance of the vertical resolution experiments seems to be less sensitive to the boundary conditions because they result in relatively small variations in WRMSE^′ and WR^′.

Unlike the apparent discrepancies noted in the metrics obtained for the domain size experiments, the differences in the rainfall-related metrics among the experiments with different numbers of vertical levels are not evident, especially during the less rainy period (6 h) and the period when convective rainfall dominates (12 h). During the first 12 h, C4 displays better agreement with the gridded observations than the other three experiments in terms of the accuracy and spatial correlation of the rainfall amount. However, over the longer time periods, C3 displays the greatest skill, according to most of the verification metrics. Comparing C3 and C1 shows that increases in the vertical resolution may increase WRF's ability to explicitly resolve small-scale physical processes and improve the accuracy of the amount and distribution of the simulated rainfall. Comparing C3 and C4 shows that, although C4 includes further refinement of the vertical resolution, the C4 performance is worse than that of C3 when the evaluated time period increases from 6 h to more than 12 h. This result may occur because progressive reductions in the vertical grid spacing magnify the propagation of surface perturbations through the vertical grid columns, potentially weakening the kinetic energy that favours precipitation. Examining the values of WRMSE^′ and WR^′ shows that the differences between the simulations and the reanalysis are more distinct in C3 and C4 than in C1. This discrepancy may occur due to the exaggeration of the initial errors introduced by the interpolation process and the incorporation of false surface perturbations introduced by the limited accuracy and resolution of the initial forcing data. C5 shows either better or worse performance than C1 in each period but produces less accurate rainfall simulations than C3 over most of the evaluated durations. As such, C3 is identified as yielding the best performance in the vertical resolution scenario.

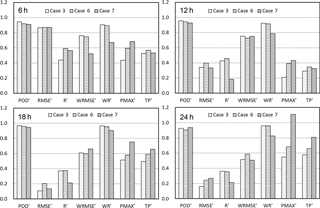
Figure 6 As in Fig. 3, but for the experiments in scenario three with different horizontal resolutions. Case 3 has an initial downscaling ratio of 1 : 3 : 3 with horizontal grid spacing of 40.5, 13.5, and 4.5 km, whereas cases 6 and 7 have the same large horizontal grid spacing with nesting ratios of 1 : 5 : 5 and 1 : 7 : 7, respectively. The innermost grid spacing is 1.62 km in Case 6 and 0.826 km in Case 7.

5.3 Results of the horizontal resolution scenario

Based on the results obtained for scenario S2, C3 is selected as the starting experiment in the horizontal resolution scenario. The modelling skill of the S3 experiments shows similar temporal trends as that of the S2 experiments (Figs. 5 and 6). However, the sensitivity of the metrics to the variation in the horizontal resolution is more evident than that with different vertical resolutions. Over most of the evaluated time periods, C6, which has a grid spacing of 1.62 km, displays better performance than C3 and C7 having grid spacings of 4.5 and 0.826 km, respectively. Comparison of C3 and C6 shows that C6 tends to produce more accurate spatial patterns of rainfall throughout the heavy rainfall event in Beijing. Higher values of PMAX^′ and TP^′ are also detected in C6 when compared to C3. This result stems in part from the explicit resolution of the convective processes by the WRF microphysics scheme, which may explain why the PMAX^′ of C7 is higher than C6 over most of the tested durations. Note that the modelling skill of C7 deteriorates rapidly after the heavy rain begins (12 h); the lowest POD^′ and R^′ values of the three experiments are obtained for this simulation and time period. Analysis of the WRMSE^′ values suggests that simulation C7 displays significant departures from the coarser-scale PW fields that are used to force the model. Thus, model simulations with excessively high horizontal resolutions may also display poor performance. Theoretically, this deterioration may be attributed to the accumulated errors introduced by the imperfect model physics or biases in the initial and boundary conditions, which can be exaggerated by the chaotic nature of NWP systems. According to the above analysis, C6 yields the best agreement with the ground truth data among the horizontal resolution experiments.

5.4 Searching for the likely ideal spin-up time

To limit the effects of the chaotic nature of NWP on the model simulations and extend the lead time, the scenario in which the spin-up time used in WRF is varied is placed at the end of the experimental design, after the possible errors introduced by inappropriate domain configuration options have been reduced. In S4, C6 is adopted as the starting experiment (OS3). Unlike the previous scenarios, the ranks of the spin-up time experiments, as sorted by the metrics, are nearly the same across the different time periods. Hence, Fig. 7 presents only the modelling skill of the spin-up time experiments over the time period of 18 h. The model performance of WRF in simulating heavy rainfall clearly varies with the spin-up time. For most of the metrics, an obvious diurnal tendency is found from 0 to 60 h, followed by a short-term decrease until 72 h; random fluctuations occur after 72 h. Before 72 h, the variations in the rainfall and PW metrics are almost consistent; thus, the good fits of the simulations produced by the model runs with longer spin-up times are also physically reasonable within this period. The discrepancies among these experiments may be due to differences in the initial conditions (e.g. the water vapour amounts and the times of day when the simulations begin).

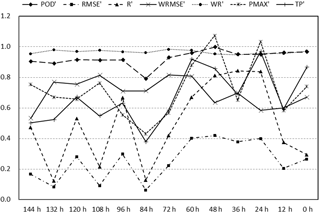
Figure 7 Spatial values of the verification metrics for the WRF spin-up experiments, calculated over 18 h periods and over domain three. Case 6 employs an initial spin-up time of 12 h; Case 8 employs a spin-up time of 0 h; and from Case 9 to Case 19, the spin-up time is increased from 24 to 144 h by every 12 h.

Table 3 Comparison of the values of the error metrics in the initial experiment and the optimum experiments identified for each scenario.

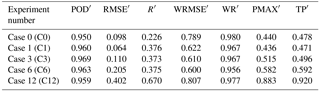
From TP^′, it is found that all of the spin-up time experiments underestimate the total rainfall amount during the heavy rainfall event. Of all of the rainfall-related metrics, POD^′ is found to display the least sensitivity to the spin-up time; however, it displays similar variations over time as PMAX^′, R^′, and RMSE^′ before 72 h, with the highest values shown in the experiment with a spin-up time of 48 h (C11). Positive biases are detected in PMAX^′ in C9 (which is run 24 h ahead) and C11, in which the largest positive biases are detected in the simulated amount of water vapour across the analysed periods and earlier (during the initialization period). This result may occur because the atmospheric water vapour content determines the maximum possible rainfall amount. C12, which includes a spin-up time of 60 h, is ranked third in terms of PMAX^′, whereas it displays better performance than C9 and C11 in terms of TP^′, WR^′, and WRMSE^′. As seen in Fig. 8, C9, C11 and C12 also rank in the top three, based on the values of the rainfall-related metrics calculated over domain two. However, larger departures from the forcing PW fields are seen in C9 and C11 than in C12. The difference is that C12 shows the best agreement with the ground truth data in terms of both the rainfall- and PW-related fields. Overall, C12 is regarded as the experiment that best reproduces the Beijing SDHR event with the optimal set of domain configuration options and the longest spin-up time.

6 Discussion

The results reveal that the initial experiment with the most commonly employed WRF domain settings does not yield the best performance in reproducing the temporal and spatial characteristics of SDHR on the convective scale. In S1, the assigned domain size of C0 is not sufficiently broad to allow the model physics to fully develop local small-scale features, resulting in obvious reductions in modelling skill as the evaluated time duration increases from 12 to 24 h. Further refinement of the grid spacing of C0 in S2 and S3 is shown to enable more explicit resolution of convective processes, leading to more accurate rainfall simulations. The comparison made in S4 suggests that the proper spin-up time is determined by both the time needed for model initialization and the accuracy of the initial conditions fed into the model run. Moreover, experiments with too large domains, too high spatial resolutions, or too long spin-up times also yield poor performance in rainfall simulations. Therefore, the reasonableness of these WRF settings should be checked before the model is used in regional NWP systems for flood forecasting or as a reference for the design of flood mitigation strategies.

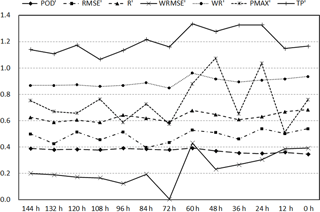
Figure 8 As in Fig. 7, but the metrics are calculated over 18 h periods and over domain two in Case 6.

In addition to exploring whether the recommended WRF domain configuration options and spin-up time are optimal for application in SDHR-prone urban areas, the performance of the model is quantified, and its total improvement is evaluated by comparing the values of the verification metrics yielded by the experiments. Table 3 compares the values of the verification metrics obtained for the optimal experiments in each scenario with the values obtained for the initial experiment. Here, the 18 h time duration is selected for evaluation because it covers most of the heavy rainfall event, and the metrics calculated over this period display a greater range and thus greater ability in identifying the simulation with the best performance. One exception is the domain size scenario, in which C0 presents the most obvious reduction in performance during the last stage of the rainfall event (24 h). Therefore, the improvement in C1 relative to C0 is mainly represented by R' and POD^′ across D03 over the 18 h time period. The improvement produced by refining the vertical resolution is indicated by all of the rainfall-related metrics but is accompanied by a decrease in WRMSE^′ that stems in part from the reduction in kinetic energy, which promotes rainfall. C6 yields higher values of POD^′, RMSE^′, R^′, and PMAX^′ when compared with C3, indicating that appropriate increases in the horizontal resolution can increase the accuracy of rainfall simulations. The largest differences in the metrics between C6 and C12 occurs for PMAX^′, which may relate to the different initial weather conditions at the different starting times of the model runs.

Overall, although the magnitudes of the increases in the rainfall metrics differ, they all reflect an increase in model skill after the re-evaluation process has been conducted. Specifically, R^′ increases from 0.226 in C0 to 0.67 in C12, RMSE^′ increases from 0.098 to 0.402, and PMAX^′ increases from 0.44 to 0.883. As the complete assessment is based on objective verification metrics and checked by subjective verification methods, it can be concluded that the domain configuration options and the spin-up time have significant effects on regional simulations of SDHR. Therefore, re-evaluating the values of those settings used in high-resolution regional studies is certainly worthwhile, and the accuracy of predictions of heavy rain clearly benefit from these analyses. For the evaluated metrics, evaluations based on a single type of metric or a single time period may clearly result in partially accurate conclusions. The use of datasets from multiple sources in verification can help increase the comprehensiveness of the analyses, such as the use of WRMSE^′ and WR^′ in this study. The use of different time periods helps to determine the optimal configurations with higher physical rationality, such as the selection of the proper domain size. In addition, the verification results may also depend on the fields and temporal–spatial scales of interest. To further understand the effects of WRF model configuration options on regional simulations of sub-daily heavy rainfall, more objective verification metrics for SDHR should be developed, and more case studies of SDHR events are also needed. Given that the uncertainties in the regional NWP studies result mainly from the inaccurate boundary conditions associated with grid nesting techniques, methods that can serve as alternate schemes to reduce these uncertainties are also worth studying. One example includes the mesh transitions approach used on irregular grids. In addition, more accurate simulations are expected when the model is driven with forcing data with higher temporal or spatial resolutions than those of the ERA-Interim reanalysis because the uncertainties and errors introduced by the input data could be further reduced.

7 Conclusions

In this study, a comparative test is designed to evaluate the effects of WRF domain configuration options and the spin-up time on simulations of the precipitation during the SDHR event that occurred on 21 July 2012 in Beijing, China. Three nested domains are established: D01 is the largest, has the coarsest resolution, and covers the leading synoptic features; and D03 is the smallest and covers the area of interest, Beijing. The initial conditions of the three domains are provided by the ERA-Interim reanalysis and the 30-second static geographical datasets. For the LBCs, D01 is forced by the ERA-Interim reanalysis, whereas D02 is forced by D01, and D03 is forced by D02. The reference ground truth data used for verification is 3-hourly 0.05 gridded rainfall observations and the coarser-scale ERA-Interim reanalysis. Five rainfall-related error metrics and two PW-related indices that monitor the departure of the model simulations from the driving fields are calculated at the convective-resolving scale over different sub-daily time spans. These metrics are then checked and considered together as part of a subjective verification process that is intended to pinpoint the likely best combination of the domain configuration options and spin-up time and to help quantify the possible improvements in the model performance of WRF in reproducing severe SDHR events after carrying out the entire re-evaluation process.

Precipitation simulations are sensitive to changes in domain size, vertical resolution, horizontal resolution, and spin-up time. Of all of the configurations, the most obvious variations are found when adjusting the domain size and the spin-up time. This analysis shows that domains that cover only the area of interest may be insufficiently broad to permit full development of small-scale features, resulting in poor performance in capturing the spatial pattern of heavy rainfall, especially in the early stages of rainfall events. Despite the dominant role of chaotic processes, it is still possible that model runs with longer spin-up times may result in better rainfall simulations, given favourable initial weather conditions. The effects of the vertical and horizontal resolutions are smaller, but the accuracy of the rainfall amount and the correct hits exhibit evident increases in runs with slightly higher spatial resolutions. A comparison of C12, which uses the evaluated optimum configurations, and C0, which uses the recommended settings, shows that the metrics clearly increase. Specifically, R^′ increases from 0.226 to 0.67, RE_PMAX rises from −56 to −11.7 %, and RMSE decreases by 33.65 %. Thus, substantial benefits may result from re-evaluating the WRF domain configuration options and spin-up times used in regional studies of SDHR.

Given the intensification of SDHR and the increased risks posed by SDHR-induced hazards, the demands of the operational flood management community for more accurate rainfall predictions with longer lead times, especially over highly affected areas with very short hydrologic response times, are increasing. One method that has now been proven to be effective is to dynamically downscale freely available global NWP products to areas of interest using high-resolution regional NWP models (e.g. WRF). Therefore, the uncertainties associated with the downscaling process, such as errors in boundary conditions and the issues associated with grid nesting, should be carefully evaluated to ensure that the rainfall simulations produced are both statistically accurate and physically reasonable before they are employed in flood forecasting systems. This study illustrates the importance of re-evaluating the domain configuration options and spin-up times used in WRF for improving regional rainfall simulations. Comparisons of the metrics indicate that evaluations based on just one category of metrics or values of metrics calculated over only one time period (e.g. 24 h) do not result in comprehensive comparisons and may lead to partially accurate conclusions. The use of PW fields calculated against reanalysis output is verified to be helpful in determining the optimal set of model configurations when analyses of rainfall-related metrics do not yield uniform conclusions. In addition, evaluations conducted over larger-scale domains are demonstrated to be useful in establishing the reasonableness of the evaluated results. Overall, the evaluation process is partly subjective. To simplify the assessment process, verification methods that can replace this subjective verification procedure should be developed. More regional case studies are also needed to further investigate the effects of configuration options in simulations of regional SDHR and to explore methods of reducing the uncertainties in regional NWP modelling associated with the scale-variation procedures. In addition, the use of more accurate forcing data with higher temporal and spatial resolutions is also expected to reduce the errors in the initial and boundary conditions and could thus be helpful in further improving the accuracy of rainfall simulations and extending the lead times of forecasts.