Technical note: An illustrative introduction to the domain dependence of spatial principal component patterns

Principal Component Analysis (PCA) of synchronous time series of one variable, e.g. water level or discharge, measured at multiple locations, has been applied in a wide spectrum of hydrological analyses. The possibility that the Principal Components (PCs) can exhibit domain dependence (DD) found only little recognition in the hydrological PCA literature so far. DD describes the situation in which the spatial PC patterns are mainly determined by the spatial extent of the analysed data set (domain size) and the spatial arrangement of the data set's locations (domain shape). Thus, instead of the hydrological functioning of the analysed system, the spatial PC patterns rather reflect the functioning of the PCA within the context of the data set's spatial domain. The effect is caused by homogeneous spatial autocorrelation in the analysed series. DD patterns are distinct, with strong gradients and contrasts. We show that it can come together with substantial accumulation of variance in the leading PCs. In addition, DD can cause effectively degenerate multiplets, i.e. PCs which are not well separable. All these features are highly suggestive and easily lead to wrong hydrological interpretations. Consequently, DD should be considered for any application in which the PCs are used to draw conclusions about spatially distinct properties of the analysed system. For most practical applications checking the first few leading PC patterns should be sufficient. Visual comparison of the spatial PC patterns from subdomains with markedly different shapes and/or sizes can serve as quick qualitative check. Reference patterns can be used to test whether spatial PC patterns differ significantly from pure DD patterns. We present two methods, one stochastic, one analytic, to calculate DD reference patterns for defined spatial correlation properties and arbitrary spatial domains. With a series of synthetic examples, we explore the DD effect with respect to (a) domain shape, (b) domain size and spatial correlation length and (c) effectively degenerate multiplets. Particular focus is given to the effect of DD on the explained variance of the PCs and the contrasts of their spatial patterns. An application example with a precipitation raster data set is presented and different options to detect and diminish DD are discussed. Accompanying this technical note, R-scripts to (i) demonstrate and explore the DD effect, and (ii) perform the presented DD reference methods are provided.

1 Introduction

In hydrology, Principal Component Analysis (PCA), also known as Empirical Orthogonal Function (EOF) analysis or Karhunen–Loève Transform, is a popular tool to analyse spatio-temporal data sets. The analysed data can be structured in various ways (Richman, 1986; Demšar et al., 2013). Here, the focus is on PCA of data sets comprising synchronous time series of one observed variable, e.g. water level, with the time series (a) being distributed in space at multiple locations and (b) being used as variables for the PCA. This is known as S-mode PCA (Richman, 1986) or atmospheric science PCA (Demšar et al., 2013). In this setting, the covariance among the time series from the different locations is analysed (Richman, 1986; Isaak et al., 2018). For each PC there is a temporal and a spatial pattern. The PCs are series of the same length as the analysed time series and can be plotted against the common time index (temporal PC patterns). The eigenvector of each PC is associated with the complete set of locations and can be plotted against the locations' coordinates (spatial PC patterns). All spatial patterns are orthogonal, all temporal patterns are mutually uncorrelated. With this, the leading PCs provide a compact description of the spatio-temporal variability of the data set. S-mode PCA can be applied to data from very different hydrological systems such as catchments or soil columns.

A non-exhaustive list of hydrological applications comprises S-mode PCA to describe the spatio-temporal variability of streamflow (Smirnov, 1972, 1973; Bartlein, 1982; Lins, 1985a, b, 1997; Kalayci and Kahya, 2006), groundwater level (Winter et al., 2000; Longuevergne et al., 2007; Lehr and Lischeid, 2020), lake water level (Lischeid et al., 2010), soil moisture (Korres et al., 2010; Nied et al., 2013; Hohenbrink et al., 2016; Bieri et al., 2021), precipitation (Kumar and Duffy, 2009; Thomas et al., 2012; Bieri et al., 2021), drought (Karl and Koscielny, 1982; Santos et al., 2010; Ionita et al., 2015), atmospheric rivers (Li et al., 2022), or river water temperature (Isaak et al., 2018). In stark contrast to its widespread use, the possibility that the PCs of such analysis can exhibit domain dependence (DD) is rather unknown in hydrological PCA literature.

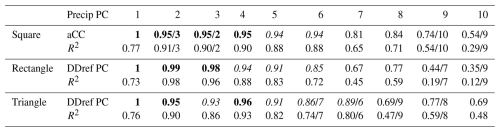
DD describes the situation in which the spatial PC patterns from S-mode PCA are mainly determined by the size and shape of the analysed spatial domain, meaning the spatial extent of the data set and the spatial arrangement of its locations (Buell, 1975, 1979; Richman, 1986). If the spatial autocorrelation of the data set's variable is homogeneous across the domain, its size and shape induce distinct sequences of spatial PC patterns due to the variance maximization of the PCs and the orthogonality constraint of the PCs` eigenvectors (Jolliffe, 2002; Wilks, 2006). Buell (1975) identified classical sequences for data sets with basic geometric domain shapes and isotropic spatial autocorrelation (e.g. Fig. 1). The spatial pattern of PC 1 is a weighted spatial average emphasizing the centroid of the network (“mean behaviour”). The PC 2 pattern is a gradient depicting the variability along the axis of the longest extent of the domain. The PC 3 pattern covers the next largest spread of spatial variability orthogonal to the spatial patterns of PC 1 and PC 2, etc. Given the functioning of the PCA, the sequence simply reflects (a) that the covariance between the locations has its maximum in the centroid of the network because it is the point which is on average closest to all other locations, and (b) that the only structure in the variability of the data set is the homogeneous decay of covariance with distance (Dommenget, 2007). On a sphere the resulting spatial PC patterns of such a data set would be the spherical harmonics (North and Cahalan, 1981).

Ignorance about DD can easily lead to wrong interpretations of PCA results. DD patterns are distinct, with strong gradients and contrasts, and therefore highly suggestive to indicate physically meaningful drivers or properties of the analysed system. In the climatological literature DD was intensely discussed (Buell, 1975, 1979; Horel, 1981; Richman, 1986, 1987, 1993; Jolliffe, 1987; Legates, 1991, 1993). Apparently, the topic did not reach the hydrological community, even though the effect of size and shape of the network geometry on the results was observed in early hydrological S-mode PCA applications (Smirnov, 1973; Bartlein, 1982; Lins, 1985b). For that reason, we want to raise attention to the DD effect among PCA users in the hydrological community again to reduce the risk of drawing wrong hydrological conclusions from spatio-temporal PCA.

DD is one aspect in the general discussion on the physical interpretation of S-mode PCs. There are strongly diverging opinions, ranging from “never physically interpret any PCs” to “distinct processes can be meaningfully assigned to single PCs”. For physical processes or modes of geosystems, the S-mode PC properties orthogonality of spatial patterns, linear uncorrelatedness of temporal patterns and successive maximization of variance are heavy constraints (Buell, 1979; Jolliffe, 2002; von Storch and Zwiers, 2003; Hannachi et al., 2007; Monahan et al., 2009). By extracting maximal variance, different sources of variability can get pulled onto the first eigenvector, thereby mixing the sources (e.g. Fig. 14A in Karl and Koscielny, 1982). The successive order of the PCs implies that they should not be interpreted isolated, but only with reference to the preceding PCs. The spatio-temporal patterns of the first PC set the reference for all subsequent PC patterns. Forced by the orthogonality constraint, prominent features of the first spatial PC pattern cascade down to the spatial patterns of the other PCs (Cahalan et al., 1996). The analysis is limited to linear relationships and assumes stationarity of mean and variance of the analysed variable. If single features are assigned to single PCs, this raises the question whether the hydrological features in the analysed system are expected to exhibit orthogonal spatial patterns, to be linearly uncorrelated in time and to successively maximize variance. If not, PCA is simply the wrong model (Jolliffe, 1987, 2002).

Rotation of PCs can relax the aforementioned PCA constraints (Richman, 1986; Hannachi et al., 2007; Monahan et al., 2009). It is regularly used in atmospheric mode detection. Several studies found that rotated PCA performed better than unrotated PCA for this purpose, and that their spatial patterns were less prone to DD (Richman, 1986; Compagnucci and Richman, 2008; Huth and Beranová, 2021). Despite these findings, unrotated PCA is still often used (Huth and Beranová, 2021). Regardless of whether rotated or unrotated PCA is used, the physical interpretation depends on the spatial PC patterns and requires that they are not domain dependent. The knowledge which locations carry the most variance can already be helpful to improve the physical understanding of the analysed system (Monahan et al., 2009). In hydrology, unrotated PCA is to our knowledge much more common than rotated PCA. Therefore, we mainly focus on unrotated PCA here.

DD is important for any application in which a PCA of observed data is used to draw conclusions about spatially distinct properties of the analysed system. This concerns descriptive applications in which the spatial PC patterns are used to identify dominant hydrological modes (Smirnov, 1972, 1973; Bartlein, 1982; Lins, 1985a, b, 1997; Kalayci and Kahya, 2006; Thomas et al., 2012; Ionita et al., 2015) or regions with similar hydrological behaviour (regionalisation) (Karl and Koscielny, 1982; Santos et al., 2010; Nied et al., 2013), as well as the interpretation that they represent the spatial variability of concrete hydrological signals (Longuevergne et al., 2007; Lewandowski et al., 2009), hydrological processes (Hohenbrink et al., 2016; Isaak et al., 2018; Scholz et al., 2024) or physical properties (Korres et al., 2010; Lischeid et al., 2010). For all those applications it is essential that there is a physical counterpart for the spatial PC patterns in the analysed system. Thus, DD touches the very basic question whether the applied combination of data set and data analysis method allows inference on the analysed system.

DD is critical in particular for any interpretation of the PCs based on correlation analysis with other variables (Korres et al., 2010; Lischeid et al., 2010; Hohenbrink et al., 2016; Isaak et al., 2018; Scholz et al., 2024). In case of “strong DD” the correlation between their spatial patterns depends mainly on the selected spatial domain. Consider for example a soil texture gradient in west-east direction and the classical Buell patterns in Fig. 1. Depending on the selected domain the spatial patterns from different PCs would correlate strongly, moderately or not at all with the gradient. Consequently, those correlations would be neither useable for the interpretation of the PCs nor for the identification of predictors for their spatio-temporal patterns. Thus, spatial PC patterns should be checked for DD prior to any interpretation implying causal relationships.

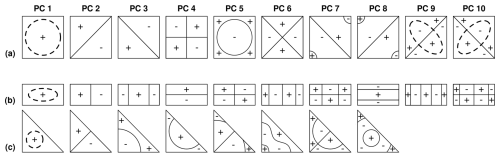
Figure 1 Exemplary reproduction of some “classical Buell patterns” for differently shaped domains of relatively similar size: (a) 6 ×6 square, (b) 5×10 rectangle and (c) 8×8 triangle (Figs. 2, 5 and 4 adapted from Buell, 1975). The signs indicate positive and negative values of the spatial PC patterns. The patterns are for data exhibiting exponentially decaying spatially isotropic autocorrelation with spatial correlation length of 2 grid cells (function F1, scale parameter L=2 in Buell, 1975). The spatial PC patterns of the rectangular shape are for the gaussian covariance function (function F2 in Buell, 1975) but Buell noted that the patterns of the exponential function are essentially the same. The dashed circle of PC 1 indicates that its pattern is of one sign in the entire domain with absolute values being highest within the circle and fading out towards the domain boundaries.

When checking for DD, it has to be considered that DD patterns are original for every combination of spatial domain and spatial correlation properties of the analysed data set. Thus, the “classical Buell patterns” are DD patterns for the distinct combinations of size and shape of the domain, spatial covariance function and spatial correlation length used in Buell's (1975) numerical experiments (e.g. Fig. 1). Spatial PC patterns of real-world data sets can be expected to deviate from those archetypes due to possible differences in all these aspects. In addition, there might be a blurring effect of measurement errors. For spatially regular distributed data sets with strong homogeneous autocorrelation and domain boundaries similar to one of Buell's basic domains the DD patterns of the leading PCs are commonly visually easy to recognize as Buell-like. This is less clear for those of the PCs with smaller eigenvalues (low ranked PCs). They are more finely detailed and less robust against deviations from Buell's settings. Furthermore, there might be intermixing of the variance structures when the eigenvalues from successive eigenvectors are of very similar size (North et al., 1982; Quadrelli et al., 2005). These PCs which are not well separated with the PCA are called effectively degenerated multiplets (North et al., 1982). For their separation, additional post-processing is required, e.g. rotation of eigenvectors (Richman, 1986; Jolliffe, 1989). DD patterns from data sets with more complex domain shapes and spatially irregular distributed locations, which is the common case in hydrology, can differ substantially from Buell's archetypes. All in all, visual recognition by comparison with Buell patterns is rather limited. Comparison with DD patterns calculated for the analysed spatial domain overcome these limitations (Cahalan et al., 1996; Dommenget, 2007). They can be used as reference to test whether spatial PC patterns differ significantly from what has to be expected from DD alone.

The objective of this technical note is to introduce (i) the DD effect and (ii) the application of DD reference patterns to the hydrological community. We illustrate our introduction primarily with synthetic examples. This ensures that the statistical properties of the examples, in particular their spatial correlation properties and spatial domains, are strictly defined. It further clarifies that all observed effects are solely caused by the specified statistical properties. Another advantage is that series of examples with systematic differences can be constructed to study the effects of specific properties, e.g. spatial correlation length or spatial extent, on the PCA results.

Note that we aim for an illustrative introduction for PCA practitioners. For a mathematically rigid introduction to the DD phenomenon see Buell (1975, 1979) and North and Cahalan (1981). All the here presented analyses were performed in R (R Core Team, 2019). Scripts to reproduce the results, explore the DD effect and calculate DD reference patterns for defined spatial correlation properties and arbitrary spatial domains are provided (Lehr, 2024). After presenting two DD reference methods, a series of synthetic examples is used to explore the DD effect with respect to (a) domain shape, (b) domain size and spatial correlation length and (c) effectively degenerate multiplets. Particular focus is given to the effect of DD on the explained variance of the PCs and the contrasts of their spatial patterns, both common indicators for the interpretation of PCA results. Finally, an application example with a precipitation raster data set is presented and different options to detect and diminish DD are discussed.

Figure 2 Three realizations of a 20×20 random field simulated with an isotropic exponential covariance model and spatial correlation length of 10 cells representing three instants of time of a synthetic data set.

2 Data

2.1 Synthetic data

The synthetic data sets consist of synchronous spatially distributed time series exhibiting spatial but no temporal autocorrelation. Each data set is produced by concatenating realizations of a random field with identical spatial correlation properties (Fig. 2). The grid cells (cells) of the random field represent the locations of a data set. The spatial autocorrelation is defined with a spatial covariance model. Each realization of the field represents one instant of time of a data set. Thus, at each location the respective time series consists of a sequence of random numbers. The number of field realizations gives the length of the simulated time series. The random fields were simulated with the “RandomFields” package (Schlather et al., 2015, 2020).

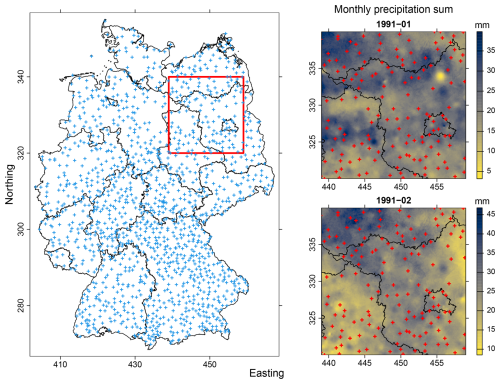
Figure 3 Maps of the precipitation data showing the permanent precipitation stations (crosses) that were used by the German Weather Service to produce raster of monthly precipitation sums in the monitoring period 1991–2020. Left panel: Federal States of Germany (black lines) and the domain selected for PCA (red square). Right panel: Sample raster of monthly precipitation sums (mm) from the first two months of the selected data set. The Northing and Easting coordinates (10 km) of the maps are in the ETRS89/LAEA Europe projection.

2.2 Precipitation data

As an application example based on observed data we use time series of monthly precipitation sums from the years 1991–2020 out of a 200 km × 200 km square in northeast Germany (Fig. 3). The precipitation series were selected from the 1 km × 1 km HYRAS-DE-PR precipitation grid provided by the German Weather Service (Deutscher Wetterdienst, 2025). Amongst others, the HYRAS-DE-PR precipitation product is suggested as input data for hydrological modeling (see the description file at Deutscher Wetterdienst, 2025). The monthly precipitation sums are based on daily measurements of precipitation height at the monitoring stations. The raster layers are interpolated by combining multiple linear regression considering topography with inverse distance weighting. The interpolation method preserves the measured precipitation values at the grid cells of the stations. For details, see Rauthe et al. (2013) and the description file of the data (Deutscher Wetterdienst, 2025). Except from z-scaling, no pre-processing of the precipitation series was applied.

3 Methods

3.1 Principal Component Analysis

PCA maps a m×n data matrix X to n new linearly uncorrelated variables, the Principal Components (PCs), such that the PCs successively maximise represented fractions of the data set's variance (Wilks, 2006). The data set's variance is defined as the sum of variances of the variables x. It equals the sum of the diagonal elements (trace) of its covariance matrix. PCA can be performed as eigenvalue decomposition of the variables' covariance matrix or as singular value decomposition of the variables' matrix with the variables being centred to their mean (Jolliffe, 2002). Unfortunately, the terminology is not used consistently throughout the literature. Here, we follow the terminology used by Jolliffe (2002) and Jolliffe and Cadima (2016) for the eigenvalue approach.

Each PC is associated with an eigenvalue λ and an eigenvector a. The values of a PC are termed scores. The variance of the scores of a PC equals its eigenvalue. The ratio of a PC eigenvalue to the sum of all PC eigenvalues gives the fraction of the data set's variance assigned to that PC. Each PC is calculated as linear combination of all n analysed variables x (non-locality).

$$\begin{array}{}\text{(1)}& {\mathrm{pc}}_j=a_{j}X=\sum _{i=\mathrm{1}}^n{a}_{ij}{x}_i\end{array}$$

The coefficients a_ij in this linear combination are termed loadings. The loadings of a PC j are the n elements of the eigenvector a_j associated with that PC. The eigenvectors of all PCs define the orthogonal basis of the new ordination system into which the analysed data is projected (orthogonality constraint). Subject to the eigenvectors being orthogonal and the PCs being uncorrelated, the linear combinations of the PCs provide the optimal linear functions to successively maximise variance accounted for (variance maximization). The maximum variance that can be described by a linear combination of the analysed variables is assigned to the first PC, the maximum of the remaining variance to the second PC, and so forth. Thus, the leading PCs provide a compact description of the data set's variance. It is quite common that a few PCs suffice to summarize a major part of a data set's variance.

For the synthetic data, PCA was performed with the function “prcomp” from the default “stats” package (R Core Team, 2019). For the precipitation data, a truncated PCA, calculating the first 20 PCs only, was performed with the “prcomp_irlba” from the “irlba” package to reduce computation time. The equivalence of the results of both PCA algorithms with respect to the leading PCs was confirmed by comparison of the results from smaller data sets.

3.1.1 S-mode PCA

In S-mode PCA, the analysed variables are synchronous time series distributed in space at multiple locations (Fig. S1 in the Supplement; Richman, 1986). Thus, the PCs are series of the same length as the analysed time series (temporal PC patterns) and the loadings yield values for each location (spatial PC patterns), describing the weighting of the analysed time series to calculate the PC scores. All temporal PC patterns are linearly uncorrelated with each other, each temporal PC pattern is associated with a spatial pattern and all spatial PC patterns are orthogonal to each other. Note that in this study, we perform S-mode PCA only.

3.1.2 Correlation matrix based PCA, correlation loadings and contrasts of spatial PC patterns

Normalizing the variables to zero mean and standard deviation one (z-scaling) prior to applying PCA ensures equal weighting of the analysed variables. This is important if the range of values between the analysed variables differs substantially. A PCA with z-scaled variables is identical to an eigenvalue decomposition of the correlation matrix of the analysed variables. In hydrology, correlation matrix based PCA is to our knowledge more common than covariance matrix based PCA.

For the eigenvectors, different scaling conventions exist (Wilks, 2006). Here, the eigenvectors that are used to calculate the PCs are of unit length (Eq. 1). In correlation matrix based PCA, normalizing the loadings from the unit length eigenvector a_j of a PC by multiplying it with the square root of its eigenvalue λ_j is equivalent to the Pearson correlation r between the scores pc_j and the analysed variables X.

$$\begin{array}{}\text{(2)}& c_j=a_j\sqrt{{\mathit{\lambda }}_j}=r\left({\mathrm{pc}}_j,X\right)\end{array}$$

Thus, the loadings are normalized to the commonly well-known Pearson correlation range from −1 to 1 which simplifies reading and interpretation of the PCA results. Here, we use the term “correlation loadings” for these normalized loadings c_j. We do so to prevent confusion with the coefficients that are used in the linear combination to calculate the PCs, which are not normalized to a common range (Eq. 1). The sum of the squared correlation loadings c_j of a PC equals its eigenvalue λ_j. Thus, they can be used to calculate the fractions of variance associated with the PCs. In the following, the spatial PC patterns are described with correlation loadings only.

For S-mode PCA, the normalization enables direct comparison of the contrasts of spatial patterns from different PCs or PCAs. Here, we define the contrast of a spatial PC pattern as the range between the minimum and maximum of the correlation loading values of that PC. Thus, the maximum contrast possible would be 2.

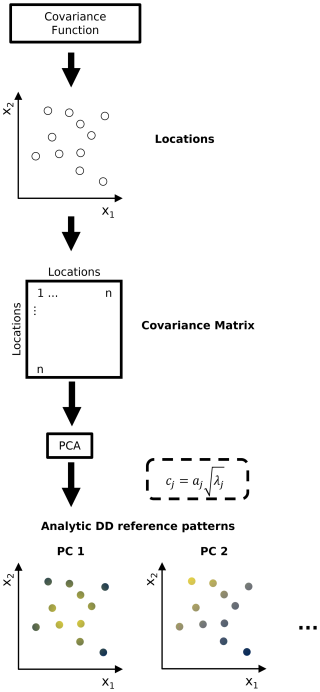
3.2 DD reference patterns

DD reference patterns are the DD patterns of a distinct combination of spatial domain and spatial correlation properties. They can be used as null hypothesis in pairwise statistical tests to test whether spatial PC patterns differ significantly from what has to be expected from DD alone.

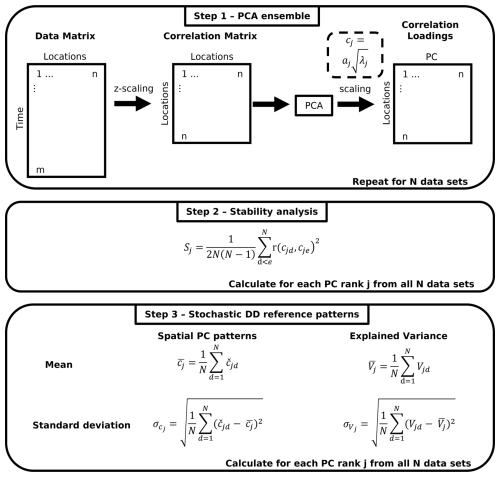
Figure 4 Stochastic DD reference method. n: number of locations, m: number of time steps, N: number of data sets, respectively PCAs. Index j: PC rank, c: correlation loadings, a: loadings, λ: eigenvalue. S: stability of the spatial PC patterns, indices d, e: running indices for PCAs from the ensemble, r: Pearson correlation. $\stackrel{\mathrm{ˇ}}{c}$: harmonized correlation loadings. V: explained variance.

3.2.1 Stochastic method

In the stochastic method, PCA is applied on synthetic data sets (Sect. 2.1) to derive DD reference patterns. As the data sets consist of spatially correlated white noise time series, their temporal PC patterns are white noise as well. The spatial PC patterns of the data sets are solely determined by the spatial domain and the spatial correlation properties defined in the simulation. The spatial PC patterns of data sets simulated with identically parameterized random fields differ due to the randomness in the simulations. Therefore, a three-step procedure is applied to get stable patterns (Fig. 4).

Step 1: An ensemble of data sets with identical spatial domain and spatial correlation properties is simulated. Each of the data sets is analysed separately with a PCA, resulting in a PCA ensemble.

Step 2: The stability of the spatial PC patterns is assessed by pairwise correlating the spatial patterns of all possible combinations of PCs with identical ranks from the PCA ensemble. For each PC rank, the mean R² of the correlations is used to describe the overall similarity of the respective spatial PC patterns.

Step 3: For each PC rank (a) the mean spatial patterns from all PCAs of the ensemble and (b) their standard deviation patterns are calculated. They are calculated as the mean and standard deviation of the correlation loadings of PCs with identical rank from the PCA ensemble.

The mean spatial PC patterns are the DD reference patterns for data sets with the spatial domain and the spatial correlation properties defined in step 1. The standard deviation patterns serve as their spatially discrete uncertainty estimation. The variance represented with the DD reference patterns (“explained variance”) is estimated with the mean and standard deviation of the explained variances of PCs with identical rank from the ensemble.

PCs with identical rank from different data sets of an ensemble might exhibit basically the same spatial pattern but with opposite signs due to the randomness of the field simulations, i.e. the pattern of one data set might be basically a negative version of another one. For the calculation of mean and standard deviation of the spatial PC patterns of an ensemble (step 3), the spatial patterns of PCs with identical rank are therefore harmonized such that they all are correlating positively. Thus, the correlation loadings of PCs that are correlating negatively with those of identically ranked PCs from the first data set are multiplied by −1 and therefore reversed.

Note that the suggested method requires the use of correlation loadings to describe the spatial PC patterns. Thus, it is restricted to correlation matrix-based S-mode PCA, meaning the analysed series have to be z-scaled (Sect. 3.1.1 and 3.1.2). Furthermore, the mean spatial PC patterns are derived from a data set ensemble, not from a distinct single data set. Thus, they cannot be used to calculate PC scores.

3.2.2 Analytic method

Another possibility to produce DD reference patterns is to perform a PCA with the “analytic”, or “exact”, covariance matrix (North et al., 1982; Cahalan et al., 1996; Dommenget, 2007) of a spatially homogeneous covariance function (Fig. 5). The analytic covariance matrix consists of the covariances among all of the data set's locations calculated directly with their interpoint distances from the function. For consistency with the stochastic method (Sect. 3.2.1), the eigenvectors (spatial patterns) were scaled to correlation loadings (Sect. 3.1.2). A brief review of different variants using the analytic covariance matrix to produce PCA reference patterns is given in Appendix A.

For the synthetic examples, the analytic method was performed as eigendecomposition of the analytic covariance matrix with the function “eigen” from the default “base” package (R Core Team, 2019). For the precipitation data, a truncated PCA, calculating the first 20 PCs only, was performed with the function “eigs_sym” from the “RSpectra” package to reduce computation time. The equivalence of the results of both algorithms with respect to the leading PCs was confirmed by comparing the results from smaller data sets.

Figure 5 Analytic DD reference method.

3.3 Matching of spatial PC patterns

The matching of the spatial patterns from different PCAs was quantified with the congruence coefficient (Lorenzo-Seva and ten Berge, 2006) and Pearson correlation. The congruence coefficient φ is defined as the cosine of the angle between two vectors of component or factor loadings a₁ and a₂, both being based at the origin.

$$\begin{array}{}\text{(3)}& \mathit{\phi }={\displaystyle \frac{\sum a_{\mathrm{1}}{a}_{\mathrm{2}}}{\sqrt{\sum a_{\mathrm{1}}^{\mathrm{2}}\sum a_{\mathrm{2}}^{\mathrm{2}}}}}\end{array}$$

In contrast, Pearson correlation gives the cosine of the angle between two vectors, both being based at the mean loading. Thus, the matching coefficient ω in the following equation gives the Pearson correlation r when $b={\stackrel{\mathrm{‾}}{a}}_{\mathrm{1}}$, $d={\stackrel{\mathrm{‾}}{a}}_{\mathrm{2}}$ and the congruence coefficient φ when $b=d=\mathrm{0}$ (see the help of R-function “factor.congruence”).

$$\begin{array}{}\text{(4)}& \mathit{\omega }={\displaystyle \frac{\sum \left(a_{\mathrm{1}}-b\right)\left(a_{\mathrm{2}}-d\right)}{\sqrt{\sum {\left(a_{\mathrm{1}}-b\right)}^{\mathrm{2}}\sum {\left(a_{\mathrm{2}}-d\right)}^{\mathrm{2}}}}}\end{array}$$

If the compared vectors have zero mean values (${\stackrel{\mathrm{‾}}{a}}_{\mathrm{1}}={\stackrel{\mathrm{‾}}{a}}_{\mathrm{2}}=\mathrm{0}$), both indices are identical. In all other cases, the results differ. The congruence coefficient is sensitive to the addition of constants, because the vector means are not removed (Lorenzo-Seva and ten Berge, 2006). Two eigenvectors with different means can be closely correlated even though their magnitude patterns differ substantially such that some variables load high on the one PC and low on the other (Richman, 1986; Lorenzo-Seva and ten Berge, 2006). In the S-mode PCA case, this means that two spatial PC patterns with different means can be closely correlated even though some locations load high on the one PC and low on the other (thus, the maximum loadings of the two PCs could be in different locations). If that is the case, the congruence coefficient would be low, indicating the difference in magnitude patterns. Thus, in contrast to Pearson correlation it incorporates vector magnitudes in the comparison (Richman, 1986). This is desirable for the comparison of eigenvectors from PCA or factor analysis because the magnitude of the loadings is important for the interpretation of the components (Richman, 1986). Therefore, the congruence coefficient is recommended as matching coefficient over Pearson correlation for the comparison of eigenvectors from PCA or factor analysis (Richman, 1986). However, a major benefit of Pearson correlation is that it is well known and the results in terms of r or R² can easily be contextualized by the analyst.

Note that the stability analysis of the stochastic DD reference method (step 2, Sect. 3.2.1) was performed with Pearson correlation only, because all compared PC patterns (i) were of identical rank and (ii) were based on synthetic data sets simulated with identical spatial correlation properties and identical domains. For this setting, we considered the effect of the pattern mean subtraction by Pearson correlation as negligible.

Both indices have a value range from −1 to 1, with 1 indicating a perfect match, 0 no relationship and −1 a perfect inverse match (Richman, 1986). Compared with Pearson correlation, the congruence coefficient is biased towards higher values (Richman, 1986). Several guidelines were suggested that assign specific ranges of absolute congruence coefficients (aCC) to categories of goodness-of-match, or specific thresholds as indication for the identity of components/factors (Richman, 1986; Lorenzo-Seva and ten Berge, 2006). Here, we follow Lorenzo-Seva and ten Berge (2006) who suggested that aCC values between 0.85 and 0.94 indicate fair similarity of the two components, values larger than 0.95 indicate that they can be considered equal and values below 0.85 should not be interpreted as indication for similar components.

The congruence coefficient was calculated with the function “factor.congruence” from the “psych” package. The statistical significance of the correlations was assessed with t-tests and the significance level 0.05 using the function “cor.test” from the default “stats” package (R Core Team, 2019).

3.4 North's rule of thumb

Confidence limits to identify clearly separated eigenvalues and eigenvectors can be estimated e.g. with North's rule of thumb (North et al., 1982; Hannachi et al., 2007) based on the data set's effective sample size n^∗, also known as number of independent observations in the sample or the number of degrees of freedom (Hannachi et al., 2007). The 95 % confidence interval of the eigenvalue λ_g is given by $\mathit{\delta }{\mathit{\lambda }}_g\sim {\mathit{\lambda }}_g\sqrt{\mathrm{2}/n^{\ast }}$. In our case here, n^∗ equals the length of the analysed time series because the series do not exhibit temporal autocorrelation. The confidence interval for the associated eigenvector u_g can then be estimated with $\mathit{\delta }{u}_g\sim \left(\mathit{\delta }{\mathit{\lambda }}_g/\mathrm{\Delta }\mathit{\lambda }\right)u_j$ where u_j is the eigenvector of λ_j, the closest eigenvalue to λ_g, and Δλ the spacing (λ_j−λ_g) between both eigenvalues.

3.5 Varimax rotation

Rotation aims at separating a subset of PCs more clearly such that the association between the eigenvectors and the PCs is more distinct. The goal is to reach a so called “simple structure” with the loadings being either close to zero or close to the maximum possible absolute values as much as the data permit (Wilks, 2006). Thus, the magnitudes of the loadings are changed. The total variance of the rotated subspace is preserved, but the variance among the rotated PCs is redistributed more evenly (Jolliffe, 2002), potentially affecting which PCs are rated dominant. Different rotation methods are available (Richman, 1986). The rotation is performed by multiplication of the selected eigenvectors by a rotation matrix. If the rotation matrix is orthogonal, the rotation is called orthogonal, otherwise oblique (Wilks, 2006). To support the interpretability of the results, the rotation matrix is chosen to optimize a simplicity criterion (Jolliffe and Cadima, 2016). Depending on the selected simplicity criterion, the rotation changes the properties of the eigenvectors and PCs. The results can depend on the number of eigenvectors that are rotated (Jolliffe, 2002; Wilks, 2006). This is different from standard PCA where the patterns and the associated variances from a set of PCs do not depend on the number of considered PCs. For example, in standard PCA the patterns and variance distributions of the first two PCs are identical, regardless of whether only the first two PCs are considered or, say, the first four PCs. Often the results are affected more by the choice of how many eigenvectors are rotated than by the choice of the simplicity criterion (Hannachi et al., 2006; Jolliffe and Cadima, 2016).

Here, we applied varimax rotation with Kaiser normalization (Kaiser, 1958). It is the most popular rotation method (Wilks, 2006). Varimax is an orthogonal rotation that maximizes the sum of the variances of the squared elements from the r selected eigenvectors b by iteratively rotating pairs of eigenvectors (Richman, 1986; Wilks, 2006). With the Kaiser normalization the eigenvectors b are normalized with the communalities h² of the n analysed variables (here the time series from the n different locations) prior rotation and renormalized afterwards. The communality $h_i^{\mathrm{2}}$ of variable i is the fraction of variance from the variable that is depicted by the k rotated PCs. The normalized varimax criterion V can be calculated as

$$\begin{array}{}\text{(5)}& V={\sum }_{j=\mathrm{1}}^k\left\{\left[n{\sum }_{i=\mathrm{1}}^n(b_{ij}^{\mathrm{2}}/h_i^{\mathrm{2}}{)}^{\mathrm{2}}-{\left[{\sum }_{i=\mathrm{1}}^n(b_{ij}^{\mathrm{2}}/h_i^{\mathrm{2}})\right]}^{\mathrm{2}}\right]/n^{\mathrm{2}}\right\}\end{array}$$

Note that the scaling of the eigenvectors that are rotated affects the varimax results (Jolliffe, 1995; Wilks, 2006). Either the orthogonality of the eigenvectors, the uncorrelatedness of the PCs or both get lost. The most popular scaling and the default in many software packages is to use eigenvectors scaled to the square root of their eigenvalues, derived from correlation matrix PCA (what we term correlation loadings here). In that case, the orthogonality of the eigenvectors and the uncorrelatedness of the PCs are lost. Other options are to use unit length eigenvectors which preserves the orthogonality of the eigenvectors, or to divide the unit length eigenvectors by the square root of their eigenvalues which preserves the uncorrelatedness of the PCs. For the introductory purpose we use the most popular variant and rotate correlation loadings only. Varimax rotation was performed with the function “varimax” from the default “stats” package (R Core Team, 2019).

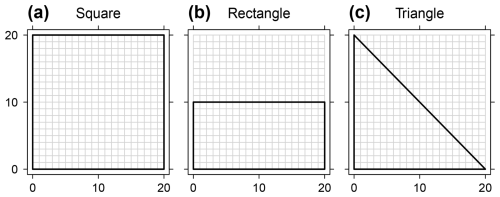
Figure 6 (a) Square, (b) rectangular and (c) triangular domain boundaries on the 20×20 grid. The grid cells represent locations from a data set.

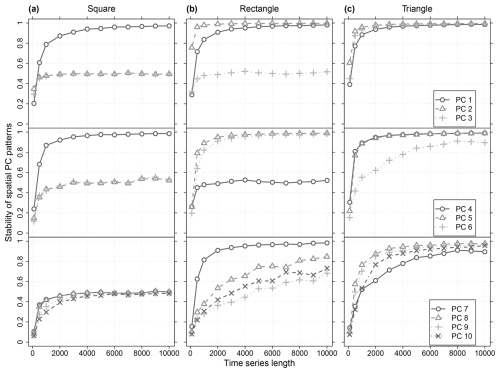
Figure 7 Stability of the spatial patterns from the leading ten PCs in relation to the time series length of the simulated data within the (a) square, (b) rectangular and (c) triangular domain boundaries of Fig. 6. All cells within the boundaries were used. For each domain the results from 12 data set ensembles are shown. Each ensemble consists of 100 data sets simulated with identical time series length, an isotropic exponential covariance model and a spatial correlation length of 10 cells. Each simulated data set was analysed separately with PCA. The stability of the spatial PC patterns is measured by the mean R² of the correlation between the spatial patterns of all PCs with identical rank derived from the respective ensemble (step 2 of the stochastic method, Sect. 3.2.1). The legends in (c) apply also to (a) and (b) of the respective row.

4 Exploring the DD effect

4.1 Exploring Buell patterns and their stability

As a start, we estimated DD reference patterns for Buell's (1975) three basic geometric domain shapes (Fig. 1) using the stochastic method (Sect. 3.2.1). Ensembles of 100 data sets were simulated for each of the three shapes. The domain boundaries are shown in Fig. 6. All cells within the boundaries were used. Note that the shape of a domain means the spatial arrangement of the data set's locations. It should not be confused with the shape of its boundary. The sides of the square, the long side of the rectangle and the legs of the perpendicular triangle were 20 cells long, the short side of the rectangle was 10 cells long. Thus, the rectangular and the triangular domain were of half the size of the square. Each data set was simulated with a spatially isotropic exponential covariance model and a spatial correlation length of 10 cells.

For the reliability of the stochastic DD reference patterns, their stability is essential. Figure 7 summarizes the results of the stability analyses (step 2 of the stochastic method, Sect. 3.2.1) from a series of ensembles with identical spatial domain and spatial correlation properties but different time series lengths. Thus, the plot shows for each PC rank the dependency of its spatial patterns' stability from the time series length if all other parameters used in the simulation are identical. Based on that information it can be decided whether additional ensembles with longer time series shall be simulated to improve the estimation. Here, we considered a time series length of 10 000 sufficient for all three domains.

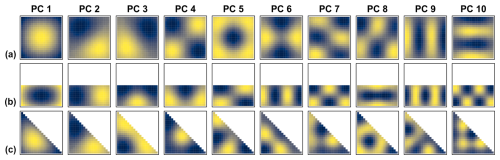
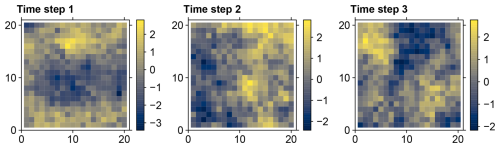
Figure 8 Overview of the leading ten mean spatial PC patterns (DD reference patterns), estimated with the stochastic method from the data set ensembles with time series length 10 000 shown in Fig. 7. All cells within the three geometric domain boundaries of Fig. 6 were used (AC). The focus is on the spatial patterns only – not their magnitudes. Therefore, no scales are shown. Instead of the ± schemes used by Buell (1975) (Fig. 1), colour gradients picture the spatial patterns. In each subplot, the gradient depicts from blue to yellow the range between the minimum and maximum values of the respective pattern.

Figure 9 As in Fig. 8 but for the standard deviation patterns (uncertainty estimation of the stochastic DD reference patterns). From blue to yellow the colour gradients depict increasing uncertainty.

Here and in the following, the results are shown for the ten leading PCs, merely for illustrative purposes. We found it to be a good balance between showing the DD pattern sequences and some degree of detail, but not too much detail that it is still visually easy to grasp. There was no other specific truncation criterion, e.g. based on eigenvalue magnitude or percent variance extracted, applied. The plots of the spatial PC patterns are overview plots designed for direct visual comparison with the classical Buell patterns shown in Fig. 1, and among each other. The focus is on the spatial patterns only – not their magnitudes. With few exceptions in Sect. 4.4 and the Supplement, we therefore do not show the scales. This is analogue to the schemes in Buell's original work (Buell, 1975). In contrast to Buell, we use colour gradients – instead of ± schemes – to picture the spatial patterns. We think that this further improves the readability of the figures, especially for the more fine-structured patterns of the PCs with small eigenvalues (lower ranked PCs). Figure 8 shows the mean spatial PC patterns of the ensembles. Those are the stochastic DD reference patterns. Most of them correspond to the Buell patterns shown in Fig. 1. Some exhibit switches in the ranking, e.g. PC 3+4 of the rectangular domain or PC 7+8 of the square domain. The uncertainty estimation of the stochastic DD reference patterns, given by the standard deviation of the spatial PC patterns from the data set ensembles, is shown in Fig. 9.

Exemplarily, the scales of the mean and standard deviation patterns of the square domain are shown in a detail plot in Fig. S2. To make use of the standard deviation patterns (Fig. S2b) as uncertainty estimation of the DD reference patterns, it is necessary to consider their magnitudes in relation to the contrast from the mean spatial patterns (Fig. S2a). In addition, the detail plot shows the percentages of variance assigned to the DD reference.

The stability of the DD patterns reflects their distinctness in the sequence of spatial PC patterns according to the PCA constraints. It depends on the specific combination of domain size and shape and spatial correlation properties of the data set. For example, for the properties here, PCs 8 to 10 of the triangle are more stable than the ones of the rectangle (Fig. 7c, b). Generally, there is the tendency that the spatial patterns of low ranked PCs, which contain also more fine-details, require longer times series to gain stability. At first, for the rectangular domain, it seems counter intuitive that PC 2 stabilizes faster than PC 1 (Fig. 7b). It indicates that for the properties of the simulated data the rectangular domain shape gives a clearer orientation for the spatial pattern of PC 2 than for the one of PC 1. Thus, especially for short time series the orientation of the gradient along the long side of the rectangle (PC 2) is more distinct than the position of the monopole in the centroid of the rectangle (PC 1) (Fig. 8b). Similarly for the triangle, the orientation of the gradient patterns of PC 2 and 3 induced by its long side are more distinct than the position of its PC 1 monopole (Figs. 7c and 8c).

PCs with ambiguous orientation of spatial patterns are more likely to occur for symmetric domain shapes than for asymmetric ones (North et al., 1982). The basic geometric domain shapes used here exhibit rotational symmetry of order 4 (square), order 2 (rectangle) and order 1 (triangle). Order 1 means no rotational symmetry. Accordingly, within the range of the analysed time series lengths the number of PCs that exhibited unstable spatial patterns differed between the domain shapes (square: 8, rectangle: 5, triangle: 2 in Fig. 7). Unstable spatial PC patterns are indicative for effectively degenerated multiplets and will be discussed in Sect. 4.4.

The R script to apply the stochastic reference method enables the production of catalogues of stability plots and DD patterns like in Figs. 7 and S2 for data sets with different spatial domains and spatial correlation properties (for sample catalogues see Lehr, 2024). The combination of both plots can be used to explore how the properties of a data set affect the DD patterns. Here, we neglect the effect of measurement errors. However, it can be simulated by adding noise to the realizations of the random field (Fig. 2).

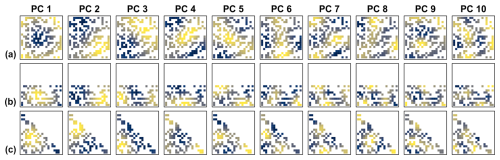
Figure 10 DD reference patterns as in Fig. 8 but for a random selection of only 40 % from the cells within the three geometric domain boundaries of Fig. 6 (Hom40). The sampling probability was homogeneous across the domain (spatially homogeneous case).

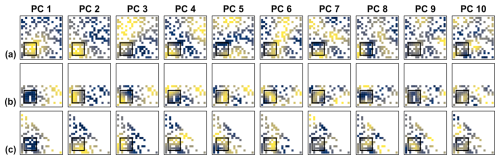
Figure 11 DD reference patterns as in Fig. 8 but for a random selection of only 40 % from the cells within the three geometric domain boundaries of Fig. 6 (Het40). The sampling probability within the small square in the lower left was three times higher than in the rest of the domain (spatially heterogeneous case).

4.2 Effects of the domain shape

For data sets with identical spatial correlation properties and similar domain size, the DD patterns are original for every domain shape. This is obvious for domains of such simple and clearly different shape like the three geometric shapes used so far. The sequence of their DD patterns is visually easy to recognize. For more complex shapes, the DD patterns are less predictable, a priori, and visual recognition is more limited.

For demonstration, we compared the DD patterns from data sets with identical spatial correlation properties in the variant in which all cells within the three geometric boundaries of Fig. 6 were selected (AC) (Fig. 8) with two variants in which only 40 % of the cells were randomly selected. In the first variant the subsampling was spatially homogeneous (Hom40) (Fig. 10), in the second spatially heterogeneous (Het40) (Fig. 11). The domain of the Het40 variant contained a subregion with higher sampling probability than the rest of the domain, i.e. within each domain there is one area in which the locations cluster. Clusters of locations have more weight in the calculation of the PCs analogue to the calculation of a weighted spatial mean (Karl et al., 1982). For the DD pattern of PC 1 the effect is obvious. Its monopole is placed in the centroid of the network. In comparison with the regular variants (Figs. 1, 8 and 10) it is therefore shifted according to the density of the locations (Fig. 11). The patterns of all other PCs are not predictable without calculating DD reference patterns.

Visually, the domains of the subsampling variants are still clearly of square, rectangular and triangular shape. Their leading DD patterns are recognizable as distinct spatial patterns. Most of the leading DD patterns from the Hom40 variant (Fig. 10) appear as noisy counterparts of the AC patterns (Fig. 8). In the Het40 case (Fig. 11), the patterns of the square domain appear again relatively similar, whereas for the triangular and rectangular domain only a few PCs exhibit visually similar patterns, e.g. PC 2.

The similarity of patterns formed by congruent selections of cells from the different variants is of particular interest. It addresses the question whether the spatial PC patterns calculated from two different domains result in different relations between the values at locations with coincident coordinates. This is visually only poorly assessable. Therefore, we correlated the patterns of the subsampling variants with the patterns formed by the corresponding subsets from their AC counterpart (that is, the AC patterns clipped with the coordinates of the subsampling variant). For example, the patterns from the Hom40 square (Fig. 10a) were correlated with the patterns from the AC square (Fig. 8a) clipped with the coordinates of the subsampled square.

For the spatial patterns of the Hom40 variant and the AC variant, the correlation analysis confirmed the visual impression of overall similarity (Table 1). But it also showed the originality of the patterns and that there are clear differences between the variants. The patterns of the Hom40 variant can be:

1. simply noisy variants of the AC patterns (e.g. PC 1 and 2 from all domains),

2. simply noisy variants of the AC patterns but with different ranking (e.g. PC 3 and 4 from the rectangular domains),

3. a mix of AC patterns (e.g. PC 4 and 5 from the square domains¹), or

4. very different from the AC patterns (e.g. PC 10 from all domains²).

Transitions between (3) and (4) are possible (e.g. PC 6 and 7 of the rectangular domain). Generally, the differences increase towards the low ranked PCs with the more detailed patterns. But there are also substantial differences between the patterns from relatively high ranked PCs possible (e.g. PC 4 and 5 from the square domains). Thus, even for rather homogeneous subsampling, like the Hom40 variant, the DD patterns are not necessarily simply noisy variants of the classical Buell patterns. The comparison with the Het40 variant yielded substantially stronger deviations (Table 2). Thus, generally, visual recognition of Buell like patterns in S-mode PCA results is a concrete indication for DD. However, it is so in particular for the leading PC patterns from domains with rather homogeneous spatial arrangement of locations within boundaries similar to Buell's archetypes. For domains of similar size and identical spatial correlation properties, deviations from strictly regular distribution of locations alone can result in DD patterns substantially deviating from what one might expect with the classical Buell patterns in mind.

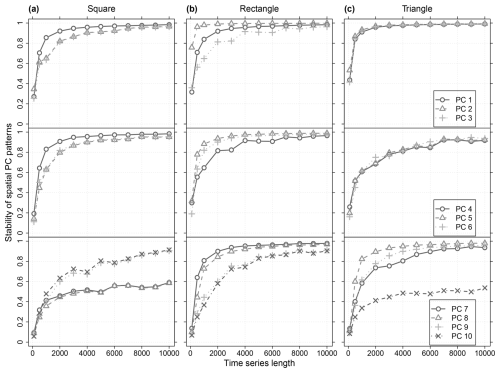
Figure 12 Stability of the spatial PC patterns as in Fig. 7 but for the patterns of the Hom40 variant (Fig. 10). The stability is measured by the mean R² of the correlation between the spatial patterns of all PCs with identical rank derived from an ensemble of 100 data sets simulated with the respective time series length. For details see the caption of Fig. 7.

Side note: The spatial PC patterns of the subsampling variants required shorter time series lengths to stabilize (Figs. 12 and S3) than the AC variant (Fig. 7). This indicates that the subsampling resulted in a more unbalanced arrangement of locations and therefore a more distinct orientation for the order of the orthogonal spatial PC patterns.

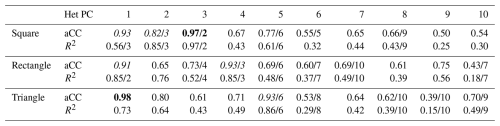
Table 1 Best matches between the DD patterns of the square, rectangular and triangular domains from the homogeneous subsampling variant (Hom40) (Fig. 10) and the patterns formed by the corresponding subsets from their all cells (AC) counterpart. That is, the AC patterns (Fig. 8a to c) clipped with the coordinates of the Hom40 variant (Fig. 10a to c), quantified by the absolute values of the Congruence Coefficient (aCC) and R². Mostly, the best matches were of identical PC rank. If the best match was with an AC pattern subset of different rank, that rank is given after the “/”. Hom PC: PC ranks from the Hom40 variant. Bold aCC values indicate PC patterns that can be considered equal; italic aCC values indicate fairly similar PC patterns (Sect. 3.3).

Table 2 As in Table 1 but for the Het40 variant (Fig. 11).

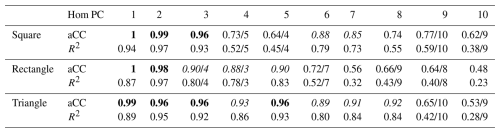
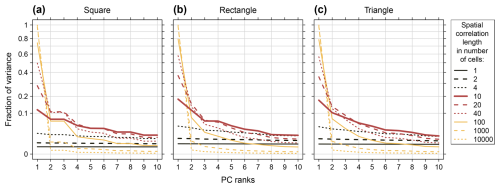
Figure 13 Variance representation of the ten leading PCs modelled with the analytic DD reference method using an isotropic exponential covariance model, nine different spatial correlation lengths and the domain boundaries (a) square, (b) rectangle and (c) triangle from Fig. 6. All cells within the boundaries were used. The scale of the Y-axis is square root transformed for better readability.

Figure 14 As in Fig. 13 but for the contrasts of the DD patterns.

4.3 Effects of the domain size and spatial correlation length

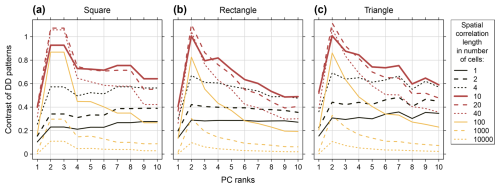
The ratio between domain size and the spatial correlation length affects the fractions of variance allocated to the PCs (Fig. 13) as well as the contrasts of the spatial PC patterns (Fig. 14). If there is no spatial correlation (spatial “white noise”), the spatial patterns of all PCs are white noise. All PCs represent the same fraction of variance, one divided by the total number of PCs. The magnitudes of the contrasts of their spatial patterns are small and on the same level. For spatial correlation length increasing from zero towards infinity, the data sets' series from all locations get more and more similar, converging towards identity of all series (perfect correlation). If the latter is reached, there is no variance in the data that could be distributed and, consequently, there are no patterns or contrasts in the PC patterns. In between the two extremes, successive allocation of variance to the PCs and spatial PC patterns with distinct contrasts appear.

For the variance allocation, increasing correlation lengths result in increasing accumulation of variance in the leading PCs, converging towards accumulation of the total variance in PC 1.

For the contrasts, it is more complex. The maximum contrasts appear for correlation lengths in the order of magnitude of the domain size. The exact maximum is specific for the different PCs and depends on the particular domain shape. For example, for the triangular domain here (Fig. 14c), the contrasts of the PC 1 patterns peak at a correlation length of 13 cells, the ones of the PC 2 patterns at a correlation length of 21 cells (not shown). The increase of the contrasts between zero correlation length and the correlation lengths of the maximum contrasts reflects the increasing fraction of covarying locations that support the poles of the DD patterns. The decrease of the contrasts between the correlation lengths of the maximum contrasts and infinite correlation length reflects the increasing similarity of all locations which leads to smoother spatial PC patterns with contrasts converging towards zero.

Within a DD sequence, the magnitude of the contrasts differs between the PCs. Generally, they peak at PC 2 (Fig. 14) and decay with decreasing PC order (Fig. S4). Starting with PC 2 it is first the coarse structures with stronger contrasts that are depicted and then the more fine-detailed structures which tend to be smoother (Figs. 8 and 14). The “spatial average” pattern of the PC 1 monopole generally exhibits contrasts on low to intermediate level compared with the “strongest contrast” pattern of the PC 2 dipole.

Substantial accumulation of variance in the leading PCs is commonly interpreted as indication for dominant processes or modes of the analysed system. In particular the combination with distinct PC patterns exhibiting strong contrasts is highly suggestive. The results demonstrate that both aspects are rather limited indicators and not sufficient for such interpretation. Quite the contrary, if spatially homogeneous autocorrelation is dominant in the data, both have to be expected.

The effect of the autocorrelation is spread over all PCs. Thus, for process identification etc., it is the question whether the features of interest cause signatures (spatio-temporal heterogeneities) distinct enough to be salient against the homogeneous background (Cahalan et al., 1996). Next question is whether they get clearly assigned to single PCs or whether they are as well smeared over several, if not all, PCs.

When rotation of PCs (Sect. 5.2.2) is applied to improve the identifiability of the features of interest, the domains size must exceed the correlation length of the respective features. Otherwise, the simplification of the PC patterns by the rotation will not be meaningful for this purpose.

4.4 Effectively degenerate multiplets

Effectively degenerate multiplets are PCs with consecutive ranks, often PC pairs, which are not well separated by the PCA (North et al., 1982). They are indicated by noticeably similar eigenvalues (fractions of explained variance) considering their position in the ranking of the PCs, e.g. PC 2+3 in Fig. 13a and PC 3+4 in Fig. 13b, both for spatial correlation length of 10 cells. Within the subspace spanned by the multiplets' eigenvectors their rotation is arbitrary. All eigenvectors of the multiplet are needed to adequately describe the multiplets' subspace (North et al., 1982). Consequently, the multiplet should not be split if the subsequent use of the PCs requires an adequate representation of multiplet subspaces, for example in rotation (Jolliffe, 1987, 1989), interpretation of PC patterns or if PCA is used as preprocessing step for other analyses. In particular, special care has to be taken that the truncation point of a PCA does not split a multiplet (North et al., 1982), especially when the amount of variance associated with the excluded PCs is relatively large compared to the amount of variance extracted by those retained. The concept of effectively degenerate multiplets (short: effective multiplets, as in Wilks, 2006) is closely related to degeneracy of eigenvalues. For clarification we provide a brief introduction in Appendix B.

In S-Mode PCA, spatial and temporal patterns are associated to the PCs. Often the hope is that the leading PCs represent the dominant spatio-temporal features of the data set. In case of effective multiplets, one spatio-temporal feature is described by the two or more PCs forming the multiplet. This feature can be described with any linear combination of the spatio-temporal patterns of the involved PCs (Appendix B). For example, a degenerated PC pair could indicate “a signal that is propagating in space” (von Storch and Zwiers, 2003; Roundy, 2015) like the Madden-Julian Oscillation (Kessler, 2001). Note that such signal might be further modified by lower ranked PCs that are clearly separated from the degenerated pair (Kessler, 2001; Roundy, 2015). Thus, at first glance an effective multiplet could be considered indicative for a rather complex spatio-temporal feature. But as we showcase here, it might as well simply result from DD.

The presented examples only consider spatial autocorrelation. Temporal autocorrelation has been excluded, resulting in white noise for the temporal PC patterns (Sect. 3.2.1). Thus, the issue of one spatio-temporal feature being represented by two or more PCs is reduced to spatial features only. Effective multiplets are built by PCs of which the orientation of their eigenvectors, i.e. their spatial patterns, in the DD sequence is ambiguous. Therefore, their patterns are very sensitive to even small variations in the analysed data. All the multiplet members in combination describe a spatial feature of the data set. Thus, in case of a degenerated pair, a variation in one pattern of the pair implies a complementary variation in the other. For the simple geometric shapes here, the pair's spatial patterns from an ensemble of data sets simulated with identical spatial domain and spatial correlation properties will usually exhibit two predominant patterns with ambiguous ranking. Gradual variations of the predominant patterns and the switches in the ranking result simply from the randomness of the simulations.

For example, the two predominant spatial patterns of the degenerated pair formed by PC 3 and 4 from data sets simulated with rectangular domain (20×10 cells), isotropic spatial correlation with exponential decay and a correlation length of 10 cells (Fig. 8b) randomly switch rank between distinct data sets (Fig. 15). This results in the low stability of the PC 3 and 4 patterns from the respective ensemble (Fig. 7b). For both PCs, the correlation of the ensemble's patterns converge for long simulated time series to a R² close to 0.5, indicating that the degeneracy of this pair cannot be resolved with longer time series. The complementarity of both parts of the pair is visible in the ensemble's mean and standard deviation patterns. The standard deviation pattern of PC 3 reflects an absolute variant of the mean spatial pattern of PC 4, and vice versa (Figs. 9b and 8b). The R²s of the correlation between the two patterns were 0.64 and 0.78, respectively. The aCCs of the two patterns were 0.95 and 0.96.

Degeneracy might cause domain dependent patterns that don't seem to be DD patterns because they are intermixed into new patterns. For example, in Fig. 15 the patterns of the multiplet pairs of simulations 1, 4 and 5 exhibit different patterns than those of simulations 2 and 3.

Symmetry of the domain shape triggers degeneracy (North et al., 1982). Thus, generally, it is recommendable to check spatial PCA results from data with symmetric domains for DD induced degeneracy. For example, the data sets simulated with the square domain yielded the four effectively degenerated PC pairs PC 2+3, PC 5+6, PC 7+8 and PC 9+10 (Fig. 7a). Again, the complementarity within the pairs yields standard deviation patterns of the one PC reflecting an absolute version of the mean spatial patterns of the counterpart PC (Fig. S2). The match of the respective two patterns was very close, with all R²s being larger than 0.80 and all aCCs being larger than 0.95.

Asymmetrical distribution of locations diminishes the probability of DD induced degeneracy. In the subsampling variants Hom40 and Het40 (Figs. 12 and S3) most of the degenerated PC pairs of the AC variant (Fig. 7) disappeared. The subsampling reduced the symmetry of the domain shape, resulting in a less ambiguous orientation for the eigenvectors. Consequently, the order of the DD sequence is clearer defined.

Effective degeneracy depends not only on the spatial domain but also on the effective sample size of the series, which equals here the time series lengths (Sect. 3.4). For example, in the triangular domain the effective degeneracy of the PC pair 6+7 which is prominent at a time series length of 2000 gradually disappears with increasing time series length (Fig. 7c). However, for very symmetric domains no sample size might be sufficient to resolve the degeneracy (e.g., see PC 2+3 and 5–10 of the square domain in Fig. 7a or Table II in Richman, 1986).

Commonly, degenerated multiplets are detected qualitatively by checking for noticeably similar eigenvalues of PCs with adjacent ranks, forming steps in the sequence of the PC eigenvalues, or quantitatively with North's rule of thumb (Fig. S6). Analogue steps in the sequence of contrasts can serve as additional indication (Fig. 14). With the stochastic DD reference method these steps are particularly pronounced, standing out as PCs of adjacent ranks with similar and rather low contrasts given their position in the DD sequence, e.g. PC 2+3, PC 5+6, PC 7+8 and PC 9+10 for most correlation lengths in Figure S5a, and PC 3+4 for spatial correlation length of 10 cells in Fig. S5b. It is an effect of averaging patterns that switch ranks between the data sets from an ensemble. The magnitude of the drop depends on the specific patterns that are averaged.

Intermixing might be easier overlooked for the smaller eigenvalues that are more closely spaced. If the analysist selects PCs to separate noise from signal, this could possibly result in truncation within a multiplet and consequently intermixing of noise and signal in the last considered PCs. Here, we selected the first ten PC merely for the illustrative purpose (Sect. 4.1). If the goal would be to further analyse PC 10, it would be necessary to check its patterns for intermixing – also with the subsequent PCs, in particular PC 11. Indications for intermixing in the PC 10 pattern can be seen in the stability plots of Figs. 7a, 12c and S3a, c. In case of Fig. 12c, PC 9 does not show sign of intermixing, thus, in this case the intermixing is probably with PC 11.

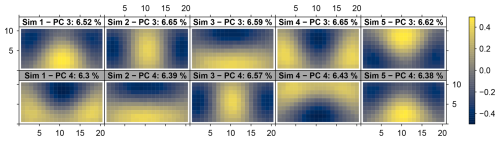
Figure 15 Spatial patterns of the degenerated PCs 3 and 4 from five distinct data sets, each simulated with rectangular domain (20 ×10 cells), isotropic exponentially decaying spatial autocorrelation of correlation length 10 cells and time series length 10 000. Identical properties were used to simulate the ensembles from Figs. 7b, 8b and 9b. The spatial patterns that belong to the same data set are plotted above each other with PC 3 on the top (white panel titles) and PC 4 on the bottom (grey panel titles). The index of the simulated data set and the fraction of assigned variance is given in the panel titles.

5 Approaches to consider DD

The preceding section introduced different aspects of DD. It demonstrated the strong effect the domain's size and shape can have on spatial PC patterns from S-mode PCA. In this section we continue with suggestions how to detect and diminish DD.

5.1 Detecting DD

5.1.1 Comparing spatial PC patterns from markedly different subdomains

The simplest way to check whether the spatial PC patterns of a data set are affected by DD is to visually compare the spatial PC patterns from sub-data sets with markedly different domains. Such a comparison can serve as quick qualitative check to detect cases in which DD is a prominent feature. We recommend partitioning of the original domain with basic geometric domain shapes like we used here. Thus, first take a subset with a square shaped domain, then taking from the square domain further subsets with rectangular and triangular domains of different orientation and compare the spatial PC patterns of these subsets. This procedure is demonstrated in the associated demo scripts (Lehr, 2024).

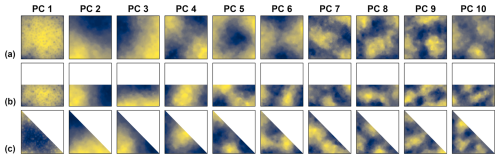
Figure 16 Overview of the leading ten spatial PC patterns from the PCAs of the precipitation data with the square, rectangular and triangular domain. The location of the square domain is marked in Fig. 3. The two other domains are fit in the square domain. In each subplot, the colour gradient depicts from blue to yellow the range between the minimum and maximum values of the respective spatial pattern.

A real-world data case is shown in Fig. 16 using raster of monthly precipitation sums from the years 1991 to 2020 in northeast Germany (Sect. 2.2). Three sets of spatial PC patterns with square, rectangular and triangular domains were derived. The square domain is the 200 km × 200 km square from the 1 km × 1 km precipitation grid in Fig. 3. The rectangular and triangular domains were fitted in the square domain, analogue to the procedure with the synthetic examples (Fig. 6). Thus, the data sets consist of time series with 360 months length and 40 000 locations in case of the square domain, and 20 000 locations in case of the rectangular and triangular domains. The DD of the spatial PC patterns is clearly visible (Fig. 16). Visually, the spatial PC patterns appear as noisy variants of the already well-known Buell patterns (Figs. 1 and 8). The very strong accumulation of variance in the centred monopole pattern of PC 1 (Table 3, Fig. 16) is another indication for DD. Thus, in this case the quick check already clarifies the DD of the PCA results.

If the subdomains are of similar size, the focus is primarily on the domain shape aspect. Analogue, the PCA results can be checked for dependency from the selected domain size. However, we assume that commonly an analysis is focused on a specific scale and the domain size as well as the interpretation of results fit to that scale. Thus, usually the dependency from the domain's shape should be more an issue than the dependency from its size.

Table 3 Percentages of assigned variances from the PCAs of the precipitation data with the square, rectangular and triangular domain (Fig. 16).

5.1.2 Comparison with DD reference patterns

DD reference patterns can be tailored for defined spatial domain and spatial correlation properties of a data set. Spatial PC patterns can be visually compared against the reference or checked for significant deviations from the reference with the congruence coefficient or simple correlation analysis (Table 1). The stability analysis of the stochastic method (Fig. 7) or the confidence intervals of the analytic method (Fig. S6) can be used to identify for each PC rank which time series length is required to reach stable and clearly defined DD patterns. Consequently, PCA results from (observed) data sets with identical spatial domain and spatial correlation properties but shorter time series have to be interpreted with the reservation that the DD might be stronger than the comparison with the reference suggests.

As a real-world data case we look again at the precipitation PCAs (Fig. 16). DD reference patterns were fitted for all three domains using an isotropic spherical covariance model and the analytic method (Fig. S7). The spatial patterns of the leading precipitation PCs exhibited strong similarity with their DD reference counterparts (Table 4), clearly indicating DD. For the first four PCs, the main difference was the separation of PCs 2+3 from the square domain in the precipitation PCAs (Fig. S8) which form a multiplet in the DD reference (Table S1 in the Supplement). In other words, although typical DD patterns occurred, the deviations of the precipitation PCA patterns from the pure theoretical DD case were strong enough to result in a clear ranking of the PC patterns. In accordance with the findings of the synthetic experiments (Fig. 13), the very large fraction of variance assigned to PC 1 of the precipitation PCAs (Table 3) is reflected in the very large theoretical correlation length of the DD reference (Fig. S7), being substantially longer than the domain size.

The patterns of the low ranked PCs exhibited stronger deviations from the DD reference than those of the leading PCs. However, this is no indication against DD. Recall that PCs should not be analysed in isolation, but only in reference to all PCs with preceding ranks. If the leading PCs exhibit DD, DD for the whole sequence of PC patterns can be concluded. It is not necessary to find DD reference patterns that perfectly fit to the patterns of the low ranked PCs for such conclusion. Because of the more finely structured spatial patterns, it can be expected that the patterns of the low ranked PCs from real-world data will deviate stronger from the DD reference than those of the leading PCs. Thus, the comparison with the DD reference confirmed the finding of strong DD from the visual comparison of the patterns from the three domains (Sect. 5.1.1).

We introduced building DD reference patterns for data sets exhibiting isotropic spatial but no temporal autocorrelation. It enables to test the null hypothesis that the spatial PC patterns from observed data merely result from simple isotropic spatial autocorrelation between random white noise time series. The main feature of the null hypothesis is the ratio of spatial correlation length to the domain size, in particular to the distances between the data set's locations. To our knowledge, such test was suggested first by Cahalan et al. (1996). They fitted models to observed precipitation and temperature data and compared the eigenvalues and spatial PC patterns of observed and modelled data. Significant differences between the two eigenvalue spectra were considered to be “signal” and indicative for spatial anisotropies and inhomogeneities, “inhomogeneous processes”, combined space and time correlation, or (secular) trends.

However, DD is not restricted to the isotropic case (see Section “Directional correlation functions” in Buell, 1975). An anisotropic example for our three basic domains is given in the Supplement. Compared with the “default” isotropic case, the DD patterns are distorted according to the direction and the ratio between longest and shortest spatial correlation length of the anisotropy (Fig. S9 vs. Fig. 8). The spatial PC patterns tend to stabilize for shorter time series length (Fig. S10 vs. Fig. 7) and the PCs which form degenerated pairs are better separated (see the bigger differences between the fractions of assigned variance and the smaller magnitudes of the standard deviation patterns in Fig. S11 vs. Fig. S2). Both aspects reflect that the anisotropy gives a less ambiguous orientation for the DD sequence.

Elaborating on the DD of PC patterns from data sets with homogeneous autocorrelation in space and time is beyond the introductory scope here. However, spatially inhomogeneous temporal trends are indicative for distinct processes, modes or alike. They are likely to spread over more than one PC (Hannachi et al., 2007; Hannachi, 2007) and to affect the variance distribution among the PCs (Vejmelka et al., 2015). Thus, if the goal is not DD assessment but to construct reference patterns for the identification of distinct features, they should be considered.

DD reference patterns are rather well behaved. The main decisions for their construction are the choice between an isotropic or an anisotropic model, and the selection of the correlation length. The first primarily defines the typical patterns that appear (e.g., Fig. 8 vs. Fig. S9), the second the variance distribution (Fig. 13, Sect. 4.3). In comparison, the effects of different spatial covariance model types like exponential, gaussian or spherical are less important. For practical applications, the comparison with the spatial patterns is the main point rather than the exact reproduction of the variance distribution. A perfect fit is not required. The spatial patterns are very similar for a wide range of correlation lengths. This holds in particular for those of the leading PCs which are commonly used in practical applications.

Table 4 As in Table 1 but for the comparison of the spatial PC patterns from the precipitation data (Fig. 16) and the corresponding DD reference patterns (Fig. S7).

5.2 Approaches to diminish DD

5.2.1 Subsampling of the spatial domain

Analysing a subsampled data set with enlarged minimal distance between the locations can be used to diminish the DD of the PCA results. Reducing the symmetry of the analysed spatial domain can remove effective multiplets. Both can help to carve out features other than DD. On the other hand, informative local details might be filtered out together with the excluded locations. If there is still DD, the new DD patterns of the subsampled data set might be harder to recognize visually because of the smaller number of locations per area. The selected minimal distance, respectively the selection of locations, is critical for the analysis. Depending on the choice, different features in the results might stick out, get diminished or even disappear. In any case, the spatial resolution of the analysed data set has to be considered in the interpretation of the results. Also, only stable PC patterns should be used to draw conclusions on the analysed system. The stable PC patterns are those which are rather insensitive to the specific selection of analysed locations. They can be identified by comparing the PCA results from different subsamples (Smirnov, 1973; Lins, 1985a; Lehr and Lischeid, 2020).

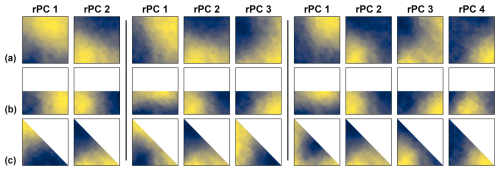
Figure 17 Leading varimax rotated spatial PC patterns from the PCAs of the precipitation data with the square, rectangular and triangular domain (Fig. 16). The rotation was performed with the first two PCs (2rPCs), the first three PCs (3rPCs) or the first four PCs (4rPCs). In each subplot, the colour gradient depicts from blue to yellow the range between the minimum and maximum values of the respective spatial pattern.

5.2.2 Rotation of PC eigenvectors

Another option that can diminish DD is to rotate the eigenvectors from the PCs of interest (Richman, 1986; Dommenget, 2007; Compagnucci and Richman, 2008). Often unrotated PCA results exhibit DD patterns, whereas rotated PCA seem to be less affected (Richman, 1986; Huth and Beranová, 2021). This finding is supported by experiments using synthetic data. Compagnucci and Richman (2008) analyzed different synthetic sequences of basic sea level pressure flow patterns (“plasmodes”). The unrotated S-mode patterns were systematically affected by DD. In the rotated variants the DD patterns vanished.

Exemplarily, we varimax rotated the leading spatial PC patterns of the precipitation PCAs (Fig. 16) in three variants, using the first two PCs (2rPCs), the first three PCs (3rPCs) and the first four PCs (4rPCs) (Fig. 17). No multiplets were split by the rotations (Fig. S7) to ensure that the results of the rotation were not affected by multiplet effects (Sect. 4.4). As expected, the variance distribution among the rotated PCs (Table 5) was much more even compared to the unrotated PCs (Table 3). The newly assigned fractions of variance did not any longer decrease continuously with the PC ranks in all cases. However, that depends on the software being used. Some packages will sort the rotated PCs by their variance explained. Note that the fractions of variance that are assigned to distinct patterns, for example to the diagonal gradient of the triangular domain, depend on the number of PCs that are rotated (Table 5). The magnitude of the pattern contrasts was more evenly distributed among the rotated PCs (Table S2) than among the unrotated PCs (Table S3). Most of the rotated patterns exhibited only positive or only negative loadings (Table S2), indicating a more “simple structure” (Sect. 3.5; Richman, 1986) than in the unrotated patterns (Table S3).

In all three varimax rotation variants, the patterns were clearly dependent on the domain geometries (Fig. 17). While the dominant PC 1 monopole of the unrotated PCA disappeared, the new dominant patterns are gradients reflecting the domain shape. For example, the patterns of the 2rPCs variant showed gradients from southwest to northeast in the square domain, from west to east in the rectangular domain and from north-west to south-east in the triangular domain. The gradients of the square domain from the 4rPCs variant reflect the rotational symmetry of the square (Fig. 17a, right panel). The gradients of the rectangular and triangular domain associated with the major fractions of variance (Table 5) depict in all three rotation variants the longest extent of the domain (Fig. 17bc). Thus, here, varimax rotation was not successful in resolving DD.

For the introductory scope here, the experiment with the three varimax rotation variants was kept deliberately simple. It is not a full-scale rotation study that would involve finding the best suitable set of rotated PCs for physical interpretation or alike. We did neither investigate which number of rotated PCs resulted in more or less DD, nor did we aim to find an optimum number of rotated PCs with respect to DD. Therefore, the results and their significance are limited. It cannot be ruled out that the DD of the presented results might be an effect of keeping too few PCs (underfactoring). In other words, unrelated signals might be forced on a single PC causing the observed DD. Keeping too many PCs (overfactoring), on the other hand, might split the correlation patterns, respectively the representation of a hydrological feature. However, overfactoring is not an issue here due to the small number of PCs retained.

Despite its limitations the experiment shows that the application of varimax rotation per se – that is without optimizing the number of rotated PCs – is not necessarily sufficient to resolve DD. For practical applications this implies that, whereas rotated eigenvectors are generally considered to be less prone to DD than unrotated ones (Richman, 1986; Wilks, 2006), it is not assured that simply taking the first few PCs of an analysis and varimax rotating them suffices to resolve DD.

Except from being less prone to DD (Richman, 1986; Wilks, 2006), rotated PCA results were found to be robust against sampling errors in case of eigenvalue degeneracy (Richman, 1986), and more robust against spatial (Richman, 1986) and temporal (Cheng et al., 1995) subsampling. Note that spatial instability may be inter-related to DD. In particular, subdomain instability can be a corollary of DD (Richman, 1986). Rotation can support the interpretation of effective multiplets if the resulting PCA patterns are of more simple structure (Jolliffe, 1987, 1989). Rotating only multiplet members limits thereby the changes in the PC properties (Sect. 3.5) to the multiplet (Jolliffe, 1989, 1995), in particular the dependency of the rotated PC patterns on which and how many PCs are rotated. That rotation results typically in a rather even variance distribution between the PCs is not much of an issue, because the variance in the multiplet is already rather equally spread between the multiplet members before rotation (Jolliffe, 1989). Also, the effects of the scaling of the eigenvectors (meaning the loss of uncorrelatedness and orthogonality in the spatial and/or temporal patterns, see Sect. 3.5) are diminished, because the eigenvalues of the multiplet are of similar size (Jolliffe, 1989, 1995).

Rotated PCA results were also found to be easier to interpret physically (Richman, 1986). Rotation can be used to systematically relax distinct PCA constraints that hamper physical interpretation (Hannachi et al., 2007; Monahan et al., 2009) by choosing between orthogonal and oblique rotation and selecting a simplicity criterion that suits best to the analysed system. In the aforementioned analysis of synthetic sea level pressure flow patterns, Compagnucci and Richman (2008) found the rotated PC patterns to be superior in depicting the “true” flow patterns. In a study using atmospheric reanalysis data, Huth and Beranová (2021) compared the spatial patterns from four PCA derived modes of climatic variability with autocorrelation maps of the analysed data to identify the true modes of climatic variability. Only the one mode based on rotated PC patterns (North Atlantic Oscillation) corresponded well to underlying autocorrelation patterns, the modes based on unrotated PCA did not. However, these studies indicating that rotated PC patterns are more suitable for physical interpretation focused primarily on atmospheric mode detection.

For future work, we suggest to perform a study similar to Compagnucci and Richman (2008), but with a hydrological focus. Synthetic data from a hydrological simulation model could be analyzed, to test which hydrological features of the model can be uncovered by the patterns of the PCs. The test data could be, for example, spatially distributed groundwater level series simulated with a groundwater model. The experiments could be used to compare the performance in hydrological feature identification of unrotated versus rotated PCA, different orthogonal and oblique rotation methods, but also of S-mode versus T-mode PCA (Richman, 1986; Compagnucci and Richman, 2008; Isaak, et al., 2018) and different scaling of the eigenvectors (Jolliffe, 1995; Wilks, 2006).

Table 5 Percentages of assigned variances from the varimax rotated spatial PC patterns from the precipitation PCAs (Fig. 17).

6 Conclusions

Spatial patterns from S-mode PCA are regularly used for hydrological interpretations. In such analysis, homogeneous spatial correlation between the data sets' time series results in spatial PC patterns that are determined by the size and shape of the analysed spatial domain (domain dependence: DD). DD patterns are distinct, with strong gradients and contrasts. We showed that DD can come together with substantial accumulation of explained variance in the leading PCs. Thus, in contrast to what one might expect, neither distinct spatial PC patterns nor large fractions of explained variance in the leading PCs do necessarily indicate dominant hydrological processes or hydrologically meaningful properties. In addition, DD can induce effectively degenerated multiplets (effective multiplets). Without knowledge about DD, the multiplets can be misinterpreted as indication for complex spatio-temporal features. Without knowledge about multiplets, the multiplet members can be mistaken as effects of independent hydrological processes. Without knowledge about the effects of multiplets, DD can be overlooked because the degeneracy can mask the expected DD patterns.

In summary, if DD is predominant, the spatial PC patterns do not reflect the hydrological functioning of the analysed system but rather the functioning of the PCA within the context of the data set's spatial domain. Ignoring DD and effective multiplets easily leads to wrong hydrological interpretations. Consequently, DD should be considered for any application in which the PCs are used to draw conclusions about spatially distinct properties of the analysed system. In other words, it should be checked whether the spatial PC patterns differ significantly from patterns that result from the trivial case of nearby locations being homogeneously more related than those further apart. If PCA is used purely for data reduction, DD is of no interest as the patterns are never examined; they serve only as an efficient set of basis vectors. If, however, the subsequent use of the PCs requires an adequate description of multiplet subspaces, for example if PCA is used as preprocessing step for other analyses, care should be taken that no multiplet is split by the selection of retained PCs. This applies in particular when the amount of variance associated with the excluded PCs is relatively large compared to the amount of variance extracted by those retained.

Classical Buell patterns (PC 1: “mean behaviour”, PC 2: gradient along the longest extent of the domain, lower ranking PCs: regular multipoles) and leading PCs with remarkably similar eigenvalues (effective multiplets) are an alert for DD. However, deviating patterns or clearly separated PCs are no contra-indication. DD patterns are original for every combination of spatial domain and spatial correlation properties. Thus, visual detection of DD is rather limited. Still, visual comparison of the spatial PC patterns from subdomains with markedly different shapes and/or sizes is practical as quick qualitative check.

To test whether spatial PC patterns differ significantly from DD patterns, reference patterns can be used as null hypothesis in pairwise statistical tests. For most practical applications checking the first few leading PC patterns should be sufficient. If the spatial PC patterns do not differ significantly from DD reference patterns, we recommend to report that and stop any interpretation of individual spatial PC patterns as distinct hydrological features.

We presented two methods to produce DD reference patterns. For the introductory purpose, we focussed on the stochastic method. The comparison of data sets simulated with identical spatial domain and spatial correlation properties showed directly the ambiguity of the PC ranking within DD induced multiplets, including the variations of the predominant patterns. Furthermore, working with simulated data is less abstract than working with the analytic covariance matrix. For practical applications the analytic method is preferable. Its short computation time is a big advantage, especially when producing DD reference patterns for data sets with many locations.

Passing the check for DD and accounting for effective multiplets in the selection of the PCs are necessary but not sufficient conditions to assure physical meaningfulness. When single PCs, or combinations of PCs, are assigned to distinct hydrological features, it should be carefully considered whether the S-mode PCA constraints (i) successive maximization of variance on the PCs, (ii) orthogonality of spatial PC patterns and (iii) linear uncorrelatedness of temporal PC patterns support such interpretation. The spatio-temporal PC patterns should not only be checked for resemblance with the postulated features, but also the invariance of the spatial and temporal PC patterns against subsampling should be approved. Building on this study, a next research task could be to conduct systematic experiments with synthetic test data derived from hydrological simulation models to evaluate which PCA modes, rotation methods and scaling of the eigenvectors work best for hydrological feature identification.

Appendix A: PCA reference patterns based on the analytic covariance matrix

Deriving reference patterns with the analytic covariance matrix to evaluate PCA results was applied earlier by Cahalan et al. (1996) and Dommenget (2007). They modelled the evolution of a continuous meteorological field as stochastic spatially isotropic diffusion process, i.e. a spatial first order auto regressive (AR(1)) or “spatial red noise” process, and used the spatial PC patterns derived from the analytic covariance matrix of the model as null hypothesis for the spatial structure of climate variability.

Dommenget (2007) presented two adaptations of the analytic covariance matrix. In the first, for each pair of locations, the product of the standard deviations from the time series of the two locations is multiplied with their covariance calculated with the covariance function. The resulting spatial PC patterns provide the smooth pattern of the globally fitted covariance function weighted with the data set's spatial distribution of covariance magnitude. In the second, the analytic covariance matrix is adapted to simulate the effect of areas with increased stochastic forcing. Areas with larger variance than the surrounding are defined and used for the weighting of the covariance matrix. In numerical experiments the effect of monopole, dipole or multipole structures in the data on the spatial PC patterns can be tested. Note that both variants are adaptations of the covariance matrix. Thus, other than in this study, the data must not be z-scaled prior PCA.

In addition, Dommenget (2007) suggested using the spatial PC patterns from an analytic covariance matrix as null hypothesis to find spatial PC patterns “that are most distinguished from those of the null hypothesis”. These so called Distinct Empirical Orthogonal Functions (DEOFs) are derived by rotating the eigenvectors of the observed data to maximum difference in explained variance between the EOFs of observed data and those of the analytic covariance matrix. A Matlab script to perform DEOF analysis is available as supplementary material to Dommenget (2007). The DEOFs were suggested as starting point to identify teleconnections patterns or physical processes. Even though not in focus, DD patterns of the null hypothesis were observed and described as hierarchy of multipoles, “starting with a monopole as EOF-1, followed by a dipole, and then by higher order multi poles”. In analogy to the spectrum of time series the DD sequence was interpreted as reflection of different spatial scales. The DEOF approach can be also used to compare the spatial variability modes from different data sets (Bayr and Dommenget, 2013). For data sets exhibiting temporal trends detrending prior applying DEOF is recommended (Hannachi and Dommenget, 2009).

Appendix B: Effectively degenerated multiplets

An eigenvalue is called degenerate if it is associated with more than one linearly independent eigenvector. That is, the eigenvalue is repeated (non-distinct), its multiplicity is larger than one. In the PCA case, the algebraic multiplicity of an eigenvalue (the multiplicity of the eigenvalue as a root of the characteristic polynomial) equals always its geometric multiplicity (the dimension of its eigenspace) (Hefferon, 2020; Meyer, 2000) because PCA performs an eigenvalue decomposition of a symmetric matrix (see “spectral theorem for symmetric matrices”, e.g. in Lay et al., 2016 or “real spectral theorem” e.g. in Larson and Falvo, 2009). A degenerate eigenvalue together with its eigenvectors is called degenerate multiplet. The eigenvectors span the subspace of the degenerate multiplet. Within this subspace their orientation is not uniquely defined and they can be arbitrarily rotated (von Storch and Zwiers, 2003). Any linear combination of the eigenvectors from the multiplet is as well an eigenvector of the eigenvalue (North et al., 1982; Hefferon, 2020).

In real-world data sets, perfectly symmetric distribution of variance such that degeneracy in the strict sense appears is unlikely to happen. However, if the eigenvalues of the “true population” are of very similar size, the sampling variability and errors can lead to “effective degeneracy” (North et al., 1982) with eigenvalues that are “indistinguishable within their uncertainties” (Hannachi et al., 2007) and eigenvectors that are random mixtures of the true population's eigenvectors (North et al., 1982).

This shall be illustrated with a slightly extended variation of an illustration given by Wilks (2006). We start with degenerated multiplets in the strict sense, i.e. an eigenvalue with more than one eigenvector. Consider a 3D point cloud with perfectly spheroid shape (idealized rugby ball). It has one long axis and two short axes of identical size. The cloud's first eigenvector is aligned with the long axis and its eigenvalue depicts the variance of the cloud in this direction. The second and the third eigenvector can be any pair of orthogonal vectors that are orthogonal to the long axis. They share a common eigenvalue. Thus, the variance representation is split in equal parts in the plane orthogonal to the first eigenvector. If we compare the eigenvectors from random subsamples of this data set, the orientation of the first one would be very stable, yet the orientation of the second and third would exhibit large sampling variability. This correctly reflects the ambiguous orientation of the second and third true population eigenvector.

In the “effective degeneracy” case the eigenvalues are merely of very similar size. Consider again a spheroid shaped cloud but this time with the two shorter axes being of slightly different size (a slightly deflated rugby ball squeezed perpendicular to its long axis). Now the orientation of the second and third true population eigenvectors is distinct and both have distinct eigenvalues. Their share to the variance representation differs. If we compare again the eigenvectors from random subsamples of the data set, the question is whether the sampling is accurate enough to detect the slight difference in size of the two shorter axes and whether the detection of the difference is stable among the subsamples? If this is not the case, the second and third sample eigenvalues are “effectively degenerate”. Together with their eigenvectors they build an “effective degenerate multiplet”. Thus, again the orientation of the second and third eigenvectors exhibits large sampling variability but this time because of the limited sampling accuracy. Due to the ambiguity of their orientation the pair is a potentially arbitrary mixture of the unknown true population eigenvectors (Wilks, 2006). Within the “accuracy range” determined by the subsampling, the fraction of the cloud's variance depicted by the plane orthogonal to the first eigenvector is approximated with the ratio of the sum of the multiplets' eigenvalues to the sum of all three eigenvalues.