Do land models miss key soil hydrological processes controlling soil moisture memory?

Soil moisture memory (SMM), which refers to how long a perturbation in soil moisture (SM) can last, is critical for understanding climatic, hydrological, and ecosystem interactions. Most land surface models (LSMs) tend to overestimate surface soil moisture and its persistency (or SMM), sustaining spuriously large soil surface evaporation during dry-down periods. We attempt to answer a question: do LSMs miss or misrepresent key hydrological processes controlling SMM? We use a version of Noah-MP with advanced hydrology that explicitly represents preferential flow and surface ponding and provides optional schemes of soil hydraulics. We test the effects of these processes, which are generally missed by most LSMs in SMM. We compare SMMs computed from various Noah-MP configurations against that derived from the Soil Moisture Active Passive (SMAP) L3 soil moisture and in situ measurements from the International Soil Moisture Network (ISMN) from the years 2015 to 2019 over the contiguous United States (CONUS). The results suggest that (1) soil hydraulics plays a dominant role and the Van Genuchten hydraulic scheme reduces the overestimation of the long-term surface SMM produced by the Brooks–Corey scheme, which is commonly used in LSMs; (2) explicitly representing surface ponding enhances SMM for both the surface layer and the root zone; and (3) representing preferential flow improves the overall representation of soil moisture dynamics. The combination of these missing schemes can significantly improve the long-term memory overestimation and short-term memory underestimation issues in LSMs. We suggest that LSMs for use in seasonal-to-subseasonal climate prediction should, at least, adopt the Van Genuchten hydraulic scheme.

1 Introduction

Land surface model (LSM) efficacy in simulating climate feedback mechanisms critically depends on soil water retention capacity and soil moisture persistency. The influence of soil moisture on climate predictions at seasonal-to-subseasonal (S2S) scales is well-recognized due to its role in the exchange of surface energy and water fluxes with the atmosphere (Koster and Suarez, 2001; Koster et al., 2002, 2009a, 2010). Water stored in soil and aquifers, which persists variably from seasons to years, is known to affect precipitation variability (Koster and Suarez, 1999, 2001). This impact is particularly pronounced in regions transitioning from dry to wet conditions, where evapotranspiration (ET) is highly sensitive to soil moisture levels (Guo et al., 2006; Koster and Suarez, 2001; Koster et al., 2004; Seneviratne et al., 2006a). While the nature and scale of soil moisture–precipitation feedback are still being debated (Findell et al., 2011; Taylor et al., 2013), numerous studies have emphasized the importance of soil moisture initialization and its persistency for accurate climate predictions (Dirmeyer, 2011; Mei and Wang, 2012; Zeng et al., 2010; Shellito et al., 2016; Tuttle and Salvucci, 2016; Yousefi Sohi et al., 2024b; Zebarjadian et al., 2024). The strength of soil moisture–precipitation coupling varies widely across different climate models (Koster and Suarez, 1999; Koster et al., 2004; Seneviratne and Koster, 2012; Moghisi et al., 2024; Taylor et al., 2013), and discrepancies in the modeled soil moisture by LSMs for climate modeling are notable (Boone, 2004; Souri et al., 2024).

Refinement of soil moisture–precipitation feedback in LSMs is hindered by the lack of large-scale observational data, challenging the improvement and validation of model simulations (Koster and Suarez, 1999, 2001; Koster et al., 2010; Koster and Mahanama, 2012; Seneviratne and Koster, 2012). This shortfall highlights the necessity for more detailed representations of land–atmosphere feedback mechanisms that are crucial for extreme weather event predictions but typically parameterized rather than explicitly resolved in models (McColl et al., 2019; Pastorello et al., 2020). Integrating extensive observational data is vital for simulating the intricacies of climate and weather and improving model predictive skill (Koster et al., 2009b, 2017; McColl et al., 2019; Shellito et al., 2018; Mohammadi et al., 2023). Recent advancements in remote sensing observations have enabled analyses of interactions between near-surface soil and the atmosphere. Nonetheless, the paucity of root zone data complicates the investigation of deep soil dynamics. Numerous studies have utilized satellite soil moisture products to evaluate and refine models, focusing on the spatial and temporal patterns of soil moisture variability (Koster et al., 2009a; Yang et al., 2020). In particular, the Soil Moisture Active Passive (SMAP) mission has been employed extensively to assess model performance (McColl et al., 2017a, b, 2019; Shellito et al., 2016, 2018).

The concept of soil moisture memory (SMM) – the duration required for a perturbation, such as rainfall, to dissipate – becomes essential for understanding land–atmosphere interactions. SMM encapsulates the temporal variations of soil moisture, reflecting the exchange of fluxes between land and the atmosphere. Therefore, SMM is an important metric for evaluating LSMs, since one of their functions is to provide surface flux exchanges and boundary conditions for atmospheric models (Koster et al., 2004; Seneviratne et al., 2006a; Koster et al., 2009a, b; Guo et al., 2006). SMM also facilitates the comparison of how quickly soil loses water between observations and various models, providing insights into the mechanisms within LSMs and their hydrometeorological responses. Moreover, analyzing SMM can yield valuable data on the configurations and hydrological parameterizations of specific LSMs, thus improving our understanding of how different configurations impact model performance, particularly in soil moisture representation. For instance, Shellito et al. (2018) measured the drying rate of surface soil moisture, which they considered to be soil moisture memory, using SMAP data and the Noah LSM during the initial 1.8 years following SMAP's launch. They concluded that Noah shows a slower drying rate and a longer surface SMM compared with SMAP, likely due to the overly strong soil water suction represented by Noah.

Determining SMM is not straightforward due to the variety of calculation methods proposed by researchers (Ghannam et al., 2016; Katul et al., 2007; Koster and Suarez, 1999, 2001; Koster et al., 2002, 2004, 2009a; Mao et al., 2020, 2017a, b, 2019; Shellito et al., 2016; Seneviratne et al., 2006a), each introducing its own level of uncertainty. Traditionally, soil moisture has been conceptualized as a red noise process, forming the basis for SMM calculations (Delworth and Manabe, 1988). This approach has led to the definition of SMM as the e-folding autocorrelation timescale within such a process (Delworth and Manabe, 1989). SMM has also been characterized using various other autocorrelation-based methods, such as the integral timescale (Ghannam et al., 2016; Nakai et al., 2014), the soil moisture variance spectrum (Katul et al., 2007; Nakai et al., 2014), and the constant time lag autocorrelation (Koster and Suarez, 2001; Seneviratne et al., 2006b). Traditionally, these models were applied to monthly datasets. However, this approach risks overlooking dynamic processes governed by limitations in water and energy (McColl et al., 2019). Consequently, there has been a shift away from their use towards recent high-resolution observational and modeling data. Therefore, there is a need for further research to refine SMM measurements that can then be used as a benchmark for assessing LSMs (McColl et al., 2019).

McColl et al. (2019) organized soil water loss into two main categories: water-limited (long-term) and energy-limited (short-term). The energy-limited regime is a process where water loss is constrained by available energy and lasts from hours to a few days. In contrast, the water-limited regime is a process where water loss depends on the available water and spans longer periods, such as weeks, months, and seasons. McColl et al. (2019) specified that ET and drainage are the main controllers of long-term and short-term memories, respectively. Utilizing a 2-year dataset from the SMAP mission and simulations from the Goddard Earth Observing System Model, Version 5 (GEOS-5), McColl et al. (2019) conducted a global analysis under various climatic and land conditions. Their analysis revealed that GEOS-5 tends to overpredict the duration of water-limited memory and underpredict energy-limited memory compared to SMM inferred from SMAP data, while the results were not affected by the SMAP sampling frequency of 3 d. Building on this, He et al. (2023) employed the hybrid memory approach proposed by McColl et al. (2019) to assess the hydrometeorological responses of various LSMs, including GLDAS-CLSM, GLDAS-Noah, MERRA-2, NCEP, ERA5, and JRA55, against SMAP observations for 2015–2020. The authors observed that LSMs generally overestimate memory in water-limited regimes and significantly underestimate it in energy-limited regimes. Moreover, their study suggested that discrepancies in SMM representation within LSMs are more attributable to the physical processes incorporated rather than factors such as soil layer thickness or the nature of model simulations (online or offline) (He et al., 2023).

A recent review of SMM identified the soil properties and processes as important controlling factors in SMM in addition to atmospheric forcings, land use, and management for future studies in order to examine the fundamental mechanisms of SMM emergence (Rahmati et al., 2024). Based on the works of McColl et al. (2019) and He et al. (2023), this study aims to examine the impacts of key soil hydrological processes and soil hydraulics on SMM that may be missed in most LSMs. Current LSMs may not be enough to address the uncertainties in SMM estimates for incomplete representations of key hydrological processes controlling SMM and uncertainties in soil hydraulic parameters (Rahmati et al., 2024). As such, we use a version of Noah-MP with advanced hydrological representations of preferential flow, surface ponding, runoff of surface-ponded water (infiltration excess runoff), and lateral infiltration (Niu et al., 2024). We conduct model experiments with various soil hydraulic parameterizations by Brooks (1964) and Van Genuchten (1980), preferential flow, and surface-ponding depth. Our analysis investigates the impact of these configurations on soil moisture persistency across ET regimes and drainage so that they provide insights into these missing physical processes affecting SMM. By comparing SMM produced by various settings of Noah-MP with SMAP L3 data and International Soil Moisture Network (ISMN) observations from 2015 to 2019 over the contiguous United States (CONUS), we seek to identify key processes and soil hydraulic schemes controlling SMM and thus provide guidance for future developments of LSMs (e.g., reducing the prevalent SMM overestimations in LSMs).

2 Materials and methods

SMM denotes the duration required for a perturbation to dissipate or the period from the start to end of a perturbation. For instance, following precipitation, the change in near-surface soil moisture marks the beginning of the perturbation. This excess moisture gradually diminishes due to flux exchange or percolation to deeper soil layers. The moisture level of the soil plays a critical role in influencing water loss patterns. Following rainfall, the upper layer of the soil initially holds more moisture than its field capacity (θ_fc), causing runoff and drainage (see Fig. 1a). Subsequently, as the soil gradually dries, its moisture content decreases to a range between θ_fc and the critical threshold (θ_c). This phase leads to consistent water loss at the maximum ET rate, known as Stage-I ET. As this process continues, the soil moisture falls below θ_c (Fig. 1a), at which point ET becomes limited by the available water, termed Stage-II ET or ET in a water-limited regime (illustrated in Fig. 1a and b). Ultimately, when the soil moisture drops below the wilting point (θ_w), water no longer leaves the soil. Therefore, the whole process of water loss depends on the soil's moisture level and has two main types: energy-limited including unresolved drainage and Stage-I ET as well as water-limited including Stage-II ET (Fig. 1b) (McColl et al., 2019; He et al., 2023). The energy-limited (green strips) and water-limited (dotted lines) types are shown in soil moisture time series at the Tonzi Ranch station (Fig. 1c).

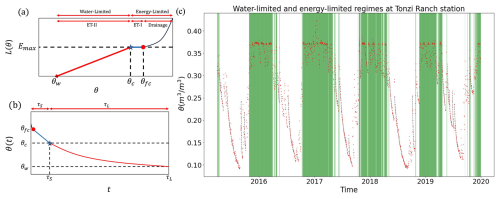
Figure 1 Schematic diagrams of the (a) surface water loss process and (b) soil moisture memory in different soil moisture regimes (adapted from McColl et al., 2017b). Note that the x axis in panel (a) refers to soil moisture (m³ m⁻³) and the y axis refers to the surface water loss rate L(θ) (mm s⁻¹). E_max is the maximum evaporation rate (mm s⁻¹). In panel (b), the x axis refers to time (e.g., days) and the y axis to SM content (m³ m⁻³). Panel (c) shows the SM time series for the Tonzi Ranch station, with the green periods indicating energy-limited regimes and the dotted lines representing water-limited regimes. θ_w, θ_c, and θ_fc refer to the wilting point, critical point, and field capacity, respectively.

2.1 Soil moisture memory of a water-limited regime (τ_L) and an energy-limited regime (τ_S)

McColl et al. (2019) considered the SMM concept as it relates to two regimes: (a) the memory of a water-limited regime (τ_L) specified by an “L” abbreviation for “long-term” and (b) the memory of an energy-limited regime (τ_S) specified by an “S” abbreviation for “short-term”. Their model incorporates a deterministic equation to represent water-limited processes during soil moisture dry-down periods. However, energy-limited processes occur over shorter timescales and present a challenge for current satellite technologies to provide precise observations. McColl et al. (2019) highlighted that drainage is not a process that is completely resolved by satellite observations. To address this gap, McColl et al. (2019) proposed a stochastic equation to capture the unresolved nature of energy-limited processes.

The hybrid model is formulated by McColl et al. (2019) as follows:

$$\begin{array}{}\text{(1)}& {\displaystyle \frac{\text{d}\mathit{\theta }\left(t\right)}{\text{d}t}}=\left\{\begin{array}{ll}{\displaystyle \frac{-\mathit{\theta }\left(t\right)-{\mathit{\theta }}_{\mathrm{w}}}{{\mathit{\tau }}_{\mathrm{L}}}},& P=\mathrm{0},\\ {\displaystyle \frac{-\mathit{\theta }\left(t\right)-\stackrel{\mathrm{‾}}{\mathit{\theta }}}{{\mathit{\tau }}_{\mathrm{S}}}}+\mathit{\epsilon }\left(t\right),& P>\mathrm{0},\end{array}\right.\end{array}$$

where θ is the volumetric soil moisture, P indicates precipitation, θ_w is the minimum soil moisture, $\stackrel{\mathrm{‾}}{\mathit{\theta }}$ is the time-averaged SM, and ε(t) is a random variable with a mean of 0. τ_L and τ_S are the SMMs for the water-limited and energy-limited regimes, respectively. McColl et al. (2019) solved these equations, demonstrating that the memories can be expressed as

$$\begin{array}{}\text{(2)}& {\displaystyle }& {\displaystyle }\mathit{\theta }\left(t\right)=\mathrm{\Delta }\mathit{\theta }\exp \left({\displaystyle \frac{-t}{{\mathit{\tau }}_{\mathrm{L}}}}\right)+{\mathit{\theta }}_{\mathrm{w}}P=\mathrm{0},\text{(3)}& {\displaystyle }& {\displaystyle }{\mathit{\tau }}_{\mathrm{S}}={\displaystyle \frac{-\frac{\mathrm{\Delta }t}{\mathrm{2}}}{\log }}.\end{array}$$

Δθ represents the soil moisture changes during dry-down, Δt is the temporal resolution of the soil moisture data, α is the precipitation intensity, Δz is the soil layer thickness, and $\stackrel{\mathrm{‾}}{\mathrm{\Delta }{\mathit{\theta }}_{+}}=\mathit{\theta }\left(t\right)-\mathit{\theta }(t-\mathrm{\Delta }t)$ represents a positive increment in soil moisture. McColl et al. (2017a) defined $\frac{\mathrm{\Delta }z\left[\stackrel{\mathrm{‾}}{\mathrm{\Delta }{\mathit{\theta }}_{+}}\right]}{\mathit{\alpha }}$ as the stored fraction of precipitation, indicating the average proportion of water that still exists in the soil layer Δt days after rainfall. McColl et al. (2019) declared that the short-term memory in their hybrid model is dominated by drainage when the sampling is relatively high (as in the case of SMAP's sampling frequency of 3 d). This approach and its rationale are further elaborated on in McColl et al. (2017a, 2019).

In the analysis of water-limited memory, we fitted Eq. (2) to the soil moisture time series during specific dry-down intervals. Then, τ_L was extracted as a parameter from the fitting curve (black dotted lines in Fig. 1c). In contrast, short-term memory was determined directly using Eq. (3), as indicated by the green periods in Fig. 1c. Further information about the criteria for calculating memories can be found in McColl et al. (2019).

2.2 Description of the datasets

We use high-resolution atmospheric forcing datasets to drive the Noah-MP LSM. This model is set up to simulate soil moisture dynamics, featuring advanced infiltration and water retention processes. Additionally, it includes a precise parameterization for ponding depth. This setup facilitated five distinct experiments. Then, we used surface and root zone soil moisture data derived from the Noah-MP experiments, SMAP L3 surface soil moisture measurements, and root zone soil moisture measurements from the ISMN to calculate the hybrid SMM. The rest of this section describes in detail the forcing and observational datasets, the Noah-MP LSM configurations, the employed infiltration and water retention schemes, and the ponding depth threshold criterion.

2.2.1 Atmospheric forcing, soil, and vegetation parameters

For modeling purposes, this study utilized the North American Data Assimilation System Phase 2 (NLDAS-2) near-surface meteorological data at an hourly interval and 0.125° spatial resolution. This dataset encompasses a range of variables, including air temperature, specific humidity, wind speed, surface pressure, shortwave and longwave radiation, and precipitation (Xia et al., 2012a). We also used precipitation data from the Integrated Multi-satellite Retrievals for Global Precipitation Measurement (IMERG-Final) dataset (Huffman et al., 2020; Yousefi Sohi et al., 2024a; Jawad et al., 2024), which offers half-hourly measurements across a 0.1° grid extending from 60° S to 60° N. Subsequently, the IMERG-Final data were mapped to the 0.125° resolution of NLDAS-2 using bilinear interpolation. These precipitation data sources were integrated into the short-term SMM computation process. To integrate the IMERG precipitation product into the model, we modified the forcing component of the Noah-MP code. Specifically, an average of NLDAS-2 and IMERG precipitation was employed when NLDAS-2 reported negative precipitation values, which was particularly significant in coastal regions. This adjustment enhanced the accuracy of precipitation inputs, contributing to more reliable simulations in these areas.

To ascertain soil and vegetation parameters, the hybrid State Soil Geographic Database (STATSGO) with 1 km resolution and the United States Geological Survey (USGS) 24-category vegetation classification were employed. The datasets were aggregated to align with a 0.125° resolution, which is consistent with the NLDAS-2 forcing data. This process included determining the dominant soil and vegetation types for each grid cell. Subsequently, the lookup tables within the Noah-MP model (Niu et al., 2020) were used to assign the relevant parameters to the corresponding soil and vegetation categories.

2.2.2 SMAP L3 surface soil moisture

Since its successful deployment on 31 January 2015, the SMAP observatory has consistently provided global volumetric soil moisture estimates every 2 or 3 d (Entekhabi et al., 2010). Its onboard radiometer, operating in the L-band frequency of the microwave spectrum, senses the top 5 cm of the soil column. In this study, we selected the SMAP L3 morning overpass due to the greater likelihood of air and surface temperature equilibrium during these hours, a critical condition for the SMAP retrieval algorithm. The SMAP L3 data used here span the period from 2015 to 2020, have a spatial resolution of 9 km, and are instrumental in calculating SMM across the CONUS.

In line with established methodologies from previous research (He et al., 2023; McColl et al., 2019), a quality control protocol was deemed necessary to refine soil moisture data in regions affected by dense vegetation, bodies of water, and permafrost, thereby mitigating noise present in satellite measurements (He et al., 2023; McColl et al., 2019; McColl et al., 2017; Wang et al., 2017). However, this study is conducted to determine SMM to deepen our knowledge of physical processes and to get closer to optimal soil hydraulic parameterizations within Noah-MP. This is achieved through a comparative analysis of SMM derived from the SMAP and Noah-MP datasets. Given that a specific parameterization within Noah-MP has a pronounced impact on the eastern region of the CONUS – a region that also corresponds to a significant portion of SMAP's low-quality data – we chose not to filter SMAP data to fully capture the parameterization effects within our study's geographical focus. This approach was intended to maintain consistency across the figures and enhance the presentation of our findings. Furthermore, our objective is to showcase the physical process involved in SMM rather than focus on model accuracy in comparison with SMAP data. Note that the SMM maps from McColl et al. (2019) and He et al. (2023) demonstrated the effect of removing SMAP low-quality data, and hence we did not include the map of locations with high-quality SMAP data. Given that the surface water balance is sensitive to the temporal resolution of the analyzed surface soil moisture data, the SMAP L3 soil moisture data are resampled to achieve a consistent sampling frequency of 1 of 3 d in each pixel (He et al., 2023; McColl et al., 2017; Wang, et al., 2017). To ensure the comparability, the Noah-MP modeled soil moisture data were selected to correspond to the SMAP observation times. This alignment minimizes potential biases introduced by temporal differences and facilitates a consistent analysis of soil moisture memory. It is important to note that the sampling frequency, as highlighted by Shellito et al. (2016), can significantly influence the computation of τ_L. This potential impact was mitigated in this study by aligning the Noah-MP data with SMAP observation times and maintaining a consistent sampling frequency of one observation every 3 d, thereby ensuring the reliability of the SMM analysis.

2.2.3 ISMN

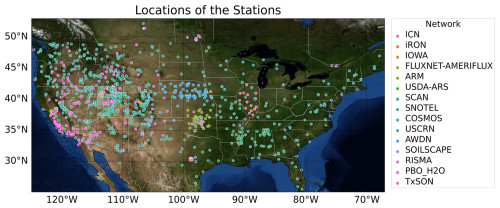
In evaluating the Noah-MP model's parameterization for the root zone soil moisture, SMM is computed using both the model's outputs and in situ observations across the CONUS. We obtained the in situ soil moisture data from the ISMN portal (Dorigo et al., 2011), which compiles quality-controlled measurements from various sensors across multiple networks (Fig. 2). We excluded stations with fewer than 90 % of their data rated as “good” quality. Despite the diversity of sensor types within the ISMN, its stringent quality control protocols suggest that it is a reliable benchmark for validating soil moisture products (Shellito et al., 2016; Colliander et al., 2017). For the representation of root zone soil moisture, we select only the data from the top 1 m of soil flagged as good quality. These measurements are averaged, i.e., hourly data aggregated to daily means, and the daily time series are used to compute both long-term and short-term SMM. For the root zone analyses, the Noah-MP outputs were sampled to ensure temporal consistency with SMAP surface layer observation times. Similarly, ISMN data were resampled to match the SMAP observation times, ensuring the same sampling frequency across all datasets used as benchmarks for the root zone SMM analysis.

Figure 2 ISMN in situ locations and networks over the CONUS.

2.3 Noah-MP with advanced soil hydrology

In this study, we choose Noah-MP (Niu et al., 2024, 2011; Yang et al., 2011) for its extensive use within the Weather Research and Forecasting (WRF) model, the Unified Forecast System (UFS) for weather and short-term climate projections, and the National Water Model (NWM) for streamflow and water resource forecasting. The “semi-tile” subgrid methodology of Noah-MP enables detailed calculation of surface energy and fluxes, differentiating effectively between bare and vegetated terrains to precisely compute variables such as latent and sensible heat fluxes (Agnihotri et al., 2023).

The Noah-MP version used in this study includes additional developments in plant hydraulics that explicitly represent plant water storage supplied by root water uptake driven by the hydraulic gradient between the soil and roots (Niu et al., 2020) and advanced soil hydrology that solves the mixed-form Richards equation and thus explicitly represents surface ponding, infiltration of surface-ponded water, and preferential flow (Niu et al., 2024). As such, the current Noah-MP accounts for water flow driven by the hydraulic gradients from the soil to the vegetation canopy to meet the plant transpiration demand. It also accounts for subgrid variability in infiltration capacity through a fractional area of preferential flow pathways caused by soil macropores in the fields. A detailed description of the underlying physical mechanisms for the schemes used in this study can be found in Niu et al. (2024), and a brief description of the equations and parameters is also included in the supporting material.

2.3.1 The mixed-form Richards equation

Most LSMs solve the mass-based (or θ-based) Richards equation (RE) for unsaturated soils (Chen and Dudhia, 2001; Oleson et al., 2010) and thus are not adequate for representing saturated conditions, e.g., surface-ponding and groundwater dynamics. The current Noah-MP adopts the methodology of Celia et al. (1990) to solve the mass-pressure (θ−h) mixed-form (MF) RE. The new solver solves the pressure head and h and conserves mass due to the mass (θ) constraint. To achieve a more accurate solution of h and the mass balance, the solver uses an adaptive time-stepping scheme.

Surface ponding occurs when the pressure head of the surface layer is greater than the air entry pressure, and the upper boundary condition (BC) shifts from a flux BC to a head BC following Paniconi and Putti (1994). Infiltration-excess runoff occurs when the surface-ponding depth, H_top, surpasses a predefined threshold, H_top,max, at which the surface-ponded water at local depressions of a model grid starts to be connected and runs off. The model extends its vertical domain to the bedrock depth (Pelletier et al., 2016) at which the lower BC is set up as a zero-flux BC. Groundwater discharge is represented simply using the TOPMODEL concept as a function of water table depth, which is determined by the modeled pressure head that is interpolated between the saturated zone and its overlying unsaturated zone.

2.3.2 Optional soil hydraulics schemes

The current Noah-MP provides optional hydraulics schemes of the Van Genuchten–Mualem (VGM) and Brooks–Corey with Clapp–Hornberger (BC/CH) parameters. To facilitate quicker convergence, particularly near saturation, we smoothed the BC/CH water retention curve using a polynomial function following Bisht et al. (2018).

2.3.3 Representing preferential flow

To represent preferential flow, the current Noah-MP adopts a Dual-Permeability Model (DPM) approach, partitioning the model grid into two domains: one representing rapid flow with a reduced suction head (macropores) and the other representing slower matrix flow, following Šimůnek and van Genuchten (2008) and Gerke and van Genuchten (1993a, b, 1996). This approach represents subgrid variability in infiltration capacity through a fractional area of soil macropores in the fields F_a (or the volumetric fraction of macropores). The DPM also represents water transfer between the two pore domains, which can be either positive (“lateral infiltration” during rainy days) or negative (diffusion from micropores to drier macropores). It also accounts for lateral movement of surface-ponded water from the matrix to macropore domains at the soil surface. The aggregated water content (θ) and vertical water flux (q) for a grid cell are given by $\mathit{\theta }=F_{\mathrm{a}}{\mathit{\theta }}_{\mathrm{a}}+(\mathrm{1}-F_{\mathrm{a}}){\mathit{\theta }}_{\mathrm{i}}$ and $q=F_{\mathrm{a}}{q}_{\mathrm{a}}+(\mathrm{1}-F_{\mathrm{a}})q_{\mathrm{i}}$, respectively, where q denotes a water flux and the subscripts a and i, respectively, indicate the macropore and micropore domains. This approach also extends to other water fluxes, such as direct evaporation from the soil surface (E_soil) and groundwater recharge.

2.4 Model experiments

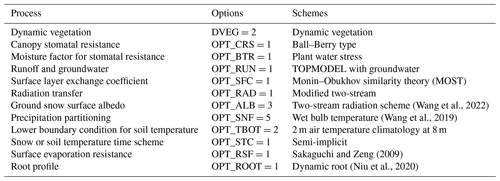
We conducted five experiments using the current Noah-MP driven by the hourly NLDAS-2 forcing data at a spatial resolution of 0.125°, starting with the same uniform initial conditions – i.e., soil moisture at 0.3 m³ m⁻³ and soil temperature at 287 K – spanning 2014 to 2019 for six iterations. The five initial iterations were dedicated to the model's spinup phase, and the resulting surface and root zone soil moisture from the last iteration were used for SMM analysis. Parameters were adopted as per the updates by Niu et al. (2020), with adjustments to the dynamic vegetation module to align with Moderate Resolution Imaging Spectroradiometer (MODIS) leaf area index observations. This study refrained from parameter calibration related to dual-domain schemes for preferential flow (Šimůnek and Van Genuchten, 2008) and ponding depth.

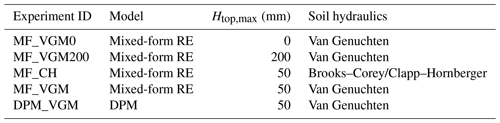
The five experiments are conducted with Noah-MP configurations with different water retention and infiltration schemes. Table 1 lists optional schemes that were the same for all these experiments for other processes, including surface layer turbulent exchange, radiation transfer, phase changes between snow and rain, and the permeability of frozen soil. For this study, we selected only those schemes that have a direct impact on the simulation of soil moisture dynamics (as detailed in Table 2). All these experiments are set with the same number of soil layers, which vary spatially from 5 to 15 vertical layers with fixed layer thicknesses: Δz_i=0.05, 0.3, 0.6, 1.0, 2.0, 2.0, 4.0, 4.0, 5.0, 5.0, 5.0, 5.0, 5.0, 5.0, and 5.0 m down to 49.0 m to match the maximum bedrock depth data of Pelletier et al. (2016) with a minimum bedrock depth of 4.0 m. The model was customized using a combination of three soil moisture solver variants, two soil hydraulics schemes, and two ponding depth thresholds.

Table 1 The Noah-MP options used in this study.

To explore the influence of surface ponding on SMM, we designed two distinct experimental conditions. The first condition, designated MF_VGM0, excluded the ponding effect by setting H_top,max to 0 mm. Conversely, the second condition, identified as MF_VGM200, incorporated a significant ponding depth of 200 mm. Both conditions utilized the mixed-form RE solver alongside the VGM model (see Table 2). Furthermore, we conducted comparative analyses to assess the role of soil hydraulic properties by conducting experiments with the BC/CH model (MF_CH) and the VGM model (MF_VGM), each with a ponding depth threshold of H_top,max=50 mm.

Table 2 Model experiment configuration.

An additional experiment employs the DPM within the VGM framework, maintaining the same ponding threshold of H_top,max=50 mm, referred to as DPM_VGM (see Table 2). The comparison of DPM_VGM with the MF_VGM setup aimed to shed light on the effects of preferential flow channels on soil moisture forecasting and runoff forecasting in future studies, thereby enhancing our comprehension of the complexities inherent in hydrological modeling.

To define the macropore volume fraction, we used the modeled soil organic matter (SOM), which is computed from Noah-MP with a microbial-enzyme model (Zhang et al., 2014) prior to the major experiments conducted in this study through a long-term (120-year) spinup simulation from 1980 to 2019 driven by the NLDAS data. The modeled SOM shows a pattern of less SOM in wet regions but more in arid regions due to more active microbial activities (decomposition and respiration) in wetter regions. The resulting macropore volume fraction ranges from 0.05 to 0.15, changing with spatially varying SOM. While we conducted sensitivity analyses of key parameters such as the ponding depth threshold and macropore fraction to identify ranges yielding realistic outcomes, we acknowledge that further model development (building relationships with global high-resolution DEM and soil data, e.g., SoilGrids 250 m; Poggio et al., 2021) is necessary for refining the parameters.

3 Results

In Sects. 2.1 and 2.2 of our study, we focus on computing the SMM for both the surface (5 cm) and root zone (up to 1 m) layers, respectively. This dual-layer analysis is fundamental to our experiments as it allows us to understand the differential impacts of various parameterizations on soil moisture. By comparing and analyzing the SMM values across these two distinct layers, we can identify specific physical processes that influence soil moisture dynamics. This comparative approach not only elucidates how these processes affect SMM but also helps in understanding the interaction between surface characteristics and subsurface moisture dynamics, which are critical for improving hydrological modeling and prediction.

3.1 Long- and short-term soil moisture memory of the surface layer

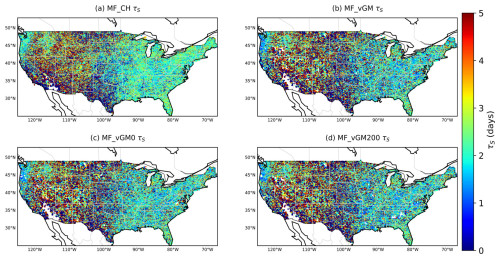
Figure 3 illustrates the spatial distribution of the median long-term memory derived from the 5-year soil moisture dataset. We also provide plots for the SMM spatial distributions to offer insights for each model experiment. However, it turns out that interpreting the fundamental mechanisms behind the distribution is very challenging regarding the spatial distributions of other controlling factors, e.g., climatic forcing, vegetation and soil types, elevation, or slope angle and aspect (affecting solar radiation), which directly or indirectly control the actual ET and runoff as well as interactions between ET and soil moisture (Rahmati et al., 2024). As such, we focus on comparing the median SMM values across model scenarios to find the dominant hydrological processes controlling SMM, because the modeled distributions from the different experiments generally show the same shape, especially for the same hydraulics (e,g., VGM). Analysis of the SMAP data revealed that long-term memory (τ_L) is significantly higher in the energy-limited and humid regions of the eastern USA and lower in the arid western regions. These findings are consistent with those of He et al. (2023) and McColl et al. (2019).

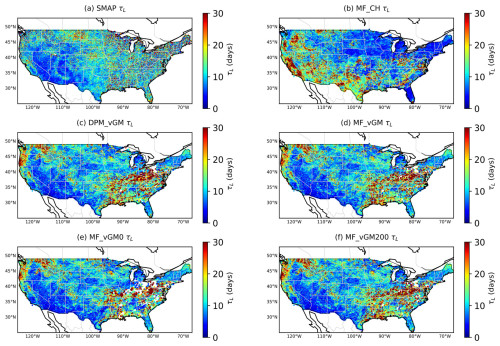
Figure 3 Long-term SMM derived from various datasets from 2015 to 2019 for the soil surface layer: (a) SMAP, (b) MF_CH, (c) DMP_VGM, (d) MF_VGM, (e) MF_VGM0, and (f) MF_VGM200. SMM: soil moisture memory.

The MF_CH experiment displays a spatial pattern that contrasts with the SMAP data, with a longer memory in the arid western regions but a shorter memory in the wet northeastern regions (Fig. 3a and b). This is likely caused by the faster drainage of topsoil water under the wetter conditions, whereas under the drier conditions the spuriously stronger suction from the CH hydraulics sustains the surface soil moisture for a longer period. Further examination reveals that models using the Van Genuchten scheme reflect SMAP's patterns. Specifically, the eastern regions display higher τ_L values, while the western regions show lower values (see Fig. 3b–f). DMP_VGM demonstrates a shorter memory in the eastern CONUS compared to MF_VGM (see Fig. 3c, d and Fig. S1 in the Supplement. The VGM scenario with zero ponding depth shows a shorter memory compared with MF_VGM200 in the eastern CONUS (Fig. 3e, f), where surface ponding happens more frequently and with a greater depth. Figure S2 shows a better match of data points with the agreement line in the DPM_VGM–SMAP scatterplot. In contrast, the MF_CH–SMAP scatterplot lacks this alignment, with a correlation of −0.10. The correlation values have risen from −0.10 to 0.15 with VGM, a sign of progress, but they are still not strong.

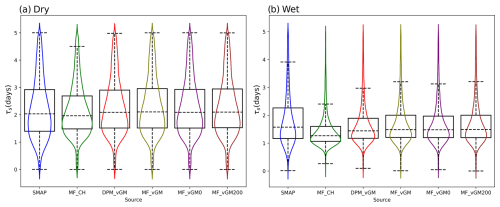
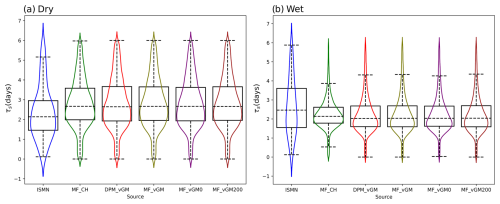
To assess the influence of plant water storage on SMAP soil moisture data and the resultant SMM, we employed the MODIS Normalized Difference Vegetation Index (NDVI) to categorize the entire CONUS into wet (NDVI>0.45) and dry (NDVI<0.45) regions. In the dry areas (see Fig. 4a), the probability distribution function (PDF) of the surface SMM from MF_CH differs from that of SMAP and exhibits a higher median of 10.53 d compared to SMAP's 8.47 d (overestimation). Other model scenarios using van Genuchten (VG) hydraulics, with an SMM median of around 8.6 d, show a PDF like SMAP's. Note that the VGM scenarios effectively tackle the problem of long-term memory overestimation, a point emphasized by He et al. (2023). This improvement is due to the refined parameterization of physical processes within the VGM experiments.

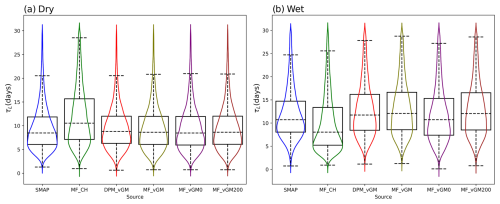
Figure 4 Violin plot of the surface τ_L estimated from the SMAP and Noah-MP scenarios for dry regions with less vegetation (NDVI<0.45) and wet regions with more vegetation (NDVI>0.45).

In the wet regions with dense vegetation (Fig. 4b), the SMM PDF of MF_CH (median of 8.03 d) significantly deviates from the SMAP PDF (median of 10.71 d), showing an underestimation of τ_L. However, due to the strong effect of plant water storage on SMAP's soil moisture retrieval (commonly in the eastern CONUS), our focus here is on model sensitivity to process representations rather than on model accuracy relative to SMAP data. Other models with the VG scheme display greater variability among themselves in wet areas (Fig. 4b) than in the dry region (Fig. 4a). MF_VGM0 (with a zero ponding depth threshold) shows a shorter long-term SMM, with a median of 10.72 d, compared to MF_VGM200 (with a 200 mm ponding threshold) with a median of 12.05 d and MF_VGM (with a 50 mm ponding threshold) with a median of 12.03 d. This suggests that extra water inputs from the surface-ponded water (MF_VGM200) can help extend the surface SMM. Changing the ponding depth threshold from 50 mm (MF_VGM) to 200 mm (MF_vGM200) has a marginal effect on τ_L, suggesting that the response does not proportionally increase with higher values. With the same 50 mm ponding threshold, DPM_VGM produces a shorter SMM, with a median of 11.73 d, than MF_VGM, indicating that the effects of faster water drainage of the topsoil water caused by the preferential flow (as represented by DPM_VGM) can last longer.

For the short-term SMM, all the scenarios produce an overall spatial pattern similar to that of the SMAP-derived τ_S, showing a longer memory in the drier western USA than in the wetter eastern USA (Fig. 5). However, MF_CH shows a shorter memory in the northwestern USA than that derived from SMAP (Fig. 5a and b). MF_CH with a median of 1.9 d underestimates SMAP with a median of 2.02 d, while VG scenarios have a median τ_S of around 2.09 d over the dry regions. This effectively rectifies the underestimation of short-term memory by LSMs, as reported in a previous study (He et al., 2023). He et al. (2023) highlighted that most LSMs tend to underestimate τ_s, which is strongly affected by soil water drainage as specified by McColl et al. (2019). Note that higher τ_s values indicate slow drainage, whereas lower τ_s values suggest faster drainage; this is exemplified by Fig. 5a, which shows more rapid drainage in the eastern CONUS compared to the western CONUS. The incorporation of surface ponding and the DPM (2.08 d) has shown fewer effects on short-term memory than the soil hydraulics for the dry region (more macropores are available in the wet regions, and hence the DPM would have a greater effect there). The introduction of surface ponding (comparing MF_VGM0 (2.11 d) to MF_VGM200 (2.108 d) in Figs. 5 and 6) contributes to more persistent surface soil moisture and drainage that is a bit quicker. The PDF of the SMM from all the VGM models more closely resembles the SMAP PDF in the western United States than in the eastern part of the country, likely due to the SMAP soil moisture retrieval being affected by the plant water storage and thus the spatial variations in canopy density.

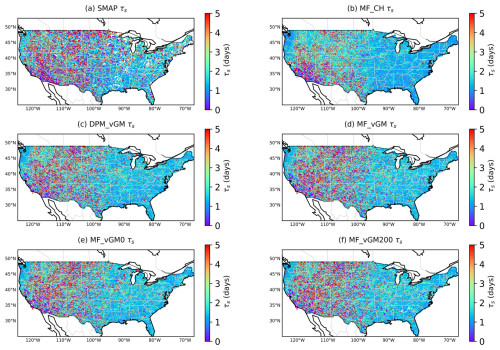
Figure 5 Short-term SMM derived from various datasets from 2015 to 2019 for the soil surface layer: (a) SMAP, (b) MF_CH, (c) DMP_VGM, (d) MF_VGM, (e) MF_VGM0, and (f) MF_VGM200.

Figure 6 Same as Fig. 4 but for short-term memory.

For the wet regions, MF_CH with a median of 1.26 d underestimates SMAP with a median of 1.56 d. DPM_VGM with faster drainage of surface soil water produces a median τ_s of 1.43 d, shorter than MF_VGM with a median of 1.48 d. The DPM accelerates the drainage of water from the topsoil. This effect is more significant in the eastern CONUS. As a result, it lowers the short-term memory in areas where the soil has macropores.

The modeling results also indicate that the long-term memory of the surface soil moisture is more sensitive to the four VGM schemes in the wet regions (Fig. 4b) than the short-term memory (Fig. 6b). This can be attributed to the differences in how topsoil water responds to surface ponding and preferential flow, as represented by the four VGM schemes across different moisture regimes. Under higher soil moisture conditions right after a rainfall event, the persistence of soil moisture is mainly dominated by drainage of topsoil water to deeper soil, whereas at relatively lower soil moisture the long-term memory is more controlled by persistent water inputs from surface-ponded water and prolonged drainage by preferential flow. This also indicates that the infiltration effects of surface-ponded water and preferential flow can last longer, up to more than 10 d. Under dry conditions (Figs. 4a and 6a), these hydrological processes become less important. However, the soil water retention curves as represented by the CH and VG schemes play a more important role under any conditions (Figs. 4a and 6a). Another possible reason could be the issue of timescales. Short-term memory has values of up to 5 d, and given the SMAP revisit time of 3 d, generating values for intervals shorter than 3 d may challenge the validity of short-term memory as a reliable measurement for soil drainage, as demonstrated by McColl et al. (2019). Since we selected Noah-MP days corresponding to the SMAP revisit time, it is possible that the effects of different VG parameterizations were diminished by this sampling. We suggest that other measurements, such as streamflow and baseflow analysis, should be considered to better quantify the effect of soil hydraulics on soil drainage (Farmani et al., 2024).

3.2 Long- and short-term soil moisture memory of the root zone layers

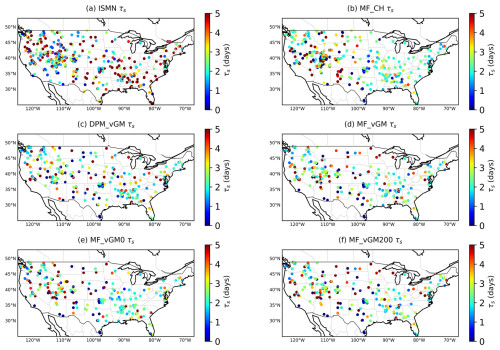
We use the ISMN dataset as the benchmark and compute SMM at the ISMN stations, as illustrated in Fig. 2. We compute the long-term SMM across 654 sites within the CONUS for the period from 2015 to 2019. The median values of these computations indicate that the root zone SMM (Figs. 7 and 9) is generally higher than the surface SMM (Figs. 3 and 5). Analysis of ISMN data reveals that the root zone τ_L (Fig. 7) generally exceeds the surface τ_L (Fig. 3), particularly in the western USA. Some eastern locations also exhibit a longer τ_L, whereas the central region demonstrates lower values.

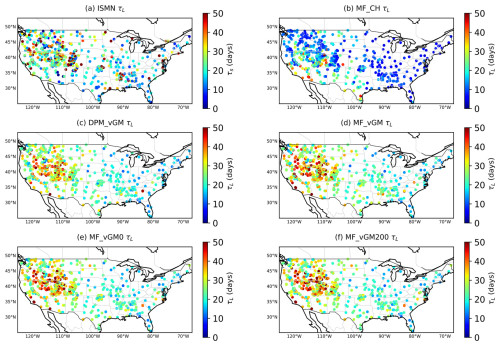
Figure 7 Long-term root zone SMM derived from various datasets from 2015 to 2019: (a) ISMN, (b) MF_CH, (c) DMP_VGM, (d) MF_VGM, (e) MF_VGM0, and (f) MF_VGM200.

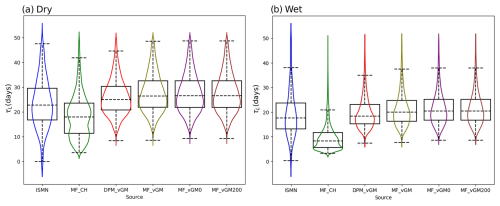
Figure 8 Violin plot of the root zone τ_L estimated from the ISMN and Noah-MP scenarios for dry regions with less vegetation (NDVI<0.45) and wet regions with more vegetation (NDVI>0.45).

MF_CH produces a shorter root zone τ_L across nearly all the sites in the CONUS (Figs. 7 and 8). The Van Genuchten scheme mirrors the ISMN-derived τ_L, albeit with slightly higher values (Figs. 7 and 8). An increase in the surface-ponding depth raises the τ_L. This is particularly true in the eastern USA, where surface ponding occurs more often, and its impact on soil moisture is more substantial. Figures S3 and S4 illustrate this effect. Additionally, DMP_VGM (Figs. 7c and 8) reduces the root zone long-term SMM across most of the CONUS relative to the other models (Figs. 7c–f and S3).

As for the surface layer, we use the MODIS NDVI to assign all the stations to wet and dry regions. In the dry regions (Fig. 8a), MF_CH has a different probability distribution function and a lower median of 19 d compared to that of the ISMN (median of 23 d). All the other scenarios using VG schemes exhibit similar SMM PDFs to each other, yet they are somewhat different from the one derived from the ISMN. Also, the presence of macropores reduces the long-term SMM, with a median of 25 d, and results in the median closest to the ISMN (Fig. 8a). The ISMN, however, shows a large range of long-term SMMs compared with all the Noah-MP experiments, indicating that the complex nature of the observed SMM needs further investigation (Fig. 8a and b). Note that the analyses were conducted at a limited number of locations, presenting challenges in fully capturing the impacts of different parameterizations on SMM.

In the wet regions, MF_CH shows a smaller τ_L value (median of 9.8 d) than that of the ISMN (median of 18 d), together with a noticeable PDF difference. The effect of dual permeability decreases the soil moisture and long-term memory compared with the other model experiments, resulting in a median (19 d) close to the ISMN (18 d) (Fig. 8b). However, it seems that the ponding depth does not show a noticeable impact on τ_L. It should be noted that the effect of ponding depth, which slightly increases the long-term memory in the root zone (RTZ), can be observed in Figs. S3 and S4 when we take a close look at them.

Further investigation reveals an enhancement in the model's ability to capture soil hydraulic dynamics when shifting from the Clapp–Hornberger scheme to the Van Genuchten scheme, with an improvement in τ_L values from 0.05 to 0.12 (Fig. S5). Also, DPM_VGM demonstrates superior performance with a correlation of 0.15 compared to all the other scenarios tested.

Figure 9 Same as Fig. 7 but for the short term.

The findings show that τ_S values in most Noah-MP scenarios are comparable to those observed in the ISMN data, as shown in Fig. 9b–f. However, there is a consistent underestimation in some eastern locations. Figure 10 highlights this pattern, showing that the wet regions tend to underestimate τ_S, with the ISMN reporting a median of 2.5 d and Noah-MP experiments a median of around 2 d. Conversely, the dry regions tend to overestimate τ_S, with the ISMN at a median of 2.1 d and Noah-MP experiments at approximately 2.7 d.

Figure 10 Same as Fig. 8 but for the short-term SSM.

Although distinguishing between MF_VGM0 and MF_VGM200 in Figs. 9 and 10 is challenging, Fig. 11 (Fig. 11c and d) reveals that an increase in ponding depth leads to a slight decrease in short-term memory in the eastern CONUS. Comparing Fig. 9 with Fig. 11 indicates that ISMN stations partially reflect the spatial pattern of long-term and short-term memory in the root zone across the CONUS. It may be concluded that the spatial patterns of long-term and short-term memory (Figs. 11 and S7) of the root zone are quite similar to those of the surface layer (Figs. 3 and 5). Hence, long-term memory is more prevalent in the eastern CONUS and mountainous areas, while longer short-term memory occurs predominantly in the western areas. However, this conclusion is not totally true, and further investigation is needed.

Figure 11 Spatial distribution of the root zone τ_s estimated from (a) MF_CH, (b) MF_VGM, (c) MF_VGM0, and (d) MF_VGM0.

4 Discussion

4.1 How do different parameterizations affect SMM?

The efficacy of LSMs in simulating climate feedback mechanisms critically depends on the soil's ability to retain moisture and how quickly the soil releases the moisture into the atmosphere through soil surface evaporation and plant transpiration and down to the aquifers through recharge. The rapid infiltration of incident water (rainfall and snowmelt) into deeper subsoil strata reduces the soil's capacity to return moisture into the atmosphere through evaporation and transpiration, thereby disrupting potential atmospheric feedback loops in LSMs (McColl et al., 2019). Conversely, if LSMs lose water too quickly through ET, they provide feedback to the atmosphere more quickly than they should. Thus, the concept of SMM becomes essential in LSMs, as it can provide information about the rate at which moisture disappears from the soil. Hence, understanding the effects of various physical processes on SMM is vital for enhancing the representation of these processes in LSMs, thereby improving their overall performance in simulating the complex interactions between the land surface and the atmosphere.

The water retention curve characteristics of the BC/CH hydraulics scheme are characterized by a strong suction force that is more pronounced than in the Van Genuchten model for various soil types (Niu et al., 2024). This stronger suction promotes moisture transfer from the deeper layers to the surface layer, causing the surface soil to retain more moisture (Fig. S6), and it has a longer τ_L (Figs. 3 and 4), which is a common issue in LSMs according to He et al. (2023). Moreover, the higher suction reduces the root zone moisture, and consequently it would have a shorter τ_L (Figs. 7 and 8). Conversely, the VG scheme, with weaker suction, transfers less moisture from the root zone to the surface, resulting in a drier surface layer and a shorter τ_L for the surface but a longer τ_L for the root zone, as depicted in Figs. 7 and 8.

Short-term memory is inversely related to moisture availability; thus, a wetter soil has a shorter τ_S, whereas a drier layer has a longer τ_S. The VG scheme produces a drier surface layer and a moister root zone, leading to a longer surface τ_S but a shorter root zone τ_S compared to the BC/CH scheme, as shown in Figs. 5, 6, and 11.

As indicated in a previous study (He et al., 2023), a common issue in LSMs is the overestimation of the long-term memory of surface soil over dry regions. This could be attributed to underestimation of evaporation within LSMs using the CH parameterization (Fig. S7a), resulting in overestimation of soil moisture. However, a shift towards the VG scheme increases the evaporation (Figs. S7b and S8), and hence it overcomes the τ_L overestimation (Figs. 3 and 4).

The presence of soil macropores promotes infiltration at the soil surface and rapid flow through preferential pathways from the surface to the root zone (Mohammed et al., 2021), consequently reducing the moisture retained in the surface layer. Moreover, macropores lead to reduced suction of the soil and hence less water from the subsurface soil was pulled up to the surface, causing the topsoil to have less moisture (Fig. S6). Therefore, macropores lead to a decrease in surface τ_L (Figs. 3d and 4b). Moreover, the presence of macropores increases the root zone soil moisture, and consequently it should prolong the root zone τ_L. However, the even distribution of macropores throughout the soil profile in the current Noah-MP configuration, DPM_VGM, increases water infiltration into deeper layers, resulting in faster flow to deep soil layers, recharge to groundwater, and thus a drier root zone. As a result, macropores reduce the root zone long-term SMM (Figs. 7d–f and S8) of DPM_VGM. This highlights the importance of calibration of the macropore profile in DPM_VGM for better representations of macropore effects and soil hydraulic dynamics.

While the soil matrix typically only allows for slow water movement due to the pressure gradient, macropores enable rapid gravitational flow (Mohammed et al., 2018). These macropores facilitate quicker infiltration into the root zone (Mohammed et al., 2021). Therefore, they increase the drainage rate to these deeper layers, which slightly reduces the short-term soil moisture memory at the surface (Figs. 5 and 6). Additionally, as water moves from the surface to the root zone, the increased moisture content there leads to quicker drainage. We speculate that this occurs in the real world; however, in the current DPM_VGM, the deep soil is wetter than the root zone, indicating a need for calibration of the macropore profile, as we have stated. Consequently, this process further decreases the short-term moisture memory in the root zone due to the higher drainage rates of wetter soil.

Finally, the ponding threshold allows water to remain on the surface before turning into runoff. This provides water with more time to percolate into the soil. The consequent increase in ponding depth allows extended water infiltration, thus enhancing soil moisture and lengthening moisture retention through the soil profile (Fig. S6e and f). So, as discussed before, wetter soil leads to prolonged τ_L and shortened τ_S (Fig. 5–7 and 11).

4.2 Limitations of our study

Some sources of uncertainty may affect our results in this study, including uncertainties in input data and models. The SMAP L-band penetration depth can indeed be shallower than 5 cm, especially over wetter regions like the eastern CONUS, which may introduce a mismatch when comparing SMAP observations with the Noah-MP 5 cm layer. SMAP reliability is affected by plant water storage change (in the eastern part of the CONUS and some mountainous sites), introducing uncertainties into SMM values for the benchmark. While SMAP observations may be less reliable over these densely vegetated areas, they still support our objective of enhancing our understanding of the physical processes in soil hydrology. Furthermore, the SMM patterns captured from SMAP can be insightful in understanding regional variabilities in SMM.

Another concern is the influence of ISMN spatial representation on SMM analysis. ISMN stations are point-based, and it is assumed that one point represents a $\mathrm{1}/\mathrm{8}$° grid area. It is possible that the point measurements cannot fully capture the spatial variability within the Noah-MP grid cells, leading to discrepancies in the representation of values and spatial patterns. The limited number of stations may further amplify this issue. One potential solution to addressing the scale mismatch between point-based observations and grid-scale simulations is the use of high-resolution or hyper-resolution models. These models can provide finer spatial detail, allowing for a more direct comparison between observational data and model outputs, thereby improving the accuracy of the analysis and reducing scale-induced biases. Incorporating such approaches into future studies would help mitigate the limitations posed by the current scale differences.

Additionally, some model representations may require further investigation. The DPM_VGM scheme uses a vertically constant macropore volume fraction, which means that macropores generated by biotic factors (formed by wormholes and dead roots) and abiotic factors (cycles of freezing–thawing and drying–wetting) are fixed down to the bedrock. However, in nature, these macropores would decrease below a few meters from the soil surface. Because the existence of macropores in nature drains the surface layer and increases the root zone soil moisture, to better represent the actual physical process, it is necessary to incorporate more soil data, e.g., the soil organic matter and coarse materials from SoilGrids 250 m (Hengl et al., 2017) for climate predictions, or to calibrate the macropore volume fraction for hydrological applications. Such a calibration is anticipated to further advance the fidelity of soil moisture simulations, enhancing the model's utility in various hydrological and climate applications.

Concerning surface water ponding, a constant ponding threshold may not be justified, and a spatially variable surface ponding may lead to improved model accuracy. Future model developments should consider microscale topographic variations to represent the hydrological connectivity of surface-ponded water. We tested a scheme of a ponding threshold as a linear function of the subgrid standard deviation of a DEM derived from a DEM at 30 m resolution (although this is not enough), resulting in higher surface-ponding thresholds over the alpine western USA. Further investigation is needed to validate and calibrate the modeled areal ponding fraction and depth against satellite (or camera) observations. We expect a more realistic representation of ponding thresholds through further calibration of the parameters in the function.

There are additional factors, such as water convergence through surface and subsurface lateral flows (e.g., Barlage et al., 2021), that may affect SMM but are not represented by the current Noah-MP version and thus not considered in our analysis. The primary focus of our study is to understand the impacts of missing processes on SMM and use this understanding to guide future LSM development for S2S climate predictions, e.g., the surface ponding and preferential flow. Consequently, we narrowed our examination down to key missing processes represented within Noah-MP. Future research would further evaluate the impact of lateral flows and other processes on SMM, expanding our understanding of these dynamics and their implications for climate prediction. Moreover, this study focuses primarily on physical process representations and parameterizations for soil moisture dynamics, while we acknowledge the strong impacts of uncertainties on hydraulic parameters.

5 Conclusion

In this study, we have explored the effects of soil hydraulic schemes and hydrological processes on SMM using the Noah-MP LSM with advanced hydrology. Our research was motivated by a need to understand how missing physical processes help solve biases in long-term and short-term SMM commonly observed by LSMs. We aim to find the key missing processes controlling SMM and thus to improve the representation of soil hydrology in LSMs, using the knowledge gained from our analysis of SMM. We designed and implemented five scenarios to focus on the impacts of key missing processes and different hydraulic parameterizations. These scenarios include two soil hydraulic models (Clapp and Hornberger and Van Genuchten), a dual-permeability model representing preferential flow, and three surface-ponding thresholds. Using soil moisture datasets from SMAP and the ISMN for surface and root zone measurements, respectively, we conducted a comprehensive analysis of the effects of different Noah-MP parameterizations on soil moisture memory.

Our findings suggest that the soil water retention curve is the most important factor controlling SMM due to its strong influence on soil water persistence through suction by soil particles. We show that the adoption of the Van Genuchten parameterization considerably mitigates the long-standing issue of overestimating SMM in LSMs employing the Brooks–Corey/Clapp–Hornberger (BC/CH) hydraulic model. The Van Genuchten model, with its reduced suction effect attributable to a drier surface layer, leads to a more accurate depiction of moisture transfer from the root zone to the surface, which is important for a more realistic description of soil moisture dynamics.

Moreover, representing surface-ponding processes allows for an extended period of soil water infiltration, thus extending both surface and root zone long-term memories and reducing the short-term memories. Implementing a dual-permeability approach fine-tunes soil moisture representation by accounting for preferential flow paths, marking a step forward in the enhancement of soil moisture memory and the overall fidelity of hydrological simulations. Macropores lead to a decrease in short-term memory and long-term memory due to faster drainage and thus decreased surface soil moisture. Given these compelling advancements, we strongly recommend that LSMs adopt the VG hydraulics to advance the prediction of hydrological and climatic phenomena.

The findings from this study have important implications for future research on SMM. By identifying the specific parameterizations that lead to discrepancies in long-term and short-term SMM, future studies should focus on refining these parameters to reduce biases in LSMs. Moreover, while this study focuses on the effect of the missing hydrological processes on the timescale of SMM, future research should analyze the impact of these parameterizations on the strength and legacy of SMM and assess whether the findings based on timescales align with those related to the strength and legacy (Rahmati et al., 2024).