Effect of floodplain trees on apparent friction coefficient in straight compound channels

The interaction of water streams in channels with a complex cross section, involving the exchange of water mass and momentum between slowly flowing water in the floodplains and fast water in the main channel, significantly depends on the diversification of the surface roughness between the main channel and floodplains. Additionally, trees increase flow resistance strongly in floodplains and significantly in the main channel by intensifying the interaction process. As a result, the water velocity and the discharge capacity of both parts of the channel decrease and, at the same time, affect the flow conditions in the main channel. The results of laboratory experiments were used to determine the effect of floodplain trees on the discharge capacity of the channel with diversified roughness. The reduction in the velocity of the main channel caused by the stream interactions is described with the apparent friction coefficients introduced at the boundary between the main channel and the floodplain. The values of resistance coefficients and their changes as a result of the significant influence of trees on the interaction process were determined for different surface roughnesses of the main-channel bottom.

1 Introduction

This paper is the result of a continuation of the study of the apparent friction coefficient at the main channel–floodplain interface for three variants of channel surface roughness described in the paper by Kubrak et al. (2019a). It is well known that the very diversification of the bottom surface roughness intensifies the momentum exchange process, as well as the creation of vortex structures in the transition area between the floodplains and the main channel (“kinematic effect”, Zheleznakov, 1971; nowadays, this is described as the streams interaction). An increase in channel surface roughness and the consequent intensification of the process of vortex formation and secondary flows in the main channel result in a reduction in water velocity and changes in the turbulent flow pattern and affect the capacity of the channel with a complex cross section (Shiono and Knight, 1991; Tominaga and Nezu, 1991; Bousmar and Zech, 1999; Rowiński et al., 1998, 2002; Van Prooijen et al., 2000; Czernuszenko et al., 2007; Tymiński, 2012; Tymiński and Kałuża, 2012; Kozioł and Kubrak, 2015). Floodplain trees further strongly increase the interaction between the main channel and the floodplain. Floodplain trees additionally cause a significant increase in flow resistance; a reduction in water velocity; a reduction in the capacity of both parts of the riverbed; and, in particular, a significant change in the turbulent flow structure (Kozioł, 2008, 2011, 2012, 2013, 2015 and 2019; Mazurczyk, 2007). The results of laboratory experiments (Kozioł, 2013) showed that trees on the floodplains did not result in significant changes in the values of relative turbulence intensity in the whole compound channel, but they did result in significant changes in the vertical distributions of the relative turbulence intensities in all three directions in the floodplains and over the bottom of the main channel.

The main goal of this unique work was to determine the influence of floodplain trees on the value of the apparent resistance coefficient in a compound channel for the different roughnesses of the main-channel bottom. The results of measurements from previous experimental studies in compound channels on the flow capacity and the turbulence structure were used to write this paper (Kozioł, 1999, 2012, 2013, 2019; Kubrak et al., 2019b). Variants W 2.0 and W 3.0 from the Kubrak et al. (2019a) study were used to show the impact of floodplain trees as a reference.

The interaction between the main channel and the floodplain, especially in the transition zone, is a complex phenomenon. Traditionally, researchers have modeled this by separating the two zones, often represented by vertical lines. These lines represent boundaries where shear stresses are estimated and applied. Wright and Carstens (1970) introduced the concept of apparent shear stresses at these boundaries within compound-channel cross sections. Since the 1980s, consistently with the concept of apparent shear stress, a number of formulas based on hydraulic experiments in channels have been introduced to calculate flow resistance due to momentum transfer between the main channel and the floodplain (Myers, 1978; Wormleaton et al., 1982; Knight and Demetriou, 1983; Prinos and Townsend, 1984; Christodoulou, 1992). An overview of these formulas can be found in Moreta and Martin-Vide (2010).

Laboratory tests allow the determination of apparent shear stresses, which enables the determination of the values of dimensionless resistance coefficients used to calculate the average velocity v_m in the steady uniform flow in the main channel of the compound cross section according to the Darcy–Weisbach formula:

$$\begin{array}{}\text{(1)}& v_{\mathrm{m}}=\sqrt{{\displaystyle \frac{\mathrm{8}g{R}_{\mathrm{m}}{S}_{\mathrm{o}}}{f_{\mathrm{m}}}}},\end{array}$$

where v_m is the average flow velocity in the main channel, g is the gravitational acceleration, R_m is the hydraulic radius of the main-channel cross section, S_o is the longitudinal channel slope, and f_m is the resistance coefficient for the main-channel cross section. The f_m resistance coefficient is calculated for the wetted perimeter, taking into account the length of the cross-sectional division plane, the side slopes, and the bottom of the main channel.

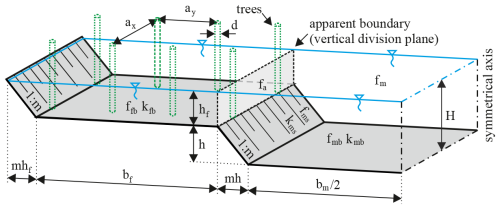
The flow resistance coefficients at the division planes of the compound cross section, calculated on the basis of apparent shear stresses, depend on the channel parameters given by Nuding (1998), but, in the case of trees on the floodplain, they also depend on additional parameters such as the following: d, which is the tree diameter; $A_v/A$, which is the degree of cover of the cross-sectional area of the channel by trees; and a_x and a_y, which are the spacings of trees in the longitudinal and transverse directions. Then the relationship for flow resistance coefficients given in the work by Kubrak et al. (2019) should be supplemented with additional channel parameters (Fig. 1):

$$\begin{array}{}\text{(2)}& f_{\mathrm{a}}=f\left(f_{\mathrm{mb}};{\displaystyle \frac{H}{h_{\mathrm{f}}}};{\displaystyle \frac{b_{\mathrm{m}}}{b_{\mathrm{f}}}};\mathrm{1}:m;{\displaystyle \frac{k_{\mathrm{mb}}}{k_{\mathrm{fb}}}};d;{\displaystyle \frac{A_v}{A}};a_x\text{and}{a}_y\right),\end{array}$$

where f_a is the apparent coefficient of resistance at the boundary between the main channel and floodplain area, f_mb is the resistance coefficient of the main-channel bottom, f_ms is the resistance coefficient of the main-channel side slopes, f_m is the resistance coefficient in the main channel, f_fb is the resistance factor of the bottom of the floodplain, H is the water depth in the main channel, h_f is the water depth on the floodplain, b_m is the bottom width of the main channel, b_f is the floodplain width, 1:m is the aspect of the side slope of the main channel and floodplains, k_mb is the absolute surface roughness of the main channel, k_ms is the absolute roughness of the main-channel side slopes, k_fb is the absolute surface roughness of the floodplain, and k_fs is the absolute roughness of the floodplain side slopes.

Figure 1 Symbols used for dimensions of the compound cross section of the channel.

Bretschneider and Özbek (1997) used a large-scale hydraulic modeling approach to determine the apparent resistance coefficients at vertical division lines in compound channels. Their research, conducted as part of the Science and Engineering Research Council (SERC) program at the Hydraulic Research Laboratory in Wallingford, England, used measurements of average water velocity in the main channel (this provided insight into flow characteristics within the main channel) and apparent tangential stresses at the division boundary of the cross section (these estimated shear stresses represent the interaction between the main channel and the floodplain). The study of the flow and structure of turbulent water flow in river channels with a compound cross section is complex and incomplete and, despite considerable research interest in the subject, still requires detailed clarification in many areas of research, especially the influence of high vegetation. In recent years, there have been many important publications on the apparent roughness coefficient and apparent shear stress in a compound channel (Devi and Khatua, 2018; Fernandes, 2021; Devi et al., 2022; Khozani et al., 2019; Zhao et al., 2024). However, much of the research to date has been conducted on compound channels without tall vegetation (bushes and trees). Kubrak et al. (2019a) performed research on a small-scale hydraulic model, and the aim of their research was to explain how the surface roughness of the main channel and floodplains affects the values of apparent resistance coefficients. In contrast, the main objective of this unique work was to extend the knowledge by determining the effect of floodplain trees on the value of the apparent drag coefficient in a complex channel for the different bed roughnesses.

2 Study of discharge capacity of channel with compound cross section with floodplain trees

A study on the capacity of the channel with the compound cross section was carried out in the hydraulic laboratory of the Department of Water Engineering of the Warsaw University of Life Sciences. A straight open channel (16 m long and 2.10 m wide) with a symmetrically trapezoidal cross section was used for the laboratory variants (Fig. 2 in this paper; Kozioł, 2013, Fig. 1; Kubrak et al., 2019a, Figs. 2 and 3). Detailed information on the research model and measurement procedures can be found in the articles by Kozioł (1999, 2012, 2013, 2019) and Kubrak et al. (2019a), while only the most relevant research parameters are included here. The cross section halfway down the channel length was selected for velocity measurements (Fig. 2b in this paper and Kozioł, 2013, Fig. 1). Two devices were used to measure the components of the flow velocity: an electromagnetic PEMS probe and an acoustic Doppler velocity meter (ADV). At the beginning, the electrostatic PEMS probe was used, and then the newly purchased acoustic ADV probe was used. The description of the electrostatic PEMS probe, the measurement technique, and the method of determining the required length of the velocity measurement time series are presented in the work of Kubrak et al. (2019a), and the description of the ADV probe is presented in the works of Kozioł (2012, 2019). The velocity measurements taken, at a point, by the PEMS probe were carried out in 77 measurement verticals and in nearly 500 cross-sectional points (Kubrak et al., 2019a), and those taken by the second probe were carried out at 250 points at 23 verticals — 6 on each floodplain and 11 in the main channel (Kozioł, 2012, 2019). The probes were mounted on a sliding measuring carriage. The differential pressure gauge and the probes were connected to a computer measurement logger. The results of measurements from two experimental studies in compound channels on the flow capacity (Kozioł, 1999; Kubrak et al., 2019a) and turbulence characteristics of the water stream (Kozioł, 1999, 2012, 2019) were used to write this paper. Diversification of the surface roughness in the channel was obtained by painting the concrete of a blurred surface with paint (called a smooth surface) or by applying a terrazzo layer with a grain diameter of 6–12 mm (called a rough surface, Fig. 2).

The studies of the capacity of the compound channel and the analysis of the apparent friction coefficient at the apparent boundary between the main channel and the floodplain were carried out for six variants and three values of floodplain roughness. The test results of the first three variants without trees (W 1.0, W 2.0, and W 3.0) are described in detail in the article by Kubrak et al. (2019a). This paper presents three variants of experiments with trees on floodplains for the following conditions:

1. In the fourth variant (W 2.T1, Fig. 2a and b), the surface of the main-channel bed was smooth and made of concrete, whereas the floodplains were covered by cement mortar composed with terrazzo. The emergent vegetation (trees) growing on the floodplains were modeled by aluminum pipes of 0.8 cm diameter, placed with both longitudinal and lateral spacings of 10 cm. There were 16 pipes in each of the 161 cross sections. The treetops were emergent, and the pipes were not subject to any elastic strains caused by overflowing water.

2. In the fifth variant (W 2.T2, Fig. 2b), the covering of the floodplains was the same as in the variant W 2.T1, but emergent vegetation (trees) growing on the floodplains was modeled to be half as much, placed with both longitudinal and lateral spacings of 20 cm (photo in Kozioł, 2013, Fig. 3). There were eight pipes in each of the 80 cross sections.

3. In the sixth variant (W 3.T2, Fig. 2c), the floodplains and all sloping banks were covered by cement mortar composed with terrazzo, and the bottom of the main channel was smooth. The emergent vegetation (trees) growing on the floodplains was modeled in accordance with the variant W 2.T2, with spacings of 20×20 cm.

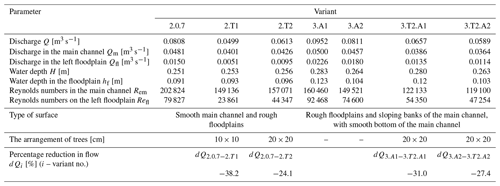
The list of tests performed during the experiments, the measured flow rates in the main channel, and the adjacent floodplains are summarized in Table 1.

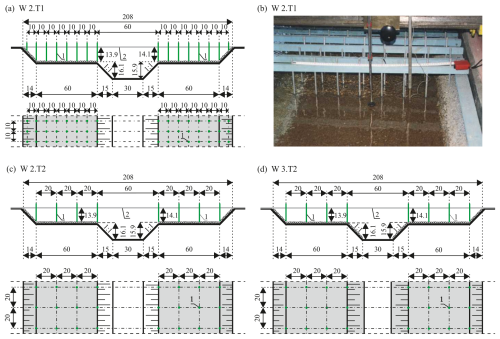
Figure 2 Scheme of the cross section of the channel in the variants analyzed (dimensions in centimeters) and a view of the model of the channel in the W 2.T1 variant.

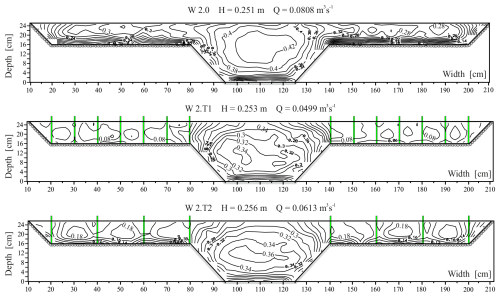
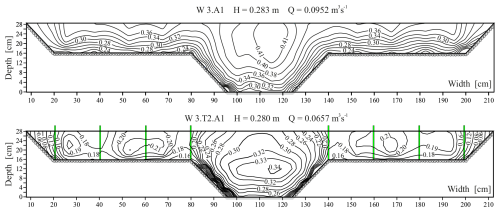
Based on the spot velocity measurements, it was possible to plot lines of constant velocities (isovels) in the cross sections of the channel for all analyzed variants. Examples of isovels in the cross section of the channel at a similar flow depth (H≈0.25 m) for variant W 2.0 and variants W 2.T1 and W 2.T2, with trees on the floodplains, are shown in Fig. 3. Figure 4 presents isovels in the cross section of the channel with a smooth surface at the bottom of the main channel and a rough surface on the side slopes of the main channel and floodplains for variant W 3.0 and variant W 3.T2, with trees on the floodplains (H=0.28 m).

Table 1 Hydraulic parameters of experiments (variants 2.0.7, 3.A1, and 3.A2 from the research of Kubrak et al., 2019a).

Figure 3 Isovels in the cross section of the channel at similar depths for variant W 2.0 and variants W 2.T1 and W 2.T2, with trees on the floodplains (variant W 2.0 from research of Kubrak et al., 2019a).

Figure 4 Isovels in the cross section of the channel at similar depths for variant W 3.A1 and variant W 3.T2.A1, with trees on the floodplains (variant W 3.A1 from research of Kubrak et al., 2019a).

3 Resistance coefficients in the main channel with the influence of the floodplain trees

In the variant with trees in the floodplain, as in the variant without trees (Kubrak et al., 2019a), the values of the dimensionless resistance coefficients in the main channel with different bottom and slope roughnesses and of the resistance coefficients in the distribution plane of the channel cross section were calculated using the Einstein method (Einstein, 1934). This method is based on a simplified approach in which the flow can be found for each surface roughness along the perimeter of the cross section, where this roughness determines the flow conditions (Fig. 5). The Einstein method simplifies the flow analysis by assuming uniform average velocities within subsections defined by surface roughness along the channel perimeter. These areas are identified using isovel plots (Fig. 5), which represent lines of equal velocity. The method divides the cross section with lines perpendicular to the isovels, starting from the wetted perimeter. This approach assumes that the dividing lines are free of shear stress and that no forces are transmitted between the separated areas.

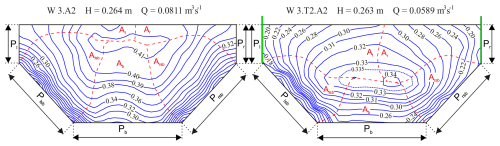
Figure 5 Surface areas of stream cross sections A_i in which the flow conditions are shaped under the influence of a constant roughness over the length of the wetted perimeter P_i (variant W 3.A2 from research of Kubrak et al., 2019a).

The Einstein method assumes a simplified approach where the average flow velocity within each subsection A_i is equivalent to the average velocity across the entire main-channel cross section (v_i=v_m). Under this assumption, the Darcy–Weisbach equation can be applied, leading to the following relationship (Kubrak et. al., 2019a):

$$\begin{array}{}\text{(3)}& \sqrt{{\displaystyle \frac{\mathrm{8}g{R}_i{S}_{\mathrm{o}}}{f_i}}}=\sqrt{{\displaystyle \frac{\mathrm{8}g{R}_{\mathrm{m}}{S}_{\mathrm{o}}}{f_{\mathrm{m}}}}}⟹f_i=f_{\mathrm{m}}{\displaystyle \frac{R_i}{R_{\mathrm{m}}}},\end{array}$$

where R_i is the hydraulic radius of the cross-sectional area per given roughness ($R_i=A_i/P_i)$; R_m is the hydraulic radius of the entire cross section of the main channel ($R_{\mathrm{m}}=A_{\mathrm{m}}/P_{\mathrm{m}}$); f_i is the resistance coefficient of the subsection; and f_m is the average Darcy's friction factor in the main channel, being the substitutionary coefficient of resistance for the cross section of the main channel calculated for the wetted perimeter P_m, which includes the lengths of the section dividing lines ($P_{\mathrm{m}}=P_{\mathrm{l}}+P_{\mathrm{lsb}}+P_b+P_{\mathrm{rsb}}+P_{\mathrm{r}}$). The coefficient of resistance f_m in the cross section of the main channel is calculated on the basis of the average velocity ($v_{\mathrm{m}}=Q_{\mathrm{m}}/A_{\mathrm{m}}$). The determined areas of the cross section A_i (Fig. 5) were used to calculate the hydraulic radius R_i and the resistance coefficients f_i.

In Fig. 6, the calculated values of the apparent resistance coefficients f_a (l and r – the left and the right side, respectively) and of the resistance coefficients of the main channel f_m, as well as of the bottom f_mb, the side slope of the main channel f_ms, and the bottom of the floodplain f_f, of the compound cross section in experiments conducted with variants W 2.0, W 2.T1, W 2.T2, W 3.0, and W 3.T2 are presented as a function of the depth ratio ($H-h)/H$. The values of the apparent resistance coefficients f_a for the compound cross section in variants W 2.0 and W 3.0 and of the resistance coefficients of the bottom of the floodplain f_f with high roughness (in variants W 2.0 and W 3.0) decrease with the increase in the flow depth (also with increase of the ratio $(H-h)/H)$ (Fig. 6). The presence of trees and the interaction process in variants W 2.T1, W 2.T2, and W 3.T2, in contrast to variants W 2.0 and 3.0, contribute to the fact that there is a significant increase in apparent resistance coefficient values above the depth of $(H-h)/H=\mathrm{0.2}$.

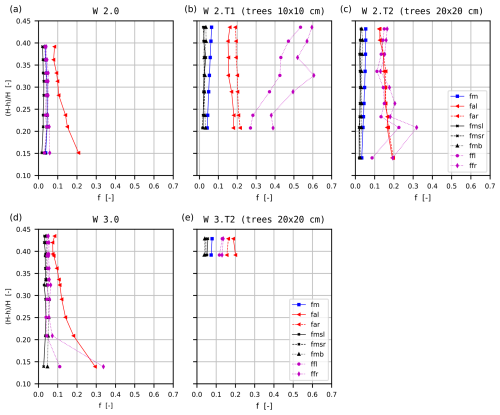
Figure 6 Variability of resistance coefficients in the cross section of the compound cross section in variants (a) W 2.0, (b) W 2.T1, (c) W 2.T2, (d) W 3.0, and (e) W 3.T2 (variants without floodplain trees – W 2.0 and 3.0; Kubrak et al., 2019a).

Figure 7a and b present the influence of floodplain trees on the values of the resistance coefficients f_m in the main channel in the second and third variants. In variant W 2.0, the values of resistance coefficients f_m would first increase above $(H-h)/H=\mathrm{0.25}$ and then start to decrease. Trees from floodplains intensify the increase in resistance and the subsequent reduction in flow. In variant W 2.T1 (trees 10×10 cm), at approximately H=0.25 m ($(H-h)/H=\mathrm{0.4}$), the value of the coefficient f_m increased by approximately 48 % in the main channel, and the flow reduction was approximately 38.2 % in the entire channel (Table 1). In variant W 2.T2, with a larger spacing (20×20 cm) and fewer trees, the f_m value increased by approximately 36 % in the smooth main channel, and the flow reduction was 24.1 % in the entire channel. The values of the resistance coefficients f_m in variants with trees (W 2.T1 and W 2.T2) increase with the increase in the flow depth (Fig. 7a). The increase in the roughness of the main-channel slopes in variant W 3.0 resulted in a significant increase in the f_m value in the main channel (Fig. 7b) of approximately 32 % ($(H-h)/H=\mathrm{0.36}$) for H=0.251 m and of approximately 36 % ($(H-h)/H=\mathrm{0.39}$) for H=0.262 m, while the flow reduction in the entire channel was approximately 12.9 % and 15 %, respectively. Figure 7b presents the influence of floodplain trees (20×20 cm) on values of resistance coefficients f_m in the main channel in the third variant. In variant W 3.T2, the f_m value in the main channel increased by approximately 57 % for H=0.263 m ($(H-h)/H=\mathrm{0.39}$) and by approximately 70 % for H=0.28 m ($(H-h)/H=\mathrm{0.43}$), while the flow reduction in the entire channel was approximately 27.4 % and 31 %, respectively (Table 1).

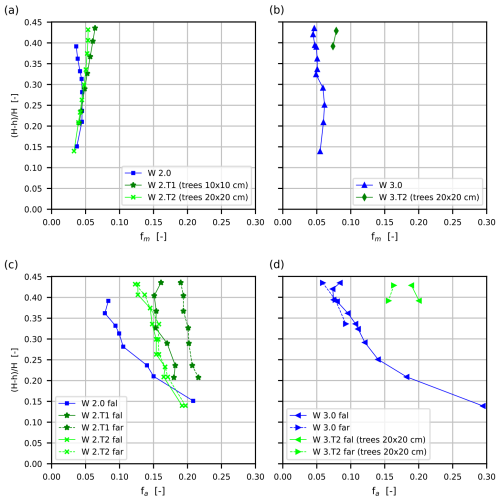
Figure 7 Variability of resistance coefficients f_m in the main channel and apparent resistance coefficients f_a at the boundary between the main channel and the floodplain as a function of the flow depth (variants without floodplain trees – W 2.0 and 3.0; Kubrak et al., 2019a).

Figure 7c and d present the influence of floodplain trees on the apparent resistance coefficients f_a at the boundary between the main channel and the floodplain in the second and third variants. In variant W 2.0, without trees at the analyzed flow depth (Fig. 7c), the f_a values decrease quite rapidly with increasing depth. However, in the variants with trees (W 2.T1 and W 2.T2), the f_a values decrease slowly with increasing depth. In variants with trees, the f_a values increase compared to the variant without trees. In both cases, the increase in the f_a value is the smallest at low depths on the floodplain and increases with depth, which is the result of the increase in interactions between the main channel and the tree-covered floodplain. At the depth of H=0.20 m ($(H-h)/H=\mathrm{0.21}$) in variant W 2.T1 in the left division plane, the f_al coefficient value increased by 20 % (Fig. 8c). In the right division plane, the f_ar coefficient value is even higher (by 24 %) than the left one, which indicates asymmetric flow in the main channel and higher flow velocities on the left side of the main channel (Fig. 3, W 2.T1). This is similar throughout the entire depth, but the variation in the coefficient value increases. At the depth of H=0.26 m ($(H-h)/H=\mathrm{0.39}$) in the left division plane, the f_al coefficient value in variant W 2.T1 increased by about 81 %, and the f_ar coefficient value is even higher (by 52 %) than the left one. In variant W 2.T2, with a larger spacing (20×20 cm) and fewer trees, the f_a values are similar on the left and right sides of the main channel, and at the depth of H=0.20 m ($(H-h)/H=\mathrm{0.21}$), the f_a coefficient value increased by about 12 % and by about 58 % at H=0.26 m ($(H-h)/H=\mathrm{0.39}$) (Fig. 7c). The increase in the roughness of the main-channel slopes in variant W 3.0 caused the greatest increase in the f_al value at small flow depths in the division planes (about 41 %, H=0.18 m, $(H-h)/H=\mathrm{0.14}$) and decreased with increasing depth (about 22 %, H=0.25 m, $(H-h)/H=\mathrm{0.36}$) until the values became equal (Fig. 7d). At greater depths ($(H-h)/H\ge \mathrm{0.39}$), trees from floodplains in variant W 3.T2 (20×20 cm) resulted in a more than 2-fold increase in the f_a value. In the left division plane, the f_a value increased by 168 % at H=0.26 m ($(H-h)/H=\mathrm{0.39}$) and by 125 % at H=0.28 m ($(H-h)/H=\mathrm{0.43}$), while in the right division plane, it increased by 101 % and 178 %, respectively.

An increase in the flow depth in the floodplain resulted in an increase in the influence of the floodplain trees on the flow conditions in the main channel and on the values of the apparent resistance coefficients f_a at the apparent boundary between the main channel and the floodplain (Fig. 7). However, at small flow depths ($(H-h)/H\mathit{<}\mathrm{0.2}$), the bottom roughness generally determines the coefficient values.

Figure 8 presents the influence of floodplain trees on the values of the resistance coefficients for the bottom f_mb and the side slopes f_ms of the main channel in the second and third tests. Figure 8a shows that, in the W 2.0 variant without trees on the floodplains, the f_mb coefficient values initially increase slightly and then decrease with increasing depth on the floodplains. The influence of trees in the W 2.T1 and W 2.T2 variants resulted in the greatest decrease in the value of the f_mb coefficient at small flow depths on the floodplain. With increasing flow depth, the value of the coefficient increases, and, already, at approximately $(H-h)/H=\mathrm{0.39}$, the value is the same as in the variant without trees. Figure 8b shows that the increase in the roughness of the main-channel side slopes in variant W 3.0 resulted in a slight increase in the f_mb value. However, the floodplain trees in variant W 3.T2 (20×20 cm) at higher flow depths ($(H-h)/H=$ 0.39–0.43) did not result in a change in the f_mb value for the bottom of the main channel.

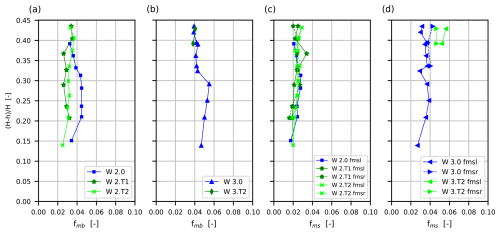
Figure 8 Variability of resistance coefficients for the bottom f_mb and the side slopes f_ms of the main channel as a function of the flow depth (variants without floodplain trees – W 2.0 and 3.0; Kubrak et al., 2019a).

Figure 8c shows that the influence of trees in the smooth main channel (W 2.T1 and W 2.T2) resulted in only a slight decrease in f_ms values at low flow depths in the floodplain, while, at higher depths, the coefficients did not change. Figure 8d shows that the increase in the surface roughness of the sloping banks of the main channel (W 3.0) resulted in an increase in the f_ms value coefficient, along with an increase in the flow depth. The influence of trees in the main channel with rough sloping banks (W 3.T2) resulted in different increases in f_msl and f_msr values at higher flow depths ($(H-h)/H=$ 0.39–0.43).

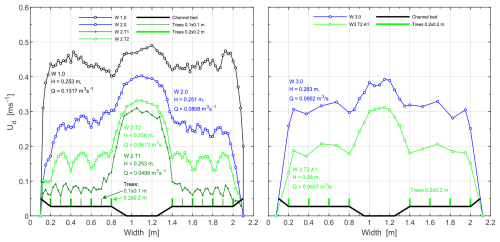
Figure 9 Distribution of average velocity in verticals in variants W 1.0, W 2.0, and W 3.0, with similar flow depths in the compound channel (the variants without floodplain trees, designated W 1.0/smooth channel/, 2.0, and 3.0, are derived from the study by Kubrak et al., 2019a).

The influence of trees on the flow in a compound channel is very significant, and the most common observed effect is a large decrease in the water flow value (Table 1) and clear changes in the distribution of the depth average velocity in the cross section of the compound channel (Fig. 9). It can be observed from the presented results that the influence of trees changes the values of resistance coefficients in the main channel to varying degrees, and the size of the changes depends on the surface roughness. Generally, the influence of trees in the smooth main channel resulted in a large increase in the apparent resistance coefficient but a slight decrease in the value of the bottom resistance coefficient, with an almost unchanged resistance coefficient of the main-channel side slopes. However, the influence of trees in the channel with the rough surface of the main-channel side slopes also resulted in a large increase in the apparent resistance coefficient and a small increase in the value of the resistance coefficient of the main-channel side slopes, with an unchanged bottom resistance coefficient at large flow depths ($(H-h)/H=$ 0.39–0.43). The value of the apparent resistance coefficient depends on the surface roughness of the channel bottom, the density of trees, and the depth of flow. Changes in the values of the apparent resistance coefficients can be explained by a change in the interaction between the parts of the compound channel, which depends on the magnitude of changes in the average depth velocity in the main channel and on the floodplain (Fig. 9). If the values of the apparent resistance coefficients are all greater then the differences between the flow velocities in the main channel and the floodplain will also be greater.

4 Conclusions

The analysis of the values of resistance coefficients determined for the main channel in the compound channel with different bottom roughnesses with and without trees on floodplains showed the following:

1. Floodplain trees cause an increase in floodplain interactions based on flow conditions in the main channel; this is to varying degrees for different coefficients depending on flow depth. The effect of floodplain trees on the value of the resistance coefficient for the entire smooth main channel was observed above the flow depth $(H-h)/H=\mathrm{0.25}$. In contrast, an effect on the value of the apparent resistance coefficient was already observed above the flow depth $(H-h)/H=\mathrm{0.15}$. The values of the apparent resistance coefficient differ little or are identical at very small flow depths in floodplains in variants without and with trees (the rough surface of the channel bottom generally has more influence than trees). As the flow depth increased, the trees resulted in a significant increase in the value of the apparent resistance coefficient and even reached values that were twice as high.

2. At large flow depths, floodplain trees in the channel with rough floodplains and rough sloping banks of the main channel resulted in a more than 2-fold increase in the value of the apparent resistance coefficient.

3. The values of the apparent resistance coefficients decrease with increasing flow depth; this happens more slowly with trees on floodplains and faster without trees.

4. In the straight compound channel in the main channel (Kubrak et al., 2019a), the values of the flow resistance coefficient increase with the flow depth up to $(H-h)/H=\mathrm{0.25}$, and then the values decrease. The floodplain trees resulted in a continuous increase in the value of the flow resistance coefficient with the flow depth.

5. The values of apparent resistance coefficients are several times greater than the resistance coefficients for the side slopes and the bottom of the main channel. The floodplains trees in the smooth main channel resulted in a decrease in the value of the resistance coefficients for the bottom of the main channel below depth $(H-h)/H\mathit{<}\mathrm{0.4}$ and only a slight decrease in the value of the side slopes of the main channel.